Dynamic Modeling and Analysis of a Flying–Walking Power Transmission Line Inspection Robot Landing on Power Transmission Line Using the ANCF Method
Abstract
1. Introduction
- A coupled FPTLIR/PTL dynamic model was derived to describe the FPTLIR landing process. The PTL was modeled using the ANCF method with a Euler–Bernoulli beam, neglecting shear and torsion to improve computational efficiency. A contact model based on the Hunt–Crossley theory was used to consider the deflection angle of the contact beam element and the traveling wheel groove, to ensure accuracy.
- A modular simulation model was conducted with different landing positions and robot masses to enhance the adaptability and generalization of the model using MATLAB (R2020b) software. The simulation performed parallel updates for the mass matrices of the robot and PTL to improve efficiency, and separated the dynamics calculations of the PTL and the FPTLIR to reduce complexity. The modular design of the simulation enhanced the adaptability to other HIRs.
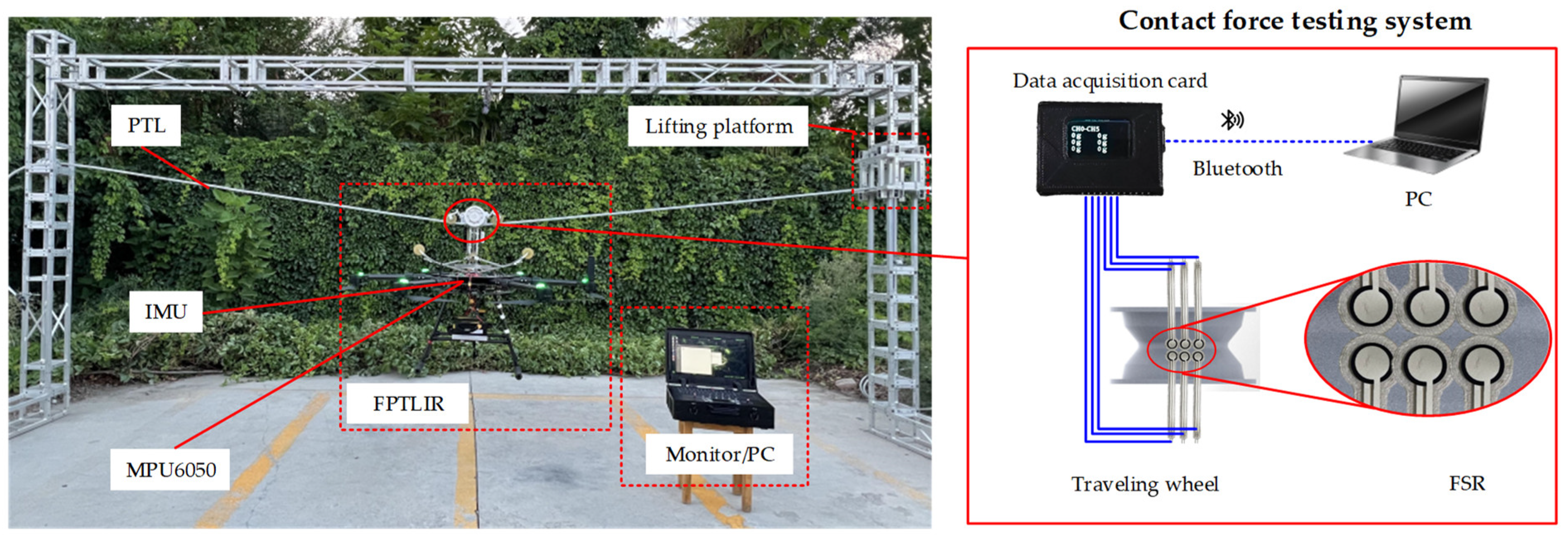
- A comprehensive test platform was established to evaluate the landing performance of the FPTLIR. Six opposing force-sensing resistors (FSRs) were employed on the platform to handle the variability in contact point locations during force measurement. The platform enabled the measurement of attitude, displacements, and contact forces, demonstrating the capability to achieve high measurement accuracy and ensuring reliable evaluation of the proposed method.
2. Problem Description
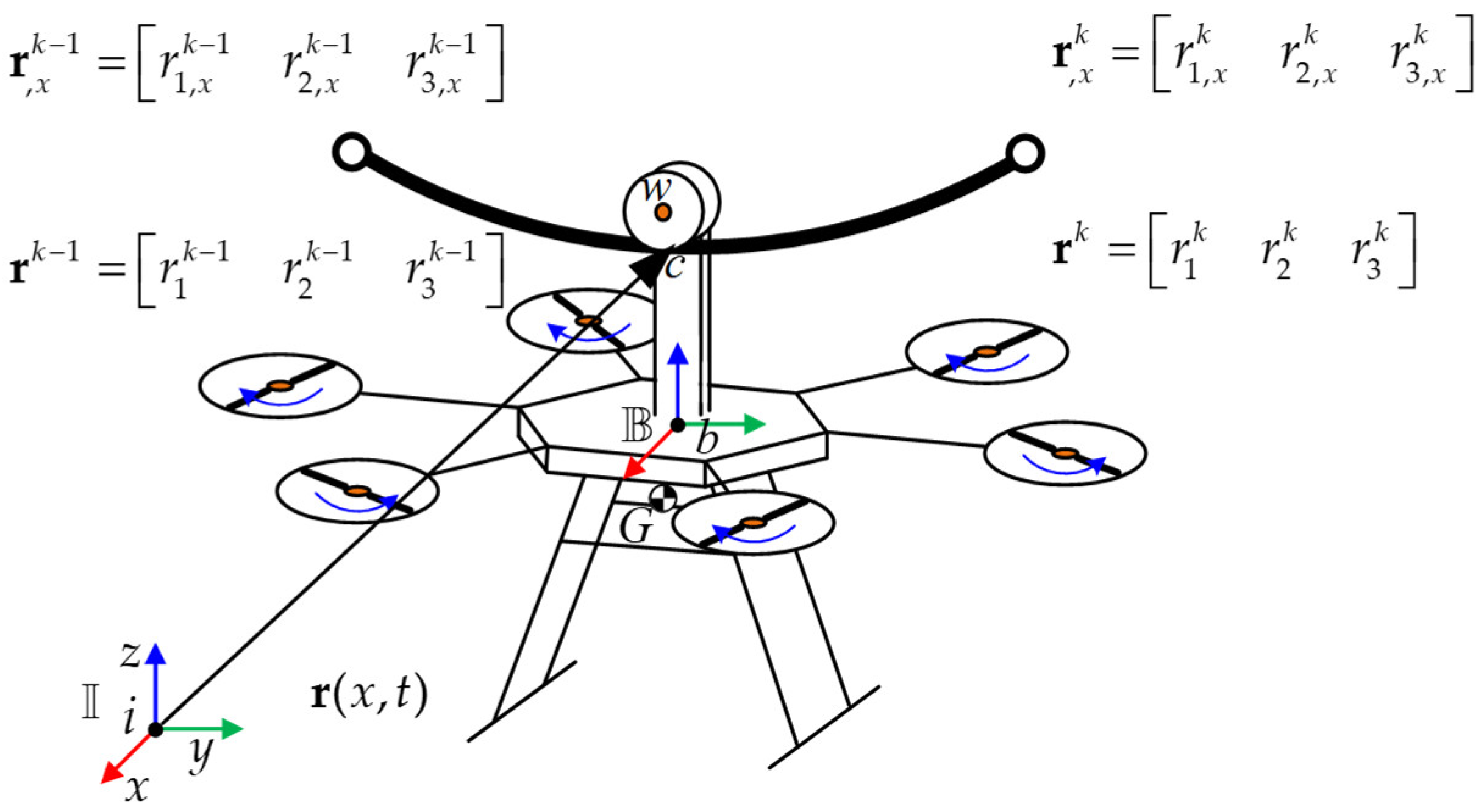
2.1. Description of FPTLIR
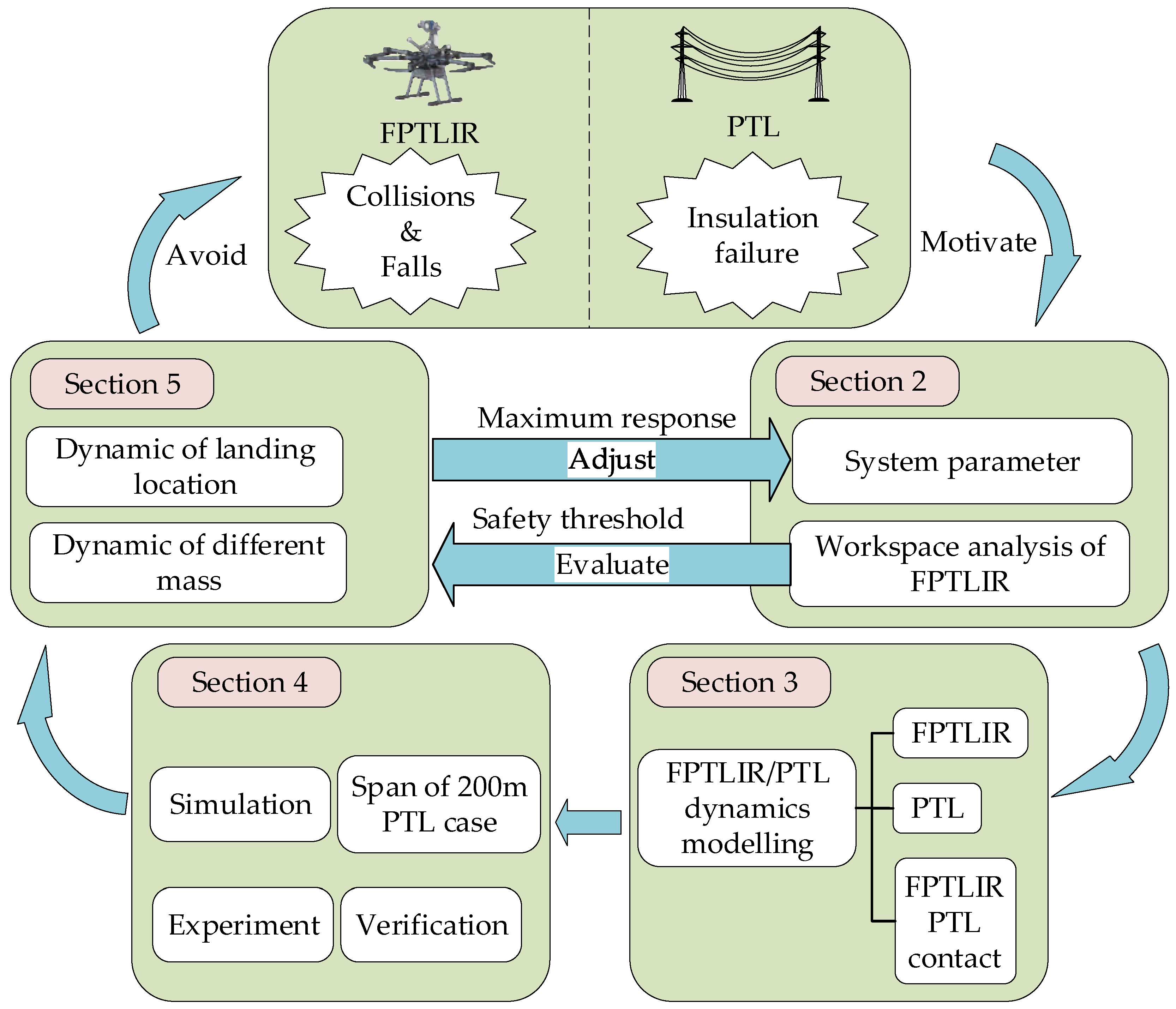
2.2. Overview of the Modeling and Analysis Framework
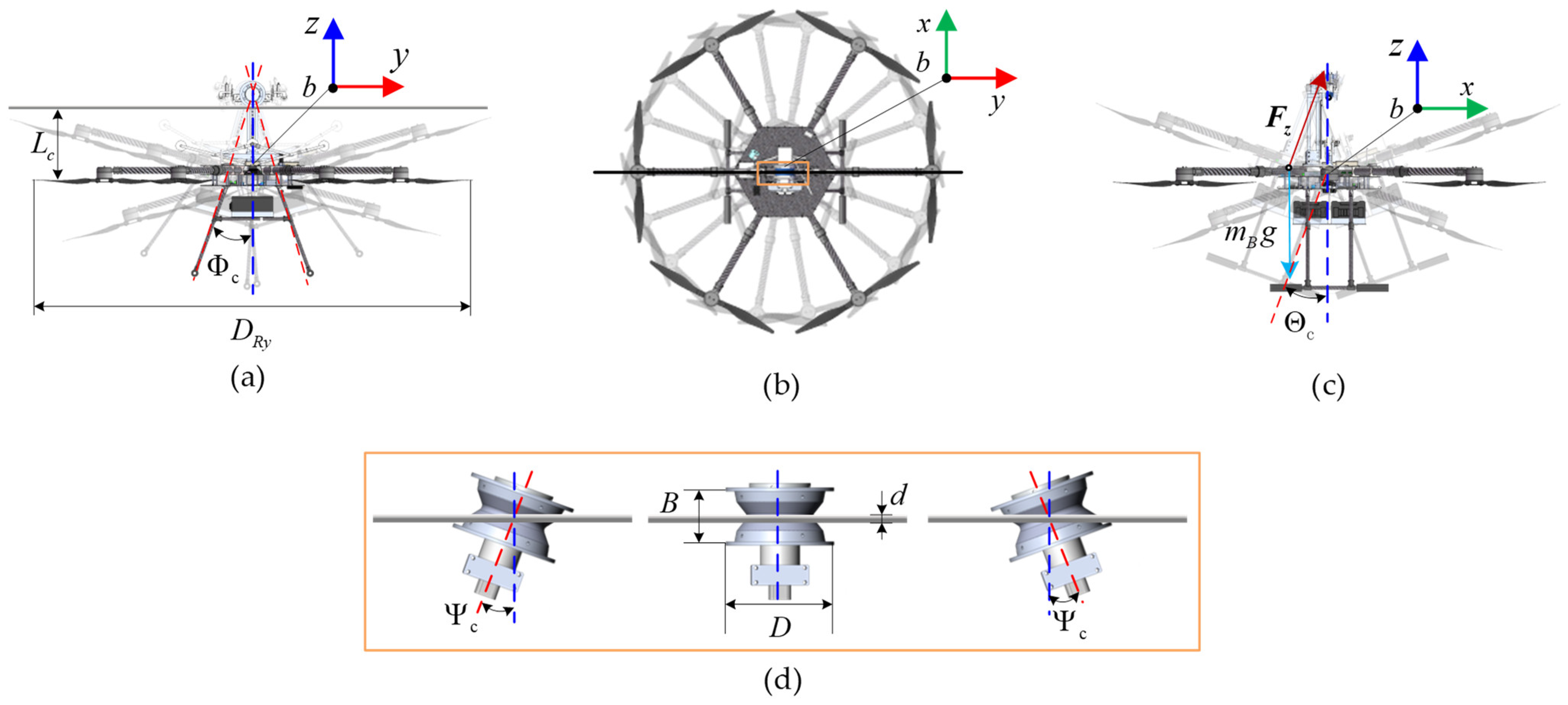
2.3. Workspace Analysis of FPTLIR
3. FPTLIR/PTL Dynamics Modelling
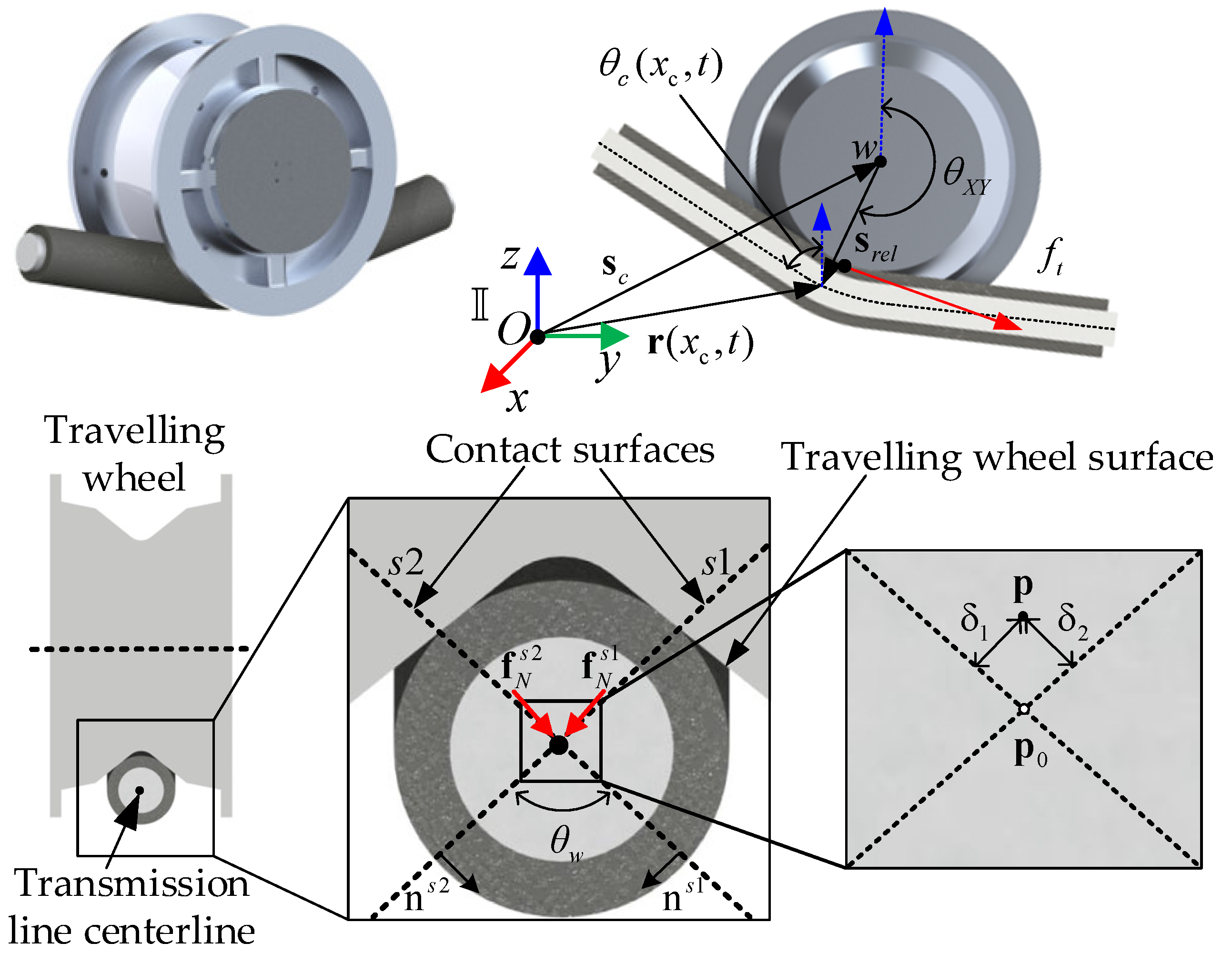
3.1. PTL Modeling
3.2. FPTLIR/PTL Contact Formulation
3.3. FPTLIR Subsystem Dynamics
3.4. Calculation of the Motion Equations of the System
4. Simulation and Experiment
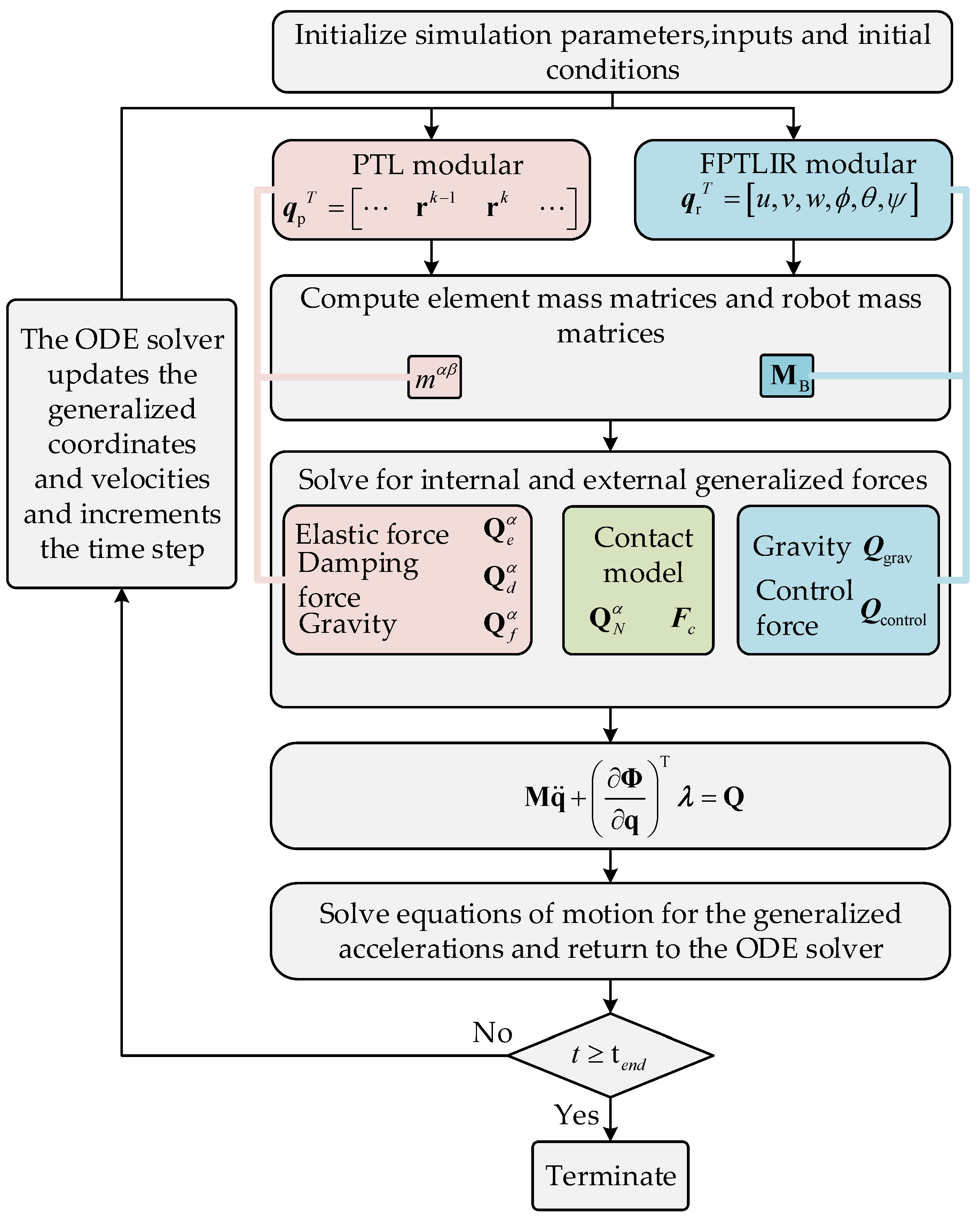
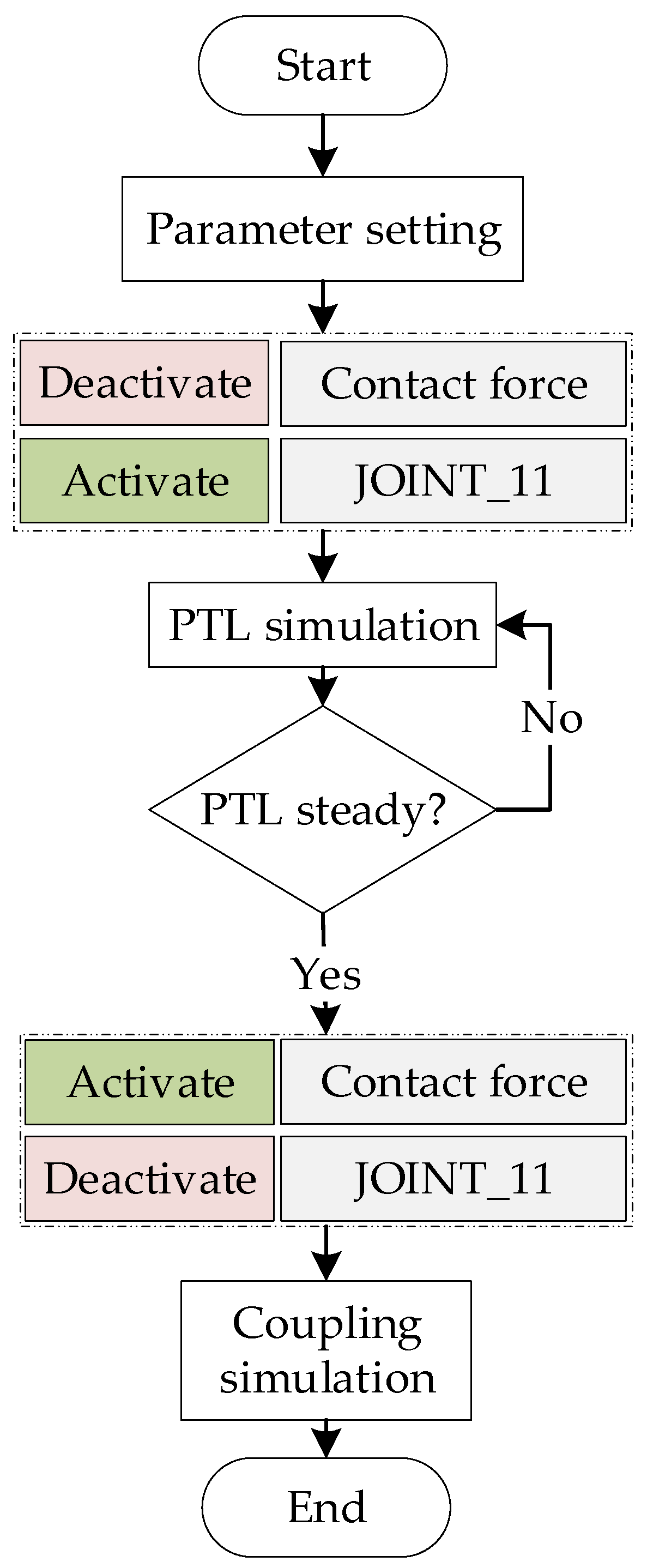
4.1. Dynamic Simulation Workflow
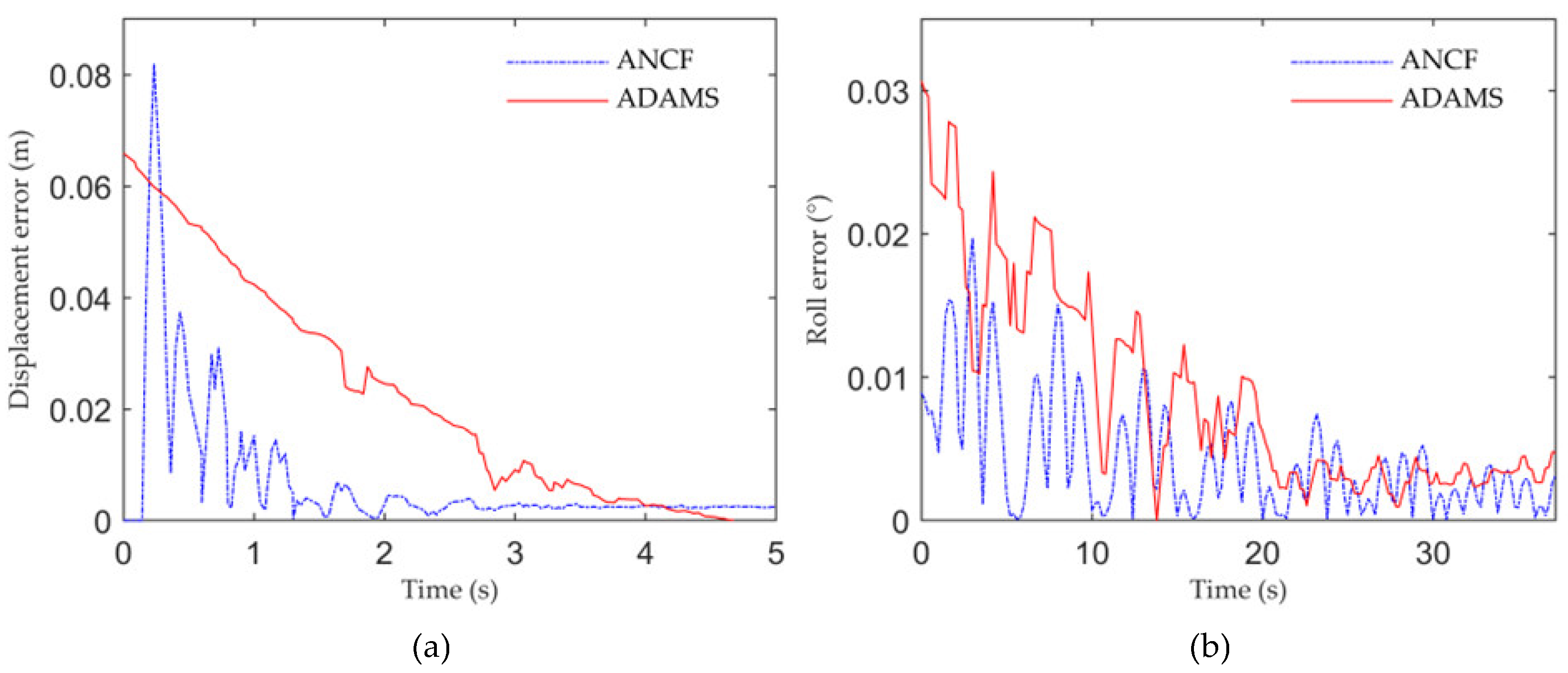
4.2. Comparison of Different Methods
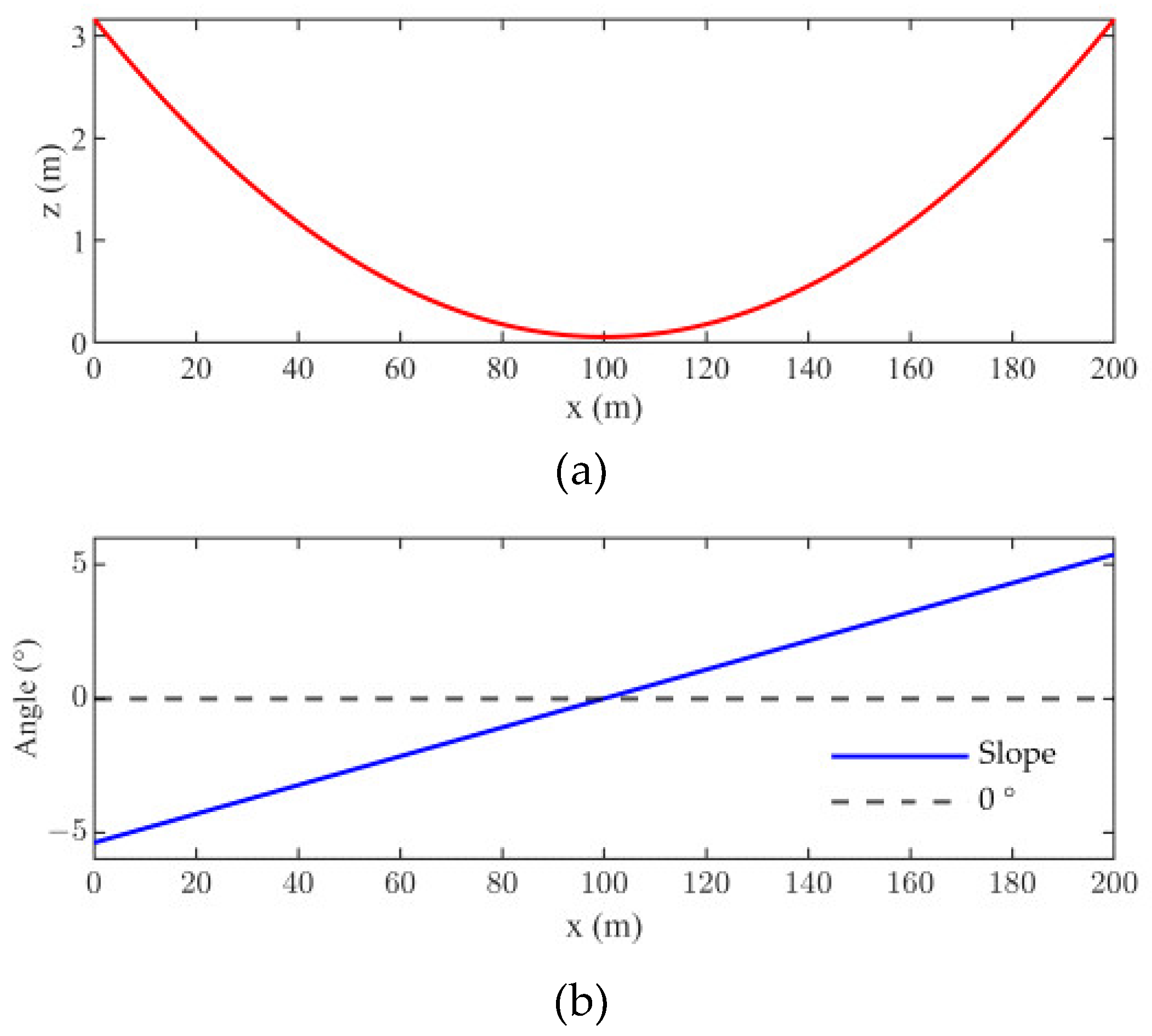
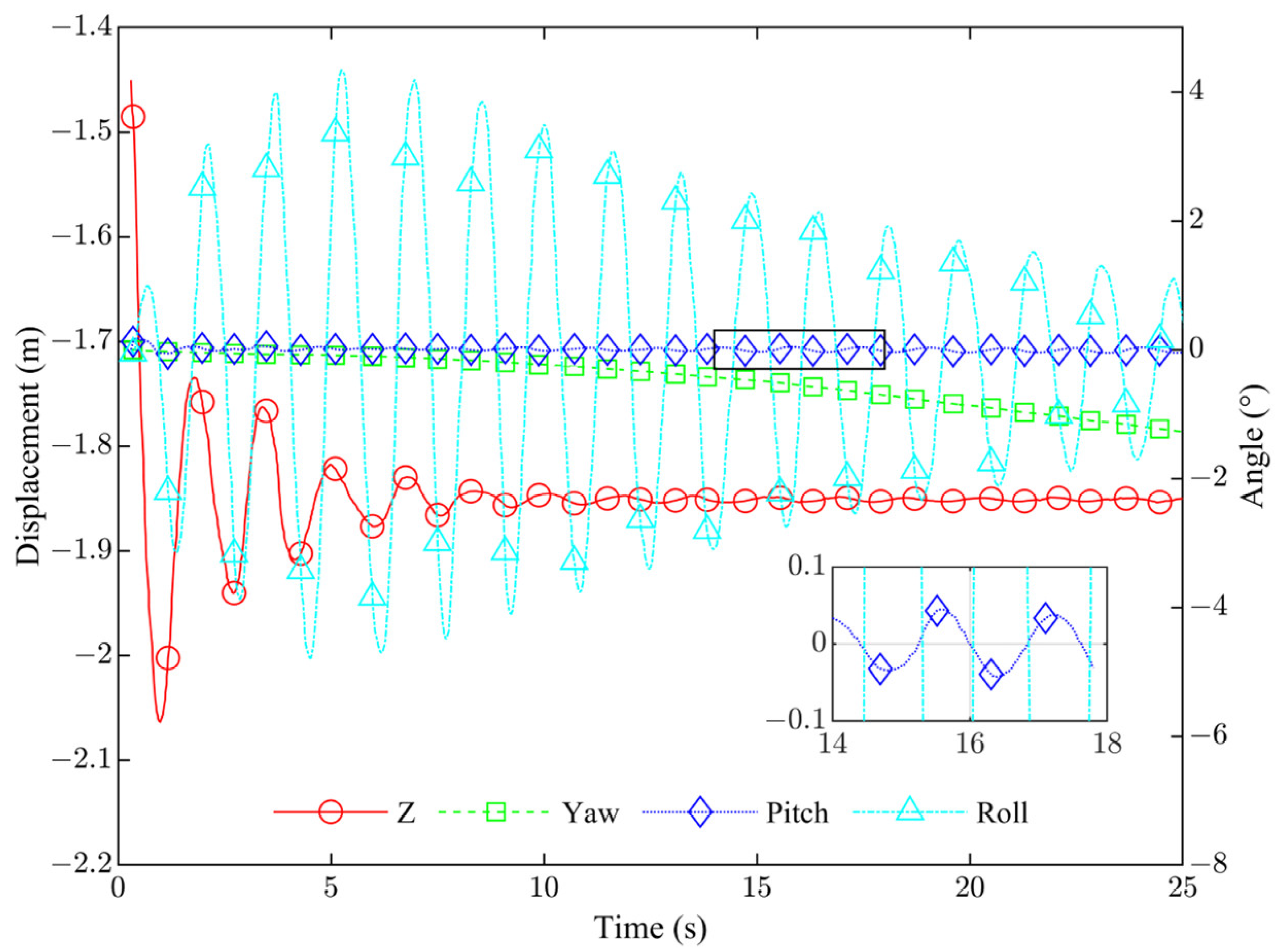
4.3. Span of 200 m PTL Case
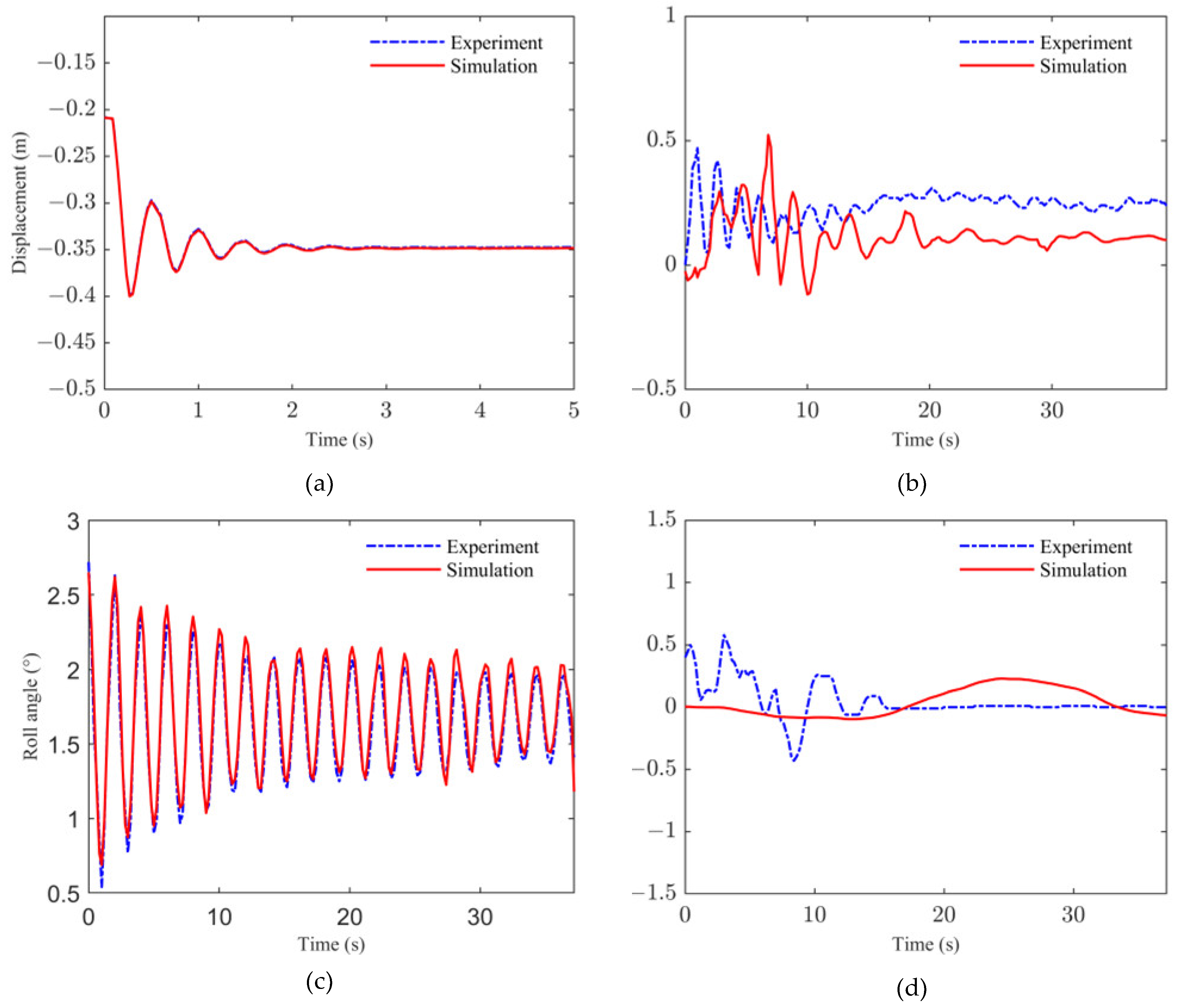
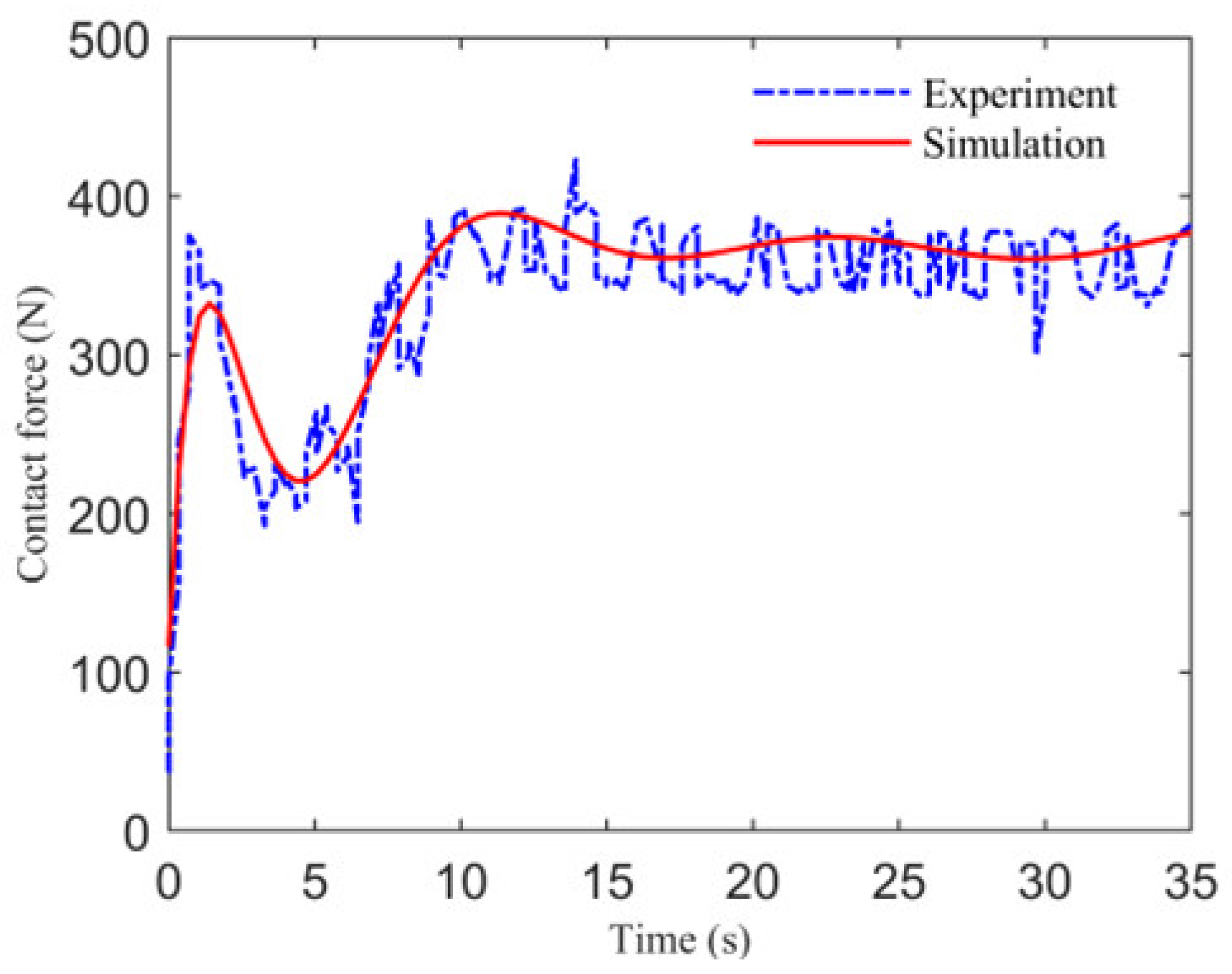
4.4. Experimental Verification of Model
5. Discussion
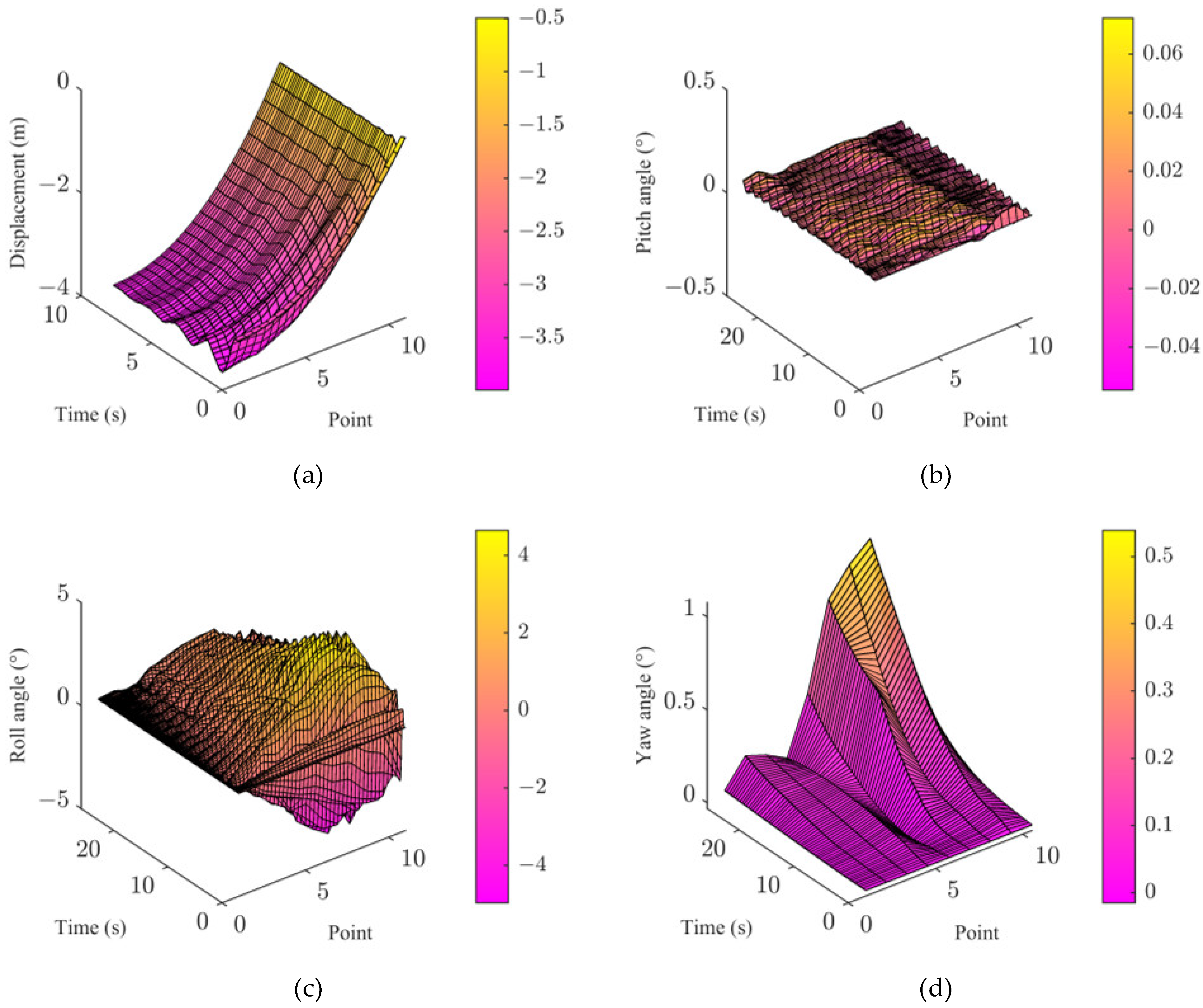
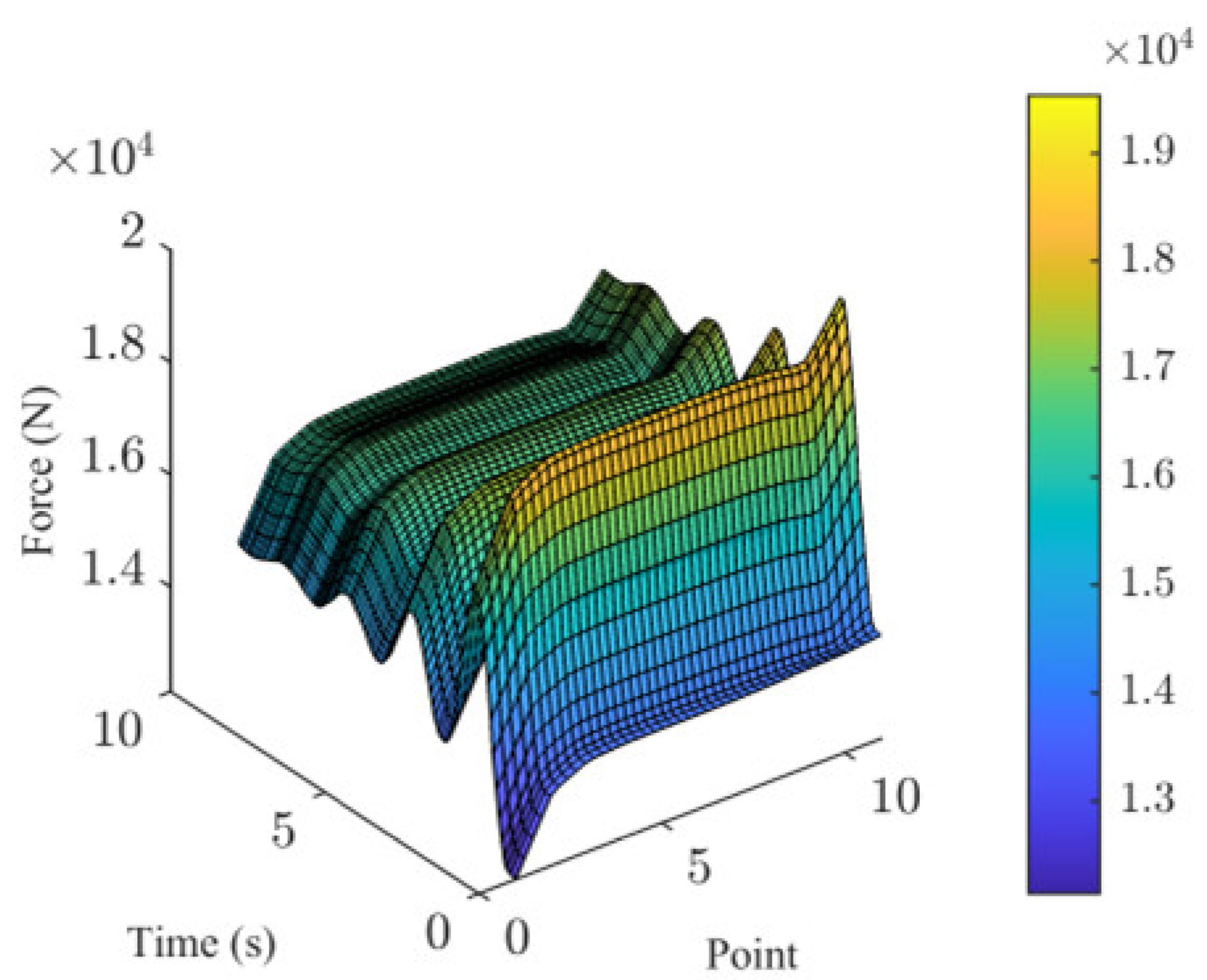
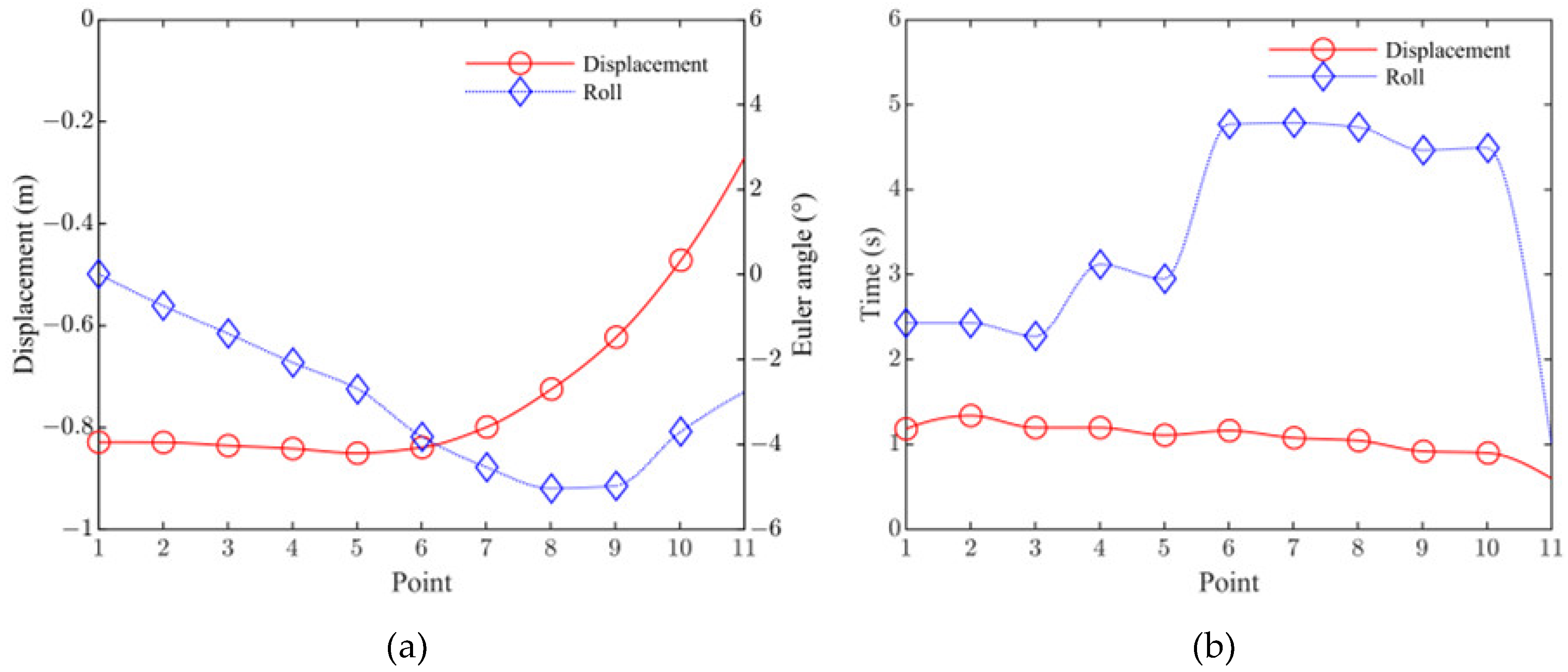
5.1. Influence of Landing Location on System Dynamics
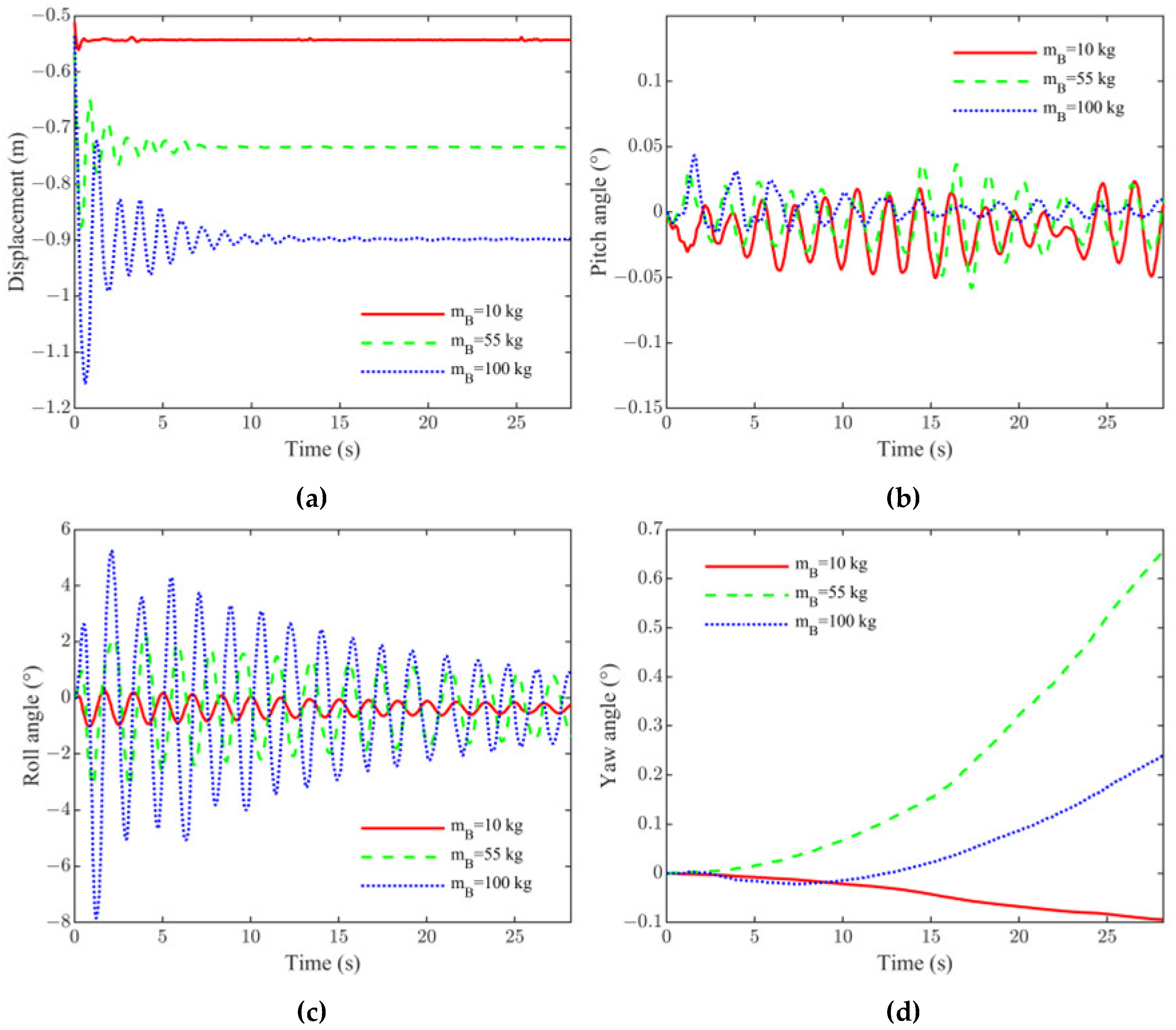
5.2. Influence of Mass of FPTLIR on System Dynamics
5.3. Comparison Between HIRs
5.4. Limitations and Future Work
6. Conclusions
- A coupled FPTLIR/PTL dynamic model was derived using the ANCF method. Shear and torsion were ignored using a Euler–Bernoulli beam to improve the efficiency. The coupled effect between the FPTLIR and PTL was formulated using the Hunt–Crossley contact model, considering the deflection angle and the groove of the of the travelling wheel to ensure the accuracy.
- A modular simulation of the model was performed with different landing positions and FPTLIR masses. Compared with the FEM, the ANCF demonstrated an accuracy improvement exceeding 50%. The results show that all dynamic responses remained within acceptable ranges. As the landing position approached the tower, the amplitude of the Z-displacement wave decreased, with the peak Z-displacement at the closest point being 34.4% of that at the farthest point while the roll angle amplitude increased, with the maximum exceeding the minimum by 3.7%. The appropriate landing point should be selected by weighing the collision risk against the insulation risk. Additionally, increasing the FPTLIR mass amplified the Z-displacement and attitude angle waves, with the lightest robot achieving a Z-displacement peak 9.2% and a roll angle peak 12.8% of those of the heaviest. Therefore, both the collision risk and the insulation risk exhibited a positive correlation with the robot’s mass.
- An integrated landing test platform was constructed to observe the landing process of the FPTLIR and to validate the accuracy of the model. The time domain variations of the attitude, Z-displacements, and contact forces were measured from the test platform, with the contact forces recorded using six opposing FSRs. The results show that the relative errors for the roll angle and Z-displacement were found to be 0.004 and 0.044, respectively, validating the accuracy of the proposed method. The platform enabled accurate analysis and prediction of FPTLIR system responses during the landing process.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PTL | Power transmission lines |
| HIR | Hybrid inspection robot |
| ANCF | Absolute nodal coordinate formulation |
| FPTLIR | Flying–walking power transmission line inspection robot |
| UAV | Unmanned aerial vehicle |
| FEM | Finite element modeling |
| DOF | Degree of freedom |
| FSR | Force-sensing resistor |
References
- Shu, Y.; Chen, W. Research and Application of UHV Power Transmission in China. High Volt. 2018, 3, 1–13. [Google Scholar] [CrossRef]
- Yang, L.; Fan, J.; Liu, Y.; Li, E.; Peng, J.; Liang, Z. A Review on State-of-the-Art Power Line Inspection Techniques. IEEE Trans. Instrum. Meas. 2020, 69, 9350–9365. [Google Scholar] [CrossRef]
- Ahmed, M.F.; Mohanta, J.C.; Sanyal, A. Inspection and Identification of Transmission Line Insulator Breakdown Based on Deep Learning Using Aerial Images. Electr. Power Syst. Res. 2022, 211, 108199. [Google Scholar] [CrossRef]
- Daisy, M.; Dashti, R.; Shaker, H.R.; Javadi, S.; Hosseini Aliabadi, M. Fault Location in Power Grids Using Substation Voltage Magnitude Differences: A Comprehensive Technique for Transmission Lines, Distribution Networks, and AC/DC Microgrids. Measurement 2023, 220, 113403. [Google Scholar] [CrossRef]
- Chen, D.; Guo, X.; Huang, P.; Li, F. Safety Distance Analysis of 500 kV Transmission Line Tower UAV Patrol Inspection. IEEE Lett. Electromagn. Compat. Pract. Appl. 2020, 2, 124–128. [Google Scholar] [CrossRef]
- Alhassan, A.B.; Zhang, X.; Shen, H.; Xu, H. Power Transmission Line Inspection Robots: A Review, Trends and Challenges for Future Research. Int. J. Electr. Power Energy Syst. 2020, 118, 105862. [Google Scholar] [CrossRef]
- Qiu, R.; Miao, X.; Zhuang, S.; Jiang, H.; Chen, J. Design and Implementation of an Autonomous Landing Control System of Unmanned Aerial Vehicle for Power Line Inspection. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 7428–7431. [Google Scholar]
- Li, Z.; Zhang, Y.; Wu, H.; Suzuki, S.; Namiki, A.; Wang, W. Design and Application of a UAV Autonomous Inspection System for High-Voltage Power Transmission Lines. Remote Sens. 2023, 15, 865. [Google Scholar] [CrossRef]
- Chen, M.; Cao, Y.; Tian, Y.; Li, E.; Liang, Z.; Tan, M. A Passive Compliance Obstacle-Crossing Robot for Power Line Inspection and Maintenance. IEEE Rob. Autom. Lett. 2023, 8, 2772–2779. [Google Scholar] [CrossRef]
- Chang, W.; Yang, G.; Yu, J.; Liang, Z.; Cheng, L.; Zhou, C. Development of a Power Line Inspection Robot with Hybrid Operation Modes. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 973–978. [Google Scholar]
- Wang, H.; Li, E.; Yang, G.; Guo, R. Design of an Inspection Robot System with Hybrid Operation Modes for Power Transmission Lines. In Proceedings of the 2019 IEEE International Conference on Mechatronics and Automation (ICMA), Tianjin, China, 4–7 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 2571–2576. [Google Scholar]
- Mirallès, F.; Hamelin, P.; Lambert, G.; Lavoie, S.; Pouliot, N.; Montfrond, M.; Montambault, S. LineDrone Technology: Landing an Unmanned Aerial Vehicle on a Power Line. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 6545–6552. [Google Scholar]
- Li, Z.; Tian, Y.; Yang, G.; Li, E.; Zhang, Y.; Chen, M.; Liang, Z.; Tan, M. Vision-Based Autonomous Landing of a Hybrid Robot on a Powerline. IEEE Trans. Instrum. Meas. 2023, 72, 1–11. [Google Scholar] [CrossRef]
- Hamelin, P.; Miralles, F.; Lambert, G.; Lavoie, S.; Pouliot, N.; Montfrond, M.; Montambault, S. Discrete-Time Control of LineDrone: An Assisted Tracking and Landing UAV for Live Power Line Inspection and Maintenance. In Proceedings of the 2019 International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 11–14 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 292–298. [Google Scholar]
- Li, Z.; Tian, Y.; Yang, G.; Zhang, Y.; Li, E.; Liang, Z.; Tan, M. Model-Based Trajectory Planning of a Hybrid Robot for Powerline Inspection. IEEE Rob. Autom. Lett. 2024, 9, 3443–3450. [Google Scholar] [CrossRef]
- Lopes, V.M.L.; Honório, L.M.; Santos, M.F.; Pancoti, A.A.N.; Silva, M.F.; Diniz, L.F.; Mercorelli, P. Design of an Over-Actuated Hexacopter Tilt-Rotor for Landing and Coupling in Power Transmission Lines. Drones 2023, 7, 341. [Google Scholar] [CrossRef]
- Lv, N.; Liu, J.; Xia, H.; Ma, J.; Yang, X. A Review of Techniques for Modeling Flexible Cables. Comput. -Aided Des. 2020, 122, 102826. [Google Scholar] [CrossRef]
- Lv, N.; Liu, J.; Ding, X.; Liu, J.; Lin, H.; Ma, J. Physically Based Real-Time Interactive Assembly Simulation of Cable Harness. J. Manuf. Syst. 2017, 43, 385–399. [Google Scholar] [CrossRef]
- Zhang, H.; Guo, J.; Liu, J.; Ren, G. An Efficient Multibody Dynamic Model of Arresting Cable Systems Based on ALE Formulation. Mech. Mach. Theory 2020, 151, 103892. [Google Scholar] [CrossRef]
- Xiao, X.; Wu, G.; Li, S. Dynamic Coupling Simulation of a Power Transmission Line Inspection Robot with Its Flexible Moving Path When Overcoming Obstacles. In Proceedings of the 2007 IEEE International Conference on Automation Science and Engineering, Scottsdale, AZ, USA, 22–25 September 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 326–331. [Google Scholar]
- Deng, X.; Deng, Z.; Ren, X. New Algorithm of Shape-Finding of Suspension Bridge with Spatial Cables. Theor. Appl. Mech. Lett. 2023, 13, 100402. [Google Scholar] [CrossRef]
- Fan, W.; Ren, H.; Zhu, W.; Zhu, H. Dynamic Analysis of Power Transmission Lines With Ice-Shedding Using an Efficient Absolute Nodal Coordinate Beam Formulation. J. Comput. Nonlin. Dyn. 2021, 16, 011005. [Google Scholar] [CrossRef]
- Gu, Y.; Lan, P.; Cui, Y.; Li, K.; Yu, Z. Dynamic Interaction between the Transmission Wire and Cross-Frame. Mech. Mach. Theory 2021, 155, 104068. [Google Scholar] [CrossRef]
- Peng, C.; Yang, C.; Xue, J.; Gong, Y.; Zhang, W. An Adaptive Variable-Length Cable Element Method for Form-Finding Analysis of Railway Catenaries in an Absolute Nodal Coordinate Formulation. Eur. J. Mech. -A/Solids 2022, 93, 104545. [Google Scholar] [CrossRef]
- Zheng, X.; Wu, G.; Jiang, W.; Fan, F.; Zhu, J. Rigid–Flexible Coupling Dynamics with Contact Estimator for Robot/PTL System. Proc. Inst. Mech. Eng. K J. Multi-Body Dyn. 2020, 234, 635–649. [Google Scholar] [CrossRef]
- Xiao, X.; Wu, G.; Du, E.; Li, S. Impacts of Flexible Obstructive Working Environment on Dynamic Performances of Inspection Robot for Power Transmission Line. J. Cent. South Univ. Technol. 2008, 15, 869–876. [Google Scholar] [CrossRef]
- Yue, X.; Wang, H.; Jiang, Y. Performance Optimization of a Mobile Inspection Robot for Power Transmission Lines. Int. J. Simul. Syst. Sci. Technol. 2016, 17, 3.1–3.3. Available online: https://ijssst.info/Vol-17/No-48/paper3.pdf (accessed on 7 February 2025).
- Westin, C.; Irani, R.A. Modeling Dynamic Cable–Sheave Contact and Detachment during Towing Operations. Mar. Struct. 2021, 77, 102960. [Google Scholar] [CrossRef]
- Wang, Y.; Qin, X.; Jia, W.; Lei, J.; Wang, D.; Feng, T.; Zeng, Y.; Song, J. Multiobjective Energy Consumption Optimization of a Flying–Walking Power Transmission Line Inspection Robot during Flight Missions Using Improved NSGA-II. Appl. Sci. 2024, 14, 1637. [Google Scholar] [CrossRef]
- Bauchau, O.A.; Craig, J.I. Euler-Bernoulli Beam Theory. In Structural Analysis; Bauchau, O.A., Craig, J.I., Eds.; Springer: Dordrecht, The Netherlands, 2009; pp. 173–221. ISBN 978-90-481-2516-6. [Google Scholar]
- Gerstmayr, J.; Irschik, H. On the Correct Representation of Bending and Axial Deformation in the Absolute Nodal Coordinate Formulation with an Elastic Line Approach. J. Sound Vib. 2008, 318, 461–487. [Google Scholar] [CrossRef]
- Atay, S.; Buckner, G.; Bryant, M. Dynamic Modeling for Bi-Modal, Rotary Wing, Rolling-Flying Vehicles. J. Dyn. Syst. Meas. Contr. 2020, 142, 111003. [Google Scholar] [CrossRef]
- Zengin, A.T.; Erdemir, G.; Akinci, T.C.; Selcuk, F.A.; Erduran, M.N.; Seker, S.S. (PREPRINT) ROSETLineBot: One-Wheel-Drive Low-Cost Power Line Inspection Robot Design and Control. J. Electr. Syst. 2019, 15, 626–634. [Google Scholar]
- Pouliot, N.; Montambault, S. Geometric Design of the LineScout, a Teleoperated Robot for Power Line Inspection and Maintenance. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 3970–3977. [Google Scholar]
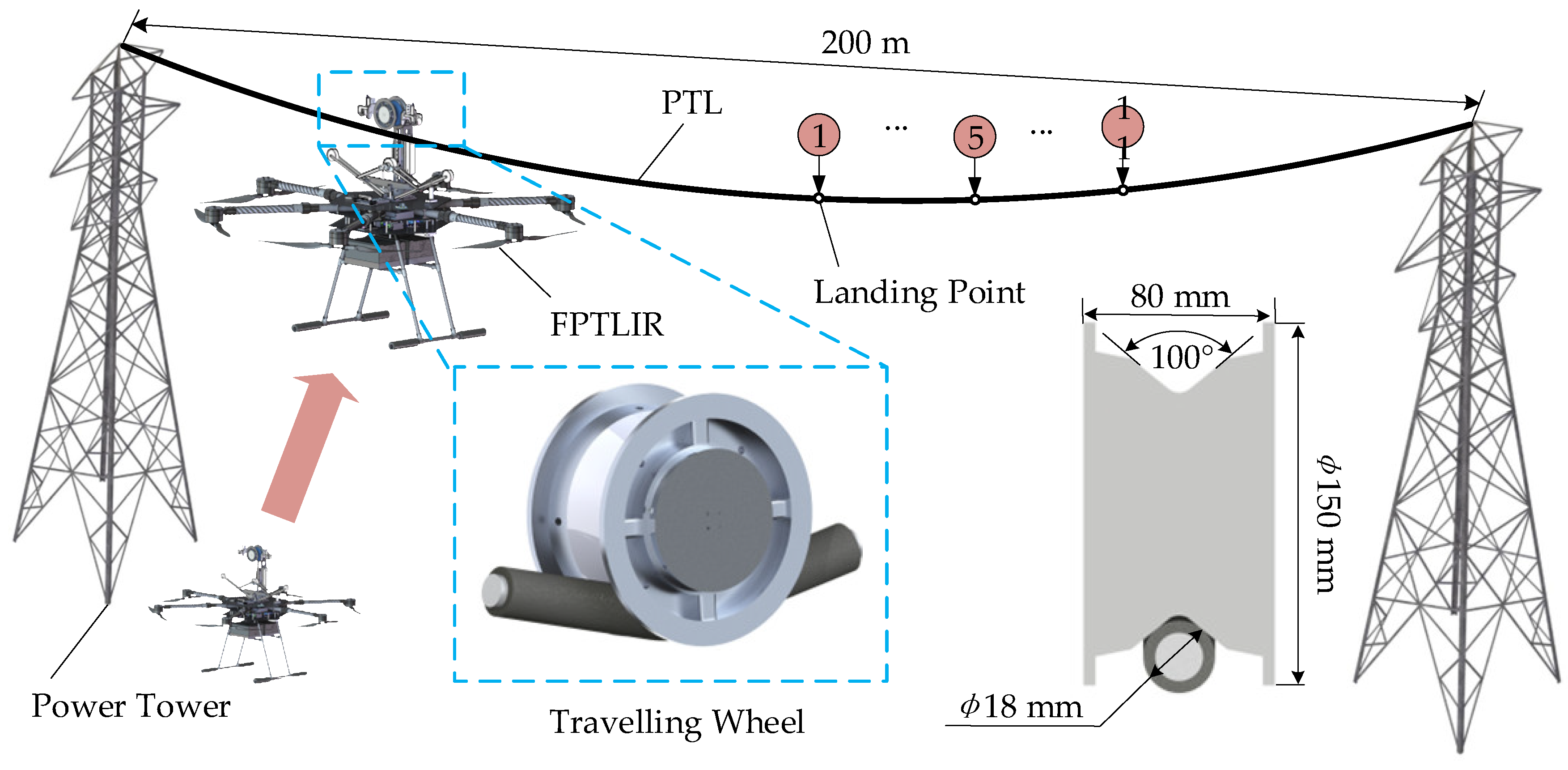



| Parameter Type | Parameter/Unit | Value |
|---|---|---|
| FPTLIR parameters | Mass/kg | 38 |
| Dimension/(mm × mm × mm) | 1250 × 1250 × 1200 | |
| Moment of inertia about the x-axis/kg | 5.8 | |
| Moment of inertia about the y-axis/kg | 5.8 | |
| Moment of inertia about the z-axis/kg | 8.5 | |
| Diameter of travelling wheel/mm | 150 | |
| Groove angle of travelling wheel/° | 100 | |
| Groove width of travelling wheel/mm | 80 | |
| PTL parameters | PTL length/m | 200 |
| Linear density kg/m | 0.91 | |
| Axial stiffness/N/m | 8.12 × 107 | |
| Bending stiffness/N·m2 | 6580 | |
| Diameter/mm | 18 |
| Value | Formula | Range |
|---|---|---|
| Roll angle | ||
| Pitch angle | ||
| Yaw angle | ||
| Z-displacement |
| Z-Displacement | Pitch | Roll | Yaw | Contact Force |
|---|---|---|---|---|
| 0.004 | 2.14 | 0.044 | 21.1 | 0.079 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, W.; Lei, J.; Qin, X.; Jin, P.; Zhang, S.; Tao, J.; Zhao, M. Dynamic Modeling and Analysis of a Flying–Walking Power Transmission Line Inspection Robot Landing on Power Transmission Line Using the ANCF Method. Appl. Sci. 2025, 15, 1863. https://doi.org/10.3390/app15041863
Jia W, Lei J, Qin X, Jin P, Zhang S, Tao J, Zhao M. Dynamic Modeling and Analysis of a Flying–Walking Power Transmission Line Inspection Robot Landing on Power Transmission Line Using the ANCF Method. Applied Sciences. 2025; 15(4):1863. https://doi.org/10.3390/app15041863
Chicago/Turabian StyleJia, Wenxing, Jin Lei, Xinyan Qin, Peng Jin, Shenting Zhang, Jiali Tao, and Minyu Zhao. 2025. "Dynamic Modeling and Analysis of a Flying–Walking Power Transmission Line Inspection Robot Landing on Power Transmission Line Using the ANCF Method" Applied Sciences 15, no. 4: 1863. https://doi.org/10.3390/app15041863
APA StyleJia, W., Lei, J., Qin, X., Jin, P., Zhang, S., Tao, J., & Zhao, M. (2025). Dynamic Modeling and Analysis of a Flying–Walking Power Transmission Line Inspection Robot Landing on Power Transmission Line Using the ANCF Method. Applied Sciences, 15(4), 1863. https://doi.org/10.3390/app15041863






