Harnessing Spatial-Frequency Information for Enhanced Image Restoration

Abstract

Image restoration aims to recover high-quality, clear images from those that have suffered visibility loss due to various types of degradation. Numerous deep learning-based approaches for image restoration have shown substantial improvements. However, there are two notable limitations: (a) Despite substantial spectral mismatches in the frequency domain between clean and degraded images, only a few approaches leverage information from the frequency domain. (b) Variants of attention mechanisms have been proposed for high-resolution images in low-level vision tasks, but these methods still require inherently high computational costs. To address these issues, we propose a Frequency-Aware Network (FreANet) for image restoration, which consists of two simple yet effective modules. We utilize a multi-branch/domain module that integrates latent features from the frequency and spatial domains using the discrete Fourier transform (DFT) and complex convolutional neural networks. Furthermore, we introduce a multi-scale pooling attention mechanism that employs average pooling along the row and column axes. We conducted extensive experiments on image restoration tasks, including defocus deblurring, motion deblurring, dehazing, and low-light enhancement. The proposed FreANet demonstrates remarkable results compared to previous approaches to these tasks.

1. Introduction

Image restoration, a classic task in computer vision, aims to recover a high-quality, clean image by removing specific types of degradation, such as haze, blur, and low light. Since images affected by degradation can adversely impact the performance of computer vision models, the importance of image restoration is emphasized in various applications, including autonomous driving, surveillance, and remote sensing. However, obtaining a single effective solution is challenging because image restoration is an inherently ill-posed problem. To address this challenge, conventional approaches [1,2] often rely on strong image priors, which are limited in producing consistent results across diverse, unseen environments and scenarios.

With the advent of deep learning, the image restoration task has experienced a rapid paradigm shift from conventional approaches to deep learning-based methods. Various deep learning models have been proposed, demonstrating substantial improvements over traditional approaches, such as multi-stage frameworks [3,4], normalization techniques [5], and attention mechanisms [6,7]. More recently, many researchers have shifted their focus to multi-head self-attention (MHA) [8], which captures long-range dependencies and demonstrates remarkable performance [7,9]. However, when an image with a resolution of $h \times w$ is given, the computational complexity of MHA is $\mathcal{O}\left(h^2{w}^2\right)$, which requires significant memory resources, making it unsuitable for high-resolution images.

Since various types of degradation distort texture, edges, and other features in an image, the discrepancy between the degraded and clean images in the frequency domain is essential. Nonetheless, only a few approaches utilize the latent space of the frequency domain [10,11,12,13,14]. Among them, most methods process features by directly transforming them using various transformation tools, such as the wavelet transform [12,13] and the Fourier transform [14,15]. Some recently published studies designed learnable low-pass filters through pooling techniques [10,11] to implicitly process frequency information. These approaches have substantially improved restoration capabilities in simple yet powerful ways, demonstrating promising potential in image restoration.

However, previous methods [14,15] related to modeling the frequency space, particularly those using the discrete Fourier transform (DFT), apply two independent convolutional neural networks (CNNs) to process complex features consisting of real and imaginary components, e.g., $Y = X_{real}{W}_{real} + j\left(X_{imag}{W}_{iamg}\right)$. This approach has an upper limit on performance due to a mathematical error in the operation.

In this study, we designed a Frequency-Aware Net work (FreANet) to efficiently the bridge frequency gaps between degraded and sharp images and capture spatial interactions with low computational complexity. Specifically, we propose a multi-domain feature extractor (MDFE) that adaptively aggregates spatial and frequency contexts for various types of degradation. The MDFE is composed of spatial and frequency branches, which utilize convolutions with large strip kernels ($1 \times k$ or $k \times 1$) to produce rich representations [16]. In the frequency branch, we introduce complex convolutions ($\mathbb{C}$CNNs) [17] to handle the complex features transformed via the DFT.

To reduce the computational complexity of the attention mechanism, we developed a multi-scale pooling attention (MPA) mechanism, which leverages unidirectional global average pooling (GAP) and strip convolutions with multiple scales. This design bypasses the quadratic computational complexity, $\mathcal{O}\left(h^2{w}^2\right)$, of MHA, allowing the network to achieve linear computational complexity, $\mathcal{O}\left(hw\right)$.

We conducted extensive experiments on four image restoration tasks, including defocus deblurring, motion deblurring, dehazing, and low-light enhancement. Compared to previous methods [18,19], the proposed FreANet demonstrates substantial restoration capacity with fewer parameters, achieving state-of-the-art performance on various datasets.

Our main contributions are summarized as follows:

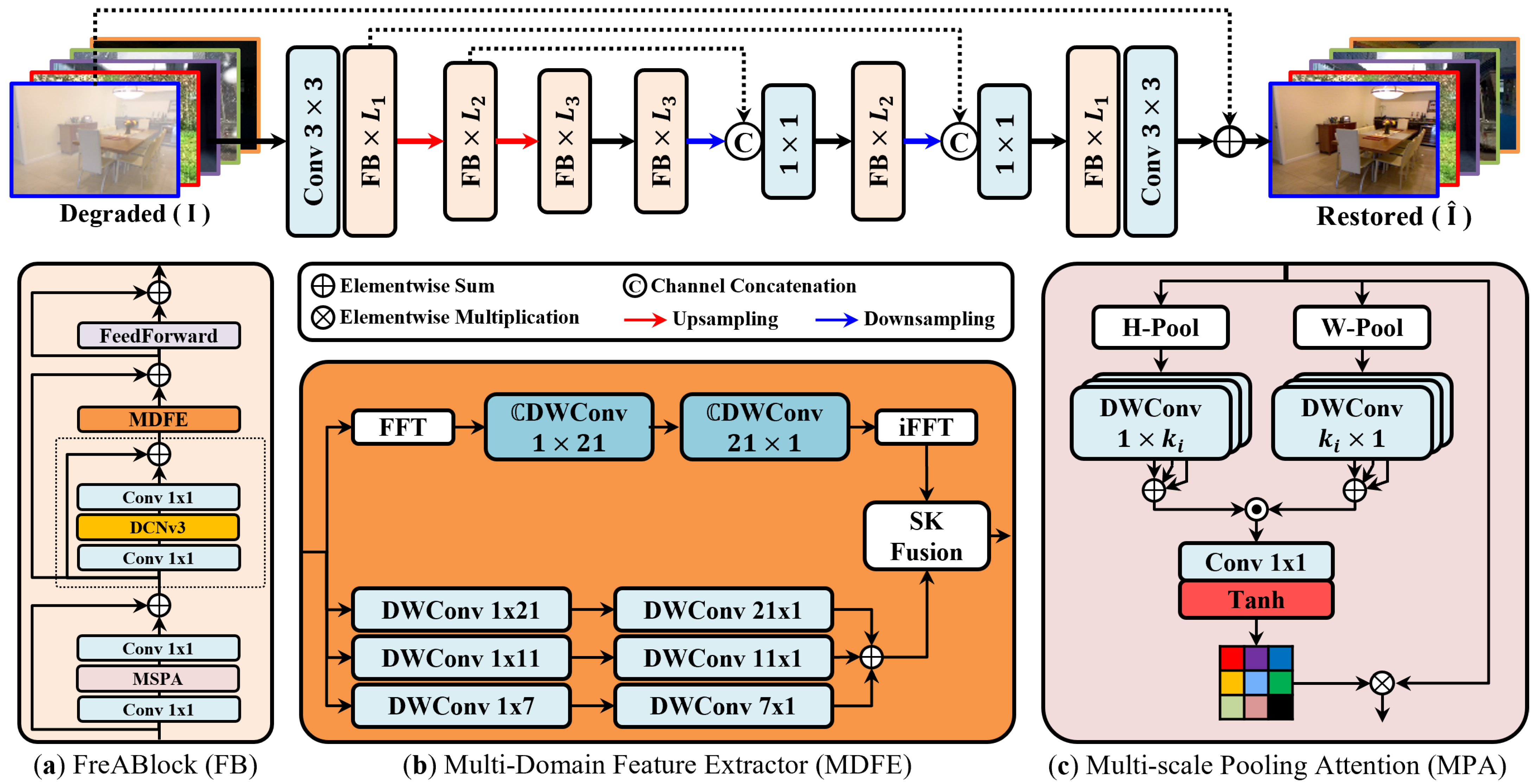
• We propose a multi-domain feature extractor (MDFE) that selectively integrates spatial and frequency information for different types of degradation and is designed to operate appropriately in the corresponding domain.
• To efficiently capture global information, we propose a multi-scale pooling attention (MPA) mechanism, which utilizes unidirectional pooling functions and convolutions with multiple strip kernels, thereby reducing the computational complexity of vanilla attention from $\mathcal{O}\left(h^2{w}^2\right)$ to $\mathcal{O}\left(hw\right)$.
• The proposed FreANet is evaluated on 11 benchmark datasets for various restoration tasks, demonstrating remarkable performance compared to other algorithms.

2. Related Works

2.1. Image Restoration

Image restoration aims to reproduce clean counterparts from images damaged by various types of degradation, and this field has been extensively studied for a long time. Conventional image restoration approaches restrict the clean latent space based on various assumptions and handcrafted preprocessing techniques [1,2]. Recently, data-driven methods designed with CNNs have shown substantial improvements in restoration capacity compared to conventional algorithms [3,4,5,20,21]. These CNN-based methods primarily utilize encoder–decoder frameworks, particularly U-shaped architectures, which can yet effectively aggregate hierarchical representations. Furthermore, advanced techniques have been introduced to enhance performance, including dilated convolutions [4,22], multi-stage frameworks [3,23], contrastive learning [20,24], dense connections [25,26], and attention mechanisms [3,21]. Recently, newly proposed methods have included the design of transformer-based and MLP-mixer-based models to capture long-range dependencies, demonstrating remarkable performance in several image restoration tasks [7,9,23,27]. While these approaches have been developed to perform restoration only in the spatial domain, we can selectively aggregate features in both the spatial and frequency domains for image restoration.

2.2. Modeling Frequency Information

Some restoration methods have been proposed to bridge the frequency gap between paired degraded and clean images [10,11,14]. Generally, numerous studies have utilized methods that decompose images into different frequency components using various transformation tools, such as the wavelet transform [12,13,28] and the Fourier transform [14,15,29]. Specifically, UHDFour [29] proposed restoring the amplitude and phase separately, as each plays a different role. Fourmer [14] introduced FPE, which consists of spatial interaction and channel evolution for efficient global modeling. Recently, some studies have proposed learnable low-pass filters using pooling techniques [10,11]. In this study, we directly access the frequency latent space using the DFT tool, similar to methods employing Fourier transforms [14,29]. However, we model their implicit interactions through complex convolutions instead of processing the real and imaginary parts separately.

2.3. Attention Mechanisms

The attention mechanism is a crucial factor in boosting performance by allowing the network to focus on essential parts. Vision transformers [30,31] divide an image into a sequence of patches to capture the relationships between these patches. Although they have demonstrated promising performance across various vision tasks, they have the drawback of requiring substantial computational resources. To address this issue, the Swin transformer [32] introduced window-based local attention that learns the interactions between elements within shifted windows. POTTER [33] proposed pooling attention that applies individual h-axis and w-axis pooling operations. Restormer [7] effectively restored clean images by designing attention in the channel direction. SegNeXt [16] was developed with convolutional attention using multi-branch depthwise strip convolutions and achieved performance comparable to that of transformer-based models. In this study, we designed a novel attention mechanism that integrates the advantages of both POTTER and SegNeXt. Our attention compresses features into global statistical information via unidirectional pooling operations and then effectively aggregates spatial information using multi-scale, depthwise strip convolutions.

3. Methodology

In this Section, we provide details on our method, starting with FreANet’s overall architecture and then introducing its core modules: the MDFE and MPA.

Before delving into the details, we define the notations and Fourier transform used throughout the paper. Let $x\in {\mathbb{R}}^{H\times W\times C}$ denote an input feature in the spatial domain. The Fourier transform $\mathcal{F}$ converts the input feature into the frequency domain, representing it as its corresponding complex component $X = X_{\mathrm{re}} + j{X}_{\mathrm{im}} \in {\mathbb{C}}^{H\times W\times C\times 2}$. Here, the last dimension, ‘2’, refers to the real $X_{\mathrm{re}}$ and imaginary $X_{\mathrm{im}}$ components. The Fourier transform is expressed as

$$\mathcal{F}\left(x\right)(u,v)={\displaystyle \frac{1}{\sqrt{HW}}}\sum _{h=0}^{H-1}\sum _{w=0}^{W-1}x(h,w)e^{-j2\pi (\frac{h}{H}u+\frac{w}{W}v)},$$

(1)

where u and v are the corresponding coordinates in the frequency domain. The inverse Fourier transform is denoted by ${\mathcal{F}}^{-1}\left(X\right)$. We employ the FFT and IFFT algorithms [34] for the Fourier transform and its inverse process.

3.1. Overall Architecture

As shown in Figure 1, our FreANet utilizes the popular U-shaped encoder–decoder architecture to achieve rich hierarchical representations. Specifically, given an input image $I \in {\mathbb{R}}^{H\times W\times 3}$, FreANet projects it into the embedding space using a single $3 \times 3$ convolution, producing features of size $H \times W \times C$, where H and W indicate the original resolution sizes, and C represents the number of channels. These features are then fed into FreABlock as input to capture high-level representations. FreABlock consists of the MDFE, MPA, and a feed-forward network (Figure 1b). Furthermore, the input features of the MDFE are flexibly enhanced through the residual deformable block (RDB) using DCNv3 [35], allowing a focus on critical features. As the features pass through deeper layers, the number of channels doubles, and their resolution halves. Upsampling and downsampling are performed using transposed and strided convolutions, respectively. Finally, the restored image $\widehat{I} \in {\mathbb{R}}^{H \times W \times 3}$ is estimated using a single $3 \times 3$ convolution.

3.2. Multi-Domain Feature Extractor (MDFE)

As illustrated in Figure 1c, the MDFE is composed of inter-multi-branches, each operating in different spaces, including the spatial and frequency domains. The spatial branch is designed with an intra-multi-branch structure consisting of parallel branches with small to large receptive fields, effectively capturing the multi-scale spatial context. We adopt two serial depthwise convolutions with strip kernels [16] to maintain a lightweight network in each branch. The process in the spatial branch is expressed as

$$f_{\mathrm{s}} =\sum _{i=0}^2{\mathrm{DWConv}}_{k_i\times 1}\left({\mathrm{DWConv}}_{1\times k_i}\left(x\right)\right),$$

(2)

where $f_{\mathrm{s}}$ represents the output features of the spatial branch. DWConv and $k_i$, with $i \in \left\{0,1,2\right\}$, refer to the depthwise convolution and the kernel size of the i-th branch, respectively.

Before being fed into the frequency branch, the input features are converted into their corresponding complex features by applying the FFT algorithm. Given that the real and imaginary components of complex features originate from corresponding spatial features, applying individual convolutions to these components is inappropriate. Therefore, we apply complex convolutions to the complex features, which involve interactions between the real and imaginary components. Complex convolutions are implemented similarly to standard convolutions, but each convolution kernel is responsible for the real $W_{\mathrm{re}}$ and imaginary $W_{\mathrm{im}}$ weights. The complex kernel W is defined as $W = W_{\mathrm{re}} + j{W}_{\mathrm{im}}$, and the complex convolution is expressed as $W ⊛ X = (W_{\mathrm{re}}{X}_{\mathrm{re}} - W_{\mathrm{im}}{X}_{\mathrm{im}}) + j(W_{\mathrm{re}}{X}_{\mathrm{im}} + W_{\mathrm{im}}{X}_{\mathrm{re}})$. Like the spatial branch, we utilize two serial depthwise convolutions with strip kernels, employing them in the manner of complex convolutions. The process in the frequency branch is expressed as

$$F_{\mathrm{f},\mathrm{re}} + j{F}_{\mathrm{f},\mathrm{im}} = \mathrm{DW}\mathbb{C}{\mathrm{Conv}}_{21\times 1}\left(\mathrm{DW}\mathbb{C}{\mathrm{Conv}}_{1\times 21}\left(X\right)\right),$$

(3)

$$X = \mathcal{F}\left(x\right),f_{\mathrm{f}}={\mathcal{F}}^{-1}(F_{\mathrm{f},\mathrm{re}} + j{F}_{\mathrm{f},\mathrm{im}}),$$

(4)

where $F_{\mathrm{f},\mathrm{re}}$ and $F_{\mathrm{f},\mathrm{im}}$ are the real and imaginary output features of the frequency branch. $\mathrm{DW}\mathbb{C}\mathrm{Conv}$ refers to the depthwise complex convolution, and $F_{\mathrm{f}}$ the output features of the frequency branch, which are converted to the spatial domain through the inverse Fourier transform. Finally, inspired by SKNet [36], the output features extracted from different domains are integrated by computing weights for each channel. The fusion process is expressed as

$$Z = \mathrm{MLP}\left(\mathrm{GAP}(f_{\mathrm{s}} + f_{\mathrm{f}})\right),$$

(5)

where $Z \in {\mathbb{R}}^{1\times 1\times D}$ represents compressed features, with the number of channels denoted by D. MLP and GAP refer to a fully connected layer and global average pooling. Next, two separate fully connected layers are applied, followed by a softmax operation, to compute the weights for each channel:

$$[\alpha ,\beta ] = \left[{\mathrm{MLP}}_{\alpha }\left(\mathrm{Z}\right),{\mathrm{MLP}}_{\beta }\left(\mathrm{Z}\right)\right],$$

(6)

$${\alpha }^{\mathrm{c}} = {\displaystyle \frac{e^{{\alpha }^{\mathrm{c}}}}{e^{{\alpha }^{\mathrm{c}}} + e^{{\beta }^{\mathrm{c}}}}},{\beta }^{\mathrm{c}} = {\displaystyle \frac{e^{{\beta }^{\mathrm{c}}}}{e^{{\alpha }^{\mathrm{c}}} + e^{{\beta }^{\mathrm{c}}}}},$$

(7)

$$f^{\mathrm{c}} = {\alpha }^{\mathrm{c}} \otimes f_{\mathrm{s}}^{\mathrm{c}} + {\beta }^{\mathrm{c}} \otimes f_{\mathrm{f}}^{\mathrm{c}},\mathrm{where}{\alpha }^{\mathrm{c}} + {\beta }^{\mathrm{c}} = 1,$$

(8)

where $f = [f^1,f^2,\cdots ,f^{\mathrm{c}}]$. $\alpha$ and $\beta$ represent the weights per channel for $f_{\mathrm{s}}$ and $f_{\mathrm{f}}$, respectively. The notation ${\alpha }_{\mathrm{c}}$ denotes the c-th channel of $\alpha$, and the same notation applies to ${\beta }^{\mathrm{c}}$, $f_{\mathrm{s}}^c$, and $f_{\mathrm{f}}^c$. The symbol ⊗ represents element-wise matrix multiplication.

3.3. Multi-Scale Pooling Attention (MPA)

The proposed MPA utilizes global average pooling on the input features along specific directions, such as the vertical and horizontal axes, to address the high complexity of spatial attention. The resulting squeezed features are then fed into several strip convolutions, encompassing both small and large receptive fields, to aggregate local and long-range information:

$$[x_{\mathrm{h}},x_{\mathrm{w}}] = \left[{\mathrm{GAP}}_{\mathrm{h}}\left(x\right),{\mathrm{GAP}}_{\mathrm{w}}\left(x\right)\right],$$

(9)

$$A_{\mathrm{h}} = \sum _{i=0}^3{\mathrm{DWConv}}_{1\times k_i}\left(x_{\mathrm{h}}\right),A_{\mathrm{w}} = \sum _{i=0}^3{\mathrm{DWConv}}_{k_i\times 1}\left(x_{\mathrm{w}}\right),$$

(10)

where ${\mathrm{GAP}}_{\mathrm{h}}$ and ${\mathrm{GAP}}_{\mathrm{w}}$ denote global average pooling in the h- and w-axis directions, respectively. $A_{\mathrm{h}} \in {\mathbb{R}}^{1\times W\times C}$ and $A_{\mathrm{w}} \in {\mathbb{R}}^{H\times 1\times C}$ represent the information aggregated from features squeezed in each direction. Then, we compute the attention map $A \in {\mathbb{R}}^{\mathrm{H}\times \mathrm{W}\times \mathrm{C}}$ by calculating the dot product between the information aggregated for each axis. After performing pointwise convolution for information exchange between channels, the attention values are projected into the range (−1, 1) using the Tanh function, which helps suppress irrelevant information while enhancing useful information. This process can be expressed as follows:

$$A = \mathrm{Tan}\mathrm{h}\left(\mathrm{PWConv}\left(A_{\mathrm{h}}{A}_{\mathrm{w}}\right)\right),\mathrm{Out} = A\otimes x.$$

(11)

In Equation (11), PWConv refers to the pointwise convolution, and Out represents the final output of the MPA.

3.4. Loss Function

Given that the proposed FreANet operates within the embedding spaces of both the spatial and frequency domains, we adopt the main spatial ${\mathcal{L}}_{\mathrm{Spatial}}$ loss and an auxiliary spectral ${\mathcal{L}}_{\mathrm{Frequency}}$ loss:

$${\mathcal{L}}_{\mathrm{Spatial}} = {\parallel \widehat{I}-Y\parallel }_1,{\mathcal{L}}_{\mathrm{Frequency}} = {\parallel \mathcal{F}\left(\widehat{I}\right) - \mathcal{F}\left(Y\right)\parallel }_1,$$

(12)

where Y is the corresponding clear image. Additionally, we employ contrastive regularization ${\mathcal{L}}_{\mathrm{CR}}$ [20] to further improve performance:

$${\mathcal{L}}_{\mathrm{CR}} = \sum _{i=0}^n{w}_i{\displaystyle \frac{{\parallel {\mathsf{\Phi }}_i\left(\widehat{I}\right) - {\mathsf{\Phi }}_i\left(Y\right)\parallel }_1}{{\parallel {\mathsf{\Phi }}_i\left(\widehat{I}\right) - {\mathsf{\Phi }}_i\left(I\right)\parallel }_1}},$$

(13)

where ${\mathsf{\Phi }}_i$ refers to the hidden features extracted from the i-th layer of the pre-trained network. $w_i$ is the weight coefficient. Then, the overall loss is expressed as a combination of the above-mentioned losses:

$$\mathcal{L} = {\mathcal{L}}_{\mathrm{Spatial}} + {\lambda }_1{\mathcal{L}}_{\mathrm{Frequency}} + {\lambda }_2{\mathcal{L}}_{\mathrm{CR}}.$$

(14)

In this work, ${\lambda }_1$ and ${\lambda }_2$ are set to 0.1 and 0.05, respectively.

4. Experiments

This Section presents extensive experiments conducted on 11 benchmark datasets for four restoration tasks, including defocus deblurring, motion deblurring, dehazing, and low-light enhancement. Summaries of all the datasets used in these experiments are provided in

Table 1. Dataset summary for four restoration tasks.

Task	Dataset	Test Subname	#Train	#Test
Defocus Deblurring	DPDD [37]	-	350	76
	LFDOF [38]	-	11,261	725
Motion Deblurring	GoPro [39]	-	2103	1111
	HIDE [40]	-	0	2025
Dehazing	RESIDE-ITS [41]	SOTS-Indoor	13,990	500
	RESIDE-OTS [41]	SOTS-Outdoor	313,950	500
	Dense-Haze [42]	-	45	5
	NH-HAZE [43]	-	45	5
	NHR [44]	-	16,146	1794
Enhancement	LOLv1 [45]	-	485	15
	LOLv2-real [46]	-	689	100
	LOLv2-syn [46]	-	900	100

. In the result tables, the best and second-best scores for each dataset are highlighted in bold and underlined, respectively.

Implementation Settings. We trained separate models to restore images degraded by different degradation factors. Considering the complexity of each problem, we redesigned the proposed FreANet by adjusting the number of encoder–decoder layers and residual blocks [${\mathrm{L}}_1,{\mathrm{L}}_2$, ${\mathrm{L}}_3$, N]. We set [1, 2, 3, 10] for defocus/motion deblurring, [1, 2, 3, 3] for dehazing, and [1, 2, 2, 1] for low-light enhancement. Additionally, to ensure a fair evaluation for dehazing, we designed a small version of FreANet [1, 1, 1, 2]. Unless mentioned otherwise, the following tunable parameters were used in all experiments. We adopted the Adam optimizer [47] with an initial learning rate of $1 \times {10}^{-4}$, which decreases to $1 \times {10}^{-6}$ in a cosine annealing manner [48]. We used a patch size of 256 × 256 with random horizontal flips and rotations for data augmentation. We trained and evaluated the proposed restoration models for all degradation types on a single NVIDIA H100 GPU (NVDIA, Santa Clara, CA, USA). FLOPs were measured on data with a resolution of $256 \times 256$.

4.1. Single-Image Defocus Deblurring Results

Following the training strategy of SFNet [10], our model was trained on LFDOF [38] and fine-tuned on DPDD [37].

Table 2. Defocus deblurring comparisons on the DPDD [37] test set.

Methods	Indoor Scenes				Outdoor Scenes				Combined				#Params
	PSNR↑	SSIM↑	MAE↓	LPIPS↓	PSNR↑	SSIM↑	MAE↓	LPIPS↓	PSNR↑	SSIM↑	MAE↓	LPIPS↓	(M)
IFAN [49]	28.11	0.861	0.026	0.179	22.76	0.720	0.052	0.254	25.37	0.789	0.039	0.217	10.47
Restormer [7]	28.87	0.882	0.025	0.145	23.24	0.743	0.050	0.209	25.98	0.811	0.038	0.178	26.13
SFNet [10]	29.16	0.878	0.023	0.168	23.45	0.747	0.049	0.244	26.23	0.811	0.037	0.207	13.27
FocalNet [11]	29.10	0.876	0.024	0.173	23.41	0.743	0.049	0.246	26.18	0.808	0.037	0.210	12.82
IRNeXt [18]	29.22	0.879	0.024	0.167	23.53	0.752	0.049	0.244	26.30	0.814	0.037	0.206	14.75
OKNet [19]	28.99	0.877	0.024	0.169	23.51	0.751	0.049	0.241	26.18	0.812	0.037	0.206	14.02
FSNet [50]	29.14	0.878	0.024	0.166	23.45	0.747	0.050	0.246	26.22	0.811	0.037	0.207	13.28
DSANet [51]	29.27	0.881	0.024	0.158	23.50	0.749	0.049	0.231	26.31	0.813	0.036	0.195	13.16
FreANet	29.32	0.881	0.023	0.131	23.55	0.757	0.049	0.195	26.36	0.817	0.036	0.164	12.74

The best and second-best scores are highlighted in bold and underlined, respectively. ↑ indicates that a higher score is better, whereas ↓ indicates that a lower score is better.

presents the quantitative results of single-image defocus deblurring on the DPDD. As can be seen in Table 2, our model improves performance on all metrics except SSIM. Compared to IRNeXt [18], the proposed FreANet, with 13.63% fewer parameters, achieves gains of 0.1 dB PNSR and 0.02 SSIM in the indoor scenes. FreANet outperforms the frequency-based SFNet [10] in the outdoor scenes, achieving improved scores of 0.1 dB in PSNR and 0.01 in SSIM. Figure 2 demonstrates that our model restores visibility-degraded parts more effectively than previous algorithms.

4.2. Motion Deblurring Results

We evaluated deblurring models on the GoPro [39] and HIDE [40] datasets and report the quantitative results in

Table 3. Motion deblurring comparisons on the GoPro [39] and HIDE [40] test sets.

Methods	GoPro [39]		HIDE [40]		#Params
	PSNR↑	SSIM↑	PSNR↑	SSIM↑	(M)
MPRNet [3]	32.66	0.959	30.96	0.939	20.1
HINet [5]	32.71	0.959	30.32	0.932	20.1
Restormer [7]	32.92	0.961	31.22	0.942	26.13
Uformer-B [53]	33.06	0.967	30.90	0.953	50.88
Stripformer [52]	33.08	0.962	31.03	0.940	20
IRNeXt [18]	33.16	0.962	-	-	14.75
FreANet	33.21	0.962	31.11	0.937	12.74

The best and second-best scores are highlighted in bold and underlined, respectively. ↑ indicates that a higher score is better.

. Our method achieves a PSNR of 33.21 dB on the GoPro, using fewer parameters compared to the transformer-based Stripformer [52]. FreANet also demonstrates remarkable generalization performance on HIDE. We visualize the deblurred results in Figure 3, where it can be seen that our FreANet restores images more sharply and distinctly than its competitors.

4.3. Dehazing Results

We conducted dehazing experiments on synthetic datasets (RESIDE/SOTS [41]) and real-world datasets (Dense-Haze [42] and NH-HAZE [43]).

Table 4. Image dehazing comparisons on the synthetic and real dehazing test sets.

Methods	SOTS-Indoor [41]		SOTS-Outdoor [41]		Dense-Haze [42]		NH-HAZE [43]		Overheads
	PSNR↑	SSIM↑	PSNR↑	SSIM↑	PSNR↑	SSIM↑	PSNR↑	SSIM↑	#Params (M)	FLOPs (G)
GridDehazeNet [54]	32.16	0.984	30.86	0.982	-	-	13.80	0.54	0.956	21.49
FFA-Net [6]	36.39	0.989	33.57	0.984	14.39	0.45	19.87	0.69	4.45	287.8
AECR-Net [20]	37.17	0.990	-	-	15.80	0.47	19.88	0.72	2.61	52.20
MAXIM [23]	38.11	0.991	34.19	0.985	-	-	-	-	14.1	-
Fourmer [14]	37.32	0.990	-	-	15.95	0.49	19.91	0.72	1.29	20.6
OKNet-S [19]	37.59	0.994	35.45	0.992	16.85	0.62	20.29	0.80	2.40	17.88
OKNet [19]	40.79	0.996	37.68	0.995	16.92	0.64	20.48	0.80	4.72	39.71
FreANet-S	39.54	0.995	36.46	0.993	17.39	0.65	20.11	0.81	1.79	19.77
FreANet	41.62	0.997	38.39	0.995	17.53	0.67	20.52	0.82	5.37	40.29

The best and second-best scores are highlighted in bold and underlined, respectively. ↑ indicates that a higher score is better.

presents the quantitative results in comparison with previous models. Compared to the most recently proposed OKNet [19], our model obtains significant gains of 0.83 dB and 0.71 dB in PSNR on the SOTS-Indoor and SOTS-Outdoor datasets. For Dense-Haze, FreANet reports PSNR gains of 0.61 dB and 1.58 dB over OKNet [19] and the frequency-based Fourmer [14], respectively. Furthermore, the qualitative results for both indoor and outdoor scenarios are presented in Figure 4. Our model generates images with sharper and more detailed object preservation, even in complex environments, outperforming previous works.

In line with previous work [19], we performed a nighttime dehazing experiment on the NHR [44] dataset, and the results can be found in

Table 5. Nighttime dehazing comparisons on the NHR [44] test set.

Method	OFSD	HCD	FocalNet	FSNet	OKNet	FreANet
	[44]	[55]	[11]	[50]	[19]	(Ours)
PSNR↑	21.32	23.43	25.35	26.30	27.92	28.76
SSIM↑	0.804	0.953	0.969	0.976	0.979	0.978

The best and second-best scores are highlighted in bold and underlined, respectively. ↑ indicates that a higher score is better.

. FreANet achieves a PSNR gain of 0.84 dB over the recently proposed OKNet [19].

4.4. Low-Light Enhancement Results

We evaluated our network on the LOLv1 [45] and LOLv2 [46] datasets. The LOLv2 dataset is divided into synthetic (LOLv2-syn) and real (LOLv2-real) datasets. According to Retinex theory, our model is equipped with an illumination estimator [56] at the forefront. The quantitative and qualitative comparison results with previous enhancement models are shown in

Table 6. Low-light image enhancement comparisons on the LOLv1 [45] and LOLv2 [46] test sets.

Method	LOLv1 [45]		LOLv2-Real [46]		LOLv2-Syn [46]		#Params
	PSNR↑	SSIM↑	PSNR↑	SSIM↑	PSNR↑	SSIM↑	(M)
DRBN [57]	20.13	0.830	20.29	0.831	23.22	0.927	5.27
Restormer [7]	22.43	0.823	19.94	0.827	21.41	0.830	26.13
MIRNet [21]	24.14	0.830	20.02	0.820	21.94	0.876	31.76
UHDFour [29]	23.09	0.870	21.78	0.870	-	-	28.52
SNR-Net [58]	24.61	0.842	21.48	0.849	24.14	0.928	4.01
FreANet	23.60	0.836	21.78	0.860	25.91	0.939	2.45

The best and second-best scores are highlighted in bold and underlined, respectively. ↑ indicates that a higher score is better.

and Figure 5, respectively. Although our method shows slightly reduced performance on LOLv1 compared to previous approaches, it demonstrates outstanding performance on both the synthetic and real datasets of LOL-v2, even with significantly fewer parameters (2.45 million). As shown in Figure 5, our method restores low-light images with color and texture similar to the target images.

5. Ablation Study

We performed ablation studies to explore the effectiveness of the proposed modules. For the ablation studies, we used variant models derived from a small version of our FreANet. All these variant models were evaluated on the SOTS-Indoor dataset.

Table 7. Ablation study on SOTS-Indoor.

Variant	MPA	RDB	MDFE		SOTS-Indoor
			Spatial	Frequency	PSNR↑	SSIM↑	#Params
(a)	✔				30.75	0.976	0.81 M
(b)		✔			36.29	0.991	1.40 M
(c)	✔	✔			37.06	0.993	1.59 M
(d)			✔		33.36	0.984	0.66 M
(e)				✔	25.06	0.941	0.66 M
(f)			✔	✔	35.83	0.991	0.81 M
(g)	✔		✔	✔	36.65	0.992	1.01 M
(h)		✔	✔	✔	39.18	0.994	1.59 M
(i)	✔	✔	✔	✔	39.54	0.995	1.78 M

The best score is highlighted in bold. ↑ indicates that a higher score is better. ✔ indicates that the corresponding component is included in the variant.

presents the quantitative results for the variant models. First, the initial model (a) results in a PSNR of 30.75 dB. The model (b) utilizing only the RDB module achieves a PSNR of 36.29 dB, while the variant model (c) with MPA yields a PSNR gain of 0.77 dB, with a slight increase of 0.19 M parameters. We investigated the components of the MDFE module, including the spatial and frequency branches. The model (d) equipped only with the spatial branch achieves a 33.36 dB PSNR. In the case of the frequency branch, model (e) causes a performance degradation due to insufficient spatial texture information. However, when combined with the spatial branch, model (f) leads to a significant gain of 2.47 dB over model (d). Finally, the progressive addition of MPA and RDB modules produces improved results. Our full model (i) outperforms other variant models, achieving an 8.79 dB boost over the initial model (a).

Visual results of each component. To analyze the impact of individual components, we provide the visual results of the MDFE and MPA in Figure 6 and Figure 7, respectively. As shown in Figure 6, the frequency branch of the MDFE captures high-frequency information, such as edges, while the spatial branch emphasizes less degraded regions, such as boxes, humans, and vines. By selectively aggregating the output features, the MDFE enhances edge signals and texture information from the initial features. Figure 7 demonstrates that MPA highlights regions with extreme low-light conditions or severe blur that require more focus for restoration.

6. Conclusions

In this paper, we propose FreANet, which selectively extracts features from multiple domains and captures long-range spatial dependencies for image restoration. Specifically, we introduce a multi-domain feature extractor (MDFE) composed of spatial and frequency branches. Each branch employs strip convolutions with large kernels in parallel. Furthermore, we propose a multi-scale pooling attention (MPA) mechanism that learns interactions among elements in the spatial embedding space, utilizing global average pooling for efficiency. Finally, our FreANet demonstrates outstanding performance on 11 benchmark datasets for various restoration tasks, including defocus deblurring, motion deblurring, dehazing, and low-light enhancement.