Experiment and Analytical Model for Pore Structure of Early-Age Composite Cement Pastes by LF-NMR
Abstract
1. Introduction
2. Experimental Materials and Methodology
2.1. Experimental Materials
2.2. Experiment Method
3. Results and Discussion
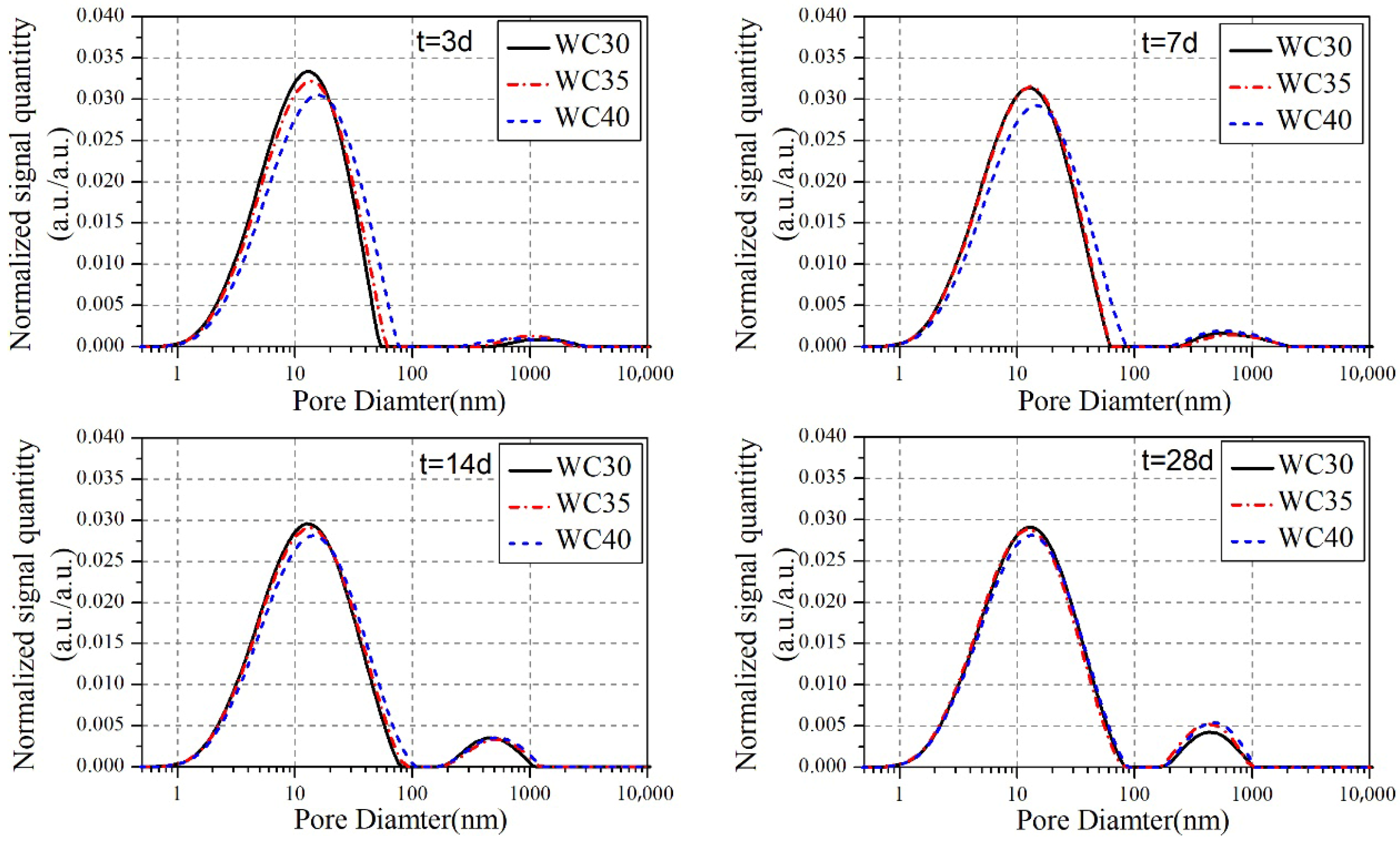
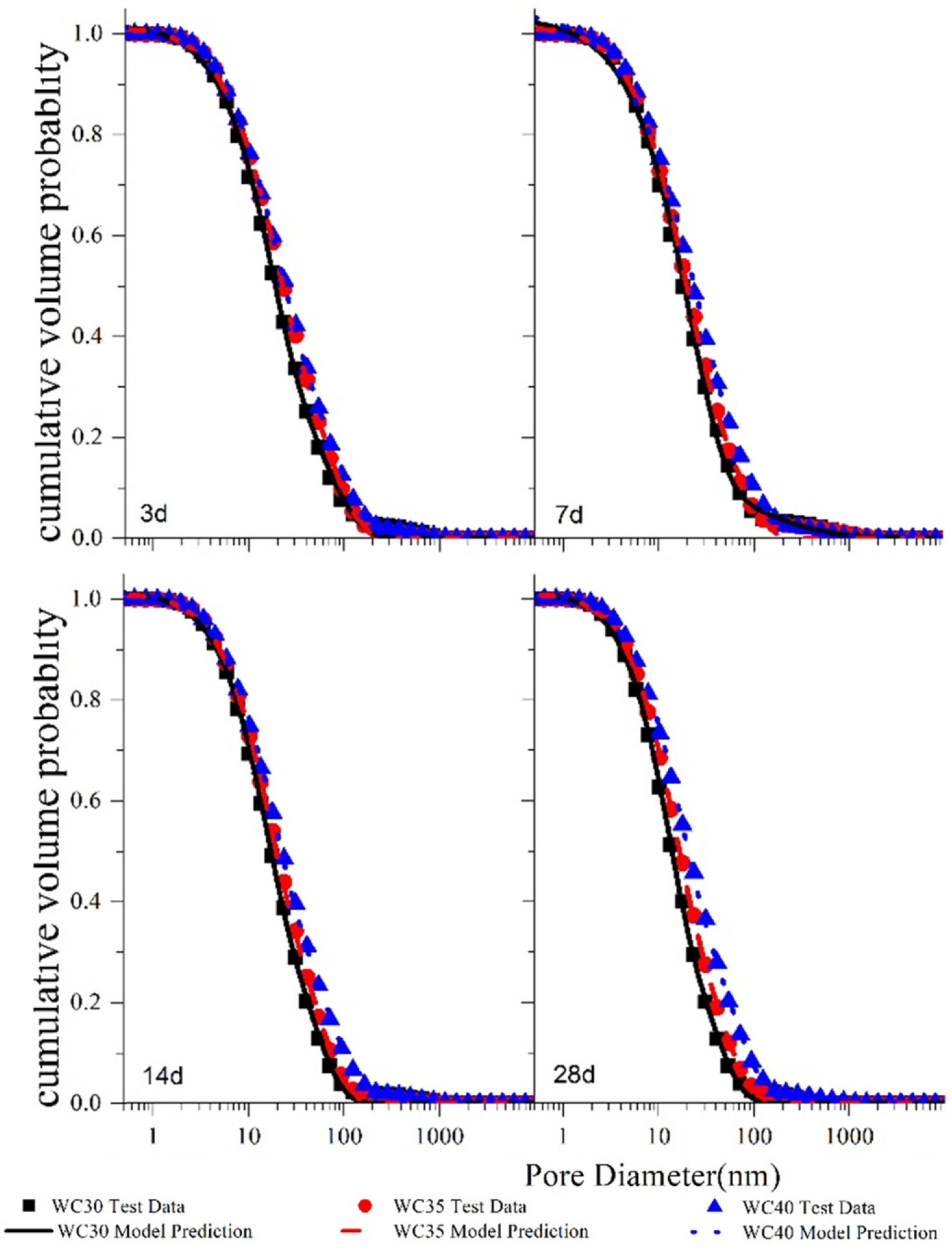
3.1. Pore Characteristics of Neat Cement Pastes
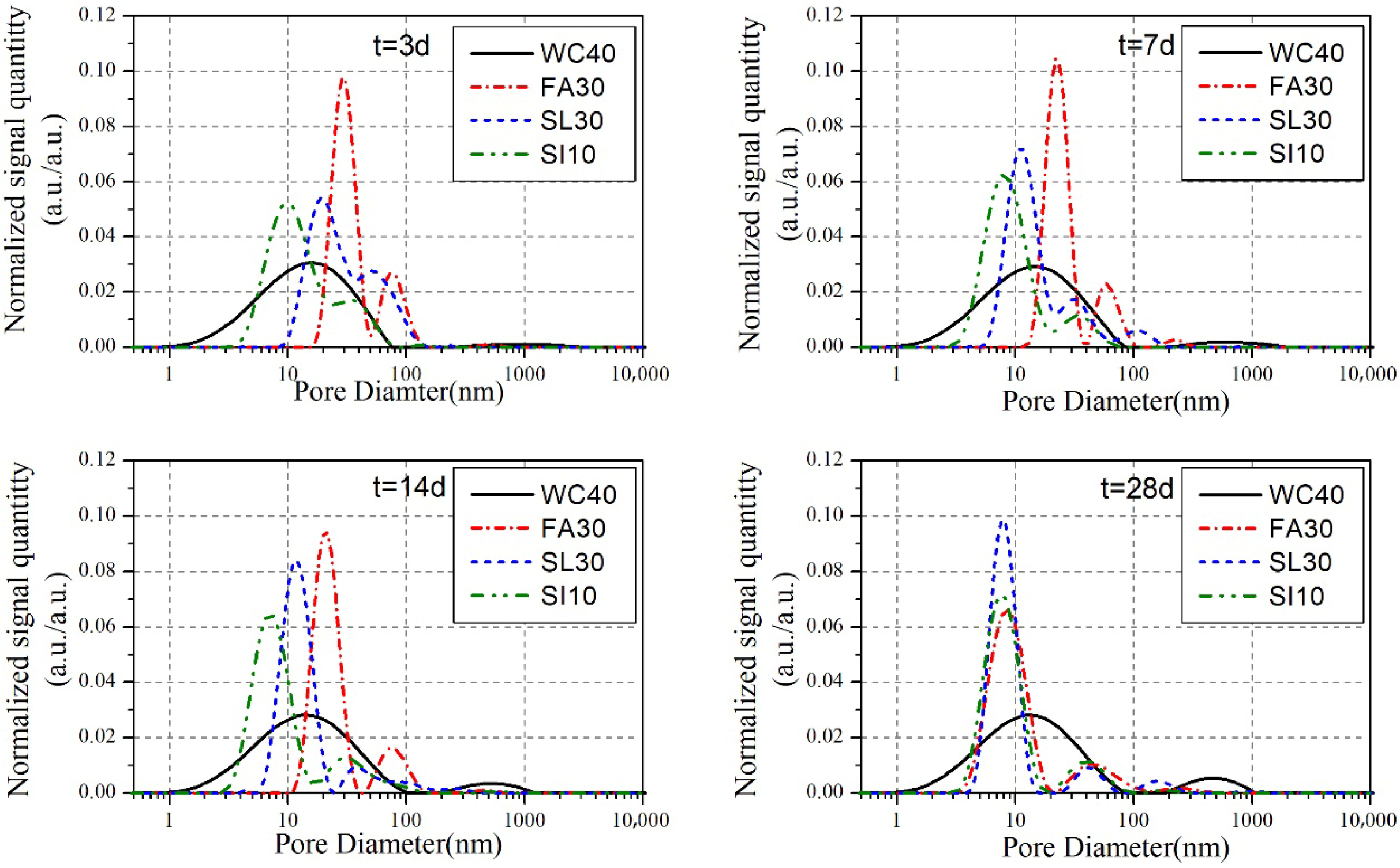
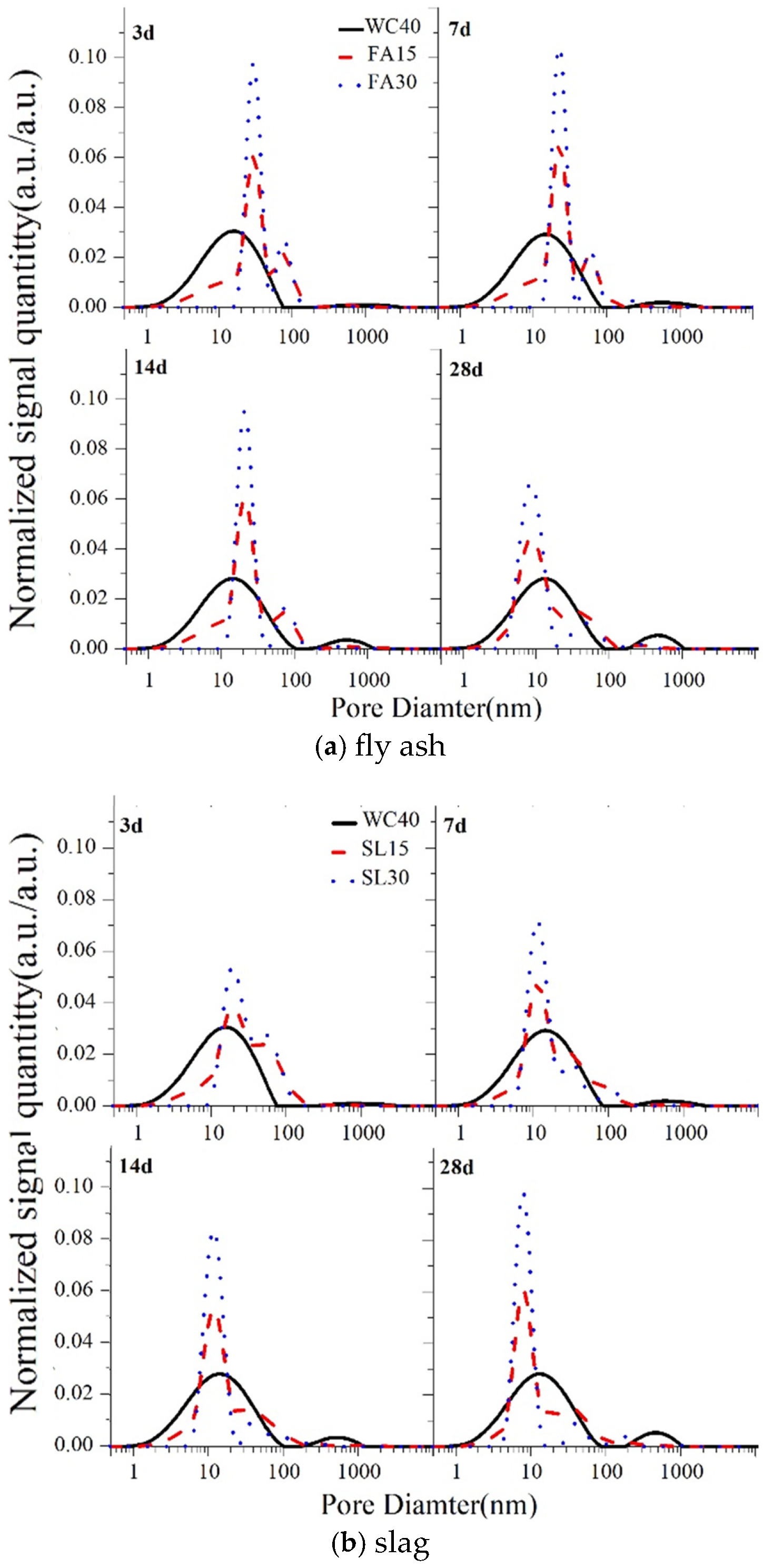
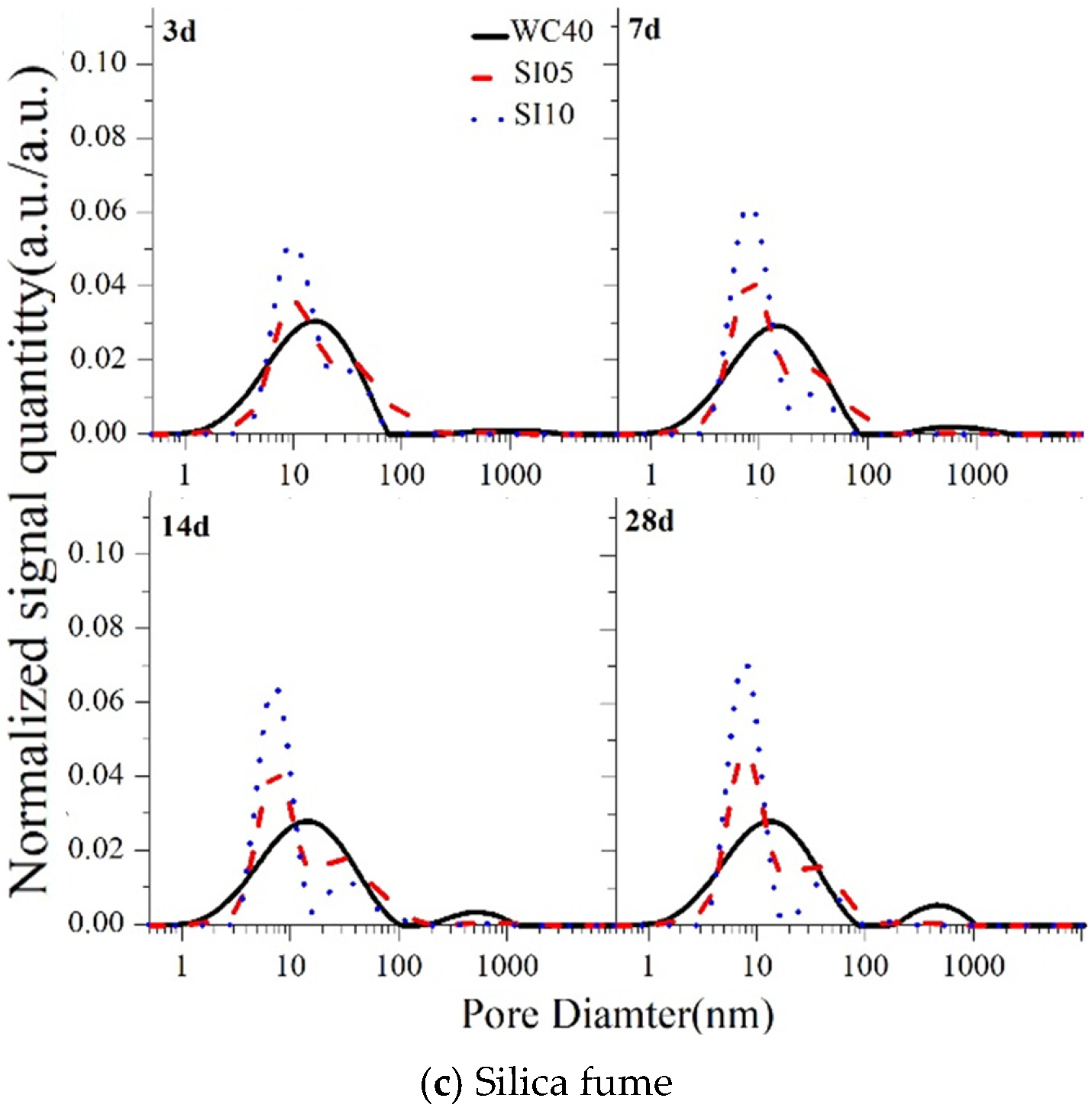
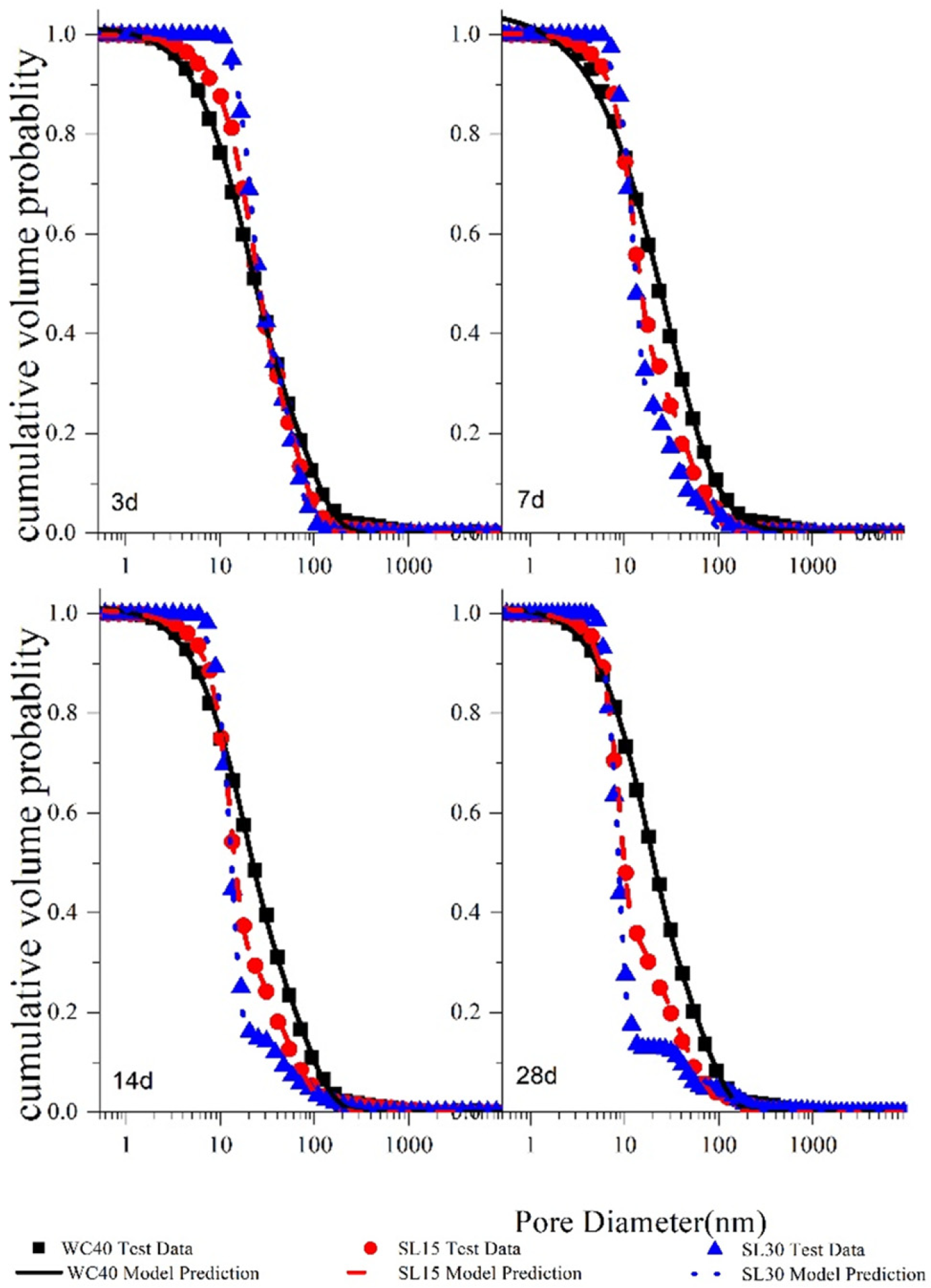
3.2. Pores of Composite Cement Pastes
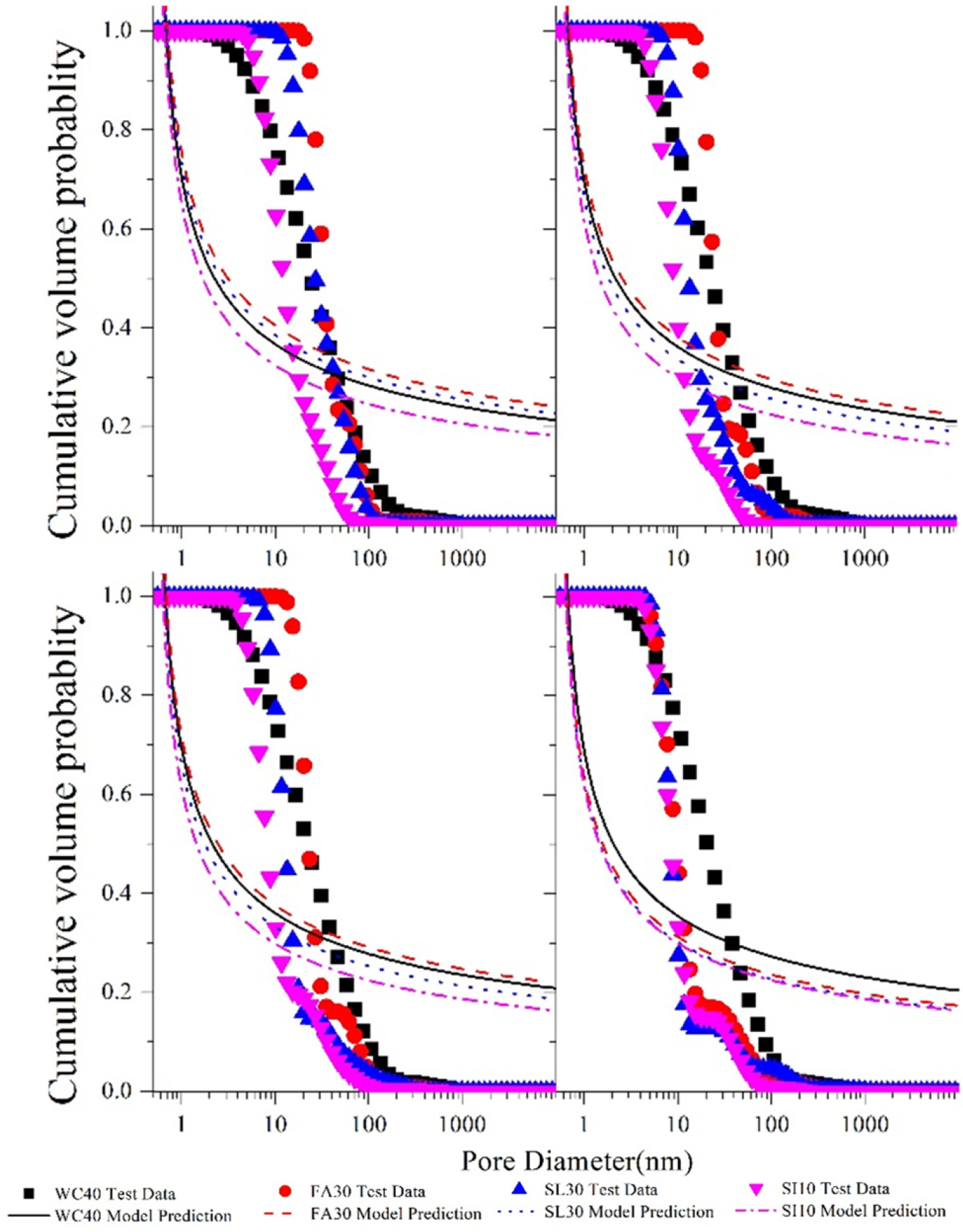
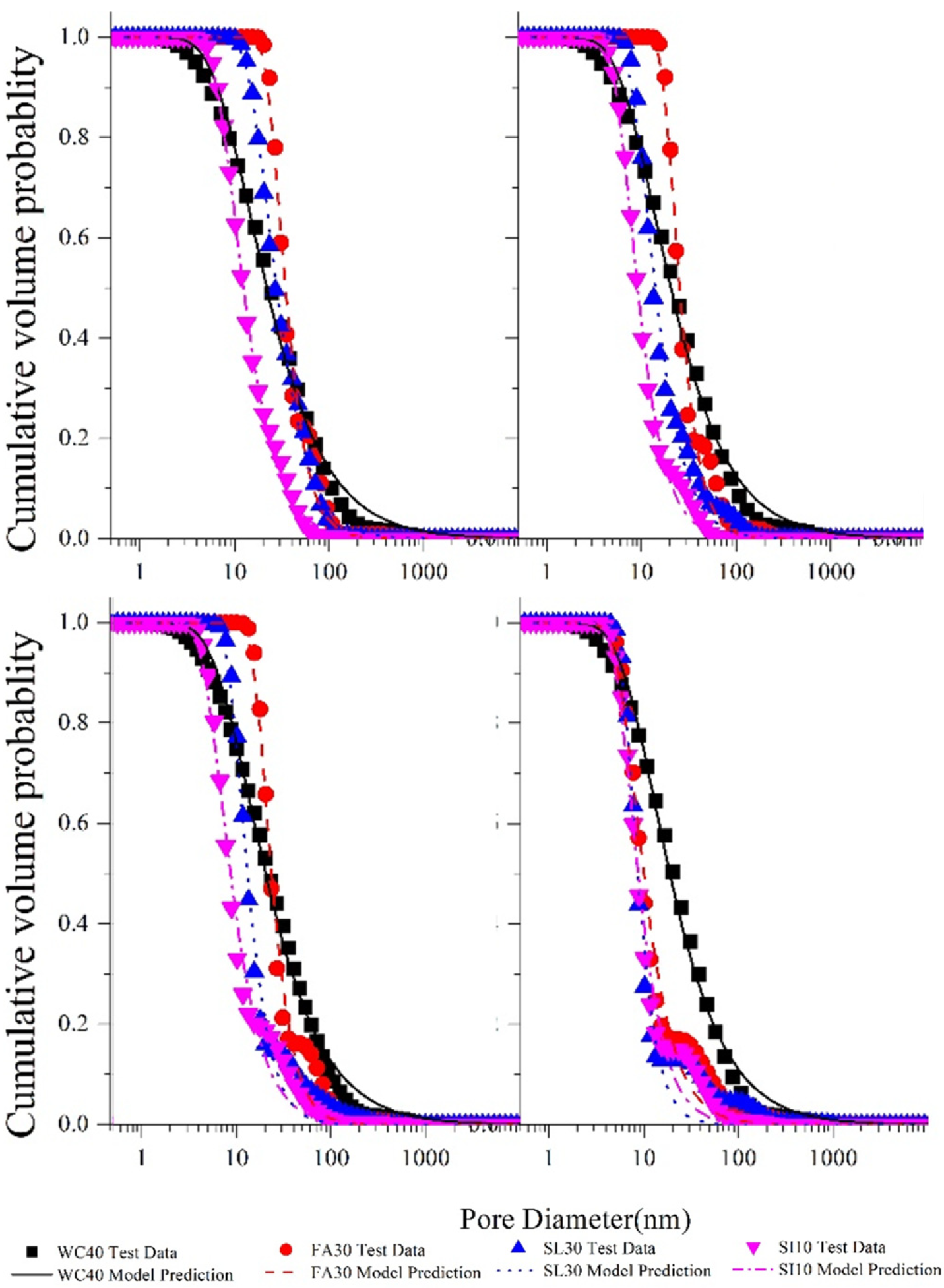
3.3. Analytical Pore Structure Model
3.3.1. Van Breugel (V.B.) Pore Structure Model
3.3.2. Shi and Brown (S. and B.) Pore Structure Model
3.3.3. Shimomura and Maekawa (S. and M.)’s Pore Structure Model
3.3.4. Optimized Pore Structure Model
4. Conclusions
- (1)
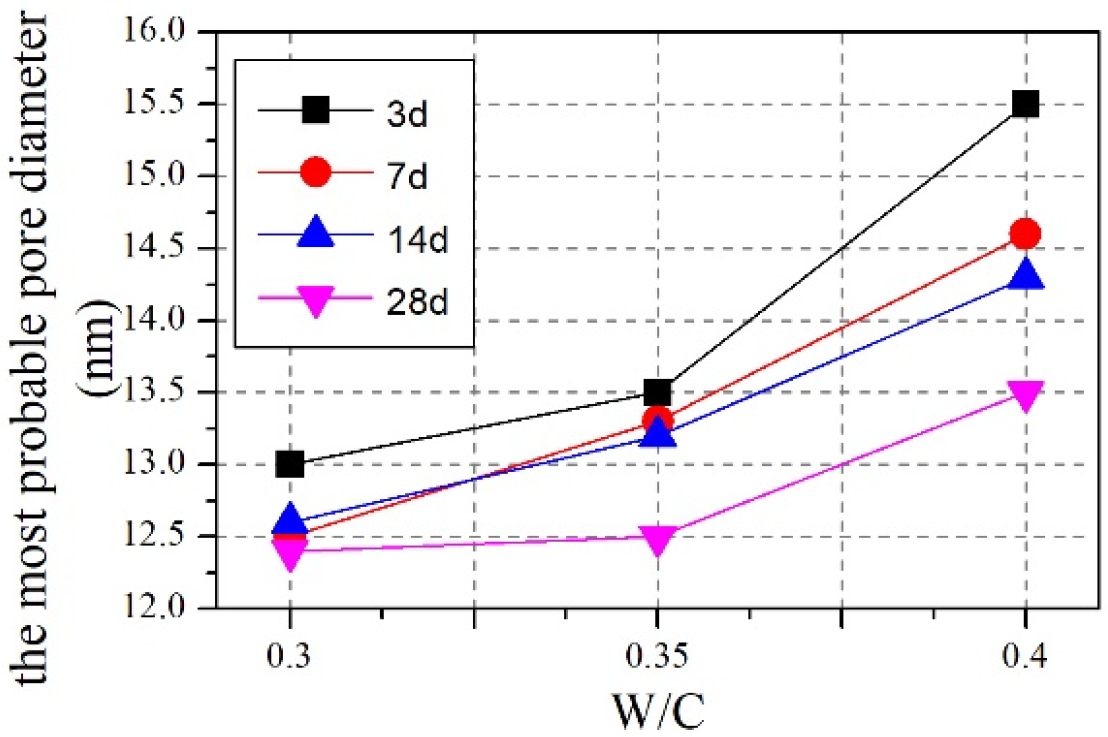
- For all the cement pastes examined in the study, the most likely pore diameter reduces progressively with increasing curing age. Fly ash-blended cement pastes show a larger likely pore diameter than neat pastes up to 14 days, but it becomes smaller by 28 days. The pore size of slag-blended pastes increases initially and then decreases at 3 days. Moreover, the pore diameter of silica fume paste remains consistently smaller than that of neat paste from 3 to 28 days.
- (2)
- The test results indicate that when the contents of fly ash, slag, and silica fume are below 30%, 30%, and 10%, respectively, the mineral admixture content has minimal impact on the most probable pore diameter. But as the admixture content increases, the proportion of gel pores increases.
- (3)
- A bimodal model, which combines the Shimomura and Maekawa model with the Weibull distribution function, was developed to account for the PSD of both the left and right peaks in cement paste with and without the addition of fly ash, slag, and silica fume. The outcomes of this model align well with the experimental data.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dao, V.T.N.; Morris, P.H.; Dux, P.F. Crack propagation in concrete at very early ages. Mag. Concr. Res. 2014, 66, 643–651. [Google Scholar] [CrossRef]
- Douglas Hooton, R. Future directions for design, specification, testing, and construction of durable concrete structures. Cem. Concr. Res. 2019, 124, 105827. [Google Scholar] [CrossRef]
- Orozco, C.; Babel, S.; Tangtermsirikul, S.; Sugiyama, T. Comparison of environmental impacts of fly ash and slag as cement replacement materials for mass concrete and the impact of transportation. Sustain. Mater. Technol. 2024, 39, e00796. [Google Scholar] [CrossRef]
- Meyer, C. The greening of the concrete industry. Cem. Concr. Compos. 2009, 31, 601–605. [Google Scholar] [CrossRef]
- Li, M.; Han, Z.; Cheng, H.; Yang, R.; Yuan, J.; Jin, T. Low-temperature performance improvement strategies for high RAP content recycled asphalt mixtures: Focus on RAP gradation variability and mixing process. Fuel 2025, 387, 134362. [Google Scholar] [CrossRef]
- Tayeh, B.A.; Hamada, H.M.; Almeshal, I.; Bakar, B.H.A. Durability and mechanical properties of cement concrete comprising pozzolanic materials with alkali-activated binder: A comprehensive review. Case Stud. Constr. Mater. 2022, 17, e01429. [Google Scholar] [CrossRef]
- Altwair, N.M.; Kabir, S. Green concrete structures by replacing cement with pozzolanic materials to reduce greenhouse gas emissions for sustainable environment. In Proceedings of the 6th International Engineering and Construction Conference, Cairo, Egypt, 28–30 June 2010; pp. 1126–1130. [Google Scholar]
- Nochaiya, T.; Wongkeo, W.; Chaipanich, A.J.F. Utilization of fly ash with silica fume and properties of Portland cement–fly ash–silica fume concrete. Fuel 2010, 89, 768–774. [Google Scholar] [CrossRef]
- Guo, Z.; Jiang, T.; Zhang, J.; Kong, X.; Chen, C.; Lehman, D.E. Mechanical and durability properties of sustainable self-compacting concrete with recycled concrete aggregate and fly ash, slag and silica fume. Constr. Build. Mater. 2020, 231, 117115. [Google Scholar] [CrossRef]
- Nazeer, M.; Kapoor, K.; Singh, S. Strength, durability and microstructural investigations on pervious concrete made with fly ash and silica fume as supplementary cementitious materials. J. Build. Eng. 2023, 69, 106275. [Google Scholar] [CrossRef]
- Ramzi, S.; Hajiloo, H. The effects of supplementary cementitious materials (SCMs) on the residual mechanical properties of concrete after exposure to high temperatures. Buildings 2023, 13, 103. [Google Scholar] [CrossRef]
- Mark, O.; Ede, A.; Olofinnade, O.; Bamigboye, G.; Okeke, C.; Oyebisi, S.; Arum, C. Influence of some selected supplementary cementitious materials on workability and compressive strength of concrete—A review. IOP Conf. Ser. Mater. Sci. Eng. 2019, 640, 012071. [Google Scholar] [CrossRef]
- Makul, N. Modern sustainable cement and concrete composites: Review of current status, challenges and guidelines. Sustain. Mater. Technol. 2020, 25, e00155. [Google Scholar] [CrossRef]
- Duan, P.; Shui, Z.; Chen, W.; Shen, C. Effects of metakaolin, silica fume and slag on pore structure, interfacial transition zone and compressive strength of concrete. Constr. Build. Mater. 2013, 44, 1–6. [Google Scholar] [CrossRef]
- Hooton, R.D. Permeability and pore structure of cement pastes containing fly ash, slag, and silica fume. In Blended Cements; ASTM International: West Conshohocken, PA, USA, 1986. [Google Scholar]
- Li, Y.; Bao, J.; Guo, Y. The relationship between autogenous shrinkage and pore structure of cement paste with mineral admixtures. Constr. Build. Mater. 2010, 24, 1855–1860. [Google Scholar] [CrossRef]
- Chindaprasirt, P.; Jaturapitakkul, C.; Sinsiri, T. Effect of fly ash fineness on microstructure of blended cement paste. Constr. Build. Mater. 2007, 21, 1534–1541. [Google Scholar] [CrossRef]
- Zhou, J.; Ye, G.; Van Breugel, K. Hydration process and pore structure of Portland cement paste blended with blast furnace slag. In Proceedings of the 6th International Symposium on Cement & Concrete, Canmet, Xi’an, China, 19–22 September 2006; pp. 1–7. [Google Scholar]
- Song, W.; Zhu, Z.; Peng, Y.; Wan, Y.; Xu, X.; Pu, S.; Song, S.; Wei, Y. Effect of steel slag on fresh, hardened and microstructural properties of high-calcium fly ash based geopolymers at standard curing condition. Constr. Build. Mater. 2019, 229, 116933. [Google Scholar] [CrossRef]
- Yajuun, J.; Cahyadi, J. Investigation on microstructure of silica fume cement pastes. WIT Trans. Built Environ. 2002, 59, 9. [Google Scholar]
- Thommes, M.; Cychosz, K.A. Physical adsorption characterization of nanoporous materials: Progress and challenges. Adsorption 2014, 20, 233–250. [Google Scholar] [CrossRef]
- Bae, Y.-S.; Yazaydın, A.O.; Snurr, R.Q. Evaluation of the BET method for determining surface areas of MOFs and zeolites that contain ultra-micropores. Langmuir 2010, 26, 5475–5483. [Google Scholar] [CrossRef] [PubMed]
- De Belie, N.; Kratky, J.; Van Vlierberghe, S. Influence of pozzolans and slag on the microstructure of partially carbonated cement paste by means of water vapour and nitrogen sorption experiments and BET calculations. Cem. Concr. Res. 2010, 40, 1723–1733. [Google Scholar] [CrossRef]
- Juenger, M.C.G.; Jennings, H.M. The use of nitrogen adsorption to assess the microstructure of cement paste. Cem. Concr. Res. 2001, 31, 883–892. [Google Scholar] [CrossRef]
- Ng, C.; Alengaram, U.J.; Wong, L.S.; Mo, K.H.; Jumaat, M.Z.; Ramesh, S. A review on microstructural study and compressive strength of geopolymer mortar, paste and concrete. Constr. Build. Mater. 2018, 186, 550–576. [Google Scholar] [CrossRef]
- Fleury, M.; Gimmi, T.; Mazurek, M. Porewater content, pore structure and water mobility in clays and shales from NMR methods. Clays Clay Miner. 2022, 70, 417–437. [Google Scholar] [CrossRef]
- Watson, A.T.; Chang, C.P. Characterizing porous media with NMR methods. Prog. Nucl. Magn. Reson. Spectrosc. 1997, 31, 343–386. [Google Scholar] [CrossRef]
- Nagel, S.M.; Strangfeld, C.; Kruschwitz, S. Application of 1H proton NMR relaxometry to building materials—A review. J. Magn. Reson. Open 2021, 6, 100012. [Google Scholar] [CrossRef]
- Halperin, W.P.; Jehng, J.-Y.; Song, Y.-Q. Application of spin-spin relaxation to measurement of surface area and pore size distributions in a hydrating cement paste. Magn. Reson. Imaging 1994, 12, 169–173. [Google Scholar] [CrossRef]
- Jehng, J.-Y.; Sprague, D.; Halperin, W. Pore structure of hydrating cement paste by magnetic resonance relaxation analysis and freezing. Magn. Reson. Imaging 1996, 14, 785–791. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Qin, X.; Liu, J.; Zhou, L.; Tian, Q.; Wang, P. Pore structure characterization of early-age cement pastes blended with high-volume fly ash. Constr. Build. Mater. 2018, 189, 934–946. [Google Scholar] [CrossRef]
- Faure, P.F.; Caré, S.; Magat, J.; Chaussadent, T. Drying effect on cement paste porosity at early age observed by NMR methods. Constr. Build. Mater. 2012, 29, 496–503. [Google Scholar] [CrossRef]
- She, A.-m.; Yao, W.; Yuan, W.-c. Evolution of distribution and content of water in cement paste by low field nuclear magnetic resonance. J. Cent. South Univ. 2013, 20, 1109–1114. [Google Scholar] [CrossRef]
- Pandey, S.; Sharma, R. The influence of mineral additives on the strength and porosity of OPC mortar. Cem. Concr. Res. 2000, 30, 19–23. [Google Scholar] [CrossRef]
- Ouellet, S.; Bussière, B.; Aubertin, M.; Benzaazoua, M. Microstructural evolution of cemented paste backfill: Mercury intrusion porosimetry test results. Cem. Concr. Res. 2007, 37, 1654–1665. [Google Scholar] [CrossRef]
- Wan, Z.; He, T.; Chang, N.; Yang, R.; Qiu, H. Effect of silica fume on shrinkage of cement-based materials mixed with alkali accelerator and alkali-free accelerator. J. Mater. Res. Technol. 2023, 22, 825–837. [Google Scholar] [CrossRef]
- Dai, J.; Wang, Q.; Xie, C.; Xie, Z.; Tian, X.; Lou, X.; Guo, H. Effect of Curing Temperature on Activity Index of Silica Fume. IOP Conf. Ser. Mater. Sci. Eng. 2018, 381, 012096. [Google Scholar] [CrossRef]
- Choi, Y.C.; Kim, J.; Choi, S. Mercury intrusion porosimetry characterization of micropore structures of high-strength cement pastes incorporating high volume ground granulated blast-furnace slag. Constr. Build. Mater. 2017, 137, 96–103. [Google Scholar] [CrossRef]
- Mehta, P.K. Pozzolanic and cementitious byproducts as mineral admixtures for concrete-a critical review. Spec. Publ. 1983, 79, 1–46. [Google Scholar]
- Van Breugel, K. Numerical simulation of hydration and microstructural development in hardening cement-based materials (I) theory. Cem. Concr. Res. 1995, 25, 319–331. [Google Scholar] [CrossRef]
- Shi, D.; Brown, P.W.; Ma, W. Lognormal simulation of pore size distributions in cementitious materials. J. Am. Ceram. Soc. 1991, 74, 1861–1867. [Google Scholar] [CrossRef]
- Shimomura, T.; Maekawa, K. Analysis of the drying shrinkage behaviour of concrete using a micromechanical model based on the micropore structure of concrete. Mag. Concr. Res. 1997, 49, 303–322. [Google Scholar] [CrossRef]







| Sample | CaO | SiO2 | Al2O3 | Fe2O3 | MgO | K2O | Na2O | TiO2 | SO3 |
|---|---|---|---|---|---|---|---|---|---|
| Cement | 64.7 | 19.6 | 4.5 | 3.1 | 0.8 | 0.6 | 0.07 | — | — |
| Fly ash | 2.13 | 54.0 | 35.1 | 3.90 | 0.512 | 1.26 | 0.47 | 1.29 | 0.45 |
| Slag | 39.9 | 30.8 | 14.6 | 0.61 | 8.65 | 0.576 | 0.40 | 1.22 | 2.19 |
| Silica fume | 1.40 | 91.4 | 0.61 | 0.88 | 2.37 | 1.68 | 0.43 | — | 0.48 |
| Sample | Mixture Parameters | Quantity of Experimental Substances (kg/m3) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| w/b | Slag Content % | Fly Ash Content % | Silica Fume Content % | Cement | Slag | Fly Ash | Silica Fume | Water | |
| WC30 | 0.30 | 0 | 0 | 0 | 1628 | 0 | 0 | 0 | 488 |
| WC35 | 0.35 | 0 | 0 | 0 | 1505 | 0 | 0 | 0 | 527 |
| WC40 | 0.40 | 0 | 0 | 0 | 1399 | 0 | 0 | 0 | 560 |
| FA15 | 0.40 | 0 | 15 | 0 | 1154 | 0 | 204 | 0 | 543 |
| FA30 | 0.40 | 0 | 30 | 0 | 922 | 0 | 395 | 0 | 527 |
| SL15 | 0.40 | 15 | 0 | 0 | 1187 | 209 | 0 | 0 | 558 |
| SL30 | 0.40 | 30 | 0 | 0 | 974 | 417 | 0 | 0 | 557 |
| SI5 | 0.40 | 0 | 0 | 5 | 1316 | 0 | 0 | 69 | 554 |
| SI10 | 0.40 | 0 | 0 | 10 | 1236 | 0 | 0 | 137 | 549 |
| Sequence | TD | SW | RFD | RG1 | DRG1 | PRG | TW | NS | NECH | TE | DL1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| FID | 1024 | 200 | 0.005 | 20 | 3 | 2 | 2000 | 4 | — | — | — |
| CPMG | AUTO | 333.33 | 0.005 | 10 | 3 | 2 | 200 | 4 | 4000 | 0.36 | 500 |
| Sample | Age (Day) | a | n | Correlation | Standard Error |
|---|---|---|---|---|---|
| WC40 | 3 | 0.610 | −0.457 | 0.7011 | 0.2896 |
| 7 | 0.604 | −0.460 | 0.7022 | 0.2884 | |
| 14 | 0.603 | −0.461 | 0.7025 | 0.2880 | |
| 28 | 0.596 | −0.465 | 0.7029 | 0.2873 | |
| FA30 | 3 | 0.657 | −0.437 | 0.6474 | 0.3458 |
| 7 | 0.630 | −0.451 | 0.6556 | 0.3362 | |
| 14 | 0.625 | −0.454 | 0.6601 | 0.3315 | |
| 28 | 0.543 | −0.497 | 0.6997 | 0.2844 | |
| SL30 | 3 | 0.635 | −0.448 | 0.6630 | 0.3299 |
| 7 | 0.574 | −0.481 | 0.6840 | 0.3039 | |
| 14 | 0.570 | −0.483 | 0.6818 | 0.3046 | |
| 28 | 0.530 | −0.504 | 0.6950 | 0.2860 | |
| SI10 | 3 | 0.558 | −0.489 | 0.6906 | 0.2958 |
| 7 | 0.526 | −0.508 | 0.6960 | 0.2857 | |
| 14 | 0.526 | −0.507 | 0.7045 | 0.2780 | |
| 28 | 0.526 | −0.507 | 0.6993 | 0.2824 |
| Sample | Age (Day) | f1/f2/f3 | μ1/μ2/μ3 | σ1/σ2/σ3 | Correlation | Standard Error |
|---|---|---|---|---|---|---|
| WC40 | 3 | −0.5543 | 2.6370 | 0.0031 | 0.9911 | 0.0380 |
| −0.5712 | 1.7574 | −0.0036 | ||||
| 0.6476 | 2.1643 | −0.0064 | ||||
| 7 | 13.0555 | 2.1997 | 0.0599 | 0.9906 | 0.0388 | |
| −0.0281 | 2.5804 | 0.0002 | ||||
| 0.2507 | 1.4048 | 0.2099 | ||||
| 14 | 10.0689 | −0.5263 | 0.0349 | 0.9912 | 0.0550 | |
| −2.7385 | −0.6080 | −30.2094 | ||||
| 0.3575 | −0.5845 | −0.0220 | ||||
| 28 | 0.0034 | −1359.4000 | 1033.9580 | 0.9904 | 0.0569 | |
| 1.0084 | −0.1766 | 0.0668 | ||||
| 0.3245 | −1.4005 | −0.0008 | ||||
| FA30 | 3 | 0.0000 | 1.1660 | 0.0000 | 0.9688 | 0.1109 |
| −0.0071 | 3.6674 | 0.0001 | ||||
| 0.9987 | 2.9082 | −0.0111 | ||||
| 7 | 29.0848 | −2.3760 | 0.0458 | 0.9735 | 0.1033 | |
| 0.0000 | −6.2538 | 0.0000 | ||||
| −28.0848 | −2.6475 | 0.0356 | ||||
| 14 | −0.0005 | 1.5239 | 0.0000 | 0.9721 | 0.1019 | |
| −1.9832 | 2.6903 | 0.0123 | ||||
| 2.1446 | 0.0117 | |||||
| 28 | −0.0851 | 2.0938 | −0.0068 | 0.9838 | 0.0697 | |
| −19,535.3000 | −0.7879 | −476.5680 | ||||
| −0.0020 | −407.2220 | |||||
| SL30 | 3 | 0.1671 | −0.1879 | 0.2365 | 0.9702 | 0.1078 |
| 0.8492 | 0.3482 | 0.0667 | ||||
| −1.2336 | −0.0013 | |||||
| 7 | −0.0031 | 0.7645 | 0.0000 | 0.9816 | 0.0781 | |
| 16.1096 | 1.3550 | 0.0304 | ||||
| 1.5903 | −0.0387 | |||||
| 14 | 198.9263 | 1.0956 | −0.3676 | 0.9770 | 0.0871 | |
| −0.0097 | 1.4498 | 0.0000 | ||||
| 0.7179 | −0.7680 | |||||
| 28 | −3.4846 | −0.3328 | 0.0157 | 0.9757 | 0.0848 | |
| 4.6319 | 0.0798 | 0.0121 | ||||
| 0.5546 | −0.0009 | |||||
| SI10 | 3 | −1.1553 | 1.3688 | 0.0044 | 0.9854 | 0.0684 |
| −35.8882 | 0.6204 | 0.1371 | ||||
| 0.9876 | 0.0734 | |||||
| 7 | 8339.1130 | 0.0000 | 37.0011 | 0.9832 | 0.0712 | |
| 0.0000 | 1.0548 | 0.0000 | ||||
| −8338.1130 | −0.3464 | 46.1337 | ||||
| 14 | −43.9595 | 0.6257 | 0.2530 | 0.9863 | 0.0632 | |
| −3.5670 | −0.2094 | 0.0137 | ||||
| 0.1489 | 0.1135 | |||||
| 28 | −0.0222 | 0.8798 | −0.0003 | 0.9827 | 0.0716 | |
| −13.9269 | −0.5535 | 0.1810 | ||||
| 0.2463 | 0.0997 |
| Sample | Age (Days) | B | C | Correlation | Standard Error |
|---|---|---|---|---|---|
| WC40 | 3 | 15.1829 | −1.0000 | 0.9991 | 0.0183 |
| 7 | 15.5102 | −1.0.288 | 0.9992 | 0.0164 | |
| 14 | 15.1023 | −1.0219 | 0.9992 | 0.0174 | |
| 28 | 15.9384 | −1.0671 | 0.9992 | 0.0170 | |
| FA30 | 3 | 12,072.4900 | −2.7557 | 0.9992 | 0.0176 |
| 7 | 11,392.3500 | −2.9982 | 0.9991 | 0.0192 | |
| 14 | 4480.3220 | −2.7742 | 0.9987 | 0.0224 | |
| 28 | 58.7800 | −1.9292 | 0.9979 | 0.0258 | |
| SL30 | 3 | 360.1463 | −1.8819 | 0.9997 | 0.0111 |
| 7 | 157.6100 | −2.0545 | 0.9992 | 0.0170 | |
| 14 | 554.1292 | −2.5940 | 0.9986 | 0.0228 | |
| 28 | 465.3938 | −3.0201 | 0.9972 | 0.0312 | |
| SI10 | 3 | 75.5010 | −1.8445 | 0.9998 | 0.0078 |
| 7 | 93.0119 | −2.2156 | 0.9996 | 0.0104 | |
| 14 | 39.0152 | −1.8644 | 0.9984 | 0.0219 | |
| 28 | 82.8129 | −2.2082 | 0.9984 | 0.0227 |
| Sample | Age (Days) | A | B | C | E | F | G | Correlation | Standard Error |
|---|---|---|---|---|---|---|---|---|---|
| WC30 | 3 | 0.5000 | 11.5818 | −1.0038 | 0.0223 | 1.1113 | 0.4800 | 0.9999 | 0.0037 |
| 7 | 0.5000 | 10.6257 | −0.9793 | 0.0183 | 1.2354 | 0.4800 | 0.9999 | 0.0044 | |
| 14 | 0.5000 | 12.2808 | −1.1087 | 0.0146 | 1.2592 | 0.4800 | 1.0000 | 0.0028 | |
| 28 | 0.5000 | 12.6788 | −1.1834 | 0.0190 | 1.2997 | 0.4800 | 1.0000 | 0.0024 | |
| WC35 | 3 | 0.5000 | 12.6478 | −1.0661 | 0.0113 | 1.1750 | 0.4800 | 1.0000 | 0.0021 |
| 7 | 0.5000 | 11.5941 | −1.0139 | 0.0153 | 1.2078 | 0.4800 | 0.9999 | 0.0034 | |
| 14 | 0.5000 | 13.3211 | −1.1251 | 0.0115 | 1.2467 | 0.4800 | 1.0000 | 0.0024 | |
| 28 | 0.5000 | 13.7422 | −1.1738 | 0.0156 | 1.2434 | 0.4800 | 1.0000 | 0.0021 | |
| WC40 | 3 | 0.5000 | 12.7710 | −1.0342 | 0.0161 | 1.0628 | 0.4800 | 1.0000 | 0.0021 |
| 7 | 0.5000 | 13.1063 | −1.0333 | 0.0194 | 1.0604 | 0.4800 | 1.0000 | 0.0028 | |
| 14 | 0.5000 | 13.4378 | −1.0708 | 0.0182 | 1.0560 | 0.4800 | 1.0000 | 0.0023 | |
| 28 | 0.5000 | 13.8415 | −1.1048 | 0.0172 | 1.1075 | 0.4800 | 1.0000 | 0.0023 | |
| FA15 | 3 | 0.5000 | 23,166.8753 | −3.0342 | 0.0304 | 0.9228 | 0.4800 | 0.9994 | 0.0105 |
| 7 | 0.5000 | 95,288.6855 | −3.7947 | 0.0300 | 0.9623 | 0.4800 | 0.9995 | 0.0096 | |
| 14 | 0.5000 | 95,381.8748 | −3.9167 | 0.0318 | 0.9269 | 0.4800 | 0.9995 | 0.0101 | |
| 28 | 0.5000 | 74.1283 | −1.4514 | 0.0019 | 2.9628 | 0.4800 | 0.9998 | 0.0051 | |
| FA30 | 3 | 0.5000 | 2970.1461 | −2.1606 | 0.0000 | 6.9915 | 0.4800 | 0.9996 | 0.0090 |
| 7 | 0.5000 | 700.3776 | −1.9719 | 0.0000 | 7.6552 | 0.4800 | 0.9996 | 0.0085 | |
| 14 | 0.5000 | 226.7626 | −1.6824 | 0.0000 | 7.1336 | 0.4800 | 0.9994 | 0.0109 | |
| 28 | 0.5000 | 16.2297 | −1.1678 | 0.0000 | 4.7858 | 0.4800 | 0.9992 | 0.0110 | |
| SL15 | 3 | 0.5000 | 183.7057 | −1.7566 | 0.0176 | 1.0854 | 0.4800 | 0.9998 | 0.0053 |
| 7 | 0.5000 | 215.7488 | −1.6727 | 0.0009 | 2.9526 | 0.4800 | 0.9999 | 0.0042 | |
| 14 | 0.5000 | 73.8583 | −1.3951 | 0.0008 | 2.9376 | 0.4800 | 0.9998 | 0.0055 | |
| 28 | 0.5000 | 42.9995 | −1.3274 | 0.0004 | 3.7793 | 0.4800 | 0.9998 | 0.0051 | |
| SL30 | 3 | 0.5000 | 91,027.6255 | −3.9221 | 0.0004 | 1.9604 | 0.4800 | 1.0000 | 0.0029 |
| 7 | 0.5000 | 92.0333 | −1.5872 | 0.0000 | 4.9719 | 0.4800 | 0.9999 | 0.0050 | |
| 14 | 0.5000 | 44.0380 | −1.4554 | 0.0000 | 6.2969 | 0.4800 | 0.9993 | 0.0106 | |
| 28 | 0.5000 | 18.9131 | −1.3615 | 0.0000 | 8.0867 | 0.4800 | 0.9978 | 0.0187 | |
| SI05 | 3 | 0.5000 | 308.0020 | −1.7386 | 0.0021 | 2.6854 | 0.4800 | 1.0000 | 0.0025 |
| 7 | 0.5000 | 320.3482 | −2.8682 | 0.0193 | 1.1243 | 0.4800 | 0.9999 | 0.0047 | |
| 14 | 0.5000 | 115.0704 | −1.5352 | 0.0018 | 3.1708 | 0.4800 | 0.9998 | 0.0048 | |
| 28 | 0.5000 | 792.4858 | −3.4112 | 0.0217 | 1.1100 | 0.4800 | 0.9998 | 0.0055 | |
| SI10 | 3 | 0.5000 | 385.7514 | −2.0812 | 0.0002 | 3.8029 | 0.4800 | 0.9998 | 0.0062 |
| 7 | 0.5000 | 51.4245 | −1.7054 | 0.0005 | 3.6095 | 0.4800 | 0.9997 | 0.0064 | |
| 14 | 0.5000 | 20.2913 | −1.2952 | 0.0002 | 4.3730 | 0.4800 | 0.9995 | 0.0088 | |
| 28 | 0.5000 | 19.9810 | −1.3501 | 0.0000 | 4.9628 | 0.4800 | 0.9992 | 0.0112 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Yang, G.; Hong, B.; Liu, X. Experiment and Analytical Model for Pore Structure of Early-Age Composite Cement Pastes by LF-NMR. Appl. Sci. 2025, 15, 1650. https://doi.org/10.3390/app15031650
Wu J, Yang G, Hong B, Liu X. Experiment and Analytical Model for Pore Structure of Early-Age Composite Cement Pastes by LF-NMR. Applied Sciences. 2025; 15(3):1650. https://doi.org/10.3390/app15031650
Chicago/Turabian StyleWu, Jincheng, Guo Yang, Bin Hong, and Xiaolin Liu. 2025. "Experiment and Analytical Model for Pore Structure of Early-Age Composite Cement Pastes by LF-NMR" Applied Sciences 15, no. 3: 1650. https://doi.org/10.3390/app15031650
APA StyleWu, J., Yang, G., Hong, B., & Liu, X. (2025). Experiment and Analytical Model for Pore Structure of Early-Age Composite Cement Pastes by LF-NMR. Applied Sciences, 15(3), 1650. https://doi.org/10.3390/app15031650







