Abstract
A novel method is proposed for a combined high and low cycle fatigue (CCF) life prediction model based on Miner’s rule, incorporating load interactions and coupled damage effects to evaluate the fatigue life of wind turbine blades under CCF loading. The method refines the CCF damage curve by modeling the complex damage evolution process under L-H loading and establishes a life prediction model linking low cycle fatigue (LCF) and high cycle fatigue (HCF) damage curves for more accurate predictions. Compared to Miner’s rule, the M-H model, and the T-K model, the proposed approach demonstrates superior prediction accuracy, with results predominantly falling within a life factor of ±1.5. To verify the model’s practical applicability, finite element analysis (FEA) was performed on critical blade sections, reducing the prediction error to 4.3%. This method introduces a novel approach for evaluating the fatigue life of wind turbine blades with improved accuracy over existing methods.
1. Introduction
The fatigue life of wind turbine blades is a critical aspect of turbine performance and reliability research. With the advancement of wind turbine technology, fatigue load analysis, particularly under combined high and low cycle fatigue (CCF) conditions, has become a key factor in optimizing blade design and enhancing turbine stability [1,2,3]. In the fatigue analysis of wind turbine blades, CCF loading plays a crucial role. Compared to traditional low cycle fatigue (LCF) and high cycle fatigue (HCF), CCF loading involves more complex load interactions that significantly impact the fatigue life of the blades [4,5]. The fatigue analysis, vibration suppression, and condition monitoring of wind turbine blades under CCF loading conditions are key areas for improving turbine performance and extending service life [6,7,8,9]. However, most of the existing research on wind turbine blade damage mechanisms typically treats HCF and LCF damage theories separately, leading to significant discrepancies between the predicted and experimental fatigue life [10,11,12,13]. Therefore, developing a damage accumulation model that considers the impact of CCF failure on blade fatigue is essential for ensuring blade safety.
The fatigue damage accumulation hypothesis is currently the most widely adopted method for predicting CCF life [14,15,16,17]. To evaluate the fatigue life under CCF loading, several researchers have looked into different fatigue prediction models [18,19]. Most of these cumulative damage models, particularly the early ones, were developed under loading conditions limited to either pure HCF or LCF. The complexity of CCF loading often leads to highly discrete life forecast errors, making it difficult to achieve the desired accuracy. Moreover, neither pure HCF nor LCF adequately models blade fatigue strength damage mechanisms or accurately represents real operational conditions when compared to CCF damage. Miner’s rule [20], one of the most traditional approaches, has been widely applied due to its simplicity and practicality. However, it fails to account for the interaction between LCF and HCF loading, leading to non-conservative predictions. To address this limitation, Manson and Halford (M-H) [21] proposed the damage curve method to model interaction effects. Similarly, Trufyakov and Kovalchuk (T-K) [22] established a damage curve approach to improve CCF fatigue life predictions. These two models demonstrated better prediction accuracy compared to Miner’s rule. In recent years, Yue et al. [23,24] introduced a pioneering nonlinear damage accumulation model that incorporates current HCF damage and threshold damage factors for a specific material type, achieving improved prediction outcomes. Building on this, Han [25] developed a life prediction model designed for turbine blades under CCF loading, yielding better results. Additionally, a dual threshold model was created by Qiu [26] to evaluate the turbine blade’s CCF fatigue life. De Maio [27] et al. provided valuable insights into advanced damage mechanics for ductile materials, which were discussed to highlight the comparative novelty of our proposed model in terms of incorporating load interactions and coupled damage effects. Ha [28] et al. focused on quasi-brittle materials and presented advanced damage simulation techniques, offering a relevant benchmark for positioning our model. However, rather than predicting the accumulation of fatigue damage in composite materials under CCF loading, the models presented above are mostly used to predict the CCF fatigue life of metallic materials. As a result, few models are able to predict the CCF fatigue life of composite materials with any degree of accuracy.
The purpose of this paper is to develop a comprehensive and accurate CCF fatigue life prediction model for wind turbine blades. This model integrates a nonlinear damage accumulation approach and considers the effects of load interactions and sequence on fatigue damage, aiming to address the limitations of traditional life prediction methods and provide a more reliable prediction framework. Additionally, this study validates the proposed method using both experimental data and finite element analysis (FEA) on critical blade sections, ensuring its practical applicability and accuracy in engineering scenarios.
The remainder of this paper is organized as follows. In Section 2, we describe the CCF load spectrum and the accumulation of fatigue damage under variable amplitude cyclic loading, along with the introduction of a nonlinear fatigue damage accumulation model. Based on this model, a nonlinear damage accumulation model considering load sequence and load interactions is established, and the CCF damage curve is modified using fatigue damage curves and equivalent damage theory. In Section 3, a new CCF fatigue life prediction model is proposed, which incorporates a coupling damage module while considering load interactions. This model establishes a connection between HCF and LCF, enabling more accurate life predictions under CCF cyclic loading. In Section 4, we briefly discuss Miner’s rule, the M-H model, and the T-K model and validate the proposed model using existing experimental data, demonstrating superior prediction accuracy. In Section 5, finite element analysis (FEA) is performed on the critical sections of the wind turbine blades, and the proposed method is applied to assess fatigue life predictions. Section 6 summarizes the main conclusions and suggests directions for further research.
2. Miner’s Rule and Fatigue Damage Accumulation Under Variable Amplitude Cyclic Load
2.1. Miner’s Rule
In fatigue damage accumulation theory, Miner’s rule, representing linear damage accumulation, is widely used in engineering for its computational simplicity. The mathematical expression of Miner’s rule [21]:
where denotes the number of loading cycles at stress level , represents the failure cycles at stress level , and k indicates the total number of loading stress cycles. Fatigue failure typically occurs when the accumulated damage D reaches 1.
Figure 1a illustrates that the load spectrum under CCF loading circumstances is made up of several identical load blocks, each of which has one LCF and n HCF cycles. A figure in Figure 1b shows indicating the number of failed load blocks , which can be calculated according to the following Equation (2) [29]:
where denotes the failure load block determined by Miner’s rule, and and denote the number of cycles to failure at high cyclic stress and low cyclic stress , respectively.
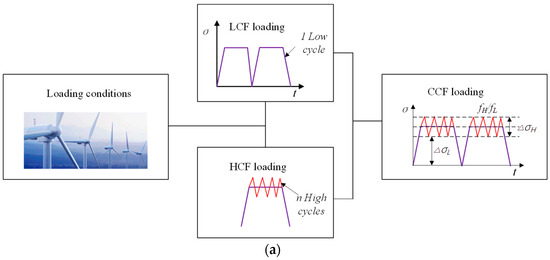
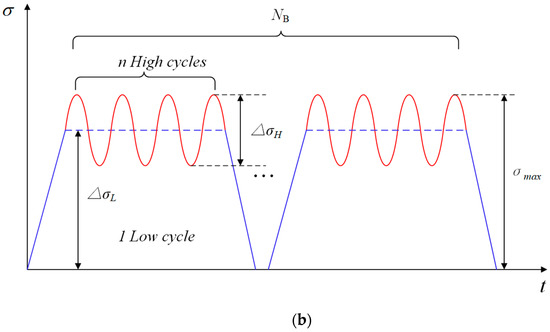
Figure 1.
Load spectrum of CCF. (a) CCF block loads; (b) number of failed load blocks.
Therefore, the cumulative damage under CCF loading according to Miner’s rule may be expressed as follows [30]:
Since Miner’s rule is independently applied at stress levels, but CCF involves complex damage accumulation, it struggles to accurately predict fatigue life in CCF.
2.2. Fatigue Damage Accumulation Under Variable Amplitude Cyclic Loading
As Miner’s rule predicts fatigue life inaccurately under variable amplitude loading, a nonlinear fatigue damage model was proposed to address its limitation in handling different stress levels independently.
Throughout the damage cycle, internal material fractures emerge as the damage rate increases under sustained stress. Interfacial debonding initiates fractures, and the damage rate gradually stabilizes as fissures expand to saturation. Subsequent fractures and damage coupling within the material result in large-scale cracking and accelerated degradation, ultimately leading to fatigue failure. Consequently, the progression of material damage exhibits significant nonlinearity [30].
In the two-stage fatigue test, the specimen is subjected to repeated second-level loading until fatigue failure occurs, following cycles of first-level loading . The number of loading cycles is recorded as . Considering the impact of load sequence, H-L represents the sequence of two-level loading, meaning that H-L stands for high load followed by low load, and L-H stands for low load followed by high load. Figure 2 illustrates the cumulative damage mode under the H-L sequence. Likewise, Figure 3 displays the cumulative damage mode under the L-H sequence.
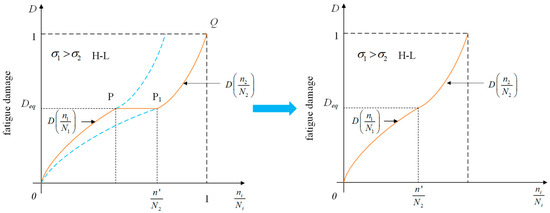
Figure 2.
Accumulated damage patterns under H-L load sequences.
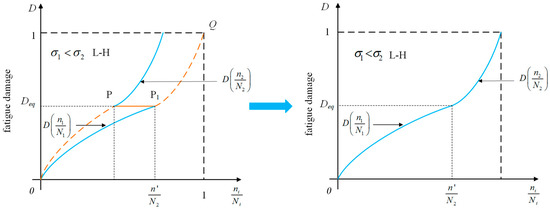
Figure 3.
Accumulated damage mode under L-H load sequence.
The equivalent damage hypothesis, which states that fatigue damage may be converted equivalently under various loadings, is used to forecast fatigue life under varying cyclic loading. Under the equivalent damage theory, during two-stage cyclic loading, loading occurs times under load and is converted to times under load . This means that the load cycle ratio at matches the equivalent conversion cycle ratio at . Equation (4) displays the corresponding damage expression at under two-level cyclic loading [31].
where represents the equivalent number of cycles after converting the first-level load to the second-level load .
The fatigue damage under primary load is converted to fatigue damage under secondary load by introducing the equivalent damage theory. The equivalent damage under secondary load is shown in Equation (5):
The microstructure within the material undergoes transformation caused by varying applied loads, leading to distinct damage patterns like cracking and fracture. Under equal amplitude cyclic loading, high loading accelerates crack formation, whereas low loading enhances fatigue and yield strengths, thereby extending fatigue life. Under CCF loading, fatigue damage from the current cycle is influenced by the loading sequence and the magnitude of the preceding load. The previous loading level affects material damage evolution and the subsequent loading level. Fatigue life predictions may deviate from expectations if load sequences and interactions are ignored [31].
2.3. Nonlinear Damage Accumulation Considering Load Interactions
The H-L sequence was analyzed to explore how load sequences and interactions influence fatigue damage accumulation, as shown in Figure 4.
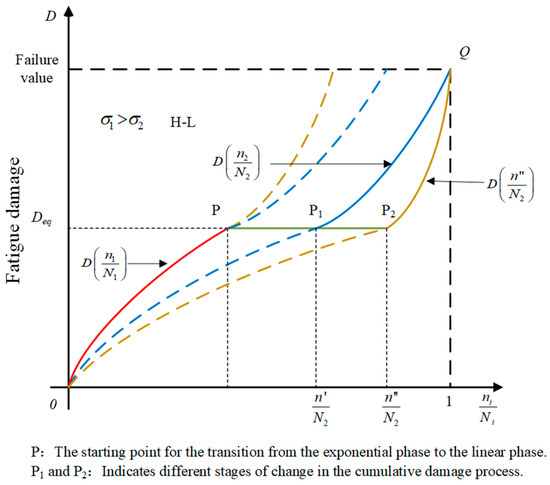
Figure 4.
Cumulative damage in H-L loading sequence.
The damage evolution route under the first-level load is represented by the red solid line in Figure 4. The damage evolution route under secondary loads is represented by the blue solid line if the interaction between loads is ignored. However, the first-level load influences the second-level load damage development due to the interaction between loads, which accelerates fatigue damage accumulation in materials. Consequently, the damage evolution path’s slope increases when secondary loads are applied [32,33]. The orange solid line in Figure 4 illustrates how the fatigue damage route appears as a red, green, and orange solid line when both load sequence and interaction are considered.
The relationship between applied loads under variable amplitude loading is modeled using their load ratio. Fatigue life prediction accuracy decreases with increasing load differences. Based on equivalent damage theory and load interaction considerations, Equation (5) is modified to Equation (6) to enhance fatigue life prediction accuracy under variable amplitude loading.
where represents the number of loading cycles under the interaction of stress levels and .
The modified Equation (6) improves fatigue life prediction accuracy by incorporating load interaction effects and nonlinear damage accumulation, which are critical for more accurate life prediction under variable amplitude loading. The modified Equation (6) considers the relationship between the applied loads under variable amplitude loading by using their load ratio, which accounts for the influence of load sequence (H-L or L-H) on the damage accumulation process. This allows the model to reflect the impact of load history, which is often neglected in simpler models like Miner’s rule. The term in Equation (6) introduces this load interaction effect, which adjusts the damage accumulation based on the varying loads. The original Equation (5) assumes linear damage accumulation, which can lead to overestimation or underestimation of fatigue life, especially when there are significant load variations. Equation (6) modifies the damage calculation by including a nonlinear factor raised to a power, which better captures the material’s response to cyclic loading. The addition of the stress ratio further enhances the model’s ability to predict fatigue life by accounting for the differing effects of high and low stress levels on damage accumulation. By integrating these factors, the modified Equation (6) enhances the model’s ability to predict fatigue life more accurately, especially under CCF loading conditions. This results in a more accurate prediction of material behavior, aligning better with experimental data and reducing errors associated with traditional models.
Based on the damage curves, for composites, the nonlinear cumulative damage model was presented [34,35]:
where material properties A and B are used. Fatigue life and applied load relate to parameter B. The expression is given in Equation (8) [33].
where K, which stands for the scaling parameter, is set at 0.06. represents the maximum stress, denotes the original strength of the material.
The linear relationship satisfied by parameters A and B [33]:
Combining Equations (4)–(7), the equivalent cyclic ratio of the variable cyclic load at the secondary load is obtained as shown in Equation (10):
3. Outline of New CCF Life Prediction Model
3.1. Nonlinear Fatigue Damage Considering Load Interactions
The evolution curve of fatigue damage under CCF loading, considering load interactions, was modified based on Miner’s rule and nonlinear fatigue damage. The load blocks were initially predicted using Miner’s rule and Equation (2). The HCF damage and LCF damage are superimposed to derive cumulative damage, calculated using Equation (3) [36].
LCF damage is expressed as
HCF damage is represented as
The fatigue damage evolution curve was modified to account for the nonlinear damage buildup of load interaction, as illustrated in Figure 5. The fatigue damage evolution initially follows the exponential curve from point 0 to P, transitions to the straight line PP1P2, and ends with the curve P2Q to Q.
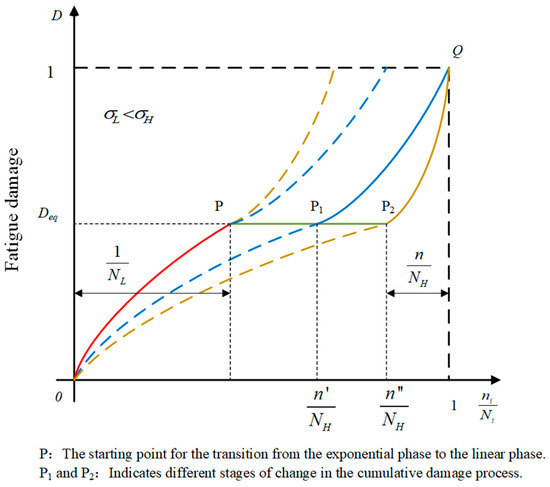
Figure 5.
Accumulated damage under CCF load.
The cumulative fatigue damage under LCF load at point P is identical to the equivalent converted cumulative fatigue damage under HCF load at point P1, as per the damage curve approach and equivalent damage theory [17]. In the meantime, the equivalent converted cumulative fatigue damage can also be used to define the cumulative fatigue damage under HCF loading at point P1, as demonstrated by the following formulations in Equations (13) and (14).
Based on the idea outlined in Section 2.3 above, Equation (14) is changed to Equation (15) to account for the impact of the interaction between loads:
By combining Equations (13)–(15), Equation (16) displays the equivalent cyclic ratio of the variable cyclic load at the secondary load:
Therefore, the following is an expression for the cumulative damage under CCF loading:
where represents the cumulative damage under CCF loading.
3.2. New CCF Life Prediction Model
A fatigue cumulative damage model with coupled damage was introduced in the CCF loading region [37]:
where indicates the coupling damage between the loads.
It is known from the model of Yue et al. [23,24]:
where denotes the stress range under CCF loading.
By substituting Equation (13) into Equation (14), a modified CCF damage accumulation model was obtained:
Therefore, the CCF life prediction model can be written as Equation (21):
4. Model Validation and Comparison
4.1. Model Validation Classical CCF Life Prediction Model
The widely used linear injury model for CCF is Miner’s rule [20], a straightforward combination of LCF and HCF injuries:
Since Miner’s rule neglects HCF-LCF interactions, it has limitations. To address this under CCF loading, several nonlinear cumulative damage techniques have been proposed, with the M-H model and T-K model being the most representative. The cumulative damage in the M-H model [21] is computed as follows:
where β denotes the material constant.
The T-K model [22] cumulative damage is calculated as follows:
where r denotes the material constant.
4.2. Model Validation
In this proposal, experimental data on the fatigue of composites under CCF loading from literature [38] are introduced for model validation. The composite material used in the experiments is CFRP, consisting of T800 carbon fiber and epoxy resin. The specimen lay-up configuration is [0/45/0/−45]2S, and the laminate consists of 16 prepreg layers. The dimensions of the specimens are 200 mm × 25 mm in length and width, respectively, with a thickness of 3 mm. The specimen gauge area is 100 mm. The LCF loading profile consisted of a trapezoidal spectrum with a stress ratio of . The maximum load levels were 80% and 75% of the tensile strength of the material, and the specimens were subjected to repeated loading cycles until failure. The test configuration and loading profile followed ASTM standard D3479 [39]. The CCF tests were conducted by superimposing HCF on the LCF loading profile. A single cycle of CCF included one LCF cycle and n HCF cycles, where the frequency ratio was maintained at . The applied stress levels for the HCF and LCF components were varied to evaluate the combined effects on fatigue life. The experimental condition parameters are shown in Table 1.

Table 1.
Experimental condition parameters in CCF.
Miner’s rule, the M-H model, and the T-K model are applied to validate the proposed life prediction model, where 0.4 and 1.6 represent the material constants β and r.
The findings of this proposed model are compared to those of other models in Figure 6. Due to Miner’s rule disregard for the interaction between HCF and LCF damage, the forecast tends to be nonconservative, and the error is within ±2 times. The M-H model’s forecast understates the CCF life and is too cautious, with some data beyond the ±2 life factor area. With several data surpassing the ±2 life factor area and significant prediction errors, the T-K model’s usefulness is restricted by the addition of extra material coefficients. With an inaccuracy of less than ±1.5 times, the projected life of this proposed model has the best agreement with the experimental life, suggesting that it may be effectively used for high-precision fatigue life evaluation under CCF loading.
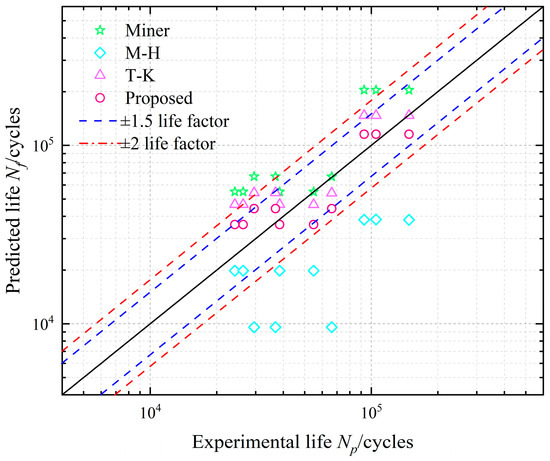
Figure 6.
Comparison between predicted life and experimental life.
4.3. Modeling Error Assessment
To visually compare the discrepancy between the predicted and experimental life, the relative error function, defined in Equation (21) [40,41], was introduced. To accurately evaluate the reliability of the predicted life, a box plot of the model’s prediction error is presented in Figure 7.
where indicates predicted life, and indicates experimental life.
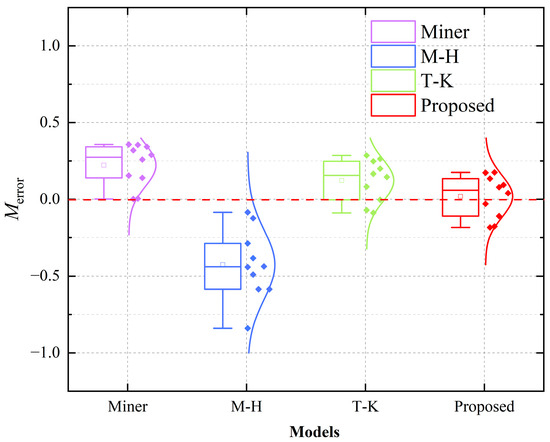
Figure 7.
Box plot of prediction error.
Figure 7 displays the prediction results and error analysis for the four models. It is evident that while Miner’s rule offers a simpler computational approach, it assumes that damage accumulates linearly with respect to the number of cycles, meaning each cycle contributes equally to the total damage, regardless of the loading sequence. This simplification fails to account for load interaction effects, where alternating H-L or L-H stress sequences induce additional damage through mechanisms such as residual stress redistribution and microcrack formation. In H-L or L-H fatigue scenarios, these interactions accelerate damage accumulation, which Miner’s rule overlooks, resulting in an underestimation of cumulative damage and an overestimation of fatigue life. The M-H model, while addressing some load sequence effects, tends to underestimate fatigue life, exhibiting lower mean values and greater dispersion in the predictions. Although the T-K model incorporates a fatigue damage accumulation method to mitigate the limitations of Miner’s rule under CCF loading, it still shows larger prediction errors. In contrast, the model proposed here provides more accurate fatigue life predictions with tighter discretization and a lower mean value, due to its focus on load sequence effects, load interactions, and coupled damage mechanisms. These results demonstrate that the proposed model outperforms the other models in predicting CCF life.
5. Wind Turbine Blade Life Prediction
The wind turbine blade used in the analysis is modeled based on the 5 MW reference turbine blade geometry. Table 2 [10] provides detailed data for each segment of the wind turbine blades studied.

Table 2.
Turbine blade geometry.
A fatigue life prediction model was developed by combining load interactions, improving the damage curve, and applying the model to predict blade life [41]. The FEA steps and CCF life prediction steps under this model are shown in Figure 8.
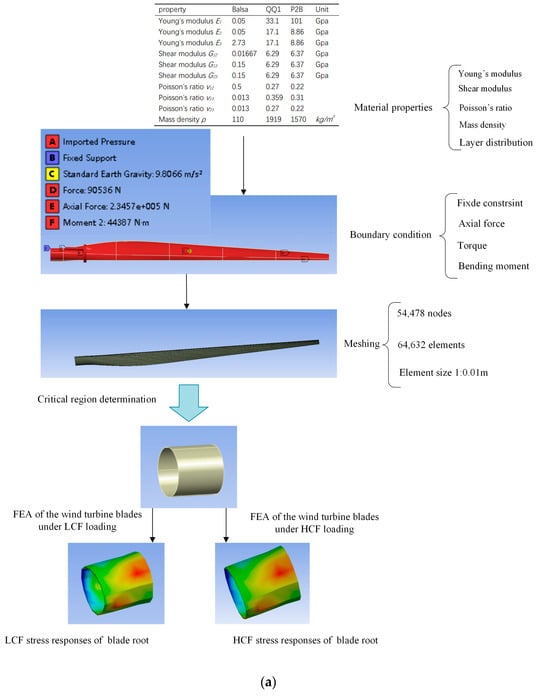
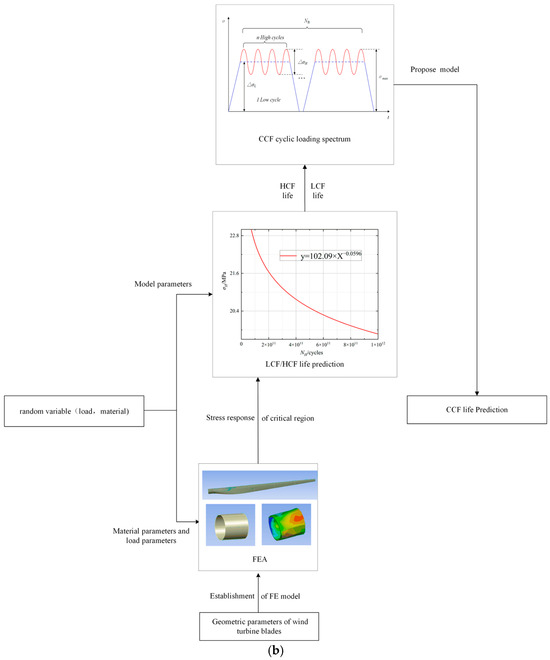
Figure 8.
CCF analysis process. (a) CCF FEA model of wind turbine blades; (b) CCF life prediction analysis process.
Since the overall fatigue life of a blade is determined by the root of the blade, which is the first to fail, the local stresses in the root were chosen to assess the fatigue condition of the blade. The loaded fatigue damage depends not only on the applied stress but also on the number of cycles over 20 years [42]. The number of cycles at each wind speed is calculated based on the Weibull wind speed distribution, and the expression is shown in Equation (26):
where denotes the number of hours per year, denotes the wind speed, denotes the wind speed increment, and and denote the corresponding probability density and distribution function, respectively.
The time expression for the distribution of effective wind speed over the year is shown in Equation (27):
When m/s, the number of hours per year at each wind speed is calculated according to Equation (27), and the results are shown in Table 3. The effective wind speed distribution time in a year is estimated according to Equation (27) h. The Weibull wind speed distribution curve is shown below in Figure 9.

Table 3.
Stress distribution table at each wind speed.
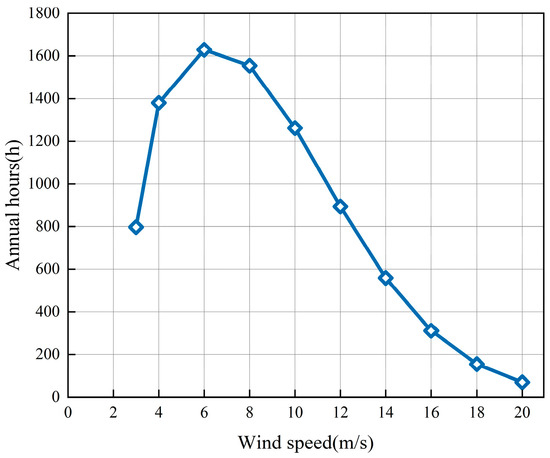
Figure 9.
Weibull wind speed distribution curve.
The tested blade is made of composite material, and its fatigue limit is MPa. The stress distribution at each wind speed is shown in Table 3. Stresses lower than the fatigue limit have no effect on fatigue performance and can be neglected. Stresses above the fatigue limit will be predicted based on Equation (21) for fatigue life.
According to Table 3, the cycles and the S-N curves of HCF [43] are shown in Figure 10. Figure 10 shows the relationship between the stress amplitude and the number of cycles for HCF loading. The data are represented by a fitted curve, described by Equation (28):
where represents the stress amplitude , and represents the number of cycles .
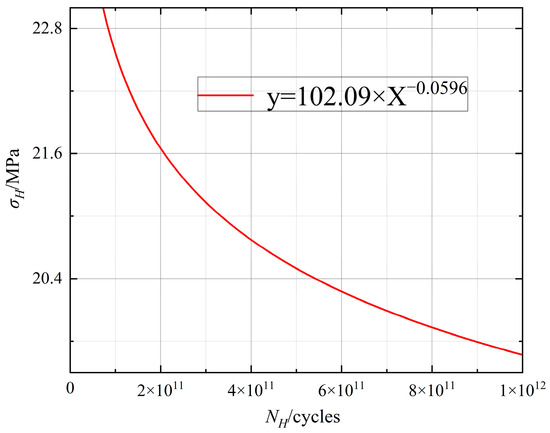
Figure 10.
HCF S-N curve.
The equation suggests a weak inverse relationship between stress and the number of cycles that as the number of cycles increases, the stress amplitude decreases, which is characteristic of fatigue behavior in materials subjected to HCF loading. This type of relationship is crucial in fatigue life prediction models, as it helps estimate the material’s endurance limit and predict failure under HCF fatigue loading.
The combination of , , and Equation (21) is shown in Table 3. cycles.
The empirical formula for blade fatigue life calculation is shown in Equation (29):
where denotes the effective wind speed distribution time in a year, and denotes the wind turbine speed.
Substituting the values of each parameter into the life expectancy Equation (29) yields years.
The number of combined failure load blocks under CCF loading and the cumulative fatigue damage can be expressed as Equation (30). The 3D damage evolution of the blade under different high and low peripheral stress frequency ratios and failure cycle load blocks was established, as shown in Figure 11.
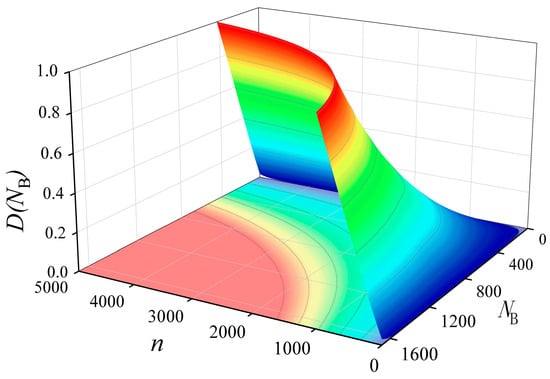
Figure 11.
Three-dimensional damage evolution process.
The estimated life of the model in this proposal is comparable to the theoretical life of the 5 MW wind turbine blade, which was determined to be 23 years by applying the stress analysis function of a finite element to calculate the stress at the blade’s root and combining it with the Weibull wind speed distribution data [42]. When the traditional Miner’s rule was used to predict the blade fatigue life, the prediction error from the theoretical life was 13%. However, the prediction error was reduced to 4.3% by the method proposed. The results show that fatigue life can be accurately predicted using the model in this proposal, leading to better design of wind turbine blades to ensure safety and lightweighting.
While the proposed model significantly improves fatigue life predictions by considering load interaction effects and nonlinear damage accumulation, it does come with an increase in computational complexity compared to traditional models, such as Miner’s rule. The complexity arises primarily from the need to solve nonlinear damage evolution equations and the integration of load interaction effects in each cycle of the fatigue life prediction. This results in an increased number of calculations per cycle, especially in scenarios involving CCF. However, the computational burden can be managed by utilizing optimization techniques and parallel computing methods. The model’s implementation can be parallelized to efficiently handle large-scale simulations, where multiple fatigue life predictions for different loading conditions can be computed simultaneously. In practice, this approach allows for scalable predictions, especially when applying the model to real-world engineering systems such as wind turbine blades, where multiple components or conditions must be evaluated simultaneously. Furthermore, simplifications and approximations can be applied to reduce computational costs when needed. In cases where load history is predictable or simplified, certain parts of the model can be approximated without significantly affecting the accuracy of the prediction. In such scenarios, the model can achieve a balance between computational efficiency and predictive accuracy, making it feasible for large-scale applications.
6. Conclusions
This article proposes a life prediction model for CCF under cyclic loading that is used for predicting the CCF life of wind turbine blades. The main advantage of this model is that it considers the influence of load sequence and load interaction, as well as load coupling damage, on CCF damage. The main conclusions can be summarized as follows:
- (1)
- Using damage curves to analyze the damage evolution process under CCF load, this paper proposes a CCF life prediction model that primarily takes into account the impacts of load sequence, load interaction, and load coupling.
- (2)
- Existing CCF experiments were used to evaluate the model’s robustness and prediction accuracy. The majority of our model’s results of prediction fall within the life factor ± 1.5 range when compared to Miner’s rule, the M-H model, and the T-K model. It is evident that the model’s anticipated life agrees well with the experimental life fitting curve, suggesting that our model is better suited to forecasting CCF life than other models due to its greater prediction accuracy and more accurate prediction error.
- (3)
- Based on Miner’s rule, this study introduces composite material damage components to present a new CCF life prediction model that can be used to estimate the CCF fatigue life of composite materials.
- (4)
- The proposed model, which integrates load interaction effects and nonlinear damage accumulation, provides highly accurate fatigue life predictions. Despite its increased computational complexity compared to traditional methods, it remains feasible for large-scale applications, such as evaluating the fatigue life of complex structures under variable amplitude loading. Future work will focus on further optimizing the model’s computational efficiency, including the use of high-performance computing and simplified versions for specific cases, ensuring its applicability to real-time and large-scale engineering problems.
Author Contributions
Methodology, conceptualization, investigation, writing—original draft, data curation, M.L.; formal analysis, writing—review and editing, funding acquisition, validation, project administration, J.G.; software, investigation, writing—review and editing, supervision, resources, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (52465019), Natural Science Foundation of Xinjiang Uygur Autonomous Region (2024D01C27), Xinjiang Uygur Autonomous Region Central Guidance Local Science and Technology Development Fund Project (ZYYD2025JD07), and Changji Hui Autonomous Prefecture Science and Technology Plan Project (2023Z02).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, Y.; Huang, R.; Li, Z. Fault Detection Method for Wind Turbine Generators Based on Attention-Based Modeling. Appl. Sci. 2023, 13, 9276. [Google Scholar] [CrossRef]
- Guo, Z.; Huang, D.; Yan, X.; Zhang, X.; Qi, M.; Fan, J. A damage coupled elastic-plastic constitutive model and its application on low cycle fatigue life prediction of turbine blade. Int. J. Fatigue 2020, 131, 105298. [Google Scholar] [CrossRef]
- Yuan, G.J.; Zhang, X.C.; Chen, B.; Tu, S.T.; Zhang, C.C. Low-cycle fatigue life prediction of a polycrystalline nickel-base superalloy using crystal plasticity modelling approach. J. Mater. Sci. Technol. 2020, 38, 28–38. [Google Scholar] [CrossRef]
- Zhang, X.; Zheng, M. Numerical Simulation of Fluid-Structure Coupling for a Multi-Blade Vertical-Axis Wind Turbine. Appl. Sci. 2023, 13, 8612. [Google Scholar] [CrossRef]
- Zhao, Y.; Gong, X.; Wang, J.; Zhang, L.; Bai, Y. Stress characteristics of horizontal-axis wind turbine blades under dynamic yaw. Appl. Sci. 2023, 13, 8418. [Google Scholar] [CrossRef]
- Gao, J.; Liu, Y.; Yuan, Y.; Heng, F. Residual strength modeling and reliability analysis of wind turbine gear under different random loadings. Mathematics 2023, 11, 4013. [Google Scholar] [CrossRef]
- Miao, Y.; Soltani, M.N.; Hajizadeh, A. A machine learning method for modeling wind farm fatigue load. Appl. Sci. 2022, 12, 7392. [Google Scholar] [CrossRef]
- Kuo, J.Y.; You, S.Y.; Lin, H.C.; Hsu, C.Y.; Lei, B. Constructing condition monitoring model of wind turbine blades. Mathematics 2022, 10, 972. [Google Scholar] [CrossRef]
- Ding, X.; Yan, X.; Guo, Z.; Guo, K. A combined low-and high-cycle life prediction model considering the closure effect of micro-defects. Fatigue Fract. Eng. Mater. Struct. 2022, 45, 2058–2071. [Google Scholar] [CrossRef]
- Schubel, P.J.; Crossley, R.J. Wind turbine blade design. Energies 2012, 5, 3425–3449. [Google Scholar] [CrossRef]
- Liu, L.; Gao, H.S.; Wang, J.D.; Zhang, C.J.; Wen, Z.X.; Yue, Z.F. Combined high and low cycle fatigue analysis of FGH96 alloy under high temperature conditions. Mater. Today Commun. 2024, 38, 108053. [Google Scholar] [CrossRef]
- Liu, L.; Gao, H.S.; Wang, J.D.; Zhang, C.J.; Wen, Z.X.; Yue, Z.F. Microstructure analysis and life prediction of DD6 superalloy under 760 °C combined high and low cycle fatigue conditions. Eng. Fract. Mech. 2024, 295, 109796. [Google Scholar] [CrossRef]
- Feng, C.; Long, Z.; Su, M.; Xu, L.; Zhao, L.; Han, Y. A physics-informed deep learning approach for combined cycle fatigue life prediction. J. Constr. Steel Res. 2024, 222, 109000. [Google Scholar] [CrossRef]
- Dowling, N.E. Estimation and correlation of fatigue lives for random loading. Int. J. Fatigue 1988, 10, 179–185. [Google Scholar] [CrossRef]
- Gao, J.; Heng, F.; Yuan, Y.; Liu, Y. A novel machine learning method for multiaxial fatigue life prediction: Improved adaptive neuro-fuzzy inference system. Int. J. Fatigue 2024, 178, 108007. [Google Scholar] [CrossRef]
- Mesmacque, G.; Garcia, S.; Amrouche, A.; Rubio-Gonzalez, C. Sequential law in multiaxial fatigue, a new damage indicator. Int. J. Fatigue 2005, 27, 461–467. [Google Scholar] [CrossRef]
- Bai, S.; Huang, H.Z.; Li, Y.F.; Yu, A.; Deng, Z. A modified damage accumulation model for life prediction of aero-engine materials under combined high and low cycle fatigue loading. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 3121–3134. [Google Scholar] [CrossRef]
- Zhu, S.P.; Yue, P.; Yu, Z.Y.; Wang, Q.Y. A combined high and low cycle fatigue model for life prediction of turbine blades. Materials 2017, 10, 698. [Google Scholar] [CrossRef]
- Liu, P.; Wang, X.; Shen, Q.; Li, F.; Liu, M.; Sun, Y. On the consideration of loading interaction in combined high and low cycle fatigue life prediction. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 2651–2661. [Google Scholar] [CrossRef]
- Yang, S.; Hu, W.; Meng, Q.; Zhao, B. A new continuum damage mechanics-based two-scale model for high-cycle fatigue life prediction considering the two-segment characteristic in S-N curves. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 387–402. [Google Scholar] [CrossRef]
- Manson, S.S.; Halford, G.R. Practical implementation of the double linear damage rule and damage curve approach for treating cumulative fatigue damage. Int. J. Fract. 1981, 17, 169–192. [Google Scholar] [CrossRef]
- Trufyakov, V.I.; Koval’chuk, V.S. Determination of life under two-frequency loading. Report no. 2. Proposed method. Strength Mater. 1982, 14, 1303–1308. [Google Scholar] [CrossRef]
- Yue, P.; Zhou, C.; Zhang, J.; Zhang, X.; Du, X.; Liu, P. A comparative study on combined high and low cycle fatigue life prediction model considering loading interaction. Int. J. Damage Mech. 2024, 10567895241292747. [Google Scholar] [CrossRef]
- Yue, P.; Ma, J.; Zhou, C.; Zu, J.W.; Shi, B. Dynamic fatigue reliability analysis of turbine blades under combined high and low cycle loadings. Int. J. Damage Mech. 2021, 30, 825–844. [Google Scholar] [CrossRef]
- Han, L.; Huang, D.; Yan, X.; Chen, C.; Zhang, X.; Qi, M. Combined high and low cycle fatigue life prediction model based on damage mechanics and its application in determining the aluminized location of turbine blade. Int. J. Fatigue 2019, 127, 120–130. [Google Scholar] [CrossRef]
- Qiu, S.; Cui, H.; Zhang, H.; Wen, W.; Guo, J. A dual-threshold modelling approach for fatigue life prediction under combined high and low cycle fatigue. Int. J. Fatigue 2022, 164, 107110. [Google Scholar] [CrossRef]
- De Maio, U.; Greco, F.; Lonetti, P.; Pranno, A. Pranno, A. A combined ALE-cohesive fracture approach for the arbitrary crack growth analysis. Eng. Fract. Mech. 2024, 301, 109996. [Google Scholar] [CrossRef]
- Ha, D.; Kim, J.H.; Kim, T.; Joo, Y.S.; Yun, G.J. Multiscale fatigue damage model for CFRP laminates considering the effect of progressive interface debonding. Mech. Adv. Mater. Struct. 2022, 31, 2321–2333. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, H.; Zhou, W. A Modified Damaged Stress Model for Fatigue Life Prediction Based on Load Interaction. Heliyon 2024, 10, e40357. [Google Scholar] [CrossRef] [PubMed]
- Hou, J.; Wang, X.; Guo, H.; Wang, Y.; Li, F.; Shen, Q. Combined high and low cycle fatigue life prediction model based on damage curve method considering loading interaction effect. Int. J. Damage Mech. 2023, 32, 185–203. [Google Scholar] [CrossRef]
- Gao, H.; Huang, H.Z.; Lv, Z.; Zuo, F.J.; Wang, H.K. An improved Corten-Dolan’s model based on damage and stress state effects. J. Mech. Sci. Technol. 2015, 29, 3215–3223. [Google Scholar] [CrossRef]
- Zhu, S.P.; Huang, H.Z.; Wang, Z.L. Fatigue life estimation considering damaging and strengthening of low amplitude loads under different load sequences using fuzzy sets approach. Int. J. Damage Mech. 2011, 20, 876–899. [Google Scholar] [CrossRef]
- Feng, Z.; Ma, Q.; An, Z.; Ma, H.; Bai, X. New fatigue life prediction model for composite materials considering load interaction effects. Int. J. Appl. Mech. 2023, 15, 1758–8251. [Google Scholar] [CrossRef]
- Strizhius, V. Fatigue damage accumulation under quasi-random loading of composite airframe elements. Mech. Compos. Mater. 2016, 52, 455–468. [Google Scholar] [CrossRef]
- Yue, P.; Li, H.; Dong, Y.; Zhang, J.F.; Zhou, C.Y. A modified nonlinear cumulative damage model for combined high and low cycle fatigue life prediction. Fatigue Fract. Eng. Mater. Struct. 2024, 47, 1300–1311. [Google Scholar] [CrossRef]
- Yue, P.; Ma, J.; Zhou, C.; Jiang, H.; Wriggers, P. A fatigue damage accumulation model for reliability analysis of engine components under combined cycle loadings. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 1880–1892. [Google Scholar] [CrossRef]
- Wang, Z.; Zheng, T.; Shi, Q.; Chen, Z.; Zhang, L.; Zhou, J.; Sun, X.; Guo, L. Damage behavior and life prediction model of composite laminates under combined high and low cycle fatigue. Int. J. Fatigue 2024, 183, 108240. [Google Scholar] [CrossRef]
- Bai, S.; Huang, T.; Li, Y.; Lu, N.; Huang, H.Z. A probabilistic fatigue life prediction method under random combined high and low cycle fatigue load history. Reliab. Eng. Syst. Saf. 2023, 238, 109452. [Google Scholar] [CrossRef]
- ASTM D3479-07; Standard Test Method for Tension-Tension Fatigue of Polymer Matrix Composite Materials. ASTM International: West Conshohocken, PA, USA, 2007.
- Wu, J.; Huang, H.Z.; Li, Y.F.; Bai, S.; Yu, A.D. Probabilistic fatigue life prediction of an aero-engine turbine shaft. Aircr. Eng. Aerosp. Technol. 2022, 94, 1854–1871. [Google Scholar] [CrossRef]
- Hou, N.X.; Wen, Z.X.; Yu, Q.M.; Yue, Z.F. Application of a combined high and low cycle fatigue life model on life prediction of SC blade. Int. J. Fatigue 2009, 31, 616–619. [Google Scholar] [CrossRef]
- Liu, X.; Lin, B.; Luo, H. Dynamical measurement system for wind turbine fatigue load. Renew. Energy 2016, 86, 909–921. [Google Scholar] [CrossRef]
- Movahedi-Rad, A.V.; Keller, T.; Vassilopoulos, A.P. Fatigue damage in angle-ply GFRP laminates under tension-tension fatigue. Int. J. Fatigue 2018, 109, 60–69. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).