Abstract
We propose the HOSA algorithm to pick P-wave arrival times on seismic arrays. HOSA comprises two stages: a single-trace stage (STS) and a multi-channel stage (MCS). STS seeks deviations in higher-order statistics from background noise to identify sets of potential onsets on each trace. STS employs various thresholds and identifies an onset only for solutions that are gently variable with the threshold. Uncertainty is assigned to onsets based on their variation with the threshold. MCS verifies that detected onsets are consistent with the array geometry. It groups onsets within an array by hierarchical agglomerative clustering and selects only groups whose maximum differential times are consistent with the P-wave travel time across the array. HOSA needs a set of P-onsets to be calibrated. These sets may be already available (e.g., preliminary catalogs) or retrieved from picking (manually/automatically) a subset of traces in the target area. We tested HOSA on 226 microearthquakes recorded by 20 temporary arrays of 10 stations each, deployed in the Irpinia region (Southern Italy), which, in 1980, experienced a devastating 6.9 Ms earthquake. HOSA parameters were calibrated using a preliminary catalog of onsets obtained using an automatic template-matching approach. HOSA solutions are more reliable, less prone to false detection, and show higher inter-array consistency than template-matching solutions.
1. Introduction
Detecting seismic wave arrival times is crucial for various geophysical and seismological applications, including crustal imaging and earthquake monitoring. The expansion of dense seismic monitoring networks in regions of high seismic activity provides an evergrowing availability of high-quality recordings, even for microseismic events, which are earthquakes with magnitudes typically below the threshold of traditional earthquake detection methods (magnitude < 3). These events are often associated with localized stress changes or fractures in the subsurface, and they can occur naturally or be triggered by human activities such as geo-resource exploitation. Dense arrays of seismic stations can lower the detection threshold of small earthquakes and improve the quality of fault imaging, and are largely adopted for seismic monitoring all over the world (e.g., [1,2,3]). This triggered a significant development of automatic techniques for efficient processing and analysis aimed at providing accurate and reliable body wave picking. The advantages of the automatic picking techniques rely on the processing capability of large volumes of seismic data rapidly, possibly facilitating real-time analysis and decision-making, as well as reducing the potential for errors or biases due to human subjectivity, as often introduced by manual picking procedures.
Various algorithms and techniques are used to automatically pick seismic phases from the data. After [4]’s pioneering work, which was based on the STA/LTA (short-term average/long-term average) technique, various algorithms for the automatic picking of seismic arrivals have been developed. These include methods based on higher-order statistics (HOS hereinafter) such as kurtosis or skewness [5,6,7], on the dominant frequency content of the seismogram [8], on the wavelet transform analysis [9], and on the polarization analysis, particularly for S-wave picking [10,11].
Nowadays, seismologists are largely adopting machine learning approaches to pick small earthquakes whose recordings are similar to or even lower than the noise. Although many different approaches are being developed, most of them train neural networks from a set of fingerprints from precisely picked earthquakes and try to identify potential hidden events in continuous seismograms. These approaches are allowing us to greatly reduce the earthquake detection threshold, with the effect of enhancing the earthquake catalogs [12,13,14,15].
On the other hand, there are various issues and limitations to the automatic picking of seismic waves that may affect their efficiency and dependability. Noise sensitivity is a critical aspect, as these approaches may fail to distinguish between seismic signal and background noise, especially in situations with high levels of ambient noise. For example, machine learning methods may present the drawbacks that only a part of the detected events are indeed small earthquakes, as a fraction of the automatically identified events must be excluded a posteriori by a user-based revision as they are actually noise [16]. Moreover, the automatic readings of the seismic phases may suffer from large inaccuracies. This is due, on one side, to the low amplitude of the events they try to catch and, on the other side, to the data reduction that is involved in these techniques to identify beforehand some effective fingerprints that implicitly lead to an undersampling of the original signal and thus to a reduction in the resolution.
Furthermore, in complicated geological settings or if multiple seismic phases reach a receiver at close times, automated systems may become ambiguous, making it difficult to precisely detect individual wave arrivals. Addressing these problems is critical for expanding the capabilities of autonomous seismic picking approaches and increasing their utility in diverse seismological applications.
Here, we propose an approach that is able to provide reliable P-wave arrival times picking by combining single-station and multi-channel numerical techniques to identify the first seismic arrival, hereinafter also denoted as onsets. Specifically, on individual traces, we analyze signal segments to detect changes in statistical properties (e.g., variance and higher-order statistics) compared to the background noise. We fix in this way the onset of an earthquake at one receiver; eventually, these picks are validated by evaluating the consistency of these solutions within an array of receivers, grouping them by a clustering approach. The proposed technique requires two inputs: a list of earthquakes whose origin time is required and the seismograms of those earthquakes, recorded at one or multiple arrays. Our algorithm comprises parameters that need to be fixed based on the features of the specific dataset under analysis. In this study, we choose to use the phase arrival times obtained from the automated method proposed by [17] and adopted in [18] as an initial reference for calibrating our method. Our method is particularly well-suited as an extra module that can complement automatic workflows for earthquake detection (f.i., machine learning or amplitude-based approaches) with the goals of automatically discarding false earthquake detection and incorrect picks, refining any eventual existing onset and integrating the catalog with new reliable picks.
2. Data
We focus on the complex normal fault system of Southern Apennines that was struck by the destructive Ms 6.9 1980 Irpinia earthquake [19]. The Irpinia region in southern Italy exhibits significant seismogenic potential due to its complex fault systems and tectonic activity, as demonstrated by the long history of powerful earthquakes that occurred in this region [20,21] (some of the most important are displayed in Figure 1). Since 2005, the seismicity in the Irpinia area has been monitored in real-time by the Irpinia Near Fault Observatory [22], which also includes the Irpinia Seismic Network (ISNet; http://isnet.unina.it [23]; last accessed on 18 January 2025). ISNet, with its 31 seismic stations equipped with accelerometers and short-period or broad-band seismometers, represents a natural laboratory for studying fault evolution and rupture processes. The seismicity of the last decades (2005–2024) is characterized by low magnitude events (maximum magnitude 3.9), mainly occurring at depths between 8 and 15 km [24,25], within the fault system that hosted the Irpinia earthquake.
With the aim of monitoring the seismicity in the Irpinia region at a finer scale, in the framework of “The DEnse mulTi-paramEtriC observations and 4D high-resolution imaging” (DETECT [26]) experiment, 200 seismic stations were deployed in 20 small-aperture arrays of ten stations from August 2021 to August 2022, integrating the existing network, as illustrated in Figure 1. Each array consisted of one broadband sensor, with a characteristic period of 120s (Trillium-Compact/g = 750), one 1 Hz broadband and eight 4.5 Hz geophones deployed in urban areas within a kilometric-size aperture. Stations belonging to the same array were placed in a confined geographical area. Table 1 shows the maximum distance between two generic stations of the same array.

Table 1.
Numerical codes used to identify the DETECT arrays, along with respective maximum distances between stations. Each array consists of 10 receivers.
In this work, we analyze the about 35,700 seismic traces registered by DETECT stations, 200 Hz-sampled, corresponding to 226 events reported in the manual catalog provided by ISNet (accessible through the Irpinia Seismic Network website: http://isnet-bulletin.fisica.unina.it/cgi-bin/isnet-events/isnet.cgi; last accessed on 18 January 2025). The events have a local magnitude ranging between −0.3 and , as extracted from the released seismic catalog and evaluated through a local magnitude scale tailored for the area [27], and they occurred during the first 6 months of the experiment (September 2021–February 2022). To obtain phase arrival times that will serve as initial references for calibrating our method, we follow the strategy and parameterization proposed by [17], tailored for the detection and phase picking of seismic sequences in Irpinia. This approach integrates the machine learning model EQTransformer [12] for detection and phase picking with a cross-correlation analysis applying the template matching algorithm EQCorrscan [28], with the aim to retrieve picks undetected by the machine learning model [29]. The approach returned 8685 P-wave arrival times. Henceforth, we will refer to these picks as catalog picks.
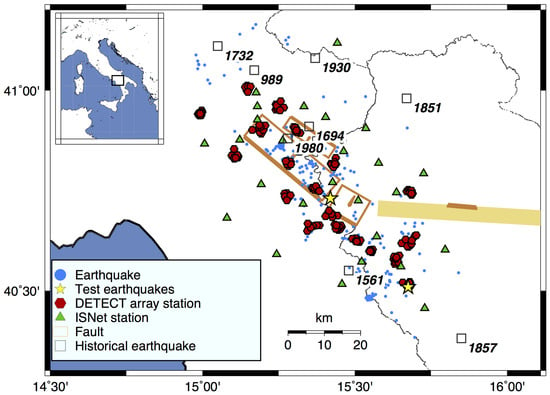
Figure 1.
Map of Southern Apennines (Italy) representing the earthquake analyzed in this study (blue dots) and DETECT seismic station locations (red hexagons). ISNet stations are represented by green triangles. Black squares refer to the historical earthquakes that occurred in Irpinia [21], highlighting the significant seismogenic potential of the region [20]. The numbers next to the black squares are the dates of the historical earthquake. The orange rectangles represent the individual seismogenic sources of the 1980 Campania-Lucania earthquakes [30]. The yellow stars represent the position of the earthquakes whose waveforms are utilized as example in Section 5.2. The inset of the figure highlights the study region’s location on the Italian peninsula.
3. Methodology
We present an algorithm for detecting onsets based on higher-order statistics (HOS), specifically designed for applications to arrays of stations. Hereinafter, we will denote our algorithm as higher-order statistics for arrays (HOSA).
As the method aims to reveal P-wave arrival times, we will use only the vertical component of motion, where P-waves are more visible.
HOSA consists of two stages: a single-trace stage (STS) and a multi-channel stage (MCS), which are outlined in Figure 2 and described in detail in Algorithm 1. STS receives the vertical components of the seismic waveforms as input. In each trace, it seeks the P-wave arrival time. When the stage successfully identifies an arrival time, it outputs the corresponding value along with a respective weight. MCS receives the arrivals from the previous stage and leverages information about the spatial arrangement of stations. It performs a second selection process, checking the coherence of arrivals within the same array and thus enhancing the reliability of predictions. In the following sections, a detailed description of the two stages is provided.
| Algorithm 1 Algorithm HOSA. |
|
|
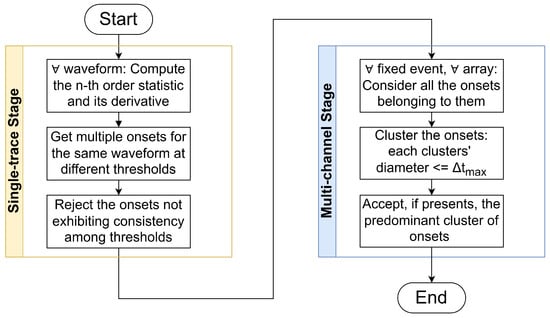
Figure 2.
Brief outline of the proposed methodology, schematically illustrating the two-stage structure of the HOSA method. For a detailed description, refer to Algorithm 1 or Section 3.
3.1. Single-Trace Stage
STS aims to determine P-wave arrival times in the waveforms. It is based on the HOS approach introduced by [5]. The basic assumption is that the sought signal and the background noise are ruled by different physical processes, resulting in distinct statistics. The method utilizes HOS gradient-based characteristic functions. These functions possess the desirable property of yielding null values when computed on time windows containing Gaussian-distributed random processes, such as those consisting solely of noise, while exhibiting non-zero values when a signal is encountered. The onset (hereinafter denoted as o) of the signal is detected among the samples where the characteristic function significantly deviates from zero.
For each seismic trace , we can define the time series , representing the n-th order relevant statistic. Indicating with the expectation operator, for a generic discrete random process with expected values , is given by the following:
where is the estimation of in a time window of length w ending at time t, and is the value of for a Gaussian variable [31]. Thus, the estimation of for Gaussian variables is zero. Explicitly, for a seismic trace we have the following:
where .
We seek the P-arrival in a part of the trace u enclosed between the event origin time (OT) and OT + . To increase the signal-to-noise ratio (SNR), we use a band-pass filter beforehand on the signals in the frequency range defined by . Each time series is then scanned by a sliding time window of length equal to w. The values of depend on the dataset and the geometry of the receivers and will be fixed later (Section 4). An HOS value is computed in each time window w sliding of one sample at each step, as described in Equation (2), resulting in a new time series: . A moving average window of three points is used to smooth the and mitigate noise fluctuations. In the following, based on previous works [31,32], we test two values: and , which are, respectively, the 4-th and 6-th order statistics. As noted in [7], the time derivative of exhibits a considerably more impulsive character, making it more appropriate as a characteristic function. Consequently, derivatives are computed, generating the time series . Some typical waveforms, along with their and , are depicted in Figure 3.
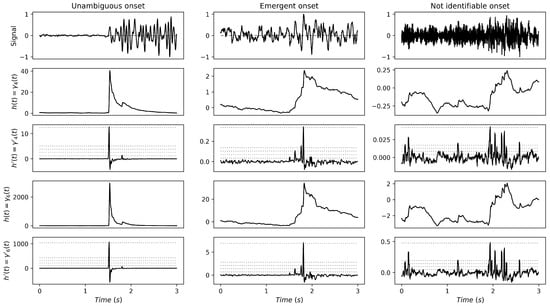
Figure 3.
Examples of vertical components of traces with respective statistics and derivatives. On the left is a typical example of a good-quality seismic signal (station S0809, M = 0.7, and epicentral distance = 7.6 km) for which it is possible to visually identify an unambiguous P-onset. In the center is a weak signal (station S0209, , and epicentral distance km) with an emergent P-arrival, which is reflected in an ambiguous P-onset. On the right is a waveform lacking distinguishable events (station S1009, , and epicentral distance km), which implies an unidentifiable P-onset. Dotted gray lines refer to the different threshold levels of the multi-threshold criterion.
How do we identify P-onsets from the functions? Several studies have simply used the maximum of . However, as explained in [32], this criterion can lead to inaccurate detection in the presence of spurious spikes before the actual P-onset or in the case of very unstable . This can be seen in Figure 3, where and have been plotted for three representative cases of seismograms in which the P-onset is clearly impulsive, emergent, and not clearly identifiable, respectively. In the first case, the functions show a sharp increase (corresponding to the maxima of ) at the correct P-onset, and for an emergent arrival, the functions increase smoother, reaching smaller maxima values both in and , highlighting an area before the maximum of , where the onset is likely to be found. Remarkably, the functions show multiple relative maxima in the case of an emergent arrival. An even smoother increase in and several relative maxima of appear in the third case, in which the P-onset is masked by the noise.
To account for this variability in and and thus of the uncertainty of the retrieved P-onset, HOSA employs a multi-threshold criterion and includes an acceptance stage to evaluate the reliability of arrival times. HOSA utilizes a set of thresholds , which are defined relatively to the maximum of ; in other words, corresponds to one-tenth of the maximum of , and corresponds to the value of the maximum of . Starting from , we obtain a set of potential onsets for each trace as follows. We first identify the time corresponding to the maximum of :
We then look for the potential onset for each , as described in Equation (4) and at the point 1.7 of Algorithm 1:
As indicated in Equation (4), the onsets are sought in a 2 s time window centered in M. This is fixed because the functions show a dispersion around M that is typically in the order of 0.3 s for emergent arrivals (see Figure 3) and is eventually connected to the uncertainty in the P-onset. To account for this uncertainty, we seek the values of in a time window centered in M and with a width equal to about ±3 ±1 s.
The onset associated with the threshold intercepts, by definition, the main peak of . Various thresholds identify any potential lower amplitude peaks preceding the main one. We assume that a time consistency among the potential onsets implies a low error definition of the P-onset. In other words, we assume that if does not change with the threshold, the estimated P-onset is robust. Conversely, if spans a wide time range, we assume that the estimated P-onset is affected by a large uncertainty. Such uncertainty is quantified as the standard deviation within each set . The user can tune the degree of accuracy of STS by allowing only solutions with lower than a threshold . We will refer to this condition as the multi-threshold criterion.
Eventually, from each set (satisfying the multi-threshold criterion), one final P-onset must be identified. As noted in the previous work by [6], the optimal picking performance occurs when the actual onset matches the earliest part of the characteristic function’s increase; this corresponds to the case when the very beginning of the sought signal accesses the time window for HOS calculation, leading to a small increase in HOS. The value of the threshold that optimally catches this increase depends on the dataset and receiver setup. In this study, we identify the final onset with the first potential onset (related to the threshold ), as Section 4 indicates that this is the best choice in our case.
From , an estimate of the uncertainty on the arrival can be assigned as the standard deviation . Specifically, we assign a weight to the P-onset ranging between 0 and 3 based on the ratio , as reported in Table 2.

Table 2.
Correspondence between the and weight assignment method of STS. The assigned weights reflect the uncertainty levels of the respective P-wave arrival times. Lower weights correspond to lower uncertainty levels (e.g., a weight equal to 0 indicates maximum reliability).
For example, considering the statistics in the cases displayed in Figure 3, the standard deviation among the set is calculated using the case in the left panel, which is equal to s. In contrast, the traces in the central and right panels exhibit standard deviations of about 0.1 s and 0.2 s, respectively. The choice = 75 ms, for example, would correspond to the assignment of a weight of 0 (the largest reliability) to the left case and to reject the onsets on the other cases. Similar outcomes can be obtained considering the 6th-order statistic.
3.2. Multi-Channel Stage
The second part of the algorithm involves a multi-channel stage (MCS) that includes the analysis of multiple channels of an array of receivers. This stage exploits the array disposition information to enhance the reliability of the previous onsets that passed the multi-threshold criterion.
In order to formalize this process, we introduce the following notation. Suppose that a seismic event is registered by the receivers , resulting in the traces , where the indices i and j run, respectively, over the number of arrays and the number of receivers of array i. Let us assume that for all or a portion of the traces, STS is assigned an onset of . For each array , we denote the set of onsets as .
To evaluate the consistency of the arrivals, we first perform a clustering analysis of the elements of .
In general, a clustering procedure is an unsupervised learning technique [33] used to group data points together, based on some similarity criterion, into subsets or clusters that are homogeneous or well separated [34]. In this study, we employed hierarchical agglomerative clustering [35,36,37,38,39] to build groups of concordant onsets. Hierarchical agglomerative clustering begins by partitioning the dataset into single dad ( in our case), each representing a cluster. A value of dissimilarity is then computed for each pair of initial clusters. Subsequently, the clustering procedure iteratively merges the current pair of mutually closest clusters into a new object, computing new dissimilarities until there is one final cluster left. The user can stop the fusion of the objects at a certain level of dissimilarity or when a desired number of clusters is reached.
Here, we adopt the complete linkage distance [37] as a measure of dissimilarity between two fused objects (clusters) of onsets and , defined as follows:
When clusters and are merged into a new cluster , the value will correspond to its diameter, that is, the maximum dissimilarity (distance) between two entities within [40,41].
A critical point of hierarchical agglomerative clustering is to establish the optimal number of final clusters or, equivalently, the maximum allowed dissimilarity between fused objects [34]. Given the nature of our objects (seismic arrival times), we fixed the maximum intra-cluster distance as the largest physically possible time difference between P-wave arrival times at receivers of array i, which we indicate as . This parameter is related to the maximum spatial distance between two generic receivers of the same array and the P-wave propagation velocity in the following way:
where is a tolerance term, which takes into account any possible uncertainty or fluctuation in the considered physical quantities.
Thus, we interrupted the clustering procedure at the fusion step, after which a new cluster with a diameter larger than was created. In this way, the clustering step returns a partition of in a set of different clusters with the largest intra-cluster distance less than or equal to . Figure 4 illustrates some possible scenarios arising from the clustering procedure in a schematic way.
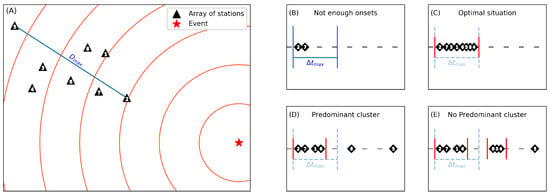
Figure 4.
Graphical representation of the clustering procedure. (A) Schematic illustration of a single array of stations. represents the maximum distance between two stations of the array. The numbers within the black triangles serve to identify the different stations. Panels (B–E) depict various example situations of arrival times, with diverse clustering scenarios. Vertical red lines delimit clusters of onsets. is the maximum allowed time that can elapse between two arrivals at the same array. Each black rhombus represents an arrival time. The numbers within them correspond to the numbers of the stations to which they belong.
Once the clusters of onsets at array i are formed, a selection of suitable onsets is performed as follows. Let be the total number of onsets in , which is, in general, less than or equal to 10; that is, the number of receivers for our arrays. If the onsets are all grouped in the same cluster, we accept them in the case ; otherwise, they are discarded. If more than one cluster is present, we denote with and the numbers of onsets present in the two most populated clusters, and . We accept the onsets of (and reject the other) if all the conditions of Equation (7) are met ( indicates the integer division).
In this case, we claim that represents a “predominant cluster”.
If any of the conditions of Equation (7) are not met, no predominant cluster can be defined, indicating very spread arrivals (and, thus, large uncertainty in the solutions). In this case, all onsets of the array are rejected.
4. Settings Configuration
As described in the previous sections, HOSA involves parameters that need to be configured according to the characteristics of the earthquakes and receivers under analysis. A comprehensive list of the parameters to be configured along with the selected setup can be found in Table 3.

Table 3.
Settings to be configured, along with respective optimal setup for our case study. Refer to Algorithm 1 and Section 3 for an explanation of their meaning.
As explained in Section 2, we detected P-wave arrival times (catalog onsets) for part of the traces in our dataset with an automatic approach. We utilize these onsets as an initial reference for calibrating the parameters of STS. We set the parameter s, as of catalog onsets occur within 8 s of their respective origin times. This conservative choice enables the method to concentrate on the significant portion of the trace, where arrivals are more likely to occur.
To optimize the remaining parameters of STS, we compare the catalog onsets with the predictions made by only the first stage of HOSA (STS) across various configuration settings. Specifically, for each trace where STS assigns an onset , we claim that the onset is in agreement with the respective catalog onset if their difference fulfills the condition of Equation (8).
This choice corresponds to focusing on an onset accuracy of the order of 0.2 s, which is the typical magnitude of a good-quality pick in similar tectonic settings, as suggested by pick accuracy for a similar tectonic context provided in [42].
With this definition, we can establish two metrics to measure performance: precision and recall. The metrics are defined in Equation (9):
where is the number of agreeing onsets, is the total number of onsets assigned by the HOSA first stage, and is the total number of onsets in the catalog. Precision is a metric that evaluates the reliability of predictions generated by our technique, while recall expresses the ability of the technique to identify onsets in traces containing a P-phase.
Figure 5 reports the performance of STS for various choices of the parameter set: , , w, and . By testing with various values of , it has been observed that changes in relative performance across the various explored configurations are not significantly affected by the value of . Therefore, in Figure 5, we present the scenario, where is kept fixed at 75 ms, as the following observations can be extended to the case of a general value of . Moreover, the value of 75 ms will result in an optimal value for , as explained in the following paragraphs.
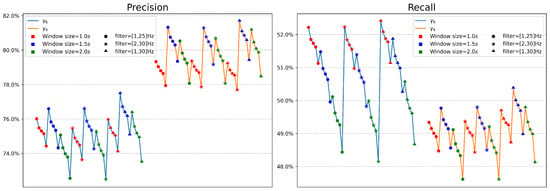
Figure 5.
Performances of STS across various settings, fixing the value ms. The trends of performances as parameters change are independent of values of sigma. Precision is displayed on the left panel, while, on the right panel, recall is displayed. Each point denotes a distinct configuration. Line colors represent the utilized statistics, marker colors denote window sizes, and marker shapes indicate the frequencies used for filtering. Each set of 5 points sharing identical markers and connected by identical line color denotes the different used for the multi-threshold criteria, with a value increasing from left to right.
We notice from Figure 5 that using the statistic (orange lines) instead of (light blue lines) leads to an improvement in precision values despite lower recall values. The plots show that a value of s (blue markers) consistently improves precision. There is no significant impact on performance among the filter frequencies used. However, setting Hz (triangular markers) leads to the highest precision and recall performances. In Figure 5, each set of five consecutive points identified with equal markers and connected by identical line color denotes the different thresholds of the multi-threshold criteria. Points are sorted in a way that the values of the respective increase from left to right: the first point belongs to the case , the second point to the case , and so on. We notice that in each case, the minimum threshold value of exhibits the best performance in terms of both precision and recall. Therefore, in our case, it is evident that the optimal value for the final P-onset corresponds to the first potential onset , related to the first threshold .
To select the optimal setup, we choose to adopt a conservative approach, prioritizing the reliability of predictions over their retrieval capacity (i.e., optimizing primarily for precision rather than recall). Therefore, we focus our attention on the behavior of the configuration exhibiting the best precision performance when varying the value. Performance indicators for this configuration and different are reported in Table 4. Precision values decrease as increases, while the opposite behavior is exhibited by recall values. We fixed ms as a good trade-off that maximizes the recall value and allows, at the same time, a high precision performance (which is not significantly lower than the optimal value).

Table 4.
Performance relative to the maximum-precision setting (i.e., the set {; Hz; s; }) across different values of . The green-highlighted row refers to the chosen value.
As expressed in Table 3, the chosen setup of the parameters of STS is {; Hz; s; ; ms}, which leads to the best precision performance.
The only parameter to be set for the MCS is the of Equation (6). We opt to set a value of s for all the arrays. This choice allows us to set a tolerance that is in accordance with the precision sought in Equation (8). Based on the values of for our arrays, presented in Table 1, we assume a propagation velocity of km/s for the area under study [43], which approximately corresponds to of the maximum of .
We remark that the ab initio availability of P-onsets for traces is not strictly necessary for the parameter setup. Parameters can be either adjusted according to specific criteria or needs as required (e.g., setting based on theoretical arrival times, in order to reflect a desired degree of precision, and so on) or optimized based on manually picked onsets from a small subset of the total traces.
5. Results
In this section, we configure the HOSA method according to the settings reported in Table 3 and apply it to the traces registered by DETECT stations derived from the catalog described in Section 2. We run HOSA on a Workstation DELL Precision 7820 Tower with 2 Intel Xeon Silver 4214R 2.4 GHz and 12 × 8 GB DDR4 2933 RDIMM ECC. Processing the entire dataset of about 30,700 traces takes less than 5 min. The method assigns a HOSA onset to 8113 of the total traces. We will refer to these onsets with the symbol . We recall that the number of traces associated with a catalog onset (indicated with ) is 8685. The two sets of traces (with an onset by HOSA and with an onset in the catalog) do not completely overlap. Specifically, the number of traces with onsets identified by both the catalog and HOSA is equal to . Traces with onsets solely detected by the catalog (and not by HOSA) are , whereas there exist traces with onsets exclusively identified by the HOSA method. In the following, we analyze the quality of the HOSA onsets.
5.1. SNR Examination and Solution Inspection
The initial evaluation of the proposed technique involves computing the signal-to-noise ratio (SNR) across the three distinct subsets , , and (see Figure 6). For each trace, SNR is calculated by dividing the standard deviation of the signal (i.e., the 4 s of waveform starting from the onset) by the standard deviation of the noise (i.e., the 4 s of waveform before the origin time).
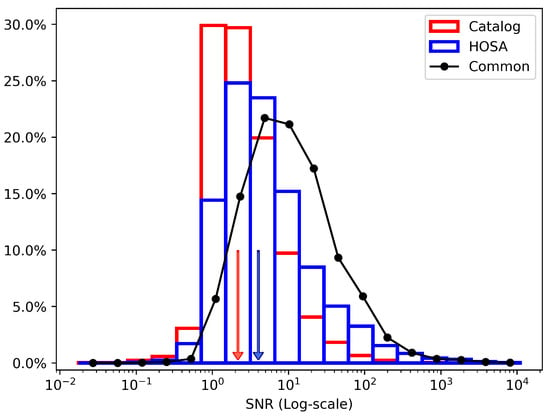
Figure 6.
Log-scaled SNR distribution of traces with onsets detected by both techniques (black line, 4797 traces), exclusively by the HOSA method (blue rectangles, 3316 traces), and only by catalog (red rectangles, 3888 traces). Red and blue arrows refer to the median of the catalog and HOSA SNR distributions, with values of and , respectively. The median SNR value for the common traces is . For common traces, considering the catalog onsets or the HOSA onsets does not affect the SNR distribution.
Figure 6 shows that the SNR distribution of traces with onsets solely in HOSA is more similar to the distribution of the common set, whereas the subset with onsets exclusively in the catalog is more concentrated towards lower SNR values, indicating that HOSA can pick traces with higher SNR. Approximately of the traces belonging exclusively to HOSA have an SNR greater than 4, compared to of the only catalog subset. Furthermore, the median values of the SNR distributions are 4.0 and 2.1 for HOSA and the catalog, respectively.
This implies that there are traces exclusively identified by HOSA that exhibit a high value of SNR. A visual examination has confirmed them to represent clear onsets of local events, correctly detected by our approach. They constitute additional high-quality onsets that were overlooked by the automated machine learning approach employed but retrieved by HOSA.
On the other hand, the catalog can pick more traces with low SNR that HOSA disregards. However, upon visually inspecting traces within the catalog’s densely populated bin where SNR < 1.5, it becomes evident that many of them consist predominantly of pure noise. In other cases, the catalog onset often shows a significant error as it is placed far from the event within the noisy segment. Only a small fraction of these traces represent reliable onsets (some examples are displayed in Figure 7).
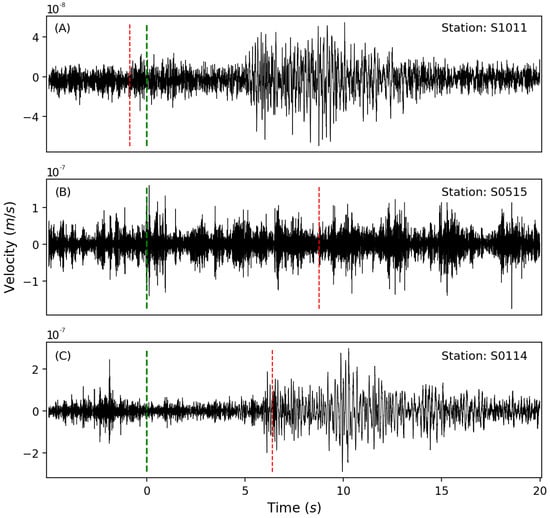
Figure 7.
Examples of traces belonging to the catalog’s high-populated bin with SNR < 1.5. Traces have been aligned by their respective event origin times, corresponding to the 0 point on the x-axis, indicated by green lines. Red lines denote the catalog arrival times. (A) Catalog onset showing a significant error. (B) Catalog onset assigned to noise. (C) Reliable catalog onset. Most of the traces in the considered bin belong to cases (A,B). HOSA doesn’t assign any onset to these traces. For cases (A,B), this is due to the barrage of the multi-threshold criterion in the STS, i.e., for the high standard deviation among the diverse potential onsets for the same trace. For case (C), the onset is rejected in the MCS barrage due to the non-satisfaction of the first criterion of Equation (7).
5.2. Consistency Examination: Semblance
A quality assessment of the HOSA onsets can be conducted by computing the semblance S, a quantity that can be interpreted as a measure of coherence for multi-channel data [44,45].
To emphasize the source component of the (ground velocity) recordings, for semblance calculations we band-pass filtered the traces in the range of Hz, which encloses the typical peak frequency of velocity seismograms produced by microearthquakes (M < 3—[46]). For a fixed event, we defined for the generic i-th array the value of the semblance , computed among the filtered traces aligned by their respective detected onsets , as explained in Equation (10):
where is the total number of traces with a detected onset for the i-th array, the integrand is referred to as temporal semblance, and the integrals are computed over , from a to a (with corresponding to the P-onset). We computed semblance values both using catalog onsets () and onsets by HOSA (). We fixed the extremes of the integral to the values s and s. This choice allowed us to focus on the first oscillation of the waveforms and to make the semblance sensitive to onset alignments. Semblance assumes values , and it is independent of individual signal amplitudes [47]. Semblance equals 1 when all the time series consist of identical values, i.e., all the waveforms are identical and perfectly aligned. In contrast, for uncorrelated noise . Examples of the semblance and temporal semblance of Equation (10) are depicted in Figure 8, where traces belonging to two events have been aligned by catalog onsets (top) and HOSA onsets (middle raw), demonstrating higher semblance values when onsets are such that waveforms exhibit higher coherence. We can notice that in the cases presented in Figure 8, the catalog onsets show an error of less than 0.1 s (manual analysis on each trace reveals a typical error of about 0.05 s). Despite the small error, semblance values on these catalog onsets are similar to those computed on noise, indicating the high sensitivity of semblance to small misalignment.
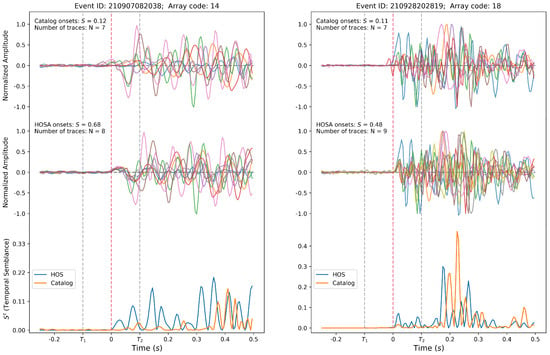
Figure 8.
Example cases of Semblance (S) computation for traces at a fixed array, along with respective temporal semblance ( last row). The waveforms belong to the events represented by yellow stars in Figure 1: the waveforms in the left panel are associated with the event located at (40°44′ N, 15°25′ E), while those in the right panel correspond to the event at (40°31′ N, 15°40′ E). Waveforms are aligned according to their respective onsets, indicated by dashed red lines. Different colors are used for the waveform lines solely to distinguish between them. In the first row, traces are aligned by catalog onsets , while, in the second row, they are aligned by HOSA onsets . Traces are considered in counts and normalized, dividing by the maximum values present in each displayed window. Dashed gray lines highlight the time interval of 0.2 s width considered to compute the residual semblance: , where corresponds to onset time minus 0.1 s and to onset time plus 0.1 s. These cases demonstrate HOSA’s ability to provide very precise predictions, as it leverages array concordance checks performed during the MCS.
It is more straightforward to evaluate the accuracy of the onset using residual semblance, which is the semblance reduced by the value expected for noise (Equation (11)).
We computed the residual semblance (Equation (11)) for all traces in each array for all events, employing the HOSA and catalog onsets, respectively. Figure 9 illustrates the distributions of residual semblance using HOSA and catalog onset, respectively. In the upper left panel, the distributions have been computed for all arrays, while the other panels show the value of residual semblance for arrays with a fixed number of detected arrivals. Due to the high sensitivity of semblance to a small misalignment, values of residual semblance slightly higher than zero indicate good alignment among the onsets.
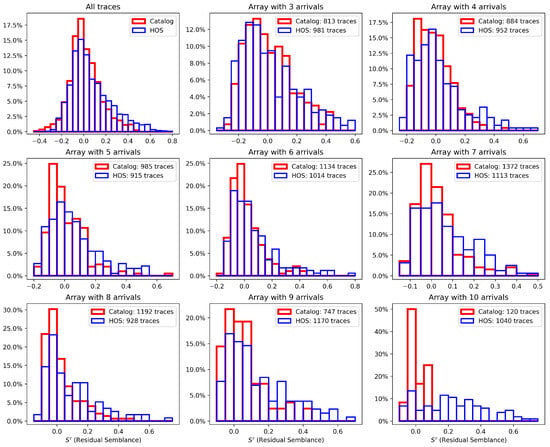
Figure 9.
Histograms of residual semblance values considering catalog and HOSA onsets. Bins have a width of 0.5. Each semblance value is computed by fixing an event and an array and utilizing all the waveforms with an onset assigned. We recall that residual semblance computed on uncorrelated noise assumes values equal to 0. Higher values correspond to better alignments of onsets. The top-left panel illustrates the case of considering all onsets, while the other panels show cases for arrays with a number of onsets specified in the respective panel’s title, varying from 3 to 10. HOSA shows higher residual semblance values, especially in the cases where the number of detected onsets per array is higher (>5), resulting in better overall alignment.
Figure 9 shows higher values of residual semblance for HOSA onsets, suggesting improved alignment compared to catalog onsets. Notably, the enhancement in residual semblance values is more pronounced when a larger number of waveforms are employed in semblance computation. In Table 5, we present the percentages of residual semblance that exhibit values greater than , i.e., significantly higher than zero, indicating a strong alignment among the respective onsets. In each case, HOSA exhibits a percentage of strong alignment greater than that of the catalog and also higher than (except for the scenario involving four detected arrivals per array). Remarkably, in cases where the number of detected arrivals exceeds eight, HOSA shows approximately half or more of the onsets with strong alignment, indicating a high capability to produce very accurate predictions.

Table 5.
Percentages of residual semblance values (a measure of onset alignment) greater than for HOSA and catalog onsets, corresponding to each case represented in Figure 9. In all cases, HOSA demonstrates higher percentages of residual semblance values above 0.1, indicating better onset alignment.
Impact of Noise Levels on Semblance
To compare the qualities of HOSA and catalog onsets based on noise levels, we examine how residual semblance varies with SNR. While SNR is computed for individual traces, semblance values are calculated using all traces of an event at a fixed array. To categorize semblance by SNR, we assign an average SNR to each array, computed as the mean SNR of its traces. The histograms in Figure 10 illustrate this categorization: the left panel includes semblance values for arrays with a mean SNR below 4, the right panel includes arrays with a mean SNR above 10, and the central panel represents all others. In each case of Figure 10, we observe that bins corresponding to higher residual semblance values are more populated for HOSA onsets than catalog onsets. The improvement is further evident in the case of SNR > 10, where, for all bins above (the condition for strong alignment defined in Section 5.2), the histogram for HOSA onsets shows values significantly higher than the catalog onsets histogram. As further demonstrated by Table 6, we notice that HOSA consistently improves prediction accuracy across all SNR ranges, with a greater improvement at higher SNR values.
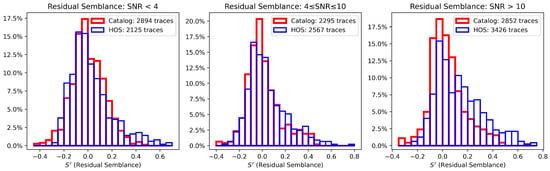
Figure 10.
Histograms of residual semblance for different SNR ranges. Bins have a width of 0.5. Each semblance value is computed by fixing an event and an array. Each panel contains semblance values of all the arrays whose mean SNR among traces falls in a fixed range (specifically SNR ≤ 4; 4 < SNR < 10; SNR ≥ 10). Bins corresponding to higher residual semblance values are consistently more populated for HOSA histograms than catalog ones across all SNR ranges.

Table 6.
Percentages of residual semblance values greater than 0.0 (a) and greater than 0.1 (b) across varying SNR ranges. In each SNR interval, HOSA demonstrates better alignment onsets. For a detailed analysis, refer to Figure 10.
5.3. False Detection Robustness: Comparison with STA/LTA
As presented here, HOSA is a versatile algorithm that combines single-trace statistical analysis with multi-channel coherence techniques, making it a reliable tool for detecting low-energy seismic events. To provide a more comprehensive analysis, we conduct a peer-to-peer comparison with the widely used STA/LTA method in this section.
STA/LTA [4] is traditionally used for single-trace triggering and detection tasks, particularly suited for continuous analysis. HOSA is designed for more refined analysis in networks with array geometry. The analysis of previous sections demonstrates HOSA’s ability to handle low-energy P-wave arrivals and low-SNR signals, where STA/LTA often struggles. Hereafter, the robustness of HOSA in terms of false detections in noise-only traces is also analyzed and compared with STA/LTA performance. To further facilitate the peer-to-peer comparison, we focus on evaluating only the single-trace stage (STS) of HOSA, noting that the second multi-channel stage can further enhance the reliability of predictions.
We analyzed two independent noise-only traces and made a comparison between the two techniques in terms of false detections. Figure 11 shows the analysis of Trace A, a trace extracted from one of the events used in our study at station 03 of array 01, while in Figure S1, Trace B from station 04 of array 02 is analyzed. Following the suggestion reported in [48], we set the parameters of STA/LTA in an appropriate way for detecting local weak earthquakes in a weak-motion context. Specifically, we set the following:
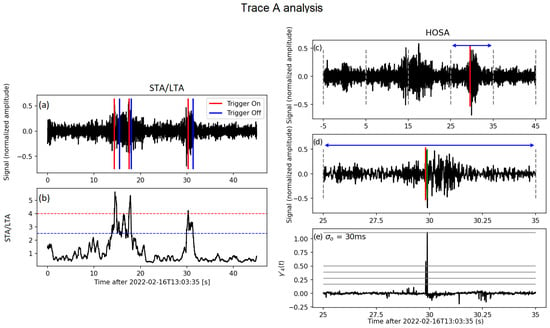
Figure 11.
Trace A analysis: Robustness to false detection for STA/LTA and single-trace stage (STS) of HOSA. Panel (a) shows the noise-only seismic trace used, along with the 3 false detections assigned by the STA/LTA technique (red vertical lines). Panel (b) represents the STA/LTA function along with the triggering thresholds, represented by blue and red dashed lines, respectively. Panel (c) depicts the same trace, along with the pick assigned by STS, marked by a red line (note that in a real application, this pick would undergo a secondary selection step performed by the MCS). To apply the STS of HOSA, the whole trace was divided into five 10 s sub-traces, each marked by vertical dashed grey lines in Panel (c). The blue arrows between 25 and 35 s highlight the window with the HOSA false detection. Panels (d,e) provide a detailed analysis of the STS application on the window that resulted in the HOSA false detection. Panel (d) zooms on the time interval between 25 and 35 s of Panel (c). Here, we indicate with green lines the different potential onsets determined by STS (only 2 are visible because they overlap). Panel (e) shows the corresponding fourth-order statistic (), along with the 5 thresholds used for the multi-threshold criterion of STS (refer to the main text for a complete explanation). This onset is accepted by STS due to the value ms < 75 ms, as reported in the upper-left part of the panel. Zoomed-in views of the other sub-traces are provided in Figure S2.
- Length of LTA windows to 15 s;
- Length of STA windows to 0.5 s;
- Triggering threshold to 4;
- Detriggering threshold to 2.5.
HOSA settings remain the same as expressed in Table 3 of Section 4, except for , which is set to 10 s here.
In both Figure 11 and Figure S1, the left panels (a and b) show the application of the STA/LTA technique. STA/LTA produces three false triggers for Trace A and three for Trace B. While higher threshold levels could reduce false detections, they would also lower detection rates in the context of microseismicity.
We applied HOSA’s STS for both Trace A and Trace B. To this end, we divided each trace analyzed with STA/LTA into five sub-traces of length equal to 10 s. We recall that STS searches for exactly one onset in only a sub-trace of 10 s and only accepts onsets whose standard deviations satisfy ms. The right panels of Figure 11 and Figure S1 demonstrate that the STS of HOSA is more robust with respect to STA/LTA, producing only one single false detection among the five windows for Trace A and none for Trace B (other potential onsets have been discarded due to high values). We remark that only the STS was used here. The application of the MCS step potentially further improves the reliability of predictions, possibly discarding some of the false detection by the STS. Figure S2 shows, in detail, the application of STS for each sub-trace deriving from Trace A analysis.
The results of this analysis demonstrate HOSA’s robustness against false detections. When applied to two 50 s noise-only traces, HOSA produced only one false detection compared to six false detections by STA/LTA, reducing the number of false alarms by a factor of six.
6. Discussions and Conclusions
Higher-order statistics for array algorithms (HOSAs) combine single-trace statistical analysis with multi-channel coherence analysis to infer P-wave onsets for a list of earthquakes. HOSA can work to refine, filter, and integrate a set of available arrival times or to define a new set of arrival times.
HOSA first includes a single-trace stage that uses a multi-threshold criterion to estimate the P arrival times, while the position of the sensors in arrays is exploited in the second part of the algorithm to refine and consolidate the arrival times estimated from the first module. The presence of two separate modules in HOSA allows its usage in cases not limited to array-like seismic sensor spatial configurations, which are only seldom available.
In this sense, HOSA differs from classical array-based approaches such as the beam-forming method, in which the single-station recordings of a seismic array are time-shifted to maximize the constructive interference between the traces and are eventually stacked. This results in the generation of one signal with a possible higher SNR than the individual recordings of the array. HOSA does not perform any similar data reduction, while the spatial redundancy of recordings due to the array-based geometry is exploited in the second module. It is worth noting that HOSA, in its current form, is not optimized for detection purposes. Instead, it requires an earthquake catalog as input and aims to integrate/refine P arrival times using an approach that complements both classical STA/LTA methods and machine learning-based techniques.
Here, we tested HOSA on a catalog of 226 microearthquakes recorded in Irpinia (Italy) by twenty 10-receiver seismic arrays deployed between 2021–2022. We compared the results of HOSA with a set of P-arrivals automatically computed using a template-matching approach (whose detections are here referred to as “catalog onsets”). In less than 5 min of computation, HOSA detected 8113 onsets out of the 30,700 analyzed traces, a number slightly lower than the 8685 catalog onsets. Among these, 3316 onsets were uniquely detected by HOSA and exhibited higher SNR values (median SNR = 4.0) than catalog-exclusive ones (median SNR = 2.1). Traces exclusively identified by HOSA exhibited high SNR values and were confirmed to represent clear onsets of local events. These high-quality onsets, overlooked by the automated machine learning approach, were successfully detected by HOSA. Residual semblance analysis revealed better onset consistency and alignment for HOSA, with up to 68% of arrays achieving strong alignment (residual semblance > 0.1), compared to 0% for the catalog in the 10-arrival case. Table 6 demonstrates the better consistency of HOSA’s prediction across all the investigated SNR ranges, achieving up to 50% strong alignment in the cases of SNR > 10.
Additionally, the single-trace Stage of HOSA is compared with the widely used STA/LTA method. The comparison demonstrated the reduced false detection rate for our technique in noise-only traces by a factor of six compared to STA/LTA.
The application of HOSA to the Irpinia microseismicity shows that this algorithm relevantly improves performance in accurately picking the P onset when the first module returns five arrivals or more within a 2–3 km spacing array (see Table 5); this implicitly implies that HOSA, similarly to other array techniques, works better for dense seismic arrays. The same test case also shows that HOSA improves its resolution in P picking mostly for SNRs larger than four (although actually, HOSA shows more accurate P picking than the template matching approach for all levels of SNR, Figure 10). These results should be taken into account when HOSA is applied to different seismic areas possibly dominated by microseismicity (for which the accurate phase picking is especially challenging though crucial), such as a tool to complement other picking systems.
The results of the HOSA algorithm support the possibility to refine and eventually increase the dataset of phase arrival times provided by advanced detection techniques. Recent studies pointed out limitations in the application of machine-learning pickers, including EQTransformer, for the identification of the phase arrival times due to fluctuations of the probability values according to the different positions of the earthquake within the considered portion of continuous data [29,49]. Increasing the overlap between adjacent time windows has been proposed as a mitigation strategy to improve the robustness of detections made by machine-learning pickers [29,49], leading to a higher computational cost when applying continuous data. Therefore, HOSA is also presented as an integrating strategy to effectively complement the application of machine-learning pickers.
HOSA does not require any special technological infrastructure. In fact, differently from other automated approaches, HOSA is not time-consuming and computer-demanding and does not require large memory allocations (it takes less than 5 min to process ≃ 30,000 traces on a Workstation DELL Precision 7820 Tower with 2 Intel Xeon Silver 4214R 2.4 GHz, and 12 × 8 GB DDR4 2933 RDIMMECC). For this reason, HOSA appears to be remarkably suitable for potential employment in automated workflows. The reliable predictions generated by HOSA make it suitable for efficiently revising or validating large volumes of data in catalogs using a consistent method. It can quickly and robustly discard incorrect P-onsets and refine inaccurate ones in databases. Moreover, HOSA can ideally integrate automatic real-time procedures for the picking of the seismic phases, such as those routinely adopted for seismic monitoring, improving the quality of the readings and eventually allowing a more precise automatic earthquake location.
In conclusion, we found that HOSA solutions have the following characteristics:
- They are reliable and less prone to false P-onset detection than STA/LTA;
- They show higher inter-array consistency than template-matching solutions, especially in cases of a high number of detected onsets per array.
Future developments of HOSA could include tailoring of method for more challenging scenarios, such as picking secondary seismic phases or emergent arrivals from volcanic or tectonic tremors. Moreover, additional enhancements in detection reliability could be investigated by testing the MCS, which leverages array-based information, to improve false detection robustness further.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/app15031172/s1. The file includes Figure S1: Trace B analysis—Robustness to false detection for STA/LTA and single-trace stage (STS) of HOSA; Figure S2: Zoomed-in views of HOSA’s application (STS) on the sub-traces from Trace A (Figure 11 in the main text).
Author Contributions
Conceptualization: G.M. and M.P.; methodology, G.M. and M.P.; software: G.M. and M.P.; validation: G.M., S.S., F.N., and O.A.; formal analysis: G.M.; data curation: F.N. and F.S.d.U.; writing—original draft preparation: G.M., S.S., F.N., O.A., M.P., and F.S.d.U.; writing—review and editing: G.M., S.S., F.N., O.A., M.P., and P.C.; visualization: G.M. and O.A.; supervision: M.P. and S.S.; project administration: P.C.; funding acquisition: O.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by TOGETHER-Sustainable geothermal energy for two Southern Italy regions: geophysical resource evaluation and public awareness financed by European Union—Next Generation EU Piano Nazionale di Ripresa e Resilienza Missione 4-Componente 2-CUP D53D23022850001 and by a PhD fellowship financed by the European Union—Next Generation EU DM 118/2023, CUP D42B23001820006.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The events used for this study are those reported in the manual catalog provided by ISNet (http://isnet-bulletin.fisica.unina.it/cgi-bin/isnet-events/isnet.cgi; last accessed on 18 January 2025) and occurred in the period September 2021–February 2022. The waveforms supporting the findings of this study are currently under embargo and Available on 2025-09-01. Further inquiries regarding data access may be found at https://doi.org/10.14470/MX7576871994 or directed to the corresponding author. The code of the presented technique will be made available by the authors on request.
Acknowledgments
All authors would like to thank the reviewers for their valuable contributions that have enhanced the quality of our paper. Figure 1 has been obtained through GMT 6.0.0 [50] software. Figure 2 has been obtained through the free online diagram maker software (https://app.diagrams.net; last accessed on 18 January 2025). All other figures have been produced using the Python library Matplotlib (Matplotlib version 3.5.2; Python 3.8.10) [51]. All authors would also like to extend their thanks to the authors of [52] for providing access to the seismic traces used in this study that formed the foundation of our analyses.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| HOSA | Higher-order statistics for srray |
| HOS | Higher-order statistics |
| STS | Single-trace stage |
| MCS | Multi-channel stage |
| SNR | Signal-to-noise ratio |
References
- Lehujeur, M.; Vergne, J.; Schmittbuhl, J.; Zigone, D.; Le Chenadec, A.; Team, E. Reservoir imaging using ambient noise correlation from a dense seismic network. J. Geophys. Res. Solid Earth 2018, 123, 6671–6686. [Google Scholar] [CrossRef]
- Zhang, Z.; Deng, Y.; Qiu, H.; Peng, Z.; Liu-Zeng, J. High-resolution imaging of fault zone structure along the creeping section of the Haiyuan fault, NE Tibet, from data recorded by dense seismic arrays. J. Geophys. Res. Solid Earth 2022, 127, e2022JB024468. [Google Scholar] [CrossRef]
- Gritto, R.; Jarpe, S.P.; Hartline, C.S.; Ulrich, C. Seismic imaging of reservoir heterogeneity using a network with high station density at The Geysers geothermal reservoir, CA, USA. Geophysics 2023, 88, WB11–WB22. [Google Scholar] [CrossRef]
- Allen, R.V. Automatic earthquake recognition and timing from single traces. Bull. Seismol. Soc. Am. 1978, 68, 1521–1532. [Google Scholar] [CrossRef]
- Saragiotis, C.D.; Hadjileontiadis, L.J.; Panas, S.M. PAI-S/K: A robust automatic seismic P phase arrival identification scheme. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1395–1404. [Google Scholar] [CrossRef]
- Baillard, C.; Crawford, W.C.; Ballu, V.; Hibert, C.; Mangeney, A. An automatic kurtosis-based P-and S-phase picker designed for local seismic networks. Bull. Seismol. Soc. Am. 2014, 104, 394–409. [Google Scholar] [CrossRef]
- Langet, N.; Maggi, A.; Michelini, A.; Brenguier, F. Continuous kurtosis-based migration for seismic event detection and location, with application to Piton de la Fournaise Volcano, La Reunion. Bull. Seismol. Soc. Am. 2014, 104, 229–246. [Google Scholar] [CrossRef]
- Hildyard, M.W.; Nippress, S.E.; Rietbrock, A. Event detection and phase picking using a time-domain estimate of predominate period T pd. Bull. Seismol. Soc. Am. 2008, 98, 3025–3032. [Google Scholar] [CrossRef]
- Zhang, H.; Thurber, C.; Rowe, C. Automatic P-wave arrival detection and picking with multiscale wavelet analysis for single-component recordings. Bull. Seismol. Soc. Am. 2003, 93, 1904–1912. [Google Scholar] [CrossRef]
- Amoroso, O.; Maercklin, N.; Zollo, A. S-wave identification by polarization filtering and waveform coherence analyses. Bull. Seismol. Soc. Am. 2012, 102, 854–861. [Google Scholar] [CrossRef]
- Diehl, T.; Deichmann, N.; Kissling, E.; Husen, S. Automatic S-wave picker for local earthquake tomography. Bull. Seismol. Soc. Am. 2009, 99, 1906–1920. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Ellsworth, W.L.; Zhu, W.; Chuang, L.Y.; Beroza, G.C. Earthquake transformer—An attentive deep-learning model for simultaneous earthquake detection and phase picking. Nat. Commun. 2020, 11, 3952. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Ross, Z.E.; Zhu, W.; Azizzadenesheli, K. Phase Neural Operator for Multi-Station Picking of Seismic Arrivals. Geophys. Res. Lett. 2023, 50, e2023GL106434. [Google Scholar] [CrossRef]
- Zhou, Y.; Yue, H.; Kong, Q.; Zhou, S. Hybrid event detection and phase-picking algorithm using convolutional and recurrent neural networks. Seismol. Res. Lett. 2019, 90, 1079–1087. [Google Scholar] [CrossRef]
- Ma, X.; Chen, T. Small seismic events in Oklahoma detected and located by machine learning–based models. Bull. Seismol. Soc. Am. 2022, 112, 2859–2869. [Google Scholar] [CrossRef]
- Jiang, C.; Fang, L.; Fan, L.; Li, B. Comparison of the earthquake detection abilities of PhaseNet and EQTransformer with the Yangbi and Maduo earthquakes. Earthq. Sci. 2021, 34, 425–435. [Google Scholar] [CrossRef]
- Scotto di Uccio, F.; Scala, A.; Festa, G.; Picozzi, M.; Beroza, G.C. Comparing and integrating artificial intelligence and similarity search detection techniques: Application to seismic sequences in Southern Italy. Geophys. J. Int. 2023, 233, 861–874. [Google Scholar] [CrossRef]
- Palo, M.; Scotto di Uccio, F.; Picozzi, M.; Festa, G. An Enhanced Catalog of Repeating Earthquakes on the 1980 Irpinia Fault System, Southern Italy. Geosciences 2023, 14, 8. [Google Scholar] [CrossRef]
- Bernard, P.; Zollo, A. The Irpinia (Italy) 1980 earthquake: Detailed analysis of a complex normal faulting. J. Geophys. Res. Solid Earth 1989, 94, 1631–1647. [Google Scholar] [CrossRef]
- Lombardi, G. Irpinia earthquake and history: A nexus as a problem. Geosciences 2021, 11, 50. [Google Scholar] [CrossRef]
- Rovida, A.; Locati, M.; Camassi, R.; Lolli, B.; Gasperini, P.; Antonucci, A. Catalogo Parametrico dei Terremoti Italiani 651 (cpti15); Istituto Nazionale di Geofisica e Vulcanologia (INGV): Rome, Italy, 2016.
- Chiaraluce, L.; Festa, G.; Bernard, P.; Caracausi, A.; Carluccio, I.; Clinton, J.F.; Di Stefano, R.; Elia, L.; Evangelidis, C.; Ergintav, S.; et al. The Near Fault Observatory community in Europe: A new resource for faulting and hazard studies. Ann. Geophys. 2022, 65, DM316. [Google Scholar] [CrossRef]
- Weber, E.; Convertito, V.; Iannaccone, G.; Zollo, A.; Bobbio, A.; Cantore, L.; Corciulo, M.; Di Crosta, M.; Elia, L.; Martino, C.; et al. An advanced seismic network in the southern Apennines (Italy) for seismicity investigations and experimentation with earthquake early warning. Seismol. Res. Lett. 2007, 78, 622–634. [Google Scholar] [CrossRef]
- De Landro, G.; Amoroso, O.; Stabile, T.A.; Matrullo, E.; Lomax, A.; Zollo, A. High-precision differential earthquake location in 3-D models: Evidence for a rheological barrier controlling the microseismicity at the Irpinia fault zone in southern Apennines. Geophys. Suppl. Mon. Not. R. Astron. Soc. 2015, 203, 1821–1831. [Google Scholar] [CrossRef]
- Palo, M.; Picozzi, M.; De Landro, G.; Zollo, A. Microseismicity clustering and mechanic properties reveal fault segmentation in southern Italy. Tectonophysics 2023, 856, 229849. [Google Scholar] [CrossRef]
- Picozzi, M.; Iaccarino, A.G.; Bindi, D.; Cotton, F.; Festa, G.; Strollo, A.; Zollo, A.; Alfredo Stabile, T.; Adinolfi, G.M.; Martino, C.; et al. The DEnse mulTi-paramEtriC observations and 4D high resoluTion imaging (DETECT) experiment, a new paradigm for near-fault observations. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 23–27 May 2022; p. EGU22-8536. [Google Scholar]
- Bobbio, A.; Vassallo, M.; Festa, G. A local magnitude scale for southern Italy. Bull. Seismol. Soc. Am. 2009, 99, 2461–2470. [Google Scholar] [CrossRef]
- Chamberlain, C.J.; Hopp, C.J.; Boese, C.M.; Warren-Smith, E.; Chambers, D.; Chu, S.X.; Michailos, K.; Townend, J. EQcorrscan: Repeating and near-repeating earthquake detection and analysis in Python. Seismol. Res. Lett. 2018, 89, 173–181. [Google Scholar] [CrossRef]
- Park, Y.; Beroza, G.C.; Ellsworth, W.L. A mitigation strategy for the prediction inconsistency of neural phase pickers. Seismol. Soc. Am. 2023, 94, 1603–1612. [Google Scholar] [CrossRef]
- Basili, R.; Burrato, P.; Fracassi, U.; Kastelic, V.; Maesano, F.; Tarabusi, G.; Tiberti, M.M.; Valensise, G.; Vallone, R.; Vannoli, P.; et al. Database of Individual Seismogenic Sources (DISS), Version 3.3.0: A compilation of potential sources for earthquakes larger than M 5.5 in Italy and surrounding areas. Istituto Nazionale di Geofisica e Vulcanologia (INGV); Istituto Nazionale di Geofisica e Vulcanologia (INGV): Sezione di Catania, Italy, 2021. [CrossRef]
- Lokajíček, T.; Klima, K. A first arrival identification system of acoustic emission (AE) signals by means of a high-order statistics approach. Meas. Sci. Technol. 2006, 17, 2461. [Google Scholar] [CrossRef]
- Li, X.; Shang, X.; Wang, Z.; Dong, L.; Weng, L. Identifying P-phase arrivals with noise: An improved Kurtosis method based on DWT and STA/LTA. J. Appl. Geophys. 2016, 133, 50–61. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R.; Taylor, J. Unsupervised learning. In An Introduction to Statistical Learning: With Applications in Python; Springer: Berlin/Heidelberg, Germany, 2023; pp. 503–556. [Google Scholar]
- Hansen, P.; Jaumard, B. Cluster analysis and mathematical programming. Math. Program. 1997, 79, 191–215. [Google Scholar] [CrossRef]
- Gordon, A.D. A review of hierarchical classification. J. R. Stat. Soc. Ser. A (Gen.) 1987, 150, 119–137. [Google Scholar] [CrossRef]
- Müllner, D. Modern hierarchical, agglomerative clustering algorithms. arXiv 2012, arXiv:1109.2378. [Google Scholar]
- Murtagh, F.; Contreras, P. Algorithms for hierarchical clustering: An overview. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2012, 2, 86–97. [Google Scholar] [CrossRef]
- Palo, M.; Ogliari, E.; Sakwa, M. Spatial pattern of the seismicity induced by geothermal operations at the Geysers (California) inferred by unsupervised machine learning. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5905813. [Google Scholar] [CrossRef]
- Palo, M.; Schubert, B.; Ogliari, E.; Wei, J.; Gu, K.; Liu, W. Detection, features extraction and classification of radio-frequency pulses in a high-voltage power substation: Results from a measurement campaign. In Proceedings of the 2020 IEEE 3rd International Conference on Dielectrics (ICD), Valencia, Spain, 5–31 July 2020; pp. 677–680. [Google Scholar]
- Guénoche, A.; Hansen, P.; Jaumard, B. Efficient algorithms for divisive hierarchical clustering with the diameter criterion. J. Classif. 1991, 8, 5–30. [Google Scholar] [CrossRef]
- Wang, Y.; Yan, H.; Sriskandarajah, C. The weighted sum of split and diameter clustering. J. Classif. 1996, 13, 231–248. [Google Scholar] [CrossRef]
- Napolitano, F.; Amoroso, O.; La Rocca, M.; Gervasi, A.; Gabrielli, S.; Capuano, P. Crustal structure of the seismogenic volume of the 2010–2014 Pollinof (Italy) seismic sequence from 3D P-and S-wave tomographic images. Front. Earth Sci. 2021, 9, 735340. [Google Scholar] [CrossRef]
- Amoroso, O.; Ascione, A.; Mazzoli, S.; Virieux, J.; Zollo, A. Seismic imaging of a fluid storage in the actively extending Apennine mountain belt, southern Italy. Geophys. Res. Lett. 2014, 41, 3802–3809. [Google Scholar] [CrossRef]
- Neidell, N.S.; Taner, M.T. Semblance and other coherency measures for multichannel data. Geophysics 1971, 36, 482–497. [Google Scholar] [CrossRef]
- Palo, M.; Tilmann, F.; Krüger, F.; Ehlert, L.; Lange, D. High-frequency seismic radiation from Maule earthquake (M w 8.8, 2010 February 27) inferred from high-resolution backprojection analysis. Geophys. J. Int. 2014, 199, 1058–1077. [Google Scholar] [CrossRef]
- Aki, K.; Richards, P.G. Quantitative Seismology; University Science Books: Herndon, VA, USA, 2002. [Google Scholar]
- Rößler, D.; Krueger, F.; Ohrnberger, M.; Ehlert, L. Rapid characterisation of large earthquakes by multiple seismic broadband arrays. Nat. Hazards Earth Syst. Sci. 2010, 10, 923–932. [Google Scholar] [CrossRef][Green Version]
- Trnkoczy, A. Understanding and parameter setting of STA/LTA trigger algorithm. In New Manual of Seismological Observatory Practice (NMSOP); Deutsches GeoForschungsZentrum GFZ: Potsdam-Süd, Germany, 2009; pp. 1–20. [Google Scholar]
- Pita-Sllim, O.; Chamberlain, C.J.; Townend, J.; Warren-Smith, E. Parametric testing of EQTransformer’s performance against a high-quality, manually picked catalog for reliable and accurate seismic phase picking. Seism. Rec. 2023, 3, 332–341. [Google Scholar] [CrossRef]
- Wessel, P.; Luis, J.F.; Uieda, L.A.; Scharroo, R.; Wobbe, F.; Smith, W.H.; Tian, D. The generic mapping tools version 6. Geochem. Geophy. Geosy. 2019, 20, 5556–5564. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Bindi, D.; Cotton, F.; Picozzi, M.; Zollo, A. The Irpinia Seismic Array 2021. Available online: https://geofon.gfz.de/doi/network/ZK/2021 (accessed on 18 January 2025). [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).