Reliability-Constrained Structural Design Optimization Using Visual Programming in Building Information Modeling (BIM) Projects
Abstract
Featured Application
Abstract
1. Introduction
2. State of the Art
2.1. Structural Design Optimization
2.2. Metaheuristic Algorithms
2.3. Relability Analysis
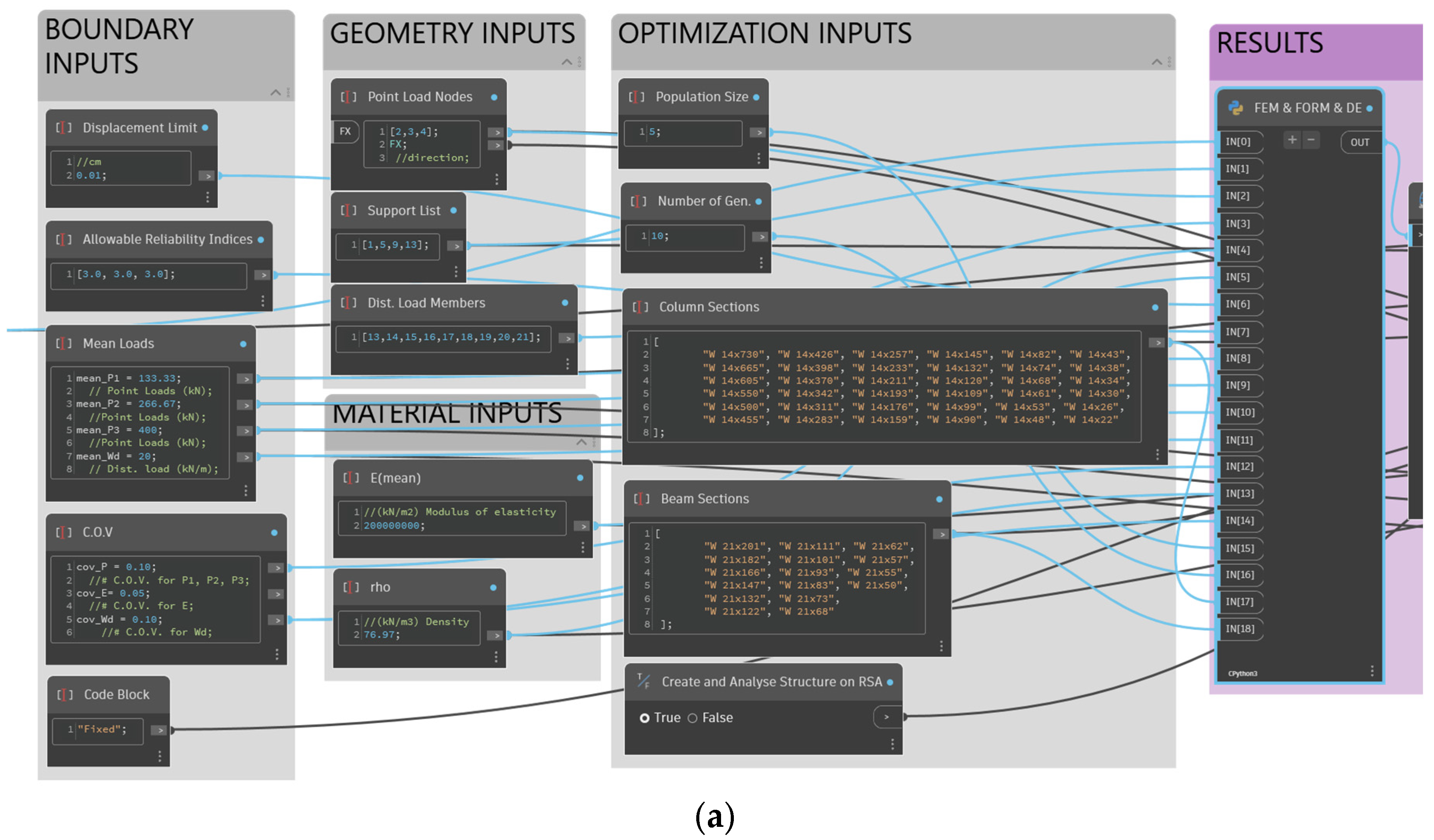
3. Materials and Methods
- Create parametric trusses by using VP (Figure 2);
- Create a FEM model to perform structural analyses (Figure 3);
- Perform reliability analysis (Figure 4);
- Change the design variables with MAs and perform multiple reliability analyses until design criteria are fulfilled (Figure 5);
- Import the optimized model to the BIM environment for refinement (Figure 6).

3.1. Problem Formulation
3.2. Computational Software and Hardware
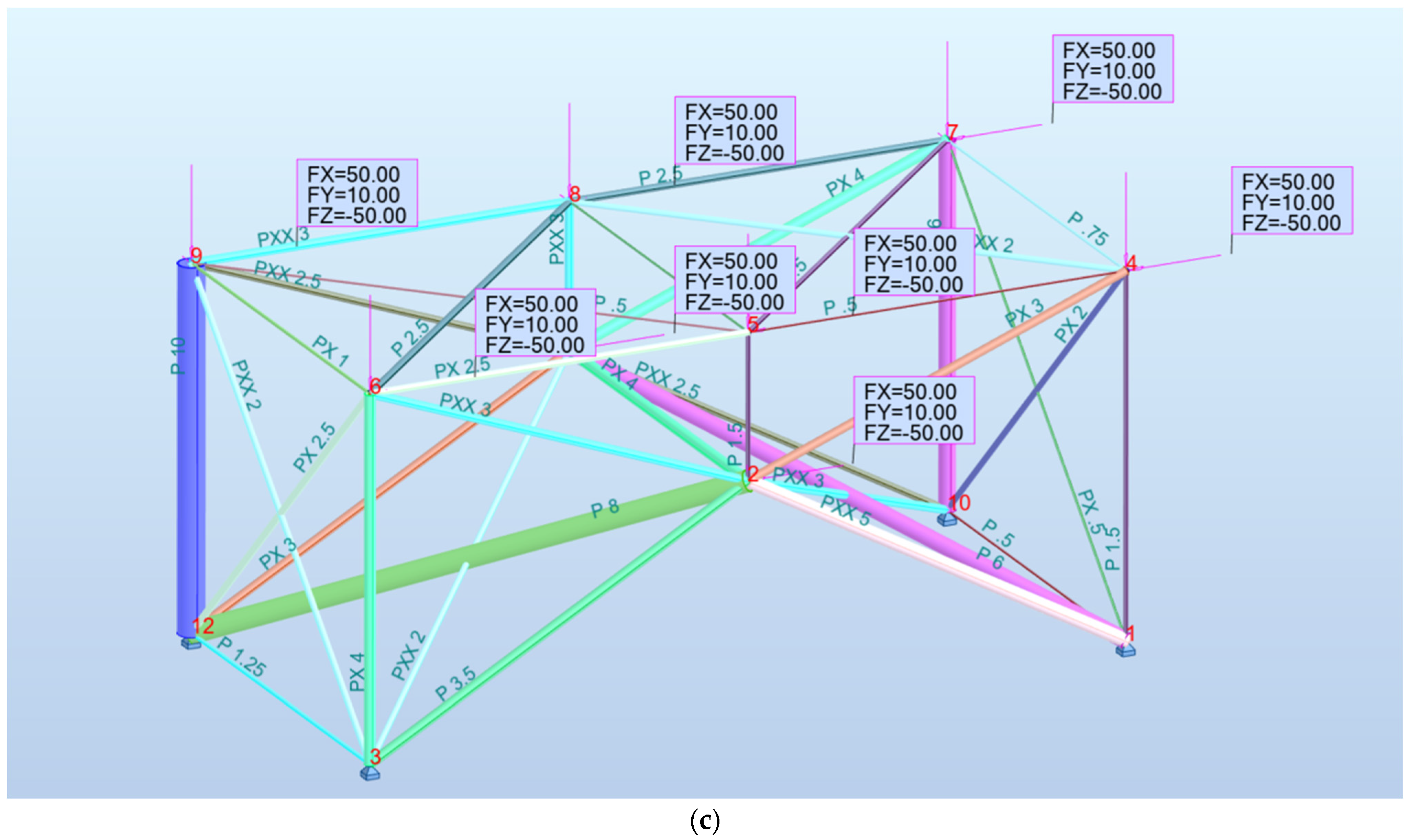
3.3. Design and Development of Parametric Models
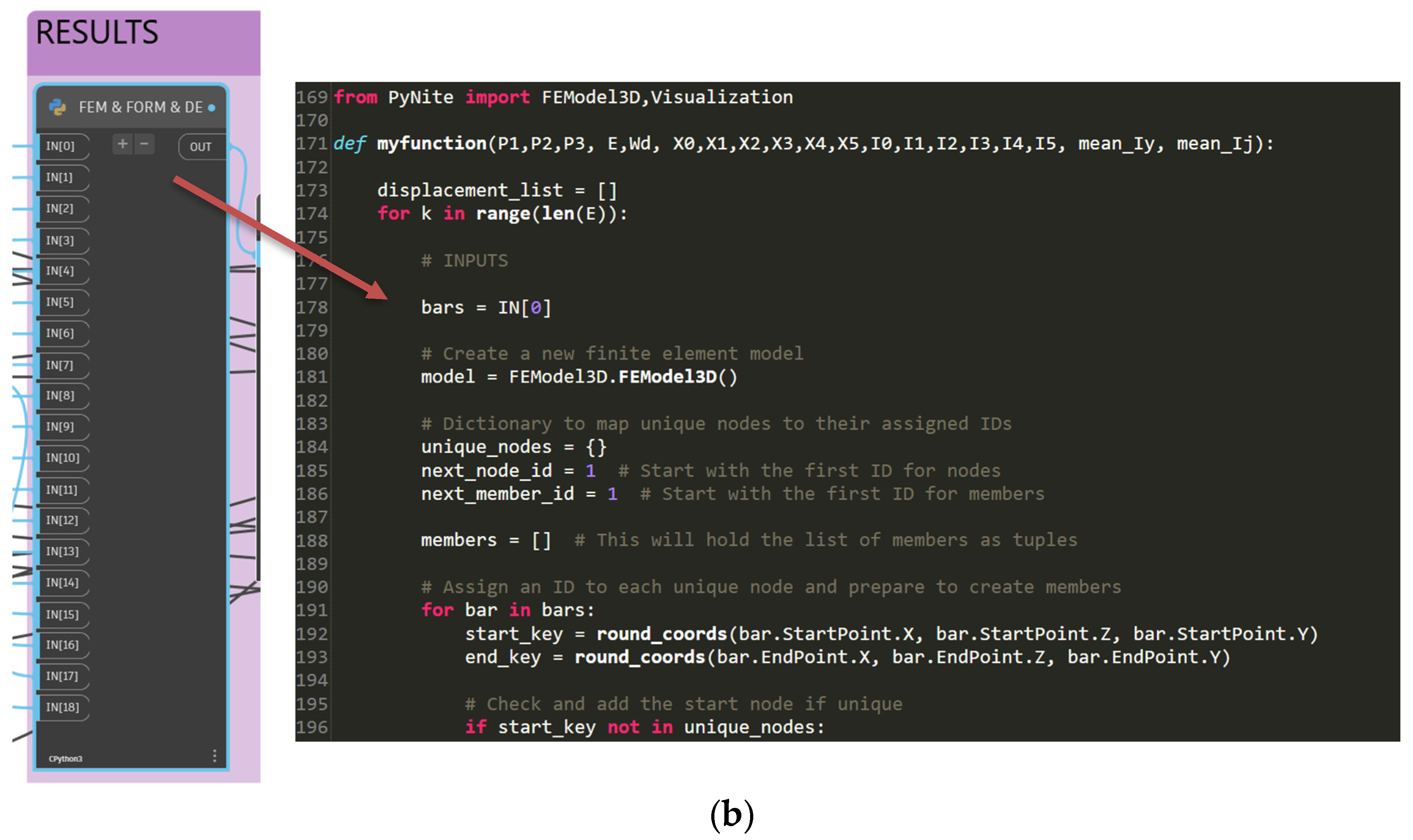
3.4. Structural Analysis in Dynamo Visual Programming
| Algorithm 1: FEM Analysis on Dynamo Through Python Node | |||
| Input: Initial design variables (e.g., loads) | |||
| Output: FEM results (e.g. displacements) | |||
| 1. | Initialize results list; | ||
| 2. | for k in design configurations do | ||
| 3. | Initialize model, nodes and member lists; | ||
| 4. | for bar in IN[0], where IN[0] is Dynamo structural elements list, do | ||
| 5. | Extract nodes and members from Dynamo; | ||
| 6. | Assign IDs to start and end nodes, create FEM model; | ||
| end | |||
| 7. | Add supports to model; | ||
| 8. | Add material properties from Dynamo inputs; | ||
| 9. | Add section properties from Dynamo inputs; | ||
| 10. | for i, member in members do | ||
| 11. | Add member to model with material and section properties; | ||
| end | |||
| 12. | Add loads from Dynamo inputs; | ||
| 13. | Analyze model; | ||
| 14. | Append FEM results to results list; | ||
| end | |||
| 15. | Return FEM results; | ||
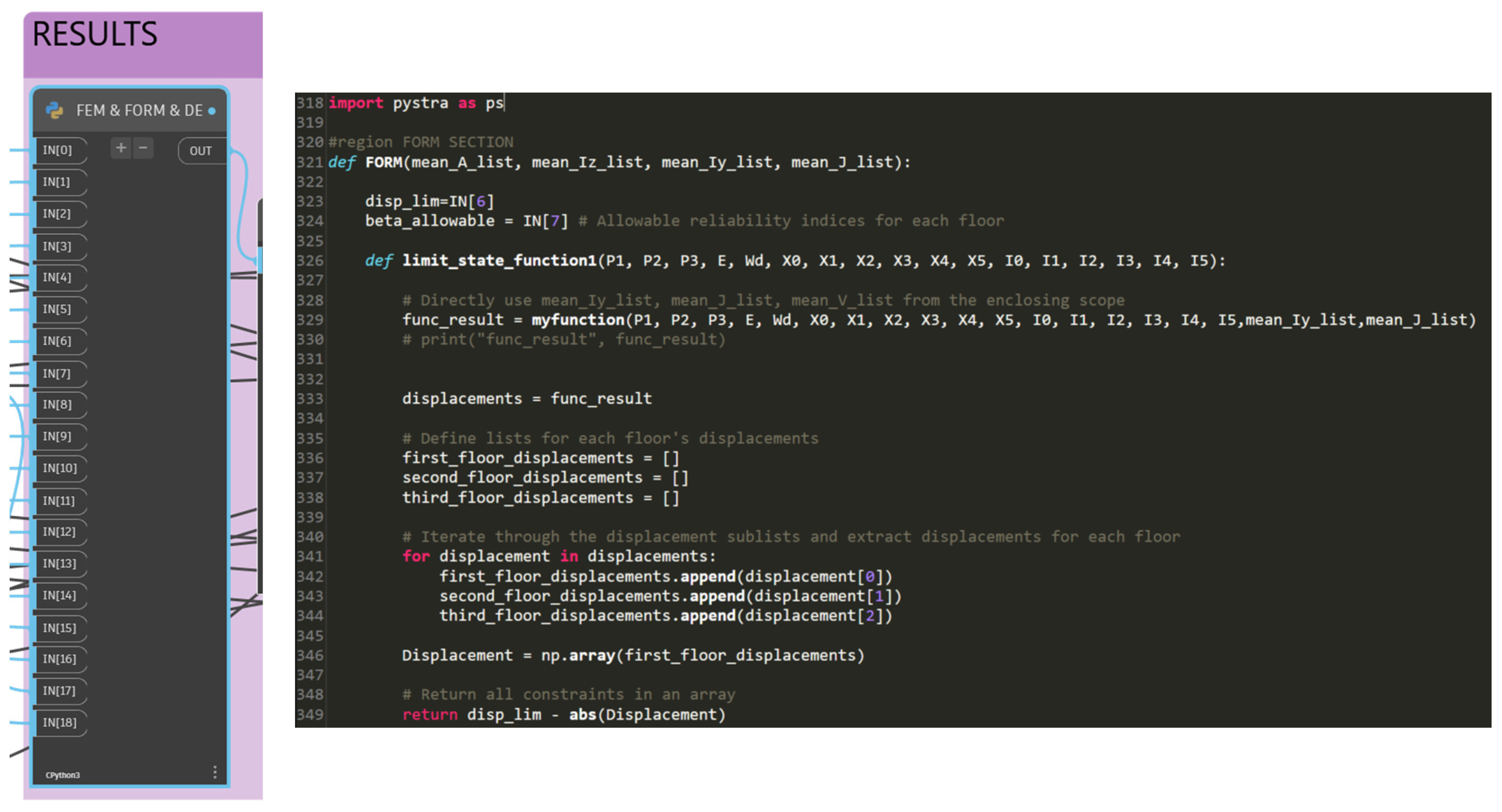
3.5. Reliability Analysis
| Algorithm 2: FORM Analysis on Dynamo Through Python Node | |||
| Input: Structure with mean-COV values for design variables (e.g., elasticity modulus) | |||
| Output: Constraint violation | |||
| 1. | Initialize violation list; | ||
| 2. | Set displacement limits from Dynamo; | ||
| 3. | Set allowable reliability from Dynamo; | ||
| 4. | Create stochastic model with predefined random variables; | ||
| 5. | Define FEM based LSF by using logic in Algorithm 1; | ||
| 6. | while i < imax, where imax is maximum iteration number, do | ||
| 7. | Compute LSF by calling FEM model; | ||
| 8. | Update the search point; | ||
| 9. | Check convergence; | ||
| 10. | if converged: break; | ||
| 11. | i ← i + 1; | ||
| end | |||
| 12. | Get beta values; | ||
| 13. | Calculate violation = (beta_allowable − beta)/beta_allowable; | ||
| 14. | Return violation list; | ||
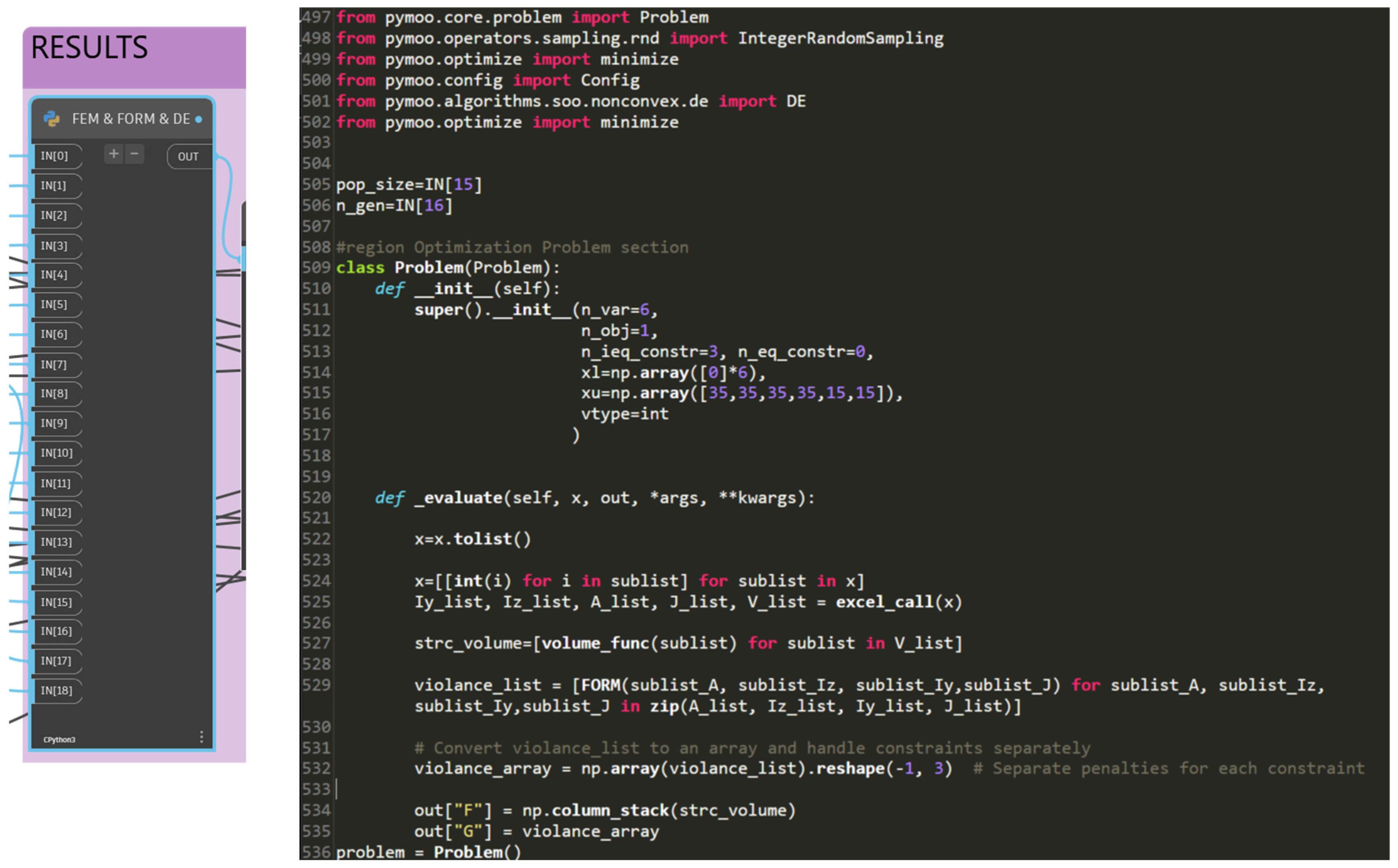
3.6. AI-Based Optimization
| Algorithm 3: RBDO Problem Definition and Optimization | |||
| Input: Optimization problem with parameters (e.g., population size) | |||
| Output: Optimized design variables (e.g., cross-sectional areas) | |||
| 1. | Define the optimization problem by using logic in Algorithm 2; | ||
| 2. | Set MA and CHT (e.g., GA with penalty method); | ||
| 3. | Set lower and upper bounds for the design variables; | ||
| 4. | Set constraints for optimization problem; | ||
| 5. | Initialize constraint violation list; | ||
| 6. | while k < kmax, where kmax is generation number, do | ||
| 7. | Compute reliability violations by employing FORM | ||
| 8. | Compute objective functions (e.g., mass) | ||
| 9. | Check convergence; | ||
| 10. | if converged: break; | ||
| 11. | k←k + 1; | ||
| 12. | Create new population; | ||
| end | |||
| 13. | Return reliability based optimized design variables; | ||
| Algorithm 4: Processing AISC Data on Dynamo | |||
| Input: AISC data path | |||
| Output: AISC section properties (e.g. cross-sectional areas) | |||
| 1. | Load Excel file from specified path on Dynamo and read into dataframe; | ||
| 2. | for each set of section indices do | ||
| 3. | Select sections from dataframe based on section indices; | ||
| 4. | Initialize lists for extracted data (e.g., moment of inertia); | ||
| 5. | foreach section in selected sections do | ||
| 6. | if section exists in dataframe then; | ||
| 7. Read section properties from dataframe; | |||
| 8. Convert extracted values to required units; | |||
| 9. Append converted properties to respective lists; | |||
| end | |||
| end | |||
| 10. | Append these lists to the corresponding overall lists; | ||
| end | |||
| 11. | Return lists of transformed section properties from an Excel file; | ||
3.7. Interoperability with BIM Software
| Algorithm 5: Generate and Analyze Model on RSA | ||
| Input: Optimized design variables along with geometry, material, boundary, etc. | ||
| Output: RSA model and FEM results | ||
| 1. | Check Boolean input from Dynamo; | |
| 2. | if RSA option on Dynamo is True then | |
| 3. | Load RSA API library and import API; | |
| 4. | Initialize Robot Application; | |
| 5. | Define unique node identification system; | |
| 6. | Assign an ID to each unique node using rounded coordinates; | |
| 7. | Create nodes and bars in RSA; | |
| 8. | Define supports and their types; | |
| 9. | Create and apply load cases from Dynamo inputs; | |
| 10. | Define material properties from Dynamo inputs; | |
| 11. | Assign sections to bars based on input indexes; | |
| 12. | Run calculation engine; | |
| 13. | Save the project; | |
| 14. | Print “Structure Created on RSA and Analysis have been started”; | |
| end | ||
| 15. | else | |
| 16. | Print “Option is not selected”; | |
| end | ||
| 17. | Return RSA file for optimized model; | |
4. Experimental Case Studies and Results
4.1. Experimental Setup
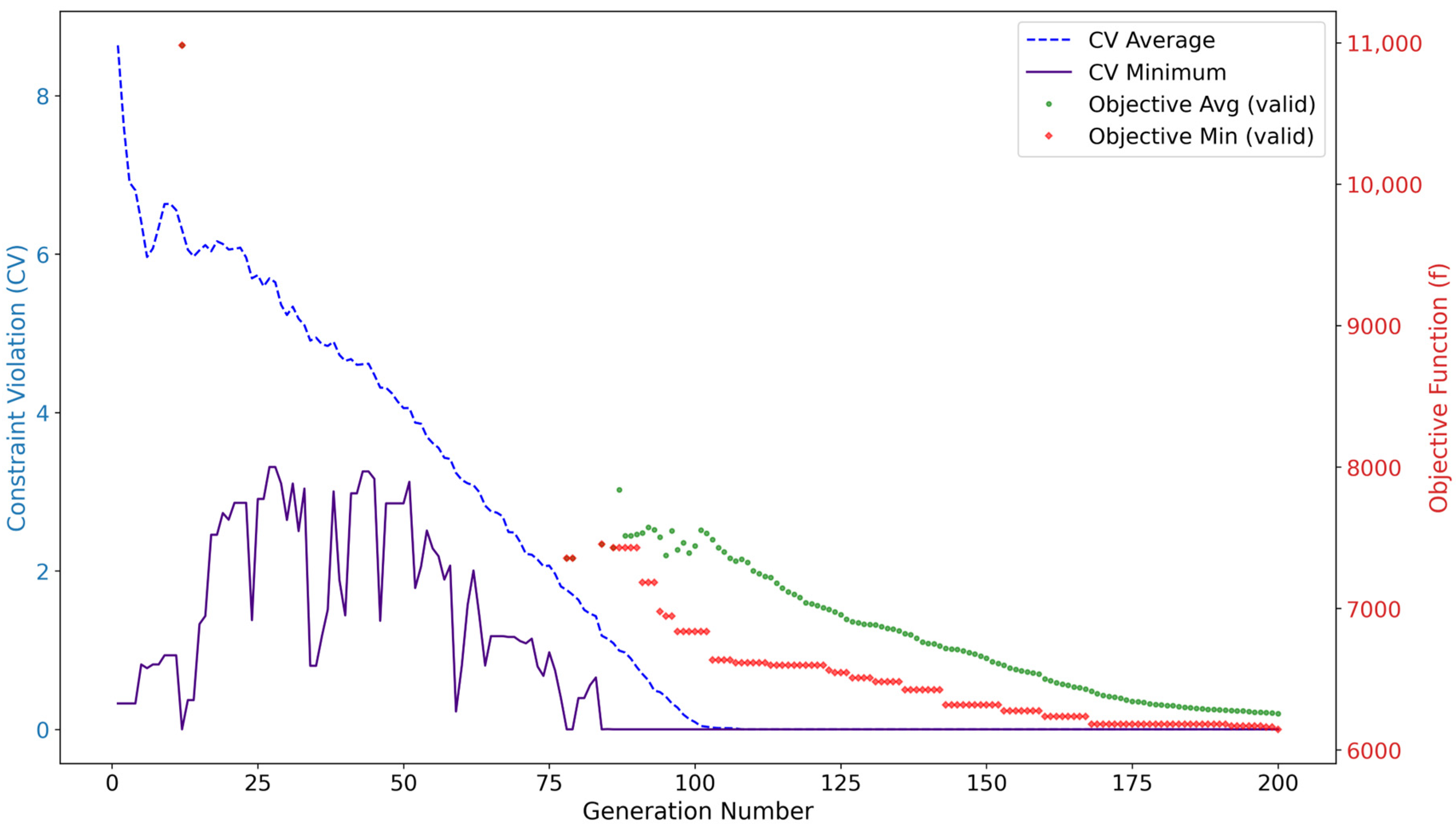
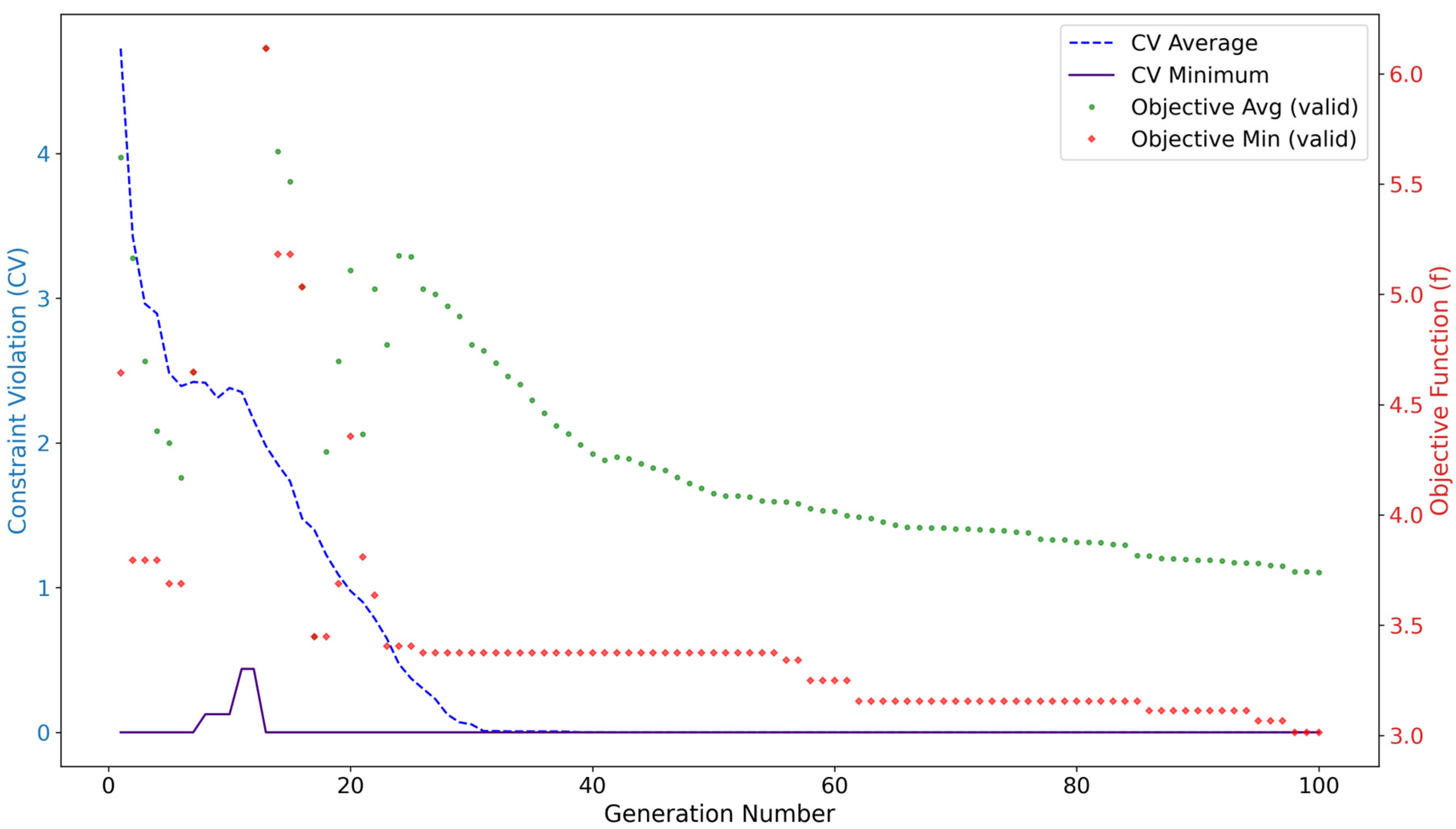
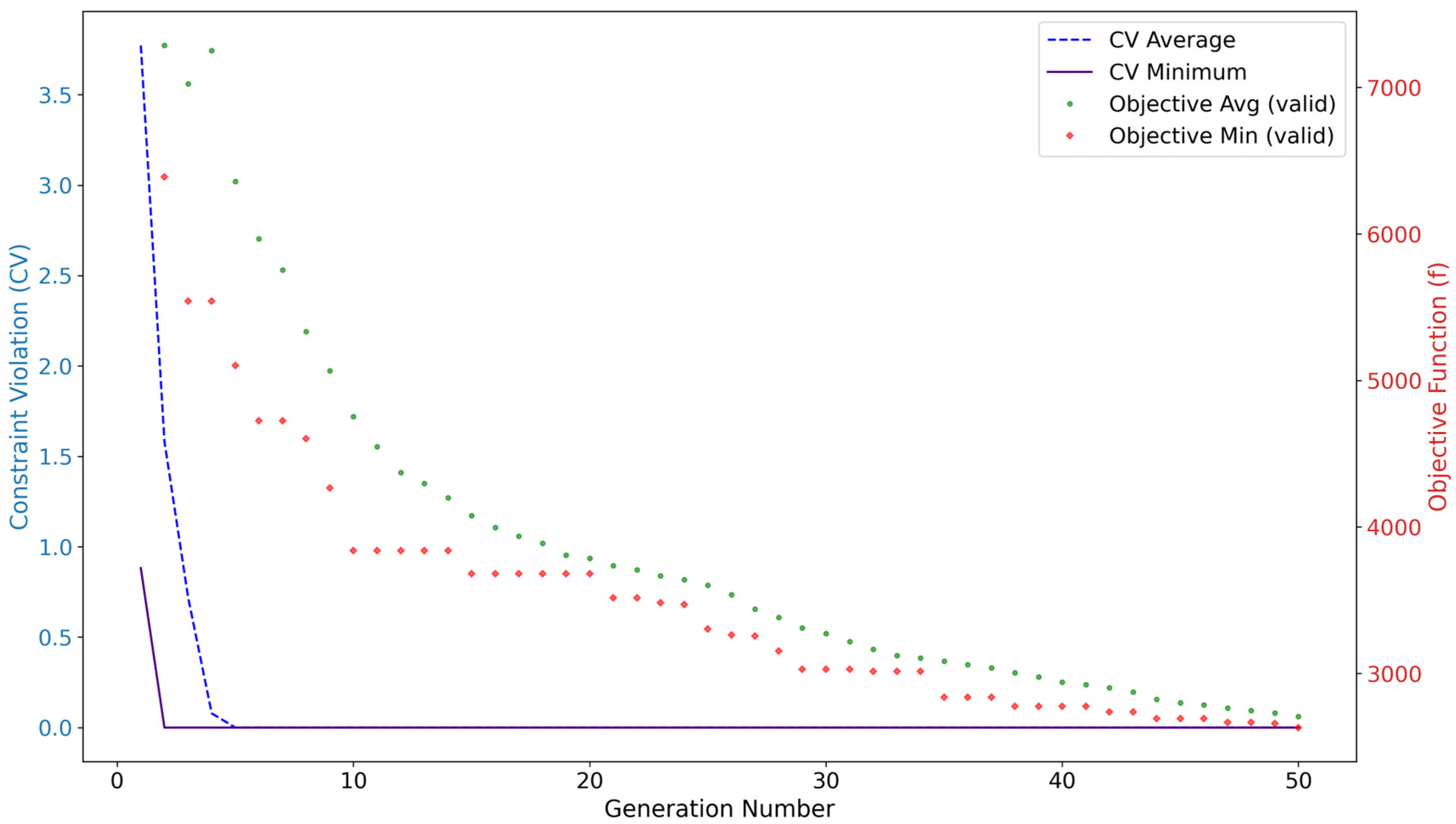
4.2. Results and Analysis
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Beaurepaire, P.; Jensen, H.A.; Schuëller, G.I.; Valdebenito, M.A. Reliability-Based Optimization Using Bridge Importance Sampling. Probabilistic Eng. Mech. 2013, 34, 48–57. [Google Scholar] [CrossRef]
- Hadjisophocleous, G.V.; Benichou, N. Performance Criteria Used in Fire Safety Design. Autom. Constr. 1999, 8, 489–501. [Google Scholar] [CrossRef]
- Kharmanda, G.; Olhoff, N.; El-Hami, A. Optimum Values of Structural Safety Factors for a Predefined Reliability Level with Extension to Multiple Limit States. Struct. Multidiscip. Optim. 2004, 27, 421–434. [Google Scholar] [CrossRef]
- Tomonaga, M. The Atomic Bombings of Hiroshima and Nagasaki: A Summary of the Human Consequences, 1945-2018, and Lessons for Homo Sapiens to End the Nuclear Weapon Age. J. Peace Nucl. Disarm. 2019, 2, 491–517. [Google Scholar] [CrossRef]
- Canpolat, N.; Saygılı, S.; Sever, L. Earthquake in Turkey: Disasters and Children Preparing for the Unexpected Supporting the Vulnerable! Turk. Arch. Pediatr. 2023, 58, 119–121. [Google Scholar] [CrossRef]
- Scawthorn, C.; Johnson, G.S. Preliminary Report: Kocaeli (Izmit) Earthquake of 17 August 1999. Eng. Struct. 2000, 22, 727–745. [Google Scholar] [CrossRef]
- Celorrio, L. Reliability-Based Design Optimization of Structures Combining Genetic Algorithms and Finite Element Reliability Analysis. Adv. Intell. Syst. Comput. 2015, 368, 143–152. [Google Scholar] [CrossRef]
- Yavan, F.; Maalek, R.; Toğan, V. Structural Optimization of Trusses in Building Information Modeling (BIM) Projects Using Visual Programming, Evolutionary Algorithms, and Life Cycle Assessment (LCA) Tools. Buildings 2024, 14, 1532. [Google Scholar] [CrossRef]
- Jensen, H.; Valdebenito, M.; Sepúlveda, J.; Becerra, L. Discrete Variable Structural Optimization of Systems under Stochastic Earthquake Excitation. In Structural Seismic Design Optimization and Earthquake Engineering: Formulations and Applications; Plevris, V., Mitropoulou, C., Lagaros, N., Eds.; IGI Global: Hershey, PA, USA, 2012; pp. 51–75. [Google Scholar] [CrossRef]
- Koch, P.; Kodiyalam, S. Variable Complexity Structural Reliability Analysis for Efficient Reliability-Based Design Optimization. In Proceedings of the 40th Structures, Structural Dynamics, and Materials Conference and Exhibit, St. Louis, MO, USA, 12–15 April 1999; p. 1210. [Google Scholar]
- Liu, Y.; Wang, Z.; Lu, H.; Ye, J.; Zhao, Y.; Min Xie, Y. Layout Optimization of Truss Structures with Modular Constraints. Structures 2023, 55, 1460–1469. [Google Scholar] [CrossRef]
- Goodarzimehr, V.; Topal, U.; Das, A.K.; Vo-Duy, T. Bonobo Optimizer Algorithm for Optimum Design of Truss Structures with Static Constraints. Structures 2023, 50, 400–417. [Google Scholar] [CrossRef]
- Aydın, Z. Size, Layout and Tendon Profile Optimization of Prestressed Steel Trusses Using Jaya Algorithm. Structures 2022, 40, 284–294. [Google Scholar] [CrossRef]
- Vasani, A.; Patel, R.; Savsani, V.; Savsani, P. Parametric Analysis of Genetic Algorithm Toolbox for Truss Problem Optimization. In Reliability and Risk Assessment in Engineering; Gupta, V.K., Varde, P.V., Kankar, P.K., Joshi, N., Eds.; Springer: Singapore, 2020; pp. 389–398. [Google Scholar]
- Machairas, V.; Tsangrassoulis, A.; Axarli, K. Algorithms for Optimization of Building Design: A Review. Renew. Sustain. Energy Rev. 2014, 31, 101–112. [Google Scholar] [CrossRef]
- Chi, H.-L.; Wang, X.; Jiao, Y. BIM-Enabled Structural Design: Impacts and Future Developments in Structural Modelling, Analysis and Optimisation Processes. Arch. Comput. Methods Eng. 2015, 22, 135–151. [Google Scholar] [CrossRef]
- Yavan, F.; Maalek, R.; Maalek, S. Enhancing Spatial Truss Designs by Integrating Metaheuristic Optimization Techniques via Visual Programming in BIM-Based Projects. In Redefining the Art of Structural Design, Proceedings of the IASS 2024 Symposium, Zürich, Switzerland, 26–30 August 2024; Block, P., Boller, G., DeWolf, C., Pauli, J., Kaufmann, W., Eds.; International Association for Shell and Spatial Structures (IASS): Madrid, Spain, 2024. [Google Scholar]
- Eleftheriadis, S.; Mumovic, D.; Greening, P.; Chronis, A. BIM Enabled Optimisation Framework for Environmentally Responsible and Structurally Efficient Design Systems. In Proceedings of the 32nd International Symposium on Automation and Robotics in Construction and Mining—ISARC 2015, Oulu, Finland, 15–18 June 2015. [Google Scholar] [CrossRef]
- Mirra, G.; Pugnale, A. Comparison between Human-Defined and AI-Generated Design Spaces for the Optimisation of Shell Structures. Structures 2021, 34, 2950–2961. [Google Scholar] [CrossRef]
- Liu, Z.; Sun, H.; Charkaoui, A.; Hassan, N.M.; Bahroun, Z.; Jiang, J.; Wang, S.; Zhao, L.; Li, W.; Yao, Q.; et al. You May Also like Nonlinear Stress Analysis of Key Joints of Steel Truss Bridge Enhancing Mechanical Properties of Cellular Core Sandwich Panels: A Review of Topological Parameters and Design Improvements Research on Parametric Finite Element Analysis Method of Escalator Truss Truss Optimization Using Genetic Algorithm and FEA. J. Phys. Conf. Ser. 1965, 1, 12134. [Google Scholar] [CrossRef]
- Rajeev, S.; Krishnamoorthy, C.S. Discrete Optimization of Structures Using Genetic Algorithms. J. Struct. Eng. 1992, 118, 1233–1250. [Google Scholar] [CrossRef]
- Rasheed, K.M. GADO: A Genetic Algorithm for Continuous Design Optimization; Rutgers University, School of Graduate Studies: New Brunswick, NJ, USA, 1998; ISBN 0591759950. [Google Scholar]
- Groenwold, A.A.; Stander, N.; Snyman, J.A. A Regional Genetic Algorithm for the Discrete Optimal Design of Truss Structures. Int. J. Numer. Methods Eng. 1999, 44, 749–766. [Google Scholar] [CrossRef]
- Toǧan, V.; Daloǧlu, A.T. An Improved Genetic Algorithm with Initial Population Strategy and Self-Adaptive Member Grouping. Comput. Struct. 2008, 86, 1204–1218. [Google Scholar] [CrossRef]
- Darko, A.; Chan, A.P.C.; Adabre, M.A.; Edwards, D.J.; Hosseini, M.R.; Ameyaw, E.E. Artificial Intelligence in the AEC Industry: Scientometric Analysis and Visualization of Research Activities. Autom. Constr. 2020, 112, 103081. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning, 1st ed.; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1989; ISBN 0201157675. [Google Scholar]
- Talatahari, S.; Gandomi, A.H.; Yang, X.S.; Deb, S. Optimum Design of Frame Structures Using the Eagle Strategy with Differential Evolution. Eng. Struct. 2015, 91, 16–25. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant Colony Optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Dorigo, M.; Di Caro, G. Ant Colony Optimization: A New Meta-Heuristic. CEC 1999, 2, 1470–1477. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Singh, P.; Kottath, R.; Tejani, G.G. Ameliorated Follow The Leader: Algorithm and Application to Truss Design Problem. Structures 2022, 42, 181–204. [Google Scholar] [CrossRef]
- Jawad, F.K.J.; Ozturk, C.; Dansheng, W.; Mahmood, M.; Al-Azzawi, O.; Al-Jemely, A. Sizing and Layout Optimization of Truss Structures with Artificial Bee Colony Algorithm. Structures 2021, 30, 546–559. [Google Scholar] [CrossRef]
- Alqattan, Z.N.; Abdullah, R. A Hybrid Artificial Bee Colony Algorithm for Numerical Function Optimization. Int. J. Mod. Phys. 2015, 26, 1550109. [Google Scholar] [CrossRef]
- Baykasoğlu, A.; Baykasoğlu, C. Weighted Superposition Attraction-Repulsion (WSAR) Algorithm for Truss Optimization with Multiple Frequency Constraints. Structures 2021, 30, 253–264. [Google Scholar] [CrossRef]
- Pradhan, C.; Bhende, C.N. Online Load Frequency Control in Wind Integrated Power Systems Using Modified Jaya Optimization. Eng. Appl. Artif. Intell. 2019, 77, 212–228. [Google Scholar] [CrossRef]
- Rao, R.V. Jaya: A Simple and New Optimization Algorithm for Solving Constrained and Unconstrained Optimization Problems. Int. J. Ind. Eng. Comput. 2016, 7, 19–34. [Google Scholar] [CrossRef]
- Jafari, M.; Salajegheh, E.; Salajegheh, J. Optimal Design of Truss Structures Using a Hybrid Method Based on Particle Swarm Optimizer and Cultural Algorithm. Structures 2021, 32, 391–405. [Google Scholar] [CrossRef]
- Liu, J.; Xia, Y. A Hybrid Intelligent Genetic Algorithm for Truss Optimization Based on Deep Neutral Network. Swarm Evol. Comput. 2022, 73, 101120. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems with Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Makkar, P.; Sikka, S.; Malhotra, A. Empirical Evaluation of NSGA II, NSGA III, and MOEA/D Optimization Algorithms on Multi-Objective Target; Springer: Singapore, 2022; pp. 23–31. [Google Scholar] [CrossRef]
- Jensen, H.A.; Valdebenito, M.A.; Schuëller, G.I. An Efficient Reliability-Based Optimization Scheme for Uncertain Linear Systems Subject to General Gaussian Excitation. Comput. Methods Appl. Mech. Eng. 2008, 198, 72–87. [Google Scholar] [CrossRef]
- Moses, F. Approaches to Structural Reliability and Optimization; University of Waterloo, Department of Civil Engineering: Waterloo, ON, Canada, 1968. [Google Scholar]
- Burton, S.; Hajela, P. Reliability-Based Shape Optimization of Truss Structures. In Proceedings of the 19th AIAA Applied Aerodynamics Conference; Fluid Dynamics and Co-located Conferences, Anaheim, CA, USA, 11–14 June 2001; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2001. [Google Scholar]
- Choi, S.-K.; Canfield, R.A.; Grandhi, R.V. Reliability-Based Structural Optimization. In Reliability-Based Structural Design; Springer: London, UK, 2007; pp. 153–202. ISBN 978-1-84628-445-8. [Google Scholar]
- Jensen, H.A. Structural Optimization of Linear Dynamical Systems under Stochastic Excitation: A Moving Reliability Database Approach. Comput. Methods Appl. Mech. Eng. 2005, 194, 1757–1778. [Google Scholar] [CrossRef]
- Vietor, T. Stochastic Optimization for Mechanical Structures. Math. Methods Oper. Res. 1997, 46, 377–408. [Google Scholar] [CrossRef]
- Enevoldsen, I.; Sørensen, J.D. Reliability-Based Optimization in Structural Engineering. Struct. Saf. 1994, 15, 169–196. [Google Scholar] [CrossRef]
- Jensen, H.A.; Valdebenito, M.A.; Schuëller, G.I.; Kusanovic, D.S. Reliability-Based Optimization of Stochastic Systems Using Line Search. Comput. Methods Appl. Mech. Eng. 2009, 198, 3915–3924. [Google Scholar] [CrossRef]
- Mathakari, S.; Gardoni, P.; Agarwal, P.; Raich, A.; Haukaas, T. Reliability-Based Optimal Design of Electrical Transmission Towers Using Multi-Objective Genetic Algorithms. Comput.-Aided Civ. Infrastruct. Eng. 2007, 22, 282–292. [Google Scholar] [CrossRef]
- Thampan, C.K.P.V.; Krishnamoorthy, C.S. System Reliability-Based Configuration Optimization of Trusses. J. Struct. Eng. 2001, 127, 947–956. [Google Scholar] [CrossRef]
- Sokołowski, D.; Kamiński, M. Stochastic Reliability-Based Design Optimization Framework for the Steel Plate Girder with Corrugated Web Subjected to Corrosion. Materials 2022, 15, 7170. [Google Scholar] [CrossRef]
- Zhang, L.-X.; Meng, X.-J.; Ding, Z.-J.; Han, H.-X. Simulation-Based Reliability Design Optimization Method for Industrial Robot Structural Design. Appl. Sci. 2023, 13, 3776. [Google Scholar] [CrossRef]
- De, S.; Maute, K.; Doostan, A. Reliability-Based Topology Optimization Using Stochastic Gradients. Struct. Multidiscip. Optim. 2021, 64, 3089–3108. [Google Scholar] [CrossRef]
- Shayanfar, M.; Abbasnia, R.; Khodam, A. Development of a GA-Based Method for Reliability-Based Optimization of Structures with Discrete and Continuous Design Variables Using OpenSees and Tcl. Finite Elem. Anal. Des. 2014, 90, 61–73. [Google Scholar] [CrossRef]
- Chun, J. Reliability-Based Design Optimization of Structures Using Complex-Step Approximation with Sensitivity Analysis. Appl. Sci. 2021, 11, 4708. [Google Scholar] [CrossRef]
- Der Kiureghian, A. Structural and System Reliability; Cambridge University Press: Cambridge, UK, 2022; ISBN 9781108991889. [Google Scholar]
- GitHub—Ugurfeyzullah/Reliability-Constrained-Structural-Design-Optimization-Using-BIM-Based-Tools. Available online: https://github.com/ugurfeyzullah/Reliability-Constrained-Structural-Design-Optimization-Using-BIM-Based-Tools/tree/main (accessed on 12 September 2024).
- Chen, J.J.; Duan, B.Y. Structural Optimization by Displaying the Reliability Constraints. Comput. Struct. 1994, 50, 777–783. [Google Scholar] [CrossRef]
- JWock82/PyNite: A 3D Structural Engineering Finite Element Library for Python. Available online: https://github.com/JWock82/PyNite (accessed on 18 July 2024).
- Blank, J.; Deb, K. Pymoo: Multi-Objective Optimization in Python. IEEE Access 2020, 8, 89497–89509. [Google Scholar] [CrossRef]
- Ma, Z.; Wu, G.; Suganthan, P.N.; Song, A.; Luo, Q. Performance Assessment and Exhaustive Listing of 500+ Nature-Inspired Metaheuristic Algorithms. Swarm Evol. Comput. 2023, 77, 101248. [Google Scholar] [CrossRef]
- Glover, F.; Sörensen, K. Metaheuristics. Scholarpedia 2015, 10, 6532. [Google Scholar] [CrossRef]
- Silberholz, J.; Golden, B.; Smith, R.H.; Gendreau, M.; Potvin, J.-Y. Comparison of Metaheuristics. Int. Ser. Oper. Res. Manag. Sci. 2010, 146, 625–640. [Google Scholar] [CrossRef]
- Lagaros, N.D.; Kournoutos, M.; Kallioras, N.A.; Nordas, A.N. Constraint Handling Techniques for Metaheuristics: A State-of-the-Art Review and New Variants. Optim. Eng. 2023, 24, 2251–2298. [Google Scholar] [CrossRef]
- Blum, C.; Roli, A. Metaheuristics in Combinatorial Optimization: Overview and Conceptual Comparison. ACM Comput. Surv. 2003, 35, 268–308. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Abdel-Fatah, L.; Sangaiah, A.K. Metaheuristic Algorithms: A Comprehensive Review. In Computational Intelligence for Multimedia Big Data on the Cloud with Engineering Applications; Sangaiah, A.K., Sheng, M., Zhang, Z., Eds.; Intelligent Data-Centric Systems; Academic Press: Cambridge, MA, USA, 2018; pp. 185–231. ISBN 978-0-12-813314-9. [Google Scholar] [CrossRef]
- Halim, A.H.; Ismail, I.; Das, S. Performance Assessment of the Metaheuristic Optimization Algorithms: An Exhaustive Review. Artif. Intell. Rev. 2021, 54, 2323–2409. [Google Scholar] [CrossRef]
- Sonmez, M. Performance Comparison of Metaheuristic Algorithms for the Optimal Design of Space Trusses. Arab. J. Sci. Eng. 2018, 43, 5265–5281. [Google Scholar] [CrossRef]
- Welcome to Pystra’s Documentation!—PySTRA 1.3.0 Documentation. Available online: https://pystra.github.io/pystra/index.html (accessed on 22 July 2024).
- AISC Shapes Database V16.0, American Institute of Steel Construction. Available online: https://www.aisc.org/publications/steel-construction-manual-resources/16th-ed-steel-construction-manual/aisc-shapes-database-v16.0/ (accessed on 11 September 2024).
- Camp, C.V.; Bichon, B.J. Design of Space Trusses Using Ant Colony Optimization. J. Struct. Eng. 2004, 130, 741–751. [Google Scholar] [CrossRef]
- Kazemzadeh Azad, S.; Kazemzadeh Azad, S. A Standard Benchmarking Suite for Structural Optimization Algorithms: ISCSO 2016–2022. Structures 2023, 58, 105409. [Google Scholar] [CrossRef]
- Optimization Problem and Winner of ISCSO 2019—Bright Optimizer. Available online: https://www.brightoptimizer.com/problem-iscso2019/ (accessed on 19 December 2024).
- American Institute of Steel Construction. Manual of Steel Construction: Load & Resistance Factor Design; American Institute of Steel Construction, Inc.: Chicago, IL, USA, 1994; Volume 2. [Google Scholar]


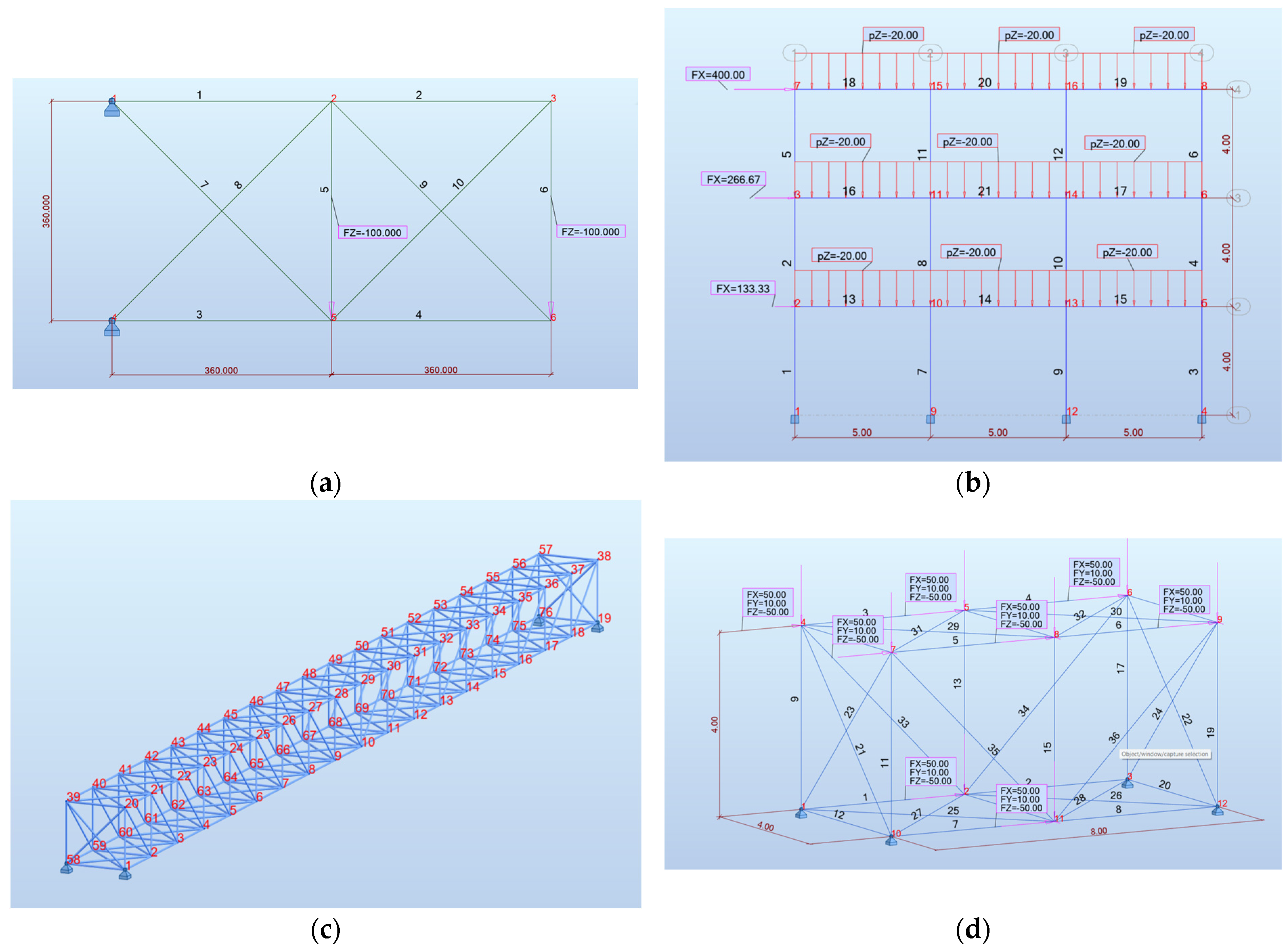

| Dynamo Nodes [8] | RSA API [34] | Python Library This Study | |
|---|---|---|---|
| Required Time (Min. Approximately) | 240 | 30 | 0.4 |
| Number of FEM Evaluation | 200 | 200 | 200 |
| Structural Optimization | RBDO | |||
|---|---|---|---|---|
| [21] | [8] | [57] | This Study | |
| Objective (kg) | 2549.22 | 2763.06 | 2817.40 | 2787.55 |
| −0.027 | 0.29 | 3.01 | 3.0022 | |
| Employed MA | GA | GA | GA | DE |
| Population Size | 20 | 20 | 100 | 50 |
| Generation Number | 20 | 20 | 500 | 100 |
| Separate Runs | - | 10 | 50 | 2 × GA, 2 × DE |
| A1 (cm2) | 216.128600 | 181.289960 | 221.625363 | 223.489362 |
| A2 (cm2) | 10.451592 | 23.161244 | 0.645160 | 0.783208 |
| A3 (cm2) | 141.935200 | 165.160960 | 191.502843 | 196.122331 |
| A4 (cm2) | 99.999800 | 128.386840 | 169.515790 | 125.815885 |
| A5 (cm2) | 10.451592 | 10.322560 | 0.645160 | 0.749852 |
| A6 (cm2) | 11.612880 | 27.225752 | 0.645160 | 0.679507 |
| A7 (cm2) | 91.612720 | 115.483640 | 21.528989 | 26.795538 |
| A8 (cm2) | 128.386840 | 125.161040 | 182.928666 | 189.808710 |
| A9 (cm2) | 128.386840 | 115.483640 | 168.631921 | 174.270183 |
| A10 (cm2) | 16.903192 | 22.516084 | 0.645160 | 0.652246 |
| Structural Optimization | RBDO | ||
|---|---|---|---|
| This Study | [57] | This Study | |
| Objective (m3) | 2.38 | 3.06 | 3.014 |
| , , | 1.75, 0.17, 0.04 | 4.65, 3.04, 3.12 | 4.11, 3.084, 3.12 |
| Employed MA | GA | GA | DE |
| Population Size | 50 | 100 | 50 |
| Generation Number | 100 | 120 | 100 |
| Separate Runs | 2 × DE, 2 × GA | 50 | 2 × DE, 2 × GA |
| A1 (cm2) | 206.45 | 334.19 | 250.32 |
| A2 (cm2) | 170.97 | 187.74 | 227.74 |
| A3 (cm2) | 441.93 | 487.74 | 487.74 |
| A4 (cm2) | 250.32 | 366.45 | 334.19 |
| A5 (cm2) | 278.71 | 345.81 | 382.58 |
| A6 (cm2) | 118.06 | 176.13 | 157.42 |
| Structural Optimization | RBDO | |
|---|---|---|
| This Study | This Study | |
| Objective (kg) | 1678.39 | 2631.06 |
| −0.48 | 3.07 | |
| Employed MA | GA | GA |
| Population Size | 30 | 30 |
| Generation Number | 50 | 50 |
| Separate Runs | 2 × DE, 2 × GA | 2 × DE, 2 × GA |
| A1 (cm2) | 6.9032 | 72.9031 |
| A2 (cm2) | 35.9999 | 17.2903 |
| A3 (cm2) | 19.4838 | 1.6129 |
| A4 (cm2) | 6.9032 | 14.5161 |
| A5 (cm2) | 19.4838 | 10.9677 |
| A6 (cm2) | 14.5161 | 35.2903 |
| A7 (cm2) | 28.4516 | 25.9999 |
| A8 (cm2) | 20.4516 | 2.7935 |
| A9 (cm2) | 39.4193 | 5.1548 |
| A10 (cm2) | 6.9032 | 2.1484 |
| A11 (cm2) | 14.5161 | 35.9999 |
| A12 (cm2) | 2.0645 | 1.6129 |
| A13 (cm2) | 28.4516 | 5.1548 |
| A14 (cm2) | 3.1871 | 2.0645 |
| A15 (cm2) | 17.1613 | 35.2903 |
| A16 (cm2) | 4.1226 | 28.4516 |
| A17 (cm2) | 17.2903 | 28.4516 |
| A18 (cm2) | 2.0645 | 4.1226 |
| A19 (cm2) | 9.5484 | 76.774 |
| A20 (cm2) | 4.1226 | 4.3161 |
| A21 (cm2) | 27.7419 | 9.5484 |
| A22 (cm2) | 2.7935 | 14.5161 |
| A23 (cm2) | 2.0645 | 2.0645 |
| A24 (cm2) | 5.6839 | 17.1613 |
| A25 (cm2) | 23.7419 | 35.9999 |
| A26 (cm2) | 6.9032 | 54.1934 |
| A27 (cm2) | 3.1871 | 35.2903 |
| A28 (cm2) | 19.4838 | 17.1613 |
| A29 (cm2) | 1.6129 | 17.1613 |
| A30 (cm2) | 4.3161 | 1.6129 |
| A31 (cm2) | 4.3161 | 5.1548 |
| A32 (cm2) | 6.9032 | 10.9677 |
| A33 (cm2) | 25.9999 | 19.4838 |
| A34 (cm2) | 19.4838 | 35.2903 |
| A35 (cm2) | 20.4516 | 28.4516 |
| A36 (cm2) | 20.4516 | 25.9999 |
| Z1 (cm) | 182 | 22.8 |
| Z2 (cm) | 2361 | 248.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yavan, F.; Maalek, R. Reliability-Constrained Structural Design Optimization Using Visual Programming in Building Information Modeling (BIM) Projects. Appl. Sci. 2025, 15, 1025. https://doi.org/10.3390/app15031025
Yavan F, Maalek R. Reliability-Constrained Structural Design Optimization Using Visual Programming in Building Information Modeling (BIM) Projects. Applied Sciences. 2025; 15(3):1025. https://doi.org/10.3390/app15031025
Chicago/Turabian StyleYavan, Feyzullah, and Reza Maalek. 2025. "Reliability-Constrained Structural Design Optimization Using Visual Programming in Building Information Modeling (BIM) Projects" Applied Sciences 15, no. 3: 1025. https://doi.org/10.3390/app15031025
APA StyleYavan, F., & Maalek, R. (2025). Reliability-Constrained Structural Design Optimization Using Visual Programming in Building Information Modeling (BIM) Projects. Applied Sciences, 15(3), 1025. https://doi.org/10.3390/app15031025







