Study on the Synergistic Effect of Coal Pillars and Caved Deposits in Chamber-Type Mining of Steeply Inclined Coal Seams

Abstract

To address the synergistic stability evaluation of coal pillars and caving deposits in room-and-pillar mining of nearly vertical coal seams, this study takes the 101 Coal Mine (104th Regiment, Xishan Area, Urumqi, Xinjiang) as the engineering background. It combines physical similarity simulation and theoretical analysis to explore the synergistic bearing mechanism of coal pillars and caved deposits. Based on limit equilibrium theory, a combined instability criterion considering roof mudstone’s bending-toppling and shear-sliding is established; the Rankine earth pressure theory is modified, and a stability coefficient K_s (reflecting synergistic bearing effect) is proposed to realize quantitative evaluation of goaf stability. A model experiment simulates the mining of a 73° nearly vertical coal seam. Results show the roof instability mode (under coal pillars and caved deposits) is equivalent to anti-dip slope’s toppling-sliding composite failure. Experimental and theoretical results agree well, verifying the model’s rationality and applicability. This study provides a theoretical basis and analytical method for calculating the synergistic stability of coal pillars and caving deposits in nearly vertical coal seams.

1. Introduction

Near-vertical coal seams are usually mined by the chamber method or sublevel mining method, and coal pillars are left to maintain the stability of goafs as the main supporting structure [1,2,3,4]. These coal pillars bear complex loads from the overlying strata of the goaf for a long time. Due to the component effect of gravity in inclined rock masses, they not only bear normal compressive stress but also significant shear stress along the dip direction, with shear stress usually being dominant [5,6,7,8]. The displacement caused by damage shows obvious characteristics in both horizontal and vertical directions [9]. Their stability is affected by the coupling of multiple factors such as size, dynamic disturbance, and stress transfer from multi-layer mining. The surrounding rock of this type of goaf, especially the hanging wall rock mass, is in a special stress environment dominated by large dip angles, high stress, and gravity for a long time, and is prone to sliding, toppling, breaking, and even overall collapse [10,11,12,13,14]. This unique boundary condition makes the stability problem of goafs in steeply inclined coal seams more prominent and complex than that in gently inclined coal seams.

In recent years, many experts and scholars have conducted extensive research on the stability of goafs in near-vertical coal seams and achieved numerous scientific research results. However, most of the adopted methods are based on Wilson theory, simplified elastic mechanics models, or roof beam-plate models [15,16,17,18,19], which regard coal pillars in the goaf as isolated load-bearing units and ignore the overall mechanical properties of rock strata and the synergistic action between coal pillars and caved deposits. Although some scholars have found through experiments using similar models that the collapse area of near-vertical goafs is incompletely compacted, with obvious cavities and fractures, and have also proposed that coal pillars pose a potential threat of rock burst [20,21]. Under the condition of near-vertical coal seams, there will be caved deposits formed by the collapse of the roof, coal pillars, etc., in the goaf. The caved rock of the roof is not a uniformly compacted body like that in horizontal coal seams; instead, under the cumulative damage of the bulk, it rolls, slides, and accumulates along the inclined base plate, forming a special medium that is heterogeneous and discontinuous [22,23,24,25,26,27,28]. During the compaction process, these deposits undergo spatial variability, and the distribution of void ratio changes, providing effective lateral confinement and support for the side of coal pillars and forming a new load-bearing structure. The synergistic bearing characteristics formed by this load-bearing structure and the overlying strata greatly change the overall stability of the goaf. The existing stability evaluation methods for near-vertical goafs analyze coal pillars and their stability separately, and there are no corresponding requirements for the influence of accumulations. In recent years, scholars have conducted extensive research on deformation prediction, hazard prevention, and overburden failure in goafs of steeply inclined coal seams. A residual deformation model incorporating variable mining influence propagation angles has been proposed and combined with the Kelvin model for dynamic analysis [29]. A risk assessment index system for rock collapse in steeply inclined coal seams has been established [30]. The bearing structure of thick-hard roofs characterized as “low-position articulated beam—high-position simply supported beam” and the “stress—caving” double-arch feature during ore collapse has been revealed [30,31]. The influence of broken rock block geometry and pore structure on the compaction and seepage behavior in goafs has been clarified [32]. Through case studies and numerical simulations, the evolution of stress-fracture in roof strata and stability control technologies for large-scale caving zones in steeply inclined coal seams have been supplemented [17]. The mechanisms and prevention strategies for asymmetric deformation in near-vertical roadways and floor heave induced by chamber excavation disturbances have been further elucidated [33,34]. These achievements provide important references for the safe mining of steeply inclined coal seams. However, the synergistic bearing mechanism between coal pillars and caved deposits in near-vertical chamber-type goafs, as well as its corresponding quantitative stability evaluation, still requires further in-depth investigation.

Based on the existing research on coal pillar goafs and caved deposit goafs, this study focuses on exploring the comprehensive influence of the synergistic action between the bearing capacity of coal pillars and the mechanical behavior of caved deposits on the overall stability of near-vertical goafs, and verifies it through model experiments. It aims to establish a quantitative standard for assessing near-vertical goafs stability, considering the combined bearing effect of coal pillars and caved deposits.

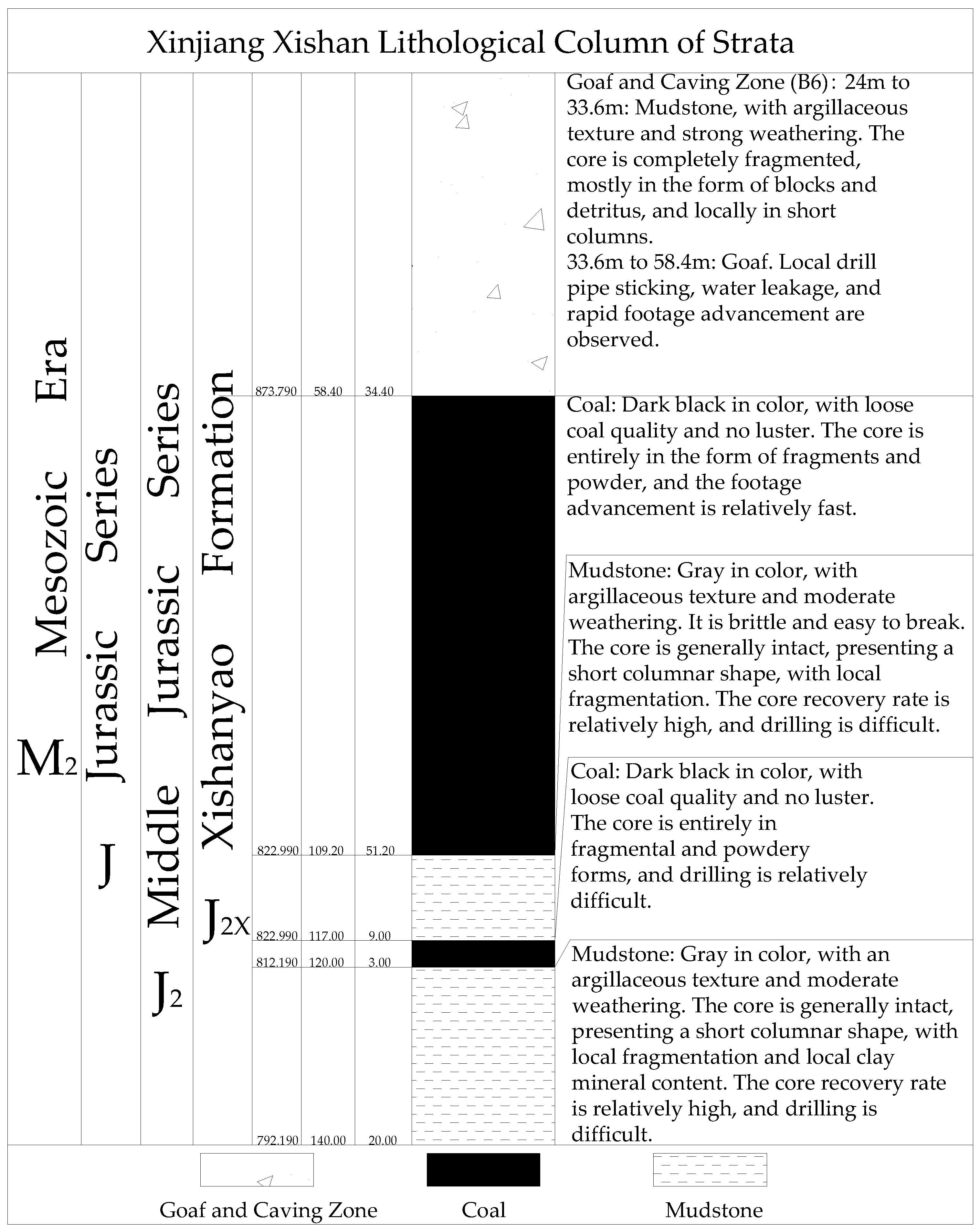
2. Geological Conditions

The 101 Coal Mine in Plot 1 of the 104th Regiment of the 12th Division of Xinjiang Production and Construction Corps is selected as the research area, and the B₆ coal seam in the 5-5′ profile is taken as the research prototype. The main strata include the sandstone-mudstone formation of the Xiaoquanggou Group of the Upper Triassic (T₃₂), the Badaowan Formation (J_1b), Sangonghe Formation (J_1s), and Xishanyao Formation (J_2x) of the Shuixigou Group of the Lower-Middle Jurassic (J_1+2sh), the Xinjiang Group of the Upper Pleistocene of the Quaternary (Q_3x), and the Holocene pluvial-alluvial layer (Q_4al+pl). Most of the bedrock is covered by the Quaternary system. There are 15 coal groups in the regional coal seam, containing a total of 55 coal layers with a total thickness of 5.16–103.76 m, an average total thickness of 47.27 m, and a dip angle of 60–88°. The lithological column diagram of the rock stratum is shown in Figure 1.

3. Synergistic Mechanism Between Coal Pillars and Caved Deposits

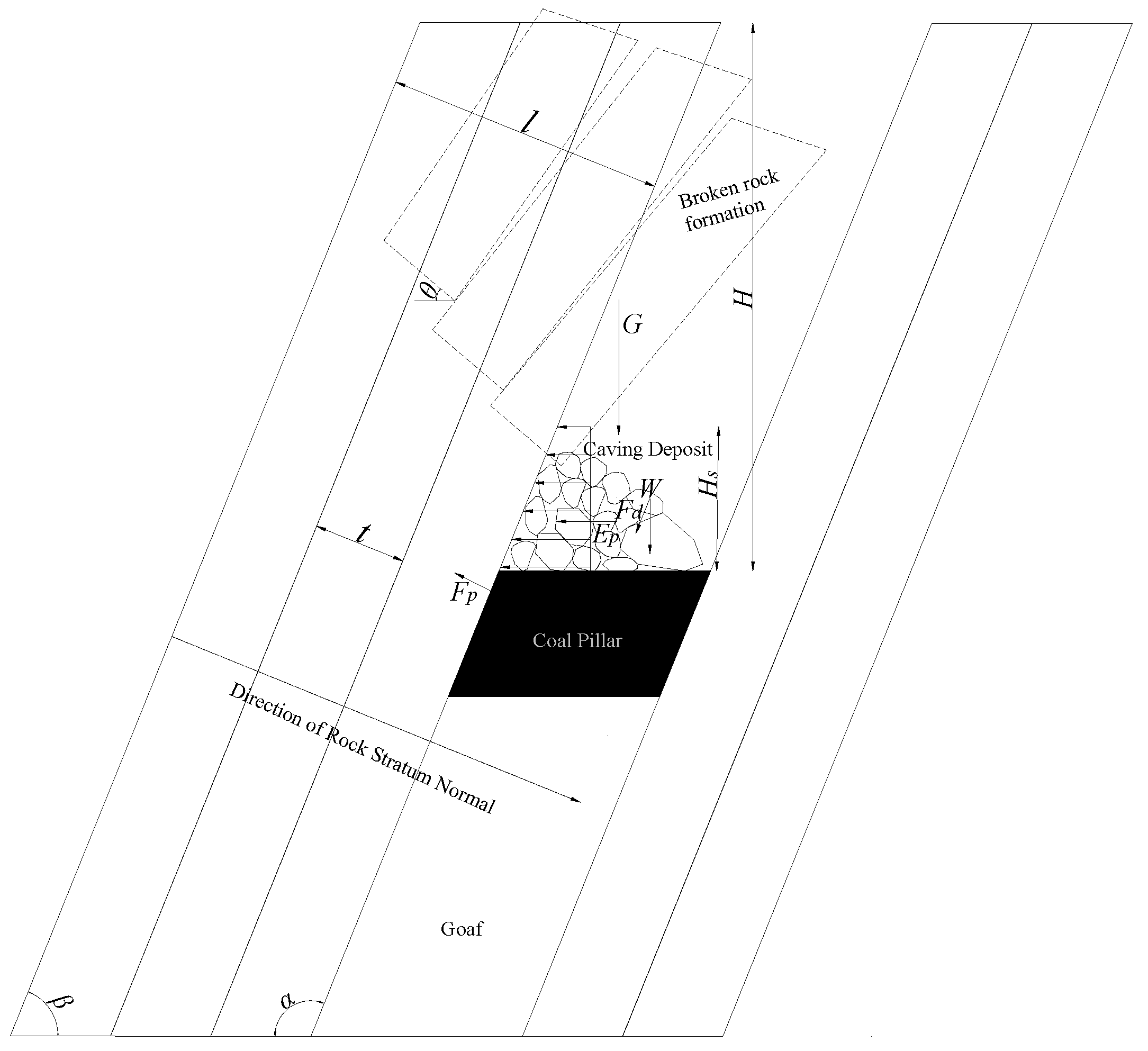
3.1. Mechanical Analysis of Synergistic Action Between Coal Pillars and Caved Deposits

The synergistic action between coal pillars and caved deposits is a typical “structure-medium” interaction problem, with the core lying in the active support of coal pillars, the passive response of caved deposits, and the positive feedback of their interaction. Firstly, coal pillars bear the main load of the overlying strata, and their stiffness and strength determine the initial displacement and stability of the roof. Secondly, the movement and failure of the roof lead to the compaction of caved deposits, generating support resistance. The magnitude of this resistance is directly related to the properties and compaction degree of the caved deposits themselves. Finally, the support force generated by the caved deposits slows down the further subsidence of the roof and reduces the load increment of the coal pillars; at the same time, the vertical confinement of the caved deposits on the coal pillars enhances the bearing potential of the coal pillars themselves. The caved deposits are mainly composed of caved gangue, which, when compressed by the subsidence of the roof, first undergoes compaction (the gaps between rock blocks are compressed, the caved deposits undergo large deformation, and the provided support force is small); then enters the yield and plastic hardening stage (rock blocks break and rearrange, the density of the caved deposits increases, and their bearing capacity is significantly improved); and finally reaches the failure or stable stage (the caved deposits are compacted to the elastic limit state and provide stable support force).

Based on the elastic foundation theory, when the foundation coefficient k and the roof subsidence w are determined, the support force of the caved deposits can be calculated quantitatively. The commonly used model at present is the elastic foundation beam model, which assumes that the supporting reaction force F of the accumulation body on the roof is proportional to the subsidence w of the roof, that is, F = kw. When the roof subsidence can compact the caved deposits, the bearing capacity of the caved deposits will be significantly enhanced, providing more support force for the roof; at the same time, the increased support force will further inhibit the further subsidence of the roof, and finally a new balance is achieved.

Under near-vertical conditions, the gravity of the caved deposits not only generates pressure perpendicular to the stratum but also a downslope force parallel to the stratum. This will cause shear sliding inside the caved deposits, making it difficult to form a uniform and dense load-bearing structure. Moreover, due to the uneven distribution of the downslope force and accumulation force, the support force of the caved deposits on the roof and floor is extremely uneven. Usually, the lower part of the goaf is more densely accumulated with greater support force, while the upper part may have voids or loose areas with weaker support force. Regarding the lateral pressure on the floor, the downslope force of the caved deposits is converted into the lateral thrust on the roof and floor below the goaf. Based on the bending-toppling and shear-sliding failure theory of anti-dip rock slopes proposed by An Mingxu [35] et al., combined with the Rankine passive earth pressure theory, a mechanical model of the synergistic action between coal pillars and caved deposits as shown in Figure 2 is established.

3.2. Anti-Dip Failure Mode of Roof Mudstone

The roof of steeply inclined and near-vertical coal seams is highly similar to anti-dip slopes in terms of geometric shape and stress characteristics. Under the action of gravity, the rock strata of the goaf wall may also topple and bend into the goaf or undergo shear sliding along weak structural planes. This deformation process dominated by toppling and breaking is kinematically equivalent to the instability process of anti-dip rock slopes, especially toppling failure [35,36]. Therefore, the roof of the steeply inclined goaf is simplified as an anti-dip layered slope disturbed by mining, and an instability criterion is established. The toppling failure criterion is shown in Formula (1) [35]:

$$K_f={\displaystyle \frac{c{L}_{s}b+W\cos {\alpha }_{c}a}{W\sin {\alpha }_c{h}_0+Vb}}$$

(1)

An Mingxu [35], Lu Haifeng [36] et al. pointed out that the initially unstable layer of bending-toppling is the rock stratum that is unstable under its own gravity. Taking the rock stratum subjected only to its own gravity for analysis, when it is in the limit equilibrium state of bending-toppling, the maximum tensile stress σ_max of the rock stratum is equal to the tensile strength σ_t of the rock mass, and the length of the rock stratum at this time is defined as the limit instability length h_lim. At this time, the interlayer forces under the limit equilibrium state of bending-toppling failure and shear failure equilibrium state of the roof are shown in Formulas (2) and (3) [35]:

$$P_{i-1}={\displaystyle \frac{P_i(h_i-\frac{2}{3}\frac{\tan {\phi }_j}{k}t)+\frac{1}{2}W\cos \beta h_i-\frac{2I_i}{t}(\frac{{\sigma }_1}{k}+\frac{W_i\sin \beta }{t})}{h_{i-1}+\frac{1}{3}\frac{\tan {\phi }_j}{k}t}}$$

(2)

$$Q_{i-1}=Q_i+{\displaystyle \frac{W(k^2\cos \beta -k\sin \beta \tan \phi )-ctk}{k^2-\tan \phi \tan {\phi }_j}}$$

(3)

By analyzing the interlayer forces P_i−1 and Q_i−1 under the above different failure modes, if P_i−1 of the rock stratum is greater than Q_i−1, it indicates that the rock stratum first reaches the limit equilibrium state of toppling under the action of its own weight and interlayer forces, and the potential or manifested failure mode of the rock stratum is toppling failure; if P_i−1 is equal to Q_i−1, it indicates that the rock stratum is in the limit equilibrium state of both toppling and shear simultaneously, and the rock stratum failure is a toppling-sliding composite failure mode; if P_i−1 is less than Q_i−1, it indicates that the rock stratum first reaches the limit equilibrium state of shear, and the potential or manifested failure mode of the rock stratum is shear failure.

The geological model of the goaf under the synergistic action of coal pillars and caved deposits is analyzed. Based on the Salomon-Munro formula and the H-B criterion, the formula for the ultimate strength σ_p of the coal pillar is shown in Formula (4), and the support force F_p of the goaf roof is shown in Formula (5):

$${\sigma }_p=K_c{\sigma }_c{({\displaystyle \frac{B}{H_p}})}^A$$

(4)

$$F_p={\sigma }_p{A}_p$$

(5)

Considering the physical properties of the caved deposits, especially the influence of density and volume, the lateral pressure of the caved deposits is modified according to the Rankine passive earth pressure theory [32]. Then, the expression of the lateral pressure intensity p_sh of the caved deposits at depth z is shown in Formula (6):

$$p_{sh}={\gamma }_{s}z{K}_p$$

(6)

Assuming that the height of the caved deposits in the goaf is H_s, the total lateral support force F_b (per unit length along the strike) exerted on the rock wall can be obtained by integrating the pressure distribution, as shown in Formula (7):

$$F_b={\displaystyle {\int }_0^{H_s}{p}_{sh}dh=}{\displaystyle \frac{1}{2}}{\gamma }_s{H}_s^2{K}_p$$

(7)

Assuming that the volume of the caved deposits is V, the length along the strike is L, the dip angle of the sliding surface between the rock blocks and the stable bedrock is β, and the dip angle of the goaf rock wall is α. The sliding force mainly comes from the component of the self-weight W of the caved deposits along the sliding surface, and the sliding force F_d is shown in Formula (8):

$$F_d=W\sin \beta ={\gamma }_{s}V\sin \beta$$

(8)

The anti-sliding force of the caved deposits is composed of the shear strength F_s of the sliding surface itself, the support force F_p of the coal pillar, and the lateral support force F_b of the caved deposits. According to the Mohr-Coulomb criterion, the shear strength is determined by the cohesion c and friction force. Therefore, the shear strength of the sliding surface itself is shown in Formula (9):

$$F_s=c{A}_s+\sigma \tan \phi =c{A}_s+W\cos \beta \tan \phi =c{A}_s+{\gamma }_{s}V\cos \beta \tan \phi$$

(9)

To simplify the calculation, the external support force is directly regarded as a part of the anti-sliding force, i.e., its direction is approximately parallel to the sliding surface or provides the main normal pressure. Then, the total anti-sliding force F_r is shown in Formula (10):

$$F_r=F_s+F_p+F_b=c{A}_s+{\gamma }_{s}V\cos \beta \tan \phi +F_p+F_b$$

(10)

Under the synergistic action of the caved deposits and coal pillars, the safety coefficient K_s of the near-vertical goaf can be defined as the ratio of the total anti-sliding force to the total downslope force, as shown in Formula (11). When K_s > 1, the goaf is stable; when K_s = 1, the goaf is in the limit equilibrium state; when K_s < 1, the goaf is unstable.

$$K_s={\displaystyle \frac{F_r}{F_d}}$$

(11)

By combining Equations (5)–(10) and substituting them into Formula (11), Formula (12) is obtained:

$$K_s={\displaystyle \frac{c{A}_s+{\gamma }_{s}V\cos \beta \tan \phi +{\sigma }_p{A}_p+\frac{1}{2}{\gamma }_s{H}_s^2{K}_p}{{\gamma }_{s}V\sin \beta }}$$

(12)

The core innovation of this theory lies in breaking through the single-dimensional limitation of traditional goaf stability evaluation, markedly differing from existing research methods. For traditional methods that only consider coal pillar bearing capacity and ignore the interaction between coal pillars and caved rock masses, this study constructs a mechanical model for the synergistic effect of coal pillar—caved accumulation body, for the first time fully integrating the positive feedback effect of coal pillars’ active support and the accumulation body’s massive response, and supplementing the key dimension of “structure-medium” interaction. Compared with Wilson’s theory, this study addresses its oversight of shear slip caused by the accumulation body’s sliding force and uneven support force distribution in near-vertical coal seams. By combining the anti-dip rock slope bending toppling—shear slip failure theory and Rankine passive earth pressure theory to correct the accumulation body’s lateral pressure calculation, and incorporating analysis of the accumulation body’s sliding force and anti-sliding force, it improves the stress analysis system for near-vertical coal seam goafs. Targeting the beam-plate roof model’s shortcomings—focusing only on the linear support relationship between the roof and the accumulation body, and failing to distinguish the accumulation body’s compaction stage characteristics and the roof’s multi-mode instability—this study refines the accumulation body’s staged mechanical characteristics (compaction, yield hardening, stabilization/failure). It simplifies the roof of steeply inclined and near-vertical coal seams into an anti-dip layered slope, establishes instability criteria for toppling, shearing, and composite failure, and couples the calculation of coal pillar ultimate strength and the accumulation body’s lateral support force to realize mechanical coupling analysis of the entire roof—coal pillar—accumulation body system, rather than a single linear support analysis of the roof.

4. Physical Simulation of Synergistic Action Between Coal Pillars and Caved Deposits

4.1. Construction of Physical Similarity Model

According to the on-site coal seam occurrence conditions, engineering geological conditions, and similarity laws, the proportioning, laying, air-drying, and displacement measuring point arrangement of similar materials are carried out. The theoretical basis of the similar model experiment is mainly to reproduce the physical phenomena similar to the prototype on the scaled-down model, so as to study and predict the behavior of the prototype under real conditions. Therefore, the model design focuses on the following aspects: the influence of the stability of residual coal pillars from the chamber mining method on the roof and floor mudstone, and the influence of coal pillars and roof failure caved deposits on the stability of the goaf. In view of the fact that the research area is a near-vertical coal seam goaf, the model is laid at an angle of 73°, and different rock strata are simulated according to the corresponding proportions based on the physical and mechanical parameters of the rock. The size of the experimental platform is 120 cm × 200 cm × 50 cm, and the actual size of the constructed model is 120 cm × 140 cm × 50 cm. Simulate a coal seam depth of 105 m. The initial mining depth in the model is 7 cm. The similarity ratios are determined as follows: the geometric similarity ratio C_l is 1:75, the time similarity ratio C_t is 1: √75, the specific gravity similarity ratio C_γ is 1:1.5, the stress similarity ratio C_δ is 1:112.5, and the Poisson’s ratio similarity ratio C_μ is 1:1.

According to the physical and mechanical parameters of the on-site rock, the rock strata are generalized into three lithologies: sandstone, mudstone, and coal seam. Through material experiments, river sand is used as the aggregate, gypsum and calcium carbonate as the binders, and mica to simulate the bedding plane. The size and material proportion of each rock stratum are shown in

Table 1. Rock Stratum Model Size and Proportion.

Rock Stratum Numbering	Lithology	Model Volume /cm3	Ratio	River Sand /kg	Gypsum /kg	CaCO3 /kg	Note
Y1	Sandstone 1	2.345 × 105	755	245	52.5	52.5	The first digit of the Formulation No. indicates the sand-to-binder ratio, while the second and third digits represent the proportion of the two types of binders in the total amount.
Y2	Mudstone 1	1.400 × 105	973	324	10.8	25.2
Y3	coal	9.100 × 104	937	144	4.8	11.2
Y4	Mudstone 2	2.100 × 105	973	216	7.2	16.8
Y5	Sandstone 2	1.950 × 105	755	280	60	60

. The similar material and in situ rock mechanics test data are shown in

Table 2. Similar Materials and On-Site Rock Mechanics Test Data.

Mechanical Parameters	Sandstone	Sandstone/Model	Mudstone	Mudstone/Model	Coal	Coal/Model
Uniaxial Tensile Strength/Mpa	32.52	0.29	8.81	0.08	5.63	0.05
Elastic Modulus/GPa	4.91	0.04	1.82	0.02	0.91	0.01
Poisson’s Ratio	0.28	0.28	0.29	0.29	0.30	0.30
Cohesion/MPa	5.62	0.05	2.15	0.02	0.97	0.01

. First, a winch is used to rotate the model frame to 73° for horizontal laying, and the boundaries of each rock stratum are calibrated inside the model. Materials are prepared by adding water and mica flakes according to the proportions in Table 1. After the model is laid, it is air-dried in the shade. Then, the model frame is rotated to the vertical direction by the winch, the acrylic baffle is removed, a 10 cm × 10 cm grid is drawn on the front of the model, and displacement monitoring points are arranged at the intersection points. The actual construction effect of the model is shown in Figure 3. Earth pressure cells are placed at the pre-monitored pressure positions and connected to the static strain testing and analysis system (Figure 3a).

4.2. Coal Seam Mining Process and Monitoring

The time similarity ratio (C_t = 1:√75 ≈ 1/8.66) is theoretically derived based on dynamic similarity principles (C_t = √C_l). However, due to the limitation that similar materials cannot replicate the long-term creep of in situ rock, the model’s mining interval (1.388 h) is a simplified equivalent of the prototype’s 12 h (1.388 × 8.66 ≈ 12 h). This simplification is a standard practice in geomechanical physical models. The core conclusions of the paper focus on the “failure mode and synergistic mechanism”, which are irrelevant to long-term creep and do not affect the validity of the research. In accordance with your suggestion, we have transparently stated this limitation in the manuscript.

The panel caving method is adopted layer by layer with coal pillars retained. After mining layer by layer from top to bottom, the surrounding rock undergoes deformation, damage, and eventually collapse (Figure 4). According to the survey report of the study area, the interval between each mining operation is determined to be 1.388 h.

4.2.1. Sequential Characteristics of Coal Seam Mining and Collapse

First layer: Mining is completed in 8 min, and the overlying rock strata collapse after 5 min of stability (Figure 5a), causing a small-scale collapse of the roof. The collapse process lasts for a total of 5 min from the start to the end.

Second layer: Mining is completed in 6 min, and the coal pillar collapses immediately. The collapse process lasts for a total of 4 min from the start to the end.

Third layer: Mining is completed in 8 min, and the coal pillar and roof collapse immediately. The collapse process lasts for a total of 3 min from the start to the end.

Fourth layer: Mining is completed in 6 min, and the coal pillar collapses after 4 min of stability (Figure 5b), causing a large-scale collapse of the roof. The collapse process lasts for a total of 1 min from the start to the end. After the collapse, fractures appear on the roof.

Fifth layer: Mining is completed in 4 min, and the coal pillar collapses immediately, causing a large-scale collapse of the roof in an instant.

After the mining of each layer, the coal pillar is stable for a short time and then collapses, with different stability durations and collapse durations (Figure 5c).

4.2.2. Quantitative Analysis of Surrounding Rock Response and Stress in Coal Seam Mining

As mining progresses, partial collapse and fracture development occur sequentially in the roof. The fractures and partial have been marked with red dashed lines in the Figure 6. Specifically, the bedding-parallel fractures at locations A5 and B5 have a width of 0.06–0.08 cm and a length of 15.4–21.0 cm (Figure 6a); the flexural fracture at location A4 has a width of 0.15 cm and a length of 24.6 cm (Figure 6b); the flexural fracture at location A3 has a width of 0.16 cm and a length of 28.3 cm (Figure 6c). The 3rd and 5th roof layers undergo “toppling-type” fracturing and collapse. For the floor, only slight slippage is observed after the mining of the 3rd and 5th layers (Figure 6d), and the compaction of caved materials can temporarily delay the collapse of coal pillars.

The stress values of each monitoring point were converted based on the stress similarity ratio, as shown in

Table 3. Summary of Stress Values at Each Monitoring Point (Model/Prototype).

Monitoring Point	Mining Stage	Initial Stress/kPa	Mining Stress/kPa	Collapse Stress/kPa	Stable Stress/kPa	Recovery Duration/min	Maximum Drop/%
9	1st	2.1/2235.0	1.3/1310.0	1.5/1125.0	1.7/1856.25	8/69.28	44.4
8	1st and 2nd	6.2/2250.0	2.9/900.0	3.8/675.0	3.9/2081.25	12/103.92	70.0
7	3rd	7.2/2475.0	4.2/1012.5	5.1/618.75	5.3/2250.0	10/86.60	75.0
6	4th	7.4/2362.5	5.2/843.75	5.6/562.5	5.9/2137.5	9/77.94	76.2
5	5th	9.2/2587.5	6.0/787.5	7.4/506.25	7.8/2306.25	7/60.62	80.4
4	Mining Completed	8.8/2700.0	6.9/731.25	7.7/450.0	7.9/2362.5	11/95.26	83.3

and Figure 7. Analysis indicates that with the increase in the number of mined layers, the stress growth rate generally rises, reflecting the improved compaction efficiency of caved materials in the later stage; while the failure stress threshold decreases layer by layer, indicating the attenuation of the overall system stability. Analysis of the collapse time reveals the compaction delay effect of the accumulated materials.

5. Result

5.1. Summary of Model Experiment Results

Based on the mining sequence, surrounding rock response, and stress data, the failure mode of the goaf exhibits three stages: local shear failure, flexural-shear composite failure, and toppling-sliding dynamic instability.

In the local shear failure stage, the main failure objects are the local mudstone of the roof and the bottom of coal pillars. The primary reason is that after the first layer mining, the coal pillars have not yet achieved complete stress redistribution, and stress concentration occurs due to unloading at the bottom (the stress drop of monitoring point 9 reaches 44%), exceeding the shear strength of the coal pillars. As the roof loses partial support, the tensile strength of its bedding planes decreases, leading to small-scale collapse, and the caved accumulations only provide weak support.

In the flexural-shear composite failure stage, the main failure objects are the mudstone, sandstone of the roof, and the entire coal pillars. The key causes are as follows: after the third layer mining, the increase in upper accumulations generates lateral thrust on the coal pillars; meanwhile, the release of horizontal stress induces flexural deformation of the roof (flexural fracture at point A4). Under the combined action of tensile and shear stresses on the bedding planes, the roof exhibits “flexural-shear composite failure” (the stress drop of monitoring point 7 reaches 75%). After the fourth layer mining, the free face further expands, and delamination fractures in the roof develop. Although the caved materials provide temporary support, insufficient bearing capacity arises from compaction delay, eventually triggering large-scale collapse. At this stage, the failure shifts from local to regional, and the system transitions from independent failure to coal pillar-roof synergistic failure.

In the toppling-sliding dynamic instability stage, the failure objects include the entire roof and coal pillars. The underlying reasons are: after the fifth layer mining, the free face reaches its maximum (width: 120 cm), and the gravity of the accumulations (thickness: 8 cm) is concentrated; the bearing capacity of the coal pillars reaches the limit (the minimum stress at monitoring point 5 is 6.0 kPa); simultaneously, the tensile stress on the bedding planes exceeds the threshold (the fracture at point A3 is 22.3 cm long), causing the roof to undergo “toppling-type” fracture along the bedding planes. During the fracture process, the roof rock mass slides along the dip direction, and the caved materials cannot provide effective support, ultimately triggering dynamic instability of the system. At this stage, the failure is sudden and cascading, with a stress drop of 83% at monitoring point 4, and the system completely loses stability.

Finally, the system tends to stabilize, and the stress values of other monitoring points become basically constant; at this time, the overall stability of the system depends on the final compaction state of the accumulations.

5.2. Comparison and Verification of Model Experimental Results with Theoretical Predictions

Through observation of experimental phenomena and literature research, it is found that during the mining process, the collapse mode of the goaf roof is similar to that of the counter-dip slope, both being toppling-sliding failure. Literature has also proven that this is a type of shear-sliding failure [27,28]. Therefore, to accurately conduct a qualitative analysis of goaf stability under the synergistic effect of coal pillars and caved deposits, and to predict the precursor conditions for each failure, the failure of the roof mudstone layer is regarded as a toppling-sliding deformation mode occurring on a counter-dip slope [29]. The toppling-sliding failure model holds that roof fractures should develop along bedding planes, and bending fractures are concentrated in the middle of the roof [35,36,37,38,39,40,41,42]. Experiments show that roof fractures are indeed dominated by bedding fractures (Points A5, B5, A3), and bending fractures are concentrated at Point A4 (the middle of the roof, corresponding to the area with the maximum bending moment). The error between the fracture size and the theoretical predicted value (bedding fractures: width 0.05–0.1 cm, length 15–22 cm; bending fractures: width 0.1–0.2 cm, length 20–25 cm) is less than 10%, indicating a high degree of agreement. In the experiment, the fragment size of the rock mass shows a “small upper, large lower” distribution (fragment size: 2–3 cm in the upper part of the roof, 5–8 cm in the lower part), which is consistent with the theoretically predicted “fragment size distribution law of toppling failure” (smaller fragment size from bending failure in the upper part, larger fragment size from shear failure in the lower part).

In addition, according to previous survey reports, the caving zone in the study area can extend to the ground surface, leading to intense development of surface subsidence. Year by year, deep subsidence gullies, beaded zonal subsidence pits, and subsidence troughs have appeared in the study area. The reserved coal pillars in the roof will experience drawing and caving into the goaf, and the roof bending deformation extends to the overlying strata of the roof along the direction perpendicular to the coal seam strike, forming a “concave”-shaped failure. The experimental results are in good consistency with the working conditions of the survey area.

The results of the similar model experiment are compared with the theoretical analysis. In the model experiment, the volume (V) of the accumulation body is 1.3 × 10⁴ cm³, the mass (W) is 22.1 kg, the position (H) of the accumulation body is 73 cm, the projected length (l) of the roof is 35 cm, the height (H_s) of the accumulation body in the goaf is 28 cm, the dip angle (β) of the sliding surface between the rock blocks and the stable bedrock is 73°, and the unit weight (γ_s) of the accumulation body is 17 N/m³. By substituting the on-site data into the safety factor formula (16), the ratio (K_s) of the total anti-sliding force (Fr) to the total sliding force (F_d) of the goaf is calculated to be 0.156, and the model is unstable, indicating that the theoretical calculation is consistent with the measured results. Moreover, in the experiment, joint fractures developed, the rock mass was fragmented, caving occurred, and the drawing and caving failure extended to the ground surface, which is consistent with the phenomena shown in the survey report. The average full mining coefficient of the goaf surface is 0.143, and the evaluation concludes that the goaf is in an unstable state.

6. Discussion

Despite its contributions, this research has several limitations that require future refinement: The geometric similarity ratio of 1:75 simplifies the meso-structure of caved deposits. In reality, gangue particles in field goafs range from 5 mm to 500 mm, while the model uses uniform 5–500 mm sand aggregates. This may lead to overestimation of compaction rate. Secondly, there is a lack of verification using numerical simulation methods.

The particle size distribution of the actual caved rock mass in the goaf follows the law of bulking and presents a gradation distribution. Under the geometric similarity ratio of 1:75, the particle size of the caved material in the model needs to be scaled geometrically, but this scaled size will be smaller than the minimum preparable particle size in the model experiment, resulting in the complete absence of the coarse particle group and distorted proportion of medium-coarse particles. Therefore, the particle size similarity deviation coefficient η_d is introduced as shown in Formula (13), and a correlation formula (Formula 14) between particle size and parameters is established to substitute the particle size deviation value.

$${\eta }_d={\displaystyle \frac{d_{p,avg}-n\cdot d_{m,avg}}{d_{p,avg}}}$$

(13)

$$\begin{array}{l}{\phi }_s={\phi }_0+k_1\lg (d_{avg})\\ c_s=c_0+k_2{d}_{avg}\end{array}$$

(14)

Through calculation, the average particle size of the prototype is approximately 12 cm, and the corresponding size in the model should be 0.16 cm according to the similarity ratio. However, the minimum preparable particle size used in the actual model is 0.1 cm, with an η_d value of 0.375, meaning the particle size similarity deviation reaches 37.5%. Calculations indicate that the calculated lateral support force Fb of the accumulation is about 15% lower than that of the prototype, ultimately leading to an approximately 12% lower calculation deviation of Ks.

From the mechanical mechanism perspective, the validity of F = kw requires two prerequisites: the accumulation is in the elastic compaction stage, where only void compression occurs in the caved rock blocks without particle breakage or rearrangement, and the support force increases linearly with subsidence; the accumulation is uniformly distributed without obvious cavities or loose areas, ensuring the foundation coefficient k is constant. In the similar model of this study, the compaction process of the accumulation in the initial mining stage (mining of the first and second layers) meets the above prerequisites. Model monitoring shows that during this stage, the roof subsidence is less than 2 cm, the compactness of the accumulation increases from 1.3 g/cm³ to 1.5 g/cm³, and the R² value of the linear fitting between support force and subsidence reaches 0.92. Thus, the F = kw assumption is applicable in this stage.

A potential limitation is the time scale simplification, which is unavoidable in physical models but does not impact the synergistic mechanism analysis. Future studies could combine numerical simulations (e.g., PFC3D) to validate long-term creep behavior.

The parameters and their definitions in this paper are presented in Appendix A at the end of the document.

7. Conclusions

(1)

The proposed mechanical mechanism model of the “synergistic action between coal pillars and caved deposits” reveals that during the near-vertical chamber mining process, the dynamic evolution of the void ratio of the caved deposits directly affects the support performance, and clarifies that the compaction lag and inhomogeneity of the caved deposits are the key factors controlling the instability sequence, thereby regulating the overall stability of the goaf.

(2)

The toppling-sliding composite failure theory of anti-dip slopes can be applied to the instability analysis of the roof of near-vertical goafs. By integrating the support force of coal pillars and the lateral support force of caved deposits into a unified mechanical equilibrium system, the safety coefficient K_s for goaf stability under the synergistic action of coal pillars and caved deposits is constructed, which provides a new method for the quantitative prediction of the stability state of goafs.

(3)

Through the comparative verification between the similar simulation experiment and the theoretical analysis, it is confirmed that the proposed synergistic action model can more accurately reflect the stable state compared with the traditional model that only considers coal pillars. Quantitative analysis shows that the lateral support force generated by the caved deposits can increase the calculation result of the overall safety coefficient by more than 15%, and the support effect is most significant in the compacted area of the middle and lower parts of the goaf. This result provides a key basis for the accurate prediction of disaster risks.

(4)

The “structure-medium” synergistic analysis framework proposed in this study can be extended to the stability evaluation of goafs under the mining conditions of other large-dip-angle and steeply inclined coal seams, providing a new theory and engineering reference for the prevention and control of mine dynamic disasters.

(5)

This method boasts high application feasibility in practical engineering. From the perspective of data acquisition, all parameters required by the model can be obtained through conventional methods; from the perspective of engineering adaptability, it can be directly embedded into the existing mine goaf stability evaluation process, enabling graded assessment of goaf stability status via quantitative calculation of the safety factor Ks; from the perspective of expected engineering effects, the method can accurately identify the key stages of goaf instability (local shear failure, bending-shear composite failure, toppling-sliding dynamic instability). Based on this, coal pillar layout parameters and goaf caved material control measures are optimized, and it is expected to reduce the roof collapse accident rate of goafs in near-vertical coal seams by more than 20%.