From Measured In Situ Stress to Dynamic Simulation: A Calibrated 3DEC Model of a Rock Quarry
Abstract
1. Introduction
2. Study Area
3. Materials and Methods
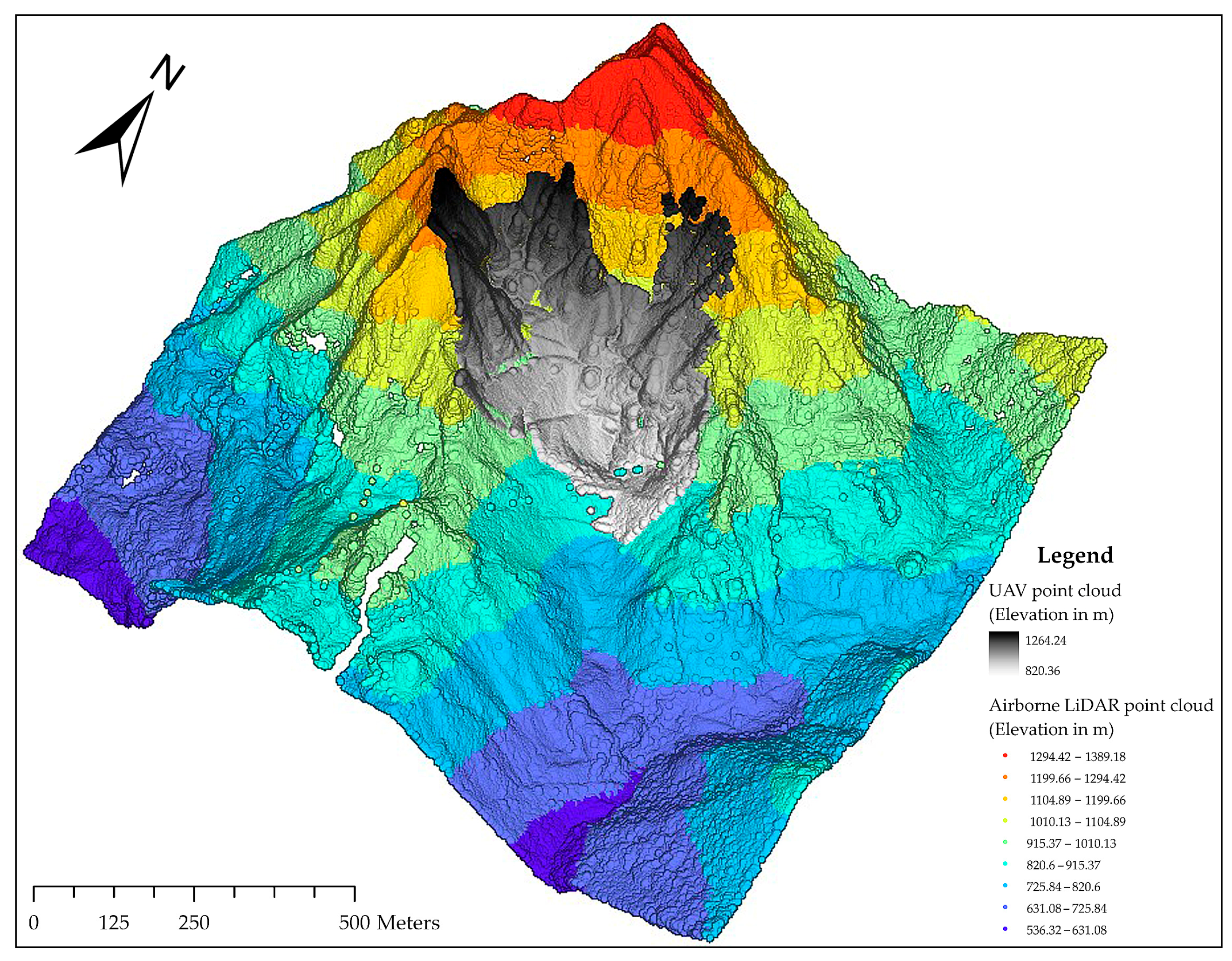
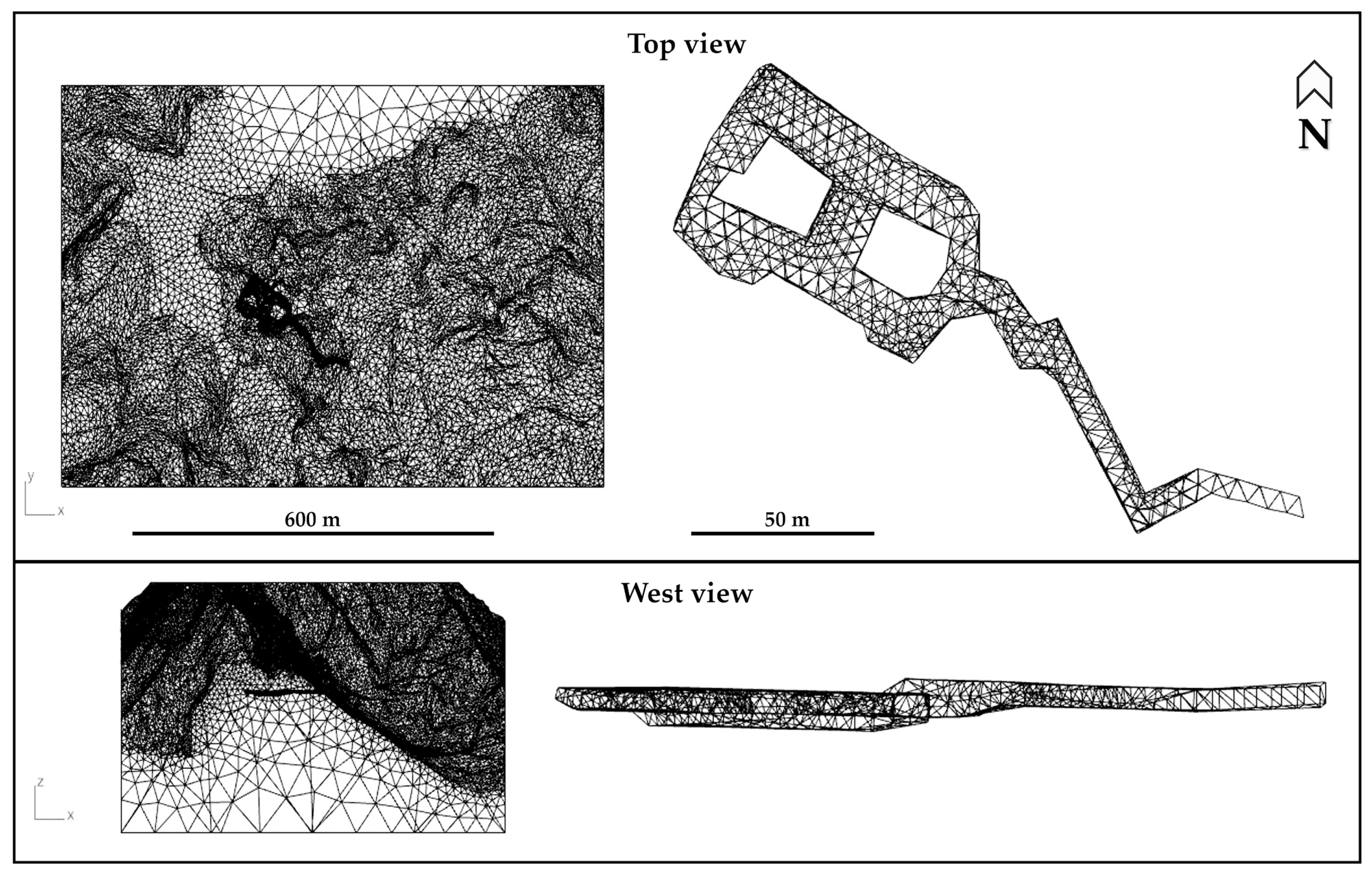
3.1. Topographic Survey and 3D Model Generation
3.2. Geomechanical Characterization
3.3. CSIRO HI Cell Overcoring Tests
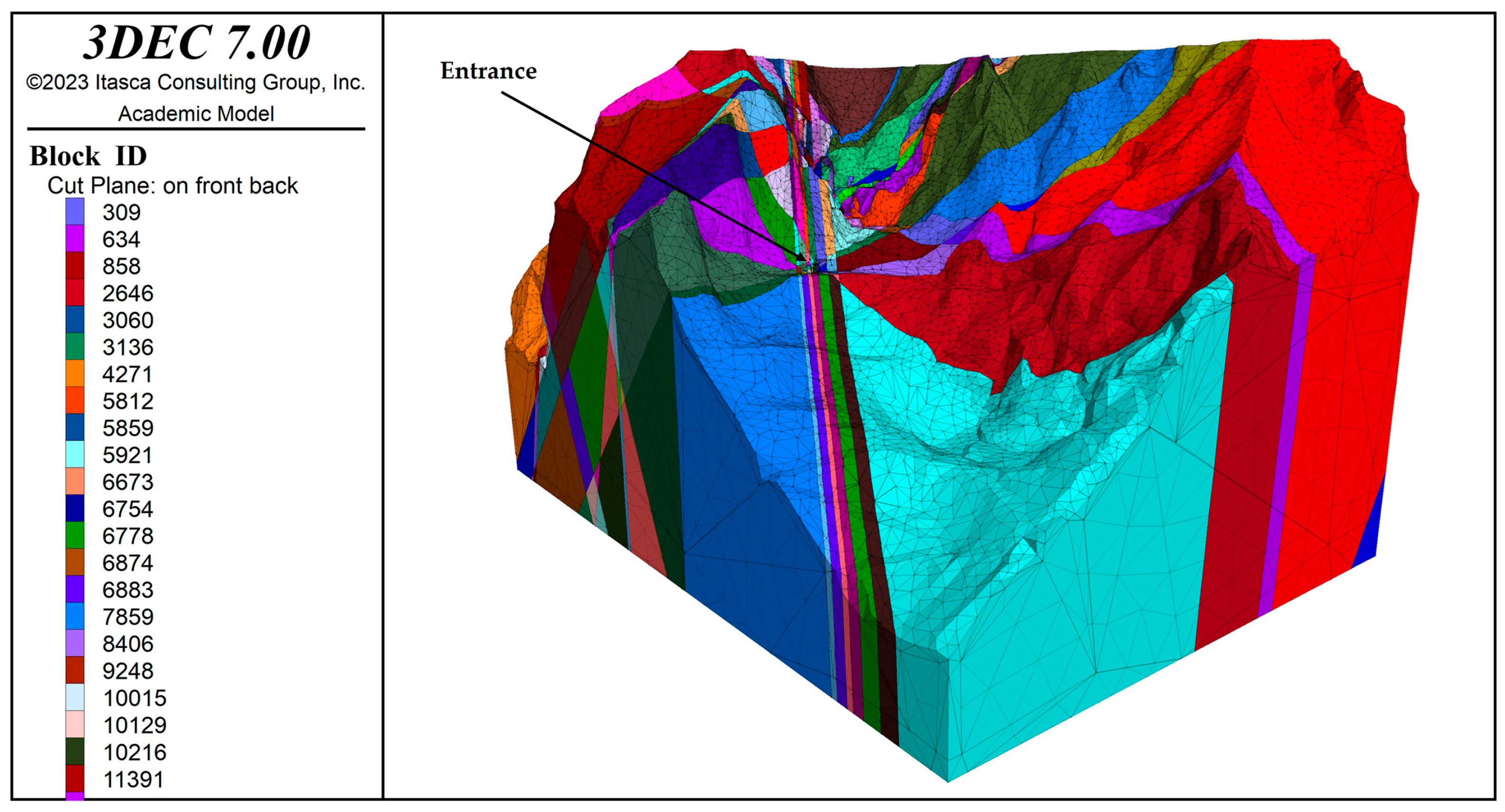
3.4. Distinct Element Numerical Modelling
4. Results
4.1. Engineering-Geological Survey
4.2. CSIRO HI Stress Measurements
4.3. DEM Modelling
5. Discussion
- -
- -
- Constructive interference of wave fronts at free surfaces, enhancing dynamic shear stress [48];
- -
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Santa, C.M.; Fernandes, I.; Chaminé, H.I. Geomechanical Classifications, Geotechnical Indexes and Fractured Rock Media: The Influence of Discontinuities on the Rock Masses Description. Civ. Environ. Eng. Rep. 2024, 3, 43–54. [Google Scholar] [CrossRef]
- Barton, N.R. A model study of rock-joint deformation. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1972, 9, 579–582. [Google Scholar] [CrossRef]
- Gottron, D.; Henk, A. Upscaling the Mechanical Properties of a Fractured Rock Mass Using the Lattice-Spring-Based Synthetic Rock Mass (LS-SRM) Modeling Approach—Comparison of Discontinuum, Continuum and Empirical Approaches. Geosciences 2022, 12, 343. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. The Hoek–Brown failure criterion—A 2018 update. J. Rock Mech. Geotech. Eng. 2019, 11, 585–592. [Google Scholar] [CrossRef]
- Brady, B.H.G.; Brown, E.T. Rock Mechanics for Underground Mining, 3rd ed.; Springer: Dordrecht, The Netherlands, 2006; pp. 1–600. [Google Scholar]
- Wang, T.; Xu, D.; Elsworth, D.; Zhou, W. Distinct element modeling of strength variation in jointed rock masses under uniaxial compression. Geomech. Geophys. Geo-Energy Geo-Resour. 2016, 2, 11–24. [Google Scholar] [CrossRef]
- An, H.; Wu, S.; Liu, H.; Wang, X. Hybrid Finite-Discrete Element Modelling of Various Rock Fracture Types. Sustainability 2022, 14, 592. [Google Scholar] [CrossRef]
- Itasca Consulting Group, Inc. 3DEC, 3-Dimensional Distinct Element Code User’s Guide; Itasca Consulting Group, Inc.: Minneapolis, MN, USA, 2024; Available online: https://www.itascacg.com/3dec (accessed on 10 October 2025).
- Ge, X.; Liu, X. Effects of Three-Directional Seismic Wave on Dynamic Response and Failure Behavior of High-Steep Rock Slide. Appl. Sci. 2022, 12, 20. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhao, Z.; Li, H.; Liu, D. DEM-Based Numerical Investigation of Seismic Stability of Jointed Rock Masses Using 3DEC. Lithosphere 2021, 2021, 613345. [Google Scholar] [CrossRef]
- Ziegler, M.O.; Heidbach, O. The 3D Stress State from Geomechanical–Numerical Modelling: Quantification of Uncertainties in Stress Tensor Components. Geotherm. Energy 2020, 8, 33. [Google Scholar] [CrossRef]
- Amadei, B.; Stephansson, O. Rock Stress and Its Measurement; Chapman and Hall: London, UK, 1997. [Google Scholar]
- Ziegler, M.O.; Heidbach, O. Rock Properties and Modelled Stress State Uncertainties. Rock Mech. Rock Eng. 2022, 55, 2753–2774. [Google Scholar] [CrossRef]
- Brown, E.T.; Hoek, E. Trends in relationships between measured rock stress and depth. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1978, 15, 211–215. [Google Scholar] [CrossRef]
- Hoek, E. Practical Rock Engineering; Rocscience: Toronto, ON, Canada, 2000. [Google Scholar]
- Ferrero, A.M.; Migliazza, M.; Segalini, A.; Gullì, D. In situ stress measurements interpretations in large underground marble quarry by 3D modeling. Int. J. Rock Mech. Min. Sci. 2013, 60, 103–113. [Google Scholar] [CrossRef]
- Bonetto, S.M.R.; Vagnon, F.; Umili, G.; Vianello, D.; Migliazza, M.R.; Ferrero, A.M. The Contribution of Remotely Sensed Data to the Stress State Evaluation in Underground Marble Quarries. Egypt. J. Remote Sens. Space Sci. 2021, 24, 1–13. [Google Scholar] [CrossRef]
- Smith, W.K. Two BASIC Computer Programs for the Determination of In Situ Stresses Using the CSIRO Hollow Inclusion Stress Cell and the USBM Borehole Deformation Gage; USGS Open-File Report 82-489; U.S. Geological Survey: Reston, VA, USA, 1982. [Google Scholar] [CrossRef]
- Jin, Z.; Li, Y.; Li, Q.; Liu, Z.; Wu, S.; Wang, Z. Modification of the CSIRO Method in the Long-Term Monitoring of Slope-Induced Stress. Front. Earth Sci. 2022, 10, 981470. [Google Scholar] [CrossRef]
- De Lucia, V.; Ermini, A.; Guido, S.; Marchetti, D.; Gullì, D.; Salvini, R. Investigations using CSIRO HI Triaxial Cells for measuring the stress states of rock masses subject to mining extraction: Numerical modelling of in-situ extracted core samples. Ital. J. Eng. Geol. Environ. 2024, 1, 95–103. [Google Scholar] [CrossRef]
- Pinheiro, A.L.; Lana, M.S.; Sobreira, F.G. Use of the Distinct Element Method to Study Flexural Toppling at the Pico Mine, Brazil. Bull. Eng. Geol. Environ. 2015, 74, 1177–1186. [Google Scholar] [CrossRef]
- Stephansson, O.; Zang, A. ISRM Suggested Methods for Rock Stress Estimation—Part 5: Establishing a Model for the In Situ Stress at a Given Site. Rock Mech. Rock Eng. 2012, 45, 955–969. [Google Scholar] [CrossRef]
- Gullì, D.; Pellegri, M.; Cortopassi, A. Experimental approach for stability evaluations of Carrara marble basins. In Landslide Science and Practice, Vol. 3: Spatial Analysis and Modelling; Springer: Berlin/Heidelberg, Germany, 2013; pp. 211–217. [Google Scholar]
- He, M.; Jia, X.; Coli, M.; Livi, E.; Sousa, L. Experimental Study of Rockbursts in Underground Quarrying of Carrara Marble. Int. J. Rock Mech. Min. Sci. 2012, 52, 1–8. [Google Scholar] [CrossRef]
- Francioni, M.; Salvini, R.; Stead, D.; Giovannini, R.; Riccucci, S.; Vanneschi, C.; Gullì, D. An Integrated Remote Sensing–GIS Approach for the Analysis of an Open Pit in the Carrara Marble District, Italy: Slope Stability Assessment through Kinematic and Numerical Methods. Comput. Geotech. 2015, 67, 46–63. [Google Scholar] [CrossRef]
- Coli, M.; Criscuolo, A. The Carrara Marble: Geology, Geomechanics and Quarrying. IOP Conf. Ser. Earth Environ. Sci. 2021, 833, 012120. [Google Scholar] [CrossRef]
- Salvini, R.; Ermini, A.; De Lucia, V.; Beltramone, L.; Silvestri, D.; Rindinella, A.; Guido, S.; Marchetti, D.; Gullì, D. Stress–strain investigation of the rock mass based on overcoring with CSIRO HI cell test and numerical modeling: A case study from an Italian underground marble quarry. Geosciences 2022, 12, 441. [Google Scholar] [CrossRef]
- De Lucia, V.; Ermini, A.; Guido, S.; Marchetti, D.; Gullì, D.; Salvini, R. Distinct Element Numerical Modelling and In Situ CSIRO HI Cell Data for Rock Slope Stability Assessment. Geosciences 2025, 15, 155. [Google Scholar] [CrossRef]
- Cortopassi, M.; Vaselli, O. Piano di Coltivazione della Cava Ravalunga n.138 (Bacino di Colonnata—Loc. Ravalunga); Technical Report (Private Communication); Comune di Carrara: Carrara, Italy, 2013. [Google Scholar]
- Cortopassi, P.F.; Daddi, M.; D’Amato Avanzi, G.; Giannecchini, R.; Lattanzi, G.; Merlini, A.; Milano, P.F. Quarry Waste and Slope Instability: Preliminary Assessment of Some Controlling Factors in the Carrara Marble Basin (Italy). Ital. J. Eng. Geol. Environ. 2008, 99–118. [Google Scholar] [CrossRef]
- Carmignani, L.; Kligfield, R. Crustal extension in the Northern Apennines: The transition from compression to extension in the Alpi Apuane core complex. Tectonics 1990, 9, 1275–1303. [Google Scholar] [CrossRef]
- ERTAG Regione Toscana. I Marmi Apuani; Nuova Grafica Fiorentina: Florence, Italy, 1980; p. 126. [Google Scholar]
- Cravero, M.; Gullì, D.; Iabichino, G. Comparative mechanical characterization of marble by means of laboratory testing. In Proceedings of the 39th U.S. Rock Mechanics Symposium (USRMS), Cambridge, MA, USA, January 2003. [Google Scholar]
- Firpo, G.; Salvini, R.; Francioni, M.; Ranjith, P.G. Use of Digital Terrestrial Photogrammetry in rocky slope stability analysis by Distinct Elements Numerical Methods. Int. J. Rock Mech. Min. Sci. 2011, 48, 1045–1054. [Google Scholar] [CrossRef]
- Cundall, P.A. The Measurement and Analysis of Acceleration in Rock Slopes. Ph.D. Thesis, University of London, London, UK, 1971. [Google Scholar]
- Coulomb, C.A. Essai sur une application des règles des maximis et minimis à quelques problèmes de statique relatifs à l’architecture. Mem. Acad. R. Sci. 1776, 7, 343–387. [Google Scholar]
- Jiao, Y.; Zhao, J.; Ge, X. New formulation and validation of the three-dimensional extension of a static relaxation method. Adv. Eng. Softw. 2004, 35, 317–323. [Google Scholar] [CrossRef]
- Lysmer, J.; Kuhlemeyer, R.L. Finite dynamic model for infinite media. J. Eng. Mech. Div. 1969, 95, 859–877. [Google Scholar] [CrossRef]
- Ministero delle Infrastrutture e dei Trasporti. Decreto Ministeriale 17/01/2018. Aggiornamento delle “Norme Tecniche per le Costruzioni” (NTC 2018); Supplemento Ordinario alla Gazzetta Ufficiale n. 42 del 20 febbraio; Ministero delle Infrastrutture e dei Trasporti: Roma, Italy, 2018. [Google Scholar]
- GeoStru Software. GeoStru Online Platform—NTC 2018 Response Spectra and Seismic Input Generator; GeoStru Software: Piacenza, Italy, 2024; Available online: https://www.geostru.eu (accessed on 6 November 2025).
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering, 4th ed.; Pearson Education: Upper Saddle River, NJ, USA, 2012. [Google Scholar]
- Rybacki, E.; Jokisch, A.; Ziegenhagen, B.; Dresen, G.; Brantut, N.; Heidbach, O.; Meier, T. Semi-Brittle Deformation of Carrara Marble: Hardening and Strengthening Mechanisms in a Massive Carbonate Rock. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022573. [Google Scholar] [CrossRef]
- Mohr, O. Welche Umstände bedingen die Elastizitätsgrenze und den Bruch eines Materials? Z. Ver. Dtsch. Ing. 1900, 44, 1524–1530. [Google Scholar]
- Martin, C.D.; Kaiser, P.K.; McCreath, D.R. Hoek-Brown parameters for predicting the depth of brittle failure around tunnels. Can. Geotech. J. 1999, 36, 136–151. [Google Scholar] [CrossRef]
- Gullì, D.; Pellegri, M.; Marchetti, D. Mechanical behaviour of Carrara marble rock mass related to geo-structural conditions and in-situ stress. In Proceedings of the 8th South American Congress on Rock Mechanics: Integrating Innovation of Rock Mechanics, Buenos Aires, Argentina, 15–18 November 2015. [Google Scholar]
- Cao, M.; Li, X.; Li, Y.; Wu, J.; Li, P.; Zhou, Y. Stress Characteristics and Mechanical Behavior of Rock Masses with an Opening under Complex Deep Underground Stress Conditions. Appl. Sci. 2024, 14, 7197. [Google Scholar] [CrossRef]
- Shan, R.; Bai, H.; Li, Y.; Wu, H.; Sun, P.; Zhao, X.; Dou, H.; Wang, H. Analytical Solution of Surrounding Rock Stress and Plastic Zone of Rectangular Roadway under Non-Uniform Stress Field. Sci. Rep. 2024, 14, 27482. [Google Scholar] [CrossRef]
- Lan, R.; Zhang, Z.; Wang, H.; Li, J.; Zou, Q.; Gao, F. The Influence of the Number of Free Surfaces on the Energy Distribution and Fragmentation Degree in Blasting of Hard Rock. Front. Earth Sci. 2023, 11, 1210650. [Google Scholar] [CrossRef]
- Martin, C.D.; Christiansson, R.; Söderhäll, J. Stress Concentrations Caused by Sharp Corners and Large Regions of Low Confinement in Underground Openings. In SKB Technical Report; TR-01-38; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 2001; Available online: https://skb.se/upload/publications/pdf/TR-01-38.pdf (accessed on 5 November 2025).
- Lei, Q.; Latham, J.-P.; Xiang, J. Implementation of an Empirical Joint Constitutive Model into Finite-Discrete Element Analysis of the Geomechanical Behaviour of Fractured Rocks. Rock Mech. Rock Eng. 2016, 49, 4799–4816. [Google Scholar] [CrossRef]
- Burjánek, J.; Gassner-Stamm, G.; Poggi, V.; Moore, J.R.; Fäh, D. Ambient Vibration Analysis of an Unstable Mountain Slope. Geophys. J. Int. 2010, 180, 820–828. [Google Scholar] [CrossRef]
- Kleinbrod, U.; Burjánek, J.; Fäh, D. Ambient Vibration Classification of Unstable Rock Slopes: A Systematic Approach. Eng. Geol. 2019, 249, 198–217. [Google Scholar] [CrossRef]
- McKinnon, S.D. Analysis of stress measurements using a numerical model methodology. Int. J. Rock Mech. Min. Sci. 2001, 38, 699–709. [Google Scholar] [CrossRef]








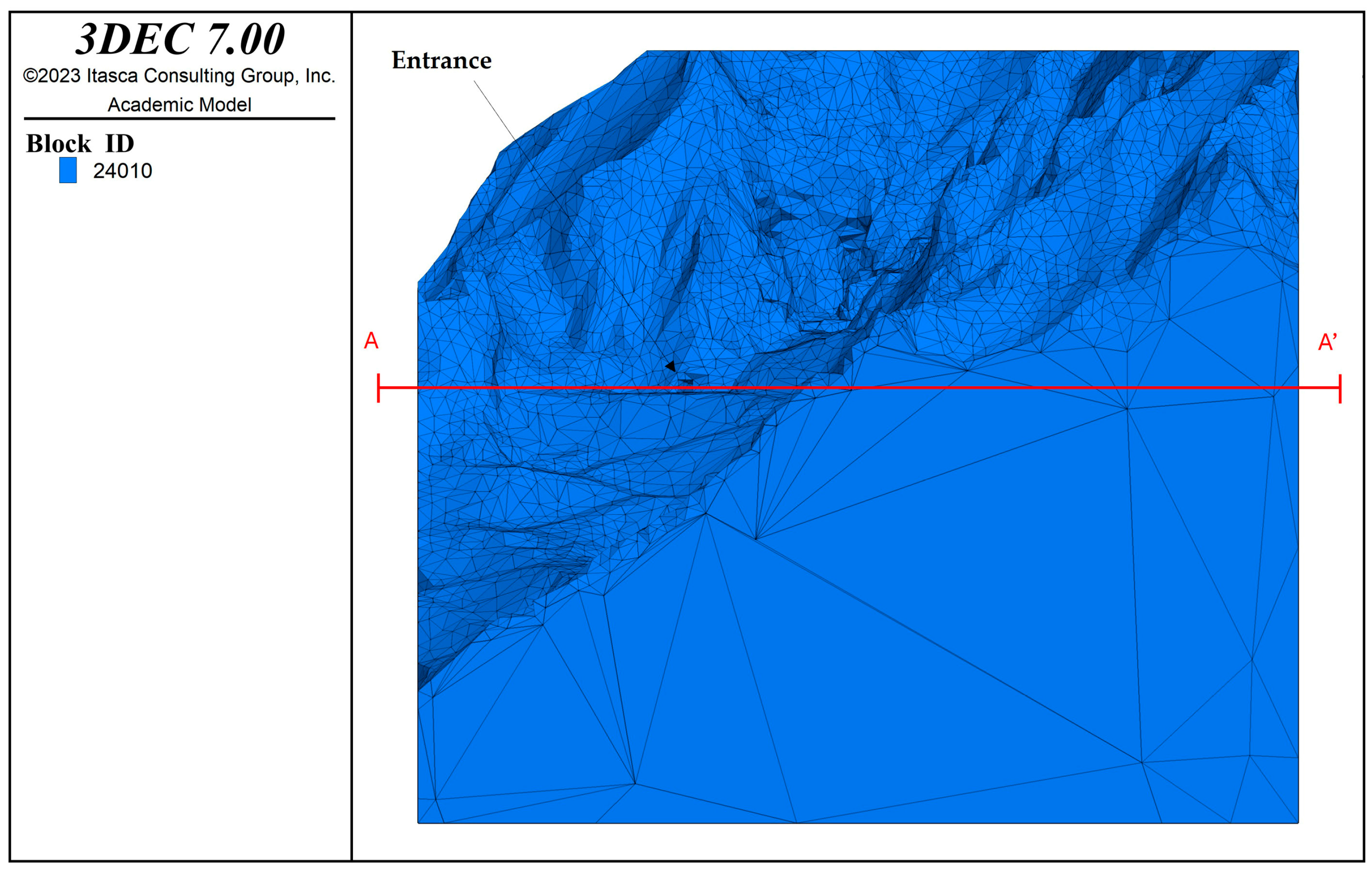

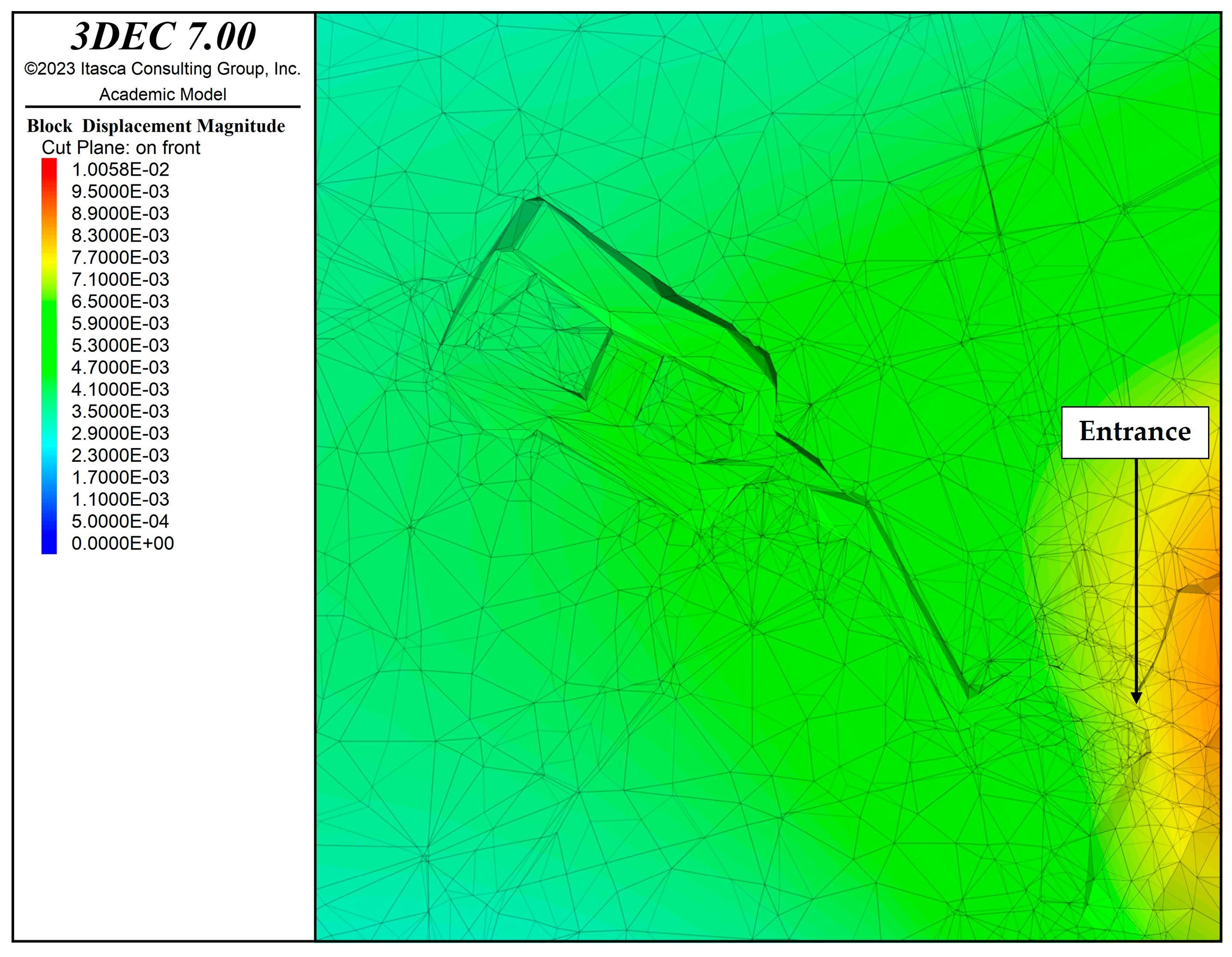
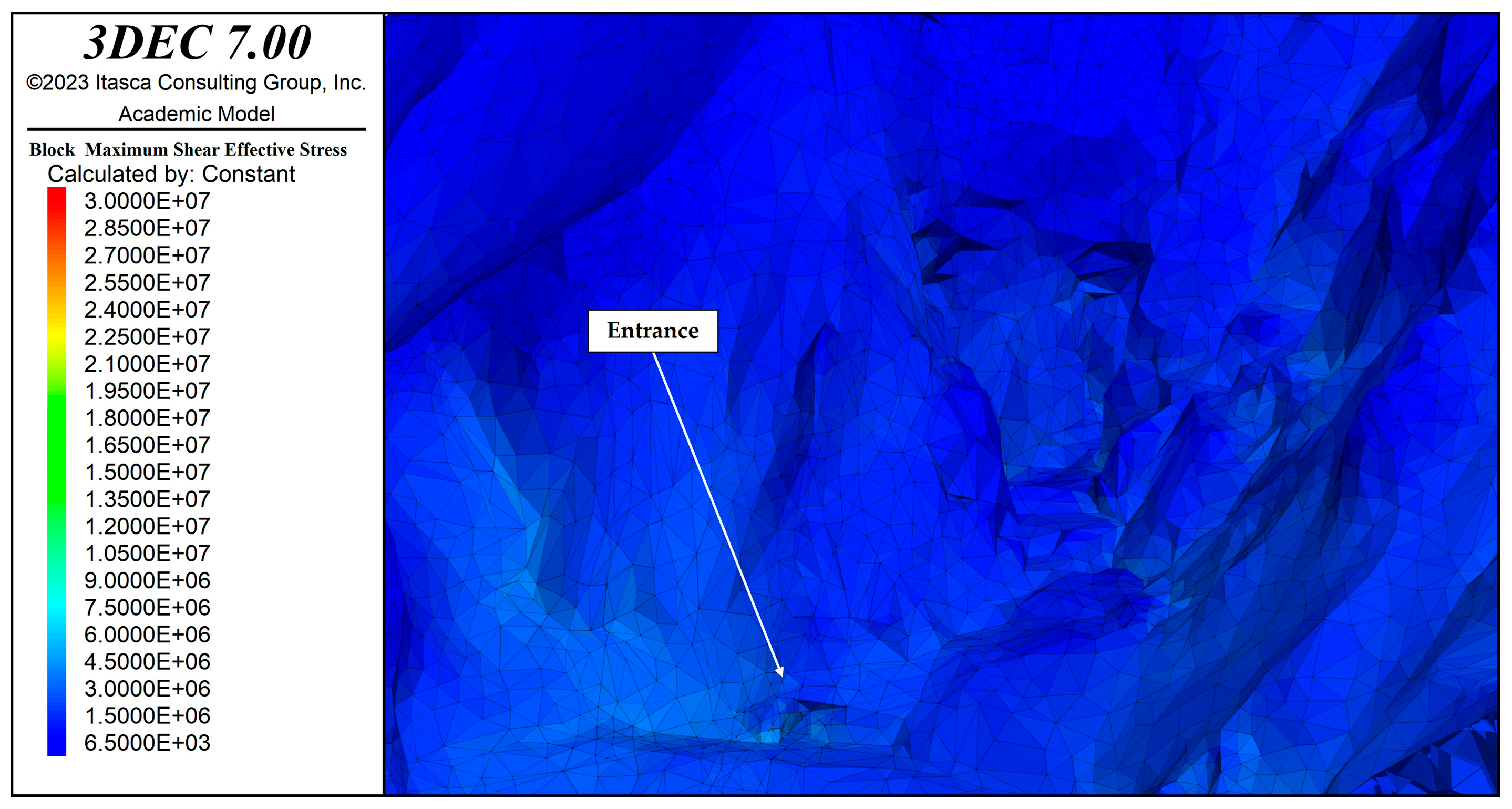







| Parameter | Value |
|---|---|
| Uniaxial Compressive Strength (MPa) | 100 |
| Tensile Strength (MPa) | 8 ± 3 |
| Cohesion (MPa) | 20 |
| Friction Angle (°) | 50 |
| Density (Kg/m3) | 2700 |
| Poisson’s coefficient (-) | 0.35 |
| Young’s Modulus (MPa) | 84,000 |
| Borehole | Bore Diameter (mm) | Dip Direction (°) | Dip (°) | Depth of the CSIRO HI Test (m) | |
|---|---|---|---|---|---|
| A | 164 | 26 | 5 | A1 | 5.65 |
| A2 | 10.65 | ||||
| B | 164 | 296 | 5 | B1 | 5.40 |
| B2 | 10.34 | ||||
| Set | Dip Direction | Dip | Frequency % | Persistence (m) | Spacing (m) |
|---|---|---|---|---|---|
| K1 | 030 | 89 | 33 | >20 | 0.6 |
| K2.1 | 128 | 71 | 25 | 3–20 | 0.8 |
| K2.2 | 296 | 72 | 7 | 1–10 | 1.2 |
| K3 | 257 | 88 | 19 | 3–20 | 1.2 |
| K4 | 165 | 87 | 10 | 1–3 | 1 |
| K5 | 255 | 46 | 3.5 | >20 | 1.2 |
| Borehole | Depth (m) | E [MPa] | ν [-] | σ1 [MPa] | σ2 [MPa] | σ3 [MPa] | σv [MPa] | |
|---|---|---|---|---|---|---|---|---|
| A | A1 | 5.65 | 82,797 ± 1036 | 0.36 ± 0.02 | 13.35 ± 0.48 | 3.74 ± 0.36 | 2.76 ± 0.65 | 10.74 ± 0.39 |
| A2 | 10.65 | 81,742 ± 1690 | 0.35 ± 0.03 | 7.90 ± 0.23 | 3.88 ± 0.15 | 2.57 ± 0.28 | 6.79 ± 0.14 | |
| B | B1 | 5.40 | 87,572 ± 1654 | 0.33 ± 0.02 | 9.26 ± 0.28 | 2.20 ± 0.38 | 0.04 ± 0.21 | 8.15 ± 0.22 |
| B2 | 10.34 | 84,749 ± 1785 | 0.32 ± 0.03 | 5.03 ± 0.31 | 2.38 ± 0.47 | 0.22 ± 0.30 | 4.55 ± 0.39 | |
| Friction Angle (°) | Cohesion [MPa] | Density [kg/m3] | Ei [MPa] | ν [-] | Gi [MPa] |
|---|---|---|---|---|---|
| 50 | 20 | 2700 | 84,000 | 0.35 | 31,111 |
| Friction Angle (°) | Em [MPa] | Gm [MPa] | L [m] | Kn [MPa/m] | Ks [MPa/m] |
|---|---|---|---|---|---|
| 35 | 58,023 | 21,490 | 1 | 187,624 | 69,491 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Lucia, V.; Gullì, D.; Marchetti, D.; Salvini, R. From Measured In Situ Stress to Dynamic Simulation: A Calibrated 3DEC Model of a Rock Quarry. Appl. Sci. 2025, 15, 13100. https://doi.org/10.3390/app152413100
De Lucia V, Gullì D, Marchetti D, Salvini R. From Measured In Situ Stress to Dynamic Simulation: A Calibrated 3DEC Model of a Rock Quarry. Applied Sciences. 2025; 15(24):13100. https://doi.org/10.3390/app152413100
Chicago/Turabian StyleDe Lucia, Vivien, Domenico Gullì, Daria Marchetti, and Riccardo Salvini. 2025. "From Measured In Situ Stress to Dynamic Simulation: A Calibrated 3DEC Model of a Rock Quarry" Applied Sciences 15, no. 24: 13100. https://doi.org/10.3390/app152413100
APA StyleDe Lucia, V., Gullì, D., Marchetti, D., & Salvini, R. (2025). From Measured In Situ Stress to Dynamic Simulation: A Calibrated 3DEC Model of a Rock Quarry. Applied Sciences, 15(24), 13100. https://doi.org/10.3390/app152413100







