A Surface Subsidence Monitoring Method for Narrow and Elongated Mining Areas by Combining InSAR and the Improved Probability Integral Method
Abstract
1. Introduction
2. Materials and Methods
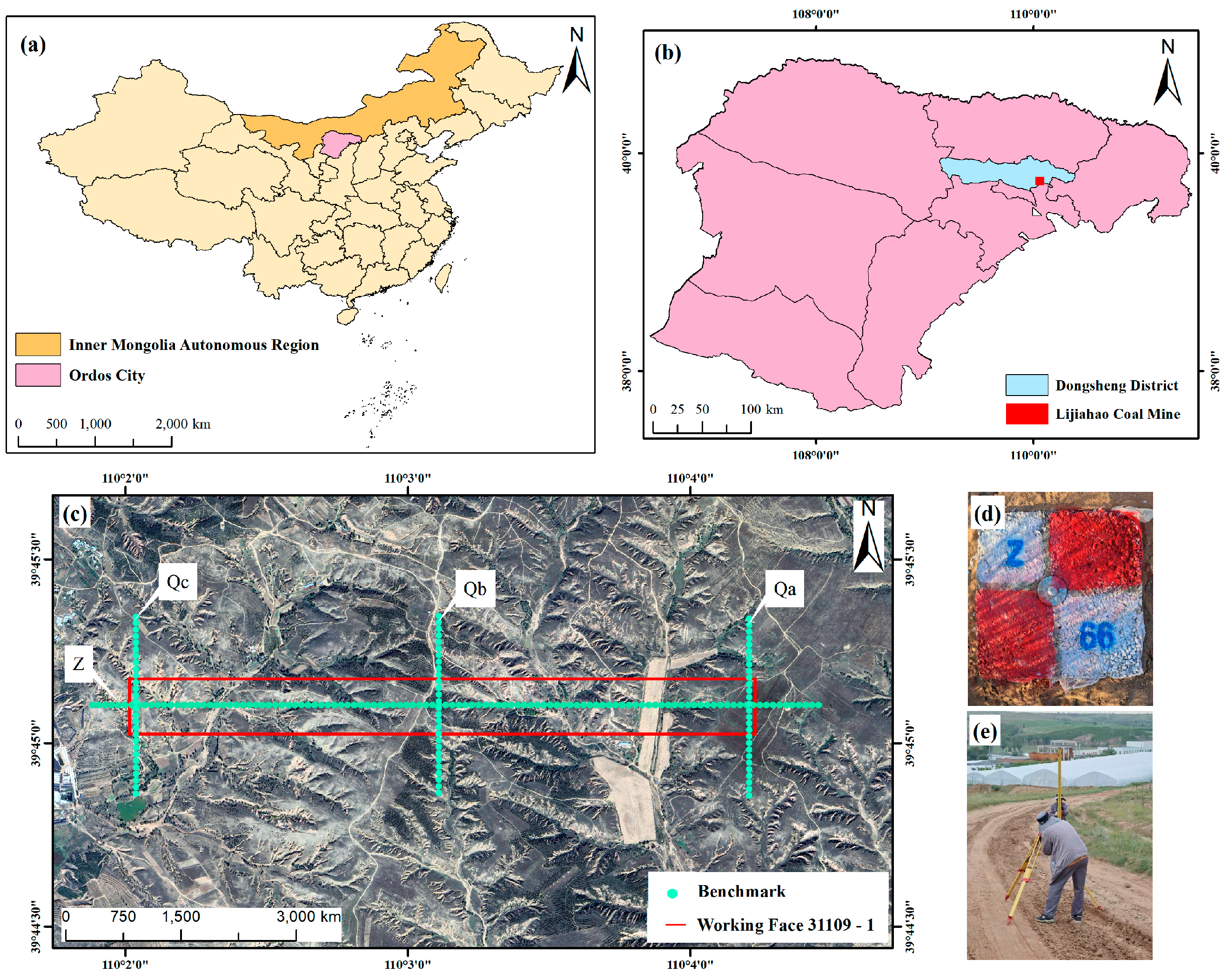
2.1. Overview of the Study Area
2.2. Selection of SAR Image Data
2.3. The Basic Principle of the Improved Probability Integral Method (IPIM)
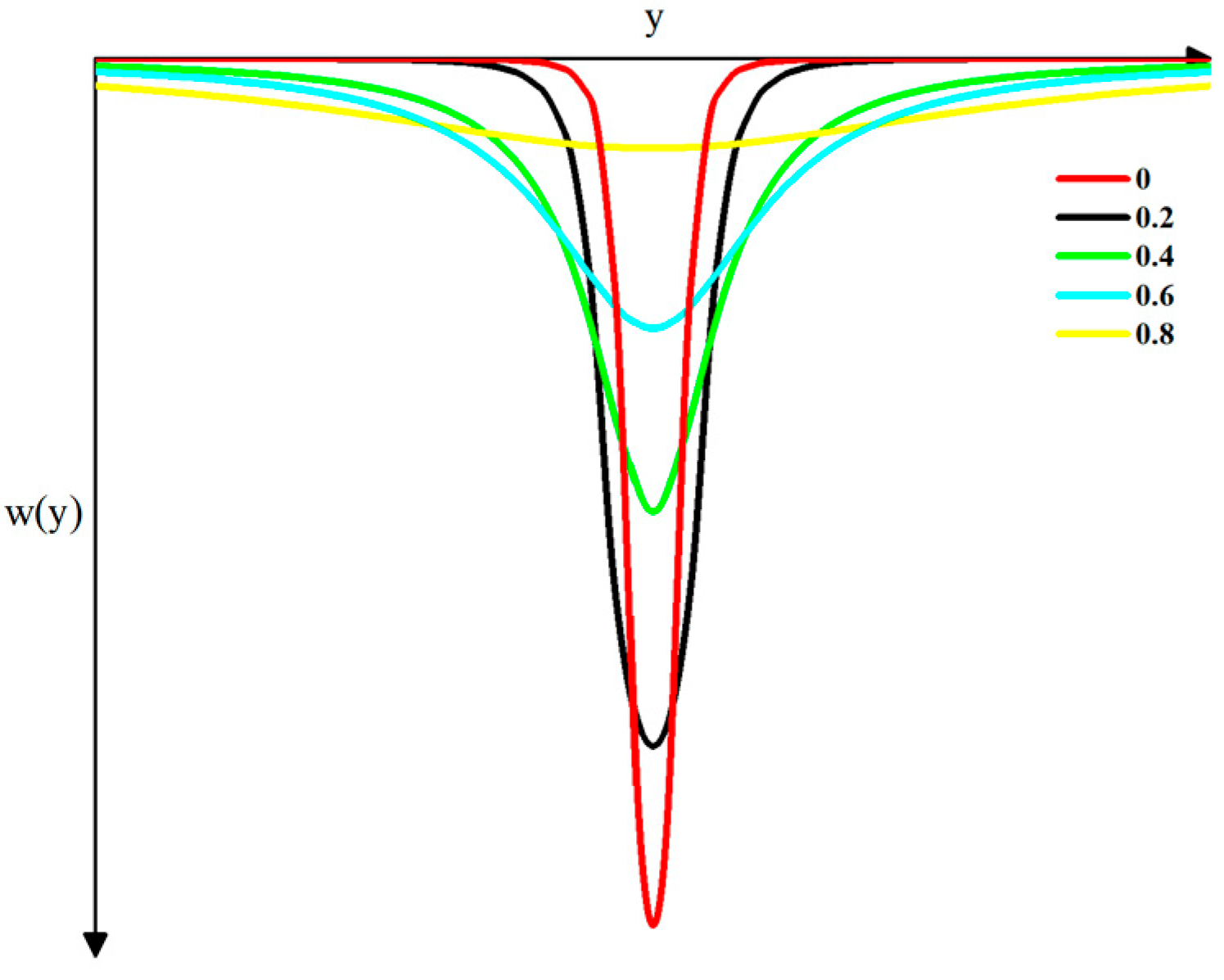
2.3.1. Probability Integral Model
2.3.2. Improved Probability Integral Method
2.4. Fusion Principle of SBAS-InSAR Technology and IPIM
2.4.1. InSAR Maximum Deformation Gradient Theory
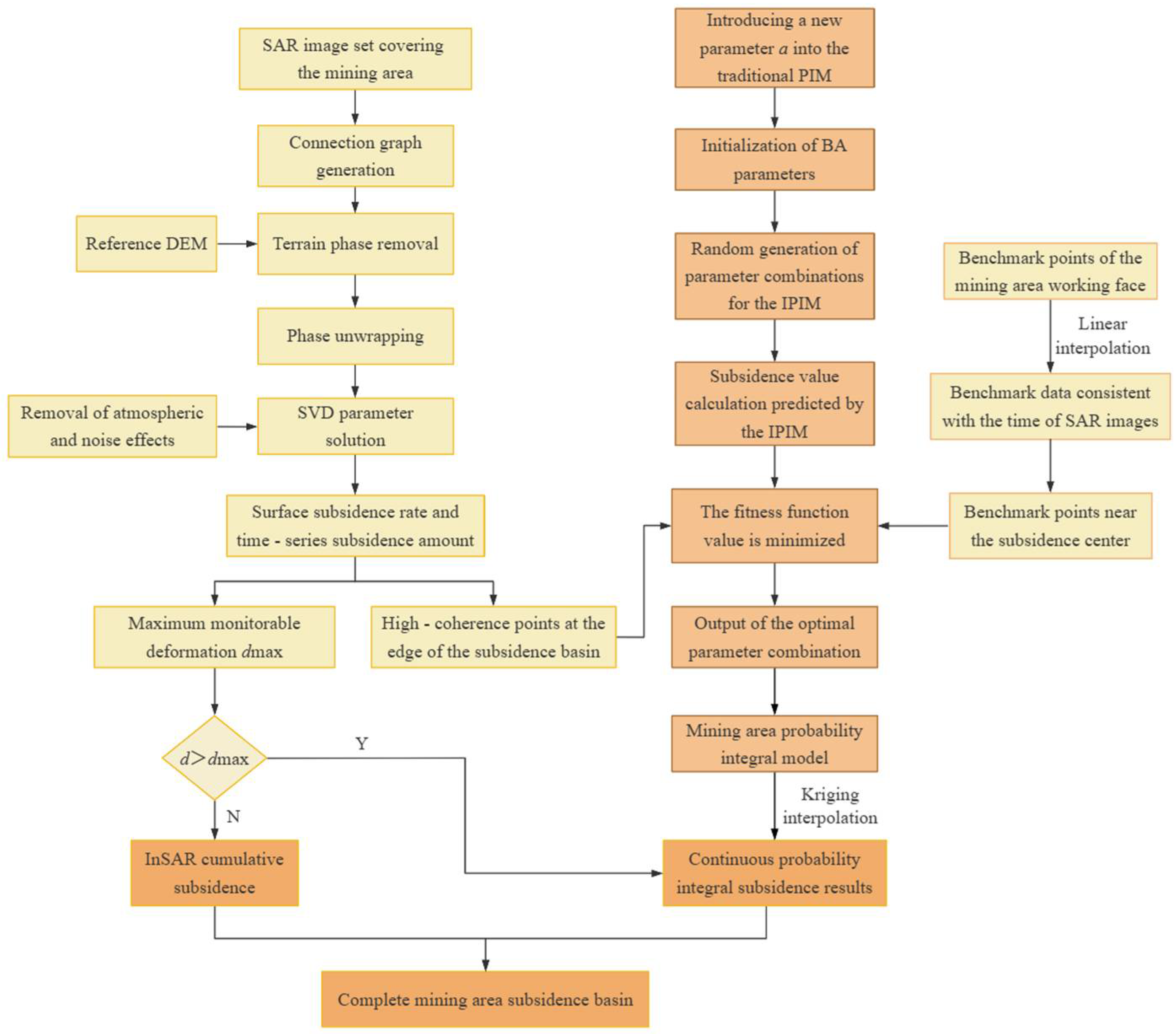
2.4.2. Specific Steps for Fusion
3. Results
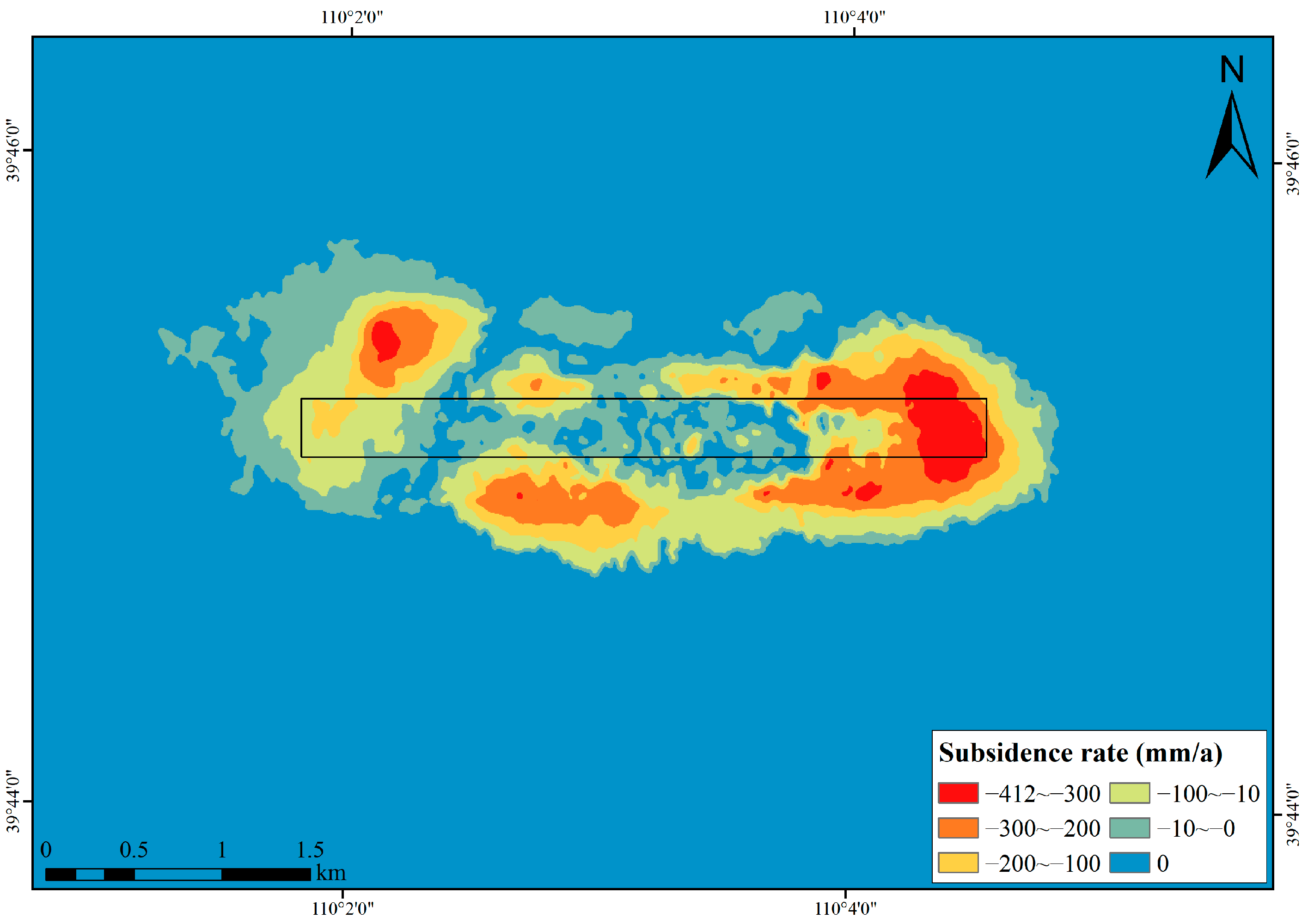
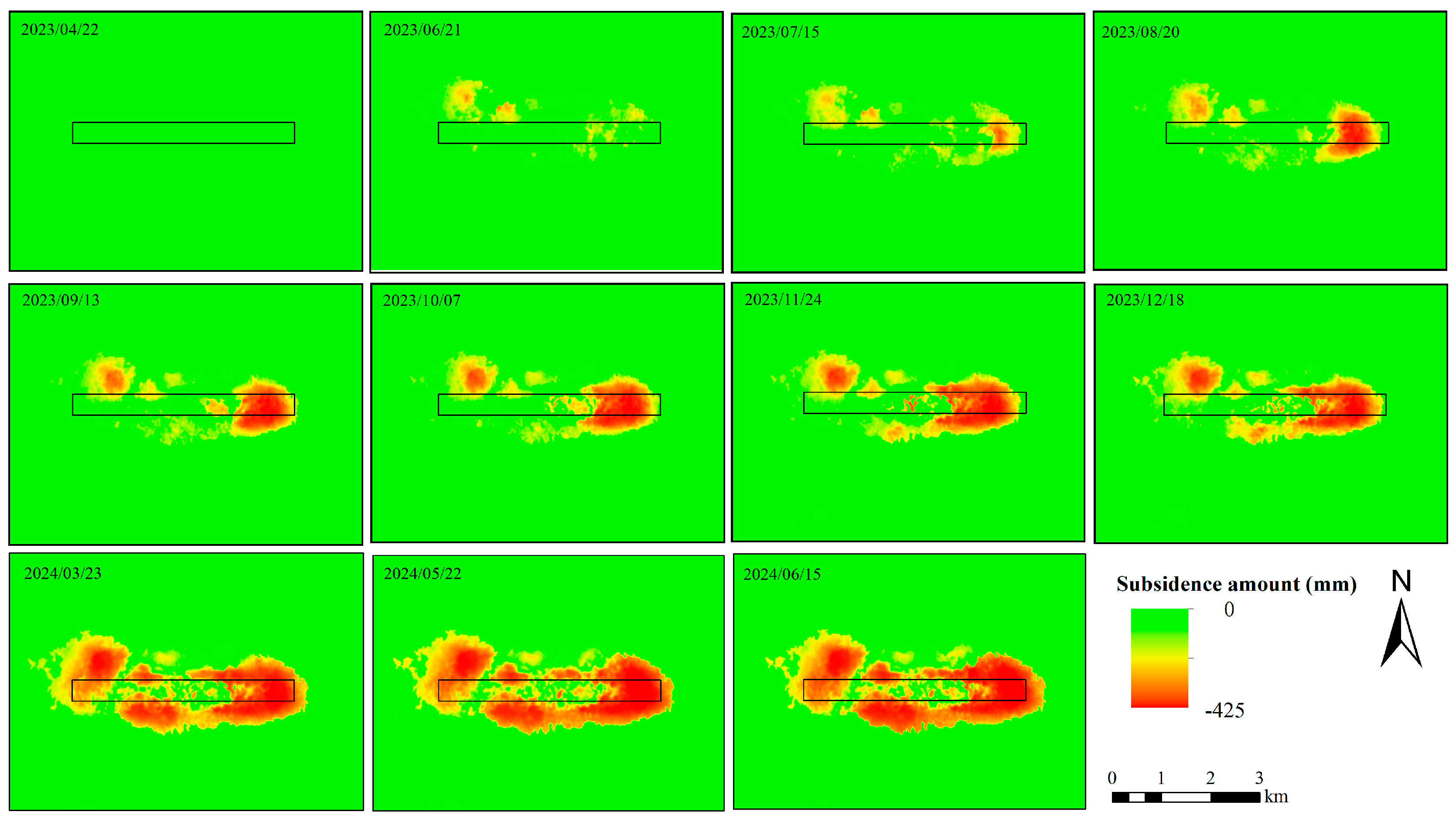
3.1. SBAS-InSAR Process and Analysis
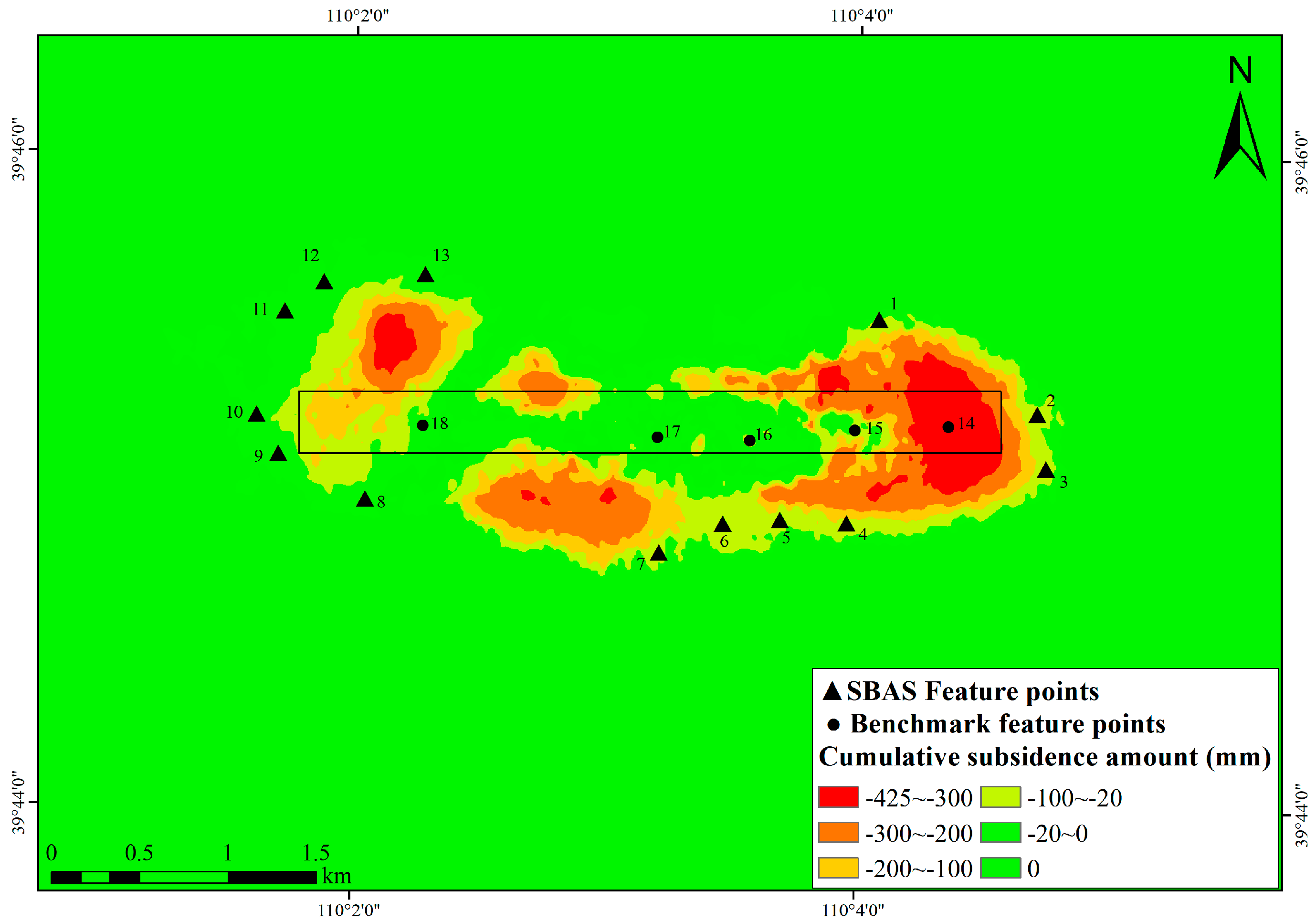
3.2. Selection of Feature Points
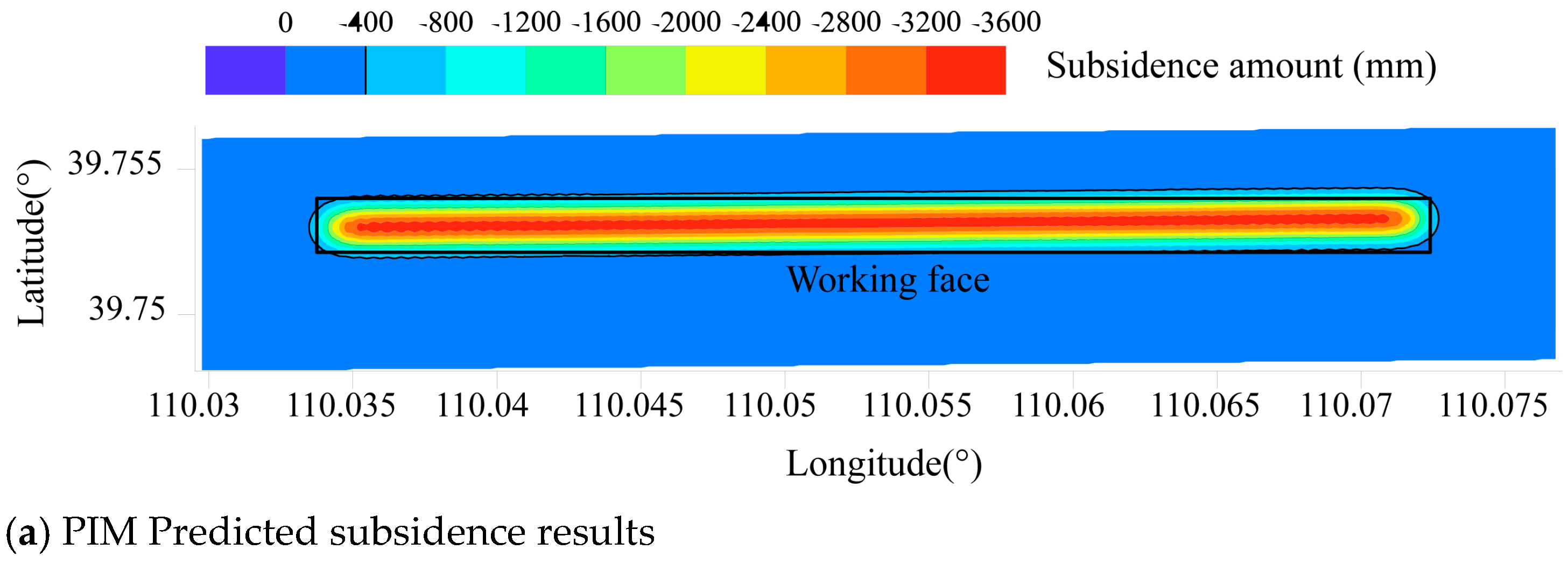
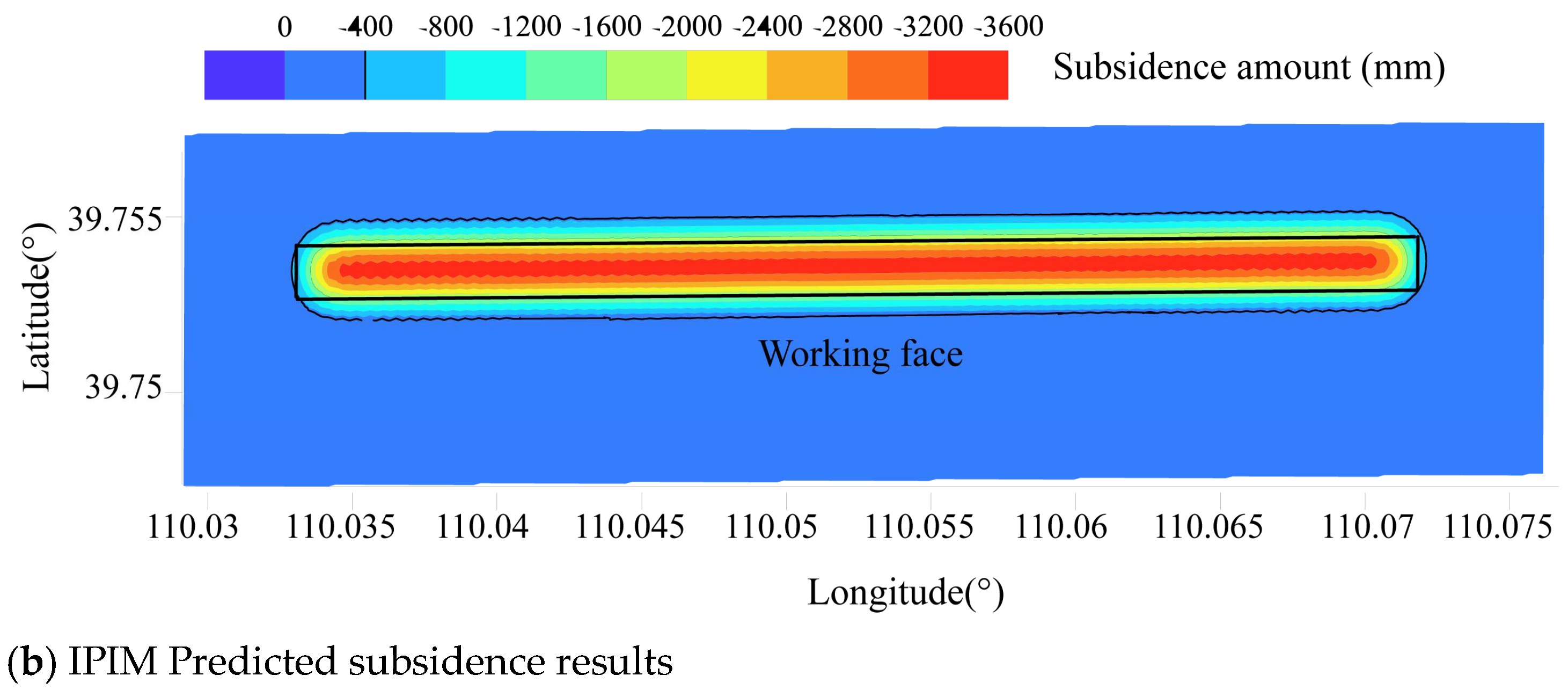
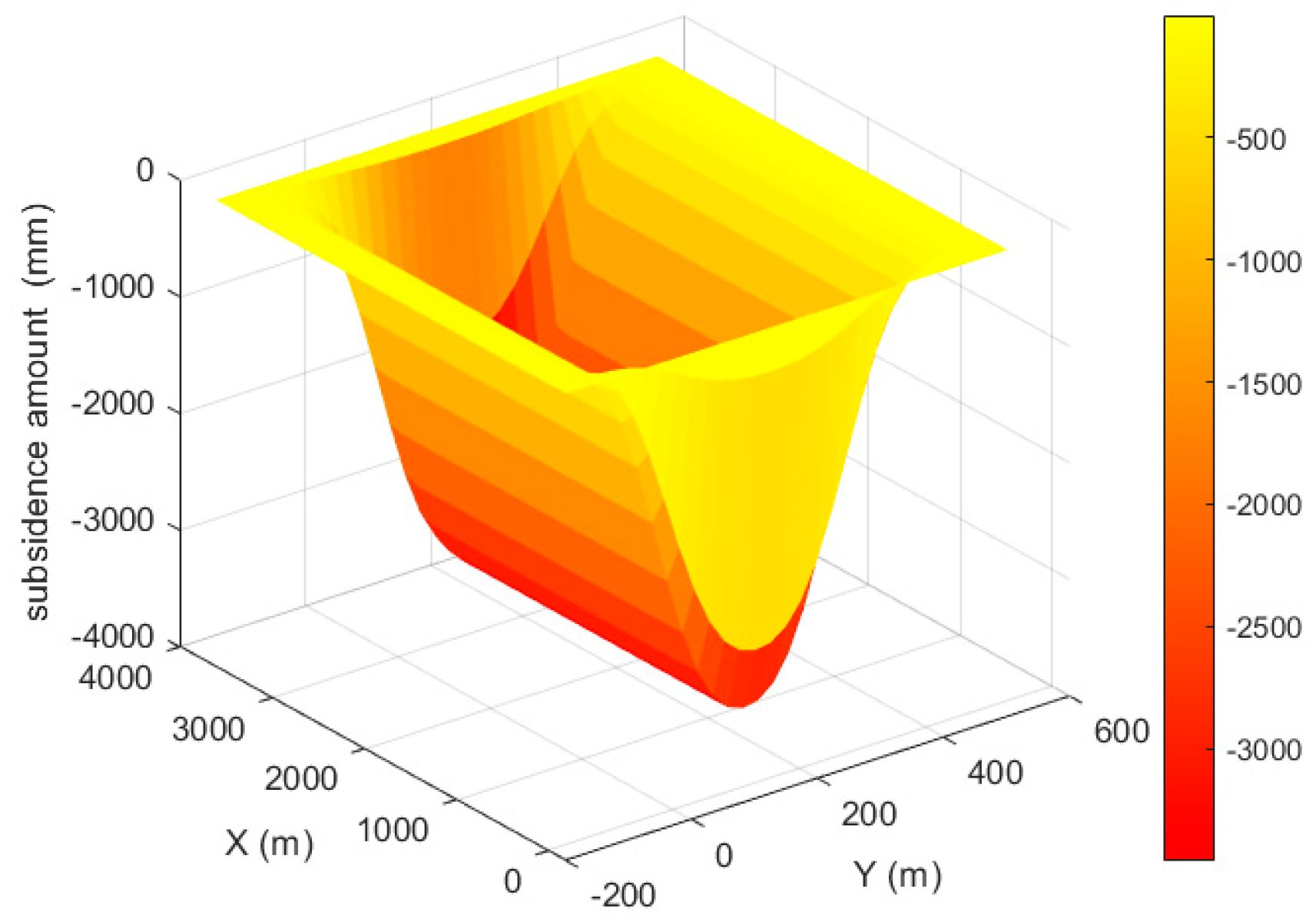
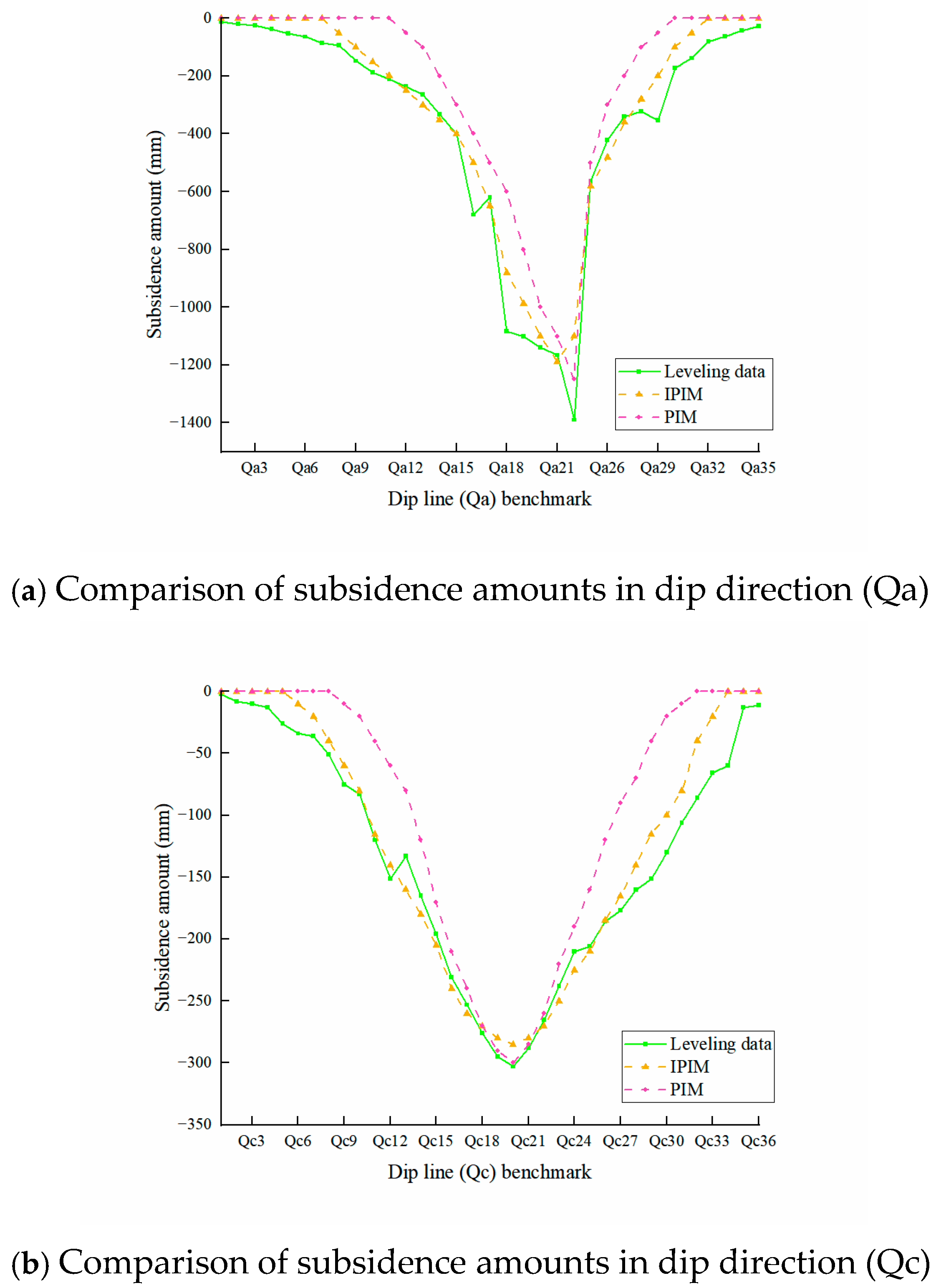
3.3. Analysis of Subsidence Monitoring Results Based on the IPIM
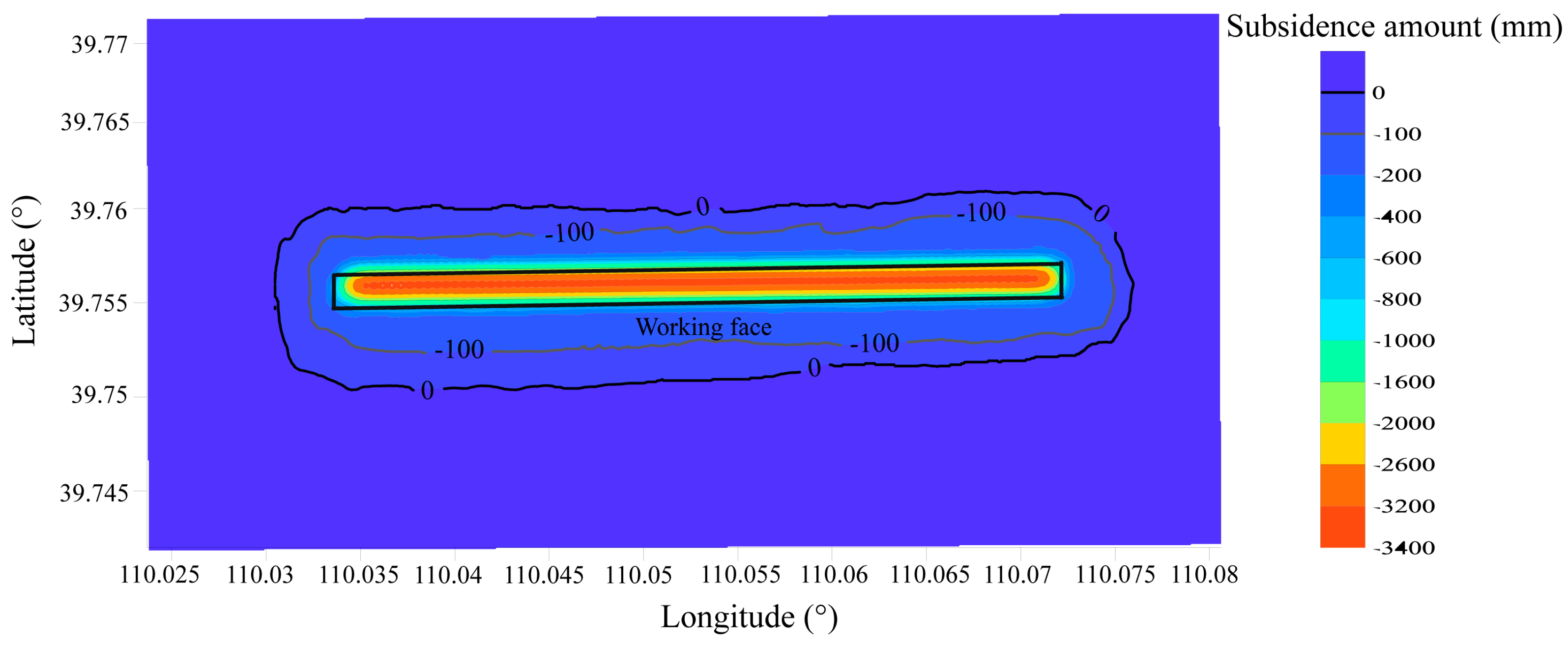
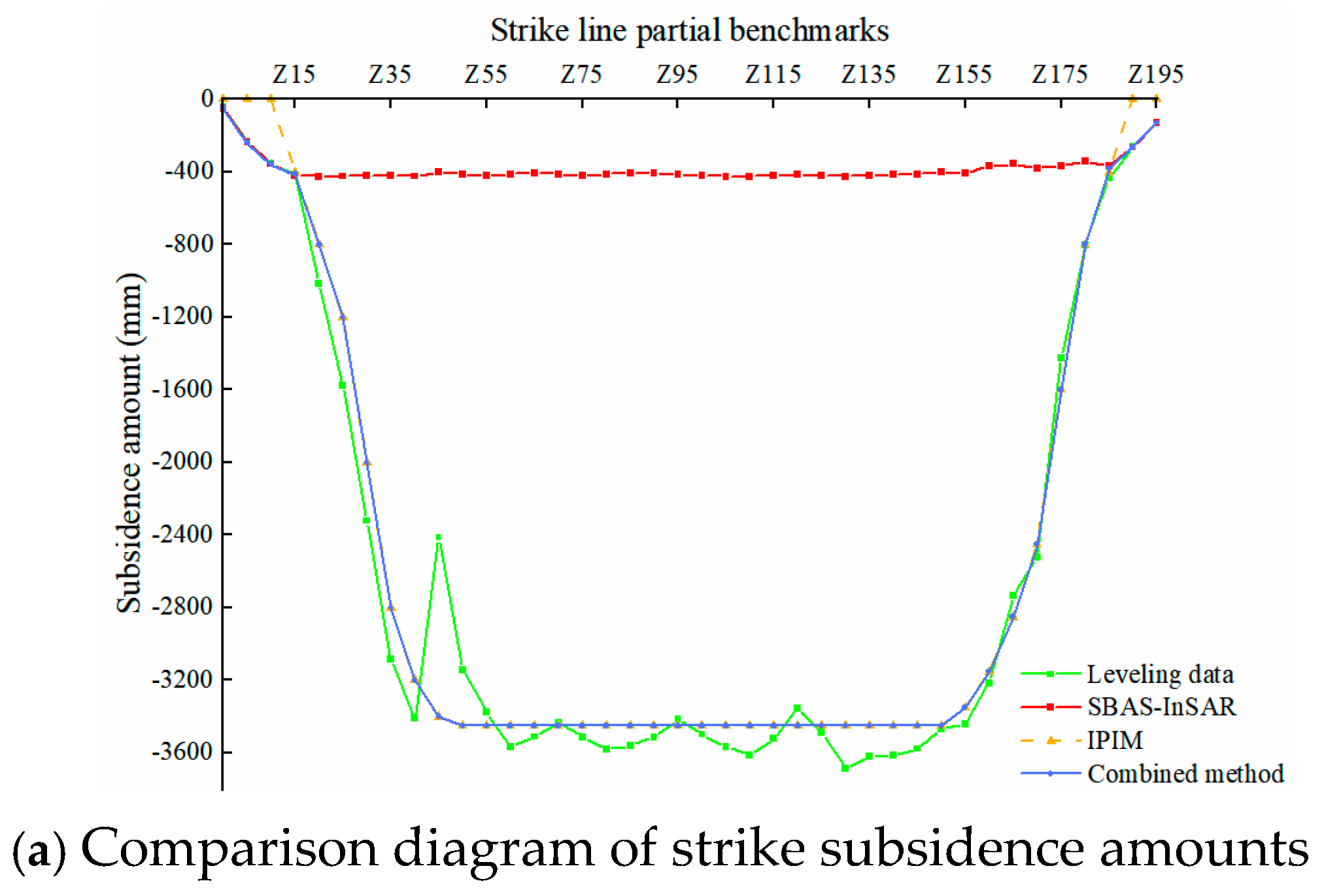
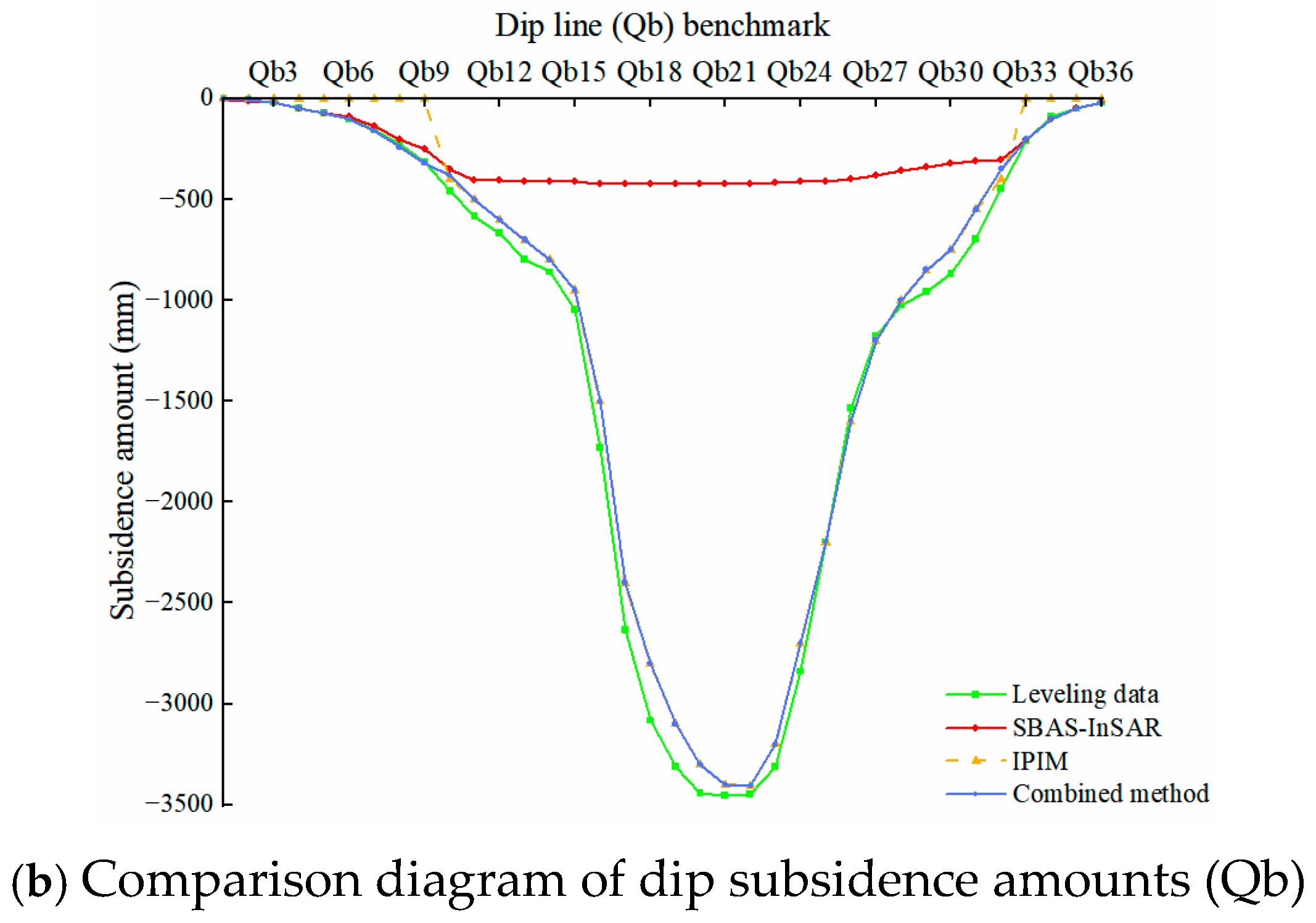
3.4. Monitoring Results of the Combined Method for Subsidence
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lee, S.-J.; Yun, H.-S.; Kim, T.-Y. Monitoring of High-Speed Railway Ground Deformation Using Interferometric Synthetic Aperture Radar Image Analysis. Appl. Sci. 2025, 15, 4318. [Google Scholar] [CrossRef]
- Witkowski, W.T.; Łucka, M.; Guzy, A.; Sudhaus, H.; Barańska, A.; Hejmanowski, R. Impact of mining-induced seismicity on land subsidence occurrence. Remote Sens. Environ. 2024, 301, 113934. [Google Scholar] [CrossRef]
- Luo, R.; Li, G.; Chen, L.; Zeng, L.; Pei, K.; Yu, X. Rock Slope Instability Mechanism Induced by Repeated Mining in Mountain Mining Areas. Appl. Sci. 2024, 14, 9634. [Google Scholar] [CrossRef]
- Peng, W.; Feng, S. Research on the Support Technology for Deep Large-Section Refuge Chambers in Broken Surrounding Rock in a Roadway. Appl. Sci. 2024, 14, 7527. [Google Scholar] [CrossRef]
- Song, J.; Han, C.; Li, P.; Zhang, J.; Liu, D.; Jiang, M.; Zheng, L.; Zhang, J.; Song, J. Quantitative prediction of mining subsidence and its impact on the environment. Int. J. Min. Sci. Technol. 2012, 22, 69–73. [Google Scholar] [CrossRef]
- Wang, F.; Liu, Q.; Li, R.; Wang, S.; Wang, H.; Wang, J.; Ma, X.; Zhou, L.; Wang, Y. Surface Deformation Monitoring and Prediction of InSAR-Hybrid Deep Learning Model for Subsidence Funnels. Remote Sens. 2025, 17, 2972. [Google Scholar] [CrossRef]
- Wang, Z.; Ren, J.; Fan, C.; Liu, J.; Lei, Y.; Feng, T. Applicability analysis of sentinei-1A in surface subsidence monitoring in southwest coal mining area. Prog. Geophys. 2021, 36, 2339–2350. [Google Scholar]
- Zhang, K.; Wang, Y.; Zhao, F.; Ma, Z.; Zou, G.; Wang, T.; Zhang, N.; Huo, W.; Diao, X.; Zhou, D.; et al. An Underground Goaf Locating Framework Based on D-InSAR with Three Different Prior Geological Information Conditions. Remote Sens. 2025, 17, 2714. [Google Scholar] [CrossRef]
- Wang, P.; Chen, H.; Wang, X. Research on the application of D-InSAR and SBAS-InSAR technologies in the monitoring of ground subsidence in mining areas. China Min. Mag. 2024, 33, 133–141. [Google Scholar]
- Ashraf, T.; Yin, F.; Liu, L.; Zhang, Q. Land Subsidence Detection Using SBAS- and Stacking-InSAR with Zonal Statistics and Topographic Correlations in Lakhra Coal Mines, Pakistan. Remote Sens. 2024, 16, 3815. [Google Scholar] [CrossRef]
- Bai, Z.; Zhao, F.; Wang, J.; Li, J.; Wang, Y.; Li, Y.; Lin, Y.; Shen, W. Revealing Long-Term Displacement and Evolution of Open-Pit Coal Mines Using SBAS-InSAR and DS-InSAR. Remote Sens. 2025, 17, 1821. [Google Scholar] [CrossRef]
- Zhang, F.; Chang, L.; Xun, Z. Surface deformation monitoring in Yanghuopan Mining Area based on SBAS-InSAR technology. China Min. Mag. 2024, 33, 152–159. [Google Scholar]
- Wang, F.; Tao, Q.; Chen, Y.; Han, Y.; Guo, Z. Monitoring and early-warning of surface deformation in mine goaf based on InSAR. Saf. Coal Mines 2022, 53, 195–203. [Google Scholar]
- Xue, X.; Ji, J.; Li, G.; Li, H.; Cao, Q.; Wang, K. Time Series Analysis of Mining-Induced Subsidence Using Small Baseline Subset Interferometric Synthetic Aperture Radar (Wanli Mining Area, Inner Mongolia, China). Appl. Sci. 2025, 15, 3998. [Google Scholar] [CrossRef]
- Zhang, X.; He, L.; Liu, C.; Wang, X.; Tang, Y.; He, R. Monitoring and Analysis of Coal Mining Subsidence based on SBAS-InSAR Method. Remote Sens. Technol. Appl. 2022, 37, 1021–1028. [Google Scholar]
- Xie, Y.; Bagan, H.; Tan, L.; Te, T.; Damdinsuren, A.; Wang, Q. Time-Series Analysis of Mining-Induced Subsidence in the Arid Region of Mongolia Based on SBAS-InSAR. Remote Sens. 2024, 16, 2166. [Google Scholar] [CrossRef]
- Tao, Q.; Liu, R.; Li, X.; Gao, T.; Chen, Y.; Xiao, Y.; He, H.; Wei, Y. A method for monitoring three dimensional surface deformation in mining areas combining SBAS-InSAR, GNSS and probability integral method. Sci. Rep. 2025, 15, 2853. [Google Scholar] [CrossRef]
- Chi, F.; Liu, G.; Tao, Q.; Xiao, Y. Subsidence monitoring and analysis of Yuncheng coal mine combined with SBAS-InSAR and probability integral model. Prog. Geophys. 2025, 40, 484–494. [Google Scholar]
- Ma, J.; Yang, J.; Zhu, Z.; Cao, H.; Li, S.; Du, X. Decision-making fusion of InSAR technology and offset tracking to study the deformation of large gradients in mining areas-Xuemiaotan mine as an example. Front. Earth Sci. 2022, 10, 962362. [Google Scholar] [CrossRef]
- Liu, B.; Dai, H. Research development and origin of probability integral method. J. Min. Strat. Control Eng. 2016, 21, 1–3. [Google Scholar]
- Wang, D.; Wang, Z.; Li, Y.; Wang, Y. Ground Subsidence Prediction and Shaft Control in Pillar Recovery During Mine Closure. Processes 2025, 13, 3274. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, P.; Ji, X.; Li, Y. Prediction of surface subsidence in Gequan coal mine based on probability integral and numerical simulation. Acad. J. Eng. Technol. Sci. 2024, 7, 8–15. [Google Scholar] [CrossRef]
- Jiang, C.; Liu, W.; Wang, L.; Zhu, X.; Tan, H. A Probability Integral Parameter Inversion Method Integrating a Selection-Weighted Iterative Robust Genetic Algorithm. Appl. Sci. 2025, 15, 8102. [Google Scholar] [CrossRef]
- Zhou, B.; Li, S.; Kang, J.; Zhang, L.; Zhang, J.; Li, M. A probability integral method modified model for accurately characterizing subsidence at the boundary of a mining area. Sci. Rep. 2025, 15, 21014. [Google Scholar] [CrossRef] [PubMed]
- Wang, N.; Wu, K.; Qin, Z. Prediction model of mining subsidence with probability integration method based on thickness influences of loose layer. Coal Sci. Technol. 2012, 40, 10–16. [Google Scholar]
- Li, J.; Yu, X.; Chen, D.; Fang, X. Research on the establishment of a mining subsidence prediction model under thick loose layer and its parameter inversion method. Earth Sci. Res. J. 2021, 25, 215–223. [Google Scholar] [CrossRef]
- Chen, Y.; Tao, Q.; Liu, G.; Wang, L.; Wang, F.; Wang, K. Detailed mining subsidence monitoring combined with InSAR and probability integral method. Chin. J. Geophys. 2021, 64, 3554–3566. [Google Scholar]
- Hou, Z.; Yang, K.; Li, Y.; Gao, W.; Wang, S.; Ding, X.; Li, Y. Dynamic prediction model of mining subsidence combined with D-InSAR technical parameter inversion. Environ. Earth Sci. 2022, 81, 307. [Google Scholar] [CrossRef]
- Massonnet, D.; Feigl, K.L. Radar interferometry and its application to changes in the Earth’s surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef]
- Baran, I.; Stewart, M.; Claessens, S. A new functional model for determining minimum and maximum detectable deformation gradient resolved by satellite radar interferometry. IEEE Trans. Geosci. Remote Sens. 2005, 43, 675–682. [Google Scholar] [CrossRef]
- Li, Y. Spatial distribution of strain energy changes due to mining-induced fault coseismic slip: Insights from a rockburst at the Yuejin coal mine, China. Rock. Mech. Rock. Eng. 2025, 58, 1693–1706. [Google Scholar] [CrossRef]

| Parameter | Corresponding Value |
|---|---|
| Acquiring satellite | Sentinel-1A |
| Resolution (m) | 5 × 20 |
| Radar wavelength (mm) | 5.6 |
| Polarization mode | VV |
| Image time | April 2023–June 2024 |
| Number of images (scene) | 14 |
| Point No. | Subsidence (mm) | Coherence Coefficient | Point No. | Subsidence (mm) | Coherence Coefficient |
|---|---|---|---|---|---|
| 1 | 43 | 0.61 | 10 | 12 | 0.77 |
| 2 | 35 | 0.57 | 11 | 18 | 0.64 |
| 3 | 38 | 0.68 | 12 | 19 | 0.68 |
| 4 | 40 | 0.51 | 13 | 22 | 0.60 |
| 5 | 32 | 0.81 | 14 | 2878 | — |
| 6 | 41 | 0.76 | 15 | 3065 | — |
| 7 | 39 | 0.53 | 16 | 3256 | — |
| 8 | 21 | 0.65 | 17 | 3685 | — |
| 9 | 25 | 0.51 | 18 | 2912 | — |
| Method | q | θ (°) | tanβ | S1 (m) | S2 (m) | S3 (m) | S4 (m) | a |
|---|---|---|---|---|---|---|---|---|
| PIM | 0.71 | 86.1° | 1.3 | 20 | 20 | −40 | −40 | — |
| IPIM | 0.81 | 87.7° | 1.4 | 8 | 8 | −20 | −20 | 0.48 |
| Directional Position | Method | Maximum Absolute Error (mm) | Average Absolute Error (mm) | Root Mean Square Error (mm) | Maximum Subsidence Relative Error (%) |
|---|---|---|---|---|---|
| Strike line | SBAS-InSAR | 3260 | 3015 | 3112 | 88.4 |
| IPIM | 232 | 175 | 193 | 6.2 | |
| Combined method | 232 | 91 | 118 | 5.2 | |
| SBAS-InSAR | 3067 | 2810 | 2901 | 87.8 | |
| Dip line (Qb) | IPIM | 193 | 112 | 154 | 5.5 |
| Combined method | 193 | 68 | 98 | 4.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Dong, H. A Surface Subsidence Monitoring Method for Narrow and Elongated Mining Areas by Combining InSAR and the Improved Probability Integral Method. Appl. Sci. 2025, 15, 13086. https://doi.org/10.3390/app152413086
Zhang Z, Dong H. A Surface Subsidence Monitoring Method for Narrow and Elongated Mining Areas by Combining InSAR and the Improved Probability Integral Method. Applied Sciences. 2025; 15(24):13086. https://doi.org/10.3390/app152413086
Chicago/Turabian StyleZhang, Zhen, and Hongjuan Dong. 2025. "A Surface Subsidence Monitoring Method for Narrow and Elongated Mining Areas by Combining InSAR and the Improved Probability Integral Method" Applied Sciences 15, no. 24: 13086. https://doi.org/10.3390/app152413086
APA StyleZhang, Z., & Dong, H. (2025). A Surface Subsidence Monitoring Method for Narrow and Elongated Mining Areas by Combining InSAR and the Improved Probability Integral Method. Applied Sciences, 15(24), 13086. https://doi.org/10.3390/app152413086




