Influencing Factor Analysis Based on Jointly Modeling for Freeway Rear-End and Sideswipe Crashes Considering Spatial and Site Correlations
Abstract
1. Introduction
2. Literature Review
2.1. Studies on Factors Influencing Traffic Crashes
2.2. Studies on Traffic Safety Analysis Models
- (1)
- We propose and apply a copula-based bivariate Poisson lognormal-CAR (PLN-CAR) model that simultaneously accounts for spatial correlation and site correlation. This type of dependence structure has rarely been examined systematically in previous traffic safety studies.
- (2)
- We construct bivariate PLN–CAR models with two alternative dependence structures: one based on multivariate normally distributed residuals and the other based on copula functions. We then systematically compare their performance in capturing site correlation across crash types and in terms of overall model fit.
- (3)
- We apply the aforementioned models to freeway rear-end and sideswipe crash data to quantify their spatial and site correlations, as well as to identify the type-specific safety contributing factors of each crash type. The findings deepen the understanding of the differential mechanisms of rear-end and sideswipe crashes and provide theoretical support for targeted freeway safety countermeasures.
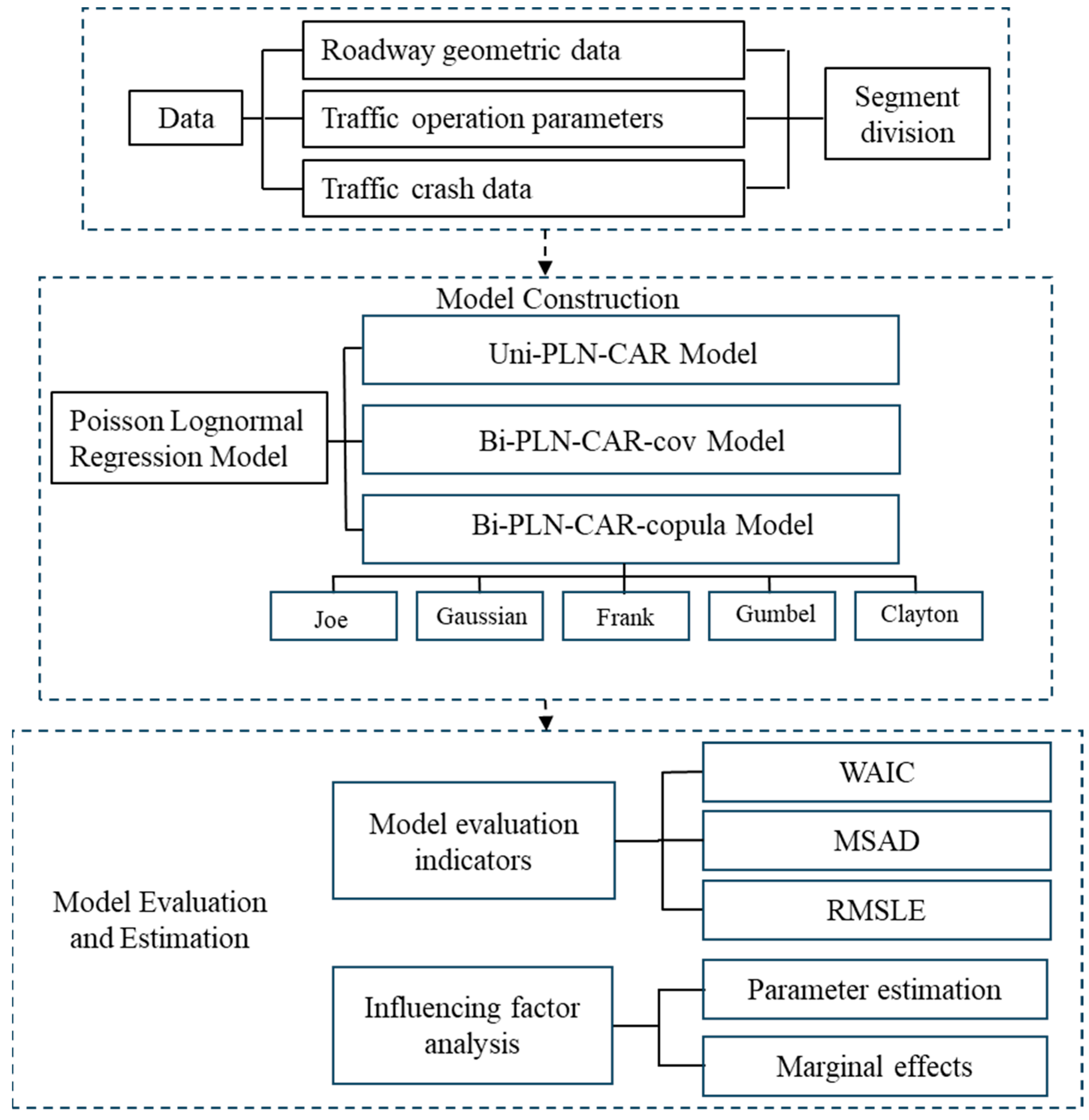
3. Data Preparation
3.1. Division of Roadway Units
3.2. Extraction of Geometric Design Parameters
3.3. Traffic Operation Parameters
3.4. Traffic Operation Features
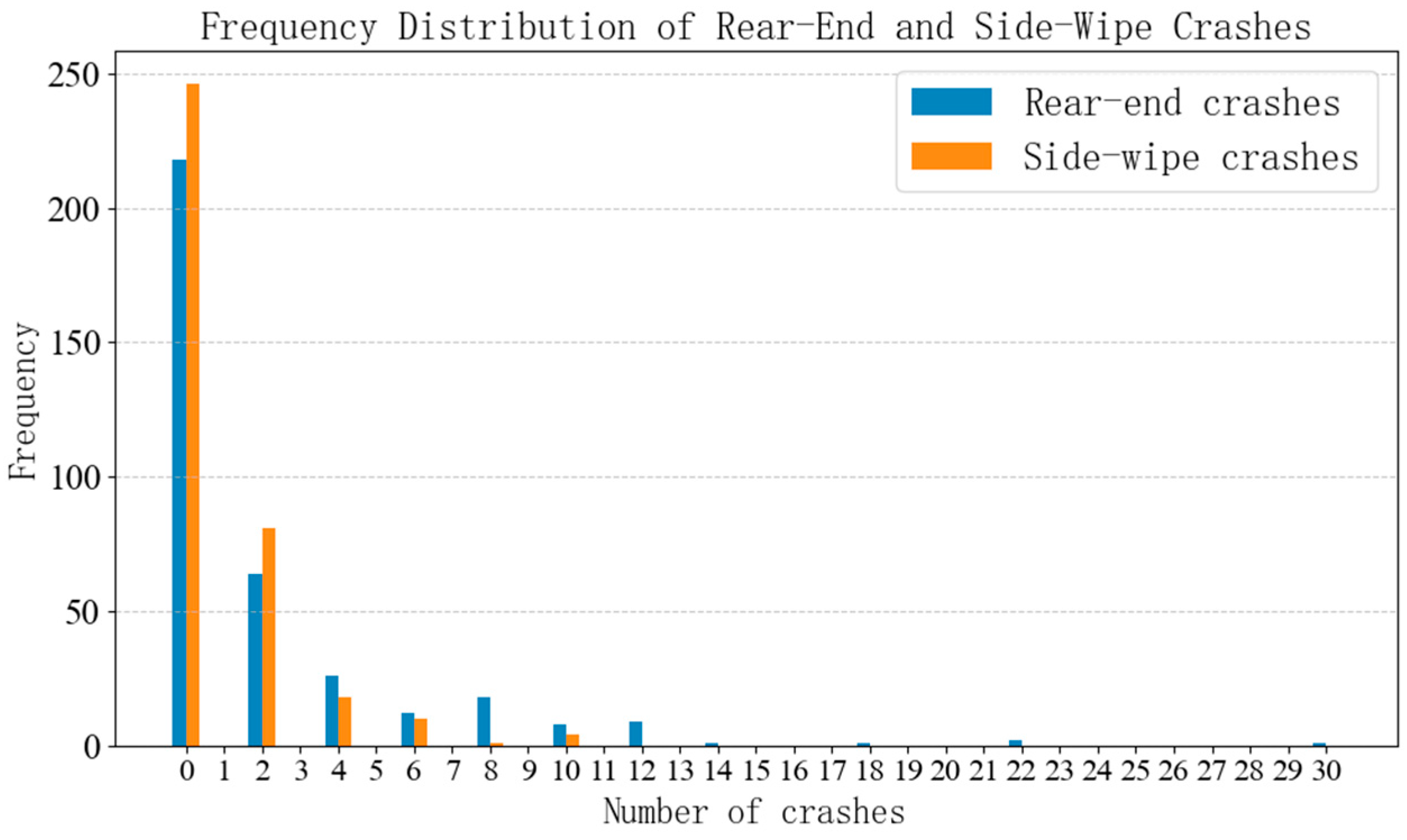
3.5. Analysis of Crash Characteristics
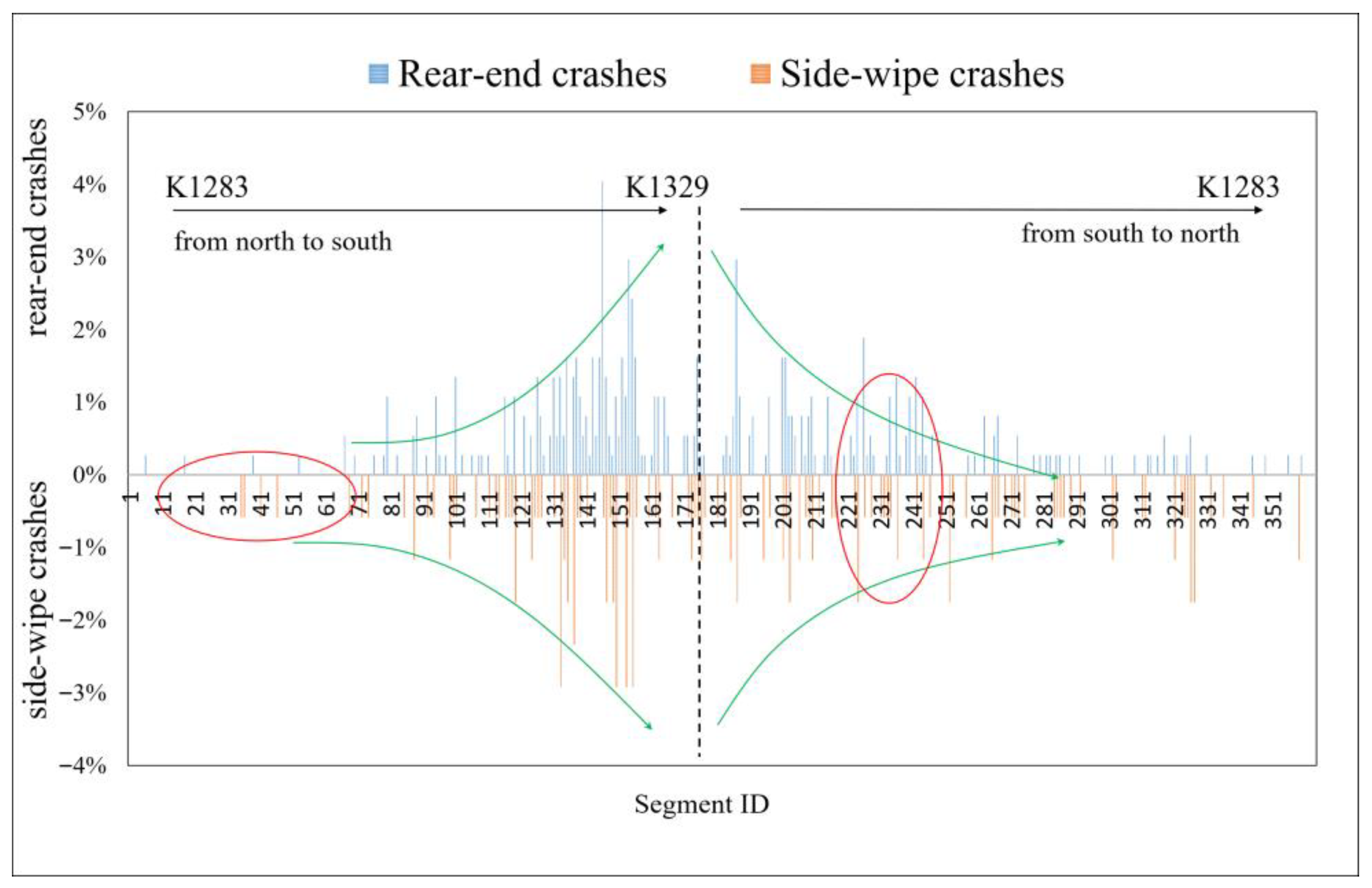
3.5.1. Spatial Correlation
3.5.2. Site Correlation
4. Safety Analysis Models and Evaluation Indicators
4.1. Model Structure
4.1.1. Poisson Lognormal Regression Model
4.1.2. Univariate PLN CAR Model
4.1.3. Bivariate PLN-CAR Model Based on the Variance Covariance of Jointly Distributed Residuals
4.1.4. Bivariate PLN-CAR Model Based on Copula Functions
4.2. Marginal Effects of Influencing Factors
4.3. Model Estimation and Evaluation
5. Model Construction and Analysis
5.1. Variable Selection
5.2. Model Performance Comparison
5.3. Parameter Estimation and Analysis
5.4. Marginal Effects Analysis
6. Conclusions
- (1)
- The Bi-PLN-CAR-Frank model exhibited superior performance. The proposed bivariate correlated models based on jointly distributed residuals and copula functions, as well as incorporating the conditional autoregressive (CAR) term, were capable of addressing site correlation and spatial correlation in crash data. According to the evaluation indicators for the model, association modeling of rear-end and sideswipe crashes effectively improved the overall performance of the model. In terms of model structure, the association model based on the Frank copula function (Bi-PLN-CAR-Frank) performed better than the model based on jointly distributed residuals (Bi-PLN-CAR-cov), which indicates that the Frank copula-based association model can be considered as an exploratory option for freeway rear-end and sideswipe crash safety analyses under similar conditions, although its applicability still needs to be validated further using broader datasets.
- (2)
- Key factors differ significantly between rear-end and sideswipe crashes. Model estimation outcomes revealed that the key determinants of rear-end and sideswipe crashes on freeways differed from each other. On one hand, some specific factors showed different levels of significance for the two crash types; on the other hand, some factors were significant only for one type of crash. Overall, the precise identification of these influencing factors provides a useful reference for improving freeway traffic safety on the studied freeway and, with due caution, at similar facilities.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PLN | Poisson lognormal regression |
| CAR | Conditional autoregressive |
| Uni-PLN | Univariate Poisson Lognormal Regression Model |
| Uni-PLN-CAR | Univariate PLN CAR Model |
| Bi-PLN-CAR-cov | Bivariate PLN-CAR Model based on the Variance Covariance of Jointly Distributed Residuals |
| WAIC | Watanabe–Akaike Information Criterion |
| RMSLE | Root Mean Squared Logarithmic Error |
| MSAD | Mean Standardized Absolute Deviance |
| Bi-PLN-CAR-copula | Bivariate PLN-CAR Model based on Copula Functions |
Appendix A. Joint Likelihood and MultiBUGS Implementation
Appendix A.1. Model Specification
Appendix A.2. Log-Likelihood of the Frank Copula
Appendix A.3. Joint Likelihood for a Single Segment and for the Full Sample
Appendix A.4. MultiBUGS Code Snippet
| Listing A1. MultiBUGS code snippet for the Bi-PLN-CAR-Frank model. |
| # Zero-trick implementation of the joint likelihood for the |
| # Frank-copula Bi-PLN-CAR-Frank model |
| C <- 100000 # large constant for the zero-trick |
| for (i in 1:regions) { |
| # ---- Marginal log-likelihoods for the two Poisson outcomes ---- |
| l_marg1[i] <- -mu1[i] + sidewipe[i] * log(mu1[i]) - loggam(sidewipe[i] + 1) |
| l_marg2[i] <- -mu2[i] + rear[i] * log(mu2[i]) - loggam(rear[i] + 1) |
| # ---- CDFs of the Poisson marginals (u_i and v_i) ---- |
| u[i] <- cdf.pois(sidewipe[i], mu1[i]) + 0.0001 |
| v[i] <- cdf.pois(rear[i], mu2[i]) + 0.0001 |
| # ---- Frank copula density c_alpha(u_i, v_i) in log form ---- |
| e_a <- 1 / exp(alphac) # exp(-alpha) |
| t[i] <- 1 - e_a - (1 - 1/exp(alphac*u[i])) * (1 - 1/exp(alphac*v[i])) |
| t1[i] <- max(t[i], 0.0001) |
| l_copula[i] <- log(max(alphac, 0.0001)) + log(1 - e_a) - alphac * (u[i] + v[i]) - |
| 2 * log(t1[i]) |
| # ---- Joint log-likelihood for segment i ---- |
| loglik[i] <- l_marg1[i] + l_marg2[i] + l_copula[i] |
| # ---- Zero-trick: introduce a Poisson(φ_i) with mean φ_i = C - loglik_i ---- |
| zeros[i] <- 0 |
| phi[i] <- -loglik[i] + C |
| zeros[i] ~ dpois(phi[i]) |
| } |
References
- World Health Organization. Global Status Report on Road Safety 2023; World Health Organization: Geneva, Switzerland, 2023. [Google Scholar]
- World Health Organization. Road Traffic Injuries. Available online: https://www.who.int/news-room/fact-sheets/detail/road-traffic-injuries (accessed on 3 November 2025).
- The Traffic Management Bureau of the Ministry of Public Security of the People’s Republic of China. Annual Report on Road Traffic Accident Statistics (2019); Traffic Management Science Research Institute of the Ministry of Public Security: Wuxi, China, 2020. [Google Scholar]
- Ministry of Transport of the People’s Republic of China. Statistical Bulletin on the Development of the Transportation Industry in 2019. Available online: https://xxgk.mot.gov.cn/2020/jigou/zhghs/202006/t20200630_3321335.html (accessed on 3 November 2025).
- Office of the State Council Leading Group on Safety Production. Public Security System’s Three-Year Action Plan for Fundamental Safety Production (2024–2026). Available online: https://www.gov.cn/lianbo/bumen/202402/content_6930470.htm (accessed on 3 November 2025).
- Skaug, L.; Nojoumian, M.; Dang, N.; Yap, A. Road Crash Analysis and Modeling: A Systematic Review of Methods, Data, and Emerging Technologies. Appl. Sci. 2025, 15, 7115. [Google Scholar] [CrossRef]
- Beijing News. A Series of 29 Traffic Pile-Ups Occurred on the Shanxi Guoyang Section of the Erguang Expressway, Resulting in 1 Death and 6 Injuries. Available online: https://baijiahao.baidu.com/s?id=1784952458455163219&wfr=spider&for=pc (accessed on 3 November 2025).
- Christoforou, Z.; Cohen, S.; Karlaftis, M.G. Identifying Crash Type Propensity Using Real-Time Traffic Data on Freeways. J. Saf. Res. 2011, 42, 43–50. [Google Scholar] [CrossRef]
- Mao, X.; Yuan, C.; Gan, J.; Zhang, S. Risk Factors Affecting Traffic Accidents at Urban Weaving Sections: Evidence from China. Int. J. Environ. Res. Public Health 2019, 16, 1542. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Song, M.; Ma, X. Investigation on the Injury Severity of Drivers in Rear-End Collisions between Cars Using a Random Parameters Bivariate Ordered Probit Model. Int. J. Environ. Res. Public Health 2019, 16, 2632. [Google Scholar] [CrossRef] [PubMed]
- Yang, B. Study on the Relationship Between Traffic Flow State and Crash Pattern on Freeway. Ph.D. Dissertation, Southeast University, Nanjing, China, 2020. [Google Scholar]
- Wang, X.; Feng, M. Freeway Single and Multi-Vehicle Crash Safety Analysis: Influencing Factors and Hotspots. Accid. Anal. Prev. 2019, 132, 105268. [Google Scholar] [CrossRef]
- Zeng, Q.; Gu, W.; Zhang, X.; Wen, H.; Lee, J.; Hao, W. Analyzing Freeway Crash Severity Using a Bayesian Spatial Generalized Ordered Logit Model with Conditional Autoregressive Priors. Accid. Anal. Prev. 2019, 127, 87–95. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Ding, X.; Yuan, C.; Liu, X.; Tang, J. Jointly Analyzing Freeway Primary and Secondary Crash Severity Using a Copula-Based Approach. Accid. Anal. Prev. 2023, 180, 106911. [Google Scholar] [CrossRef]
- Qi, W.; Qin, S.; Zhu, S.; Fu, C. A Random Parameter Bivariate Approach for Modelling Freeway Crash Frequency by Severity Level. Transp. A Transp. Sci. 2025, 2466471. [Google Scholar] [CrossRef]
- Alsaleh, R.; Walia, K.; Moshiri, G.; Alsaleh, Y.T. Traffic Collision Severity Modeling Using Multi-Level Multinomial Logistic Regression Model. Appl. Sci. 2025, 15, 838. [Google Scholar] [CrossRef]
- Wang, J.; Ma, S.; Jiao, P.; Ji, L.; Sun, X.; Lu, H. Analyzing the Risk Factors of Traffic Accident Severity Using a Combination of Random Forest and Association Rules. Appl. Sci. 2023, 13, 8559. [Google Scholar] [CrossRef]
- Mothafer, G.I.M.A.; Yamamoto, T.; Shankar, V.N. A Multivariate Heterogeneous-Dispersion Count Model for Asymmetric Interdependent Freeway Crash Types. Transp. Res. Part B Methodol. 2018, 108, 84–105. [Google Scholar] [CrossRef]
- Hosseinpour, M.; Sahebi, S.; Zamzuri, Z.H.; Yahaya, A.S.; Ismail, N. Predicting Crash Frequency for Multi-Vehicle Collision Types Using Multivariate Poisson–Lognormal Spatial Model: A Comparative Analysis. Accid. Anal. Prev. 2018, 118, 277–288. [Google Scholar] [CrossRef]
- Zhang, C.; He, J.; Bai, C.; Yan, X.; Wang, C.; Guo, Y. Exploring Relationships between Months and Different Crash Types on Mountainous Freeways Using a Combined Modeling Approach. J. Adv. Transp. 2022, 2022, 6716275. [Google Scholar] [CrossRef]
- Bisht, L.S.; Tiwari, G. Assessment of Fatal Rear-End Crash Risk Factors of an Expressway in India: A Random Parameter NB Modeling Approach. J. Transp. Eng. Part A Syst. 2023, 149, 04022111. [Google Scholar] [CrossRef]
- Guo, H.; Xie, K.; Keyvan-Ekbatani, M. Modeling Driver’s Evasive Behavior During Safety–Critical Lane Changes: Two-Dimensional Time-to-Collision and Deep Reinforcement Learning. Accid. Anal. Prev. 2023, 186, 107063. [Google Scholar] [CrossRef] [PubMed]
- Rusli, R.; Haque, M.M.; Afghari, A.P.; King, M. Applying a Random Parameters Negative Binomial Lindley Model to Examine Multi-Vehicle Crashes along Rural Mountainous Highways in Malaysia. Accid. Anal. Prev. 2018, 119, 80–90. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Li, S.; Li, X.; Wang, Y.; Zeng, Q. Effects of Geometric Attributes of Horizontal and Sag Vertical Curve Combinations on Freeway Crash Frequency. Accid. Anal. Prev. 2023, 186, 107056. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Gao, J.; Zuo, F.; Ozbay, K. Estimating Urban Traffic Safety and Analyzing Spatial Patterns through the Integration of City-Wide Near-Miss Data: A New York City Case Study. Appl. Sci. 2024, 14, 6378. [Google Scholar] [CrossRef]
- Aguero-Valverde, J. Multivariate Spatial Models of Excess Crash Frequency at Area Level: Case of Costa Rica. Accid. Anal. Prev. 2013, 59, 365–373. [Google Scholar] [CrossRef]
- Ma, X.; Chen, S.; Chen, F. Multivariate Space–Time Modeling of Crash Frequencies by Injury Severity Levels. Anal. Methods Accid. Res. 2017, 15, 29–40. [Google Scholar] [CrossRef]
- Wei, F.; Cai, Z.; Wang, Z.; Guo, Y.; Li, X.; Wu, X. Investigating Rural Single-Vehicle Crash Severity by Vehicle Types Using Full Bayesian Spatial Random Parameters Logit Model. Appl. Sci. 2021, 11, 7819. [Google Scholar] [CrossRef]
- Champahom, T.; Jomnonkwao, S.; Karoonsoontawong, A.; Ratanavaraha, V. Spatial Zero-Inflated Negative Binomial Regression Models: Application for Estimating Frequencies of Rear-End Crashes on Thai Highways. J. Transp. Saf. Secur. 2022, 14, 523–540. [Google Scholar] [CrossRef]
- Hu, Y.; Wei, H.; Zeng, Q. Analysis of Freeway Crash Severity Based on Spatial Generalized Ordered Probit Model. J. South China Univ. Technol. 2023, 51, 114–122. [Google Scholar]
- Rahman, M.A.; Moomen, M.; Khan, W.A.; Codjoe, J. An Analysis of the Impact of Injury Severity on Incident Clearance Time on Urban Interstates Using a Bivariate Random-Parameter Probit Model. Stats 2024, 7, 863–874. [Google Scholar] [CrossRef]
- Alanazi, F.; Alruwaili, A.; Shtayat, A. MRI-Copula: A Hybrid Copula–Machine Learning Framework for Multivariate Risk Indexing in Urban Traffic Safety. Sustainability 2025, 17, 9210. [Google Scholar] [CrossRef]
- Tahir, H.B.; Yasmin, S.; Haque, M.M. A Poisson Lognormal-Lindley Model for Simultaneous Estimation of Multiple Crash-Types: Application of Multivariate and Pooled Univariate Models. Anal. Methods Accid. Res. 2024, 41, 100315. [Google Scholar] [CrossRef]
- Ahmad, N.; Gayah, V.V.; Donnell, E.T. Copula-Based Bivariate Count Data Regression Models for Simultaneous Estimation of Crash Counts Based on Severity and Number of Vehicles. Accid. Anal. Prev. 2023, 181, 106928. [Google Scholar] [CrossRef]
- Faden, A.; Abdel-Aty, M.; Wang, C.; Yang, S. Short-Term Safety Analysis and Interdependencies of Mixed-Operation Freeways with Fully Separated Express Lanes: A Copula-Based Poisson Lognormal Lindley Approach. Accid. Anal. Prev. 2025, 217, 108050. [Google Scholar] [CrossRef]
- American Association of State Highway and Transportation Officials. Highway Safety Manual, 1st ed.; AASHTO: Washington, DC, USA, 2010. [Google Scholar]
- Wang, J.; He, S.; Zhai, X.; Wang, Z.; Fu, X. Estimating Mountainous Freeway Crash Rate: Application of a Spatial Model with Three-Dimensional (3D) Alignment Parameters. Accid. Anal. Prev. 2022, 170, 106634. [Google Scholar] [CrossRef] [PubMed]
- Gedamu, W.T.; Plank-Wiedenbeck, U.; Wodajo, B.T. A Spatial Autocorrelation Analysis of Road Traffic Crash by Severity Using Moran’s I Spatial Statistics: A Comparative Study of Addis Ababa and Berlin Cities. Accid. Anal. Prev. 2024, 200, 107535. [Google Scholar] [CrossRef]
- BUGS User Manual—MultiBUGS v2.0. Available online: https://www.multibugs.org/documentation/latest/spatial/SpatialDistributions.html (accessed on 3 November 2025).
- Besag, J.; York, J.; Mollié, A. Bayesian Image Restoration, with Two Applications in Spatial Statistics. Ann. Inst. Stat. Math. 1991, 43, 59. [Google Scholar] [CrossRef]
- Sklar, A. Fonctions de Répartition à N Dimensions et Leurs Marges. Publ. Inst. Stat. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 2006. [Google Scholar]
- Bedford, T.; Cooke, R.M. Probability Density Decomposition for Conditionally Dependent Random Variables Modeled by Vines. Ann. Math. Artif. Intell. 2001, 32, 245–268. [Google Scholar] [CrossRef]
- Tamakloe, R.; Hong, J.; Park, D. A Copula-Based Approach for Jointly Modeling Crash Severity and Number of Vehicles Involved in Express Bus Crashes on Expressways Considering Temporal Stability of Data. Accid. Anal. Prev. 2020, 146, 105736. [Google Scholar] [CrossRef] [PubMed]
- Feng, M.; Wang, X.; Li, Y. Analyzing Single-Vehicle and Multi-Vehicle Freeway Crashes with Unobserved Heterogeneity. J. Transp. Saf. Secur. 2023, 15, 59–81. [Google Scholar] [CrossRef]
- Brooks, S.P.; Gelman, A. General Methods for Monitoring Convergence of Iterative Simulations. J. Comput. Graph. Stat. 1998, 7, 434–455. [Google Scholar] [CrossRef]
- Barua, S.; El-Basyouny, K.; Islam, M.T. Multivariate Random Parameters Collision Count Data Models with Spatial Heterogeneity. Anal. Methods Accid. Res. 2016, 9, 1–15. [Google Scholar] [CrossRef]
- Li, P.; Abdel-Aty, M.; Yuan, J. Using Bus Critical Driving Events as Surrogate Safety Measures for Pedestrian and Bicycle Crashes Based on GPS Trajectory Data. Accid. Anal. Prev. 2021, 150, 105924. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, W.; Wushour, S. Traffic Accident Prediction Based on LSTM–GBRT Model. J. Control Sci. Eng. 2020, 2020, 4206919. [Google Scholar] [CrossRef]
- Yu, R.; Abdel-Aty, M. Multi-Level Bayesian Analyses for Single- and Multi-Vehicle Freeway Crashes. Accid. Anal. Prev. 2013, 58, 97–105. [Google Scholar] [CrossRef]
- Qin, X.; Ivan, J.N.; Ravishanker, N.; Liu, J.; Tepas, D. Bayesian Estimation of Hourly Exposure Functions by Crash Type and Time of Day. Accid. Anal. Prev. 2006, 38, 1071–1080. [Google Scholar] [CrossRef] [PubMed]
- Phan, D.C.; Truong, L.T. Traffic Congestion and Safety: Mixed Effects on Total and Fatal Crashes. Sustainability 2024, 16, 8911. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, Q. Quantitative Causality Assessment between Traffic States and Crash Risk in Freeway Segments with Closely Spaced Entrance and Exit Ramps. Phys. A Stat. Mech. Appl. 2024, 637, 129587. [Google Scholar] [CrossRef]

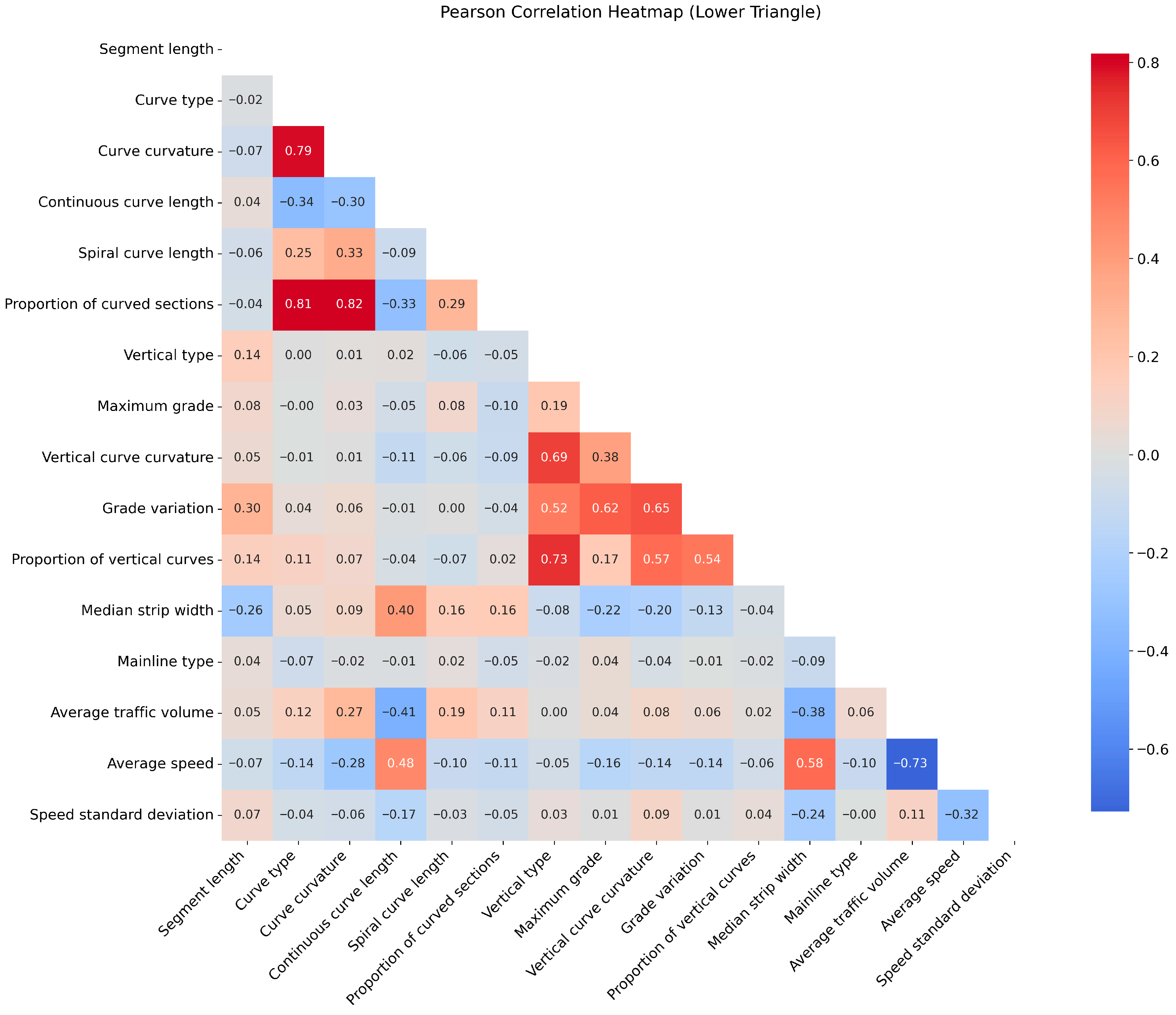
| Variable | Code and Description | Statistics | |
|---|---|---|---|
| Horizontal Alignment | Curve type | 1: Straight section | N: 198 |
| 2: Circular curve | N: 140 | ||
| 3: Combined straight and curve section | N: 22 | ||
| Curve curvature (10−4 m−1) | Reciprocal of curve radius | Mean: 2.47 SD: 1.91 | |
| Spiral curve length (km) | Length of transition curve between straight and circular segments | Mean: 0.17 SD: 0.13 | |
| Continuous curve length (km) | Length of consecutive curves in design drawings | Mean: 2.50 SD: 1.86 | |
| Proportion of curved sections (%) | Ratio of curved length within each analysis unit | Mean: 42.06 SD: 48.12 | |
| Vertical Alignment | Vertical type | 0: Level | N: 110 |
| 1: Upgrade | N: 6 | ||
| 2: Downgrade | N: 8 | ||
| 3: Crest curve | N: 87 | ||
| 4: Sag curve | N: 76 | ||
| 5: Combined slope and vertical curve | N: 73 | ||
| Maximum grade (%) | Maximum slope within each analysis unit | Mean: 0.88 SD: 0.88 | |
| Vertical curve curvature (10−4 m−1) | Reciprocal of vertical curve radius | Mean: 0.63 SD: 0.65 | |
| Grade variation (%) | Grade variation within a segment | Mean: 1.00 SD: 1.23 | |
| Proportion of vertical curves (%) | Proportion of vertical curve length in the segment | Mean: 56.86 SD: 44.78 | |
| Cross-Sectional | Mainline Type | 0: Regular mainline | N: 316 |
| 1: Mainline with entrance ramp | N: 23 | ||
| 2: Mainline with exit ramp | N: 21 | ||
| Number of Lanes | 1: Two lanes | N: 146 | |
| 2: Three lanes | N: 193 | ||
| 3: Four lanes | N: 21 | ||
| Median Strip Width (m) | 0: 2 m | N: 45 | |
| 1: 3 m | N: 91 | ||
| 2: > 3 m | N: 224 | ||
| Length (m) | Segment Length | Length of analysis unit | Mean: 224.32 SD: 94.92 |
| Variable | Description | Mean | SD | Min | Max |
|---|---|---|---|---|---|
| Daily traffic volume (104 vehicles) | Daily traffic volume per direction for each segment | 2.21 | 1.08 | 0.68 | 5.43 |
| Average speed (km/h) | Mean speed of vehicles traversing the segment | 82.56 | 6.90 | 66 | 92 |
| Speed deviation (km/h) | Standard deviation of vehicle speeds along the segment | 42.41 | 41.90 | 16 | 225 |
| Crash Type | Mean | SD | Min | Max |
|---|---|---|---|---|
| Rear-end crashes | 2.06 | 3.80 | 0 | 30 |
| Sideswipe crashes | 0.95 | 1.76 | 0 | 10 |
| Crash Type | Direction | |
|---|---|---|
| North-to-South | South-to-North | |
| Rear-end crashes | 0.290 (p < 0.001) | 0.119 (p < 0.001) |
| Sideswipe crashes | 0.151 (p < 0.001) | 0.026 (p < 0.001) |
| Spearman’s Correlation Test | ||
|---|---|---|
| Segment Ranking Index | Rear-End Crashes | Sideswipe Crashes |
| Rear-end crashes | 1 | 0.527 (p < 0.0001) |
| Sideswipe crashes | 0.527 (p < 0.0001) | 1 |
| Copula | Function Form | Range of Parameter θ | Kendall’s Tau | Range of Kendall’s |
|---|---|---|---|---|
| Gaussian | ||||
| Frank | ||||
| Clayton | ||||
| Joe | ||||
| Gumbel |
| Model | Rear-End | Sideswipe | ||||
|---|---|---|---|---|---|---|
| WAIC | MSAD | RMSLE | WAIC | MSAD | RMSLE | |
| Uni-PLN | 1549.0 | 0.481 | 0.749 | 1023.0 | 0.591 | 0.590 |
| Uni-PLN-CAR | 782.8 | 0.213 | 0.408 | 744.4 | 0.426 | 0.454 |
| Bi-PLN-CAR-cov | 838.1 | 0.211 | 0.415 | 775.5 | 0.417 | 0.453 |
| Bi-PLN-CAR-Joe | 693.4 | 0.249 | 0.316 | 489.3 | 0.318 | 0.258 |
| Bi-PLN-CAR-Frank | 678.9 | 0.219 | 0.283 | 484.7 | 0.305 | 0.249 |
| Bi-PLN-CAR-Clayton | 769.9 | 0.214 | 0.288 | 542.1 | 0.303 | 0.273 |
| Bi-PLN-CAR-Gaussian | 1136.0 | 0.253 | 0.443 | 840.9 | 0.312 | 0.399 |
| Bi-PLN-CAR-Gumbel | 1125.0 | 0.442 | 0.476 | 917.9 | 0.775 | 0.507 |
| Variable | Uni-PLN-CAR | Bi-PLN-CAR-Cov | Bi-PLN-CAR-Frank | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rear-End | Sideswipe | Rear-End | Sideswipe | Rear-End | Sideswipe | |||||||
| Coef. | SD | Coef. | SD | Coef. | SD | Coef. | SD | Coef. | SD | Coef. | SD | |
| Intercept | −1.922 ** | 0.2804 | −2.086 ** | 0.3627 | −2.08 ** | 0.340 | −3.789 ** | 1.546 | −0.91 ** | 0.111 | 0.412 | 0.405 |
| Proportion of horizontal curves | 0.047 ** | 0.080 | −0.333 * | 0.169 | 0.594 ** | 0.240 | −0.070 | 0.347 | ||||
| Continuous curve length | −0.115 ** | 0.026 | −0.019 * | 0.023 | −0.281 ** | 0.029 | −0.191** | 0.052 | −0.252** | 0.014 | −0.009 | 0.078 |
| Spiral curve length | 2.759 ** | 0.5846 | 1.084 ** | 0.364 | 1.159 ** | 0.219 | 0.200 | 0.482 | 0.395 ** | 0.173 | 2.059 | 1.756 |
| Mainline type (baseline: regular mainline) | ||||||||||||
| with entrance ramp | −1.15 | 0.581 | −1.319 | 1.012 | 0.274 | 0.512 | 0.604 | 0.520 | 0.537 | 0.572 | 0.544 | 0.617 |
| with exit ramp | −1.276 | 0.925 | −0.966 ** | 1.112 | 0.573 | 0.437 | 1.126 ** | 0.432 | 0.055 | 1.007 | 1.214 * | 0.702 |
| Median strip width (baseline: 2 m) | ||||||||||||
| =3 m | 0.281 ** | 0.069 | 0.486 ** | 0.079 | 0.575 ** | 0.149 | 0.856 ** | 0.24 | 0.245 ** | 0.037 | −0.016 | 0.532 |
| >3 m | −1.443 ** | 0.1455 | −0.736 ** | 0.103 | −2.038 ** | 0.211 | −1.234 ** | 0.271 | −2.411 ** | 0.650 | −1.882 ** | 0.528 |
| Log(segment length) | 0.589 ** | 0.043 | 0.383** | 0.046 | 0.560 ** | 0.047 | 0.405 * | 0.209 | 0.612 ** | 0.007 | 0.419 ** | 0.048 |
| Average speed | −0.015 ** | 0.003 | 0.001 | 0.004 | −0.001 ** | 0.001 | 0.018 | 0.015 | −0.015 ** | 0.001 | −0.023 ** | 0.004 |
| Log(traffic volume) | −0.013 ** | 0.021 | −0.030 ** | 0.237 | 1.532 | 1.414 | −0.038 ** | 0.008 | −0.149 ** | 0.003 | −0.247 ** | 0.036 |
| Site correlation | -- | 0.873 | 0.993 | |||||||||
| 0.0001 | 0.0077 | 0.0055 | ||||||||||
| Variable | Rear-End | Sideswipe |
|---|---|---|
| Proportion of horizontal curves | 0.0292 ** | −0.0073 |
| Continuous curve length | −0.0124 ** | −0.0009 |
| Spiral curve length | 0.0194 ** | 0.2132 |
| Mainline type (baseline: regular mainline) | ||
| with entrance ramp | 0.0264 | 0.0564 * |
| with exit ramp | 0.0027 | 0.1257 |
| Median strip width (baseline: 2 m) | ||
| =3 m | 0.0121 ** | −0.0016 |
| >3 m | −0.1187 ** | −0.1949 ** |
| Log(segment length) | 0.0301 ** | 0.0434 ** |
| Average speed | −0.0007 ** | −0.0024 ** |
| Log(traffic volume) | −0.0073 ** | −0.0255 ** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, J.; Zhou, L.; Feng, M.; Zhao, J.; Lin, Y. Influencing Factor Analysis Based on Jointly Modeling for Freeway Rear-End and Sideswipe Crashes Considering Spatial and Site Correlations. Appl. Sci. 2025, 15, 13015. https://doi.org/10.3390/app152413015
Wei J, Zhou L, Feng M, Zhao J, Lin Y. Influencing Factor Analysis Based on Jointly Modeling for Freeway Rear-End and Sideswipe Crashes Considering Spatial and Site Correlations. Applied Sciences. 2025; 15(24):13015. https://doi.org/10.3390/app152413015
Chicago/Turabian StyleWei, Jianluo, Lulu Zhou, Mingjie Feng, Jing Zhao, and Yu Lin. 2025. "Influencing Factor Analysis Based on Jointly Modeling for Freeway Rear-End and Sideswipe Crashes Considering Spatial and Site Correlations" Applied Sciences 15, no. 24: 13015. https://doi.org/10.3390/app152413015
APA StyleWei, J., Zhou, L., Feng, M., Zhao, J., & Lin, Y. (2025). Influencing Factor Analysis Based on Jointly Modeling for Freeway Rear-End and Sideswipe Crashes Considering Spatial and Site Correlations. Applied Sciences, 15(24), 13015. https://doi.org/10.3390/app152413015






