Discrete Element Simulations of Fracture Mechanism and Energy Evolution Characteristics of Typical Rocks Subjected to Impact Loads

Abstract

The dynamic fracture behavior of rocks subjected to impact loading is a fundamental issue within the field of rock dynamics. This study aims to construct microstructure models of heterogeneous minerals representative of various typical rocks and establish a coupled SHPB impact simulation system with FLAC-PFC to examine the mechanisms of fracture, energy dissipation law, and the characteristics of acoustic emission (AE) responses in rocks acted upon by impact loads. The main results obtained reveal the following: (i) The fracture mechanisms of various lithologies under impact loading exhibit common characteristics, predominantly behaving as composite failure mechanisms. The observed distribution characteristics are mixed and interwoven with shear-tension-implosion failures, with a tendency to aggregate from the boundaries towards the interior of samples. (ii) The AE fracture strength of various lithologies predominantly ranges from −8.25 to −5.25, with peak frequencies observed between −7 to −6. The sequence of AE-based B-values, ranked from highest to lowest, is as follows: red sandstone > green sandstone > slate > granite > blue sandstone > basalt. (iii) The T-k distribution for various lithologies follows CLVD (+)-first. (iv) A significant correlation exists between the energy-time density and the B-value. Rocks exhibiting high energy dissipation capacity are characterized primarily by small-amplitude AE events and small-scale fractures, whereas those with low energy dissipation capacity are mostly marked by large-amplitude AE events and large-scale fractures. These research findings provide a fairly solid theoretical basis for understanding the fracture mechanisms and energy dissipation behaviors of rocks subjected to impact loading.

1. Introduction

The dynamic fracture behavior of rock under impact loading is a critical area of study in rock dynamics. Such long-duration impact loads are prevalent in high-dynamic disturbance environments, including mining, tunnel excavation, hydraulic engineering, and earthquake engineering. Understanding the fracture modes, energy evolution, and acoustic emission responses of rocks under these conditions is essential for further rational elucidation of the fracture instability mechanisms of rock materials. However, the inherent heterogeneity and multi-scale structure of rock lead to various uncertainties regarding its fracture behavior under high strain rates. Consequently, it is imperative to methodically examine the micro–macro response differences across various lithologies subjected to impact loading.

In recent years, numerical simulation technologies have emerged as vital tools for exploring the dynamic fracture behavior of rocks, with the discrete element method (PFC) demonstrating unique advantages in simulating the microscopic fracture mechanisms at the particle level. Wang yang et al. [1] developed a PFC-GBM and SHPB system to investigate the influence of grain size on dynamic tensile strength. Wei Zhu et al. [2] unveiled the heterogeneous characteristics of crack propagation in sandstone by constructing a heterogeneous model. Jian Zhou et al. [3] discovered that mineral composition significantly affects the uniaxial compression properties of granite. Hu et al. [4] and Lei et al. [5] emphasized that the macro-mechanical response and failure mechanisms of rocks are profoundly affected by microstructural factors, specifically grain contact heterogeneity and grain size heterogeneity, respectively. Additionally, Hu et al. [6], Xu et al. [7], and Han et al. [8] incorporated various physical field factors into their models, enhancing the applicability of PFC in tackling complex rock fracture scenarios.

The choice between using a two-dimensional or three-dimensional model in numerical simulations has been a subject of ongoing debate in the rock mechanics community. While three-dimensional models can more directly capture the spatial heterogeneity and complex stress redistribution of real rocks, they come with a high computational cost, which becomes prohibitive when extensive comparison of operational conditions and parameter scanning is required. In contrast, under reasonable calibration of the microscopic parameters, two-dimensional models can retain key failure mechanisms such as crack initiation, propagation, and coalescence, while significantly reducing degrees of freedom and computational time. This makes it more feasible for systematic parametric studies, fracture mode comparisons, and the exploration of characteristics across multiple lithologies and conditions. Existing numerical studies have also shown that the stress–strain response, crack morphology, and acoustic emission (AE) statistical characteristics obtained from two-dimensional models exhibit good qualitative consistency with experimental results and three-dimensional simulations. These can provide reliable trend information for engineering criteria, rather than relying solely on absolute values under a single operational condition [9]. On the other hand, the coupled continuum-discrete FLAC–PFC model, while capable of describing both macroscopic deformation and microfracture evolution in jointed rock masses, has been shown in numerous studies to be highly sensitive to particle size, contact stiffness, bonding strength, and coupling strategies with respect to its macroscopic stiffness, ultimate bearing capacity, and energy dissipation [10]. This sensitivity is primarily reflected in quantitative indicators such as peak strength and equivalent stiffness, with relatively limited impact on the dominant trends in crack topology, failure modes, and AE evolution. Therefore, this does not preclude the model from being used for mechanism studies and trend identification after proper calibration [11]. Based on the aforementioned considerations, this study adopts a unified two-dimensional particle flow modeling framework to conduct comparative simulations of different lithologies under identical dynamic loading conditions, focusing on the analysis of crack evolution characteristics, AE event clustering, b-value evolution, and multi-scale energy dissipation pathways. The objective of this study is to identify the common patterns of damage localization and energy release, rather than providing precise predictions for a specific engineering case. In doing so, it offers transferable mechanistic insights for geotechnical problems such as tunnel stability assessment and blasting optimization, without relying on complex FLAC–PFC coupling or cumbersome sensitivity analyses.

Building upon this foundation, researchers have increasingly focused on acoustic emission (AE) and moment tensor (MT) inversion techniques to facilitate dynamic identification and quantitative analysis of micro-fracture mechanisms. In this regard, Ohtsu et al. [12] laid the groundwork for moment tensor theory, establishing a correlation between AE signals and tensile/shear fracture modes, which provided a theoretical basis for analyzing AE source mechanisms. Following this, Graham et al. [13] compared the polarity method with moment tensor inversion, highlighting the latter’s superior capability in rationally predicting the shear fracture behavior. Aker et al. [14] elucidated the dynamic evolution law of fracture events within both isotropic and anisotropic contexts during rock instability. Liu et al. [15] and Ren et al. [16] discovered the tensile-shear characteristics and transformation phenomena through experimental investigations, validating the advantages of AE and moment tensor methodologies in elucidating the crack and fracture evolution mechanisms in rocks. Ma et al. [17], Zhou et al. [18], and Bu et al. [19] integrated PFC or FDEM simulation with AE-MT analysis to examine the evolution of fracture modes and tensile-shear mechanisms, confirming the effectiveness of this approach in the rock mechanics domain. Cai et al. [20] and Wang et al. [21] further explored the trends in the tension-shear ratio and provided insights into the comprehensive evolution processes of the tension-shear mechanism through moment tensor methods, demonstrating the extensive application potential of AE-MT techniques for analyzing multi-scale fracture evolution in both temporal and spatial dimensions.

The investigation into the dynamic fracture mechanisms of rocks has increasingly adopted an energy perspective as a pivotal approach for understanding rock fracture behavior. Particularly under impact loading conditions, energy characteristics not only embody the fundamental nature of the rock failure process but also serve as critical indicators for assessing precursors to instability. Wang et al. [22] demonstrated that the failure evolution in hard rocks is closely associated with the accumulation of strain energy through the development of a stress–energy coupling model. Gao et al. [23] observed that the energy dissipation ratio exhibits a negative correlation with post-peak intensity, revealing distinct energy evolution characteristics across various lithologies. In terms of energy evolution, Chen et al. [24] proposed a brittleness criterion grounded in the energy damage curve, while Xie et al. [25] established a critical relationship between the dissipation ratio and strength, offering a novel methodology for identifying brittle rock instability. Zhang et al. [26] examined the impact of diverse loading paths on energy distribution, uncovering that axial pressure and confining pressure significantly influence energy release modes, thereby providing essential indicators for instability predictions. In a theoretical expansion, Wang and Cui [27] put forward the concept of “energy intensity”, developed an energy evolution equation, and highlighted that the proportion of dissipated energy can serve as a strength characterization parameter under confining pressure. Furthermore, Meng et al. [28] and Li et al. [29] identified the energy evolution laws associated with fatigue failure and sudden instability by analyzing energy density and time curves. Zhou et al. [30] further divided the energy response under static–dynamic combined loading into three stages, elastic accumulation, nonlinear growth, and failure mutation, which comprehensively delineated the entire energy evolution process of rocks subjected to impact loading.

Although the moment tensor simulation method has been applied to analyze the failure mechanism of acoustic emission events, as a new method, there are still some key problems to be solved urgently. The existing research work mostly focuses on the acoustic emission of a single lithology under uniaxial compression, and there is still room for further research on cross-rock and cross-working conditions. The dynamic mechanical properties and energy characteristics of rock have always been a hot issue, but the energy index is relatively simple. The energy–time density index considering time factor is introduced to make up for the lack of coupling between energy index and AE statistics, so the relationship between energy–time density and AE B value is worth further study.

In the current investigation, we examine several typical rock types as research subjects, constructing a heterogeneous microstructure model based on XRD test results. A numerical simulation of SHPB impact tests is performed using a FLAC-PFC coupled impact loading system, enabling a detailed examination and analysis of the fracture mechanism, acoustic emission characteristics, and energy dissipation behaviors of rocks under impact loading. The present work aims to clarify the fracture evolution modes of various lithologies subjected to impact loading and explore the coupling relationships among the energy consumption characteristics and the acoustic emission traits of rocks under such conditions. Therefore, this provides theoretical insights and technical references for the dynamic response mechanisms of rocks under impact disturbances.

2. Establishment of Numerical Simulation Model and Parameter Calibration

2.1. Establishment of Numerical Simulation Model

To examine the fracture evolution characteristics of typical rocks under impact loading, this study employs PFC2D discrete element software for the simulation and analysis of various rock types. The mineral composition of six representative rocks was first determined through XRD experiments, focusing on the four primary components exhibiting the highest contents for PFC-GBM modeling. X-ray diffraction (XRD) analyses were performed using a D/MAX-2600 X-ray diffractometer manufactured by Rigaku Company, Tokyo, Japan. Figure 1 illustrates the mass fraction distribution of the main minerals present in each rock sample.

In the development of a rock sample model, a Voronoi polygonal mesh is incorporated into the software, employing a parallel bonding model for mineral grains and a smooth joint model for interactions between these grains. This approach effectively facilitates the modeling of micro-mineral structures present in heterogeneous rocks [31]. Rocks, as a typical heterogeneous material, arise from complex physical and chemical transformations involving various crystals. Based on different fracture mechanisms, cracks at the crystal scale (intragranular/intergranular) induced by contact failures among particles can be essentially classified into tensile cracks and shear cracks. When the normal tensile stress exerted on particles within mineral crystals surpasses their tensile strength, tensile failure occurs at the contacts, leading to the formation of intra-crystal tensile cracks. Conversely, when the tangential shear stress on particles exceeds their shear strength, shear damage occurs, resulting in intracrystalline shear cracks. The underlying fracture principles governing both tensile and shear cracks between mineral crystals reflect those described in the preceding discussion [32].

To examine the two-dimensional evolution process of typical rock specimens subjected to impact loading, a SHPB impact system coupled with FLAC and PFC was constructed. For this purpose, an elastic rod model was developed in FLAC to facilitate the simulation of stress wave propagation and loading. Additionally, a heterogeneous rock model was constructed using PFC numerical simulation software in conjunction with PFC-GBM. The coupled SHPB impact system was employed to conduct impact numerical simulation tests on typical rocks. The results regarding the mineral crystal model and the Hopkinson impact test model have been illustrated in Figure 2.

Numerical simulations were performed using PFC2D (version 7.0) and FLAC (version 7.0), developed by Itasca Consulting Group Inc. In the PFC2D simulations, the time step was selected based on a safety factor of 0.5 relative to the critical time step to ensure numerical stability. Through the built-in coupling mechanism, the time step in FLAC was synchronized with PFC, and during the quasi-static calibration stage, the ratio of unbalanced forces to total applied forces in the FLAC domain was maintained below ε (e.g., 10⁻⁴).

In numerical simulation experiments, methods for simulating incident loads are typically categorized into two types: the first involves replicating the impact of structural bullets under real conditions, while the second employs an equivalent load application method based on impact waveforms. The structural bullet impact technique allows for a comprehensive inversion of the test process; however, it necessitates calibration between the bullet and rod within the simulation, which complicates the overall process. Conversely, the equivalent load application method facilitates the mapping of the functional relationship between the waveform and loading time onto the incident rod, thereby enabling not only the simulation of the impact load form but also allowing for easier adjustments in the simulation and execution.

In this study, the equivalent load application method is utilized to implement the application of a sine wave as the incident load. The incident load p and the loading time t satisfy a functional relationship as follows: p = p_m[1 − cos(2πf₀t)]/2, where p_m is the peak value of incident load, f₀ is the incident frequency, such that for the case of load application time of T is denoted by T = 1/f₀.

The coupling procedure between FLAC and PFC in the SHPB system involves modeling the rod domain in FLAC and a particle-based PFC2D rock sample, with the two being coupled through the Itasca data file interface. The detailed coupling procedure is as follows:

(1)

An axisymmetric elastic rod is generated in FLAC, with both the incident and transmission rods having a length of 1.8 m, a diameter of 50 mm, a density of 7.89 g/cm³, an elastic modulus of 220 GPa, and a Poisson’s ratio of 0.21.

(2)

A PFC2D specimen with a diameter of 50 mm and a height of 50 mm is created at the center of the rod-to-rod interface.

(3)

The FLAC grid surfaces at both ends of the specimens are defined as coupling boundaries, and the corresponding PFC particle groups at the specimen ends are designated as coupling boundaries. At each global time step, the average normal stress on the FLAC coupling boundary is transferred as a boundary load to the PFC coupling boundary, while the reaction force on the PFC side is fed back as an equivalent nodal force to FLAC.

(4)

In FLAC, an incident stress wave is applied at the left end of the incident rod in the form of a half-sine pulse p(t), and the transmitted and reflected waves are recorded through monitoring points.

(5)

During dynamic loading, FLAC and PFC apply load waveforms to the units at specified intervals, while exchanging force-velocity data at a frequency of 1 kHz to maintain synchronization between the two software programs.

Figure 3 illustrates the time-history curve of the stress wave within the bar. The peak value of the incident stress measured by the monitoring circle is 100 MPa, which aligns with the predetermined data. Furthermore, the incident waveform corresponds closely with the equivalent applied load. Consequently, this approach satisfies the requirements for simulation.

Figure 4 illustrates the stress wave propagation in bars and rock specimens.

Although dynamic fracture and wave propagation in rocks are inherently three-dimensional phenomena, this study employs a two-dimensional particle-based discrete element model (PFC2D-FLAC) to simulate the fracture behavior of rocks under a Split-Hopkinson Pressure Bar (SHPB) configuration. The primary reason for choosing the two-dimensional model is that the specimens used in the experiments have an approximately cylindrical geometry, with axisymmetric loading and boundary conditions. As such, the two-dimensional model effectively simulates the in-plane mechanical response of the specimens and can capture the primary fracture modes and acoustic emission (AE) source mechanisms of the rock, especially in the cross-sectional view. The two-dimensional model offers lower computational costs, making it suitable for large-scale cross-lithology parameter studies. By calibrating the laboratory stress–strain curves, the two-dimensional model successfully reproduces macroscopic responses such as peak strength, stiffness, loading rate effects, and overall failure modes. However, the two-dimensional simplification also introduces limitations. Due to the inability to fully simulate out-of-plane crack branching and three-dimensional crack morphology, the two-dimensional model may underestimate the total energy dissipation. Additionally, the two-dimensional model fails to capture the complex evolution of cracks in three-dimensional space, leading to discrepancies between the estimated energy density and crack geometry and the results from full three-dimensional simulations. Nevertheless, the two-dimensional model effectively reflects fracture evolution trends, acoustic emission statistics, and energy-time density variations under different lithologies, providing valuable insights into the study of rock fracture behavior. To verify numerical stability, a halved time step and refined grid settings were employed, and the consistency of the numerical results was confirmed through repeated simulations, ensuring that the chosen numerical settings do not affect the main conclusions.

Although the two-dimensional model performs well in the current study, future research will extend to three-dimensional models to gain a more comprehensive understanding of the complex fracture processes of rocks under dynamic loading. The three-dimensional model can more accurately capture the three-dimensional crack morphology, particle size effects, and the influence of different lithologies on failure modes, especially under non-axisymmetric loading conditions. Additionally, three-dimensional simulations can provide deeper insights into rock stability analysis, energy dissipation characteristics, and scale effects in the fracture process. Therefore, future work will focus on developing three-dimensional particle flow-finite difference models and further investigating the effects of particle size and lithological variations on rock fracture behavior.

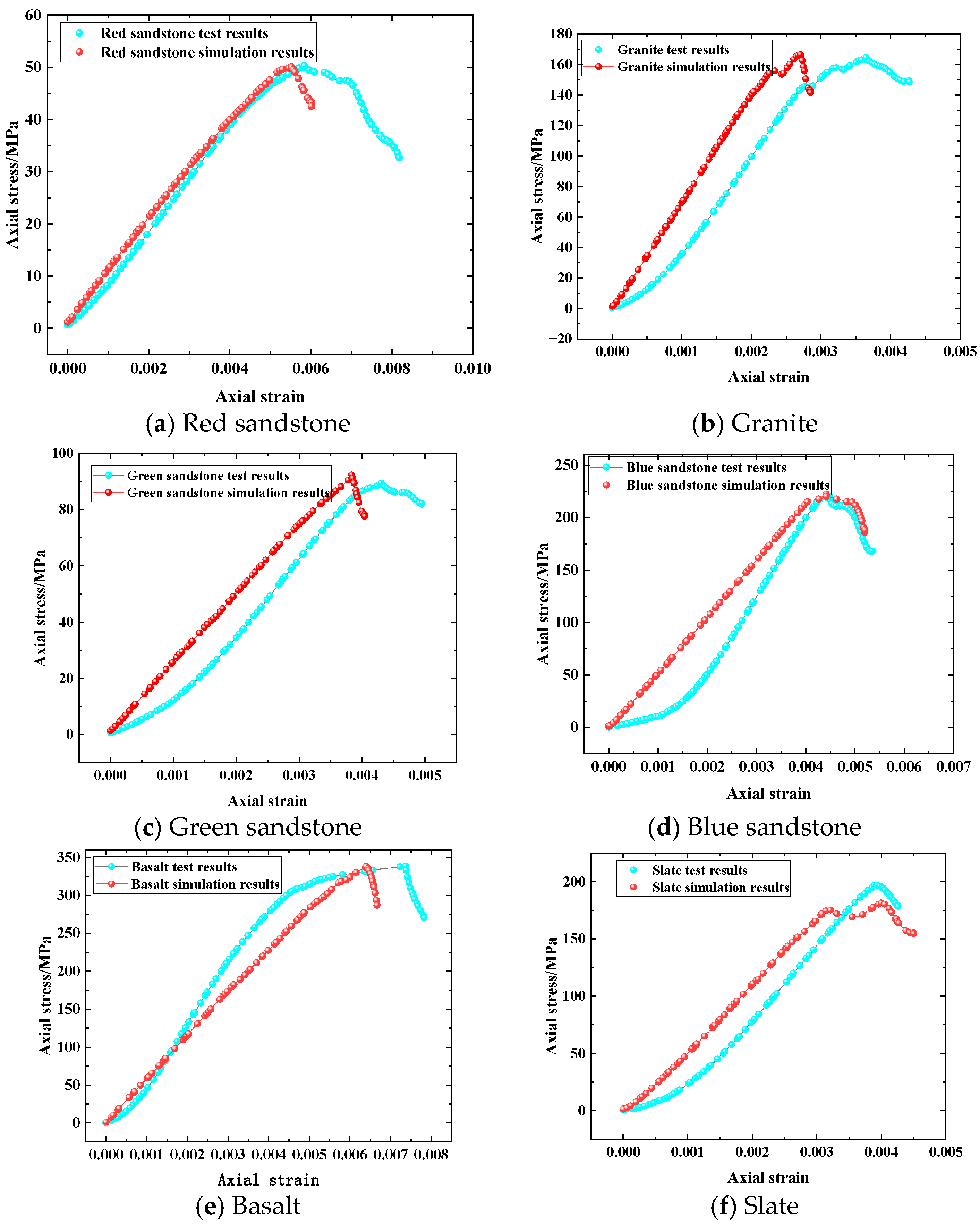
2.2. Parameter Calibration

In the numerical simulation testing of PFC, accurately determining and rationally selecting meso-parameters that characterize the intrinsic properties of materials is of great significance. There exists a correlation between the meso-parameters employed in simulations and the macro-parameters displayed by rock samples; however, this relationship is not strictly one-to-one, as a single meso-parameter can simultaneously influence multiple macro-parameters. Currently, an effective method for calibrating meso-parameters remains a trial-and-error approach [33,34,35].

When simulating rock samples and rock-like materials, the inherent complexity of typical rocks—comprising various minerals—renders the use of a singular bonding model inadequate to represent the characteristics and properties both between and within grains effectively. The parallel bonding model is primarily utilized to simulate the bonding state within the material, providing a more accurate representation of the bonding and force transfer processes of the internal crystal structure. Conversely, the smooth joint model is more adept at simulating the bonding state between grains, as it effectively captures the weak connections and ease of sliding at grain boundaries.

Parameter calibration is an indispensable link in PFC simulation, and its core function is to verify whether microscopic parameters can make the simulated materials have the expected macroscopic characteristics. Numerical uniaxial compression test, as a common calibration method, has the same model size as the uniaxial size of the specimen.

To achieve macro-mechanical parameters that closely align with experimental results, a uniaxial numerical simulation test was executed, wherein the upper and lower walls were subjected to a fixed loading speed of 0.05 m/s. In this scenario, the time step was automatically set as 7 × 10⁻⁸ time step/s. This loading speed meets the requirements for a quasi-static test as detailed in the literature [36]. Figure 5 illustrates the comparative analysis between the experimental and simulation results for typical rocks. Due to the diversity of rock types, the calibration methods are standardized, with the mesoscopic parameters exemplified using red sandstone.

Table 1. Calibration results of meso-parameters of red sandstone.

Attribute Group	Parameter	Red Sandstone
Basic particle group	Minimum particle radius Rmin (mm)	0.05
	Particle radius ratio Rmax/Rmin	1.66
	Grain density ρ (kg·m−3)	2500
	Elastic modulus of particles E (GPa)	36
	Particle friction coefficient μ	0.5
Mineral particle group	Mineral matter group	Plagioclase	Quartz	Calcite	Other
	Parallel bond modulus E* (GPa)	5.57	5.41	5.09	4.61
	Parallel bond tensile strength σt* (MPa)	6.24	5.61	4.98	4.88
	Parallel bonding cohesion c*	8.31	7.48	6.65	6.44
	Parallel bonding friction angle φ*	30
	Parallel bond stiffness ratio K*	1.5
Mineral boundary group	SJM stiffness ratio k*sj	2.6
	SJM friction factor μsj	0.3
	SJM tensile strength σt_sj (MPa)	2.22
	SJM cohesive strength csj	27.44

presents the calibration results for the mesoscopic parameters of red sandstone.

We performed error analysis on the peak strength and elastic modulus from both experimental and simulation results for each rock type, and the corresponding values are summarized in

Table 2. Main mechanical parameters of the rock specimen.

Rock	Experiment		Simulation		Error
	σ/MPa	E/GPa	σ/MPa	E/GPa	σ/%	E/%
Red sandstone	50.26	8.61	50.04	9.08	0.43	5.46
Granite	164.49	65.96	166.49	71.93	1.22	9.05
Green sandstone	89.43	27.57	92.36	24.65	3.27	10.59
Blue sandstone	220.70	76.77	222.37	54.26	0.76	29.32
Basalt	338.65	82.72	338.52	55.74	0.04	32.62
Slate	197.19	65.48	181.52	60.25	7.95	7.98

. For all rock types, the maximum error in peak strength is 7.95%, and the maximum error in elastic modulus is 32.62%. While there are some cases with relatively large errors, these do not affect the identification of the regular characteristics of the rocks in subsequent studies. During the initial experiment design, we performed tests with random seeds and found that their impact on the results was minimal. To eliminate the effect of random seeds in subsequent studies, we used a uniform random seed value for each lithology, which facilitates clear comparison of crack patterns and acoustic emission (AE) statistics across different rock types. We acknowledge that discrete element simulations may exhibit statistical variability when different random seeds are used. Systematic analysis based on multiple trials for each lithology, combined with formal statistical tests, will allow for a more rigorous estimation of the dispersion and confidence intervals. This will be the focus of future work.

3. Discrete Element Simulation Method of Moment Tensor Acoustic Emission

In the numerical simulation of PFC, the fracture of particle contacts can be conceptualized as the initiation of internal cracks within materials, leading to energy dissipation, a process analogous to the principle of acoustic emission. Current research is indicative of the existence of two distinct methods for simulating acoustic emission using discrete elements. The first involves treating the formation of a single crack as the source of acoustic emission signals, which is relatively straightforward. The second method utilizes the moment tensor approach to compute the relevant acoustic emission parameters.

Utilizing the single microcrack approach as the acoustic emission signal source presents challenges, particularly because the particle sizes within the sample are similar. This similarity can lead to closely aligned fracture intensities of AE events, which may result in an overestimation of the number of such events and consequently yield inaccurate acoustic emission parameters. Furthermore, this method diverges from the experimental principles of acoustic emission acquisition. In experimental setups, the acoustic emission apparatus primarily detects signals produced by similar microcracks occurring simultaneously, which may be singular or multiple. Therefore, the results obtained by the single crack method may not align with the established power-law frequency-amplitude distribution law [37].

The acoustic emission simulation method, grounded in the moment tensor approach, addresses both temporal and spatial proximity criteria, thereby incorporating the effects of time and space into the analysis. If the direct distance between two cracks and the elapsed time between their occurrences fall below specified thresholds, these cracks are considered a single AE event. This aligns more closely with experimental acquisition principles, allowing for more stable and accurate statistical results. However, this approach is not without limitations; specimens typically fail due to multiple AE events. The calculations of the moment tensor necessitate the components of particle contact forces, which demand considerable computational resources and data storage.

In the current study, the moment tensor method is employed to simulate AE events due to its practical advantages. Hazzard et al. [38] were the first to introduce an acoustic emission calculation method in PFC software, based on the discrete element method, wherein the moment tensor is computed using contact force data and the distances from contact points to the centers of the AE events. This method considers the collective changes in contact forces on particles adjacent to the crack, as well as relevant force arm products. As a result, by analyzing the forces and displacements of affected particles during crack formation, one can determine the position and intensity of AE events, as well as investigate the tensile and shear properties of the corresponding sources.

The moment tensor can be stated by:

$$M_{ij}={\displaystyle \sum _S\left(\mathrm{\Delta }{F}_i{R}_j\right)},$$

(1)

where M_ij denotes the moment tensor; ΔF_i represents the i-th component of the change of contact force; R_j is the j-th component of the distance between the contact force and the center of the microcrack.

Hanks et al. [39] proposed the following formula for calculating the torque tensor:

$$M_w={\displaystyle \frac{2}{3}}\log M_0-6,$$

(2)

$$M_0=\sqrt{{\displaystyle \frac{{\displaystyle \sum _{i=1}^n{m}_i^2}}{2}}},$$

(3)

where n denotes the dimension, and m_i signifies the i-th eigenvalue of the moment tensor matrix. The amplitude serves as an indicator of the energy release intensity associated with crack formations or failure events within the rock mass. High-amplitude signals typically signify substantial stress release or pronounced fracture processes, often linked to extensive crack propagation or localized failure. By analyzing the amplitude of acoustic emission, it is possible to gain insights into the degree of damage, the evolution of cracks, and the areas of stress concentration in the rock mass.

To conduct an in-depth examination of the various types of acoustic emission, the R-value method as proposed in Ref. [40] is employed for classification, while the enhanced discrimination technique outlined in Ref. [41] is utilized for further analysis. The specific calculations and discrimination methodologies are detailed as follows:

$$R={\displaystyle \frac{tr(M)\times 100}{\left(|tr(M)|+{\displaystyle \sum _{i=1}^n\left|m_i^{\ast }\right|}\right)}}$$

(4)

$$\left\{\begin{array}{l}R>30(Tensile)\hfill \\ -30<R<30(shear)\hfill \\ R<-30(\mathrm{Im}plosion)\hfill \end{array}\right.,$$

(5)

where tr(M) represents the trace of the moment tensor, and m_i^* denotes the i-th deviatoric stress eigenvalue of the moment tensor matrix. The R-value serves as an indicator of the stress state, failure mechanism, and type of particle internal fracture during each AE event. Events categorized as tensile and implosion types suggest that the sample experiences localized stretching and compression, which generates local tensile stress. Conversely, shear-type events predominantly indicate that the sample undergoes localized damage due to shear stress.

Eaton et al. [42] described the amplitude and cumulative percentage of AE events as the Gutenberg-Richter relationship:

$$LogN=a-b{M}_w,$$

(6)

where N denotes the cumulative AE count greater than or equal to the amplitude M_w, a is the average activity level, and b is the frequency ratio of AE events with smaller amplitude to AE events with larger amplitude. A lower value of b suggests that AE events with higher amplitudes (indicative of strong damage or crack propagation) are more frequent than those with lower amplitudes. This implies a more intense and abrupt rock mass damage, with crack propagation potentially being more concentrated and localized. Conversely, a higher value of b signifies the predominance of AE events characterized by smaller amplitudes (representing smaller cracks or micro-cracks), indicating that strong failure events are rare. Rock masses exhibiting a large b value tend to be more stable, exhibiting a gentler development of cracks and a more gradual failure process, which reduces the likelihood of sudden large-scale fractures.

Since the moment tensor is asymmetry two-tensor, the three feature values are all real numbers and there are three orthogonal feature vectors. If the principal feature values of the three feature vectors are M₁, M₂, and M₃ (M₁ ≥ M₂ ≥ M₃) with corresponding feature vector values of t₁, t₂, and t₃, the moment tensor can be diagonalized in a principal axes system as [43]:

$$\begin{array}{l}{M}_w=\left[\begin{array}{lll}{M}_{11}\hfill & M_{12}\hfill & M_{13}\hfill \\ M_{21}\hfill & M_{22}\hfill & M_{23}\hfill \\ M_{31}\hfill & M_{32}\hfill & M_{33}\hfill \end{array}\right]=\left[\begin{array}{ccc}{M}_1& 0& 0\\ 0& M_2& 0\\ 0& 0& M_3\end{array}\right]=\\ {\displaystyle \frac{1}{3}}\left(M_1+M_2+M_3\right)\left[\begin{array}{lll}1\hfill & 0\hfill & 0\hfill \\ 0\hfill & 1\hfill & 0\hfill \\ 0\hfill & 0\hfill & 1\hfill \end{array}\right]+{\displaystyle \frac{1}{2}}\left(M_1-M_3\right)\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& -1\end{array}\right]\\ +{\displaystyle \frac{1}{6}}\left(2M_2-M_3-M_1\right)\left[\begin{array}{ccc}-1& 0& 0\\ 0& 2& 0\\ 0& 0& -1\end{array}\right]=M^{ISO}+M^{PSC}+M^{CLVD}\end{array},$$

(7)

where M^ISO is the isotropy part of the moment tensor (ISO); M^PSC the pure shear crack part (PSC); and M^CLVD the compensated linear vector dipole part (CLVD).

The pure shear crack part MPSC of the moment tensor can be calculated as follows:

$$M^{\mathrm{PSC}}={\displaystyle \frac{1}{2}}\left(M_1-M_3\right)\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& -1\end{array}\right],$$

(8)

To enhance the analysis and understanding of the mechanisms of rock fracture, Hudson [44] introduced the moment tensor T-k diagram. In this framework, the moment tensor is divided into two parameters: T and k. The equations governing these two factors are:

$$T={\displaystyle \frac{2M_2}{\max \left(\left|M_1\right|,\left|M_3\right|\right)}},$$

(9)

$$k={\displaystyle \frac{M^{ISO}}{\left|M^{ISO}\right|+\max \left(\left|M_1\right|,\left|M_3\right|\right)}},$$

(10)

The factor T is utilized to control the characteristics of the constant volume component, while the k parameter serves to assess the expansion component of the source. The values for both parameters are constrained within the range of −1 to 1. A smaller T-value approaches −1 for the CLVD, whereas a larger T-value trends towards 1. Additionally, a lower k-value indicates a more uniform compression degree, whereas a higher k-value suggests a more uniform stretching degree. This study quantitatively demonstrates the magnitude type, and fracture mechanism of the AE moment tensor, applying both quantitative demonstration and qualitative analysis methods.

4. Experimental Results and Analysis

4.1. Analysis of Acoustic Emission Characteristics Under Impact Load

To systematically investigate the fracture and acoustic emission (AE) characteristics of typical rock types under impact loading, we utilized the integrated FISH language function in PFC. Acoustic emission (AE) monitoring was achieved through four dedicated FISH programs. Specifically, the ae_record function scans newly broken contact points at each time step and stores their position, normal force, and shear force variations; the ae_cluster function performs spatiotemporal clustering based on the criteria described in Section 3; the ae_mtensor function calculates the moment tensor components and eigenvalues for each AE event; and the ae_output function outputs event time, position, magnitude, R-value, and T-k parameters for subsequent statistical analysis. In this study, individual contact failure events and their corresponding time and spatial coordinates were first recorded. To replicate the experimental collection principle, where one AE event corresponds to a set of nearly simultaneous microcracks, these contact failure events are clustered into AE events based on their temporal and spatial proximity. If the spatial distance between two contact points is less than R_c and the time interval is less than Δt_c, the two events are merged into a single AE event. In the simulation, R_c is set to twice the average particle radius, and Δt_c is set to 0.1 microseconds. To filter out numerical noise, only clusters containing at least three contact failure events are recorded as valid AE events.

Due to the differences among the six rock types, a quantitative approach was used to quantify and implement the six lithologies in this study. However, the differences between these lithologies are primarily explained qualitatively, with the focus on the distribution of AE source types, AE b-values, and trends observed in the energy-time density.

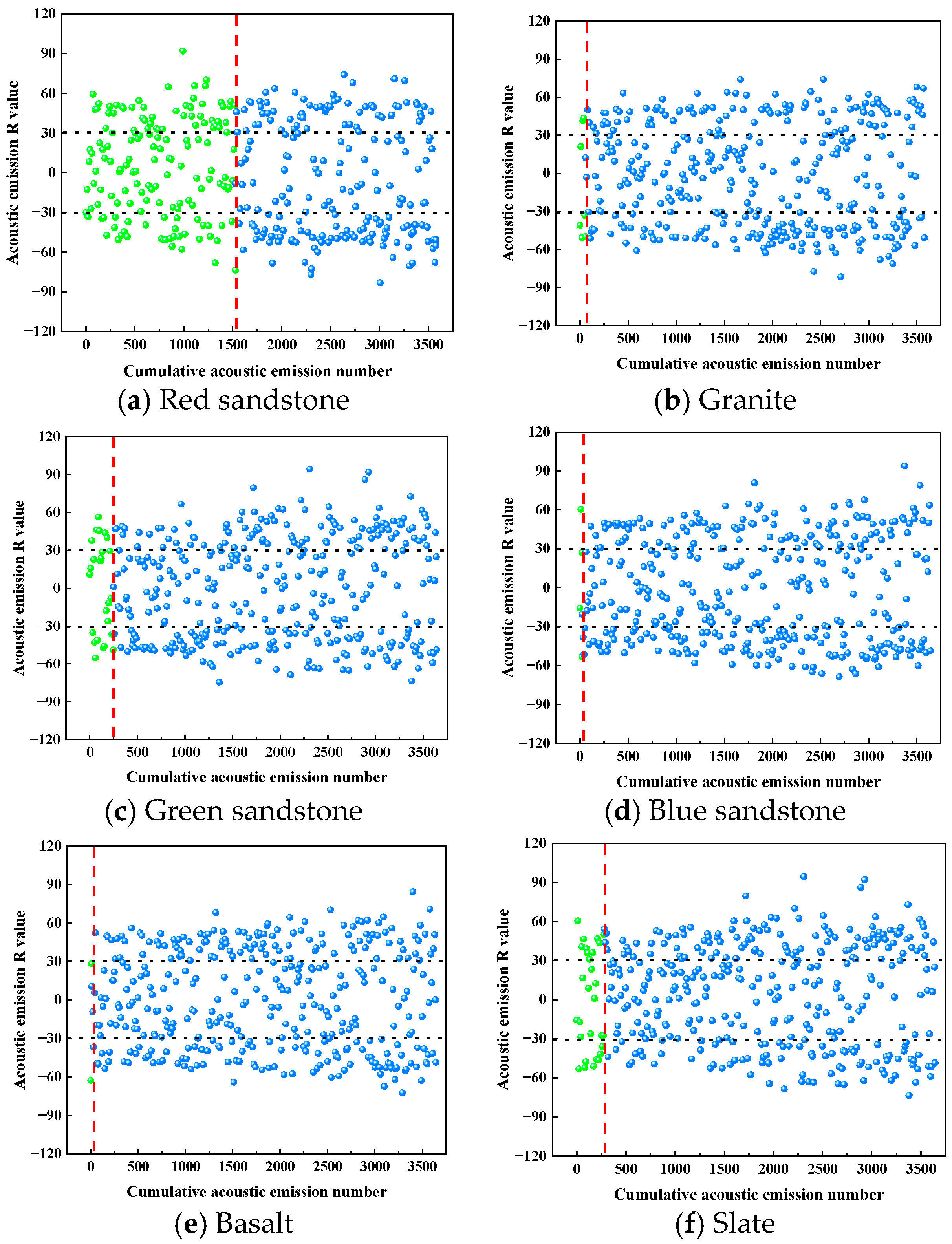
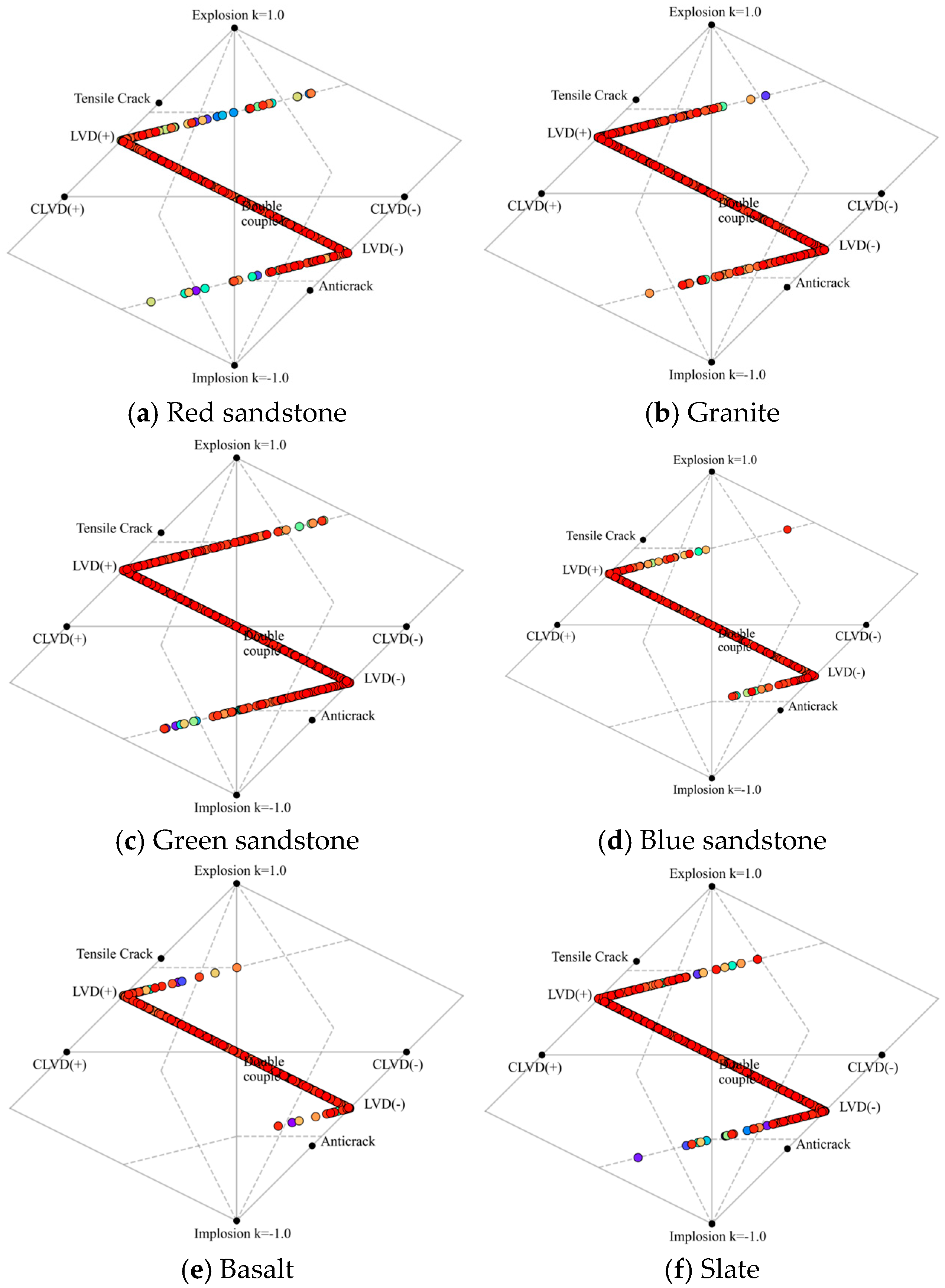
4.1.1. Characteristics of Acoustic Emission R-Value and Distribution of Focal Types

In this study, we systematically recorded and analyzed the variations in the AE event R-values of various rock samples subjected to the same impact load. Figure 6 illustrates the evolutionary trends of the AE R-values for the selected typical rocks.

Under impact loading, the distribution of R-values across various rock samples exhibits an identical pattern, characterized by a relatively scattered and uniform overall distribution. Most values are primarily concentrated within the range of −30 to 30, correlating predominantly with shear-type failures. However, there are notable instances of distributions outside this central range, suggesting the occurrence of tensile and implosion-type failures as well, which indicates that the failure modes of rocks under impact loading are generally multifaceted. Differences in the behavior of rock samples before and after the stress peak under impact load are evident. A greater concentration of R-values is observed before the peak for red sandstone, whereas other rock types display a higher distribution post-peak. This pre-peak concentration in red sandstone suggests that the material has undergone extensive microstructural adjustments before reaching its failure limit. Under these impact conditions, red sandstone is more susceptible to the initiation of micro-cracks, which subsequently lead to macro-fractures. In contrast, other rock types display a tendency to cluster more around the post-peak distribution, indicating a relative resistance to internal micro-crack formation under the same impact conditions. Furthermore, the stress peak correlates with an increase in the severity of AE events during testing, contributing to the escalation of damage within the sample.

Figure 7 and Figure 8 illustrate the distribution of source types and their respective proportions of AE events in typical rocks subjected to impact loads. Through statistical analysis of R-values, source types can be rationally categorized into three groups: tension type, shear type, and implosion type. The differing proportions of these types among various rocks demonstrate the distinct fracture mechanisms inherent to each rock material.

Under impact loading, the spatial distribution of various rock samples exhibits increased density at the boundaries, while the central regions are comparatively less dense. This distribution reveals a tendency for particles to aggregate towards the boundaries and subsequently expand into the interior zone of the samples. This reveals the leading role of boundary stress concentration and intergranular weakening in the impact failure process. The three types of events classified according to the R-value mechanism are shear-type, tensile-type, and implosion-type, which are mixed and interwoven. Overall, the distribution is more concentrated between the grains.

Understanding the fracture process of rocks is crucial not only for assessing their strength and stability but also for comprehending fluid transport and the migration of dissolved chemicals in fractured rock layers. When rocks fracture, the formation of microcracks and the opening of existing cracks significantly increase the material’s permeability, facilitating the migration and diffusion of fluids or contaminants. For instance, in low-permeability rocks such as granite, fractures may create local channels for fluid flow, affecting the diffusion of contaminants (such as water or carbon dioxide) within the rock. The dynamics of contaminant diffusion are influenced by fracture modes, crack propagation rates, and material porosity.

Recent experimental and theoretical studies on anomalous diffusion behavior in natural porous rocks have shown that the connectivity and geometry of microcracks can lead to highly non-Fickian breakthrough curves and heterogeneous concentration fields of contaminants or tracers. As long as the matrix-fracture system exhibits strong heterogeneity and critical connectivity, the tracer breakthrough curve typically deviates from Fickian diffusion, showing early arrival with long-tail drag and accompanying non-Gaussian concentration fields, which can be characterized using continuous-time random walk and fractional diffusion frameworks [45]. Based on the fracture characteristics observed in this study, at least three scenarios directly related to the diffusion of contaminants or reactive fluids can be envisioned: First, in dense rocks such as granite and basalt, where shear dominates and energy release is concentrated, impact loading may trigger a few high-porosity, high-opening dominant channels, leading to pronounced channelized flow and non-Fickian breakthrough curves with “sharp peaks and long tails,” consistent with transport simulation results based on real fracture networks and stress-driven crack propagation [46]. Second, in lithologies with more densely distributed microcracks, such as red sandstone and green sandstone, impact-induced fracture is more likely to form numerous terminally closed branches and weakly connected multi-stage crack clusters, leading to repeated retention and release of solutes, thereby enhancing the long-term tailing and time-scale dependence of the apparent diffusion coefficient. Third, when considering CO₂ or reactive contaminants, impact-induced fractures not only increase effective permeability but also significantly enhance the specific surface area and material exchange flux between the matrix and fractures, potentially forming a reaction-diffusion front controlled by a “fast channel + slow matrix” coupling in different lithologies. These findings suggest that the fracture mechanisms discussed in this study are directly relevant to understanding the propagation and diffusion of water and other reactive fluids in rock fractures.

Under the impact load, the proportion of source shear-type failure across all rock types ranges from 36% to 61%, demonstrating a shear-based failure pattern. In contrast, the proportion of tensile-type failures is between 26% and 32%, exhibiting small fluctuation across various lithologies. This suggests that tensile cracking is not only a significant contributor to rock failure under impact loads but is also influenced by the nature of the impact load and constrained by lithological characteristics. The implosion-type failures account for between 13% and 32%, with some variability; however, the overall proportion is comparable to that of the tensile type, while still showing a notable gap relative to the shear type. This indicates that implosion-type failure is influenced by lithological factors.

Additionally, by combining damage ratio data and distribution characteristics of different rock types under impact loading, it is further demonstrated that rock failure under impact is a complex process influenced by the stratification and structural features of the rock. In this sample set, basalt and red/green/blue sandstones can be considered approximately isotropic at the sample scale, whereas shale, granite, and basalt exhibit clear foliation or preferential mineral alignment. In both laboratory SHPB tests and numerical simulations, the loading direction is along the axial direction of the cylindrical samples. For anisotropic rocks, the effect of impact direction on rock strength and fracture mode characteristics can be further explored in future studies.

4.1.2. Acoustic Emission B-Value Characteristics

The magnitude-frequency relationship of AE events across different lithologies is modeled using the Gutenberg-Richter (G-R) law, allowing for the extraction of the b-value, which elucidates the scale distribution and distinctive characteristics of rupture events.

Figure 9 illustrates the correlation between the cumulative number of AE events, frequency, and fracture strength across various rock samples. The linear trend is derived from curve fitting using the least squares method, with the slope of this linear relationship representing the B-value. As depicted in Figure 9, the fracture strength distribution of AE events for all rock samples is predominantly concentrated between −8.25 and −5.25. The relationship between AE amplitude and frequency exhibits a normal distribution, with AE frequency peaking around the fracture strength values of −7 and −6. This observation suggests that lithology does not significantly influence the distribution of fracture strength. However, a comparative analysis of the B-values across various rock samples reveals the following order: red sandstone (2.35) > green sandstone (2.09) > slate (2.04) > granite (1.89) > blue sandstone (1.87) > basalt (1.70). This indicates that, under impact loading, weakly cemented rocks such as red sandstone and green sandstone tend to generate fewer, smaller AE events, which are mainly characterized by more gradual ruptures and a higher propensity for small-scale fractures. Conversely, under similar loading conditions, strongly cemented rocks like slate, granite, blue sandstone, and basalt demonstrate a greater occurrence of AE events with higher amplitudes. This pattern highlights a more intense and abrupt degree of damage, suggesting that once the main fracture zone is established, it tends to propagate rapidly, aligning with the behavior observed in the sudden instability of dense brittle materials.

4.1.3. Analysis of AE T-K Diagram

To further identify the pivotal mechanism of rock fracture events under impact load, this paper aims to extract a T-k diagram based on the moment tensor decomposition results of AE events.

The T-k diagram disaggregates the source properties of each acoustic emission (AE) event into two independent components: the source moment tensor is divided into volume deformation (k) and compensated linear vector dipole (CLVD) components. The T-k diagrams for various lithologies under impact loading are illustrated in Figure 10. Analysis of the T-k diagram reveals that the distribution of all rock types under impact loading exhibits an inverted Z-shape. AE events are primarily located along the connecting line between LVD(+) and LVD(−), indicating a predominance of single-crack events during this phase. Over time, the point cloud gradually extends toward the CLVD region, suggesting an enhanced interaction between cracks, where micro-cracks interconnect to form a fracture zone, progressing towards macro-instability.

Overall, the dominant fracture mechanism across various rock types during loading is generally tensile fracture. However, the structural characteristics of the rocks significantly influence the distribution patterns of AE events: red sandstone and green sandstone predominantly demonstrate tensile-dominant fractures, characterized by a single mechanism and a broad distribution of events, which implies a more gradual and gentle fracture process. In contrast, slate, basalt, granite, and blue sandstone demonstrate more complex mechanisms accompanied by a higher concentration of events, suggesting that their fracture processes are more localized and explosive. This indicates that anti-cracking and CLVD events are more likely to occur in rocks with well-developed shear and structural planes.

4.2. Study on the Relationship Between Energy-Time Density and B-Value

In the related research of rocks, AE can be employed as a typical means to appropriately examine the evolution of damage and fracture, which can effectively analyze the failure types of rocks. However, in the study of rock characteristics under impact loading, energy characteristics represent a crucial path to methodically analyzing rocks. For this purpose, energy-time density is introduced as an index of energy dissipation rate, and the AE b-value is analyzed correspondingly to explore the energy dissipation characteristics and the corresponding relationship of rock materials when damage and fracture occur.

In Hopkinson’s test, the energy of the incident wave is transmitted to the specimen via an elastic rod. A portion of this energy is reflected and transmitted, while another part is absorbed by the rock specimen itself. The absorbed energy primarily facilitates the development of crack propagation within the rock. A minor fraction of the energy is dissipated through various modes, including acoustic, optical, thermal, radiant, and kinetic processes. In this context, the dissipated energy is often negligible. Thus, the rock specimen utilizes the absorbed energy for the deformation and damage processes associated with the expansion of cracks, as a result of energy dissipation. The quantification of this energy can be performed as follows [47]:

$$W_{\mathrm{i}}={\displaystyle \frac{A_0}{{\rho }_0{C}_0}}{\displaystyle {\int }_0^t{\sigma }_{\mathrm{i}}^2}(t)\mathrm{d}t,$$

(11)

$$W_{\mathrm{r}}={\displaystyle \frac{A_0}{{\rho }_0{C}_0}}{\displaystyle {\int }_0^t{\sigma }_{\mathrm{r}}^2}(t)\mathrm{d}t,$$

(12)

$$W_{\mathrm{t}}={\displaystyle \frac{A_0}{{\rho }_0{C}_0}}{\displaystyle {\int }_0^t{\sigma }_{\mathrm{t}}^2}(t)\mathrm{d}t,$$

(13)

$$W_{\mathrm{d}}=W_{\mathrm{i}}-W_{\mathrm{r}}-W_{\mathrm{t}},$$

(14)

where W_i, W_r, W_t, and W_d, are incident, reflected, transmitted, and absorbed energies, respectively; in addition, σ_i, σ_r, and σ_t in order are incident, reflected, and transmitted stresses, A₀ is the cross-sectional area of the rod, C₀ is the elastic wave velocity in the compression rod, and ρ₀ is the density of the elastic rod.

To minimize the effect of specimen volume, the energy dissipated per unit volume is defined as the energy density:

$$U_d={\displaystyle \frac{W_d}{V}},$$

(15)

where U_d is the energy density, W_d is the absorbed energy, and V is the volume.

Energy-time density reflects the energy dissipation per unit volume of rock in unit time, which is commonly formulated by [48]:

$$E_{VT}={\displaystyle \frac{U_d}{T}}$$

(16)

where E_VT denotes the energy-time density, U_d represents the energy consumption density, and T is the reflected wave action time.

Figure 11 presents the energy-time density time-history curve for various rocks subjected to impact loading. Green sandstone and red sandstone exhibit the highest peak energy-time densities, at 0.00128 J·cm⁻³·ms⁻¹ and 0.00163 J·cm⁻³·ms⁻¹, respectively, and demonstrate superior energy dissipation capacity. This suggests a violent release during the fracture phase and a significant degree of fragmentation under loading. In contrast, the peak energy-time densities of blue sandstone, granite, slate, and basalt are relatively lower, at 0.000835 J·cm⁻³·ms⁻¹, 0.00089 J·cm⁻³·ms⁻¹, 0.00114 J·cm⁻³·ms⁻¹, and 0.000764 J·cm⁻³·ms⁻¹, respectively, indicating moderate energy dissipation capacity and a more gradual energy release during the fracture stage of the loading process. Red sandstone and green sandstone reach their peak energy-time density later compared to other rocks, primarily due to the more pronounced gradual expansion and slow accumulation of microcracks in these two rock types, and also exhibiting a more progressive fracture pattern, consistent with the b-value study in acoustic emission research.

The overall trend observed across all rock types follows a consistent pattern: the energy-time density initially increases to a peak, subsequently declines, and ultimately stabilizes, embodying the characteristic energy evolution behavior of rocks—namely, “first increasing, then decreasing, and finally stabilizing”.

Figure 12 illustrates the data diagram depicting peak energy-time density alongside the AE B-value for various typical rock types. Both red sandstone and green sandstone have peak energy-time densities of 0.00128 J·cm⁻³·ms⁻¹ and 0.00163 J·cm⁻³·ms⁻¹, respectively, and AE B-values of 2.35 and 2.09. Both of these values are relatively high, suggesting that these lithologies are primarily characterized by their high energy dissipation capacity and the occurrence of low-amplitude AE events. This further indicates a prevalence of numerous small-scale fractures within these rock types. In contrast, slate, granite, blue sandstone, and basalt exhibit comparatively lower energy dissipation capacities and the presence of large-amplitude AE events, implying a tendency toward the formation of fewer, large-scale fractures. At the same time, this supports the finding that there is a certain correlation between the energy-time density and AE B-value under impact loading in rocks.

5. Conclusions

This study presents a coupled two-dimensional FLAC–PFC model, utilizing the discrete element method and moment tensor method to investigate the fracture behavior and energy dissipation characteristics of different rock types under dynamic loading conditions. Compared to previous studies that typically focus on a single lithology or quasi-static loading, the main innovation of this work lies in the cross-lithology analysis of moment tensor-based AE characteristics under impact loading, as well as the introduction of an energy–time density metric that further combines dynamic energy dissipation characteristics with acoustic emission features. The key findings of this study can be summarized as follows:

(1)

Under impact loading, the R-values for each lithology display considerable variability and are generally uniform, indicative of a typical composite failure mechanism. The R-values tend to cluster before the stress peak, suggesting that the material undergoes significant microstructural adjustments before reaching peak stress, resulting in an increased presence of microcracks. The variations in rock types do not appear to influence the distribution characteristics of R-values under impact loading; however, they do affect the failure characteristics observed before and after the stress peak.

(2)

During impact loading, seismic sources associated with lithologies exhibit a greater density at the boundaries, demonstrating a pattern of aggregation from the boundary into the interior of the sample. The observed distribution features are almost intricate, mainly characterized by shear–tension–implosion interactions, with point clouds predominantly located at grain–grain interfaces. This reflects the critical roles of stress concentration and interface weakening in facilitating impact failure. Notably, the proportion of shear-type sources ranges between 36% and 61%, indicating that tensile cracking is the predominant mode of rock failure.

(3)

The AE fracture strength across different lithologies primarily ranges from –8.25 to –5.25, with peak frequencies situated between –7 and –6. The B-values for lithologies under study obey the following order: red sandstone > green sandstone > slate > granite > blue sandstone > basalt. The T-k diagram evolves in an inverted “Z” shape, with initial AE events distributed along the LVD (+)-LVD (–) line, dominated by singular crack types. As loading advances, the distribution gradually extends into the CLVD region, signifying an enhancement in crack interactions that culminates in the formation of a fracture zone, leading to macro instability. Rocks possessing a loose structure are more predisposed to progressive failures driven by tensile fractures, while those exhibiting a dense structure or pronounced weak surfaces tend to exhibit more complex failure mechanisms, primarily dominated by CLVD or reverse fractures.

(4)

The time–density plots of all rock types almost reveal a steady trend of initially increasing, followed by a subsequent decrease. There exists a correlation between the peak value of energy–time density and the B-value. Rocks characterized by high energy dissipation capacity predominantly display small-amplitude AE events and small-scale fractures, whereas rocks with lower dissipation capacity are primarily associated with large-amplitude AE events and substantial fractures.

(5)

It is important to emphasize that there are several limitations in the study, and the numerical results reported here are based on the two-dimensional PFC2D–FLAC model. Since the specimen is approximately in a plane strain state, it may not fully capture the out-of-plane crack branching. In the simulation process, only one random seed was used for each rock type. Future work should involve repeated simulations using multiple random seeds to account for statistical variability. However, this method fails to capture the potential out-of-plane crack branching and the full three-dimensional distribution of dissipated energy. Future work will extend the current approach to three-dimensional coupled PFC–FLAC simulations and incorporate statistical analysis to better quantify the material properties and fracture behavior of different rock types. This will further validate and refine the conclusions drawn in this study.