Timing Usage of Technical Analysis in the Cryptocurrency Market

Abstract

The cryptocurrency landscape underwent significant changes in 2024 with the regulatory approval of spot Bitcoin ETFs, opening the market to institutional investors and millions of new clients. As Bitcoin reached new price peaks, the market attracted many retail traders using speculative approaches, evidenced by the surge in meme coins at the end of 2024. In such an environment, properly examining trading strategies can offer substantial advantages over the majority of market participants. Many traders, however, fail to test their strategies adequately, limiting evaluations to selected time periods and risking overfitting. This paper introduces the Rolling Strategy–Hold Ratio (RSHR), which uses a rolling-window approach to evaluate how strategies would perform from thousands of different starting points. This method helps mitigate recency bias and provides a more comprehensive understanding of strategy performance across diverse market conditions and cycles. By comparing strategies results against buy-and-hold results, traders can make informed decisions about whether to refine their strategies further or opt for index-based investing or alternative analytical methods. This study demonstrates the RSHR’s applications across technical, on-chain, sentiment analysis, and dollar cost averaging strategies, with initial research suggesting potential applications in traditional markets.

1. Introduction

The cryptocurrency landscape underwent a transformational shift in 2024, marked by significant institutional acceptance. The watershed moment occurred on 10 January, when the U.S. Securities and Exchange Commission granted approval for eleven investment firms to offer spot-based Bitcoin ETF funds, including industry leaders BlackRock and Vanguard Group, organizations that collectively manage assets exceeding $30 trillion and serve a client base numbering in the tens of millions [1]. Following this regulatory milestone, BlackRock published strategic guidance titled “Bitcoin: A Unique Diversifier,” highlighting Bitcoin’s exceptional portfolio diversification characteristics and recommending a modest 1–2% capital allocation, noting that even this conservative positioning could substantially impact Bitcoin’s valuation if widely implemented across institutional portfolios [2]. This institutional endorsement contributed to Bitcoin’s price trajectory, which exceeded $100,000 for the first time by December 2024 [3].

The momentum continued into 2025, with cryptocurrency market participation expanding substantially in response to appreciating asset values, corporate adoption acceleration, and supportive regulatory policies from the Trump administration [4]. This participation surge parallels the patterns observed in 2022, when the retail investor base in cryptocurrency markets expanded by millions [5]. Despite the increasing sophistication of trading infrastructure, analysis of exchange user data and search trends indicates that most new market participants lack familiarity with advanced analytical methods [3,6]. This knowledge gap creates vulnerability similar to that observed in traditional financial markets, where research indicates approximately 70–80% of retail investors experience losses when employing leverage [7], a risk particularly pronounced in the inherently volatile cryptocurrency ecosystem.

Many of these traders, including both newcomers and seasoned professionals, choose to build their market engagement around algorithms or technical-analysis-based strategies. As shown by the authors in the article “Effectiveness of the Relative Strength Index on the Cryptocurrency Market,” under certain market conditions, properly applied TA can offer a tangible edge [8]. Nonetheless, a substantial portion of users fall victim to overfitting—tailoring their strategies so precisely to historical data that the approach underperforms in live markets [9]. Moreover, inappropriate testing methods, such as using overly short or unrepresentative historical periods, often lead to misleading conclusions about a given technique’s viability.

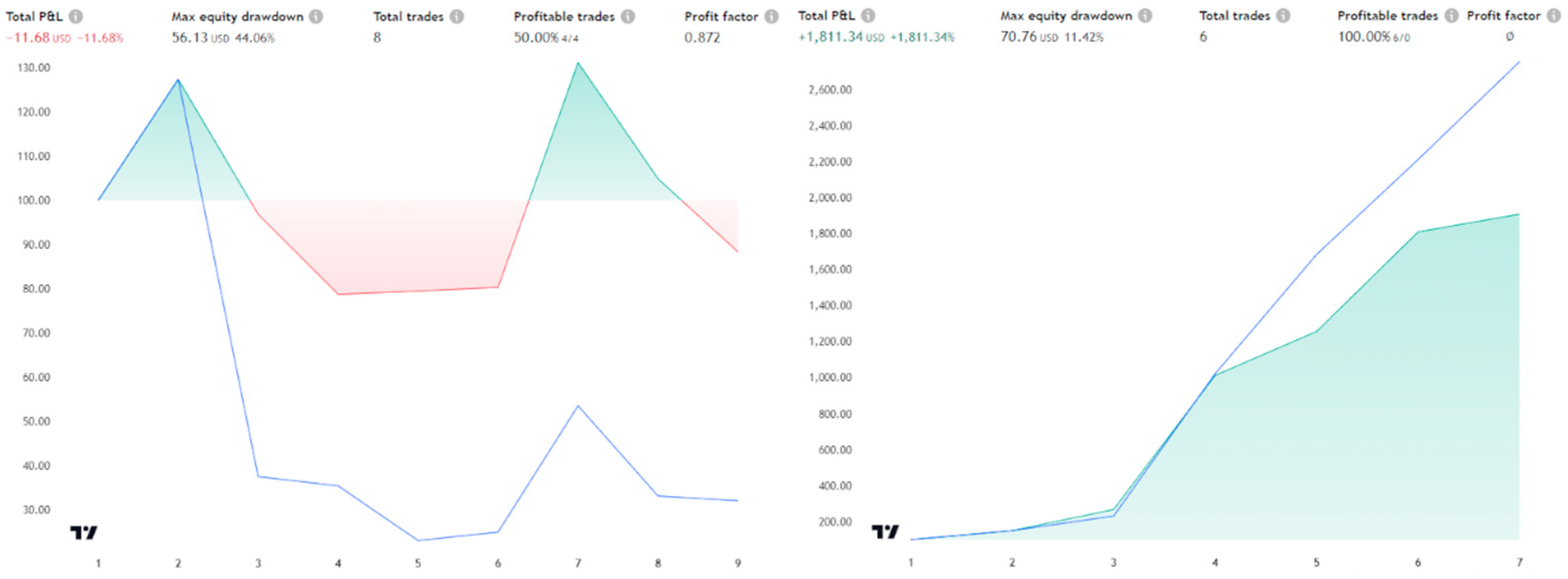
Most traders who assess the effectiveness of their chosen trading strategy measure its performance from the inception of the relevant index or from an arbitrarily selected start date, extending through the current day. This is also the default backtesting method on widely used platforms for building one’s own strategies (e.g., TradingView), which serves millions of users daily [10]. However, such an approach carries a significant risk of period bias: even a small shift in the examined timeframe can yield dramatically different outcomes. For example, Figure 1 illustrates a single strategy achieving stellar results during a bear market but performing poorly in a bull market, thereby putting traders at risk of losses or causing them to abandon an otherwise promising approach.

An alternative to this solution is the use of rolling metrics, also referred to as moving-window calculations, which are frequently employed in finance to track how various performance and risk indicators evolve over time. Rather than utilizing the entire dataset to produce a single estimate, rolling metrics repeatedly compute statistics over a shorter, fixed-length interval that is shifted successively by one period [11,12]. This approach not only mitigates the noise introduced by isolated outliers but also reveals subtle shifts in performance or risk profiles under different market regimes. It is also commonly applied in genetic algorithms for market research and related methods [13,14].

In this paper, authors present the Rolling Strategy–Hold Ratio (RSHR), a method developed for evaluating trading and investing strategy performance. The presented method enables comprehensive analysis of an examined strategy’s performance in all historical market conditions by employing a rolling window approach. In essence, the strategy is evaluated every candle, after playing with the chosen strategy and consecutive number of candles, which allows users to assess the strategy’s simulation-based outcomes when starting at any date in the index’s history, examine the historical maximum gains and risks associated with using a given investment technique compared to buy-and-hold, and compare the strategy’s performance against a traditional buy-and-hold baseline. This multi-faceted perspective not only reveals the market conditions under which a given system works best but also identifies periods that pose substantial risks. Although this method was initially conceived for the cyclic cryptocurrency market, preliminary tests indicate that it may also prove effective in more conventional market contexts, including emerging stock markets.

Our research framework applies sophisticated signal processing methods to cryptocurrency market data, conceptualizing price movements and technical indicators as complex time-series signals requiring specialized analysis techniques. The Rolling Strategy–Hold Ratio (RSHR) method incorporates digital signal processing principles to extract meaningful patterns from highly volatile market data streams.

To rigorously examine the solutions presented in this publication, the authors developed a model simulating the functionality of a cryptocurrency exchange and deployed a broad range of strategies, timeframes, and cryptocurrencies. Detailed experiments were then conducted, with outcomes compared against widely accepted market beliefs and commonly employed technical-analysis-based trading evaluation methods and more mature markets. Drawing from these findings, the authors derived practical conclusions and constructed an instruction manual for using the new tool, one that can significantly reduce the risk of choosing an unsuitable trading or investing strategy.

The remainder of the paper is organized in the following manner: Section 2 offers an overview of related studies and describes previous works that form the foundation for this novel solution. Section 3 introduces the presented method. Section 4 articulates the market and exchange presumptions made during the research. Section 5 presents the results of research and examples of potential usage of the presented method. Section 6 encapsulates the paper’s conclusions.

2. Related Work and Motivation

In the authors’ previous research, “Effectiveness of the Relative Strength Index Signals in Timing the Cryptocurrency Market,” one of the main challenges involved selecting an appropriate time period that would test the solution across a diverse range of market conditions [8]. The research team initially used a fixed time interval corresponding to a single Bitcoin market cycle, which in theory allowed evaluation across all market conditions experienced by Bitcoin. However, this approach limited their ability to analyze how the strategy performed during specific market phases. Additionally, extending the analysis across multiple market cycles would have made it difficult to determine how the strategy behaved within each individual cycle [15]. These limitations motivated the authors to explore and develop rolling window analytical frameworks, which address the constraints of fixed-period analysis while providing more detailed performance evaluation across different market conditions.

A prime example of a rolling metric is the Rolling Sharpe Ratio, which extends the Sharpe Ratio first introduced by William F. Sharpe in 1966 [16]. The Sharpe Ratio evaluates the excess return of an investment—above the risk-free rate—relative to its volatility. By computing this measure over a moving window (e.g., a 12- or 36-month period), one obtains a time series of Sharpe values that reveals how a strategy’s risk–return trade-off behaves under evolving market conditions [17]. Practitioners employ these rolling estimates to identify periods of abnormal performance, facilitate ongoing risk assessment, and detect whether strong overall results stem from consistent long-term gains or sporadic, short-lived spikes in returns.

A simplified alternative to the proposed indicator is Rolling Returns (RR). This measure indicates the strategy’s performance relative to its initial portfolio value. Evaluating results in this manner provides a more absolute sense of gains or losses and is particularly useful in traditional markets or other environments with lower growth than cryptocurrencies [18]. By focusing on changes in the initial portfolio value, RR can help investors gauge how well a strategy performs in less volatile or rapidly rising markets. The authors observe, however, that while this information has value, significantly more actionable insight comes from understanding how a selected strategy performs relative to a benchmark index when evaluating trading and investment strategies, particularly within the context of Bitcoin and the broader cryptocurrency market ecosystem.

The authors’ objective is to present an alternative to conventional strategy evaluation methods that substantially mitigates the utilization of predetermined testing timeframes. Technical analysis represents a primary domain where practitioners may derive significant benefit from the proposed analytical framework. Historical academic investigation has established evidence supporting technical analysis efficacy within conventional financial systems. Notable research contributions by Kuang and colleagues, alongside Jegadeesh’s work, have documented these findings [19,20]. Conversely, scholarly perspectives from researchers such as Allen and Taylor present arguments challenging technical analysis utility [21]. This academic dichotomy has shifted contemporary research’s focus predominantly toward developing economies [22,23], where empirical evidence suggests the possibility of generating superior returns through technical methods under specific market conditions. The authors’ previous publication, “Effectiveness of the Relative Strength Index Signals in Timing the Cryptocurrency Market,” similarly identified potential validity for technical analysis application within cryptocurrency markets [8]. Contemporary trading methods frequently incorporate fundamental technical instruments including the Moving Average Convergence Divergence (MACD), Relative Strength Index (RSI), Simple and Exponential Moving Averages (SMA, EMA), alongside newer trend identification systems such as the Supertrend indicator [24,25,26].

Another area of market analysis where the new solution may prove particularly advantageous is on-chain analysis. On-chain analysis involves examining data recorded on a blockchain to gain insights into network activity, investor behavior, and overall market sentiment [27,28]. Because blockchains store public and immutable transaction records, analysts have access to a wealth of real-time data to inform investment decisions [29]. Common on-chain metrics include exchange inflows and outflows, transaction volume, active addresses, and the cost of mining. This last point has gained particular attention from researchers such as Charles Edwards of Capriole Investments, who has analyzed how Bitcoin’s production cost encompassing energy consumption and hardware overhead can function as a fundamental floor for price [30]. In essence, the transparency of on-chain data makes the cryptocurrency market significantly more open than most traditional markets, where comparable metrics might be subject to lengthy reporting delays or insider access. Services like Glassnode, CryptoQuant, and Capriole Investments’ dashboards represent a new frontier in data-driven finance, offering specialized tools for exploring how block-by-block events can shape market outcomes [31].

The method may also prove useful in the case of sentiment analysis. Sentiment analysis assesses public opinion and social attitudes toward cryptocurrencies by examining data from social media, forums, news articles, or even Wikipedia pageview counts, as demonstrated by Stolarski [32], to capture shifts in general interest and sentiment over time [33]. Widely used tools include the Fear and Greed Index, which measures market sentiment on a continuum from extreme fear to extreme greed using inputs like volatility, market momentum, and social media trends [34,35]. Other techniques rely on analyzing the frequency of cryptocurrency-related searches (e.g., via Google Trends), monitoring social media engagement (Twitter, Reddit, Telegram), and evaluating the impact of endorsements or critiques by influencers and industry leaders. While these approaches can yield valuable insights, they also carry heightened risk due to rapid shifts in public opinion and misinformation. Consequently, sentiment metrics are best employed alongside additional analytic methods, such as fundamental or on-chain analysis.

The authors believe that Dollar Cost Averaging represents the domain with the most significant practical potential for RSHR implementation, an application frequently overlooked in conventional backtesting methods. Dollar Cost Averaging (DCA) represents an investment method wherein participants deploy predetermined capital amounts at consistent intervals, irrespective of prevailing markets [36]. This structured approach diminishes volatility exposure while limiting emotionally driven decision-making that often characterizes market timing attempts [37]. The strategy confers notable psychological benefits through anxiety reduction and investment discipline reinforcement [38]. DCA’s fundamental mechanism automatically acquires greater asset quantities during price depressions and smaller quantities during price elevations, potentially creating advantageous average acquisition costs over extended implementation periods [39].

The cryptocurrency market presents an ideal environment for rolling window analytical approaches due to its continuous 24/7/365 operation, enabling consistent analysis intervals without interruptions typical of traditional markets. Cryptocurrency exchanges such as Binance and Coinbase serve as the ecosystem’s cornerstone by providing essential liquidity and price discovery mechanisms. They provide competitive trading fees, year-round operation, extensive trading pair availability, and various trading options including leverage capabilities. Through sophisticated Application Programming Interfaces (APIs), they enable direct connection without brokerage intermediaries, facilitating rapid execution and seamless integration of trading algorithms [40,41]. This technological framework, combined with high liquidity and continuous operation, creates unprecedented opportunities for portfolio management through complex trading strategies, potentially generating substantial returns for sophisticated market participants [42].

3. The Rolling Strategy–Hold Ratio (RSHR)

In this paper, the authors present the Rolling Strategy–Hold Ratio (RSHR), a method developed for evaluating trading and investing strategy performance. This analytical framework provides a comprehensive approach to assessing strategy effectiveness against a traditional buy-and-hold benchmark by implementing a rolling analysis window. The RSHR method distinctive feature lies in its dynamic evaluation process, where each trading strategy is effectively reset daily and its performance is measured over a fixed subsequent period, typically one year. This approach enables the analysis of overlapping performance intervals, offering a nuanced understanding of strategy effectiveness across varying market conditions. By continuously recalculating and comparing strategy returns against the passive benchmark, the RSHR provides insights into both short-term performance variations and long-term effectiveness patterns.

3.1. Inspiration

The Rolling Sharpe Ratio (RS) served as an initial source of inspiration for developing the Rolling Strategy–Hold Ratio (RSHR). The RS is widely applied in performance analysis and risk assessment, particularly within diversified portfolios, where it provides a dynamic perspective on how the return-to-risk relationship evolves over time. By computing the Sharpe Ratio for consecutive, overlapping periods (e.g., monthly or quarterly), it helps investors monitor the stability of returns and the effectiveness of risk management practices in a long-term context. This rolling method addresses the limitations of single-period Sharpe Ratio calculations by offering a clearer view of how real-world market fluctuations impact performance in an ongoing manner.

Rolling Returns (RR) served as an additional inspiration for the authors. The metric represented the initial focus of their research efforts. The authors soon recognized that, despite its usefulness, the indicator suffers from similar limitations to the Rolling Sharpe Ratio. Although it successfully determines whether a strategy generates profits, it does not address whether the strategy should be implemented.

While motivated by the Rolling Sharpe Ratio and Rolling Returns concepts, the Rolling Strategy–Hold Ratio (RSHR) shifts the focus toward assessing a strategy’s incremental value compared to a simple buy-and-hold approach as shown on Figure 2. Instead of emphasizing the return-to-volatility perspective, the RSHR aims to give investors a more direct understanding of what returns they might realistically expect from an active trading strategy, including those based on technical analysis. By tracking these overlapping, rolling performance intervals and contrasting them with a baseline buy-and-hold, the RSHR framework makes it easier to determine whether the potential advantages of active market entry and exit decisions justify the extra effort, or if a passive investment posture remains the more effective option in the long run.

3.2. The Rolling Strategy–Hold Ratio (RSHR) Formula

Mathematically, the Rolling Strategy–Hold Ratio (RSHR) at time i can be expressed as follows:

$$\mathrm{R}\mathrm{S}\mathrm{H}{R}_i ={\displaystyle \frac{ \left( \left(Portfolio Valu{e}_i\right) / \left(Portfolio Valu{e}_{\left(i-n\right)}\right) \right)}{\left( \left(Pric{e}_i\right) / \left(Pric{e}_{\left(i-n\right)}\right) \right)}}$$

where

• $Portfolio Valu{e}_i$ denotes the total value of the investment portfolio on candle I;
• $Portfolio Valu{e}_{\left(i-n\right)}$ is the value of that same portfolio exactly n candles earlier;
• $Pric{e}_i$ is the price of a selected instrument (e.g., a stock index) on candle I;
• $Pric{e}_{\left(i-n\right)}$ is the price of that same instrument n candles earlier.

This formula compares the return achieved by the analyzed strategy and the portfolio’s growth over the past n periods, usually 365 days, with the return from a simple buy-and-hold approach for the underlying asset and the asset’s price growth over the same period. As a result, it provides a clearer perspective on how the strategy performs relative to a passive benchmark.

3.3. The Rolling Strategy–Hold Ratio (RSHR) Pine Script Code

The indicator was implemented in Pine Script for the TradingView platform, as it is expected to be the primary environment in which the RSHR will be used. The full source Cited.code is provided below for reproducibility as Algorithm 1.

Algorithm 1. Rolling Strategy–Hold Ratio in PineScript 6

//@version=6 strategy(“Rolling Strategy–Hold Ratio-RSHR–Marek Zatwarnicki”, overlay = false) // INPUT x = input.int(365, minval = 1, title = “RSHR length”) // STRATEGY LOGIC if ta.sma(close, 50) > close strategy.entry(“SMA50”, strategy.long) else strategy.close(“SMA50”) // RSHR CALCULATION portfolio_return = strategy.equity / strategy.equity[x] price_return = close / close[x] rshr = portfolio_return / price_return // PLOTTING RSHR plot(rshr, title = “RSHR”, offset = -x)

3.4. The Rolling Strategy–Hold Ratio (RSHR) Recommended Applications

The researchers advocate for the implementation of the aforementioned indicator primarily as an instrument for evaluating the empirical validity of trading strategies and assessing whether such approaches confer statistically significant advantages, either persistent or transitory, compared to passive index acquisition strategies. Financial market participants frequently allocate substantial temporal resources to the refinement of trading methods that demonstrate efficacy exclusively within circumscribed temporal parameters, typically predetermined through a priori selection processes. The utilization of the proposed indicator may facilitate the avoidance of significant resource expenditure directed toward the development of strategies with limited probability of successful implementation.

Furthermore, the indicator’s application may frequently provide sufficient analytical evidence to prompt investors or market participants to completely abandon certain investment strategies, thereby conserving considerable effort otherwise required for the configuration of automated trading systems and mitigating operational expenditures associated with server maintenance. The researchers’ objective is not to discourage strategic investment approaches but rather to enable rapid evaluation of conceptual frameworks and prioritization of those demonstrating enhanced probability of positive returns. Additionally, this approach may be implemented in conjunction with analyses of cryptocurrency market cyclicality and capital flow periodicity within financial systems.

In summation, the researchers identify three primary applications for the indicator:

• Facilitating quantitative decision-making regarding the implementation of trading or investment strategies versus passive index acquisition approaches;
• Providing analytical support for the selection of strategies demonstrating comparative advantages relative to alternative methods;
• Enabling retrospective analysis of trading and investment strategy performance relative to index benchmarks, with specific reference to Bitcoin market cycles and capital flow dynamics.

The authors intend to initiate a series of follow-up publications aimed at further developing the theoretical foundations and practical applications of the proposed indicator. These future studies will build upon the preliminary findings and exploratory analyses presented in the latter sections of this article, with the goal of systematically exploring the indicator’s performance across different market conditions, asset classes, and analytical contexts. Through these contributions, the authors aim to establish a broader methodological framework for the use of the RSHR in both academic research and practical investment strategy development.

3.5. Combining the Rolling Strategy–Hold Ratio (RSHR) with Other Indicators

The researchers identify substantial potential in the implementation of rolling-type indicators for strategy assessment. Their forthcoming research endeavors will utilize both the fundamental variant of the indicator and various combinations with alternative metrics designed for trading and investment strategy evaluation.

A prime example would be combining the RSHR with the maximum drawdown metric. Specifically, one could analyze a rolling RSHR ratio multiplied by the largest percentage drop in capital over an n-day period. This approach offers insights into both performance relative to a buy-and-hold benchmark and the magnitude of potential losses within the same time window.

This methodological integration represents a significant advancement in comprehensive strategy assessment, allowing for simultaneous evaluation of relative performance and risk parameters. Such multivariate analysis provides market participants with more robust decision-making frameworks than single-metric evaluations.

3.6. Statistical Methods of Interpretation of the RSHR

Similarly to the Rolling Sharpe Ratio, the RSHR serves primarily as a tool for rapid, visual analysis of strategies by experts. While this visual approach provides valuable insights, statistical methods for evaluating strategy effectiveness offer complementary analytical capabilities that can prove particularly effective in strategy parameter selection or when screening entire markets to identify indices with the highest and, most importantly, relatively stable historical returns.

It is important to note that strategy performance is typically assessed using metrics such as the Sharpe Ratio, Profit Factor, and similar indicators. The RSHR however, does not address the question of a strategy’s profitability, but rather the justification for using it in the first place. Therefore, to quickly assess this aspect, one can refer to the average value of the RSHR over the past year or preferably over a longer period, such as four years, which corresponds to a full market cycle in the case of Bitcoin.

To statistically compare different strategies or the same strategy with different parameters, focusing on both performance level and temporal stability, the following tests and measures should be employed:

• Highest Rolling Sharpe Ratio of Rolling Strategy–Hold Ratio—to quantify how consistently each index produced positive risk-adjusted returns;
• One-way ANOVA—to test for significant differences in the mean Rolling Strategy–Hold Ratios across indices, assuming normality and equal variances;
• Kruskal–Wallis test—a non-parametric alternative to ANOVA when the assumptions of normality or homoscedasticity are violated;
• Levene’s test—to compare the variances of Rolling Strategy–Hold Ratios across indices, serving as a measure of performance stability;
• Tukey’s HSD test—to perform post hoc pairwise comparisons after a significant ANOVA result;
• Dunn’s test—to perform post hoc pairwise comparisons after a significant Kruskal–Wallis result;
• Coefficient of variation (CV)—to assess the relative stability of performance across indices by normalizing standard deviation by the mean.

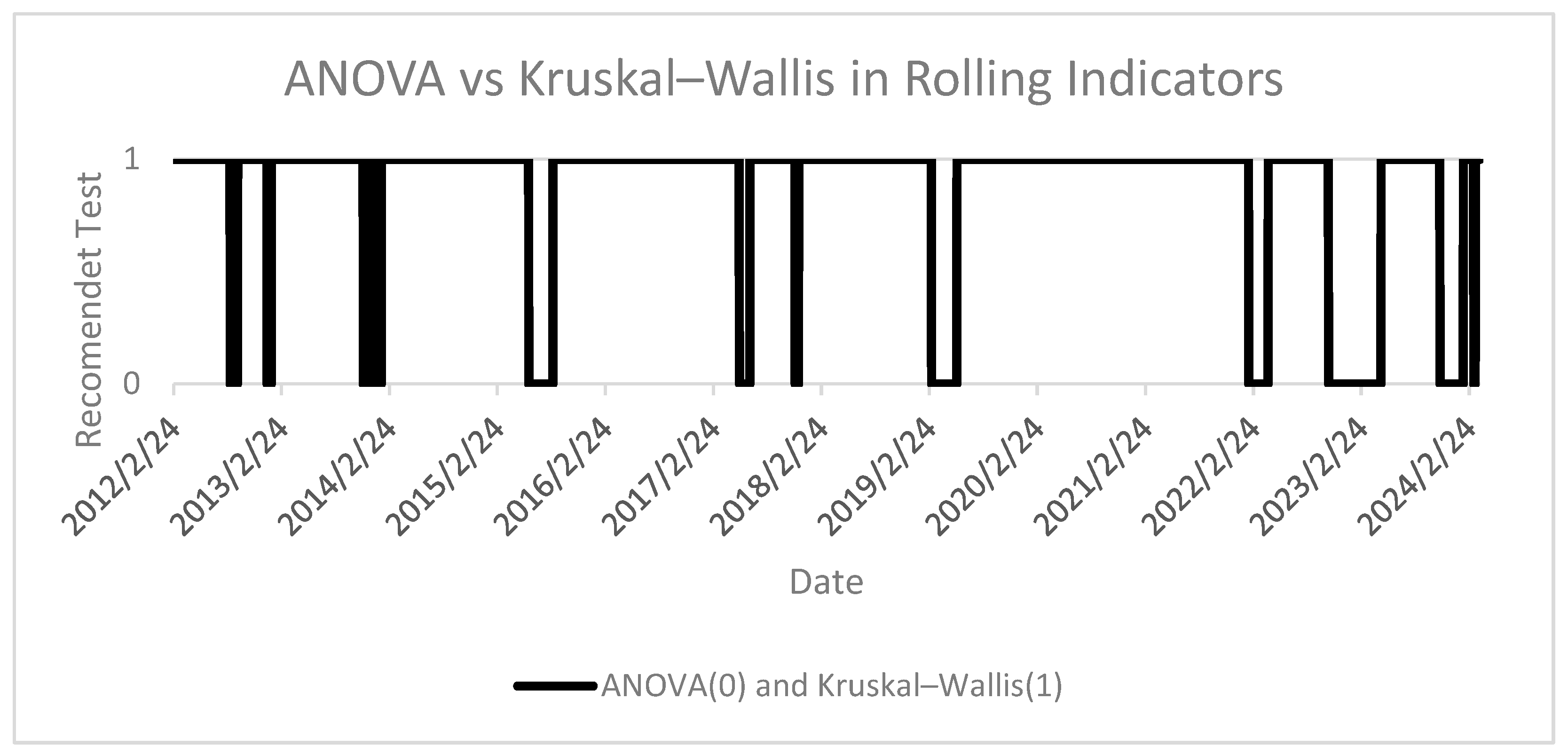
It is worth noting that the fundamental operation of these tests, even in their basic versions, relies on fixed data ranges. For this reason, their use may negate the advantages of utilizing rolling-type tools as shown on Figure 3. The authors encourage the use of these tools also in rolling window versions, and such an example of application will be presented by the authors.

4. The Experiment Assumptions and Initial Studies

The establishment of accurate foundational assumptions is critical when developing investment strategies. These assumptions must reflect the actual market conditions in which investors operate to ensure research validity and practical applicability. After conducting comprehensive analysis of cryptocurrency market conditions and exchange functionalities, the authors have identified key assumption categories that frame their research method.

The subsequent section will detail these foundational parameters that align the research with market realities:

• Selection of the strategies;
• Selection of the instruments;
• Selection of the data range;
• Selection of the time intervals;
• Selection of the exchanges;
• Selection of research method.

4.1. Selection of the Strategies for Empirical Testing

The research method employs a comprehensive framework to assess the versatility and applicability of the proposed analytical model across various trading approaches. By systematically evaluating multiple strategy types derived from fundamentally different analytical paradigms, this study establishes the model’s effectiveness as a universal evaluation tool.

The selected strategies represent the full spectrum of contemporary cryptocurrency trading methods, incorporating technical indicators, blockchain-specific metrics, market sentiment analysis, systematic investment approaches, and contrarian positioning:

• Technical Analysis Indicators: The research evaluates a Simple Moving Average (SMA-50) strategy, which initiates cryptocurrency acquisition when the opening price exceeds the 50-day moving average of closing prices. The strategy was selected due to its popularity and simplicity [43]. Additionally, in strategy selection with statistical methods, the Relative Strength Index (RSI-14) is examined within an oversold market framework, with acquisition signals generated at values below 30 and liquidation signals at values exceeding 70.
• Systematic Investment Approach: The Dollar Cost Averaging method is evaluated, implementing daily acquisitions of 1/365 of the total investment capital, with performance measured relative to initial entry prices.
• On-chain Metrics: The analytical framework incorporates the Spent Output Profit Ratio (SOPR), implementing acquisition when the indicator exceeds 1.0 and liquidation when values fall below this threshold.
• Sentiment Analysis: The research examines the efficacy of the Fear and Greed Index as a decision-making parameter, with acquisition occurring at values exceeding 50 and liquidation at values below this threshold.
• Short Position Strategy: A contrarian approach utilizing the SMA-50 indicator for short positions is examined. The researchers have limited short strategy implementation to specific cases due to the predominantly appreciating market environment and previously documented ineffectiveness.

It is important to note that the presented analytical framework can be applied to any individual indicator or combination of indicators. The strategies evaluated in this study serve as implementation examples rather than investment recommendations from the authors.

4.2. Selection of the Time Intervals for Empirical Testing

The researchers selected a daily interval as the primary timeframe for index analysis. This choice provides a balanced perspective, capturing market dynamics effectively while avoiding potential noise from shorter-term fluctuations. The interval used in the study is counted based on universal time to ensure standardization across all data points.

To demonstrate the versatility of the presented method when applied to higher-frequency trading approaches, the researchers also included a case study based on 4 h intervals. This supplementary analysis employs a rolling window equivalent to one month, effectively illustrating the analytical framework’s applicability to shorter timeframes. This dual-interval approach validates the method’s flexibility across different temporal resolutions while maintaining analytical integrity.

4.3. Selection of the Data Source for Empirical Testing

The research utilizes TradingView as the primary platform for data acquisition and analysis. TradingView represents one of the most comprehensive financial data visualization and analysis platforms available to market participants globally [10]. The platform aggregates market data from multiple exchanges, ensuring a high level of data integrity and consistency across various cryptocurrency pairs.

The researchers selected TradingView due to its standardized data normalization processes, which minimize discrepancies that might otherwise occur when sourcing data from individual exchanges directly. Furthermore, TradingView’s widespread adoption among both retail and institutional investors ensures that the research findings maintain practical relevance to actual market participants.

For on-chain data acquisition, the researchers utilized CryptoQuant, a comprehensive blockchain analytics platform that specializes in providing institutional-grade cryptocurrency intelligence. CryptoQuant offers extensive historical data covering various network metrics, miner activities, and exchange flows, which are essential for implementing sophisticated on-chain trading strategies [44]. The Fear and Greed Index data was obtained from alternative.me, the standard reference source for this particular market sentiment indicator used by both retail and institutional investors.

4.4. Selection of the Instruments for Empirical Testing

Bitcoin provides the conceptual foundation for introducing the new indicator and served as a primary source of inspiration for the creation of the RSHR. Launched in 2009, Bitcoin is the first decentralized digital currency, using blockchain to operate a peer-to-peer network. As of March 2025 it is the largest digital asset globally with a total market capitalization exceeding one trillion dollars. For the experimental phase, Bitcoin price data was sourced from TradingView’s weighted price index across multiple exchanges, accessible under the identifier INDEX:BTCUSD.

To demonstrate the universality of the approach, examples were also applied to the following:

• Digital Asset—Ethereum—Second largest cryptocurrency by market capitalization that introduced smart contract functionality. TradingView name—INDEX:ETHUSD.
• Digital Asset—Cryptocurrency Market ex-BTC/ETH—Aggregate index representing the entire cryptocurrency market excluding Bitcoin and Ethereum. TradingView name—CRYPTOCAP:TOTAL3.

Additionally, to illustrate the method’s broad applicability, examples from traditional markets were evaluated:

• Traditional Market—S&P 500—Stock market index tracking the performance of 500 large companies listed on U.S. exchanges and primary indicator of U.S. market performance. TradingView name—SP:SPX.
• Emerging Market—NIFTY 50—Weighted average of 50 Indian company stocks across various sectors with growth patterns demonstrating certain similarities to Bitcoin’s trajectory. TradingView name—NSE:NIFTY.
• Precious Metal—Gold—Humanity’s oldest store of value representing the largest precious metal asset class by market capitalization. TradingView name—TVC:GOLD.
• Currency Pair—Euro/Dollar—Exchange rate between two of the world’s most traded currencies with high liquidity and global economic significance. TradingView name—FXCM:Euro/U.S. Dollar.
• Commodity—Crude Oil—World’s primary energy commodity and fundamental input for industrial production reflecting complex geopolitical and economic factors. TradingView name—TVC:USOIL.

For traditional markets, the rolling window was configured to span 252 days, representing the average number of annual trading days between 2000 and 2025.

4.5. Selection of the Data Range for Empirical Testing

The analytical approach presented in this paper does not require predetermined or arbitrary date ranges. Consequently, the research encompasses the complete historical data of the Bitcoin market and altcoin markets, excluding only the initial periods necessary for indicator value calculations.

For traditional market instruments the testing period begins from the dot-com bubble burst (10 March 2000). This starting point represents an ideal threshold for analysis as it marks the beginning of modern electronic trading prevalence. Prior to this period, markets demonstrated lower levels of accessibility and reduced automation, which would create potential methodological inconsistencies in the comparative analysis. The post-2000 timeframe better reflects contemporary market dynamics characterized by high-frequency algorithmic trading and broader retail participation.

The research method will also place significant emphasis on analyzing market cyclicality, both within the Bitcoin ecosystem and across traditional financial markets. This cyclical analysis provides valuable insights into strategy performance across varying market conditions and economic cycles.

4.6. Selection of the Exchange Parameters and Simulation Assumptions for Empirical Testing

In any market research, establishing assumptions regarding broker operations is essential—or in the case of cryptocurrencies, the exchange platform where simulations are conducted. The following parameters were adopted in the researchers’ simulations:

• Initial Capital: The experiments conducted incorporated an initial capital of $100 to match percentage growth measurements. Given Bitcoin’s subdivision into 100,000,000 Satoshi, it is possible to purchase a fraction of Bitcoin that closely matches any fiat currency value [45]. For traditional markets, to simplify calculations and facilitate easier comparison of results, the researchers assumed the use of ETFs.
• Fee Structure: The fee value for this analysis was determined based on the standard spot market fees of Binance and other large cryptocurrency exchanges, which equates to 0.1% of the transaction value. For traditional markets, a fee of 0.05% was applied.
• Market Impact: This study did not account for slippage or the potential impact of large orders from the simulated trader on the market dynamics, due to the research being conducted on relatively large and liquid markets. For plans involving high investment amounts in less liquid markets such as altcoin markets or operations on very low time intervals, the authors recommend prior estimation of the impact of one’s own investments based on order book depth or adding a constant additional fee to simulate slippage. For operations involving substantial capital amounts, the authors additionally recommend employing the same strategy with similar but varying parameters to partition investments into smaller tranches without materially impacting overall performance outcomes.
• Execution Latency: The researchers did not factor in delays associated with data retrieval, calculations, and subsequent order execution on the exchange platform. In the conducted experiment, the purchase and sale operations using the server took less than one second, which statistically should not affect the experimental results.
• Trading Metrics: Due to the instantaneous calculations achieved through the Automated Trading System (ATS), the opening values of market indices were used for all calculations.
• Taxation: Due to varying regulations across different countries, tax considerations were omitted from the analysis.

4.7. Selection of Research Method for Empirical Testing

The exhaustive search method was used to obtain a complete set of combinations of the results found for the strategies [46,47]. This method is sufficient for simple strategies, with no more than a few analyzed indexes. In the case of the advanced strategies that use more parameters, it is recommended to use a more sophisticated approach, such as evolutional algorithms, discrete optimization techniques, etc. [48]. The method of evaluating the obtained results in the case of using both techniques remains similar. For the purpose of thoroughly evaluating the indicator, the research team conducted approximately 50,000 distinct simulations across various market conditions and parameter combinations.

5. Results of the Experiments and Discussion

When deciding to invest in financial markets, the investor or trader tries to make the trades as good as possible. The trading strategy should minimize the risk while maximizing profits. Proper knowledge and research can allow traders to choose the best solutions. The wide range of the uses of the RSHR was examined in order to understand its strengths and weaknesses. The results were confronted with the generally prevailing opinions.

5.1. The Research Environment

To begin the experimental phase, the authors built a cryptocurrency exchange simulation in Python 2024.3.1.1 that accurately reflected how actual exchanges function during the study period. This simulation allowed for transactions based on price movements and volume data from the selected market indices. The authors developed an automated trading system (ATS) that independently executed trades when specific technical analysis conditions were met [46]. This approach allowed them to efficiently analyze large datasets spanning extended time periods, which was essential for their comprehensive research goals. After completing the initial data collection, the authors analyzed the results to identify the most effective ways to implement the selected analytical components.

For quick calculation of technical analysis indicators, the authors used Pine Script from the TradingView platform. This specialized programming language is designed specifically for developing custom indicators, creating trading strategies, and visualizing market data. Pine Script’s efficient structure helped them handle the computational requirements of calculating multiple indicators across extensive historical datasets, which significantly enhanced their analytical capabilities.

The chapter has been organized into six distinct subchapters. Each subsequent section examines all experimental results derived from different classes of market indices. The subchapter structure is as follows:

• RSHR in comparison with solutions from the literature;
• RSHR in parameter selection;
• RSHR in Dollar Cost Averaging;
• RSHR on lower timeframes, sentiment analysis, and on-chain analysis;
• RSHR in Ethereum and altcoin markets;
• RSHR in traditional financial markets.

5.2. RSHR in Comparison with Solutions from the Literature

The following subsection introduces the RSHR and illustrates how it compares to similar indicators found in the literature, as well as to the price dynamics. The illustrative RSHR implementations examined using annual settings include the following:

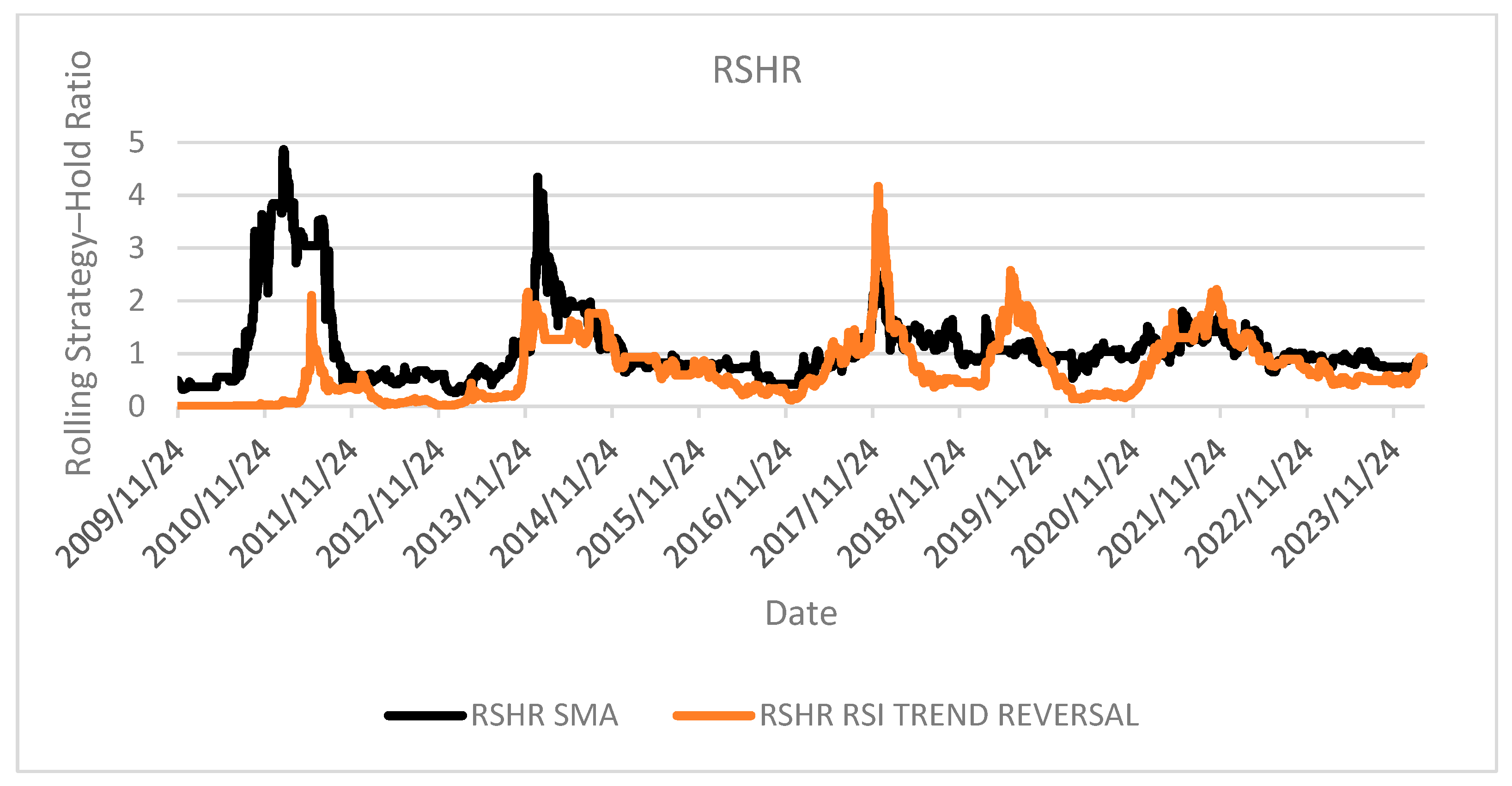
• RSHR of Bitcoin SMA50 strategy;
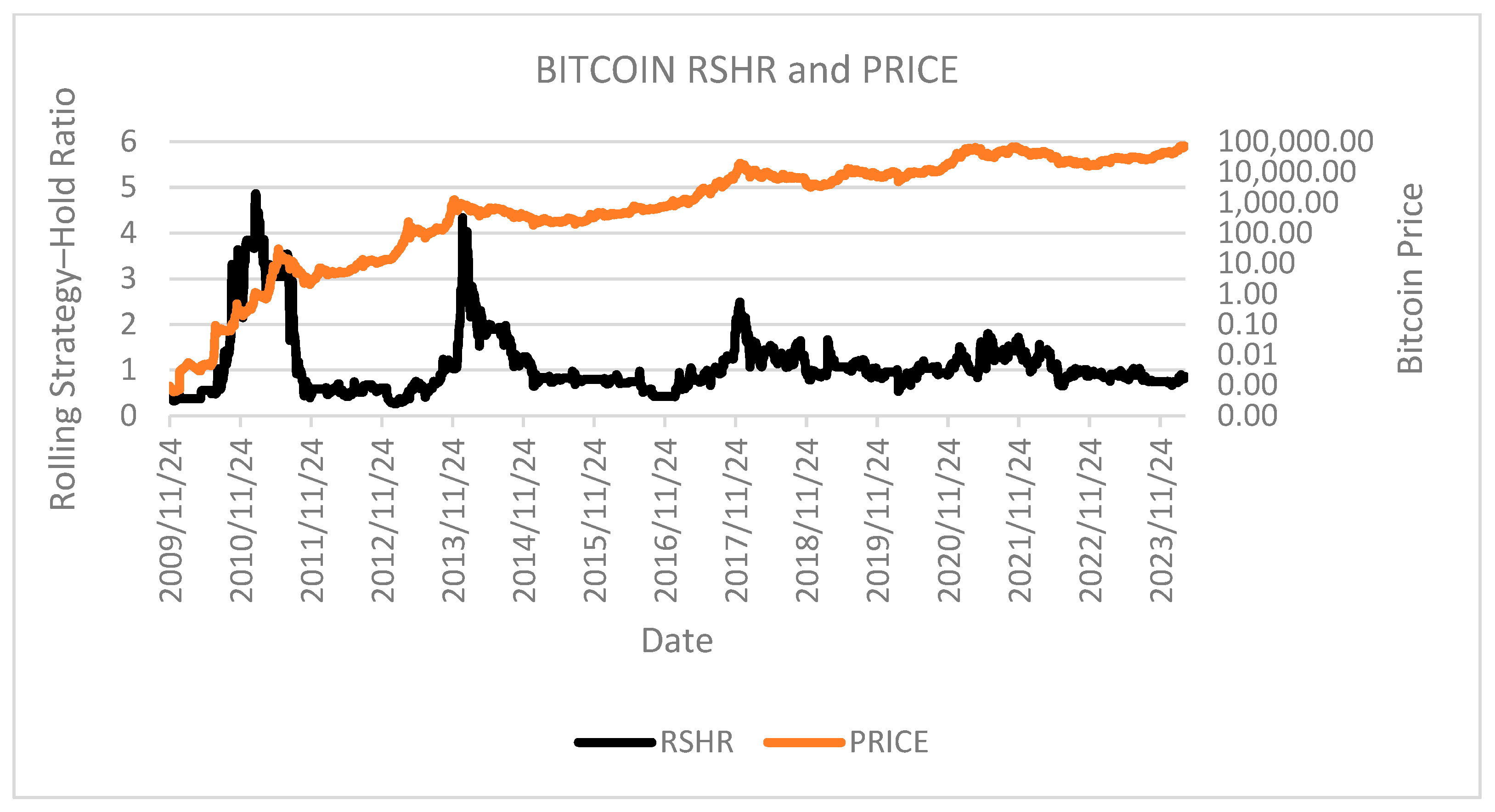
• RSHR of Bitcoin SMA50 strategy compared with Bitcoin price;
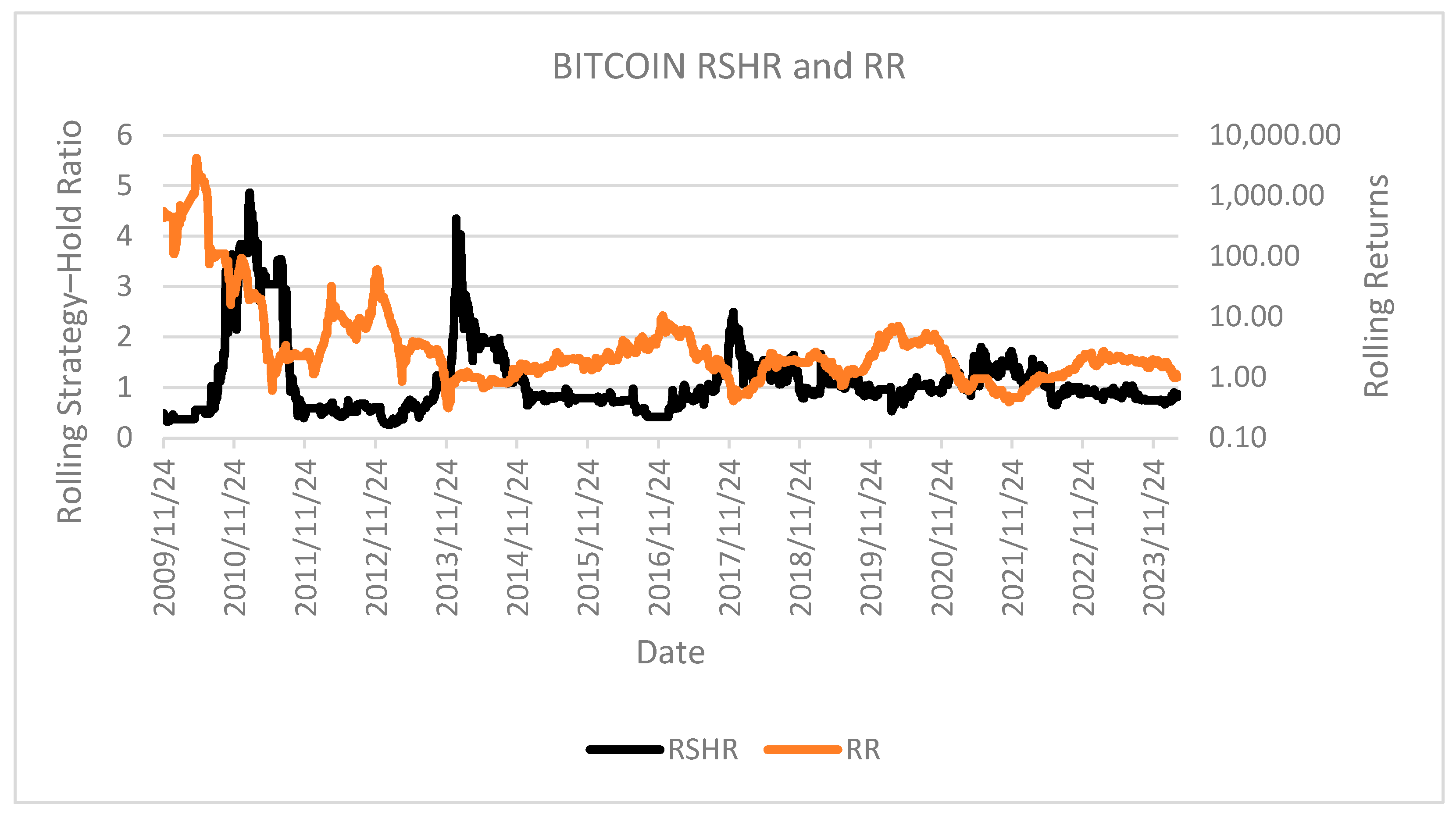
• RSHR of Bitcoin SMA50 strategy compared with Rolling Returns;
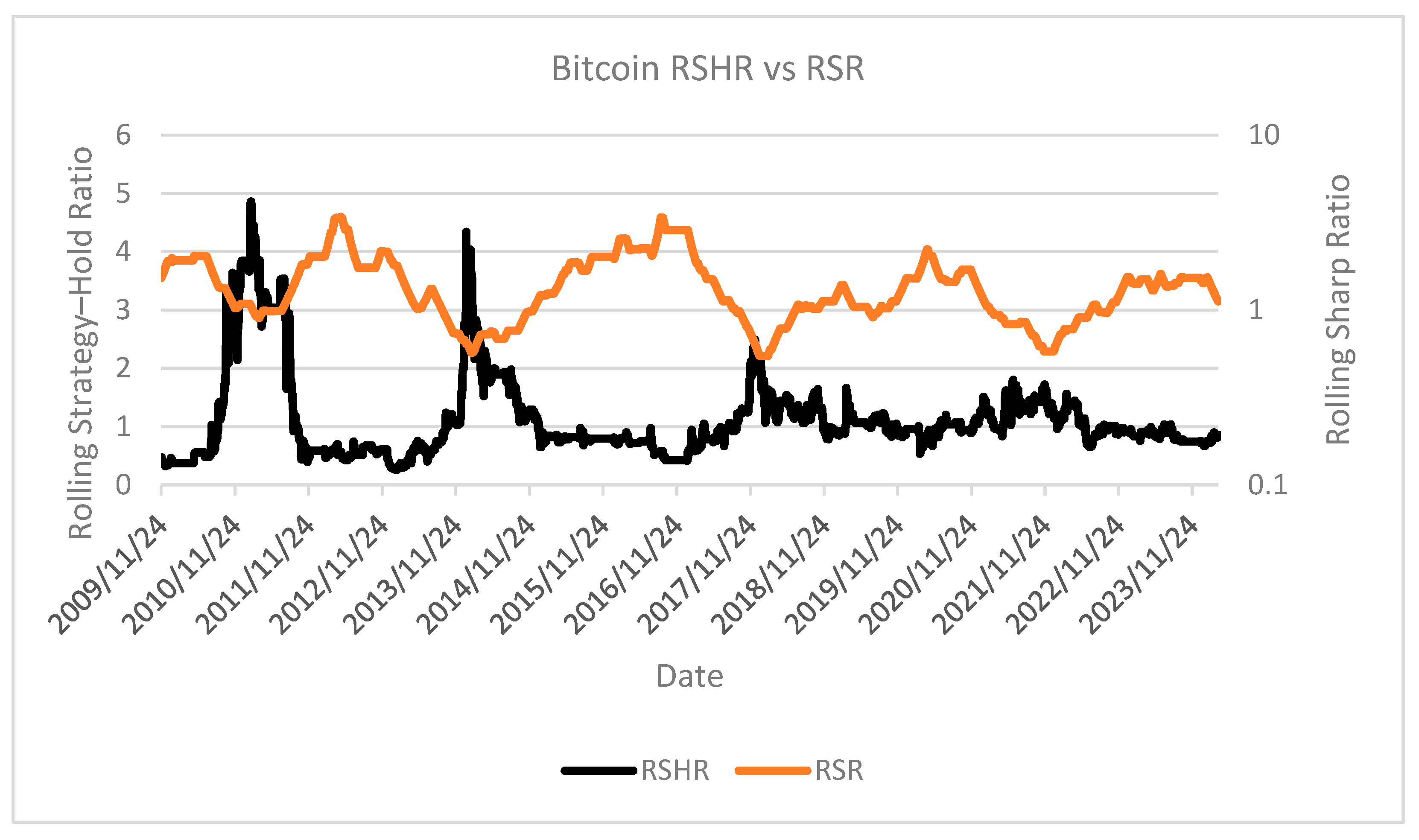
• RSHR of Bitcoin SMA50 strategy compared with Rolling Sharpe Ratio;

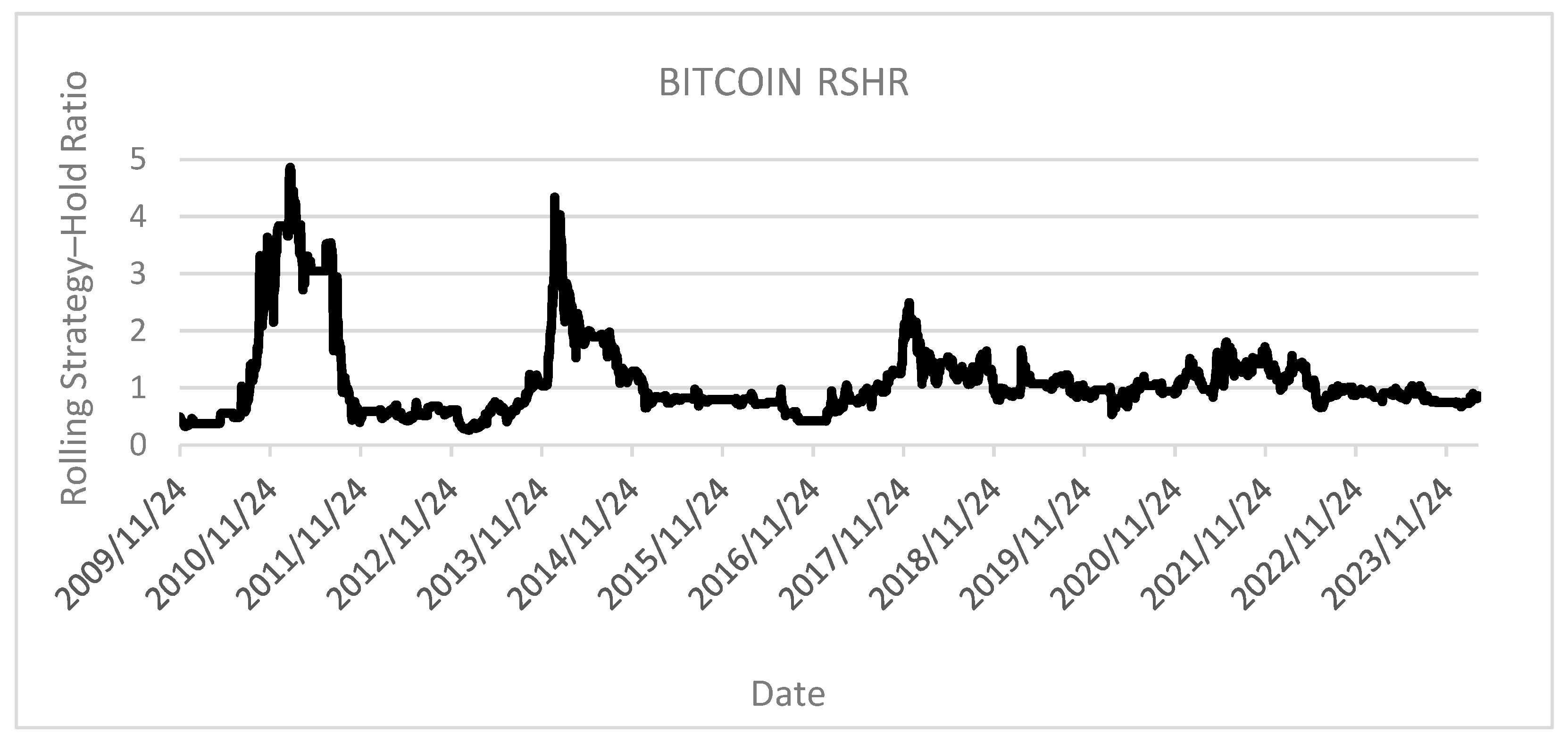
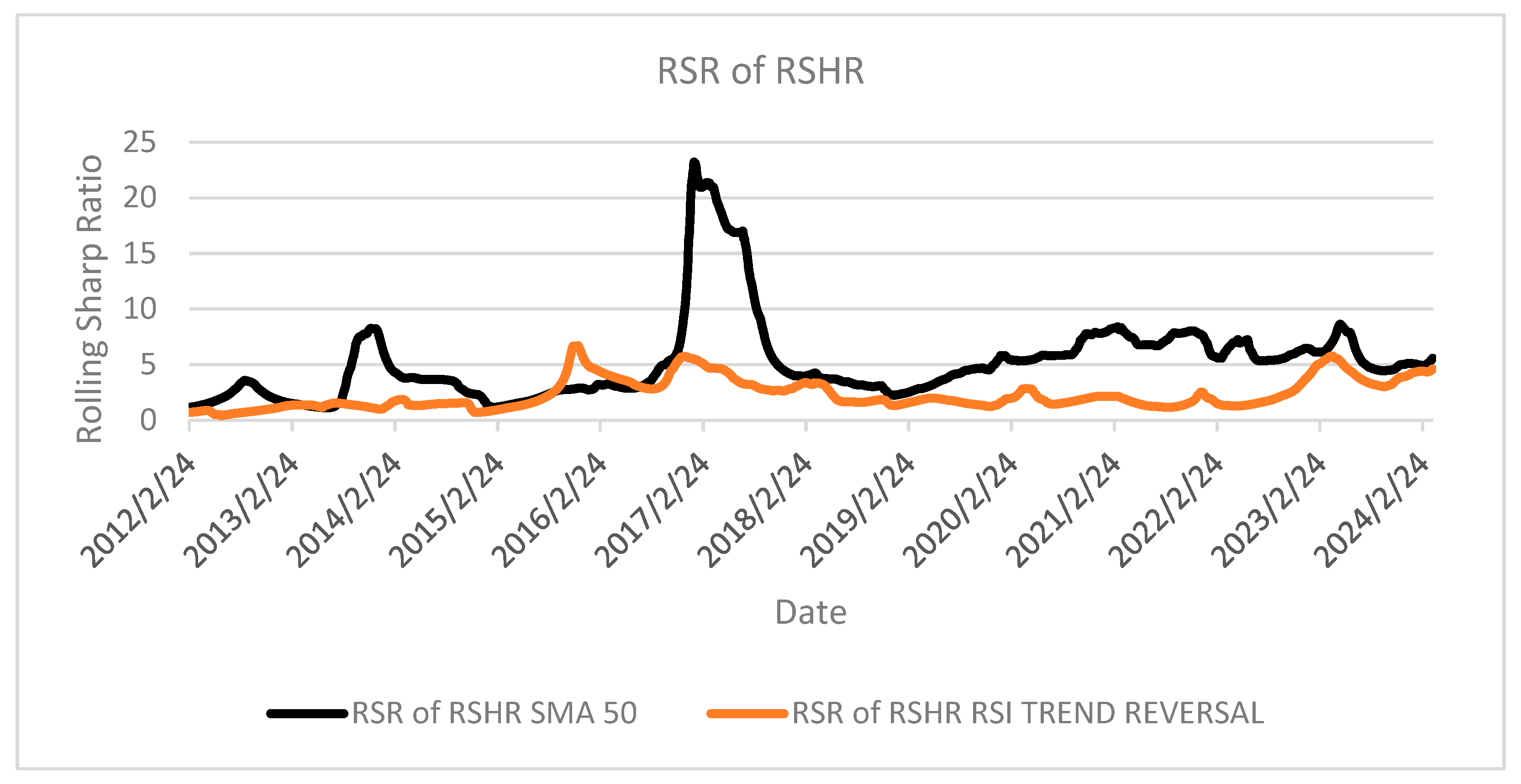
RSHR basic application, as shown on Figure 4, can provide traders with multiple analytical insights. Primary observable correlation can be drawn between strategy effectiveness and Bitcoin market cycles. Notably, each successive cycle demonstrates diminishing performance fluctuations, potentially indicating increasing market maturity and efficiency. The data reveals a progressively increasing mean strategy effectiveness, with the examined approach consistently achieving above-average performance throughout most of the 2017–2024 period. The visualization substantiates the methodological validity of rolling analysis frameworks by demonstrating that identical strategic implementations can yield performance differentials ranging from 500% outperformance to 50% underperformance relative to the benchmark index, depending entirely on the specific implementation period. This performance variability underscores the importance of comprehensive temporal testing rather than relying on arbitrary period selection.

Comparative analysis of RSHR metrics against Bitcoin price charts on Figure 5 reveals significant temporal patterns in technical analysis strategy effectiveness. The data demonstrates that methods based on technical indicators exhibit their greatest efficacy during periods initiating at cycle apexes. This observation suggests that technical analysis frameworks provide maximum utility during market contractions by facilitating strategic capital preservation through position avoidance during pronounced downtrends. Conversely, the strategy demonstrates suboptimal performance during periods of accelerated price growth. This latter insight holds considerable value for implementation optimization, as it potentially identifies temporal windows where alternative approaches, such as leveraged investment strategies, may yield superior results. This application effectively illustrates the necessity of integrating diverse analytical methods to achieve comprehensive market understanding and optimize capital deployment across varying market conditions.

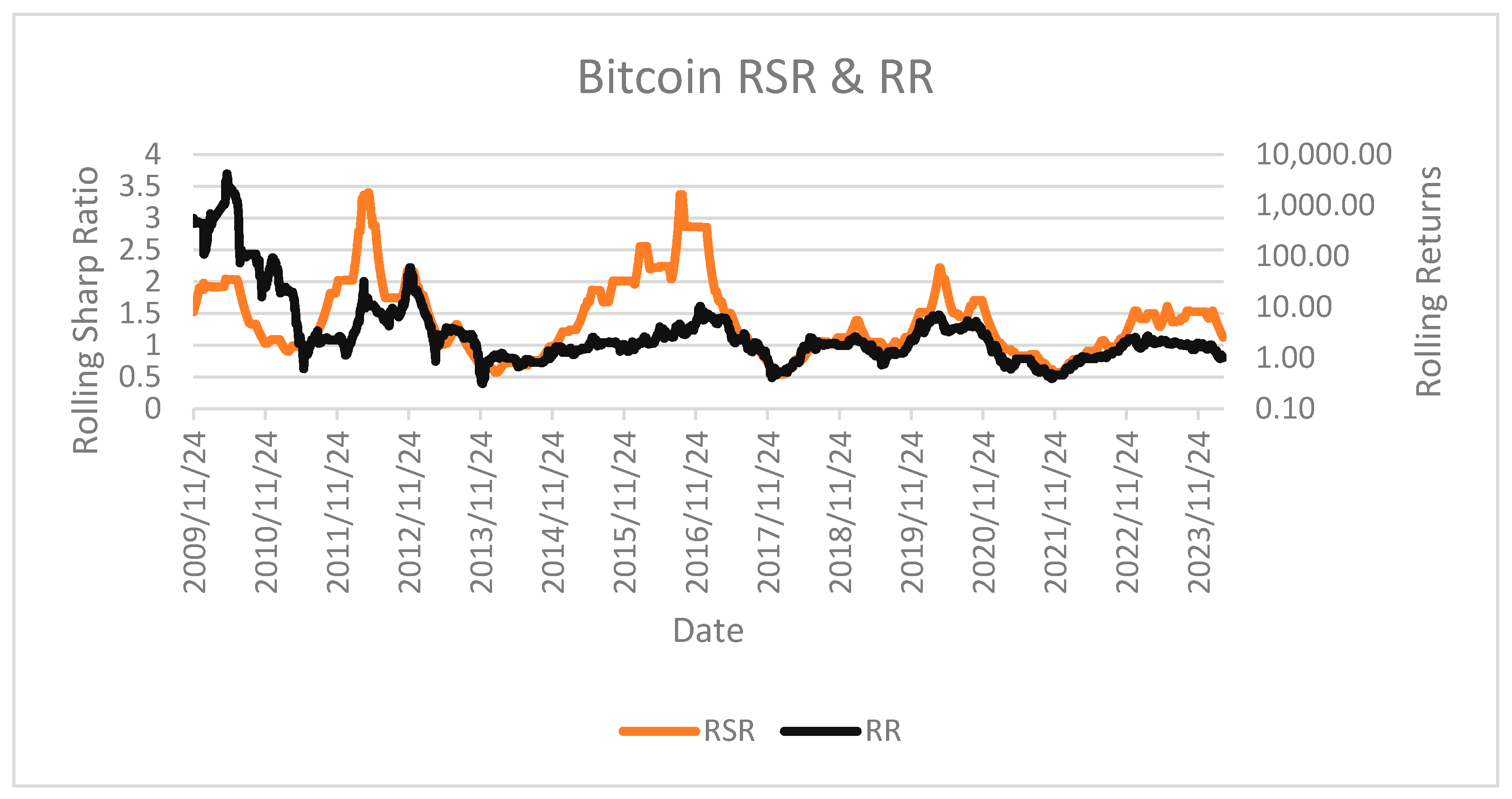
The comparative examination of the RSHR against Rolling Returns (RR) on Figure 6 revealed notable analytical divergences. A significant observation emerges in the frequently inverse, occasionally mirror-image relationship between these performance indicators. Despite the RR strategy demonstrating absolute profitability, periods exhibiting maximum absolute returns frequently coincide with intervals of minimal relative performance compared to the buy-and-hold benchmark. This pattern provides empirical support for the hypothesis presented in the preceding discussion regarding technical analysis limitations during bull market phases. This finding substantiates the methodological validity of implementing the RSHR for comprehensive performance evaluation and underscores the necessity of employing multiple analytical frameworks when assessing strategy efficacy. The data suggests that exclusive reliance on RR method could potentially lead practitioners to erroneous strategic conclusions and suboptimal capital allocation decisions.

The comparative analysis of the RSHR against both Rolling Returns (RR) and the Rolling Sharpe Ratio (RSR) on Figure 7, reveals that both metrics yield highly similar results and lead to comparable conclusions. This consistency confirms that RR and the RSR capture the same underlying performance dynamics. However, the RSR serves as a more normalized and statistically robust version of RR, making it more suitable for comparative analysis across different time periods and strategies. This reinforces the methodological validity of using the RSHR alongside them while also highlighting the risk of relying solely on RR and the RSR, which may obscure relative performance in certain market conditions.

5.3. RSHR in Parameter Selection

The following subsection illustrates how RSHR can be used in Technical Analysis parameter and strategy selection. The illustrative RSHR implementations examined using annual settings include the following:

• RSHR of Bitcoin SMA50 strategy and RSI Trend Reversal strategy;
• RSR of RSHR of Bitcoin SMA50 strategy and RSI Trend Reversal strategy;

The strategies tested on Figure 8 exhibit fundamentally different characteristics. The strategy based on the 50-day SMA is marked by lower profits and losses but demonstrates significantly greater stability. The authors argue that, when selecting strategies responsibly, one should favor those offering moderate and consistent returns, thereby avoiding excessive exposure to risk. This rationale aligns with the original purpose of the Sharpe Ratio, which was designed to capture this precise trade-off. The authors believe that combining both indicators in this manner enables researchers to make more informed and rational decisions when evaluating investment strategies.

The authors recommend calculating the RSHR for each tested strategy and subsequently deriving the RSR using a consistent rolling window. In this way, the strategy with the highest resulting value will be the one that most consistently achieved superior performance relative to the buy-and-hold benchmark.

As illustrated in Figure 9, the strategy based on the 50-day SMA consistently achieves a higher RSHR over the majority of the analyzed period, which corroborates the expert assessment provided in the case study. The presented approach enables the automation of this evaluation process and supports comparative analysis across an arbitrary number of strategies. The authors posit that, in addition to expert judgment, pure RSHR-based assessment constitutes one of the primary applications of the proposed metric. Future research will aim to refine and expand this methodology. In scenarios involving a larger set of strategies, the authors advocate for the application of statistical tests to ensure that comparisons are not conducted on overly similar or collinear cases, thereby preserving the validity of the evaluation.

5.4. RSHR in Dollar Cost Averaging

The following subsection will examine one of the primary applications of the RSHR, namely Dollar Cost Averaging. The illustrative RSHR-based DCA implementations analyzed in this section are presented using annual settings, including the following:

• RSHR of Bitcoin DCA based on SMA50 strategy.

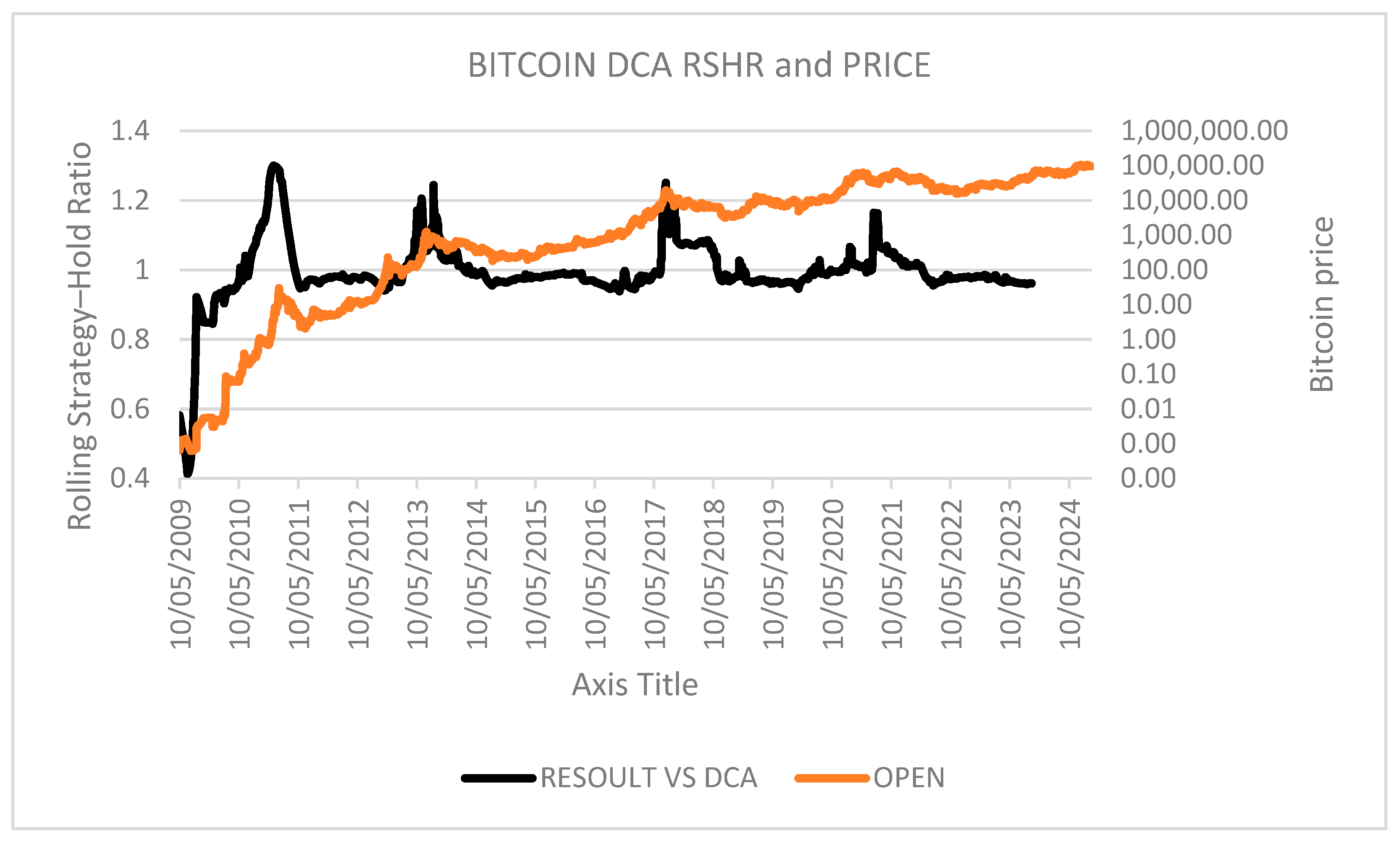
The RSHR analysis of Dollar Cost Averaging produces findings that contradict commonly held perceptions regarding periodic investment distribution advantages. Contrary to the widespread assumption that dividing investments across sequential time periods yields improved entry price averages, the data suggests limited efficacy in Bitcoin markets. Low average efficacy potentially attributable to the asset’s predominantly appreciating trajectory. While DCA demonstrates superior performance during specific intervals, particularly when initiated near cyclical price maxima, the potential return enhancement rarely justifies the substantial underperformance risk, which reached approximately 40% in the most recent market cycle. This empirical contradiction with established investment principles has motivated the authors to focus on comprehensive examination of DCA methods in future studies utilizing the RSHR framework.

The RSHR analysis of Dollar Cost Averaging on Figure 10, produces findings that contradict commonly held perceptions regarding periodic investment distribution advantages. Contrary to the widespread assumption that dividing investments across sequential time periods yields improved entry price averages, the data suggests limited efficacy in Bitcoin markets. Low average efficacy is potentially attributable to the asset’s predominantly appreciating trajectory. While DCA demonstrates superior performance during specific intervals, particularly when initiated near cyclical price maxima, the potential return enhancement rarely justifies the substantial underperformance risk, which reached approximately 40% in the most recent market cycle. This empirical contradiction with established investment principles has motivated the authors to focus on comprehensive examination of DCA methods in future studies utilizing the RSHR framework.

The RSHR method has enabled multifaceted analytical approaches and generated substantive conclusions regarding Bitcoin market dynamics. The authors propose that RSHR implementation, when integrated with existing analytical frameworks, provides enhanced capacity for comprehensive trading and investment strategy evaluation, potentially facilitating the avoidance of significant implementation errors that might otherwise result in substantial opportunity cost and suboptimal capital deployment.

5.5. RSHR on Lower Timeframes, Sentiment Analysis, and On-Chain Analysis

The following subsection will examine various RSHR applications across different Bitcoin analysis. The illustrative RSHR implementations examined using annual settings include the following:

• RSHR of Bitcoin SMA50 strategy on 4 h timeframe;
• RSHR of Bitcoin SMA50 shorting strategy;
• RSHR of Bitcoin Fear and Greed strategy;
• RSHR of Bitcoin Spent Output Profit Ratio strategy;

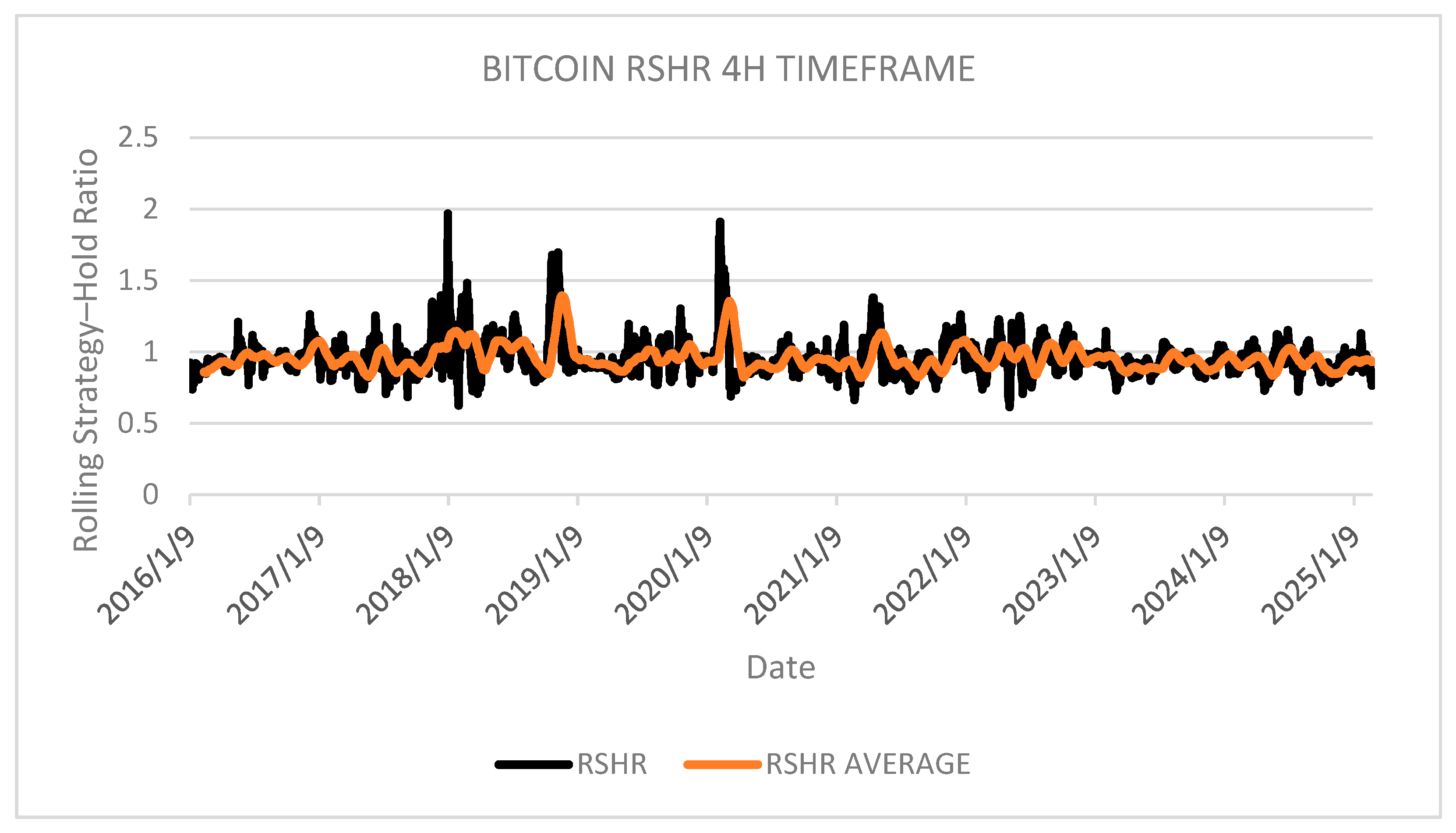
When applying the RSHR to shorter time intervals such as on Figure 11, the resulting visualization exhibits reduced interpretability due to increased signal noise. In such scenarios, the authors recommend implementing indicator averaging techniques to mitigate noise interference and enhance analytical clarity. The empirical findings from this specific implementation reveal that the strategy achieves marginally inferior performance compared to the buy-and-hold benchmark on average, though it maintains potential utility across various applications. To supplement this analysis, the authors propose integrating additional statistical metrics by conducting a sequential month-by-month examination of quartile distributions, extreme deviation values, and median performance. This chronological statistical analysis would enable identification of potential seasonal effectiveness patterns and cyclical variations within the shorter timeframe implementation.

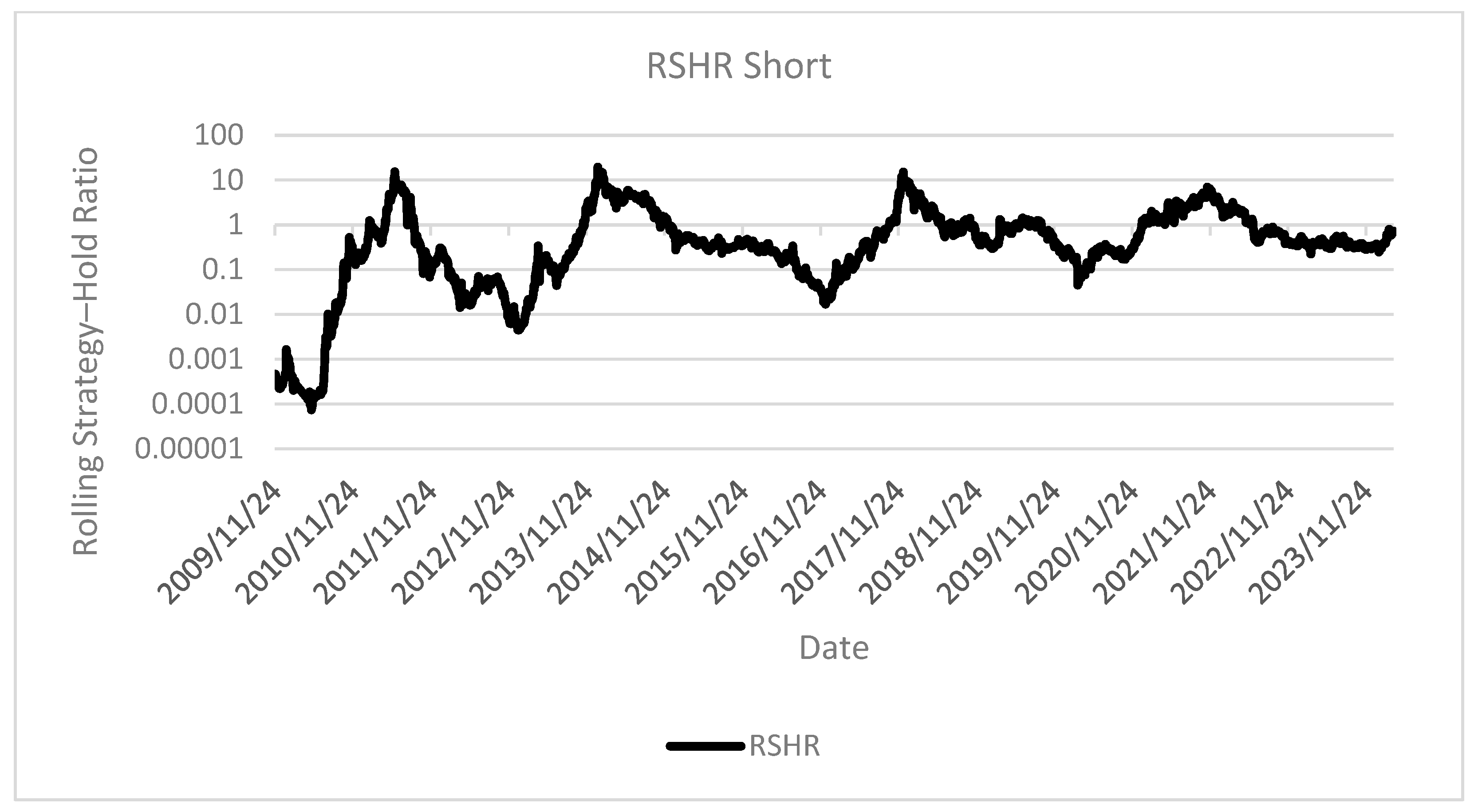
The short-selling strategy from Figure 12, illustrates the significant risks associated with shorting a market as structurally bullish as cryptocurrencies. The strategy exhibited extreme outcomes—ranging from gains exceeding those of a buy-and-hold approach by a factor of ten during bear markets, to losses of up to 99.99% during bull runs. In the past two years alone, it recorded an average loss of nearly 80%.

It is worth noting that selling near the top of a market cycle could have yielded comparable returns to those of a short strategy, highlighting the critical role of timing. These findings once again underscore the strong dependency of strategy performance on Bitcoin’s cyclical nature and motivate the authors to further investigate this phenomenon in future research.

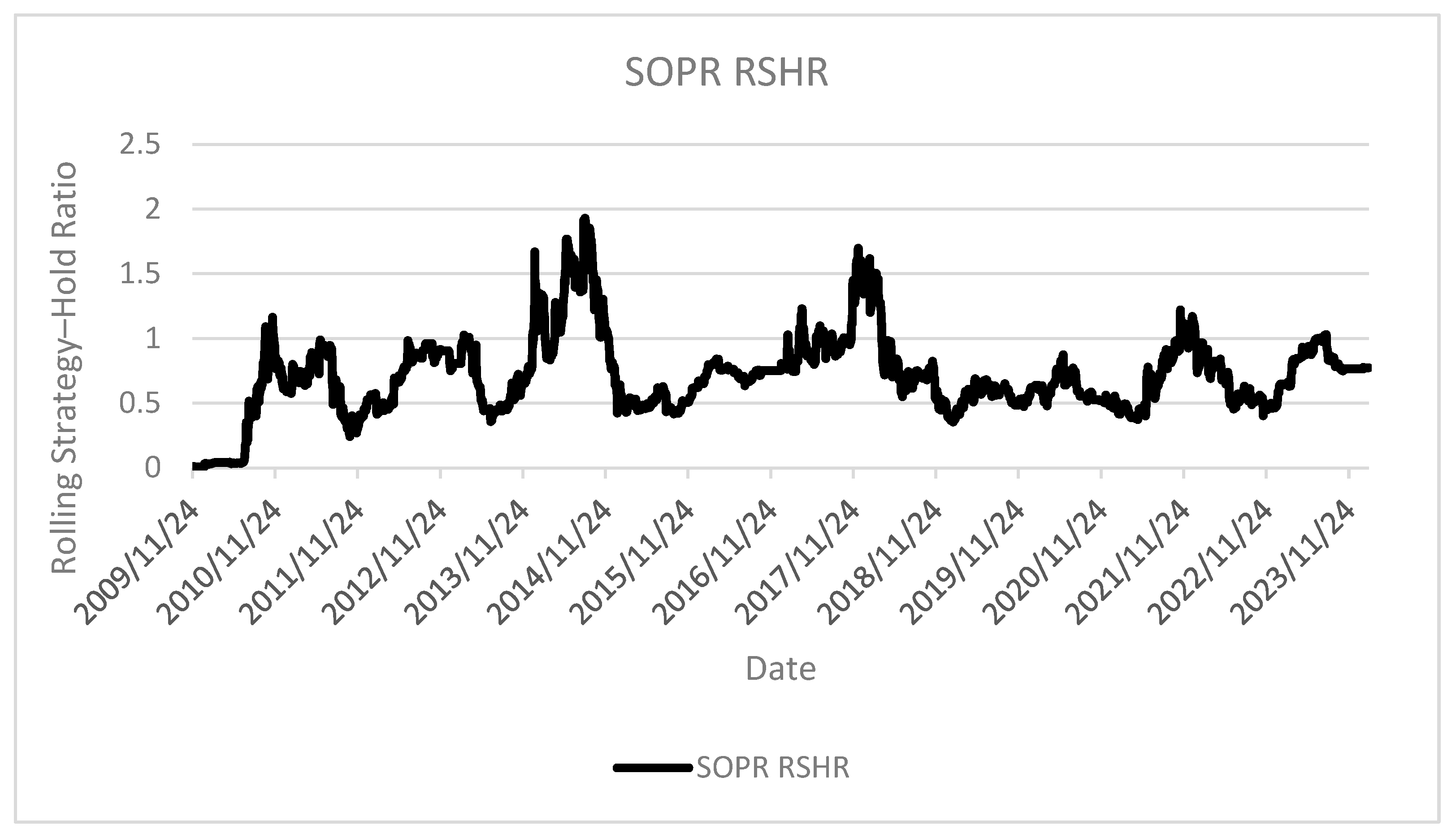
The SOPR-based strategy on Figure 13 delivered exceptionally weak results, achieving on average only around 60% of the returns generated by a simple buy-and-hold approach. This suggests that on-chain data cannot always be utilized directly and may require additional preprocessing, assumptions, or temporal adjustments. The authors intend to continue their research in the area of on-chain indicators and further investigate their effectiveness in the context of trading strategies.

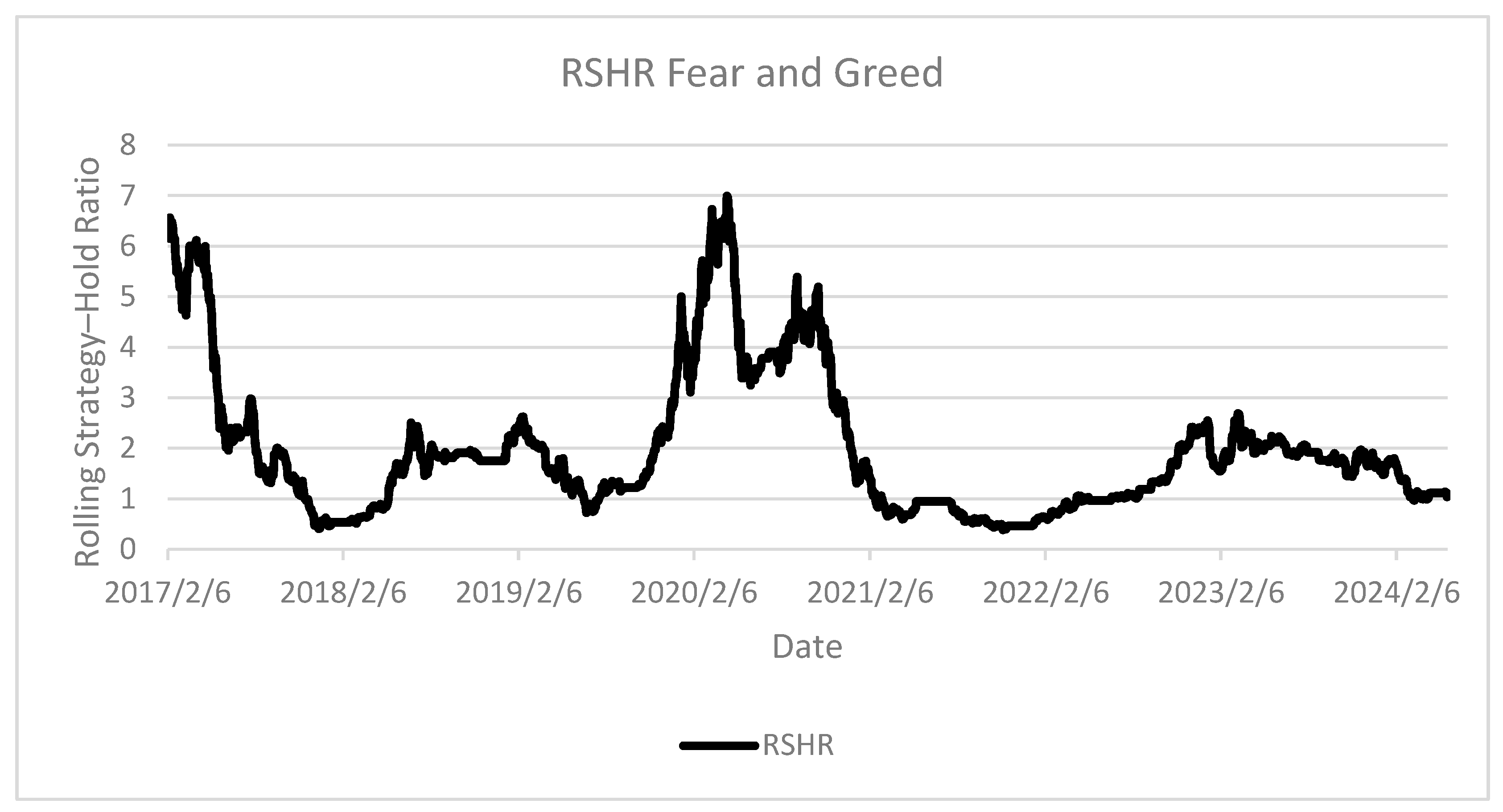
The Fear and Greed Index strategy from Figure 14, demonstrated relatively stable and consistently strong performance, delivering above-average returns in recent years. It is worth noting, however, that the strategy underperforms when initiated at the bottom of a market cycle. In all other scenarios, it tends to outperform the average.

The Fear and Greed Index serves as a compelling example of a modern indicator that aggregates multiple sources of information into a single, actionable signal. As the results suggest, it exhibits greater effectiveness than any of the previously tested indicators, making it a promising tool for strategy development and market timing.

5.6. Altcoins

The following subsection will examine various RSHR applications across different altcoin markets. The illustrative RSHR implementations examined using annual settings include the following:

• RSHR of Etherneum using the SMA50 strategy;
• RSHR of Altcoin Market using the SMA50 strategy.

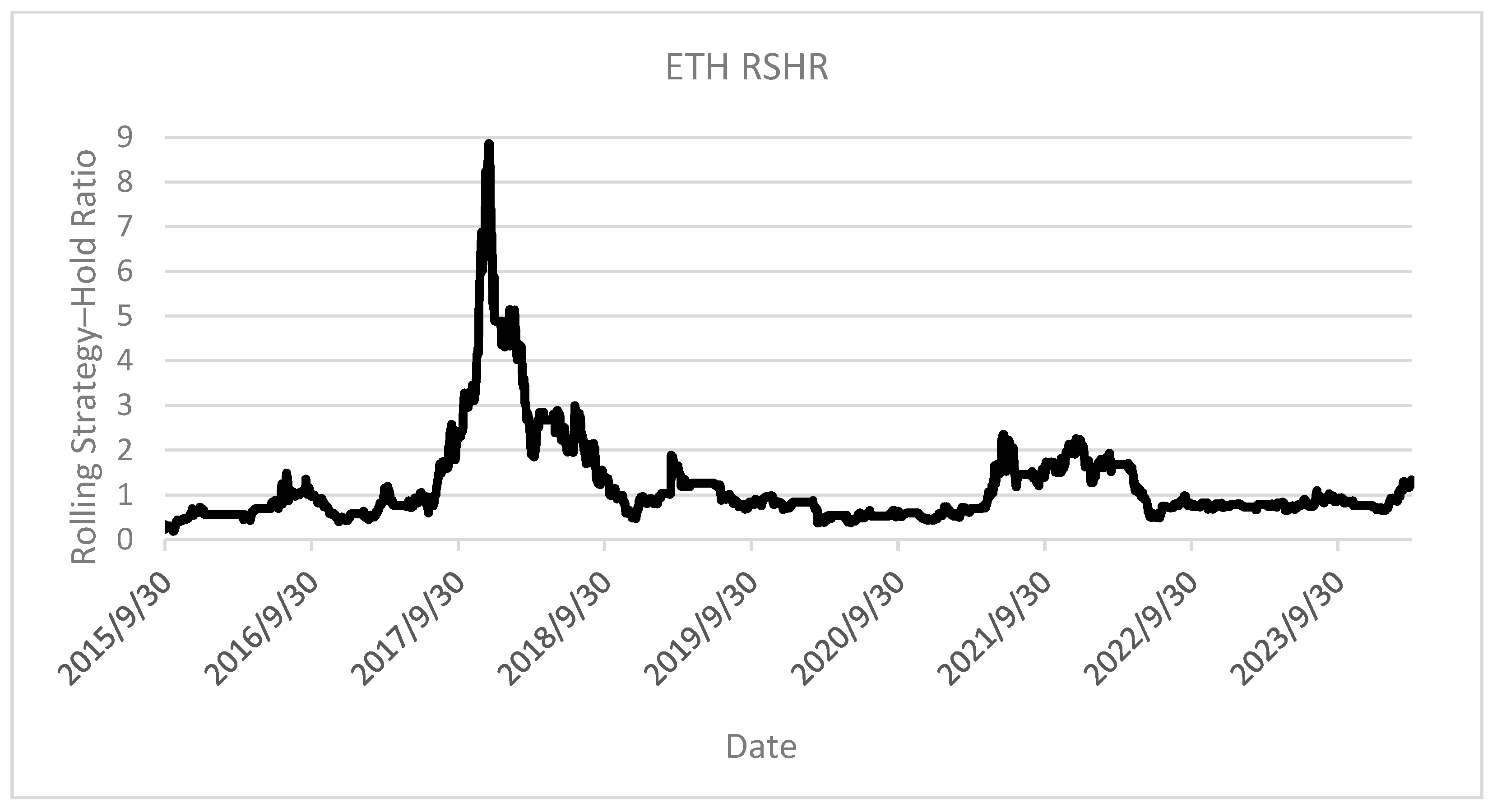
The analysis of Ethereum utilizing the SMA50 strategy on Figure 15, reveals consistent performance characteristics throughout the asset’s historical data, with strategy returns averaging approximately 80% of the buy-and-hold. This persistent performance differential may indicate insufficient market maturity for optimal technical analysis implementation. The authors, however, hypothesize that the remarkable consistency of return patterns suggests the potential for developing alternative technical methods capable of achieving persistent outperformance. This performance stability, while suboptimal in absolute terms, provides a potentially valuable foundation for strategy refinement and optimization.

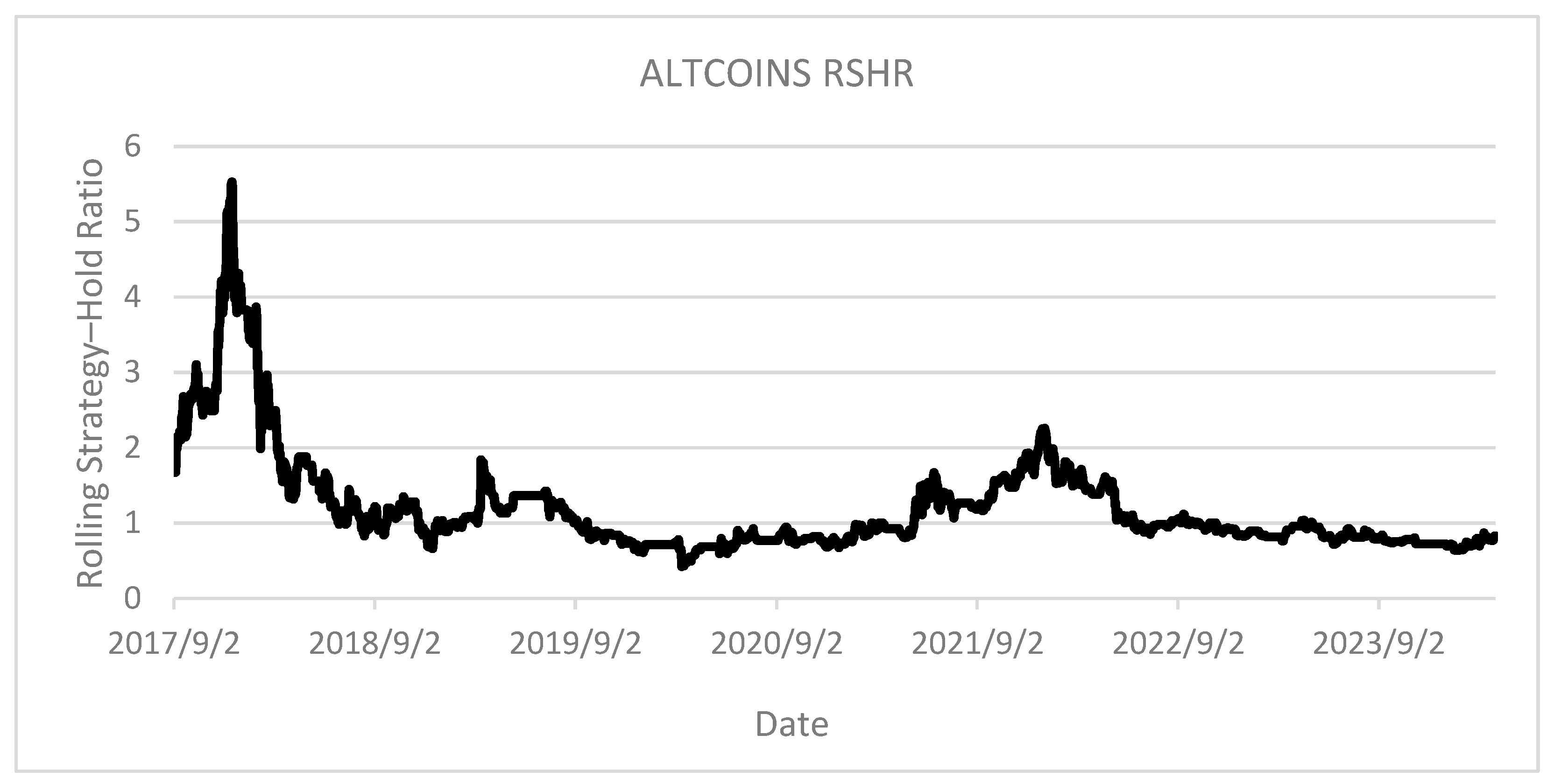
The examination of the broader Altcoin Market on Figure 16 yields analytical conclusions parallel to those observed in the Ethereum analysis, potentially indicating significant correlation between these market indices. This observed relationship suggests underlying structural similarities in market behavior across non-Bitcoin cryptocurrencies.

In subsequent research initiatives, the authors intend to implement the RSHR method to investigate interrelationships between Bitcoin, Ethereum, and the broader altcoin ecosystem. This analysis will incorporate cryptocurrency trading pairs and Bitcoin market dominance metrics to provide enhanced understanding of market dynamics and potential lead–lag relationships between different segments of the cryptocurrency market.

5.7. Traditional Markets

In the following subsection, the effectiveness of the RSHR indicator will be examined across traditional financial markets. This analysis aims to demonstrate the method’s versatility and promote rolling window analytical approaches beyond cryptocurrency applications. The assessment will include examples from diverse market categories:

• S&P 500 Index;
• NIFTY 50 Index;
• Gold;
• Crude oil;
• EUR/USD.

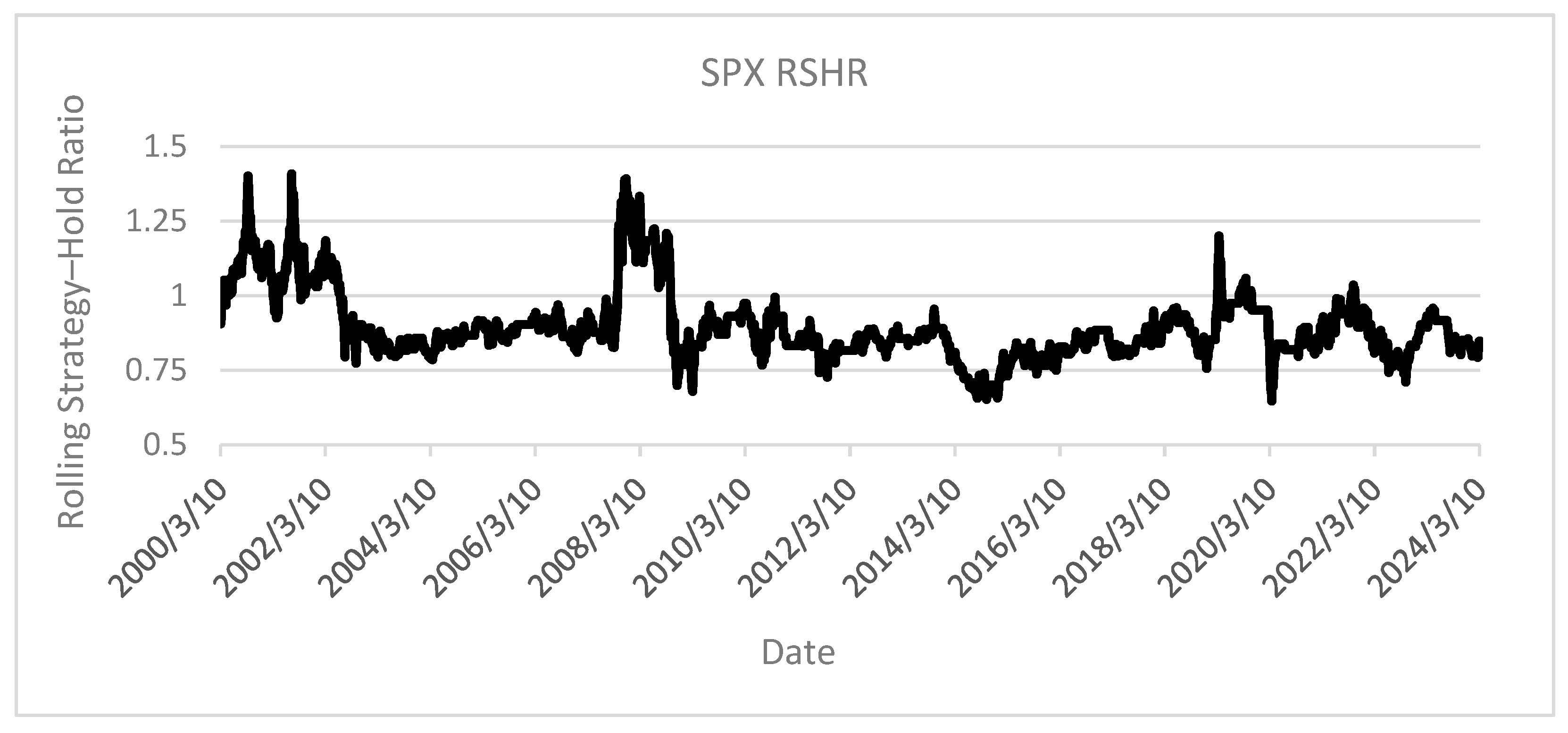
As hypothesized, the application of elementary technical analysis methodologies to the S&P 500 on Figure 17, demonstrates notably suboptimal performance, with RSHR values predominantly fluctuating within the 0.75 to 1.0 range. The sole exceptions occur during significant market contractions, suggesting that technical analysis frameworks may provide limited utility in avoiding substantial drawdowns, though typically at the expense of potential appreciation capture. Considering the advanced maturity of this market and the prevalence of algorithmic trading implementations, the empirical evidence leads the authors to recommend against technical analysis application in this particular market environment.

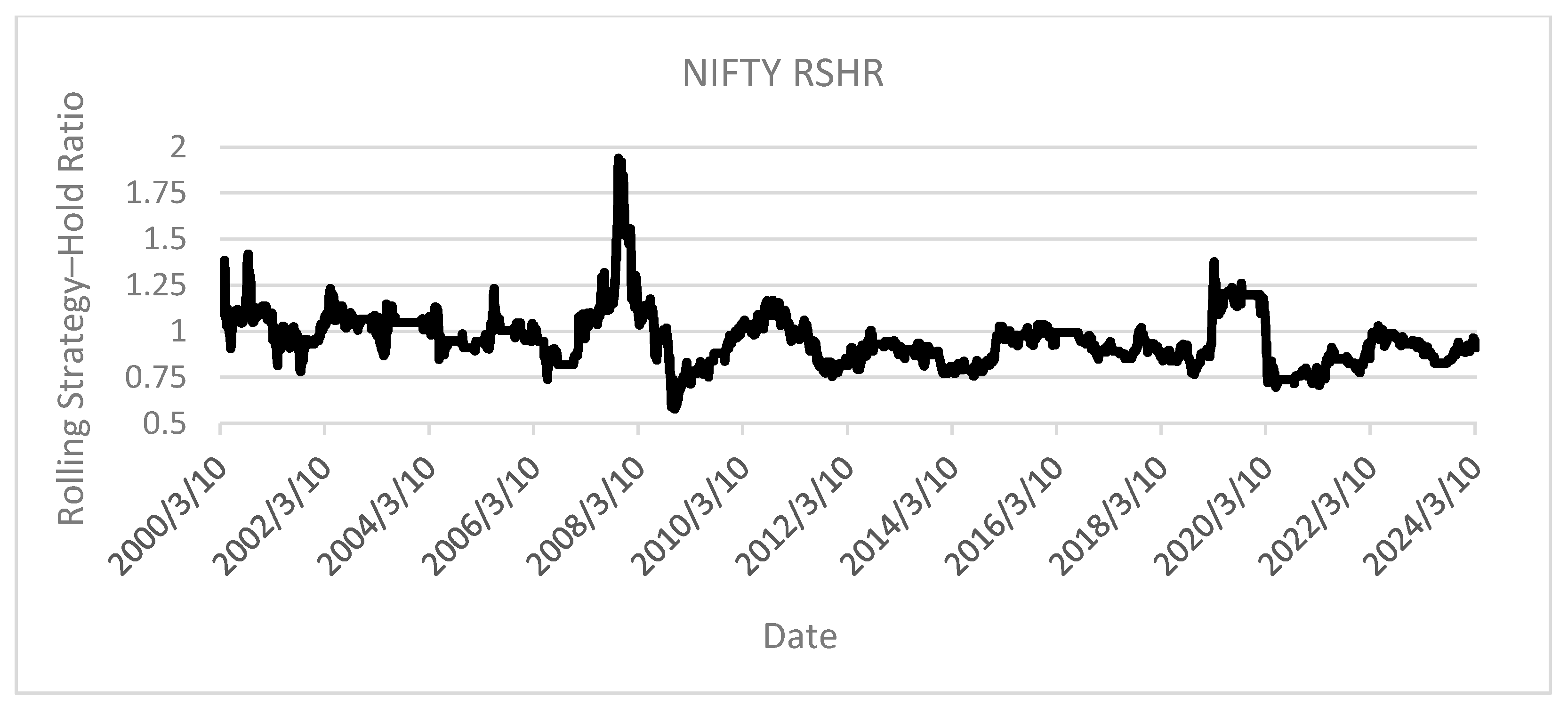
The examination of the NIFTY 50 index on Figure 18, representing India’s emerging market, presents particularly noteworthy findings. Throughout the past twenty-five years, substantial temporal intervals existed during which the elementary SMA50 strategy consistently generated above-average performance metrics. However, recent data demonstrates performance convergence with S&P 500 patterns, potentially indicating progressive market maturation. These empirical observations provide corroborative evidence for theoretical frameworks proposed by Ratner and Leal in “Tests of Technical Trading Strategies in the Emerging Equity Markets of Latin America and Asia,” which postulate the achievability of superior returns through technical analysis implementation in emerging market environments. Based on these findings, the authors suggest potential implementation of strategies validated on the Indian market to less developed market environments that may exhibit similar structural inefficiencies to historical NIFTY 50 patterns.

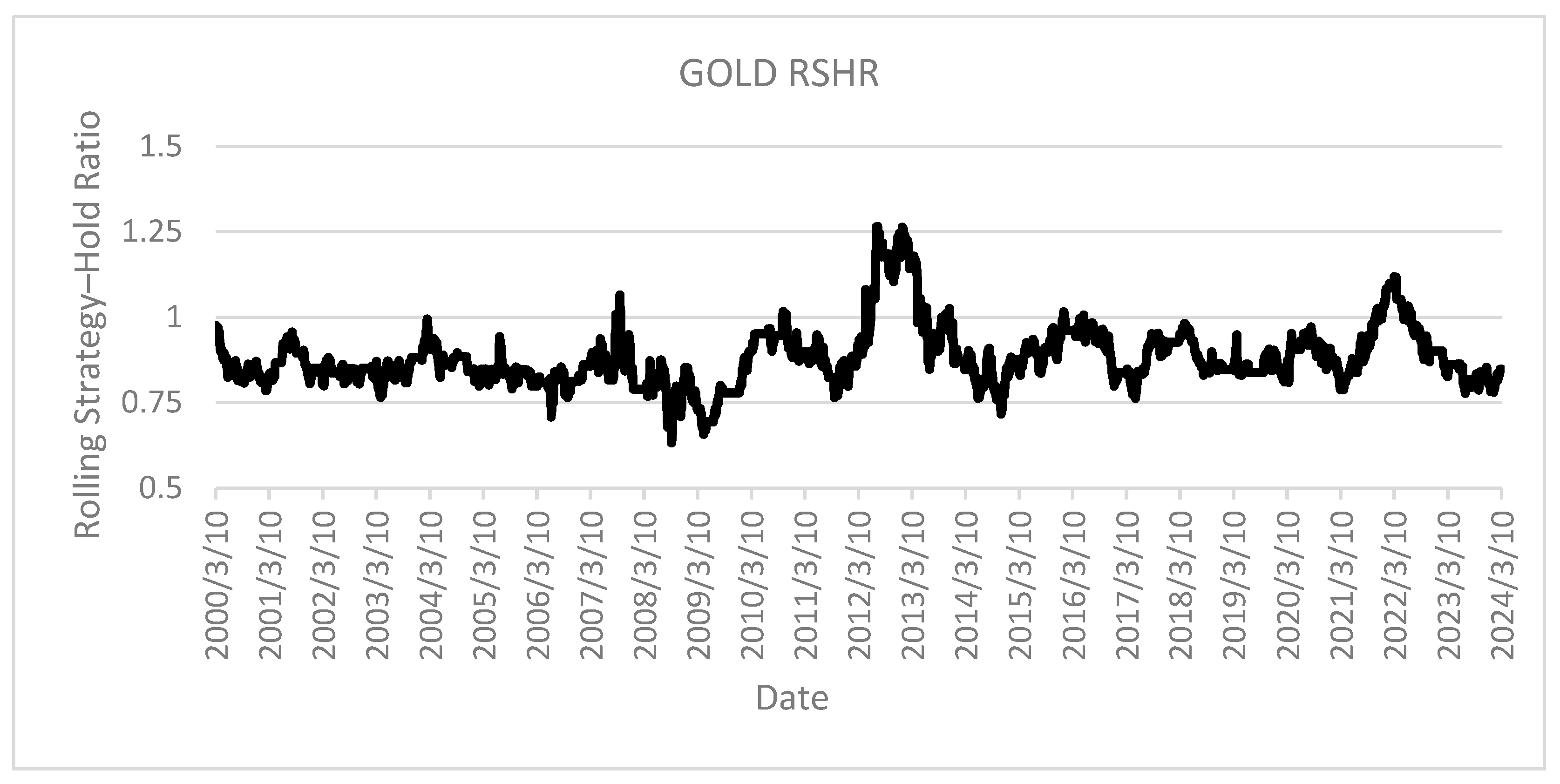
In the case of gold, RSHR analysis provides definitive evidence that implementation of the selected strategy results in approximately 15% reduced returns compared to the buy-and-hold approach within a single annual period. The compounding effect of this performance differential indicates that over multi-year implementation horizons, strategy utilization would potentially generate cumulative returns of approximately half those achieved through simple index acquisition. Given this substantial and consistent underperformance, the authors would recommend complete abandonment of simple technical analysis methods for this particular asset class.

In the case of gold, RSHR analysis provides definitive evidence that implementation of the selected strategy on Figure 19, results in approximately 15% reduced returns compared to the buy-and-hold approach within a single annual period. The compounding effect of this performance differential indicates that over multi-year implementation horizons, strategy utilization would potentially generate cumulative returns of approximately half those achieved through simple index acquisition. Given this substantial and consistent underperformance, the authors would recommend complete abandonment of simple technical analysis methods for this particular asset class.

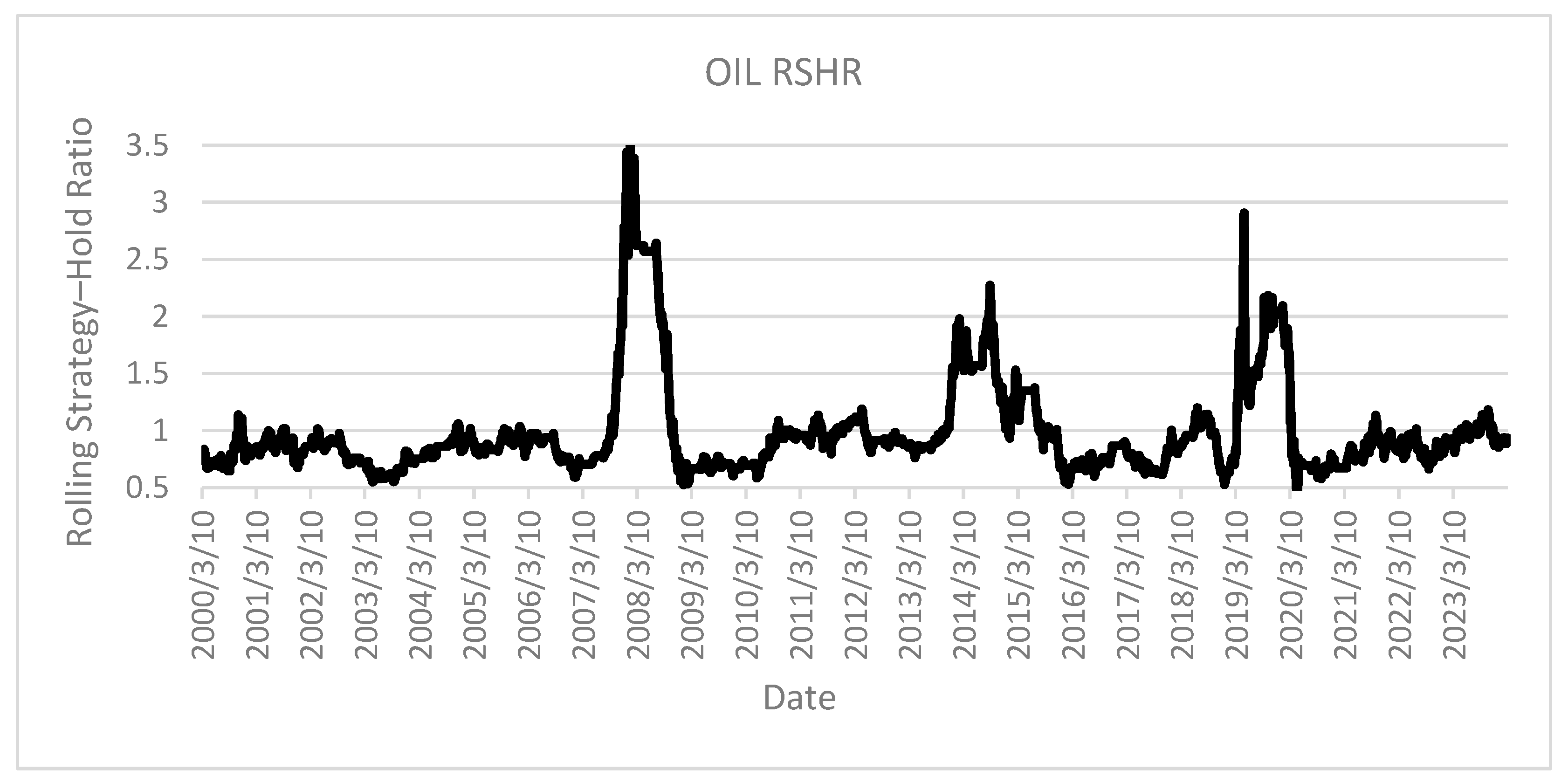
The crude oil market demonstrates extreme RSHR variability, with values oscillating between 0.5 and 3.5 as shown on Figure 20. This substantial fluctuation range confirms the asset’s characteristic high volatility profile. Despite the presence of extended periods during which strategy performance approximated buy-and-hold returns, the empirical evidence suggests this particular market environment likely represents a suboptimal domain for implementing elementary technical analysis methods. The extreme performance variability indicates potentially unpredictable strategy reliability that could present significant implementation challenges.

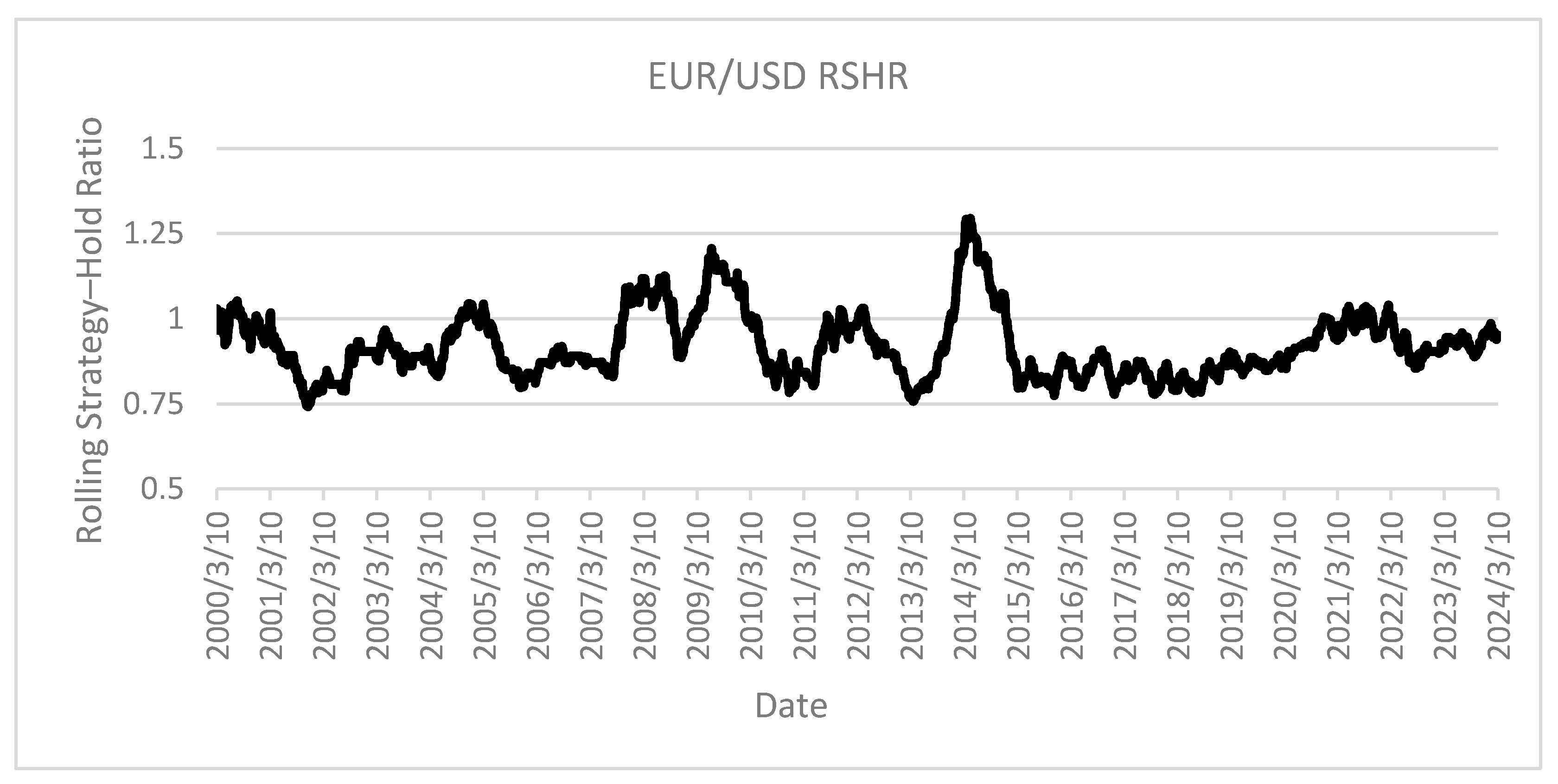
The SMA50 strategy demonstrates exceptionally poor performance when applied to the EUR/USD pair, achieving returns equivalent to the buy-and-hold benchmark for only brief intervals during the past decade as shown on Figure 21. This underperformance aligns with the authors’ expectations given the significant regulatory framework and substantial central bank intervention characterizing currency markets. These results strongly suggest the complete absence of utility for technical analysis methods in this particular market environment.

In summary, this research enabled rapid assessment of representative indices across major traditional market categories. The RSHR method facilitated efficient evaluation of continued strategy development potential for specific indices, mitigating the risk of analytical bias from testing during periods of anomalous performance. The approach successfully identified historical intervals exhibiting both substantial outperformance and significant underperformance. The empirical evidence demonstrates the efficiency characteristics of mature markets while confirming opportunities for above-average returns in emerging market environments, thereby validating theoretical frameworks prevalent in the existing literature.

The authors acknowledge that a more comprehensive analysis would benefit from examining multiple indices within each market category. However, they opted for a focused approach using representative indices to enhance presentation clarity. This methodological decision also enabled more targeted assessment of how exogenous factors, including significant events, fundamental analysis metrics, and market liquidity cycles, influence performance outcomes across different market environments.

5.8. Directions for Future Research

The promising results obtained during the experiments demonstrate the significant value that rolling-type evaluation methods can provide for trading and investment strategy assessment. The authors believe further development and promotion of both the RSHR and similar analytical frameworks is essential for advancing quantitative finance methods. The approaches presented in this paper will serve as foundational elements in the authors’ subsequent research initiatives.

During the examination of various applications for the indicator, the authors identified a notable cyclicality in performance metrics that correlates strongly with Bitcoin market cycles. While this observation may appear intuitive, the authors believe that the RSHR can help establish consistent timeframes within the Bitcoin cycle where trading strategies demonstrate optimal effectiveness. Furthermore, the method shows potential for identifying altcoin seasons and may synchronize effectively with liquidity cycles in traditional markets [49].

The research team intends to expand their investigation into Dollar Cost Averaging strategies, incorporating all analytical approaches available for cryptocurrency markets. This comprehensive assessment will aim to determine whether systematic investment approaches can be optimized through selective application during specific market conditions, potentially enhancing returns while maintaining the risk-management benefits inherent to periodic investment strategies.

Given the specialized expertise of one of the authors, the research team also intends to explore the potential of the RSHR and rolling-type strategies in developing algorithmic trading strategies based on genetic algorithms. This investigation will be conducted in collaboration with a domain expert in evolutionary computation, aiming to leverage machine learning optimization techniques to enhance strategy performance. The proposed research will examine how rolling metrics can serve as fitness functions within genetic algorithm frameworks, potentially creating adaptive trading systems that evolve based on market conditions and historical performance indicators.

The authors also plan to dedicate an entire article exclusively to statistical methods employed in conjunction with rolling-type indicators, including the RSHR. They intend to present their proprietary approach to conducting the aforementioned statistical tests, providing a comprehensive methodological framework for evaluating rolling metrics in financial analysis.

Considering the demonstrated efficacy of the proposed method and the analytical insights it provides across various research domains, the authors intend to implement this approach in the majority of their forthcoming research initiatives and scientific publications.

6. Summary

This article presents a scientific introduction to a new method for evaluating trading and investment strategies—the Rolling Strategy–Hold Ratio (RSHR). The proposed solution applies an algorithmic approach that can help better predict investment returns and significantly reduce risks associated with cryptocurrency trading and investing.

The authors have developed a new method for analyzing the effectiveness of trading and investment strategies, which represents a modification of Rolling Returns and Rolling Sharpe Ratio concepts. This method was developed based on a comprehensive literature review and original research conducted for this study. The RSHR allows for the analysis of thousands of simulations using straightforward calculations and presents the results in a single visualization. The research demonstrates the limitations of commonly applied evaluation methods and identifies specific contexts where RSHR application can provide advantages in the decision-making process.

Additionally, the authors proposed a novel approach that combines the RSHR with the Rolling Sharpe Ratio, enabling the identification of strategies that most consistently achieve above-average performance. This dual-metric evaluation allows for a statistically grounded selection of the most robust solution among multiple competing strategies, significantly enhancing the objectivity and precision of the strategy selection process.

The approach presented in this article effectively determines the validity of strategies based on technical, on-chain, and sentiment analysis across both cryptocurrency markets and traditional financial markets. The market model constructed by the authors enabled extensive preliminary research, which was executed using the TradingView platform and Python.

The Rolling Strategy–Hold Ratio method presented in this article demonstrates considerable versatility across various market contexts, asset classes, and analytical frameworks. The empirical evidence supports its applicability to both cryptocurrency and traditional financial markets, regardless of the underlying analytical approach employed. This universality represents a significant advancement in strategy evaluation capabilities. The authors do believe the RSHR will help educated traders and institutions make better decisions while discouraging excessive risk-taking, ultimately contributing to healthier, more stable markets.

By providing a standardized framework for comparative analysis, the RSHR enables market participants to efficiently assess multiple strategies without extensive computational resources or prolonged testing periods. This efficiency can substantially reduce the time investment typically required for strategy validation and help practitioners avoid potentially costly investment decisions based on strategies that perform well only under specific historical conditions. Furthermore, the method serves as a valuable component in the development of sophisticated automated trading systems by providing a quantitative foundation for strategy selection and optimization. As markets continue to evolve and increase in complexity, robust analytical tools like the RSHR will become increasingly essential for both individual investors and institutional market participants seeking to maintain competitive advantages in dynamic financial environments. The authors express confidence that this publication will make a meaningful contribution to the further development and implementation of rolling ratios in financial analysis, establishing a foundation for more sophisticated methods in cryptocurrency market strategy optimization.