Braking Force Coordination Control Strategy for Electric Vehicles Considering Failure Conditions

Abstract

This paper presents a braking force coordination control strategy for electric vehicles based on a hierarchical control architecture. The proposed strategy integrates electronic brakeforce distribution (EBD), direct yaw control (DYC), anti-lock braking system (ABS), and braking force reconstruction functions to effectively enhance braking stability under brake actuator failure conditions. First, a full-vehicle model is established to investigate the braking force coordination process during braking. Then, by analyzing the coupling relationship between the yaw moment and DYC control, a dynamic ABS/DYC coordination strategy is developed. A dynamic computation model of the braking force limited weight coefficient is established, and a three-level braking force coordination mechanism is constructed according to the braking force limited state of each wheel. This mechanism achieves integrated coordination and reconstruction of longitudinal and lateral braking forces. Considering road adhesion, failure sequence, and failure location, eleven typical verification scenarios are designed. Simulation results show that, compared with uncoordinated control methods, the proposed method not only can effectively handle with muti-wheel failure scenarios, but also can reduce the braking distance by up to 7.05% and the lateral deviation by 26.74%, effectively improving the braking safety of electric vehicles.

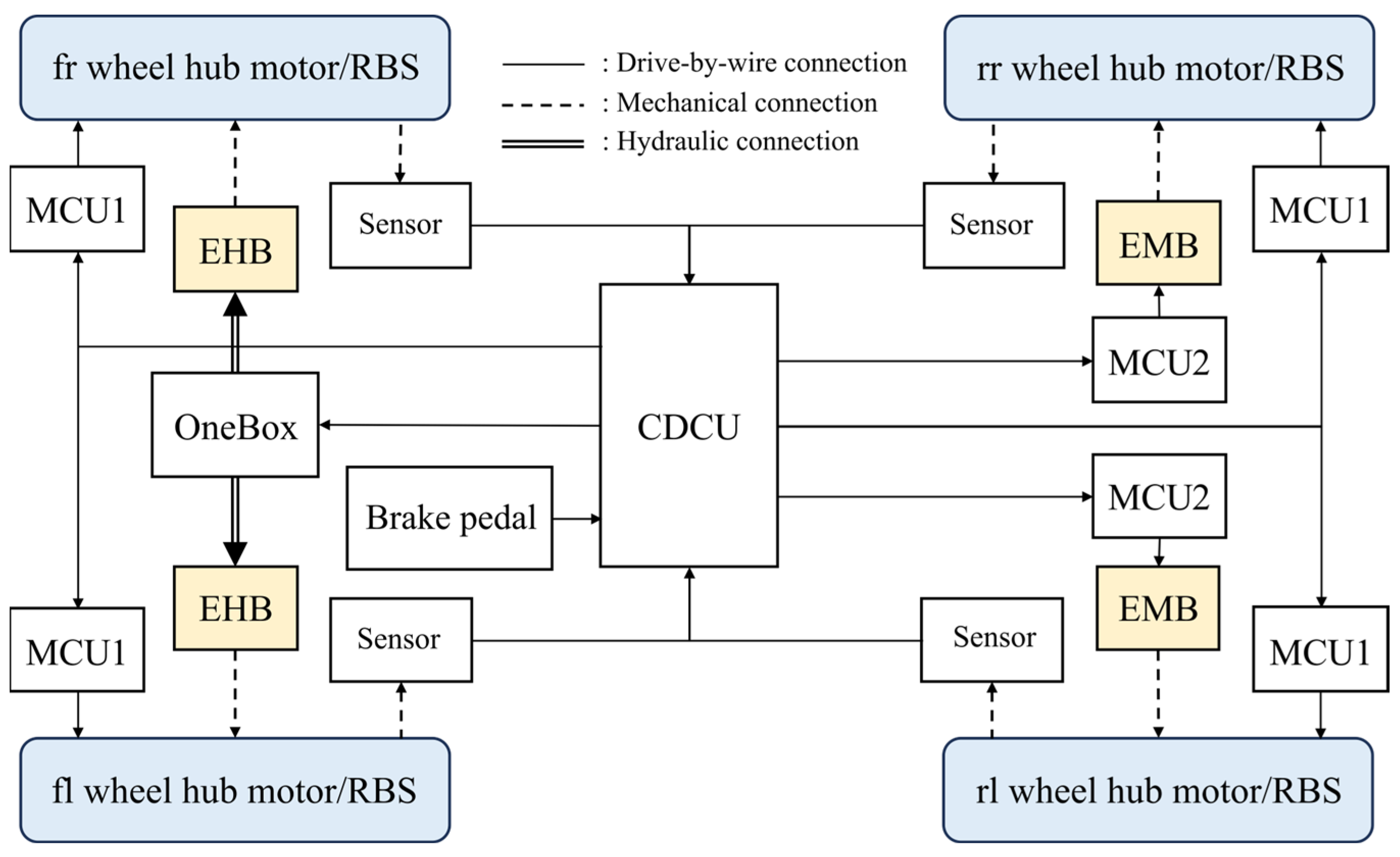
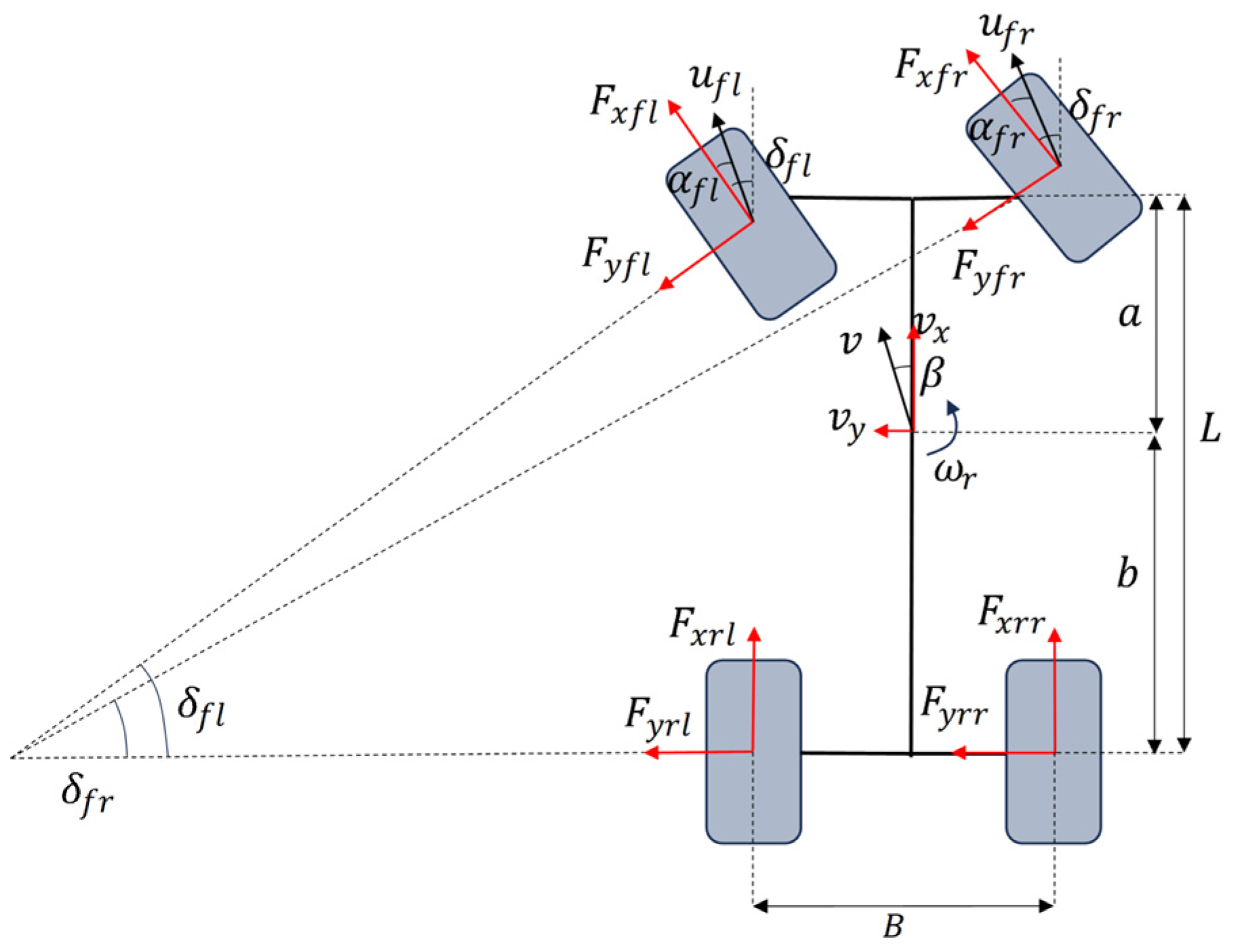
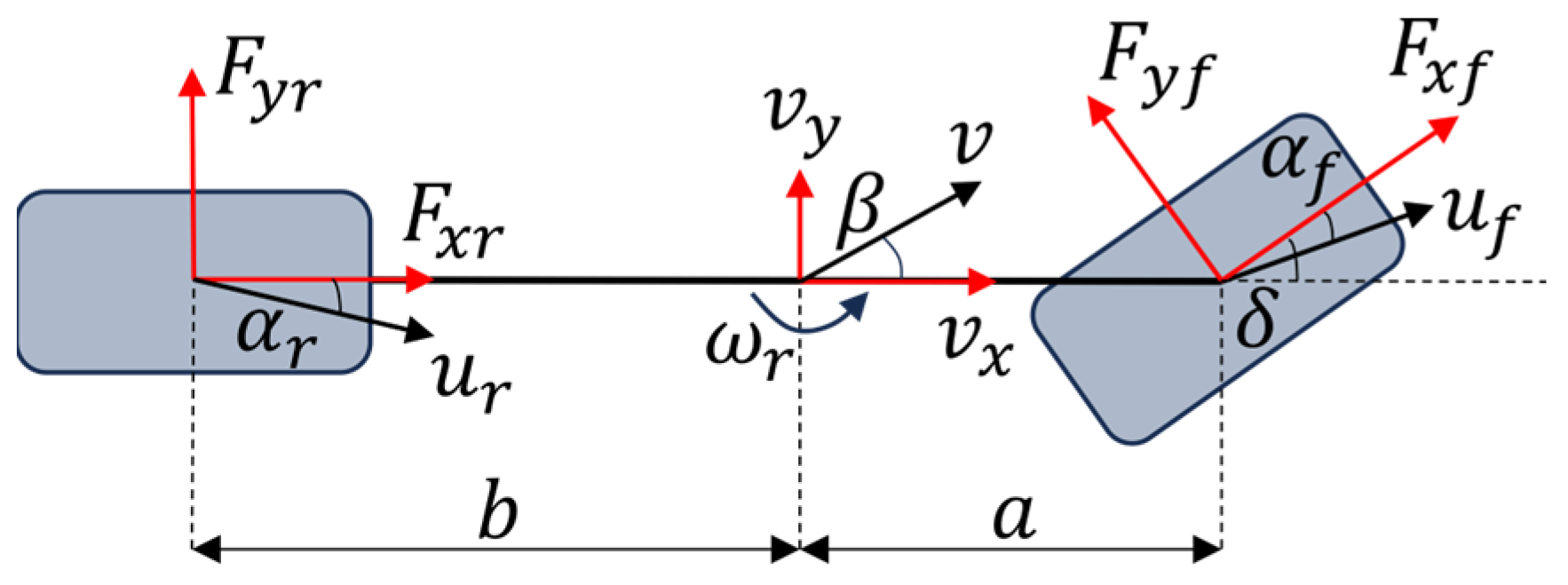
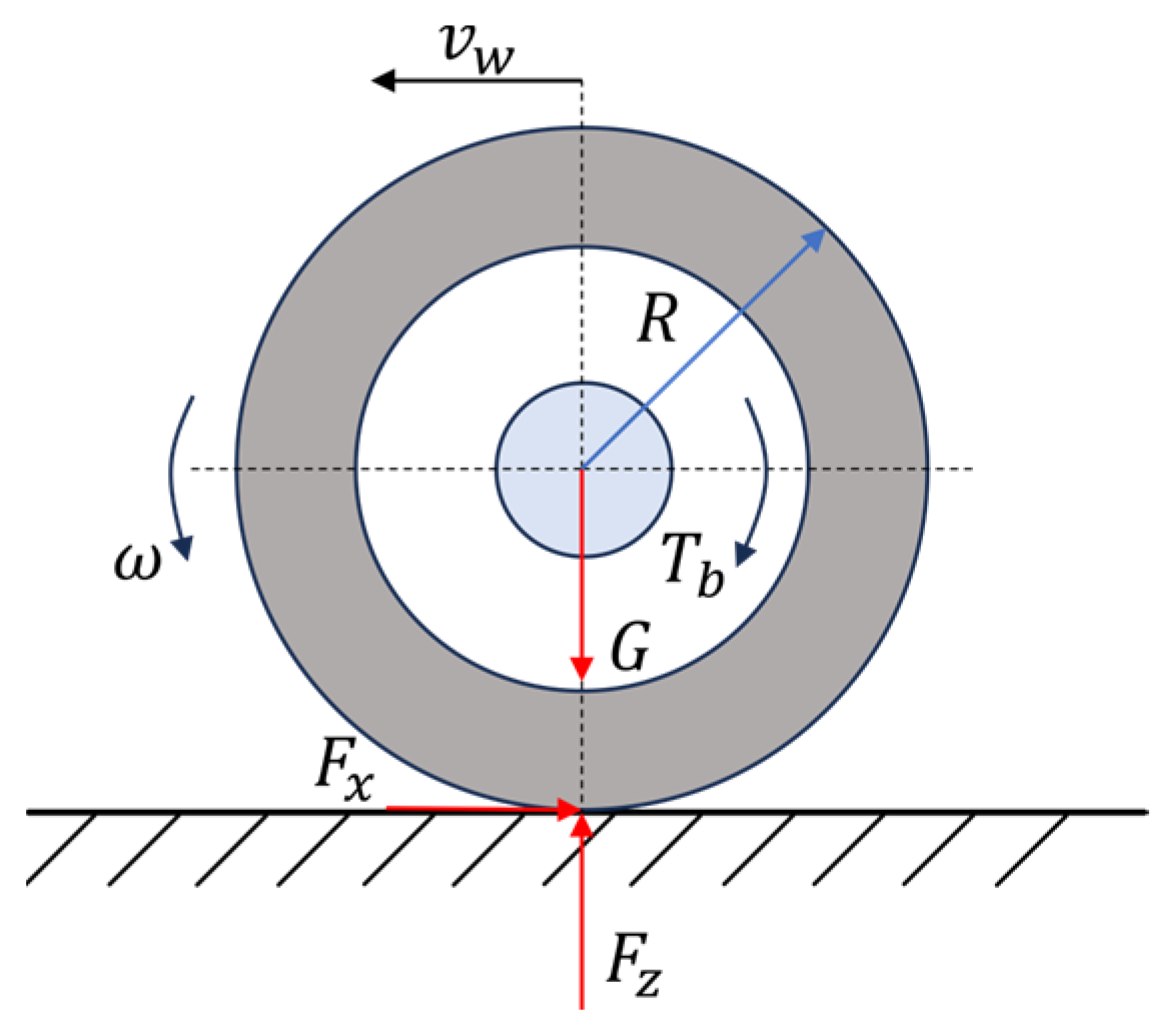
1. Introduction

With the increasing popularity of automobiles, environmental pollution poses severe challenges to improving the fuel economy of internal combustion engine vehicles. As an alternative solution, electric vehicles (EVs) attract significant attention for their potential to alleviate environmental pollution and energy shortages [1]. Meanwhile, vehicle chassis systems are evolving from the mechanically actuated configurations of conventional vehicles toward brake-by-wire, steer-by-wire, and suspension-by-wire systems in EVs. The brake-by-wire system addresses the issue of high coupling of braking forces among wheels in traditional braking systems, thereby enhancing the flexibility and freedom of braking force distribution. However, this also presents new challenges for braking force coordination. Traditional braking force distribution control utilizes a decentralized architecture, wherein subsystems such as electronic brakeforce distribution (EBD), anti-lock braking system (ABS), and direct yaw-moment control (DYC) collect vehicle data through their respective sensors and issue commands to the brake actuators based on their own control objectives [2]. Although this decentralized architecture offers a high degree of in-dependence among subsystems, it does not meet the requirements of the brake-by-wire system for flexible braking force coordination. Additionally, conflicts among subsystem commands can arise, reducing braking effectiveness. Consequently, a coordinated braking force control strategy is necessary to improve braking safety in EVs. On distributed drive platforms with four in-wheel motors, each drive motor, under the control of the regenerative brake system (RBS), can generate independent electric braking force at its corresponding wheel. This produced electric braking force is redundant with the mechanical braking force generated by the mechanical brake actuators, presenting new opportunities for coordinated braking force control. However, as the complexity of brake-by-wire systems in-creases, the likelihood of failures also grows, making it increasingly urgent to investigate braking force distribution and coordination strategies that can address braking force failure.

Braking force coordination control needs to reconcile the different requirements of sub-systems such as ABS, EBD, and DYC for braking force distribution, while also considering coordination strategies under brake system failure conditions. Tang et al. [3] proposed an MPC-based RBS-ABS coordination control strategy employing a nonlinear three-degree-of-freedom predictive model to compute the required braking torque corresponding to the desired wheel slip ratio. Xu et al. [4] designed a coordination control method for RBS and ABS in hybrid electric vehicles with compound motor structures. Liang et al. [5] proposed a coordination controller based on functional allocation, where the upper layer designs a dynamic stability envelope boundary using the phase plane method, the mid-layer employs robust $H_{\infty }$ feedback control and an improved PSO algorithm to calculate the additional yaw moment required by DYC, and the lower layer utilizes the Sequential Quadratic Programming (SQP) algorithm to coordinate wheel torque and braking torque. Zheng et al. [6] developed an extensible hierarchical coordination controller that considers the bounded rationality of control systems, where the monitoring layer uses an extension phase-plane method to classify vehicle states, and the coordination decision layer treats active front-wheel steering and DYC control as game-theoretic agents. Anh et al. [7] proposed compensating for the delay of hydraulic braking by leveraging the fast response of regenerative braking (RBS), thereby improving braking performance. Zhu et al. [8] optimized the distribution of longitudinal force, lateral force, and yaw moment to enhance vehicle stability, while supplementing the limitations of hydraulic braking with the fast response of electric braking, which shortened the braking distance. Chu et al. [9] addressed the conflict between RBS and ABS in regulating hydraulic braking during electric vehicle braking and proposed an ABS-RBS coordinated control strategy that balanced control performance and real-time response. Wang et al. [10] presented an adaptive fault-tolerant control strategy that generated additional tire forces and constrained yaw moments under braking system failures, thereby improving the tracking performance of target yaw rate and lateral velocity. Bai et al. [11] developed a longitudinal-lateral stability coordinated controller for a battery electric vehicle equipped with distributed EMB braking and centralized drive, based on an MPC algorithm and a hierarchical control architecture, which integrated ABS, DYC, and other braking force distribution functions. Yu et al. [12] focused on the integrated coordinated control of braking force distribution systems, including ABS, EBD, DYC, and RBS, within two-dimensional vehicle dynamics control.

For braking failure conditions in brake-by-wire vehicles, Wang et al. [13] proposed a control strategy that redistributed the braking torque lost due to a single actuator failure among the remaining wheel braking systems while counteracting the additional yaw moment. Zhang et al. [14] addressed braking failures in hub-motor electric vehicles and proposed a hierarchical fault-tolerant architecture that integrated regenerative braking and differential torque control to maintain both longitudinal and lateral stability. Feng et al. [15] developed a control allocation algorithm that redistributed braking force and compensated the yaw moment through steering angle adjustment, thereby ensuring safe braking performance under partial or complete braking failures. Zhou et al. [16] designed a dual-layer control architecture in which braking force redistribution was combined with yaw moment compensation based on sliding mode control, improving braking efficiency and stability under single-wheel failure in brake-by-wire systems. Tang et al. [17] presented a stability control strategy for single-wheel braking failure, which reconstructed torque through predefined rules and applied a front wheel steering controller to maintain braking stability. For regenerative braking system (RBS) failure conditions, Wang et al. [18] combined torque cut-off control, electro-hydraulic braking (EHB) torque compensation, and yaw stability control to achieve efficient coordination during regenerative braking failures. Fang et al. [19] proposed a front-rear axle braking force compensation and distribution strategy that integrated EHB compensation control with deviation-assisted control, selecting appropriate electro-hydraulic brake compensation schemes according to the se-verity of regenerative braking failure and the location of the failed wheel. For EMB failure scenarios, Wu et al. [20] proposed a multi-factor coupling fault-tolerant control strategy with a hierarchical architecture and dynamic braking force distribution. The HIL test results under a complete left-front actuator failure show that this strategy effectively handled the failure by reducing lateral displacement to 0.03 m while maintaining a deceleration of 3.7 m/s². Peng et al. [21] designed a fault-tolerant electro-mechanical brake architecture using Markov chains and force redistribution, and the probability of a dangerous failure per hour for the system was 6.14 FIT in hard-ware-in-the-loop (HIL) tests, satisfying ASIL-D requirements.

In summary, most existing braking force coordination studies employ a hierarchical control architecture integrating EBD, ABS, and DYC subsystems to coordinate braking demands based on LQR control and phase-plane stability boundaries, with optimization typically based on SQP algorithms and slip ratio or adhesion coefficient targets. However, existing research on braking force coordination mainly focuses on coordination under normal braking conditions, EMB redundancy backup during RBS failure, coordination of the remaining wheel braking forces during EMB failure, or cooperative control with steering systems. While mechanical and RBS can form mutually redundant relationships, research on braking force coordination strategies under mechanical braking failure compensated by RBS redundancy remains limited. Furthermore, above mentioned braking coordination control method based on LQR control and phase-plane stability boundaries is very difficult to dynamically handle conflicts between ABS and DYC, and it is also not applicable to multi-wheel sequential failures.

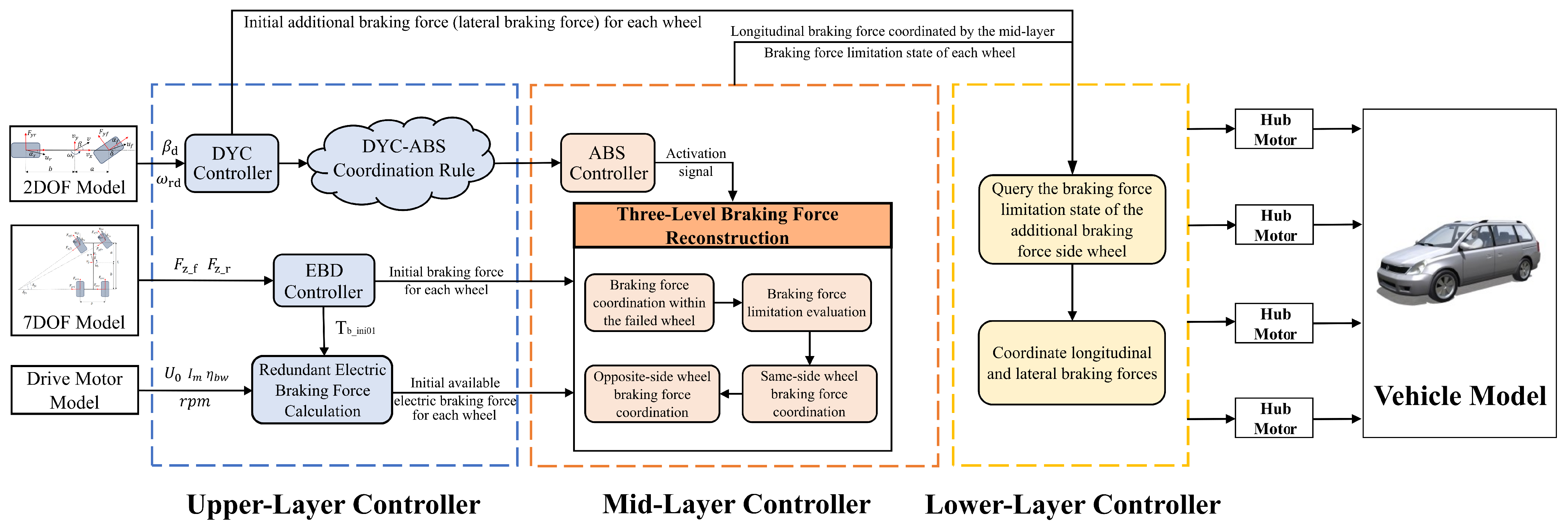
To address these issues, this paper proposes a braking force coordination control strategy for electric vehicles based on a hierarchical control architecture, aiming to resolve conflicts among dynamic braking force allocations during coordination of ABS, EBD, DYC, and RBS, as well as to compensate braking force dynamically under brake actuator failure. The proposed architecture consists of three layers: the upper-layer controller, which integrates EBD, DYC, and the available electric braking force computation module while establishing DYC-ABS coordination rules; the mid-layer controller, which incorporates a braking force limited state evaluation module and integrates ABS functionality to construct a three-level braking force reconstruction mechanism based on the temporal sequence and spatial position of failures; and the lower-layer controller, which coordinates longitudinal and lateral braking forces in response to actuator failure states. The main contributions of this paper are as follows.

• A dynamic computation model of the braking force limited coefficient is established to support braking force reconstruction and coordination.
• A braking force coordination control strategy for electric vehicles under actuator failure conditions is proposed, employing RBS as a full redundant braking actuator, which effectively improves braking stability and safety under fault scenarios.

2. System Model and Key Parameter Estimation

This study focuses on a four in-wheel motor distributed-drive electric vehicle equipped with steer-by-wire and a brake-by-wire system that adopts a front electro-hydraulic braking (EHB) and rear electromechanical braking (EMB) configuration. This structure combines the maturity of EHB with the fast response and flexible packaging advantages of EMB. The overall vehicle architecture is illustrated in Figure 1.

2.1. 7-DOF Vehicle Dynamics Model

The 7-DOF vehicle model includes yaw motion about the z-axis, lateral motion along the y-axis, longitudinal motion along the x-axis, and rotational motion of the four wheels, as shown in Figure 2. The corresponding dynamic equations are expressed as follows:

$$\begin{array}{c}m({\dot{v}}_x-v_y{\mathrm{\omega }}_r)=(F_{xfl}\cos {\delta }_{fl}+F_{xfr}\cos {\delta }_{fr})+(F_{xrl}+F_{xrr})\\ -(F_{yfl}\sin {\delta }_{fl}+F_{yfr}\sin {\delta }_{fr})\end{array}$$

(1)

$$\begin{array}{c}m({\dot{v}}_y+v_x{\mathrm{\omega }}_r)=(F_{xfl}\sin {\delta }_{fl}+F_{xfr}\sin {\delta }_{fr})+(F_{yrl}+F_{yrr})\\ +(F_{yfl}\cos {\delta }_{fl}+F_{yfr}\cos {\delta }_{fr})\end{array}$$

(2)

$$\begin{array}{l}{I}_z{\dot{\omega }}_r=(F_{yfl}\cos {\delta }_{fl}+F_{yfr}\cos {\delta }_{fr})a-(F_{yrl}+F_{yrr})b+(F_{yfl}\sin {\delta }_{fl}-F_{yfr}\sin {\delta }_{fr}){\displaystyle \frac{B}{2}}\\ \hspace{1em}\hspace{1em} +(F_{xfl}\sin {\delta }_{fl}+F_{xfr}\sin {\delta }_{fr})a-(F_{xfl}\cos {\delta }_{fl}-F_{xfr}\cos {\delta }_{fr}){\displaystyle \frac{B}{2}}-(F_{xrl}-F_{xrr}){\displaystyle \frac{B}{2}}\end{array}$$

(3)

where $F_{xij}$ and $F_{yij}$ represent the longitudinal and lateral forces acting on each wheel, respectively, ${\mathrm{\delta }}_{ij}$ is the steering angle of the front wheels; subscripts $\mathrm{ij}$ = $fl, fr, rl, rr$ correspond to the left-front, right-front, left-rear, and right-rear wheels, $\mathrm{m}$ is the vehicle mass, $v_x$ and $v_y$ are the longitudinal and lateral velocities at the vehicle’s center of gravity (CG), ${\mathrm{\omega }}_r$ is the yaw rate, $I_z$ is the yaw moment of inertia about the z-axis, $\mathrm{a}$ and $\mathrm{b}$ are the distances from the CG to the front and rear axles, respectively, $\mathrm{B}$ is the track width, and $\beta$ is the sideslip angle at the CG.

Considering the load transfer caused by longitudinal and lateral accelerations, the vertical load on each wheel can be expressed as shown in Equation (4).

$$\left\{\begin{array}{l}{F}_{zfl}={\displaystyle \frac{mgb-m{a}_x{h}_g}{2L}}-{\displaystyle \frac{m{a}_y{h}_{g}b}{LB}}\\ F_{zfr}={\displaystyle \frac{mgb-m{a}_x{h}_g}{2L}}+{\displaystyle \frac{m{a}_y{h}_{g}b}{LB}}\\ F_{zrl}={\displaystyle \frac{mga+m{a}_x{h}_g}{2L}}-{\displaystyle \frac{m{a}_y{h}_{g}a}{LB}}\\ F_{zrr}={\displaystyle \frac{mga+m{a}_x{h}_g}{2L}}+{\displaystyle \frac{m{a}_y{h}_{g}a}{LB}}\end{array}\right.$$

(4)

where $a_x$ and $a_y$ are the longitudinal and lateral accelerations, respectively, and $h_g$ is the height of the vehicle’s CG.

Roll and pitch are primarily caused by longitudinal and lateral accelerations. The impact of these accelerations on tire load variations has been revealed by Equation (4). The model directly couples real-time longitudinal and lateral accelerations into the calculation of wheel vertical loads, effectively capturing the influence of vehicle pitch and roll motions on tire load variations.

When a single failure occurs, the asymmetric braking force generated at the moment of failure induces changes in both longitudinal and lateral accelerations, directly exciting vehicle roll and pitch motions, which lead to load transfer from the failed side to the opposite-side wheel. Simultaneously, the continuous braking deceleration induces pitch motion, causing load redistribution from the rear axle to the front axle. In the case of dual-wheel failure, the complete loss of braking force on one side of either the front or rear axle results in severe pitch motion, causing a significant load transfer to the opposite side, thereby substantially reducing the load on the failed side.

2.2. 2-DOF Vehicle Dynamics Model

The linear 2-DOF vehicle model is utilized to calculate the ideal sideslip angle at the vehicle’s center of gravity and the ideal yaw rate, which serve as reference targets for the subsequent DYC control. The dynamic equations of the 2-DOF model are expressed in Equation (5), where $v_x$ is assumed to be constant, and the corresponding model is shown in Figure 3.

$$\left\{\begin{array}{l}m\left({\dot{v}}_y+2{\mathrm{\omega }}_r\cdot v_x\right)=F_{yf}\cos \mathrm{\delta }+F_{yr}\\ I_z{\dot{\mathrm{\omega }}}_r=a{F}_{yf}\cos \mathrm{\delta }-b{F}_{yr}\end{array}\right.$$

(5)

where $F_{yf}$ and $F_{yr}$ are the lateral forces on the front and rear axles, respectively, $F_{yf}=k_f\cdot {\alpha }_f$, $F_{yr}=k_r\cdot {\alpha }_r$, $k_f$ and $k_r$ are the cornering stiffness coefficients of the front and rear tires, and $\mathrm{\delta }$ represents the front wheel steering angle.

2.3. Wheel Dynamics Model During Braking

When developing the longitudinal braking force distribution controller, the control law must be derived from the wheel dynamics equations. Therefore, a wheel dynamics model during braking is established, and the corresponding model is illustrated in Figure 4, where $v_w$ is the wheel center velocity; $\mathrm{G}$ is the gravitational load on the wheel; $F_x$ is the longitudinal braking force acting on the tire-road interface, and $F_z$ is the normal reaction from the road surface.

The rotational dynamics of each wheel are given by:

$$I_w\dot{\mathrm{\omega }}=F_{x}r-T_b-T_f$$

(6)

where $\mathrm{\omega }$ is the angular velocity, $T_b$ is the braking torque, and $T_f$ is the rolling resistance torque.

2.4. In-Wheel Motor Model

Permanent magnet synchronous motors (PMSMs) are employed as the driving motors, arranged in a distributed drive configuration with hub-reduction gearboxes. The relationship between the output torque of the drive motor and the demanded torque is given by:

$$T_m={\displaystyle \frac{1}{1+{\mathrm{\iota }}_{t}s}}\max (T_{\max },T_d)$$

(7)

where $T_m$ is the motor output torque, ${\mathrm{\iota }}_t$ is the time constant of the first-order system, $T_{\max }$ is the maximum torque available at the current motor speed derived from the external characteristic curve, and $T_d$ is the target output torque.

The external characteristic curve of the drive motor is shown in Figure 5.

The MAP diagram of the target drive motor and its operating efficiency are shown in Figure 6.

2.5. Key Parameter Estimation

The longitudinal vehicle velocity serves as a key input for DYC and other subsystems, while the Tire-Road Peak Adhesion Coefficient (TRPAC) directly affects braking force allocation strategies. This chapter presents a longitudinal vehicle velocity estimation algorithm that fuses wheel speed and acceleration data. The approach is validated through both simulations and physical vehicle tests. Due to the space limitation of this article, a detailed description of the TRPAC estimation method based on excitation assessment, as well as its validation, can be referred to in the papers previously published by our team [22].

2.5.1. Longitudinal Vehicle Speed Estimation

The process flow of the proposed longitudinal velocity estimation algorithm is shown in Figure 7.

Wheel speed signals are measured by sensors mounted on all four wheels. However, due to the different turning radii of inner and outer wheels during cornering, their rotational speeds differ. Therefore, the four-wheel speeds must be converted to the equivalent velocity at the center of the rear axle before being used as inputs for longitudinal velocity estimation. The conversion relationship could be given as follows:

$$\left\{\begin{array}{l}{v}_{Tfl}={\displaystyle \frac{v_{wfl}-{\mathrm{\omega }}_{r}L\sin \mathrm{\delta }}{\cos \mathrm{\delta }}}+0.5{\mathrm{\omega }}_{r}B\\ v_{Tfr}={\displaystyle \frac{v_{wfr}+{\mathrm{\omega }}_{r}L\sin \mathrm{\delta }}{\cos \mathrm{\delta }}}-0.5{\mathrm{\omega }}_{r}B\\ v_{Trl}=v_{wrl}+0.5{\mathrm{\omega }}_{r}B\\ v_{Trr}=v_{wrr}-0.5{\mathrm{\omega }}_{r}B\end{array}\right.$$

(8)

where $v_{Tij}$ and $v_{wij}$ are the converted and original wheel speeds, respectively, and the converted wheel speeds are sorted in descending order as $v_1\sim v_4$.

The velocity change gradients ${\nabla }_1\sim {\nabla }_4$ are determined according to Equation (9) based on the longitudinal acceleration and the current vehicle speed; among these, ${\nabla }_1$ and ${\nabla }_2$ correspond to the velocity change gradients when ABS is inactive, while ${\nabla }_3$ and ${\nabla }_4$ correspond to the gradients when ABS is active.

$$\begin{array}{l}{\nabla }_1=\min \left(\max (0.1,{\displaystyle \frac{a_x}{g}}+0.2),0.85\right)\cdot g\\ {\nabla }_2=\left\{\begin{array}{l}-0.35g, \mathrm{if} v_{x0}\le 2.56 \mathrm{m}/\mathrm{s}\\ -0.85g, \mathrm{else}\end{array}\right.\\ {\nabla }_3=0.85g\\ {\nabla }_4=0.985a_x\end{array}$$

(9)

When ABS is activated, the maximum wheel speed $v_1$ is used as the reference velocity. When ABS is inactive, the maximum wheel speed $v_1$ together with the third-largest wheel speed $v_3$ are selected as the reference velocities. The velocity constraint rule is defined as shown, where $v_x$ is the estimated longitudinal velocity; $v_{x0}$ is the previously estimated longitudinal velocity; ${\nabla }_i$ is the velocity change gradient, and $T_s$ is the sampling period.

$$v_x=v_{x0}+{\nabla }_i{T}_s$$

(10)

The iterative process for correcting the reference velocity based on the velocity constraint rule is illustrated in Figure 8, where ${\tilde{v}}_{x0}$ is the previously estimated longitudinal velocity $v_{x0}$ from the last control cycle.

2.5.2. Validation of the Estimation Algorithm

To evaluate the effectiveness of the proposed longitudinal velocity estimation algorithm, a straight-line emergency braking test was conducted, which represents an extreme operating condition where the difference between wheel speed and true vehicle speed is most significant. The test was performed from an initial velocity of 100 km/h with braking initiated at 0.5 s under road adhesion coefficients of μ = 0.85 and μ = 0.3.

The results, shown in Figure 9, indicate that the estimated longitudinal velocity closely follows the true value, unaffected by wheel speed fluctuations. The maximum absolute error occurs during ABS activation, recorded at 0.85 m/s and 1.06 m/s, respectively. Both error values are below 1.5 m/s, with corresponding percentage errors of 3.27% and 3.89%, each remaining under 5%. Therefore, the estimation accuracy of the longitudinal vehicle speed fully satisfies the requirements for braking force coordination control.

The architecture of the real-vehicle test platform is shown in Figure 10. The installation and layout of the experimental equipment are shown in Figure 11.

To further evaluate algorithm adaptability under mixed driving conditions, a composite steering step test involving acceleration, deceleration, and steering maneuvers was conducted. The test procedure initiates with the steering wheel in the neutral position. The vehicle then accelerates while simultaneously turning the steering wheel to a 90° step input and maintaining this angle. The vehicle speed increases from 0 to approximately 9 m/s, maintains this velocity for a period, and subsequently undergoes braking until a complete stop, which concludes the test.

A 25-s data segment is extracted from the longitudinal vehicle speed estimation experiment, with the results shown in Figure 12. A left-turn steering maneuver is performed during the experiment. As shown in Figure 12b, the wheel speeds on the right side are significantly higher than those on the left. The maximum absolute error of the longitudinal velocity estimation occurs at 16.09 s, with a value of 0.4 m/s, which is below the 1.5 m/s. The corresponding percentage error is 4.73%, still remaining within the 5%. These results demonstrate that the proposed wheel-speed and acceleration fusion-based longitudinal velocity estimation algorithm achieves high accuracy and meets engineering application requirements.

3. Design of Braking Force Coordination Control Strategy

To address braking instability under actuator failure conditions, this paper proposes a braking force coordination control strategy based on a hierarchical control architecture, as shown in Figure 13. The strategy consists of three layers: The upper-layer controller integrates EBD, DYC, and the available electric braking force computation module while establishing DYC-ABS coordination rules. The mid-layer controller includes braking force limited state evaluation and integrates ABS functionality to construct a three-level braking force reconstruction mechanism based on failure timing and location. The lower-layer controller coordinates longitudinal and lateral braking forces according to actuator failure states. Since EMB replaces mechanical and hydraulic components with electronic devices, concerns regarding reliability and insufficient redundancy remain [23]. Therefore, this study mainly addresses EMB failure scenarios.

3.1. Upper-Layer Controller

The proposed upper-layer controller is composed of the EBD, DYC, and the available electric braking force computation module, as well as the DYC–ABS coordination rules. The specific analysis is presented as follows.

3.1.1. EBD Controller

Since the EBD requires the driver’s desired braking force, a driver model is designed to track the target vehicle speed, essentially functioning as a longitudinal speed tracking controller. Proportional–integral–derivative (PID) control is employed to minimize the speed error between the desired and actual vehicle speeds and to generate the required longitudinal torque.

EMB outputs the initial braking force for each wheel based on the driver’s desired braking force. In this study, the EBD controller is designed based on a dynamic axle-load and wheel-speed deviation correction method. The initial front-rear braking force distribution coefficient ${\beta }_{ini}$ is first determined using the dynamic vertical loads of each wheel. Then, ${\beta }_{ini}$ is corrected according to the wheel-speed deviation between the front and rear wheels, resulting in the final braking force distribution coefficient ${\beta }_b$.

Based on the 7-DOF vehicle dynamics model, the vertical load on the front and rear axles can be obtained as follows:

$$\left\{\begin{array}{l}{F}_{z\_f}=m\left(gb-a_x{h}_g\right)/L\\ F_{z\_r}=m\left(gb+a_x{h}_g\right)/L\end{array}\right.$$

(11)

where $F_{z\_f}$ and $F_{z\_r}$ are the vertical loads acting on the front and rear axles, respectively.

The initial braking force distribution coefficient is given by:

$${\beta }_{ini}=F_{z\_f}/\left(F_{z\_f}+F_{z\_r}\right)$$

(12)

During vehicle braking, wheels with lower speeds exhibit a greater tendency to lock up compared to those with higher speeds. Wheel speed can reflect this locking tendency, and the ratio of the wheel speeds between the front and rear axles can be utilized to correct the initial coefficient ${\beta }_{ini}$.

The front-rear wheel-speed ratio $\mathrm{\Lambda }$ is defined as:

$$\mathrm{\Lambda }=\left(n_{rl}+n_{rr}\right)/\left(n_{fl}+n_{fr}\right)$$

(13)

The ideal front-rear wheel-speed ratio is ${\mathrm{\Lambda }}_d=1$, and the wheel-speed ratio error is defined as:

$$E_{\mathrm{\Lambda }}={\mathrm{\Lambda }}_d-\mathrm{\Lambda }$$

(14)

Using a discrete PID algorithm, the front-rear wheel-speed ratio error is employed to provide feedback compensation for ${\beta }_{ini}$:

$$\left\{\begin{array}{l}{\Delta }_{\beta }=E_{\mathrm{\Lambda }}\left(z\right)\left(P_{EBD}+I_{EBD}\cdot T_s{\displaystyle \frac{1}{z-1}}+D_{EBD}{\displaystyle \frac{N}{1+N\cdot T_s\frac{1}{z-1}}}\right)\\ {\beta }_b={\beta }_{ini}+{\Delta }_{\mathrm{\beta }}\end{array}\right.$$

(15)

where $E_{\mathrm{\Lambda }}\left(z\right)$ is the transformed value of $E_{\mathrm{\Lambda }}$ after the z-domain conversion, $P_{EBD}$, $I_{EBD}$, and $D_{EBD}$ are the weighting coefficients of the proportional, integral, and derivative terms, respectively, and $N$ is the filtering factor, with $N=100$.

The front-rear braking force distribution coefficient must also satisfy the following constraint:

$$\left\{\begin{array}{l}{\beta }_d\le {\displaystyle \frac{\left(z+0.07\right)\left(b+z{h}_g\right)}{0.85zL}}, 0.1< z < 0.61\\ {\beta }_d\ge 1-{\displaystyle \frac{\left(z+0.05\right)\left(a-z{h}_g\right)}{L}}, 0.3< z < 0.45\\ {\beta }_d\ge {\displaystyle \frac{\left(b+z{h}_g\right)}{L}}, 0.15< z < 0.6\end{array}\right.$$

(16)

Based on the corrected front-rear braking force distribution coefficient ${\beta }_b$, the system limits the braking force of the rear axle to ensure that the braking force distribution between the front and rear brake actuators reaches the ideal ratio.

3.1.2. DYC Controller

The DYC system calculates the required additional yaw moment using an LQR controller, and this moment is allocated through an additional braking force distributor. By applying unilateral braking, the corresponding additional yaw moment is generated to suppress understeer or oversteer tendencies during vehicle cornering.

Considering the neutral-steer steady-state characteristics represented by the 2-DOF linear vehicle dynamics model, the model outputs, namely the sideslip angle at the vehicle’s center of gravity ${\beta }_d$ and the yaw rate ${\mathrm{\omega }}_{rd}$, are constrained dynamically based on the road adhesion coefficient μ, thereby forming the theoretical reference values for the closed-loop DYC control system.

$$\begin{array}{l}{\beta }_d={\displaystyle \frac{b/L+ma{v}_x^2/(L^2{k}_r)}{1+K{v}_x^2}}\\ {\mathrm{\omega }}_{rd}={\displaystyle \frac{v_x/L}{1+K{v}_x^2}}\end{array}$$

(17)

where $\mathrm{K}$ is the stability factor of the vehicle during steering.

The reference values for the sideslip angle at the center of gravity and the yaw rate are given as follows:

$$\begin{array}{l}{\beta }_{ref}=\min \left\{{\beta }_d\mathrm{sgn}(\delta ), \arctan (0.02\mu g)\mathrm{sgn}(\delta )\right\}\\ {\mathrm{\omega }}_{ref}=\min \left\{{\mathrm{\omega }}_d\mathrm{sgn}(\delta ), 0.85\mathrm{\mu }g/v_x\mathrm{sgn}(\mathrm{\delta })\right\}\end{array}$$

(18)

The state-space representation is derived from Equation (17) as follows:

$$\begin{array}{c}\left[\begin{array}{c}\Delta \dot{\beta }\\ \Delta {\dot{\mathrm{\omega }}}_r\end{array}\right]=M\left[\begin{array}{c}\Delta \beta \\ \Delta {\mathrm{\omega }}_r\end{array}\right]+N\Delta M\\ M=\left[\begin{array}{cc}{\displaystyle \frac{k_f+k_r}{m{v}_x}}& {\displaystyle \frac{a{k}_f-b{k}_r}{{m{v}_x}^2}}-1\\ {\displaystyle \frac{a{k}_f-b{k}_r}{I_z}}& {\displaystyle \frac{a{k}_f-b{k}_r}{I_z{v}_x}}\end{array}\right], N=\left[\begin{array}{c}0\\ {\displaystyle \frac{-1}{I_z}}\end{array}\right]\end{array}$$

(19)

where $\Delta \beta ={\beta }_{ref}-\beta$ and $\Delta {\mathrm{\omega }}_r={\mathrm{\omega }}_{ref}-\mathrm{\omega }$, and $\Delta M$ is the additional yaw moment.

Let $x={\left[\Delta \beta , \Delta {\mathrm{\omega }}_r\right]}^{\mathrm{T}}$ and $u=\Delta M$, and Equation (19) can be rewritten as:

$$\dot{x}=Mx+Nu$$

(20)

The optimal control input $u^{*}$ is given as follows:

$$\begin{array}{l}{u}^{*}=-K_{L}x(t)\\ \left\{\begin{array}{l}{K}_L=R_L^{-1}\cdot N^{\mathrm{T}}\cdot P\\ M^{\mathrm{T}}P+PM+Q_L-PN{R}^{-1}{N}^{\mathrm{T}}P=0\end{array}\right.\end{array}$$

(21)

where $Q_L$ and $R_L$ are the weighting matrices for the state vector $x$ and the input vector $u$, respectively.

The additional yaw moment applied to the front and rear wheels is distributed according to the rule specified in Equation (22).

$$\begin{array}{l}\Delta M_f=\Delta M\cdot \left(b+z\cdot h_g\right)/L\\ \Delta M_r=\Delta M\cdot \left(a-z\cdot h_g\right)/L\end{array}$$

(22)

When $\Delta M$ is positive, the additional braking force is applied to the left-side wheels according to the following rule:

$$\begin{array}{l}\Delta F_{bfl}={\displaystyle \frac{\Delta M_f}{\sin (\left|\mathrm{\delta }\right|)\cdot a+\cos (\left|\mathrm{\delta }\right|)\cdot 0.5B}}\\ \Delta F_{brl}={\displaystyle \frac{2}{B}}\Delta M_r\end{array}$$

(23)

When $\Delta M$ is negative, the additional braking force is applied to the right-side wheels according to the following rule:

$$\begin{array}{l}\Delta F_{bfr}={\displaystyle \frac{-\Delta M_f}{-\sin (\left|\mathrm{\delta }\right|)\cdot a+\cos (\left|\mathrm{\delta }\right|)\cdot 0.5B}}\\ \Delta F_{brr}={\displaystyle \frac{2}{B}}\Delta M_r\end{array}$$

(24)

3.1.3. Computation of Available Electric Braking Force

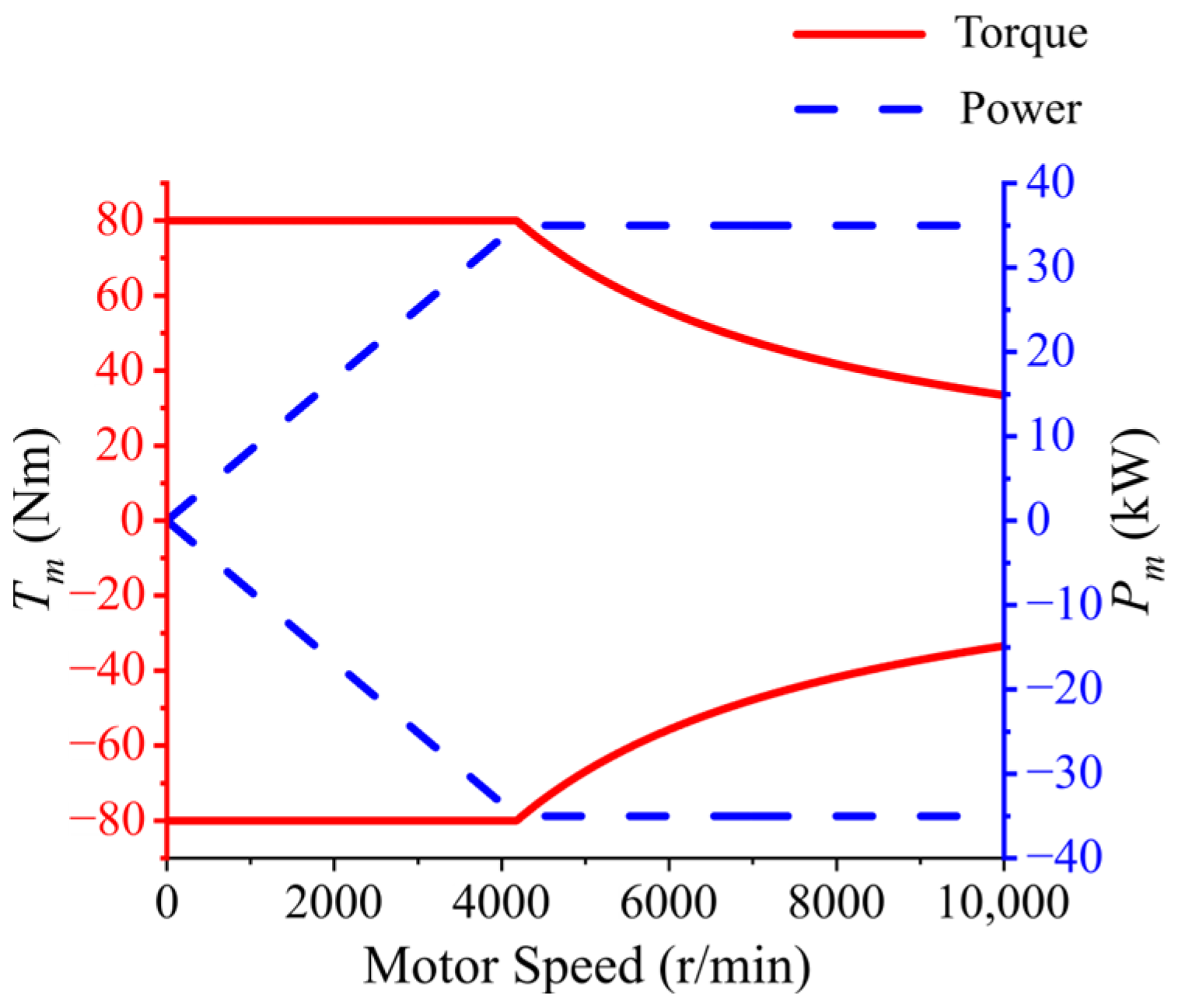
When the electric braking mode is activated on a specific wheel, such as during EMB failure conditions where RBS functions as a redundant braking system, the redundant electric braking force calculation module delivers both the initial electric braking force and the available electric braking force for all four wheels. Conversely, when the electric braking mode is not activated on a wheel, such as when it is operating under EHB or EMB actuation states, both the available electric braking force and the initial electric braking force for that wheel remain zero.

The available output power of the motor under regenerative braking conditions is given as follows:

$$P_{bm\_w}={\displaystyle \frac{U_0{\mathrm{I}}_{\mathrm{m}}}{n_{bw}}}$$

(25)

where $U_0$ is the rated voltage of the power battery, $I_m$ is the dynamic maximum charging current of the power battery, and ${\mathrm{\eta }}_{bw}$ is the dynamic operating efficiency of the drive motor for a given wheel.

The mechanical power required by the load is given as follows:

$$P_{b\_w}={\displaystyle \frac{T_{b\_ini01}\cdot rpm}{9550}}$$

(26)

where $T_{b\_\mathrm{ini}01}$ is the torque corresponding to the initial braking force on a given wheel, and $rpm$ is the rotational speed of the drive motor.

When $P_{bm\_w}\ge P_{b\_w}$, the motor braking torque can fully meet the demand, and the motor braking torque is set to the target value as follows:

$$T_{b\_ini02}=T_{b\_ini01}$$

(27)

The corresponding available electric braking torque of the motor is given as follows:

$$T_{b\_surplus\_ini01}={\displaystyle \frac{9550P_{bm\_w}}{rpm}}-T_{b\_ini02}$$

(28)

When $P_{bm\_w}<P_{b\_w}$, the motor braking torque is limited and is determined by the maximum available power.

$$T_{b\_ini02}={\displaystyle \frac{9550P_{bm\_w}}{rpm}}$$

(29)

Due to insufficient motor power, the available electric braking torque is zero.

$$T_{b\_surplus\_ini01}=0$$

(30)

Thus, the initial electric braking force and the initial available electric braking force are calculated as shown in Equation (31).

$$\begin{array}{l}{F}_{bij\_RBS\_ini}={\displaystyle \frac{T_{b\_ini02}}{R}}\\ F_{bij\_RBS\_surplus\_ini}={\displaystyle \frac{T_{b\_surplus\_ini01}}{R}}\end{array}$$

(31)

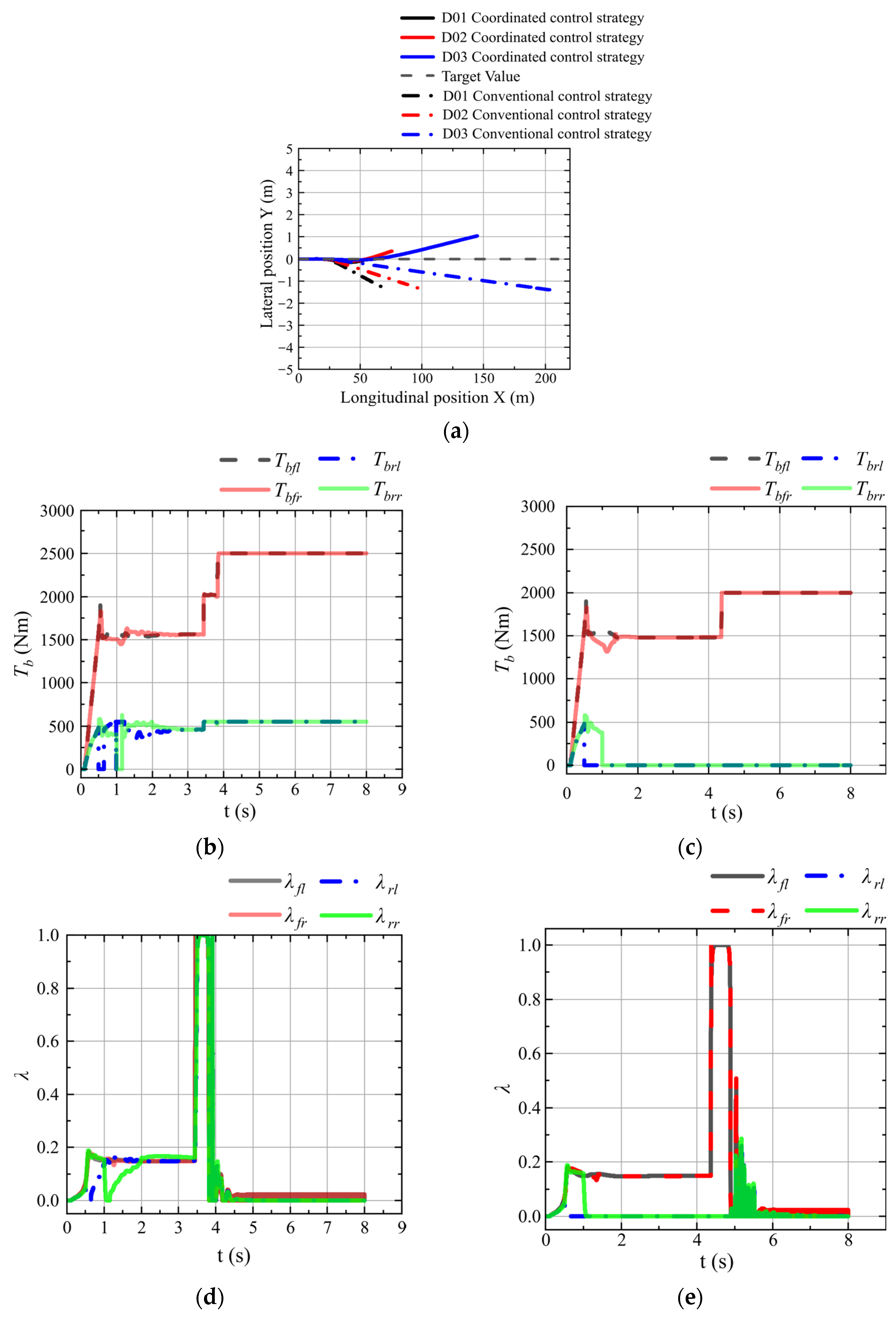
When the RBS on a failed wheel cannot generate sufficient target braking force, the coordination mechanism is activated to engage the mechanical brakes on functional wheels, thereby compensating for the deficient braking force or executing relevant dynamics control actions.

3.1.4. Coordination Strategy Between DYC and ABS

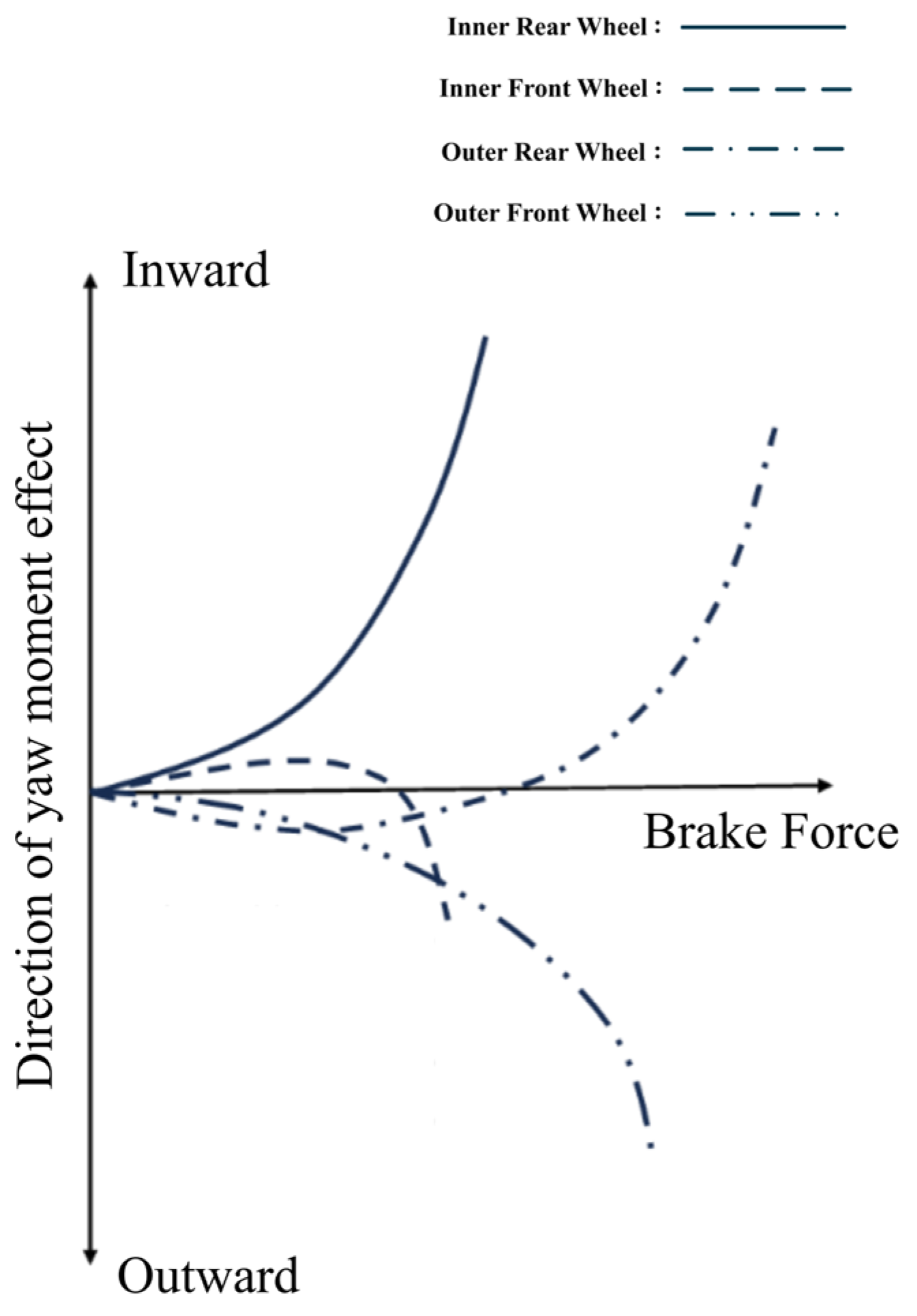
The application of excessive additional braking force by the DYC system on a wheel may trigger the ABS control system, necessitating coordination between DYC and ABS. The DYC system generates the additional yaw moment through unilateral braking, where the left side is defined as the inner wheel during a left turn and vice versa [24]. As shown in Figure 14, braking should be prioritized on the inner rear wheel in understeer conditions, whereas the outer front wheel should be prioritized in oversteer conditions. The braking force distribution for the inner front and outer rear wheels must adhere to the adhesion ellipse theory. Based on this, the DYC system control strategy is established as follows: actuators for the inner rear and outer front wheels may adopt an unrestricted regulation strategy without activating the ABS control module; whereas the inner front and outer rear wheels require a restricted regulation strategy, where the ABS control is synchronously activated when the wheel slip ratio exceeds the critical threshold. The coordination control rules of DYC and ABS are provided in

Table 1. Coordination control rule table of DYC and ABS.

Steering Status	Wheel Without ABS Control	Wheel Receiving ABS Control
Left turn, understeer	rl	fl, fr, rr
Left turn, oversteer	fr	fl, rl, rr
Right turn, oversteer	fl	fr, rl, rr
Right turn, understeer	rr	fl, fr, rl

.

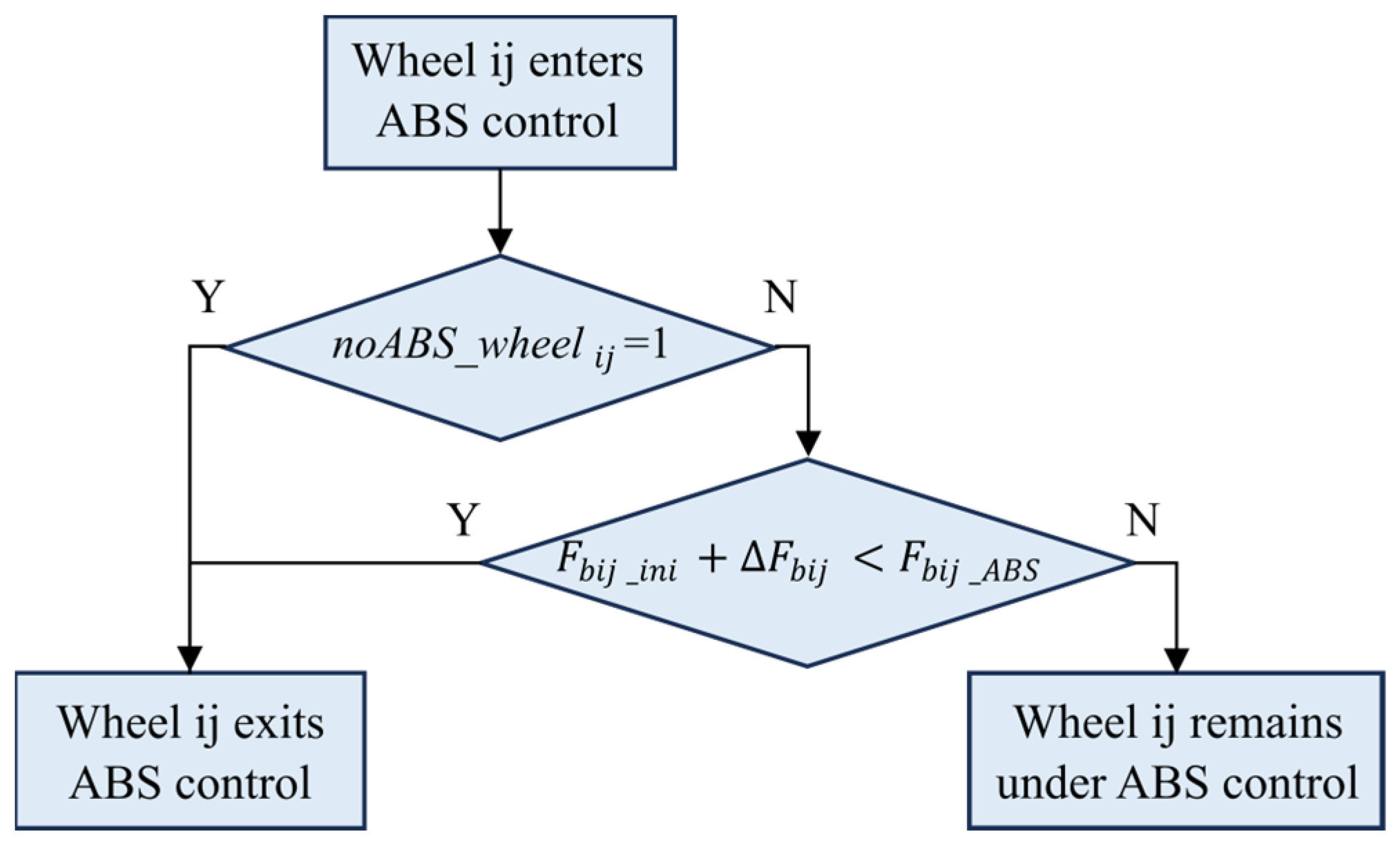
When the slip ratio of a wheel increases due to the additional braking force applied by the DYC system, triggering ABS intervention, the ABS control should be promptly deactivated after the demand for additional braking force ceases and no braking demand exists for that wheel. The coordination exit strategy between ABS and DYC is illustrated in Figure 15, where $F_{bij\_ABS}$ is the target braking force output by the ABS controller for ij-wheel, and $noABS\_whee{l}_{ij}$ is the ABS activation signal for ij-wheel. When $noABS\_whee{l}_{ij}=1$, the ABS control is not activated for the corresponding wheel.

Eventually, the upper-layer controller outputs to the middle/lower layers the initial braking forces for all four wheels, the initial electric braking forces, the available electric braking forces, and the additional braking forces and the $noABS\_whee{l}_{ij}$ signal.

3.2. Mid-Layer Controller

The proposed mid-layer controller is composed of the ABS and the braking force limited state evaluation module, and a three-level braking force reconstruction mechanism based on the temporal sequence and spatial position of failures. The detailed analysis is provided below.

3.2.1. ABS Controller

An ABS control strategy is established based on Sliding Mode Control (SMC). The dynamic model of the wheel during braking is shown in Figure 4. The wheel center velocity $v_w$, the wheel angular velocity $\mathrm{\omega }$, and the wheel slip ratio $\mathrm{\lambda }$ are selected as the state variables, i.e., $x_{S1}=v_w$, $x_{S2}=\mathrm{\omega }$, $x_{S3}=\mathrm{\lambda }=\left(x_{S1}-r{x}_{S2}\right)/x_{S1}$, with the braking torque $T_b$ as the input. The state-space representation is given by Equation (32).

$$\left\{\begin{array}{l}{\dot{x}}_{S1}=-F_x/m\\ {\dot{x}}_{S2}=\left(F_{x}r-T_b\right)/I_z\\ {\dot{x}}_{S3}=-\left({\dot{x}}_{S1}/x^2{S}_1\right)\left(x_{S1}-r{x}_{S2}\right)+\left(1/x_{S1}\right)\left({\dot{x}}_{S1}-r\cdot {\dot{x}}_{S2}\right)\end{array}\right.$$

(32)

The state-space representation can be reformulated as follows:

$$\left\{\begin{array}{l}{\dot{x}}_{S1}=-F_x/m\\ {\dot{x}}_{S2}=\left(F_{x}r-T_b\right)/I_z\\ {\dot{x}}_{S3}={\displaystyle \frac{F_x}{v_w}}f\left(\mathrm{\lambda }\right)+{\displaystyle \frac{r{T}_b}{v_w{I}_z}}\\ f\left(\mathrm{\lambda }\right)=\left({\displaystyle \frac{\mathrm{\lambda }-1}{m}}-{\displaystyle \frac{r^2}{I_z}}\right)\end{array}\right.$$

(33)

The error tracking function is defined as follows:

$$S=ce$$

(34)

where $e=\left(\mathrm{\lambda }-{\mathrm{\lambda }}_d\right)$, ${\mathrm{\lambda }}_d$ is the target slip ratio, and $c>0$.

The Lyapunov function is defined as follows:

$$V={\displaystyle \frac{1}{2}}{S}^2$$

(35)

Thus, $\dot{V}=S\dot{S}\le 0$, $\dot{S}=c\dot{\mathrm{\lambda }}=c{\dot{x}}_3=c\left[{\displaystyle \frac{F_x}{v_w}}f\left(\mathrm{\lambda }\right)+{\displaystyle \frac{r{T}_b}{v_w{I}_z}}\right]$.

An exponential reaching law is selected.

$$\dot{S}=c\left[{\displaystyle \frac{F_x}{v_w}}f\left(\mathrm{\lambda }\right)+{\displaystyle \frac{r{T}_b}{v_w{I}_z}}\right]=-\mathrm{\epsilon }\mathrm{sgn}(S)-pS$$

(36)

where $\mathrm{\epsilon }>0$, $p>0$, and $\mathrm{sgn}(S)$ is the sign function of.

Based on Equation (36), the control law for the braking torque $T_b$ can be derived as follows:

$$T_b=-{\displaystyle \frac{v_{\mathrm{\omega }}{I}_z}{rc}}\left[\mathrm{\epsilon }\mathrm{sgn}\left(S\right)+pS\right]-{\displaystyle \frac{F_x{I}_z}{v_{\mathrm{\omega }}r}}\cdot f\left(\mathrm{\lambda }\right)$$

(37)

To mitigate the chattering issue in the sliding mode controller, the sign function is replaced with a saturation function. This substitution ensures a smooth transition of the control input when the error tracking function changes sign. The modified control law for $T_b$ after incorporating the saturation function is given as follows:

$$T_b=-{\displaystyle \frac{v_{\mathrm{\omega }}{I}_z}{rc}}\left[\mathrm{\epsilon }\mathrm{sat}\left(S\right)+pS\right]-{\displaystyle \frac{F_x{I}_z}{v_{\mathrm{\omega }}r}}\cdot f\left(\mathrm{\lambda }\right)$$

(38)

3.2.2. Three-Level Braking Force Reconfiguration

The mid-layer controller primarily coordinates the braking force through its three-level braking force redistribution function, adhering to the principle of maintaining equal braking forces on both sides during redistribution. When EHB or EMB serves as the brake actuator, control is managed by a conventional ABS controller; while when RBS acts as the brake actuator, control is implemented by the RBS_ABS controller.

When a wheel does not trigger ABS and enters the failure mode, a three-level braking force redistribution is executed in four steps: (1) Braking force coordination within the failed wheel; (2) Braking force limited state evaluation; (3) Same-side wheel braking force coordination; (4) Opposite-side wheel braking force coordination.

When the wheel triggers ABS and enters the failure mode, due to EMB failure, the RBS_ABS controller is utilized for control. Once the wheel enters the ABS control state, it cannot participate in the braking force coordination within the failed wheel. Therefore, the ABS activation status and the braking force of the ABS-activated wheels are directly input into the braking force limited evaluation module, which subsequently provides a reference for the following brake force coordination process.

(1)

Braking force coordination within the failed wheel: when EMB fails and the RBS is used as the redundant braking system, the available electric braking force of the failed wheel is assessed. If the initial available electric braking force of the failed wheel is greater than zero, the failed wheel can achieve full redundant braking. However, if the initial available electric braking force of the failed wheel is less than or equal to zero, it indicates that the electric braking force provided by the drive motor has reached its limit, and full redundant braking cannot be achieved within the failed wheel. In this case, the coordination of the same-side wheel is requested to compensate for the missing brake force of the failed wheel.

(2)

Braking force limited state evaluation: before performing the same-side wheel braking force coordination control, it is necessary to determine the extent of brake force limitation for each wheel. The rules for determining the braking force limited weight are shown in

Table 2. The rules for determining the braking force limited weight.

Braking Force Limited Weight	Wheel Status
	ABS Not Activated			ABS Activated
	RBS Not Activated	RBS Activated		RBS Not Activated	RBS Activated
	/	Available Electric Braking Force > 0	Available Electric Braking Force ≤ 0
${\mathrm{Lim}\text{\_}\mathrm{Weight}}_{ij}$	0	0	1.1	1	1.2

, where ${\mathrm{Lim}\text{\_}\mathrm{Weight}}_{ij}$ is the braking force limited weight for each wheel. When designing the specific values for the braking force limited weight, it is important to note that when the wheels on both sides are in different states, the sum of the braking force limited weights for the single-side wheels should not be equal, as this would affect the braking force coordination of the opposite-side wheel. A braking force limited weight less than 0.5 indicates an unrestricted brake force state, greater than 0.5 indicates a fully limited brake force state, and equal to 0.5 indicates a partially limited brake force state. The selection of weight values is intended to distinguish the severity of the failure conditions.

(3)

Same-side wheel braking force coordination: when the backup braking force available from the failed wheel is limited and full redundant braking cannot be achieved, the coordination of the same-side wheel braking force is requested. This coordination allows the wheel with unrestricted brake force on the same side to compensate for the missing brake force portion.

The same-side wheel braking force coordination module first evaluates the braking force limitation coefficient of the same-side front wheel. If the limitation coefficient ${\mathrm{Lim}\text{\_}\mathrm{Weight}}_{ij}\le 0.5$, indicating that the wheel is in an incompletely limited braking state, the same-side front wheel compensates for the required braking force. If the front wheel is in a fully limited braking state, coordination with the opposite-side wheel is requested to ensure equal braking forces on both sides.

$$\begin{array}{l}{F}_{b\_opp\_l}=F_{brl\_ini}-F_{brl\_RBS\_ini}\\ F_{b\_opp\_r}=F_{brr\_ini}-F_{brr\_RBS\_ini}\end{array}$$

(39)

where $F_{b\_opp\_l}$ and $F_{b\_opp\_r}$ are the braking forces requested from the opposite-side wheels for coordination on the left and right sides, respectively; $F_{brl\_\mathrm{ini}}$ and $F_{brr\_\mathrm{ini}}$ are the initial braking forces of the rear-left and rear-right wheels; $F_{brl\_\mathrm{RBS}\_\mathrm{ini}}$ and $F_{brr\_\mathrm{RBS}\_\mathrm{ini}}$ are the initial electric braking forces of the rear-left and rear-right wheels, respectively.

(4)

Opposite-side wheel braking force coordination: when the braking force of the front wheel on the same side as the failed wheel is in a fully limited state, the coordination of the opposite-side wheel braking force should be requested.

The opposite-side wheel braking force coordination module first compares the braking force limited weights of the left and right wheels. The side with the higher limited weight indicates a more severe braking failure situation, with a smaller available brake force coordination space. Therefore, the braking force coordination request from the side with the larger braking force limited weight is taken as the target coordination braking force $F_{b\_opp}$, and the wheel on the side with the smaller braking force limited weight responds to this target coordination braking force. If the braking force limited weights on both sides are equal, then $F_{b\_opp}=0$.

Next, the braking force limited state of the wheel with the smaller limited weight is checked. If both wheels are fully limited in braking force, opposite-side braking force coordination cannot be performed. If only one wheel is in a non-fully limited braking force state, that wheel will handle the coordination. If both wheels have non-fully limited braking forces, the SQP algorithm is used to coordinate $F_{b\_opp}$ with the wheel on the side with the smaller limited braking force. The side with the larger braking force limited weight is the coordinated side, while the side with the smaller limited weight is the coordinating side. If $F_{b\_opp}$ is less than zero, indicating that the coordinated side’s braking force is fully limited, the coordinating wheel must reduce its braking force to ensure that the braking forces on both sides are balanced. Since maintaining directional stability is generally more important than minimizing braking distance, the coordinating wheel can reduce some of its braking force to ensure stability, but the reduction should not exceed 20% of its original braking force.

When coordinating braking force based on the SQP algorithm, the optimization criterion is to minimize the total tire force utilization on that side of the vehicle, adjusting the front and rear braking forces accordingly. The expression for tire force utilization is as follows:

$${\mathrm{\eta }}_{ij}={\displaystyle \frac{\sqrt{{F_{xij}}^2+{F_{yij}}^2}}{{\mathrm{\mu }}_{ij}{F}_{zij}}}$$

(40)

where $i=f, r$ and $j=l, r$ are the front, rear, and left, right wheels, respectively; $F_{xij}$, $F_{yij}$, and $F_{zij}$ are the longitudinal force, lateral force, and vertical load on each wheel, respectively; ${\mathrm{\mu }}_{ij}$ is the peak tire-road adhesion coefficient for each wheel. Since the lateral force is generally uncontrollable, only the distribution of longitudinal force is optimized [25]. When using the SQP algorithm to coordinate the braking forces, the wheels on the side with the smaller braking force limited weight have not yet activated ABS. In this case, the braking force is equal to the ground adhesion force. The optimization objective function is to minimize the sum of the squared tire force utilization on the side with the smaller braking force limited weight:

$$\min \mathrm{J}=\min {\displaystyle \sum \frac{{F_{bij}}^2}{{({\mathrm{\mu }}_{ij}{F}_{zij})}^2}}$$

(41)

where $F_{bij}$ is the braking force of each wheel.

The constraint function is shown below:

$$\left\{\begin{array}{l}{F}_{bfl}+F_{brl}=F_{bfr}+F_{brr}\\ F_{bfj}\le {\mathrm{\mu }}_{fj}{F}_{zfj}\\ F_{brj}\le {\mathrm{\mu }}_{rj}{F}_{zrj}\end{array}\right.$$

(42)

The mid-layer controller ultimately outputs the coordinated braking force for each wheel, along with the braking force limited state signals, which are used to control the lower-layer controller.

3.3. Lower-Layer Controller

The lower-layer controller primarily coordinates the longitudinal braking forces from the mid-layer controller with the additional braking forces output by the upper-layer controller. The process begins by checking the braking force limited state of the wheel on the side where the additional braking force is applied (left or right). If both wheels on that side have fully limited braking forces, the initial additional braking force for the front and rear wheels cannot be coordinated. If only one wheel has a non-fully limited braking force, the additional braking force $\Delta F_{bfj}+\Delta F_{brj}$ is applied by the wheel with the non-fully limited braking force. If both wheels have non-fully limited braking forces, the additional braking forces $\Delta F_{bfj}$ and $\Delta F_{brj}$ are applied separately to the front and rear wheels. Here, $\Delta F_{bfj}$ and $\Delta F_{brj}$ represent the initial additional braking forces for the front and rear wheels, respectively. Specifically, when $j=l$, $\Delta F_{bfl}$ and $\Delta F_{brl}$ represent the initial additional braking forces for the left-side front and rear wheels; when $j=r$, $\Delta F_{bfr}$ and $\Delta F_{brr}$ represent the initial additional braking forces for the right-side front and rear wheels.

Finally, the target braking force for each wheel is determined by the lower-layer controller and delivered to the corresponding brake actuator.

4. Simulation Verification

To verify the effectiveness of the proposed strategy, simulation analyses are conducted under brake actuator failure conditions and compared with an uncoordinated control method, in which the ABS, EBD, and DYC subsystems operate independently. The simulation platform is built based on CarSim and MATLAB R2022a/Simulink. The vehicle control model used is a Class C car from CarSim, with its parameters listed in

Table 3. Basic parameters of the target vehicle.

Parameter	Value	Parameter	Value
Mass m (kg)	1413	Distance from CM to front axle a (m)	1.015
Wheelbase L (m)	2.910	Distance from CM to rear axle b (m)	1.895
Track width B (m)	1.655	$\mathrm{Height} \mathrm{of} \mathrm{CM} h_g$ (m)	0.54
Rolling radius R (m)	0.325	$\mathrm{Wheel} \mathrm{rotational} \mathrm{inertia} I_w$$(\mathrm{kg}\cdot {\mathrm{m}}^2$)	1.5
Inertia moment about the z-axis $I_z (\mathrm{kg}\cdot {\mathrm{m}}^2$)	1536.7	$\mathrm{Steering} \mathrm{transmission} \mathrm{ratio} I_s$	14.46

. The parameters of the drive motor and wheel-side reduction gear are referenced from the team’s distributed drive vehicle, with details provided in

Table 4. Key parameters of drive motor and transmission system.

Rated/Peak Torque (Nm)	Rated/Peak Speed (r/min)	Rated/Peak Power (kW)	Wheel-Side Reducer $\mathbf{Transmission} \mathbf{Ratio} {\mathit{i}}_0$
30/80	5456/10,500	19/35	6.9

, in which CM denotes the vehicle’s center of mass.

4.1. Single-Wheel Failure

The left rear wheel is selected as the failed wheel under single-wheel failure condition, and the simulation conditions are summarized in

Table 5. Summary table of simulation conditions under single-wheel failure.

Working Condition	Base Condition	$\mathbf{Speed} {\mathit{v}}_0$ (km/h)	TRPAC	EMB Failure Time(s)	Start Time(s)	Remark
A01	Straight-line emergency braking	100	0.85	Before braking	Braking: 0.5	/
A02	Straight-line emergency braking	100	0.6	Before braking
A03	Straight-line emergency braking	100	0.3	Before braking
B01	Cornering braking	80	0.85	Before braking	Braking: 0.5 Steering: 0.5	Steering wheel angle: [−45,0]°
B02	Cornering braking	80	0.6	Before braking

.

The simulation results and data for the A01 to A03 conditions are shown in Figure 16 and

Table 6. Simulation data for conditions A01-A03.

Working Condition	Coordinated Control		Uncoordinated Control		Braking Distance Reduction (%)	Lateral Deviation Reduction (%)
	Braking Distance (m)	Lateral Deviation (m)	Braking Distance (m)	Lateral Deviation (m)
A01	61.300	0.002	68.654	4.630	10.71	99.96
A02	79.000	0.002	90.912	6.210	13.10	99.97
A03	145.400	0.006	176.492	13.092	17.62	99.95

, respectively. Among these, Figure 16c,d present the simulation results at μ = 0.6. From Figure 16, it can be observed that when the left rear wheel’s EMB fails, the braking force coordination control system quickly engages the left rear wheel’s RBS to supplement the missing braking force from the EMB, ensuring the vehicle maintains a straight trajectory during straight-line braking. According to Table 6, under high, medium, and low adhesion conditions, the braking force coordination control system effectively reduces both the braking distance and the lateral deviation.

Figure 17 shows a comparison of the vehicle’s braking trajectory, CM side-slip angle, and yaw rate under the B01 and B02 conditions, considering both the coordinated control strategy and the uncoordinated control strategy. In the B01 condition, the braking distances are 92.38 m and 99.39 m, respectively, while in the B02 condition, the distances are 84.37 m and 92.41 m. The braking distances are reduced by 7.05% and 8.7% in the two conditions, respectively. As shown in Figure 17, the coordinated control strategy performs significantly better than the uncoordinated control strategy. In Figure 17a, the uncoordinated control strategy under the μ = 0.6 condition shows a clear braking trajectory deviation, and both the CM side-slip angle and yaw rate are much higher than those observed under the μ = 0.85 condition. This confirms that the vehicle experiences lateral sliding during cornering braking on a μ = 0.6 road surface, which is highly detrimental to braking safety.

4.2. Dual-Wheel Failure

The simulation conditions for dual-wheel failure are summarized in

Table 7. Summary table of simulation conditions under dual-wheel failure.

Working Condition	Base Condition	$\mathbf{Speed} {\mathit{v}}_0$ (km/h)	TRPAC	Failed Actuator and Failure Time (s)	Braking Start Time (s)	Remark
C01	Straight-line emergency braking	100	0.85	EMB Before braking	0.1	/
C02	Straight-line emergency braking	100	0.6
C03	Straight-line emergency braking	100	0.3
D01	Straight-line emergency braking	100	0.85	EMB rl wheel: 0.5 rr wheel: 1	0.1	/
D02	Straight-line emergency braking	100	0.6
D03	Straight-line emergency braking	100	0.3

.

Due to the dual-wheel failure condition, the braking forces on both sides of the vehicle remain balanced after the braking failure. As a result, both the coordinated control and the uncoordinated control strategies show minimal lateral deviation, close to zero. Figure 18 and

Table 8. Braking distance and lateral deviation for conditions C01-C03.

Working Condition	Coordinated Control		Uncoordinated Control		Braking Distance Reduction (%)
	Braking Distance (m)	Lateral Deviation (m)	Braking Distance (m)	Lateral Deviation (m)
C01	55.452	8.7 × 10−7	73.442	5.3 × 10−7	24.50
C02	75.094	7.7 × 10−8	105.127	2.2 × 10−7	28.57
C03	143.793	8.9 × 10−6	214.290	8.8 × 10−7	32.90

present the simulation results for the C01 to C03 conditions. From Figure 18b, it can be seen that at 4.7 s, the vehicle exits ABS control because the speed drops below the activation threshold for ABS. Similarly, Figure 18c shows that the vehicle exits ABS control at 6.6 s for the same reason. Under the C02 condition with coordinated control, after exiting ABS control, the braking torque on the front wheels is 2500 Nm. In contrast, under the uncoordinated control strategy, the braking torque is only 2000 Nm. This difference is due to the fact that, under the coordinated control strategy, the two rear wheels, due to the limited power of the drive motor, are unable to apply the full required braking torque. The missing torque is compensated by the front wheels, resulting in a higher front wheel braking torque in the coordinated control case compared to the uncoordinated control strategy.

Figure 19 and

Table 9. Simulation data for conditions D01-D03.

Working Condition	Coordinated Control		Uncoordinated Control		Braking Distance Reduction (%)	Lateral Deviation Reduction (%)
	Braking Distance (m)	Lateral Deviation (m)	Braking Distance (m)	Lateral Deviation (m)
D01	56.851	0.004	69.172	1.323	17.81	99.70
D02	75.621	0.353	98.185	1.340	22.98	73.66
D03	144.776	1.041	205.850	1.421	29.67	26.74

present the simulation results for the D01 to D03 conditions. Due to the failure of the left rear wheel before the right rear wheel, the uncoordinated control strategy results in the vehicle losing part of the left-side braking force, causing the vehicle to deviate to the right of the ideal braking trajectory. Later, the failure of the right rear wheel leads to a balance in the braking forces on both sides, and the vehicle eventually deviates to the right of the ideal braking trajectory. Under the coordinated control strategy, the vehicle initially deviates to the right of the ideal braking trajectory due to the failure of the left rear wheel. However, the activation of the RBS on the left rear wheel provides backup braking force, balancing the braking forces on both sides and eliminating the yaw moment. Following this, the failure of the right rear wheel causes the vehicle to deviate to the left of the ideal braking trajectory, ultimately leading to the vehicle deviating to the left of the ideal trajectory under the coordinated control strategy.

5. Conclusions

This paper addresses the key issue of braking force coordination control under braking actuator failure conditions for steer-by-wire electric vehicles. A hierarchical braking force coordination strategy is proposed and its effectiveness in enhancing braking safety is validated. The strategy integrates EBD, DYC, ABS, and braking force reconstruction functions, establishing a three-layer braking force distribution mechanism. By analyzing the coupling mechanism between braking yaw moment and DYC control, an ABS/DYC dynamic coordination strategy is formulated, followed by the development of a dynamic model for calculating the braking force limit weight. This model enables the collaborative reconstruction of longitudinal and lateral braking forces. Simulation results indicate that, compared to uncoordinated strategies, the proposed strategy effectively controls vehicle braking stability and significantly improves braking safety performance.

In future work, the impact of motor temperature on redundant electric braking force will be analyzed. Additionally, the reliability of the braking force coordination control strategy under braking actuator failure conditions will be validated through hardware-in-the-loop (HIL) testing or real vehicle experiments.