Design and Experimentation of a Roller-Type Precision Seed Metering Device for Rapeseed with Bezier Curve-Based Profiled Holes
Abstract
1. Introduction
2. Materials and Methods
2.1. Structure and Working Principle
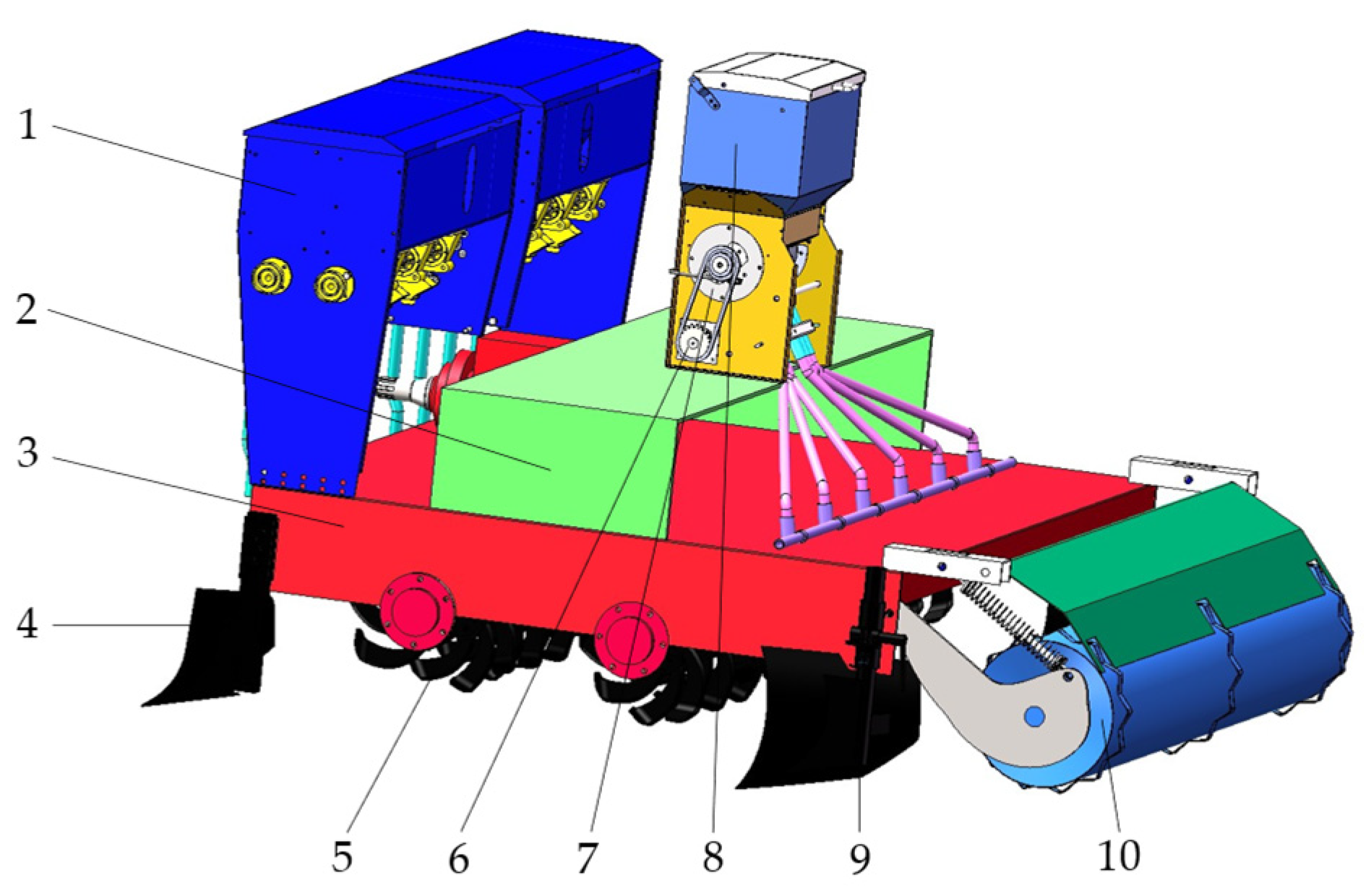
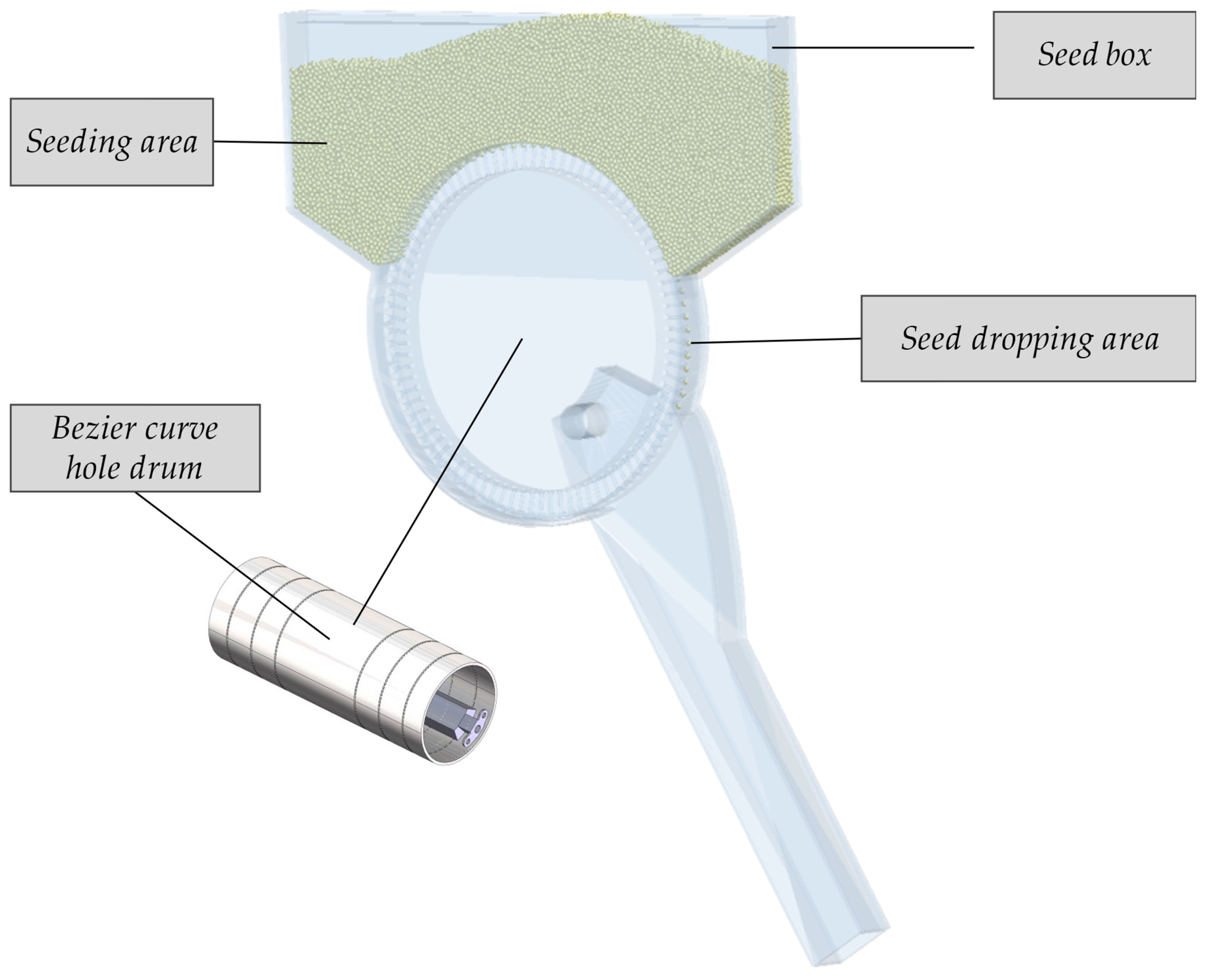
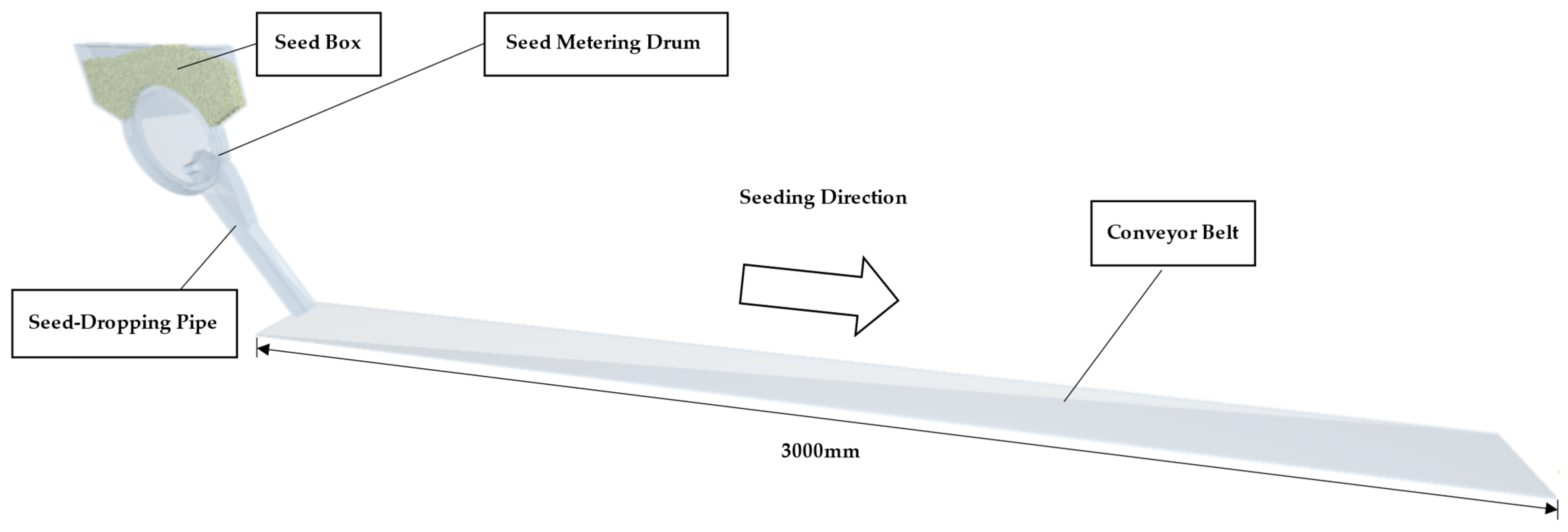
2.1.1. Overall Structure
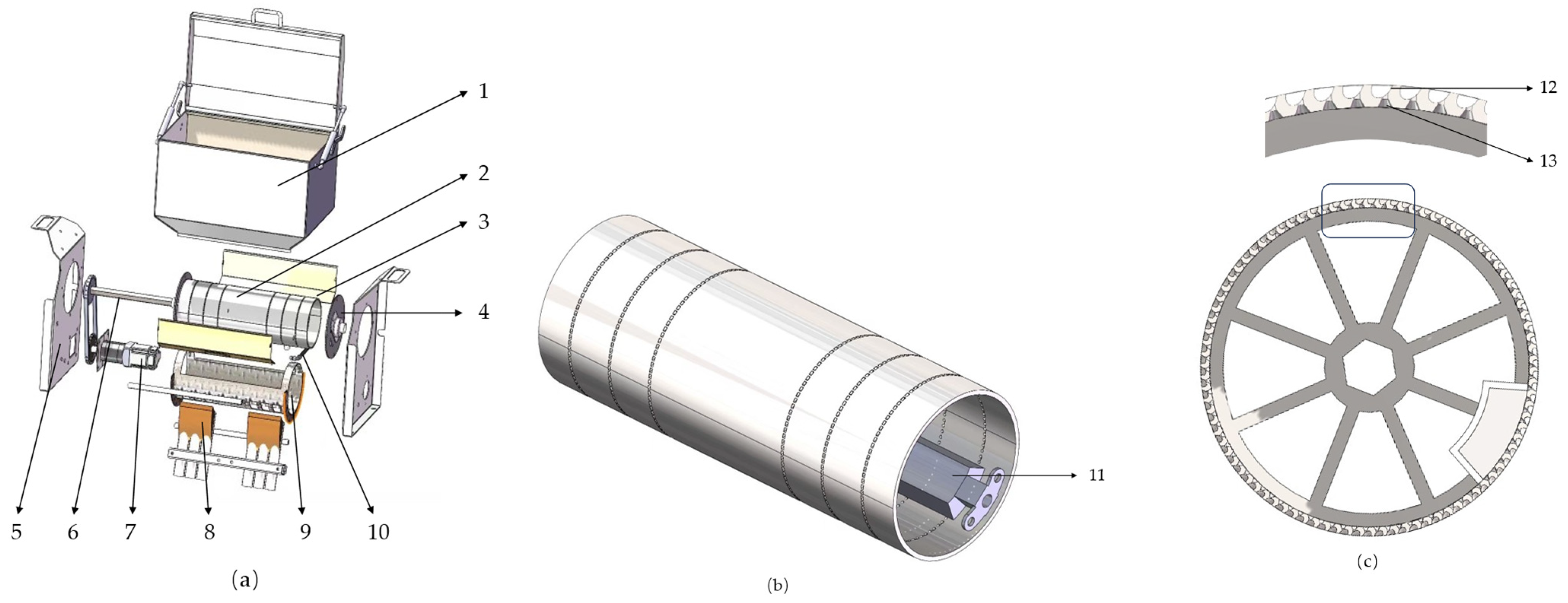
2.1.2. Structure of the Seed Metering Device
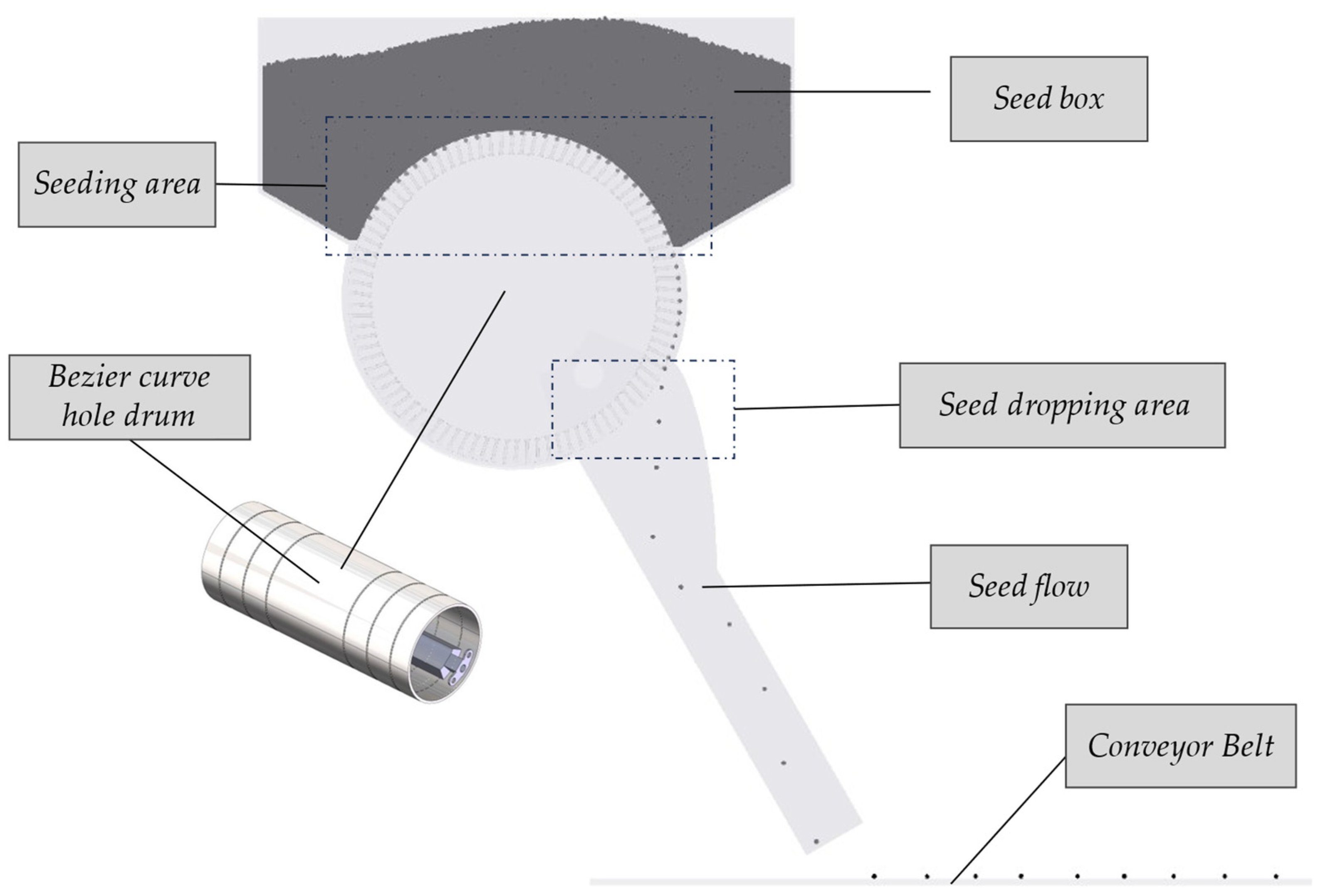
2.1.3. Working Principle of the Seed Metering Device
2.2. Design of Key Structures of the Seed Metering Device
2.2.1. Design of the Seed Metering Roller
2.2.2. Design of the Number of Radial Holes
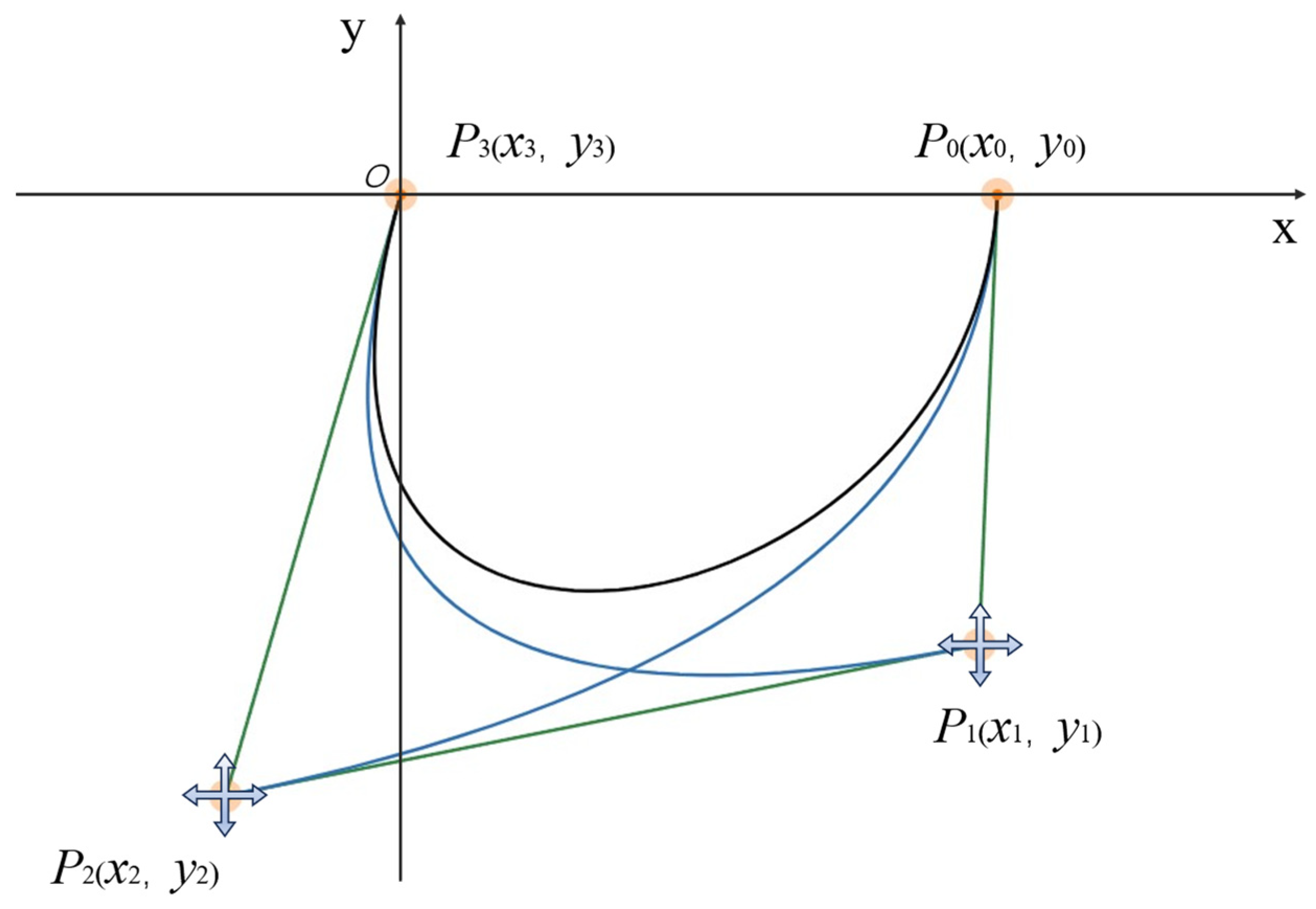
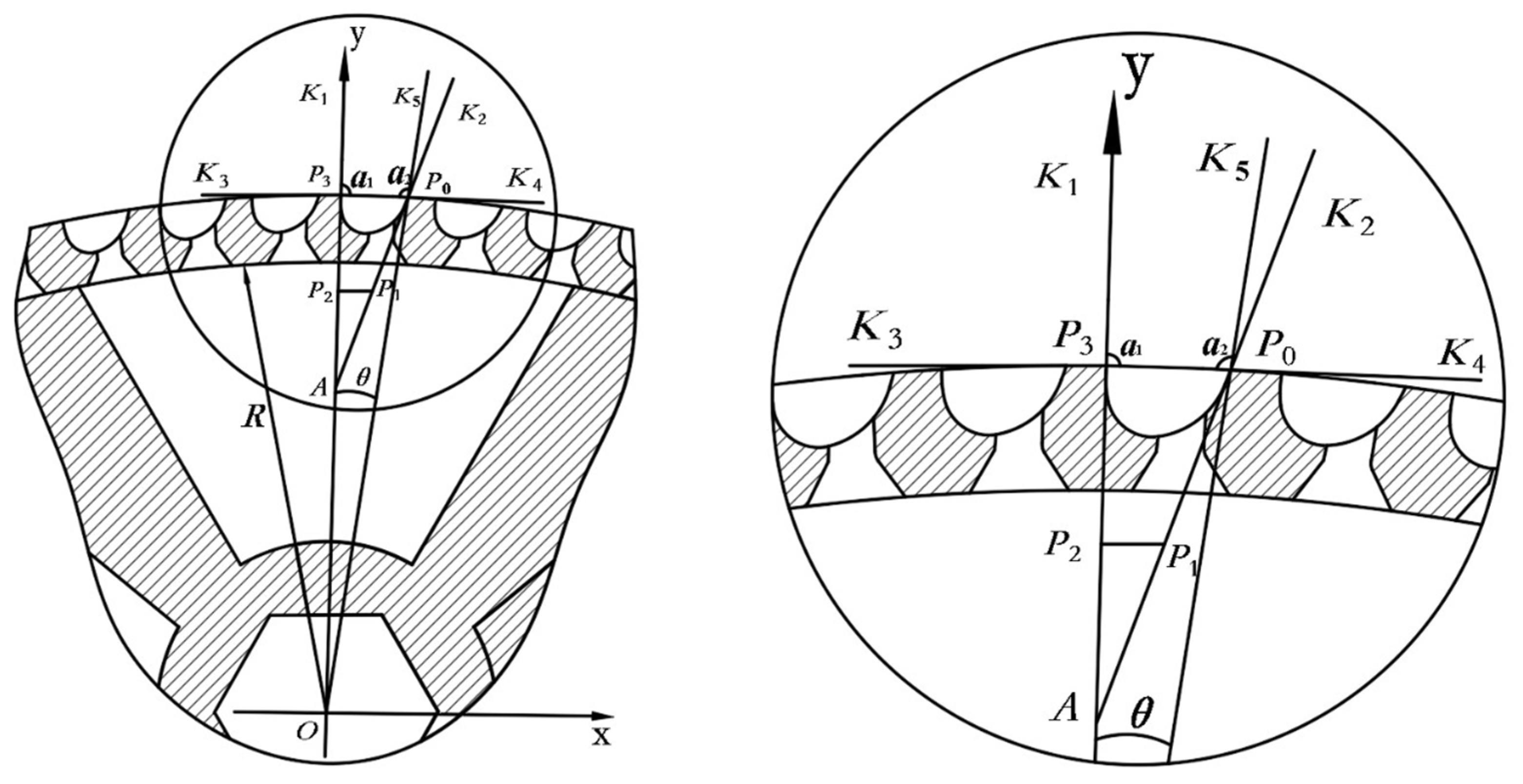
2.2.3. Design of Hole Contour
Cubic Bezier Curve
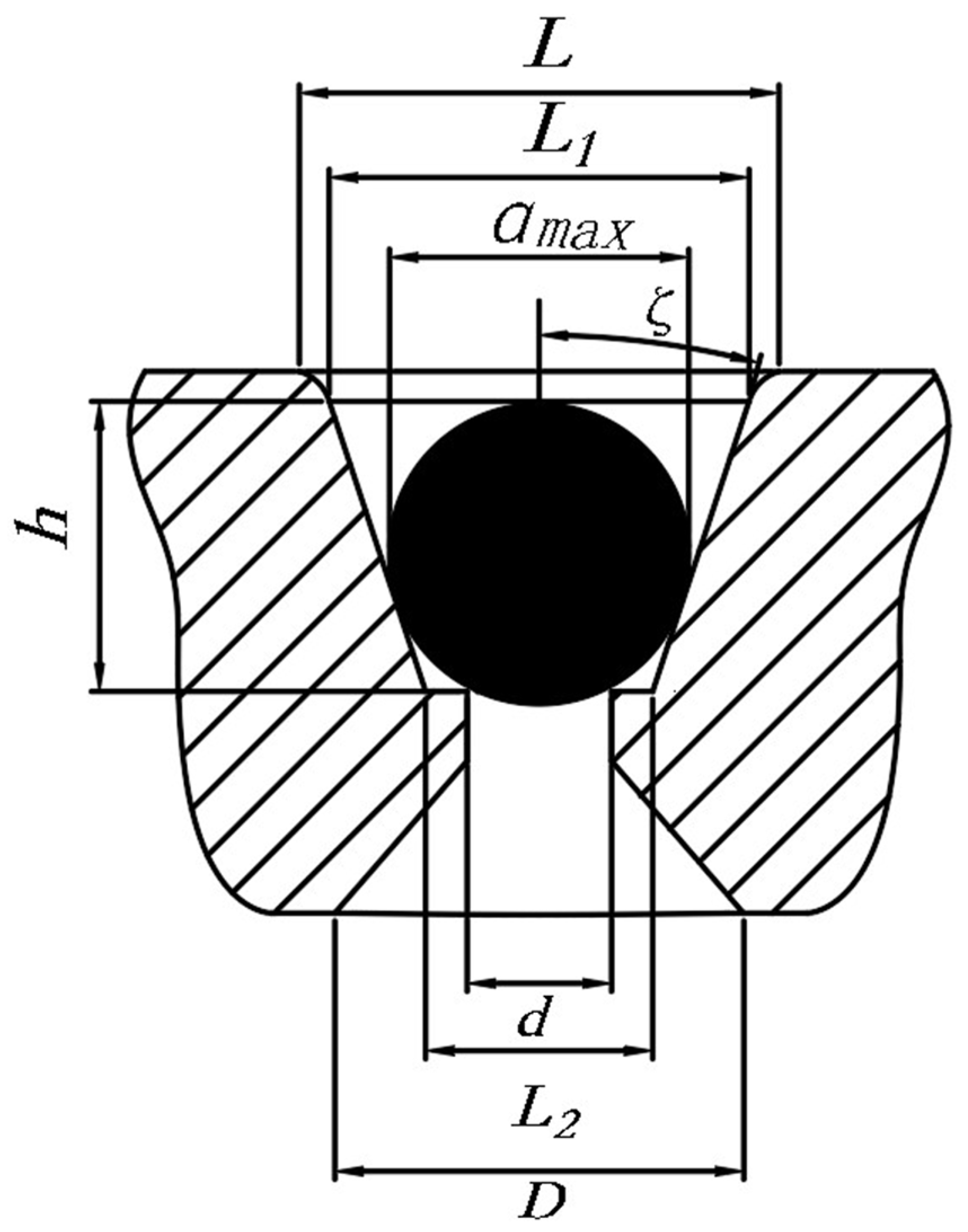
Radial Cross-Section Structure of the Hole
Axial Cross-Sectional Structure of the Holes
2.3. Mechanical Analysis of the Seed-Filling and Seed-Dropping Process
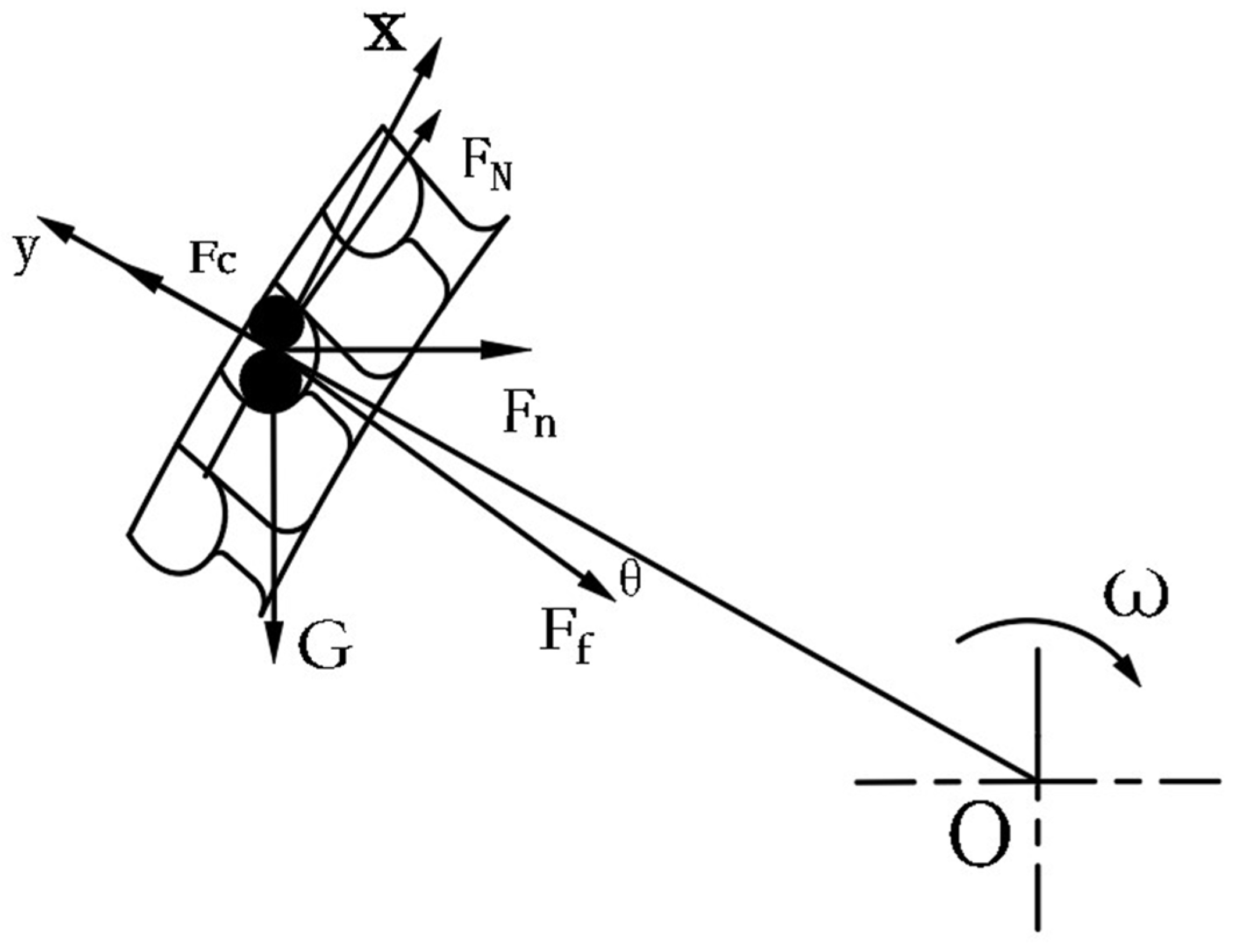
2.3.1. Seed-Filling Process
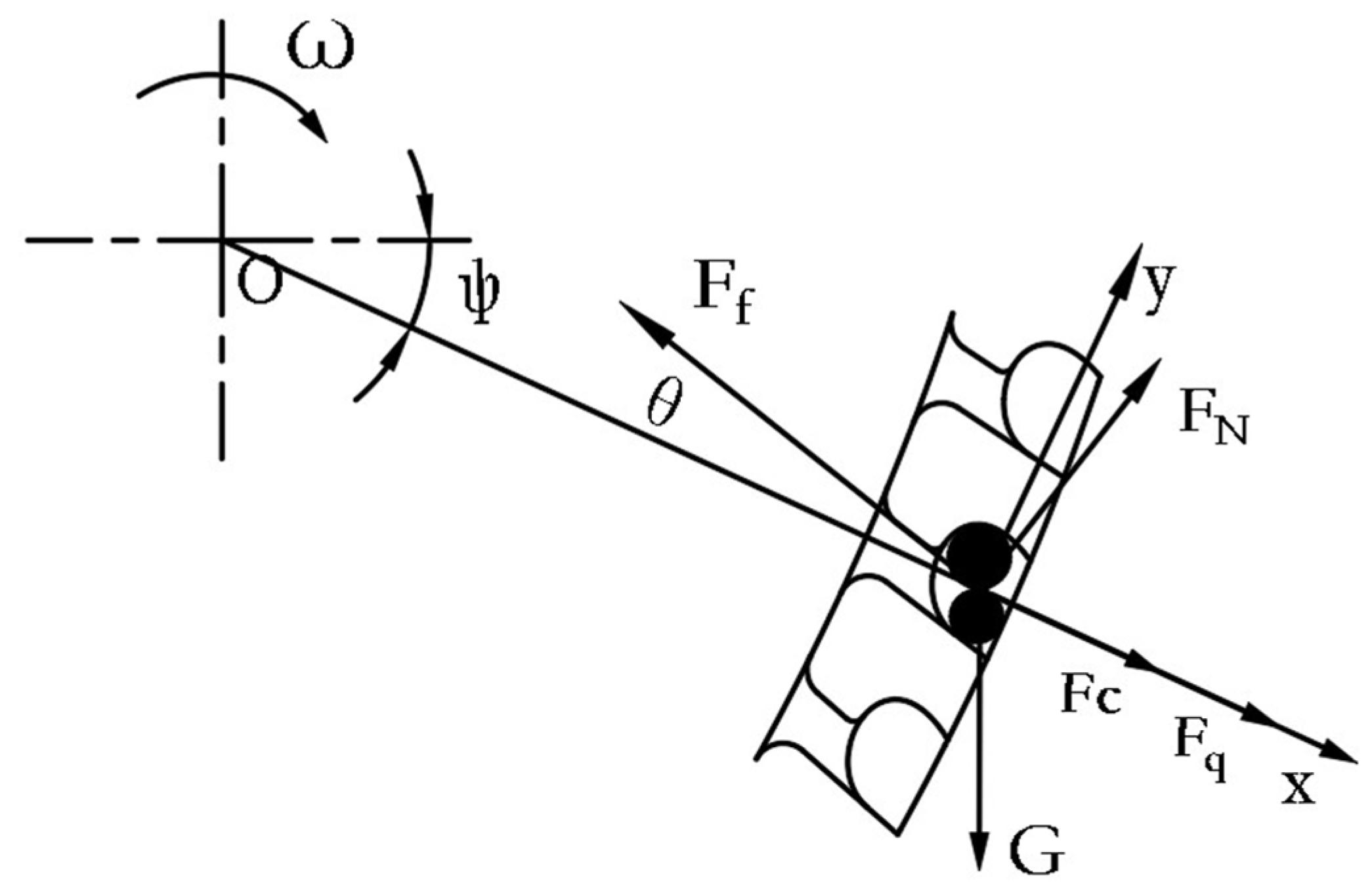
2.3.2. Seed-Dropping Process
2.4. Simulation Experiments
2.4.1. Model Establishment
2.4.2. Test Method
2.5. Seed Metering Performance Bench Test
3. Results
3.1. Analysis of Simulation Results and Parameter Optimization
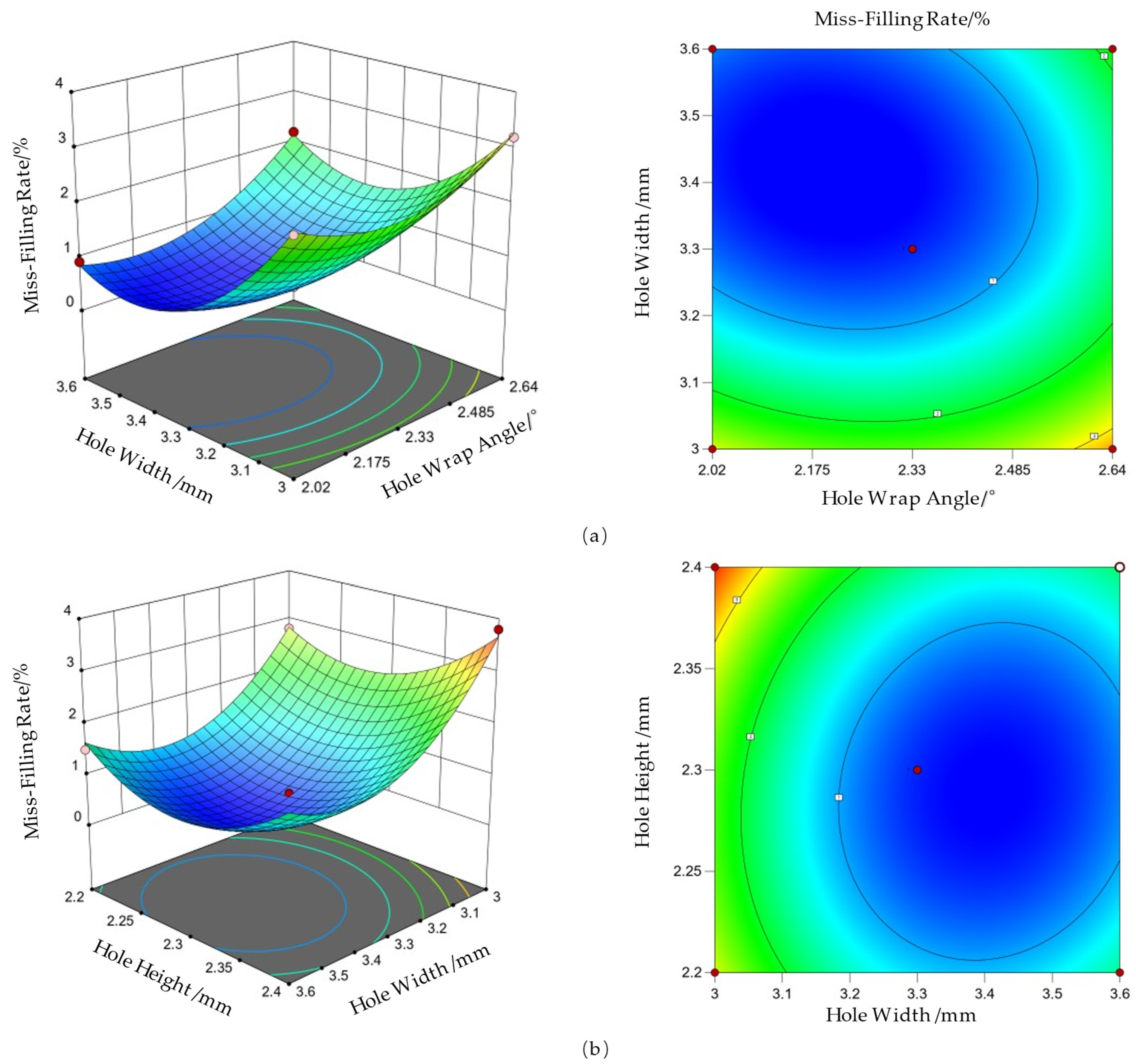
3.1.1. Analysis of Miss-Filling Rate
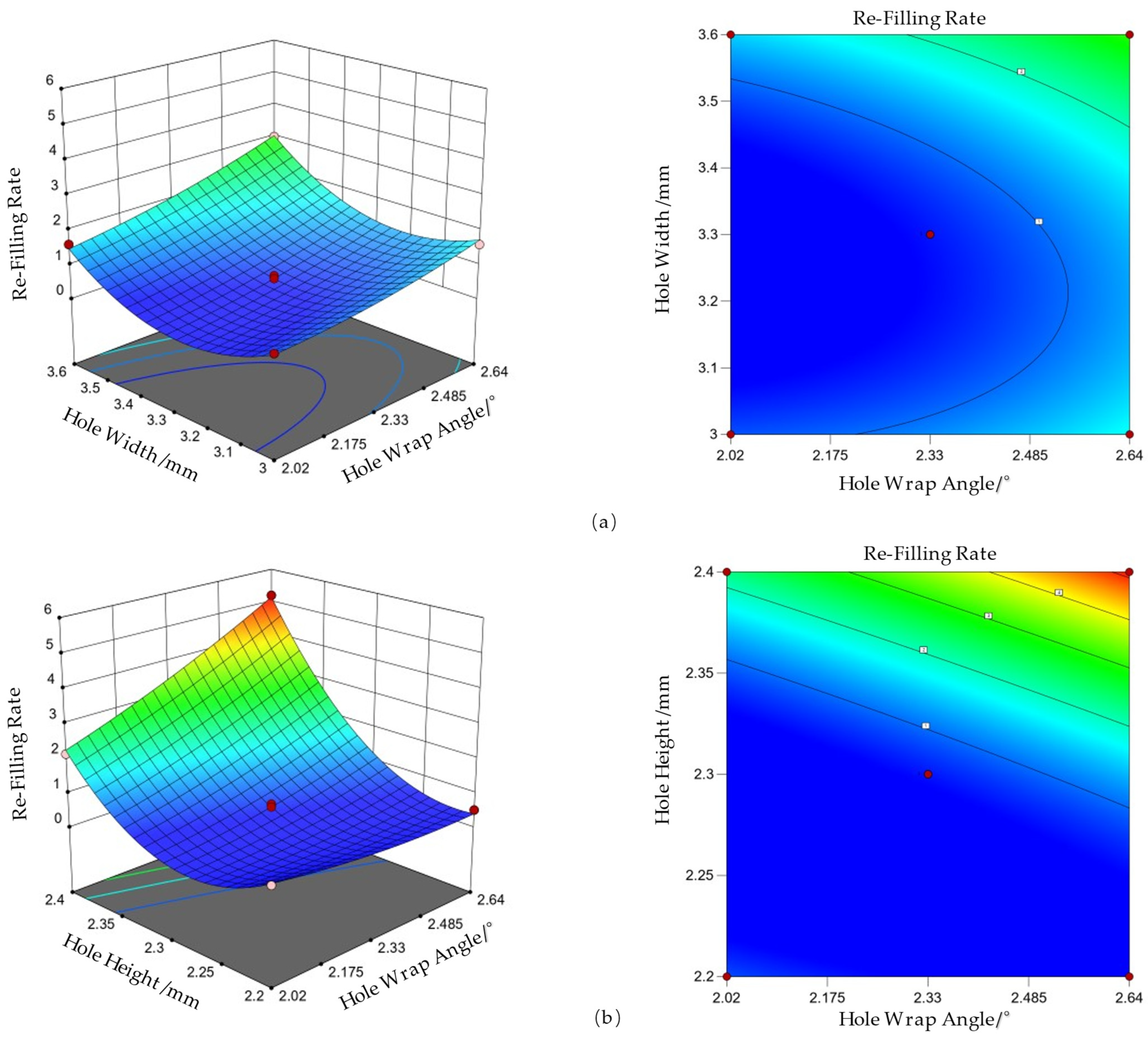
3.1.2. Analysis of Multiple-Filling Rate
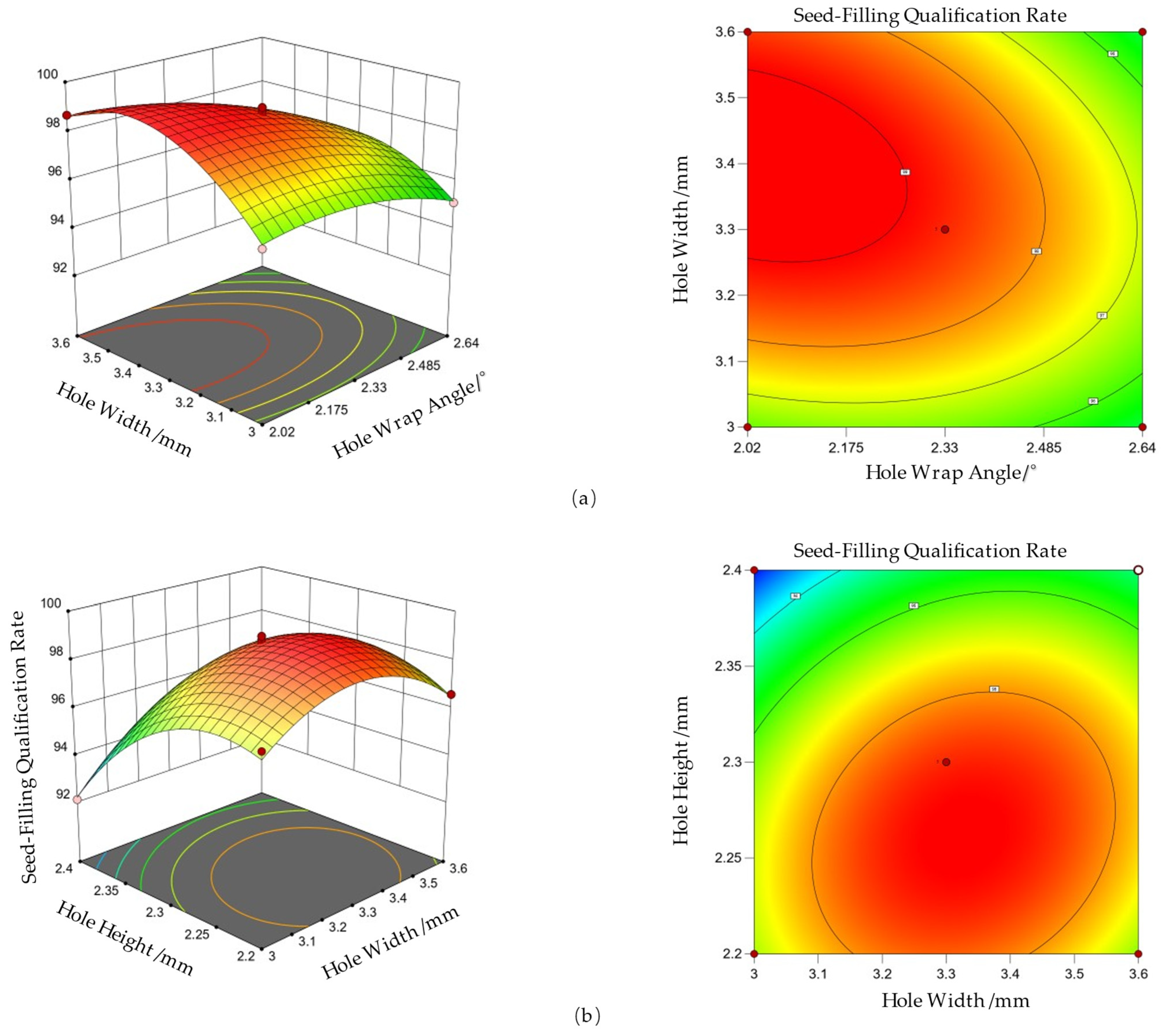
3.1.3. Analysis of and Seed-Filling Qualification Rate
3.1.4. Parameter Optimization
3.2. Bench Test Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liao, Y.T.; Shi, B.B.; Wang, C.Q.; Liao, Q.X.; Wu, A.Y.; Ou, Y.H. Current Situation and Development Trend of Mechanized Seeding for Rapeseed and Wheat in Southern Hilly and Mountainous Areas. Trans. Chin. Soc. Agric. Eng. 2025, 41, 12–26. [Google Scholar] [CrossRef]
- Xia, X.L. Practice and Exploration of Full-Process Mechanization Technology for Rapeseed Production. Agric. Mach. Technol. Promot. 2021, 29–31. [Google Scholar] [CrossRef]
- Zhang, Y.Y. Major Rapeseed-Producing Counties Are Expected to Realize Fully Mechanized Production. Hunan Agric. 2019, 14–15. [Google Scholar] [CrossRef]
- Liao, Q.X.; Cao, M.; Wang, B.S.; Wang, L.; Shen, W.H.; Pei, L.M. Design and Experiment of Slotted-tooth Spoon Hole and Air-assisted Precision Centralized Metering Device for Sesame. Trans. Chin. Soc. Agric. Mach. 2023, 54, 65–76. [Google Scholar] [CrossRef]
- Tan, Y.; Zhang, Y.; Jin, Y. Design and Test of a Pneumatically Assisted Seed Guiding and Integrated Seed-Meter for Both Oilseed Rape and Wheat. Trans. Chin. Soc. Agric. Mach. 2025, 56, 105–116+187. [Google Scholar] [CrossRef]
- Wang, B.S.; Wang, L.; Liao, Y.T.; Wu, C.; Cao, M.; Liao, Q.X. Design and Experiment of Seeding Wheels for Precision Hole-seeding Centralized Metering Device for Small-Particle-Size Seeds. Trans. Chin. Soc. Agric. Mach. 2022, 53, 64–75, 119. [Google Scholar] [CrossRef]
- Yuan, W.S.; Wu, C.Y.; Jin, C.Q. Design and Experiment of Special-Shaped Hole Pocket Wheel-Type Rapeseed Seed Metering Device. Trans. Chin. Soc. Agric. Mach. 2009, 40, 72–75. [Google Scholar]
- Zhong, J.Y. Design and Experiment of Inverted Fin-Shaped Hole Wheel-Type Variable Seed Metering Device for Dual-Use of Wheat and Rapeseed. Master’s Thesis, Anhui Agricultural University, Hefei, China, 2022. [Google Scholar]
- Luo, X.W.; Liu, T.; Jiang, E.C.; Li, Q. Design and Experiment of Seeding Wheel for Rice Precision Hill-Direct Seeding. Trans. Chin. Soc. Agric. Eng. 2007, 23, 108–112. [Google Scholar] [CrossRef]
- Lei, X.L.; Yang, W.H.; Yang, L.J.; Liu, L.Y.; Liao, Q.X.; Ren, W.J. Design and Experiment of Centralized Seeding Device for Rapeseed Precision Hill Seeding. Trans. Chin. Soc. Agric. Mach. 2020, 51, 54–64. [Google Scholar] [CrossRef]
- Yao, L.; Liao, Q.X.; Shen, W.H.; Wang, L.; Li, M.L.; Hu, Q.L. Design and Experiment of Rapeseed Rotary Disc-Type Precision Cluster Metering Device Based on Bezier Curve. Trans. Chin. Soc. Agric. Mach. 2022, 53, 56–66+83. [Google Scholar] [CrossRef]
- Ahmadi, E.; Ghassemzadeh, H.R.; Moghaddam, M.; Kim, K.U. Development of a Precision Seed Drill for Oilseed Rape. Turk. J. Agric. For. 2008, 32, 451–458. [Google Scholar]
- Lei, X.; Hu, H.; Yang, W.; Liu, L.; Liao, Q.; Ren, W. Seeding Performance of Air-Assisted Centralized Seed-Metering Device for Rapeseed. Int. J. Agric. Biol. Eng. 2021, 14, 79–87. [Google Scholar] [CrossRef]
- Aliyev, E.B.; Bezverkhniy, P.E. Numerical modelling of the seed retarder of a precision pneumatic seeder. National interdepartmental scientific and technical collection. Des. Manuf. Oper. Agric. Mach. 2022, 52, 86–98. [Google Scholar] [CrossRef]
- Zheng, G.; Qi, B.; Zhang, W.; Shao, W.; Zhang, L.; Wang, Y.; Ding, Y. Engineering Discrete Element Method-Based Design and Optimization of the Key Components of a Spoon-Wheel Spinach Seed-Metering Device. Agronomy 2024, 14, 2096. [Google Scholar] [CrossRef]
- Nikolay, Z.; Nikolay, K.; Gao, X.; Wei Li, Q.; Peng Mi, G.; Xiang Huang, Y. Design and Testing of Novel Seed Miss Prevention System for Single Seed Precision Metering Devices. Comput. Electron. Agric. 2022, 198, 107048. [Google Scholar] [CrossRef]
- Guo, P.; Sun, B.; Shang, S.; Hou, J.; Wang, D.; Zhao, Z.; Elshafie, A.; Zheng, X.; Eltoum, F. Effect of Auxiliary Air-Suction Seed-Filling Structure on Seed Discharge Performance of Peanut High-Speed Seed-Metering Machine. Agriculture 2025, 15, 1678. [Google Scholar] [CrossRef]
- Vladimir, N.; Nikolai, K.; Alexandr, K.; Yulia, N. Design and study of seeding devices for small selection seeding machines. E3S Web Conf. 2019, 126, 00008. [Google Scholar] [CrossRef]
- Chinese Academy of Agricultural Mechanization Sciences. Agricultural Machinery Design Manual; China Agricultural Science and Technology Press: Beijing, China, 2007. [Google Scholar]
- Lin, P. Experiment and Analysis of Rapeseed and Sesame Dual-Purpose Precision Seeding Device. Master’s Thesis, Huazhong Agricultural University, Wuhan, China, 2021. [Google Scholar]
- Kuai, J.; Wang, J.J.; Zuo, Q.S.; Chen, H.L.; Gao, J.Q.; Wang, B.; Zhou, G.S.; Fu, T.D. Effects and Mechanism of Higher Plant Density on Directly-Sown Rapeseed in the Yangtze River Basin of China. Sci. Agric. Sin. 2018, 51, 4625–4632. [Google Scholar] [CrossRef]
- Kuai, J.; Sun, Y.Y.; Zuo, Q.S.; Liao, Q.X.; Leng, S.H.; Cheng, Y.G.; Cao, S.; Wu, J.S.; Zhou, G.S. Optimization of Planting Density and Row Spacing for Direct-Seeded Winter Rapeseed under Mechanical Harvesting Mode. Acta Agron. Sin. 2016, 42, 898–908. [Google Scholar] [CrossRef]
- Cao, X.L.; Ma, X.; Li, H.W.; Wen, Z.C.; Li, Z.H.; Wang, X.C. Design and Experiment of Precision Seed Metering Device for Air-Suction roller -Type Rapeseed Plug Seedling. Trans. Chin. Soc. Agric. Eng. 2021, 37, 51–60. [Google Scholar] [CrossRef]
- Ding, L.; Yang, L.; Zhang, D.X.; Cui, T. Parametric Design and Experiment of Seed Cleaning Mechanism for Air-Suction Corn Seed Metering Device. Trans. Chin. Soc. Agric. Mach. 2019, 50, 47–56. [Google Scholar] [CrossRef]
- Shen, H.; Zhang, J.; Chen, X.; Dong, J.; Huang, Y.; Shi, J. Development of a Guiding-Groove Precision Metering Device for High-Speed Planting of Soybean. Am. Soc. Agric. Biol. Eng. 2021, 64, 1113–1122. [Google Scholar] [CrossRef]
- Gao, L.P.; Shi, B.B.; Liao, Q.X.; Zhang, B.X.; Zheng, J.; Liao, Y.T. Seeding Performance of Conical Hole Disc in Rapeseed Precision Seed Metering Device with Combined Positive and Negative Air Pressure. Trans. Chin. Soc. Agric. Eng. 2022, 38, 22–33. [Google Scholar] [CrossRef]
- Zhang, C.L.; Liu, T.; Zheng, Z.H.; Fang, J.; Xie, X.D.; Chen, L.Q. Design and Test of Precision Seeding Dispenser with Staggered Convex Teeth for Wheat Wide—Seedling—Belt Sowing. Trans. Chin. Soc. Agric. Eng. 2024, 40, 47–59. [Google Scholar] [CrossRef]
- Wu, W.; Chang, C.; Li, T.; Hu, H.; Zhou, Z.; Yang, W.; Guo, J.; Zhu, P.; Li, J.; Hu, J.; et al. Seed-Filling Characteristics of a Centralized Seed-Metering Device for Rapeseed Caused by Vibration. Agriculture 2022, 12, 965. [Google Scholar] [CrossRef]
- Li, T.; Zhang, Y.; Liao, Q.X.; Chen, H.; He, K.W.; Liao, Y.T. Design and Experiment of Pneumatic Roller—Type Single—Grain Precision Seed—Metering Device for Multi—Crop Compatibility. Trans. Chin. Soc. Agric. Eng. 2025, 14, 1–10. [Google Scholar] [CrossRef]
- GB/T 6973-2005; Testing Methods of Single Seed Drills (Precision Drills). China Standards Press: Beijing, China, 2005.
- Yan, B.; Gao, N.; Meng, Z. Design and Test of a Gravity-Assisted Vacuum Seed-Meter for Maize. In Proceedings of the 2020 4th International Workshop on Advances in Energy Science and Environment Engineering (AESEE 2020), Hangzhou, China, 10–12 April 2020; Yan, B., Gao, N., Meng, Z., Eds.; Beijing Research Center of Intelligent Equipment for Agriculture: Beijing, China; Beijing Research Center for Information Technology in Agriculture: Beijing, China, 2020; Volume 2, pp. 29–35. [Google Scholar] [CrossRef]
- Wei, G.L.; Ji, H.; Pan, H.L. Design and Test of a Simplified Intelligent Control Integrated Seed-Meter for Oilseed Rape. Digital Agriculture and Intelligent Agricultural Machinery. Digit. Agric. Intell. Agric. Mach. 2025, 1–5. [Google Scholar] [CrossRef]


| Variety | Planting Density/(Plants·hm−2) | Hill Spacing/mm | Row Spacing/mm | Number of Rows |
|---|---|---|---|---|
| Deyouza 988 | 3 × 105–6 × 105 | 60–150 | 150–300 | 6–8 |
| Variety | Length/mm | Width/mm | Height/mm |
|---|---|---|---|
| Deyouza 988 | 2.01 ± 0.29 | 1.98 ± 0.27 | 1.88 ± 0.22 |
| Item | Parameter | Value |
|---|---|---|
| Rapeseed seed | Poisson’s ratio | 0.25 |
| Shear modulus/Pa | 1.1 × 107 | |
| Density/(kg·m−3) | 1060 | |
| ABS engineering plastic | Poisson’s ratio | 0.394 |
| Shear modulus/Pa | 8.9 × 108 | |
| Density/(kg·m−3) | 1060 | |
| Seed–seed | Restitution coefficient | 0.6 |
| Static friction coefficient | 0.5 | |
| Dynamic friction coefficient | 0.01 | |
| Seed–ABS engineering plastic | Restitution coefficient | 0.75 |
| Static friction coefficient | 0.3 | |
| Dynamic friction coefficient | 0.01 |
| Code | Factor | Value of Each Level | ||
|---|---|---|---|---|
| −1 | 0 | 1 | ||
| X1 | Hole wrap angle (°) | 2.02 | 2.33 | 2.64 |
| X2 | Hole width (mm) | 2.5 | 2.7 | 2.9 |
| X3 | Hole height (mm) | 2.2 | 2.3 | 2.4 |
| Serial Number | Level | Miss-Filling Rate Y1 (%) | Multiple-Filling Rate Y2 (%) | Seed-Filling Qualification Rate Y3 (%) | ||
|---|---|---|---|---|---|---|
| X1 | X2 | X3 | ||||
| 1 | −1 | −1 | 0 | 2.78 | 0.9 | 96.1 |
| 2 | 1 | −1 | 0 | 3.2 | 1.6 | 95.1 |
| 3 | −1 | 1 | 0 | 0.92 | 1.6 | 98.68 |
| 4 | 1 | 1 | 0 | 2.2 | 3 | 95.3 |
| 5 | −1 | 0 | −1 | 1.4 | 0.8 | 98.3 |
| 6 | 1 | 0 | −1 | 2.4 | 0.5 | 96.7 |
| 7 | −1 | 0 | 1 | 1.82 | 2.15 | 96.33 |
| 8 | 1 | 0 | 1 | 2.6 | 5.2 | 93.2 |
| 9 | 0 | −1 | −1 | 2.8 | 1.1 | 97 |
| 10 | 0 | 1 | −1 | 1.5 | 1.8 | 96.6 |
| 11 | 0 | −1 | 1 | 3.8 | 4.1 | 92.1 |
| 12 | 0 | 1 | 1 | 1.8 | 5.1 | 94.4 |
| 13 | 0 | 0 | 0 | 0.58 | 0.54 | 98.4 |
| 14 | 0 | 0 | 0 | 0.55 | 0.64 | 98.85 |
| 15 | 0 | 0 | 0 | 0.45 | 0.59 | 98.99 |
| 16 | 0 | 0 | 0 | 0.64 | 0.5 | 98.7 |
| 17 | 0 | 0 | 0 | 0.62 | 0.68 | 98.75 |
| Source of Variance | Sum of Squares | Degrees of Freedom | Mean Square | F | p |
|---|---|---|---|---|---|
| Model | 17.59 | 9 | 1.95 | 130.23 | <0.0001 ** |
| X1 | 1.51 | 1 | 1.51 | 100.84 | <0.0001 ** |
| X2 | 4.74 | 1 | 4.74 | 315.97 | <0.0001 ** |
| X3 | 0.4608 | 1 | 0.4608 | 30.70 | 0.0009 ** |
| X1X2 | 0.1849 | 1 | 0.1849 | 12.32 | 0.0099 ** |
| X1X3 | 0.0121 | 1 | 0.0121 | 0.8061 | 0.3991 |
| X2X3 | 0.1225 | 1 | 0.1225 | 8.16 | 0.0245 * |
| X12 | 1.74 | 1 | 1.74 | 116.15 | <0.0001 * |
| X22 | 4.76 | 1 | 4.76 | 317.24 | <0.0001 ** |
| X32 | 3.00 | 1 | 3.00 | 199.57 | <0.0001 ** |
| Residual | 0.1051 | 7 | 0.0150 | ||
| Lack of fit | 0.0828 | 3 | 0.0276 | 4.96 | 0.0781 |
| Error | 0.0223 | 4 | 0.0056 | ||
| Total | 17.70 | 16 |
| Source of Variance | Sum of Squares | Degrees of Freedom | Mean Square | F | p |
|---|---|---|---|---|---|
| Model | 40.61 | 9 | 4.51 | 310.19 | <0.0001 ** |
| X1 | 2.94 | 1 | 2.94 | 202.13 | <0.0001 ** |
| X2 | 1.80 | 1 | 1.80 | 124.09 | 0.0009 ** |
| X3 | 19.07 | 1 | 19.07 | 1310.65 | <0.0001 ** |
| X1X2 | 0.1225 | 1 | 0.1225 | 8.42 | 0.0229 * |
| X1X3 | 2.81 | 1 | 2.81 | 192.87 | <0.0001 ** |
| X2X3 | 0.0225 | 1 | 0.0225 | 1.55 | 0.2536 |
| X12 | 0.1095 | 1 | 0.1095 | 7.53 | 0.0288 * |
| X22 | 4.41 | 1 | 4.41 | 303.37 | <0.0001 ** |
| X32 | 8.39 | 1 | 8.39 | 576.48 | <0.0001 ** |
| Residual | 0.1018 | 7 | 0.0145 | ||
| Lack of fit | 0.0806 | 3 | 0.0269 | 5.07 | 0.0754 |
| Error | 0.0212 | 4 | 0.0053 | ||
| Total | 40.71 | 16 |
| Source of Variance | Sum of Squares | Degrees of Freedom | Mean Square | F | p |
|---|---|---|---|---|---|
| Model | 70.61 | 9 | 7.85 | 86.34 | <0.0001 ** |
| X1 | 10.37 | 1 | 10.37 | 114.16 | <0.0001 ** |
| X2 | 2.74 | 1 | 2.74 | 30.13 | 0.0009 ** |
| X3 | 19.75 | 1 | 19.75 | 217.35 | <0.0001 ** |
| X1X2 | 1.42 | 1 | 1.42 | 15.58 | 0.0055 ** |
| X1X3 | 0.5852 | 1 | 0.5852 | 6.44 | 0.0388 * |
| X2X3 | 1.81 | 1 | 1.82 | 20.06 | 0.0029 ** |
| X12 | 1.88 | 1 | 1.88 | 20.66 | 0.0027 ** |
| X22 | 13.27 | 1 | 13.27 | 146.02 | <0.0001 ** |
| X32 | 15.81 | 1 | 15.81 | 173.98 | <0.0001 ** |
| Residual | 0.6361 | 7 | 0.0909 | ||
| Lack of fit | 0.4442 | 3 | 0.1481 | 3.09 | 0.1523 |
| Error | 0.1919 | 4 | 0.0480 | ||
| Total | 71.25 | 16 |
| Rotational Speed/(r·min−1) | Average Breakage Rate/% | Miss-Seeding Rate/% | Multiple-Seeding Rate/% | Hole Seed Count Qualification Rate/% |
|---|---|---|---|---|
| 10 | 0.05 | 0 | 4.63 | 95.37 |
| 15 | 0.12 | 0.65 | 2.06 | 97.29 |
| 20 | 0.18 | 2.35 | 1.29 | 96.36 |
| 25 | 0.35 | 3.61 | 0.22 | 96.17 |
| 30 | 0.48 | 4.84 | 0.27 | 94.89 |
| Evaluation Indicator (s) | Simulation Optimization Value | Bench Test Value (20 r/min) | Error |
|---|---|---|---|
| Seed-filling qualification rate% | 99.122 | 96.36 | 2.762 |
| Miss-filling rate% | 0.448 | 2.35 | 1.902 |
| Multiple-filling rate% | 0.416 | 1.29 | 0.874 |
| Breakage rate% | - | 0.18 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, H.; Ji, H.; Hu, X.; Zhan, Y.; Wei, G. Design and Experimentation of a Roller-Type Precision Seed Metering Device for Rapeseed with Bezier Curve-Based Profiled Holes. Appl. Sci. 2025, 15, 12786. https://doi.org/10.3390/app152312786
Pan H, Ji H, Hu X, Zhan Y, Wei G. Design and Experimentation of a Roller-Type Precision Seed Metering Device for Rapeseed with Bezier Curve-Based Profiled Holes. Applied Sciences. 2025; 15(23):12786. https://doi.org/10.3390/app152312786
Chicago/Turabian StylePan, Huaili, Hua Ji, Xinyu Hu, Yongqi Zhan, and Guoliang Wei. 2025. "Design and Experimentation of a Roller-Type Precision Seed Metering Device for Rapeseed with Bezier Curve-Based Profiled Holes" Applied Sciences 15, no. 23: 12786. https://doi.org/10.3390/app152312786
APA StylePan, H., Ji, H., Hu, X., Zhan, Y., & Wei, G. (2025). Design and Experimentation of a Roller-Type Precision Seed Metering Device for Rapeseed with Bezier Curve-Based Profiled Holes. Applied Sciences, 15(23), 12786. https://doi.org/10.3390/app152312786





