Neural Key Agreement Protocol with Extended Security

Abstract

Key agreement protocols based on neural synchronization with Tree Parity Machines (TPMs) offer promising security advantages: they do not rely on trapdoor functions, making them resistant to quantum attacks, and they avoid the need for specialized hardware required by quantum-based schemes. Nevertheless, these protocols face a significant vulnerability: the large number of public message exchanges required for synchronization increases the risk that an attacker, acting as a Man-in-the-Middle, can successfully synchronize their own TPMs with those of the legitimate parties and ultimately recover the shared key. Motivated by the need to reduce this risk, we propose a novel probabilistic protocol that enables two parties to securely estimate the size of the shared key during intermediate steps, without revealing any key material. This estimation allows the protocol to terminate as soon as sufficient key material has been established, thereby reducing the number of synchronization rounds and limiting the opportunity for an attacker to synchronize. We integrate our estimation mechanism into a neural key agreement protocol and evaluate its performance and security, demonstrating improved efficiency and enhanced resistance to attacks compared to existing approaches.

1. Introduction

Key agreement protocols are fundamental to the security of modern cryptographic systems. From securing web traffic via the TLS protocol to enabling end-to-end encrypted messaging platforms such as Signal, the majority of cryptographic applications depend on robust key agreement mechanisms [1]. The primary objective of these protocols is to establish a shared secret between two or more parties over potentially insecure communication channels.

Traditionally, most key agreement protocols rely on hard number-theoretic problems, including the discrete logarithm problem (DLP), the Diffie–Hellman problem (DHP), the decisional Diffie–Hellman problem (D-DHP), and the integer factorization problem [2]. A significant drawback of these approaches is their susceptibility to attacks by large-scale quantum computers. Shor’s seminal work [3] introduced a quantum algorithm capable of solving both the DLP and the factorization problem in polynomial time. Although quantum computers of sufficient scale do not yet exist to threaten widely deployed cryptographic protocols, it is widely anticipated that such technology will emerge in the foreseeable future [4].

In response to these challenges, three principal alternatives to conventional key agreement protocols have been developed:

• Post-quantum key agreement protocols,
• Quantum key agreement protocols,
• Neural key agreement protocols.

Post-quantum key agreement protocols are based on mathematical problems for which no efficient solution is known on either classical or quantum computers [5]. However, these schemes often involve computationally intensive operations over finite fields, which can hinder their practical deployment [6]. Quantum key agreement protocols, on the other hand, leverage quantum phenomena such as wave function collapse, entanglement, and the no-cloning theorem [7]. While these protocols provide strong security guarantees even against quantum adversaries, they require specialized hardware that is both costly and challenging to maintain.

Neural key agreement protocols, first introduced in [8], offer an alternative to both quantum and post-quantum approaches. The core concept involves synchronizing the weights of two neural networks, specifically Tree Parity Machines (TPMs), through iterative updates between the communicating parties. The resulting synchronized weights are then used as a shared secret key. Unlike post-quantum protocols, whose security is predicated on mathematical problems that may eventually be solved, or quantum protocols, which necessitate dedicated and expensive hardware, neural key agreement protocols do not rely on such assumptions or infrastructure.

A central challenge in neural key agreement protocols is the large number of rounds typically required for two parties to achieve full synchronization of their TPMs. In existing protocols, the process continues until the entire set of weights is identical, at which point the shared key is established. However, this approach leads to a substantial communication overhead and, more critically, increases the risk that an adversary can synchronize their own TPM with those of the legitimate parties by observing the public exchanges [9]. This vulnerability is exacerbated as the number of rounds grows, since each additional round provides further opportunities for an attacker to align their weights.

It is important to note that the weight vector of a TPM generally contains far more elements than the length required for a standard cryptographic key (e.g., 128 bits). This observation suggests that it is not necessary to wait for complete synchronization; the protocol could be terminated once a sufficient number of weights have been aligned to provide the desired level of security. Early termination would not only reduce the number of communication rounds—thereby improving efficiency—but also significantly limit the window in which an attacker might succeed in synchronizing their own TPM.

The main obstacle to implementing early termination is the lack of a secure mechanism for the parties to determine the extent of synchronization without revealing any information about the actual weights. Without such a mechanism, the parties cannot safely assess whether enough key material has been established to halt the protocol. To address this limitation, we introduce a privacy-preserving comparison protocol that enables the two parties to securely estimate the number of synchronized weights after each round, without disclosing the weight values themselves. By integrating this mechanism into the neural key agreement protocol, we enable secure early termination based on the amount of shared key material, thereby enhancing both the efficiency and the security of the protocol.

1.1. Related Work

The concept of employing neural synchronization for key agreement protocols was first introduced by Kanter et al. [8], who proposed a method enabling two parties to synchronize the weights of their respective three-layer neural networks, known as Tree Parity Machines (TPMs), over a public channel. This approach was designed to prevent any third party from reconstructing the weights, even with access to all exchanged information. Shortly thereafter, Klimov et al. [9] identified three classes of attacks against this protocol, demonstrating through extensive experimentation that a geometric attack could allow an adversary to recover up to 90% of the shared key. In response to these vulnerabilities, Mislovaty et al. [10] provided experimental evidence that increasing the range of possible weight values can enhance the protocol’s security. Nevertheless, Shacham et al. [11] subsequently introduced a more advanced attack that remains effective even when the weight range is expanded, underscoring the persistent challenges in securing neural synchronization-based protocols.

To further strengthen the security of neural key agreement protocols, a variety of alternative strategies have been explored [12]. For instance, Ruttor et al. [13] proposed dynamically generating TPM inputs based on the current internal state of the network, thereby increasing the unpredictability of the synchronization process. In a different approach, Allam et al. [14,15] developed algorithms that perturb the TPM output, making it more difficult for adversaries to reconstruct the original information while still enabling legitimate parties to achieve synchronization. Although these methods enhance security under the assumption that an eavesdropper can intercept all public communications, they often result in increased synchronization times.

Recent research has also focused on novel TPM architectures and input representations. Stypinski et al. [16] introduced nonbinary input values to accelerate protocol execution, while Jeong et al. [17] demonstrated that vector-valued inputs can further improve both efficiency and security. Similarly, Dong et al. [18] investigated the use of complex-valued inputs in TPMs. The security implications of nonbinary inputs were systematically analyzed by Stypinski et al. [19], providing deeper insights into the robustness of these protocols. In addition to architectural innovations, parameter selection for TPMs has been systematically studied by Salguero et al. [20], who analyzed various parameter sets and reported their effects on both synchronization time and security.

Beyond theoretical advancements, several studies have examined practical applications of neural cryptography. For example, Sarkar et al. [21] utilized TPM-based mechanisms to enable secure access to medical data, while Sarkar et al. [22] developed a chaos-based neural synchronization method for secret sharing within a public-key framework. Gupta et al. [23] applied neural cryptography to the secure distribution of image shares. Additionally, Plesa et al. [24] proposed a TPM architecture based on spiking neural networks, evaluating its performance and resilience to man-in-the-middle attacks. Notably, the efficiency gains of this protocol are most pronounced when implemented on neuromorphic hardware [25].

Table 1. Comparison of TPM-based key agreement protocols.

Protocol	Core Idea/Modification	Advantages	Limitations/Comparison to Our Protocol
Kanter et al. [8]	Original TPM synchronization protocol over public channel	Simple, does not rely on trapdoor functions	Vulnerable to geometric attacks; no early termination mechanism
Mislovaty et al. [10]	Increased weight range to improve security	Reduces success rate of some attacks	Still vulnerable to advanced attacks; no protocol-level fix
Ruttor et al. [13]	Dynamic input generation based on internal state	Increases unpredictability, improves security	Increases synchronization time; more complex implementation
Allam et al. [14,15]	Output perturbation to confuse adversaries	Harder for attacker to reconstruct weights	Slower synchronization; more rounds required
Stypiński et al. [16]	Nonbinary input vectors for TPMs	Faster synchronization, improved efficiency	Security depends on parameters; geometric attacks still possible
Jeong et al. [17]	Vector-valued inputs for TPMs	Improves efficiency and security	Implementation complexity; not immune to all attacks
Dong et al. [18]	Complex-valued TPMs	Novel input representation; potential for higher security	Security analysis limited; practical deployment unclear
Salguero et al. [20]	Parameter optimization for TPMs	Systematic study of security vs. efficiency trade-offs	Does not address protocol-level vulnerabilities
Plesa et al. [24]	Spiking neural network TPMs	Improved efficiency on neuromorphic hardware	Security against geometric attacks not fully resolved
Our Protocol	Privacy-preserving synchronization check with early termination	Significantly reduces rounds; effectively mitigates geometric attacks	Readily integrates with existing TPM frameworks; offers promising potential for practical deployment

provides a comparison of the main TPM-based key agreement protocols, highlighting their core ideas, advantages, and limitations relative to our proposal.

1.2. Our Contribution

The primary contributions of this study are summarized as follows:

• We introduce a novel probabilistic algorithm that allows two parties engaged in a neural key agreement protocol to privately compute the proportion of synchronized weights at intermediate stages, without revealing the actual weight values.
• Leveraging this algorithm, we develop a new key agreement protocol based on the non-binary TPM model proposed by [16].
• We perform a comprehensive security analysis of our protocol, evaluating its resilience against both naive and geometric attacks, and benchmark its robustness against the protocol presented in [16].
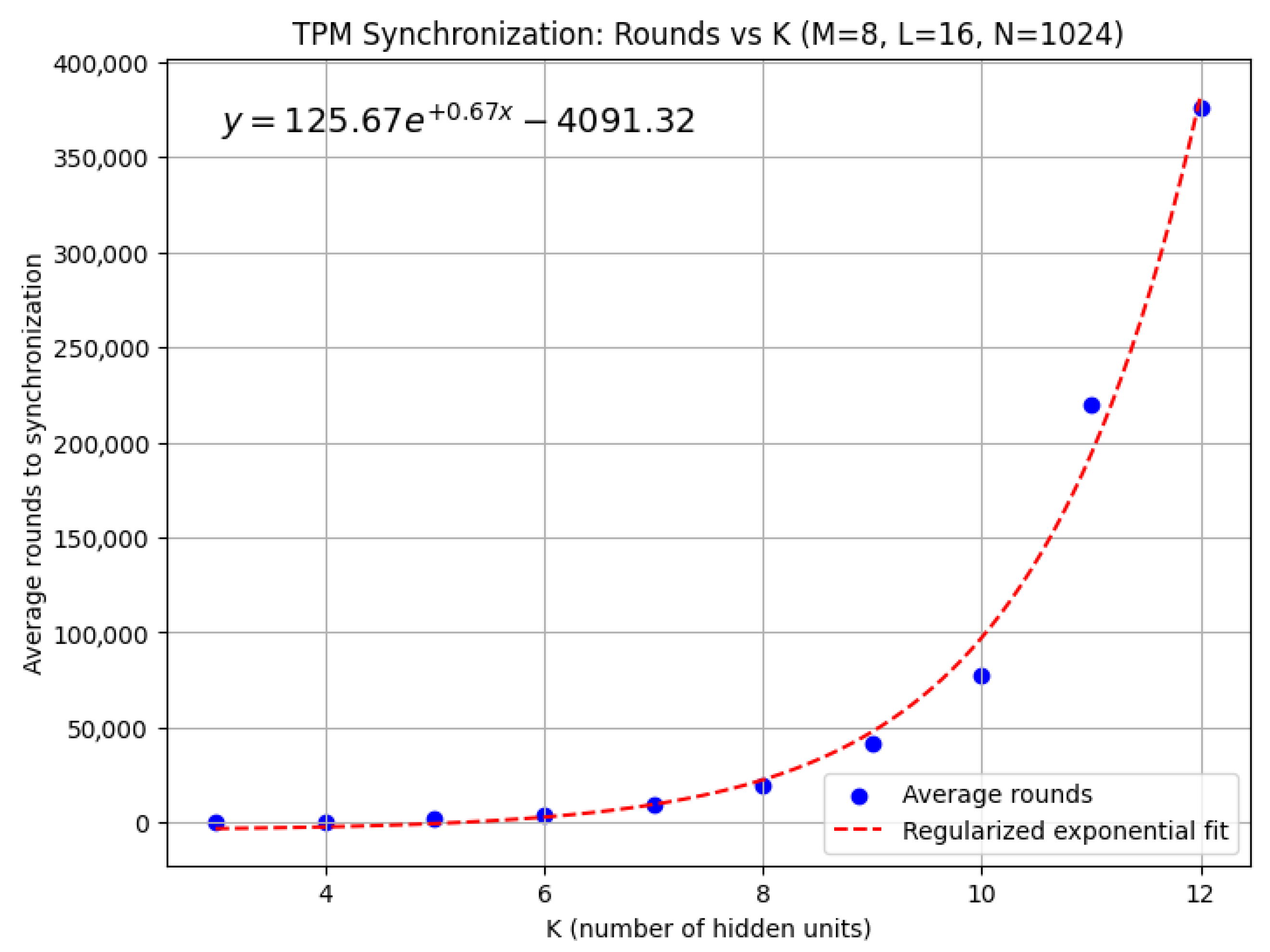
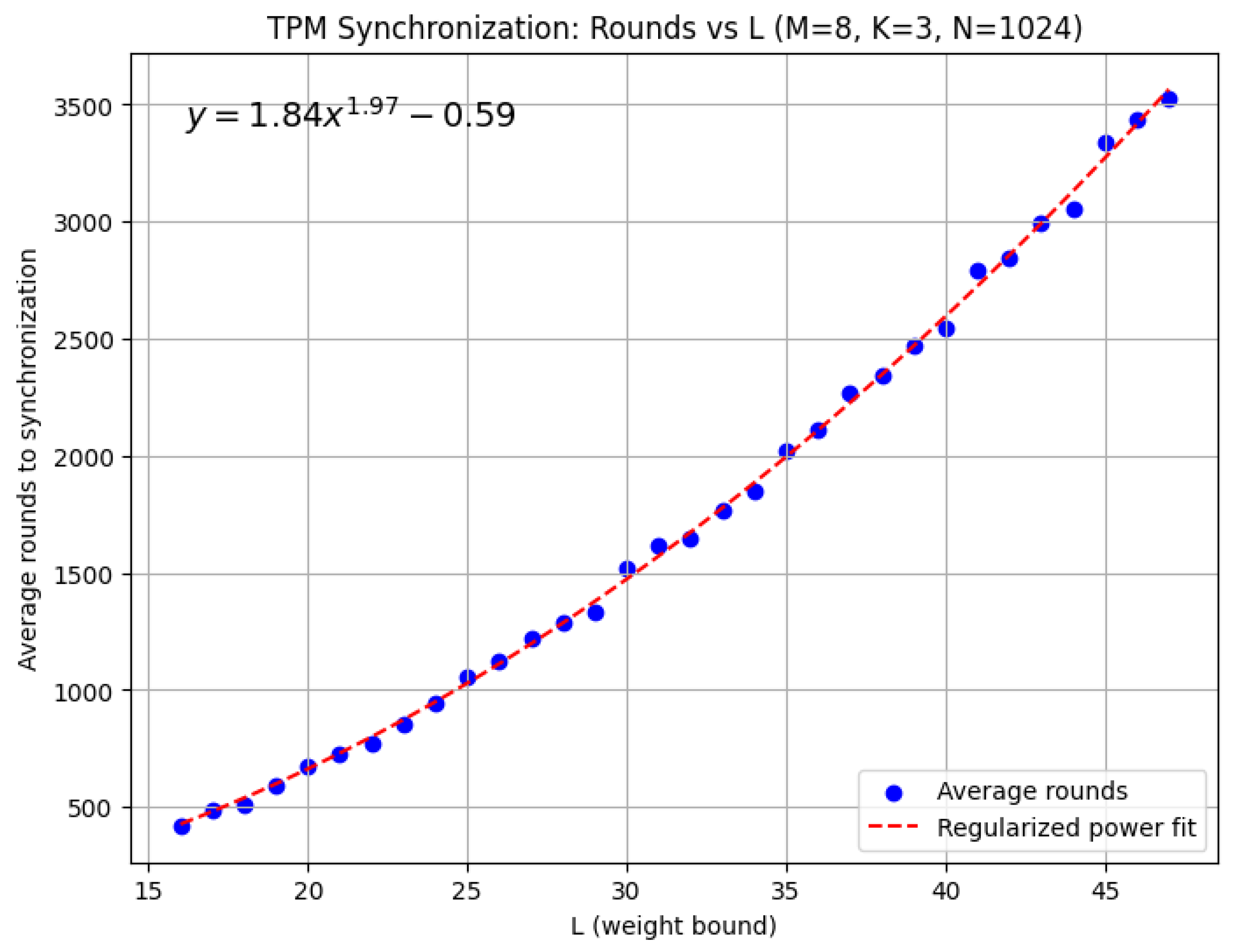
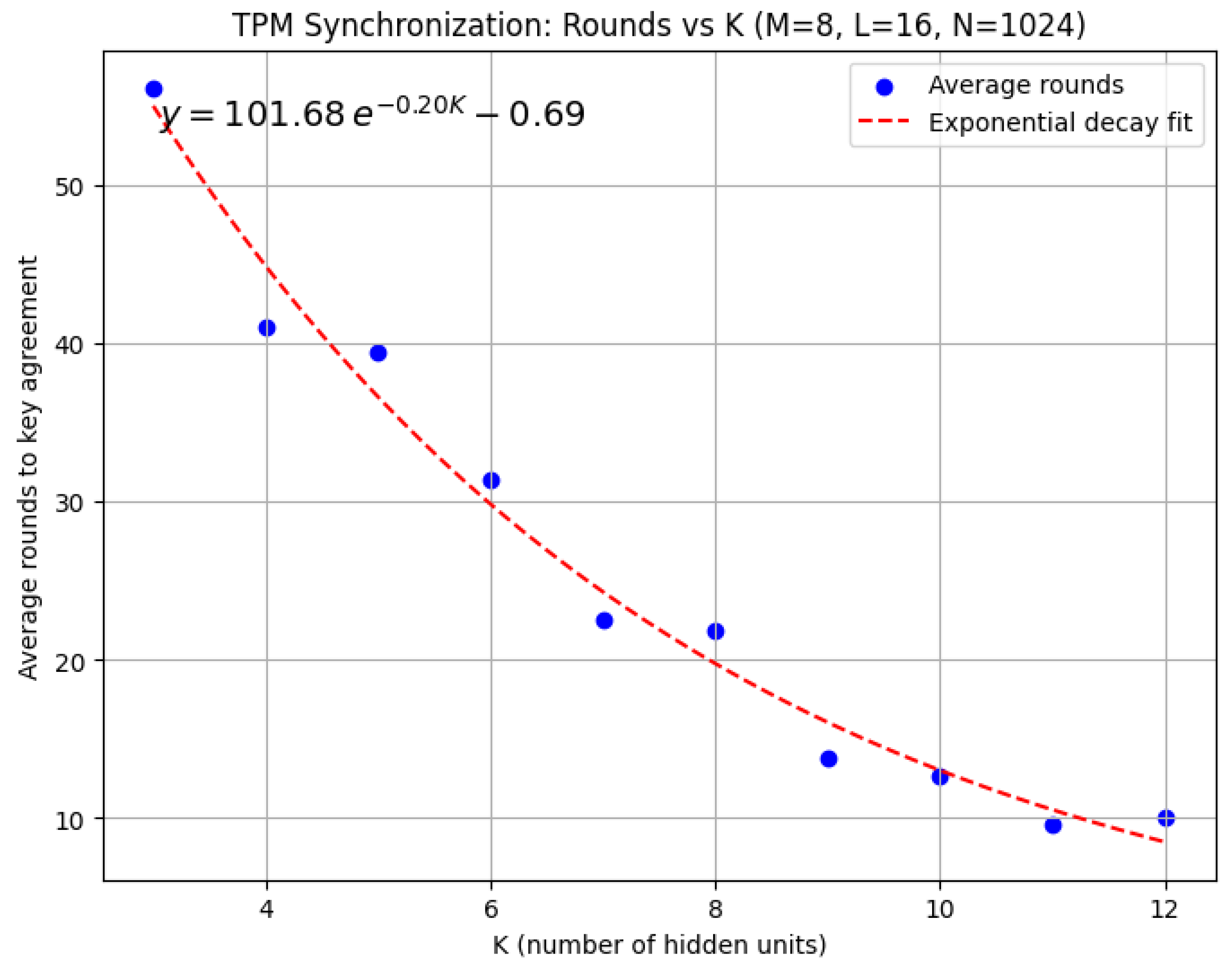
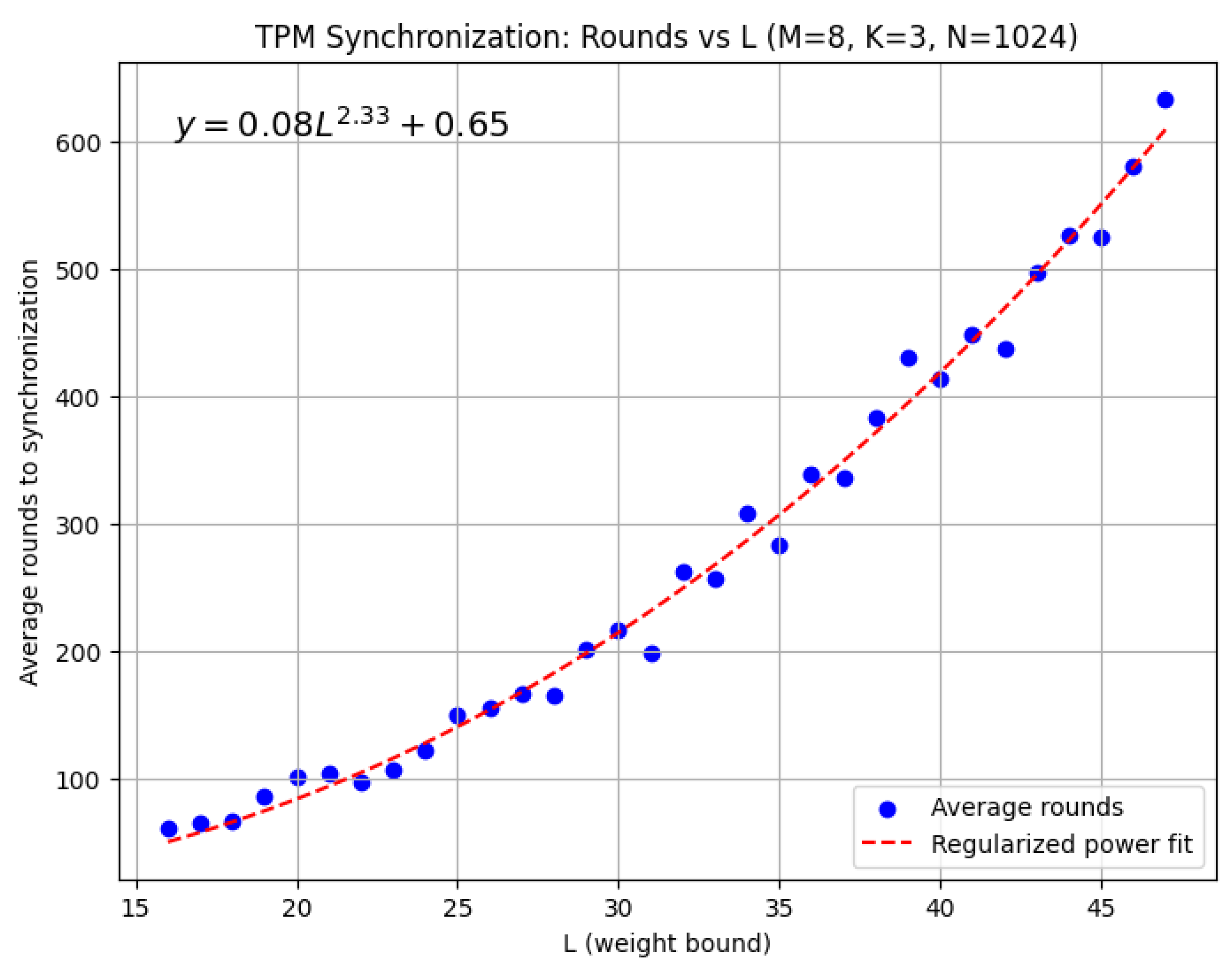
• We empirically demonstrate the efficiency of our protocol by analyzing its complexity in terms of the number of rounds required for synchronization, as a function of the number of hidden units in the TPM and the weight range, and compare these results with those of [16].

The remainder of the paper is organized as follows. Section 2 introduces the Tree Parity Machine (TPM) model, providing the necessary background as described in [16]. Our main technical contributions begin in Section 3, where we present our novel algorithm for privacy-preserving weight comparison. Section 4 builds on this by detailing our proposed neural key agreement protocol, which integrates the privacy-preserving mechanism. In Section 5, we provide a comprehensive experimental evaluation of our protocol, analyzing both its security and efficiency compared to existing approaches. Finally, Section 6 concludes the paper and discusses directions for future research.

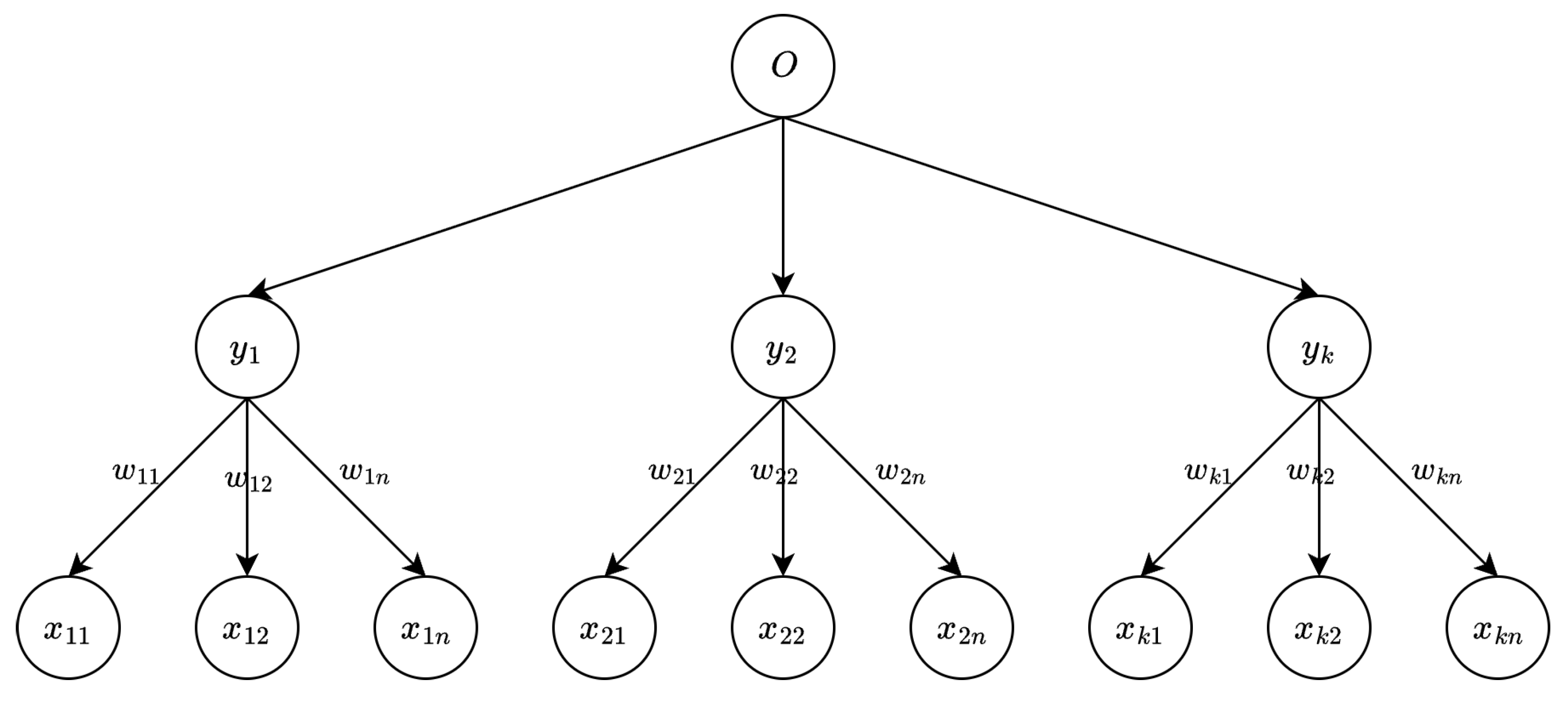
2. Tree Parity Machine

The Tree Parity Machine (TPM) model utilized in this study, as originally introduced in [16], is a three-layer neural network consisting of an input layer, a hidden layer, and an output layer. The input layer is partitioned into K groups, each comprising N neurons. Each neuron within a group is connected to a corresponding neuron in the hidden layer, and all hidden neurons are collectively connected to a single output neuron.

The network inputs, denoted by $x_{ji}$ for $1\le i\le N$ and $1\le j\le K$, are integer values constrained by $-M\le x_{ji}\le M$, where $M\in \mathbb{Z}$. The synaptic weights connecting the input and hidden layers, represented as $w_{ji}$, are also integers, bounded by $-L\le w_{ji}\le L$, with $L\in \mathbb{Z}$.

The activation of each hidden neuron, $y_j$, is computed by applying the sign function to the weighted sum of its inputs:

$$y_j=\sigma \left(\sum _{i=1}^N{x}_{ji}{w}_{ji}\right),$$

(1)

where $\sigma \left(x\right)$ denotes the sign function.

The output neuron, denoted by O, calculates the product of the activations of all hidden neurons:

$$O=\prod _{j=1}^K{y}_j$$

(2)

The weights of the network are updated according to the Hebbian learning rule, as described in [26]:

$$w_{ji}\leftarrow w_{ji}+O{x}_{ji}\Phi \left(y_j,O\right),$$

(3)

where

• $w_{ji}$ is the weight of the i-th input to the j-th hidden neuron,
• $x_{ji}$ is the corresponding input value,
• $y_j$ is the output of the j-th hidden neuron,
• O is the global output of the TPM,
• $\Phi (a,b)$ is the indicator function:

  $$\Phi (a,b)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if} a=b,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Figure 1 illustrates the structure of the TPM.

3. Weights Comparison Algorithm

Consider two parties, ${\mathcal{P}}_1$ and ${\mathcal{P}}_2$, participating in a neural key agreement protocol. Let $w^{{\mathcal{P}}_1}$ and $w^{{\mathcal{P}}_2}$ denote the respective $KN$-dimensional weight vectors of their TPMs. The proposed comparison protocol, $\mathsf{PrivComp}$, enables the parties to privately compute not only the number of synchronized weights, but also to identify which specific weights have been synchronized, without revealing the actual values of the weights to any external observer. This is achieved under the honest-but-curious security model, where both parties are assumed to follow the protocol correctly, but an adversary may passively intercept all messages exchanged during $\mathsf{PrivComp}$ in an attempt to infer the secret weights. The protocol proceeds as follows:

Initially, ${\mathcal{P}}_1$ constructs a vector $d^1$ by flattening its weight matrix $w^{{\mathcal{P}}_1}$, and generates a decoy vector $d^2$ of the same length, where each entry is independently sampled from the range $-L\le d_i^2\le L$. For each position $1\le i\le KN$, ${\mathcal{P}}_1$ randomly decides whether to swap the values of $d_i^1$ and $d_i^2$, thereby obscuring the correspondence between the actual weights and the decoy elements. After performing these random swaps, ${\mathcal{P}}_1$ transmits both $d^1$ and $d^2$ to ${\mathcal{P}}_2$.

Upon receiving the vectors, ${\mathcal{P}}_2$ compares each of its own weights with the corresponding entries in $d^1$ and $d^2$. Specifically, ${\mathcal{P}}_2$ constructs a binary vector $\mathrm{mask}$, where ${\mathrm{mask}}_i=1$ if $w_i^{{\mathcal{P}}_2}$ matches either $d_i^1$ or $d_i^2$, and ${\mathrm{mask}}_i=0$ otherwise. The Hamming weight S of the mask vector, representing the number of matches, is then computed. If S exceeds a predefined security threshold $\tau$, ${\mathcal{P}}_2$ returns the mask vector to ${\mathcal{P}}_1$; otherwise, the protocol terminates with output ⊥.

An adversary intercepting the vectors sent by ${\mathcal{P}}_1$ cannot deduce the actual weights, as the random swapping introduces $2^{KN}$ possible configurations. Although the mask vector could potentially reduce the brute-force search space by indicating positions of possible matches, the threshold $\tau$ ensures that an attacker must still consider at least $2^{\tau }$ possibilities, thereby preserving the desired level of security.

The underlying intuition is that, due to the synchronization process, the probability that ${\mathcal{P}}_2$ observes a match at position i without the actual weights being synchronized is low. Consequently, if ${\mathrm{mask}}_i=1$, it is highly likely that the corresponding weights are synchronized.

The output of the $\mathsf{PrivComp}$ protocol is the common set weights, or ⊥ if the number of matches is below the threshold $\tau$.

The following theorems establish the correctness and security of our construction.

Theorem 1 (Correctness). 

Let $w^{{\mathcal{P}}_1},w^{{\mathcal{P}}_2}\in {\{-L,\dots ,L\}}^{KN}$ denote the weight vectors of parties ${\mathcal{P}}_1$ and ${\mathcal{P}}_2$. Let $d^1,d^2$ be constructed as specified in the protocol, and let $\mathrm{mask}\in {\{0,1\}}^{KN}$ be the output of ${\mathcal{P}}_2$. Then, for any position $i\in \{1,\dots ,KN\}$:

• If $w_i^{{\mathcal{P}}_1}\ne w_i^{{\mathcal{P}}_2}$, the probability that ${\mathrm{mask}}_i=1$ (i.e., a false positive) is at most ${\displaystyle \frac{2}{2L+1}}$.
• If $w_i^{{\mathcal{P}}_1}=w_i^{{\mathcal{P}}_2}$, then ${\mathrm{mask}}_i=1$ with probability 1 (i.e., a true positive).

Proof. 

Fix any position $i\in \{1,\dots ,KN\}$.

Case 1: $w_i^{{\mathcal{P}}_1}\ne w_i^{{\mathcal{P}}_2}$ (False Positive Probability).

According to the protocol, for each index i, one of $\{d_i^1,d_i^2\}$ contains the true value $w_i^{{\mathcal{P}}_1}$, while the other contains a randomly generated decoy. The assignment is governed by the swap bit $s{w}_i$: if $s{w}_i=0$, then $d_i^1=w_i^{{\mathcal{P}}_1}$ and $d_i^2$ is a decoy; if $s{w}_i=1$, then $d_i^2=w_i^{{\mathcal{P}}_1}$ and $d_i^1$ is a decoy.

Let r be the random decoy sampled uniformly from $\{-L,\dots ,L\}$.

There are two cases, each occurring with probability $1/2$:

• With probability $1/2$, $(d_i^1,d_i^2)=(w_i^{{\mathcal{P}}_1},r)$.
• With probability $1/2$, $(d_i^1,d_i^2)=(r,w_i^{{\mathcal{P}}_1})$.

In both cases, $w_i^{{\mathcal{P}}_2}$ can match $d_i^1$ or $d_i^2$ only if $w_i^{{\mathcal{P}}_2}=r$ (since $w_i^{{\mathcal{P}}_1}\ne w_i^{{\mathcal{P}}_2}$ by assumption).

Since r is uniformly distributed over $2L+1$ values, the probability that $r=w_i^{{\mathcal{P}}_2}$ is ${\displaystyle \frac{1}{2L+1}}$.

There are two opportunities (either $d_i^1$ or $d_i^2$), so by the union bound, the probability that $w_i^{{\mathcal{P}}_2}$ matches either $d_i^1$ or $d_i^2$ is at most $2·{\displaystyle \frac{1}{2L+1}}={\displaystyle \frac{2}{2L+1}}$.

Case 2: $w_i^{{\mathcal{P}}_1}=w_i^{{\mathcal{P}}_2}$ (True Positive Probability).

Regardless of the value of $s{w}_i$, either $d_i^1$ or $d_i^2$ will be equal to $w_i^{{\mathcal{P}}_1}$.

Therefore, $w_i^{{\mathcal{P}}_2}$ will always match at least one of $d_i^1$ or $d_i^2$, so ${\mathrm{mask}}_i=1$ with probability 1. □

Theorem 2 (Security). 

Let ${\mathcal{P}}_1$ send the vectors $d^1,d^2\in {\{-L,\dots ,L\}}^{KN}$ to ${\mathcal{P}}_2$ as specified in the protocol, where each position is randomly swapped. Let $\mathrm{mask}\in {\{0,1\}}^{KN}$ be the binary vector sent by ${\mathcal{P}}_2$ to ${\mathcal{P}}_1$ only if the number of 1s in $\mathrm{mask}$ is at least τ. Then, for any eavesdropper intercepting the communication:

• Before $\mathrm{mask}$ is sent, the eavesdropper must consider all $2^{KN}$ possible swap configurations to recover the real weights of ${\mathcal{P}}_1$.
• After $\mathrm{mask}$ is sent, the eavesdropper must consider at least $2^{\tau }$ possible swap configurations.

In both cases, the attacker faces an exponential search space in the relevant parameter.

Proof. 

(1) Security Before $\mathrm{mask}$ is Sent:

When ${\mathcal{P}}_1$ sends $d^1$ and $d^2$, each entry is either the real weight or a random decoy, determined by the secret swap vector $sw\in {\{0,1\}}^{KN}$. For each position i, the attacker does not know whether $d_i^1$ or $d_i^2$ is the real weight. Thus, to recover the real weight vector, the attacker must guess the entire swap vector $sw$, which has $2^{KN}$ possible configurations.

(2) Security After $\mathrm{mask}$ is Sent:

When ${\mathcal{P}}_2$ sends the mask vector $\mathrm{mask}$, the attacker learns which positions i have a match with ${\mathcal{P}}_2$’s weights. For each position i where ${\mathrm{mask}}_i=1$, the real weight of ${\mathcal{P}}_1$ could be either $d_i^1$ or $d_i^2$. For positions where ${\mathrm{mask}}_i=0$, the attacker knows neither value is the real weight, so these positions can be ignored in the brute-force search.

Let S be the number of bits of 1 in the $\mathrm{mask}$. The attacker must guess the swap bits for these S positions, resulting in $2^S$ possible configurations. By protocol, $S\ge \tau$, so the brute-force complexity is at least $2^{\tau }$.

Conclusion: In both cases, the attacker must consider an exponential number of possible swap configurations, either $2^{KN}$ or at least $2^{\tau }$, to recover the real weights. This ensures the protocol’s security against brute-force attacks by an eavesdropper. □

The protocol is described in Box 1.

Box 1. The $\mathsf{PrivComp}$ protocol for privacy-preserving weight comparison.

• Decoy Generation: ${\mathcal{P}}_1$ initializes $d^1$ with its actual weights $w^{{\mathcal{P}}_1}$ and generates a decoy vector $d^2$, where each entry is sampled uniformly from the weight range:

  $$d_i^1\leftarrow w_i^{{\mathcal{P}}_1},\forall i\in \{1,\dots ,KN\}$$

  (4)

  $$\begin{array}{l}{d}_i^2\sim \mathrm{Unif}\{-L,-L+1,\dots ,L\},\forall i\in \{1,\dots ,KN\}\end{array}$$

  (5)
• Random Swapping and Transmission: ${\mathcal{P}}_1$ generates a random binary vector $sw$, where each entry is sampled uniformly from $\{0,1\}$. For each index i, if $s{w}_i=1$, the entries $d_i^1$ and $d_i^2$ are swapped. Both vectors are then sent to ${\mathcal{P}}_2$:

  $$\begin{array}{c}s{w}_i\sim \mathrm{Unif}\{0,1\},\forall i\in \{1,\dots ,KN\}\hfill \end{array}$$

  (6)

  $$\begin{array}{c}(d_i^1,d_i^2)\leftarrow (d_i^2,d_i^1),\mathrm{if} s{w}_i=1\hfill \end{array}$$

  (7)

  $$\begin{array}{c}{\mathcal{P}}_1⟶{\mathcal{P}}_2:(d^1,d^2)\hfill \end{array}$$

  (8)
• Comparison: ${\mathcal{P}}_2$ compares each of its weights $w_i^{{\mathcal{P}}_2}$ with $d_i^1$ and $d_i^2$, constructing the mask vector:

  $$\begin{array}{c}\hfill \mathrm{mask}\left[i\right]=\left\{\begin{array}{cc}1,\hfill & \mathrm{if} w_i^{{\mathcal{P}}_2}\in \{d_i^1,d_i^2\}\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.\forall i\in \{1,\dots ,KN\}\end{array}$$

  (9)
• Threshold Verification and Response: ${\mathcal{P}}_2$ computes $S={\sum }_{i=1}^{KN}\mathrm{mask}\left[i\right]$. If $S>\tau$, ${\mathcal{P}}_2$ returns the mask vector to ${\mathcal{P}}_1$:

  $$\begin{array}{c}\hfill \mathrm{If} S>\tau ,{\mathcal{P}}_2⟶{\mathcal{P}}_1:\mathrm{mask}\end{array}$$

  (10)
• Output: If $S>\tau$, both parties output the set of synchronized weights:

  $$w^c=\{w_i^{{\mathcal{P}}_1}\mid \mathrm{mask}\left[i\right]=1\}=\{w_i^{{\mathcal{P}}_2}\mid \mathrm{mask}\left[i\right]=1\}.$$
  Otherwise, both parties output ⊥.

4. Neural Key Agreement Protocol

In this section, we present the neural key agreement protocol, which incorporates our privacy-preserving comparison protocol, $\mathsf{PrivComp}$, to securely determine the extent of synchronization between the parties. The protocol is detailed in Box 2. All computations, including weight updates, are performed within the range $[-L,L]$ with appropriate clipping.

The proposed protocol follows the general architecture of neural key agreement schemes, as outlined in [8,16]. Its primary innovation, however, is the integration of a privacy-preserving comparison protocol, which allows the participating parties to terminate the synchronization process as soon as a sufficient number of weights have been aligned. This enhancement not only increases the protocol’s efficiency by reducing the number of required rounds, but also significantly improves its security. As noted in [9], the probability that an adversary can successfully synchronize a third TPM with those of the legitimate parties grows with the number of rounds observed. By minimizing unnecessary rounds, the protocol effectively mitigates this risk.

Regarding correctness, it has been established in [8] that two TPMs will eventually synchronize, as the process can be modeled as a random walk within a finite weight space. Each party updates its weights only when the outputs of the corresponding hidden neurons are identical. This selective update rule ensures that the weight vectors do not diverge, but instead gradually converge towards synchronization. In essence, updates are performed exclusively under conditions that promote alignment, thereby guaranteeing convergence of the protocol.

Box 2. Neural key agreement protocol with privacy-preserving synchronization check.

• Parameter Setup and Initialization: The parties ${\mathcal{P}}_1$ and ${\mathcal{P}}_2$ agree on the protocol parameters $K,N,M,L$, and independently initialize their TPM weights uniformly at random:

  $$\begin{array}{cc}{w}_{ji}^{{\mathcal{P}}_1}\sim \mathrm{Unif}\{-L,\dots ,L\},\hfill & \hfill \forall (j,i)\in \{1,\dots ,K\}\times \{1,\dots ,N\},\end{array}$$

  (11)

  $$\begin{array}{cc}{w}_{ji}^{{\mathcal{P}}_2}\sim \mathrm{Unif}\{-L,\dots ,L\},\hfill & \hfill \forall (j,i)\in \{1,\dots ,K\}\times \{1,\dots ,N\}.\end{array}$$

  (12)
• Input Generation: Both parties agree on a common random input vector x, either by exchanging the vector directly or by sharing a common random seed:

  $$\begin{array}{cc}{x}_{ji}\sim \mathrm{Unif}\{-M,\dots ,M\},\hfill & \hfill \forall (j,i)\in \{1,\dots ,K\}\times \{1,\dots ,N\}.\end{array}$$

  (13)
• Computation and Output Exchange: Each party computes the activations of the hidden neurons and the TPM output, then exchanges the output value with the other party:

  $$\begin{array}{cc}{y}_j^{{\mathcal{P}}_1}=\sigma \left(\sum _{i=1}^N{x}_{ji}{w}_{ji}^{{\mathcal{P}}_1}\right),\hfill & \hfill \forall j\in \{1,\dots ,K\},\end{array}$$

  (14)

  $$\begin{array}{cc}{y}_j^{{\mathcal{P}}_2}=\sigma \left(\sum _{i=1}^N{x}_{ji}{w}_{ji}^{{\mathcal{P}}_2}\right),\hfill & \hfill \forall j\in \{1,\dots ,K\},\end{array}$$

  (15)

  $$\begin{array}{c}{O}^{{\mathcal{P}}_1}=\prod _{j=1}^K{y}_j^{{\mathcal{P}}_1},\hfill \end{array}$$

  (16)

  $$\begin{array}{c}{O}^{{\mathcal{P}}_2}=\prod _{j=1}^K{y}_j^{{\mathcal{P}}_2},\hfill \end{array}$$

  (17)

  $$\begin{array}{c}{O}^{{\mathcal{P}}_1}\leftrightarrow O^{{\mathcal{P}}_2}.\hfill \end{array}$$

  (18)
• Weight Update: If the outputs coincide, each party updates its weights according to the Hebbian learning rule, but only for those hidden neurons whose activation matches the global output:

  $$\begin{array}{c}\mathrm{If} O^{{\mathcal{P}}_1}=O^{{\mathcal{P}}_2}=O, \mathrm{then}\hfill \end{array}$$

  (19)

  $$\begin{array}{cc}{w}_{ji}^{{\mathcal{P}}_1}\leftarrow w_{ji}^{{\mathcal{P}}_1}+O{x}_{ji}\Phi (y_j^{{\mathcal{P}}_1},O),\hfill & \hfill \forall (j,i)\in \{1,\dots ,K\}\times \{1,\dots ,N\},\end{array}$$

  (20)

  $$\begin{array}{cc}{w}_{ji}^{{\mathcal{P}}_2}\leftarrow w_{ji}^{{\mathcal{P}}_2}+O{x}_{ji}\Phi (y_j^{{\mathcal{P}}_2},O),\hfill & \hfill \forall (j,i)\in \{1,\dots ,K\}\times \{1,\dots ,N\}.\end{array}$$

  (21)
• Synchronization Check and Output: Both parties execute the $\mathsf{PrivComp}$ protocol to privately estimate the number of synchronized weights. If the result is ⊥, indicating insufficient synchronization, the protocol returns to Step 2. Otherwise, both parties output the set of synchronized weights $w^c$ as the shared secret key.

There are two principal types of attacks on neural key agreement protocols, both of which are relevant in the context of the honest-but-curious adversarial model. In this model, the adversary is assumed to have full access to all messages exchanged over the public channel and may attempt to infer secret information by passively observing the protocol, but does not deviate from the prescribed protocol steps or actively interfere with the communication.

In a naive attack (illustrated in Box 3, the honest-but-curious adversary attempts to synchronize its own TPM with those of the legitimate parties by simply following the same protocol as the participants. The success of such an attack is directly influenced by the number of synchronization rounds observed, which highlights the importance of minimizing protocol duration to limit the adversary’s opportunity for synchronization.

Box 3. Naive attack against the neural key agreement protocol.

• Attacker Initialization: The adversary $\mathcal{A}$ independently initializes the weights of its own TPM:

  $$\begin{array}{cc}{w}_{ji}^{\mathcal{A}}\sim \mathrm{Unif}\{-L,\dots ,L\},\hfill & \hfill \forall (j,i)\in \{1,\dots ,K\}\times \{1,\dots ,N\}.\end{array}$$

  (22)
• Local Computation: The attacker $\mathcal{A}$ observes the public input vector x used by the legitimate parties and computes the activations of its hidden neurons and the output of its TPM:

  $$\begin{array}{cc}{y}_j^{\mathcal{A}}=\sigma \left(\sum _{i=1}^N{x}_{ji}{w}_{ji}^{\mathcal{A}}\right),\hfill & \hfill \forall j\in \{1,\dots ,K\},\\ O^{\mathcal{A}}=\prod _{j=1}^K{y}_j^{\mathcal{A}}.\hfill \end{array}$$
• Synchronization Attempt: The attacker $\mathcal{A}$ monitors the outputs $O^{{\mathcal{P}}_1}$ and $O^{{\mathcal{P}}_2}$ exchanged between the legitimate parties. Whenever $O^{{\mathcal{P}}_1}=O^{{\mathcal{P}}_2}=O^{\mathcal{A}}$, the attacker updates its weights according to the same Hebbian learning rule:

  $$\begin{array}{c}{w}_{ji}^{\mathcal{A}}\leftarrow w_{ji}^{\mathcal{A}}+O^{\mathcal{A}}{x}_{ji}\Phi (y_j^{\mathcal{A}},O^{\mathcal{A}}),\forall (j,i)\in \{1,\dots ,K\}\times \{1,\dots ,N\}.\hfill \end{array}$$

  (23)
• Output: The attacker $\mathcal{A}$ continues this process for as long as ${\mathcal{P}}_1$ and ${\mathcal{P}}_2$ execute the protocol. Upon termination, $\mathcal{A}$ outputs its current weight vector $w^{\mathcal{A}}$ as its estimate of the shared secret.

In a geometric attack, the adversary leverages additional information from the protocol execution to improve its chances of synchronization, even when its own output does not match those of the legitimate parties. Specifically, when the attacker’s output differs, the adversary identifies the hidden neuron whose associated weights are closest to the input hyperplane and selectively flips its activation. This advanced technique, introduced by [9], allows the honest-but-curious adversary to make progress toward synchronization despite output mismatches, thereby posing a more significant threat than the naive attack. The geometric attack is detailed in Box 4.

Box 4. Geometric attack against the neural key agreement protocol.

• Attacker Initialization: The adversary $\mathcal{A}$ independently initializes the weights of its TPM:

  $$\begin{array}{c}{w}_{ji}^{\mathcal{A}}\sim \mathrm{Unif}\{-L,\dots ,L\},\forall (j,i)\in \{1,\dots ,K\}\times \{1,\dots ,N\}.\hfill \end{array}$$
• Local Computation: The attacker $\mathcal{A}$ observes the public input vector x and, for each hidden unit j, computes:

  $$\begin{array}{c}\hfill p_j^{\mathcal{A}}=\sum _{i=1}^N{x}_{ji}{w}_{ji}^{\mathcal{A}},\forall j\in \{1,\dots ,K\},\\ y_j^{\mathcal{A}}=\sigma \left(p_j^{\mathcal{A}}\right),\forall j\in \{1,\dots ,K\},\hfill \\ O^{\mathcal{A}}=\prod _{j=1}^K{y}_j^{\mathcal{A}}.\hfill \end{array}$$
• Geometric Update: The attacker $\mathcal{A}$ observes the outputs $O^{{\mathcal{P}}_1}$ and $O^{{\mathcal{P}}_2}$ exchanged by the legitimate parties and proceeds as follows:

  $$\begin{array}{cc}\hfill & \mathrm{If} O^{{\mathcal{P}}_1}=O^{{\mathcal{P}}_2}=O \mathrm{and} O^{\mathcal{A}}\ne O:\hfill \\ \hfill & \mathrm{Let}{j}_0=arg\underset{j}{min}|p_j^{\mathcal{A}}| (\mathrm{the} \mathrm{hidden} \mathrm{neuron} \mathrm{closest} \mathrm{to} \mathrm{its} \mathrm{hyperplane}).\hfill \\ \hfill & \mathrm{Define} \mathrm{the} \mathit{flipped} \mathrm{hidden} \mathrm{vector}:\hfill \\ \hfill & {\tilde{y}}_j^{\mathcal{A}}=\left\{\begin{array}{cc}-y_j^{\mathcal{A}}\hfill & \mathrm{if} j=j_0,\hfill \\ y_j^{\mathcal{A}}\hfill & \mathrm{otherwise}\hfill \end{array}\right.\forall j\in \{1,\dots ,K\}.\hfill \\ \hfill & w_{ji}^{\mathcal{A}}\leftarrow w_{ji}^{\mathcal{A}}+O^{\mathcal{A}}{x}_{ji}\Phi ({\tilde{y}}_j^{\mathcal{A}},O^{\mathcal{A}}),\forall (j,i)\in \{1,\dots ,K\}\times \{1,\dots ,N\}.\hfill \\ \hfill & \mathrm{If} O^{{\mathcal{P}}_1}=O^{{\mathcal{P}}_2}=O \mathrm{and} O^{\mathcal{A}}=O:\hfill \\ \hfill & w_{ji}^{\mathcal{A}}\leftarrow w_{ji}^{\mathcal{A}}+O{x}_{ji}\Phi (y_j^{\mathcal{A}},O),\forall (j,i)\in \{1,\dots ,K\}\times \{1,\dots ,N\}.\hfill \end{array}$$
• Output: The attacker $\mathcal{A}$ repeats the above steps for as long as ${\mathcal{P}}_1$ and ${\mathcal{P}}_2$ are executing the protocol. When the protocol terminates, $\mathcal{A}$ outputs its current weight vector $w^{\mathcal{A}}$.

5. Experiments

The experimental evaluation focuses on two key aspects of the neural key agreement protocol: efficiency and security. Efficiency is measured in terms of the number of rounds required for synchronization, while security is assessed by the percentage of the shared key that can be recovered by an attacker. We consider two types of attacks: naive and geometric [9]. While naive attacks generally pose little threat to neural key agreement protocols, geometric attacks represent a significant vulnerability and are the primary reason such protocols are not widely regarded as secure. In each experiment, we compare our protocol to that of [16], which follows an identical message flow, with the only difference being that synchronization steps (1–4) from Box 2 are executed until all weights are equal. For all experiments involving our protocol, we set the threshold $\tau =128$, reflecting a realistic scenario in which an attacker would need to brute-force $2^{128}$ possible swap configurations, as established in Theorem 2.

Efficiency: In the first set of experiments, we assess the efficiency of the protocol with respect to K (the number of hidden neurons) and L (the range of weight values). For both experiments, we fix $N=128$ and $M=8$. In the first experiment, with $L=16$, we compute the number of rounds required to synchronize the TPMs in 50 trials for each value of $K\in \{3,4,\dots ,12\}$, and report the average. Similarly, in the second experiment, with $K=3$, we average the number of rounds over 50 trials for each value of $L\in \{16,17,\dots ,47\}$. Figure 2 and Figure 3 present the results for the classic protocol of [16], while Figure 4 and Figure 5 show the results for our protocol. Although both protocols exhibit similar complexity with respect to the weight range L, our protocol demonstrates superior efficiency as K increases. Specifically, while the protocol of [16] exhibits exponential growth in the number of rounds with increasing K, our protocol shows an exponential decrease. This improvement is attributable to the early termination mechanism: as K increases, the parties reach the key length threshold more rapidly, allowing the protocol to halt sooner.

To evaluate the practical efficiency of our proposed protocol, we conducted a series of experiments comparing its average running time to that of the classic protocol of [16]. The experiments were performed on a system equipped with an Intel^® Xeon^® Gold 5512U processor (12 cores per socket) manufactured by Intel Corporation, Santa Clara, CA, USA, along with approximately 60 GB of RAM.

Table 2. Comparison of average running time (in seconds) for key agreement between the Protocol of [16] and our protocol, for various values of K.

K	Protocol of [16]	Our Protocol
3	0.03	0.22
4	0.05	0.22
5	0.13	0.24
6	0.37	0.20
7	0.83	0.20
8	1.69	0.18
9	3.81	0.16

summarizes the average running time (in seconds) required to achieve key agreement for both protocols, across a range of values for the hidden layer size K.

As shown in the table, while the classic protocol is slightly faster for small values of K, our protocol demonstrates a dramatic improvement in efficiency as K increases. For example, at $K=9$, our protocol achieves key agreement in an average of just $0.16$ s, compared to $3.81$ s for the protocol of [16]—a speedup of more than an order of magnitude. This trend becomes increasingly pronounced for larger K, which is of paramount importance for security, as higher values of K are known to significantly enhance resistance against known attacks. These results highlight the practical advantage of our protocol in scenarios where strong security is required.

Security: In the second set of experiments, we evaluate the resilience of both protocols against naive and geometric attacks by measuring the proportion of the shared key that an attacker can recover. For all security experiments, we set $K=3$, a common choice in the literature [8,16]. In our protocol, the threshold for the shared key length is set to 180, meaning that once 180 weights are synchronized, the protocol terminates. The success of an attack is quantified as the synchronization percentage, defined as the ratio of the number of weights correctly recovered by the attacker to the total length of the shared key.

Table 3. Comparison of synchronization percentages between the two protocols for $k=3$ in the naive attack.

Protocol	Average (%)	Maximum (%)
Protocol of [16]	9.75	28.32
Our Protocol	6.90	27.27

presents the results for the naive attack. As expected from prior work [8,16], neural key agreement protocols are robust against naive attacks. This robustness arises from the synchronization process itself: while the legitimate parties update their weights only when their output neurons agree, the attacker can update only when all three outputs coincide. This discrepancy allows the legitimate parties to synchronize before the attacker can recover a significant portion of the key. Notably, since our protocol halts synchronization once sufficient key material has been established, both the average and maximum synchronization percentages for the attacker are lower compared to the protocol of [16].

The results for the geometric attack, shown in

Table 4. Comparison of synchronization percentages between the two protocols for $k=3$ in the geometric attack.

Protocol	Average (%)	Maximum (%)
Protocol of [16]	65.02	100.00
Our Protocol	6.90	27.27

, reveal a stark contrast between the two protocols. While the protocol of [16] yields an average attacker synchronization percentage of 65.02%, our protocol limits this to only 6.90%. More importantly, the maximum synchronization percentage for the attacker reaches 100% in the classic protocol, indicating that the attacker can occasionally recover the entire shared key. In contrast, the maximum in our protocol is approximately 27%. Given that our shared key consists of 180 weights, even recovering 30% of the key still leaves the attacker with more than 126 unknown weights, corresponding to a brute-force search space of $2^{630}$ when $L=16$.

6. Conclusions and Further Directions of Research

In this paper, we introduced a novel protocol that enables two parties engaged in a neural key agreement process to privately determine which weights have been synchronized at intermediate stages. This capability allows the parties to terminate the synchronization process as soon as sufficient key material has been established, thereby improving both the efficiency and security of the protocol. We formally proved the correctness and security of our approach and demonstrated how it can be seamlessly integrated into a neural key agreement protocol.

Our experimental results show that the proposed protocol not only reduces the number of rounds required for synchronization, but also significantly enhances security, particularly against geometric attacks, the primary vulnerability in existing neural key agreement schemes. By comparing our protocol to the state-of-the-art approach from [16], we demonstrated substantial improvements: in our protocol, the number of rounds required for synchronization decreases as the number of hidden units increases, whereas in the alternative protocol, this number grows exponentially. Furthermore, our protocol effectively mitigates the geometric attack, limiting the attacker’s ability to recover the shared key, while the alternative protocol remains vulnerable to complete key recovery by an adversary.

While our results are promising, we do not claim that neural key agreement protocols incorporating our privacy-preserving comparison procedure are ready for immediate deployment in real-world scenarios. Rather, our work demonstrates that the main limitation of such protocols, i.e., the vulnerability to geometric attacks, can be addressed. An important direction for future research is to establish the security of these protocols within a standard cryptographic framework, which remains an open challenge for all neural key agreement protocols. The implementation is available at https://github.com/miiip/Neural-Key-Agreement- (accessed on 26 November 2025).