Seismic Data Enhancement for Tunnel Advanced Prediction Based on TSISTA-Net

Abstract

Tunnel seismic advanced prediction is a widely used technique in geotechnical engineering due to its non-destructive characteristics and deep detection capability. However, limitations in acquisition space and complex on-site conditions often result in missing traces, damaged channels, and low-resolution data, thereby hindering accurate geological interpretation. Although deep learning models such as U-Net have shown promise in seismic data reconstruction, their emphasis on local features and fixed parameter configurations limits their capacity to capture global and long-range dependencies, thereby constraining reconstruction accuracy. To address these challenges, this study proposes a novel deep unrolling network, TSISTA-Net (Tunnel Seismic Iterative Shrinkage–Thresholding Algorithm Network), specifically designed to improve seismic data quality. Built upon the ISTA-Net architecture, TSISTA-Net incorporates three distinct innovations. First, reflection padding is utilized to minimize boundary artifacts and effectively recover edge information. Second, multi-scale dilated convolutions are employed to extend the receptive field, thereby facilitating the extraction of long-range and multi-scale features from seismic signals. Third, a lightweight and patch-based processing strategy is adopted, guaranteeing high computational efficiency while maintaining reconstruction quality. The effectiveness of the proposed method was validated on both synthetic and real tunnel seismic datasets. On synthetic data, TSISTA-Net achieved a PSNR of 37.28 dB, an SSIM of 0.9667, and an LCCC of 0.9357, outperforming U-Net (35.93 dB, 0.9480, 0.9087) and conventional ISTA-Net (34.04 dB, 0.9167, 0.8878). These results demonstrate superior signal fidelity, structural similarity, and local correlation relative to established baselines. Consistent improvements were also observed on real tunnel datasets, indicating that TSISTA-Net provides an efficient, data-driven solution for tunnel seismic data processing with strong potential for practical engineering applications.

1. Introduction

Tunnel seismic advanced prediction is a key technical approach to ensuring the safety of tunnel construction. This method analyzes the propagation characteristics of seismic waves within rock masses to identify adverse geological structures (such as faults, fracture zones, karst cavities, etc.) ahead of the excavation face, thereby providing critical support for engineering decision-making [1,2]. In recent years, as China’s transportation, water conservancy, and other infrastructure projects have extended into complex geological regions, increasingly challenging tunnel rock mass conditions have imposed higher demands on the precision and reliability of seismic exploration data [3]. However, in practical tunnel engineering, seismic data acquisition often faces significant challenges. Firstly, heterogeneous and discontinuous geological conditions play a critical role. For instance, unfavorable geological structures such as fault fracture zones, karst cavities, and shear zones can cause abrupt velocity changes, strong scattering, mode conversions, and energy attenuation of seismic waves within the medium, resulting in highly non-stationary and spatially complex wavefields [4]. These natural factors lead to multipath propagation, superposition of multiple wave modes, and phase distortions in tunnel seismic records, which directly affect data interpretability and the stability of subsequent processing. Secondly, engineering environmental factors can exert significant influence. Abate G et al. reported that, under construction-induced vibrations, a pronounced bidirectional dynamic coupling exists between aboveground buildings and underground tunnels, whereby the dynamic response of the surface structures can, in turn, affect the tunnel and the surrounding soil, altering the propagation paths and spectral characteristics of near-field vibrations [5]. To mitigate such effects, Maleska T et al. applied expanded polystyrene (EPS) geofoam beneath a soil–steel composite bridge. This material was found to effectively absorb and redistribute seismic energy, thereby reducing structural deformation and stress [6]. This method demonstrates good adaptability for bridge structures; nevertheless, the direct treatment of seismic energy can modify the propagation and recording characteristics of seismic signals. The combined effect of the two factors leads to seismic records with insufficient acquisition channels, low spatial sampling rates, severe noise, and signal degradation [7]. Therefore, the development of efficient and robust methods for seismic data enhancement and reconstruction, aimed at improving data quality and spatial continuity, has become an important research focus in tunnel seismic advanced prediction.

Traditional methods for seismic data reconstruction can be broadly categorized into predictive-filter-based approaches [8,9] wave-equation-based approaches [10,11], mathematical-transformation techniques [12,13], and matrix rank reduction methods [14,15], among others. These methods typically rely on predefined prior assumptions such as sparsity or low-rank properties or explicitly defined geophysical models, and they often perform well under simple and homogeneous geological conditions. However, in the complex and heterogeneous geological environments frequently encountered in actual tunneling projects, such assumptions often fail to align with actual geological complexities, leading to limited reconstruction effectiveness. Furthermore, traditional algorithms are frequently computationally intensive and exhibit slow iterative convergence, thus making it difficult to meet the efficiency demands of practical engineering applications [16].

To overcome the aforementioned limitations, compressed sensing theory has been introduced into seismic data processing. This theory, by leveraging the sparsity of signals, can reconstruct complete information from undersampled data [17]. The Iterative Shrinkage-Thresholding Algorithm (ISTA) and its accelerated version (FISTA), as classical algorithms within the framework of compressed sensing, have demonstrated excellent performance in seismic data reconstruction when combined with sparse transforms such as wavelets or curvelets [18,19,20]. However, the performance of ISTA-based methods heavily depends on the choice of sparse transform bases and parameters, which are typically determined through expert knowledge. Such reliance limits adaptability under complex geological conditions, and the iterative process is computationally expensive.

In recent years, deep learning, with its powerful feature learning and nonlinear mapping capabilities, has provided novel solutions for seismic data reconstruction. Encoder–decoder architectures such as U-Net have been widely applied to seismic data interpolation and reconstruction tasks, demonstrating superior performance in scenarios involving randomly missing or regularly missing data [21]. For instance, Chai et al. investigated the efficacy of U-Net in reconstructing both regular and irregular missing seismic data, validating the network’s advantage in leveraging data feature information through 3D seismic data verification [22]. He et al. proposed a method employing U-Net neural networks to reconstruct continuous multi-channel seismic data with missing traces [23]. Additionally, Gao and Zhang proposed a small-scale, multi-component joint reconstruction scheme by integrating U-Net with CNN modules, providing a novel technical framework for reconstructing complex seismic data [24]. However, the U-Net architecture primarily focuses on extracting local features, with limited capability for modeling the global dependencies and long-range correlations inherent in seismic signals. Furthermore, the design of its network architecture and parameter settings often lacks consideration of the unique physical properties of seismic data, thereby constraining further improvements in reconstruction accuracy [25].

In response to the aforementioned challenges, several researchers have attempted to integrate traditional iterative algorithms with deep learning to develop interpretable Deep Unrolling Networks. In the field of image processing, Zhang et al. mapped each iteration of ISTA to a single layer in a neural network, enabling the network to learn the parameters and transformations involved in each iteration, thereby significantly improving reconstruction efficiency and flexibility [26]. In remote sensing data processing, some studies have combined models such as GSISTA with optimization theory, further enhancing reconstruction performance [27]. In civil engineering, digital twin technology and genetic algorithms have been applied to bridge inspection, providing a scalable framework suitable for real-time structural health monitoring of complex structural systems [28]. Rabi R.R. et al. have integrated machine learning with empirical models and engineering principles to improve the accuracy of shear capacity prediction for rectangular hollow reinforced concrete bridge piers [29]. Their approach offers a precise, interpretable, and practically applicable prediction framework, which holds significant value for advancing structural design practice and reliability in engineering assessment. Similar approaches have also been explored in disciplines such as medicine [30], hydrology [31], and agriculture [32]. In the seismic domain, Ding et al. proposed an SA-PINN (Self-Adaptive Physics-Informed Neural Network) model that incorporates a sequential learning strategy based on time-domain decomposition, thereby improving scalability and accuracy in complex wavefields [33]. Lan et al. introduced a low-dimensional manifold model for seismic data reconstruction, achieving better results than many traditional methods [34]. Zhang et al. combined deep-learning-based denoising with conventional algorithms to design the CNN-POCS framework for seismic data processing [35], while Chen et al. integrated the convex projection method with deep learning for three-dimensional seismic data reconstruction [36].These approaches offer novel paradigms for seismic data reconstruction; however, in the specific application scenario of tunnel seismic data, the limited spatial aperture and complex acquisition environment present unique challenges, and thus the adaptability and optimization of these methods remain to be further investigated.

Inspired by the aforementioned applications of Deep Unrolling Networks, and considering the strong non-uniformity, multi-scale characteristics, and low signal-to-noise ratio inherent to tunnel seismic data, this paper proposes a TSISTA-Net model for enhancing tunnel seismic data, building upon the ISTA-Net framework. The main contributions of this study are as follows:

(1)

Introducing a reflection padding technique to effectively suppress boundary artifacts and improve the reconstruction quality of edge information;

(2)

Embedding a multi-scale dilated convolution module to expand the receptive field and enhance the capability to capture long-range correlated features in seismic signals;

(3)

Adopting lightweight and block-based processing strategies to enhance computational efficiency while ensuring reconstruction accuracy, thereby satisfying the demands of practical engineering applications.

The remainder of this paper is organized as follows. The theoretical section first presents the classical ISTA framework and ISTA-Net, and then provides a detailed description of the proposed TSISTA-Net method. The experimental section outlines the dataset construction process, followed by experiments conducted in two-dimensional scenarios using both synthetic and field data. The results derived from various evaluation metrics verify the effectiveness and superiority of TSISTA-Net. Subsequently, the discussion section offers an in-depth analysis of the experimental results, identifies the limitations of the method, and explores potential directions for future research. Finally, the conclusion section summarizes the work and proposes a feasible approach and research perspective for tunnel engineering data enhancement.

2. Theory

2.1. Iterative Shrinkage Threshold Algorithm

The Iterative Shrinkage-Thresholding Algorithm (ISTA) is an optimization algorithm for sparse signal recovery. It has been widely applied in signal processing, image reconstruction, and seismic data processing, particularly for solving linear inverse problems where the signals of interest exhibit sparsity or compressibility. The algorithm combines gradient descent with shrinkage (thresholding) operations, thereby enabling signal recovery and denoising through iterative optimization.

In seismic data processing, the goal is to recover the original seismic signal from noisy and possibly incomplete observations. ISTA is primarily employed to solve sparsity-regularized convex optimization problems, where the objective function typically consists of a data fidelity term and a sparse regularization term. Specifically, the optimization problem can be formulated as follows:

$$\underset{x}{\min }{\displaystyle \frac{1}{2}}{‖Ax-b‖}_2^2+\lambda {‖\psi x‖}_1,$$

(1)

Here, x ∈ Rⁿ represents the seismic signal to be recovered, which is typically assumed to be sparse in a specific transform domain (e.g., the frequency or wavelet domain). A ∈ R^m×n is the observation matrix for seismic data, b ∈ R^m×n represents the observed seismic data, λ > 0 is the regularization parameter that controls the trade-off between sparsity and data fidelity, and ψ denotes the coefficients of x in the chosen sparse transform domain.

In seismic data processing, ISTA iteratively refines the estimate of the seismic signal x. Its core idea is to combine gradient descent (to optimize the data fidelity term) with shrinkage–thresholding operations (to enforce sparsity constraints). The detailed calculation procedure is presented in

Table 1. Ista Iteration Steps.

Input: Observation data: b; Initial value: x(0) = 0; Observation Matrix: A; Regularization parameter: λ; Step: t; Number of iterations: Niter

For k = 1: Nite

$\mathrm{Gradient} \mathrm{update}: y^{(k)}=x^{(k)}-t{A}^T(A{x}^{(k)}-b)$

$\mathrm{Soft} \mathrm{threshold} \mathrm{operation}: x^{(k+1)}=S_{\lambda t}(y^{(k)})$

End

Output: x(k+1)

.

Assume the following linear model in seismic data processing:

$$b=Ax,$$

(2)

Here, x denotes the sparse seismic signal to be recovered. By applying ISTA, the above-described steps are integrated, and the iterative update equation for seismic data processing can be expressed as:

$$x^{(k+1)}=S_{\lambda t}(x^{(k)}-t{A}^T(A{x}^{(k)}-b)),$$

(3)

Here, x^(k) denotes the seismic signal estimate at the k-th iteration; t is the step size (also referred to as the learning rate), which must satisfy 0 < t < 1/L to guarantee the convergence of the algorithm; S_λt(·) denotes the soft-thresholding function for imposing sparsity constraints. Therefore, based on ISTA, the iteration can be divided into two steps: a gradient update and a proximal mapping. The equations are given as follows:

$$r^{(k+1)}=x^{(k)}-t{A}^T(A{x}^{(k)}-b),$$

(4)

$$x^{(k+1)}=\arg \underset{x}{\min }{\displaystyle \frac{1}{2}}{‖x-r^{(k+1)}‖}_2^2+\lambda {‖\psi x‖}_1,$$

(5)

In each iteration, the gradient descent step first minimizes the data fitting error, and the soft-thresholding function then enforces the sparsity of the seismic signal, thereby approximating the true signal. It is worth noting that ISTA typically requires a large number of iterations to achieve satisfactory reconstruction results, rendering the algorithm computationally expensive. This issue is particularly pronounced when processing high-dimensional data, in which the computational cost increases substantially. Moreover, pre-defined, fixed transformations and parameters limit ISTA’s flexibility and generalization capability, making it difficult to adapt to diverse signal characteristics. Additionally, the complexity of solving the proximal mapping further constrains ISTA’s effectiveness and efficiency when employing more powerful or adaptive transformations. The difficulty of parameter tuning exacerbates the challenges of applying the algorithm in practice, particularly in scenarios lacking prior knowledge or automated parameter adjustment tools.

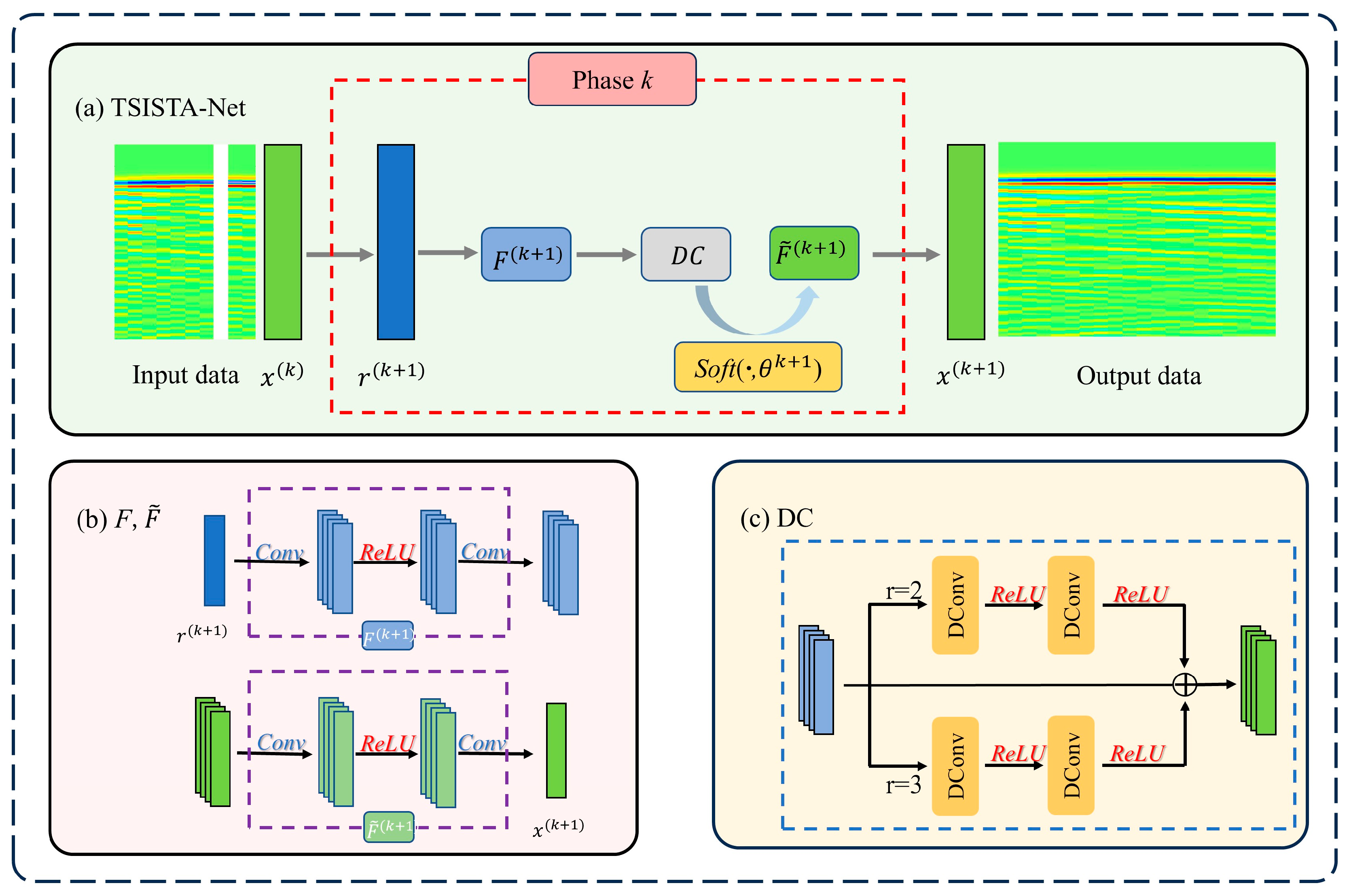
2.2. Tunnel Seismic Iterative Shrinkage Threshold Algorithm Net

To adapt to the complex tunnel environment and overcome the shortcomings of the traditional ISTA, this paper proposes a deep unfolded network, hereafter referred to as TSISTA-Net. The core idea is to unfold ISTA iterations into network layers, enabling the learning of adjustable parameters and adaptive transformations to address the limitations of the traditional ISTA. Meanwhile, to effectively capture the complex features of tunnel seismic data, techniques such as random medium modeling for dataset generation, dilated convolution, and reflection padding are incorporated into the network design to enhance reconstruction performance. Figure 1 illustrates the various modules of the proposed network.

2.2.1. Iterative Shrinkage Threshold Algorithm Net

Figure 2 shows the specific structure of the ISTA-Net. The network employs a generic nonlinear transformation function F(·) to sparsity the seismic data, whose parameters are learnable. Leveraging CNN’s strong representation and universal approximation capabilities, we design F(·) as two linear convolution layers followed by a ReLU activation function. Specifically, the first layer consists of 32 convolution kernels of size 3 × 3 × 32, whereas the second layer contains a single convolution kernel of size 3 × 3 × 32. This architecture ensures that the spatial dimensions of the output remain consistent with those of the input.

$$F(x)=Con{v}_2(ReLU(C{\mathrm{onv}}_1(x))),$$

(6)

In ISTA-Net, Equations (4) and (5) can be modified as follows:

$$r^{(k+1)}=x^{(k)}-t^{(k)}{A}^T(A{x}^{(k)}-b),$$

(7)

$$x^{(k+1)}=\arg \underset{x}{\min }{\displaystyle \frac{1}{2}}{‖x-r^{(k+1)}‖}_2^2+\lambda ‖{F(x)‖}_1,$$

(8)

It can be observed that the parameter t in Equation (7) allows the transformation to be updated during iterations (whereas it remains constant in the traditional ISTA). To efficiently solve the proximal mapping problem in Equation (8), we follow the method proposed by Zhang et al. [26]. First, it is important to note that r^(k+1) represents the direct reconstruction of x^(k) obtained in the k-th iteration. When dealing with image inverse problems, a frequently used and reasonable assumption is that every component of the difference vector (x^(k) − r^(k)) can be considered to follow an independent normal distribution with zero mean and identical variance σ² [37]. Here, we also make this assumption, and then we further prove the following theorem:

Theorem 1:

Let X₁, …, X_n be independent normal random variables with common zero mean and variance σ2. Denote the random vector X′ = [X₁,…,X_n]^T. Given matrices A ∈ R^m×n and B ∈ R^m×n, define Y′ = BReLU(AX′) = Bmax(0,AX′). ReLU(z) = max(0,z) is applied element-wise. Then, the variance of Y′ and the variance of X′ are linearly related:

$$E[{‖Y^{\prime }-E[Y^{\prime }]‖}_2^2]=\alpha E[‖{X^{\prime }-E[X^{\prime }]‖}_2^2],$$

(9)

where α is only a function of A and B.

Theorem 1 can be easily extended to a normal distribution. Suppose that r^(k+1) and F(r^(k+1)) are the mean values of x and F(x), respectively, then we can make the following approximation based on Theorem 1:

$${‖F(x)-F(r^{(k+1)})‖}_2^2\approx \alpha {‖x-r^{(k+1)}‖}_2^2,$$

(10)

Here, α is a scalar associated only with the parameters of F(). Substituting this relationship into Equation (8) and combining λα into a single parameter θ, the optimization problem reduces to:

$$x^{(k+1)}=\arg \underset{x}{\min }{\displaystyle \frac{1}{2}}{‖F(x)-F(r^{(k+1)})‖}_2^2+\theta {‖F(x)‖}_1,$$

(11)

The closed-form solution to this optimization problem is obtained via the soft-thresholding operation:

$$F(x^{(k+1)})=\mathrm{soft}(F(r^{(k+1)}),\theta ),$$

(12)

To reconstruct F(x^(k+1)) from x^(k+1), we introduce the left-inverse transformation F(·) of $\tilde{F}(\cdot )$ satisfying $F(\cdot )\ast \tilde{F}(\cdot )=I$.

$$x^{(k+1)}=\tilde{F}(\mathrm{soft}(F(r^{(k+1)}),\theta )),$$

(13)

Therefore, at the (k + 1)-th stage of the network, the complete update formula for x^(k+1) can be written as:

$$x^{(k+1)}={\tilde{F}}^{(k+1)}(\mathrm{soft}(F^{(k+1)}(r^{(k+1)}),{\theta }^{(k+1)})),$$

(14)

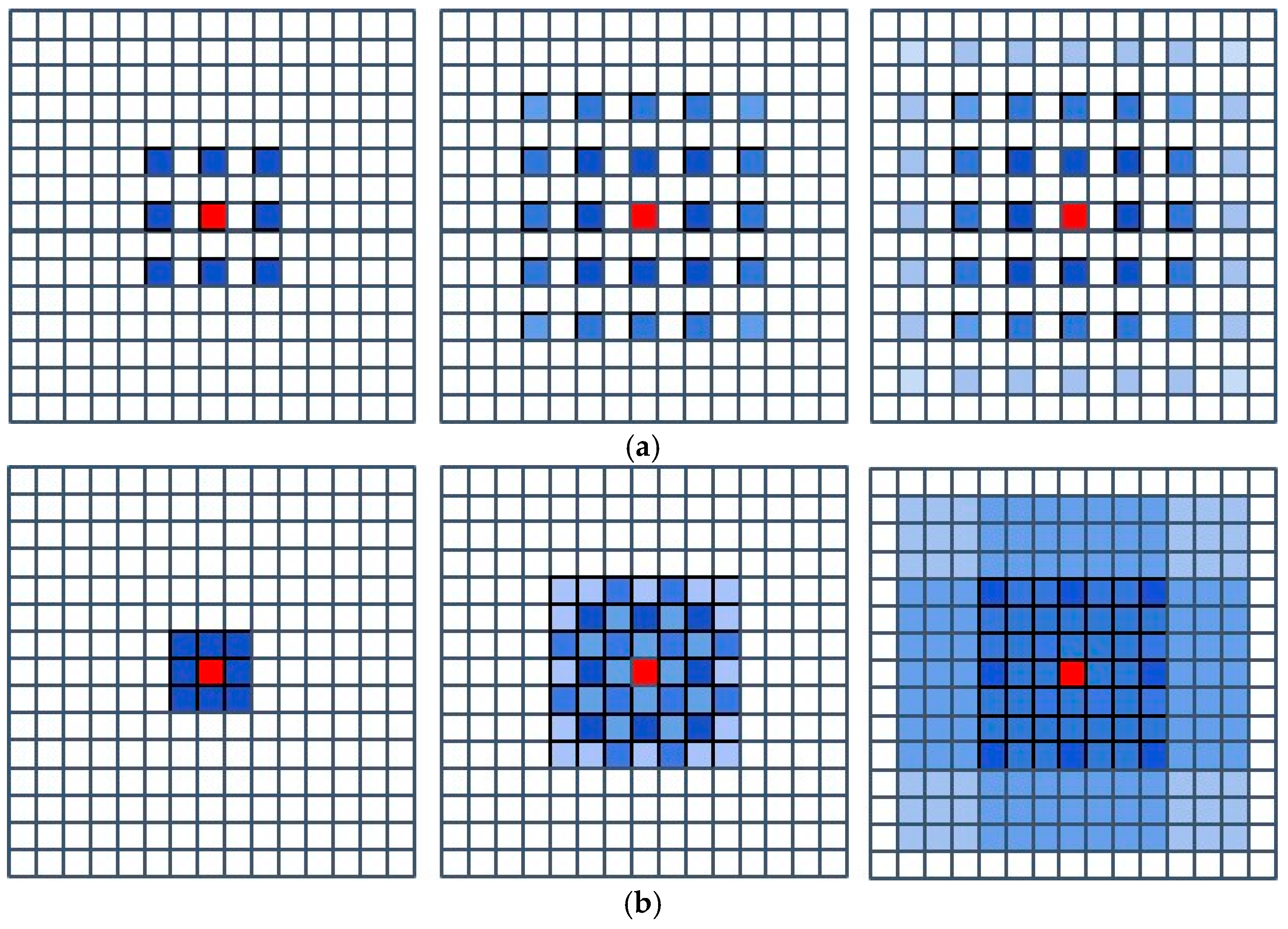
2.2.2. Dilated Convolution

Conventional convolution effectively extracts informative features from data, but is less effective for complex multi-scale data. To capture multi-scale information in tunnel data and integrate multi-scale features from deep learning, with the aim of reconstructing missing tunnel measurements more effectively, we adopt a combination of dilated convolution and conventional convolution. Integrating the feature extraction capabilities of both methods enhances the reconstruction quality of tunnel data. The fundamental principle of the dilated convolution kernel is described as follows:

$$K=k+(k-1)(r-1),$$

(15)

Here, k denotes the size of the original convolution kernel, and r is the dilation rate, a parameter of the dilated convolution. Adjusting the dilation rate enlarges the receptive field, which enables the capture of multi-scale information. However, due to sparse sampling of the input signal in dilated convolution, the information from long-range convolution lacks strong correlation, which leads to the grid effect. As shown in Figure 3a, after three layers of dilated convolution with dilation rates of 2, 2, and 2, the receptive field of the red pixel expands to a size of 13 pixels, but only about 70% of the actual pixels contribute to the computation. In Figure 3b, the red pixel undergoes dilated convolution with dilation rates of 1, 2, and 3, which also expands the receptive field to 13 pixels. However, it can access information from a wider range of pixels, thereby avoiding the grid effect.

Therefore, considering the actual missing patterns in seismic trace data, we adopt the aforementioned approach using dilated convolution with varying dilation factors. Specifically, the module comprises three dilated convolution layers with a 1 × 3 kernel and dilation rates of 1, 2, and 3, along with a standard convolution layer using a 3 × 3 kernel. These convolutions are arranged in parallel branches and integrated into the ISTA-Net framework. Figure 1c presents the schematic structure of this module.

2.2.3. Padding

During convolution operations, the kernel traverses the image space for computation, but edge pixels might be only partially covered. Moreover, in practical training and testing scenarios, the network’s reconstruction performance for edge regions tends to be suboptimal. To ensure that edge pixels contribute effectively to the computation and to maintain the original image dimensions, padding is added around the outermost pixels. This allows the convolution kernel to process even the boundary pixels, thereby enhancing the preservation of global features in the image or signal.

Building on the previous step, specific padding strategies are designed to meet the unique requirements of dilated convolution and to preserve information integrity when expanding the receptive field. In this study, we apply different padding methods to standard and dilated convolution. Standard convolution adopts reflective padding with a width of 1 pixel, whereas dilated convolution employs asymmetric horizontal reflective padding with widths of 2 and 3 pixels. This ensures accurate reconstruction of missing data points and preserves the integrity of temporal information. Figure 4 shows the receptive field sizes of standard convolution and dilated convolution.

2.3. Loss Function

Given the data pairs $\left\{d_{obs}^i,d^i\right\}$, where $d_{obs}^i$ is used as the input and dⁱ as the label, the reconstructed result at the N-th iteration is denoted by $d_N^i$. To formulate an appropriate loss function, we incorporate the previously introduced constraint $F(\cdot )\ast \tilde{F}(\cdot )=I$, while minimizing the discrepancy between $d_N^i$ and dⁱ. Consequently, the loss function of the deep unrolling network combines L₁ and L₂ loss terms, expressed as follows:

$$L_{total}=L_1+\gamma L_2,$$

(16)

$$\left\{\begin{array}{c}{L}_1={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{‖d_N^i-d^i‖}_F^2}\\ L_2={\displaystyle \frac{1}{n}}{\displaystyle {\sum }_{i=1}^n{\displaystyle {\sum }_{k=1}^N{‖{\tilde{F}}^k(F^k(d^i))-d^i‖}_F^2}}\end{array}\right.,$$

(17)

where N is the number of training iterations, n the size of the training set, and γ the regularization parameter.

3. Experiment

3.1. Model Construction

Tunnel seismic advance prediction aims to identify the velocity distribution and geological structures within 100–200 m ahead of the tunnel face, in order to detect unfavorable geological bodies such as faults and fractured zones, thereby reducing construction risks. A numerical model with dimensions of 100 m × 200 m is developed based on actual detection requirements. The wave velocity of the surrounding rock is set to 1500–4500 m/s in order to reflect discontinuous geological features such as joints and fissures. The first 50 m of the model represents the excavated tunnel area, where a 20 m-wide air region with a wave velocity of 340 m/s is defined to simulate the tunnel cavity. The section from 50 m to 200 m represents the detection area. Specific parameters for various types of rock masses are listed in

Table 2. Tunnel model parameters.

Stratum Classification	Stratum-Related Parameters
	P-Wave Velocity vp (m/s)	S-Wave Velocity vs (m/s)	Density p (kg/m3)	Thickness Along the Tunnel Axis (m)
Tunnel cavity	340	0	1.29	50
Tunnel surrounding rock	3300~3700	1900~2150	2300~2400	/
Karst cave	1000~1400	600~900	1750~1900	2~4
Fracture zone	1800~2200	1000~1350	2000~2150	8~12
Stratum	3900~4300	2250~2400	2450~2510	/

. Figure 5 shows a partial model used for forward modeling

To enhance the stability of numerical simulations, a finite difference grid of 1 m × 1 m is employed. Ricker wavelets with dominant frequencies of 100 Hz, 150 Hz, and 200 Hz are selected as seismic sources to cover commonly observed seismic frequency bands [38]. The time step is set to 1.2 × 10⁻⁴ s, with 800 sampling points and a recording duration of 0.096 s, effectively avoiding numerical dispersion. The observation method involves excitation and reception at the tunnel face, with both seismic sources and receivers spaced at 1 m intervals, totaling 20 each.

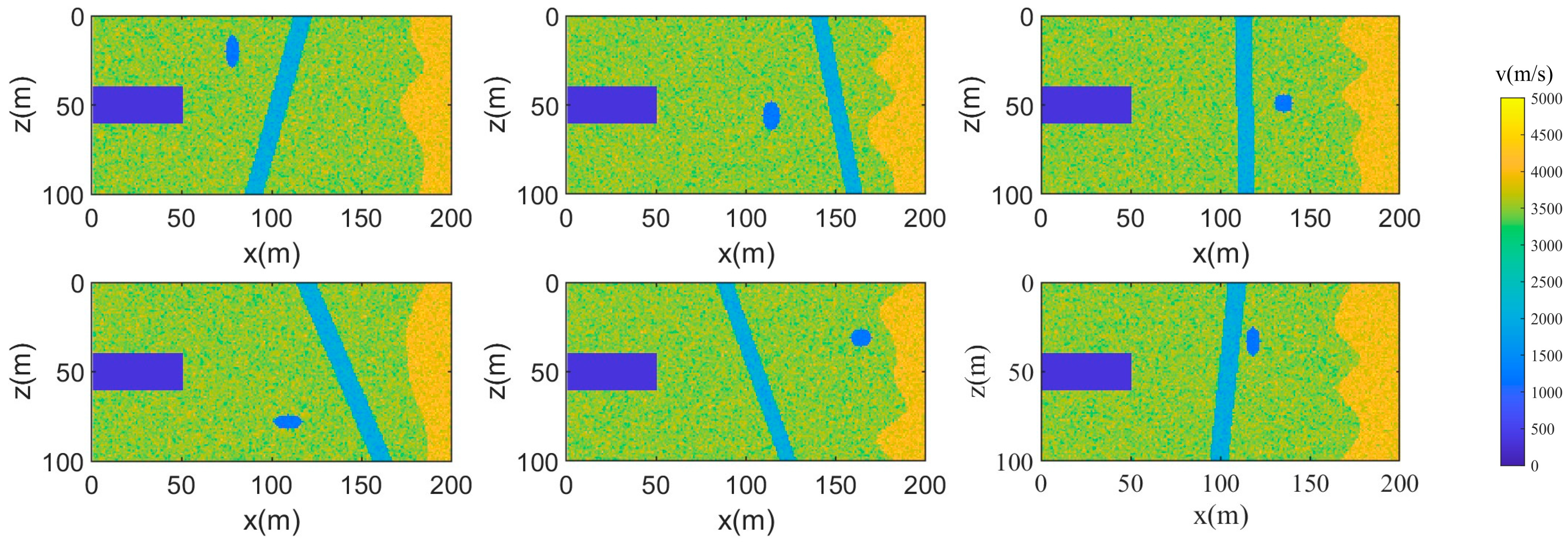
3.2. Dataset Construction

A total of 2000 randomly generated velocity models and corresponding forward seismic records (dimensions 800 × 20) were produced as label data. To simulate the missing and faulty traces commonly observed in actual tunnel data acquisition, each dataset was uniformly downsampled to 10 traces, with up to 2 faulty traces randomly added, forming the input data. The 2 faulty traces were simulated by setting their values to zero. To further expand the sample size and enhance generalization, the seismic records were divided into blocks for processing. The block size was set to 32 × 20 for labels and 32 × 10 for inputs, with a 16-channel overlap between blocks. Ultimately, 98,000 datasets were obtained and divided into training, validation, and testing sets in the ratio of 8:1:1. All data were normalized to the range [0, 1] to reduce amplitude differences and improve training stability. Figure 6 shows some input data and label data in the dataset.

3.3. Evaluation Indicators

We evaluate reconstruction quality using PSNR, SSIM, and LCCC. PSNR reflects the error level between the reconstructed signal and the ground-truth signal; a higher value indicates better reconstruction quality. SSIM assesses the similarity between two images in terms of luminance, contrast, and structural information; values closer to 1 denote higher structural consistency. LCCC measures the correlation of two signals within a local region phase consistency; values closer to 1 indicate a higher degree of phase matching. The equations are given as follows:

$$PSNR=20{\log }_{10}({\displaystyle \frac{1}{\sqrt{MSE}}}),$$

(18)

$$SSIM(x,y)={\displaystyle \frac{(2{\mu }_x{\mu }_y+C_1)(2{\sigma }_{xy}+C_2)}{({\mu }_x^2+{\mu }_y^2+C_1)({\mu }_x^2+{\mu }_y^2+C_2)}},$$

(19)

$$LCCC(W)={\displaystyle \frac{{\displaystyle {\sum }_{i\in W}(X_i-{\mu }_X)(Y_i-{\mu }_Y)}}{\sqrt{{\displaystyle {\sum }_{i\in W}{(X_i-{\mu }_X)}^2}}\cdot \sqrt{{\displaystyle {\sum }_{i\in W}{(Y_i-{\mu }_Y)}^2}}}}$$

(20)

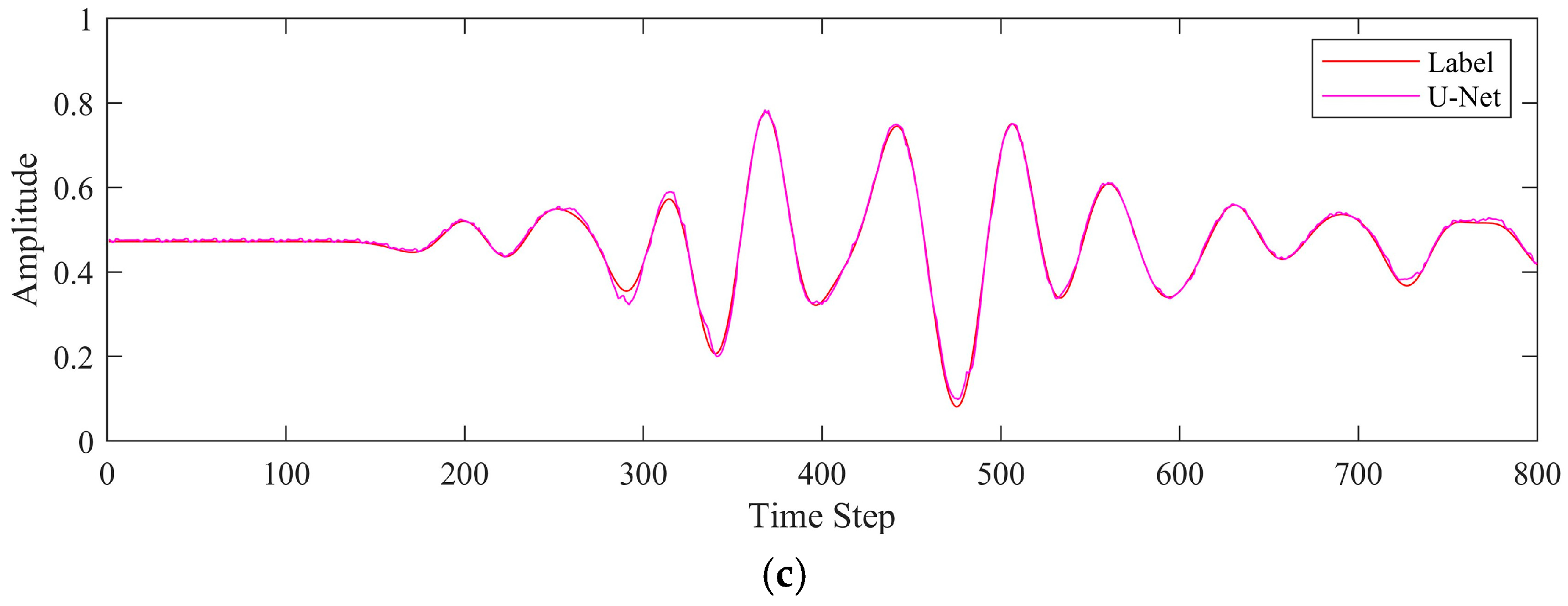
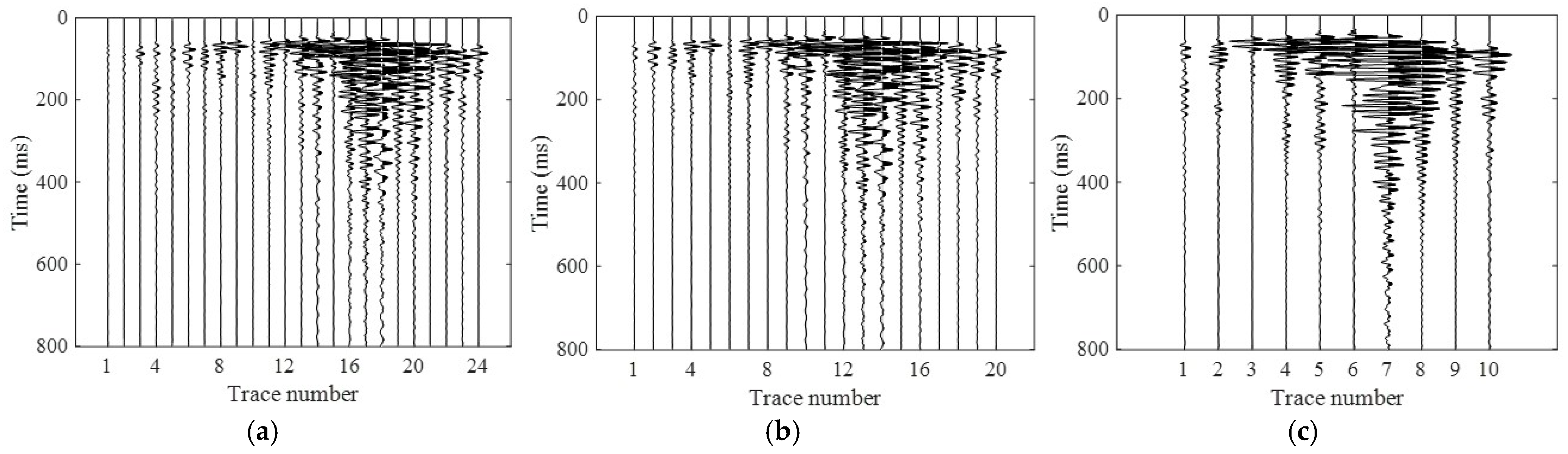
3.4. Synthetic Data Experiment

The experiment employed the Adam optimizer and the OneCycleLR learning rate scheduling strategy (maximum learning rate of 0.0001). The batch size was set to 128, and the model was trained for 50 epochs. The hardware platform was an NVIDIA GeForce GTX 1660 Ti with 13.9 GB of video memory.

To determine the optimal network depth, we evaluated performance across different numbers of phases as seen in Figure 7a. The results show that when the phase number ranges from 5 to 13, PSNR remains high and stable, with only minor variations. Although nine phases do not yield the absolute maximum PSNR, this configuration lies near the center of the plateau region and achieves a good balance between accuracy and stability. Compared with 11 or 13 phases, increasing the depth yields a PSNR improvement of less than 0.1 dB, which is negligible, while markedly increasing computational load and runtime, thus wasting computational resources. Therefore, considering both performance stability and computational efficiency, a phase number of 9 is selected as the network depth. During training, the loss value gradually decreased and stabilized at approximately 3 × 10⁻⁴, while PSNR increased steadily to around 35 dB, indicating good model convergence.

In TSISTA-Net, we introduce a lightweight strategy that partitions the input data into smaller blocks, aiming to enhance computational efficiency and reduce resource consumption. This approach mitigates the excessive memory usage observed in the non-partitioned setting, which otherwise requires an extremely small batch size or may even prevent normal training. To quantitatively assess computational efficiency across proposed methods, we adopt the per-sample training time and per-sample inference time as evaluation metrics. For the experiments, a subset of the dataset was used for training, with the Batch Size set to 128 for the block method and 16 for the unblock method. As summarized in

Table 3. TSISTA-Net: Performance Evaluation for Block Method and Unblock Method.

Method	Per-Sample Training Time	Per-Sample Inference Time	Memory Usage (GPU/CPU)	PSNR
Block	0.088 s	0.0015 s	23.44 MB/ 1142.81 MB	34.79 dB
Unblock	1.8524 s	0.0415 s	31.15 MB/ 1725.05 MB	32.07 dB

: the per-sample training time decreases from 1.8524 s (unblock) to 0.088 s, yielding an approximate 21 speed-up; the per-sample inference time decreases from 0.0415 s to 0.0015 s, corresponding to a 27 acceleration. In terms of memory usage, the unblock method exhibits relatively high GPU and CPU memory consumption even with a much smaller Batch Size. By contrast, the block method approach allows for larger batch processing while markedly lowering resource usage, thereby enabling higher throughput on the same hardware. Regarding reconstruction quality, the block method achieves a PSNR of 34.79 dB, outperforming the unblock method’s 32.07 dB. These results indicate that the proposed partitioning strategy not only delivers notable improvements in efficiency and resource savings but also maintains, and even enhances, reconstruction performance.

Figure 8 shows a sample of synthetic data, where the input data contains 8 channels, including 2 faulty channels, and the label data consists of a complete 20-channel record. To evaluate adaptability and reconstruction capability on complex tunnel data, comparative experiments were conducted using TSISTA-Net and U-Net, with ISTA-Net included under the same conditions to satisfy the requirements of an ablation study. The enhancement results are shown in Figure 9a–c, and the residuals between the enhanced results and the original data are presented in Figure 9d–f. From Figure 9a–c, all three methods achieved significant signal enhancement. Among them, TSISTA-Net and U-Net demonstrated better continuity along the same-phase axis, with more complete preservation of shallow texture details. In contrast, ISTA-Net shows discontinuities, likely due to the absence of multi-scale spatial information. Furthermore, the residuals in Figure 9d–f illustrate that TSISTA-Net yielded the smallest error, while ISTA-Net and U-Net left the larger residual signals especially at the edges.

To quantitatively compare the performance of different reconstruction methods,

Table 4. PSNR, SSIM and LCCC Values for Different Methods under Synthetic Data.

	TSISTA-Net	ISTA-Net	U-Net
PSNR (dB)	37.28	34.04	35.93
SSIM	0.9667	0.9167	0.9480
LCCC	0.9357	0.8878	0.9087

summarizes the PSNR, SSIM, and LCCC values obtained by TSISTA-Net, ISTA-Net, and U-Net. Across all three metrics, TSISTA-Net demonstrates clear superiority. Specifically, it achieves a PSNR of 37.28 dB, which is 1.35 dB higher than U-Net and 3.24 dB higher than ISTA-Net, indicating a marked reduction in reconstruction error. Its SSIM score reaches 0.9667, representing improvements of approximately 0.0187 and 0.05 over U-Net and ISTA-Net, respectively, and reflecting enhanced preservation of fine structural details. Furthermore, TSISTA-Net attains an LCCC of 0.9357, exceeding U-Net and ISTA-Net by 0.027 and 0.0479, respectively; this higher correlation suggests better spatial trend alignment and improved phase consistency with respect to the reference. Collectively, these findings confirm that the proposed method achieves superior intensity fidelity, structural detail retention, and phase accuracy.

Figure 10a–c presents a single-channel signal comparison among the three methods and the original data. As shown in the figure, ISTA-Net and U-Net exhibit a certain degree of mismatch in reconstructing the signal’s initial segment and some detailed regions. In particular, in the signal’s initial segment, both methods show slight shifts and residual errors. These errors primarily manifest as oscillations, which compromise the integrity of the waveform to some extent. Moreover, these methods also display minor distortions when fitting the main energy region and show relatively weaker recovery of fine details.

The experimental evidence indicates that TSISTA-Net exhibits greater adaptability and stability than the other two architectures. It effectively captures multi-scale structures and edge information in seismic data, yielding phase-coherent reflector continuity, reduced residual energy, and per-trace phase alignment that more closely matches the label data.

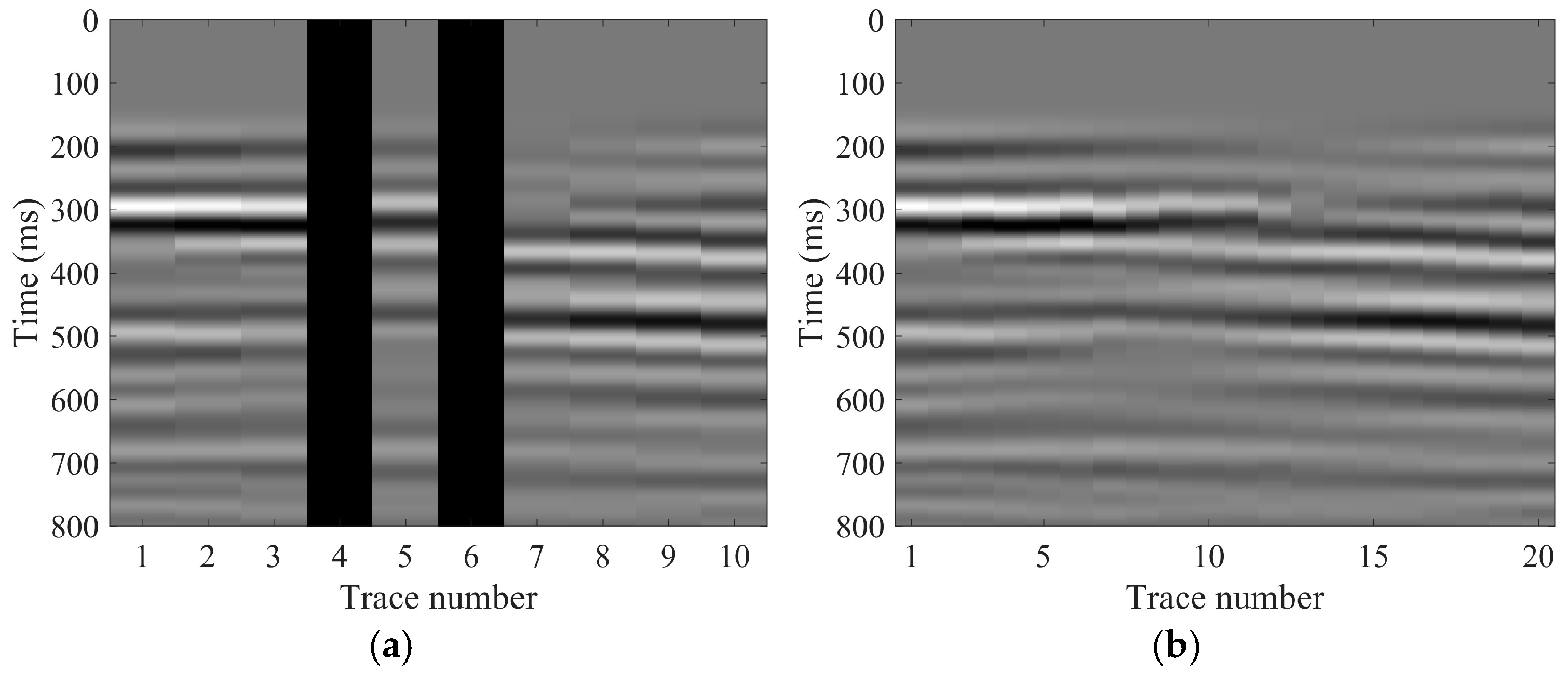
3.5. Real Data Experiment

Field data from a tunnel at the Songzi Water Station in Hebei Province were used to validate the effectiveness of the method. The raw data underwent FIR band-pass filtering (70–300 Hz) and gain adjustment (automatic gain control, AGC), as illustrated in Figure 11a. The primary signal characteristics of the seismic record are concentrated within the 0–400 millisecond time window. A notably dense distribution is observed across channels 8 to 16, exhibiting pronounced high-frequency features. In contrast, low-amplitude background signals predominantly occur beyond 400 milliseconds, demonstrating overall high spatiotemporal consistency. To meet the input requirements of the network model, the processed seismic records were further subjected to channel-wise extraction and sparsification, resulting in input–label data pairs as shown in Figure 11b,c.

After data preprocessing and segmentation, the processed data were fed into the proposed and pre-trained deep learning network model. To intuitively assess the network’s performance, the prediction results were visualized and compared, as shown in Figure 12. The reconstruction results of TSISTA-Net exhibit the highest overall consistency, with only slight amplitude deviations in a few channels, as illustrated in Figure 12a. In contrast, ISTA-Net shows abnormal amplitude values and significant waveform distortion, as seen in Figure 12b, while U-Net produces reconstruction signals with lower amplitudes and noticeable temporal lag, as presented in Figure 12c.

To provide a more detailed comparison of the enhancement effects,

Table 5. PSNR, SSIM and LCCC Values for Different Methods under Real Data.

	TSISTA-Net	ISTA-Net	U-Net
PSNR (dB)	30.33	21.93	28.31
SSIM	0.8893	0.8087	0.8546
LCCC	0.8288	0.6981	0.7386

presents the PSNR, SSIM and LCCC values for the different methods. It achieves the highest PSNR (30.33 dB), SSIM (0.8893), and LCCC (0.8288) among the compared methods. These results indicate that TSISTA-Net excels in accurate signal recovery, structural fidelity, and local correlation, enabling a more precise reconstruction of the salient features in the ground-truth labels. In contrast, U-Net yields a PSNR of 28.31 dB, SSIM of 0.8546, and LCCC of 0.7386, while ISTA-Net attains 21.93 dB, 0.8087, and 0.6981, respectively. This suggests that both U-Net and ISTA-Net are less effective in preserving fine details and mitigating distortion, leading to noticeable structural blurring and limited adaptability to real-world data. Overall, the superior performance of TSISTA-Net substantiates the effectiveness and robustness of its improved data enhancement strategy for complex seismic signal processing tasks.

On field data, TSISTA-Net delivers accurate and stable seismic signal reconstructions. Its temporal–spatial iterative framework effectively captures multi-scale structural cues and edge continuity, enabling phase-consistent recovery while suppressing localized distortions. In contrast, U-Net’s feed-forward architecture shows moderate adaptability but suffers from amplitude attenuation and timing offsets, and ISTA-Net’s limited information leads to pronounced waveform distortion. Overall, these trends confirm that integrating iterative refinement with deep learning enhances reconstruction accuracy and reliability in complex tunnel seismic processing tasks.

4. Discussion

4.1. Comparison with Existing Studies

Among conventional algorithms, multichannel singular spectrum analysis (MSSA) has demonstrated unique advantages in seismic data enhancement through its iterative optimization framework and customizable constraints. For instance, ref. [39] applied MSSA to noisy seismic records, achieving a 12.85 dB SNR improvement on a typical test dataset, with robust performance particularly in random noise suppression. However, MSSA relies critically on the assumption of linear time-invariant signal characteristics, restricting its applicability to linear event reconstruction; for complex structures (e.g., non-linear events induced by faults, salt domes, or karst caves), MSSA often fails to accurately recover geological details, resulting in event discontinuities or blurring [15]. In the deep learning domain, U-Net and its variants have been widely adopted for seismic data processing due to their powerful feature extraction capabilities. The Attention-U-Net (AU-Net), which optimizes feature weight allocation via spatial attention mechanisms, has yielded reconstruction results superior to traditional methods in both visual quality and quantitative metrics [40]. Nevertheless, this model relies purely on data-driven learning without incorporating physical constraints of seismic wave propagation, leading to poor generalization in complex geological scenarios lacking labeled data and potentially generating physically implausible artifacts in reconstructed results. To balance global and local feature modeling, researchers have proposed adaptive feature fusion networks that dynamically adjust multi-scale feature weights for reconstruction, achieving a PSNR of 19.0567 dB and SSIM of 0.9056 on test datasets [41]. While this method excels in detail recovery for high-SNR regions, its signal fidelity in low-SNR regions remains suboptimal, characterized by poor continuity or excessive energy attenuation of weak reflection events.

Although absolute numerical comparisons with existing methods are limited by dataset discrepancies and inconsistent evaluation metrics, these studies still provide a valuable benchmark for assessing the performance of our proposed TSISTA-Net. In contrast, TSISTA-Net integrates the iterative optimization philosophy of traditional ISTA with the non-linear mapping capabilities of deep learning, incorporating physical information constraints into the network training process to mitigate the generalization limitations of purely data-driven models like AU-Net. Additionally, the model employs dilated convolution with adjustable dilation rates to expand the effective receptive field without significantly increasing computational burden, thereby enhancing the detection of weak reflection signals and preserving event continuity in low-SNR regions. Furthermore, an asymmetric reflection padding strategy is introduced to effectively suppress boundary artifacts and improve reconstruction consistency in edge regions (Figure 9, Figure 10 and Figure 12; Table 4 and Table 5). These integrated designs enable TSISTA-Net to exhibit superior performance in tunnel seismic data enhancement, validating its stability, adaptability, and strong generalization capability for practical tunnel seismic scenarios.

4.2. Limitation

Although TSISTA-Net demonstrates high accuracy and efficiency in tunnel seismic data reconstruction tasks, its performance can be affected when processing seismic data containing strong random noise. This limitation arises from the method’s integration of physics-constrained algorithms with deep learning. As shown in Equation (7), during the iterative process the noisy raw data are repeatedly involved, inevitably leading to cumulative errors. Such influence persists even after a large number of iterations and is therefore considered unavoidable. Consequently, the method is most suitable for enhancing data that have undergone prior filtering to remove the majority of noise from field measurements. Moreover, it is noteworthy that the construction of the dataset plays a pivotal role in determining the prediction accuracy of the network. If the training data can be more closely aligned with the actual geological conditions ahead of the tunnel, the accuracy of enhancement and prediction results can be significantly improved. Therefore, future research could consider incorporating field-acquired seismic data into the training and validation processes, thereby enhancing the model’s applicability and generalization capability in real engineering environments.

4.3. Future Work

The enhanced data quality from TSISTA-Net not only optimizes geological anomaly detection and advance prediction in tunnel construction but also provides a foundation for broader seismological studies. For instance, in regional seismology, accurate body wave signals are critical for calculating moment magnitude (Mwg), a rapid and reliable parameter for estimating earthquake size, which relies on waveform phase consistency and amplitude fidelity [42,43]. Future work will focus on further validating the applicability of TSISTA-Net for feature enhancement in natural earthquake signals, which may facilitate its use in earthquake monitoring, source mechanism inversion, and other seismological applications. In addition, efforts will be directed toward extending the method to three-dimensional seismic data reconstruction, optimizing algorithms for real-time processing, and investigating its adaptability under various noise conditions. These advances are expected to further support the deployment and application of the technology in practical engineering projects.

5. Conclusions

This paper addresses the challenges of low-quality tunnel seismic data and the difficulty of accurate signal reconstruction by proposing TSISTA-Net, a deep unfolding network–based enhancement framework. Based on experimental evaluations using both synthetic and field data, three key conclusions are drawn:

(1)

A deep unfolding network architecture that incorporates reflection padding and multi-scale dilated convolution is proposed. The reflection padding operation effectively mitigates boundary artifacts, while the multi-scale dilated convolution substantially expands the receptive field, thereby enhancing the capability to model long-range dependencies and capture multi-scale seismic features. This design directly addresses the lack of global information modeling inherent in conventional networks such as U-Net.

(2)

High-precision and efficient tunnel seismic data reconstruction is achieved. TSISTA-Net significantly outperforms comparative methods in PSNR, SSIM and LCCC, particularly excelling in the restoration of high-frequency details and waveform continuity. Furthermore, its lightweight architecture and block-wise processing ensure low computational overhead, meeting practical efficiency requirements in engineering applications.

(3)

A novel approach for intelligent seismic data processing in tunnel engineering is established. This study confirms the effectiveness of integrating physics-informed algorithms with deep learning. TSISTA-Net not only offers strong interpretability but also demonstrates robust generalization performance, showing considerable promise for improving the reliability and practicality of tunnel advanced forecasting systems.