A Component-Oriented Model for Risk Assessment in the Design of High-Tech Products

Abstract

This study proposes a component-based model for assessing risks in the design of high-tech products. The model took into account the novelty of components, which affected the risk level in the development process. The risk assessment was based on fuzzy set theory, which allowed determination of the degree of importance of risk-generating factors, such as technical, economic, and organizational risks. The components were divided into “old” ones with the possibility of adaptation and “new” ones being implemented for the first time. The structure of the project included adaptation, acquisition, and development of new components. The component-oriented approach allowed for a reduction in the negative impact of risks in the early stages of development while optimizing decision-making on further product development. A case study involving the development of unmanned aerial vehicles (UAVs) was conducted to demonstrate the model’s applicability. The assessed aggregated project risk varied from 0.0992 for projects based primarily on reusable components to 0.1902 for those involving a high proportion of newly developed components. The model’s sensitivity to component novelty made it possible to differentiate between low- and moderate-risk design scenarios. This is especially valuable for early-stage project selection and risk-informed “go/no-go” decisions in the design of complex systems.

1. Introduction

At the initial stages of design, it is essential to consider the complexity of the product being developed, market stochasticity, the state of war, and various types of uncertainties that affect the success of the technical system being designed. The process of creating a high-tech product (HTP) is influenced by negative impacts from groups of risk-generating factors, which in turn form various types of risks. Risks are often understood as the likelihood of unfavorable events that may lead to material, time, financial, and other losses during the development of a technical system [1,2]. Among HTPs, drones are increasingly used for a wide range of tasks, such as agriculture, mining, and military operations, but also for exploration, rescue, product delivery, mapping, and even entertainment [3]. These systems are usually equipped with various sensors, cameras, controllers, and other Micro-electromechanical Systems (MEMSs), and they have to meet safety and functionality requirements related to the mechanics [4], operation [5], or noise [6]. However, to the best of our knowledge, no research has been undertaken on project risk assessment models related specifically to unmanned aerial vehicles so far.

The multifaceted nature of the concept of risk is due to the diversity of risk-generating factors. There are many integral risk-generating factors that have a combined impact on several types of risks. Thus, it is necessary to perform a comprehensive analysis of all related types of risks.

Thus, it is necessary to identify the risk-generating factors, taking into account their individual importance, and evaluating the potential negative impact of various risks on achieving the required scientific and technical results during the development of an HTP. High risks at early stages can lead to an iterative design process (redesign cycles). At the conceptual stage, risk assessment is applied to decide whether to proceed with the development of the given concept or not. Risk assessment refers to the overall process of risk identification, risk analysis, and risk evaluation. Let us introduce some concepts and definitions:

• Risk analysis refers to the process of understanding the origin of risk and determining the level of risk (the systematic use of information to identify sources and quantify risk);
• Risk evaluation is the process of comparing the results of risk analysis with established risk criteria to determine whether the risk and/or its magnitude are acceptable or tolerable;
• Risk level is the magnitude of risk or a combination of risks, expressed as the combination of consequences and the likelihood of their occurrence.

This study proposes a component-oriented model for risk assessment, including degree of novelty of the components in the new product. Then the example of project risk assessment is provided for two different options. In the first case, the synthesis of a new UAV (unmanned aerial vehicle) structure was carried out based on a component-oriented approach [7]. The calculations were made first considering the novelty of the product and components, and then considering the adaptation of reused ones. In the second case, the architecture of the projected UAV was formed without drawing on the formalized experience of past developments.

2. Development of a Component-Oriented Model for Risk Assessment

2.1. Existing Models and the Methodological Basis for the Component-Oriented One

The design of a complex technical product is based on a component-oriented approach, which allows for detailed consideration of the multi-level component architecture of the product being created. For project risk assessment, this study proposes determining the degree of novelty of the components of the high-tech product being developed. To achieve this, the components of the synthesized product structure are divided into the following groups: “old” components (proven technical solutions), which can serve as reusable components (RCs), and new components that undergo a full cycle of design work and are being implemented for the first time within this high-tech sample, as well as the elements of “old” and “new” components located at a lower level of system decomposition [7]. In some cases, “old” components may require adaptation if such a solution is deemed appropriate. In turn, “new” components ensure the innovative nature of the designed product.

In this study, project risk is understood as the probability that, during the execution of design work for the creation of a new high-tech product, the result will not meet the requirements of the technical specifications.

When assessing risks, it is important to consider difficulties in formalization and quantification of certain types of risks, e.g., operational ones, due to the presence of the “human” factor. Therefore, to assess project risk, it is necessary to quantitatively or qualitatively evaluate the components’ degree of novelty in the developed high-tech system.

One of the most comprehensive methods used to analyze and evaluate various factors in many industries is risk assessment [8,9,10,11,12]. These methods are widely used in construction, energy, economics, and other industries to assess the reliability of systems under the influence of various factors [13,14,15,16,17,18,19].

In assessment of the project risk when designing a high-tech system considering the novelty degree of its components, it is advantageous to apply a fuzzy set approach for qualitative evaluations, incorporating expert information (expert assessments) [20,21]. Fuzzy set theory (fuzzy logic) allows for the use of both quantitative and qualitative characteristics in assessments, and it enables the analysis of heterogeneous and insufficiently large data samples, which can be helpful when available information is limited or costly [22].

The paper [23] introduces an integrated risk assessment model combining Pythagorean Fuzzy Dimensional Analysis (PFDA) and Failure Mode and Effect Analysis (FMEA), with a machined detail as a case study. The study [24] proposes a multi-criteria decision-making method combining AHP (Analytic Hierarchy Process) and TOPSIS (Technique for Order Preference by Similarity to the Ideal Solution) to prioritize project risks at the activity level, addressing limitations of traditional risk assessments. Applied to Global Furniture Ltd., the hybrid AHP-TOPSIS model enables quantitative risk analysis, enhancing project time, quality, and cost management.

Another direction of risk assessment is the theory of qualimetry. Scientific publications [25,26] present the methodology of risk assessment of the quality of technological processes. The methodology for assessing the quality risks of socio-economic systems is presented in scientific publications [27,28,29,30], which is characterized by the use of function-dependent statistics. These methodologies have not been tested in assessing the risks of project works.

Although a wide range of risk assessment methods has been developed, including FMEA, PFDA, AHP–TOPSIS hybrid approaches, and qualimetric models, they have several important limitations when applied at the early design stage of a high-tech product, especially UAVs.

First of all, most existing models do not account for component-level novelty. They consider a product as a uniform system and do not distinguish between reusable, adapted, and newly developed components. As a result, these methods cannot adequately reflect the innovation-driven risks that arise when integrating new components into a complex architecture.

Secondly, the traditional approaches poorly handle the inherent fuzziness and uncertainty typical for early design phases. At this stage, quantitative data are usually unavailable, while expert information is often incomplete or subjective. Consequently, the methods relying on precise numerical inputs lose accuracy or applicability.

Thirdly, existing models are primarily activity-oriented rather than component-oriented. For example, FMEA–PFDA or AHP–TOPSIS hybrids prioritize project activities or process-level risks but do not provide a means to link risk assessment directly to individual components within a multi-level system decomposition.

And finally, most traditional methods are static, and cannot dynamically adjust risk levels when the degree of novelty of components changes due to iterative design processes or architecture updates.

To overcome these limitations, the present study proposes a component-oriented model for risk assessment that incorporates fuzzy set theory and explicitly accounts for the degree of component novelty. This enabled both qualitative and quantitative evaluation of risks under uncertainty and provided more accurate decision support at the conceptual and preliminary design stages of complex high-tech systems like UAVs.

Recently, research in the domains of modular product architectures and fuzzy-logic risk assessment has advanced significantly. For example, Xuan et al. developed a fuzzy Petri-net-based model to evaluate risk and vulnerability in complex engineering projects [31]. Mansor & Flayyih applied fuzzy synthetic evaluation to assess the risks of modular (prefabricated) construction systems [32]. Similarly, quality risk in prefabricated steel components was addressed using a fuzzy Bayesian-network approach [33].

While these studies contribute important advances, they often focus either on modularization decisions or on fuzzy risk evaluation in isolation. By contrast, the model proposed in this paper integrates component-level novelty (reuse, adaptation, new development) within a modularized product architecture and applies a fuzzy linguistic evaluation framework to capture the early-stage uncertainty typical of high-tech design. This coupling of modular component categorization with fuzzy risk modeling, at the early design phase, represents a distinctive incremental contribution to the state of the art.

2.2. The Component-Oriented Model for Risk Assessment

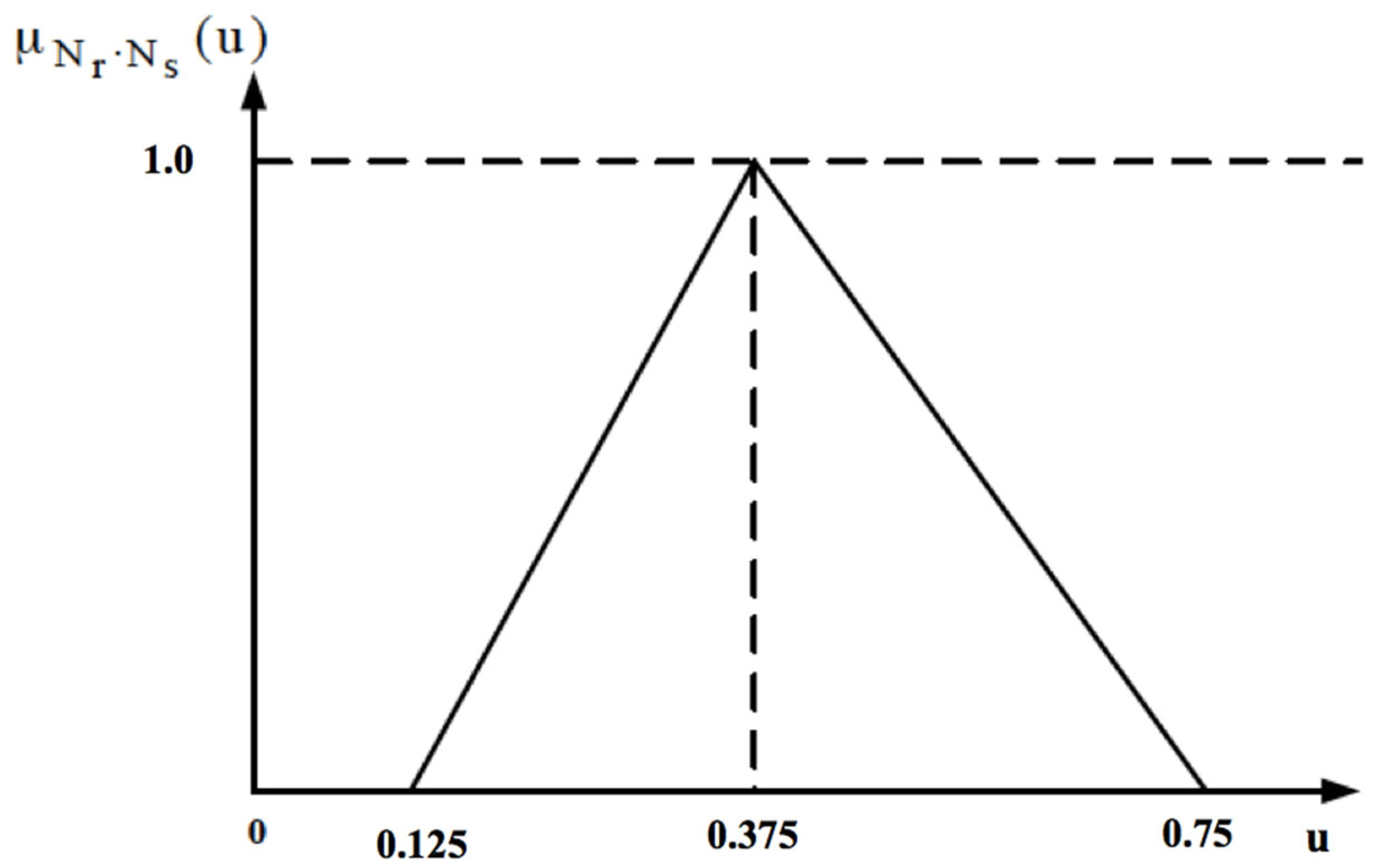
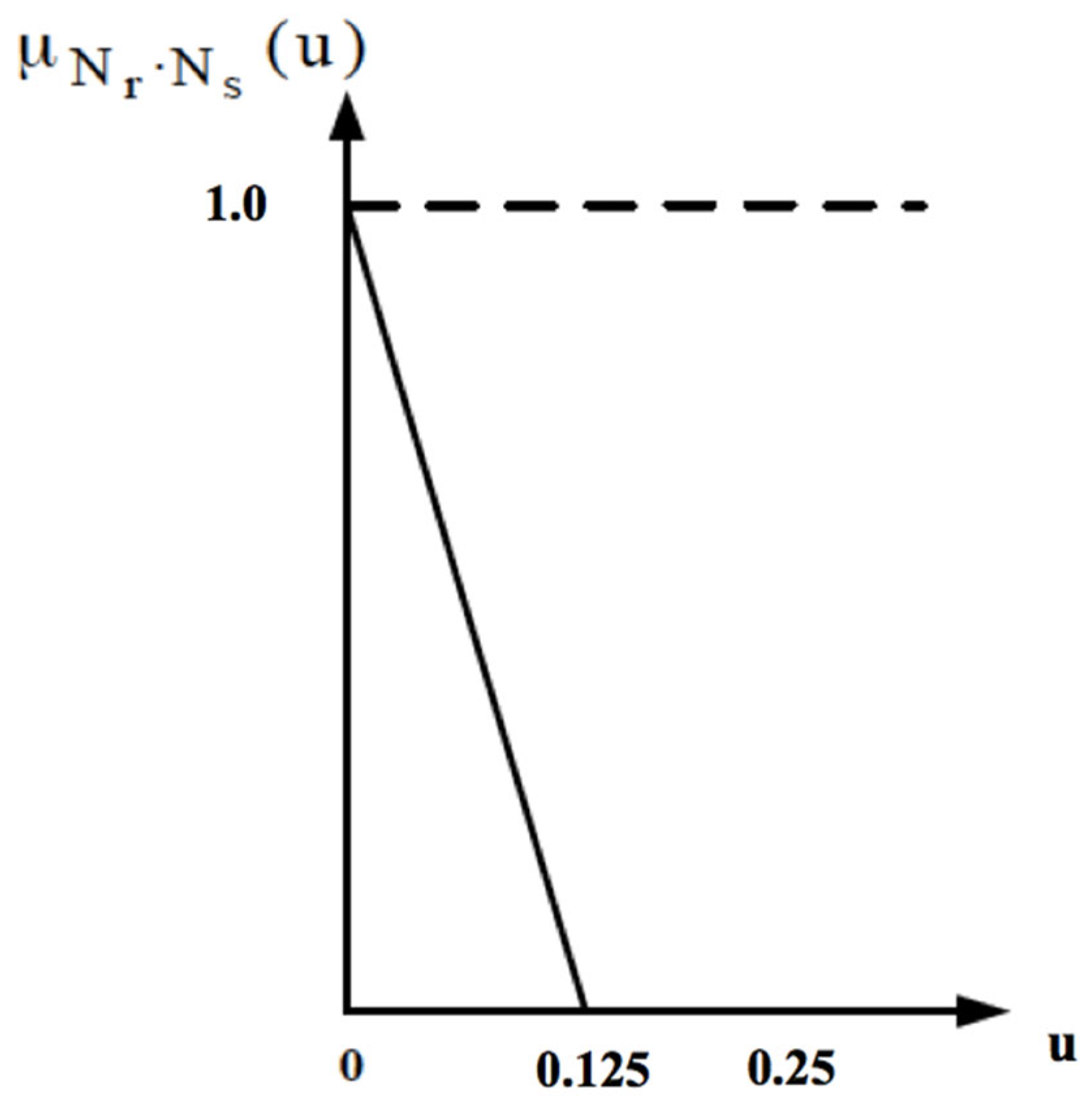
For project risk analysis, i.e., determining the level of risk, the novelty degree of the components of the new high-tech product and the concept of the impact of risk-generating factors are used, which can be represented as linguistic variables [34]. The values of each of these linguistic variables must be converted into respective fuzzy values. For this purpose, a triangular membership function is commonly used.

The proposed component-oriented model for project risk assessment in the early stages of developing a technical system includes the following steps:

Step 1. Risk identification and identification of risk-generating factors.

In the design of an HTP, it is necessary to distinguish between basic groups of risks and the intra-group risk factors that contribute to the occurrence of specific types of risks and relate to the basic risk group x₁, x₂, …, x_n, j = 1…n.

Step 2. Formation of the scope of project work for the creation of the HTP.

The project work includes tasks related to the adaptation of reusable components, acquisition of reusable components, and development of new components. Acquiring ready-made components for the creation of the HTP from available markets helps reduce the development costs.

Step 3. In this step, the values of linguistic variables are assigned via a triangular membership function, making it possible to consider the risk factor r and the indicator of the risk factor importance s. It is important to note that the membership functions µ_Vf (r) and µ_Vf (s) take the same form as the general triangular membership function [35].

At this stage, a scale is constructed to map linguistic variables to fuzzy numbers. This scale facilitates the transformation of qualitative assessments (linguistic descriptions) into corresponding fuzzy values, allowing for a more structured and quantifiable analysis of the risk level and the importance of each risk factor. The scale of relations between linguistic variables and fuzzy numbers is shown in

Table 1. Scale of relations between linguistic variables and fuzzy numbers.

Number of the Linguistic Variable Value	Values of Linguistic Variables Describing the Risk Level of the Factor (r) and the Importance Level of the Factor (s)	Fuzzy Triangular Numbers N, Representing the Value of the Linguistic Variables for the Risk Level of the Factor (r) and the Importance Level of the Factor (s) (in Accordance with the Membership Function)
1	r1; s1	Nr1; Ns1
i	ri; si	Nri; Nsi
k	rk; sk	Nrk; Nsk

.

In Table 1, N_r^k and N_s^k denote the fuzzy numbers describing the linguistic variables for the importance of the risk factor and the risk level of the risk-generating factor, respectively; i represents the number of a single linguistic variable value (i = 1…k); and k denotes the number of linguistic variables representing the risk level r and importance of the risk factor s.

For example, the number of values of linguistic variables for assessing the risk level and the importance of the risk factor can be equal to 5 (k = 5): V₁—very low; V₂—low; V₃—medium; V₄—high; and V₅—very high. This number of linguistic variable values was selected because a five-level linguistic scale is widely used in fuzzy risk assessment practice [36], providing an optimal balance between the accuracy of differentiation and the simplicity of expert judgment. Using fewer levels (e.g., three) would reduce the resolution of evaluations, while a larger number of levels would not significantly improve precision and might increase subjectivity and inconsistency in expert assessments. Thus, it was assumed that k = 5 ensured both methodological soundness and comparability with other fuzzy evaluation studies.

Linguistic variables are shown in

Table 2. Variables for risk levels and importance of risk factors.

Number of the Linguistic Variable Value	Values of Linguistic Variables Representing the Risk Level of the Given Factor (r) and Its Importance Level (s)	Designations	Numbers N That Correspond to the Values for the Risk Level of the Given Factor (r) and the Importance Level of the Factor (s) (in Accordance with the Membership Function)
1	Very Low	vl	<0; 0; 0.25>
2	Low	l	<0; 0.25; 0.5>
3	Medium	m	<0.25; 0.5; 0.75>
4	High	h	<0.5; 0.75; 1.00>
5	Very High	vh	<0.75; 1.00; 1.00>

, for both risk levels and importance of risk factors.

Next, the linguistic variables of the risk s and r are replaced by the respective fuzzy triangular numbers N_s and N_r.

Step 4. Assessment of the importance of factors s_j based on the preliminary classification of project work, considering the novelty degree of the HTP components.

The novelty of the components in the new product always affects the importance of the factor that generates the risk. This means that components with a higher degree of novelty are likely to have a greater influence on the significance of the associated risk-generating factors s_j:

s₁₁     s_j1… s_n1    
s₁₂     s_j2… s_n2
s₁₃     s_j3… s_n3

(1)

where s_j1—the linguistic evaluation of the importance of the j-th factor generating a risk, associated with acquisition of a reusable component; s_j2—the linguistic evaluation of the importance of the j-th risk-generating factor for the group of work related to the adaptation of RCs; and s_j3—the linguistic evaluation of the importance of the j-th risk-generating factor for the group of project work related to the creation of new components.

Formula (1) represents a matrix of linguistic evaluations of the importance of each risk-generating factor s_j in relation to the groups of project tasks classified by the degree of novelty of the components of the high-tech product. Each row of the matrix corresponds to a particular group of project works: acquisition of reusable components (RCs), adaptation of RCs, and development of new components. Each column represents an individual risk-generating factor. Accordingly, the elements s_j1, s_j2, and s_j3 denote the linguistic values (e.g., very low, low, medium, etc.) expressing the importance of the j-th factor for the corresponding group of project works.

This representation enables the formalization of expert assessments that capture how the novelty of components influences the weight of the specific risk factors. The obtained matrix serves as an initial dataset for further fuzzy processing and defuzzification procedures aimed at determining the aggregated project risk at the early design stage.

Dependent on the novelty of the designed components, the project work is analyzed in three groups, as follows: project work related to the acquisition of RCs, project work for the adaptation of RCs, and project work for the creation of new components. It was assumed that the value describing the importance assessment for all risk-generating factors in the project works related to the acquisition of RCs, which do not require adaptation, will be approximately the same. It should be noted that this group of work is the least exposed to risk-generating factors.

At the same time, in the creation of an HTP, part of the components of the structure of the new technical product may be RCs that require adaptation. The second group of project work is more sensitive to external economic risks. The third group consists of work related to the novelty and uniqueness of the HTP being developed. It is the most vulnerable to the impact of risk-generating factors related to the technical risk.

Step 5. Evaluation of the specific risk-generating factors r_j.

For each specific factor, the probability of the risk factor manifesting and its potential impact were assessed. To evaluate the level of each risk-generating factor r_j, a special probability and impact matrix is used. The probability and impact matrix is created based on survey results and expert assessments, establishing a correlation between the probability level and the impact of a single factor [37,38]. The matrix allowed for the factors to be prioritized according to the importance of their possible effects on the HTP being developed.

In the points of intersection between the rows and columns in the probability and impact matrix, the risk level values for the factor r_j are assigned. The risk levels of the factors r_j are determined based on the characteristics of each specific risk-generating factor. For the factor r_j, the risk level value depends on the nature of that particular risk-generating factor.

Step 6. Since r_j and s_jt (where t is the number of the project work group based on the novelty degree of the parts of the system, t = 1…3) are represented as linguistic variable values by fuzzy numbers, a defuzzification procedure, i.e., elimination of fuzziness, is necessary.

To assess project risk at the initial stages of system development, a matrix must be created, with project works as rows and risk-generating factors as columns. At the intersection of the matrix’s rows and columns, the values g_jtw (r_j, s_jt) are indicated, representing the risk level of each factor r_j, taking into account its importance s_jt, depending on the work grouped by the degree of novelty of the components of the HTP. Here, refers to the number of the project task. And w is the number of the project work.

Operations with triangular numbers are reduced to operations with the abscissas of the vertices of the membership functions, as follows:

(a₁, b₁, c₁)·(a₂, b₂, c₂) ≡ (a₁·a₂, b₁·b₂, c₁·c₂),

(2)

where (a₁, b₁, c₁)—the first fuzzy triangular number; and (a₂, b₂, c₂)—the second fuzzy triangular number.

Calculations for defuzzification are performed using the centroid method of defuzzification [39]. Finally, a matrix of values g_jtw (r_j, s_jt) can be built.

A matrix for all values of g(r, s) containing all intersections of the values for each r_j and s_j can be predefined in order to simplify calculations.

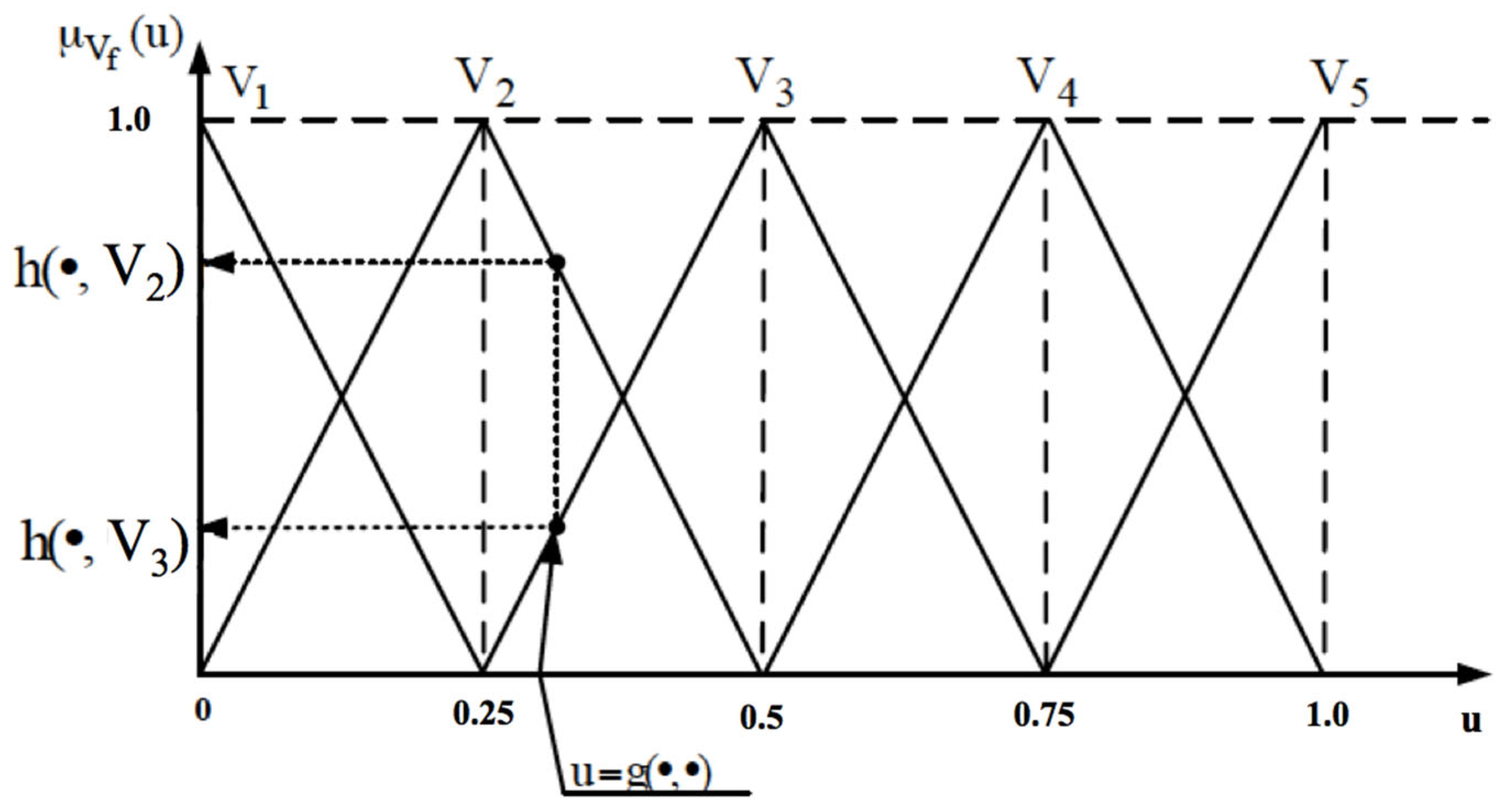
Step 7. Determining the fuzzy matrix H of intersections, considering importance and the membership functions of the triangular numbers for each project task w_it. As a result, produced pairs of values provide the bounds of the confidence interval.

The fuzzy matrix is determined by intersecting each value from the matrix created when performing step 6, g_jtw (r_j, s_jt), with the membership functions of the triangular numbers, µ_vφ(u) and µ_vφ+1(u); moreover, φ = 1, 2, …, k − 1. Thus, h(g_jtw(r_j, s_jt), V_φ−1) = 1 − h (g_jtw(r_j, s_jt), V_φ), and h(g_jtw(r_j, s_jt), V_f) = 0, for any f, where f ≠ φ and f ≠ φ + 1.

The fuzzy matrix H is as follows:

$$\begin{array}{ccc}\begin{array}{l}h\left(g_{1t_1}\left(r_1,s_{1t}\right),V_1\right)\\ h\left(g_{2t_1}\left(r_2,s_{2t}\right),V_1\right)\\ h\left(g_{1t_2}\left(r_1,s_{1t}\right),V_1\right)\\ h\left(g_{j{t}_w}\left(r_j,s_{jt}\right),V_1\right)\\ h\left(g_{n{t}_m}\left(r_n,s_{nt}\right),V_1\right)\end{array}& \begin{array}{l}h\left(g_{1t_1}\left(r_1,s_{1t}\right),V_2\right)\\ h\left(g_{2t_1}\left(r_2,s_{2t}\right),V_2\right)\\ h\left(g_{1t_2}\left(r_1,s_{1t}\right),V_2\right)\\ h\left(g_{j{t}_w}\left(r_j,s_{jt}\right),V_2\right)\\ h\left(g_{n{t}_m}\left(r_n,s_{nt}\right),V_2\right)\end{array}& \begin{array}{l}h\left(g_{1t_1}\left(r_1,s_{1t}\right),V_k\right)\\ h\left(g_{2t_1}\left(r_2,s_{2t}\right),V_k\right)\\ h\left(g_{1t_2}\left(r_1,s_{1t}\right),V_k\right)\\ h\left(g_{j{t}_w}\left(r_j,s_{jt}\right),V_k\right)\\ h\left(g_{n{t}_m}\left(r_n,s_{nt}\right),V_k\right)\end{array}\end{array}$$

(3)

where m represents the number of all project tasks.

The fuzzy matrix of intersections of all possible risk level values for the factors H’ can be pre-evaluated, considering importance g (r, s) and the respective membership functions of the triangular numbers µ_vφ(u) and µ_vφ+1(u).

Step 8. Assessment of a fuzzy risk based on the aggregation of the possible risk factors for every project task related to RC adaptation or fabrication of new components for the high-tech product, using the following formula:

$$R_f^w={\displaystyle \sum {\alpha }_j}\cdot h(g_{jtw}(r_j,s_{jt}),V_f), f=1\dots k,$$

(4)

where j is the index of the intra-group risk factor, with j = 1…n; α_j = 1/(n·d), so, accordingly, 0 ≤ α_j ≤ 1; d is the total number of groups of project tasks related to the adaptation of RCs and fabrication of new components required for the product being created; n is the number of intra-group risk factors; and V_f is the membership functions for linguistic variables, with f = 1…k.

Step 9. Assessment of a fuzzy risk based on the aggregation of all risk factors for each group of project tasks related to the adaptation of RCs or the fabrication of new components R_f^h, using the following formula:

$$R_f^h={\displaystyle \sum R_f^w,} f=1\dots k,$$

(5)

where the sum is over w = 1…L, and L is the number of project tasks included in the group of tasks for the adaptation (modernization) of RCs or the creation of new components.

Step 10. Assessment of a fuzzy risk based on the aggregation of all risk factors across all project tasks grouped in relation to the adaptation of RCs or the fabrication of new components R_f^pr:

$$R_f^{pr}={\displaystyle \sum R_f^h,} f=1\dots k,$$

(6)

where the sum is over h = 1…d; h refers to the number of the project task group related to the adaptation of RCs and the fabrication of new components.

Step 11. g(V_f)—the centroid value of V_f of the linguistic variable V:

$$g(V_f)={\displaystyle \int u\cdot {\mu }_{Vf}}(u)du/\int {\mu }_{Vf}(u)du f=1\dots k,$$

(7)

where [a_f, c_f]—the limits of the integrals.

The risk assessment for a group of project tasks related to the adaptation (modernization) of RCs or the creation of new components is conducted as follows:

$$R^h={\displaystyle \sum g(V_f)\cdot }{R}_f^h/{\displaystyle \sum R_f^h},$$

(8)

where the sums are over f = 1…k.

The risk assessment of the project for creating a new product, related to its novelty, is determined by defuzzifying the fuzzy assessment using the centroid method.

$$R^{pr}={\displaystyle \sum g(V_f)\cdot }{R}_f^{pr}/{\displaystyle \sum R_f^{pr}},$$

(9)

where the sums are over f = 1…k; R^pr is the probability of achieving a non-satisfactory result.

One of the distinguishing features of the proposed component-oriented risk assessment model at the early stages of design is that this model is applicable not only for assessing the overall project risk of the HTP being developed but also for individual groups of project tasks related to the adaptation (modernization) of selected precedent RCs or the creation of new components.

Another feature of the proposed model is that the risk levels of factors r_j are determined based on the characteristics of each risk-generating factor using a probability and impact matrix. Thus, the impact of risk on the execution of tasks is defined by two key characteristics: the novelty of the part or subunit in the structure of the HTP being created and the risk level of each factor.

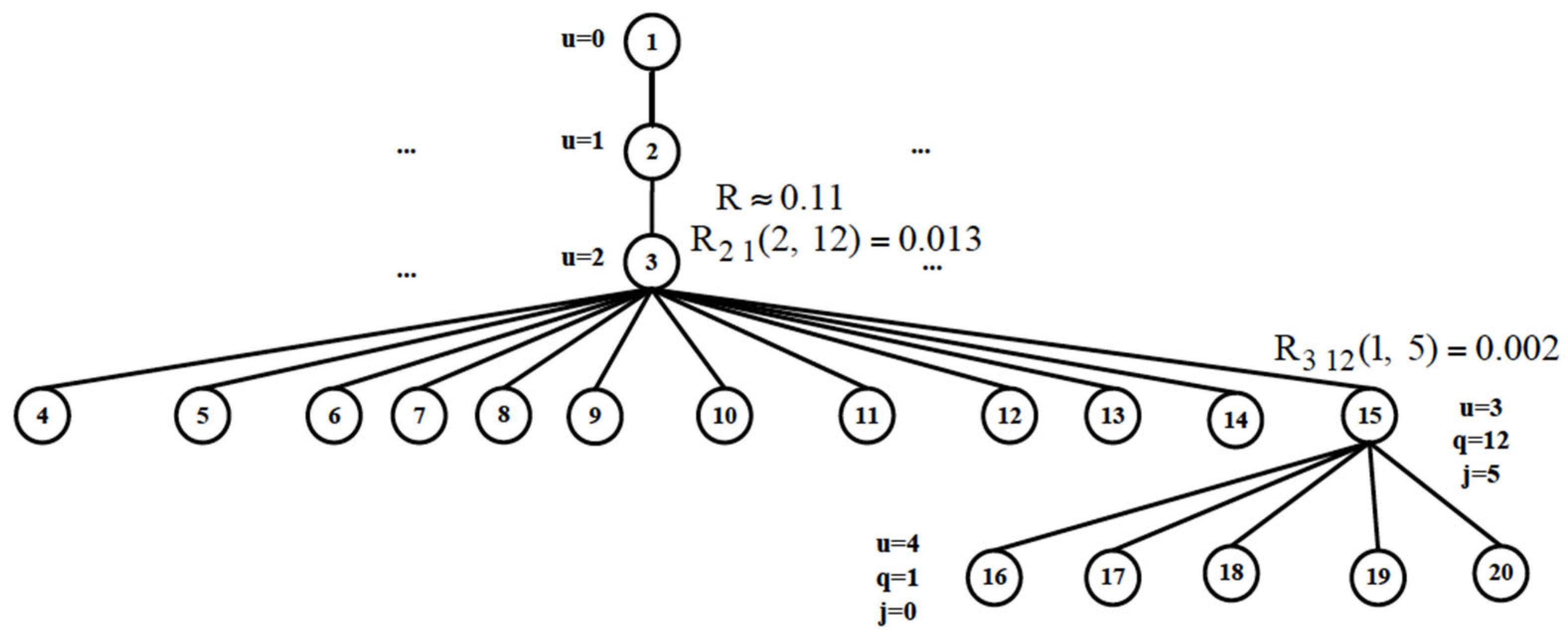
When assessing project risk, in addition to the novelty of the components, the complexity of the structure of the high-tech product is also considered in this study. A multi-level system decomposition is analyzed, including the risk of integrating components at nodes, the complexity of the node, and the number of components (lower-level sub-nodes) in the designed node. Thus, the project risk assessment associated with the complexity and novelty of the product being developed is carried out using the following formula:

$$R=1-\left({\displaystyle {\prod }_{u=m-2}^0}{\displaystyle {\prod }_{q=1}^{nu}}\left(1-R_{uq}\left(i,j\right)\right)\right)\cdot (1-R^{pr}),$$

(10)

where m is the number of decomposition levels of the high-tech product being designed. Project risk assessment is carried out starting from the lowest level of the product structure (u = m − 2) and concludes at the system level as a whole (u = 0). R_uq(i, j) is the risk of integration for the q-th node at the u-th decomposition level of the product, with i-th complexity and the number of components (sub-nodes at (u + 1)-th level) in the node j; nu represents the number of components at the u-th decomposition level of the high-tech product.

The proposed component-oriented fuzzy model is conceptually consistent with the general risk management process defined in ISO 31000 [40] and IEC 31010 [41] standards, particularly addressing the “risk assessment” phase, which includes the stages of risk identification, analysis, and evaluation. Within the model, risk identification is achieved through decomposition of the high-tech product into components and linking the corresponding risk-generating factors to groups of project works according to the degree of novelty of components. Risk analysis is conducted using fuzzy set theory, which allows for the inclusion of linguistic expert judgments and uncertainty inherent to the early design stage. Risk evaluation is performed through defuzzification and aggregation procedures, enabling the comparison of calculated risk levels with acceptable thresholds.

In contrast to traditional ISO-based approaches that operate mainly at the system or organizational level, the proposed model introduces a component-oriented representation of risk, allowing for detailed assessment of how component novelty and integration complexity affect project outcomes. Consequently, it serves as a methodological extension of existing frameworks by providing a practical tool for component-level and early-stage design risk assessment in high-tech product development.

3. Risk Assessment for the Projected UAV: A Case Study

In the case study, the assessment of project risk is associated with the complexity and novelty of the projected UAV for two different approaches. In the first case, the synthesis of the new UAV structure is carried out based on the component-oriented approach described in Section 2. In the second case, the architecture of the UAV is formed without drawing on the formalized experience of past developments.

3.1. Risk Assessment with Experience of Previous Developments

The selection of the 14 risk-generating factors used in this study was carried out through a two-stage expert-based screening procedure. At the first stage, a comprehensive review of the relevant literature, including international standards ISO 31000:2018 [40] and ISO/IEC 16085:2021 [42], as well as scientific publications on engineering and product design risk assessment, was performed. This allowed identification of more than thirty potential risk factors affecting high-tech product development.

At the second stage, the preliminary list was refined by a panel of ten domain experts from the fields of mechanical, aerospace, and systems engineering. The experts applied the Nominal Group Technique (NGT) to assess the relevance and significance of each factor. Only factors with a consensus score above 70% were retained.

As a result, fourteen risk factors were selected, representing the main risk dimensions relevant to high-tech product design—socio-economic, organizational, scientific and technical, and financial–economic. This ensures the comprehensiveness and methodological validity of the subsequent risk assessment.

The component-oriented model for assessing project risk in the early stages of creating a high-tech product was applied according to the steps described in Section 2, as outlined below.

Step 1. A list of basic risk groups was determined, identifying intra-group factors that affect the creation of a high-tech product. An excerpt of 14 factors from the list is given in

Table 3. Excerpt from the list of the basic risk factor groups and their intra-group factors that affect project work.

Risk Factor Number	Basic Risk Group	Intra-Group Risk Factor
1	Socio-economic risks	Increase in freight transportation tariffs
2	Socio-economic risks	Changes in consumer requirements
3	Socio-economic risks	New rules for conducting foreign economic activity
4	Organizational risks	Lack of coordination of work
5	Scientific and technical risks	Deviations in the timing of project design stages
6	Scientific and technical risks	Inadequacy of personnel to meet the professional requirements of the project
7	Scientific and technical risks	Emergence of unforeseen scientific and technical problems
8	Scientific and technical risks	Risk of financial losses as a result of failure to achieve planned technical parameters during design and technological development
9	Scientific and technical risks	Competitors mastering new technology
10	Scientific and technical risks	High level of external R&D
11	Scientific and technical risks	Industrial espionage and technology copying
12	Financial and economic risks	Currency market instability
13	Financial and economic risks	Budget cuts
14	Financial and economic risks	Changes in tax rates

.

Step 2. As a result of the synthesis of the component structure of the technical system, the composition of project works for the creation of a high-tech product was determined.

Table 4. Fragment of the project work tree.

Work Code	UAV Structure Components	Work Content	WGC
1.1.1	Receiver–monitor (for ground part)	Purchase of a receiver–monitor (for the ground part)	1
1.1.2	Onboard transmitter	Purchase of an onboard transmitter	1
1.1.3	Onboard computer	Purchase of an onboard computer	1
1.1.4	Air pressure receiver for measuring flight speed and barometric altitude	Purchase of an air pressure receiver for measuring flight speed and barometric altitude	1
1.1.5	Air speed and barometric altitude sensors	Purchase of air speed and barometric altitude sensors	1
1.1.6	Engine temperature sensor	Purchase of engine temperature sensors	1
1.1.7	Cables	Purchase of USB cable, 4-Y cable	1
1.1.8	Mounting hardware	Purchase of mounts	1
1.1.9	Software	Purchase of software	1
1.1.10	Fuel gauge sensor	Purchase of fuel gauge sensor	1
1.1.11	Hall effect RPM sensor	Purchase of Hall effect RPM sensor	1
1.1.12.1	GPS receiver	Purchase of GPS receiver	1
1.1.12.2	Software	Purchase of software	1
1.1.12.3	Cables	Purchase of cables	1
1.1.12.4	Mounting hardware	Purchase of mounts	1
1.1.12.5	Batteries	Purchase of batteries	1

shows a list of works for the considered project of creating a UAV. When compiling a list of project works, relevant standards and regulations were followed.

In the present study, the design work group code (WGC) according to the novelty criterion of components can take one of three values: 1—acquisition of reusable components (RCs); 2—work for the RC adaptation; and 3—work for the development of the new components specified in Table 4.

Step 3. The number of linguistic variable values for assessing the risk level and importance of the risk factor has already been selected as k = 5 (see Table 2). This set of values is quite complete and entirely acceptable.

Membership functions of values V_f, f = 1…k for both linguistic variables can be written in the form of the following expressions:

• When f = 1 and V₁ = <0; 0; 0.25>,

  $${\mu }_{V_f}(u)=\left\{\begin{array}{l}1-4\cdot u; 0\le u\le 0.25\\ 0; 0.25\le u\le 1\end{array}\right.;$$

  (11)
• When f = 2, 3, 4 and $V_f=〈{\displaystyle \frac{f-2}{4}};{\displaystyle \frac{f-1}{4}};{\displaystyle \frac{f}{4}}〉$,

  $${\mu }_{V_f}(u)=\left\{\begin{array}{l}0; u\le {\displaystyle \frac{(f-2)}{4}}\\ 4\cdot u-(f-2); {\displaystyle \frac{(f-2)}{4}}\le u\le {\displaystyle \frac{(f-1)}{4}}\\ f-4\cdot u; {\displaystyle \frac{(f-1)}{4}}\le u\le {\displaystyle \frac{f}{4}}\\ 0; {\displaystyle \frac{f}{4}}\le u\le 1.0\end{array}\right.;$$

  (12)
• When f = 5 and V₅ = <0.75; 1.0; 1.0>,

  $${\mu }_{V_f}(u)=\left\{\begin{array}{l}0; 0\le u\le 0.75\\ 4\cdot u-3; 0.75\le u\le 1.0\end{array}\right..$$

  (13)

It should be noted that the membership function μ_Vf (u) at some intervals of the universal set U takes the value 0 [43]. This is presented in Figure 1.

Step 4. Based on the degree of novelty of the components of the designed UAV, we determined the importance of the risk factor s_j affecting the project work. The impact of risks caused by risk-generating factors on the first group of works was assessed by experts as very low. The analysis showed that the group of project works with RC adaptation might be the most susceptible to socio-economic risks, as well as financial and economic risks. The impact of organizational, scientific, and technical risks on the third group of works will be the greatest, as is seen in

Table 5. Determining the importance of a risk factor s_jt dependent on the novelty of the components in the designed UAV.

Groups of Project Works According to the Degree of Novelty of Components	Unique Risk Factor Numbers (See Table 3)
	1	2	3	4	5	6	7	8	9	10	11	12	13	14
Project work on the acquisition of RCs	vl	vl	vl	vl	vl	vl	vl	vl	vl	vl	vl	vl	vl	vl
Project work on the adaptation of RCs	vl	l	l	vl	l	vl	l	vl	l	l	l	vl	vl	l
Project work on the development of new components	l	l	m	l	l	l	m	l	m	l	m	l	l	l

. In this example, all works belonged to the first group, as is specified in Table 4. Thus, the impact of risk-generating factors associated with the acquisition of RCs will be very low, denoted as vl.

Step 5. A compilation of a probability and consequence matrix was made to assess the risk level of each risk factor r_j for all project works. It is shown in

Table 6. Probability of the occurrence and consequence matrix for the risk factors.

Probability of the Risk Factor Occurrence	Impact of the Risk Factor
	Very Low (vl)	Low (l)	Medium (m)	High (h)	Very High (vh)
0.1	vl	vl	vl	m	m
0.3	vl	vl	l	m	h
0.5	vl	l	l	h	h
0.7	vl	l	m	h	vh
0.9	vl	m	m	vh	vh

. Next, the level of each risk factor was determined and is presented in

Table 7. The risk level determined for a factor rⁱ_j.

Numbers of Values of the Linguistic Variable of the Risk Level of the Factor rj	Unique Risk Factor Numbers (See Table 3)
	1	2	3	4	5	6	7	8	9	10	11	12	13	14
1 (vl)	1	1	1	0	1	1	1	0	1	1	1	1	1	1
2 (l)	0	0	0	1	0	0	0	1	0	0	0	0	0	0
3 (m)	0	0	0	0	0	0	0	0	0	0	0	0	0	0
4 (h)	0	0	0	0	0	0	0	0	0	0	0	0	0	0
5 (vh)	0	0	0	0	0	0	0	0	0	0	0	0	0	0

.

The probability values (0.1, 0.3, 0.5, 0.7, 0.9) used in the probability–impact matrix were established through a combined expert- and literature-based approach. These five levels correspond to the linguistic variables “very low,” “low,” “medium,” “high,” and “very high” and represent evenly distributed points within the [0, 1] interval. This quasi-linear scale is widely adopted in fuzzy risk assessment methods [21,22], providing a consistent mapping between qualitative expert judgments and quantitative probability estimates. The numerical values were further validated by a panel of experts in engineering risk management to ensure that they realistically reflect the likelihood of risk occurrence under the uncertainty typical of the early design stage of high-tech products.

Step 6. Next, the defuzzification procedure [44] was performed and all values of g(r, s) for all possible combinations of pairs r and s were determined using the centroid method, as follows:

$$g(r,s)={\displaystyle \frac{{\displaystyle \underset{a}{\overset{c}{\int }}u\cdot {\mu }_{N_r\cdot N_s}(u)du}}{{\displaystyle \underset{a}{\overset{c}{\int }}{\mu }_{N_r\cdot N_s}(u)du}}}.$$

(14)

Some different combinations of r and s values can be considered, as follows:

• First example: r is average, s is high;
• Second example: r is very low, s is low;
• Third example: r is very low, s is very high.

For the first example, N₃ = <0.25; 0.5; 0.75>, N₄ = <0.5; 0.75; 1.00>, and N₃·N₄ = <0.125; 0.375; 0.75>. A diagram of the membership function μ_N3·N4 (u) is presented in Figure 2.

After the calculations from Equation (14) for r = 3 and s = 4, g(3, 4) ≈ 0.4190 was obtained.

For the second example, where r = 1 and s = 2, N₁ = <0; 0; 0.25>, N₂ = <0; 0.25; 0.5>, and N₁·N₂ = <0; 0; 0.125>. A diagram of the respective membership function μ_N1·N2 (u) is presented in Figure 3. After the calculations, g(1, 2) ≈ 0.0417 was obtained.

For the third example, where r = 1 and s = 5, N₁ = <0; 0; 0.25>, N₅ = <0.75; 1.00; 1.00>, and N₁·N₅ = <0; 0; 0.25>. A diagram of the respective membership function μ_N1·N2 (u) is presented in Figure 3. After the respective calculations, g(1, 5) ≈ 0.0833 was obtained.

Other combinations of risk levels r and levels of importance s are shown in

Table 8. Values of g(r, s) for different risk levels of the factor, taking into account its importance.

Risk Level of the Factor, r	Level of Importance of the Factor, s
	1	2	3	4	5
1	0.0208	0.0417	0.0625	0.0833	0.0833
2	0.0417	0.0938	0.1667	0.2292	0.2500
3	0.0625	0.1667	0.2917	0.4190	0.4792
4	0.0833	0.2292	0.4190	0.6042	0.7083
5	0.0833	0.2500	0.4792	0.7083	0.8542

with respective values of g(r, s).

Next, a calculation table was compiled with project works and risk factors.

Table 9. Risk levels of the respective factors, considering their importance in dependence on the group of design works, and novelty of the components.

Work Code	Unique Risk Factor Numbers (See Table 3)
	1	2	3	4	5	6	7	8	9	10	11	12	13	14
1.1.1	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0208	0.0208	0.0208
1.1.2	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0208	0.0208	0.0208
1.1.3	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0208	0.0208	0.0208
1.1.4	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0208	0.0208	0.0208
1.1.5	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0208	0.0208	0.0208
1.1.6	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0208	0.0208	0.0208
1.1.7	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0208	0.0208	0.0208
1.1.8	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0208	0.0208	0.0208
1.1.9	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0208	0.0208	0.0208
1.1.10	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0208	0.0208	0.0208
1.1.11	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0208	0.0208	0.0208
1.1.12.1	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0208	0.0208	0.0208
1.1.12.2	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0208	0.0208	0.0208
1.1.12.3	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0208	0.0208	0.0208
1.1.12.4	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0208	0.0208	0.0208
1.1.12.5	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0417	0.0208	0.0208	0.0208	0.0208	0.0208	0.0208

contains the values of the risk levels of the factors with consideration of their importance, determined on the basis of the degree of novelty of the components g_jtw(r_j, s_jt). The data presented in Table 8 was used for the compilation, and details behind the work codes can be found in Table 4.

Step 7. The results presented in Table 8 allowed for calculation of the H’ matrix, where importance g(r, s) and membership functions μ_Vφ(u) and μ_Vφ+1(u) are taken into account.

The obtained matrix values were used to determine the fuzzy matrix of risk factor intersections, considering their importance and the membership functions of triangular numbers for the respective project works h(g_jtw(r_j, s_jt), V_f). A fragment of the fuzzy matrix is presented in

Table 10. Fragment of a fuzzy matrix built with consideration of importance and membership functions for each project work.

Work Code	Unique Risk Factor Numbers (See Table 3)	h1	h2	h3	h4	h5
1.1.1	1	0.9167	0.0833	0.0000	0.0000	0.0000
1.1.1	2	0.9167	0.0833	0.0000	0.0000	0.0000
1.1.1	3	0.9167	0.0833	0.0000	0.0000	0.0000
1.1.1	4	0.8333	0.1667	0.0000	0.0000	0.0000
1.1.1	5	0.9167	0.0833	0.0000	0.0000	0.0000
1.1.1	6	0.9167	0.0833	0.0000	0.0000	0.0000
1.1.1	7	0.9167	0.0833	0.0000	0.0000	0.0000
1.1.1	8	0.9167	0.1667	0.0000	0.0000	0.0000
1.1.1	9	0.9167	0.0833	0.0000	0.0000	0.0000
1.1.1	10	0.9167	0.0833	0.0000	0.0000	0.0000
1.1.1	11	0.9167	0.0833	0.0000	0.0000	0.0000
1.1.1	12	0.9167	0.0833	0.0000	0.0000	0.0000
1.1.1	13	0.9167	0.0833	0.0000	0.0000	0.0000
1.1.1	14	0.9167	0.0833	0.0000	0.0000	0.0000
1.1. 2	1	0.9167	0.0833	0.0000	0.0000	0.0000
1.1. 2	2	0.9167	0.0833	0.0000	0.0000	0.0000
1.1. 2	3	0.9167	0.1667	0.0000	0.0000	0.0000
1.1. 2	4	0.8333	0.0833	0.0000	0.0000	0.0000
1.1. 2	5	0.9167	0.0833	0.0000	0.0000	0.0000

.

For convenience, Table 10 shows the newly introduced values h_f representing the intersection of the risk level of the factor, considering its importance h(g_jtw(r_j,s_jt), V_f) based on a specific risk factor for a particular project task and the functions of triangular numbers μ_Vf(u).

To clarify the computational procedure, an illustrative example is provided below for risk-generating factor 4 (“Lack of coordination of work”) and project work 1.1.1 (“Purchase of a receiver–monitor”). The purpose is to demonstrate the step-by-step derivation of the h-values shown in Table 10, including substitution into the membership functions and the intersection operation.

According to Equation (11), the scalar value u = g_jtw(r_j,s_jt) represents the combined fuzzy evaluation of the risk-generating factor and the corresponding project work.

For this particular pair, the calculated value equals u = 0.0417.

Following Equations (12) and (13), the triangular membership functions μ_Vf(u) for the five linguistic variables V_f (“very low”, “low”, “medium”, “high”, “very high”) are defined as

V₁ = <0; 0; 0.25>, V₂ = <0; 0.25; 0.5>, V₃ = <0.25; 0.5; 0.75>, V₄ = <0.5; 0.75; 1.0>, V₅ = <0.75; 1.0; 1.0>.

(15)

The membership function for each triangular fuzzy number (a, b, c)(a, b, c)(a, b, c) is expressed as

$${\mu }_{(a,b,c)}(u)=\left\{\begin{array}{l}0, u<a \mathrm{or} u<c,\\ {\displaystyle \frac{u-a}{b-a}}, a\le u\le b,\\ {\displaystyle \frac{c-u}{c-b}}, b\le u\le c.\end{array}\right.$$

(16)

Substituting u = 0.0417 yields the following membership degrees:

• For V₁ = <0; 0; 0.25>,

  $$a=b=0, c=0.25 \Rightarrow {\mu }_{Vi}\left(u\right)={\displaystyle \frac{c-u}{c-b}}={\displaystyle \frac{0.25-0.0417}{0.25}}=0.8333;$$

  (17)
• For V₂ = <0; 0.25; 0.5>,

  $$a=0, 0.25 \Rightarrow {\mu }_{Vi}\left(u\right)={\displaystyle \frac{u-a}{b-a}}={\displaystyle \frac{0.0417}{0.25}}=0.1667$$

  (18)
• For V₃, V₄, and V₅, μ_Vf(u) = 0 since u < 0.25.

Thus, the intersection vector of membership degrees, i.e., the corresponding row of the fuzzy matrix H for this pair, is (h₁, h₂, h₃, h₄, h₅) = (0.8333, 0.1667, 0, 0, 0). These values correspond exactly to the data presented in Table 10. Minor numerical differences may occur due to rounding of intermediate results, e.g., 0.8332 → 0.8333 or 0.1668 → 0.1667. The same computational logic applies to all other combinations of risk-generating factors and project works. This worked example illustrates how the fuzzy intersection operation is implemented in practice, ensuring reproducibility and interpretability of the fuzzy evaluation process.

Steps 8 and 9. In the example of the UAV project, steps 8 and 9 of the proposed component-oriented model coincide, since, in this case, the acquisition of a separate component is associated not with a group of project works, but with a single work. A fuzzy risk assessment can be performed taking into account all risk factors for each project work.

Table 11. Fuzzy risk assessment matrix for each project work taking into account a group of risks.

Work Code	Description of the Work	h1	h2	h3	h4	h5
1.1.1	Purchase of a receiver–monitor	0.0565	0.0060	0.0000	0.0000	0.0000
1.1.2	Purchase of an onboard transmitter	0.0565	0.0060	0.0000	0.0000	0.0000
1.1.3	Purchase of an onboard computer	0.0565	0.0060	0.0000	0.0000	0.0000
1.1.4	Purchase of an air pressure receiver for measuring airspeed and barometric altitude	0.0565	0.0060	0.0000	0.0000	0.0000
1.1.5	Purchase of airspeed and barometric altitude sensors	0.0565	0.0060	0.0000	0.0000	0.0000
1.1.6	Purchase of engine temperature sensors	0.0565	0.0060	0.0000	0.0000	0.0000
1.1.7	Purchase of a USB cable, 4-Y cable	0.0565	0.0060	0.0000	0.0000	0.0000
1.1.8	Purchase of mounts	0.0565	0.0060	0.0000	0.0000	0.0000
1.1.9	Purchase of software	0.0565	0.0060	0.0000	0.0000	0.0000
1.1.10	Purchase of fuel gauge	0.0565	0.0060	0.0000	0.0000	0.0000
1.1.11	Purchase of Hall effect RPM sensor	0.0565	0.0060	0.0000	0.0000	0.0000
1.1.12.1	Purchase of GPS receiver	0.0565	0.0060	0.0000	0.0000	0.0000
1.1.12.2	Purchase of software	0.0565	0.0060	0.0000	0.0000	0.0000
1.1.12.3	Purchase of cables	0.0565	0.0060	0.0000	0.0000	0.0000
1.1.12.4	Purchase of mounts	0.0565	0.0060	0.0000	0.0000	0.0000
1.1.12.5	Purchase of batteries	0.0565	0.0060	0.0000	0.0000	0.0000

presents the results of the risk assessment.

Step 10. In this step, the risk was assessed for the entire work. The resulting fuzzy risk assessments, taking into account all risk factors, for all project adaptation works (in this case, the acquisition of components) are presented in

Table 12. Fuzzy risk assessment for the entirety of the project work, taking into account all risk factors.

h1	h2	h3	h4	h5
0.9048	0.0952	0.0000	0.0000	0.0000

.

Step 11. The risk assessment was made for adaptation works. In this case, this meant acquisition of the reused components, RCs. The results are collected in

Table 13. Risk assessments for adaptation (acquisition) work components for reuse.

Work Code	Job Description	Risk Assessment
1.1.1	Purchase of a receiver–monitor	0.0992
1.1.2	Purchase of an onboard transmitter	0.0992
1.1.3	Purchase of an onboard computer	0.0992
1.1.4	Purchase of an air pressure receiver for measuring airspeed and barometric altitude	0.0992
1.1.5	Purchase of airspeed and barometric altitude sensors	0.0992
1.1.6	Purchase of engine temperature sensors	0.0992
1.1.7	Purchase of a USB cable, 4-Y cable	0.0992
1.1.8	Purchase of mounts	0.0992
1.1.9	Purchase of software	0.0992
1.1.10	Purchase of fuel gauge	0.0992
1.1.11	Purchase of Hall effect RPM sensor	0.0992
1.1.12.1	Purchase of GPS receiver	0.0992
1.1.12.2	Purchase of software	0.0992
1.1.12.3	Purchase of cables	0.0992
1.1.12.4	Purchase of mounts	0.0992
1.1.12.5	Purchase of batteries	0.0992

.

Thus, the project risk associated with the novelty of the product being created was calculated as 0.0992.

Considering necessity and possibility of application of the 6R framework, including reduction, repair, reuse, recover, remanufacturing, and recycling [45], the project risk associated with the complexity and novelty was assessed. In this study, the 6R framework was treated not as an additional risk factor, but as a conceptual foundation that supported the classification of components according to their degree of reusability. The 6R principles aligned with the three groups of project works defined in the proposed model: acquisition of reusable components, adaptation (modernization) of existing ones, and development of new components. Therefore, the framework provided a sustainability-oriented context for differentiating component categories and interpreting the associated risk levels during the design process.

This project risk for a product node in our example is influenced by two factors. The first one is the risk of complexing the components that make up the node, and the second one is related to the novelty of the product.

Table 14. Matrix for the probability of occurrence of the R_uq(i, j) complexification risk for the components of a new high-tech product.

i	Node Complexity	Number of Components in a Node, j
		1–2	3–5	6–10	11–79	80–100
1	Very low	0.001	0.002	0.011	0.017	0.028
2	Low	0.003	0.004	0.013	0.02	0.033
3	Medium	0.005	0.006	0.014	0.024	0.04
4	High	0.007	0.008	0.015	0.031	0.044
5	Very high	0.009	0.01	0.016	0.036	0.048

shows the matrix for determining the probability of occurrence of the R_uq(i, j) component of Equation (10), where i is the complexity of the node and j is the number of components in the node. Figure 4 shows a schematic representation of a fragment of the multi-level component composition of a new UAV aviation product.

Figure 4 emphasizes the role of the following components and subsystems: 1—UAV; 2—automatic control subsystem; 3—set of telemetry equipment; 4—monitor receiver (for ground part); 5—onboard transmitter; 6—onboard computer; 7—air pressure receiver for measuring airspeed and barometric altitude; 8—airspeed and barometric altitude sensors; 9—engine temperature sensor; 10—cables; 11—mountings; 12—software; 13—fuel level sensor; 14—Hall effect RPM sensor; 15—GPS module; 16—GPS receiver (with antenna); 17—software (GPS); 18—cables (GPS); 19—fasteners (GPS); and 20—power supply elements. Figure 4 also includes an example of calculated project risk for the considered fragment of the technical system, which is associated with the complexity and novelty of the product, according to Equation (10).

The calculations were based on the data presented in Table 13 and Table 14. As a result, the project risk of creating the analyzed UAV at the initial stages of building up the technical system was assessed as equal to 0.11.

3.2. Risk Assessment Without Experience of Previous Developments

For comparison, the project risk of the UAV of the same product architecture was assessed without using the formalized experience of previous developments. Thus, practically all works in the creation of components of the fragment under consideration represented by Figure 4 belong to the third group, i.e., the one considering development of new components. A fragment of the project work tree is shown in

Table 15. Fragment of the project work tree and results of the risk assessment.

Work Code	UAV Structure Components	Work Content	WGC	Risk Assessment
1.1.1	Receiver–monitor (for ground part)	Design of a receiver–monitor	3	0.1625
1.1.2	Onboard transmitter	Design of an onboard transmitter	3	0.1625
1.1.3	Onboard computer	Design of an onboard computer	3	0.1625
1.1.4	Air pressure receiver for measuring flight speed and barometric altitude	Design of air pressure receiver for measuring flight speed and barometric altitude	3	0.1625
1.1.5	Air speed and barometric altitude sensors	Design of air speed and barometric altitude sensors	3	0.1625
1.1.6	Engine temperature sensor	Design of engine temperature sensors	3	0.1625
1.1.7	Cables	Adaptation of USB cable, 4-Y cable	2	0.1625
1.1.8	Mounting hardware	Fabrication of mounts	3	0.1625
1.1.9	Software	Software development	3	0.1209
1.1.10	Fuel gauge sensor	Design of fuel gauge	3	0.1625
1.1.11	Hall effect RPM sensor	Design of Hall effect RPM sensor	3	0.1625
1.1.12.1	GPS receiver	Design of GPS receiver	3	0.1625
1.1.12.2	Software	Software development	3	0.1625
1.1.12.3	Cables	Fabrication of cables	3	0.1625
1.1.12.4	Mounting hardware	Manufacture of mounts	3	0.1625
1.1.12.5	Batteries	Fabrication of power supply elements	3	0.1625

along with the respective WGCs.

For the sake of methodological correctness of the comparative analysis, the same number of linguistic variable values was used to assess the level of risk and the importance of the risk factor. The values of linguistic variables describing the risk and the importance levels were taken from Table 2, Section 2. In addition, to assess the risk of project works, the same list of basic risk groups and intra-group factors was selected and taken from Table 3. The same risk factor level values were taken from Table 7. When determining the risk of work, the importance of the risk factor presented in Table 5 for the respective group of project works was used. As a result of the calculations, the project risks for the design and fabrication of new components and the adaptation of reusable components were assessed and are collected in Table 15.

It appears that the project risk of creating a UAV, which is associated with the novelty of the designed product, the synthesis of whose structure was carried out without the use of formalized positive experience from previous developments, is equal to 0.1902. This is almost 2 times higher than the value of 0.0992 of the project risk in a component-oriented approach, described in Section 3.1, and more than 1.7 times higher than the 0.11 associated with the complexity and novelty of the product, calculated in Section 3.2.

Thus, when the synthesis of the UAV structure fragment was carried out without both the component-oriented approach and the positive experience of previous developments, the assessed risks rose by almost two times. On the other hand, the project risk associated with the complexity and novelty of the same fragment of the structure, obtained on the basis of a component-oriented approach, appeared to be the lowest, i.e., 0.11.

The obtained risk values can be practically interpreted as quantitative indicators of project feasibility at the early design stage. In the proposed fuzzy-based model, the risk value ranges between 0 and 1, where 0 corresponds to the absence of risk and 1 indicates a critical level of uncertainty. For example, the project risk value of 0.0992 obtained for the component-oriented approach corresponds to a low level of uncertainty, meaning that the design process can continue with regular control procedures. In contrast, a value of 0.1902 represents a moderate risk level, implying the need for additional verification of new components, design iteration, or implementation of risk mitigation actions before further development. Thus, the resulting quantitative values directly support managerial decision-making: projects with R < 0.1 can be approved for continuation (“go”), while those with 0.1 ≤ R < 0.2 require targeted corrective measures, and projects exceeding R ≥ 0.2 should be temporarily suspended or redesigned (“no-go”). This connection between numerical results and decision-making criteria strengthens the practical applicability of the proposed model.

In order to assess the model’s sensitivity to component novelty, an additional analysis was conducted by varying the share of newly developed components in the system structure from 10% to 60% while keeping other parameters constant. The results indicated a nearly linear increase in the total risk index, from 0.0992 for predominantly reused components to 0.1902 when the proportion of new components is dominant. Thus, it was demonstrated that the proposed model effectively captures the relationship between the degree of novelty and the overall project risk.

Furthermore, the model’s stability was verified by adjusting the weighting coefficients of component novelty within a range of ±10%. The resulting changes in aggregated risk values did not exceed 5%, confirming that the model maintained consistent behavior under small perturbations of expert-assigned weights. Consequently, the fuzzy aggregation mechanism can be considered both sensitive and stable, making it suitable for early-stage evaluation, where uncertainty and qualitative judgments prevail.

It should be noted that the proposed risk aggregation procedure assumed independence among the evaluated components. This simplification allowed for transparent fuzzy computation at the early design stage, where detailed information about component interrelations is typically unavailable. Nevertheless, in complex systems such as UAVs, interdependencies and common-cause failures may occur, which can lead to an underestimation of the overall system risk.

To address this limitation, future research could extend the model by introducing correlation coefficients between component risk values or by employing probabilistic network approaches such as Bayesian networks. Additionally, methods based on fault tree analysis or reliability block diagrams could be integrated to explicitly capture common-cause effects. Such developments would enhance the precision of the system-level risk evaluation as more detailed design and operational data become available.

Although the present study did not include a direct quantitative comparison with conventional methods such as FMEA, AHP, or TOPSIS, a qualitative analysis highlights the distinctive advantages of the proposed component-oriented fuzzy model. Traditional approaches are primarily applicable at later design stages, when detailed data on failure modes, criteria weights, and performance indicators are available. By contrast, the proposed model enables structured risk assessment under the high uncertainty characteristic of the conceptual design stage.

Furthermore, it provides a component-level decomposition of risks, linking them to the degree of novelty and reuse, and employs fuzzy linguistic variables to formalize expert judgments where numerical data are scarce. These features make the approach particularly suitable for early decision support in complex high-tech projects. Future research will focus on performing a benchmarking study comparing the proposed fuzzy model with FMEA and hybrid AHP–TOPSIS methods to quantify performance differences and validate the model’s predictive capability.

It should be noted that the three UAV project types analyzed in the case study are intentionally similar in their overall architecture and functionality. This choice was made to ensure controlled conditions for testing the sensitivity of the proposed model to changes in the proportion of reused, adapted, and newly developed components. Although the resulting risk values differ moderately, they reflect the expected trend of increasing overall project risk with higher component novelty, confirming the model’s internal consistency.

However, the similarity of the examined projects limits the demonstration of the model’s generalizability to systems with more diverse risk structures. Future research will therefore focus on applying the component-oriented fuzzy model to heterogeneous and mixed-type projects—for instance, hybrid UAV–UGV platforms, robotic subsystems, and other high-tech products—to evaluate its robustness and adaptability across different engineering domains.

A more detailed analysis of the obtained results shows that the overall project risk is primarily determined by a few dominant groups of risk-generating factors. In the UAV case study, the scientific and technical risks (related to the design feasibility and technological maturity of new components) and organizational risks (associated with coordination, schedule delays, and resource allocation) exhibited the highest weighted importance. These factors are most pronounced in the development and integration of new components, such as flight control and power subsystems, which contribute the largest share to the total risk index.

In contrast, risks associated with reused or adapted components have relatively low weights, confirming that their contribution to total risk remains limited. From a managerial standpoint, this decomposition provides actionable insight: project managers can prioritize risk mitigation efforts for components with the highest novelty and uncertainty, rather than applying uniform control across all system parts. Thus, the proposed model supports more targeted decision-making, helping to optimize development resources and improve overall project reliability at the early design stage.

4. Conclusions

Project risk represents potential unfavorable events for the project, the occurrence of which leads to material, time, financial, and other additional costs. In the proposed component-oriented model, project risk assessment is based on the novelty of the components being developed for the high-tech product. This allows the classification of project tasks into three groups based on the degree of novelty: project tasks for the adaptation of reusable components, project tasks for the acquisition of RCs that do not require adaptation, and project tasks for the creation of new components. This approach enables the consideration of varying impacts of the same risk on different project tasks.

The considered model for determining project risk, based on assessing the degree of novelty of the components in the HTP, not only allows for a reduction in the influence of a range of risks, such as innovation, scientific–technical, and organizational risks, among others, but also provides the most accurate determination of the negative impact of the identified risk-generating factors on the development of the HTP.

The component-oriented model for project risk assessment allows for consideration of the probability of risk occurrence when integrating components for each node at the specified decomposition level of the HTP, depending on the complexity of the node and the number of components (sub-nodes at the neighboring lower level) in the designed node. Although the UAV case study primarily involved purchased or reused components, it successfully demonstrated the model’s capability to detect variations in project risk resulting from the introduction of new components. Nevertheless, further validation on products with a higher proportion of design-intensive and innovative components—such as robotic platforms, smart sensor systems, and advanced manufacturing modules—will be pursued in future research. This will allow a more comprehensive demonstration of the model’s applicability and its sensitivity to innovation-driven risk dynamics in complex high-tech systems. This approach enables a more accurate assessment of project risk, which is crucial at the initial stage of creating a technical system, as it facilitates decision-making regarding the feasibility of further development of the HTP.