Simultaneous Broadband Sound Absorption and Vibration Suppression in Gradient-Symmetric Multilayer Metamaterials

Abstract

Metamaterials show perfect physics characteristics for controlling elastic wave propagation. Their potential offers a lot of useful applications in low-frequency sound absorption and vibration reduction systems. However, traditional materials have inherent deficiencies in terms of functionality. There are a few designs in both acoustic and solid-mechanics domains that simultaneously exhibit sound attenuation bands and vibration bandgaps. The question poses new challenges for metamaterial development. To address this, we propose a gradient-symmetric multilayered metamaterial. The structure is capable of concurrent sound and vibration absorption. First, we established an acoustic model based on Helmholtz resonators and a vibration model by spring-mass systems. This model can predict the sound attenuation frequencies and natural frequency positions accurately. Second, through a combined simulation and experimental approach, we investigated how variations in the number of structural layers affect sound attenuation bandwidth. In addition, we analyzed the mechanisms of sound pressure distribution inside and outside the bandgaps. Finally, we elucidated the influence of lattice constants on vibration bandgap positions, demonstrating possibilities for passive control of metamaterials. This research provides robust support for the dynamic design of acoustic and mechanical metamaterials, structural modeling methodologies, bandwidth regulation strategies, and the development of sound-absorbing and vibration-damping devices.

1. Introduction

The control of low-frequency noise and vibration remains a significant challenge across various engineering fields. For example, transportation, building acoustics, and precision manufacturing [1,2,3,4]. Traditional porous materials and microperforated panels [5,6,7] are often ineffective at these frequencies. The reason is the inherent mass-density law, which causes impractical thicknesses and weights for substantial performance. Nowadays, the emergence of artificial metamaterials has opened new avenues for tackling this problem. They can control sound or mechanical waves beyond the capabilities of natural materials. Among these, acoustic metamaterials [8,9,10] and phononic crystals [11,12,13] have demonstrated exceptional potential for generating bandgaps, where wave propagation is prohibited.

Acoustic metamaterials offer valuable applications across many fields. They can reduce low-frequency noise in many systems, such as the automotive and aircraft industries. In addition, they can improve sound insulation in architecture. For industrial equipment, these materials provide effective vibration reduction that enhances operational precision. In addition, their unique wave control capabilities enable approaches to structural health monitoring and damage detection. These applications show the broader impact and technological relevance of acoustic metamaterial research.

Phononic crystals achieve bandgaps through Bragg scattering or local resonance mechanisms. While Bragg-type [14,15] are scale-dependent and mainly occur at wavelengths, locally resonant [16,17] can attenuate waves at frequencies much lower than this limit. This advantage makes them more useful for low-frequency applications. Since the work by Liu [18] on local resonance, studies have been conducted to find the bandgap characteristics of PCs through design and material parameters. On the other hand, acoustic metamaterials often rely on subwavelength resonators like Helmholtz resonators. Their mass-spring systems exhibit negative effective properties, which lead to strong wave attenuation [19,20]. These structures can achieve remarkable sound absorption or insulation within small dimensions [21,22,23].

Despite these advances, a limitation of many acoustic metamaterials is their narrow bandwidth, which is linked to the high-quality factor of the local resonators. This restricts their practical application in broadband attenuation. Furthermore, the simultaneous reduction in vibration and noise is seldom addressed by a single design. Recent methods to broaden the effective bandwidth have included the use of multiple systems, complex structures [24,25,26], and designs with graded parameters [27,28,29]. The concept of “gradient” or “asymmetric” metamaterials has shown particular promise for creating broadband or multi-band gaps by adjacent absorption frequency [30,31,32,33,34].

Inspired by these developments, this study introduces and investigates a gradient-symmetric metamaterial structure. The metamaterial shows broadband sound absorption and vibration reduction. Unlike previous designs focusing on specific combinations, our proposed materials employ a systematic gradient to achieve wideband performance. We conclude that this graded symmetry can effectively adjust stopbands in both the elastic and acoustic domains, causing continuous and wide attenuation zones, respectively.

Although this study employs a conventional design method, artificial intelligence (AI) is now fundamentally reshaping the design for acoustic metamaterials. The study offers promising directions for future research. Its core advantage lies in transcending the limitations of traditional numerical simulations. Moreover, it can enable automated performance optimization. Specifically, future research in our work could focus on the following directions: Inverse design and performance breakthroughs, multi-objective and multi-physics co-optimization, and deep integration with smart materials:

In this paper, Section 2 describes the design of the gradient-symmetric metamaterials and establishes simulation models for their vibration and acoustic behavior. Section 3 presents numerical simulations and corresponding experiments to validate the structure’s performance. The results show the transmission loss for acoustic waves and the vibration transmissibility for elastic waves. This metamaterial demonstrates a significant broadband attenuation effect. Finally, Section 4 summarizes the principal findings and discusses the potential applications. Future research directions for this class of gradient-symmetric metamaterials. The main contributions of this article are as follows:

• A four-layer metamaterial is designed, and the structure is gradient-symmetric. We derived the analytical formulas for its underlying physical mechanisms by using the name Helmholtz resonance and the spring-mass equivalent model.
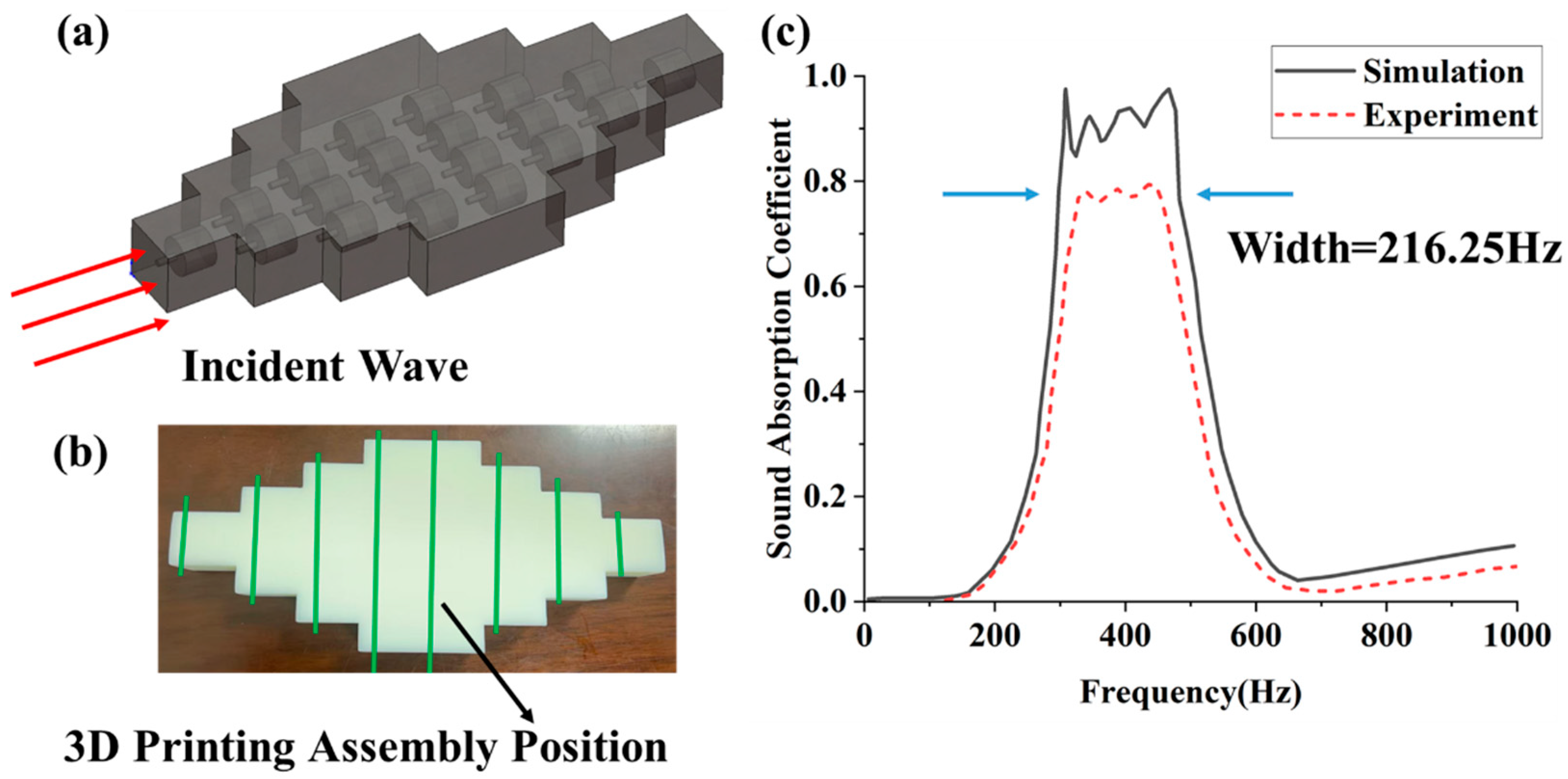
• The sound absorption characteristics were verified both numerically and experimentally. The findings demonstrate an absorption bandwidth of 216.25 Hz for coefficients greater than 0.8. The results represent an almost 20-fold increase compared to a single unit cell. Additionally, the average absorption coefficient was around 0.9 within this broad band.
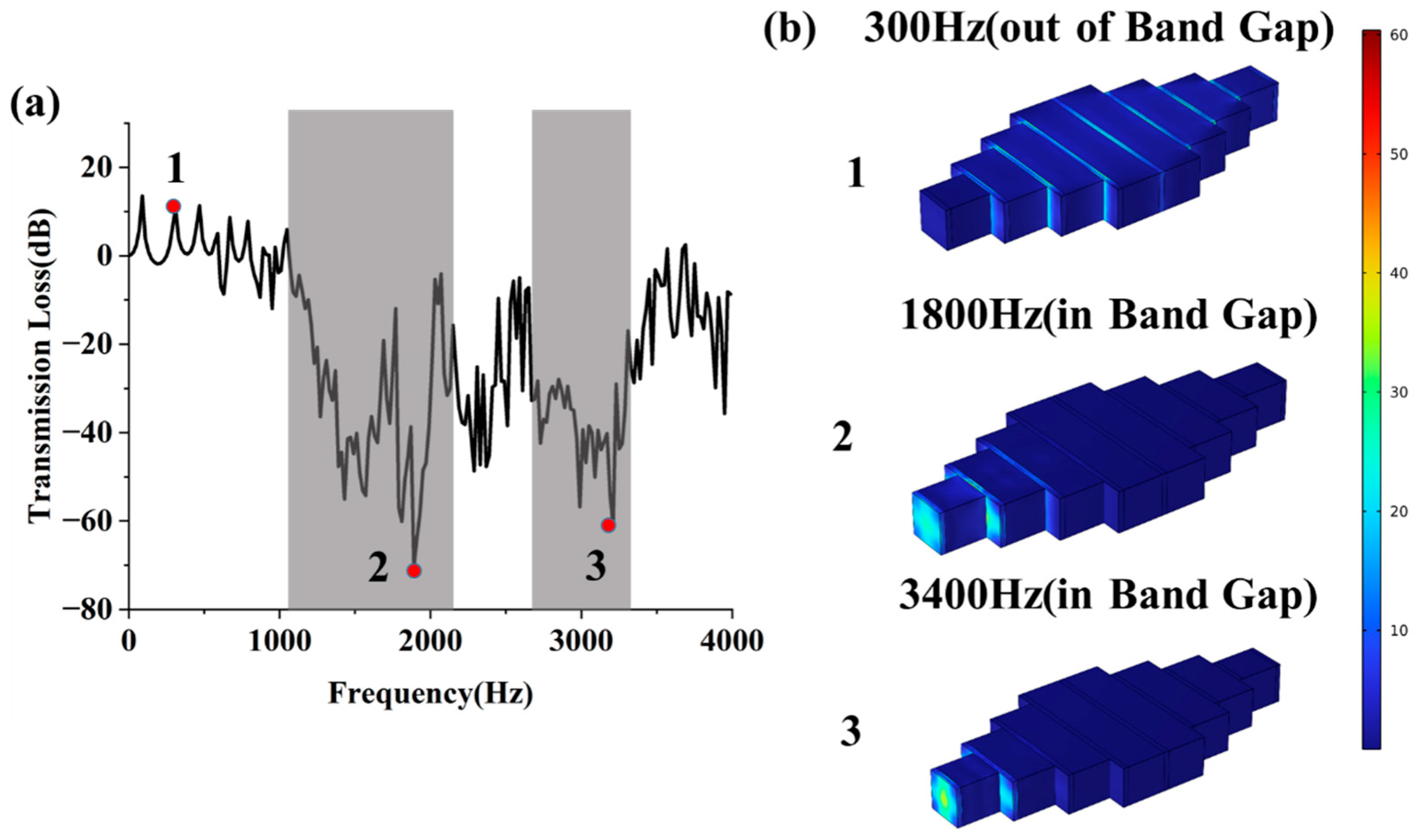
• Numerical simulations confirmed its vibration reduction capabilities in the solid mechanics domain. The results reveal two distinct effective bandgaps with an average transmission loss below −20 dB, located approximately within 1100–2200 Hz and 2700–3400 Hz. As the lattice constant increases, both bandgaps shift toward lower frequencies, while their bandwidths remain largely unchanged.

2. Theory and Model

To simultaneously verify the suppression capabilities of the metamaterial, it is necessary to model and analyze the structure separately in the pressure acoustics and solid mechanics physics fields. The model in our paper is shown in Figure 1; the lattice constant, thickness, internal dimensions of Helmholtz resonators, and overall configuration are all labeled in the figures. As validated in this work, the gradient array configuration effectively broadens the sound absorption bandwidth in acoustic fields. Moreover, the graded arrangement mitigates manufacturing challenges in 3D printing, such as sealing requirements. The specific rationale is based on the following two perspectives:

• Acoustics Domain: This domain consists of a gradient array of Helmholtz resonators. The specific frequencies for sound attenuation can be theoretically derived using Euler’s fluid equations.
• Solid Mechanics Domain: This domain is equivalent to a spring-mass system. The corresponding natural frequency range can then be calculated numerically using the finite element method.

2.1. Acoustic Model Analysis

We consider a typical Helmholtz resonator system [35]. As is well known, a Helmholtz resonator consists of a cavity and a neck. The gas in the neck can be assumed to be stationary; the Euler fluid equation is

$$\rho {\displaystyle \frac{\mathsf{\partial }v}{\mathsf{\partial }t}}+\nabla p=0$$

(1)

By performing a line integration of Equation (1) over the entire neck domain, the following is obtained:

$${\displaystyle {\int }_{L_0}^0\left(\rho \frac{\mathsf{\partial }v}{\mathsf{\partial }t}+\nabla p\right)dx}=0$$

(2)

Within the entire Helmholtz resonator, according to the plane wave approximation theory, the following conditions must be satisfied: $\lambda \gg L_0,\lambda \gg \sqrt{S_0}, v=v{e}^{jwt}$. Thus, Equation (2) can be shown as the following expression:

$$-j\omega \rho L_{0}v+p_0-p_{L_0}$$

(3)

It readily follows that:

$$X={\displaystyle \frac{P}{v{S}_0}}=j\omega {\displaystyle \frac{P{L}_0}{S_0}}\Rightarrow Ma={\displaystyle \frac{\rho L_0}{S_0}}$$

(4)

In the air cavity, since the gas is fluid, the mass equation and the equation of state can be combined, yielding the following expression [36]:

$${\displaystyle \frac{\mathsf{\partial }p}{\mathsf{\partial }t}}+\rho c^2\nabla ·v=0$$

(5)

Integrating Equation (5) over the volume domain gives

$${\displaystyle \int \left(\frac{\mathsf{\partial }p}{\mathsf{\partial }t}+\rho c^2\nabla ·v\right)}dV=0$$

(6)

Performing a surface integral and linearization on Equation (6) yields

$$-j\omega p{V}_0+p{c}^{2}v{S}_0=0$$

(7)

Consequently, the acoustic impedance in the metamaterials can be further derived as:

$$X={\displaystyle \frac{P}{v{S}_0}}={\displaystyle \frac{p{c}^2}{j\omega V_0}}\Rightarrow C_a={\displaystyle \frac{V_0}{\rho c^2}}$$

(8)

Combining the effects of the slender neck and the cavity volume, the final impedance is:

$$X=j\omega {\displaystyle \frac{\rho L_0}{S_0}}+{\displaystyle \frac{p{c}^2}{j\omega V_0}}$$

(9)

We set $X=0$; the reduction frequency can be obtained:

$$\omega =c\sqrt{{\displaystyle \frac{S_0}{V_0{L}_0}}} f={\displaystyle \frac{\omega }{2\pi }}$$

(10)

where c is the speed of sound. $S_0,L_0,V_0$ are the area and length of the neck and the volume of the cavity, respectively.

2.2. Solid Mechanics Model Analysis

The solid domain is composed of resin components with different elastic moduli, interconnected by rubber. Given that the elastic modulus of the resin is significantly higher than that of the rubber, it can be assumed that the rubber is compressible while the resin is effectively incompressible. This allows for an equivalent analysis of the solid domain, where the resin components are represented as mass blocks, and the rubber layers are modeled as equivalent springs. The natural frequency is calculated using the finite element method. During the simulation, the coupling between the solid mechanics and acoustic domains is neglected, meaning the acoustic modes and vibration modes are computed independently. Based on this approach, the equation of motion for a unit cell is shown as follows:

$$\left(K-{\omega }^{2}M\right)U=0$$

(11)

where K and M are stiffness and mass matrices, respectively.

$U={\left[\begin{array}{cccc}{U}_1& U_2& \cdots & U_n\end{array}\right]}^{\mathrm{T}}$ is the displacement matrix, which comprises the displacements at the nodal points of its constituent elements $U_i={\left[\begin{array}{ccc}{u}_i& v_i& w_i\end{array}\right]}^{\mathrm{T}}$. In accordance with Bloch’s theorem, the displacement vector U can be expressed in the form:

$$u\left(r\right)=u_k\left(r\right)e^{\left(ik·r\right)}$$

(12)

Here, $k=\left(k_x,k_y\right)$ is the wave vector. $u_k\left(r\right)$ correspond to the periodic function, respectively. Applying Bloch’s theorem leads to the following periodic boundary condition:

$$U\left(r+a\right)=U\left(r\right)e^{\left(ik·a\right)}$$

(13)

where $a$ is the lattice constant of the unit cell.

For the evaluation of vibration transmission in the solid domain, a uniform acceleration with a magnitude of ‘1’ is applied to the left boundary, aligned with the direction of the structure’s periodicity. Similarly, to assess acoustic performance, a plane wave radiation condition is imposed to calculate the transmission loss in the acoustic domain. The numerical results are obtained by the software COMSOL Multiphysics 6.2, and the results are compared with the band structure.

The transmission characteristic is quantified by the following equation:

$$H=10\log \left({\displaystyle \frac{{\displaystyle {\int }_{s_1}\left|p_1\right|d{S}_1}}{{\displaystyle {\int }_{s_1}\left|p_2\right|d{S}_2}}}\right)$$

(14)

In this equation, $p_1$ and $p_2$ refer to the transmitted and incident physical quantities, respectively. Specifically, the parameters $S_1$ and $S_2$ are the areas of the outside and inside boundaries. All the variables mentioned in the paper and their physical meanings are listed in

Table 1. Variables mentioned in the paper and their physical meanings.

$\rho$	Air Density	v	Acoustic Velocity	p	Sound Pressure	t	Time
λ	Wavelength	ω	Resonant frequency	c	Sound speed in air	M	Mass matrices
S0	Area of slender neck	L0	Length of slender neck	V0	Volume of the cavity	K	Stiffness matrices
U	Displacement matrix	k	Wave vector	r	Position vector	uk(r)	Periodic function
a	Lattice constant	H	Cavity depth	R	Cavity radius	r	Neck radius
L	Neck length	α	Sound absorption coefficient	Z	Acoustic impedance

.

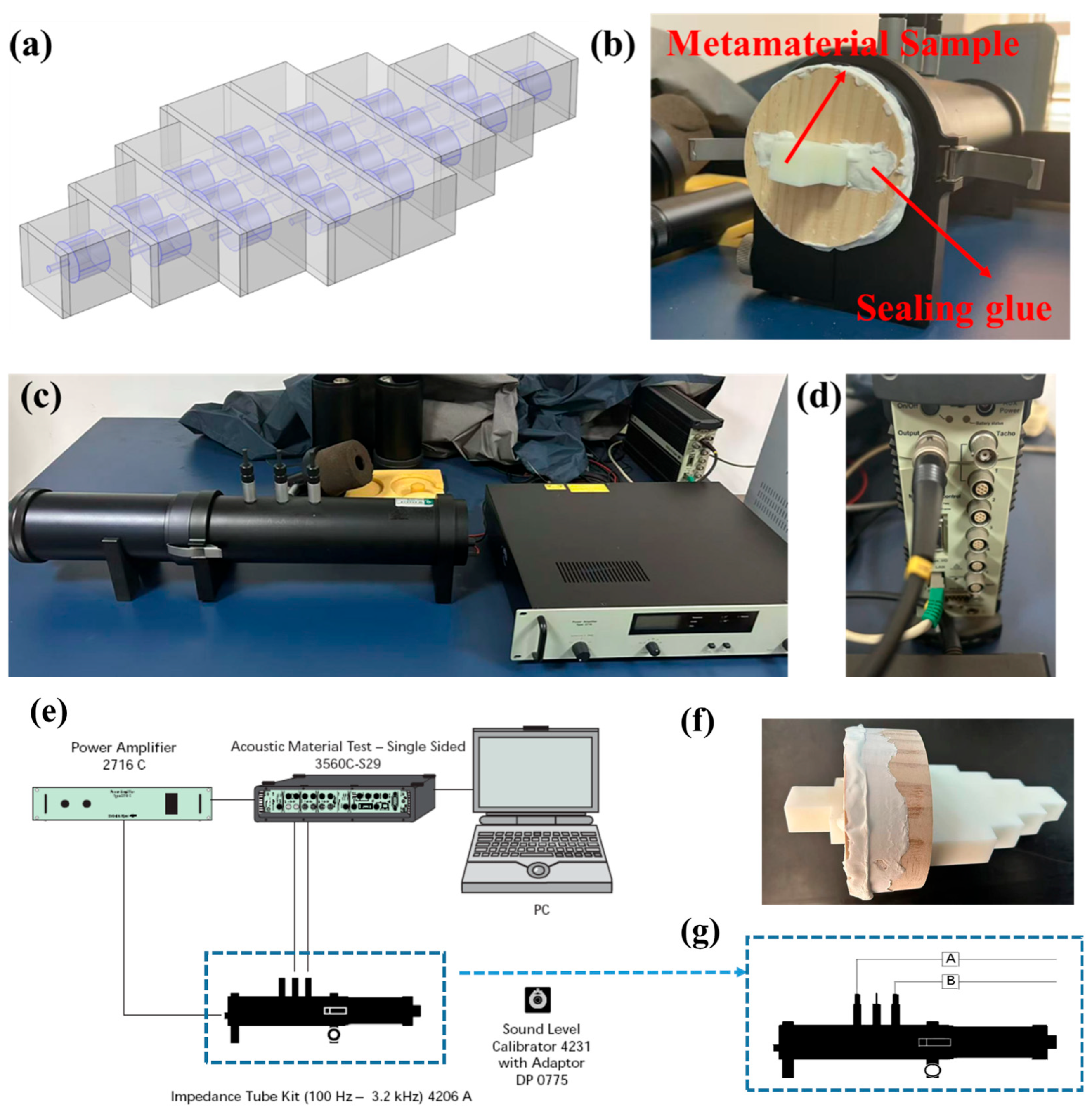
3. Simulation and Experiment Results

We first studied the sound absorption performance. The sample was fabricated via 3D printing using Somos GP Plus resin. Its mechanical properties are as follows: tensile modulus of 2649–2711 MPa, tensile strength of 41–60 MPa, and flexural strength of 69–79 MPa. The elongation at break ranges from 8% to 13%, and the notched impact strength is 36–50 J/m. These strength parameters meet the requirements for processing and experimental applications. The geometric parameters of the unit cell are as follows: lattice constant a = 20 mm, neck length L = 6 mm, neck radius r = 1 cm, cavity depth H = 10 mm, cavity radius R = 6 mm, and rubber thickness h = a/8 = 2.5 mm. The physical parameters of the material properties are listed in

Table 2. The parameters of the acoustic metamaterials.

Component	Density (kg/m3)	Young’s Modulus (GPa)	Poisson’s Ratio
Somos GP Plus Resin	1150	2.35	0.38
Rubber	1300	5.54 × 10−3	0.5

. A schematic of the simulation model and the experimental setup is shown in Figure 2.

For the corresponding experiments, an SW422 impedance tube was employed. The manufacturer is Brüel & Kjær (B & K) from Denmark, model 4206A, with a frequency range of 100 Hz to 3200 Hz. Regarding sensitivity, multiple measurements confirm sufficient accuracy within the 50–100 Hz range; however, significant measurement error occurs below 50 Hz. Therefore, this study only analyzes experimental results from 100 Hz to 1600 Hz. A VA-LAB4 system was used for data acquisition and excitation control. The models of each component are as follows: Sensor: 4187, Data Acquisition Card: 3590c-s29, Power Amplifier: 2716C. Sealant was applied to ensure air tightness, thereby effectively simulating the intended sound absorption environment. The sound absorption coefficient was derived using the following equation:

$$\alpha =1-\left|{\displaystyle \frac{Z_{\mathrm{HR}}-\rho \mathrm{c}}{Z_{\mathrm{HR}}+\rho \mathrm{c}}}\right|$$

(15)

The experimental procedure was conducted as follows: First, the impedance tube sensors were connected to the data acquisition system using the configuration shown in Figure 2. Second, channel calibration was performed within the same PULSE project by selecting microphones with identical serial numbers and conducting routine amplitude gain calibration with a Type 4231 calibrator. Third, signal-to-noise ratio measurements were carried out by sequentially performing background noise measurements and signal measurements, allowing the system to automatically calculate the SNR. Proceeding to the next step required the absence of warnings. Fourth, transfer function correction was implemented through swapped and normal microphone position measurements. Absence of warnings permitted continuation (for frequency analyses up to 6.4 kHz, while amplitude errors generally remained within tolerance, phase errors could exceed limits, requiring return to Step 1 settings to adjust phase error tolerance). During measurements, Autorange was typically selected for automatic ranging. Fifth, sample measurements were conducted by adding measurement repetitions and sample names in the Add New Measurement section, clicking Add to confirm, then initiating measurements via Start in the Measurement Control section. Finally, post-processing and report storage involved entering the desired averaged name in the Average section, selecting specific measurements, and executing averaging. The Combine section enabled merging of large and small tube measurement data through the Combine function. The Extract section allowed synthesis of 1/n-octave band results from FFT frequency response measurements according to tube type. Ultimately, functional selections were checked in the Result section for graphical display.

The SW (SolidWorks software 2023) model of the single Helmholtz resonator (one-layer) structure is shown in Figure 3a, where the direction of sound wave propagation is indicated by the red arrow. Since simulating the hard sound field boundary is sufficient for calculating the sound absorption coefficient. It is not necessary to consider the solid mechanics domain; the rubber section was also replaced with resin, which does not affect the results. Since 3D printing cannot produce sealed cavities, we customized the test prototype by printing it in sections and assembling them. The assembly positions and the sample are shown in Figure 3b, Figure 4b, Figure 5b, and Figure 6b. The green lines indicate the assembly positions.

Figure 3c presents the simulated and experimentally measured sound absorption coefficients of the one-layer sample. It can be observed that an absorption peak appears near 400 Hz, which is determined by the geometric dimensions of the Helmholtz resonator, with the resonant frequency given by Equation (10). However, the effective bandwidth of this absorption peak is very narrow. Considering a sound absorption coefficient above 0.7, the bandwidth is only 10.3 Hz. This poses a significant limitation in practical applications, as minor changes in the external environment or structural parameters can substantially compromise the metamaterial’s absorption performance.

To address this drawback, it is necessary to broaden the absorption bandwidth without altering the peak absorption frequency. Therefore, instead of modifying the dimensions of the Helmholtz resonator, we increased the number of resonators within a unit cell, aiming to achieve this goal through the coupling effects between adjacent Helmholtz resonators.

The double-layer Helmholtz resonator structure is shown in Figure 4a,b. Without altering the direction of sound wave propagation or the manufacturing method, the simulation and experimental results are presented in Figure 4c. It can be observed that, compared to the single-layer Helmholtz resonator, an additional resonance peak appears at 380 Hz, and an absorption dip emerges between 380 Hz and 400 Hz. This phenomenon results from the coupled sound absorption effect between the two Helmholtz resonators. Although the overall absorption bandwidth is slightly wider than that of the single-layer structure, two drawbacks remain: first, the effective bandwidth with an absorption coefficient above 0.7 is still narrow and is primarily determined by the resonance peak near 400 Hz, second, the absorption dip between the two peaks does not broaden the overall absorption range but may instead compromise the effectiveness of the original sound-absorbing structure. Further structural adjustments are required to address these issues.

The three-layer Helmholtz resonator structure is depicted in Figure 5a,b, with corresponding simulation and experimental results presented in Figure 5c. As shown in the figure, the increased number of Helmholtz resonators generates three distinct resonant peaks, without producing significant absorption dips. The sound attenuation bandwidth is also noticeably widened. Overall, while the three-layer configuration addresses the issues observed in the two previous structures, its average sound absorption coefficient within the effective frequency range remains only about 0.6, with experimental results being even lower.

As shown in Figure 6a,b, we further increased the number of Helmholtz resonators. The simulation and experimental results are presented in Figure 6c. This configuration exhibits four resonant peaks. Considering the frequency band where the sound absorption coefficient exceeds 0.8, the absorption bandwidth reaches 216.25 Hz—nearly 20 times that of the single unit cell. Furthermore, the average absorption coefficient achieves approximately 0.9. This optimization successfully resolves the previous issues of poor absorption performance and narrow bandwidth. The experimental results align well with the simulations, though slightly lower, which can be attributed to minor sound energy leakage despite the use of sealant, as well as the inability of the wooden partition to perfectly simulate rigid acoustic boundary conditions.

Based on the results in Figure 6c, two frequencies were selected to further investigate the sound absorption performance of the metamaterial: one is in the sound attenuation range (400 Hz), and another is outside it (800 Hz). The sound pressure distribution calculated solely in the acoustic domain is shown in Figure 7a,b. It is clearly observed that at 400 Hz, the sound pressure is predominantly concentrated within the cavities of the first three layers, with almost no sound pressure in the subsequent Helmholtz resonators. This indicates excellent sound attenuation by the metamaterial at 400 Hz. In contrast, at 800 Hz, the sound pressure exhibits a modal distribution throughout the entire metamaterial, with significant pressure still present even in the last Helmholtz resonator. Under this condition, the acoustic metamaterial does not provide effective sound attenuation.

Subsequently, the vibration reduction performance of the metamaterial was analyzed. Simulations conducted for the one, two, and three-layer acoustic metamaterials did not reveal significant vibration reduction effects. However, for the four-layer acoustic metamaterial, two vibration bandgaps were identified—one approximately between 1100 and 2200 Hz and another between 2700 and 3400 Hz. The corresponding transmission loss plot is shown in Figure 8a, where the average transmission loss in these bands exceeds 20 dB. The stress contour plots in the solid domain at two frequencies within the bandgaps and one outside are presented in Figure 8b. For the frequency of 300 Hz, which lies outside the bandgap, stress is distributed across various locations of the metamaterial in a modal pattern. In contrast, at 1800 Hz and 3400 Hz (frequencies within the bandgaps), stress remains confined to the left end where excitation is applied and does not propagate through the structure.

To further investigate the influence of lattice constant on the bandgap positions of metamaterials for vibration reduction, we adjusted the lattice constant a while keeping all other physical parameters unchanged. The simulation results are illustrated in Figure 9a–d, which display the transmission loss plots for a values of a = 18 mm, 25 mm, 30 mm, and 35 mm, respectively. It is evident that the metamaterial maintains two distinct bandgaps with comparable bandwidths across all lattice constants. As the lattice constant increases, both bandgaps shift toward lower frequencies. Specifically, the central frequency of the first bandgap shifts from approximately 1700 Hz to 1100 Hz, while the second bandgap shifts from around 3400 Hz to 2500 Hz. These observations demonstrate the feasibility of passive control over the band structure of metamaterials.

We compared our results with those reported by Li [37] and our previous work [38]. The noise reduction frequency band described in the literature corresponds to the absorption mode of a single Helmholtz resonator, which exhibits a relatively narrow absorption bandwidth with an average width of less than 100 Hz. In contrast, our study employs a 4 × 4 array configuration of Helmholtz resonators, transforming the single resonance mode into multiple coupled modes. This approach achieves an absorption bandwidth of 216.25 Hz, demonstrating significantly improved applicability compared to the structures reported in the literature. Furthermore, this work systematically investigates the influence of lattice constant on vibration modes, providing potential pathways for passive control of acoustic metamaterial frequencies [39,40].

4. Conclusions

In this work, we developed a gradient-symmetric metamaterial composed of resin, rubber, and Helmholtz resonators. The physical properties of this structure were systematically investigated through theoretical modeling, simulation analysis, and experimental validation. We have summarized the findings in the conclusion, as detailed in

Table 3. The acoustic performance of the metamaterial.

Acoustic Performance	Type 1 × 1	Type 2 × 2	Type 3 × 3	Type 4 × 4
Width of Absorption frequency (Hz)	10.3	20	50.35	216.25

and

Table 4. The mechanical performance of the metamaterial.

Mechanical Performance of Type 4 × 4	a = 18 mm	a = 25 mm	a = 30 mm	a = 35 mm
Center frequency of band 1 (Hz)	1700	1500	1300	1100
Center frequency of band 2 (Hz)	3400	3100	3000	2500

:

Based on the data from Table 3 and Table 4, it can be concluded that the 4 × 4 configuration of acoustic metamaterial exhibits superior sound absorption performance. Furthermore, larger lattice constants demonstrate enhanced low-frequency vibration-damping capabilities. Results demonstrate that the four-layer metamaterial exhibits excellent sound absorption and vibration reduction capabilities simultaneously in both acoustic and solid mechanics domains. The main conclusions are summarized as follows:

1.

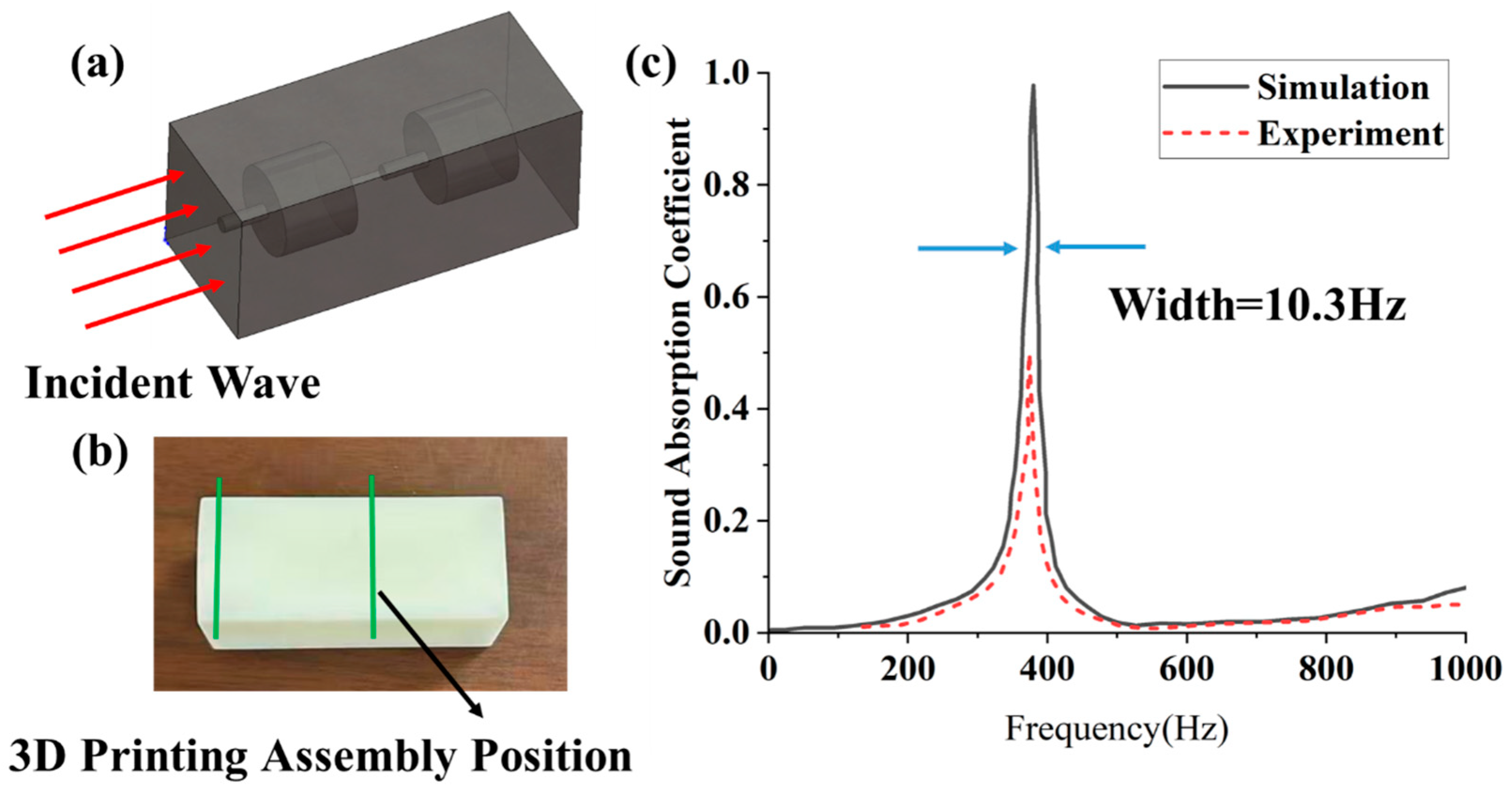
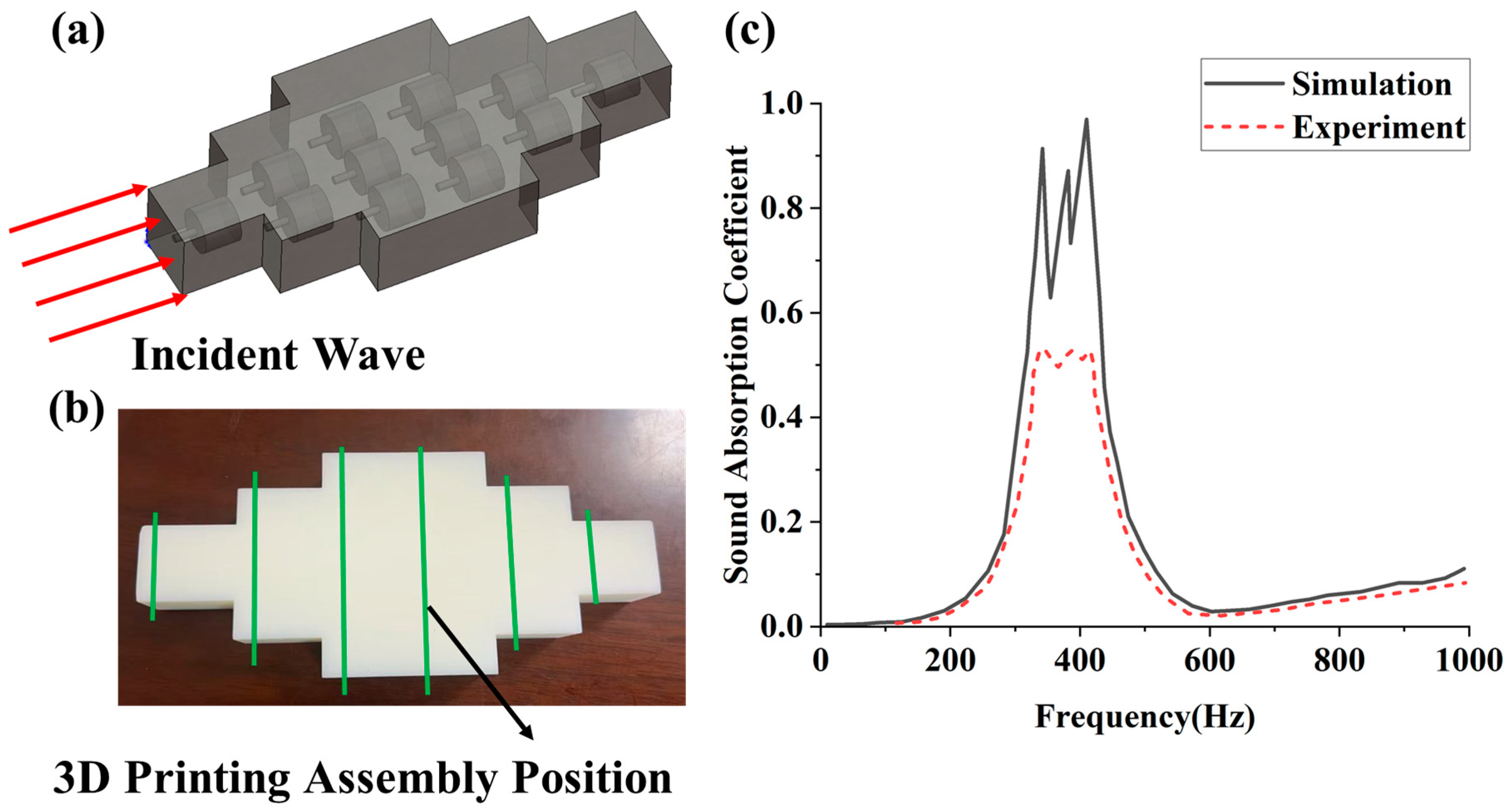
By designing the geometric parameters of a single-layer Helmholtz resonator, near-perfect sound absorption (approaching unity) can be achieved around 400 Hz. However, this configuration suffers from an extremely narrow absorption bandwidth. Increasing the number of Helmholtz resonator layers effectively broadens the absorption frequency range, though it may introduce absorption dips that partially reduce the absorption coefficient.

2.

Through structural optimization, a highly symmetric four-layer Helmholtz resonator configuration was designed. Both experimental and simulation results confirm that for absorption coefficients above 0.8, the achieved bandwidth reaches 216.25 Hz—approximately 20 times wider than that of the single-unit structure. Furthermore, the average absorption coefficient within this broad band reaches approximately 0.9.

3.

The four-layer Helmholtz resonator metamaterial also demonstrates excellent vibration suppression performance within two frequency ranges: approximately 1100–2200 Hz and 2700–3400 Hz, with an average transmission loss exceeding −20 dB.

4.

The influence of lattice constant a on vibration bandgaps was investigated. Results show that as the lattice constant increases, both the first and second bandgaps shift toward lower frequencies, while their bandwidths remain largely unchanged.

The metamaterial presented in this study exhibits superior noise attenuation and vibration reduction characteristics in both acoustic and structural domains. The comprehensive methodology—integrating theoretical analysis, numerical simulation, and experimental validation—provides valuable insights and establishes an effective framework for designing novel acoustic and mechanical metamaterials.