Explainable Machine Learning for Bubble Leakage Detection at Tube Array Surfaces in Pool
Abstract
1. Introduction
2. Materials and Methods
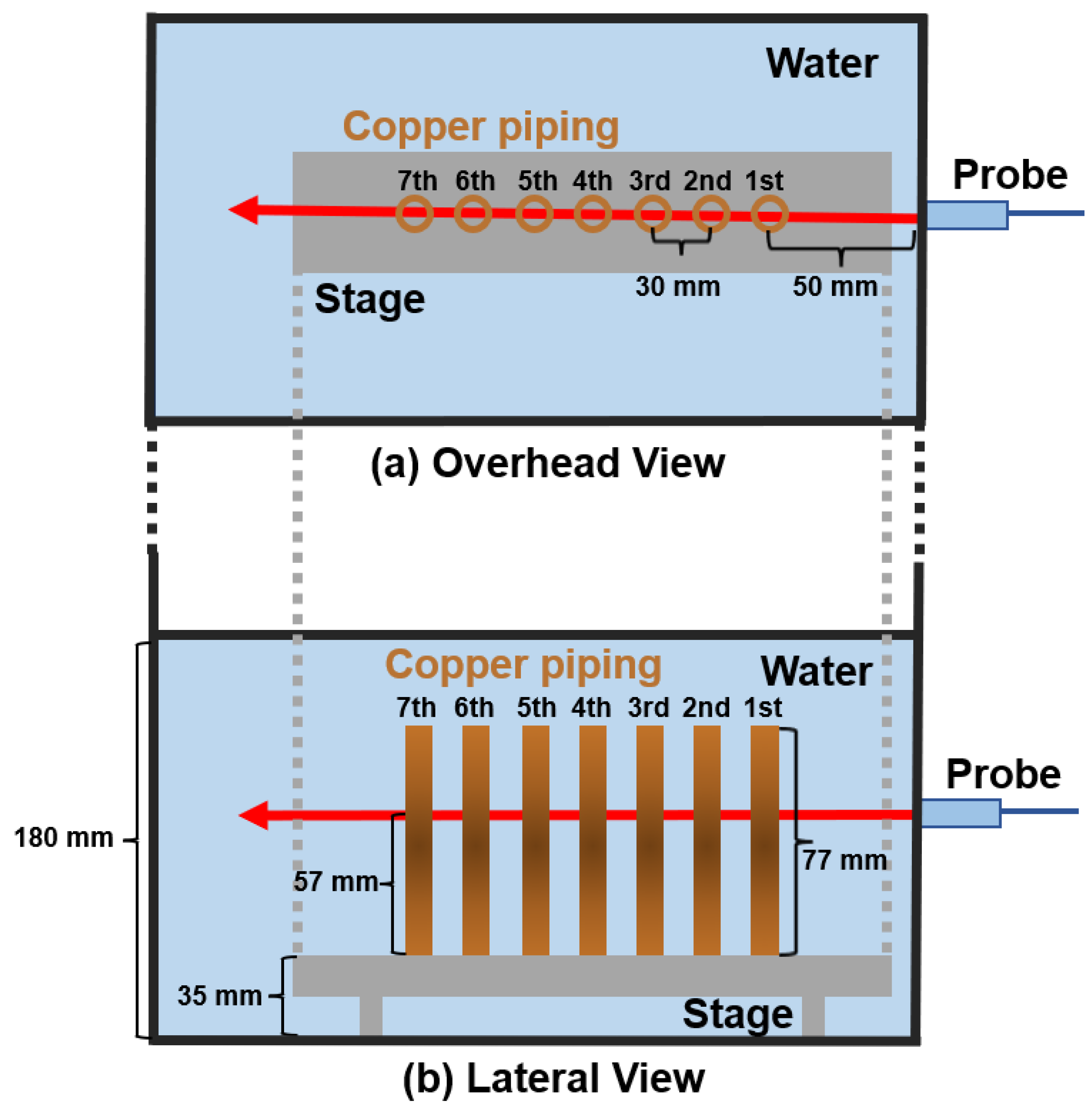
2.1. Ultrasonic Testing
2.2. Machine Learning
2.2.1. Transfer Learning for Convolutional Neural Network
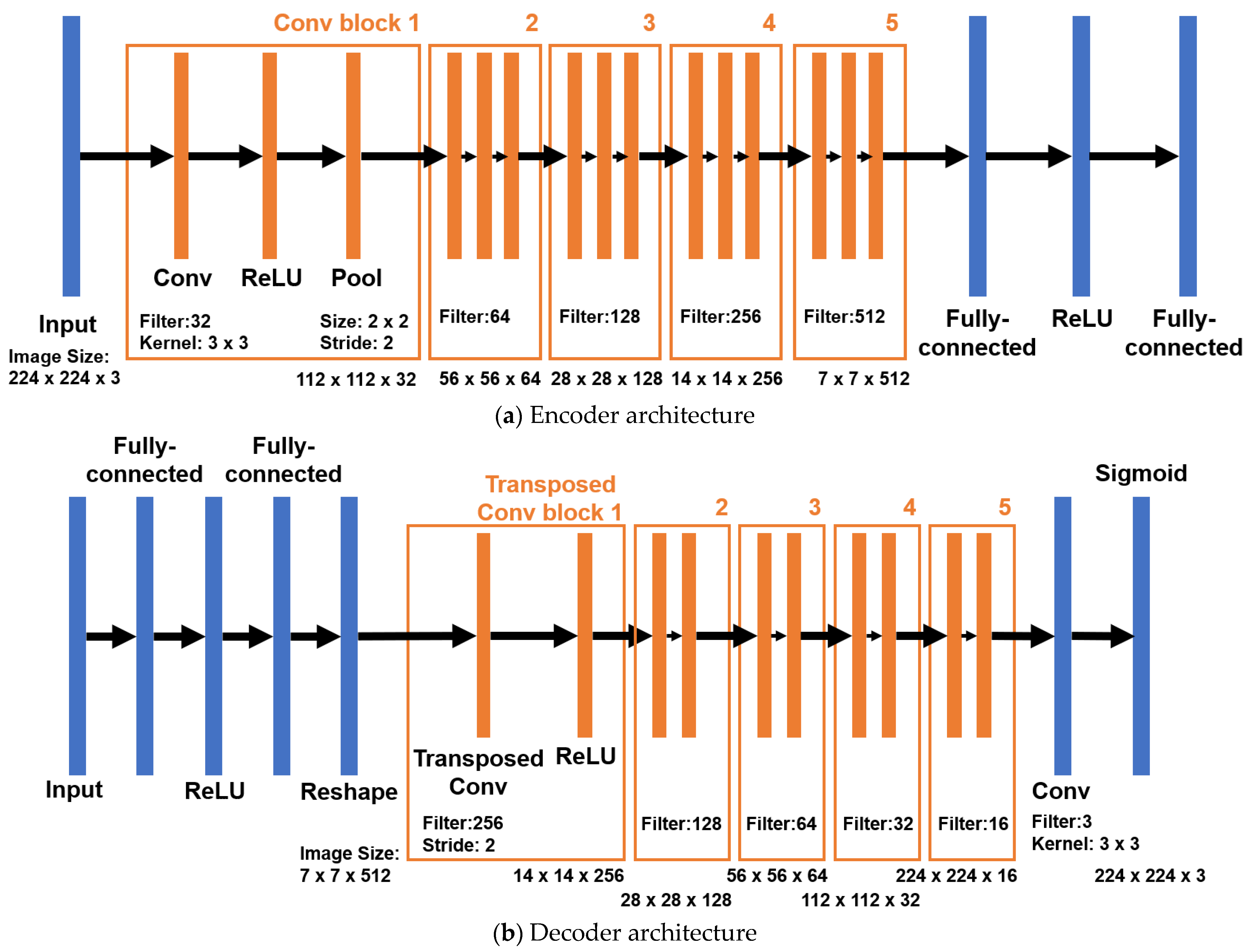
2.2.2. Autoencoder
3. Results and Discussion
3.1. Phased-Array Ultrasonic Testing Image Results
3.2. Bubble Detection Using a CNN with EfficientNet-b0
3.2.1. CNN Training Results
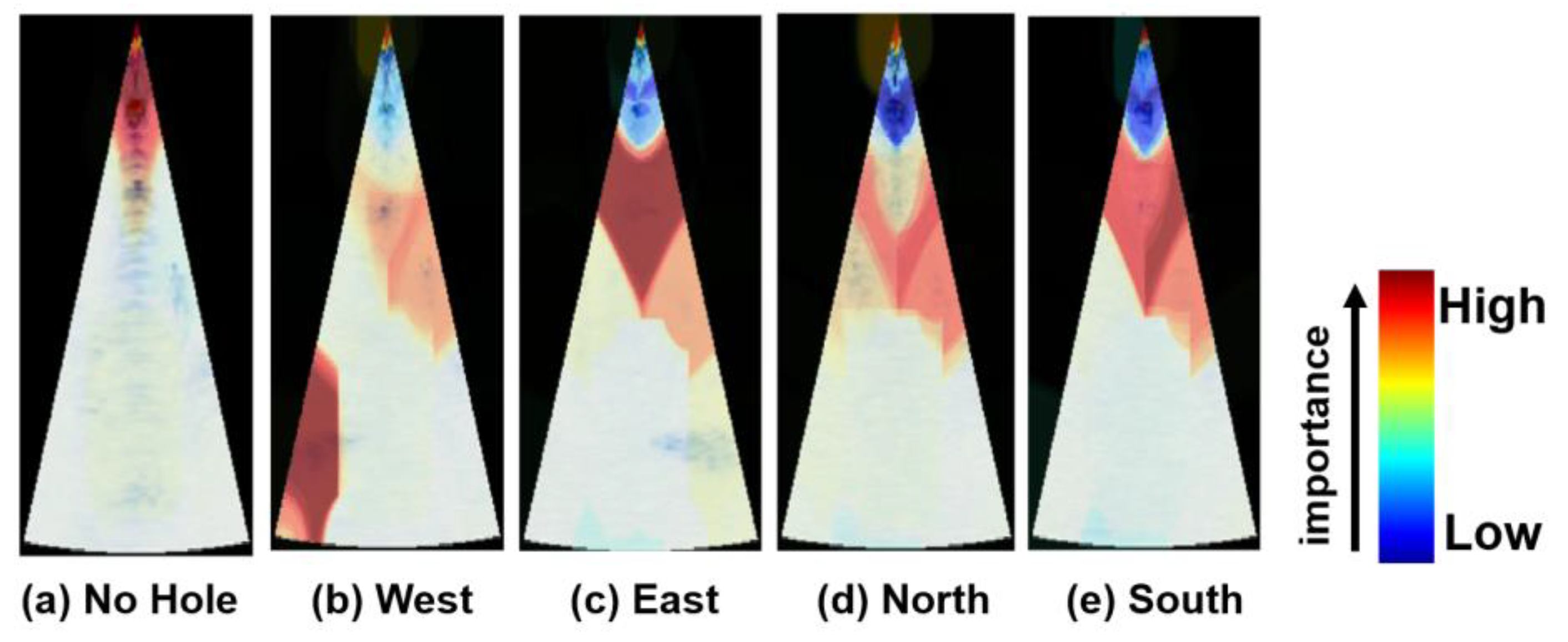
3.2.2. CNN Model Explainability
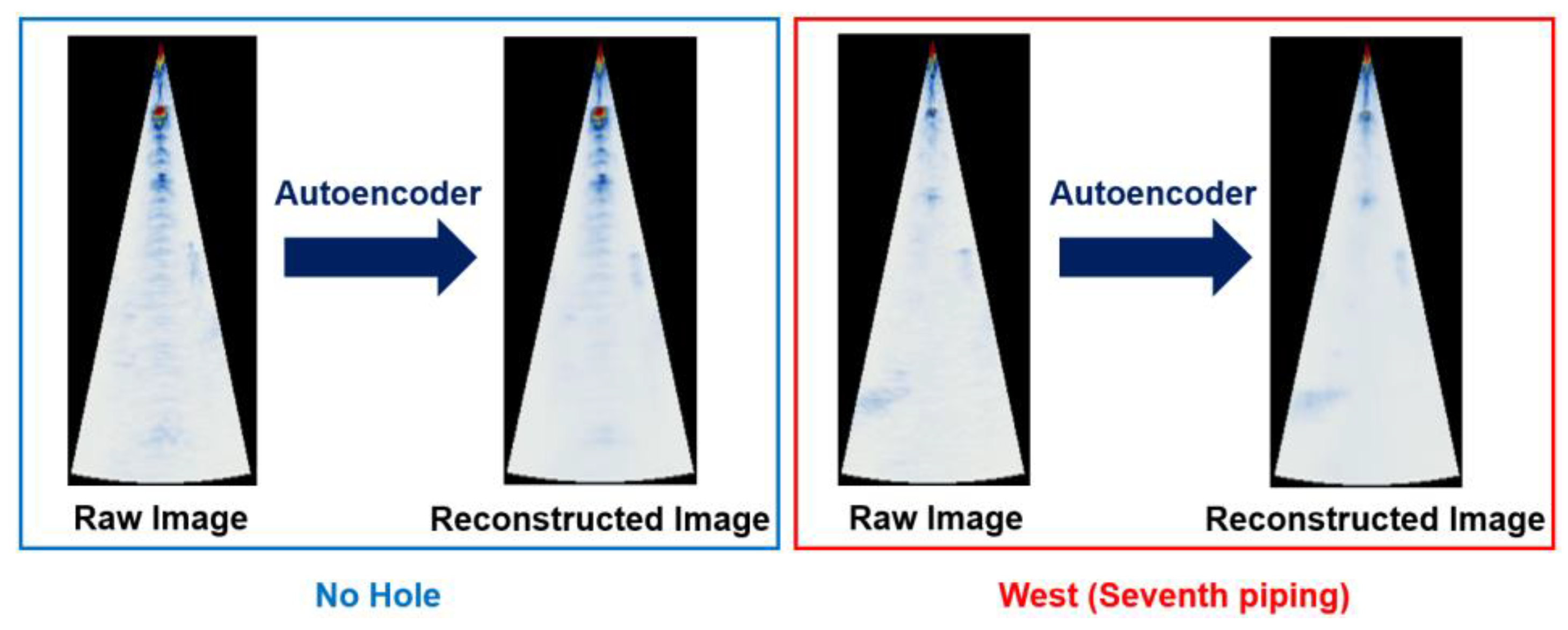
3.3. Bubble Detection Using Autoencoder
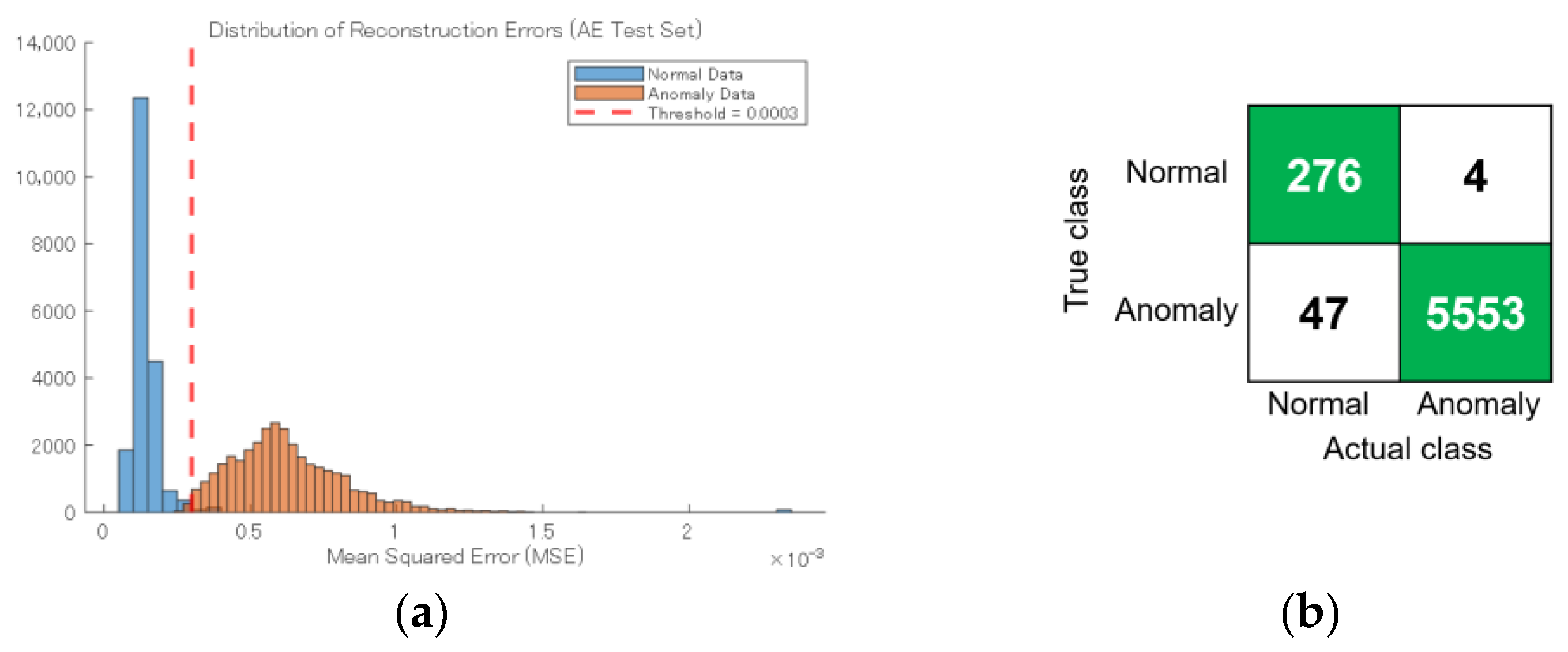
3.3.1. Detection of Unseen Anomalies
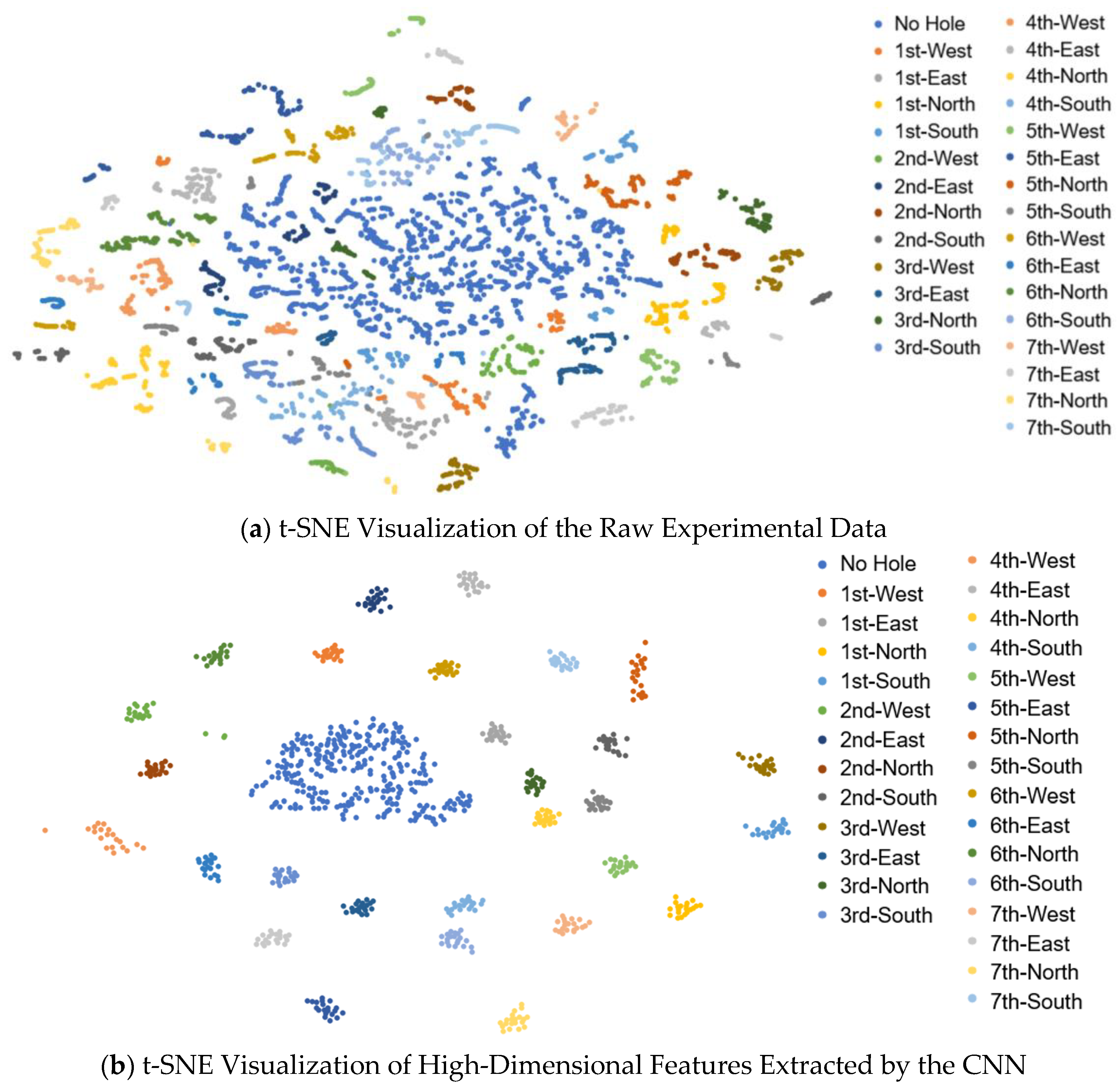
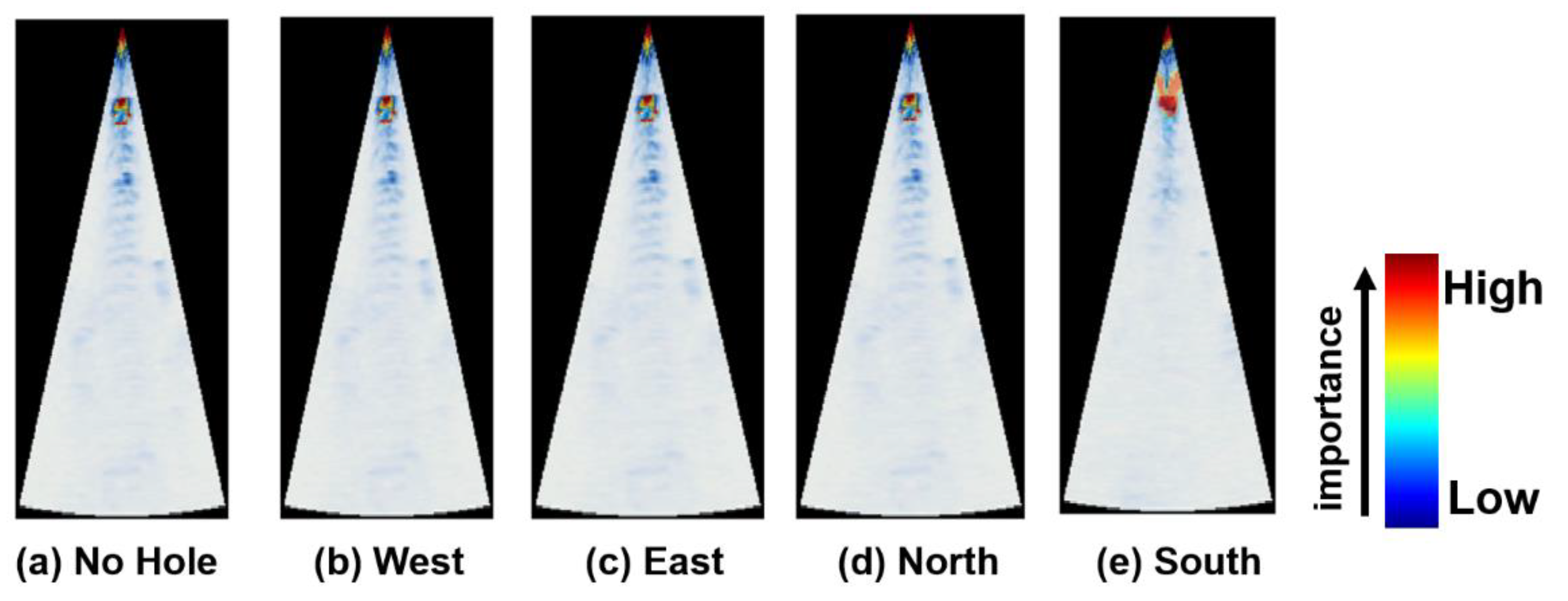
3.3.2. Autoencoder Explainability and Feature Extraction
3.3.3. Identifying Anomaly Location and Direction Using an Autoencoder and K-Means
3.4. Anomaly Detection and Multi-Class Classification by Autoencoder-Based Feature Extraction
3.4.1. Autoencoder Limitations in Rationale and Classification and Proposed Method
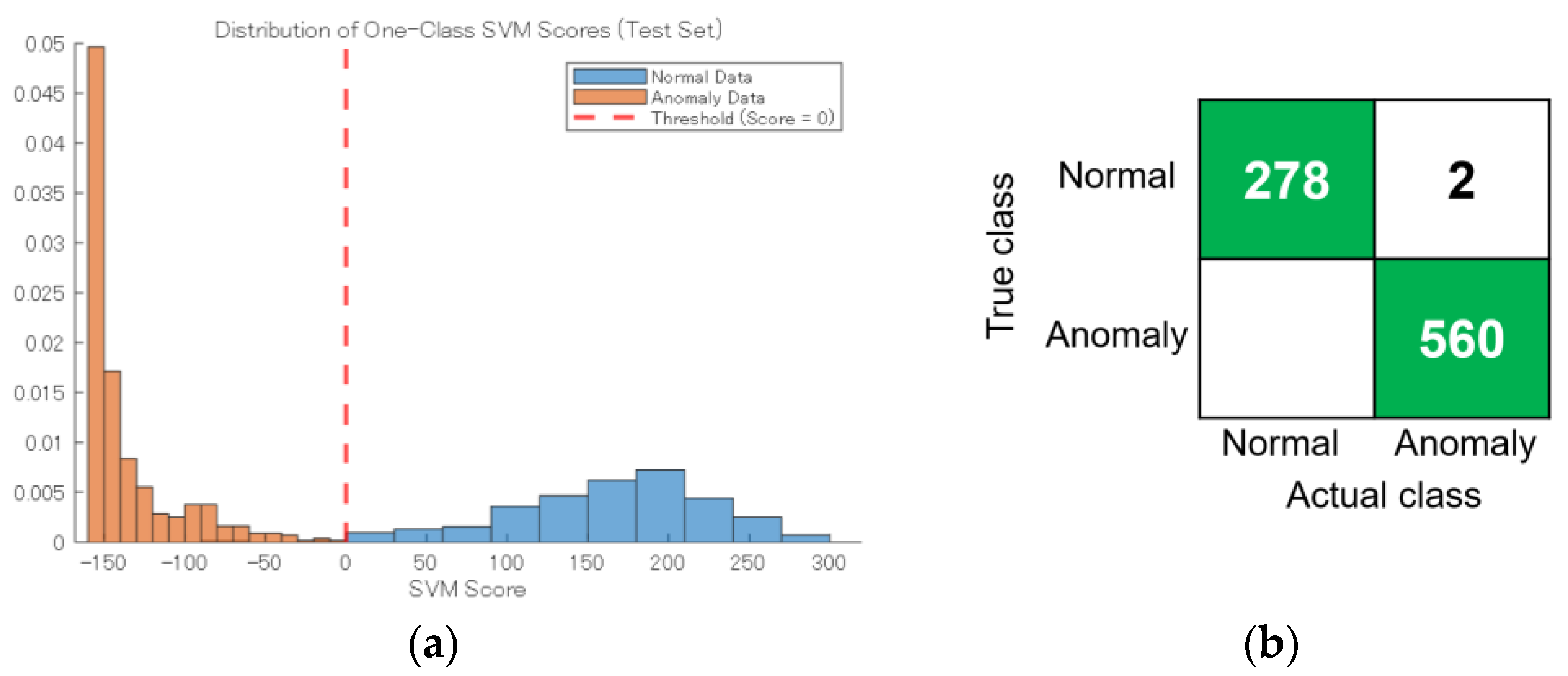
3.4.2. Identifying Anomaly Location and Direction by Autoencoder and One Class SVM
3.4.3. K-Means Multi-Class Classification by Autoencoder-Based Feature Extraction
3.4.4. Comparison with the Autoencoder Using Per-Class Feature Visualization
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclatures
| AUC | Area Under the Curve |
| CHF | Critical Heat Flux |
| CNN | Convolutional Neural Network |
| FC | Fully Connected (layer) |
| Grad-CAM | Gradient-weighted Class Activation Mapping |
| HMM | Hidden Markov Model |
| LIME | Local Interpretable Model-agnostic Explanations |
| LNG | Liquefied Natural Gas |
| ML | Machine Learning |
| ORV | Overpressure Relief Valve |
| PWR | Pressurized Water Reactor |
| RMSE | Root Mean Square Error |
| RPT | Reactor Pressure Test |
| SLIC | Simple Linear Iterative Clustering |
| SNR | Signal-to-Noise Ratio |
| SVM | Support Vector Machine |
| t-SNE | t-distributed Stochastic Neighbor Embedding |
| UT | Ultrasonic Testing |
| Roman symbols | |
| Value at position of the k-th feature map | |
| Set of all data points in cluster | |
| Prediction of the original model for instance z | |
| Prediction of the simple model for instance z | |
| h | A data point |
| K | Total number of clusters |
| Fidelity loss | |
| Grad-CAM heatmap for class c | |
| Cluster index | |
| Conditional probability of point j given point i in high-dimensional space | |
| Joint probability between points i and j in low-dimensional space | |
| t | Temperature |
| x | Data points in high-dimensional space |
| y | Data points in low-dimensional space |
| Score for class c | |
| Z | Acoustic impedance |
| Greek symbols | |
| Weight of the k-th feature map for class c | |
| Centroid of cluster | |
| Proximity measures relative to instance x | |
| ρ | Density |
| Variance of the Gaussian kernel centered on point i | |
| υ | Sound velocity |
References
- Mikami, N.; Ueki, Y.; Shibahara, M.; Aizawa, K.; Ara, K. State Sensing of Bubble Jet Flow Based on Acoustic Recognition and Deep Learning. Int. J. Multiph. Flow 2023, 159, 104340. [Google Scholar] [CrossRef]
- Korolev, I.; Aliev, T.; Orlova, T.; Ulasevich, S.A.; Nosonovsky, M.; Skorb, E.V. When Bubbles Are Not Spherical: Artificial Intelligence Analysis of Ultrasonic Cavitation Bubbles in Solutions of Varying Concentrations. J. Phys. Chem. B 2022, 126, 3161–3169. [Google Scholar] [CrossRef]
- Sun, S.; Xu, F.; Cai, L.; Salvato, D.; Dilemma, F.; Capriotti, L.; Xian, M.; Yao, T. An Efficient Instance Segmentation Approach for Studying Fission Gas Bubbles in Irradiated Metallic Nuclear Fuel. Sci. Rep. 2023, 13, 22275. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Niu, X.; Guo, X.; Mu, G.; Pang, Y. Method for Acoustic Leak Detection of Fast Reactor Steam Generator Based on Wavelet Noise Elimination. In Proceedings of the 2006 International Conference on Machine Learning and Cybernetics, Dalian, China, 13–16 August 2006; pp. 957–961. [Google Scholar]
- Brunet, M.; Garnaud, P.; Ghaleb, D.; Kong, N. Water Leak Detection in Steam Generator of Super Phenix. Prog. Nucl. Energy 1988, 21, 537–544. [Google Scholar] [CrossRef]
- Riber Marklund, A.; Michel, F.; Anglart, H. Demonstration of an Improved Passive Acoustic Fault Detection Method on Recordings from the Phénix Steam Generator Operating at Full Power. Ann. Nucl. Energy 2017, 101, 1–14. [Google Scholar] [CrossRef]
- Yoshitaka, C. Acoustic Leak Detection System for Sodium-Cooled Reactor Steam Generators Using Delay-and-Sum Beamformer. J. Nucl. Sci. Technol. 2010, 47, 103–110. [Google Scholar] [CrossRef]
- Yamamoto, T.; Kato, A.; Hayakawa, M.; Shimoyama, K.; Ara, K.; Hatakeyama, N.; Yamauchi, K.; Eda, Y.; Yui, M. Fundamental Evaluation of Hydrogen Behavior in Sodium for Sodium-Water Reaction Detection of Sodium-Cooled Fast Reactor. Nucl. Eng. Technol. 2024, 56, 893–899. [Google Scholar] [CrossRef]
- Mathews, C.K. Liquid Sodium—The Heat Transport Medium in Fast Breeder Reactors. Bull. Mater. Sci. 1993, 16, 477–489. [Google Scholar] [CrossRef]
- Mingyu, H.; Tao, W.; Jinbing, C.; Xiaoran, W. Study on Ultrasonic Location Based on Sound Pressure and TDOA Switching. In Proceedings of the 2020 Chinese Control and Decision Conference (CCDC), Hefei, China, 22–24 August 2020; IEEE: New York, NY, USA, 2020; pp. 3153–3158. [Google Scholar]
- Griffin, J.W.; Peters, T.J.; Posakony, G.J.; Chien, H.-T.; Bond, L.J.; Denslow, K.M.; Sheen, S.-H.; Raptis, P. Under-Sodium Viewing: A Review of Ultrasonic Imaging Technology for Liquid Metal Fast Reactors; Pacific Northwest National Laboratory (PNNL): Richland, WA, USA, 2009.
- Massacret, N.; Ploix, M.A.; Corneloup, G.; Jeannot, J.P. Modelling of Ultrasonic Propagation in Turbulent Liquid Sodium with Temperature Gradient. J. Appl. Phys. 2014, 115, 204905. [Google Scholar] [CrossRef]
- Barathula, S.; Srinivasan, K. Review on Research Progress in Boiling Acoustics. Int. Commun. Heat Mass Transf. 2022, 139, 106465. [Google Scholar] [CrossRef]
- Shumskii, B.E.; Vorob’eva, D.V.; Mil’to, V.A.; Semchenkov, Y.M. Investigation of Spatial Effects Accompanying Local Boiling of Coolant in VVER Core on the Basis of Neutron Flux Noise Analysis. Energy 2019, 126, 345–350. [Google Scholar] [CrossRef]
- Shu, L.; Zhu, X.; Huang, X.; Zhou, Z.; Zhang, Y.; Wang, X. A Review of Research on Acoustic Detection of Heat Exchanger Tube. EAI Endorsed Trans. Ind. Netw. Intell. Syst. 2015, 2, e5. [Google Scholar] [CrossRef]
- Hu, Z.; Xu, L.; Chien, C.-Y.; Yang, Y.; Gong, Y.; Ye, D.; Pacia, C.P.; Chen, H. Three-Dimensional Transcranial Microbubble Cavitation Localization by Four Sensors. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 3336–3346. [Google Scholar] [CrossRef] [PubMed]
- Hans, R.; Dumm, K. Leak Detection of Steam or Water into Sodium in Steam Generators of Liquid-Metal Fast Breeder Reactors. At. Energy Rev. 1977, 15, 611–699. [Google Scholar]
- Desai, P.D.; Ng, W.C.; Hines, M.J.; Riaz, Y.; Tesar, V.; Zimmerman, W.B. Comparison of Bubble Size Distributions Inferred from Acoustic, Optical Visualisation, and Laser Diffraction. Colloids Interfaces 2019, 3, 65. [Google Scholar] [CrossRef]
- Shung, K.K. High Frequency Ultrasonic Imaging. J. Med. Ultrasound 2009, 17, 25–30. [Google Scholar] [CrossRef] [PubMed]
- Wajman, R. Computer Methods for Non-Invasive Measurement and Control of Two-Phase Flows: A Review Study. Inf. Technol. Control 2019, 48, 464–486. [Google Scholar] [CrossRef]
- Boháčik, M.; Mičian, M.; Sládek, A. Evaluating the Attenuation in Ultrasonic Testing of Castings. Arch. Foundry Eng. 2018, 18, 151–156. [Google Scholar] [CrossRef]
- Matz, V.; Kreidl, M.; Smid, R. Classification of Ultrasonic Signals. Int. J. Mater. Prod. Technol. 2006, 27, 145–155. [Google Scholar] [CrossRef]
- Guichou, R.; Tordjeman, P.; Bergez, W.; Zamansky, R. Experimental Study of Bubble Detection in Liquid Metal. In Proceedings of the VIII International Scientific Colloquium “Modelling for Materials Processing”, Riga, Latvia, 21–22 September 2017; Volume 53, p. 667. [Google Scholar]
- Sun, H.; Ramuhalli, P.; Meyer, R. An Assessment of Machine Learning Applied to Ultrasonic Nondestructive Evaluation; Oak Ridge National Laboratory (ORNL): Oak Ridge, TN, USA, 2023.
- Zhang, X.; Yu, Y.; Yu, Z.; Qiao, F.; Du, J.; Yao, H. A Scoping Review: Applications of Deep Learning in Non-Destructive Building Tests. Electronics 2025, 14, 1124. [Google Scholar] [CrossRef]
- Matsuura, M.; Ikeda, M. Modification of Steam Generator System to Prevent Overheating Tube Rapture Accidents at MONJU. In Proceedings of the 18th International Conference on Structural Mechanics in Reactor Technology, Beijing, China, 7–12 August 2005. [Google Scholar]
- Chetal, S.C. Evolution of Design of Steam Generator for Sodium Cooled Reactors; International Atomic Energy Agency: Vienna, Austria, 1997. [Google Scholar]
- Haynes, W.M. (Ed.) CRC Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Rusman, J. Klasifikasi Cacat Biji Kopi Menggunakan Metode Transfer Learning dengan Hyperparameter Tuning Gridsearch. J. Teknol. Dan Manaj. Inform. 2023, 9, 37–45. [Google Scholar] [CrossRef]
- Tan, M.; Le, Q. EfficientNetV2: Smaller Models and Faster Training. In Proceedings of the 38th International Conference on Machine Learning Research, Online, 18–24 July 2021; pp. 10096–10106. [Google Scholar]
- Chang, D.T. Bayesian Hyperparameter Optimization with BoTorch, GPyTorch, and Ax. arXiv 2019, arXiv:1912.05686. [Google Scholar]
- Ando, K.; Onishi, K.; Bale, R.; Tsubokura, M.; Kuroda, A.; Minami, K. Nonlinear Mode Decomposition and Reduced-Order Modeling for Three-Dimensional Cylinder Flow by Distributed Learning on Fugaku. In High Performance Computing, Proceedings of the ISC High Performance Digital 2021 International Workshops; Jagode, H., Anzt, H., Ltaief, H., Luszczek, P., Eds.; Springer International Publishing: Cham, Switzerland, 2021; Volume 12761, pp. 122–137. [Google Scholar]
- Ma, H.; Zhang, Y.; Haidn, O.J.; Thuerey, N.; Hu, X. Supervised Learning Mixing Characteristics of Film Cooling in a Rocket Combustor Using Convolutional Neural Networks. Acta Astronaut. 2020, 175, 11–18. [Google Scholar] [CrossRef]
- Serafim Rodrigues, T.; Rogério Pinheiro, P. Hyperparameter Optimization in Generative Adversarial Networks (GANs) Using Gaussian AHP. IEEE Access 2024, 13, 770–788. [Google Scholar] [CrossRef]
- Huang, P.; Yan, H.; Song, Z.; Xu, Y.; Hu, Z.; Dai, J. Combining Autoencoder with Clustering Analysis for Anomaly Detection in Radiotherapy Plans. Quant. Imaging Med. Surg. 2023, 13, 2328–2338. [Google Scholar] [CrossRef]
- Aktar, S.; Nur, A.Y. Advancing Network Anomaly Detection: An Ensemble Approach Combining Optimized Contractive Autoencoders and k-Means Clustering. In Proceedings of the 2024 IEEE 3rd International Conference on Computing and Machine Intelligence (ICMI), Mt Pleasant, MI, USA, 11 July 2024; IEEE: New York, NY, USA, 2024; pp. 1–5. [Google Scholar]
- Dumont, V.; Ju, X.; Mueller, J. Hyperparameter Optimization of Generative Adversarial Network Models for High-Energy Physics Simulations. arXiv 2022, arXiv:2208.07715. [Google Scholar] [CrossRef]
- Alarsan, F.I.; Younes, M. Best Selection of Generative Adversarial Networks Hyper-Parameters Using Genetic Algorithm. SN Comput. Sci. 2021, 2, 283. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You?”: Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 1135–1144. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- van der Maaten, L.; Hinton, G. Visualizing Data Using T-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Maaten, L. van der Accelerating T-SNE Using Tree-Based Algorithms. J. Mach. Learn. Res. 2014, 15, 3221–3245. [Google Scholar]
- Laguna, S.; Heidenreich, J.N.; Sun, J.; Cetin, N.; Al-Hazwani, I.; Schlegel, U.; Cheng, F.; El-Assady, M. ExpLIMEable: A Visual Analytics Approach for Exploring LIME. In Proceedings of the 2023 Workshop on Visual Analytics in Healthcare (VAHC), Melbourne, Australia, 22 October 2023; pp. 27–33. [Google Scholar] [CrossRef]
- Anwar, S.; Griffiths, N.; Bhalerao, A.; Popham, T.J. MASALA: Model-Agnostic Surrogate Explanations by Locality Adaptation. In Proceedings of the 1st KDD Workshop on Human-Interpretable AI, Barcelona, Spain, 26 August 2024. [Google Scholar]
- Marquina-Araujo, J.J.; Cotrina-Teatino, M.A.; Cruz-Galvez, J.A.; Noriega-Vidal, E.M.; Vega-Gonzalez, J.A. Application of Autoencoders Neural Network and K-Means Clustering for the Definition of Geostatistical Estimation Domains|IIETA. Math. Model. Eng. Probl. 2024, 11, 1207. [Google Scholar] [CrossRef]
- Nguyen, V.; Viet Hung, N.; Le-Khac, N.-A.; Cao, V.L. Clustering-Based Deep Autoencoders for Network Anomaly Detection; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 290–303. [Google Scholar]
- Akbarian, H.; Mahgoub, I.; Williams, A. Autoencoder-K-Means Algorithm for Efficient Anomaly Detection to Improve Space Operations. In Proceedings of the 2024 International Conference on Smart Applications, Communications and Networking (SmartNets), Harrisonburg, VA, USA, 28–30 May 2024; IEEE: New York, NY, USA, 2024; pp. 1–6. [Google Scholar]
- Chang, L.-K.; Wang, S.-H.; Tsai, M.-C. Demagnetization Fault Diagnosis of a PMSM Using Auto-Encoder and K-Means Clustering. Energies 2020, 13, 4467. [Google Scholar] [CrossRef]
- Xie, J.; Girshick, R.; Farhadi, A. Unsupervised Deep Embedding for Clustering Analysis. Proc. Mach. Learn. Res. 2016, 48, 478–487. [Google Scholar]
- Aytekin, C.; Ni, X.; Cricri, F.; Aksu, E. Clustering and Unsupervised Anomaly Detection with L2 Normalized Deep Auto-Encoder Representations. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; IEEE: New York, NY, USA, 2018; pp. 1–6. [Google Scholar]
- Islam, M.M.; Faruque, M.O.; Butterfield, J.; Singh, G.; Cooke, T.A. Unsupervised Clustering of Disturbances in Power Systems via Deep Convolutional Autoencoders. In Proceedings of the 2023 IEEE Power & Energy Society General Meeting (PESGM), Orlando, FL, USA, 16–20 July 2023; IEEE: New York, NY, USA, 2023; pp. 1–5. [Google Scholar]
- Schölkopf, B.; Platt, J.C.; Shawe-Taylor, J.; Smola, A.J.; Williamson, R.C. Estimating the Support of a High-Dimensional Distribution. Neural Comput. 2001, 13, 1443–1471. [Google Scholar] [CrossRef] [PubMed]
- Tax, D.M.; Duin, R.P. Support vector data description. Mach. Learn. 2004, 54, 45–66. [Google Scholar] [CrossRef]






| Monju (325 °C) [MRayl] | Monju (469 °C) [MRayl] | This Study (25 °C) [MRayl] | |
|---|---|---|---|
| Vessel | 44 (2.25Cr-1Mo steel) | 42 (2.25Cr-1Mo steel) | 46.32 (Type-304 Stainless steel) |
| Heat transfer tube | 44 (2.25Cr-1Mo steel) | 42 (2.25Cr-1Mo steel) | 42.65 (Copper) |
| Solvent | 2.1 (Sodium) | 1.9 (Sodium) | 1.49 (Water) |
| bubbles | 9.3 × 10−4 (Hydrogen) | 8.3 × 10−4 (Hydrogen) | 4.08 × 10−4 (Air) |
| Copper Piping Order | Bubbles Direction | Precision | Recall | F1-Score |
|---|---|---|---|---|
| - | No Hole | 0.956 | 0.929 | 0.942 |
| 1st | West | 0.215 | 0.700 | 0.329 |
| East | 0.00 | 0.00 | 0.00 | |
| North | 0.256 | 0.550 | 0.349 | |
| South | 0.00 | 0.00 | 0.00 | |
| 2nd | West | 0.00 | 0.00 | 0.00 |
| East | 0.155 | 0.750 | 0.256 | |
| North | 0.682 | 0.750 | 0.714 | |
| South | 0.267 | 0.600 | 0.369 | |
| 3rd | West | 0.00 | 0.00 | 0.00 |
| East | 0.0989 | 0.450 | 0.162 | |
| North | 0.563 | 0.450 | 0.500 | |
| South | 0.00 | 0.00 | 0.00 | |
| 4th | West | 0.455 | 0.500 | 0.476 |
| East | 0.00 | 0.00 | 0.00 | |
| North | 0.00 | 0.00 | 0.00 | |
| South | 0.00 | 0.00 | 0.00 | |
| 5th | West | 0.00 | 0.00 | 0.00 |
| East | 0.00 | 0.00 | 0.00 | |
| North | 0.00 | 0.00 | 0.00 | |
| South | 0.00 | 0.00 | 0.00 | |
| 6th | West | 0.00 | 0.00 | 0.00 |
| East | 0.00 | 0.00 | 0.00 | |
| North | 0.00 | 0.00 | 0.00 | |
| South | 0.00 | 0.00 | 0.00 | |
| 7th | West | 0.235 | 0.950 | 0.376 |
| East | 0.00 | 0.00 | 0.00 | |
| North | 0.174 | 0.750 | 0.283 | |
| South | 0.00 | 0.00 | 0.00 | |
| Average | 0.140 | 0.254 | 0.164 | |
| Copper Piping Order | Bubbles Direction | Precision | Recall | F1-Score |
|---|---|---|---|---|
| - | No Hole | 0.996 | 0.968 | 0.982 |
| 1st | West | 0.576 | 0.950 | 0.717 |
| East | 0.826 | 0.950 | 0.884 | |
| North | 1.00 | 0.900 | 0.947 | |
| South | 0.679 | 0.950 | 0.792 | |
| 2nd | West | 0.783 | 0.900 | 0.837 |
| East | 0.349 | 0.750 | 0.476 | |
| North | 1.00 | 0.750 | 0.857 | |
| South | 0.314 | 0.550 | 0.40 | |
| 3rd | West | 0.00 | 0.00 | 0.00 |
| East | 1.00 | 1.00 | 1.00 | |
| North | 0.950 | 0.950 | 0.950 | |
| South | 0.387 | 0.60 | 0.471 | |
| 4th | West | 0.929 | 0.650 | 0.765 |
| East | 0.00 | 0.00 | 0.00 | |
| North | 0.541 | 1.00 | 0.702 | |
| South | 0.00 | 0.00 | 0.00 | |
| 5th | West | 0.667 | 1.00 | 0.80 |
| East | 0.436 | 0.850 | 0.576 | |
| North | 0.00 | 0.00 | 0.00 | |
| South | 0.00 | 0.00 | 0.00 | |
| 6th | West | 1.00 | 1.00 | 1.00 |
| East | 0.870 | 1.00 | 0.930 | |
| North | 0.00 | 0.00 | 0.00 | |
| South | 0.00 | 0.00 | 0.00 | |
| 7th | West | 0.833 | 1.00 | 0.909 |
| East | 0.00 | 0.00 | 0.00 | |
| North | 0.513 | 1.00 | 0.678 | |
| South | 0.377 | 1.00 | 0.548 | |
| Average | 0.518 | 0.645 | 0.559 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ota, Y.; Nukaga, S.; Kanda, Y.; Furuya, M. Explainable Machine Learning for Bubble Leakage Detection at Tube Array Surfaces in Pool. Appl. Sci. 2025, 15, 12587. https://doi.org/10.3390/app152312587
Ota Y, Nukaga S, Kanda Y, Furuya M. Explainable Machine Learning for Bubble Leakage Detection at Tube Array Surfaces in Pool. Applied Sciences. 2025; 15(23):12587. https://doi.org/10.3390/app152312587
Chicago/Turabian StyleOta, Yosei, Shun Nukaga, Yuna Kanda, and Masahiro Furuya. 2025. "Explainable Machine Learning for Bubble Leakage Detection at Tube Array Surfaces in Pool" Applied Sciences 15, no. 23: 12587. https://doi.org/10.3390/app152312587
APA StyleOta, Y., Nukaga, S., Kanda, Y., & Furuya, M. (2025). Explainable Machine Learning for Bubble Leakage Detection at Tube Array Surfaces in Pool. Applied Sciences, 15(23), 12587. https://doi.org/10.3390/app152312587







