Control System for an Open-Winding Permanent Magnet Synchronous Motor Fed by a Four-Leg Inverter

Featured Application

This study presents an enhanced hysteresis current control strategy applied to a four-leg inverter driving an open-winding permanent magnet synchronous motor (OW-PMSM). Here, ‘open-winding’ refers to a motor topology where both ends of each phase winding are independently accessible, forming a six-terminal connection to the power converter, distinct from standard star or delta connections. The proposed system is particularly suited for industrial and electric vehicle applications that require high dynamic response, operational reliability, and cost efficiency. Key application scenarios include traction systems for electric vehicles, high-speed spindles, precision servo drives, and robotic joint systems, where effective zero-sequence current suppression, stable switching frequency, and high efficiency are essential. The four-leg inverter topology, combined with the improved hysteresis control, achieves high DC-link voltage utilization while minimizing current ripple and switching losses, thus enhancing system stability and prolonging component service life. This approach provides a practical and high-performance motor drive solution.

Abstract

This paper employs a four-leg inverter topology to mitigate the high cost and zero-sequence current suppression challenges associated with dual-inverter open-winding permanent magnet synchronous motor (OW-PMSM) systems. Building on this topology, an improved current hysteresis control strategy incorporating a switching-state lookup table is proposed to suppress switching frequency fluctuations and current ripple. The developed system maintains high DC-link utilization and low cost while addressing the modulation complexity of conventional vector control and the switching frequency instability inherent in traditional hysteresis control. The study establishes a mathematical model of the OW-PMSM, analyzes the voltage vector distribution of the four-leg inverter, and designs an enhanced hysteresis control algorithm. By utilizing a predefined switching table to regulate switching logic in real time, the strategy achieves fixed switching frequency and effective harmonic suppression while preserving the fast-response characteristics of conventional hysteresis control. The experimental results demonstrate that the proposed control strategy achieves superior performance, effectively suppressing current ripple and providing ample stability margin, thereby validating its feasibility and effectiveness for practical engineering applications.

1. Introduction

Permanent Magnet Synchronous Motors (PMSMs) are widely used in industrial drives and new energy vehicles due to their high efficiency, high power density, and excellent dynamic performance [1,2]. However, due to the unadjustable nature of the permanent magnet flux, conventional PMSMs exhibit limited flux-weakening speed expansion capability and restricted output torque in wide-speed-range and high-power applications [3]. To address these limitations, the Open-Winding PMSM (OW-PMSM) has been proposed and attracted increasing attention [4,5]. This topology, which employs a dual-inverter six-leg structure by decoupling the neutral point of the star-connected windings [6], significantly enhances the DC bus voltage utilization and speed regulation range while retaining the advantages of PMSMs. Nevertheless, the dual-inverter six-leg configuration increases the number of switching devices and hardware costs. More critically, it introduces a challenge in suppressing the zero-sequence current that can circulate between the two inverters [7,8], which seriously hinders its widespread practical application. To address these issues while preserving the benefits of the open-winding structure, this paper investigates a four-leg inverter topology for the OW-PMSM drive. This topology reduces the number of switching devices and associated gate drivers from twelve to seven (a 42% reduction) compared to the dual-inverter system, leading to a direct and substantial reduction in hardware cost and complexity. This cost saving is achieved while maintaining high DC-link voltage utilization, which is directly linked to the system’s torque output capability and operational speed range—key factors influencing energy output performance.

Research on dual-inverter OW-PMSM drives has evolved along several key trajectories to address inherent challenges. Early work focused on modulation strategies to improve performance and suppress zero-sequence current [9]. For instance, a foundational method using error voltage calculation was introduced to minimize current ripple [10]. This was followed by developments in optimized voltage vector selection [11], dedicated zero-sequence suppression schemes [12], and advanced space vector modulation techniques [13,14,15]. In parallel, the system reliability concerns arising from the high switch count spurred significant research into fault-tolerant control strategies [16,17,18,19]. A notable contribution in this area is an advanced field-oriented control method that ensures operational continuity under open-circuit faults [20]. Another research direction has pursued topological simplification. Studies on multi-leg inverter architectures demonstrate a viable path to reducing hardware cost and complexity without sacrificing core functionality [21,22,23,24,25]. Furthermore, alternative control paradigms, such as the direct model predictive torque control pioneered in [26], have emerged to simultaneously enhance tracking accuracy and drive efficiency, highlighting a distinct approach to achieving high performance.

Building on these research directions, our work investigates the four-leg inverter topology, which effectively forms a three-H-bridge configuration. This topology reduces the conventional six-H-bridge structure to three H-bridges, decreasing the number of switching devices by 33%. A fundamental distinction lies in the winding connectivity: in the proposed three-H-bridge structure, the endpoint of one phase winding is electrically connected to the starting point of another phase. This contrasts with the conventional six H-bridge topology, where all three motor windings can be switched completely independently, with each winding fed by a dedicated H-bridge. This connectivity difference represents a key trade-off: while the three H-bridge topology offers advantages in cost and component count, it introduces inherent coupling between phase voltages due to the shared power devices. In comparison, the six H-bridge topology provides superior control independence and potential performance at the expense of higher hardware complexity and cost. Furthermore, the independent fourth leg in our proposed topology enables active zero-sequence current control [27,28,29,30,31], significantly improving suppression efficiency and providing an effective solution for system performance optimization [32,33]. The selection of this four-leg OEW configuration is therefore justified by its compelling combination of performance and cost-effectiveness. It retains the key advantage of high DC-link voltage utilization inherent to open-winding motors, while the simplified hardware addresses the cost and complexity issues of the dual-inverter system. Moreover, the independent control of the fourth leg is crucial for effective zero-sequence current suppression, a critical requirement for high-performance applications such as electric vehicle traction systems, renewable energy conversion, and precision industrial drives, where system reliability and waveform quality are paramount.

The motivation for developing a dedicated control system for this topology stems from its potential to address pressing engineering challenges in these very applications. For instance, in electric vehicle traction systems, the concurrent demands for high torque density, a wide speed range, and compliance with strict electromagnetic compatibility (EMC) standards pose a significant challenge. The four-leg OW-PMSM drive addresses this by providing high DC-link voltage utilization for superior torque output, inherent flux-weakening capability for extended speed operation, and—crucially—active zero-sequence current suppression to mitigate common-mode emissions and prevent bearing currents, thereby enhancing system longevity. Similarly, in renewable energy conversion systems like wind turbines and in high-performance industrial servo drives, the topology’s inherent structural redundancy offers valuable fault-tolerant capability, while its high efficiency and dynamic response contribute to improved system robustness and energy efficiency. The primary objective of this work is, therefore, to leverage these inherent advantages of the four-leg OW-PMSM topology while overcoming a key limitation in its practical implementation: the variable switching frequency and associated current ripple of traditional hysteresis control. The improved control strategy proposed herein is designed to fully unlock the topology’s potential for the demanding applications cited above.

Given these application demands and the specific capabilities of the topology, the unique structure of the four-leg inverter imposes higher requirements on its modulation strategies. Although traditional hysteresis current control offers advantages such as fast response and simple implementation, it suffers from variable switching frequency and significant current ripple, making it unsuitable for high-performance drive systems [34]. To address this, this paper proposes an improved hysteresis current control strategy, which regulates the switching behavior of power devices by introducing a switch state lookup table within a fixed period. Theoretical analysis and experimental verification confirm that the method maintains the system’s fast dynamic response, stabilizes the switching frequency, and achieves a substantial reduction in current ripple, contributing to an extended service life for power devices. Furthermore, the four-leg topology possesses inherent structural redundancy, enabling continued operation through leg reconfiguration in the event of a single-leg fault, thereby enhancing its reliability and fault tolerance.

This paper focuses on a four-leg inverter open-winding motor control system to address issues such as hardware complexity and zero-sequence current suppression challenges in conventional six-leg configurations. First, based on the characteristics of this topology, the distribution and synthesis mechanism of space voltage vectors are thoroughly analyzed, and a corresponding vector synthesis voltage control strategy is proposed. Second, an improved hysteresis current control algorithm is designed, which effectively suppresses current harmonics by fixing the power switching frequency, thereby enhancing system reliability and extending hardware lifespan. The remainder of this paper is structured to provide a logical progression from theoretical foundation to experimental validation. Section 2 begins by establishing the mathematical model of the OW-PMSM, which is fundamental for controller design. It then provides a detailed analysis of the voltage vector distribution for the four-leg inverter, defining the available control actions. Building upon this theoretical basis, Section 3 introduces the proposed improved hysteresis current control strategy, detailing the design of the switching-state lookup table and stability analysis. Finally, Section 4 presents experimental results to comprehensively validate the performance of the proposed system and control strategy under both steady-state and dynamic conditions.

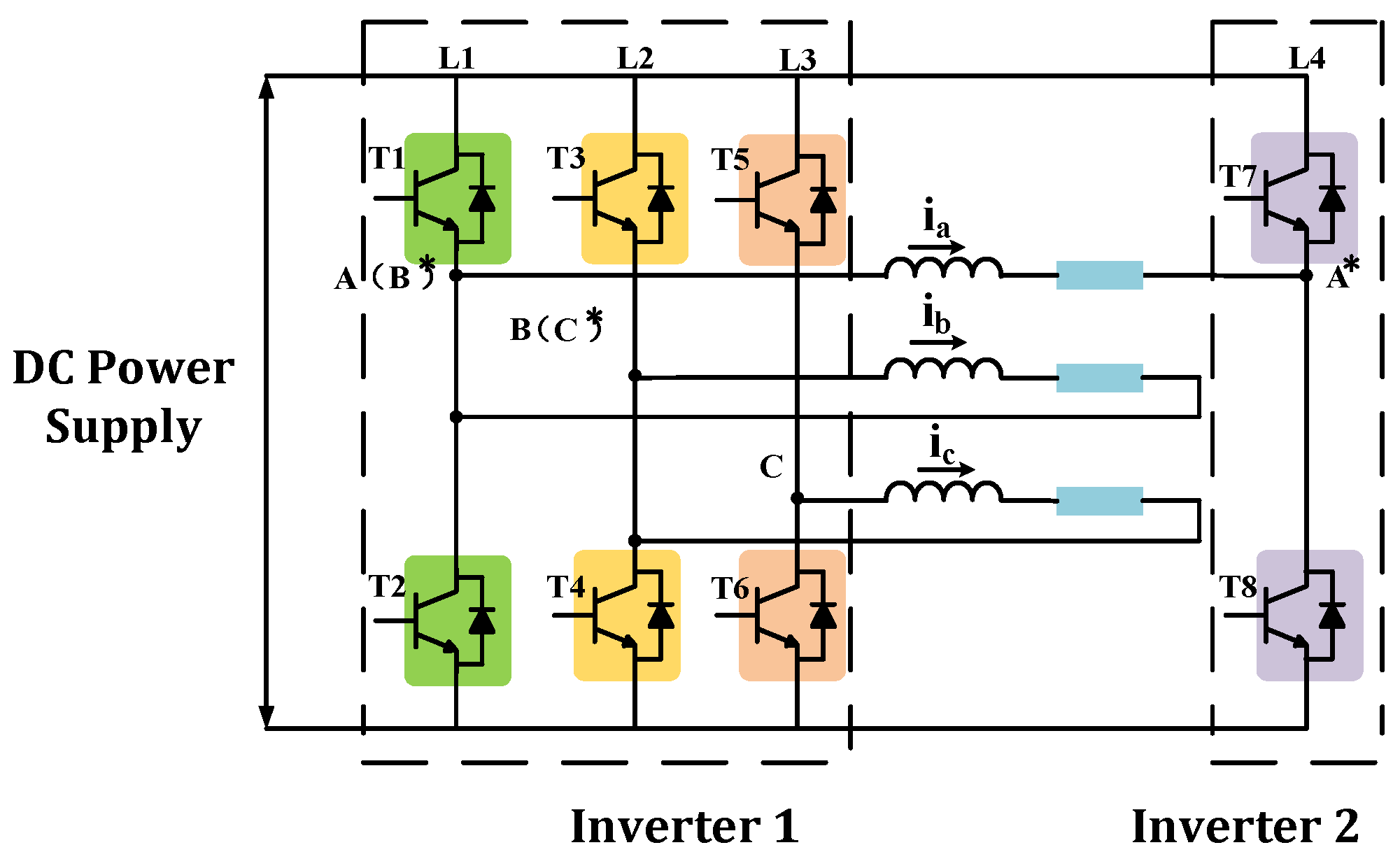
2. Four-Leg Inverter Open-Winding Motor Control System

As the foundation for the control system design, this section first presents the mathematical model of the open-winding PMSM. The drive topology of the four-leg inverter open-winding motor control system used in this paper is shown in Figure 1. In this topology, the negative terminal of phase B winding is shared with the positive terminal of phase A winding, and the negative terminal of phase C winding is shared with the positive terminal of phase B winding. The positive terminals of phases A, B, and C windings of the open-winding motor are connected to the midpoints of legs L1, L2, and L3, respectively, while the negative terminal of phase A winding is connected to the midpoint of leg L4.

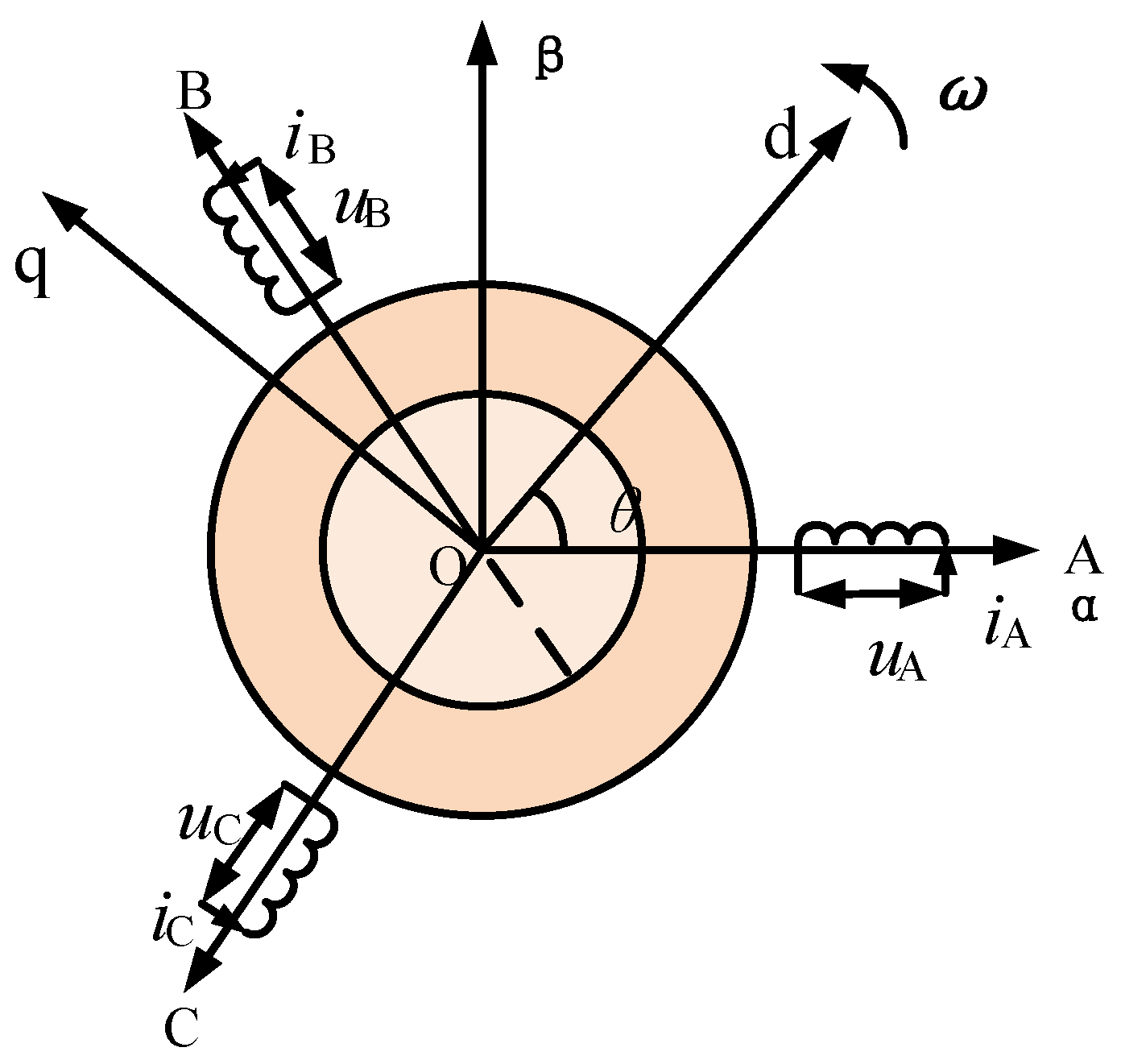
2.1. Open-Winding Motor Mathematical Model

The mathematical model of the open-winding motor is illustrated in Figure 2. For coordinate system definitions, the ABC frame represents the three-phase stationary coordinate system, the αβ frame denotes the two-phase stationary coordinate system, and the dq frame corresponds to the two-phase rotating coordinate system. Here, the α-axis aligns with the A-axis, and the angle between the d-axis and α-axis equals the rotational angle of the motor rotor.

In the two-phase rotating coordinate system, the voltage equations of the open-winding permanent magnet synchronous motor are given by:

$$\left[\begin{array}{l}{u}_d\hfill \\ u_q\hfill \\ u_0\hfill \end{array}\right]=\left[\begin{array}{ccc}R+L_d{\displaystyle \frac{d}{dt}}& -\omega L_q& 0\\ \omega L_{\mathrm{d}}& R+L_q{\displaystyle \frac{d}{dt}}& 0\\ 0& 0& R+L_0{\displaystyle \frac{d}{dt}}\end{array}\right]\left[\begin{array}{c}{i}_d\\ i_q\\ i_0\end{array}\right]+\left[\begin{array}{c}0\\ \omega \\ 0\end{array}\right]{\psi }_f$$

(1)

Here, where u_d, u_q, u₀ represent the d-axis, q-axis, and zero-sequence voltages of the open-winding motor; i_d, i_q, i₀ denote the corresponding d-axis, q-axis, and zero-sequence currents; ω is the electrical angular velocity; R is the phase resistance; L_d, L_q, L₀ are the d-axis, q-axis, and zero-sequence inductances; and Ψ_f is the permanent magnet flux linkage.

The flux linkage equations are expressed as:

$$\left[\begin{array}{l}{\psi }_d\\ {\psi }_q\\ {\psi }_0\end{array}\right]=\left[\begin{array}{ccc}{L}_d& 0& 0\\ 0& L_q& 0\\ 0& 0& L_0\end{array}\right]\left[\begin{array}{l}{i}_d\\ i_q\\ i_0\end{array}\right]+\left[\begin{array}{l}{\psi }_f\\ 0\\ 0\end{array}\right]$$

(2)

where Ψ_d, Ψ_q, Ψ₀ are the d-axis, q-axis, and zero-sequence components of the open-winding motor flux linkage, respectively.

The electromagnetic torque equation and the motion equation of the open-winding motor are given, respectively, by:

$$T_e={\displaystyle \frac{3}{2}}p\left[{\psi }_f{i}_q+(L_d-L_q)i_d{i}_q\right]$$

(3)

$$T_e-T_L={\displaystyle \frac{\mathrm{J}}{\mathrm{P}}}{\displaystyle \frac{d\omega }{dt}}$$

(4)

where T_e is the electromagnetic torque; L_d, L_q are the d-axis and q-axis inductances, respectively, T_L is the load torque, J is the moment of inertia, and P is the number of motor pole pairs.

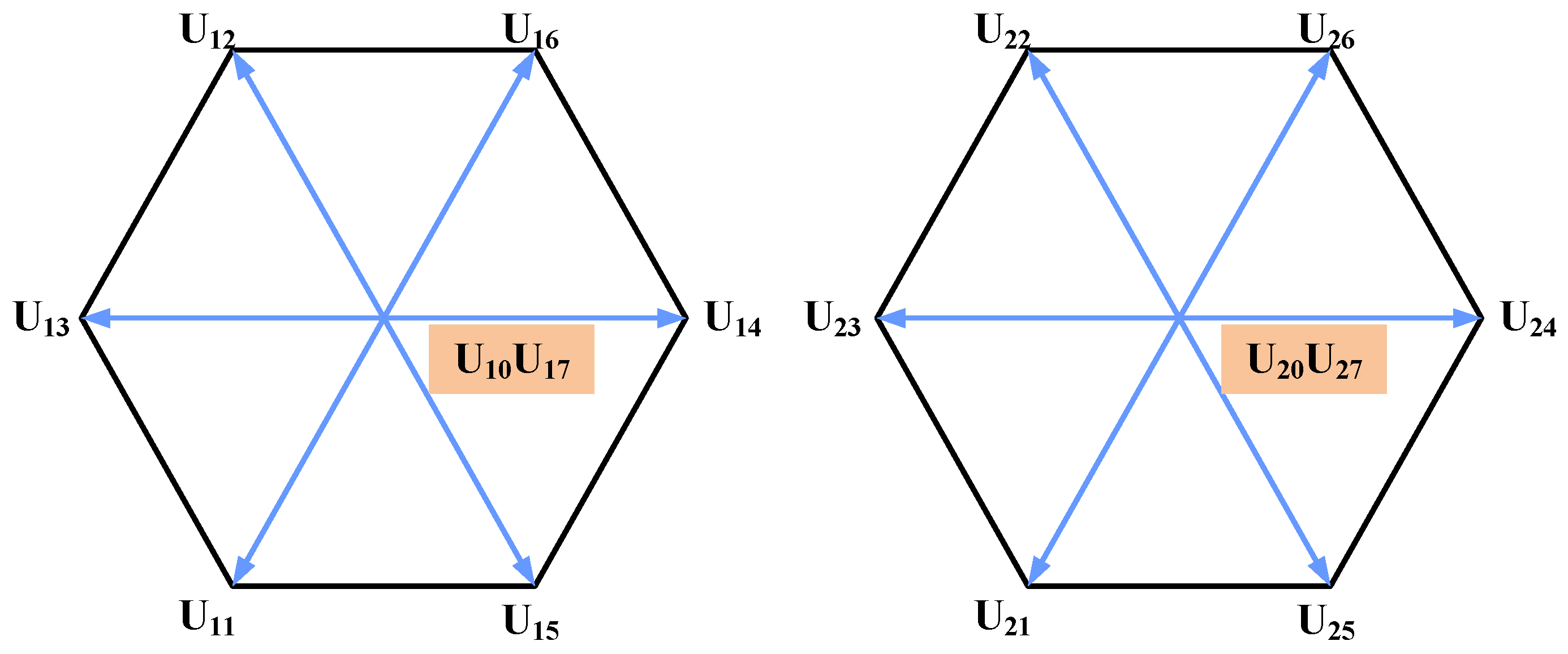
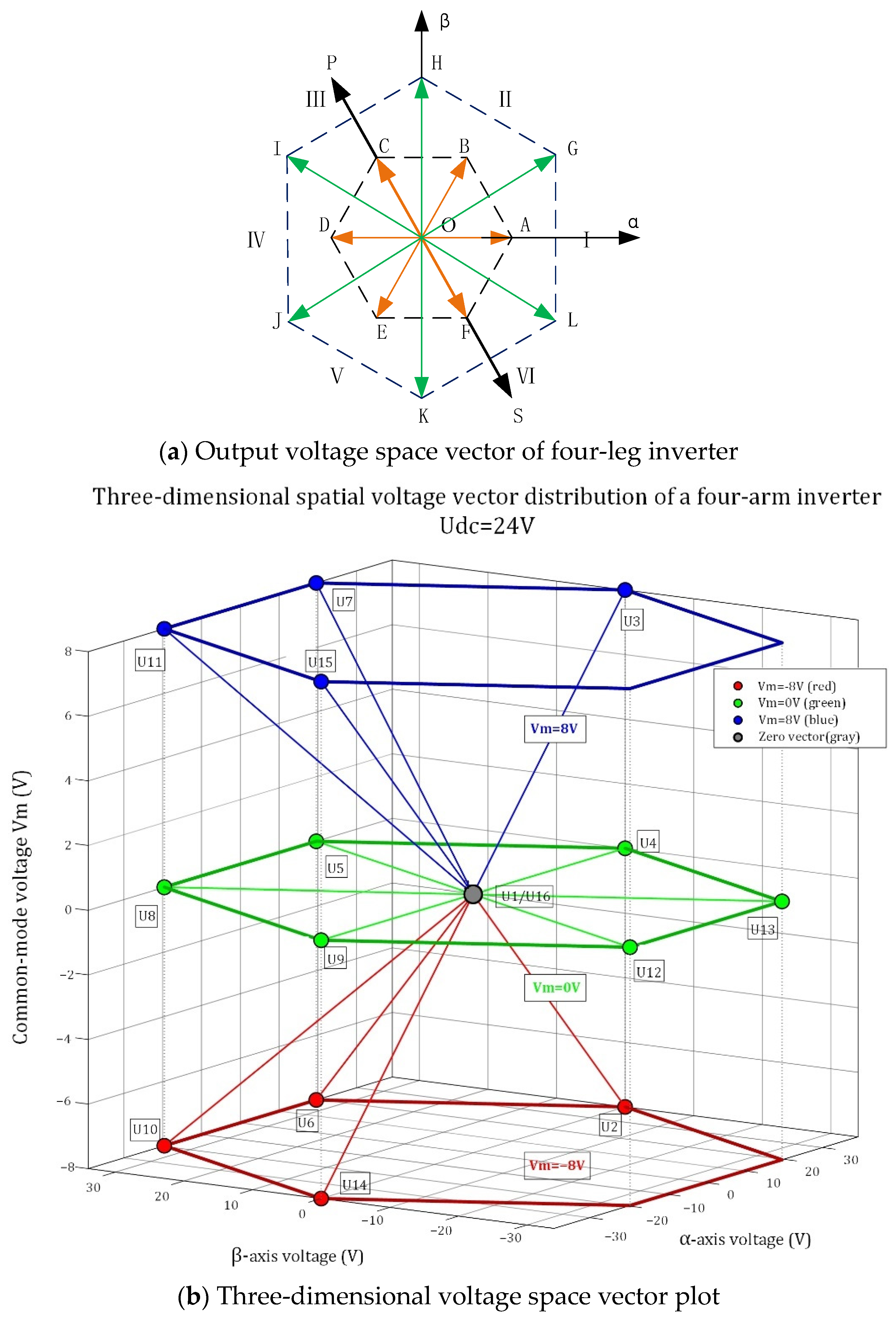
2.2. Four-Leg Inverter Voltage Vector Analysis

To accurately represent the switching states of the inverter legs, a space vector analysis of the three-leg inverter topology is conducted. Let the variable S_x (x = A, B, C) denote the switching state of each leg, defined as follows:

$$S_{\mathrm{x}}=\left\{\begin{array}{l}1,When the upper switch of a leg is ON \\ 0,When the lower switch of a leg is ON \end{array}\right.$$

(5)

The switching states and corresponding voltage vectors of the standard three-phase inverter are well-established, comprising six active vectors and two zero vectors distributed in the α-β plane as shown in Figure 3. U₁₀ and U₁₇ are zero vectors located at the center of the space vector distribution. U₁₁ to U₁₆ are non-zero vectors, each separated by 60° and evenly distributed around the center of the space vector diagram. For the dual-inverter system, the output voltage vectors are synthesized from both inverters, but under the specific winding connection constraints of the four-leg topology.

The output space vector voltage of the dual-inverter system is obtained by synthesizing the space vector voltages of Inverter 1 and Inverter 2. However, when synthesizing the space vectors of the four-leg inverter, the phase A winding shares one inverter leg with phase B, and the phase B winding shares another leg with phase C. Consequently, during space vector synthesis, the potentials of Inverter 1 and Inverter 2 must satisfy the constraints ${\mathrm{A}=\mathrm{B}}^{*}$ and $\mathrm{B}={\mathrm{C}}^{*}$. According to Equation (5), the four-leg inverter has a total of 2⁴ = 16 switching combinations. These 16 space vector voltage states are arranged in sequence and encoded according to their power switch state combinations.

The four-leg inverter produces 16 possible operating voltage combinations for the three-phase A, B, and C windings. As shown in Figure 1, taking state 1 as an example, the switching states S_AS_BS_CS_A* are 0, 0, 0, and 1, respectively. In this state, only switching devices T2 and T7 are turned on, while all other switching devices remain off. Current flows from the positive terminal of the DC source, passes through switching device T7 into the negative terminal of phase A winding, and returns to the DC source negative terminal via power switch T2. Since current enters through the winding’s negative terminal and exits from the positive terminal, the operating voltage across phase A winding is −U_dc.

Following the switching state definition in Equation (5),

Table 1. Four-leg inverter switch status table.

${\mathbf{U}}_{\mathbf{i}}$	${\mathbf{U}}_{\mathbf{a}}$	${\mathbf{U}}_{\mathbf{b}}$	${\mathbf{U}}_{\mathbf{c}}$	${\mathbf{U}}_{\mathsf{\alpha }}$	${\mathbf{U}}_{\mathsf{\beta }}$	${\mathbf{U}}_{\mathbf{m}}$
${\mathrm{U}}_1$	0	0	0	0	0	0
${\mathrm{U}}_2$	$-{\mathrm{U}}_{\mathrm{dc}}$	0	0	$-2/3$	0	$-1/3{\mathrm{U}}_{\mathrm{dc}}$
${\mathrm{U}}_3$	0	0	${\mathrm{U}}_{\mathrm{dc}}$	$-1/3$	$-\sqrt{3}/3$	$1/3{\mathrm{U}}_{\mathrm{dc}}$
${\mathrm{U}}_4$	$-{\mathrm{U}}_{\mathrm{dc}}$	0	${\mathrm{U}}_{\mathrm{dc}}$	−1	$-\sqrt{3}/3$	0
${\mathrm{U}}_5$	0	${\mathrm{U}}_{\mathrm{dc}}$	$-{\mathrm{U}}_{\mathrm{dc}}$	0	$-2\sqrt{3}/3$	0
${\mathrm{U}}_6$	$-{\mathrm{U}}_{\mathrm{dc}}$	${\mathrm{U}}_{\mathrm{dc}}$	$-{\mathrm{U}}_{\mathrm{dc}}$	$-2/3$	$2\sqrt{3}/3$	$-1/3{\mathrm{U}}_{\mathrm{dc}}$
${\mathrm{U}}_7$	0	${\mathrm{U}}_{\mathrm{dc}}$	0	$-1/3$	$\sqrt{3}/3$	$1/3{\mathrm{U}}_{\mathrm{dc}}$
${\mathrm{U}}_8$	$-{\mathrm{U}}_{\mathrm{dc}}$	${\mathrm{U}}_{\mathrm{dc}}$	0	−1	$\sqrt{3}/3$	0
${\mathrm{U}}_9$	${\mathrm{U}}_{\mathrm{dc}}$	$-{\mathrm{U}}_{\mathrm{dc}}$	0	1	$-\sqrt{3}/3$	0
${\mathrm{U}}_{10}$	0	$-{\mathrm{U}}_{\mathrm{dc}}$	0	$1/3$	$-\sqrt{3}/3$	$-1/3{\mathrm{U}}_{\mathrm{dc}}$
${\mathrm{U}}_{11}$	${\mathrm{U}}_{\mathrm{dc}}$	$-{\mathrm{U}}_{\mathrm{dc}}$	${\mathrm{U}}_{\mathrm{dc}}$	$2/3$	$-2\sqrt{3}/3$	$1/3{\mathrm{U}}_{\mathrm{dc}}$
${\mathrm{U}}_{12}$	0	$-{\mathrm{U}}_{\mathrm{dc}}$	${\mathrm{U}}_{\mathrm{dc}}$	0	$-2\sqrt{3}/3$	0
${\mathrm{U}}_{13}$	${\mathrm{U}}_{\mathrm{dc}}$	0	$-{\mathrm{U}}_{\mathrm{dc}}$	1	$\sqrt{3}/3$	0
${\mathrm{U}}_{14}$	0	0	$-{\mathrm{U}}_{\mathrm{dc}}$	$1/3$	$\sqrt{3}/3$	$-1/3{\mathrm{U}}_{\mathrm{dc}}$
${\mathrm{U}}_{15}$	${\mathrm{U}}_{\mathrm{dc}}$	0	0	$2/3$	0	$1/3{\mathrm{U}}_{\mathrm{dc}}$
${\mathrm{U}}_{16}$	0	0	0	0	0	0

comprehensively lists all 16 possible switching combinations $S_A{S}_B{S}_C{S}_A$ for the four-leg inverter and their corresponding output phase voltages $U_a$, $U_b$, $U_c$, which are defined relative to the DC-link midpoint. The switching state $S_x$ (where $x=A,B,C,A$) is defined as 1 when the top switch in leg $x$ is ON and the bottom switch is OFF, resulting in a phase voltage of $+U_{dc}/2$; conversely, it is 0 when the bottom switch is ON, resulting in a phase voltage of $-U_{dc}/2$.

Here, U_dc is the DC supply voltage. In the Clark transformation, the per-unit system is adopted with U_dc as the base unit to simplify the calculation, and $\mathrm{K}=2/3$.

The three-phase output voltages ($U_{\mathrm{a}}$, $U_b$, $U_c$) corresponding to each switching state in Table 1 are transformed into the two-phase stationary coordinate system (α-β) and the zero-sequence component using the Clarke transformation. The complete transformation is defined as:

$$\left[\begin{array}{c}{U}_{\alpha }\\ U_{\beta }\\ U_m\end{array}\right]={\displaystyle \frac{2}{3}}\times \left[\begin{array}{ccc}1& -1/2& -1/2\\ 0& \sqrt{3}/2& -\sqrt{3}/2\\ 1/2& 1/2& 1/2\end{array}\right]$$

(6)

In Equation (6), $U_m$ denotes the zero-sequence voltage component, which corresponds to the common-mode voltage. In the four-leg inverter, this component can be actively controlled via the fourth leg to suppress zero-sequence current. In conventional three-phase systems with isolated neutral points, this common-mode voltage circulates through parasitic capacitances, potentially causing bearing currents and electromagnetic interference. However, in the four-leg inverter topology, the independent fourth leg enables active control of $U_m$. The three-dimensional space vector diagram in Figure 4b explicitly shows the distribution of these common-mode voltage levels, with vectors grouped into three distinct planes corresponding to $U_0=-U_{dc}/3$, $0$, and $U_{dc}/3$.

The phase voltages $U_a,U_b,U_c$ listed in Table 1 are transformed into their two-phase stationary counterparts ($U_{\alpha }$, $U_{\beta }$) via the Clarke transformation (Equation (6)). This enables the subsequent space vector analysis. The distribution of all resultant voltage vectors is comprehensively illustrated in Figure 4, which categorizes them into large, medium, and small vectors based on their magnitude, thereby providing a complete representation of the inverter’s output capability.

With the coordinate origin as the center, a voltage vector coordinate system is established. The four-leg inverter can still output 14 non-zero vectors. Based on their magnitudes, the non-zero vectors are classified into three categories: large vectors, medium vectors, and small vectors. The six small vectors, denoted as OA, OB, OC, OD, OE, and OF, have a magnitude of 2U_dc/3. The six medium vectors, labeled OG, OH, OI, OJ, OK, and OL, have a magnitude of $2\sqrt{2}{U}_{\mathrm{dc}}/3$. The two large vectors, OP and OS, have a magnitude of 4U_dc/3. The two-dimensional space vector distribution of the output voltage of the four-leg inverter is shown in Figure 4a, and the three-dimensional voltage vector diagram is shown in Figure 4b.

As shown in Figure 4a, the six voltage vectors divide the plane evenly into six sectors (Ⅰ to Ⅵ). Compared to the six-leg inverter topology, the small and medium vectors in the four-leg inverter topology remain unchanged, while four large vectors are eliminated. Therefore, using medium vectors to drive the open-winding motor in the four-leg inverter system remains feasible. Figure 4b shows a three-dimensional space voltage vector diagram illustrating the distribution of all possible output voltage vectors of the four-leg inverter in the α-β-0 coordinate system. In the diagram, red points represent bottom-layer vectors with a common-mode voltage of −8 V (−1Udc/3), green points represent middle-layer vectors at 0 V (including two zero vectors at the center), and blue points represent top-layer vectors at 8 V (1Udc/3), all arranged on three parallel hexagonal planes. The lines from the origin to each point indicate the voltage vectors generated by corresponding switching states. The overall structure forms a hexagonal prism, clearly illustrating the layered distribution of space voltage vectors across three common-mode voltage levels and the magnitude and phase relationships of the vectors in the α-β plane.

3. Improved Hysteresis Current Control Strategy for Four-Leg Inverter

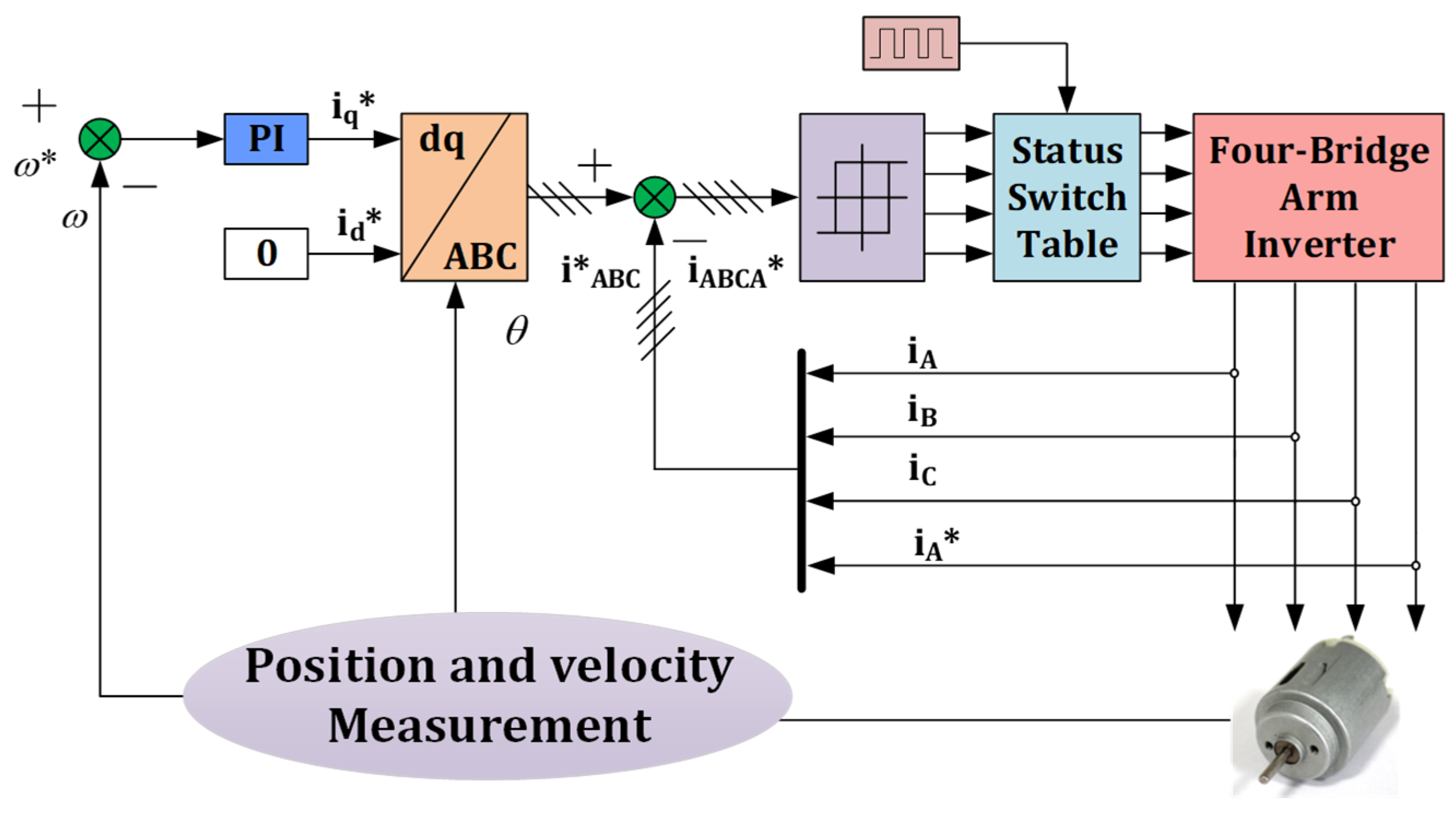
3.1. Open-Winding PMSM Control System Based on Improved Hysteresis Current Control for Four-Leg Inverter

The mathematical model and voltage vector analysis established in Section 2 provide the necessary foundation for the controller design. The insights gained from the vector analysis—specifically, the complete set of available voltage vectors and the role of the independent fourth leg in zero-sequence control—are directly utilized in this section to construct the improved hysteresis current control strategy. The core objective of this strategy is to address the variable switching frequency issue of traditional hysteresis control while leveraging the unique advantages of the four-leg topology.

Based on the system model and voltage vector analysis established in the previous section, this section presents the improved hysteresis current control strategy for the four-leg inverter. Figure 5 shows the control block diagram of the open-winding motor drive system based on the improved hysteresis current control for the four-leg inverter. The control strategy consists of the following steps: first, the actual motor speed and rotor position are measured using Hall sensors. The rotor position is used to derive the electrical angle θ for coordinate transformation, while the speed is obtained by differentiating the position signal and processed by a speed regulator to obtain the q-axis reference current i_q*; then, the four-phase motor currents are sampled by current sensors, and the current errors are calculated by comparing them with the reference currents; based on the output of the hysteresis comparator (current error), high-frequency pulse signals are generated to directly control the switching of the four-leg inverter (T1–T7) and drive the open-winding motor.

The key distinction between the improved hysteresis current control and conventional methods lies in its decoupling of the error signal from direct switch control. Unlike traditional strategies where the hysteresis comparator directly drives the power switches—resulting in a variable switching frequency—the improved version incorporates a switching-state lookup table operating at a fixed period $T_s$. This architectural innovation stabilizes the switching frequency, which is its primary advantage. In conventional methods, the hysteresis comparator directly controls the power switches, resulting in unstable switching frequency, which tends to cause current harmonics and hardware losses. In contrast, the improved strategy maintains fast response and strong tracking capability while stabilizing the switching frequency, reducing current distortion, and extending device lifespan. Experimental results validate its superiority in speed regulation and load disturbance rejection, achieving an overall balance between dynamic response and system stability. In conventional hysteresis current-controlled four-leg inverter open-winding motor drive systems, the operating frequency of the power switching devices is highly unstable due to inherent limitations of the hysteresis comparator. When the operating frequency range is too wide, the motor current becomes distorted, generating significant harmonics. Therefore, this paper proposes an improved hysteresis current control strategy.

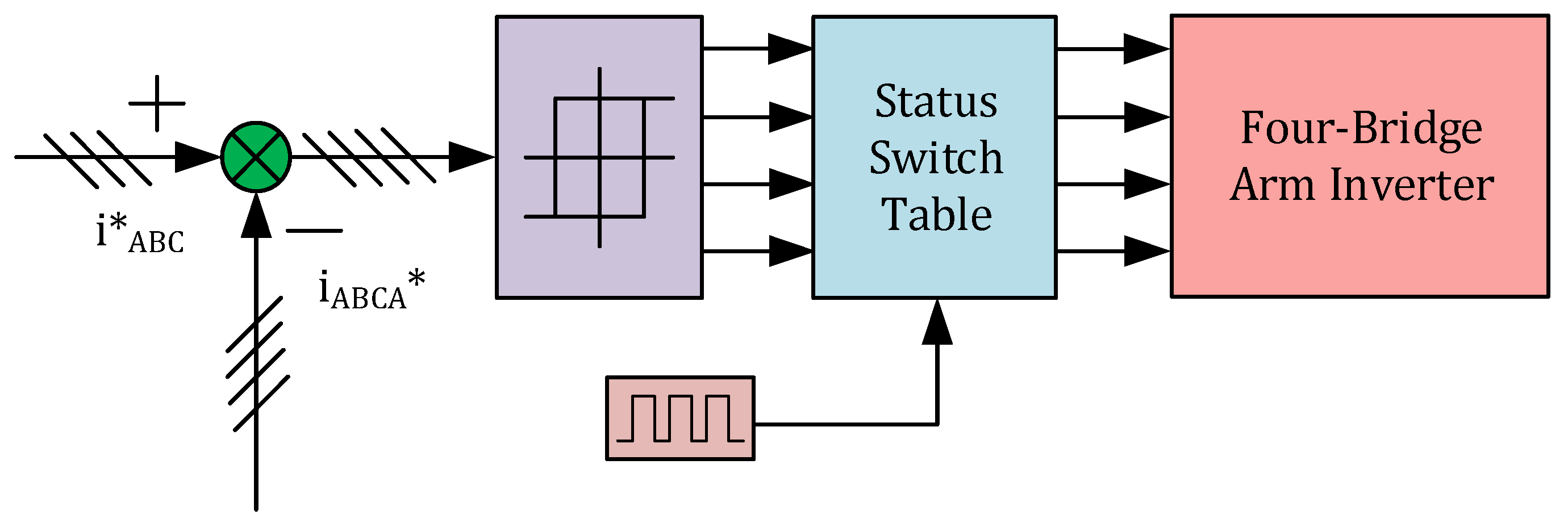
3.2. Operating Principle of Improved Hysteresis Current Control

The proposed improved hysteresis current control strategy is distinguished from both conventional hysteresis control and generic lookup table approaches by its tailored integration with the four-leg OW-PMSM topology. While the use of a lookup table to stabilize frequency is known, its application here is uniquely constrained by the system’s coupled phase voltages and the critical requirement for zero-sequence current suppression. The core innovation is the synthesis of the lookup table (

Table 2. Improved current hysteresis inverter status table.

Status	${\mathbf{K}}_{\mathbf{A}}$	${\mathbf{K}}_{\mathbf{B}}$	${\mathbf{K}}_{\mathbf{C}}$	${\mathbf{K}}_{{\mathbf{A}}^{*}}$
1	0	0	0	0
2	0	0	0	1
3	0	0	1	0
4	0	0	1	1
5	0	1	0	0
6	0	1	0	1
7	0	1	1	0
8	0	1	1	1
9	1	0	0	0
10	1	0	0	1
11	1	0	1	0
12	1	0	1	1
13	1	1	0	0
14	1	1	0	1
15	1	1	1	0
16	1	1	1	1

) based on the comprehensive voltage vector analysis from Section 2.2. Its selection logic is engineered not only to minimize current error but also to intrinsically prioritize switching states that contribute to zero-sequence voltage control, thereby achieving simultaneous current tracking and zero-sequence suppression within a single, fixed-frequency control framework. While using a lookup table to stabilize switching frequency is a recognized technique, its application to the four-leg OW-PMSM topology presents unique challenges, such as coupled phase voltages and the imperative need for zero-sequence current suppression, which generic approaches cannot address. The core innovation of this work, therefore, lies in the specialized synthesis of a pre-defined switching-state lookup table (Table 2). Derived from a comprehensive voltage vector analysis of the four-leg inverter (Section 2.2, Figure 4), this table is engineered with a selection logic that not only minimizes current error but also intrinsically prioritizes states for zero-sequence voltage control. This dual functionality enables simultaneous accurate current tracking and inherent zero-sequence suppression within a single, fixed-frequency control framework, representing a significant advancement over conventional implementations.

The operating principle of the improved hysteresis current control is illustrated in Figure 6.

The current error vector is defined as $i_e={\left[\begin{array}{cccc}{i}_{e\_A}& i_{e\_B}& i_{e\_C}& i_{e\_A^{*}}\end{array}\right]}^T$, where $i_{e\_j}={i^{*}}_j-i_j(j=A,B,C,A^{*})$. Taking the positive terminal of phase A winding in the open-winding motor as an example, the phase A current deviation is given by:

$$i_{\mathrm{e}\_\mathrm{A}}=i_{\mathrm{A}}^{*}-i_{\mathrm{A}}$$

(7)

where i_{e_A} is the current deviation, i*_A is the reference current, and i_A is the actual feedback current.

In inverter leg L4, the current direction of the A* phase is opposite to that of the A phase. The switching state of L4 is determined by the relationship between the actual current of the A* phase and reference current of the A phase. The current deviation of the A* phase is then given by:

$$i_{{\mathrm{e}\_\mathrm{A}}^{*}}=i_{{\mathrm{A}}^{*}}^{*}-i_{{\mathrm{A}}^{*}}$$

(8)

where i_{e_A}* is the current deviation of the A^* phase, $i_{{\mathrm{A}}^{*}}^{*}$ is the reference current, and i_A* is the actual feedback current of the A* phase.

The dynamic variation in the current error, influenced by the inverter output voltage and the motor back EMF, can be expressed as:

$${\displaystyle \frac{d{i}_e}{dt}}=-{\displaystyle \frac{R}{L}}{i}_e+{\displaystyle \frac{1}{L}}\left(V_{inv}-V_{emf}\right)-{\displaystyle \frac{d{i}^{\ast }}{dt}}$$

(9)

where V_inv is the inverter output voltage vector, which depends on the switching states; V_emf is the motor back EMF vector; and R and L are the winding resistance and inductance, respectively.

The output signal of the hysteresis comparator is given by:

$${\mathrm{H}}_{\mathrm{j}}=\left\{\begin{array}{c}1\\ 0\\ Maintain the previous state\end{array} \right.\begin{array}{c}{i}_{e\_j}>h\\ i_{e\_j}<-h\\ Other circumstances\end{array}$$

(10)

where $j=A,B,C,A^{*}$, h are the upper and lower thresholds of the hysteresis comparator, and h > 0.

Therefore, within a fixed period T_s, the state of the power switches in the inverter leg is determined as:

$${\mathrm{K}}_j=\mathrm{T}({\mathrm{H}}_A,{\mathrm{H}}_B,{\mathrm{H}}_C,{\mathrm{H}}_{A^{*}}){|}_{\mathrm{T}=\mathrm{Ts}, j=(1~6)}$$

(11)

Here, K_j represents the operating state of the power switches in the inverter leg during the fixed period T_s With four inverter legs, there are 16 possible switching state combinations through permutation. The corresponding driving states of K_j are listed in Table 2.

Table 2 enumerates the 16 possible switching state combinations $({\mathrm{K}}_{\mathrm{A}},{\mathrm{K}}_{\mathrm{B}},{\mathrm{K}}_{\mathrm{C}},{\mathrm{K}}_{{\mathrm{A}}^{*}})$ for the four-leg inverter. Each state corresponds to a unique output voltage vector, which is selected based on the output of the hysteresis comparator to minimize the current tracking error. Using this switching state table, the improved hysteresis current control drives the power switches to turn on and off, thereby enabling accurate tracking of the actual current. Consequently, this approach directly addresses the primary limitation of traditional hysteresis control—variable switching frequency. It reduces the impact of current harmonics, extends the lifespan of the power switches by avoiding stressful high-frequency switching bursts, stabilizes the operating frequency, and simplifies the thermal design of the inverter. The computational efficiency is maintained as the table lookup is a low-overhead operation.

3.3. Mathematical Model of the Improved Hysteresis Current Control

To simplify the analysis of the system’s frequency response, the dynamic variation in the current error can be approximated as linear over a sufficiently short switching period Ts. This approximation holds under the condition that the rate of change in the reference current is constrained by the motor armature time constant (L/R), and that load disturbances do not vary significantly within T_s, the system’s transfer function can be modeled as:

$$G_e(s)={\displaystyle \frac{{\widehat{i}}_e(s)}{{\widehat{i}}^{*}(s)}}={\displaystyle \frac{1}{1+\frac{R}{L}s+\frac{1}{LC}{s}^2}}$$

(12)

where C is the equivalent capacitive load, determined by the hysteresis bandwidth and switching frequency.

To maintain a fixed frequency $f_s=1/T_s$, the Nyquist stability criterion must be satisfied:

$$\left|G_e\right(j{\omega }_s\left)\right|<1\hspace{1em}{\omega }_s=2\pi f_s$$

(13)

In this linearized model (Equation (12)), the equivalent capacitance C characterizes the dynamics introduced by the hysteresis control. Its value is closely related to the hysteresis bandwidth h and the switching period T_s: a smaller h or a shorter T_s generally results in a smaller equivalent C, thereby increasing the system bandwidth but potentially increasing susceptibility to high-frequency noise; conversely, a larger h or a longer T_s provides stronger filtering but reduces the dynamic response speed. Thus, by co-adjusting h and T_s, the system’s frequency response can be optimized to effectively suppress higher-order harmonics near the switching frequency. The subsequent Bode and Nyquist analyses are based on this model, considering the specific designed values of h and T_s.

The Bode magnitude-frequency characteristic curve in Figure 7 reveals the unique frequency response characteristics of the improved hysteresis control system. The system exhibits a significant resonant peak at 503 Hz, with a high quality factor of 63.25 and an extremely low damping ratio of 0.01, indicating a highly resonant system. At the designed switching frequency of 15 kHz, the system gain sharply attenuates to −58.9 dB. This deep attenuation strictly satisfies the stability condition |G(jω)| ≪ 1, providing ample stability margin for the system. The high-frequency range demonstrates excellent attenuation characteristics, effectively suppressing switching noise and high-frequency harmonic interference. Through rational frequency planning, the switching frequency is set two orders of magnitude away from the resonant frequency, successfully avoiding the inherent resonance risk of oscillation-prone systems. This demonstrates that the control system maintains excellent stability and anti-interference performance even under strong resonance conditions.

It is important to note that the aforementioned linear approximation model is primarily used for frequency-domain design and stability analysis. In the practical system, abrupt changes in load torque can act as unknown disturbances that violate this local linearity. Therefore, the stability analysis in Section 3.4 and the experimental validation in Section 4 account for these nonlinearities to ensure controller robustness under real-world conditions.

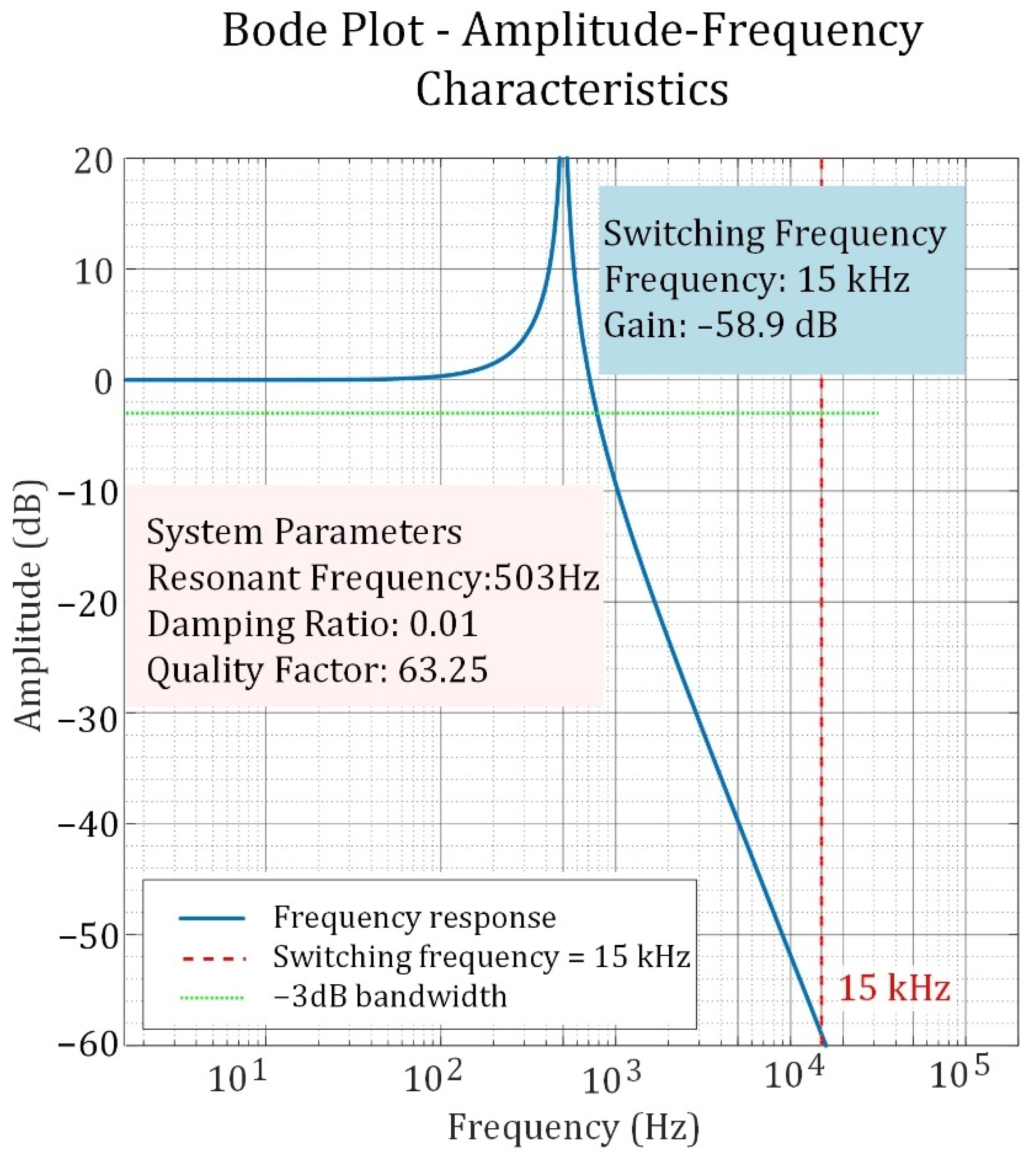
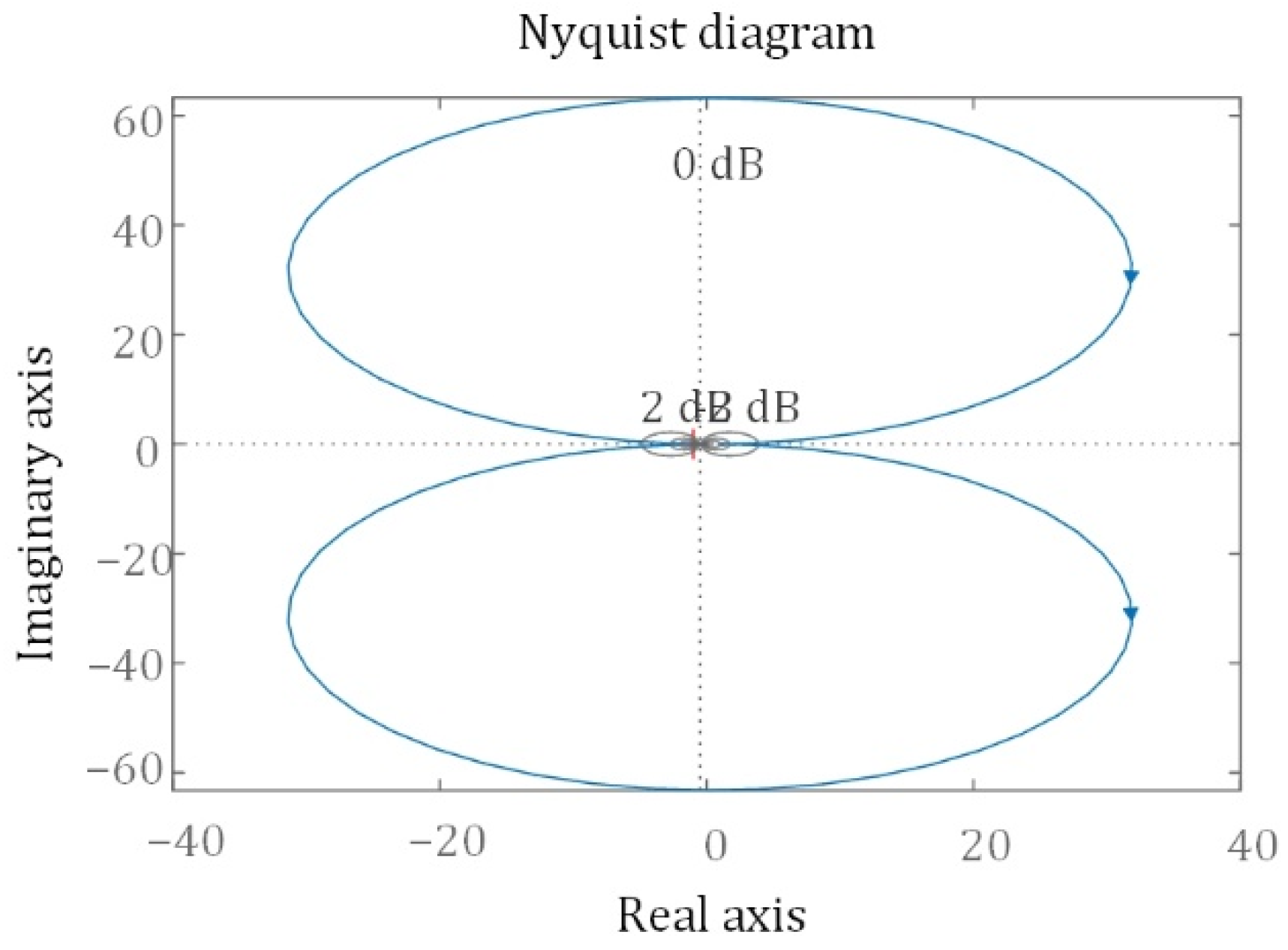
3.4. Stability Analysis of the Improved Hysteresis Current Control

The frequency-domain stability is rigorously analyzed using the Nyquist criterion. As shown in Figure 8, the Nyquist plot of the open-loop transfer function Ge(s) exhibits a smooth trajectory in the complex plane that does not encircle the critical point (−1, 0), thereby satisfying the stability criterion. Quantitative analysis further confirms robust stability, with a gain margin of 6 dB and a phase margin of 62°. These values significantly exceed typical engineering requirements (e.g., gain margin > 3–6 dB, phase margin > 45°), demonstrating substantial robustness against parameter variations and disturbances.

A comprehensive stability analysis is conducted to rigorously verify the global stability of the proposed control system. The analysis combines frequency-domain and time-domain methods to provide complementary insights. First, the Nyquist criterion is employed to assess robustness and stability margins in the frequency domain. Subsequently, Lyapunov’s direct method is utilized to establish global asymptotic stability in the time domain, considering the system’s nonlinear characteristics. For time-domain stability verification, Lyapunov’s direct method is applied. Consider the positive definite Lyapunov function candidate shown in Equation (14), which represents the energy of the current tracking error.

$$W({\mathit{i}}_{\mathit{e}})={\displaystyle \frac{1}{2}}{{\mathit{i}}_{\mathit{e}}}^{\mathit{T}}{\mathit{i}}_{\mathit{e}},$$

(14)

Its physical meaning represents the energy of the system’s current tracking error. Taking the time derivative of W(i_e) and combining it with the motor dynamic equation $L\stackrel{•}{{\mathit{i}}_{\mathit{e}}}+R{\mathit{i}}_{\mathit{e}}={\mathit{v}}_{\mathit{inv}}-{\mathit{V}}_{\mathit{emf}}-L\stackrel{•}{{\mathit{i}}^{*}}$ yields:

$$\stackrel{•}{W}={{\mathit{i}}_{\mathit{e}}}^{\mathit{T}}\stackrel{•}{{\mathit{i}}_{\mathit{e}}}={{\mathit{i}}_{\mathit{e}}}^{\mathit{T}}\left(-{\displaystyle \frac{R}{L}}{\mathit{i}}_{\mathit{e}}+{\displaystyle \frac{1}{L}}(v_{\mathit{inv}}-{\mathit{V}}_{\mathit{emf}})-{\displaystyle \frac{d{i}^{\ast }}{dt}}\right)$$

(15)

After simplification:

$$\stackrel{•}{W}=-{\displaystyle \frac{R}{L}}{{\mathit{i}}_{\mathit{e}}}^{\mathit{T}}{\mathit{i}}_{\mathit{e}}+{\displaystyle \frac{1}{L}}{{\mathit{i}}_{\mathit{e}}}^{\mathit{T}}(v_{\mathit{inv}}-{\mathit{V}}_{\mathit{emf}}-L{\displaystyle \frac{d{i}^{\ast }}{dt}}).$$

(16)

If the inverter voltage $v_{\mathit{inv}}$ can accurately track

$${\mathit{V}}_{\mathit{inv}}={\mathit{V}}_{\mathit{emf}}+L{\displaystyle \frac{d{i}^{\ast }}{dt}}-k{\mathit{i}}_{\mathit{e}},\hspace{1em}(k>0)$$

(17)

then the derivative satisfies:

$$\stackrel{•}{W}=-\left({\displaystyle \frac{R}{L}}+k\right)\parallel i_e{\parallel }^2\le 0.$$

(18)

It is worth noting that the control law in Equation (17) relies on the assumption that the back-EMF vector V_emf remains approximately constant and known within the short switching period T_s. This common assumption simplifies the controller design by facilitating feedforward compensation. However, its validity decreases during high-speed operation or severe transients, where V_emf varies significantly, potentially leading to tracking errors. While the experimental results in Section 4 demonstrate robust performance under tested conditions, this limitation should be considered for designs targeting an extremely wide operating range.

According to the Lyapunov stability theorem: if $\stackrel{•}{W}\le 0,W(i_e)>0$, the system is globally stable; if $||i_e||\ne 0,\stackrel{•}{W}<0$, the error asymptotically converges to zero.

The improved hysteresis control utilizes a state switching table with a fixed period T_s, forcing V_inv to approach its ideal value within a finite time and avoiding high-frequency oscillations. Meanwhile, the hysteresis bandwidth h limits the maximum error $\left|\left|e\right|\right|\le h$, ensuring that the derivative of W is negative definite and satisfying the stability condition. Additionally, the independent control of leg A* ensures that $e_0$ approaches zero, effectively suppressing zero-sequence current and avoiding the associated risk of instability.

The Lyapunov analysis demonstrates stability under the ideal assumption that the inverter output voltage V_inv can perfectly track the continuous reference V_emf. In the practical system, V_inv is quantized to the discrete voltage vectors defined by the switching-state lookup table (Table 2). However, the core design principle of the lookup table is to select the available voltage vector that minimizes the current tracking error at each fixed sampling instant. When the switching frequency $f_s=1/T_s$ is sufficiently high relative to the system dynamics, the average behavior of the inverter output over a short period effectively approximates the desired reference. This ensures that the practical system operates in close alignment with the theoretical stability conditions, as confirmed by the robust experimental performance shown in Section 4.

4. Experimental Analysis

To quantitatively evaluate the performance of the improved hysteresis current control strategy developed in Section 3, a comprehensive experimental study was conducted. This section begins with a description of the experimental setup and its parameters. Subsequently, it presents and discusses the results of two key tests: speed regulation and load variation. The aim is to validate the theoretical claims regarding fixed switching frequency, reduced current ripple, effective zero-sequence current suppression, and robust dynamic performance under disturbances.

This section presents experimental validation of the proposed control strategy using a 60 W laboratory prototype. The prototype serves as a controlled platform to rigorously investigate three fundamental control challenges: switching frequency stabilization, current ripple minimization, and zero-sequence current suppression. These issues are scalable in nature and independent of power rating. By enabling precise measurement and analysis under repeatable conditions, the prototype provides critical proof-of-concept for the control principles. The results thus not only demonstrate the effectiveness of the strategy at this level but also form an essential foundation for its future application in higher-power systems. Two types of experiments—speed regulation and load variation tests—are conducted to evaluate the system’s comprehensive performance. These experiments verify the speed regulation capability and disturbance rejection performance of the proposed control system, respectively.

The effectiveness of the improved hysteresis current control strategy for the four-leg inverter is validated using the experimental platform with parameters listed in

Table 3. Parameters of the experimental platform.

Parameters	Values
Rated Voltage (V)	24
Rated Current (A)	2
Rated Power (W)	60
Rated Speed (r/min)	3000
Number of Pole Pairs	4
Stator Flux Linkage (Wb)	0.175
D-Q Inductance (mH)	8.5

.

An experimental platform for the four-leg inverter open-winding motor control system was constructed based on the improved hysteresis current control strategy. The hardware platform is shown in Figure 9.

The experimental setup, implemented at a 60 W power level, is designed to accurately replicate the critical control challenges of higher-power OW-PMSM drives, as the underlying system dynamics and coupling effects scale with the fundamental principles being tested. To emulate realistic industrial conditions, load torque was applied to the motor shaft using a precision powder brake (KRYSTAL, Model PMB-J.05, Wenzhou, China). Its braking torque, which is proportional to the excitation current, was precisely regulated by a dedicated tension controller to generate controlled and repeatable load disturbances, as utilized in the subsequent experiments. System performance—including current ripple and zero-sequence current suppression—was evaluated by comparing experimental results from this setup against well-established benchmarks: current ripple was benchmarked against standard hysteresis control, while zero-sequence suppression was assessed relative to the typical performance levels and known challenges in dual-inverter OW-PMSM systems that lack dedicated control.

(1)

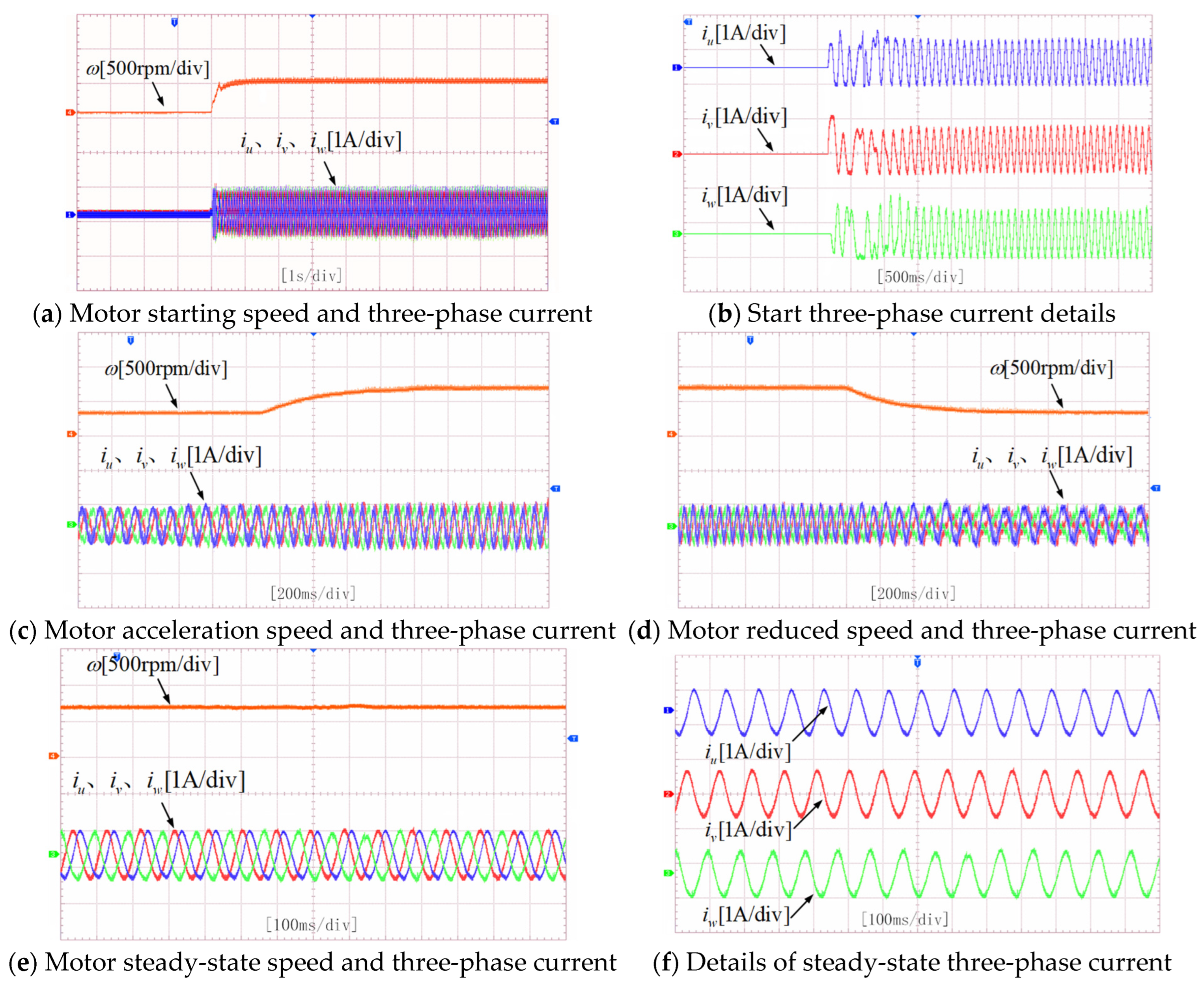
Speed Regulation Test: To evaluate the speed control capability, the initial reference speed of the open-winding motor was set to 500 r/min with an initial load of 2 N·m. After motor startup, the reference speed was increased to 800 r/min to test the acceleration performance of the system. The reference speed was then returned to 500 r/min to examine the deceleration performance. Variations in key parameters were observed throughout the speed regulation process. The experimental results are shown in Figure 10.

The speed regulation tests comprehensively evaluate both the dynamic and steady-state performance of the system. As shown in Figure 10, the controller exhibits excellent dynamic tracking during transients. The controller exhibits precise dynamic tracking during transients, with a speed overshoot of less than 2% and a settling time of approximately 100 ms during step changes. Specifically, when the speed reference steps between 500 r/min and 800 r/min (Figure 10c,d), the actual speed responds rapidly with a minimal overshoot of less than 2% and a short settling time of approximately 100 ms. Crucially, this dynamic capability is complemented by outstanding steady-state performance. Once stabilized (Figure 10e,f), the motor operates with negligible steady-state error and extremely low-speed ripple, while the three-phase currents maintain balanced, sinusoidal waveforms with low harmonic distortion. This combination of fast transient response and stable, precise steady-state operation validates the controller’s robustness and high performance across different operating conditions.

(2)

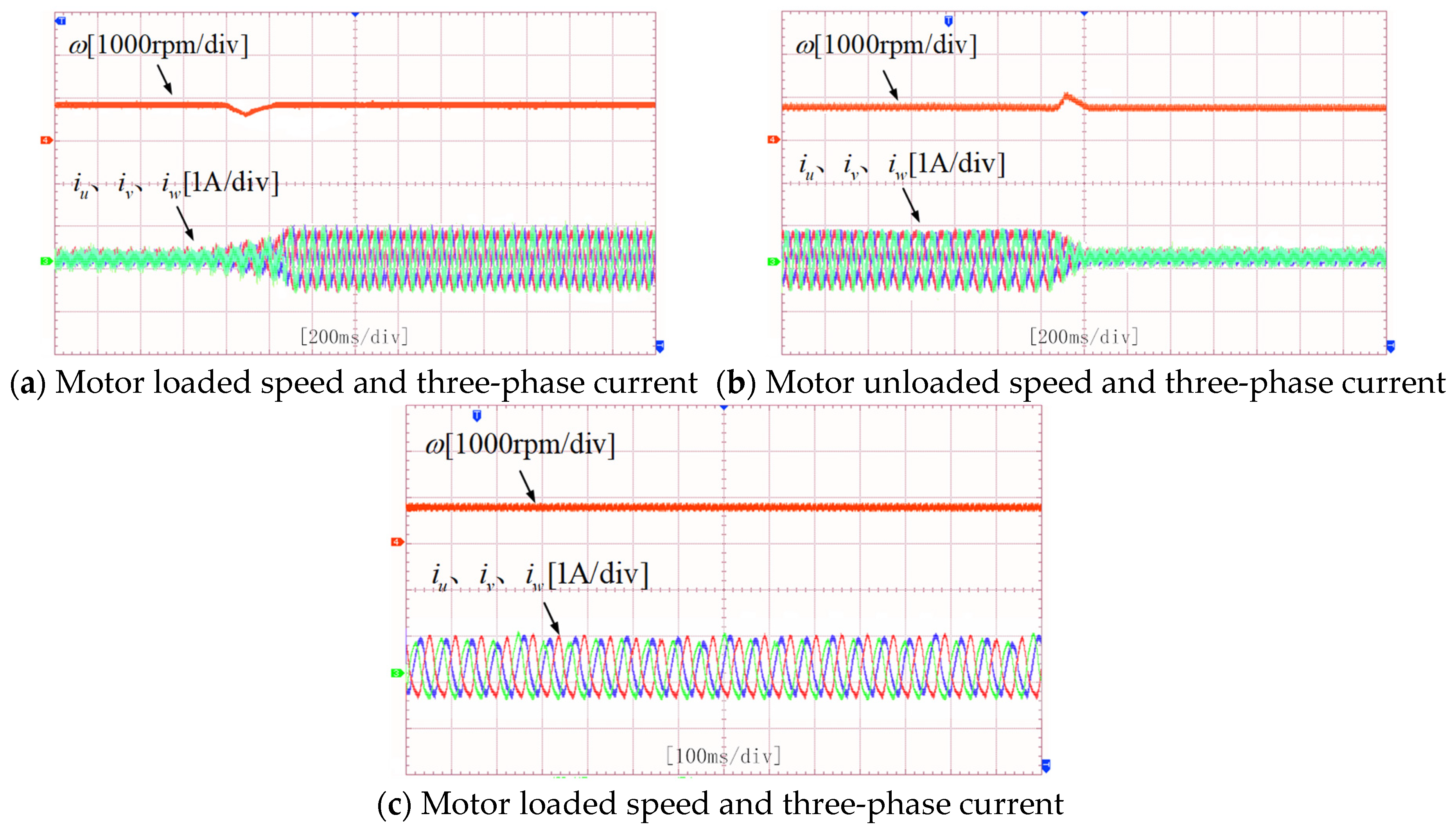
Load Variation Test: To evaluate the load disturbance rejection capability, the open-winding motor’s reference speed was set to 800 r/min, and the reference torque was set to 0 N·m. After the motor reached steady-state operation, a load disturbance was applied, and the variations in motor parameters were observed. The load was then removed to restore no-load conditions, and the parameter changes were monitored again. The experimental results are shown in Figure 11.

The system’s performance under load disturbance, detailed in Figure 11, further demonstrates its robustness. The dynamic speed response analysis during a step load increase (Figure 11a,c) shows that the maximum speed dip is confined to within 3% of the 800 r/min setpoint, with the system recovering to its steady-state within 150 ms, indicating excellent speed holding capability under sudden torque demands. Concurrently, the DC-link voltage exhibits robust regulation, with its deviation limited to within 5% of the nominal value and a recovery within 200 ms, ensuring a stable power supply during the transient. This stable electrical environment, in turn, supports the precise speed regulation observed. The three-phase currents adjust instantaneously and smoothly to compensate for the load torque without excessive overshoot. Following this transient, the system re-establishes a stable steady-state operation (Figure 11b), with all parameters, including speed and current, maintaining their values steadily. This consistent performance during both the transient and subsequent steady-state under load validates the controller’s effective disturbance rejection and reliable load-handling capability.

The experimental results validate the key achievement of the proposed control strategy: the stabilization of the inverter switching frequency at approximately 15 kHz. This stabilization directly mitigates the high-frequency spectral spreading and associated loss peaks inherent to variable-frequency hysteresis control, as evidenced by the consistent current ripple patterns. Consequently, it leads to more predictable and generally lower average switching losses. Furthermore, the observed reduction in current waveform distortion and the effective containment of the zero-sequence current collectively ensure higher current tracking accuracy and improved common-mode performance. These improvements—achieved while preserving the inherent fast dynamic response of hysteresis control—simultaneously enhance system efficiency by reducing the root-mean-square (RMS) current for the same torque output, thereby minimizing conduction losses. A comprehensive quantitative analysis of system efficiency will be addressed in future work.

In summary, the improved hysteresis current controlled four-leg inverter open-winding motor system effectively drives the motor with satisfactory dynamic and static characteristics. Therefore, the improved hysteresis current control algorithm proposed in this paper is validated as feasible.

5. Conclusions

This paper presents a novel control solution for four-leg inverter-driven OW-PMSMs that effectively addresses key limitations in prior work. The main contribution is the development of an improved hysteresis current control strategy featuring a systematically designed switching-state lookup table. Compared to existing methods, the proposed approach offers a unique combination of fixed switching frequency, inherent zero-sequence current suppression, and fast dynamic response. This integrated control advancement, coupled with the inherent cost advantage of the four-leg topology, provides a distinct and valuable alternative for practical OW-PMSM drive applications. This strategy maintains the advantages of high DC-link voltage utilization and low cost in conventional systems. The cost reduction, achieved by a 42% decrease in power switching devices, enhances the system’s cost-effectiveness without compromising the key performance metrics that govern energy output, such as torque capability and speed range. Based on the three-dimensional space vector modulation principle, the system categorizes switching states appropriately and introduces a fixed-period T_s lookup table mechanism, effectively mitigating issues such as switching frequency variation and significant current ripple in traditional hysteresis control. Experimental and theoretical analyses demonstrate that the proposed method maintains fast dynamic response while significantly improving current tracking accuracy and system stability. It not only achieves effective zero-sequence current suppression but also exhibits robust DC-link voltage regulation under step load changes, excellent speed regulation and disturbance rejection capabilities. Furthermore, the scheme features a simple structure and clear control logic, ensuring high performance while reducing cost, which highlights its strong practical value for engineering applications.

This paper has developed an improved hysteresis current control strategy with a switching-state lookup table for four-leg inverter-driven OW-PMSM systems. The main advancement lies in the integration of a fixed-period lookup table mechanism within the hysteresis control framework, which provides a systematic approach to maintaining stable switching frequency. Combined with the inherent cost advantage of the four-leg topology (42% fewer power switches than dual-inverter systems), this control strategy achieves enhanced performance without compromising cost-effectiveness. The experimental results demonstrate the effectiveness of this approach, showing significant reduction in current ripple, stable DC-link voltage regulation under load disturbances, and robust zero-sequence current suppression, while preserving the fast dynamic response characteristic of hysteresis control. This work provides a balanced solution that addresses both performance and practical implementation considerations in OW-PMSM drives, offering a valuable reference for future research and industrial applications.