Optimization of Pile Reinforcement in Soft Soils: A Numerical Analysis
Abstract
1. Introduction
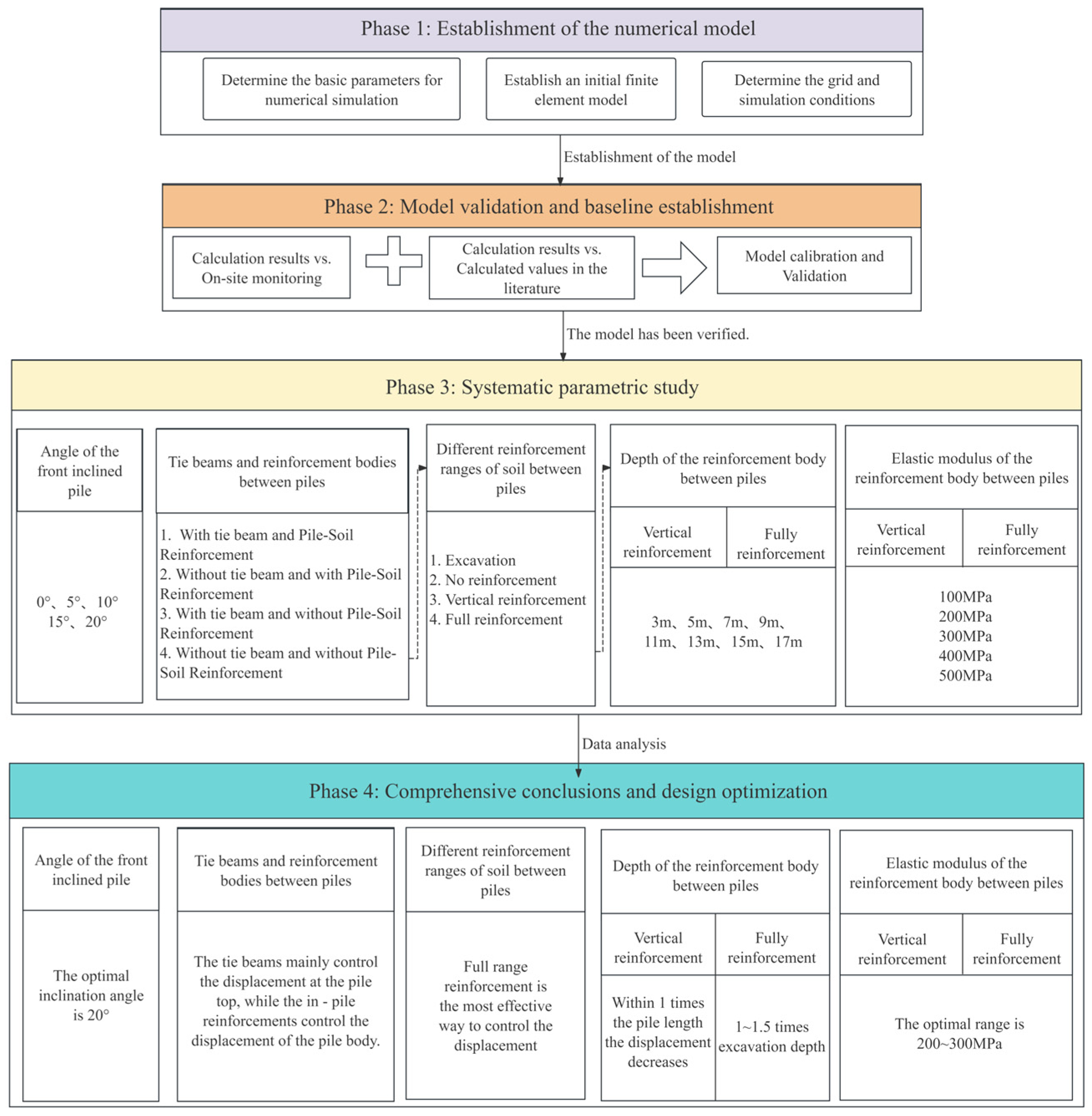
2. Methods
2.1. Mechanical Characteristics
2.2. Hardening Soil Constitutive Model (HS)
3. Project Overview and Numerical Simulation
3.1. Project Overview
3.2. Numerical Simulation
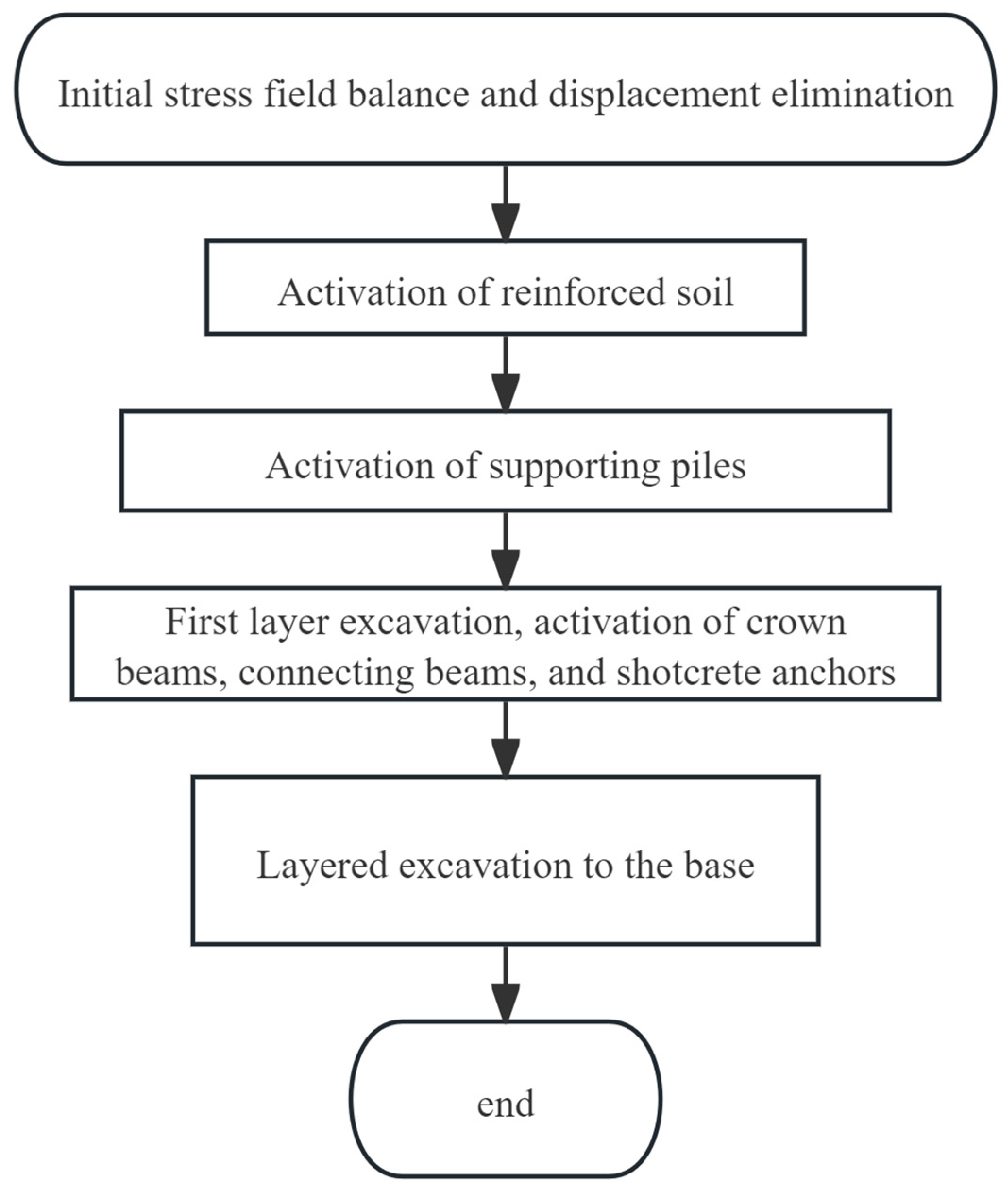
3.2.1. Numerical Model Establishment
3.2.2. Numerical Analysis Procedure
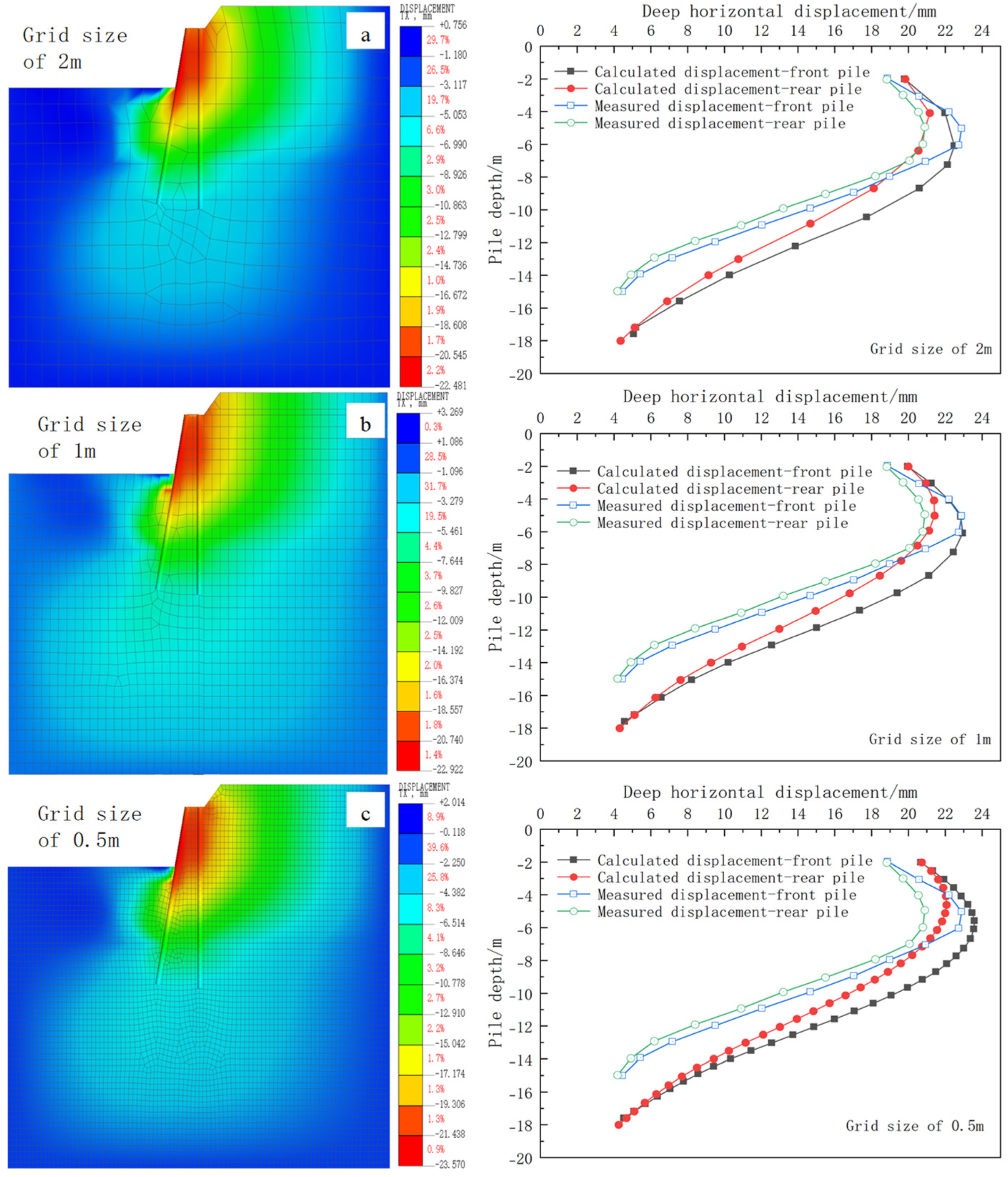
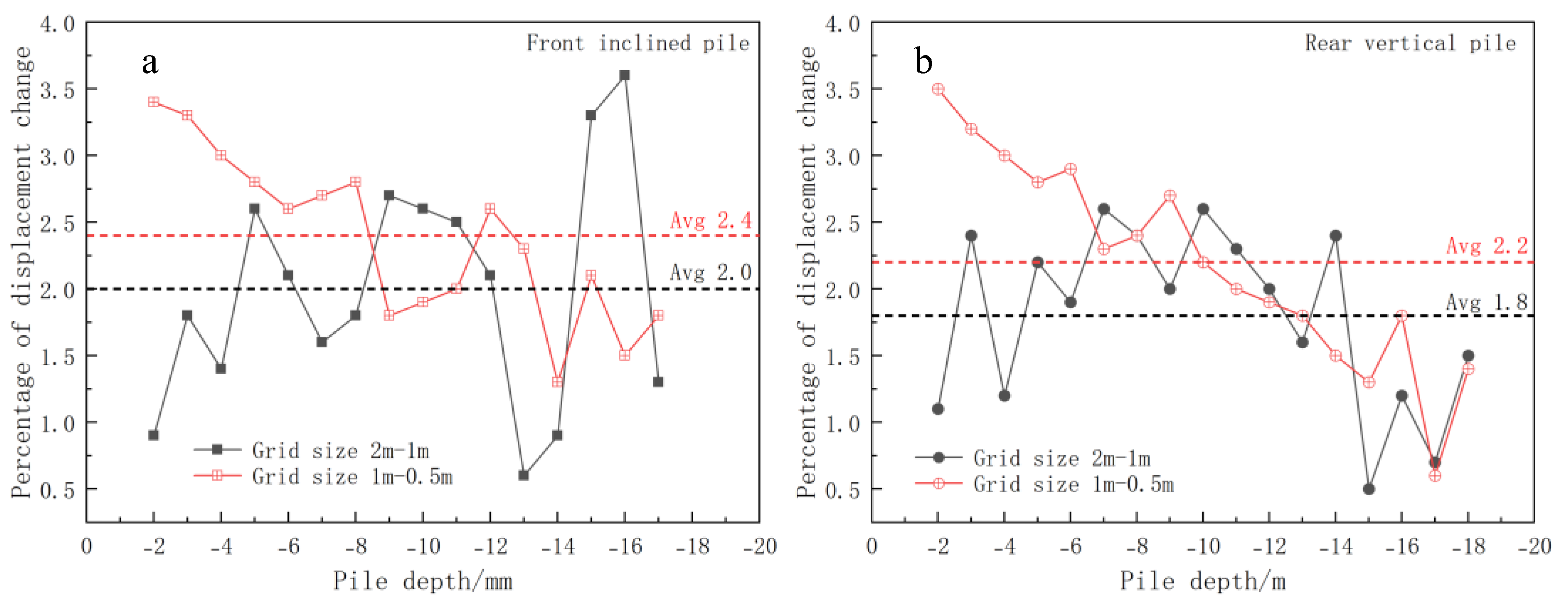
3.3. Mesh Size Sensitivity Analysis
3.4. Comparative Analysis of Results
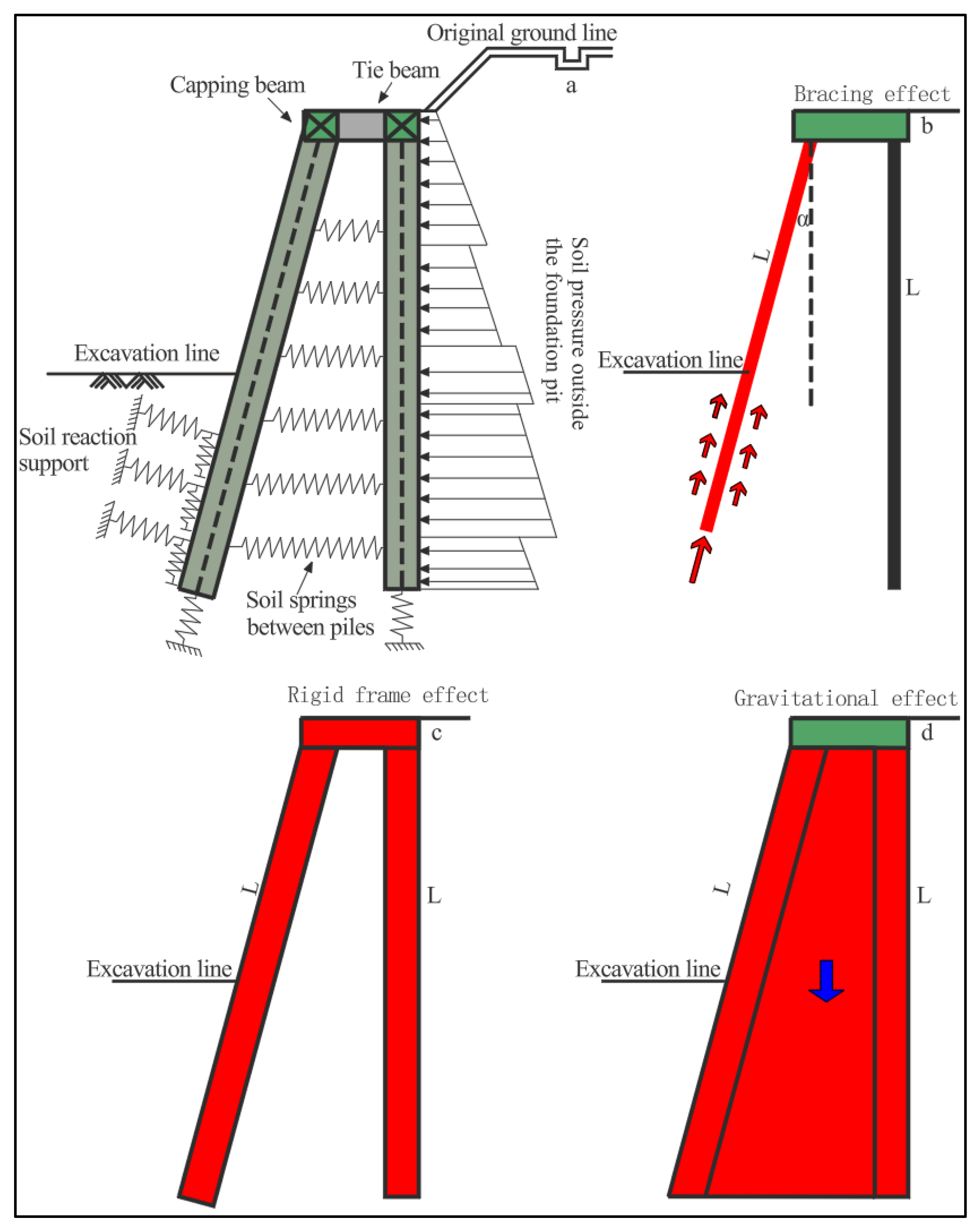
4. Study of the Displacement Characteristics and Influencing Factors of Inclined-Front, Vertical-Rear, Double-Row Piles
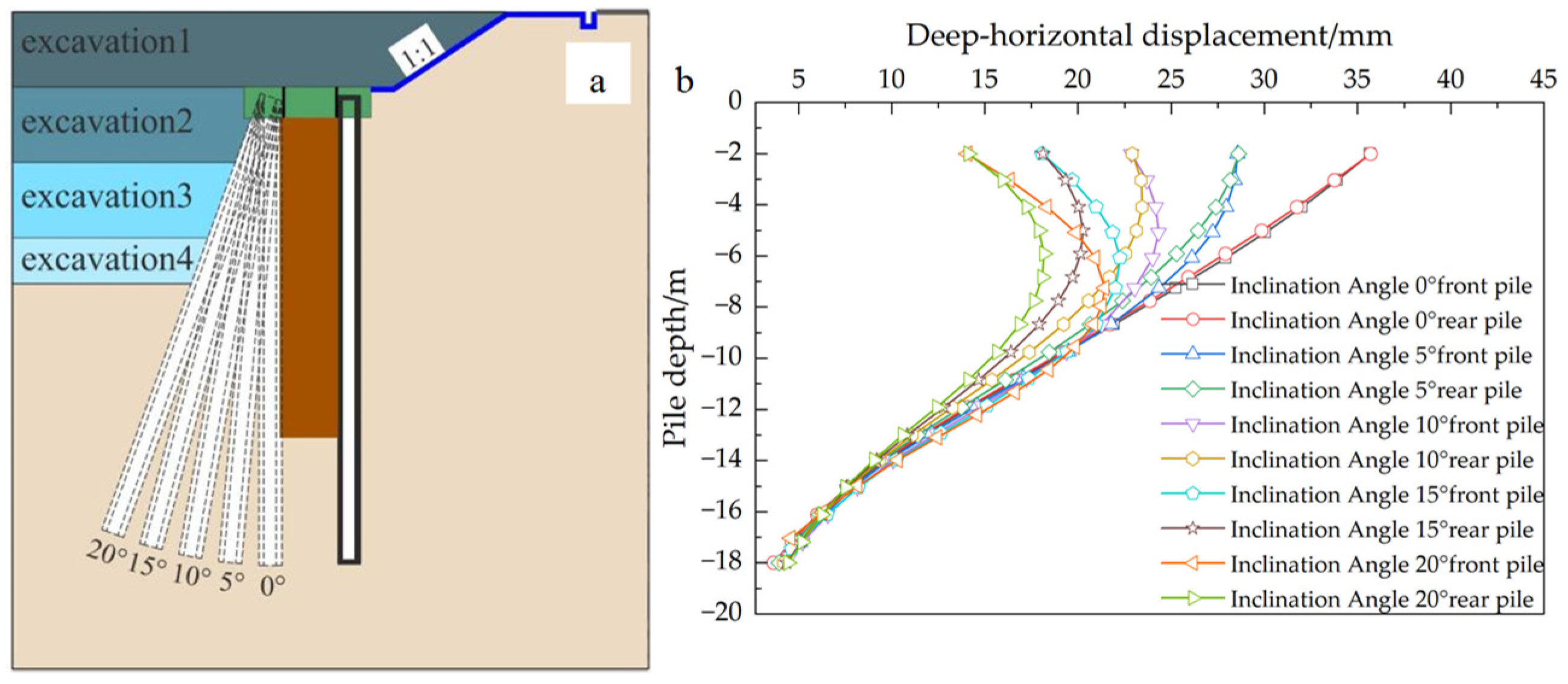
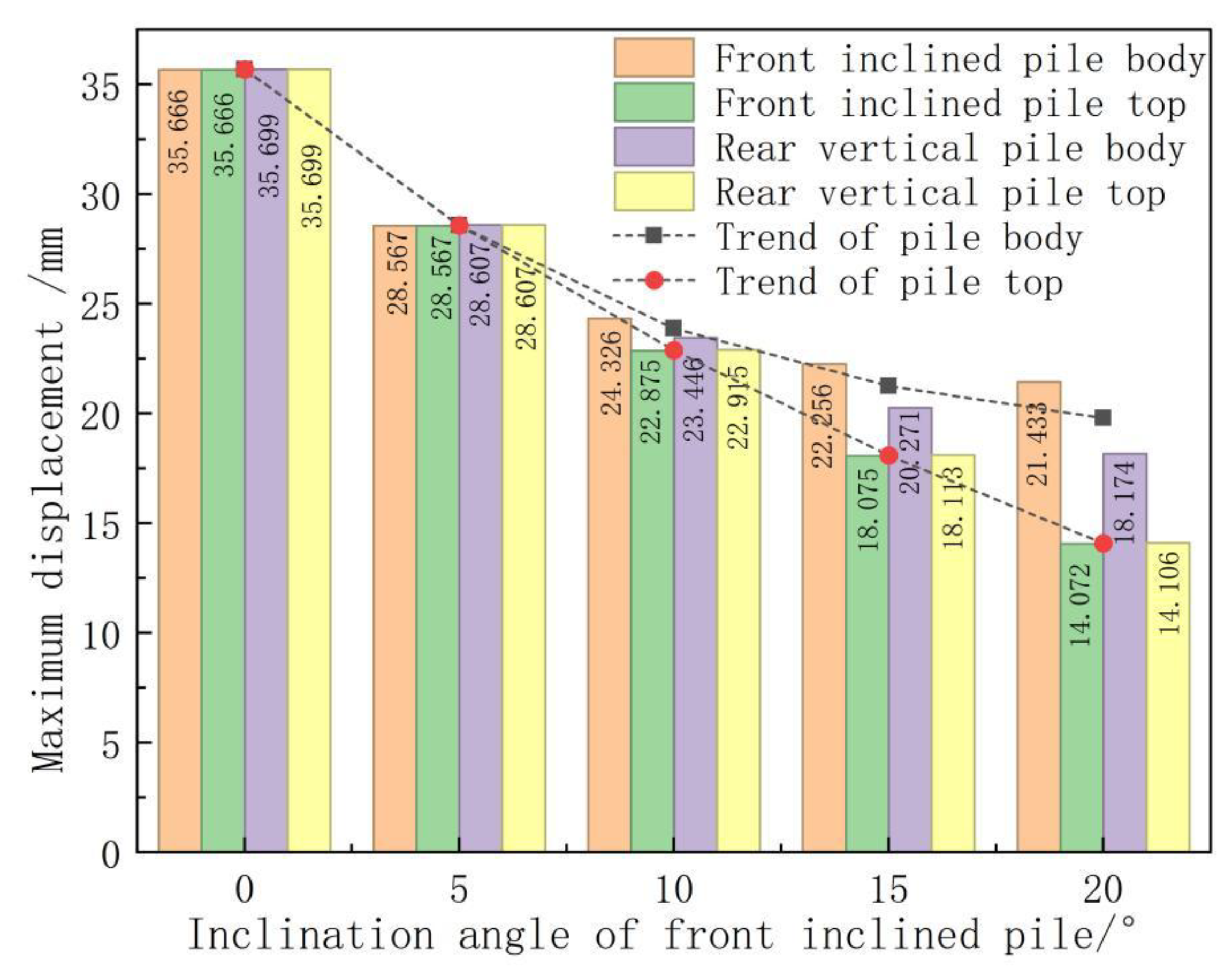
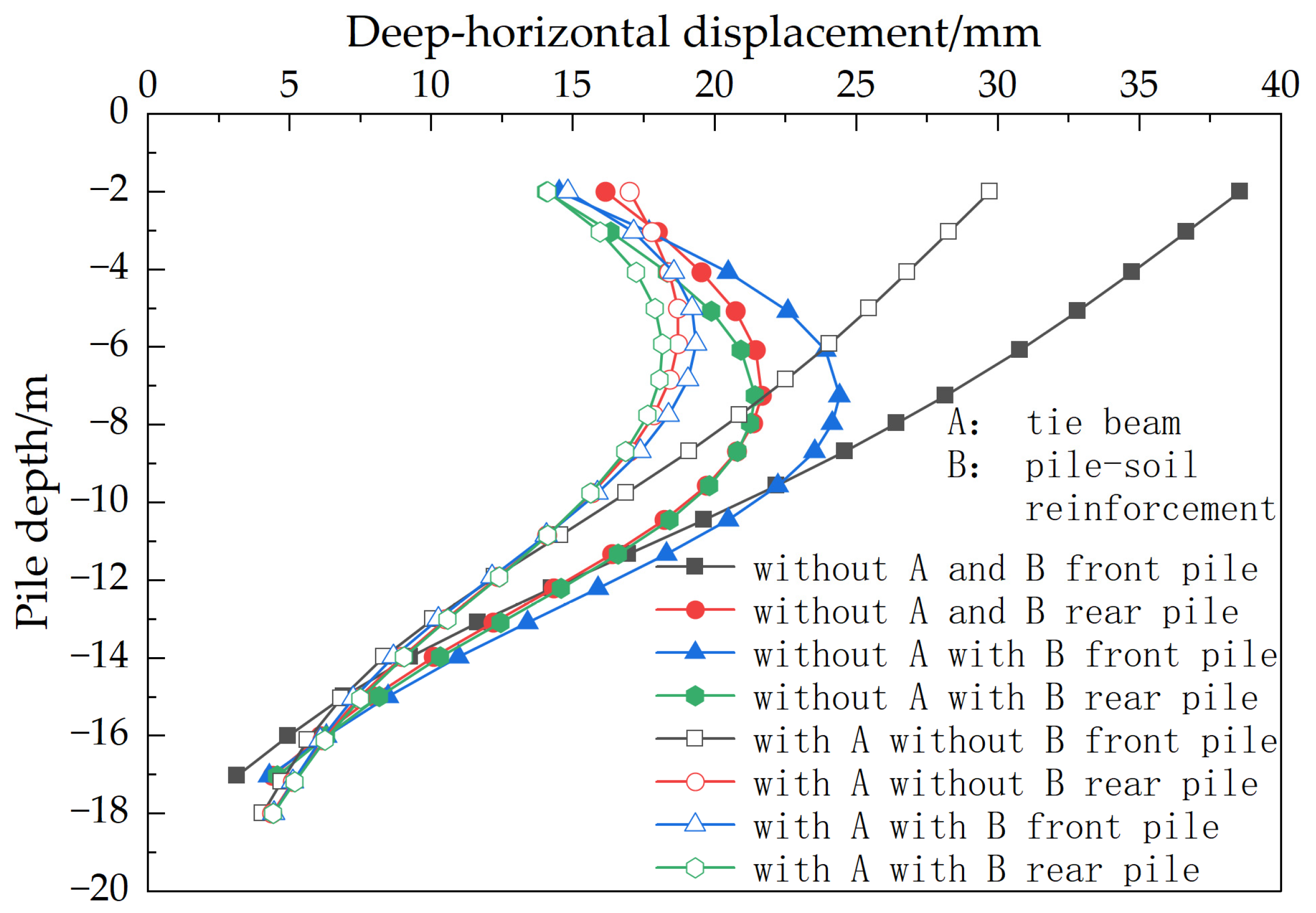
4.1. Inclination Angle’s Influence on Support System Deformation
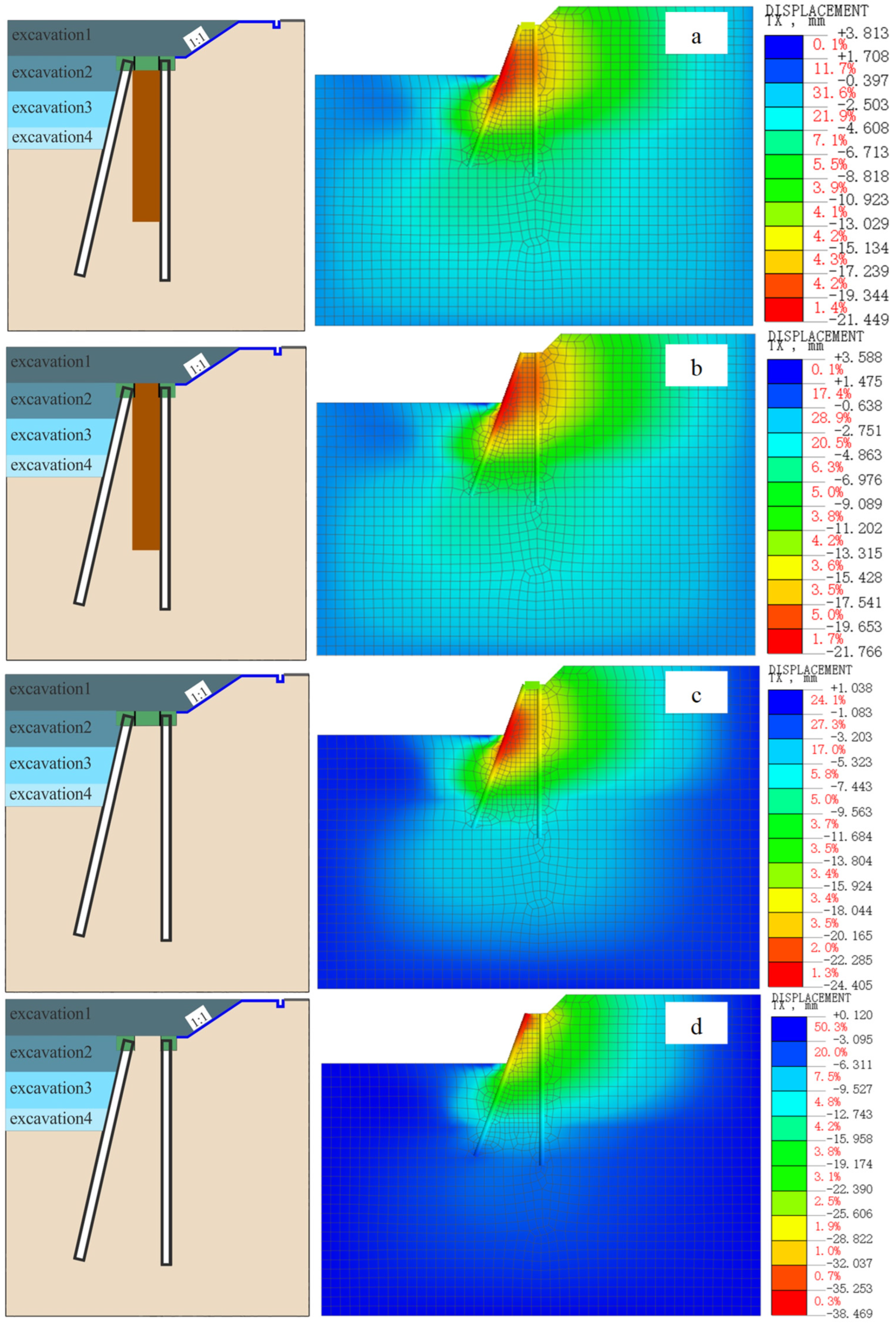
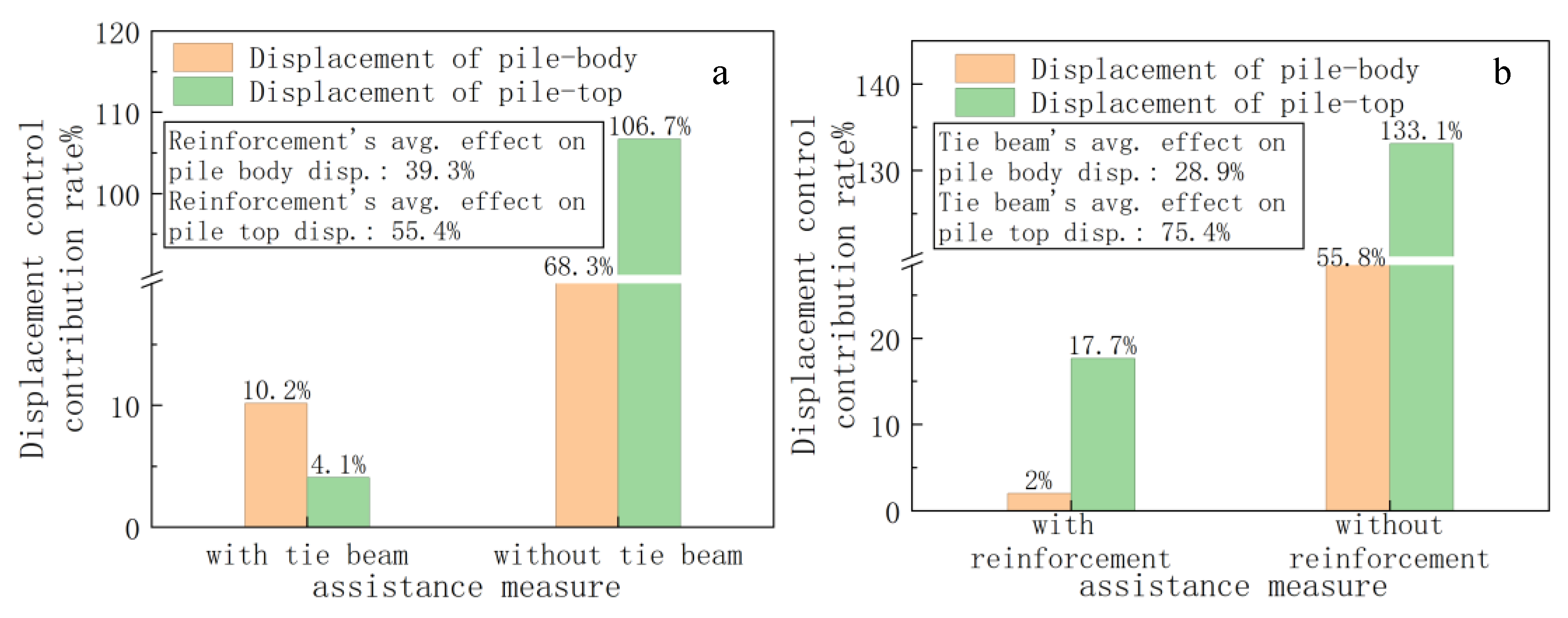
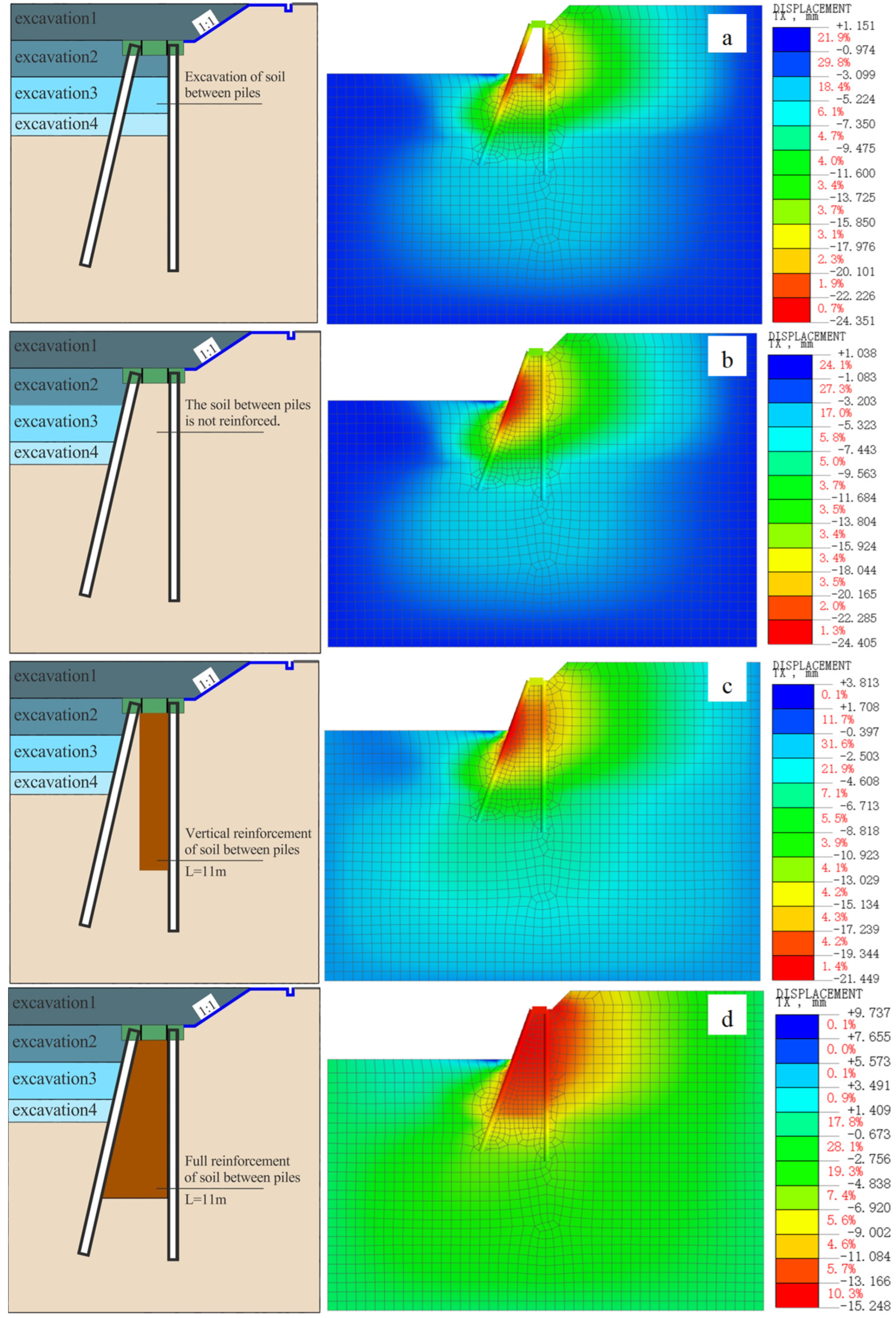
4.2. Influence of the Top Crown Beam of Piles and the Soil Between Piles on the Deformation of the Retaining and Protecting System
5. Parameter Analysis of Reinforcement Between Inclined-Front, Vertical-Rear, Double-Row Piles
5.1. Influence of Reinforcement Range on Deformation Characteristics of the Support System
5.2. Analysis of the Depth of Reinforced Soil Between Piles
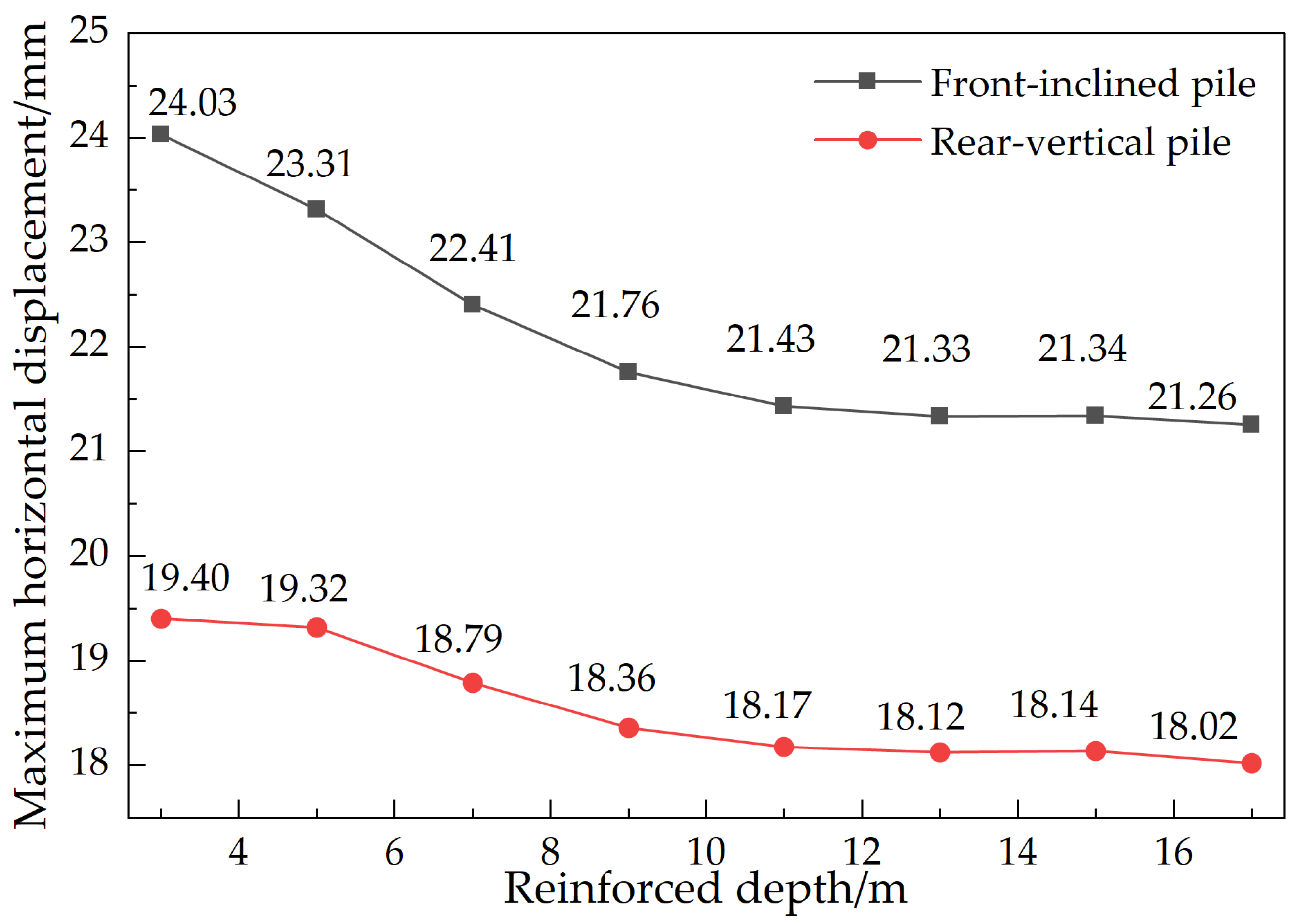
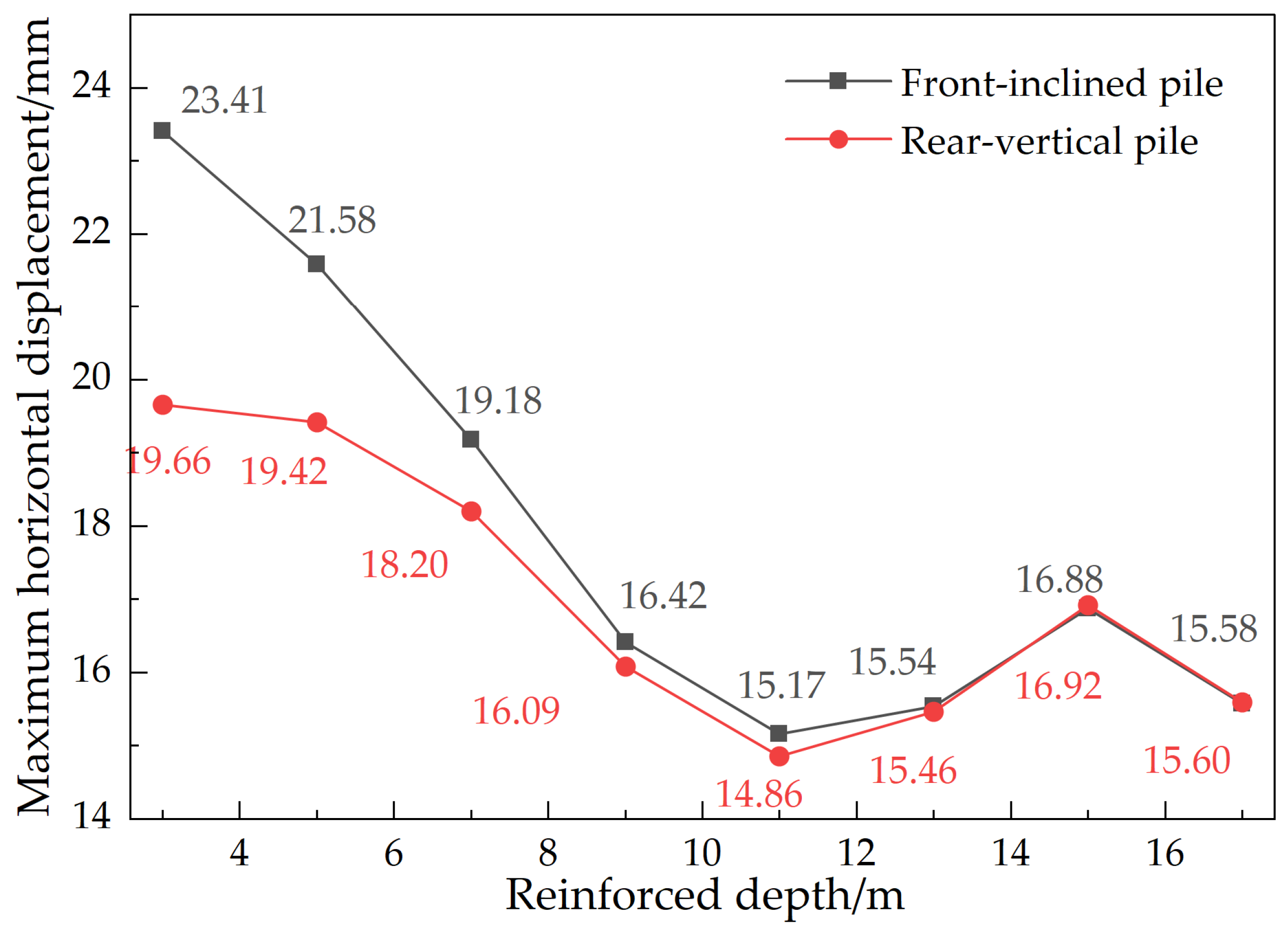
5.2.1. Influence of Reinforcement Depth on Pile Displacement
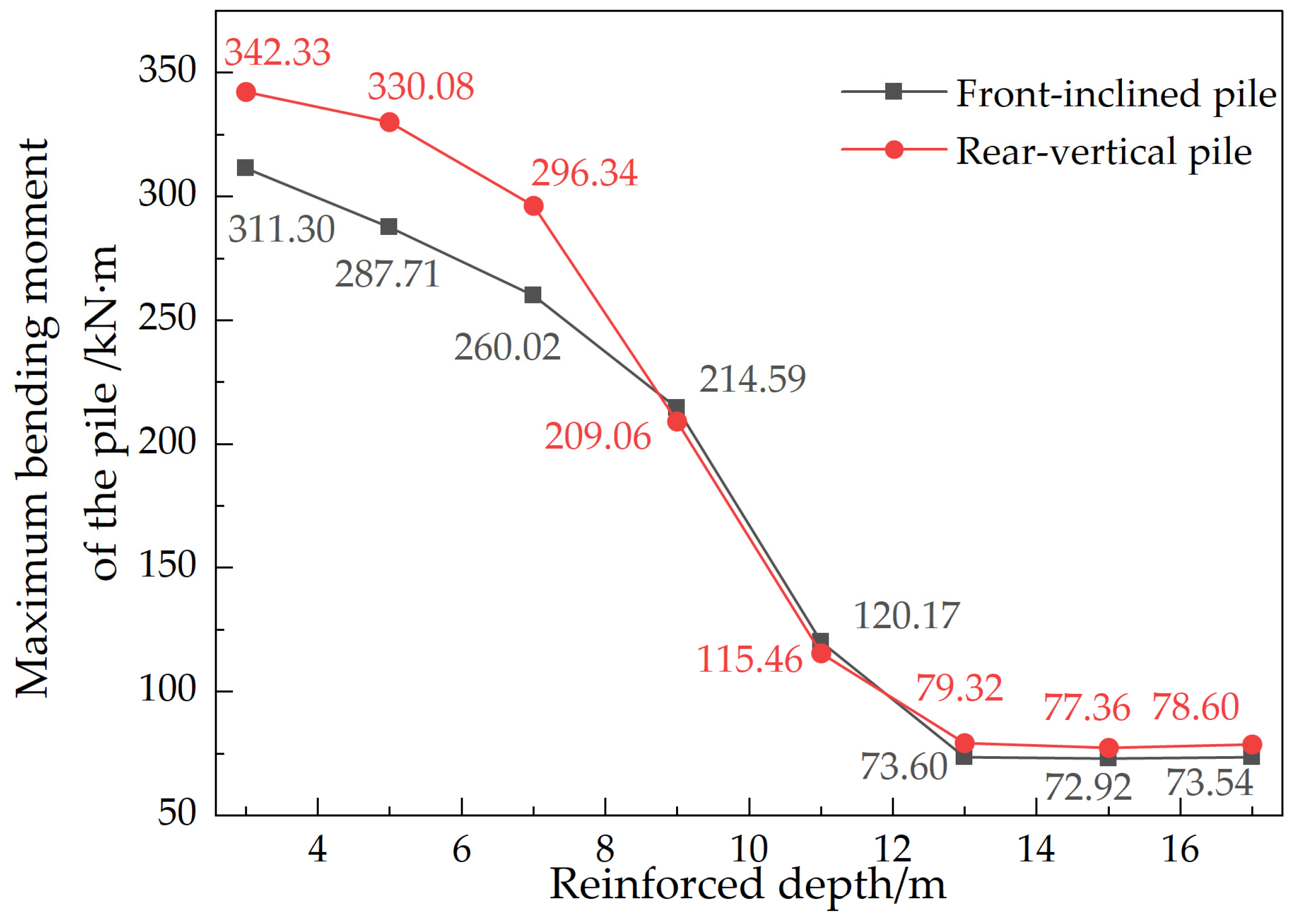
5.2.2. Influence of Reinforcement Depth on Pile Bending Moment
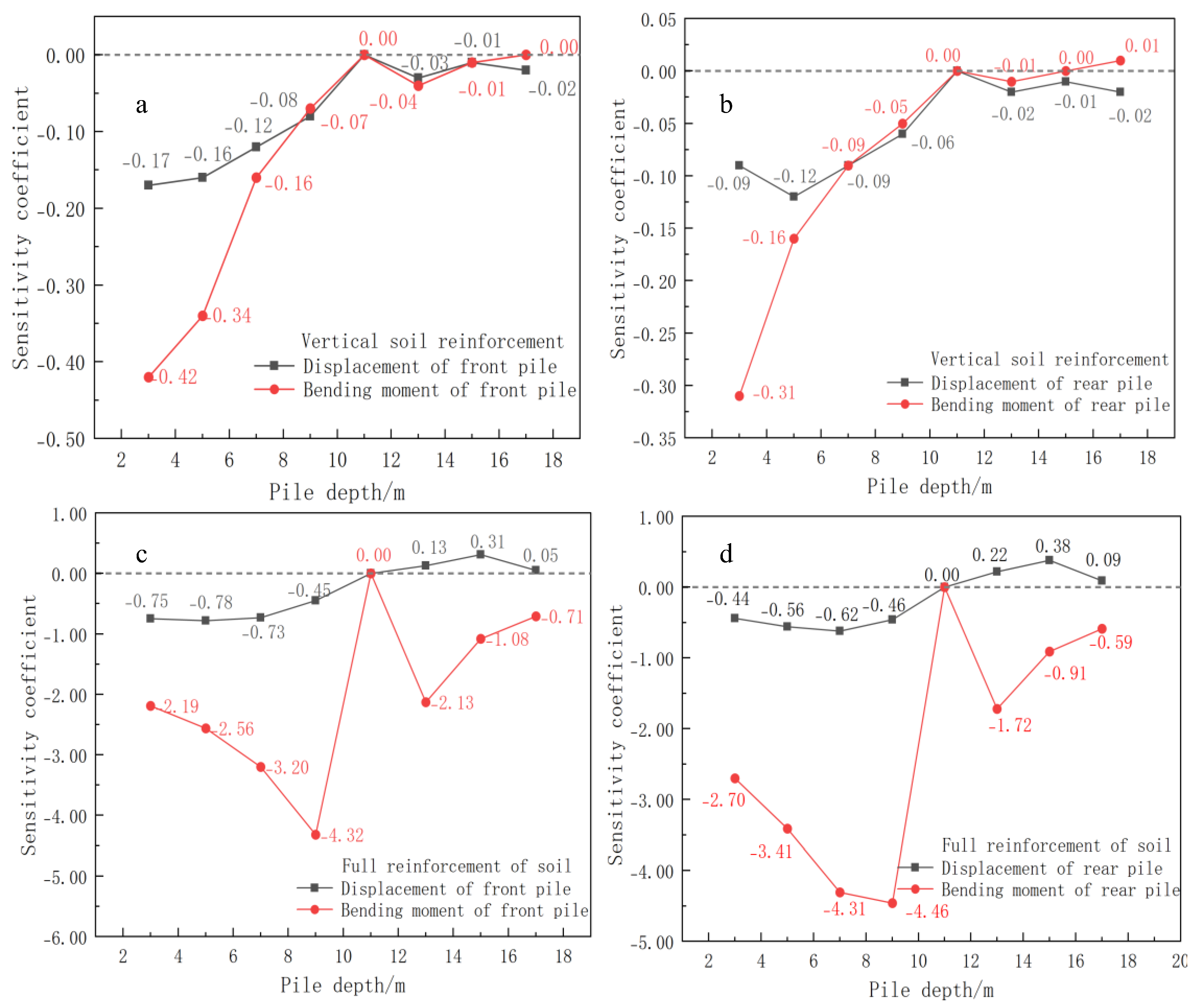
5.3. Sensitivity Analysis of Reinforcement Depth
5.4. Analysis of the Elastic Modulus of Soil Reinforcement Between Piles
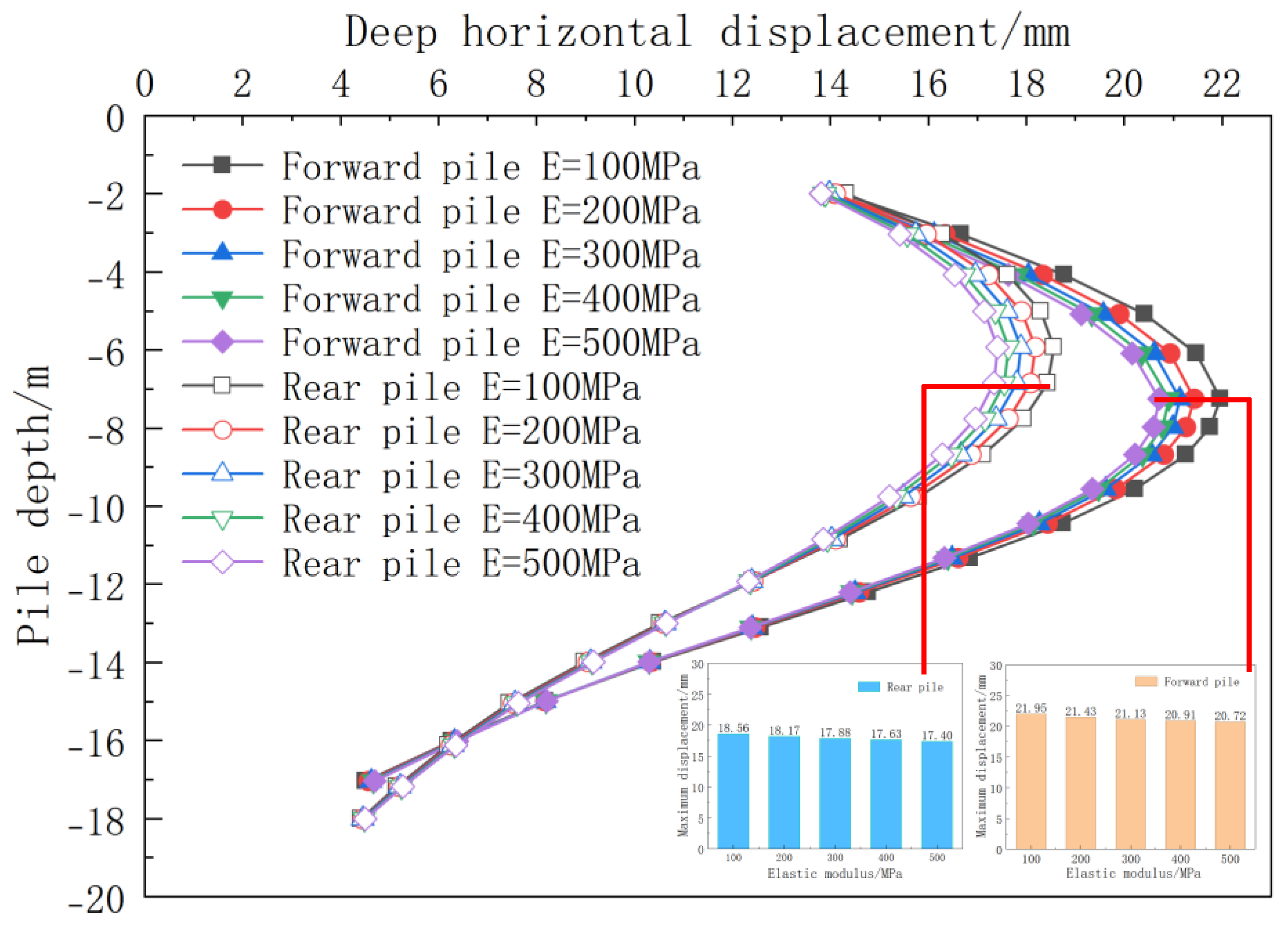
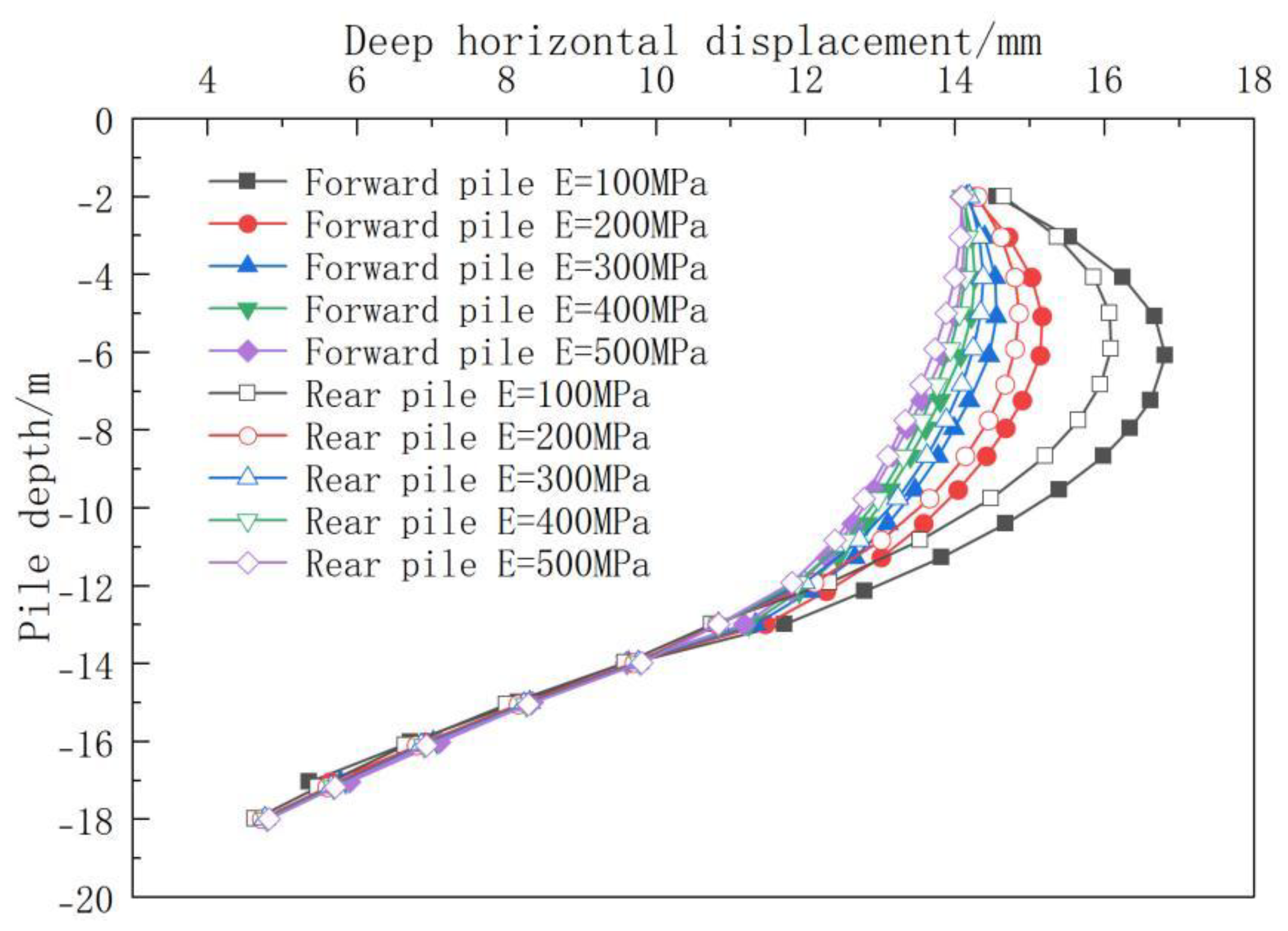
5.4.1. Influence of Elastic Modulus on Pile Displacement
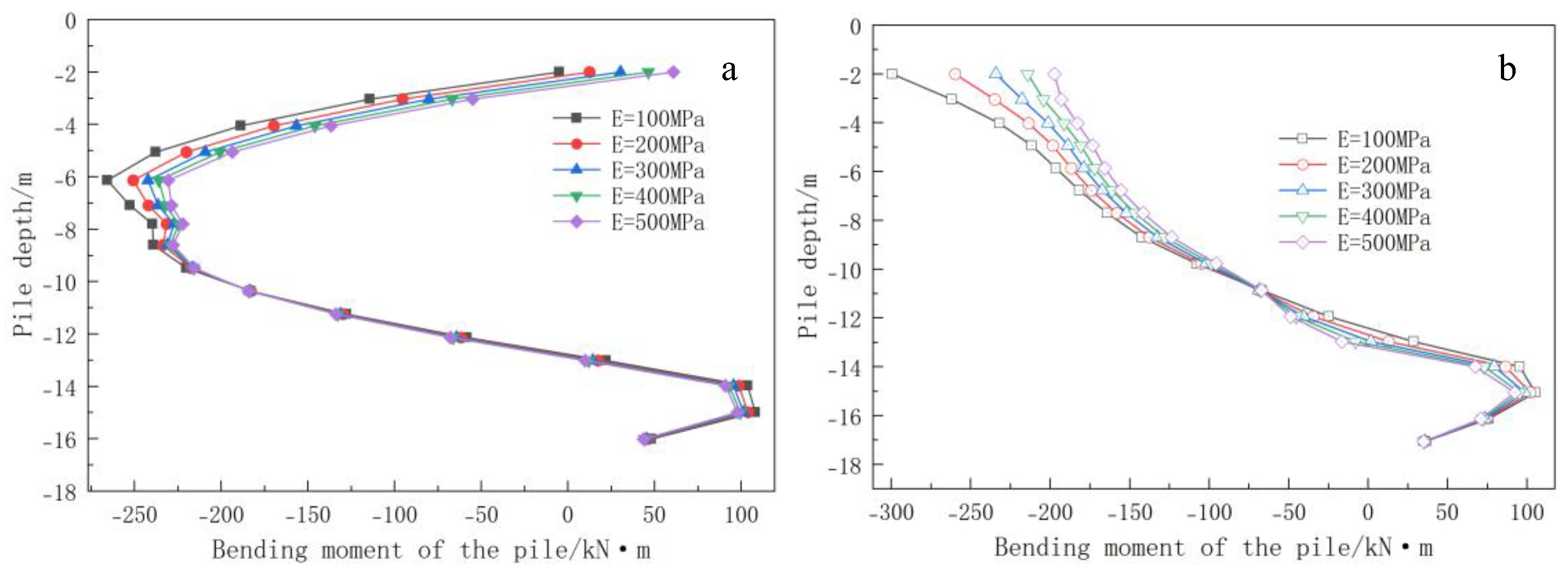
5.4.2. Influence of Elastic Modulus on the Bending Moment of the Pile Shaft
5.5. Sensitivity Analysis of Elastic Modulus
6. Conclusions
- The displacement distribution of double-row piles, comprising inclined front-row piles and vertical rear-row piles, demonstrates a characteristic deformation resembling an “inward convex drum shape.” Greater inclination angles of the front-row piles enhance the structural deformation control capacity, leading to a pile displacement curve that closely aligns with the pile-brace supporting form’s displacement characteristics.
- In the supporting system of double-row piles comprising inclined front piles and vertical rear piles, the soil reinforcement between the piles predominantly controls the overall displacement of the pile body (contribution rate: 39.3%). Conversely, the capping beam at the pile top exerts a more pronounced constraint on the displacement at the pile top (contribution rate: 75.4%). In the event of simultaneous failure of both mechanisms, there is a sharp 50% decrease in lateral resistance, leading to a shift in displacement pattern from the previous “inward convex” distribution resulting from coordinated force-bearing to a “cantilever” distribution under single-pile bearing. This transition underscores the essential nature of the dual constraint mechanism.
- The depth of reinforcement significantly influences the displacement and bending moment of supporting piles. Vertical reinforcement leads to a decrease in both displacement and bending moment as the reinforcement depth increases. Specifically, at a depth equal to the pile length, displacement decreases by 7.0–11.5%. Moreover, for h/H ≥ 1, the bending moment of rear-row piles surpasses that of front-row piles. Under full reinforcement, displacement exhibits a three-stage pattern of “decrease–increase–re-decrease.” The optimal range for controlling displacement is between 0.75 and 1 times the pile length, resulting in a reduction of 30–35%. The bending moment experiences its maximum reduction (53–61%) when h/H = 1–1.5. Notably, the cost-effectiveness of ultra-deep reinforcement (>1.5 times the excavation depth) diminishes significantly. Increasing the elastic modulus of soil reinforcement between piles can effectively reduce the displacement and bending moment of supporting piles. However, the benefits exhibit diminishing returns, with a weakening effect observed beyond 300 MPa. In vertical reinforcement scenarios, front-row piles typically experience 15–20% greater displacement compared to rear-row piles. While full reinforcement improves coordination and overall stability, it amplifies the peak bending moment within the stiffness mutation zone.
- The sensitivity of reinforcement depth to pile displacement and bending moment is significantly higher than that of elastic modulus, and the sensitivity strength under full reinforcement conditions is generally greater than that under semi-reinforcement conditions.
- In practical engineering applications, optimizing the reinforcement depth of the soil between piles is essential. The optimal reinforcement depth is typically established at 1.0 to 1.5 times the excavation depth. For foundation pit projects sensitive to the surrounding environment, full-depth reinforcement is recommended, as it more effectively controls deformation in the vicinity. The elastic modulus of the added solid should be set between 200 and 300 MPa. This range facilitates a balance among displacement control, engineering economy, and risk management within the stiffness mutation zone.
- The research presented in this paper on the parameters of soil reinforcement between piles has been initially completed. However, continuous monitoring of similar projects is necessary to assess potential failure risks and to verify the analysis results discussed herein.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Bulk Density (kN/m3) | Shear yield function | ||
| C | Cohesion (kPa) | Compression yield functions | |
| Internal Friction Angle (°) | Tensile yield function | ||
| Dilatancy angle (°) | Preconsolidation pressure (kPa) | ||
| n | Porosity | Average principal stress (kPa) | |
| Reference secant stiffness in standard hydraulic triaxial test (kPa) | Tensile strength (kPa) | ||
| Reference tangent stiffness for consolidated loading (kPa) | Plastic shear strain | ||
| Reference unloading/reloading stiffness (kPa) | Asymptotic deviation stress | ||
| m | Power of Stress Level Dependency | Ultimate deviation stress | |
| Coefficient of Static Earth Pressure | Shear plastic potential function | ||
| Failure ratio | Compression plastic potential function | ||
| v | Poisson’s ratio | Stretching plastic potential function | |
| Critical friction angle (°) | Mobilized friction angle (°) | ||
| Reference preconsolidation pressure (kPa) | Plastic volumetric strain |
References
- Zheng, G. Method and application of deformation control of excavations in soft ground. Chin. J. Geotech. Eng. 2022, 44, 1–36. [Google Scholar]
- Huang, J.; Liu, J.; Guo, K.; Wu, C.; Yang, S.; Luo, M.; Lu, Y. Numerical Simulation Study on the Impact of Deep Foundation Pit Excavation on Adjacent Rail Transit Structures—A Case Study. Buildings 2024, 14, 1853. [Google Scholar] [CrossRef]
- Ge, C.; Yang, M.; Li, P.; Zhang, M.; Zhang, Z. Performance and environmental impacts of deep foundation excavation in soft soils: A field and modeling-based case study in Nanjing, China. Undergr. Space 2024, 18, 218–238. [Google Scholar] [CrossRef]
- Liu, R.; Sun, H.; Qin, J.; Zheng, Z. A multi-geophysical approach to assess potential sinkholes in an urban area. Eng. Geol. 2023, 318, 107100. [Google Scholar] [CrossRef]
- Kong, H.; Dong, M.; Cao, X.; Lin, S.; Zhao, S.; Zheng, H. Global analysis approach of stability of deep foundation pit slopes reinforced by underground diaphragm walls and prestressed anchor cables. Comput. Geotech. 2023, 163, 105744. [Google Scholar] [CrossRef]
- He, B.; Lin, B.; Li, H.; Zhu, S. Suggested method of utilizing soil arching for optimizing the design of strutted excavations. Tunn. Undergr. Space Technol. 2024, 143, 105450. [Google Scholar] [CrossRef]
- Wang, J.H.; Xu, Z.H.; Wang, W.D. Wall and Ground Movements due to Deep Excavations in Shanghai Soft Soils. J. Geotech. Geoenviron. Eng. 2010, 136, 985–994. [Google Scholar] [CrossRef]
- Yang, J.; Kong, D. Deformation of deep and large foundation pit in soft soil of Fuzhou Subway. Arab. J. Geosci. 2020, 13, 36. [Google Scholar] [CrossRef]
- Zhou, N.; Vermeer, P.A.; Lou, R.; Tang, Y.; Jiang, S. Numerical simulation of deep foundation pit dewatering and optimization of controlling land subsidence. Eng. Geol. 2010, 114, 251–260. [Google Scholar] [CrossRef]
- Guo, C.C.; Zhu, C.X. Excavation and Support Analysis of Prefabricated Recyclable Double-Row Pile Supporting Structure. J. Zhengzhou Univ. (Eng. Sci.) 2022, 43, 78–83. [Google Scholar]
- Ou, X.D.; Lu, Z.F.; Jiang, J.; Luo, F.Z.; Liang, Y.H. Deformation Characteristics of Double-row Pile in Deep Foundation Pit with Water-rich Circular Gravel Layer. Sci. Technol. Eng. 2021, 21, 5484–5490. [Google Scholar]
- Zhang, L.; Ou, Q.; Zhu, X.R. Analysis on Forced Deformation of Double Row Piles Considering Pile-pile Interaction in Layered Foundation. J. Hunan Univ. (Nat. Sci.) 2020, 47, 120–126. [Google Scholar]
- Lu, Q.X. Research on deformation control of double-row piles near metro deep foundation pit with deep silty sand layer. Build. Struct. 2022, 52, 2423–2427. [Google Scholar]
- Zhao, S.F.; Huang, G.L.; Ma, S.Q.; Zhou, W.Y.; Zhang, X. Application of precast concrete pipe piles in a deep excavation project. Chin. J. Geotech. Eng. 2014, 36, 91–96. [Google Scholar]
- Ye, J.; He, X. Evaluation of flexural stiffness on mechanical property of dual row retaining pile wall. Mech. Adv. Mater. Struct. 2022, 29, 963–974. [Google Scholar] [CrossRef]
- Wang, R.; Yang, H.; Ni, P.; Zhao, C.; Guo, C.; Ma, H.; Dong, P.; Liang, H.; Tang, M. Model test and numerical simulation of a new prefabricated double-row piles retaining system in silty clay ground. Undergr. Space 2023, 13, 262–280. [Google Scholar] [CrossRef]
- Huang, K.Y.; Liang, Z.R.; Wei, X. Application and analysis of double-row constant thickness steel cement-soil walls on a large-scale deep excavation. Build. Struct. 2023, 53, 2902–2907. [Google Scholar]
- Lan, B.; Wang, Y.; Wang, W. Review of the Double-Row Pile Supporting Structure and Its Force and Deformation Characteristics. Appl. Sci. 2023, 13, 7715. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, J. Three-dimensional numerical simulation and earth pressure analysis on double-row piles with consideration of spatial effects. J. Zhejiang Univ.-Sci. A 2011, 12, 758–770. [Google Scholar] [CrossRef]
- Du, P.C.; Peng, X.; Ma, L.; Li, M.Y.; Xu, H.R.; Yang, K.X. Research on spatial effect of double-row piles supporting structure for deep foundation pit. Build. Struct. 2021, 51, 2038–2043. [Google Scholar]
- Ou, X.D.; Tan, Z.J.; Luo, F.Z.; Jiang, J.; Liang, Y.H. Numerical Analysis of Influence of Design Parameters on the Double-row Pile Support Structure of Deep Foundation Pit. Sci. Technol. Eng. 2021, 21, 2873–2878. [Google Scholar]
- Gao, Y.; Sun, H.K.; Liu, R.C. Slope deformation and parameters sensitivity in the design of double-row supporting piles. J. Shandong Univ. (Eng. Sci.) 2019, 49, 86–94. [Google Scholar]
- Hu, X.; Liu, D.; Niu, L.; Liu, C.; Wang, X.; Fu, R. Development of soil–pile interactions and failure mechanisms in a pile-reinforced landslide. Eng. Geol. 2021, 294, 106389. [Google Scholar] [CrossRef]
- Yu, F.; Xie, Z.; Duan, N.; Liu, N.; Shan, H. Performance of double-row piles retaining excavation beneath existing underground space. Int. J. Phys. Model. Geotech. 2019, 19, 167–180. [Google Scholar] [CrossRef]
- Dong, B.; Wang, Q.; Ma, F.; Zhang, C.; Zou, L. Calculation Theory of Counterweight Double-Row Pile Support for Deep Foundation Pit in Reclamation Area and Influence Analysis of Core Pile Parameters. Sustainability 2023, 15, 6184. [Google Scholar] [CrossRef]
- Wang, X.Q.; Liao, Z.Y.; Zheng, T.Y.; Zhu, D.L. Model test study on bearing characteristics of double-row piles based on reinforcement effect of soil around piles. J. Civ. Environ. Eng. 2021, 43, 19–25. [Google Scholar]
- Seo, M.; Im, J.; Kim, C.; Yoo, J. Study on the applicability of a retaining wall using batter piles in clay. Can. Geotech. J. 2016, 53, 1195–1212. [Google Scholar] [CrossRef]
- Zheng, G.; He, X.P.; Zhou, H.Z.; Wang, E.Y.; Yang, S.F.; Wei, J.H. Working mechanism of inclined-vertical retaining piles in excavations. Chin. J. Geotech. Eng. 2019, 41, 97–100. [Google Scholar]
- Fan, P.C.; Hu, Z.W. Simulation of Single-row Oblique Straight Alternate Piles in Soft Soil Foundation Pit Support. J. Water Resour. Archit. Eng. 2018, 16, 134–137. [Google Scholar]
- Wang, E.Y.; Zhou, H.Z.; Zheng, G.; He, X.P.; Yang, S.F.; Wei, J.H. Numerical analyses of deformation of inclined pile-retained excavations. Chin. J. Geotech. Eng. 2019, 41, 73–76. [Google Scholar]
- Diao, Y.; Su, Y.M.; Zheng, G. Numerical study on oblique-straight alternate piles for active support of excavations. Chin. J. Geotech. Eng. 2019, 41, 161–164. [Google Scholar]
- Xu, Y.; Zheng, G.; Lu, P. Behaviors of double-row contiguous retaining piles with raking front-row piles under horizontal loads. Chin. J. Geotech. Eng. 2010, 32, 93–98. [Google Scholar]
- Tian, Y.; Yu, D.H.; Lai, G.L.; Chen, G.; Song, Z.; Liu, Y. Calculation and monitoring analysis of inclined precast pile foundation pit support in soft soil area of Hanjiang River terrace. Build. Sci. 2023, 39, 168–174. [Google Scholar]
- Xiao, H.N.; Cao, W.P.; Zhao, M.; Luo, L.P.; Xi, M.Y. Numerical Analysis on Force and Deformation of Composite Piles for Loess Foundation Pit Inclination. J. Wuhan Univ. Technol. (Transp. Sci. Eng.) 2024, 48, 1199–1204. [Google Scholar]
- Zheng, G.; Wang, Y.P.; Cheng, X.S.; Yu, D.H.; Huang, X.C.; Li, X.H. Field Experiment and Working Mechanism of Foundation Pit Excavation Retained by Front-row Inclined Double Row Piles in Soft Soil Area. J. Yangtze River Sci. Res. Inst. 2024, 41, 98–105, 113. [Google Scholar]
- Qiu, H.; Zhou, Y.; Ayasrah, M.M. Impact Study of Deep Foundations Construction of Inclined and Straight Combined Support Piles on Adjacent Pile Foundations. Appl. Sci. 2023, 13, 1810. [Google Scholar] [CrossRef]
- Wu, Y.; Ye, J.; Ge, H.; Liu, G.; Liu, H. Numerical investigation of dual-row batter pile wall in deep excavation. Mech. Adv. Mater. Struct. 2022, 29, 5793–5807. [Google Scholar] [CrossRef]
- Teo, P.L.; Wong, K.S. Application of the Hardening Soil model in deep excavation analysis. IES J. Part A Civ. Struct. Eng. 2012, 5, 152–165. [Google Scholar] [CrossRef]
- Zhao, Y.; Lu, Z.; Liu, J.; Zhang, J.; Yao, H. Influence of different infill materials on the performance of geocell-reinforced cohesive soil beds. Sci. Rep. 2023, 13, 12330. [Google Scholar] [CrossRef]
- Schanz, T.; Vermeer, P.A.; Bonnier, P.G. The hardening soil model: Formulation and verification. Beyond Comput. Geotech. 1999, 11, 281–296. [Google Scholar]
- Liu, H.; Li, K.; Wang, J.; Cheng, C. Numerical Simulation of Deep Foundation Pit Construction under Complex Site Conditions. Adv. Civ. Eng. 2021, 2021, 6669466. [Google Scholar] [CrossRef]
- Goh, A.T.C.; Zhang, F.; Zhang, W.; Zhang, Y.; Liu, H. A simple estimation model for 3D braced excavation wall deflection. Comput. Geotech. 2017, 83, 106–113. [Google Scholar] [CrossRef]

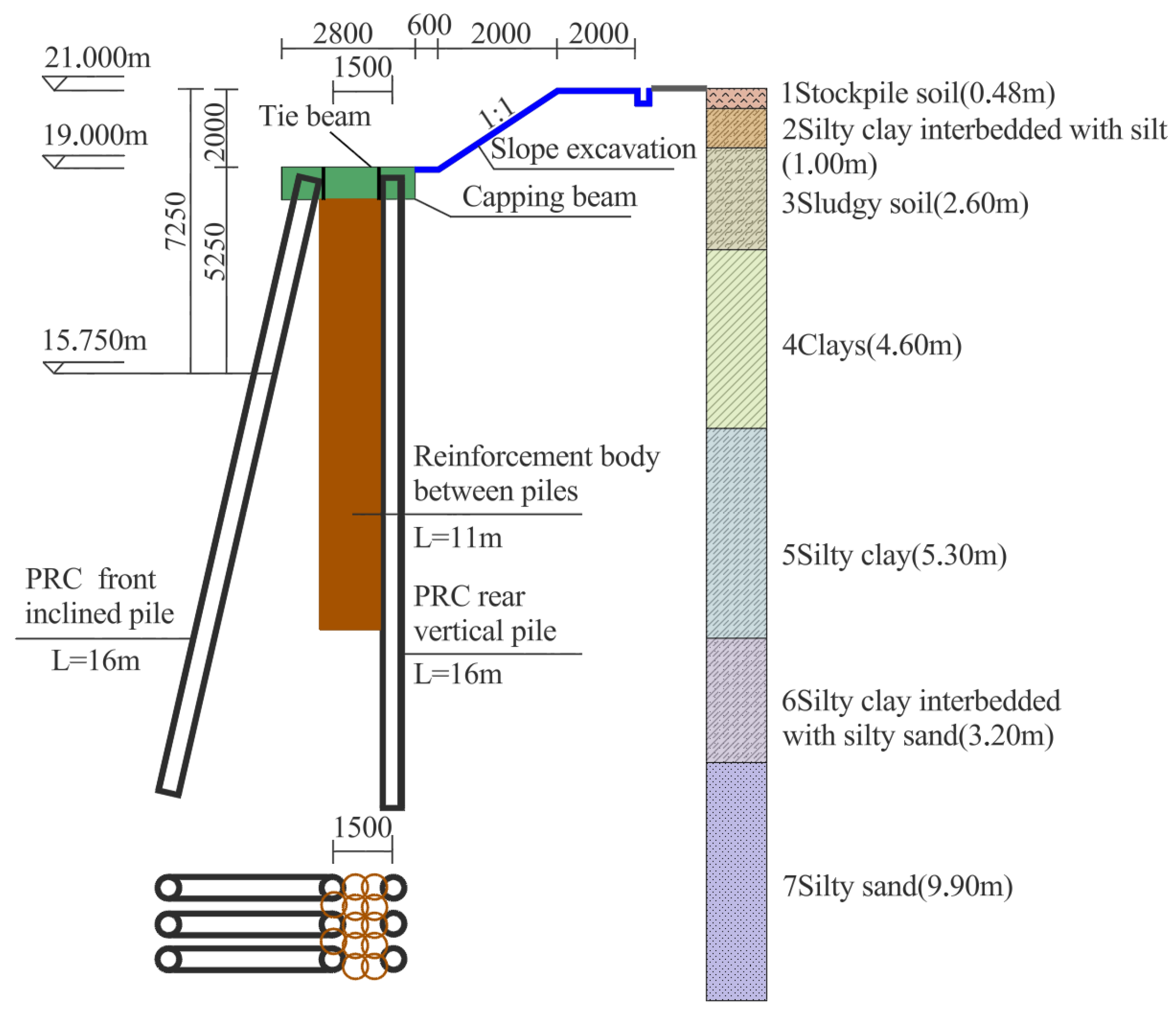











| Layer Name | Depth of Stratum/m | v | γ/kN/m3 | /MPa | /MPa | /MPa | /kPa | /° |
|---|---|---|---|---|---|---|---|---|
| ② Silty clay interbedded with silt (Q4ml) | 1.48 | 0.2 | 17.9 | 4.8 | 4.8 | 13.44 | 14 | 9 |
| ③ Sludgy soil (Q4l) | 2.60 | 0.2 | 16.7 | 2.9 | 2.9 | 8.12 | 10 | 4 |
| ④ Clays (Q4al) | 4.60 | 0.2 | 18.4 | 6.2 | 6.2 | 17.36 | 23 | 12 |
| ⑤ Silty clay (Q4al+pl) | 5.30 | 0.2 | 18.0 | 5.0 | 5.0 | 14.0 | 14 | 7 |
| ⑥ Silty clay interbedded with silty sand (Q4al+pl) | 3.20 | 0.2 | 18.2 | 10.5 | 10.5 | 47.25 | 18 | 10 |
| ⑦ Silty sand (Q4al+pl) | 9.90 | 0.2 | 19.0 | 15.5 | 15.5 | 77.5 | 1 | 31 |
| solid between piles | 11.00 | / | 22.0 | / | / | / | / | / |
| Structure Name | Unit Type | Cross-Sectional Dimension | γ/kN/m3 | E/GPa | v |
|---|---|---|---|---|---|
| PRC pile | Beam | Outer diameter 0.6 m, wall thickness 0.11 m | 25 | 80 | 0.2 |
| Crown beam | Beam | Width 1 m, height 0.8 m | 25 | 30 | 0.2 |
| Concrete spraying surface | Board | Thickness 0.1 m | 23 | 20 | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Cai, J.; Wei, P.; Yang, X.; Xu, Y. Optimization of Pile Reinforcement in Soft Soils: A Numerical Analysis. Appl. Sci. 2025, 15, 12443. https://doi.org/10.3390/app152312443
Wang Z, Cai J, Wei P, Yang X, Xu Y. Optimization of Pile Reinforcement in Soft Soils: A Numerical Analysis. Applied Sciences. 2025; 15(23):12443. https://doi.org/10.3390/app152312443
Chicago/Turabian StyleWang, Ziqi, Jihua Cai, Pengfei Wei, Xianyu Yang, and Yangqing Xu. 2025. "Optimization of Pile Reinforcement in Soft Soils: A Numerical Analysis" Applied Sciences 15, no. 23: 12443. https://doi.org/10.3390/app152312443
APA StyleWang, Z., Cai, J., Wei, P., Yang, X., & Xu, Y. (2025). Optimization of Pile Reinforcement in Soft Soils: A Numerical Analysis. Applied Sciences, 15(23), 12443. https://doi.org/10.3390/app152312443







