Thermal–Hydraulic–Mechanical Coupling Effects and Stability Analysis of Surrounding Rock in Ultra-Deep Mine Shaft Excavation
Abstract
1. Introduction
2. Engineering Background
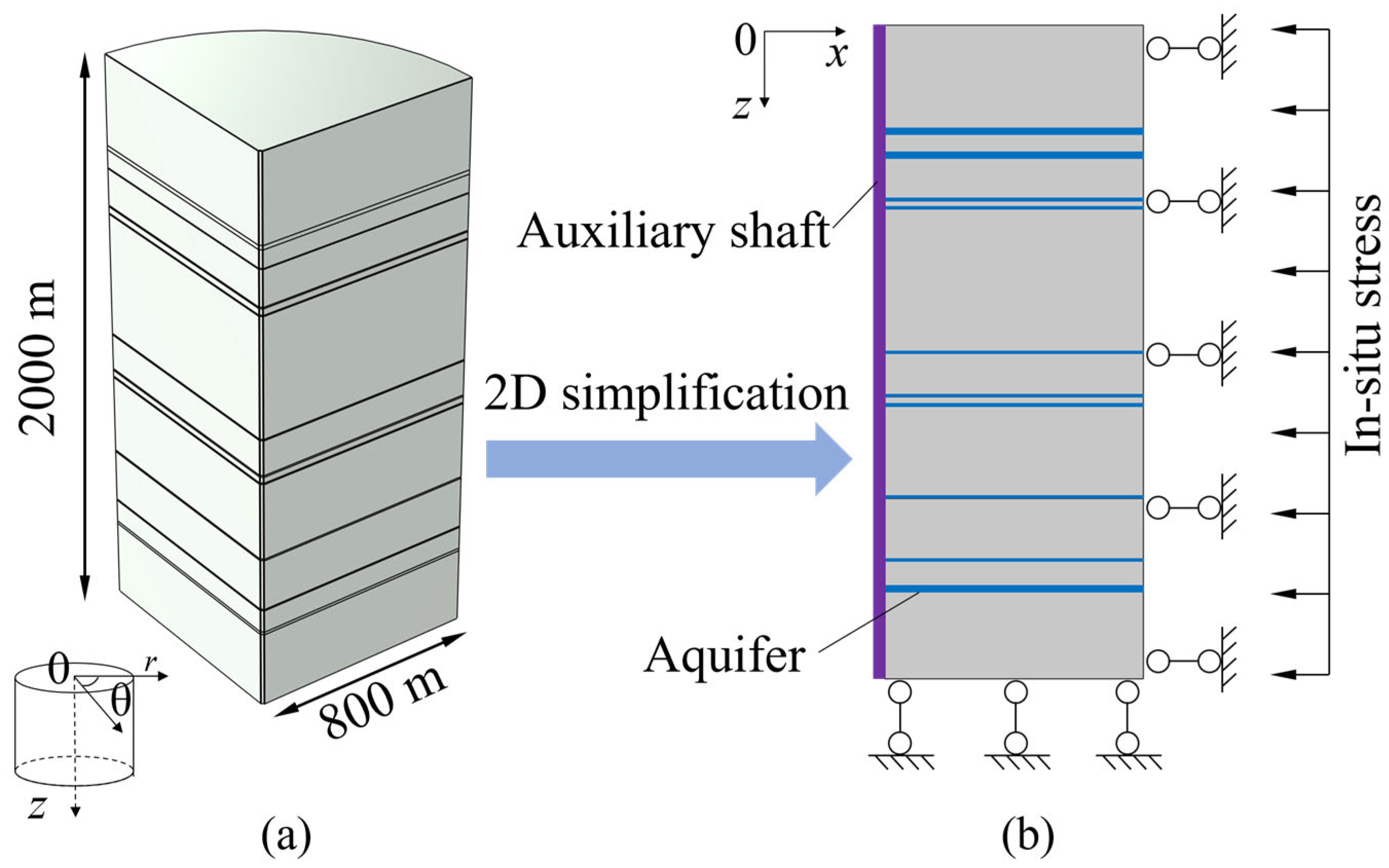
2.1. Geographical Location
2.2. Geological Characteristics
3. Numerical Model
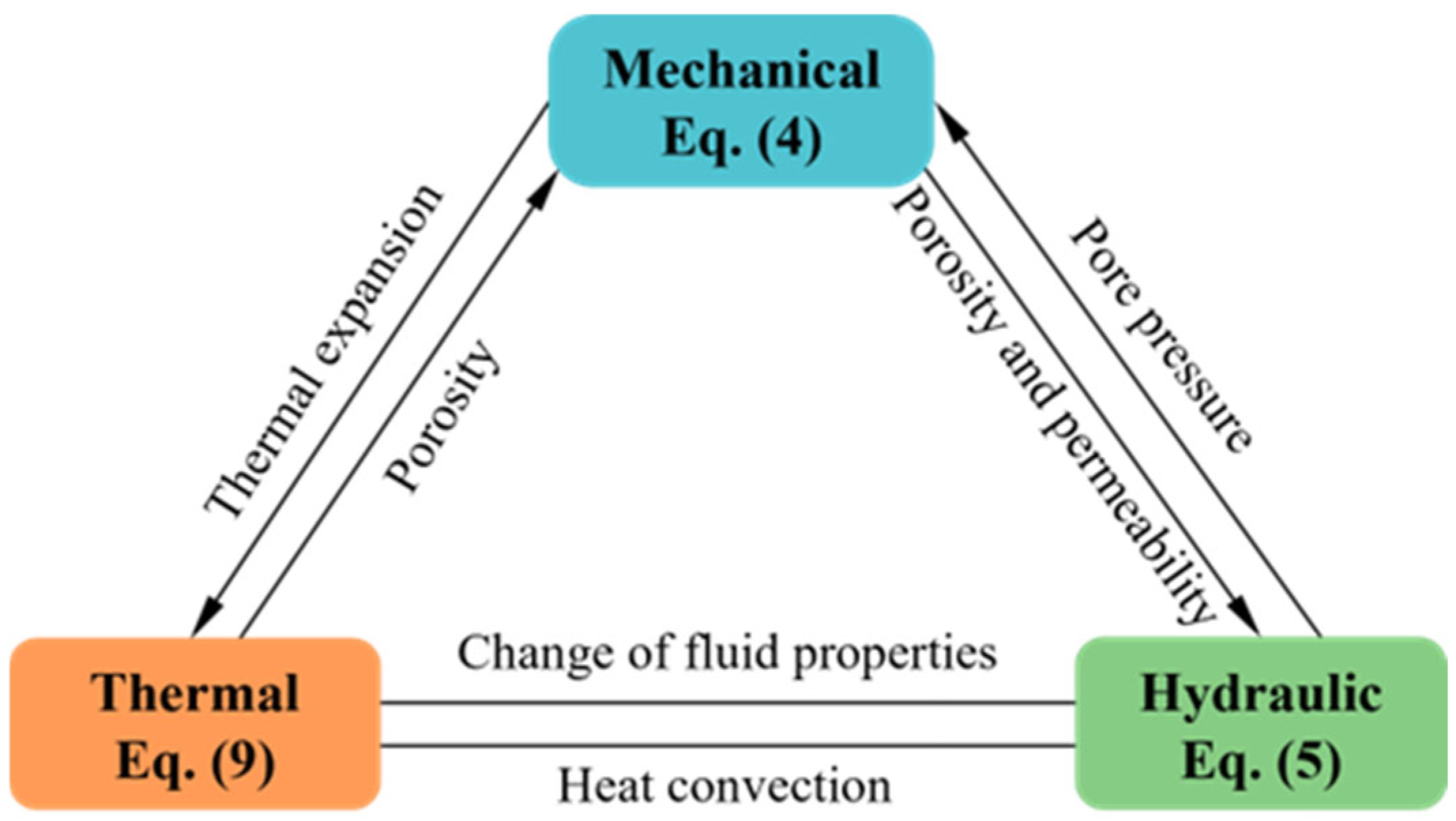
3.1. Governing Equations of the THM Coupling Model
3.1.1. Stress Field
3.1.2. Seepage Field
3.1.3. Temperature Field
3.1.4. Coupling Effects
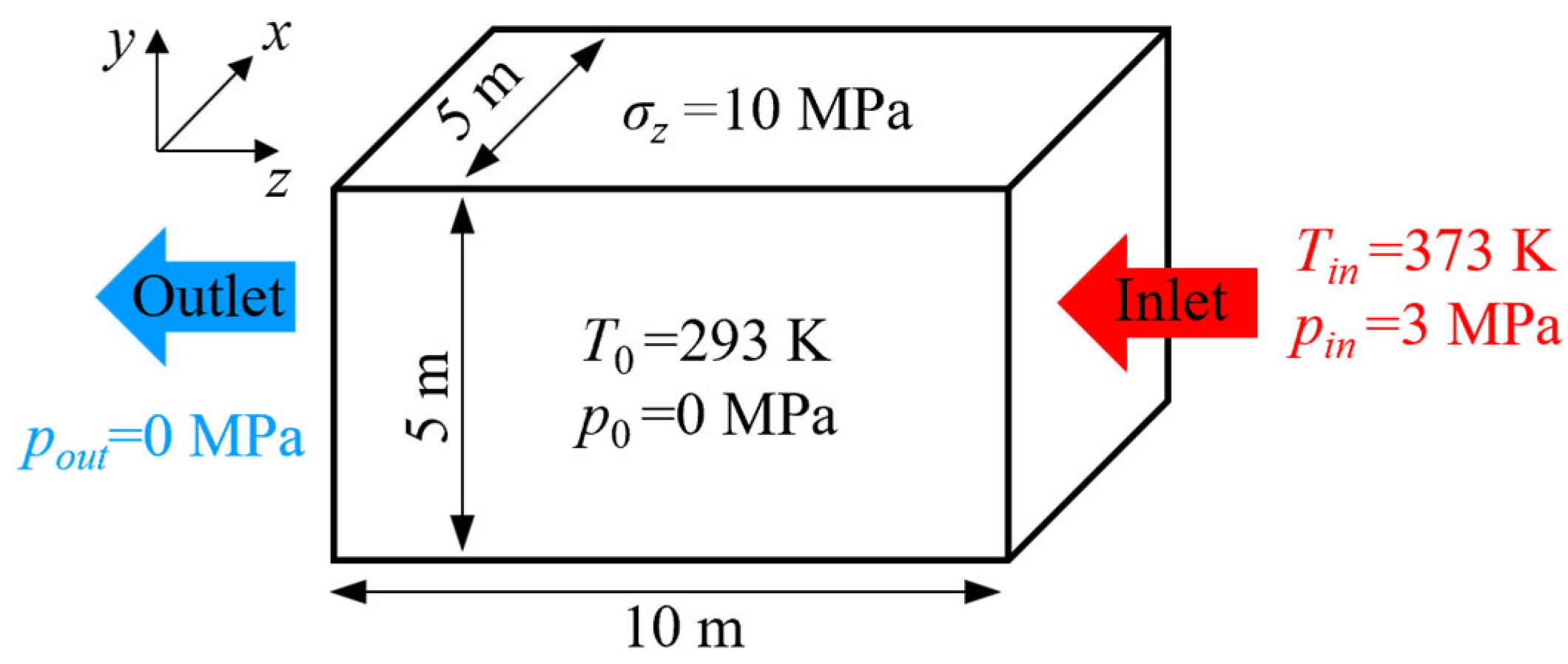
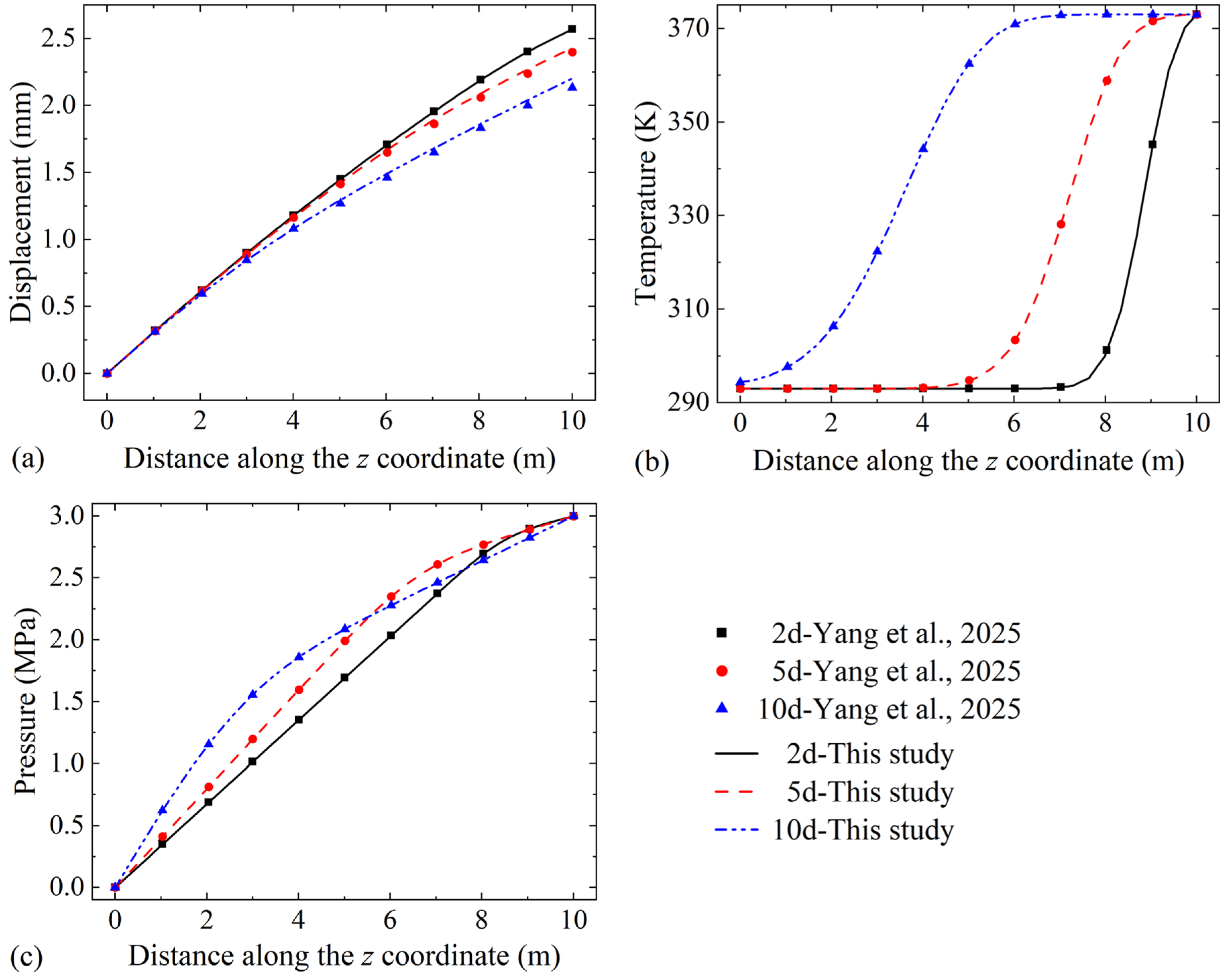
3.2. Model Validation
3.3. Model Implementation
4. Results and Discussion
4.1. Stability Analysis
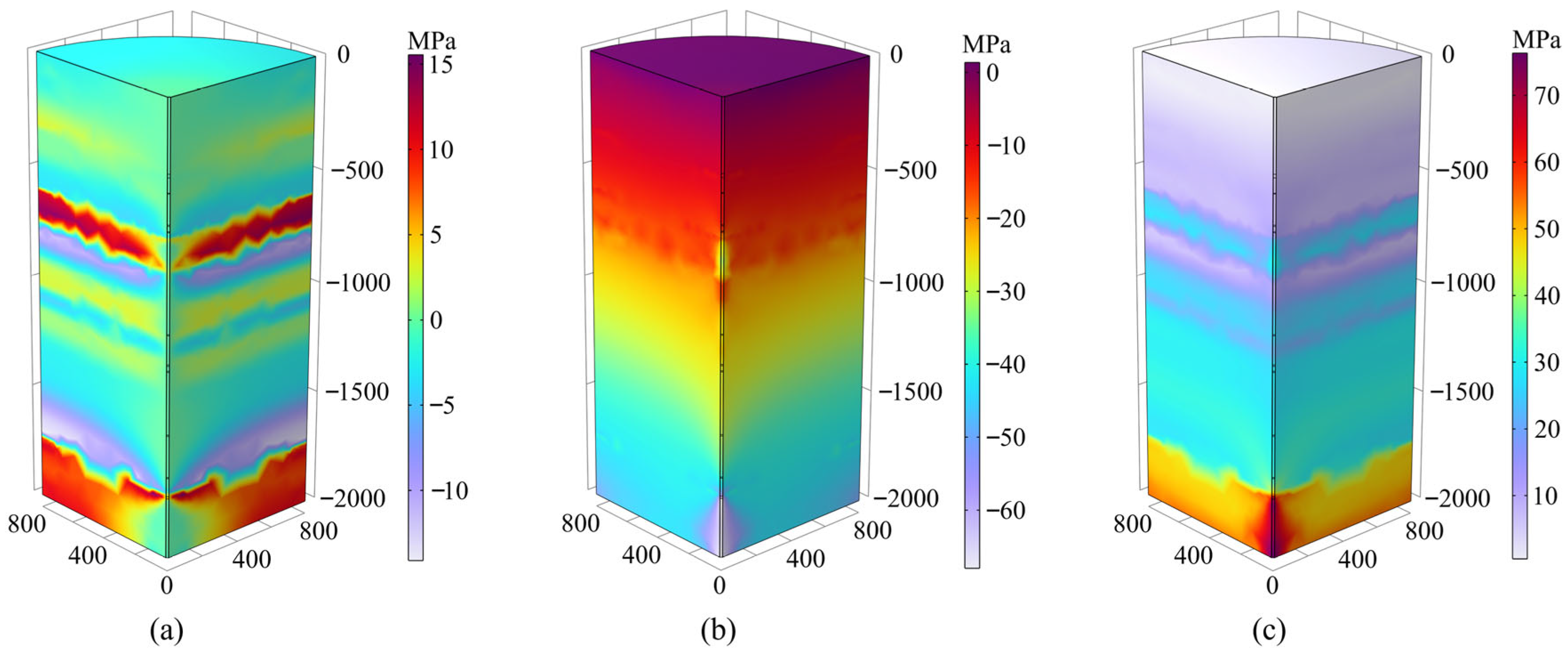
4.1.1. Stress Distribution Results
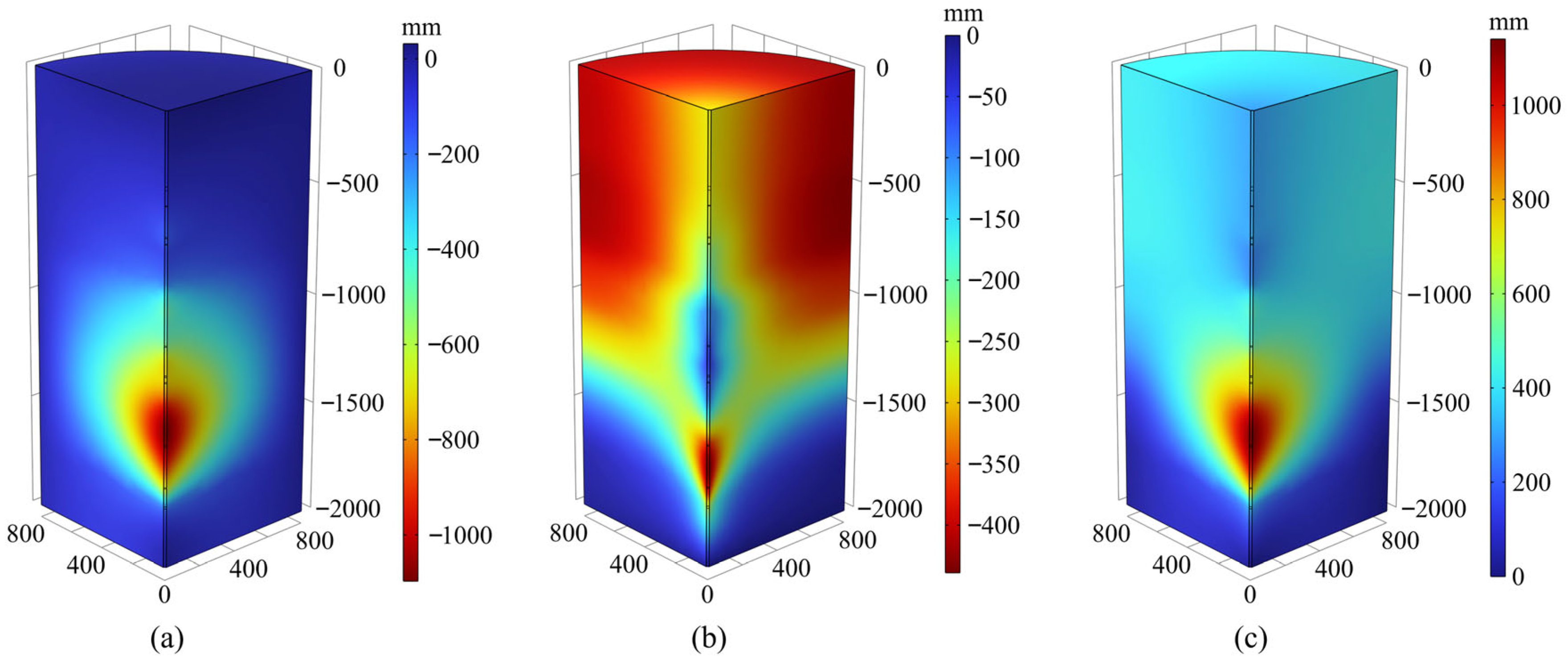
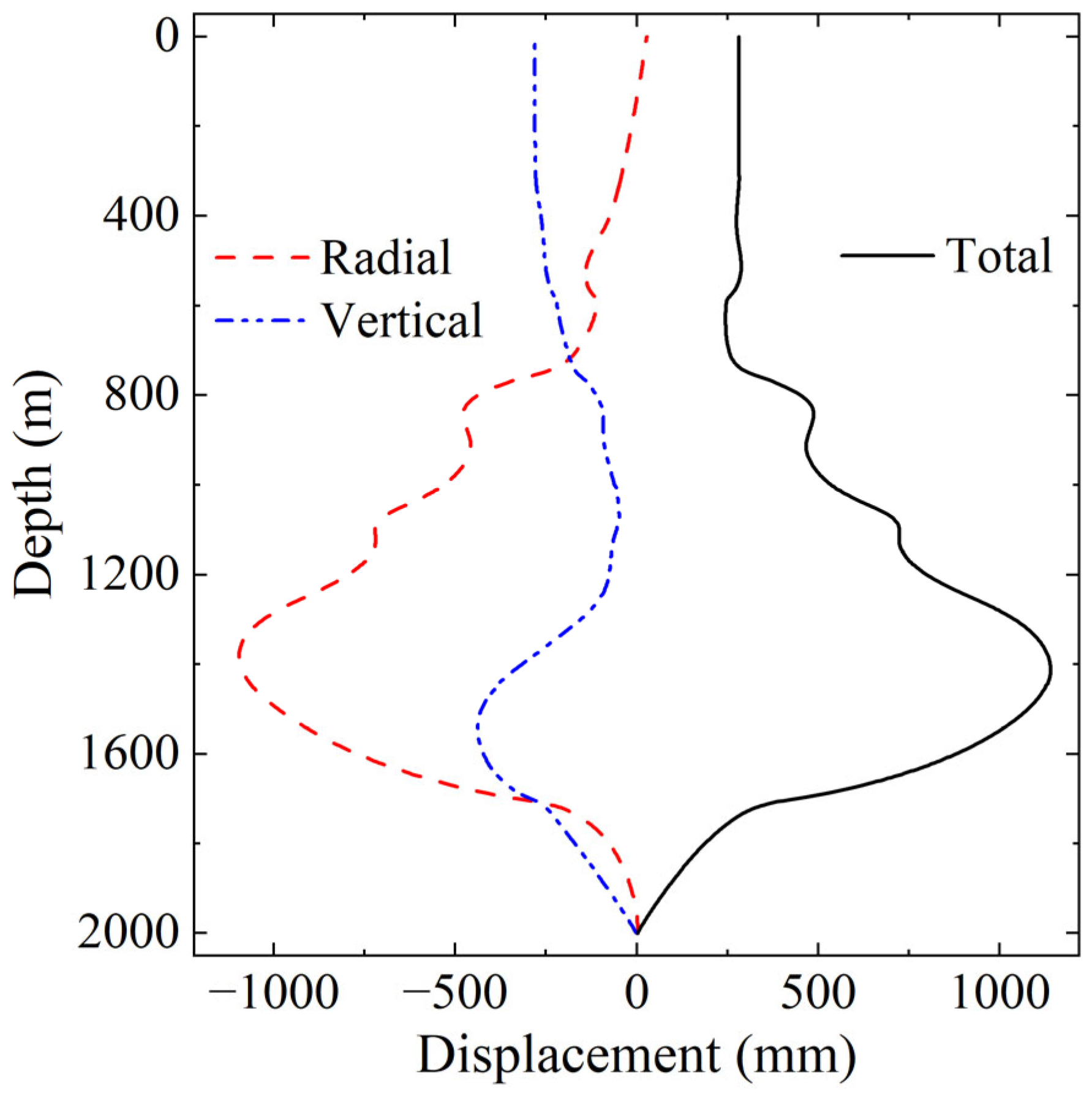
4.1.2. Displacement Distribution Results
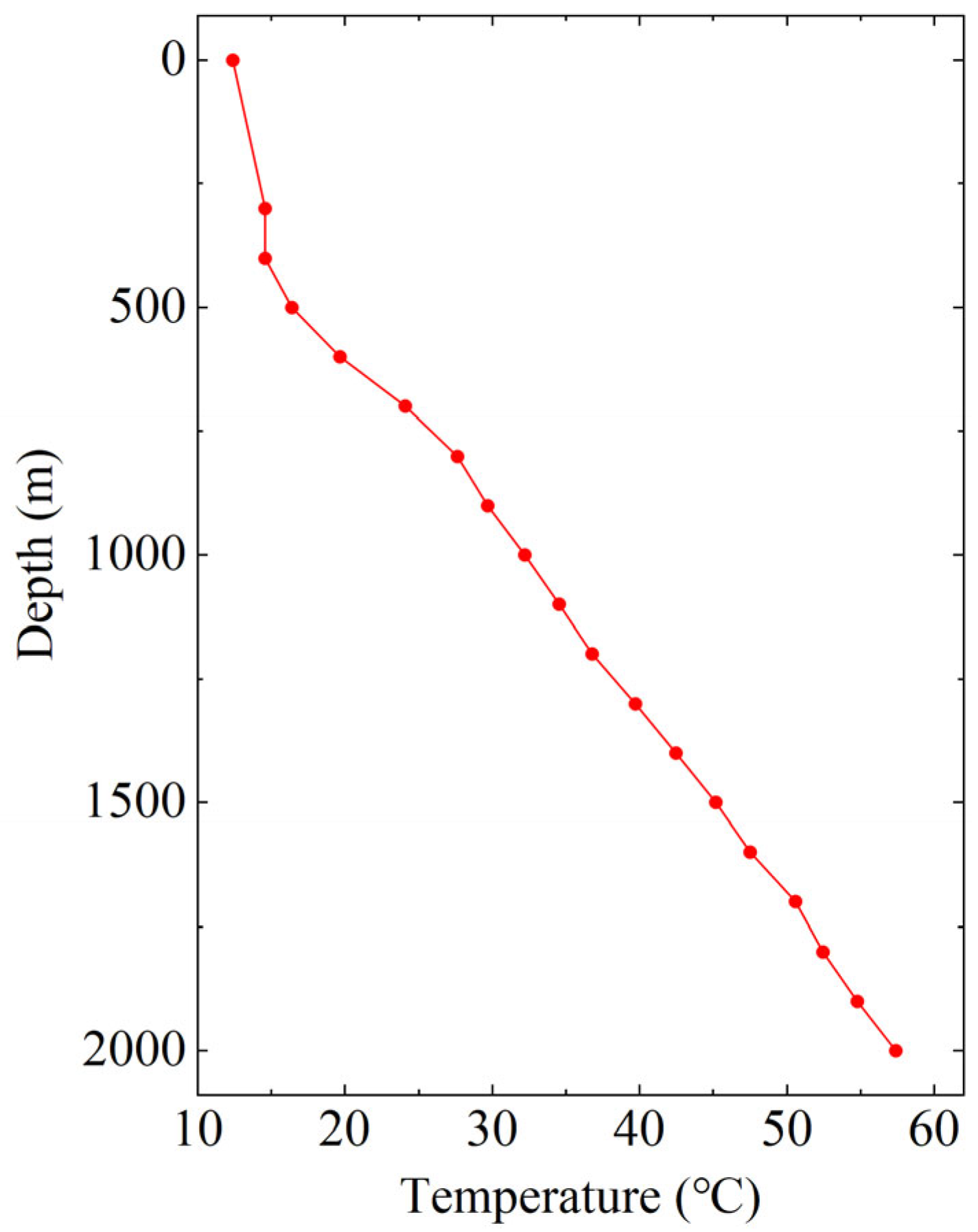
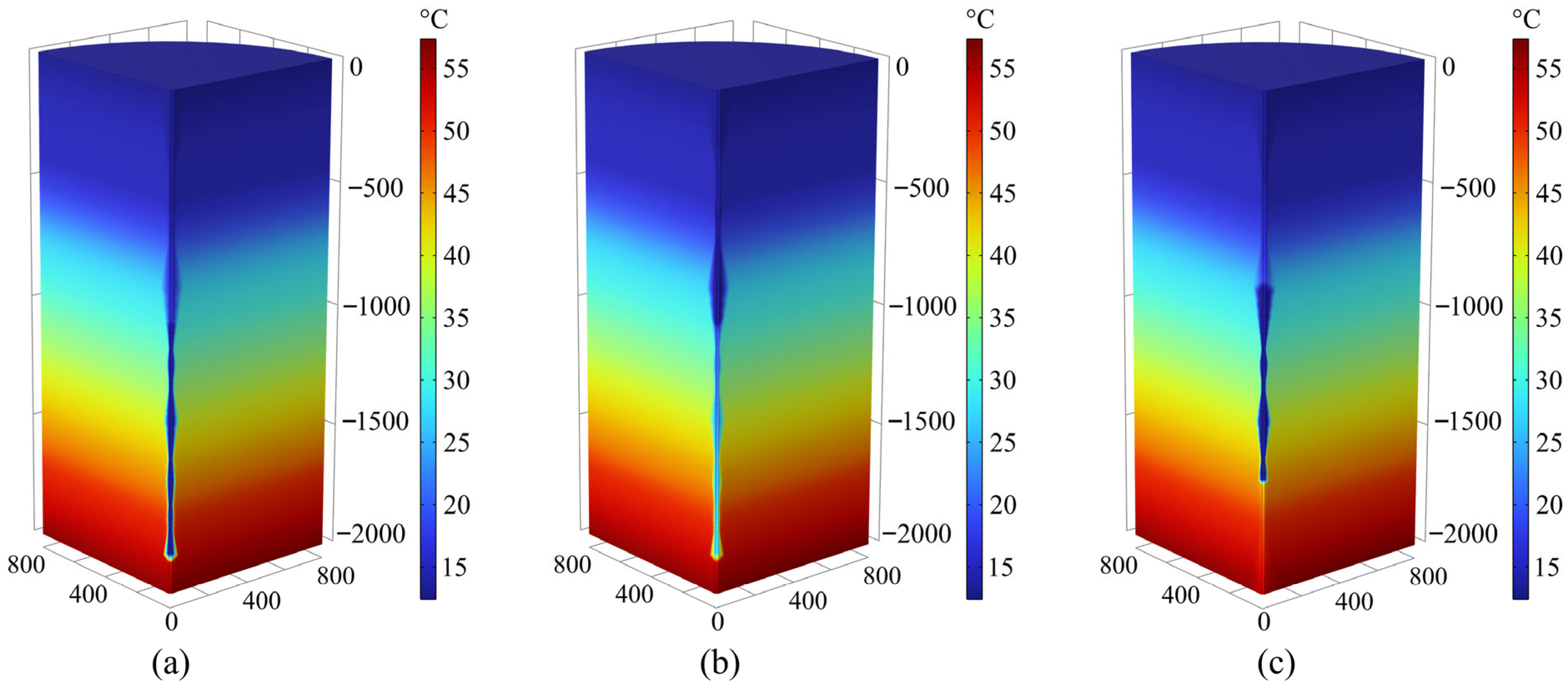
4.1.3. Pressure and Temperature Distribution Results
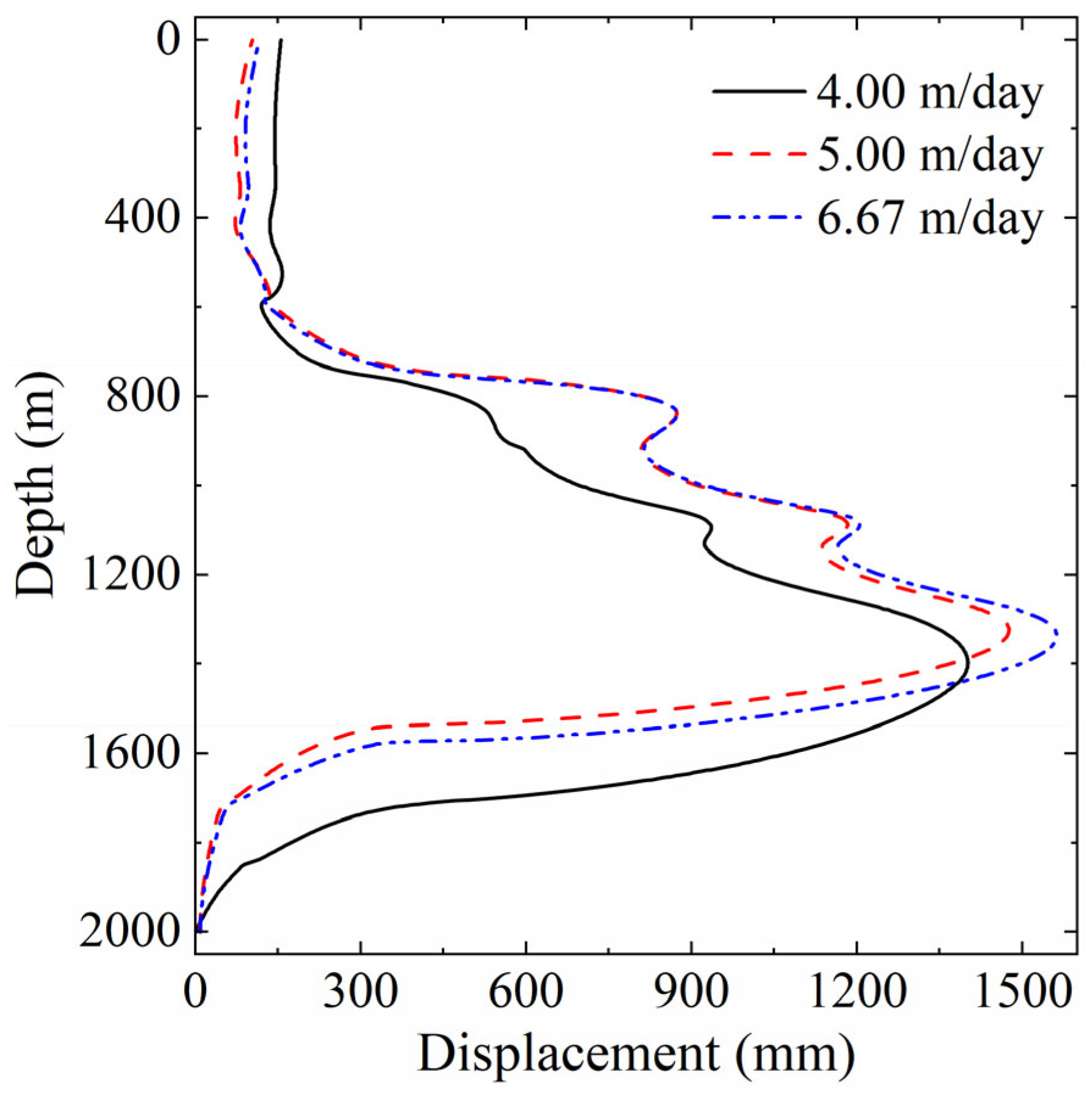
4.2. The Effect of Excavation Rates
4.3. Discussion
5. Conclusions
- (1)
- Stress redistribution induced by auxiliary shaft excavation is significantly influenced by the spatial variability of rock mechanical properties. Stress concentration occurs in rock layers with high elastic modulus (depth 500–1000 m and 1500–2000 m), where compressive stress peaks at 15.9 MPa and tensile stress reaches 14.1 MPa, making compressive-shear or tensile failure likely. The vertical stress, mainly resulting from the overburden weight, reaches a maximum of 70.0 MPa, aggravating the risk of compressive deformation in the surrounding rock.
- (2)
- Surrounding rock deformation strongly depends on lithology and the THM coupling process. The maximum displacement occurs in the low elastic modulus zone (around 1400 m depth), with a total displacement of 1139 mm. This is primarily manifested as radial displacement toward the shaft and settlement in the gravity direction, jointly induced by unloading, pore pressure reduction, and thermal contraction.
- (3)
- Excavation rate has a significant impact on deformation response. Faster excavation (e.g., 6.67 m/day) causes more pronounced instantaneous displacement, while slower excavation (e.g., 4 m/day) partially suppresses displacement due to the persistent effect of thermal contraction. Post-excavation, the thermo-mechanical coupling process continues, indicating a pronounced time-dependent and delayed deformation effect.
- (4)
- Special attention should be paid to the low-stiffness rock strata around 1400 m depth during excavation. A combined support strategy is recommended, involving high-preload rock bolts, lining, and grouting reinforcement, along with optimized excavation rates. Long-term monitoring of temperature, pore pressure, and displacement is essential to achieve dynamic risk control.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| THM | thermal–hydraulic–mechanical |
References
- Wu, F.; Qin, Y.; Xu, H.; Zhang, F.; Chu, X. Numerical Simulation of Deformation and Failure Mechanism of Main Inclined Shaft in Yuxi Coal Mine, China. Appl. Sci. 2022, 12, 5531. [Google Scholar] [CrossRef]
- Li, C.; Chunlong, W.; Xi, W.; Kexu, C.; Song, Z. Stability Analysis of Surrounding Rock of Large Section Ultradeep Shaft Wall. Adv. Mater. Sci. Eng. 2021, 2021, 4391759. [Google Scholar] [CrossRef]
- Yang, S.-Q.; Chen, M.; Jing, H.-W.; Chen, K.-F.; Meng, B. A case study on large deformation failure mechanism of deep soft rock roadway in Xin’An coal mine, China. Eng. Geol. 2017, 217, 89–101. [Google Scholar] [CrossRef]
- Hou, K.; Zhu, M.; Hao, Y.; Yin, Y.; An, L. Stability analysis and evaluation of surrounding rock of ultra-deep shaft under complicated geological conditions. Front. Earth Sci. 2023, 11, 1216667. [Google Scholar] [CrossRef]
- Tan, J.; Liu, Z.; Song, Z.; Liu, Q.; Long, Z.; Ning, F. Status and Development Trend of Mine Shaft Sinking Technique in China. Met. Mine 2021, 539, 12–24. [Google Scholar]
- Hall, A.; Cai, M.; Simser, B.; Lindsay, J. Notch formation in vertical excavations in a deep hard rock mine and rock stabilization methodologies. Deep Resour. Eng. 2024, 1, 100003. [Google Scholar] [CrossRef]
- Wang, E.; Yin, S.; Cheng, Z.; Xie, S.; Chen, L.; Kang, Q.; Duan, Y. Failure mechanism analysis of ultra-large-section soft-rock roadway in kilometer deep coal mine and its collaborative control of “grouting-anchoring-pouring”. Eng. Fail. Anal. 2025, 170, 109338. [Google Scholar] [CrossRef]
- Shu, S.; Yao, Z.; Xu, Y.; Fang, Y.; Wang, J.; Wang, F. Permeability characteristics and damage constitutive model of CA-UHPC in deep frozen shaft linings under stress-seepage coupling. Constr. Build. Mater. 2025, 484, 141824. [Google Scholar] [CrossRef]
- Lu, G.; Liu, J.; Ma, C.; Liu, L.; Tao, J. Thermal-mechanical stability of subsurface excavation in hostile geothermal environment subject to active cooling protocols. Tunn. Undergr. Space Technol. 2025, 166, 106939. [Google Scholar] [CrossRef]
- Zhang, L.; Dieudonné, A.-C.; Daniilidis, A.; Dong, L.; Cao, W.; Thibaut, R.; Tas, L.; Hermans, T. Thermo-hydro-mechanical modeling of geothermal energy systems in deep mines: Uncertainty quantification and design optimization. Appl. Energy 2025, 377, 124531. [Google Scholar] [CrossRef]
- Qin, S.; Zhao, X.; Wu, T.; Song, J.; Cao, X. Comprehensive prevention and control research on rockburst in ultradeep shaft based on theoretical deepening and practical verification. Tunn. Undergr. Space Technol. 2025, 164, 106805. [Google Scholar] [CrossRef]
- Xiao, P.; Li, D.; Zhao, G.; Zhu, Q. Characteristics and mechanism of rockburst at five deep gold mines in Jiaodong Peninsula of China. Int. J. Rock Mech. Min. Sci. 2023, 171, 105574. [Google Scholar] [CrossRef]
- Wen, J.; Zuo, J.; Wang, Z.; Wen, Z.; Wang, J. Failure mechanism analysis and support strength determination of deep coal mine roadways—A case study. Constr. Build. Mater. 2024, 443, 137704. [Google Scholar] [CrossRef]
- Hall, A.; Cai, M.; O’Connor, C.; Yadav, P.; Simser, B. Simulation of progressive notch failure in deep bored raises using an iterative approach in FLAC3D. Deep Resour. Eng. 2025, 2, 100197. [Google Scholar] [CrossRef]
- Yang, J.; Wang, J.G.; Liang, W.; Li, P.; Sun, R. Optimal selection of working fluid for enhanced geothermal systems: A comparative analysis of supercritical carbon dioxide and water under various reservoir and extraction conditions. Appl. Therm. Eng. 2024, 246, 122947. [Google Scholar] [CrossRef]
- Li, P.; Wang, J.; Liang, W.; Yang, J.; Zhang, Z.; Xu, K. A New Machine Learning-Based Prediction Approach for the Fracability of Deep Reservoirs. Nat. Resour. Res. 2025, 34, 2599–2626. [Google Scholar] [CrossRef]
- Hu, B.; Wang, J.; Ma, Z.; Sang, S. Permeability and thermal conductivity models of shale matrix with a bundle of tortuous fractal tree-like branching micropore networks. Int. J. Therm. Sci. 2021, 164, 106876. [Google Scholar] [CrossRef]
- Yang, J.; Wang, J.; Hu, B. Numerical Analysis of the Impacts of Multiscale Fractures on Geothermal Reservoir Capacity. J. Energy Eng. 2023, 149, 04023046. [Google Scholar] [CrossRef]
- Chen, S.; Zhu, H.; Zhao, P.; Wang, Y.; Song, R.; Zuo, Y.; Shi, Y.; Zhou, T. Influence of fracture network characteristics of hot dry rock on heat extraction performance: A numerical simulation study. Geoenergy Sci. Eng. 2025, 245, 213523. [Google Scholar] [CrossRef]
- Li, P.; Wang, J.; Liang, W.; Yang, J. Study on CO2 fracturing in deep tight sandstone considering the in-situ stress gradient and thermal stress. Comput. Geotech. 2024, 174, 106599. [Google Scholar] [CrossRef]
- Lu, W.; Zhang, X. Coupled thermo-hydro-mechanical modelling of carbon dioxide sequestration in saline aquifers considering phase change. Curr. Sci. 2020, 119, 973–983. [Google Scholar] [CrossRef]
- Xue, K.; Pu, H.; Li, M.; Luo, P.; Liu, D.; Yi, Q. Fractal-based analysis of stress-induced dynamic evolution in geometry and permeability of porous media Available to Purchase. Phys. Fluids 2025, 37, 036630. [Google Scholar] [CrossRef]
- Xu, T.; Pruess, K.; Apps, J. Numerical studies of fluid-rock interactions in Enhanced Geothermal Systems (EGS) with CO2 as working fluid. In Proceedings of the Thirty-Third Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 28–30 January 2008. [Google Scholar]
- Yang, J.; Wang, J.G.; Li, P.; Liang, W.; Leung, C. A Novel Progressive Many-Objective Optimization Approach for Engineering-Controllable Parameters of an Enhanced Geothermal System in the Gonghe Basin, China. Math. Geosci. 2025, 57, 1327–1355. [Google Scholar] [CrossRef]
- Gong, F.; Guo, T.; Sun, W.; Li, Z.; Yang, B.; Chen, Y.; Qu, Z. Evaluation of geothermal energy extraction in Enhanced Geothermal System (EGS) with multiple fracturing horizontal wells (MFHW). Renew. Energy 2020, 151, 1339–1351. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, H.; Li, T.; Wang, Y.; Ren, F.; Ma, G. Evaluation of geothermal development considering proppant embedment in hydraulic fractures. Renew. Energy 2020, 153, 985–997. [Google Scholar] [CrossRef]
- Pu, H.; Xue, K.; Wu, Y.; Zhang, S.; Liu, D.; Xu, J. Estimating the permeability of fractal rough rock fractures with variable apertures under normal and shear stresses. Phys. Fluids 2025, 37, 036635. [Google Scholar] [CrossRef]
- Li, M.-G.; Yan, Y.-H.; Xu, Z.-H.; Chen, H.-B.; Peng, C.-X.; Chen, J.-J. Fully hydro-mechanical coupled analyses of the deep excavation above a multi-aquifer-aquitard system. Tunn. Undergr. Space Technol. 2025, 156, 106259. [Google Scholar] [CrossRef]
- Zhu, X.; Ji, H.; Liu, R.; Yu, L.; Wang, Y. Numerical study of hydraulic characteristics of shale fractures during unloading-induced slipping: Effects of inclination angle and unloading rate. Comput. Geotech. 2023, 164, 105811. [Google Scholar] [CrossRef]
- Chu, Z.; Wu, Z.; Liu, B.; Wu, K.; Shi, X.; Liu, Q. Mechanical response of inclined TBM tunnel due to drainage settlement of deep sandstone aquifer. Tunn. Undergr. Space Technol. 2022, 122, 104393. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, R.; Li, W.; Qiao, W.; Wei, M.; Yu, L. Correcting the Permeability Evaluation of Elliptical Rock Fractures in Triaxial Shear-Flow Experiments Considering Channeling Flow. Rock Mech. Rock Eng. 2023, 57, 1509–1523. [Google Scholar] [CrossRef]
- Li, C.C. Field observations and interpretation of extensional fracture in hard rock surrounding deep underground openings. Deep Resour. Eng. 2024, 1, 100006. [Google Scholar] [CrossRef]
- Hashemi, S.; Ashcroft, B.; Chittenden, N.; Gwildis, U.; Heine, J.; Luxford, J.; Marquis, F.; Nasri, V.; Preene, M.; Shaterpour-Mamaghani, A.; et al. Selection of shaft construction method. Tunn. Undergr. Space Technol. 2025, 164, 106654. [Google Scholar] [CrossRef]
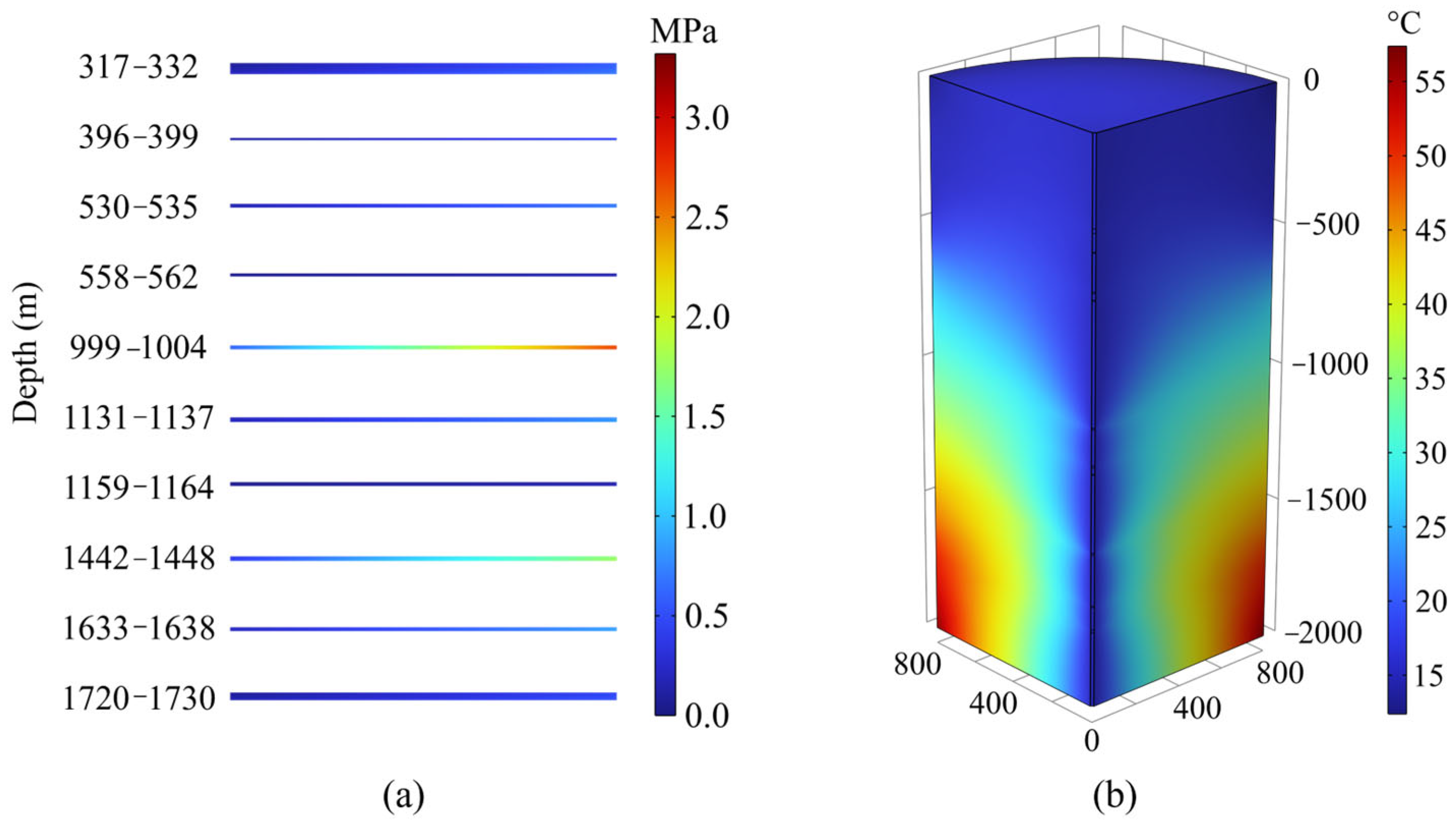
| Number | Depth | Tensile Strength | Uniaxial Compressive Strength | Friction Angle | Elastic Modulus | Poisson’s Ratio | |
|---|---|---|---|---|---|---|---|
| m | MPa | MPa | ° | GPa | 1 | ||
| SSD19-1 | ① | 4.73–16.93 | 1.84 | 26.10 | 43.6 | 23.30 | 0.23 |
| ② | 3.98 | 32.70 | 19.70 | 0.30 | |||
| ③ | 2.3 | 44.50 | 31.60 | 0.18 | |||
| SSD19-2 | 38.00–55.00 | 6.43 | 42.72 | 59.4 | 3.75 | 0.11 | |
| SSD19-19 | ① | 100.00–300.00 | 6.63 | 132 | 56.5 | 67.3 | 0.06 |
| ② | 10.2 | 135 | 55.2 | 0.05 | |||
| ③ | 8.98 | 150 | 47.9 | 0.08 | |||
| SSD19-3 | 340.00–400.00 | 4.91 | 37.66 | 5.98 | 0.02 | ||
| SSD19-4 | 525.00–580.00 | 4.49 | 54.40 | 42.83 | 7.69 | 0.27 | |
| SSD19-20 | ① | 600.00–700.00 | 8.23 | 145 | 56.3 | 57.5 | 0.06 |
| ② | 6.44 | 123 | 58.8 | 0.05 | |||
| ③ | 6.93 | 112 | 64.7 | 0.11 | |||
| SSD19-5 | 760.00–800.00 | 6.05 | 60.79 | 58.07 | 5.30 | 0.40 | |
| SSD19-6 | 935.00–1000.00 | 5.35 | 28.99 | 53.11 | 5.50 | 0.05 | |
| SSD19-7 | 1000.00–1050.00 | 5.46 | 73.00 | 44.21 | 4.76 | 0.21 | |
| SSD19-8 | 1050.00–1064.00 | 6.15 | 28.27 | 55.86 | 3.96 | 0.24 | |
| SSD19-9 | 1140.00–1170.00 | 5.83 | 46.34 | 44.58 | 2.75 | 0.05 | |
| SSD19-10 | 1300.00–1400.00 | 5.31 | 46.71 | 45.17 | 1.84 | 0.12 | |
| SSD19-11 | 1650.00–1700.00 | 3.25 | 35.10 | 36.43 | 5.17 | 0.27 | |
| SSD19-13 | ① | 1722.96–1728.16 | 3.38 | 60.60 | 53.5 | 21.8 | 0.20 |
| ② | 4.56 | 42.60 | 20.5 | 0.11 | |||
| ③ | 4.82 | 45.90 | 26.1 | 0.09 | |||
| SSD19-14 | ① | 1728.66–1740.46 | 3.94 | 58.70 | 54.3 | 36.2 | 0.14 |
| ② | 4.99 | 62.30 | 38.8 | 0.12 | |||
| ③ | 5.83 | 68.90 | 46.3 | 0.05 | |||
| SSD19-15 | ① | 1740.46–1756.76 | 7.30 | 116 | 53.3 | 43.5 | 0.09 |
| ② | 6.68 | 107 | 57.3 | 0.13 | |||
| ③ | 6.53 | 72.9 | 42.3 | 0.06 | |||
| SSD19-16 | ① | 1800.00–1870.00 | 7.36 | 126 | 53.4 | 50.5 | 0.10 |
| ② | 8.31 | 117 | 47.9 | 0.09 | |||
| ③ | 9.13 | 144 | 48.8 | 0.03 | |||
| SSD19-17 | ① | 1960.00–1980.00 | 7.16 | 113 | 54.4 | 59.8 | 0.07 |
| ② | 8.81 | 126 | 45.4 | 0.12 | |||
| ③ | 6.71 | 103 | 47.4 | 0.04 | |||
| SSD19-18 | ① | 1974.00–1983.00 | 7.54 | 141 | 58.3 | 85.7 | 0.03 |
| ② | 12.0 | 118 | 92.2 | 0.09 | |||
| ③ | 9.48 | 161 | 95.2 | 0.10 | |||
| SSD19-21 | ① | 1990.00–2000.00 | 7.58 | 87.8 | 53.6 | 52.5 | 0.11 |
| ② | 5.70 | 110 | 63.8 | 0.12 | |||
| ③ | 6.16 | 117 | 53.9 | 0.13 | |||
| SSD19-22 | ① | 2000.00–2015.00 | 2.53 | 19.2 | 45.2 | 9.32 | 0.45 |
| ② | 2.17 | 28.9 | 11.0 | 0.34 | |||
| ③ | 2.94 | 27.2 | 7.95 | 0.24 | |||
| Pumping Test Stage | Depth | Depth of Static Water Level | Water Level Drops | Aquifer Thickness | Hydraulic Conductivity | Water Inflow |
|---|---|---|---|---|---|---|
| m | m | m | m | m/d | m3/d | |
| II | 317.00–332.00 | 218.50 | 113.50 | 15.00 | 0.084331 | 174.33 |
| 396.00–399.00 | 332.00 | 67.00 | 3.00 | 0.084331 | 25.72 | |
| 530.00–535.00 | 399.00 | 136.00 | 5.00 | 0.084331 | 69.31 | |
| 558.00–562.00 | 535.00 | 27.00 | 4.00 | 0.084331 | 19.41 | |
| I | 999.00–1004.00 | 562.00 | 442.00 | 5.00 | 0.046170 | 97.02 |
| 1131.00–1137.00 | 1004.00 | 133.00 | 6.00 | 0.046170 | 47.45 | |
| 1159.00–1164.00 | 1137.00 | 27.00 | 5.00 | 0.046170 | 14.51 | |
| 1442.00–1448.00 | 1164.00 | 284.00 | 6.00 | 0.046170 | 82.82 | |
| 1633.00–1638.00 | 1448.00 | 190.00 | 5.00 | 0.046170 | 51.29 | |
| 1720.00–1730.00 | 1638.00 | 92.00 | 10.00 | 0.046170 | 59.81 |
| Parameters | Unit | Value |
|---|---|---|
| Elastic modulus of rock | GPa | 30 |
| Poisson’s ratio | 1 | 0.15 |
| Biot’s coefficient | - | 1.0 |
| Water storage coefficient | 1/Pa | 1 × 10−9 |
| Thermal expansion coefficient | 1/K | 5.0 × 10−7 |
| Rock permeability | m2 | 1 × 10−14 |
| Rock porosity | - | 0.2 |
| Fluid density | kg/m3 | 1000 |
| Thermal conductivity of fluid | J/(m·K·s) | 0.6 |
| Thermal conductivity of rock | J/(m·K·s) | 3.5 |
| Heat capacity of fluid | J/(kg·K) | 4200 |
| Heat capacity of rock | J/(kg·K) | 790 |
| Parameters | Unit | Value |
|---|---|---|
| Initial rock porosity | - | 0.15 |
| Biot’s coefficient | - | 1.0 |
| Thermal expansion coefficient | 1/K | 5.0 × 10−6 |
| Density of rock | kg/m3 | 2500 |
| Thermal conductivity of rock | W/(m·K) | 3.0 |
| Heat capacity of rock | J/(kg·K) | 800 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Fan, W.; Deng, X.; Yu, L.; Song, Z.; Hu, B. Thermal–Hydraulic–Mechanical Coupling Effects and Stability Analysis of Surrounding Rock in Ultra-Deep Mine Shaft Excavation. Appl. Sci. 2025, 15, 12433. https://doi.org/10.3390/app152312433
Wang G, Fan W, Deng X, Yu L, Song Z, Hu B. Thermal–Hydraulic–Mechanical Coupling Effects and Stability Analysis of Surrounding Rock in Ultra-Deep Mine Shaft Excavation. Applied Sciences. 2025; 15(23):12433. https://doi.org/10.3390/app152312433
Chicago/Turabian StyleWang, Guoyuan, Wenbo Fan, Xiansong Deng, Liyuan Yu, Zhaoyang Song, and Bowen Hu. 2025. "Thermal–Hydraulic–Mechanical Coupling Effects and Stability Analysis of Surrounding Rock in Ultra-Deep Mine Shaft Excavation" Applied Sciences 15, no. 23: 12433. https://doi.org/10.3390/app152312433
APA StyleWang, G., Fan, W., Deng, X., Yu, L., Song, Z., & Hu, B. (2025). Thermal–Hydraulic–Mechanical Coupling Effects and Stability Analysis of Surrounding Rock in Ultra-Deep Mine Shaft Excavation. Applied Sciences, 15(23), 12433. https://doi.org/10.3390/app152312433









