Issue of Selecting Stress Field Parameters for the Analysis of Mining Excavation Stability Using Numerical Methods in the Conditions of the LGCB Mines
Abstract
1. Introduction
- −
- The geological structure of the rock mass (the arrangement of rock layers);
- −
- The strength and strain parameters of the rock layers;
- −
- The dimensions, shape, and location of the underground headings within the rock mass;
- −
- The parameters of the stress field.
- σz—vertical stress [MPa];
- γ—unit weight of the overburden rocks [MN/m3];
- H—depth of the analyzed rock layer [m].
- σz—vertical stress [MPa];
- γi—unit weight of the i-th rock layer [MN/m3];
- hi—thickness of the i-th rock layer [m].
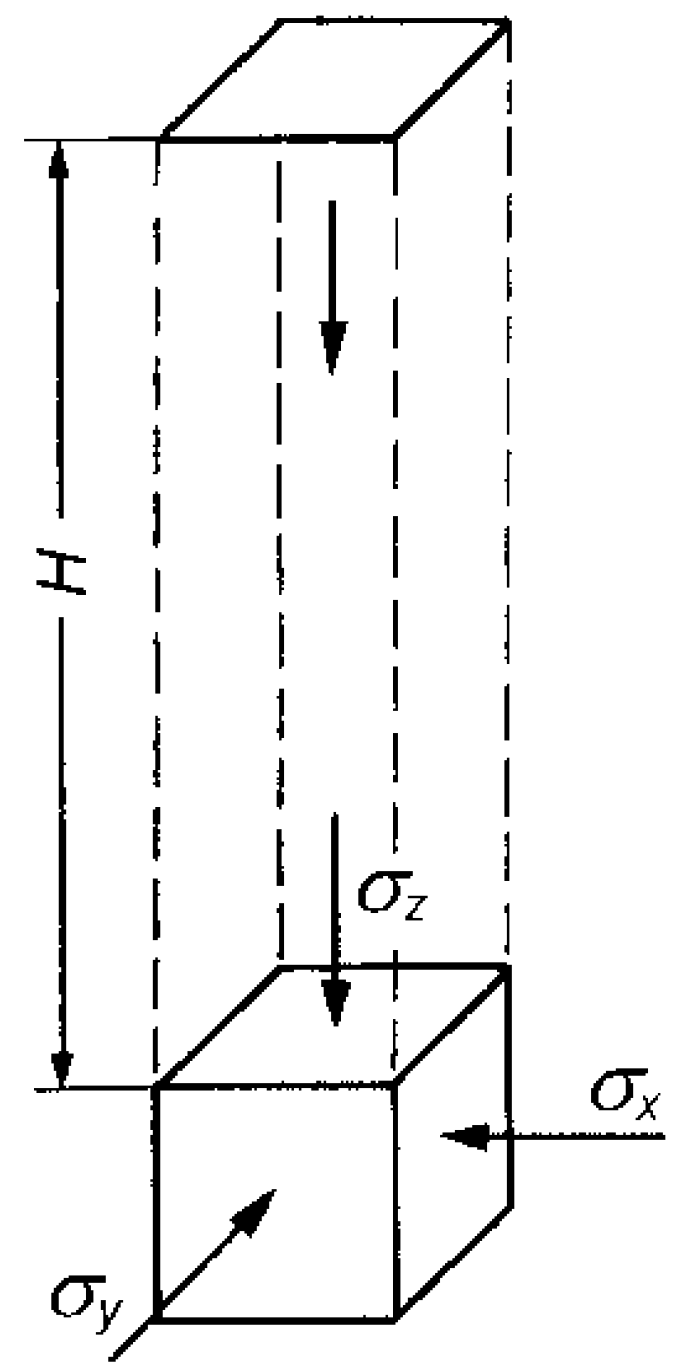
- σx—horizontal stress along the x-axis [MPa];
- σy—horizontal stress along the y-axis [MPa];
- ν—Poisson’s ratio [-];
- σz—vertical stress along the z-axis [MPa].
- −
- Gravitational stress field, related to the weight of the overlying rocks.
- −
- σBxy—horizontal stress in geostatic areas [MPa];
- H—depth at which horizontal stress is calculated [m].
- σz—vertical stress in geostatic areas [MPa];
- σz grav—vertical stress resulting from gravitational forces [MPa].
- −
- Vertical stress increases with depth;
- −
2. Prediction of the Mining Excavations Stability at the Rudna Mine
- σ1 and σ3—values of maximum and minimum effective principal stress at failure;
- mb—Hoek–Brown constant for the rock mass;
- s and a—constants dependent on the rock mass properties;
- σci—uniaxial compressive strength of the intact rock sample.
- σ1 and σ3—values of maximum and minimum effective principal stress at failure;
- φ—friction angle;
- c—cohesion;
- σt—uniaxial tension strength.
- −
- Rod diameter: 18.2 mm;
- −
- Rod length: 1.8 m;
- −
- Rod material: steel;
- −
- Young’s modulus: 210,000.0 MPa;
- −
- Ultimate load capacity: 170.0 kN;
- −
- Residual load capacity: 17.0 kN;
- −
- Initial pretension force: 30.0 kN.
| Excavation Hight [m] | Width of Excavation Roof [m] | Width of Excavation Floor [m] | Average Width [m] | Area of the Excavation [m2] | Sidewall Inclination Angle [°] |
|---|---|---|---|---|---|
| 3.5 | 7.0 | 5.8 | 6.4 | 22.4 | 10.0 |
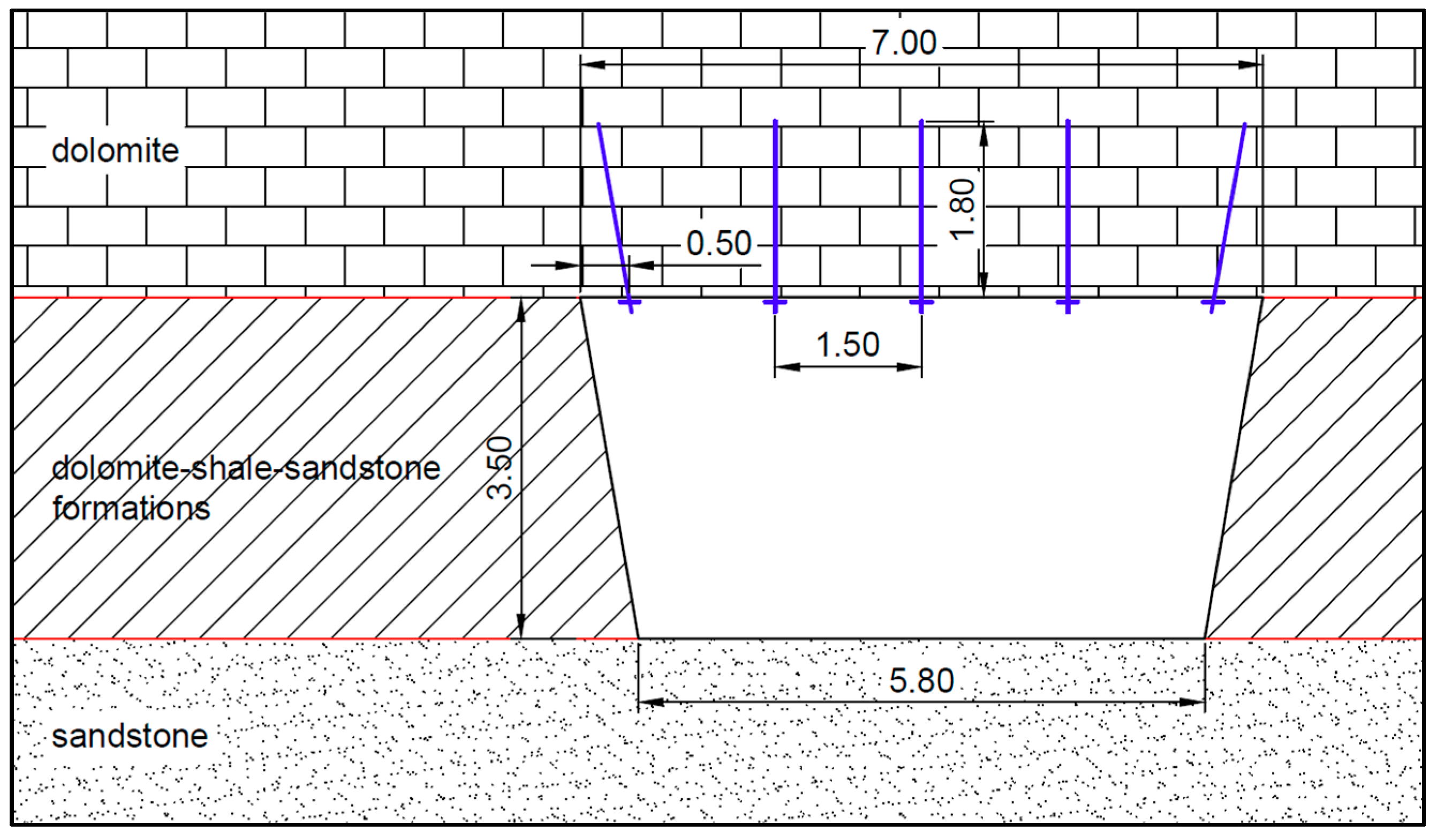
- −
- Variant 1: the stress field in the rock mass was determined for a depth of 1200 m below ground level based on Bulin’s formulas (Formulas (6) and (7));
- −
- Variant 2: hydrostatic stress state in the rock mass for a depth of 1200 m below ground level (Formula (5));
- −
- Variant 3 and variant 4: stress values derived from in situ measurements at the Rudna mine in 2012 (Table 1, measurement station no. 4 and measurement point no. 4 (S4P4)).
| Modeling Variant | Horizontal Stress σx [MPa] | Horizontal Stress σy [MPa] | Vertical Stress σz [MPa] |
|---|---|---|---|
| 1 (based on Bulin’s formulas) | 18.10 | 18.10 | 24.50 |
| 2 (hydrostatic stress state) | 24.50 | 24.50 | 24.50 |
| 3 (in situ measurements) | 19.60 | 26.40 | 23.90 |
| 4 (in situ measurements) | 26.40 | 19.60 | 23.90 |
- Loading variant 1 (stress state determined based on Bulin’s formulas for depth H = 1200 m b.g.l.):
- −
- Lateral edges: px = 18.10 MPa;
- −
- Upper and lower edges: pz = 24.50 MPa;
- −
- Direction perpendicular to the plate: py = 18.10 MPa.
- Loading variant 2 (hydrostatic stress state in the rock mass for depth H = 1200 m b.g.l.):
- −
- Lateral edges: px = 24.50 MPa;
- −
- Upper and lower edges: pz = 24.50 MPa;
- −
- Direction perpendicular to the plate: py = 24.50 MPa.
- Loading variant 3 (stress state determined based on in situ measurements at the Rudna mine; the maximum horizontal stress component acts parallel to the direction of driving the heading):
- −
- Lateral edges: px = 19.60 MPa;
- −
- Upper and lower edges: pz = 23.90 MPa;
- −
- Direction perpendicular to the plate: py = 26.40 MPa.
- Loading variant 4 (stress state determined based on in situ measurements at the Rudna mine; the maximum horizontal stress component acts perpendicular to the direction of driving the heading):
- −
- Lateral edges: px = 26.40 MPa;
- −
- Upper and lower edges: pz = 23.90 MPa;
- −
- Direction perpendicular to the plate: py = 19.60 MPa.
3. Results of Numerical Modeling and Discussion
- −
- The area and shape of the yielded rock mass zone around the headings vary depending on the magnitude of the stress field components and are closely related to the strength and deformation parameters of the rock layers in which the excavations are driven.
- −
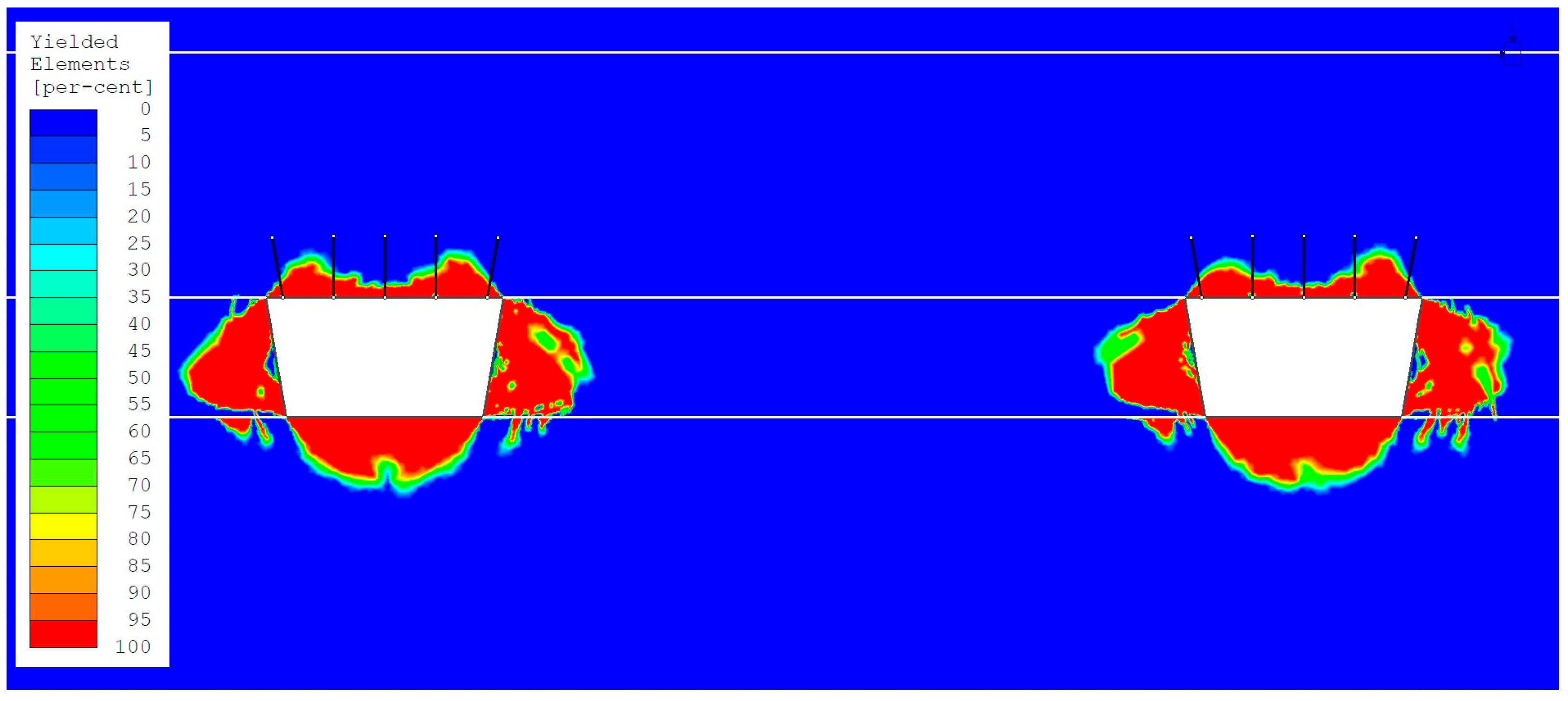
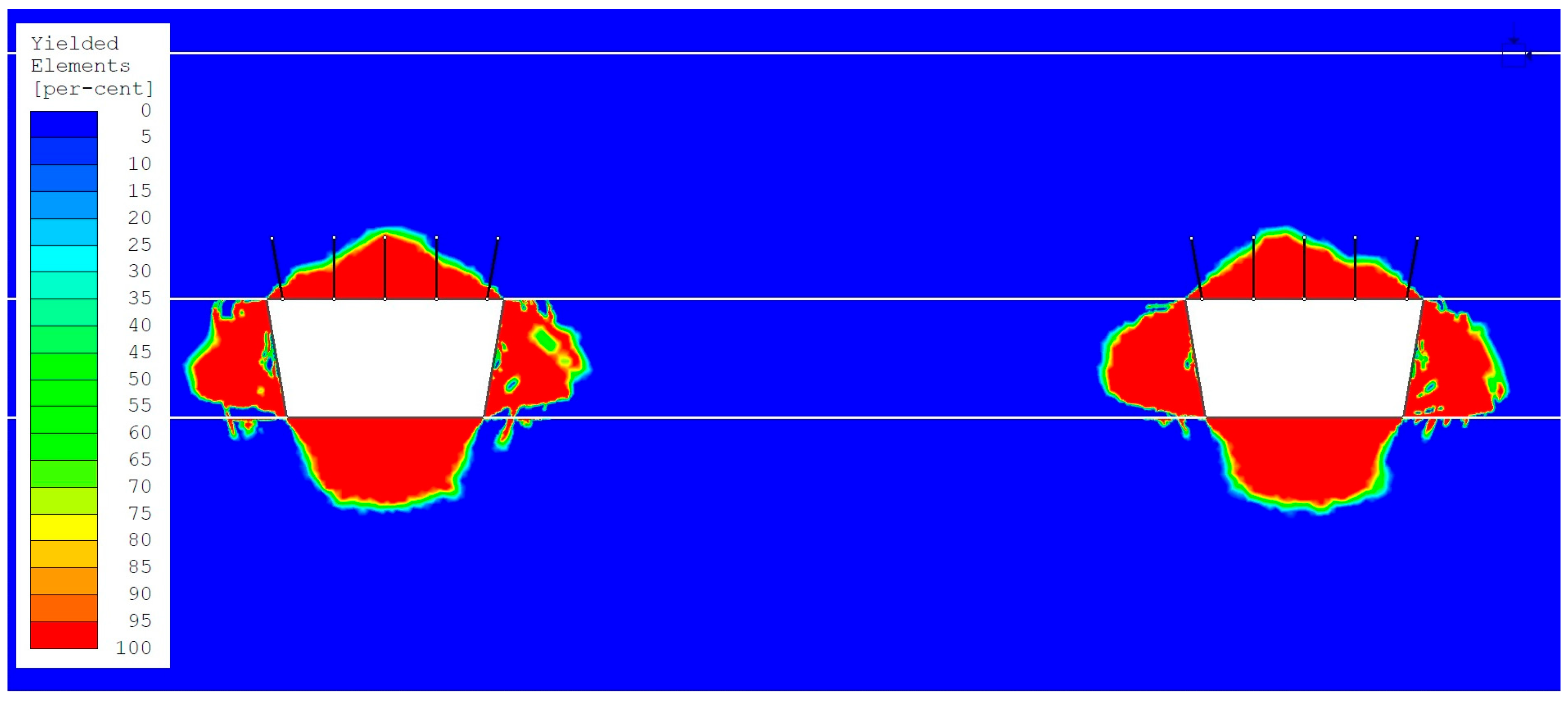
- The area of the yielded rock mass zone (ranging from 50% to 100%) in the roof of the headings in the numerical model with variant 1 loading (stress state determined based on Bulin’s formulas) is significantly smaller than the anchorage zone (ranging from 0.46 m to 0.56 m). Values from 1.24 m to 1.34 m were observed (Figure 5 and Figure 6). The yielded zone in the roof has a characteristic shape. The smallest yielded zone occurs in the center of the excavations, while the largest area of the yielded zone is observed in the roof near the upper corners of the excavations.
- −
- The area of the yielded zone (ranging from 50% to 100%) in the roofs of headings in the numerical model with variant 2 loading (hydrostatic stress state) is generally larger than the anchorage zone in the roofs of headings no. 1 to no. 3 (ranging from 0.18 m to 0.28 m), where values from 1.98 m to 2.08 m were observed (Figure 7 and Figure 8). In heading no. 4, the area of the yielded zone in the roof (50% to 100%) is 1.78 m, which is only 0.02 m less than the anchorage zone.
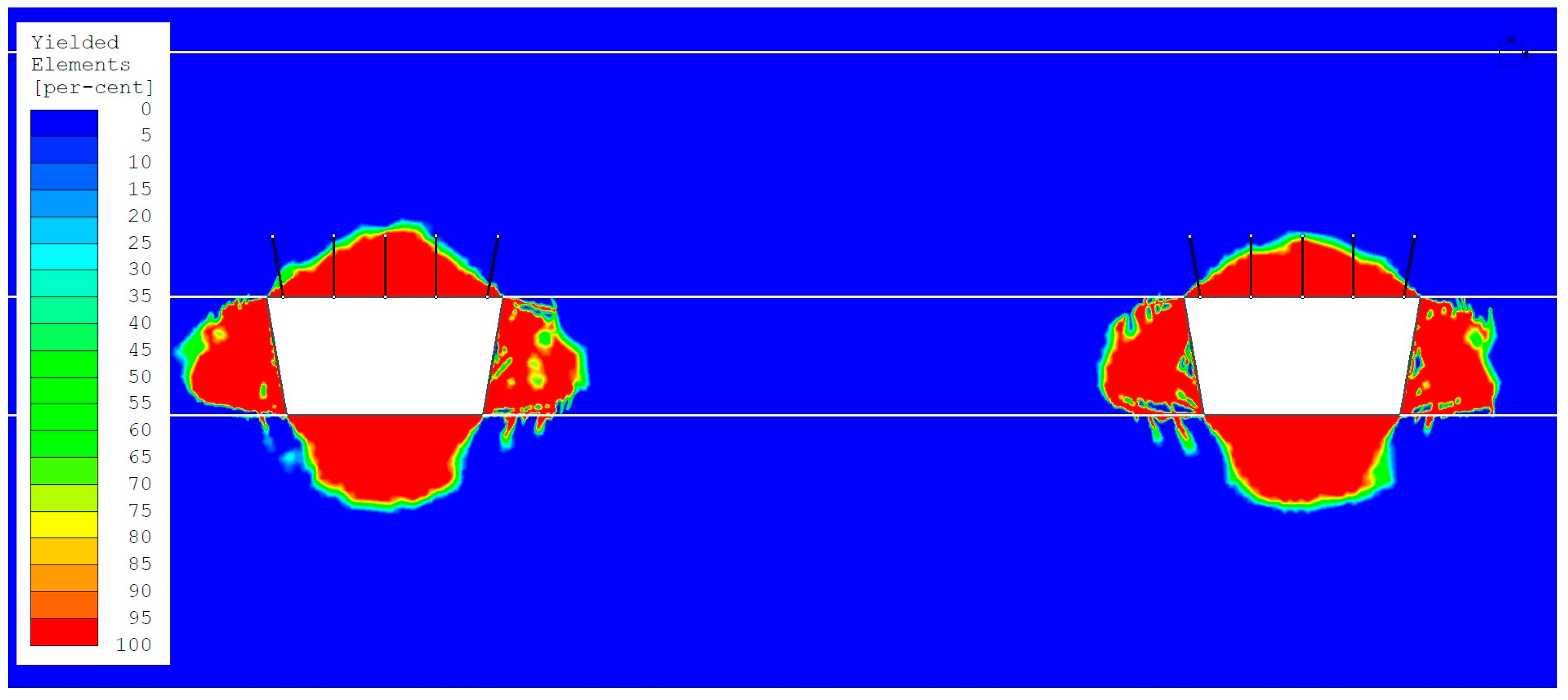
- −
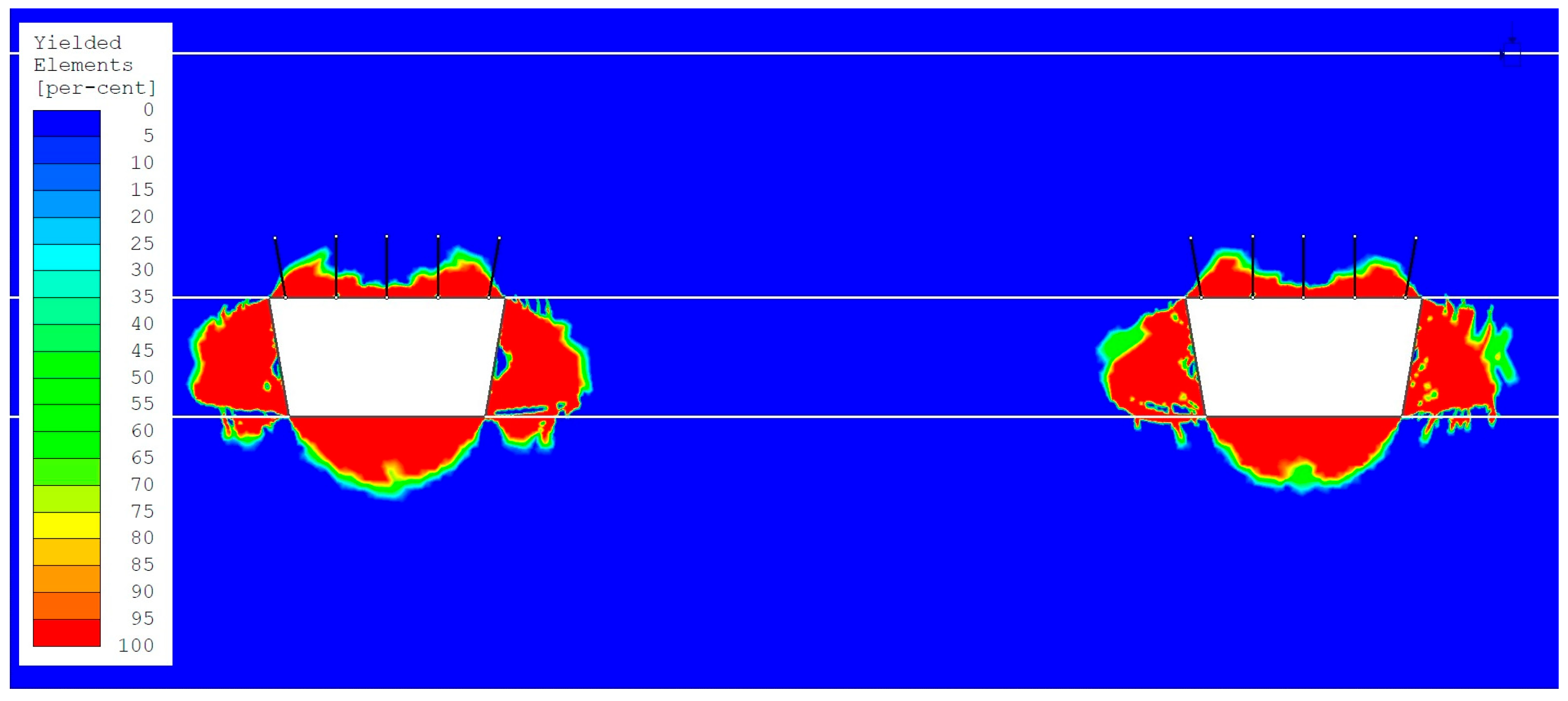
- The smallest size of the yielded zone (ranging from 50% to 100%) in the roofs of headings occurred in the numerical model with variant 3 loading (the maximum horizontal stress component, determined based on in situ measurements, acting parallel to the heading excavation direction). Values from 1.18 m to 1.25 m were observed (Figure 9 and Figure 10). These are significantly smaller (ranging from 0.55 m to 0.62 m) than the anchorage zone in the roofs of the headings.
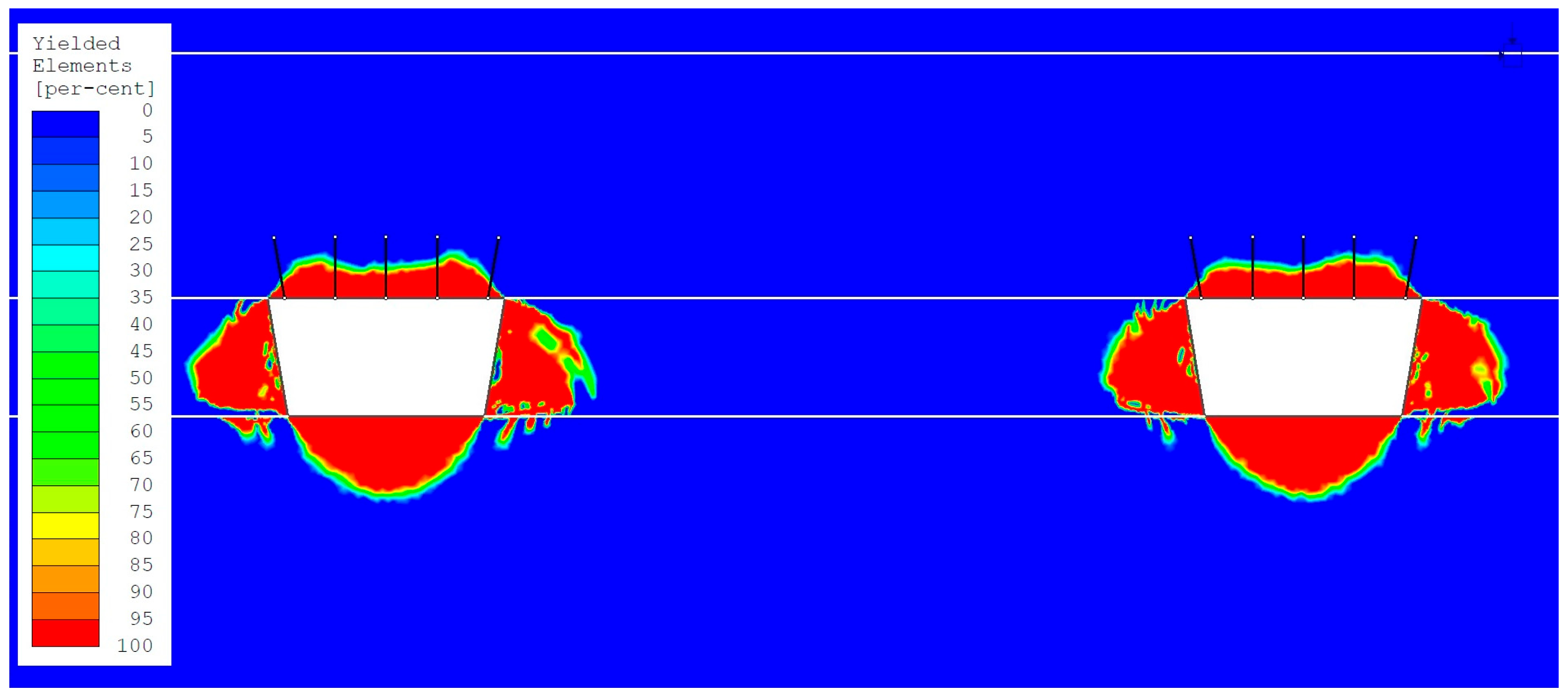
- −
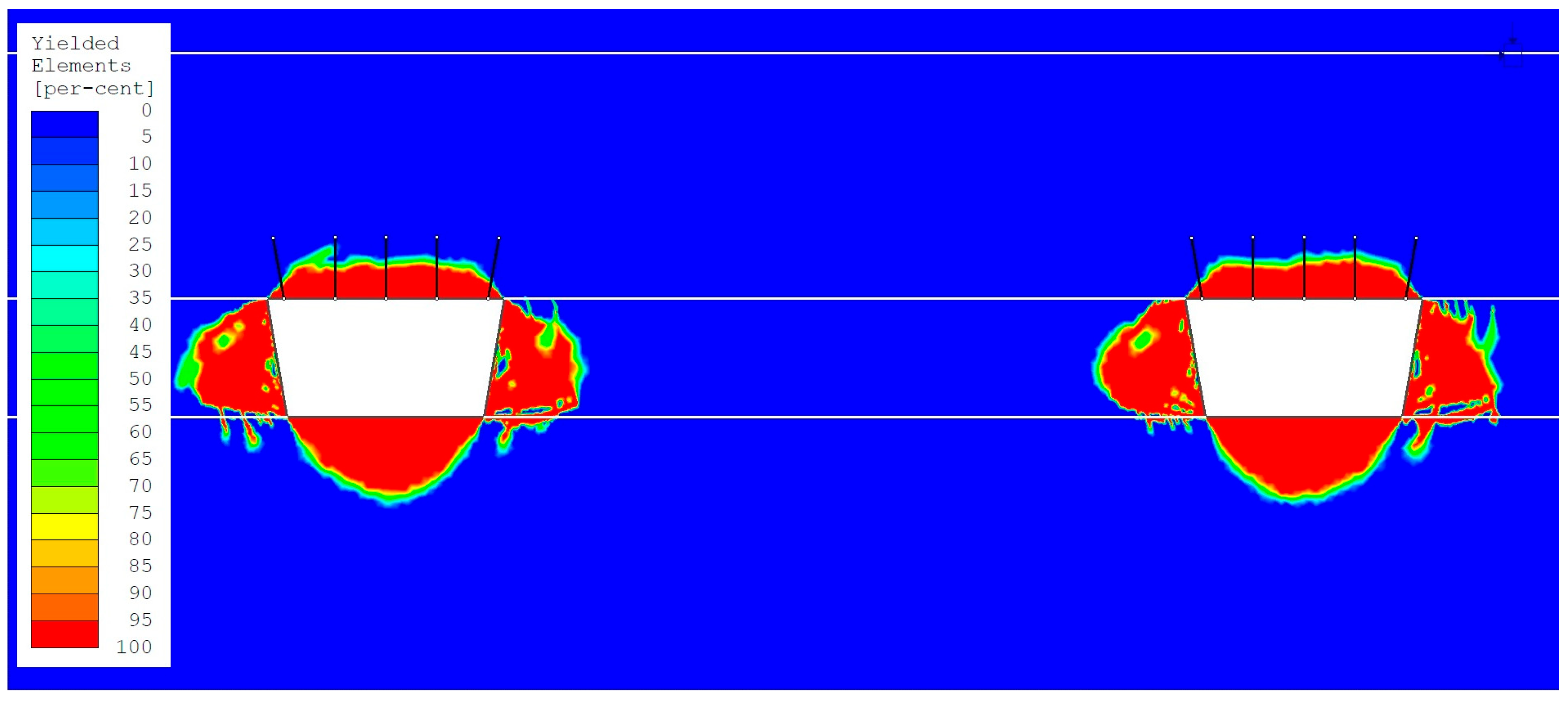
- The largest size of the yielded zone (ranging from 50% to 100%) in the roofs of headings occurred in the numerical model with variant 4 loading (the maximum horizontal stress component, determined based on in situ measurements, acting perpendicular to the direction of heading excavation). Observed values ranged from 1.97 m to 2.18 m (Figure 11 and Figure 12). These significantly exceed the anchorage zone in the heading roofs by 0.17 m to 0.38 m.
- −
- The maximum size of the yielded zone (ranging from 50% to 100%) in the sidewalls of the headings (Table 8), depending on the values of the stress field parameters, reached the following values:
- ▪
- From 2.86 m to 3.22 m (variant 1 loading);
- ▪
- From 2.83 m to 3.03 m (variant 2 loading);
- ▪
- From 2.83 m to 3.24 m (variant 3 loading);
- ▪
- From 2.83 m to 3.11 m (variant 4 loading).
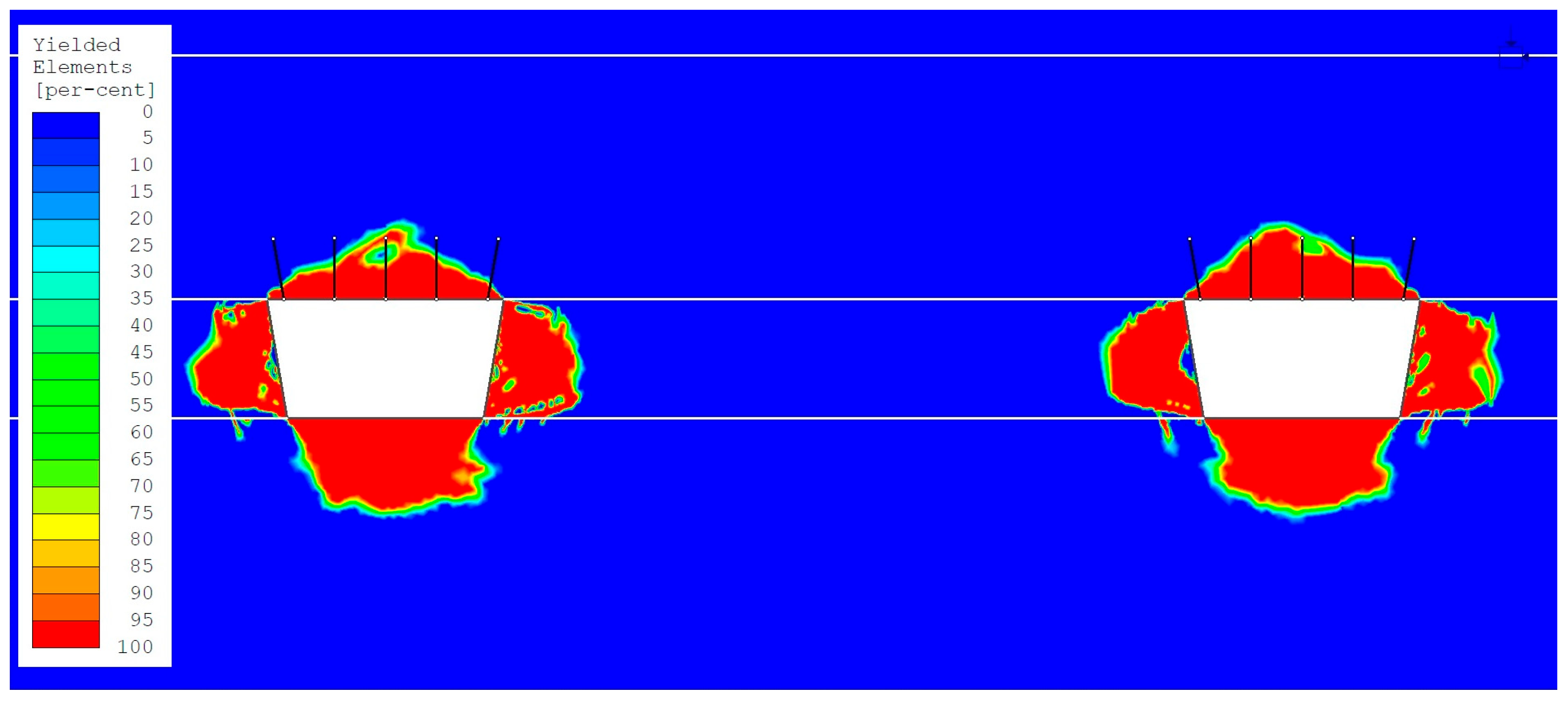
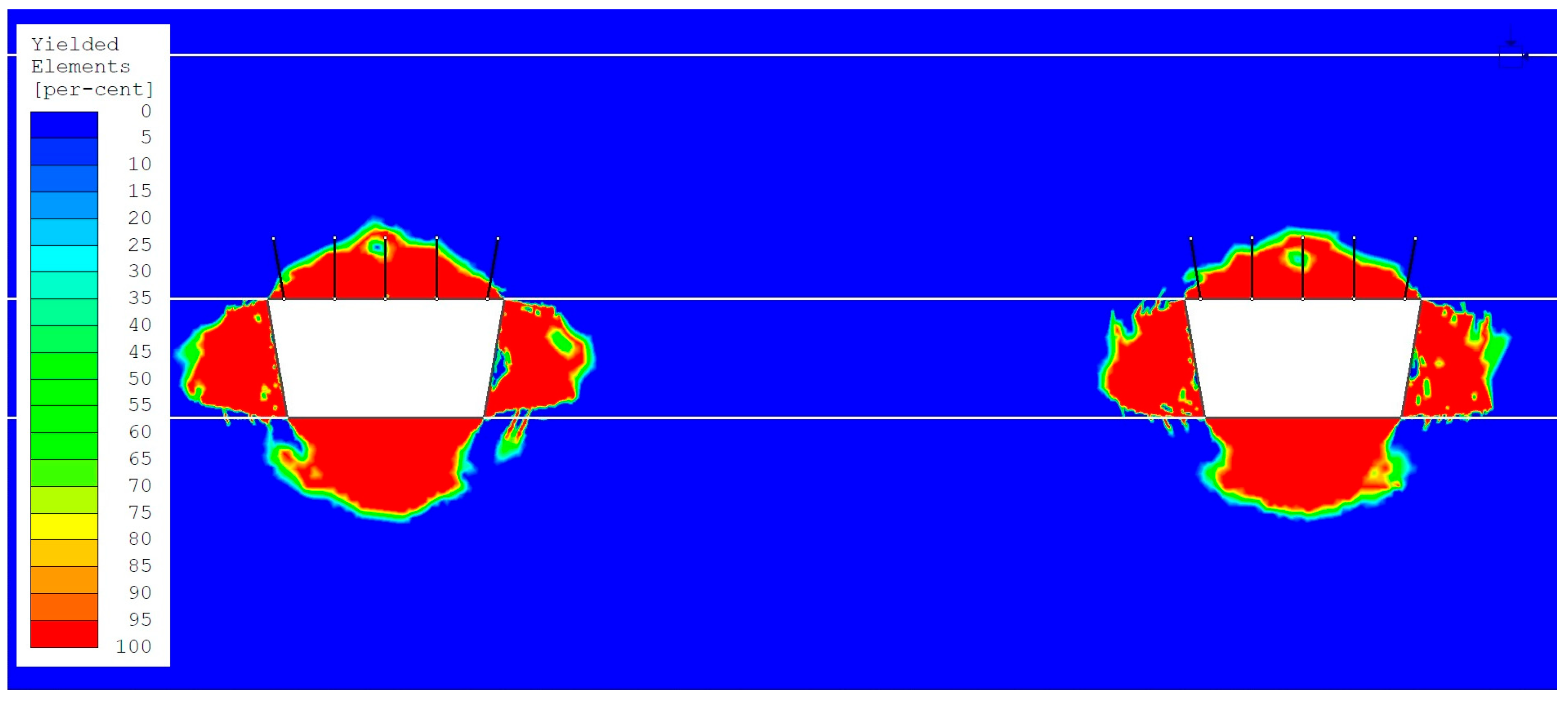
| Heading | Size of Yielded Zones in the Roof [m] | |||
|---|---|---|---|---|
| Loading Variant 1 | Loading Variant 2 | Loading Variant 3 | Loading Variant 4 | |
| 1 | 1.24 | 1.99 | 1.24 | 2.15 |
| 2 | 1.34 | 1.98 | 1.21 | 2.17 |
| 3 | 1.30 | 2.08 | 1.18 | 2.18 |
| 4 | 1.30 | 1.78 | 1.25 | 1.97 |
| Heading | Size of Yielded Zones in the Sidewalls [m] | |||
|---|---|---|---|---|
| Loading Variant 1 | Loading Variant 2 | Loading Variant 3 | Loading Variant 4 | |
| 1 (left sidewall) | 2.98 | 2.83 | 2.83 | 2.83 |
| 1 (right sidewall) | 3.05 | 2.98 | 3.24 | 2.84 |
| 2 (left sidewall) | 3.00 | 3.00 | 2.95 | 2.89 |
| 2 (right sidewall) | 3.02 | 3.03 | 2.97 | 2.88 |
| 3 (left sidewall) | 2.86 | 2.97 | 3.18 | 3.02 |
| 3 (right sidewall) | 3.05 | 2.98 | 2.85 | 3.11 |
| 4 (left sidewall) | 2.94 | 3.00 | 3.18 | 2.99 |
| 4 (right sidewall) | 3.22 | 2.83 | 2.89 | 3.02 |
| Average value | 3.02 | 2.95 | 3.01 | 2.95 |
4. Conclusions
- −
- For headings driven in a stress field determined using Bulin’s formulas (for a depth of 1200 m below ground level), RM-18 resin-grouted bolts with a length of 1.6 m and a bolt pattern of 1.5 × 1.5 m were selected.
- −
- For headings driven in a rock mass characterized by a hydrostatic stress state (at a depth of 1200 m below ground level), RM-18 resin-grouted bolts with a length of 2.2 m and a bolt pattern of 1.5 × 1.5 m were selected.
- −
- For headings driven parallel to the maximum horizontal stress component (based on in situ measurements conducted in the Rudna mine in 2012), RM-18 resin-grouted bolts with a length of 1.6 m and a bolt pattern of 1.5 × 1.5 m were selected.
- −
- For headings driven perpendicular to the maximum horizontal stress component (based on in situ measurements conducted in the Rudna mine in 2012), RM-18 resin-grouted bolts with a length of 2.6 m and a bolt pattern of 1.5 × 1.5 m were selected.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zeller, S.S.; Pollard, D.D. Boundary conditions for rock fracture analysis using the boundary element method. J. Geophys. Res. Solid Earth 1992, 97, 1991–1997. [Google Scholar] [CrossRef]
- Beer, G.; Pousen, A. Efficient numerical modelling of faulted rock using the boundary element method. Int. J. Rock Mech. Min. Sci. 1995, 31, 485–506. [Google Scholar] [CrossRef]
- Cerrolaza, M.; Garcia, R. Boundary elements and damage mechanics to analyze excavations in rock mass. Eng. Anal. Bound. Elem. 1997, 20, 1–16. [Google Scholar] [CrossRef]
- Pan, E.; Amadei, B.; Kim, Y.I. 2D BEM analysis of anisotropic half-plane problems—Application to rock mechanics. Int. J. Rock Mech. Min. Sci. 1998, 35, 69–74. [Google Scholar] [CrossRef]
- Shou, K.J. A three-dimensional hybrid boundary element method for non-linear analysis of a weak plane near an underground excavation. Tunn. Undergr. Space Technol. 2000, 15, 215–226. [Google Scholar] [CrossRef]
- Jing, L.; Hudson, J.A. Numerical methods in rock mechanics. Int. J. Rock Mech. Min. Sci. 2002, 39, 409–427. [Google Scholar] [CrossRef]
- Jing, L. A review of technics, advances and outstanding issues in numerical modelling for rock mechanics and rock engineering. Int. J. Rock Mech. Min. Sci. 2003, 40, 283–353. [Google Scholar] [CrossRef]
- Yasitli, N.E.; Unver, B. 3D numerical modelling of longwall mining with top-coal caving. Int. J. Rock Mech. Min. Sci. 2005, 42, 219–235. [Google Scholar] [CrossRef]
- Henning, J.G.; Mitri, H.S. Numerical modelling of ore dilution in blasthole stoping. Int. J. Rock Mech. Min. Sci. 2007, 44, 692–703. [Google Scholar] [CrossRef]
- Wang, J.; Apel, D.B.; Pu, Y.; Hall, R.; Wei, C.; Sepehri, M. Numerical modeling for rockbursts: A state-of-the-art review. J. Rock Mech. Geotech. Eng. 2021, 13, 457–478. [Google Scholar] [CrossRef]
- Kruszewski, M.; Montegrossi, G.; Balcewicz, M.; Igbokwe, O.A.; Backers, T.; Saenger, E.H. 3D in situ stress state modelling and fault reactivation risk exemplified in the Ruhr region (Germany). Geomech. Energy Environ. 2022, 32, 100386. [Google Scholar] [CrossRef]
- Wang, J.; Apel, D.B.; Dyczko, A.; Walentek, A.; Prusek, S.; Xu, H.; Wei, C. Analysis of the damage mechanism of strainbursts by a global-local modeling approach. J. Rock Mech. Geotech. Eng. 2022, 14, 1671–1696. [Google Scholar] [CrossRef]
- Chen, D.; Zhu, J.; Ye, Q.; Ma, X.; Xie, S.; Guo, W.; Li, Z.; Wang, Z.; Feng, S.; Yan, X. Application of gob-side entry driving in fully mechanized caving mining: A review of theory and technology. Energies 2023, 16, 2691. [Google Scholar] [CrossRef]
- Adach-Pawelus, K.; Pawelus, D. Influence of remnant size on the geomechanical situation and safety in the mining field based on numerical modeling. Min. Sci. 2025, 32, 47–63. [Google Scholar] [CrossRef]
- Zhu, D.; Tu, S. Mechanisms of support failure induced by repeated mining under gobs created by two-seam room mining and prevention measures. Eng. Fail. Anal. 2017, 82, 161–178. [Google Scholar] [CrossRef]
- Feng, G.; Wang, P. Simulation of recovery of upper remnant coal pillar while mining the ultra-close lower panel using longwall top coal caving. Int. J. Min. Sci. Technol. 2020, 30, 55–61. [Google Scholar] [CrossRef]
- Kudelko, J.; Bodlak, M. Evaluation significance of differences between the geotechnical parameters of the lithological rocks roof layers, above mining excavation. Min. Sci. 2020, 27, 183–197. [Google Scholar] [CrossRef]
- Sepehri, M.; Apel, D.B.; Adeeb, S.; Leveille, P.; Hall, R.A. Evaluation of mining induced energy and rockburst prediction at a diamond mine in Canada using a full 3D elastoplastic finite element model. Eng. Geol. 2020, 266, 105457. [Google Scholar] [CrossRef]
- Wang, J.; Qiu, P.; Ning, J.; Zhuang, L.; Yang, S. A numerical study of the mining-induced energy redistribution in a coal seam adjacent to an extracted coal panel during longwall face mining: A case study. Energy Sci. Eng. 2020, 8, 817–835. [Google Scholar] [CrossRef]
- Wei, C.; Zhang, C.; Canbulat, I. Numerical analysis of fault-slip behaviour in longwall mining using linear slip weakening law. Tunn. Undergr. Space Technol. 2020, 104, 103541. [Google Scholar] [CrossRef]
- Feng, X.; Zhang, Q.; Ali, M. 3D modelling of the strength effect of backfill-rock on controlling rockburst risk: A case study. Arab. J. Geosci. 2020, 13, 128. [Google Scholar] [CrossRef]
- Zhang, Z.; Deng, M.; Wang, X.; Yu, W.; Zhang, F.; Dao, V.D. Field and numerical investigations on the lower coal seam entry failure analysis under the remnant pillar. Eng. Fail. Anal. 2020, 115, 104638. [Google Scholar] [CrossRef]
- Jendrys, M.; Hadam, A.; Cwiekala, M. Directional Hydraulic Fracturing (DHF) of the roof, as an element of rock burst prevention in the light of underground observations and numerical modelling. Energies 2021, 14, 562. [Google Scholar] [CrossRef]
- Adach-Pawelus, K. Back-calculation method for estimation of geomechanical parameters in numerical modeling based on in-situ measurements and statistical methods. Energies 2022, 15, 4729. [Google Scholar] [CrossRef]
- Wang, J.; Apel, D.B.; Xu, H.; Wei, C. Evaluation of the performance of yielding rockbolts during rockbursts using numerical modeling method. Int. J. Coal Sci. Technol. 2022, 9, 87. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Luo, L.; Wang, C. Research on fault activation and its influencing factors on the barrier effect of rock mass movement induced by mining. Appl. Sci. 2023, 13, 651. [Google Scholar] [CrossRef]
- Jaiswal, A.; Shrivastva, B.K. Numerical simulation of coal pillar strength. Int. J. Rock Mech. Min. Sci. 2009, 46, 779–788. [Google Scholar] [CrossRef]
- Lucas, D.S.; Vakili, A.; Hutchison, B.J. Three-dimensional numerical modelling for successful design of steep slopes at the Kanmantoo copper mine. In Slope Stability 2020: Proceedings of the 2020 International Symposium on Slope Stability in Open Pit Mining and Civil Engineering; Dight, P.M., Ed.; Australian Centre for Geomechanics: Perth, Australia, 2020; pp. 1083–1096. [Google Scholar] [CrossRef]
- Adach-Pawelus, K.; Pawelus, D. Influence of driving direction on the stability of a group of headings located in a field of high horizontal stresses in the Polish underground copper mines. Energies 2021, 14, 5955. [Google Scholar] [CrossRef]
- Batugin, A.; Wang, Z.; Su, Z.; Sidikovna, S.S. Combined support mechanism of rock bolts and anchor cables for adjacent roadways in the external staggered split-level panel layout. Int. J. Coal Sci. Technol. 2021, 8, 659–673. [Google Scholar] [CrossRef]
- Skrzypkowski, K. 3D Numerical modelling of the application of cemented paste backfill on displacements around strip excavations. Energies 2021, 14, 7750. [Google Scholar] [CrossRef]
- Tahmasebinia, F.; Yang, A.; Feghali, P.; Skrzypkowski, K. A numerical investigation to calculate ultimate limit state capacity of cable bolts subjected to impact loading. Appl. Sci. 2023, 13, 15. [Google Scholar] [CrossRef]
- Tahmasebinia, F.; Yang, A.; Feghali, P.; Skrzypkowski, K. Structural evaluation of cable bolts under static loading. Appl. Sci. 2023, 13, 1326. [Google Scholar] [CrossRef]
- Feng, C.; Liu, S.; Jia, H.; Fu, M.; He, D. Strengthening device for improving shear performance of anchor cable in rock support. Materials 2024, 17, 197. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.; Zhang, J. Characteristics of overburden failure and fracture evolution in shallow buried working face with large mining height. Sustainability 2021, 13, 13775. [Google Scholar] [CrossRef]
- Ren, Y.; Yuan, Q.; Chen, J.; Wang, Z.; Zhang, D.; Li, S. Evolution characteristics of mining-induced fractures in overburden strata under close-multi coal seams mining based on optical fiber monitoring. Eng. Geol. 2024, 343, 107802. [Google Scholar] [CrossRef]
- Li, X.; Ren, Z.; Cao, Z.; Hao, R. Study on coal drawing parameters of deeply buried hard coal seams based on PFC. Sci. Rep. 2025, 15, 21934. [Google Scholar] [CrossRef]
- Sun, C.; Shi, C.; Zhu, Z.; Lin, H.; Li, Z.; Du, F.; Cao, Z.; Lu, P.; Liu, L. Overburden failure characteristics and fracture evolution rule under repeated mining with multiple key strata control. Sci. Rep. 2025, 15, 28029. [Google Scholar] [CrossRef]
- Zhi, B.; Guo, R.; Guo, G.; Zhang, S.; Yuan, J.; Lei, C.; Xu, Z. Study on fracture development and failure characteristics of repeated mining overlying strata in multi-coal seams with faults. Sci. Rep. 2025, 15, 32215. [Google Scholar] [CrossRef]
- Wang, X.; Liu, F. Characteristics of overburden failure and evolution of fractures in fully mechanized top coal mining face. Sci. Rep. 2025, 15, 37431. [Google Scholar] [CrossRef]
- Song, S.; Liu, X.; Tan, Y.; Li, X.; Yang, S.; Zhang, Y. Failure characteristics and evolution law of overburden structure under repeated mining of close-distance coal seam group in Ningdong Mining Area. Energy Sci. Eng. 2025, 13, 5627–5644. [Google Scholar] [CrossRef]
- Pawelus, D.; Butra, J. Numerical methods as an aid in the selection of roof bolting systems for access excavations located at different depths in the LGCB mines. Appl. Sci. 2024, 14, 7052. [Google Scholar] [CrossRef]
- Saati, V.; Mortazavi, A. Numerical modelling of in situ stress calculation using borehole slotter test. Tunnell. Undergr. Space Technol. 2011, 26, 172–178. [Google Scholar] [CrossRef]
- Hijazo, T.; González de Vallejo, L.I. In-situ stress amplification due to geological factors in tunnels: The case of Pajares tunnels, Spain. Eng. Geol. 2012, 137–138, 13–20. [Google Scholar] [CrossRef]
- Li, H.; Lin, B.; Hong, Y.; Gao, Y.; Yang, W.; Liu, T.; Wang, R.; Huang, Z. Effects of in-situ stress on the stability of a roadway excavated through a coal seam. Int. J. Min. Sci. Technol. 2017, 27, 917–927. [Google Scholar] [CrossRef]
- Kleczek, Z. Mining Geomechanics; Silesian Technical Publishing House: Katowice, Poland, 1994. (In Polish) [Google Scholar]
- Goszcz, A. Elements of Rock Mechanics and Rock Bursts in Polish Coal and Copper Mines; Mineral and Energy Economy Research Institute of the Polish Academy of Sciences: Krakow, Poland, 1999. (In Polish) [Google Scholar]
- Polish Standard PN-G-05016:1997; Mining Shafts, Casing, Loads. Polish Committee for Standardization (PKN): Warsaw, Poland, 1997. (In Polish)
- Gergowicz, Z. Mining Geotechnics; Wroclaw University of Science and Technology Publishing House: Wroclaw, Poland, 1974. (In Polish) [Google Scholar]
- Kidybinski, A. Basics of Mining Geotechnics; Silesia Publishing House: Katowice, Poland, 1982. (In Polish) [Google Scholar]
- Amadei, B.; Stephansson, O. Rock Stress and Its Measurement; Chapman & Hall: London, UK, 2009. [Google Scholar]
- Hoek, E.; Brown, E.T. Trends in relationships between measured in-situ stresses and depth. Int. J. Rock Mech. Min. Sci. 1978, 15, 211–215. [Google Scholar]
- Fabich, S.; Lis, J.; Pytel, W.; Szadkowski, T.; Szlązak, M. Determination of Stresses in the Rock Mass in Various Geological and Mining Conditions Based on In-Situ Tests, Stage 1; KGHM Cuprum Research & Development Centre: Wroclaw, Poland, 2003. (In Polish) [Google Scholar]
- Nemcik, J.; Gale, W.J.; Fabjanczyk, M. Methods of interpreting ground stress based on underground stress measurements and numerical modelling. In Proceedings of the Coal Operators Conference, Wollongong, Australia, 6–7 July 2006. [Google Scholar]
- Hoek, E. Practical Rock Engineering; Evert Hoek Consulting Engineer, Inc.: North Vancouver, BC, Canada, 2007. [Google Scholar]
- Han, J.; Zhang, P.T. The in-situ stress state of Kailuan mining area. In Proceedings of the 5th Intrernational Symposium ISRM “In-Situ Rock Stress”, Beijing, China, 25–27 August 2010. [Google Scholar]
- Butra, J.; Pawelus, D.; Madziarz, M.; Debkowski, R.; Fabich, S.; Hanzel, S.; Nitek, D.; Sadecki, Z.; Szpak, M.; Struzik, H. Magnitude and Directions of In-Situ Stress in the Deep Part of a Copper Ore Deposit with an Appendix “Determination of the Impact of the Primary Stress Directions and Magnitudes on the Optimal Geometry of Mining Fields”; KGHM Cuprum Research & Development Centre: Wroclaw, Poland, 2012. (In Polish) [Google Scholar]
- Hoek, E. Strength of rock and rock masses. ISRM News J. 1994, 2, 4–16. [Google Scholar]
- Hoek, E.; Brown, E.T. Practical estimates of rock mass strength. Int. J. Rock Mech. Min. Sci. 1997, 34, 1165–1186. [Google Scholar] [CrossRef]
- Hoek, E.; Marinos, P. GSI: A geologically friendly tool for rock mass strength estimation. In Proceedings of the ISRM International Symposium, Melbourne, Australia, 19–24 November 2000. [Google Scholar]
- Hoek, E.; Carranza-Torres, C.T.; Corkum, B. Hoek-Brown failure criterion—2002 edition. In Proceedings of the North American Rock Mechanics Society Meeting, Toronto, ON, Canada, 7–10 July 2002. [Google Scholar]
- Pawelus, D. Influence of Horizontal Stress on the Stability of Underground Excavations in Copper Mines. Ph.D Thesis, Wroclaw University of Science and Technology, Wroclaw, Poland, 2010. (In Polish). [Google Scholar]
- Butra, J.; Madziarz, M.; Pawelus, D.; Bodlak, M.; Dziurla, J.; Madziarz, A.; Olchawa, M.; Spiewak, A.; Brych-Butra, K.; Jaskiewicz, K. Geomechanical Analysis of the Stability of Excavations Related to the Main Dewatering System in the Area of Shaft SW-4; KGHM Cuprum Research & Development Centre: Wroclaw, Poland, 2023. (In Polish) [Google Scholar]
- Butra, J.; Madziarz, M.; Pawelus, D.; Mlynarczyk, J.; Dziurla, J.; Lipniarski, M.; Spiewak, A.; Sobolewski, W.; Madziarz, A.; Kulik, W.; et al. Design of Support for Excavations Stability for to the Main Dewatering System in the Area of Shaft SW-4; KGHM KGHM Cuprum Research & Development Centre: Wroclaw, Poland, 2024. (In Polish) [Google Scholar]
- Minova. Available online: https://www.minovaglobal.com/emea-cis/products/steel-gfrp/rock-bolts/resin-bolts-type-rm-18/ (accessed on 15 April 2025).
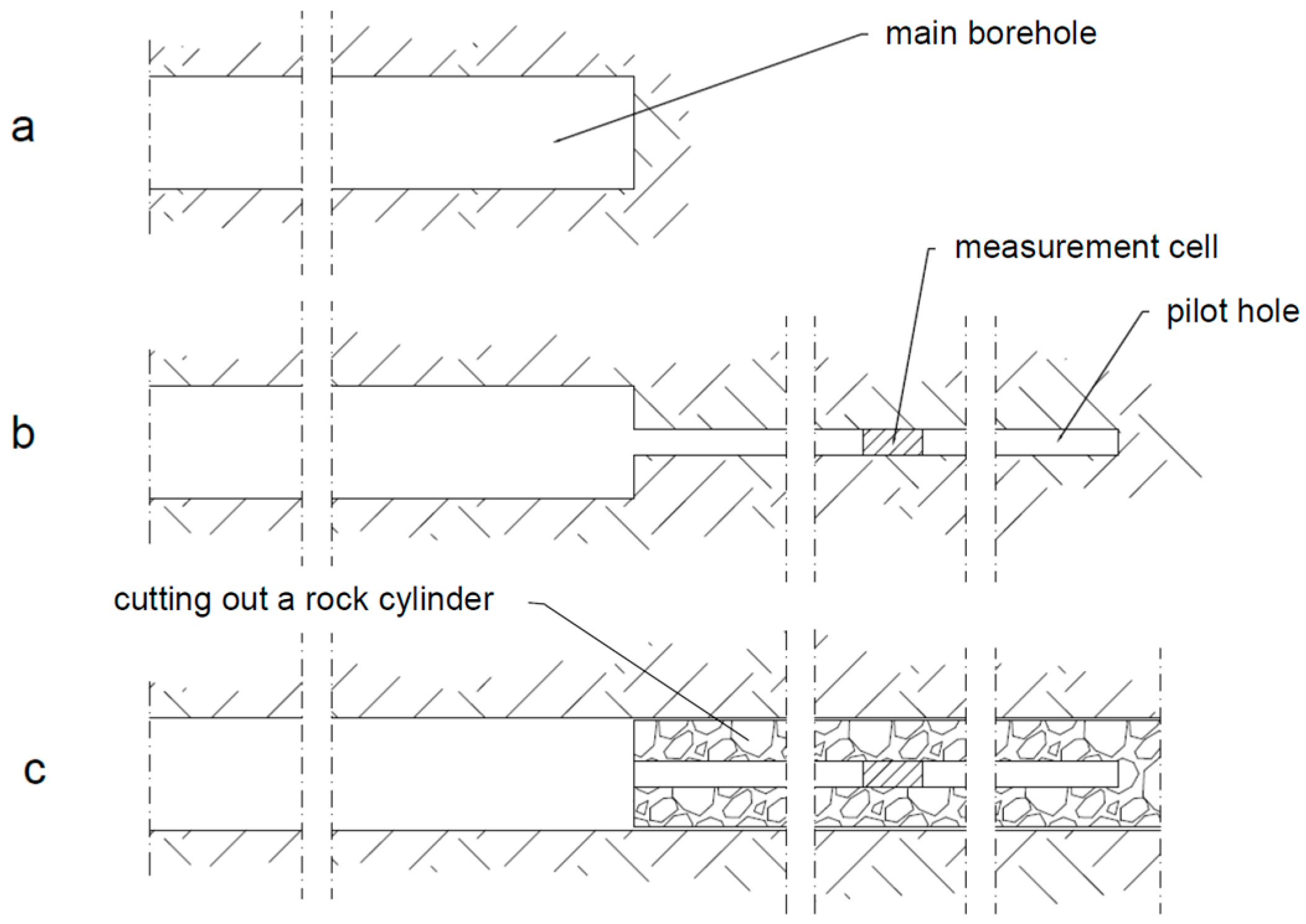
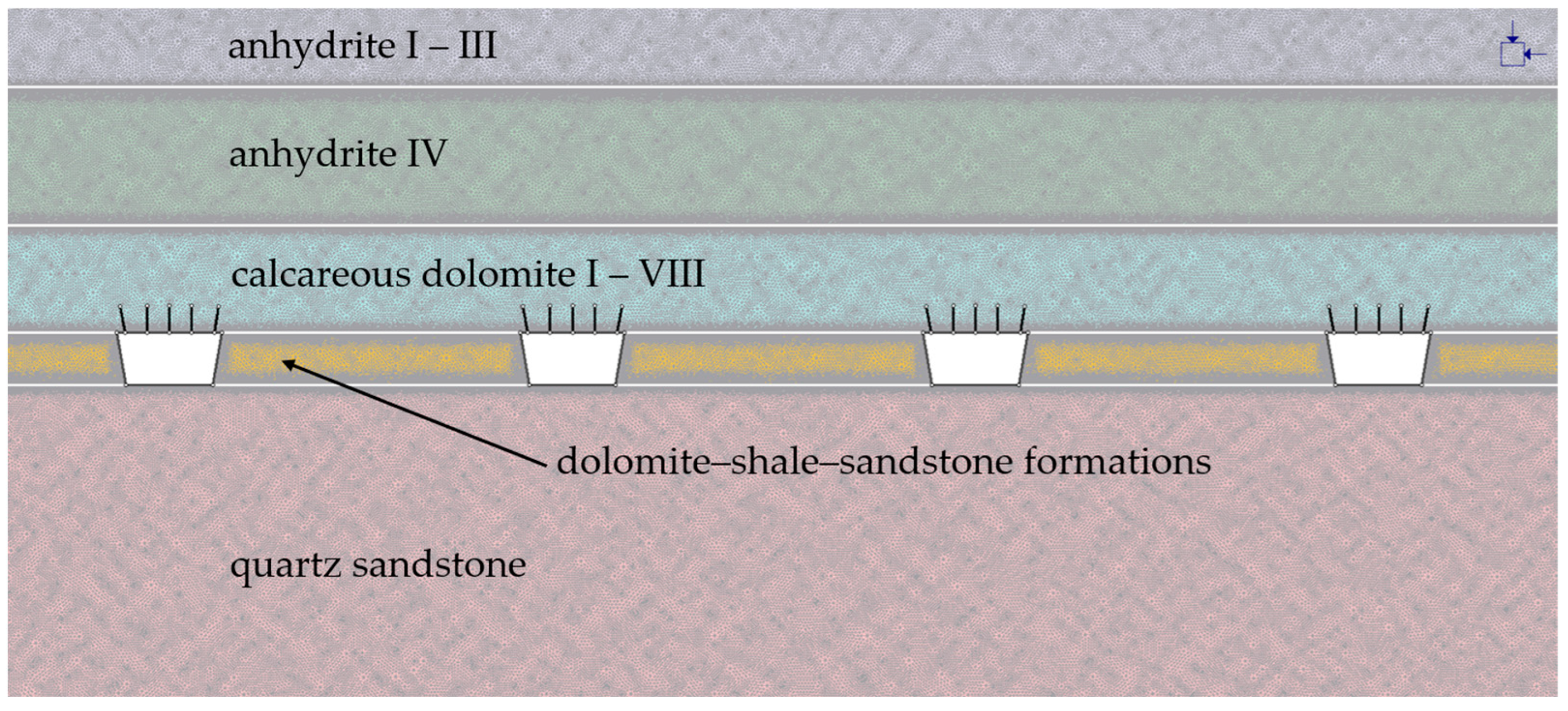
| Parameter | Measurement Station (S) and Measurement Point (P) | ||||||
|---|---|---|---|---|---|---|---|
| S1P2 | S1P3 | S2P2 | S2P4 | S3P2 | S4P3 | S4P4 | |
| σH [MPa] | 24.7 | 30.8 | 22.2 | 11.4 | 16.8 | 33.6 | 26.4 |
| αH [°] | 110.0 | 118.0 | 55.0 | 42.0 | 158.0 | 124.0 | 131.0 |
| σh [MPa] | 18.0 | 25.3 | 19.0 | 7.3 | 11.8 | 26.8 | 19.6 |
| αh [°] | 20.0 | 28.0 | 145.0 | 132.0 | 68.0 | 34.0 | 41.0 |
| σv [MPa] | 22.1 | 27.8 | 18.6 | 9.4 | 20.0 | 22.1 | 23.9 |
| Location | Rock Type | h [m] | ρ [kg/dm3] | Rc [MPa] | Rr [MPa] | Ei [GPa] | v [-] |
|---|---|---|---|---|---|---|---|
| Roof | Anhydrite I–III | 5.50 | 2.94 | 108.74 | 5.58 | 40.06 | 0.24 |
| Anhydrite IV | 9.30 | 2.94 | 86.93 | 5.94 | 38.30 | 0.24 | |
| Calcareous dolomite I–VIII | 7.20 | 2.74 | 163.13 | 7.81 | 60.18 | 0.25 | |
| Sidewall | Calcareous dolomite IX | 1.60 | 2.71 | 95.00 | 10.16 | 27.17 | 0.22 |
| Dolomitic shale | 0.60 | 2.69 | 111.49 | 9.06 | 28.89 | 0.23 | |
| Quartz sandstone I | 1.20 | 2.40 | 47.85 | 2.93 | 16.94 | 0.17 | |
| Floor | Quartz sandstone II | 9.50 | 2.33 | 36.19 | 2.78 | 13.60 | 0.14 |
| Location | Rock Type | c [MPa] | φ [°] | σt [MPa] | Erm [MPa] |
|---|---|---|---|---|---|
| Roof | Anhydrite I–III | 8.137 | 38.66 | 0.871 | 29,356.00 |
| Anhydrite IV | 6.505 | 38.66 | 0.696 | 28,066.78 | |
| Calcareous dolomite I–VIII | 14.879 | 39.00 | 3.611 | 52,975.30 | |
| Sidewall | Calcareous dolomite IX | 7.579 | 37.69 | 1.442 | 22,180.23 |
| Dolomitic shale | 6.447 | 30.41 | 1.327 | 18,250.37 | |
| Quartz sandstone I | 3.589 | 40.54 | 0.180 | 10,701.33 | |
| Floor | Quartz sandstone II | 2.520 | 39.06 | 0.093 | 7072.00 |
| Location | Rock Type | h [m] | Es [MPa] | ν [-] | σt [MPa] | φ [°] | c [MPa] | δ [°] | φres [°] | cres [MPa] |
|---|---|---|---|---|---|---|---|---|---|---|
| Roof | Anhydrite I–III | 5.50 | 29,356.00 | 0.24 | 0.871 | 38.66 | 8.137 | 2.00 | 36.73 | 1.627 |
| Anhydrite IV | 9.30 | 28,066.78 | 0.24 | 0.696 | 38.66 | 6.505 | 2.00 | 36.73 | 1.301 | |
| Calcareous dolomite I–VIII | 7.20 | 52,975.30 | 0.25 | 3.611 | 39.00 | 14.879 | 2.00 | 37.05 | 2.976 | |
| Sidewall | Dolomite-shale-sandstone formations | 3.50 | 17,435.35 | 0.20 | 0.976 | 37.41 | 5.971 | 2.00 | 35.54 | 1.194 |
| Floor | Quartz sandstone | 9.50 | 7072.00 | 0.14 | 0.093 | 39.06 | 2.520 | 2.00 | 39.06 | 2.520 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pawelus, D.; Adach-Pawelus, K.; Butra, J. Issue of Selecting Stress Field Parameters for the Analysis of Mining Excavation Stability Using Numerical Methods in the Conditions of the LGCB Mines. Appl. Sci. 2025, 15, 12365. https://doi.org/10.3390/app152312365
Pawelus D, Adach-Pawelus K, Butra J. Issue of Selecting Stress Field Parameters for the Analysis of Mining Excavation Stability Using Numerical Methods in the Conditions of the LGCB Mines. Applied Sciences. 2025; 15(23):12365. https://doi.org/10.3390/app152312365
Chicago/Turabian StylePawelus, Daniel, Karolina Adach-Pawelus, and Jan Butra. 2025. "Issue of Selecting Stress Field Parameters for the Analysis of Mining Excavation Stability Using Numerical Methods in the Conditions of the LGCB Mines" Applied Sciences 15, no. 23: 12365. https://doi.org/10.3390/app152312365
APA StylePawelus, D., Adach-Pawelus, K., & Butra, J. (2025). Issue of Selecting Stress Field Parameters for the Analysis of Mining Excavation Stability Using Numerical Methods in the Conditions of the LGCB Mines. Applied Sciences, 15(23), 12365. https://doi.org/10.3390/app152312365





