Research on Ultrasonic Guided Wave Damage Detection in Internally Corroded Pipes with Curved Random Surfaces
Abstract
1. Introduction
2. Modeling Method for Random Surfaces with Curvature
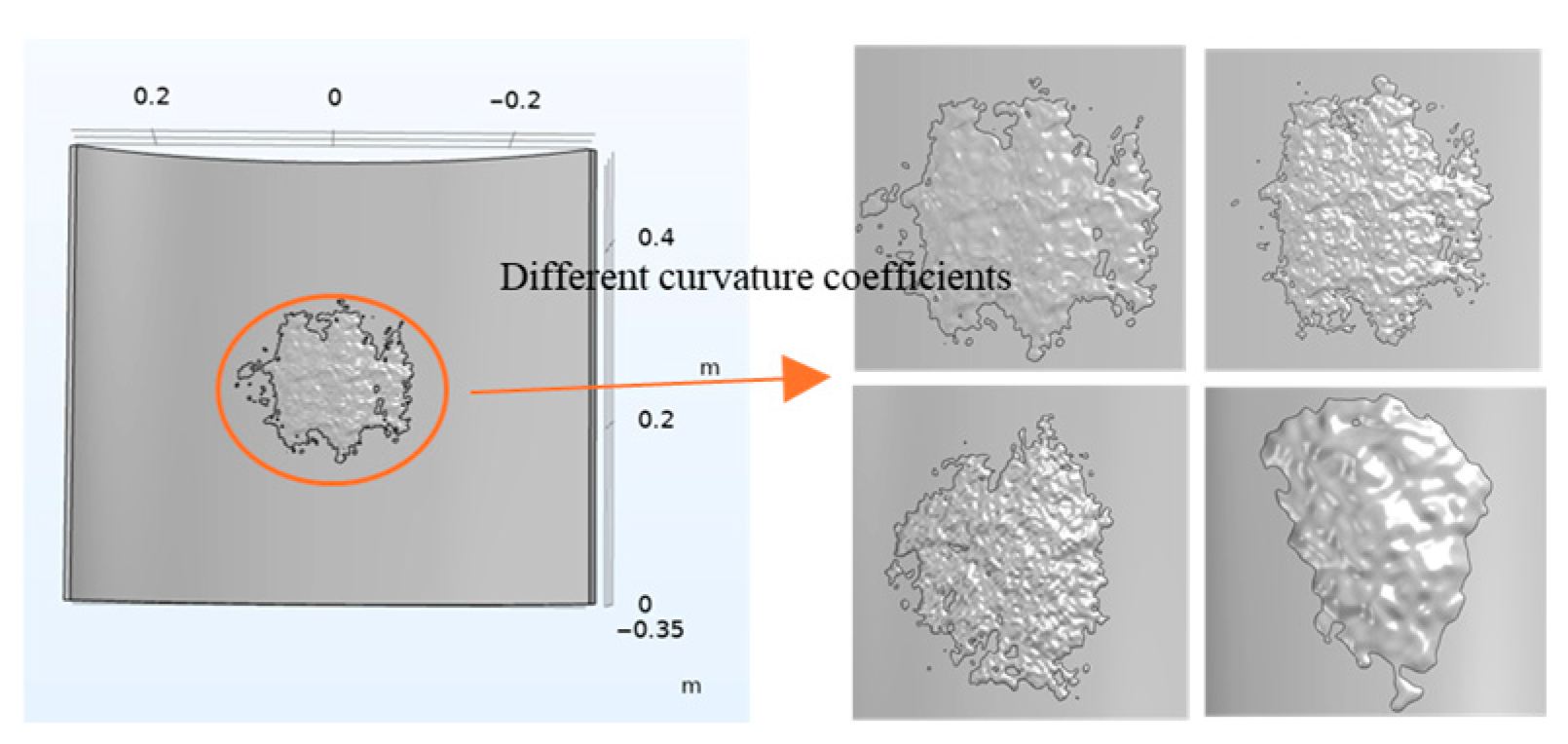
2.1. Surface Height Function
2.2. Root Mean Square Roughness, Sq
3. Finite Element Model of Layered Pipelines with Internal Corrosion
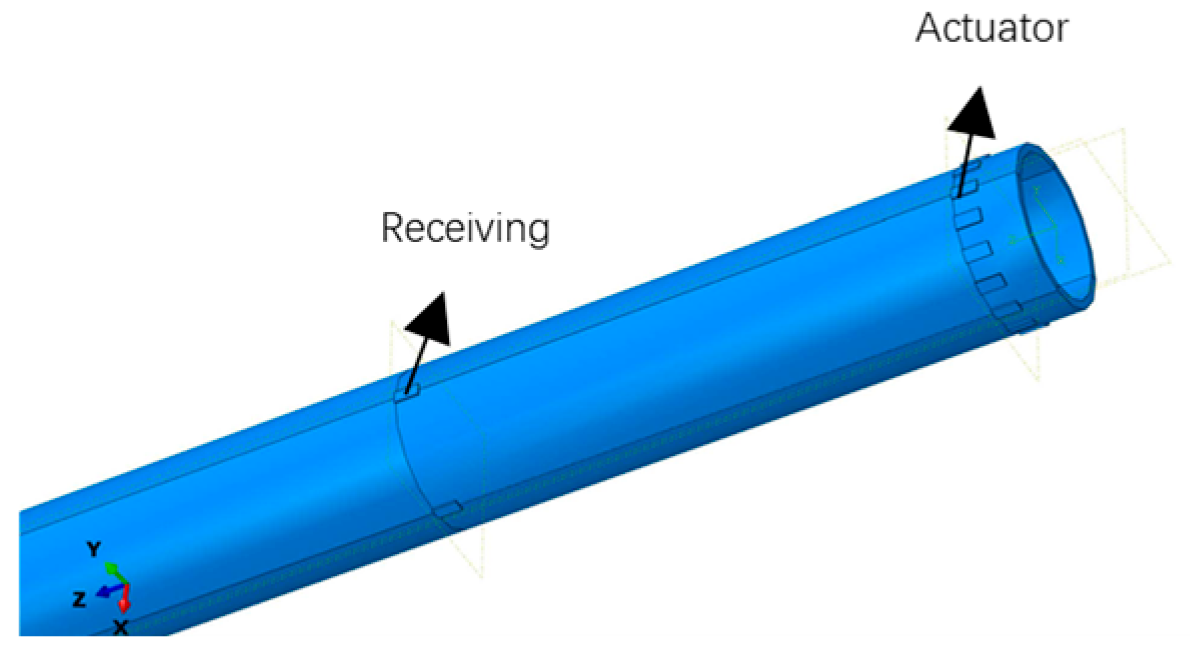
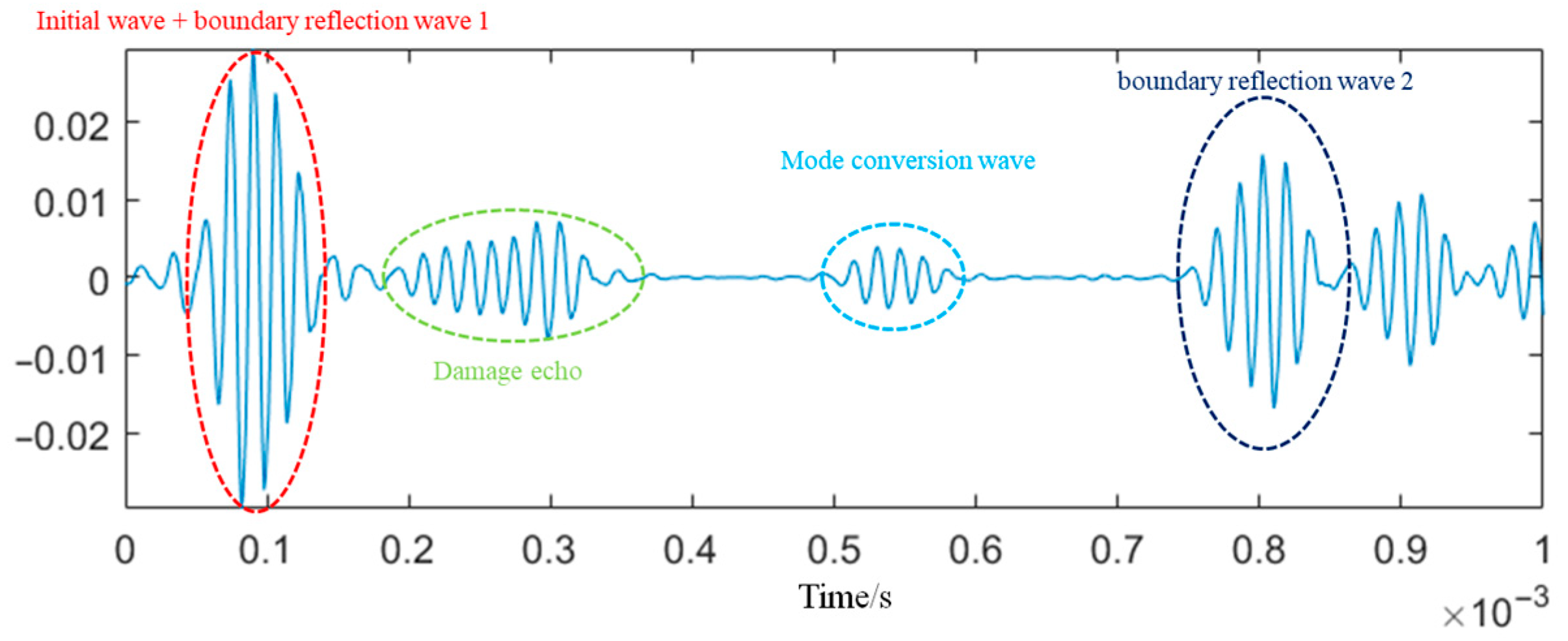
3.1. Detection Method Based on Ultrasonic Guided Waves
3.2. Characteristics of Corrosion Morphology Inside Pipelines
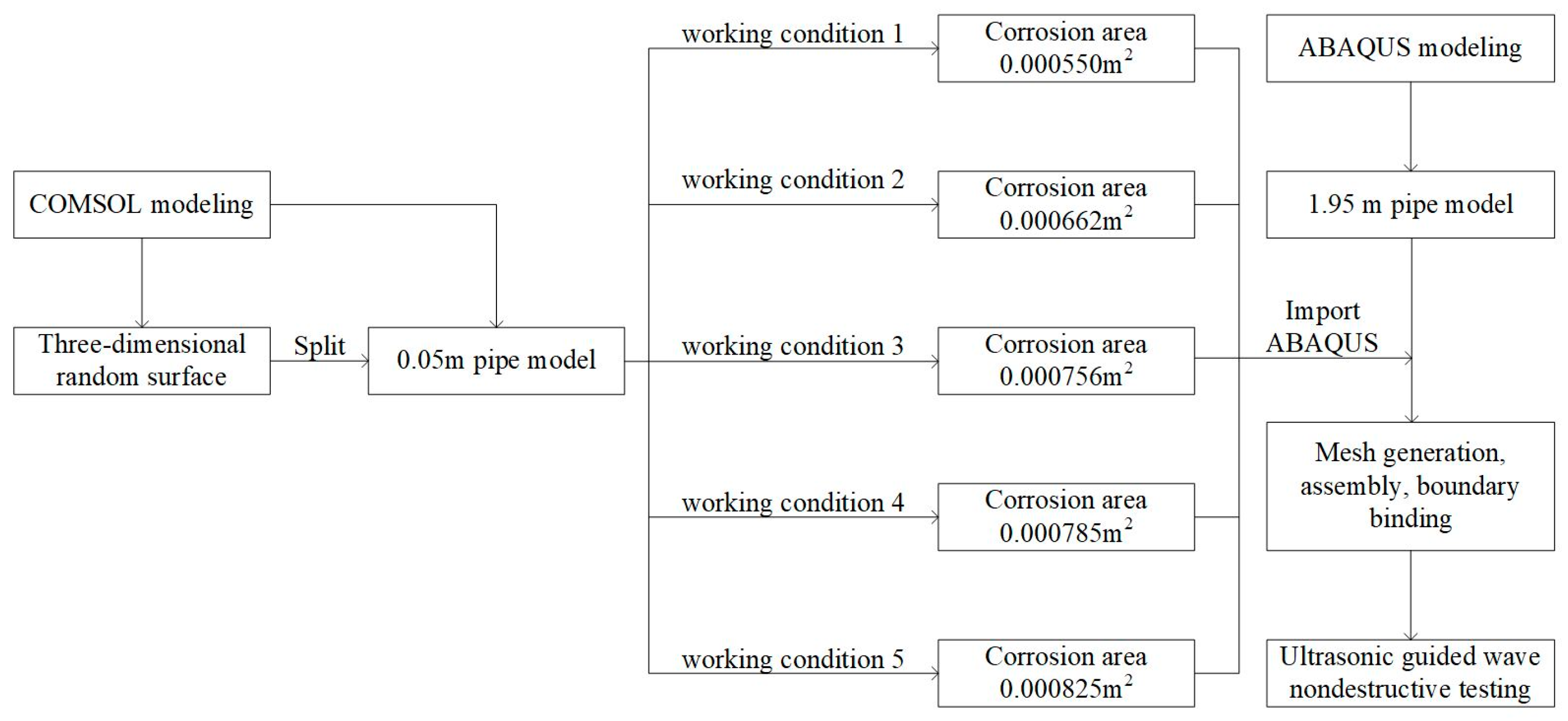
3.3. Application of the Combined Modeling Method of COMSOL and ABAQUS
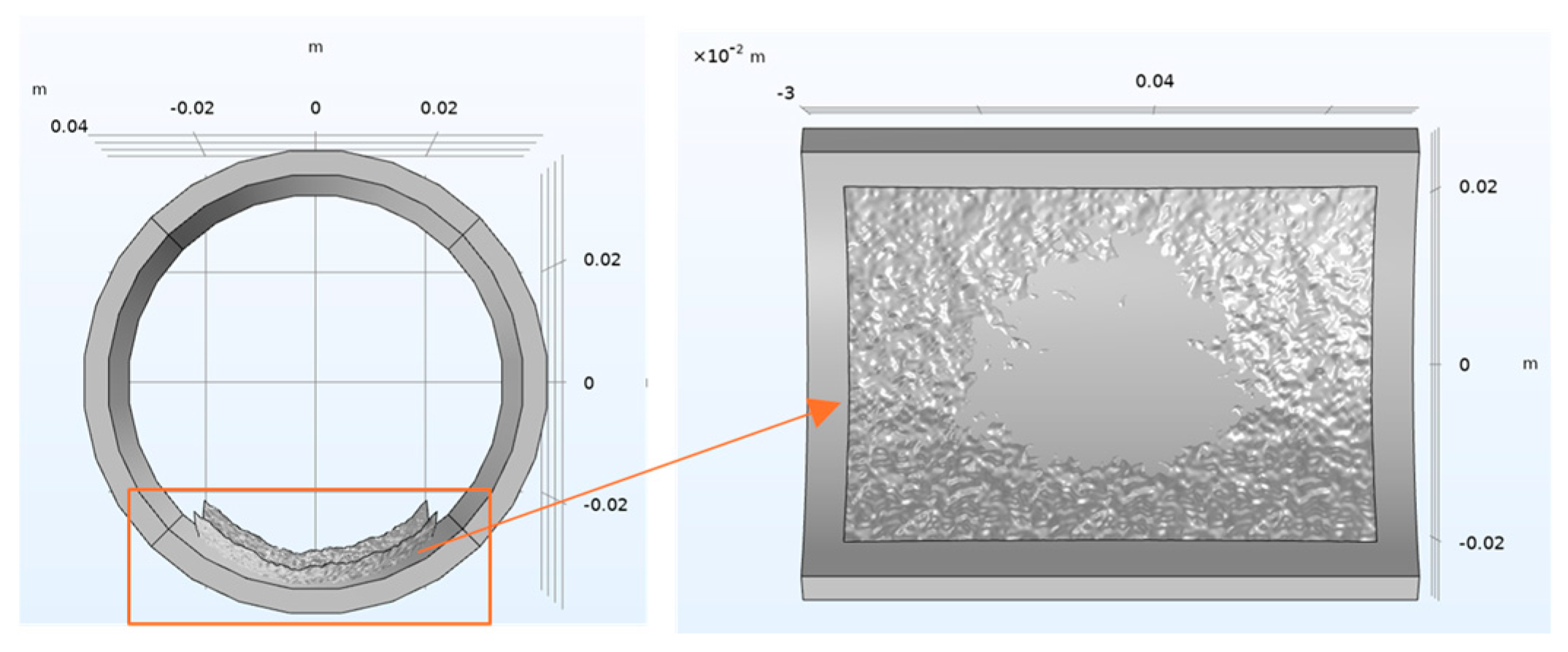
3.3.1. Establish a Finite Element Model for Internal Corrosion of Random Surfaces with Curvature
3.3.2. Establish a Finite Element Model of Layered Pipelines and Piezoelectric Elements
4. Research on Damage Detection of Layered Pipelines with Internal Corrosion
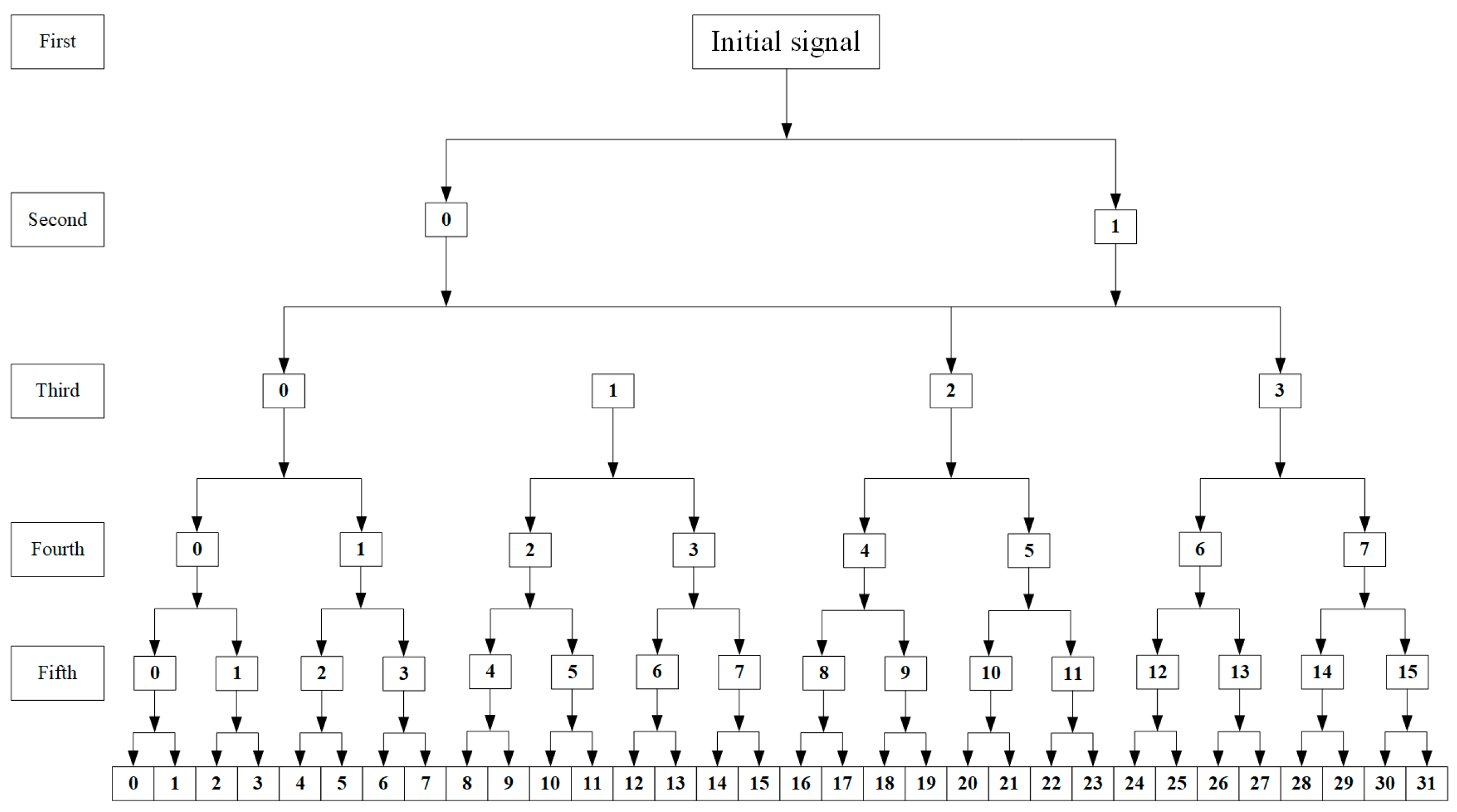
4.1. Wavelet Packet Decomposition Method
4.2. Damage Index Matrix
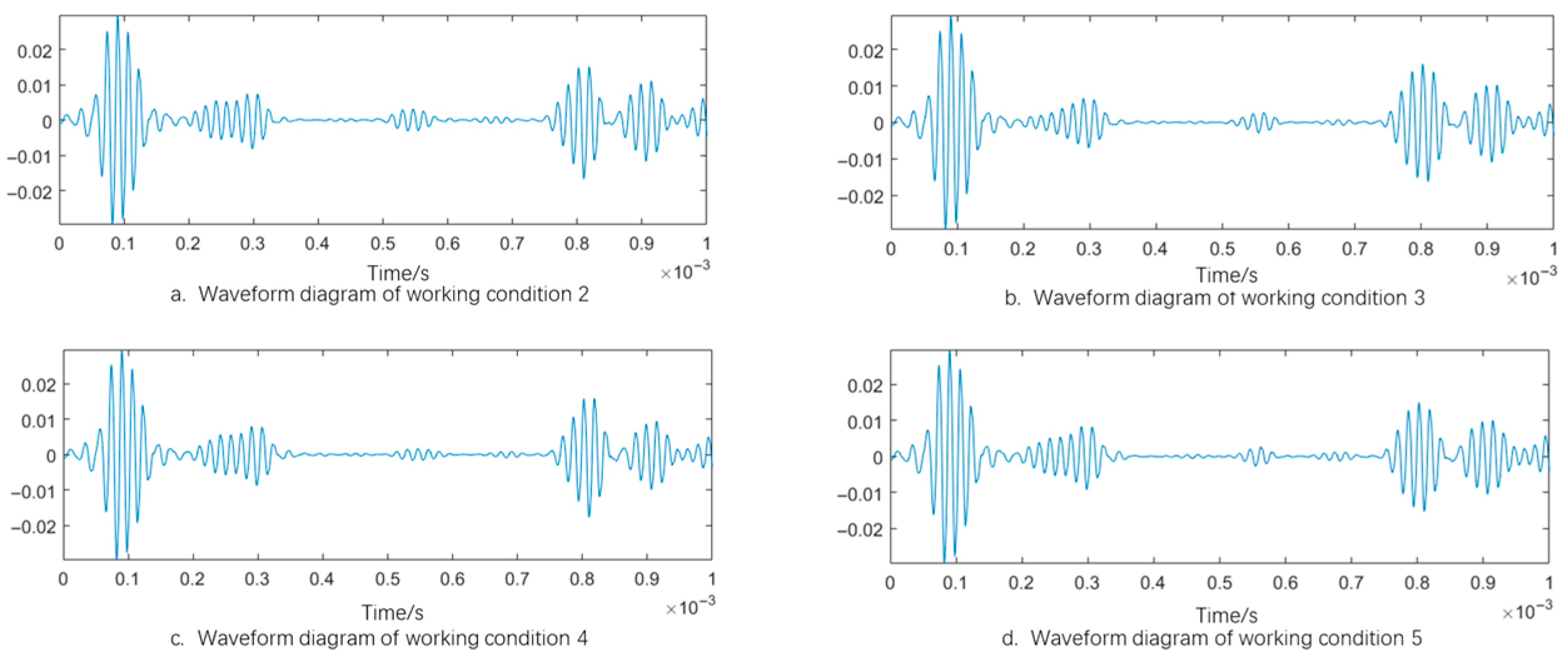
4.3. Research on Damage Detection of Different Corrosion Areas
5. Analysis and Discussion
5.1. Effectiveness Analysis of Curved Random Surface Simulation for Internal Corrosion
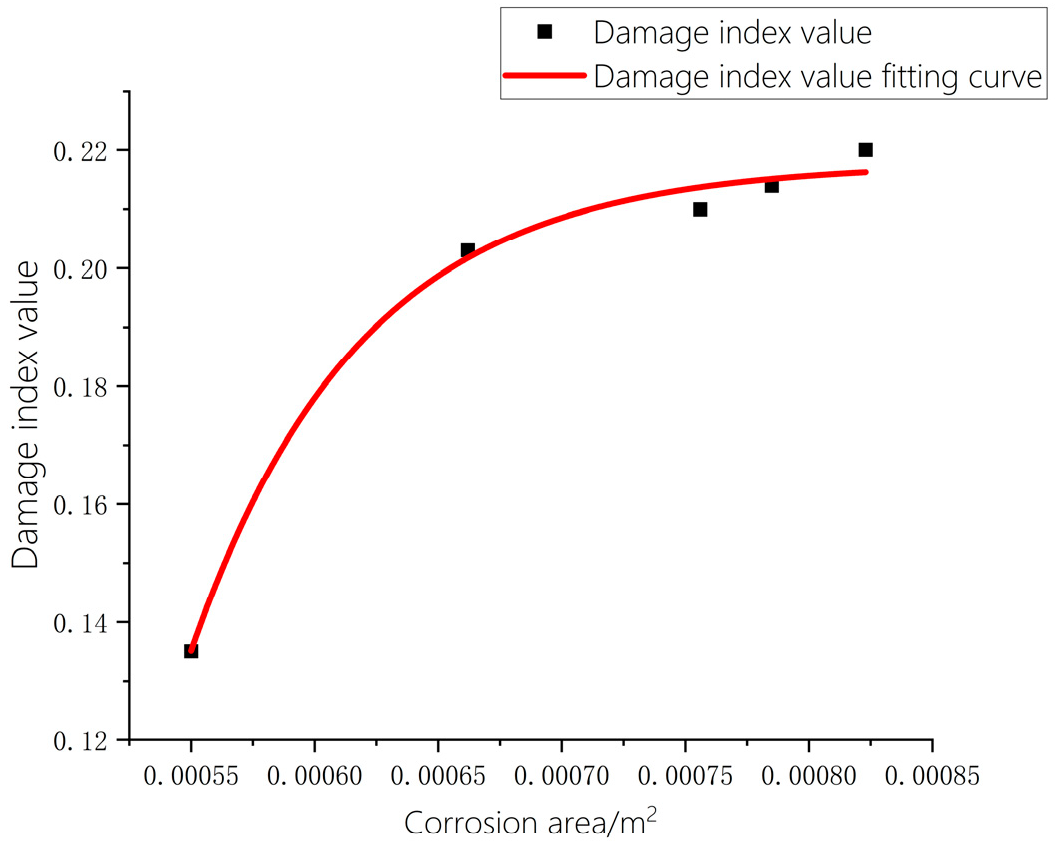
5.2. Results and Analysis of Internal Corrosion Damage Detection in Pipelines
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ID | Inner diameter |
| OD | Outer diameter |
| WT | Wall thickness |
| ρ | Density |
| E | Elastic modulus |
| ν | Poisson’s ratio |
| L | Pipe length |
References
- Meng, F. The Pipeline Industry is Accelerating the Transition from a Single Means of Transport to a Multi Type Energy Hub. 2025. Available online: https://www.cinn.cn/yw/2025/04-09/qkNaWbvD.html (accessed on 29 June 2025).
- Valor, A.; Caleyo, F.; Alfonso, L.; Rivas, D.; Hallen, J.M. Stochastic modeling of pitting corrosion: A new model for initiation and growth of multiple corrosion pits. Corros. Sci. 2007, 49, 559–579. [Google Scholar] [CrossRef]
- Caleyo, F.; Velázquez, J.C.; Valor, A.; Hallen, J.M. Markov chain modelling of pitting corrosion in underground pipelines. Corros. Sci. 2009, 51, 2197–2207. [Google Scholar] [CrossRef]
- Valor, A.; Caleyo, F.; Rivas, D.; Hallen, J.M. Stochastic approach to pitting-corrosion-extreme modelling in low-carbon steel. Corros. Sci. 2010, 52, 910–915. [Google Scholar] [CrossRef]
- Beben, D. Backfill Corrosivity around Corrugated Steel Plate Culverts. J. Perform. Constr. Facil. 2015, 29, 04014159. [Google Scholar] [CrossRef]
- Sun, Z.; Du, H. Estimation of the dispersion curves of pipe guided waves by field measurement. Mech. Syst. Signal Process. 2020, 140, 106693. [Google Scholar] [CrossRef]
- Pang, G.; Wang, N.; Fang, H.; Liu, H.; Huang, F. Study of Damage Quantification of Concrete Drainage Pipes Based on Point Cloud Segmentation and Reconstruction. Buildings 2022, 12, 213. [Google Scholar] [CrossRef]
- Demma, A.; Cawey, P.; Lowe, M.; Roosenbrand, A.; Pavlakovic, B. The reflection of guided waves from notches in pipes: A guide for interpreting corrosion measurements. NDT E Int. 2004, 37, 167–180. [Google Scholar] [CrossRef]
- Li, D.; Zhang, S.; Yang, W.; Zhang, W. Corrosion Monitoring and Evaluation of Reinforced Concrete Structures Utilizing the Ultrasonic Guided Wave Technique. Int. J. Distrib. Sens. Netw. 2014, 10, 827130. [Google Scholar] [CrossRef]
- Rao, J.; Ratassepp, M.; Lisevych, D.; Hamzah Caffoor, M.; Fan, Z. On-Line Corrosion Monitoring of Plate Structures Based on Guided Wave Tomography Using Piezoelectric Sensors. Sensors 2017, 17, 2882. [Google Scholar] [CrossRef]
- Wang, N.; Qiao, L.; Fang, H.; Pang, G.; Du, X.; Zhai, K.; Di, D.; Duan, Y. Corrosion segmentation method of concrete drainage pipes based on point transformer. Measurement 2024, 234, 114893. [Google Scholar] [CrossRef]
- Wang, X.; Yang, F.; Wang, C.; Zhao, K.; Zheng, Y. Pipeline corrosion modeling and simulation for guided-waves-based inspection. Chin. J. Sci. Instrum. 2023, 44, 71–80. [Google Scholar] [CrossRef]
- Mu, X.; Sun, Q.; Xu, J.; Chai, Z.; Sun, W.; Zhao, B. Feasibility Analysis of the Replacement of the Actual Machining Surface by a 3D Numerical Simulation Rough Surface. Int. J. Mech. Sci. 2018, 150, 135–144. [Google Scholar] [CrossRef]
- Li, X.; Lan, X.; Li, Z.; Guo, L. Discussion on the Present Situation and Development of Corrosion Detection Technology in Oil and Gas Pipelines. Constr. Des. Proj. 2019, 8, 183–184. [Google Scholar] [CrossRef]
- Xiao, R.; Hu, Q.; Li, J. Leak detection of gas pipelines using acoustic signals based on wavelet transform and Support Vector Machine. Measurement 2019, 146, 479–489. [Google Scholar] [CrossRef]
- GB/T 6461-2002; Metallic and Other Inorganic Coatings—Rating of Test Specimens and Manufactured Articles Subjected to Corrosion Tests. Standards Press of China: Beijing, China, 2002.
- ISO 10289:1999; Methods for Corrosion Testing of Metallic and Other Inorganic Coatings on Metallic Substrates—Rating of Test Specimens and Manufactured Articles Subjected to Corrosion Tests. ISO Copyright Office: Geneva, Switzerland, 1999.
- ASME B31.8S-2022; Managing System Integrity of Gas Pipelines. ASME: New York, NY, USA, 2022.
- Chen, G.; Yang, D.; Wang, Y.; Wang, T. Pipeline Corrosion Monitoring Method Based on Frequency Tracking Method. Chin. J. Sens. Actuators 2023, 36, 1148–1152. [Google Scholar] [CrossRef]
- Maleska, T.; Beben, D. Behaviour of Soil–Steel Composite Bridges under Strong Seismic Excitation with Various Boundary Conditions. Materials 2023, 16, 650. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.; Zhang, B.; Song, G.; Lin, J. PZT-Based Ultrasonic Guided Wave Frequency Dispersion Characteristics of Tubular Structures for Different Interfacial Boundaries. Sensors 2018, 18, 4111. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, K.; Zheng, Y. Characteristics of symmetric mode conversion of longitudinal guided—Wave modes in pipeline. Chin. J. Sci. Instrum. 2020, 41, 151–160. [Google Scholar] [CrossRef]
- Wasim, M.; Djukic, M. External corrosion of oil and gas pipelines: A review of failure mechanisms and predictive preventions. J. Nat. Gas Sci. Eng. 2022, 100, 104467. [Google Scholar] [CrossRef]
- Popov, B.N. Chapter 1—Evaluation of Corrosion. In Corrosion Engineering, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2025; pp. 1–29. ISBN 9780443220111. [Google Scholar] [CrossRef]
- Javaherdashti, R. Microbiologically Influenced Corrosion—An Engineering Insight. Br. Corros. J. 2008, 29, 181–182. [Google Scholar] [CrossRef]
- Revie, R.W.; Uhlig, H.H. Corrosion and Corrosion Control: An Introduction to Corrosion Science and Engineering, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Zajam, S.; Joshi, T.; Bhattacharya, B. Application of wavelet analysis and machine learning on vibration data from gas pipelines for structural health monitoring. Procedia Struct. Integr. 2019, 14, 712–719. [Google Scholar] [CrossRef]
- Shaik, N.B.; Pedapati, S.R.; Taqvi, S.A.A.; Othman, A.R.; Dzubir, F.A.A. A Feed-Forward Back Propagation Neural Network Approach to Predict the Life Condition of Crude Oil Pipeline. Processes 2020, 8, 661. [Google Scholar] [CrossRef]
- Li, S.; Wen, Y.; Li, P.; Yang, J.; Dong, X.; Mu, Y. Leak location in gas pipelines using cross-time–frequency spectrum of leakage-induced acoustic vibrations. J. Sound Vib. 2014, 333, 3889–3903. [Google Scholar] [CrossRef]
- Wang, X.; Qu, L.; Li, Y. Finite element simulation for damage identification of layered pipe structures based on damage index matrix. Earthq. Eng. Eng. Dyn. 2023, 43, 189–197. [Google Scholar] [CrossRef]
- Mallat, S. Chapter 7—Wavelet Bases. In A Wavelet Tour of Signal Processing; Academic Press: Cambridge, MA, USA, 2009; pp. 263–376. [Google Scholar]
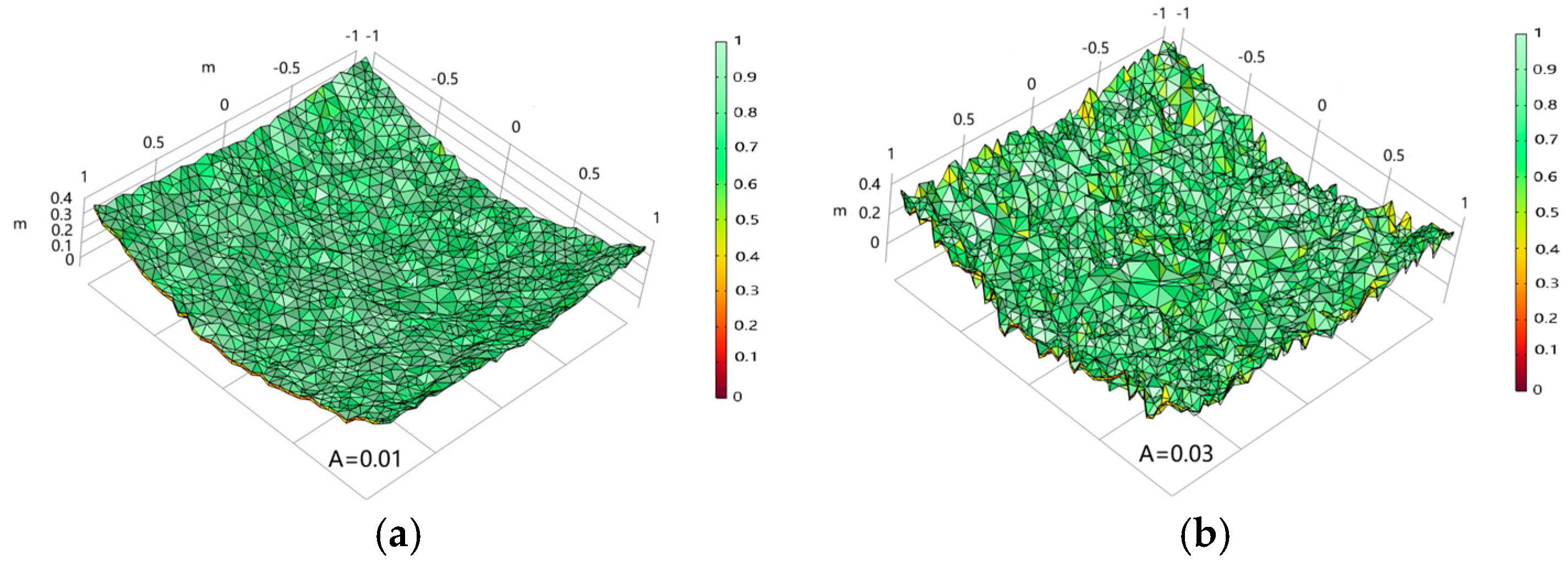
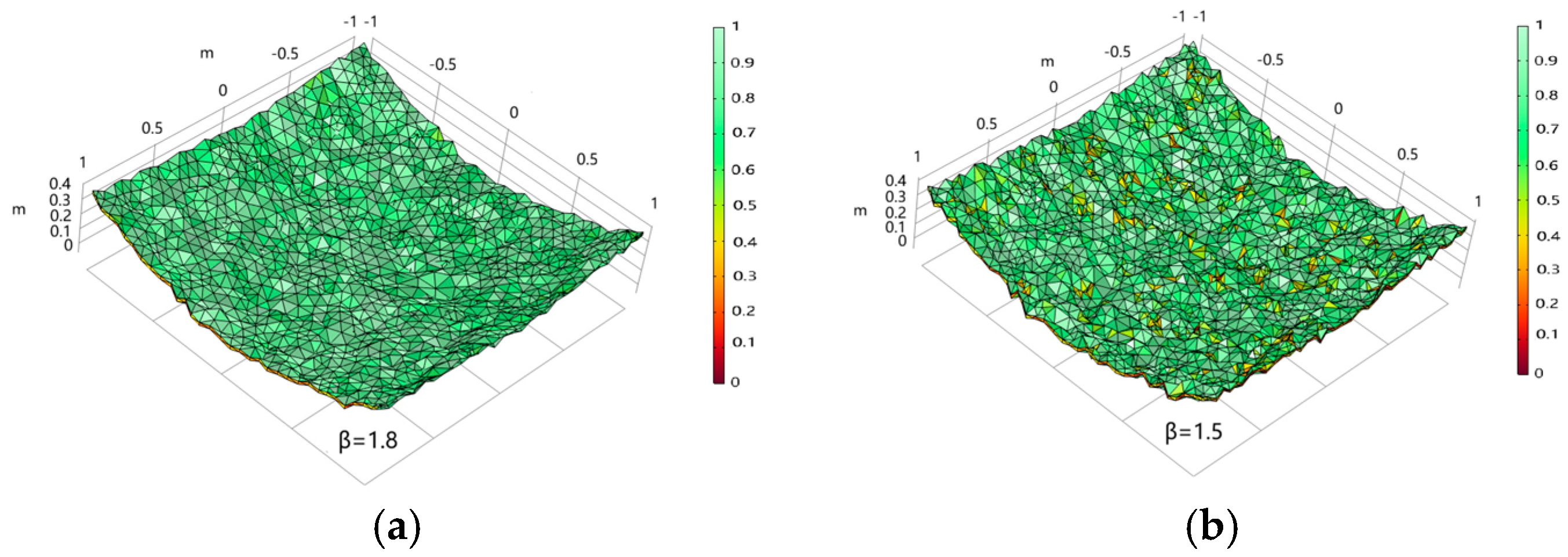
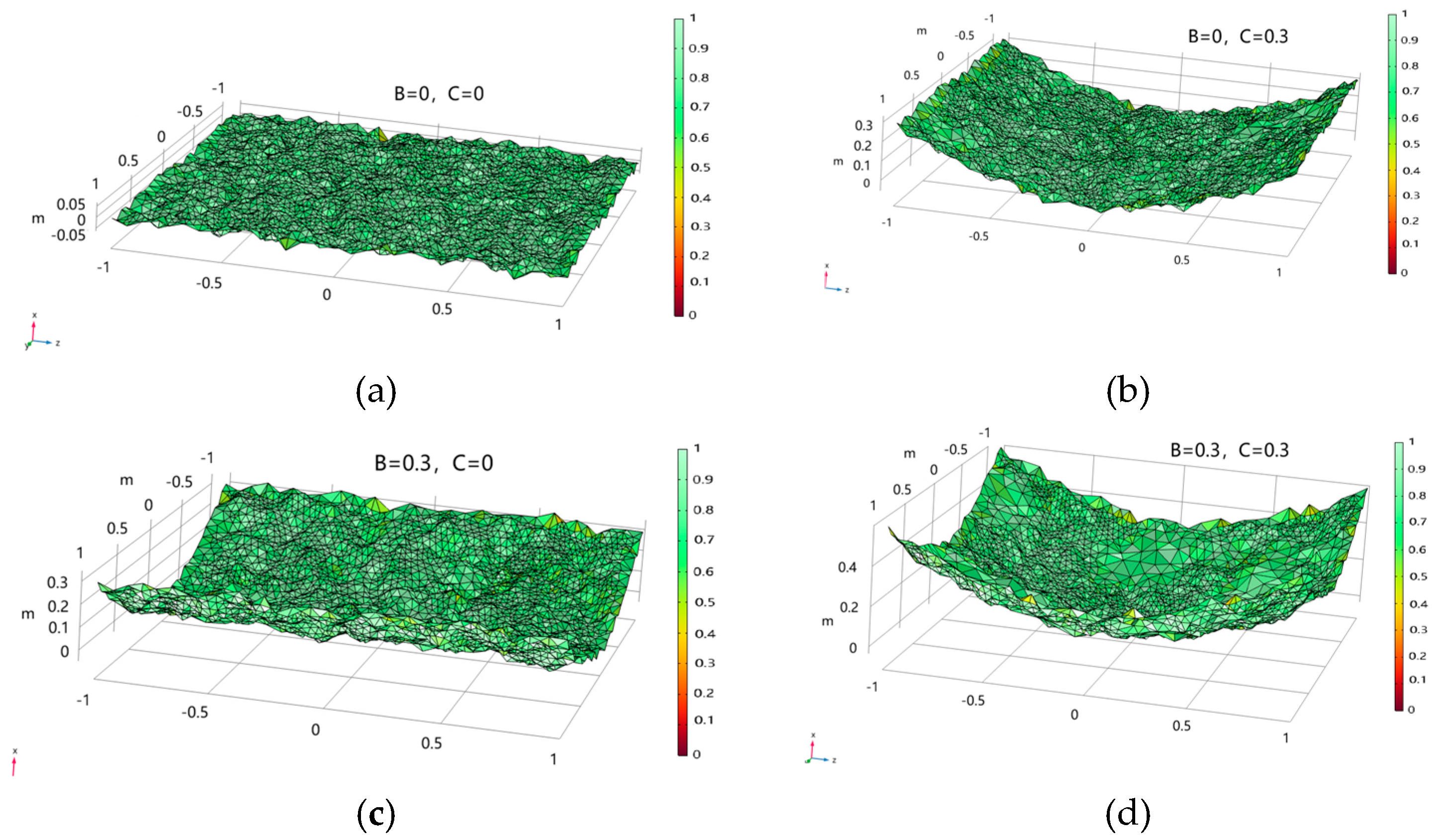
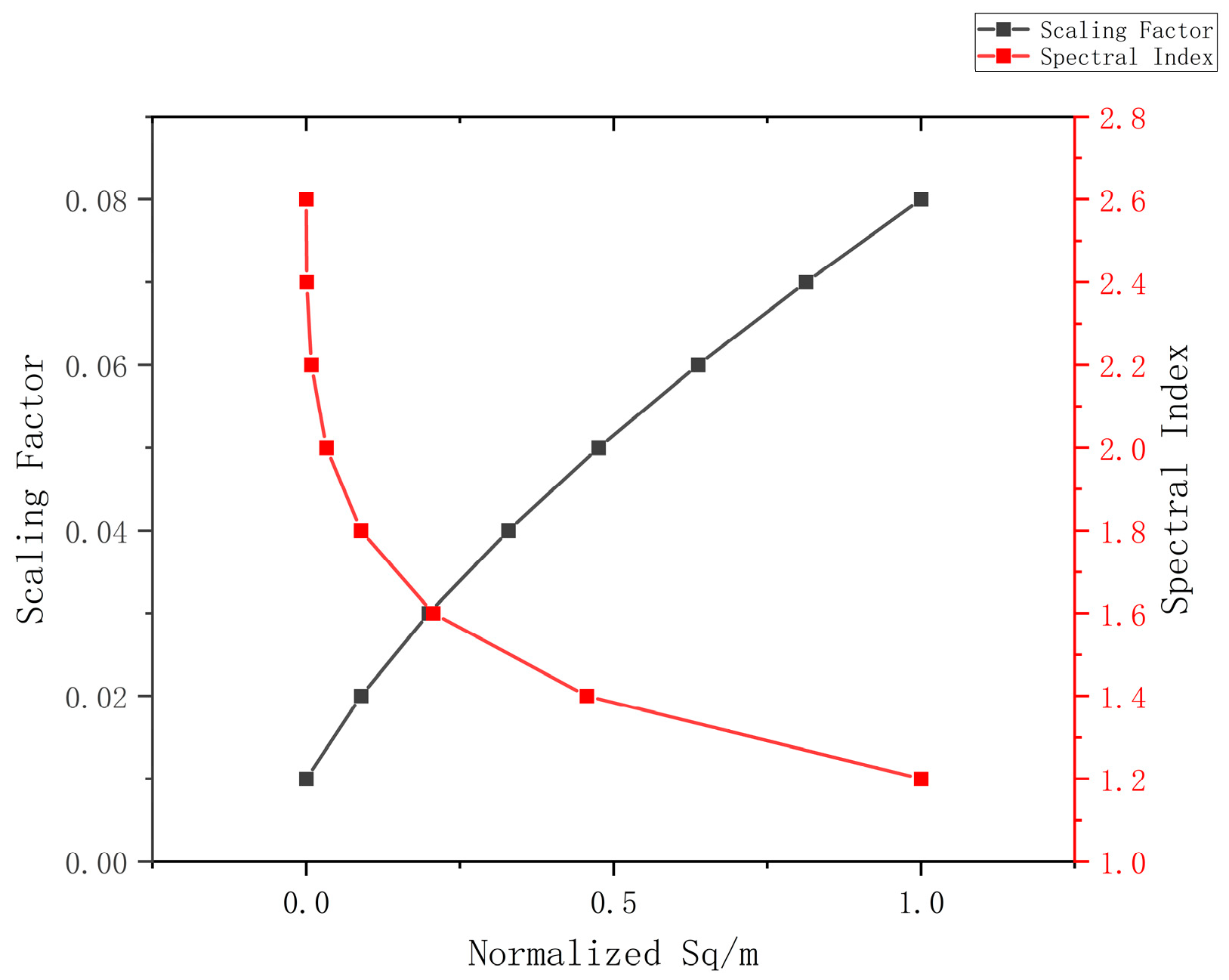


| Scaling Factor | Sq/m | Normalized Sq/m | Spectral Index | Sq/m | Normalized Sq/m |
|---|---|---|---|---|---|
| 0.01 | 0.134866 | 0 | 1.2 | 0.136166 | 1 |
| 0.02 | 0.138487 | 0.089277 | 1.4 | 0.135459 | 0.456572 |
| 0.03 | 0.142961 | 0.199586 | 1.6 | 0.135134 | 0.206764 |
| 0.04 | 0.148211 | 0.329027 | 1.8 | 0.134981 | 0.089162 |
| 0.05 | 0.154157 | 0.475628 | 2.0 | 0.134908 | 0.033052 |
| 0.06 | 0.160722 | 0.637417 | 2.2 | 0.134876 | 0.008455 |
| 0.07 | 0.167833 | 0.812803 | 2.4 | 0.134866 | 0.000768 |
| 0.08 | 0.175425 | 1 | 2.6 | 0.134865 | 0 |
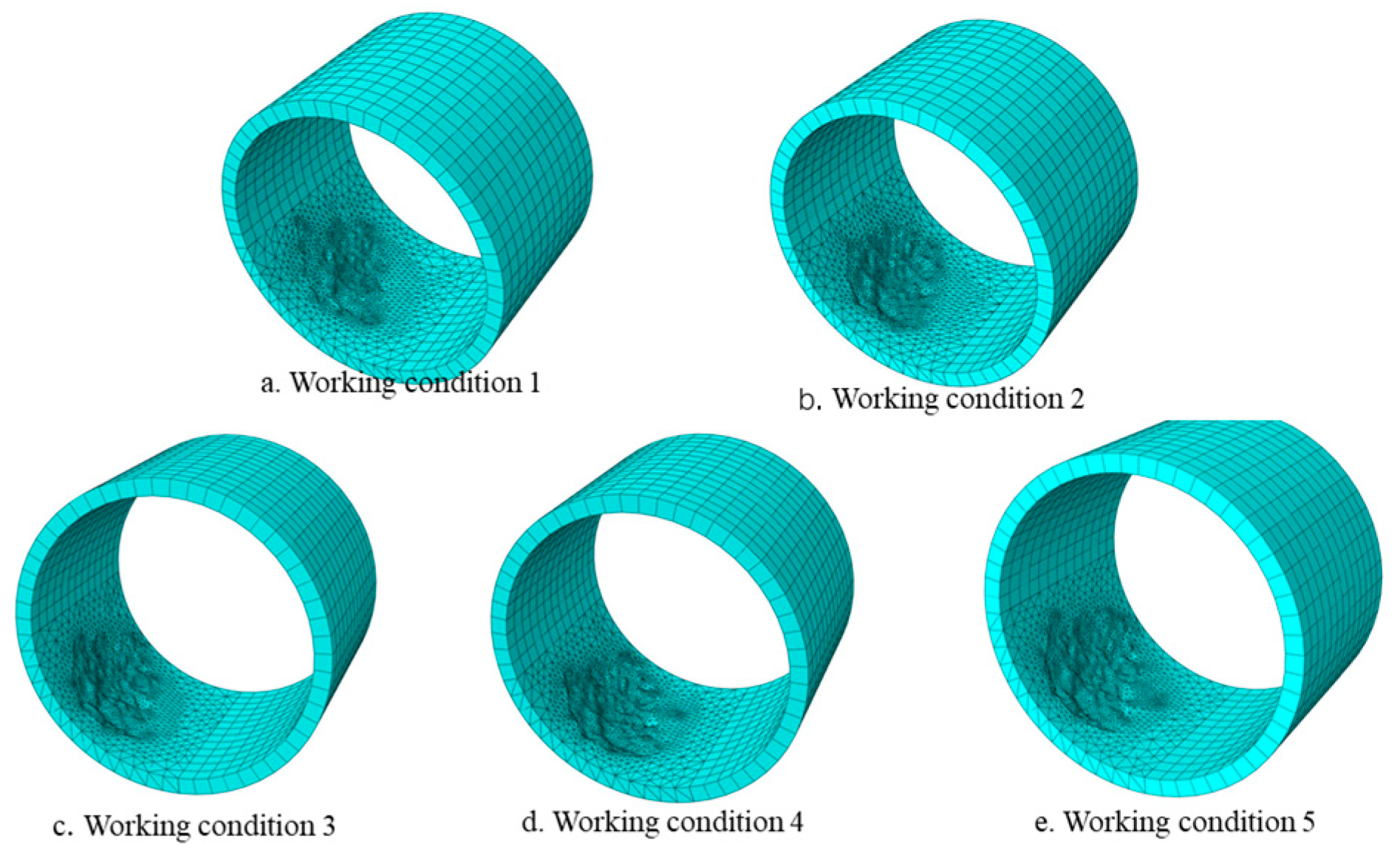
| Working Condition Number | Pipe Length/m | Pipe Wall Thickness/m | Corrosion Area/m2 | Depth of Corrosion/m |
|---|---|---|---|---|
| Working condition 1 | 0.05 | 0.04 | 0.000550 | 0.003 |
| Working condition 2 | 0.05 | 0.04 | 0.000662 | 0.003 |
| Working condition 3 | 0.05 | 0.04 | 0.000756 | 0.003 |
| Working condition 4 | 0.05 | 0.04 | 0.000785 | 0.003 |
| Working condition 5 | 0.05 | 0.04 | 0.000825 | 0.003 |
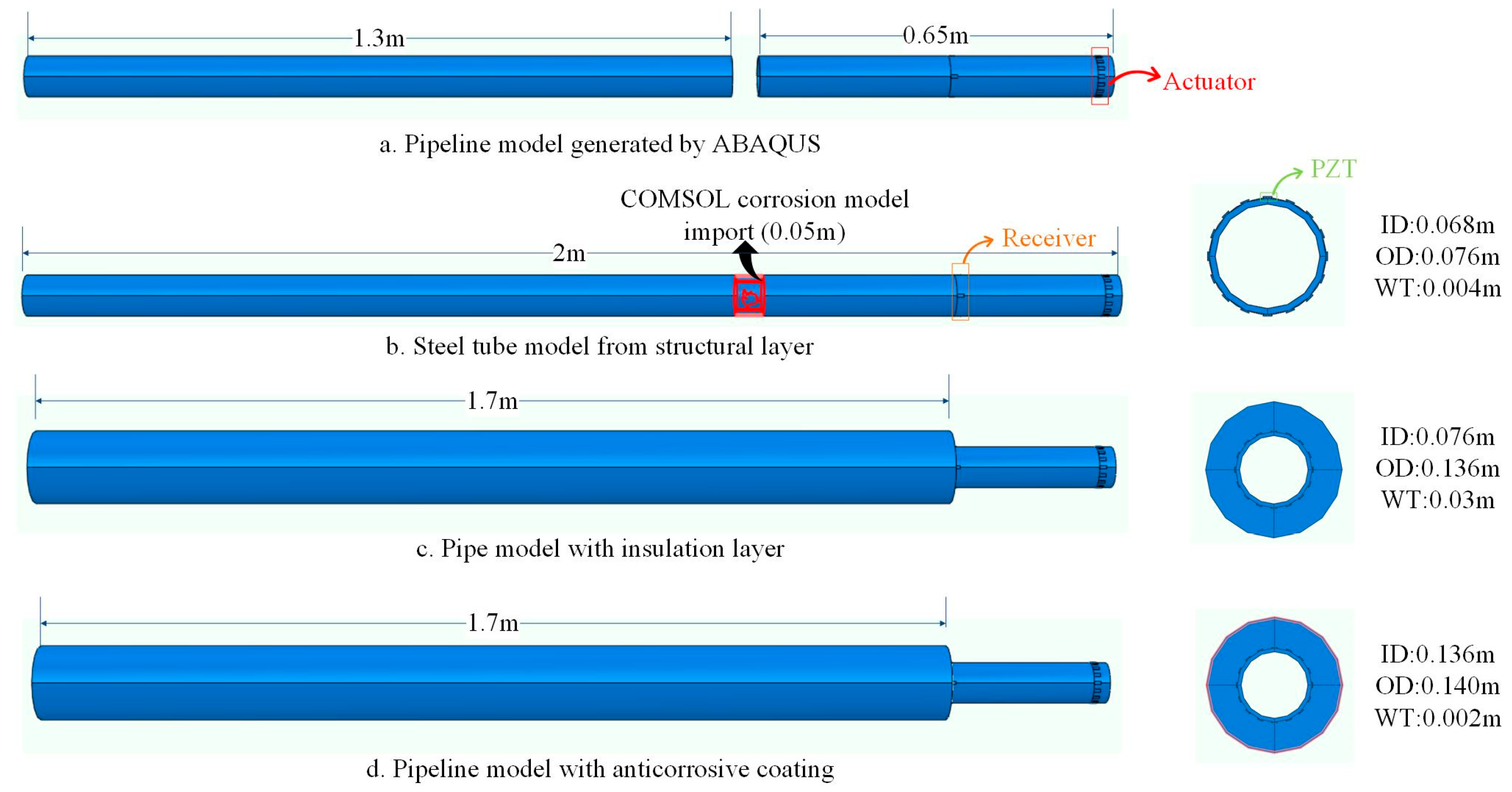
| Structure Type | ID/m | OD/m | WT/m | ρ/kg·m−3 | E/Pa | ν | L/m | |
|---|---|---|---|---|---|---|---|---|
| Material Properties | ||||||||
| Steel pipe | 0.068 | 0.076 | 0.004 | 7850 | 2.10 × 1011 | 0.32 | 2 | |
| Polyurethane rigid foams | 0.076 | 0.136 | 0.03 | 80 | 7.80 × 108 | 0.25 | 1.7 | |
| High-density polyethylene | 0.136 | 0.14 | 0.002 | 946 | 5.52 × 108 | 0.4 | 1.7 | |
| Working Condition Number | Corrosion Area/m | Damage Index Value |
|---|---|---|
| 1 | 0.000550 | 0.135 |
| 2 | 0.000662 | 0.203 |
| 3 | 0.000756 | 0.21 |
| 4 | 0.000785 | 0.214 |
| 5 | 0.000823 | 0.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Liang, Q.; He, F. Research on Ultrasonic Guided Wave Damage Detection in Internally Corroded Pipes with Curved Random Surfaces. Appl. Sci. 2025, 15, 12372. https://doi.org/10.3390/app152312372
Li Y, Liang Q, He F. Research on Ultrasonic Guided Wave Damage Detection in Internally Corroded Pipes with Curved Random Surfaces. Applied Sciences. 2025; 15(23):12372. https://doi.org/10.3390/app152312372
Chicago/Turabian StyleLi, Ying, Qinying Liang, and Fu He. 2025. "Research on Ultrasonic Guided Wave Damage Detection in Internally Corroded Pipes with Curved Random Surfaces" Applied Sciences 15, no. 23: 12372. https://doi.org/10.3390/app152312372
APA StyleLi, Y., Liang, Q., & He, F. (2025). Research on Ultrasonic Guided Wave Damage Detection in Internally Corroded Pipes with Curved Random Surfaces. Applied Sciences, 15(23), 12372. https://doi.org/10.3390/app152312372





