Vibration Analysis of Cantilever Beam with Free End Resting on 3D-Printed Spring and Considering the Effect of Accelerometer and Exciter Masses

Abstract

A cantilever beam is a mechanical structure fixed at one end and free at the other. It converts the applied external forces into bending and shear force; therefore, it should be designed to resist deflection. The fundamental natural frequency of the cantilever beam depends on its material properties, geometry, and supporting conditions. This work studied the effect of adding an accelerometer and a motor, which represent multiple masses, on the fundamental natural frequency of a cantilever beam. The beam is also supported by a 3D-printed spring at its free end. Three-dimensional-printed springs with different infill percentages (20%, 50%, 80%, and 100%) were used with different infill patterns (concentric, grid, and triangle) to study the effect of these parameters on natural frequency. The results showed that the triangle pattern gives the best results for fundamental natural frequency and resulting force values. In addition to that, the triangle pattern with 80% infill percentage is preferred for printing as compared with 100% infill percentage because it gives better vibration results.

1. Introduction

Vibration of cantilever beams is one of the topics that has been studied by many researchers over the past decade [1,2,3,4,5,6,7,8,9] due to the importance of these parts and their uses in many engineering applications, for example, but not limited to, robot arms, aeroplane wings, actuators, sensors, and vibratory feeders [10,11,12,13]. Operating conditions generally expose these parts to varying forces, determining their efficiency, durability, safety, and performance. The dynamic behaviour of these parts is an important topic for study.

In robotics applications, the effective end is equipped with special equipment (welding devices, painting guns, inspection tools, etc.) that can be treated as additional weights mounted at the free end of the shaft. In aircraft wings, engines and fuel tanks can be treated as additional weights mounted anywhere along the wing. In this work, adding a motor to the system will serve as an exciter, which subsequently introduces nonlinear effects, including inertial forces. The added mass’s value, position, stiffness, and centre of mass affect the natural frequency [14,15]. The maximum decrease in natural frequency is obtained when the mass is located at the free end, while the frequency value is not affected when this mass is located at the fixed end. Adding more than one mass (two motors, for example) will also influence the dynamic behaviour of the system [16].

Adding a spring to support the free end of the beam will change the boundary conditions, which in turn affect the mode shapes and natural frequencies of the system. A numerical analysis was conducted [17,18] to obtain the natural frequencies for a cantilever beam with a motor and spring attached to its free end. Size, location, stiffness, and number of springs that support a cantilever beam affect the amount of deflection at the free end [19]. An analytical solution for a spring-like actuator was performed [20] to study the effect of actuator stiffness and frequency on the resonance frequency and mode shapes of the system.

The vibration of the cantilever beam can be used as an energy harvester by converting this vibration from mechanical energy into electrical energy for components like sensors [21,22,23]. Vibration of a diesel engine can be used as another source of electrical power. Integrating a piezoelectric system with a cantilever beam can make use of limited space effectively because its structure is simple. Utilizing multiple piezoelectric systems or multiple beams can harvest more electrical power resulting from the surrounding vibration [24,25,26,27,28].

Three-dimensional printing is a modern technology used to manufacture various parts by combining a series of layers to produce the final product without the need for a special mould. This technology is used to manufacture prototypes for testing purposes, resulting in lower final costs and the ability to manufacture highly complex engineering models. One of the important features of this technology is the ability to control the internal specifications of the model by controlling the infill pattern or the infill percentage. Springs of the same shape and dimensions can be printed with variable stiffness and mass by controlling the infill pattern and infill percentage [29,30,31,32,33,34,35,36,37].

When studying the vibration of lightweight components, the accelerometer mass must be considered. In this paper, vibration analysis is considered for a system of cantilever beams with two masses on its top and a 3D-printed spring under its free end, as shown in Figure 1. One of the two masses is located at the free end of the beam and represents the accelerometer, while the other mass is located near the clamped end and represents an exciting motor.

The objective of this work is to utilize the vibration of the free edge of a cantilever beam by transferring the movement of the free edge to a 3D-printed spring mounted under this free edge. The novelty of our procedure is studying the amount of force resulting from the spring movement, which is affected by its stiffness. The spring stiffness depends on the printing parameters, like printing pattern and infill percentage.

2. Theory

For a cantilever beam, the natural frequency is given as follows:

$${\omega }_{beam}= {\lambda }^2 \sqrt{{\displaystyle \frac{EI}{\rho A L_{beam}^4}}}$$

(1)

where

• E = Modulus of elasticity (N/m²);
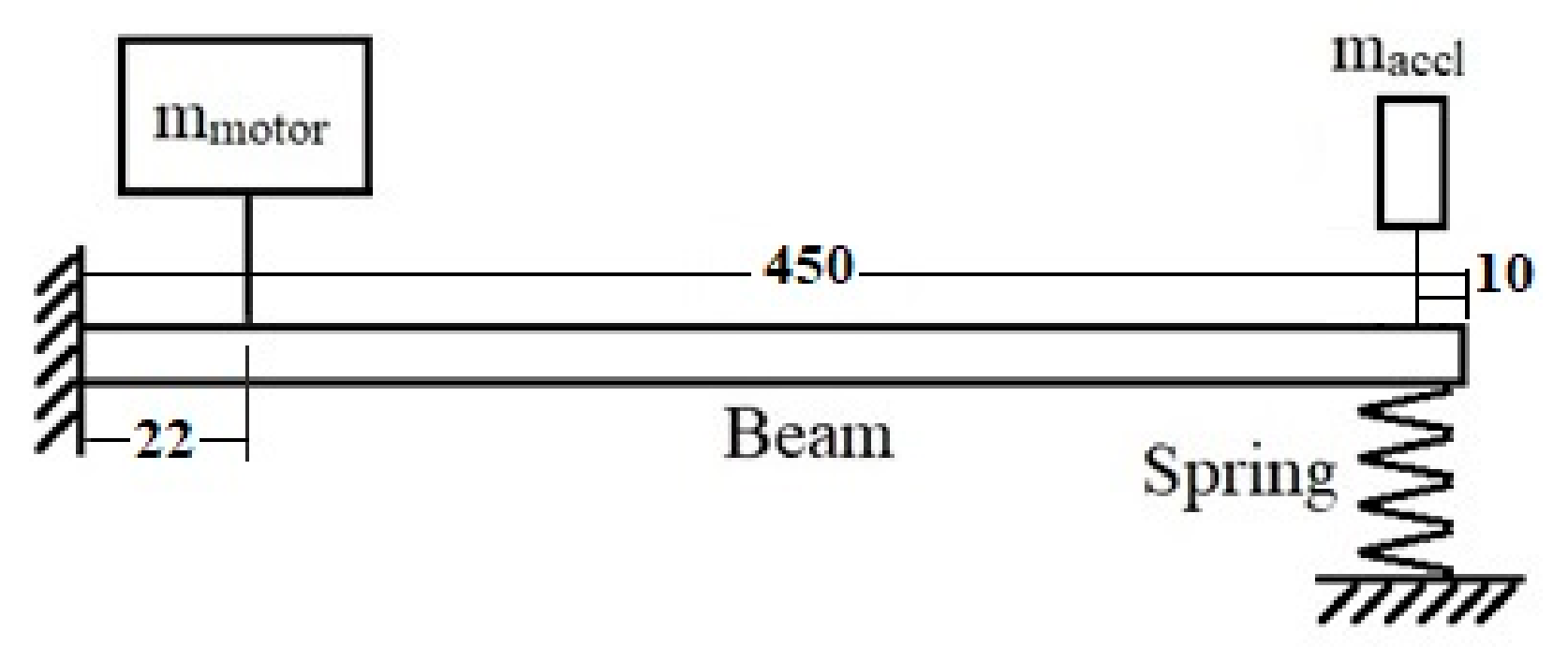
• L_beam = Length of beam (m) = 0.45 m;
• I = Moment of inertia (m⁴), $I= {\displaystyle \frac{b h^3}{12}}$;
• b, h = Width, thickness of beam (m);
• $\mathsf{\rho }$ = Mass density (kg/m³);
• A = Cross-sectional area (m²).

When adding an accelerometer with mass (m_accl) at the end of the cantilever beam and taking the mass of the beam into consideration, Dunkerley’s approximation was used to calculate the frequency of the system ω_s1 [38]:

$${\displaystyle \frac{1}{{\omega }_{s1}^2}}= {\displaystyle \frac{1}{{\omega }_{beam}^2}}+ {\displaystyle \frac{1}{{\omega }_{accl}^2}}$$

(2)

$${\omega }_{accl}=\sqrt{{\displaystyle \frac{3EI}{m_{accl} \ast L_{accl}^3}}}$$

(3)

where

• ${\omega }_{beam}$ = The original frequency of the beam without the accelerometer mass.
• ${\omega }_{accl}$= Natural frequency of massless beam and accelerometer.
• L_accl = The centre of mass for the accelerometer from the free end.

The centre of the mass in this study is located 0.01 m away from the free end; therefore, the effective length will be L_accl = 0.44 m.

When a motor (exciter) of mass (m_motor) is added near the fixed end of the previous system (Figure 1), and Dunkerley’s approximation is applied again, the frequency of the new system, f_s2, will be as follows [39]:

$${\displaystyle \frac{1}{{\omega }_{s2}^2}}= {\displaystyle \frac{1}{{\omega }_{beam}^2}}+ {\displaystyle \frac{1}{{\omega f}_{accl}^2}}+ {\displaystyle \frac{1}{{\omega }_{motor}^2}}$$

(4)

$${\omega }_{motor}=\sqrt{{\displaystyle \frac{3EI}{m_{motor} \ast L_{motor}^3}}}$$

(5)

where L_motor is the centre of the motor mass from the fixed end.

Finally, when adding a spring of stiffness (K_spring) under the free end of the system, the spring and beam will both resist displacement at the free end, and the total stiffness will act in parallel.

For a cantilever massless beam with a mass attached to its free end, the effective mass acting on this spring needs to be calculated. If a load (P) applied is on the beam’s free end, the amount of deflection will be as follows:

$$\delta = {\displaystyle \frac{P{L}^3}{3EL}}$$

(6)

Therefore, the stiffness of the beam will be as follows:

$$K_{beam}= {\displaystyle \frac{P}{\delta }}= {\displaystyle \frac{3EI}{L^3}}$$

(7)

The system now has the following two springs: the spring of stiffness (K_spring) under the free end of the cantilever beam and the flexural spring of the beam (K_beam). The spring and beam will both resist displacement at the free end, and the total stiffness will act in parallel.

$$K_{total}=K_{spring}+K_{beam}$$

(8)

The total stiffness for this system will be considered as the effective stiffness.

$$K_{eff}=K_{spring}+{\displaystyle \frac{3EI}{L^3}}$$

(9)

For a cantilever beam, the effective mass m_eff = 0.25 mL.

The frequency of this spring–mass system is as follows:

$${\omega }^2= {\displaystyle \frac{K_{eff}}{m_{eff}}}$$

(10)

$${\omega }^2={\displaystyle \frac{K_{spring}+\frac{3EI}{L^3}}{0.25 \mathrm{mL}}}$$

(11)

$${\displaystyle \frac{1}{{\omega }_{Spring}^2}}={\displaystyle \frac{0.25 \mathrm{mL}}{K_{spring}+\frac{3EI}{L^3}}}$$

(12)

Applying Dunkerley’s method, the fundamental frequency of the final system will be as follows:

$${\displaystyle \frac{1}{{\omega }_{s2}^2}}= {\displaystyle \frac{1}{{\omega }_{beam}^2}}+ {\displaystyle \frac{1}{{\omega f}_{accl}^2}}+ {\displaystyle \frac{1}{{\omega }_{motor}^2}}+ {\displaystyle \frac{1}{{\omega }_{Spring}^2}}$$

(13)

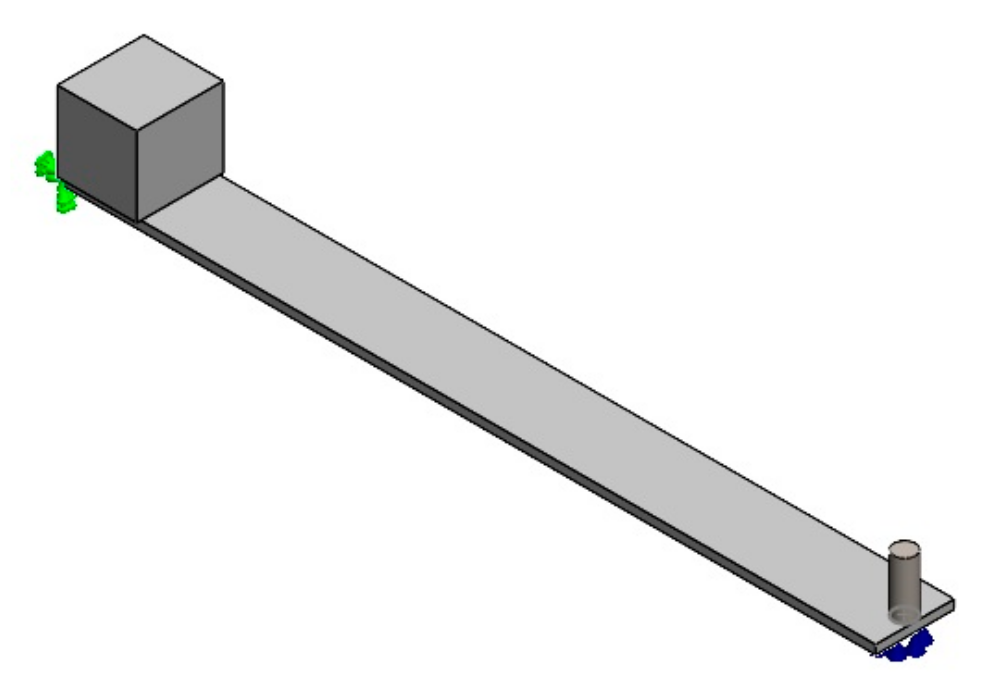
3. Numerical Modelling

To analyse the different configurations of the system, the 3D design software SolidWorks 2023 (SP3.1 version) (SolidWorks Corp., Waltham, MA, USA) was used to model the different parts of the system, as shown in Figure 2.

The beam was modeled as a box with dimensions (450 × 34.6 × 5 mm). Its material was defined as a custom material with an elastic modulus of 71,000 N/mm², Poisson’s ratio 0.33, tensile strength 273 N/mm², and mass density 2800 kg/m³. The motor was modeled as a cube (44 mm edge length) and a custom material was defined with an elastic modulus of 2000 N/mm², a Poisson’s ratio of 0.33, a tensile strength of 30 N/mm², and a mass density of 3874 kg/m³. The accelerometer was modeled as a cylinder (12 mm diameter × 31.5 mm height). ASTM A36 steel material was assigned with an elastic modulus of 200,000 N/mm², a Poisson’s ratio of 0.26, a tensile strength of 400 N/mm², and a mass density of 7850 kg/m³.

The parts were assembled as shown in Figure 3. For boundary conditions, the beam was fixed at one end and free at the other. The motor was at the fixed end of the beam, while the accelerometer was at the free end. The spring was added as an “elastic support” fixture at the beam’s free end with a stiffness that varies according to the values obtained from the printed springs.

The system was meshed with “solid high-quality” mesh type and an element size of 3 mm, which results in total nodes and total elements of 30,503 and 18,322, respectively.

4. Experimental Works

4.1. Material and Methods

4.1.1. Aluminium Beam

A beam with dimensions (0.45 × 0.0436 × 0.005 m) was cut from a commercial aluminium sheet. Its mechanical properties were measured in the material laboratory at the Engineering Technical College—Baghdad, Iraq using the LARYEE Computer Control Electronic Universal Testing Machine, Model UE3450 [40]. These properties were as follows: elastic modulus 71 GPa, tensile strength 271 MPa, and yield strength 221 MPa. The mass density was found to be 2800 kg/m³.

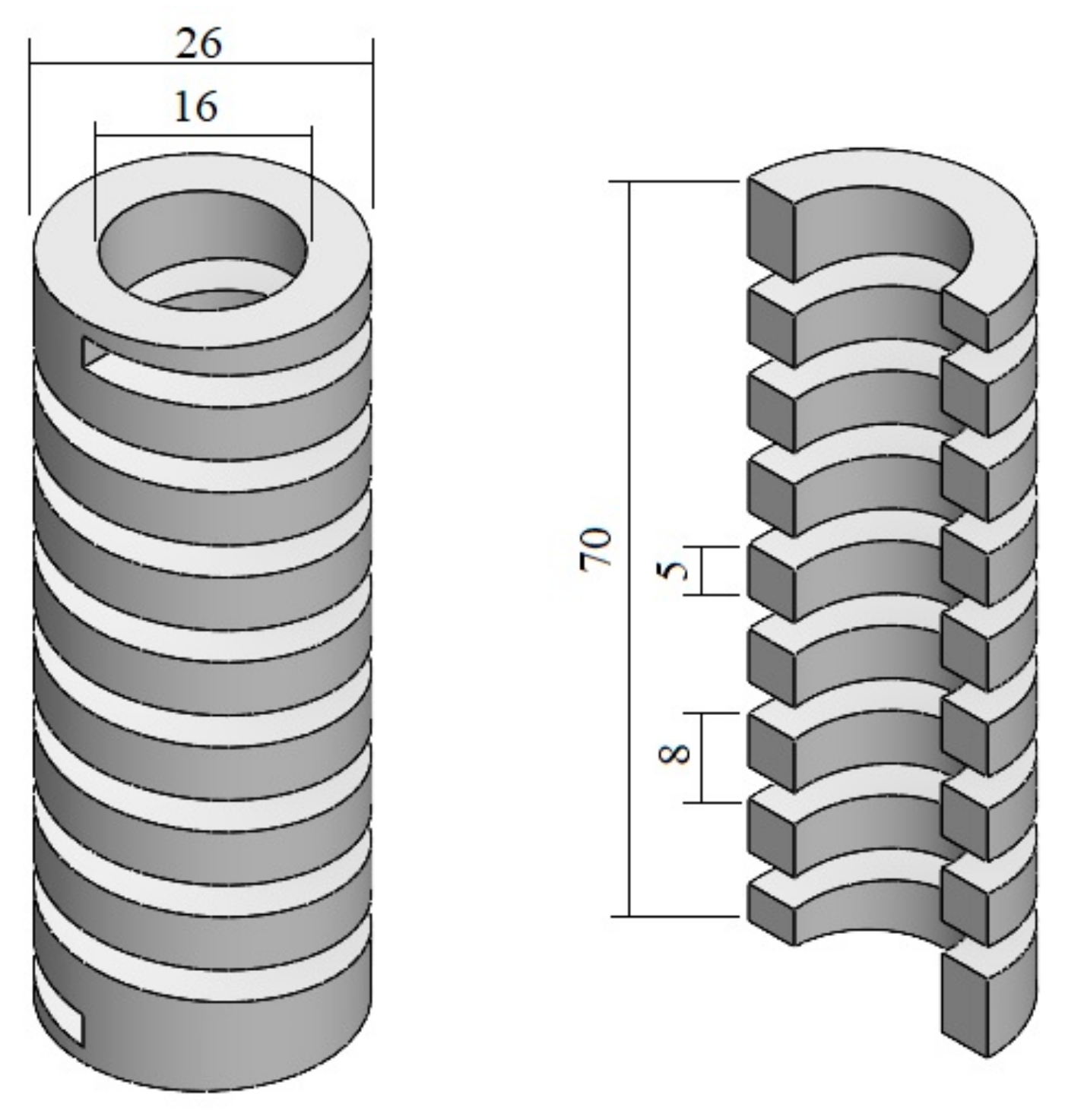
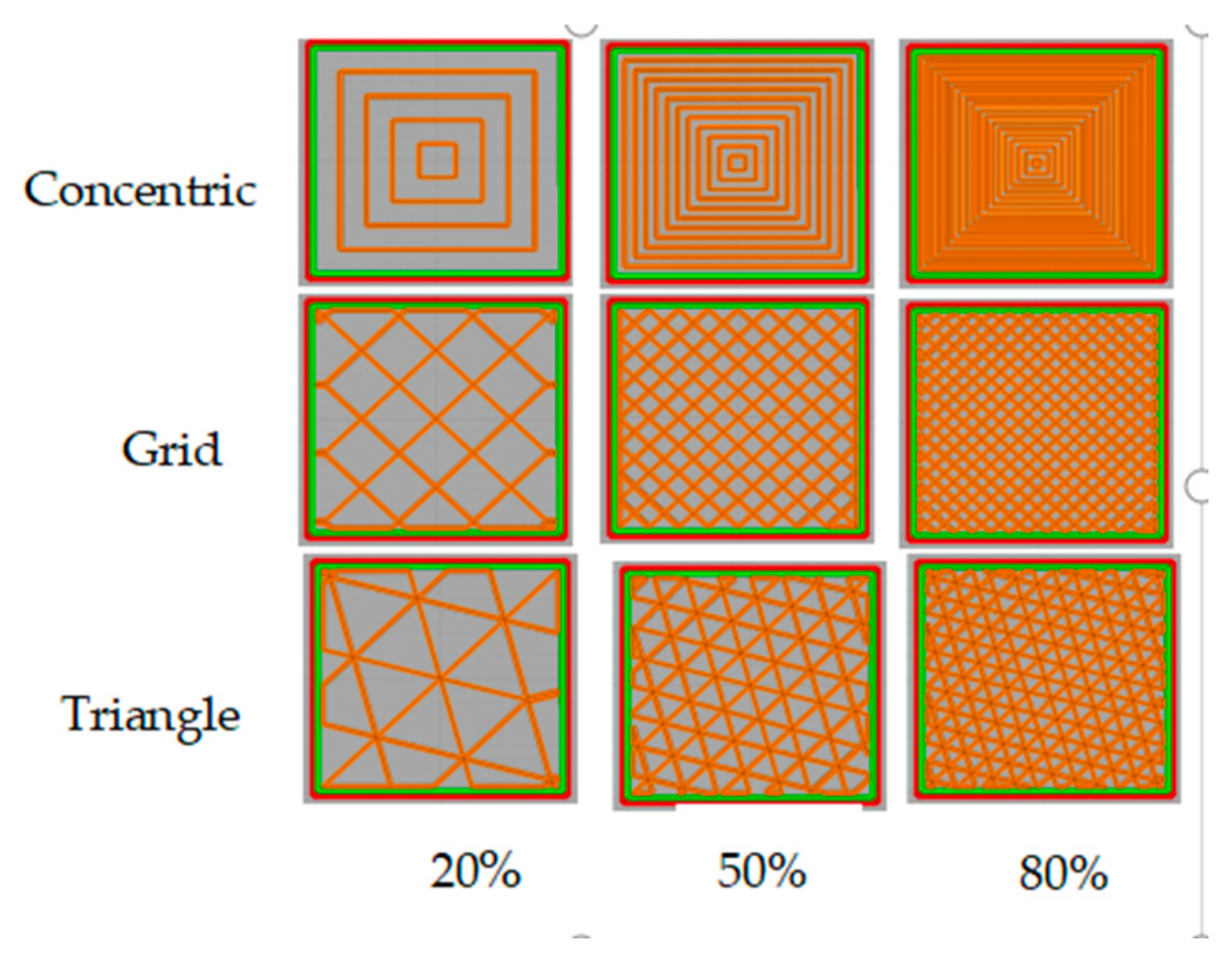
4.1.2. Springs

The Creality K1C 3D Printer [41] was used to print ten springs made from PLA filament. These printed springs had dimensions of 0.026 m outer diameter, 0.016 m inner diameter, and 0.07 m height. The spring contains eight active turns with a 0.008 m pitch. The rectangular cross-section was 0.005 × 0.005 m, as shown in Figure 4.

Three different infill patterns were used (concentric, grid, and triangle, which were denoted by C, G, and T symbols, respectively). For each pattern, three infill density percentages were used (20%, 50%, and 80%), as shown in Figure 5. To model the solid state, the tenth spring was printed with a triangle pattern (100% infill percentage). These three patterns were chosen because their printing lines are spaced far enough apart to show the effect of changing the infill percentage, compared with other patterns where the printing lines are close together and intertwined, making it difficult to notice the effect of changing the infill percentage of 50% or more.

The volume of each spring was 15.182 × 10⁻⁶ m³, but their mass density varies depending on the printing infill pattern and infill percentage. Therefore, the equivalent density for each spring was calculated. To obtain the equivalent density, the weight of each spring was measured in the material laboratory at the Engineering Technical College—Baghdad, Iraq using the RADWAG Model AS 220.X2 scale [42]. From the weight and volume of the springs, the equivalent density was found, and the results are listed in

Table 1. Spring–mass and equivalent density for different patterns at different infill %.

Infill %	Concentric		Grid		Triangle
	Weight ×10−3 (kg)	Density (kg/m3)	Weight ×10−3 (kg)	Density (kg/m3)	Weight ×10−3 (kg)	Density (kg/m3)
20	10.773	709.625	13.299	876.015	15.181	999.984
50	11.301	744.405	13.739	905.051	16.015	1054.92
80	11.455	754.549	14.109	929.37	16.137	1062.96
100	-----	-----	-----	-----	17.677	1164.4

.

The LARYLARYEE Universal Testing Machine was also used to conduct a compression test for the printed spring specimens and obtain the (load/extension) results for each value, from which the experimental stiffness for the different springs was estimated, as listed in

Table 2. Spring stiffness for different patterns at different infill %.

Infill %	Spring Stiffness (N/m)
	Concentric	Grid	Triangle
20	893.4	964.2	1123
50	1236	1243	1339.2
80	1379.1	1481.7	1503.8
100	------	------	1558.4

.

It can be noted from Table 2 that the stiffness depends on both infill percentage and infill patter, with triangle and grid patterns showing a greater effect than the concentric pattern.

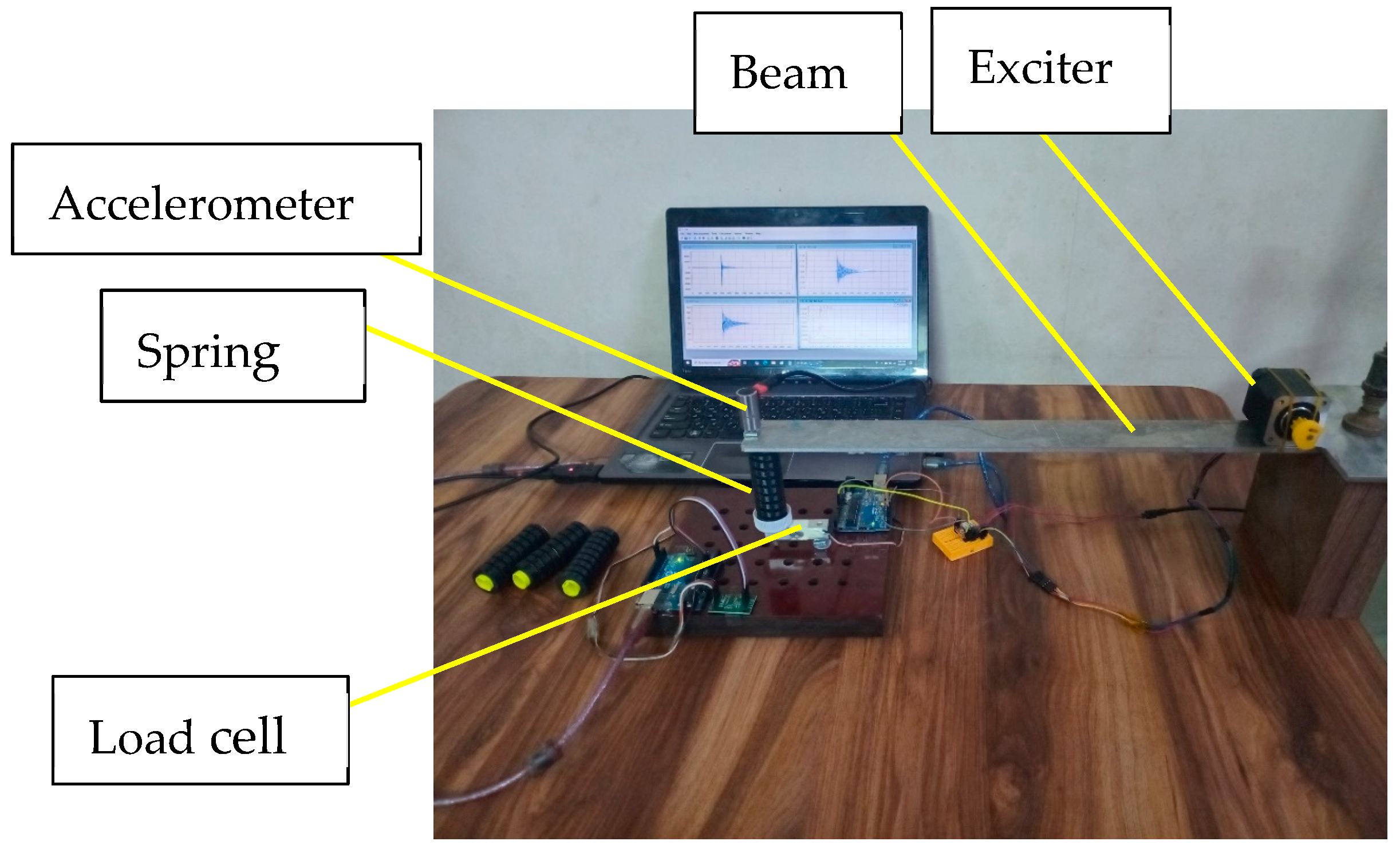
4.2. Rig Setup

The parts attached to the aluminium cantilever beam are the accelerometer, printed spring, load cell, and stepper motor. These parts are shown in Figure 6.

4.2.1. Aluminium Cantilever Beam

As explained in Section 4.1.1.

4.2.2. Accelerometer

DigivibeMX^® Version 2.1.0.4 [43] from Erbessd Instruments was used to collect and analyse the vibration data with the help of EI-CALC software 2020. The mass of the accelerometer is 0.028 kg, located at 0.01 m from the free end.

4.2.3. Printed Springs

As explained in Section 4.1.2.

4.2.4. Load Cell

A 50 kg four-wire micro load cell [44] was used to measure the applied force. The magnitude of the voltage change inside the load cell was amplified through the amplifier module and then an Arduino Uno was used to convert the numerical value into a weight value.

4.2.5. Stepper Motor

To create vibration at different frequencies, an NEMA 17 stepper motor with an A4988 driver module was used [45]. An Arduino Uno was also used to control the rotational speed of the motor. The NEMA 17 stepper motor typically has HX711 200 steps/revolution (PBC Linear company, Roscoe, IL, USA). The low and high delays for the motor were controlled by Arduino code to pulse at different times, where the step frequency f_step and the rotational speed RPM were calculated as follows:

$$f_{step}= {\displaystyle \frac{1}{total delay time}} = {\displaystyle \frac{1}{“\mathrm{High}”delay + “\mathrm{Low}”delay}} (\mathrm{Hz})$$

(14)

The motor rotational speed can be calculated as follows:

$$motor speed= {\displaystyle \frac{f_{step} \ast 60}{steps per revolution}} (\mathrm{rpm})$$

(15)

Vibration can be created at desired frequencies by adjusting the step frequency of the stepper motor. Three different delay times were used (1000, 750, and 500) for high and low delay in the Arduino code. The total delay per step equals the summation of the high delay and low delay. The rotational speeds were 150, 200, and 300 rpm, respectively. The mass of the motor is 0.36 kg, located at 0.022 m from the fixed end.

Figure 7 shows the arrangement of the different parts in the assembly.

5. Results

5.1. Free Vibration

For a cantilever beam without an accelerometer and by using Equation (1), the fundamental natural frequency was found to be 20.083 Hz.

When adding an accelerometer of mass 0.028 kg at the free end of the beam (the centre of mass is 0.01 m away from the free end) and using Equations (2) and (3), the theoretical, practical, and numerical (SolidWorks 2023, SP3.1 version) fundamental natural frequencies were 17.018, 17.614, and 17.119 Hz, respectively. The deviation between theoretical and practical, and between theoretical and numerical natural frequency was 0.35% and 0.59%, respectively. Adding an additional motor of mass 0.36 kg near the fixed end and using Equations (4) and (5), the theoretical, practical, and numerical fundamental natural frequencies became 17.014, 17.277, and 17.751 Hz, respectively. The deviation between theoretical and practical and between theoretical and numerical natural frequency was 1.54% and 4.33%, respectively. Installing the accelerometer near the free end results in a significant decrease in vibration value; this illustrates the importance of using Dunkerley’s approximation to calculate the frequency. Adding the mass of the motor has a negligible effect on the frequency because the mass is located near the fixed end, which acts as a supported node.

Springs with different printing parameters were used in two systems; the first system consists of an accelerometer (mass 0.028 kg) and spring at the free end of the beam. In the second system, a motor (mass 0.36 kg) is located at the fixed end. The fundamental natural frequency varies with spring stiffness, as listed in

Table 3. Fundamental natural frequencies for two systems.

Infill % and Infill Pattern	Stiffness (N/m)	Accelerometer–Spring System					Accelerometer–Spring–Motor System
		Practical (Hz)	Theoretical (Hz)	Deviation %	Numerical (Hz)	Deviation %	Practical (Hz)	Theoretical (Hz)	Deviation %	Numerical (Hz)	Deviation %
20C	893.4	23.047	23.107	0.26	22.718	1.68	23.222	23.384	0.69	22.662	3.09
50C	1236	24.624	25.050	1.70	24.505	2.18	24.392	24.394	0.01	24.435	0.17
80C	1379.1	24.897	25.818	3.57	25.21	2.35	24.565	24.685	0.49	25.136	1.83
20G	964.2	23.553	23.522	0.13	23.099	1.80	23.216	23.216	0.00	23.04	0.76
50G	1243	24.676	25.088	1.64	24.54	2.18	24.230	24.391	0.66	24.47	0.32
80G	1481.7	25.297	26.355	4.01	25.702	2.48	25.237	25.404	0.66	25.626	0.87
20T	1123	23.830	24.426	2.44	23.931	2.03	23.553	23.496	0.24	23.866	1.57
50T	1339.2	25.011	25.606	2.32	25.016	2.30	24.561	24.562	0.00	24.942	1.55
80T	1503.8	25.459	26.470	3.82	25.807	2.50	24.900	24.900	0.00	25.73	3.33
100T	1558.4	25.914	26.750	3.13	26.064	2.56	25.908	25.908	0.00	25.985	0.30

.

Adding the spring will act as an additional support to the free ends, which in turn increases the fundamental frequency. Also, it can be noted that the frequency depends on the printing parameters, as they determine the stiffness of the printed spring. Again, adding the motor has a small effect on the frequency value.

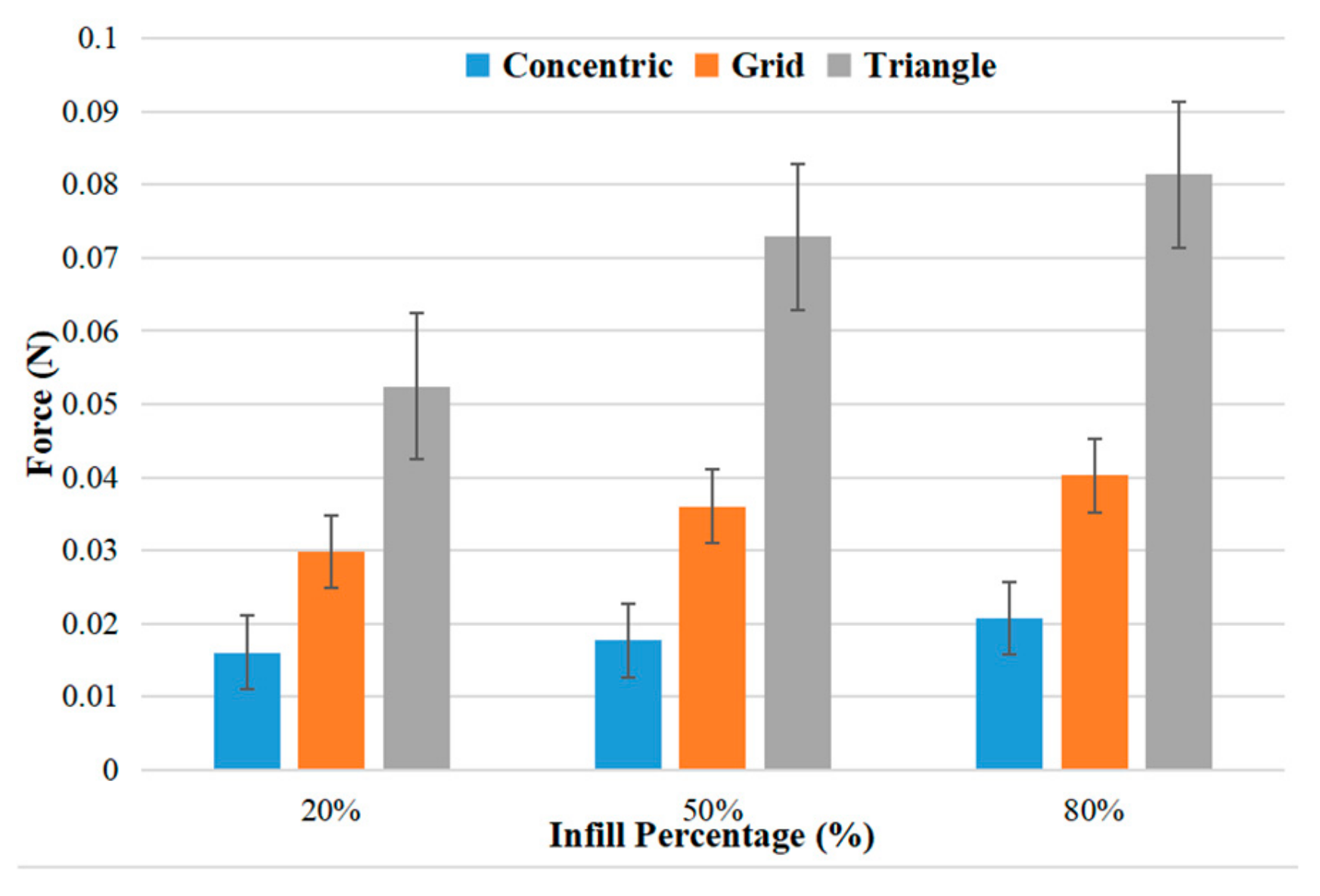
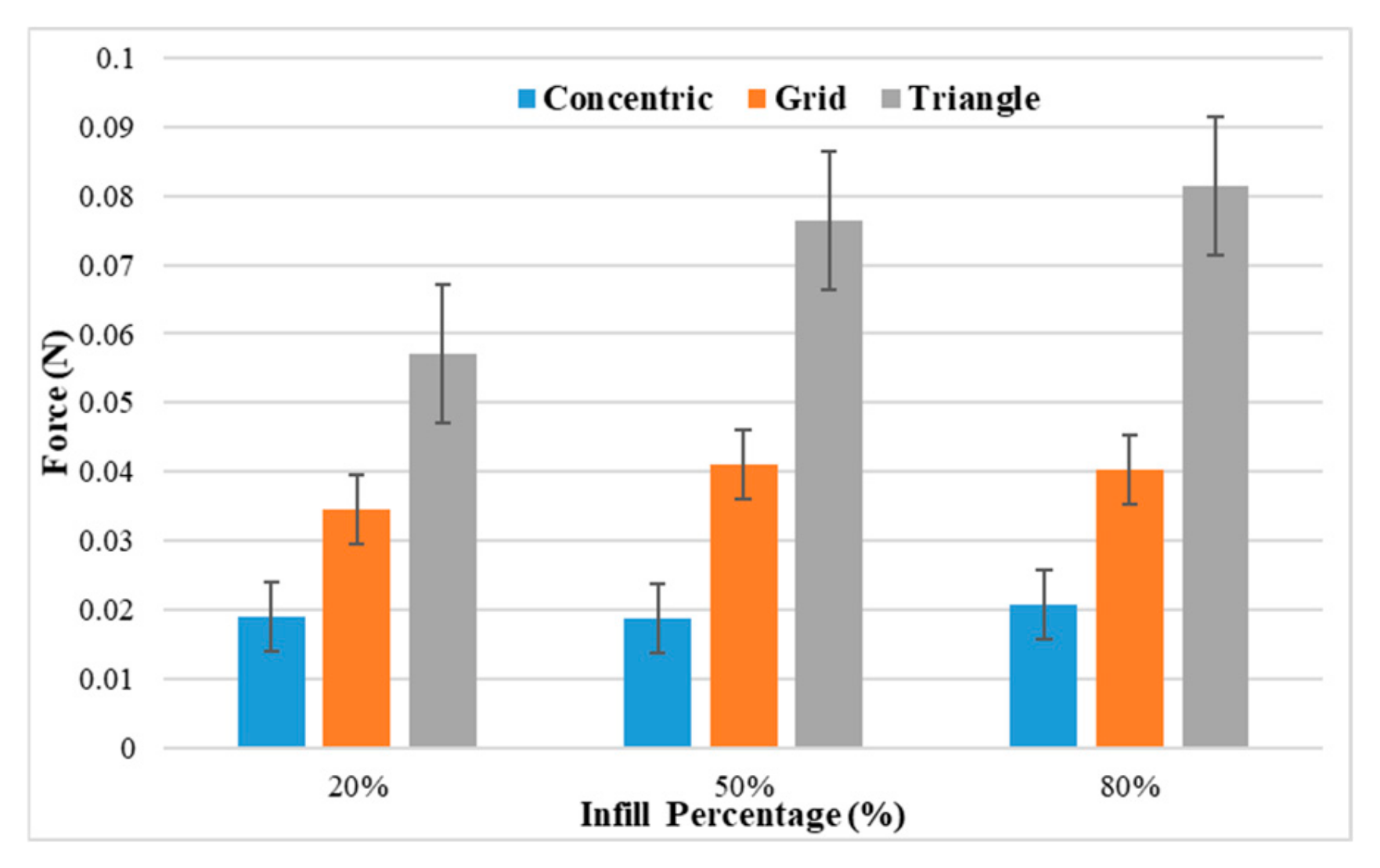
5.2. Force Measurement

The cantilever beam force variation was studied by using the load cell mentioned in Section 4.2.3 according to motor rotational speeds, infill percentages, and patterns. The resulting force was in grams, which was then converted to force in N.

The load cell measurement signals for the cantilever beam supported by a spring printed with 20%, 50%, and 80% infill and different patterns are shown in Figure 8, Figure 9 and Figure 10.

The average force values at motor rotational speeds of 150 rpm, 200 rpm, and 300 rpm are illustrated in

Table 4. Force measurement due to 150 rpm rotational speed.

Infill %	Force (N)
	Concentric	Grid	Triangle
20	0.016	0.03	0.052
50	0.018	0.036	0.072
80	0.021	0.04	0.081

,

Table 5. Force measurement due to 200 rpm rotational speed.

Infill %	Force (N)
	Concentric	Grid	Triangle
20	0.019	0.035	0.056
50	0.019	0.041	0.076
80	0.023	0.043	0.082

and

Table 6. Force measurement due to 300 rpm rotational speed.

Infill %	Force (N)
	Concentric	Grid	Triangle
20	0.021	0.041	0.061
50	0.022	0.047	0.079
80	0.024	0.049	0.087

, respectively.

It is possible to conclude that the average force is affected by changing the printing pattern more than changing the rotational speed. Also, increasing the infill percentage slightly increases the resulting force.

The average force signals for the cantilever beam supported by a spring printed with a 100% infill triangle pattern are shown in Figure 11 The average force values were 0.023, 0.041, and 0.078 N at motor rotational speeds of 150, 200, and 300 rpm, respectively. Increasing the rotational speed increases the average force.

6. Discussions

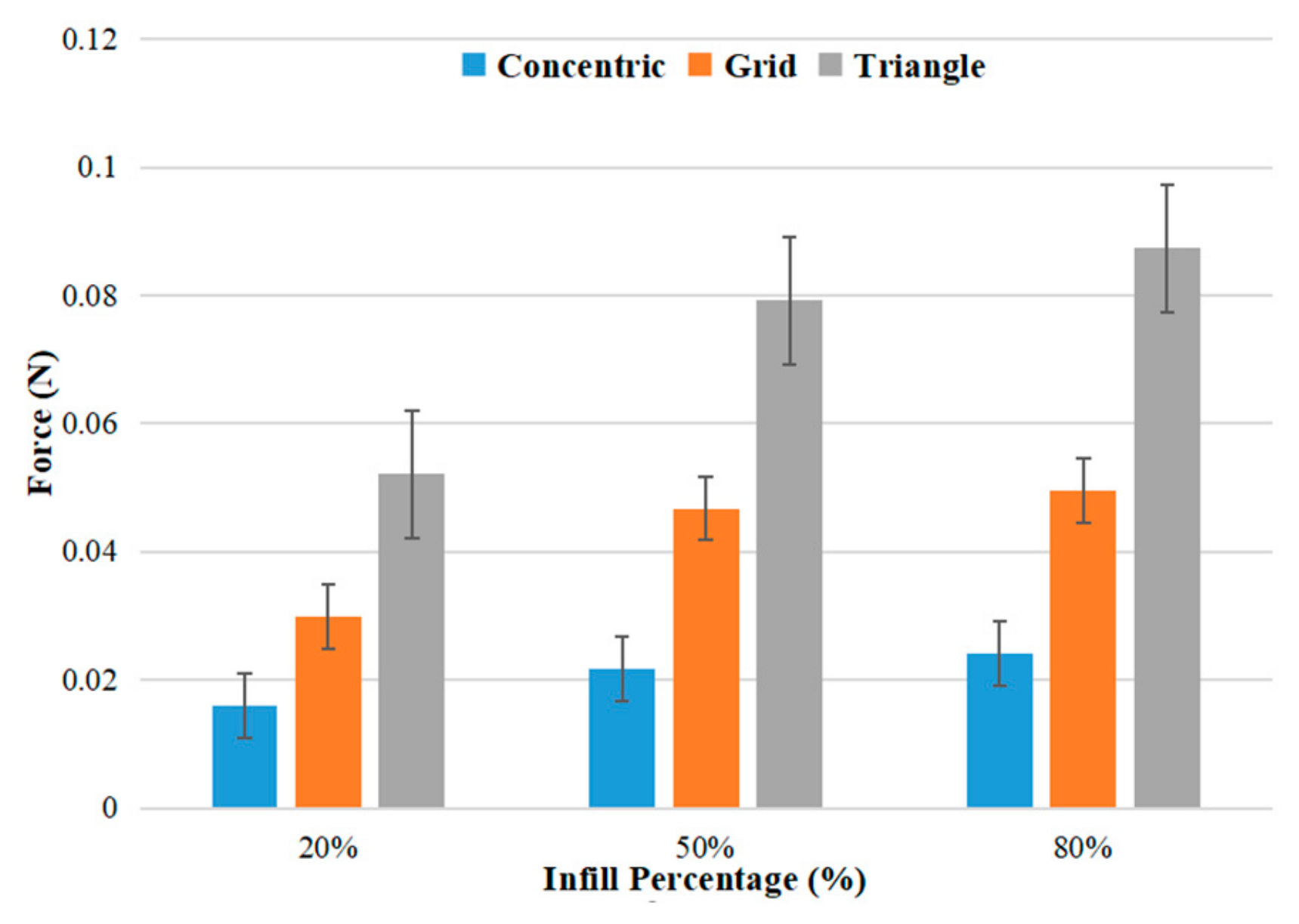
• The motor has a dynamic effect which causes beam vibration. Increasing the rotational speed causes the motor to exert more energy into the beam at a specific time. For the “grid” pattern at 50% infill percentage, increasing the rotational speed from 150 to 300 rpm increases the resulting force from 0.036 N to 0.047 N, which means an increase in force by 30%.
• When the motor rotates, the excitation force is small and the vibration resulting from it is far from the resonance value; therefore, the beam properties can be modified so that the fundamental natural frequency can be lowered to be close to the motor frequency.
• The “triangle” printing pattern results in the highest force. It creates a “truss-like” structure which is efficient for carrying loads because the resulting forces act as axial tension along the filament lines. The “grid” pattern, which is composed of square shapes, is less efficient because these shapes are deformed by filament bending at the joints, which results in less stiffness and resulting force. The “concentric” pattern shows the lowest force because this pattern acts as multiple unsupported rings, which have the lowest stiffness and resulting force. At 80% infill and 300 rpm, the force resulting from the “triangle” pattern was 0.087 N, which is 3.6 times greater than the force of the “concentric” pattern (0.024 N).
• For the “triangle” pattern at a rotational speed of 150 rpm, increasing the infill percentage from 20% to 80% increases the force from 0.052 N to 0.081 N, which means an increase of 56%.
• The “triangle” pattern with 80% infill density is recommended for printing when compared with 100% infill density because the difference in results is very small; this reduces cost and weight when using 80% infill density.
• This system can be used to harvest electrical signals resulting from the vibration of the beam if a piezoelectric sensor is mounted under the spring.
• There was a slight difference between theoretical and experimental results of natural frequency, which may arise due to clamping conditions or effective stiffness of the spring.

7. Conclusions

• The stiffness of a printed spring is not just a material property; it is also affected by its internal geometry, which is defined by the printing pattern.
• The printing pattern is the most powerful factor affecting the printed spring stiffness, while infill percentage is used for fine-tuning the spring stiffness.
• Increasing the infill percentage means more printing material within the same volume, which increases spring stiffness.
• The stepper motor can be replaced by an electrical DC motor to obtain higher rotational speed. Also, an eccentric mass can be attached to this motor to control the value of the excitation vibration.

8. Future Works

• It is suggested to perform the study using other different printing patterns to find out the best pattern to use.
• Adding a piezoelectric sensor under the spring to harvest electrical signals resulting from beam vibration.