Noninvasive Left Ventricular Pressure–Volume Loops Based on Combined 4D Flow MRI and CFD
Abstract
1. Introduction
2. Materials and Methods
2.1. Acquisition
2.2. Data Analysis
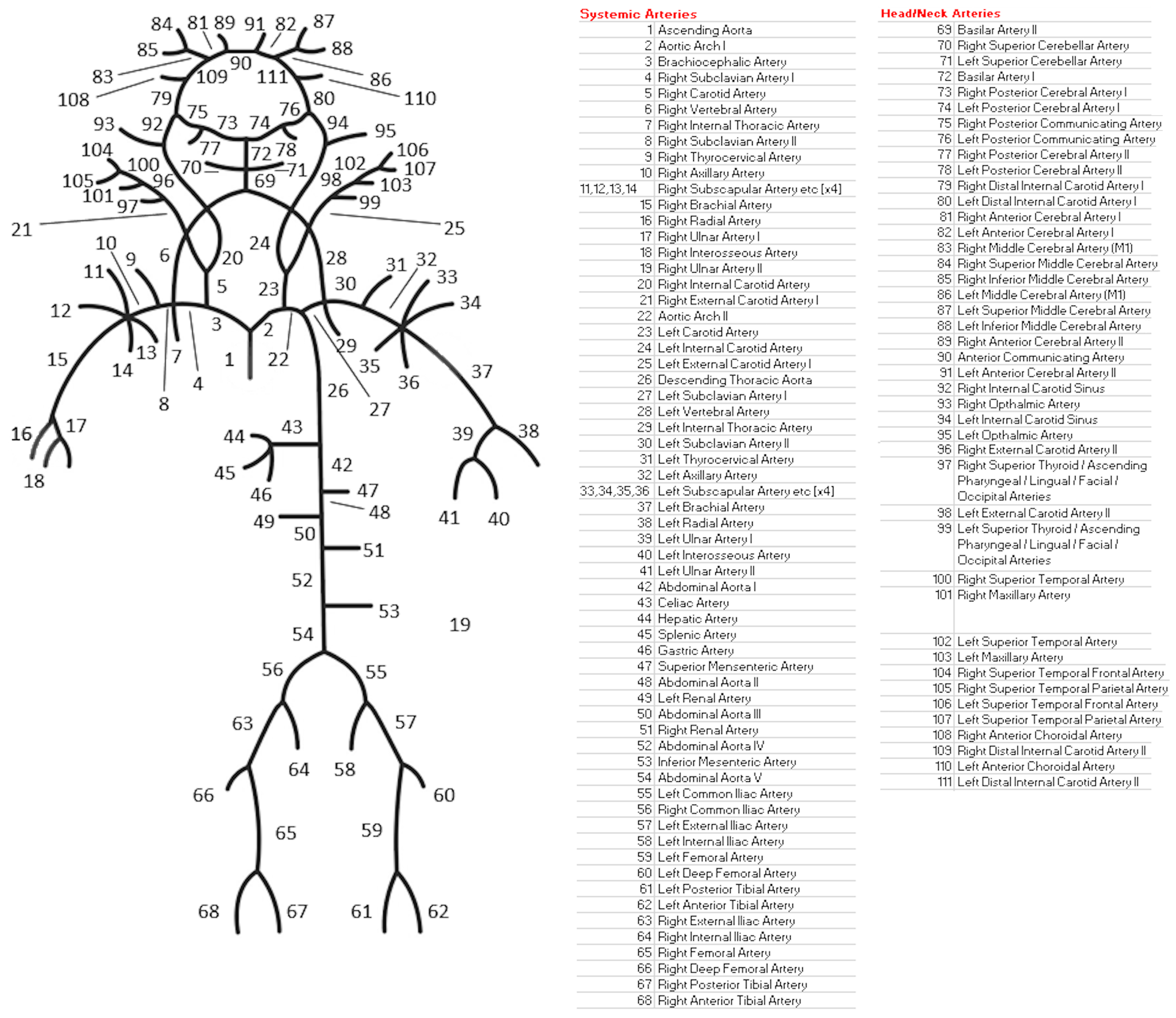
2.3. One-Dimensional 111-Artery CFD Model (1D CFD)
2.4. Four-Dimensional Left Ventricular CFD Model (3D CFD)
2.5. Pressure–Volume Loops Analysis
2.6. Variability
2.7. Statistical Analysis
3. Results
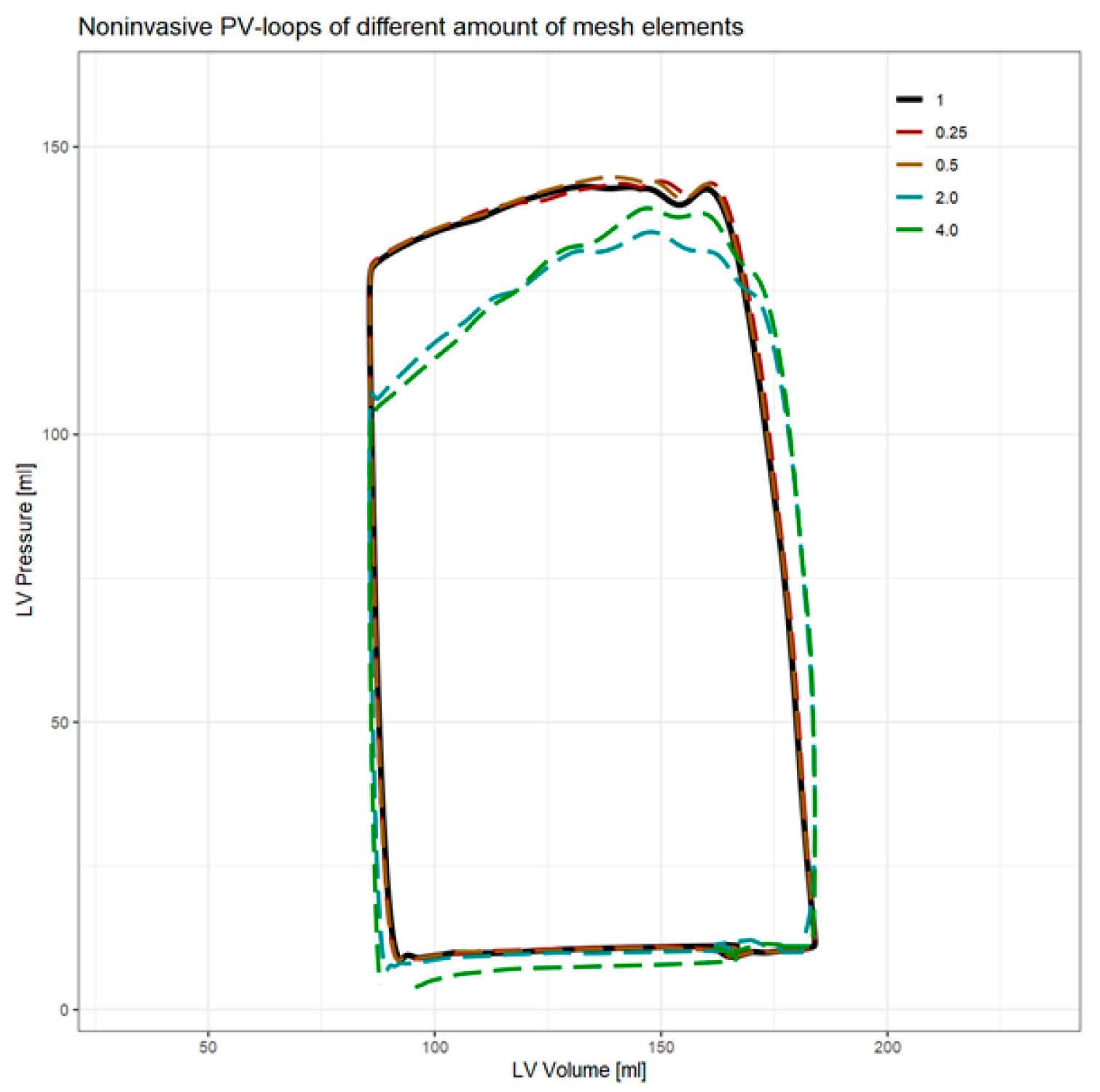
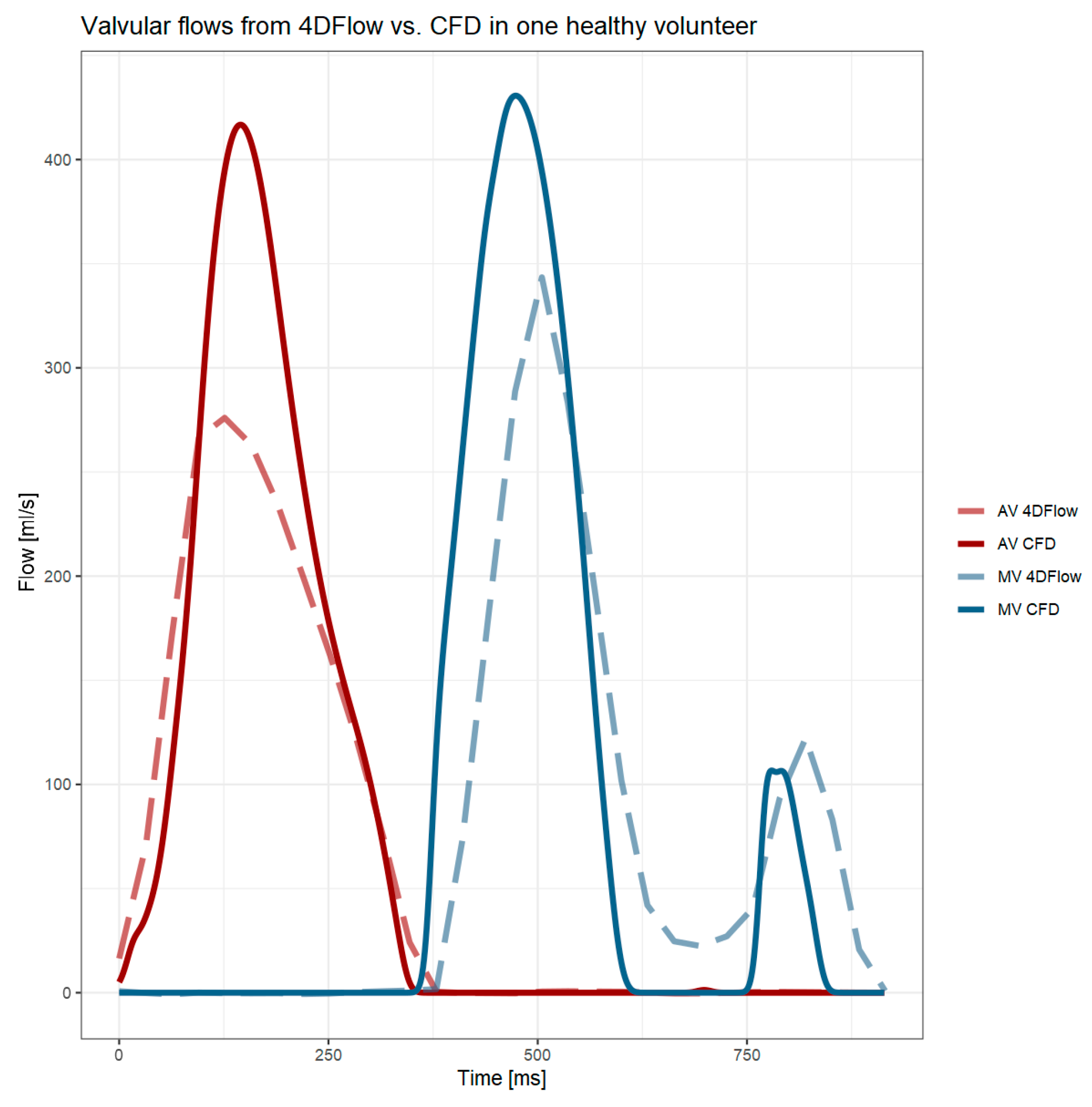
3.1. Computational Fluid Dynamics
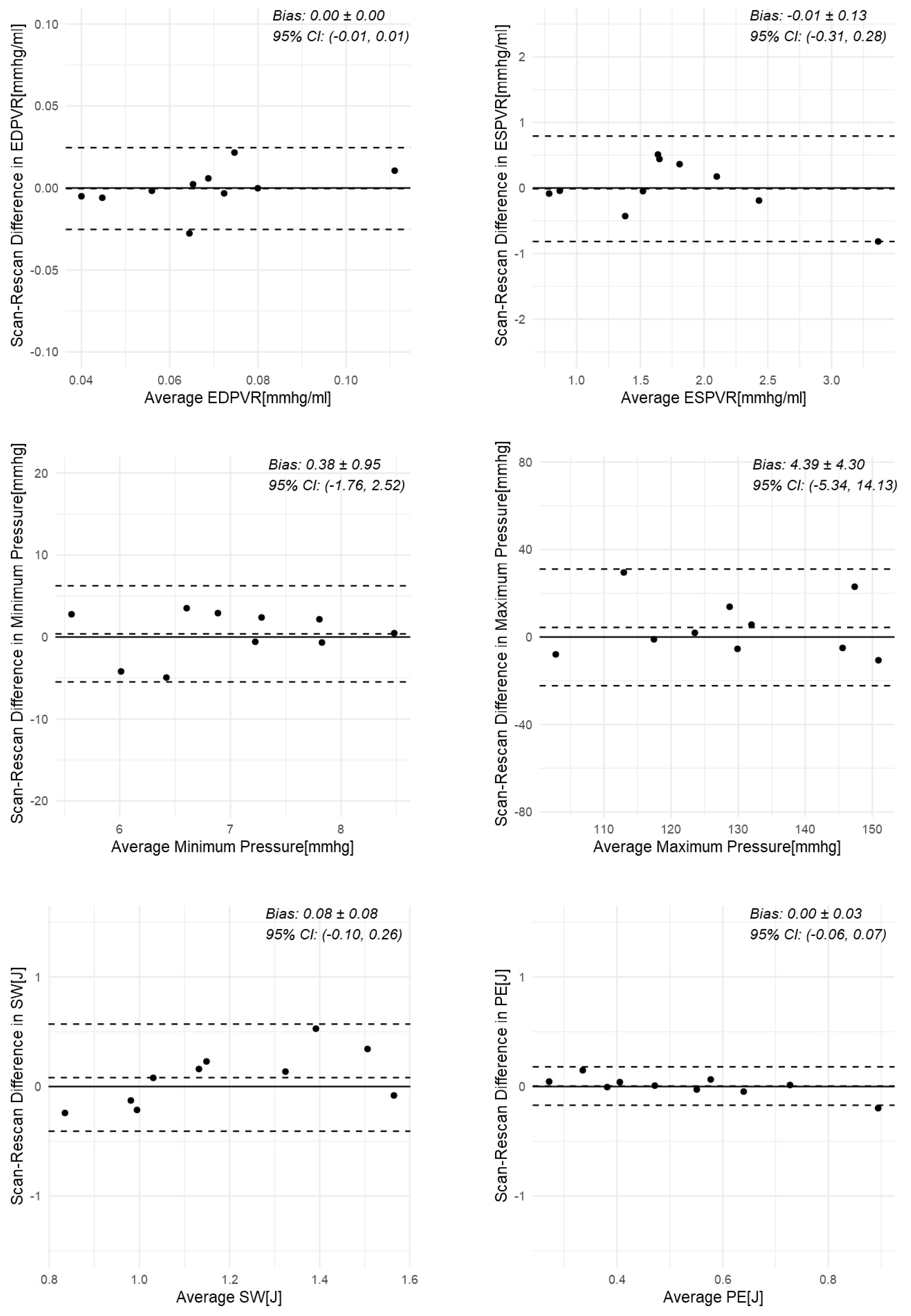
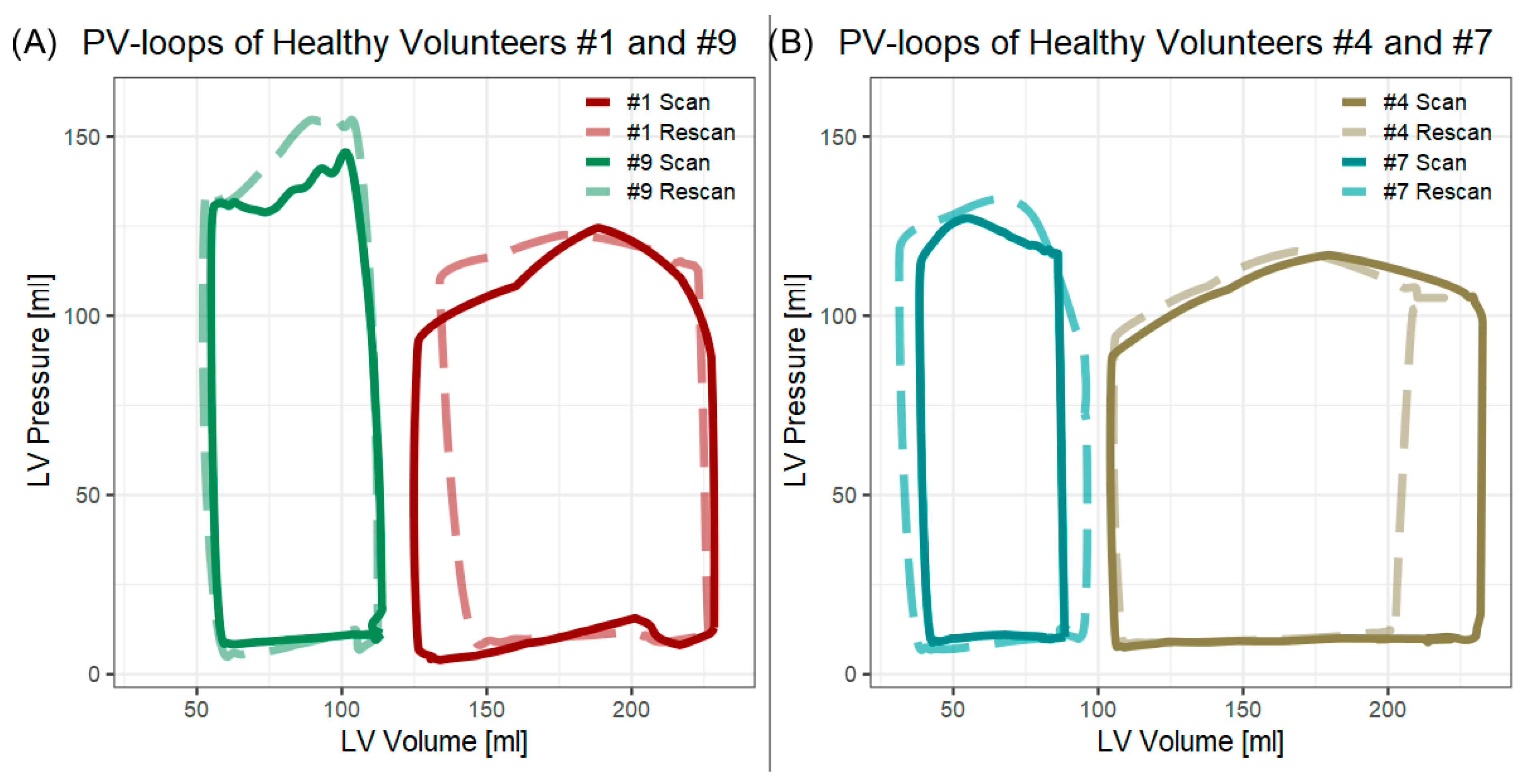
3.2. Scan–Rescan in Healthy Volunteers
3.3. Variability in Healthy Volunteer
3.4. Initial Patient Single-Case Comparison Results
4. Discussion
4.1. Scan Rescan
4.2. Valvular Flows
4.3. Variability
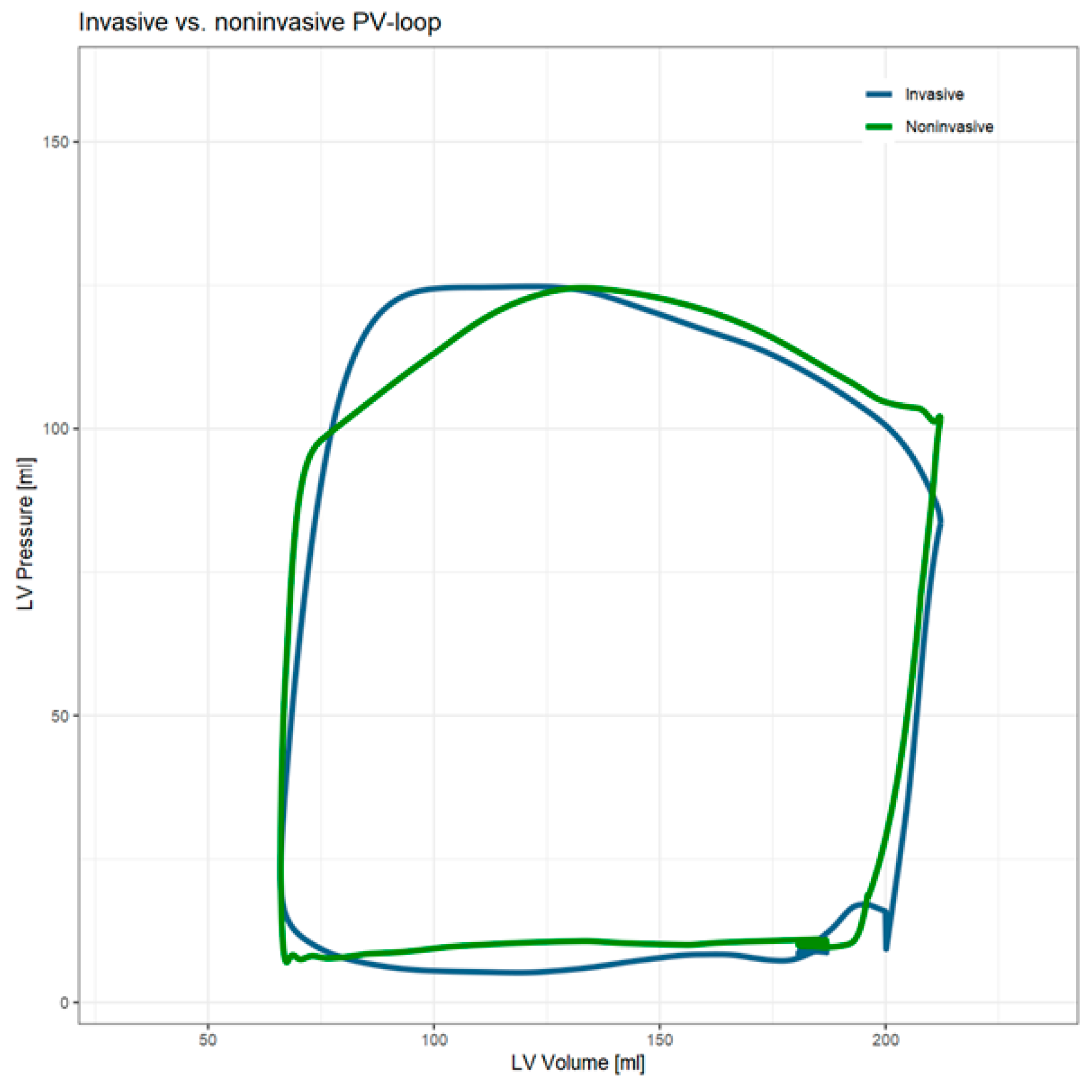
4.4. Initial Single-Case Comparison
4.5. Noninvasive PV Loop Method
4.6. Limitations
4.7. Future Developments
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 1D | One-dimensional |
| 2Ch | Two chamber |
| 4Ch | Four chamber |
| 4D | Four-dimensional |
| CFD | Computational fluid dynamics |
| EDPVR | End-diastolic pressure–volume relationship |
| ESPVR | End-systolic pressure–volume relationship |
| ICC | Intraclass correlation coefficient |
| KE | Kinetic energy |
| LV | Left ventricle/left ventricular |
| MR | Magnetic resonance |
| MRI | Magnetic resonance imaging |
| PE | Potential energy |
| PV | Pressure volume |
| SAx | Short axis |
| SW | Stroke work |
Appendix A
| Parameter | Value |
|---|---|
| Mesh elements | ~150,000 |
| Model | K-ω turbulence model |
| Solver | Pressure-based |
| Pressure-velocity coupling | SIMPLE |
| Spatial discretization | |
| - Gradient | Least Squares Cell-based |
| - Pressure | Second order |
| - Momentum | Second-order upwind |
| Residuals | <1 × 10−4 |
| Boundary conditions | 2 |
| - Input | 1330 mmHg |
| - Output | Peak systole aortic pressure + 5 mmHg |
| - Prevent reverse flow | Yes |
| Iterations | |
| - Steady-state | Unlimited (~4000) |
| - Transient | 100 |
| Timestep | 1 ms |
| Dynamic mesh | |
| - Mesh deformation | User-defined Function |
| - Remeshing interval | 1 step |
| - Max smoothing iterations | 250 |
| - Edge length | >0.001 and <0.005 |
| - Cell skew | <0.7 |
| - Face skew | <0.7 |
| # Elements | Computation Time | Converged Timesteps | Min. P [mmHg] | Max. P [mmHg] | EDPVR [mmHg/mL] | ESPVR [mmHg/mL] | SW [J] | PE [J] | PVA [J] | VE | MEP [J/s] | EEV [J/L] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.25 | −58.7% | 6.9% | −0.2% | 0.7% | 1.1% | 0.6% | 1.1% | 0.4% | 0.9% | 0.2% | 1.1% | 0.9% |
| 0.5 | −16.9% | 3.7% | −2.2% | 1.2% | 1.3% | 0.2% | 0.9% | 0.2% | 0.7% | 0.2% | 0.9% | 0.7% |
| 1 | - | - | - | - | - | - | - | - | - | - | - | - |
| 2 | 15.3% | −9.2% | −21.1% | −5.5% | 9.8% | −16.9% | −4.7% | −17.1% | −8.8% | 4.4% | −4.7% | −8.8% |
| 4 | 58.4% | −9.4% | −107.5% | −2.6% | 8.1% | −19.8% | −1.1% | −18.7% | −6.7% | 6.2% | −1.1% | −6.9% |
References
- Roth, G.A.; Mensah, G.A.; Johnson, C.O.; Addolorato, G.; Ammirati, E.; Baddour, L.M.; Barengo, N.C.; Beaton, A.Z.; Benjamin, E.J.; Benziger, C.P.; et al. Global Burden of Cardiovascular Diseases and Risk Factors, 1990–2019. J. Am. Coll. Cardiol. 2020, 76, 2982–3021. [Google Scholar] [CrossRef] [PubMed]
- Borlaug, B.A.; Kass, D.A. Invasive Hemodynamic Assessment in Heart Failure. Heart Fail. Clin. 2009, 5, 217–228. [Google Scholar] [CrossRef] [PubMed]
- Burkhoff, D.; Mirsky, I.; Suga, H. Assessment of systolic and diastolic ventricular properties via pressure-volume analysis: A guide for clinical, translational, and basic researchers. Am. J. Physiol. Heart Circ. Physiol. 2005, 289, H501–H512. [Google Scholar] [CrossRef] [PubMed]
- Stonko, D.P.; Edwards, J.; Abdou, H.; Elansary, N.N.; Lang, E.; Savidge, S.G.; Morrison, J.J. A technical and data analytic approach to pressure-volume loops over numerous cardiac cycles. JVS Vasc. Sci. 2022, 3, 73–84. [Google Scholar] [CrossRef]
- Bissell, M.M.; Raimondi, F.; Ait Ali, L.; Allen, B.D.; Barker, A.J.; Bolger, A.; Burris, N.; Carhäll, C.-J.; Collins, J.D.; Ebbers, T.; et al. 4D Flow cardiovascular magnetic resonance consensus statement: 2023 update. J. Cardiovasc. Magn. Reson. 2023, 25, 40. [Google Scholar] [CrossRef]
- Demirkiran, A.; van Ooij, P.; Westenberg, J.J.M.; Hofman, M.B.M.; van Assen, H.C.; Schoonmade, L.J.; Asim, U.; Blanken, C.P.S.; Nederveen, A.J.; van Rossum, A.C.; et al. Clinical intra-cardiac 4D flow CMR: Acquisition, analysis, and clinical applications. Eur. Heart J. Cardiovasc. Imaging 2022, 23, 154–165. [Google Scholar] [CrossRef]
- Maroun, A.; Quinn, S.; Dushfunian, D.; Weiss, E.K.; Allen, B.D.; Carr, J.C.; Markl, M. Clinical Applications of Four-Dimensional Flow MRI. Magn. Reson. Imaging Clin. N. Am. 2023, 31, 451–460. [Google Scholar] [CrossRef]
- Eerdekens, R.; Tonino, P.; Zelis, J.; Adrichem, R.; Ahn, J.M.; Demandt, J.; Eftekhari, A.; El Farissi, M.; Freeman, P.; Rahman Ihdayhid, A.; et al. Rationale and design of SAVI-AoS: A physiologic study of patients with symptomatic moderate aortic valve stenosis and preserved left ventricular ejection fraction. Int. J. Cardiol. Heart Vasc. 2022, 41, 101063. [Google Scholar] [CrossRef]
- Antiga, L.; Piccinelli, M.; Botti, L.; Ene-Iordache, B.; Remuzzi, A.; Steinman, D.A. An image-based modeling framework for patient-specific computational hemodynamics. Med. Biol. Eng. Comput. 2008, 46, 1097–1112. [Google Scholar] [CrossRef]
- Kamphuis, V.P.; Roest, A.A.W.; Ajmone Marsan, N.; van den Boogaard, P.J.; Kroft, L.J.M.; Aben, J.P.; Bax, J.J.; de Roos, A.; Lamb, H.J.; Westenberg, J.J.M. Automated Cardiac Valve Tracking for Flow Quantification with Four-dimensional Flow MRI. Radiology 2019, 290, 70–78. [Google Scholar] [CrossRef]
- Childs, H.; Ma, L.; Ma, M.; Clarke, J.; Cocker, M.; Green, J.; Strohm, O.; Friedrich, M.G. Comparison of long and short axis quantification of left ventricular volume parameters by cardiovascular magnetic resonance, with ex-vivo validation. J. Cardiovasc. Magn. Reson. 2011, 13, 40. [Google Scholar] [CrossRef] [PubMed]
- Forbat, S.M.; Sakrana, M.A.; Darasz, K.H.; El-Demerdash, F.; Underwood, S.R. Rapid assessment of left ventricular volume by short axis cine MRI. Br. J. Radiol. 1996, 69, 221–225. [Google Scholar] [CrossRef] [PubMed]
- Breall, W.S.; Shaffer, A.B. Effect of Heart Irregularity on Left Ventricular and Arterial Peak Systolic Pressures in Aortic Stenosis. Circulation 1959, 20, 1049–1052. [Google Scholar] [CrossRef]
- Xu, F.; Kenjeres, S. Numerical simulations of flow patterns in the human left ventricle model with a novel dynamic mesh morphing approach based on radial basis function. Comput. Biol. Med. 2021, 130, 104184. [Google Scholar] [CrossRef]
- Tezzele, M.; Demo, N.; Mola, A.; Rozza, G. PyGeM: Python Geometrical Morphing. Softw. Impacts 2021, 7, 100047. [Google Scholar] [CrossRef]
- Sieger, D.; Menzel, S.; Botsch, M. RBF morphing techniques for simulation-based design optimization. Eng. Comput. 2014, 30, 161–174. [Google Scholar] [CrossRef]
- Perinajová, R.; Van De Ven, T.; Roelse, E.; Xu, F.; Juffermans, J.; Westenberg, J.; Lamb, H.; Kenjereš, S. A comprehensive MRI-based computational model of blood flow in compliant aorta using radial basis function interpolation. Biomed. Eng. OnLine 2024, 23, 69. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Sagawa, K. The end-systolic pressure-volume relation of the ventricle: Definition, modifications and clinical use. Circulation 1981, 63, 1223–1227. [Google Scholar] [CrossRef]
- Stevenson, D.; Revie, J.; Chase, J.G.; Hann, C.E.; Shaw, G.M.; Lambermont, B.; Ghuysen, A.; Kolh, P.; Desaive, T. Beat-to-beat estimation of the continuous left and right cardiac elastance from metrics commonly available in clinical settings. Biomed. Eng. OnLine 2012, 11, 73. [Google Scholar] [CrossRef]
- Suga, H. Ventricular energetics. Physiol. Rev. 1990, 70, 247–277. [Google Scholar] [CrossRef]
- Seemann, F.; Arvidsson, P.; Nordlund, D.; Kopic, S.; Carlsson, M.; Arheden, H.; Heiberg, E. Noninvasive Quantification of Pressure-Volume Loops From Brachial Pressure and Cardiovascular Magnetic Resonance. Circ. Cardiovasc. Imaging 2019, 12, e008493. [Google Scholar] [CrossRef]
- Moody, W.E.; Edwards, N.C.; Chue, C.D.; Taylor, R.J.; Ferro, C.J.; Townend, J.N.; Steeds, R.P. Variability in cardiac MR measurement of left ventricular ejection fraction, volumes and mass in healthy adults: Defining a significant change at 1 year. Br. J. Radiol. 2015, 88, 20140831. [Google Scholar] [CrossRef] [PubMed]
- Sakuma, H.; Globits, S.; Bourne, M.W.; Shimakawa, A.; Foo, T.K.; Higgins, C.B. Improved reproducibility in measuring LV volumes and mass using multicoil breath-hold cine MR imaging. J. Magn. Reson. Imaging 1996, 6, 124–127. [Google Scholar] [CrossRef] [PubMed]
- RStudio Team. RStudio: Integrated Development Environment for R; Rstudio PBC: Boston, MA, USA, 2020. [Google Scholar]
- The R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- Morris, P.D.; Narracott, A.; Von Tengg-Kobligk, H.; Silva Soto, D.A.; Hsiao, S.; Lungu, A.; Evans, P.; Bressloff, N.W.; Lawford, P.V.; Hose, D.R.; et al. Computational fluid dynamics modelling in cardiovascular medicine. Heart 2016, 102, 18–28. [Google Scholar] [CrossRef] [PubMed]
- Kamphuis, V.P.; van der Palen, R.L.F.; de Koning, P.J.H.; Elbaz, M.S.M.; van der Geest, R.J.; de Roos, A.; Roest, A.A.W.; Westenberg, J.J.M. In-scan and scan–rescan assessment of LV in- and outflow volumes by 4D flow MRI versus 2D planimetry. J. Magn. Reson. Imaging 2018, 47, 511–522. [Google Scholar] [CrossRef]
- Bartoli, A.; Fournel, J.; Bentatou, Z.; Habib, G.; Lalande, A.; Bernard, M.; Boussel, L.; Pontana, F.; Dacher, J.N.; Ghattas, B.; et al. Deep Learning-based Automated Segmentation of Left Ventricular Trabeculations and Myocardium on Cardiac MR Images: A Feasibility Study. Radiol. Artif. Intell. 2021, 3, e200021. [Google Scholar] [CrossRef]
- Arvidsson, P.M.; Green, P.G.; Watson, W.D.; Shanmuganathan, M.; Heiberg, E.; De Maria, G.L.; Arheden, H.; Herring, N.; Rider, O.J. Non-invasive left ventricular pressure-volume loops from cardiovascular magnetic resonance imaging and brachial blood pressure: Validation using pressure catheter measurements. Eur. Heart J. Imaging Methods Pract. 2023, 1, qyad035. [Google Scholar] [CrossRef]
- Edlund, J.; Arvidsson, P.M.; Nelsson, A.; Smith, J.G.; Magnusson, M.; Heiberg, E.; Steding-Ehrenborg, K.; Arheden, H. Noninvasive Assessment of Left Ventricular Pressure-Volume Relations: Inter- and Intraobserver Variability and Assessment Across Heart Failure Subtypes. Am. J. Cardiol. 2022, 184, 48–55. [Google Scholar] [CrossRef]
- Markl, M.; Schnell, S.; Barker, A.J. 4D Flow Imaging: Current Status to Future Clinical Applications. Curr. Cardiol. Rep. 2014, 16, 481. [Google Scholar] [CrossRef]
- Sherwin, S.J.; Formaggia, L.; Peiró, J.; Franke, V. Computational modelling of 1D blood flow with variable mechanical properties and its application to the simulation of wave propagation in the human arterial system. Int. J. Numer. Methods Fluids 2003, 43, 673–700. [Google Scholar] [CrossRef]
- Olufsen, M.S. Structured tree outflow condition for blood flow in larger systemic arteries. Am. J. Physiol. 1999, 276, H257–H268. [Google Scholar] [CrossRef]
- Mynard, J.P.; Smolich, J.J. One-Dimensional Haemodynamic Modeling and Wave Dynamics in the Entire Adult Circulation. Ann. Biomed. Eng. 2015, 43, 1443–1460. [Google Scholar] [CrossRef]


| Cine 2ch/4ch/Ao | Cine Short-Axis | 4D Flow | |
|---|---|---|---|
| Scan time (approximately) | 10 s | 12 × 5 s | 15 min |
| FoV [mm3] | 350 × 350 × 8.0 | 350 × 350 × 104 * | 370 × 395 × 104 * |
| Acquired resolution [mm3] | 2.0 × 1.6 × 8.0 | 1.5 × 1.5 × 8.0 | 3.5 × 3.5 × 3.5 |
| Reconstructed resolution [mm3] | 1.0 × 1.0 × 8.0 | 0.73 × 0.73 × 8.0 | 2.0 × 2.0 × 1.75 |
| Temporal resolution | 46.8 ms | 48.0 ms | 40.8 ms |
| Slice gap [mm] | 0 | 0 | −1.5 |
| TR [ms] | 2.6 | 3.0 | 5.1 |
| TE [ms] | 1.3 | 1.5 | 3.0 |
| Flip Angle [°] | 45 | 45 | 5 |
| Sense factor | 2 | 2.5 | 3/1.4 |
| Segmentation factor | 17–18 | 16 | 2 |
| Respiratory compensation | Breath-hold | 1 Breath-hold per slice | Navigator gating |
| Cardiac phases ** | 30 | 30 | 30 |
| Venc [cm/s] | - | - | 200 |
| Participant | Scan | ESV [mL] | EDV [mL] | Min. P [mmHg] | Max. P [mmHg] | EDPVR [mmHg/mL] | ESPVR [mmHg/mL] | SW [J] | PE [J] | PVA [J] | VE | MEP [J/s] | EEV [J/L] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | #1 | 125 | 228 | 3.9 | 124.5 | 0.04 | 0.74 | 1.39 | 0.80 | 2.19 | 0.64 | 1.99 | 21.1 |
| #2 | 134 | 227 | 8.1 | 122.6 | 0.04 | 0.83 | 1.26 | 0.99 | 2.25 | 0.56 | 1.64 | 24.1 | |
| 2 | #1 | 54 | 138 | 8.5 | 135.6 | 0.07 | 2.19 | 1.21 | 0.43 | 1.64 | 0.74 | 1.41 | 19.5 |
| #2 | 53 | 135 | 6.1 | 121.8 | 0.07 | 2.01 | 1.05 | 0.39 | 1.44 | 0.73 | 1.16 | 17.7 | |
| 3 | #1 | 70 | 136 | 7.0 | 158.9 | 0.07 | 1.87 | 1.07 | 0.61 | 1.68 | 0.64 | 1.55 | 25.4 |
| #2 | 75 | 143 | 4.2 | 135.9 | 0.07 | 1.43 | 0.99 | 0.54 | 1.54 | 0.65 | 1.31 | 22.8 | |
| 4 | #1 | 104 | 233 | 7.5 | 116.9 | 0.04 | 0.85 | 1.68 | 0.62 | 2.29 | 0.73 | 1.58 | 17.9 |
| #2 | 105 | 219 | 8.2 | 118.0 | 0.05 | 0.89 | 1.33 | 0.66 | 2.00 | 0.67 | 1.22 | 17.5 | |
| 5 | #1 | 55 | 151 | 8.3 | 127.7 | 0.08 | 1.99 | 1.26 | 0.41 | 1.67 | 0.76 | 1.56 | 17.5 |
| #2 | 48 | 148 | 5.4 | 98.2 | 0.08 | 1.63 | 1.03 | 0.26 | 1.30 | 0.80 | 1.26 | 12.9 | |
| 6 | #1 | 86 | 184 | 8.7 | 143.1 | 0.06 | 1.50 | 1.52 | 0.73 | 2.26 | 0.67 | 1.70 | 23.0 |
| #2 | 84 | 190 | 8.2 | 148.1 | 0.06 | 1.54 | 1.61 | 0.72 | 2.33 | 0.69 | 1.76 | 21.9 | |
| 7 | #1 | 38 | 88 | 8.9 | 127.2 | 0.12 | 2.96 | 0.71 | 0.29 | 1.01 | 0.71 | 0.81 | 20.1 |
| #2 | 31 | 96 | 6.7 | 132.6 | 0.11 | 3.77 | 0.96 | 0.25 | 1.20 | 0.79 | 1.06 | 18.6 | |
| 8 | #1 | 69 | 153 | 6.9 | 98.8 | 0.07 | 1.17 | 0.89 | 0.38 | 1.27 | 0.70 | 0.86 | 15.2 |
| #2 | 59 | 158 | 7.5 | 106.8 | 0.06 | 1.60 | 1.10 | 0.38 | 1.49 | 0.74 | 1.07 | 15.1 | |
| 9 | #1 | 55 | 114 | 8.4 | 145.6 | 0.09 | 2.33 | 0.92 | 0.48 | 1.39 | 0.66 | 1.39 | 23.6 |
| #2 | 52 | 114 | 4.8 | 156.2 | 0.06 | 2.53 | 1.04 | 0.47 | 1.51 | 0.69 | 1.44 | 24.5 | |
| 10 | #1 | 65 | 170 | 4.0 | 134.8 | 0.05 | 1.89 | 1.66 | 0.54 | 2.19 | 0.75 | 1.66 | 20.9 |
| #2 | 69 | 156 | 8.9 | 129.2 | 0.08 | 1.38 | 1.13 | 0.56 | 1.69 | 0.67 | 1.06 | 19.5 | |
| Mean diff. (SD) | 1 (6) | 1 (8) | 0.4 | 4.4 | 0.00 | −0.01 | 0.08 | 0.00 | 0.09 | 0.00 | 0.15 | 0.9 | |
| t-test p-value | 0.62 | 0.71 | 0.69 | 0.33 | 0.93 | 0.93 | 0.33 | 0.87 | 0.31 | 0.95 | 0.12 | 0.18 | |
| ICC | 0.98 * | 0.99 * | −0.54 | 0.68 * | 0.83 * | 0.87 * | 0.59 * | 0.91 * | 0.82 * | 0.57 * | 0.55 * | 0.81 * |
| Variation | ESV [mL] | EDV [mL] | Min. P [mmHg] | Max. P [mmHg] | EDPVR [mmHg/mL] | ESPVR [mmHg/mL] | SW [J] | PE [J] | PVA [J] | VE | MEP [J/s] | EEV [J/L] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Segmentation | ||||||||||||
| Smaller (−7%) | 80 | 171 | 7.8 | 144.3 | 0.06 | 1.66 | 1.19 | 0.70 | 1.89 | 0.63 | 1.33 | 20.7 |
| Normal | 86 | 184 | 8.7 | 143.1 | 0.06 | 1.50 | 1.52 | 0.73 | 2.26 | 0.67 | 1.70 | 23.0 |
| Bigger (+7%) | 92 | 197 | 7.4 | 145.3 | 0.06 | 1.44 | 1.48 | 0.80 | 2.28 | 0.65 | 1.65 | 21.7 |
| Mean | 86 | 184 | 8.0 | 144.2 | 0.06 | 1.53 | 1.40 | 0.75 | 2.15 | 0.65 | 1.56 | 21.8 |
| Std | 6 | 13 | 0.7 | 1.1 | 0.00 | 0.12 | 0.18 | 0.05 | 0.22 | 0.02 | 0.20 | 1.1 |
| Rel. Std | 7% | 7% | 8% | 1% | 6% | 8% | 12% | 7% | 10% | 3% | 12% | 5% |
| Flow | ||||||||||||
| Lower (−9.8%) | 86 | 184 | 8.4 | 131.2 | 0.06 | 1.34 | 1.41 | 0.66 | 2.07 | 0.68 | 1.57 | 21.0 |
| Normal | 86 | 184 | 8.7 | 143.1 | 0.06 | 1.50 | 1.52 | 0.73 | 2.26 | 0.67 | 1.70 | 23.0 |
| Higher (+9.8%) | 86 | 184 | 8.5 | 159.5 | 0.06 | 1.68 | 1.73 | 0.82 | 2.56 | 0.68 | 1.93 | 26.0 |
| Mean | 86 | 184 | 8.6 | 144.6 | 0.06 | 1.50 | 1.55 | 0.74 | 2.29 | 0.68 | 1.74 | 23.3 |
| Std | 0 | 0 | 0.1 | 14.2 | 0.00 | 0.17 | 0.17 | 0.08 | 0.25 | 0.00 | 0.18 | 2.5 |
| Rel. Std | 0% | 0% | 2% | 10% | 0% | 11% | 11% | 11% | 11% | 0% | 11% | 11% |
| Variation | ESV [mL] | EDV [mL] | Min. P [mmHg] | Max. P [mmHg] | EDPVR [mmHg/mL] | ESPVR [mmHg/mL] | SW [J] | PE [J] | PVA [J] | VE | MEP [J/s] | EEV [J/L] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Invasive | 66 | 212 | 5.2 | 124.8 | 0.047 | 1.368 | 1.96 | 0.51 | 2.47 | 0.79 | 1.62 | 16.9 |
| Noninvasive | 66 | 212 | 7.0 | 124.6 | 0.051 | 1.315 | 1.91 | 0.47 | 2.38 | 0.80 | 1.58 | 16.3 |
| Difference | - | - | 1.8 | −0.2 | 0.005 | −0.053 | −0.05 | −0.04 | −0.09 | 0.01 | −0.04 | −0.6 |
| Rel. difference | - | - | 35% | 0% | 10% | −4% | −3% | −8% | −4% | 1% | −3% | −4% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roos, P.R.; Thijs, J.J.; in de Braekt, T.; Eerdekens, R.; Houthuizen, P.; Tonino, P.A.L.; van den Bosch, H.C.M.; Hamel, D.; Vuik, C.; Kenjeres, S.; et al. Noninvasive Left Ventricular Pressure–Volume Loops Based on Combined 4D Flow MRI and CFD. Appl. Sci. 2025, 15, 12305. https://doi.org/10.3390/app152212305
Roos PR, Thijs JJ, in de Braekt T, Eerdekens R, Houthuizen P, Tonino PAL, van den Bosch HCM, Hamel D, Vuik C, Kenjeres S, et al. Noninvasive Left Ventricular Pressure–Volume Loops Based on Combined 4D Flow MRI and CFD. Applied Sciences. 2025; 15(22):12305. https://doi.org/10.3390/app152212305
Chicago/Turabian StyleRoos, Paul R., Jonathan J. Thijs, Thomas in de Braekt, Rob Eerdekens, Patrick Houthuizen, Pim A. L. Tonino, Harrie C. M. van den Bosch, David Hamel, Cornelis Vuik, Sasa Kenjeres, and et al. 2025. "Noninvasive Left Ventricular Pressure–Volume Loops Based on Combined 4D Flow MRI and CFD" Applied Sciences 15, no. 22: 12305. https://doi.org/10.3390/app152212305
APA StyleRoos, P. R., Thijs, J. J., in de Braekt, T., Eerdekens, R., Houthuizen, P., Tonino, P. A. L., van den Bosch, H. C. M., Hamel, D., Vuik, C., Kenjeres, S., Westenberg, J. J. M., & Lamb, H. J. (2025). Noninvasive Left Ventricular Pressure–Volume Loops Based on Combined 4D Flow MRI and CFD. Applied Sciences, 15(22), 12305. https://doi.org/10.3390/app152212305





