GNSS for High-Precision and Reliable Positioning: A Review of Correction Techniques and System Architectures
Abstract
1. Introduction
- INS/GNSS integration with visual data for sky segmentation and determining which satellites are actually in the line of sight (LOS), and which are most likely in the NLOS zone [31].
2. GNSS Accuracy Factors and Techniques of Accuracy Improvement
2.1. Ionospheric Effects and Their Correction
| Correction Method for Absolute Positioning | Example Model/Product | Description/Principle | Accuracy |
| Broadcast ionospheric model [24,64,71] | Klobuchar (GPS), NeQuick-G (Galileo) | Empirical model broadcast in the navigation message; corrects ~50–70% of the ionospheric delay | Horizontal 5–7 m, vertical 8–12 m [24]; 7.7 m (winter)/9.8 m (summer) (single freq L1); 5.6 m (winter)/7.6 m (summer) (dual-freq L1/L2) [64] |
| Global ionospheric maps (GIM) [65] | IGS, CODE, ESA GIM | Data-driven global TEC maps updated every 15 min; applied for PPP and SBAS corrections | , , [65] |
| DMD-enhanced GIM forecast [65] | Dynamic Mode Decomposition | Supplementing ionospheric forecasts based on CODE products with RMS statistics | , , [65] |
| Use of ML [66] | ML (ANN, RF, LSTM) models | Improvement of ionospheric GIMs | Horizontal ~1–2 m, vertical ~2–3 m [66] |
| Regional interpolation models (PPP-RTK) [26,69] | BLUP, Kriging | Interpolate ionospheric delays from CORS stations | <10 cm at a distance of 237 km between stations; ≈1.3–3.2 cm at a distance of 500 km between stations [69] |
| Multi-frequency PPP (ionosphere-free IF) [70] | Dual-frequency L1/L2 PPP | Linear combination removes first-order ionospheric delay | ~2 cm horizontally, ~3.5 cm vertically [70] |
| Correction Method for Relative Positioning | Example Model/Product | Description/Principle | Accuracy |
| Ionosphere-weighted network RTK [68] | VRS/MAC networks | Double-difference approach with network-wide corrections | Horizontal 1–2 cm, vertical 2–3 cm in calm atmosphere; vertical 5–7 cm in disturbed atmosphere [68] |
2.2. Orbit and Clock Errors and Their Correction
| Correction Method for Absolute Positioning | Example Model/Product | Description/Principle | Accuracy |
| Broadcast ephemerides and clock data [71,72] | GPS LNAV, Galileo FNAV, BDS CNAV | Parameters transmitted in navigation message; updated periodically for SPP/PPP users | ~3–5 m horizontally and ~5–10 m vertically [71], 1–3 m [72] |
| Post-processed precise products [73,74] | IGS Final | Derived from global tracking networks | Within <1 m or <10 cm [73,74] |
| Rapid/Ultra-rapid IGS products [75] | IGS Rapid | Near-real-time solutions for low-latency PPP applications | 3–5 cm horizontally and 5–10 cm vertically [75] |
| Real-Time Service [76] | IGS services + linear clock model | Real-time corrections for PPP solutions | (E) ~1.9 cm, (N) ~2.4 cm, (U) ~4.9 cm in kinematic mode [76] |
| Multi-frequency PPP [77] | Uncombined Decoupled Clock Model (UDCM) for four systems and four frequencies for PPP | Real-time corrections for PPP solutions | <2.5 cm [77] |
| SSR corrections for PPP-RTK [79] | IGS RTS | Real-time State Space Representation corrections for PPP-RTK. | ~2–4 cm horizontally, ~5–8 cm vertically in kinematic mode [79] |
| Correction Method for Relative Positioning | Example Model/Product | Description/Principle | Accuracy |
| RTK/Network RTK with orbit and clock corrections [78] | VRS, MAC | Double-differencing cancels satellite clock and ephemeris errors; network models extend precision to longer baselines | Horizontal accuracy < 2.5 cm; vertical accuracy < 5 cm [78] |
2.3. Multipath Effects and Their Mitigation
| Correction Method for Absolute Positioning | Example Model/Product | Description/Principle | Accuracy |
| Antenna design [84,85,86] | Multipath-resistant GNSS antenna, ground plane, choke-ring structure | Reduces reflections from the ground and nearby objects by suppressing low-elevation signals | - |
| Correlator optimization [87] | Multi-correlator structure | Creation a high-resolution “snapshot” of the signal’s full autocorrelation function | 0.5–1 m [87] |
| RAIM, ARAIM [80,81,82] | Integrity monitoring | Detects faulty or multipath-affected satellites via consistency tests and exclusion | 4–10 m vertically, 30 m horizontally [80], 13–17 m horizontally [81], horizontal 7.7 m in static mode and 4.7 m in kinematic mode [82] |
| Clustering of satellite measurements [83] | Cluster-based weighting | Groups satellites with similar error signatures to reduce multipath correlation in position estimation | 2.4 m [83] |
| Adaptive filtering [88] | Elevation- and C/N0-dependent weighting of measurements | Dynamically updates observation weights based on signal strength and multipath indices | 22 m [88] |
| Machine learning (ML) classification [27,89,96,101,108] | SVM, CNN, LSTM trained on C/N0, residuals, elevation | Classifies LOS/NLOS signals and dynamically suppresses reflected measurements | 2.5 m horizontally, 3.3 m vertically [89], 1.6 mm (E), 1.9 mm (N), 4.5 mm (U) [101] |
| Model-based multipath detection for PPP [93,95] | Siderial Filtering, Multipath Hemispherical Map (MHM) | Exploits satellite geometry periodicity to detect/filter repeating multipath patterns | 2.1 mm (N), 1.7 mm (E), 4.4 (U) [93], 1.7 mm (E), 2.0 mm (N), 4.0 mm (U) [95] |
| Integration with other sensors [91,98,109] | EKF [109], FGO-based GNSS/INS fusion [91] | Detects reflective surfaces; filters inconsistent pseudorange residuals | 2.8 m [91], 0.055 m (E), 0.048 m (N), 0.037 m (U) [109], 1.41 m (E), 1.25 (N), 1.70 (U) [98] |
| Multi-frequency PPP [97] | Overlap frequency | Uses redundant multi-frequency carrier signals to decorrelate multipath and improve ambiguity fixing | 0.34 cm (East), 0.46 cm (North), 0.81 cm (Up) [97] |
| Robust filters [107] | Robust adaptive Kalman filter for PPP-RTK | Filters inconsistent pseudorange residuals | ~1 mm horizontally and ~2 mm vertically [107] |
| Correction Method for Relative Positioning | Example Model/Product | Description/Principle | Accuracy |
| Adaptive filtering [99] | Elevation- and C/N0-dependent weighting of measurements | Dynamically updates observation weights based on signal strength and multipath indices | 2.8 m [99] |
| RAIM [102] | MS-CRAIM | Detects faulty or multipath-affected satellites via consistency tests and exclusion | Horizontally 2.8 mm; vertically 4.7 mm [102] |
| Robust filters [104] | RIF, GM-KF, V-KF | Filters inconsistent pseudorange residuals | 10–15 mm horizontal and 20–25 mm vertical [104] |
| Integration with other sensors [27,105] | EKF [105], FGO [27] | Detects reflective surfaces, filters inconsistent pseudorange residuals | GNSS+INS+LiDAR+HD map: 0.21 m (E), 0.33 m (N), 1.52 m (U) [105], GNSS+LiDAR+IMU: 0.44–0.79 m [27] |
2.4. Tropospheric Effects and Their Correction
| Correction Method for Absolute Positioning | Example Model/Product | Description/Principle | Accuracy |
| Empirical models [110] | Saastamoinen, Hopfield, UNB3m, GPT2, GPT2w, GPT3, VMF3 | Empirical hydrostatic and wet delay models | Up to 20 cm UNB3m; up to 5 cm GPT2, GPT2w, GPT; 1.3 cm VMF3 [110] |
| Numerical Weather Prediction (NWP) models [124] | WRF, ERA5-based ZTD estimation | Combine WRF with UNB3m, VMF1-FC | 13.7 mm [124] |
| ML for ZWD forecasting and NWP model building [121] | Feedforward Neural Network (FNN), Long Short-Term Memory RNN | Provide tropospheric parameter forecasts (ZHD, ZWD, ZTD) | 1–2 cm [121] |
| Regional corrections ZTD/ZWD [125,126,127] | ZTD/ZWD estimation | Provide ZTD/ZWD corrections with network, grid, or polynomial models | Horizontal accuracy 13 cm, vertical accuracy 12.4 cm [125]; 2–3 cm horizontally, 4–5 cm vertically at PPP [127] |
| Network corrections [134] | Interpolation of ZTD gradients from dense networks | Global troposphere models + correction through network Interpolation models (e.g., Kriging or DIM2) for PPP-RTK | 2.5 cm horizontally; 5 cm vertically |
| SSR products [79] | Interpolated SSR corrections for PPP-RTK | SSR products with tropospheric corrections to correct tropospheric delays in PPP-RTK | Horizontal accuracy 1–3 cm in static mode, 0.1 m in dynamic mode |
| Correction Method for Relative Positioning | Example Model/Product | Description/Principle | Accuracy |
| Network RTK interpolation [132] | VRS, MAC, FKP tropospheric interpolation | Networks estimate and interpolate tropospheric gradients | Horizontal accuracy 1–2 cm, vertical accuracy 2–4 cm [132] |
| Regional corrections [133] | Correction of tropospheric errors using regional NWP | Meteorological fields are used and the zenith tropospheric delay (ZTD) | on a long base 2.3 cm (N), 2.1 cm (E), 4.3 cm (U) and 1.3 cm (N), 1.0 cm (E), 2.6 cm (U) on a short base [133] |
2.5. Receiver Noise and Methods of Correction
| Correction Method for Absolute Positioning | Example Model/Product | Description/Principle | Accuracy |
| Weighted filtering [138] | Elevation- and C/N0-dependent weighting of measurements | Weighting of observations by C/N0 and elevation angle and local redundancy of measurements [138]; C/N0 weighting and prediction of missing data for PPP [140] | Horizontal errors < 5 m [138], 4.6 m [140] |
| Kalman filtering [135,139] | Adaptive/Robust KF | Robust Adaptive Extended Kalman Filter [135]; robust adaptive filter for PPP [139] | 0.74 m [135] 201 mm (E), 77 mm (N), 160 mm (U) [139] |
| Filtering and smoothing [142,143] | Smoothing methods | Classical inverse smoothing for PPP [142]; incremental smoothing [143] | RMS: 0.139 m (N), 0.163 m (E), 0.137 m [142] 1.80 m [143] |
| Noise component separation | Wavelet analysis | Wavelet signal transformation [136] | 0.21 m [136] |
| Correction Method for Relative Positioning | Example Model/Product | Description/Principle | Accuracy |
| Weighted filtering [142] | Elevation- and C/N0-dependent weighting of measurements | Exclusion of observations with low elevation and C/N0 | 1–2.2 cm [142] |
| Kalman filtering [144] | Adaptive/Robust KF | Adaptive Kalman filter based on Integer Ambiguity Validation (IAVAKF) | Improved by 26% compared to classic KF [144] |
| Integration with other sensors [146] | GNSS/INS integration with EKF or factor graph | Tight coupling PPP-RTK, INS, vision sensor | 11 cm (E), 7 cm (N), 13 cm (U) [146] |
| Hardware improvement [55] | Use of improved antennas | Use of helix antennas | 0.32 m (E), 0.23 m (N), 0.97 m (U) [55] |
3. Architectures for GNSS High-Precision and Reliable Solutions
3.1. Conventional GNSS Receiver Architecture
3.2. Software-Defined GNSS Receivers
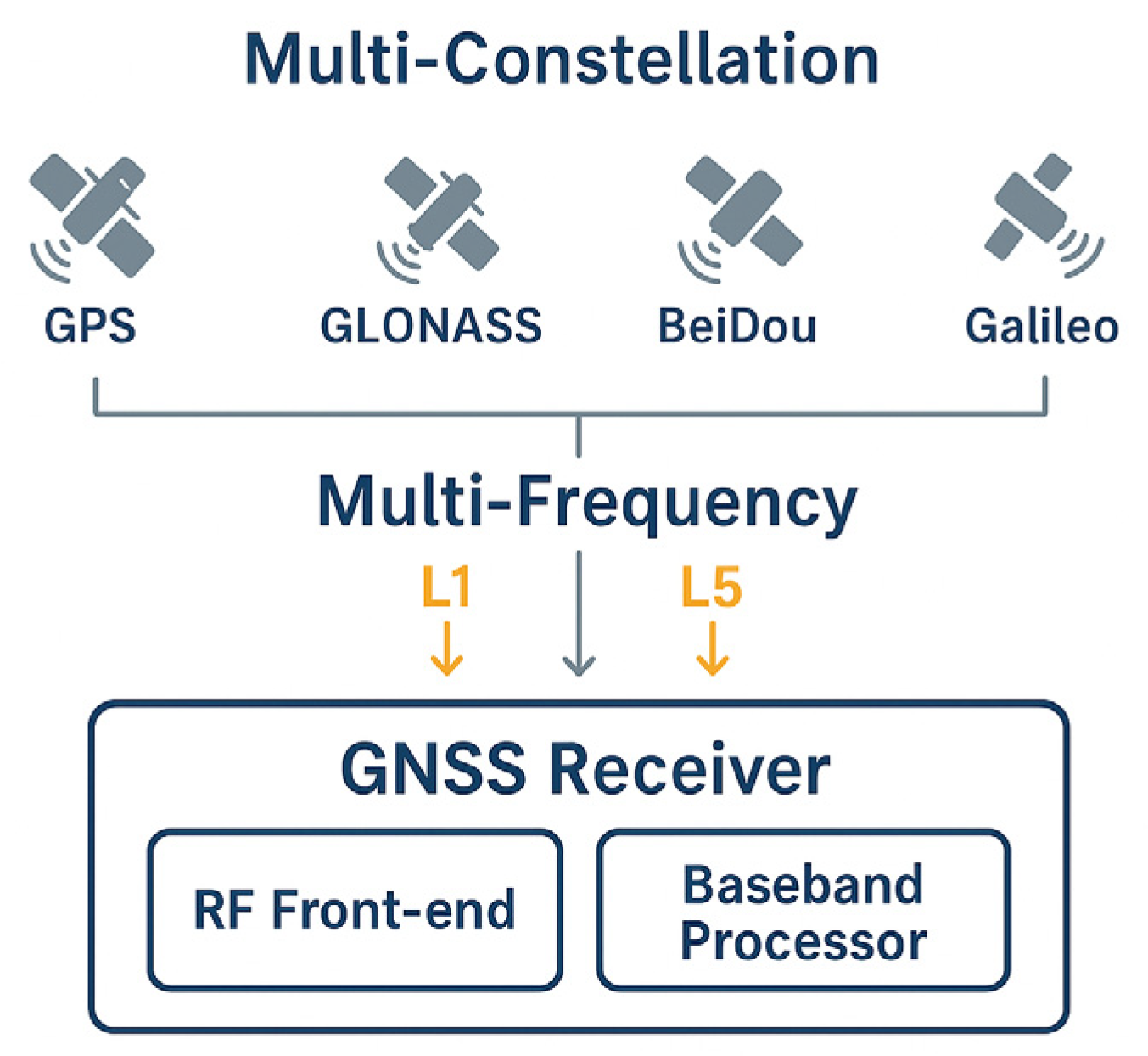
3.3. Multi-Frequency and Multi-Constellation Architectures
| Solution Type | Correction Methods/Features | Examples of Configurations/Services | Convergence Time | Positioning Accuracy | Experimental Conditions |
|---|---|---|---|---|---|
| Absolute PPP (single frequency) [163] | IF model PPP, basic ionospheric correction | GPS L1 | >30 min | Decimeter level | Static processing |
| Absolute PPP (dual-frequency) [163] | IF model PPP, ionospheric error correction | GPS + Galileo | ~15 min | Horizontal accuracy 7–12 mm | Static processing (160 stations) |
| Absolute PPP (triple-frequency) [163] | TIF PPP model, using BDS-3 and Galileo | BDS-3 (triple-frequency) | ~11 min | 4.9–12.1 mm | Static processing |
| PPP with multi-GNSS [134] | Combination of orbital and temporal products + multi-frequency signals | GPS + Galileo + BeiDou | <10 min (floating solution) | 1–2 cm | Vehicle testing |
| Hybrid PPP-RTK [134] | PPP-AR + network corrections | GPS + Galileo + BeiDou, HAS, BDS-3 PPP-B2b | <5 min (fixed solution) | ~2.5 cm | Vehicle testing |
| Multi-GNSS PPP (dynamic) [164] | MGEX products (GFZ), multi-constellation | GPS + GLONASS + Galileo + BeiDou | ~10–15 min | Centimeter -decimeter level | Sea trials |
| PPP (dynamics, single constellation) [164] | GPS-only, standard PPP products | GPS | ~20–30 min | 0.3–0.5 m | Bathymetric mapping |
| GNSS in interference conditions [165] | Analysis of signal degradation in multipath and under foliage | GPS L2 vs. L2C, Galileo | - | Accuracy degradation | Stationary tests on construction equipment |
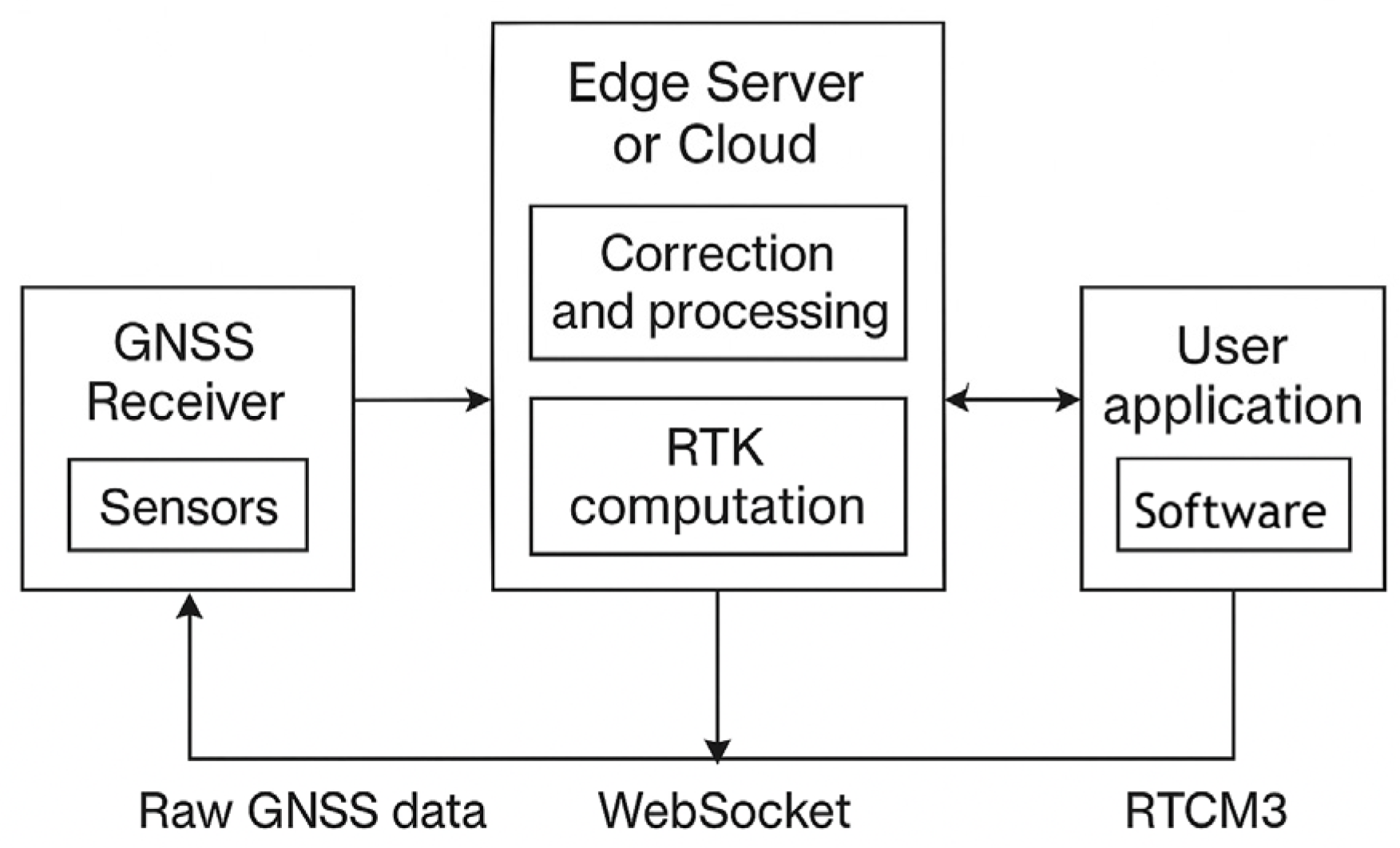
3.4. Cloud and Edge Architectures
| Type of Solution | Correction Methods/Features | Examples of Configurations/Services | Convergence Time | Positioning Accuracy | Experimental Conditions |
|---|---|---|---|---|---|
| Cloud-PPP (NavCm) [167] | PPP with using global ephemerides; support for BDS and Galileo | NavCm | Minutes (typical for PPP) | Without services: 0.06–0.08 m (horizontal), 0.08–0.10 m (vertical); with PPP-B2b: 5 cm (horizontal) and 13 cm (vertical) | Static tests, dynamic tests on vehicles |
| Cloud-PPP (PRIDE PPP- AR) [167] | PPP-AR (ambiguity resolution) in the cloud | PRIDE PPP-AR | Minutes | <4 cm (horizontal and vertical accuracy) | Dynamic tests on transport |
| Cloud-PPP for smartphones and IoT [168] | Transmission of “raw” observations to the server | Android application | Depends on the service | Sub-decimeter accuracy (2 cm horizontally and 5 cm vertically) | Mobile devices |
| Centralized cloud [170] | Full processing on cloud server | - | Depends on network and load | 1–2 cm in static, when moving, positioning error is determined by network latency: from <1 m | Mobile devices |
| Edge architecture [171] | Transfer of computations to edge servers; the cloud performs the final calculation | Edge servers + cloud | Less latency than in a centralized cloud | Centimeter accuracy (PPP/RTK) is maintained | Tractor movement under shading conditions |
3.5. Integrated GNSS/INS/LiDAR Architectures
| Type of Solution | Correction Methods/Features | Examples of Configurations/Services | Convergence Time | Positioning Accuracy | Experimental Conditions |
|---|---|---|---|---|---|
| GNSS/INS/LiDAR-SLAM + factor graph optimization [175] | Joint optimization by carrier phase and LiDAR points; INS drift compensation | Mobile mapping, geodesy | Stable convergence, even during GNSS interruptions | RMSE reduction: N ≈ 82%, E ≈ 79%; relative error at simple GNSS −0.26% distance traveled | Tests with modeling of losses GNSS, urbanized conditions |
| GNSS/INS/LiDAR (close integration) [176,177,178] | Use of carrier GNSS and LiDAR phases in filters; hybrid schemes | UAV for mapping, autonomous vehicles | Convergence is maintained during GNSS interruptions | Improved accuracy 60–75% compared to GNSS/INS; support for sub-meter accuracy | Field tests under conditions of partial/complete GNSS loss |
| GNSS/SINS Systems [179] | Use of several inexpensive receivers + cascaded/centralized filters | Low-cost integrated platforms | Rapid recovery in failures | - | Laboratory and field tests |
| GNSS/INS + ML (Cascade LSTM) [180] | The ML model predicts pseudovelocities for filtering in the absence of GNSS | Autonomous platforms | Stability is maintained during prolonged losses | Improved accuracy during prolonged downtime; reduction in INS drift | Tests on long GNSS outages |
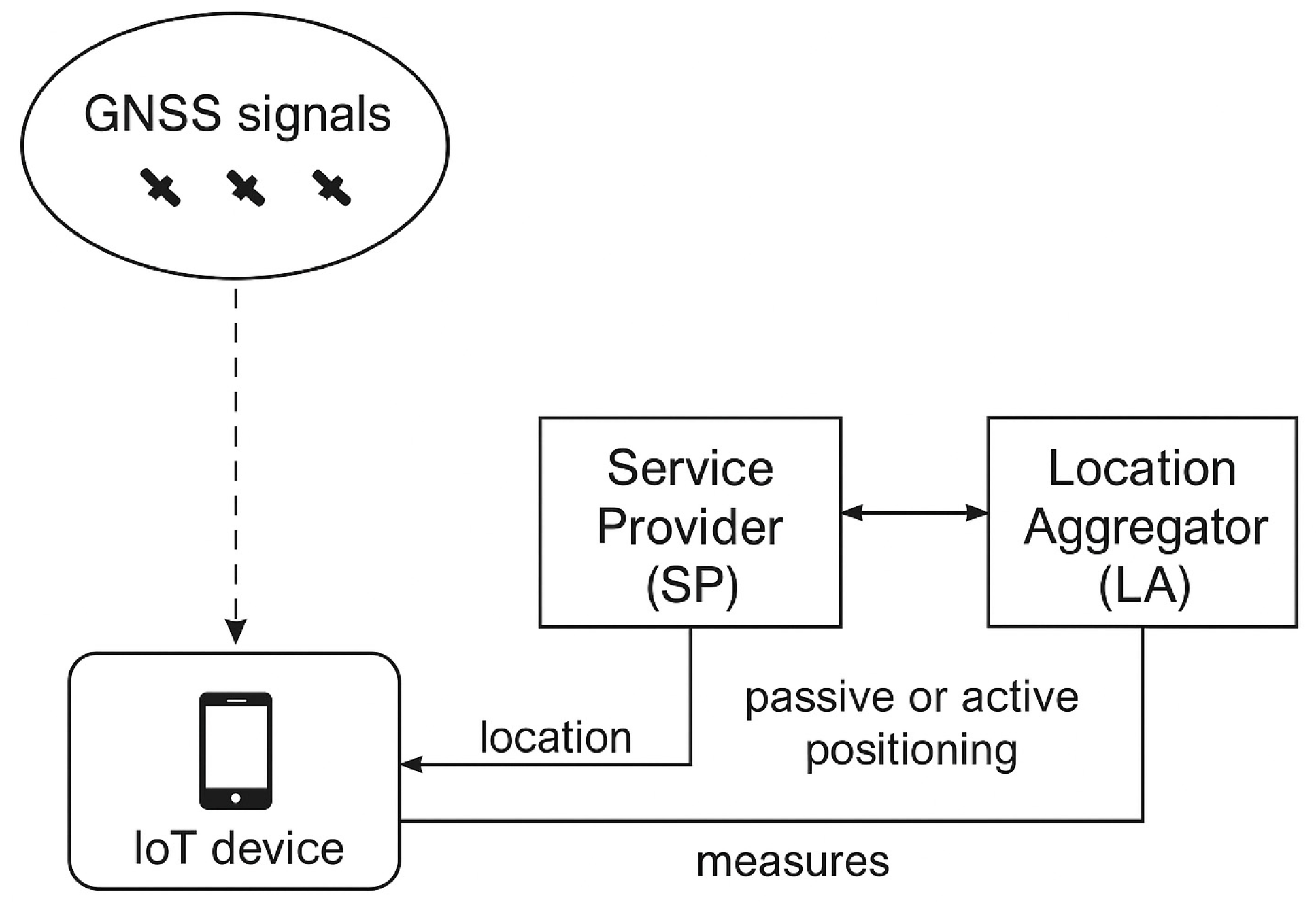
3.6. Integrated GNSS/IoT Architectures
| Type of Solution | Correction Methods/Features | Examples of Configurations/Services | Convergence Time | Positioning Accuracy | Experimental Conditions |
|---|---|---|---|---|---|
| Specialized GNSS chip for IoT [184] | Support for ultra-low power consumption, NLOS operation and multipath | Proprietary chip, comparison with the NovAtel GNSS/INS reference | - | - | Multipath |
| IoT device with PPP-RTK [57] | Integration of u-blox ZED-F9P with IoT controller, transmission of corrections via IP | u-blox ZED-F9P + network controller | Minutes (typical for PPP-RTK) | Decimeter accuracy in urban conditions | Kinematic tests, data transmission via IoT |
| GNSS-IoT for monitoring water surface (WSE) [185] | GNSS + ultrasonic sensors + accelerometer; long-term monitoring | Multi-sensor GNSS-IoT system | 6-hour averaging | 7 mm (averaged over 6 h), 28 mm (epochal values) | Field tests, Hugong Reservoir (Australia) |
| IoT platform for infrastructure [46] | Dual-band GNSS (L1/L2) + RTK; simulation of reduced number of measurements | Low-cost receivers + IoT platform | - | About 0.5 cm CEP, maximum—up to 2.5 cm | Infrastructure monitoring |
| GNSS/IoT + ML/DL [187] | Classification LOS/NLOS, prediction of missing measurements, adaptive models | ML/DL models integrated with GNSS-IoT | Depends on the algorithm | Decimeters or centimeters (under optimal conditions) for RTK | Urban environment |
4. Discussion About Research Challenges and Open Problems
| Architecture | Accuracy | Disadvantages | Positive Aspects | Applicability |
|---|---|---|---|---|
| Hardware-based receivers | SF-LC: 0.2–1 m in open sky, 0.5–3 m in the city [150,154]; DF-LC: up to 2–5 cm in RTK at short bases < 10 km [151]; Aviation: 1–3 m with SBAS/GB AS [148] | Low resistance to spoofing and jamming; reliability limited by multipath; moderate energy consumption (80–150 mW [153], up to 1 W [148]) | High predictability of operation; certified solutions; low cost of mass-produced chips | Aviation, automotive navigation, agriculture, smartphones |
| SD-based receivers | Comparable to geodetic receivers: tracking at C/N0 > 28 dB-Hz [152]; RTK: 1–2 cm [191] | High computational and energy load (1–2 W [156]); integration difficulty; vulnerability to overload [157] | Versatility, signal reproduction, support for new systems (GPS, Galileo, BeiDou) [155,191] | Scientific research, ionosphere monitoring [191], anti-spoofing [157], RFI direction finding [158] |
| Multifrequency and multi-constellation receiver | PPP: 7–12 mm static (2 freq.) [163]; 4.9–12.1 mm (3 freq.) [163]; PPP-RTK: 2.5 cm [134] | Sensitive to multipath; moderate energy (100–250 mW [57]); antenna cost; partial susceptibility to signal degradation [165] | Centimeter accuracy even on inexpensive equipment; high fault tolerance [134] | Geodesy, unmanned vehicles, UAVs, maritime navigation [161,164] |
| Cloud and edge architectures | Cloud-PPP: 6–8 hor., 8–10 cm vert. [167]; PPP-B2b: 5–13 cm [167]; Edge-CB-GNSS: 2–4 cm [171] | Risk of data compromise [172]; network latency (2–5 s [170]); reliance on connectivity; low terminal energy (20–50 mW [45]) | Scalability [57], energy efficiency, high accuracy with inexpensive terminals [45] | Smartphones, IoT terminals, autonomous transport, agricultural monitoring [45,168,171] |
| GNSS/INS/LiDAR integrated | Improved accuracy: reduction in RMSE to 82.2% and 79.6% [175]; sub-meter accuracy in the city [178]; with GNSS turned off, RMSE reduction by 51–78% [176] | High energy (15–20 W [175]); calibration complexity; costly sensors [181]; high computational load | High robustness; ability to navigate without GNSS [176] | Geodesy, mobile mapping, UAVs, autonomous machines [174,179] |
| GNSS/IoT integrated | PPP-RTK on a low-cost receiver: decimeter level in the city [57]; hydrology: 7 mm [185] | Medium-low security (vulnerable comm. channels [46]); network dependency; low energy (20–80 mW [184]); transmission delay | Low cost, mass production, integration with ML/DL for reducing energy consumption [187] | Hydrology [185], ionospheric maps [186], transport and agriculture [57] |
5. Conclusions and Future Directions
- -
- Real-time data fusion frameworks for GNSS/INS/LiDAR/vision integration;
- -
- Calibration standards and adaptive noise models for low-cost multi-frequency receivers;
- -
- Unified open-source platforms for testing and benchmarking hybrid GNSS architectures;
- -
- The development of ML-based troposphere and ionosphere forecasting integrated directly into PPP-RTK services;
- -
- The integration of GNSS with IoT, cloud-edge, and ML-based processing for real-time PPP-RTK solutions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, J. Autonomous navigation for an unmanned mobile robot in urban areas. In Proceedings of the 2011 IEEE International Conference on Mechatronics and Automation, Beijing, China, 7–10 August 2011; pp. 2243–2248. [Google Scholar] [CrossRef]
- Jurišica, L.; Duchoň, F.; Kaštan, D.; Babinec, A. High Precision GNSS Guidance for Field Mobile Robots. Int. J. Adv. Robot. Syst. 2012, 9, 169. [Google Scholar] [CrossRef]
- Suzuki, T.; Kitamura, M.; Amano, Y.; Kubo, N. Autonomous Navigation of a Mobile Robot Based on GNSS/DR Integration in Outdoor Environments. J. Robot. Mechatron. 2014, 26, 214–224. [Google Scholar] [CrossRef]
- Zhang, G.; Hsu, L.-T. Intelligent GNSS/INS integrated navigation system for a commercial UAV flight control system. Aerosp. Sci. Technol. 2018, 80, 368–380. [Google Scholar] [CrossRef]
- Xia, L.; Li, J. Autonomous Landing of a Fixed-Wing UAV with RTK GNSS and MEMS IMU. Int. J. Aerosp. Eng. 2025, 2025, 9430096. [Google Scholar] [CrossRef]
- Dlamini, S.M.; Ouma, Y.O. Large-Scale Topographic Mapping Using RTK-GNSS and Multispectral UAV Drone Photogrammetric Surveys: Comparative Evaluation of Experimental Results. Geomatics 2025, 5, 25. [Google Scholar] [CrossRef]
- Lin, M.; Yoon, J.; Kim, B. Self-Driving Car Location Estimation Based on a Particle-Aided Unscented Kalman Filter. Sensors 2020, 20, 2544. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Bi, Y.; Li, K.; Wang, K.; Lin, F.; Chen, B.M. Real-time self-driving car navigation and obstacle avoidance using mobile 3D laser scanner and GNSS. Multimed. Tools Appl. 2017, 76, 23017–23039. [Google Scholar] [CrossRef]
- Shytermeja, E.; Rakipi, A.; Cakaj, S.; Kamo, B.; Koliçi, V. Performance Impact of Ionospheric and Tropospheric Corrections of User Position Estimation Using GPS Raw Measurements. In ICT Innovations 2013; Trajkovik, V., Anastas, M., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; Volume 231, pp. 157–165. [Google Scholar] [CrossRef]
- Ma, H.; Psychas, D.; Xing, X.; Zhao, Q.; Verhagen, S.; Liu, X. Influence of the inhomogeneous troposphere on GNSS positioning and integer ambiguity resolution. Adv. Space Res. 2021, 67, 1914–1928. [Google Scholar] [CrossRef]
- Lee, T.; Bettinger, P.; Merry, K.; Cieszewski, C. The effects of nearby trees on the positional accuracy of GNSS receivers in a forest environment. PLoS ONE 2023, 18, e0283090. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Lian, J.; Zhang, G.; Hsu, L.-T. Performance Assessment of GNSS Positioning in Different Vegetated Environments. In Proceedings of the ION 2024 Pacific PNT Meeting, Honolulu, HI, USA, 21–24 May 2024; pp. 430–443. [Google Scholar] [CrossRef]
- Uzodinma, V.N.; Nwafor, U. Degradation of GNSS Accuracy by Multipath and Tree Canopy Distortions in a School Environment. Asian J. Appl. Sci. 2018, 6, 4. [Google Scholar] [CrossRef]
- Ali, K.; Chen, X.; Dovis, F.; De Castro, D.; Fernández, A.J. Multipath Estimation in Urban Environments from Joint GNSS Receivers and LiDAR Sensors. Sensors 2012, 12, 14592–14603. [Google Scholar] [CrossRef]
- Seddiki, B.; Moulay Lakhdar, A.E.M.; Beldjilali, B. Performance Evaluation of Different GNSS Positioning Modes. Indones. J. Electr. Eng. Inform. 2022, 10, 604–613. [Google Scholar] [CrossRef]
- Choy, S.; Kuckartz, J.; Dempster, A.G.; Rizos, C.; Higgins, M. GNSS satellite-based augmentation systems for Australia. GPS Solut. 2017, 21, 835–848. [Google Scholar] [CrossRef]
- Jansen, P. The Impact of Jamming and Spoofing on GNSS Signals. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2022. [Google Scholar]
- Ehrler, R.; Luo, Y.; Schade, C.; Bähr, A.; Lehner, A.; Boyero, J.P.; Pulido, J.Á. Jamming and Spoofing Impact on GNSS Signals for Railway Applications. In Proceedings of the 36th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2023), Denver, CO, USA, 11–15 September 2023; pp. 4153–4167. [Google Scholar] [CrossRef]
- Rajasekhar, C.; Srilatha Indira Dutt, V.B.S.; Sasibhushana Rao, G. Weighted GDoP for improved position accuracy using NavIC and GPS hybrid constellation over Indian sub-continent. Int. J. Intell. Netw. 2021, 2, 42–45. [Google Scholar] [CrossRef]
- Kaplan, E.D.; Hegarty, C.J. Understanding GPS: Principles and Applications, 2nd ed.; Artech House: Boston, MA, USA, 2006. [Google Scholar]
- Acosta, N.; Toloza, J. Techniques to improve the GPS precision. Int. J. Adv. Comput. Sci. Appl. 2012, 3, 125–130. [Google Scholar] [CrossRef]
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Wasle, E. GNSS—Global Navigation Satellite Systems: GPS, GLONASS, Galileo, and More; Springer: Vienna, Austria, 2008. [Google Scholar] [CrossRef]
- Arnold, L.L.; Zandbergen, P.A. Positional accuracy of the Wide Area Augmentation System in consumer-grade GPS units. Comput. Geosci. 2011, 37, 883–892. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Montenbruck, O. (Eds.) Springer Handbook of Global Navigation Satellite Systems; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Trimble Navigation Limited. GPS the First Global Navigation Satellite System; Trimble Navigation Limited: Sunnyvale, CA, USA, 2007. [Google Scholar]
- Psychas, D.; Verhagen, S. Real-Time PPP-RTK Performance Analysis Using Ionospheric Corrections from Multi-Scale Network Configurations. Sensors 2020, 20, 3012. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Wen, W.; Huang, F.; Gao, H.; Wang, Y.; Hsu, L.-T. 3D LiDAR Aided GNSS NLOS Mitigation for Reliable GNSS-RTK Positioning in Urban Canyons. arXiv 2022, arXiv:2212.05477. [Google Scholar] [CrossRef]
- Wen, W.; Zhang, G.; Hsu, L.-T. Object-Detection-Aided GNSS and Its Integration with Lidar in Highly Urbanized Areas. IEEE Intell. Transp. Syst. Mag. 2020, 12, 53–69. [Google Scholar] [CrossRef]
- Wen, W.; Pfeifer, T.; Bai, X.; Hsu, L.-T. It is time for Factor Graph Optimization for GNSS/INS Integration: Comparison between FGO and EKF. arXiv 2020, arXiv:2004.10572. [Google Scholar] [CrossRef]
- Wang, K.; Zhao, L. GPS/INS integrated urban navigation system based on vehicle motion detection. In Proceedings of the 2014 IEEE Chinese Guidance, Navigation and Control Conference, Yantai, China, 8–10 August 2014; pp. 667–670. [Google Scholar] [CrossRef]
- Wang, J.; Xu, B.; Liu, J.; Gao, K.; Zhang, S. Sky-GVIO: Enhanced GNSS/INS/Vision Navigation with FCN-Based Sky Segmentation in Urban Canyon. Remote Sens. 2024, 16, 3785. [Google Scholar] [CrossRef]
- Munin, E.; Blais, A.; Couellan, N. Convolutional Neural Network for Multipath Detection in GNSS Receivers. arXiv 2019, arXiv:1911.02347. [Google Scholar] [CrossRef]
- Ozeki, T.; Kubo, N. GNSS NLOS Signal Classification Based on Machine Learning and Pseudorange Residual Check. Front. Robot. AI 2022, 9, 868608. [Google Scholar] [CrossRef]
- Lee, Y.; Park, B. Nonlinear Regression-Based GNSS Multipath Modelling in Deep Urban Area. Mathematics 2022, 10, 412. [Google Scholar] [CrossRef]
- Suzuki, T.; Amano, Y. NLOS Multipath Classification of GNSS Signal Correlation Output Using Machine Learning. Sensors 2021, 21, 2503. [Google Scholar] [CrossRef]
- Gao, W.; Feng, Y. Assessing the robustness of machine learning strategy for GNSS/INS vehicle positioning solutions enhancement. GPS Solut. 2025, 29, 167. [Google Scholar] [CrossRef]
- Tao, A.-L.; Jan, S.-S. Optimal Navigation with Multi-constellation GNSS: A Satellite Selection Algorithm. In Proceedings of the 29th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2016), Portland, OR, USA, 12–16 September 2016; pp. 128–139. [Google Scholar] [CrossRef]
- Fang, R.; Lv, H.; Shu, Y.; Zheng, J.; Zhang, K.; Liu, J. Improved performance of GNSS precise point positioning for high-rate seismogeodesy with recent BDS-3 and Galileo. Adv. Space Res. 2021, 68, 3255–3267. [Google Scholar] [CrossRef]
- Marques, H.A.; Marques, H.A.S.; Aquino, M.; Veettil, S.V.; Monico, J.F.G. Accuracy assessment of Precise Point Positioning with multi-constellation GNSS data under ionospheric scintillation effects. J. Space Weather Space Clim. 2018, 8, A15. [Google Scholar] [CrossRef]
- Pireaux, S.; Defraigne, P.; Wauters, L.; Bergeot, N.; Baire, Q.; Bruyninx, C. Influence of ionospheric perturbations in GPS time and frequency transfer. Adv. Space Res. 2010, 45, 1101–1112. [Google Scholar] [CrossRef]
- Rougerie, S.; Carrié, G.; Israel, J.; Ries, L.; Monnerat, M.; Thevenon, P. Multipath Mitigation Methods Based on Diversity Algorithms. In Proceedings of the 26th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2013), Nashville, TN, USA, 16–20 September 2013. [Google Scholar]
- Pereira, P.M.C.; Da Silva, H.D.M.; Lima, C.M.G.S. Advancements in Multipath Mitigation for GNSS Receivers: Review of Channel Estimation Techniques. Space Sci. Technol. 2025, 5, 0278. [Google Scholar] [CrossRef]
- An, X.; Meng, X.; Jiang, W. Multi-constellation GNSS precise point positioning with multi-frequency raw observations and dual-frequency observations of ionospheric-free linear combination. Satell. Navig. 2020, 1, 7. [Google Scholar] [CrossRef]
- Romero-Holguín, L.M.; Lucas-Sabola, V.; del Peral-Rosado, J.A.; Seco-Granados, G.; López-Salcedo, J.A.; García-Molina, J.A. Prototype of IoT GNSS Sensor for Cloud GNSS Signal Processing. In Proceedings of the European Navigation Conference 2017, Lausanne, Switzerland, 9–12 May 2017. [Google Scholar]
- Lucas-Sabola, V.; Seco-Granados, G.; López-Salcedo, J.A.; García-Molina, J.A.; Crisci, M. Efficiency Analysis of Cloud GNSS Signal Processing for IoT Applications. In Proceedings of the 30th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2017), Portland, OR, USA, 25–29 September 2017; pp. 3843–3852. [Google Scholar] [CrossRef]
- Beber, R.; Morelli, L.; Remondino, F.; Hernandez, F. An IoT-based GNSS platform for infrastructure monitoring. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2024, XLVIII-2/W8-2024, 17–23. [Google Scholar] [CrossRef]
- Wang, L.; Qiu, R. BeiDou Satellite Positioning Method Based on IoT and Edge Computing. Sensors 2020, 20, 889. [Google Scholar] [CrossRef] [PubMed]
- GNSS Receiver Trimble-R12i. Available online: https://geospatial.trimble.com/en/products/hardware/trimble-r12i (accessed on 1 October 2025).
- GNSS Receiver Leica-GS18-T. Available online: https://leica-geosystems.com/en-us/products/gnss-systems/smart-antennas/leica-gs18-t (accessed on 1 October 2025).
- Hiper-HR. Available online: https://mytopcon.topconpositioning.com/support/products/hiper-hr (accessed on 1 October 2025).
- GNSS Receiver Mosaic-X5. Available online: https://www.septentrio.com/en/products/gnss-receivers/gnss-receiver-modules/mosaic-x5 (accessed on 1 October 2025).
- GNSS Receiver OEM7700. Available online: https://novatel.com/products/receivers/gnss-gps-receiver-boards/oem7700 (accessed on 1 October 2025).
- GNSS Receiver ZED-F9P-Module. Available online: https://www.u-blox.com/en/product/zed-f9p-module (accessed on 1 October 2025).
- Bose, A.; Mahato, S.; Dan, S.; Santra, A. Compact, Low-cost GNSS Modules for Precise Point Positioning. E3S Web Conf. 2021, 310, 03001. [Google Scholar] [CrossRef]
- Li, X.; Huang, J.; Li, X.; Shen, Z.; Han, J.; Li, L.; Wang, B. Review of PPP–RTK: Achievements, challenges, and opportunities. Satell. Navig. 2022, 3, 28. [Google Scholar] [CrossRef]
- Wang, P.; Gao, Y.; Zhao, Q.; Wang, Y.; Zhou, F.; Zhang, D. An Enhanced, Real-Time, Low-Cost GNSS/INS Integrated Navigation Algorithm and Its Platform Design. Sensors 2025, 25, 2119. [Google Scholar] [CrossRef]
- Amalfitano, D.; Cutugno, M.; Robustelli, U.; Pugliano, G. Designing and Testing an IoT Low-Cost PPP-RTK Augmented GNSS Location Device. Sensors 2024, 24, 646. [Google Scholar] [CrossRef] [PubMed]
- Zuo, X.; Chen, Y.; Li, C.; Pan, G.; Shi, X. Single Frequency GPS/BDS Precise Positioning Algorithm for Low-cost Receivers. In Proceedings of the 29th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2016), Portland, OR, USA, 12–16 September 2016; pp. 152–158. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, Y.; Yang, Y.; Liang, C.; Liu, R. Spoofing and Anti-Spoofing Technologies of Global Navigation Satellite System: A Survey. IEEE Access 2020, 8, 165444–165496. [Google Scholar] [CrossRef]
- Li, X.; Chen, J.; Zhao, G.; Feng, W. Overview of Jamming Technology for Satellite Navigation. Machines 2023, 11, 768. [Google Scholar] [CrossRef]
- Héroux, P.; Kouba, J. GPS precise point positioning using IGS orbit products. Phys. Chem. Earth Part A Solid Earth Geod. 2001, 26, 573–578. [Google Scholar] [CrossRef]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Wang, N.; Yuan, Y.; Li, Z.; Huo, X. Impact of Ionospheric Correction on Single-Frequency GNSS Positioning. In China Satellite Navigation Conference (CSNC) 2013 Proceedings; Sun, J., Jiao, W., Wu, H., Shi, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 244, pp. 471–486. [Google Scholar] [CrossRef]
- Bandyopadhyay, K. Comparative Analysis of the Effect of Ionospheric Delay on User Position Accuracy Using Single and Dual Frequency GPS Receivers over Indian Region. Master’s Thesis, Indian Institute of Technology Bombay, Mumbai, India, 2009. [Google Scholar]
- Landa, V.; Reuveni, Y. Toward Real-Time GNSS Single-Frequency Precise Point Positioning Using Ionospheric Corrections. Remote Sens. 2023, 15, 3333. [Google Scholar] [CrossRef]
- Poniatowski, M.; Nykiel, G.; Hoque, M.M.; Szmytkowski, J. Deep learning approach for combining global ionospheric maps for GNSS positioning. GPS Solut. 2025, 29, 111. [Google Scholar] [CrossRef]
- Paziewski, J. Study on desirable ionospheric corrections accuracy for network-RTK positioning and its impact on time-to-fix and probability of successful single-epoch ambiguity resolution. Adv. Space Res. 2016, 57, 1098–1111. [Google Scholar] [CrossRef]
- Paziewski, J.; Sieradzki, R. Enhanced wide-area multi-GNSS RTK and rapid static positioning in the presence of ionospheric disturbances. Earth Planets Space 2020, 72, 110. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, J.; Khodabandeh, A. Regional ionospheric correction generation for GNSS PPP-RTK: Theoretical analyses and a new interpolation method. GPS Solut. 2024, 28, 139. [Google Scholar] [CrossRef]
- Li, X.; Wang, B.; Li, X.; Huang, J.; Lyu, H.; Han, X. Principle and performance of multi-frequency and multi-GNSS PPP-RTK. Satell. Navig. 2022, 3, 7. [Google Scholar] [CrossRef]
- Misra, P.; Enge, P. Global Positioning System: Signals, Measurements, and Performance, 2nd ed.; Ganga-Jamuna Press: Lincoln, MA, USA, 2006. [Google Scholar]
- Wisniewski, B.; Bruniecki, K.; Moszynski, M. Evaluation of RTKLIB’s Positioning Accuracy Using low-cost GNSS Receiver and ASG-EUPOS. TransNav 2013, 7, 79–85. [Google Scholar] [CrossRef]
- Kouba, J. A Guide to Using International GPS Service (IGS) Products; International GNSS Service: Pasadena, CA, USA, 2009. [Google Scholar]
- Youssef, M.A.; Hamid, A.M.A.; Elashiry, A.A. Enhancement of the Single Point Positioning Accuracy (Using the Observations of IGS Service). Available online: https://www.fig.net/resources/proceedings/fig_proceedings/fig2009/papers/ts06b/ts06b_youssef_hamid_et_al_3390.pdf (accessed on 1 October 2025).
- Kouba, J.; Héroux, P. Precise Point Positioning Using IGS Orbit and Clock Products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Li, H.; Luojie, D.; Ding, H. Real-time service performances of BDS-3 and Galileo constellations with a linear satellite clock correction models. Satell. Navig. 2023, 4, 23. [Google Scholar] [CrossRef]
- Naciri, N.; Bisnath, S. RTK-Quality Positioning with Global Precise Point Positioning Corrections. NAVIGATION 2023, 70, navi.575. [Google Scholar] [CrossRef]
- Garrido, M.S.; Giménez, E.; De Lacy, M.C.; Gil, A.J. Testing precise positioning using RTK and NRTK corrections provided by MAC and VRS approaches in SE Spain. J. Spat. Sci. 2011, 56, 169–184. [Google Scholar] [CrossRef]
- An, X.; Ziebold, R.; Lass, C. PPP-RTK with Rapid Convergence Based on SSR Corrections and Its Application in Transportation. Remote Sens. 2023, 15, 4770. [Google Scholar] [CrossRef]
- Blanch, J.; Walter, T.; Enge, P.; Lee, Y.; Pervan, B.; Rippl, M.; Spletter, A.; Kropp, V. Advanced RAIM User Algorithm Description: Integrity Support Message Processing, Fault Detection, Exclusion, and Protection Level Calculation; GPS Directorate: Washington, DC, USA, 2015. [Google Scholar]
- Tran, H.T.; Lo Presti, L. Kalman filter-based ARAIM algorithm for integrity monitoring in urban environment. ICT Express 2019, 5, 65–71. [Google Scholar] [CrossRef]
- El-Mowafy, A.; Xu, B.; Hsu, L.-T. Integrity monitoring using multi-GNSS pseudorange observations in the urban environment combining ARAIM and 3D city models. J. Spat. Sci. 2022, 67, 91–110. [Google Scholar] [CrossRef]
- Gutierrez, J.; Gilabert, R.; Dill, E.; Hernandez, G.; Kaeli, D.; Closas, P. Multipath Mitigation via Clustering for Position Estimation Refinement in Urban Environments. In Proceedings of the ION 2024 Pacific PNT Meeting, Honolulu, HI, USA, 21–24 May 2024; pp. 556–568. [Google Scholar] [CrossRef]
- Dong, J.; Hua, Q. Overview and Progress of GNSS Anti-multipath Antenna Designs. Sens. Mach. Learn. Appl. 2023, 2, 3. [Google Scholar] [CrossRef]
- Lin, D.; Wang, E.; Wang, J. New Choke Ring Design for Eliminating Multipath Effects in the GNSS System. Int. J. Antennas Propag. 2022, 2022, 1527674. [Google Scholar] [CrossRef]
- Maqsood, M.; Gao, S.; Brown, T.W.C.; Unwin, M.; De Vos Van Steenwijk, R.; Xu, J.D. A Compact Multipath Mitigating Ground Plane for Multiband GNSS Antennas. IEEE Trans. Antennas Propag. 2013, 61, 2775–2782. [Google Scholar] [CrossRef]
- Siebert, C.; Konovaltsev, A.; Meurer, M. Development and Validation of a Multipath Mitigation Technique Using Multi-Correlator Structures. NAVIGATION 2023, 70, navi.609. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, B.; Shen, Y.; Gao, Y.; Wang, M. Site-Specific Unmodeled Error Mitigation for GNSS Positioning in Urban Environments Using a Real-Time Adaptive Weighting Model. Remote Sens. 2018, 10, 1157. [Google Scholar] [CrossRef]
- Li, L.; Elhajj, M.; Feng, Y.; Ochieng, W.Y. Machine learning based GNSS signal classification and weighting scheme design in the built environment: A comparative experiment. Satell. Navig. 2023, 4, 12. [Google Scholar] [CrossRef]
- Cheng, Q.; Sun, R. GNSS Pseudorange Correction Using Machine Learning in Urban Areas. In Positioning and Navigation Using Machine Learning Methods; Yu, K., Ed.; Springer Nature: Singapore, 2024; Volume 14, pp. 1–31. [Google Scholar] [CrossRef]
- Hassan, T.; Fath-Allah, T.; Elhabiby, M.; Awad, A.; El-Tokhey, M. Detection of GNSS no-line of sight signals using LiDAR sensors for intelligent transportation systems. Surv. Rev. 2022, 54, 301–309. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Yigit, C.O.; El-Mowafy, A.; Dindar, A.A.; Bezcioglu, M.; Hu, J.W. Hybrid Wavelet and Principal Component Analyses Approach for Extracting Dynamic Motion Characteristics from Displacement Series Derived from Multipath-Affected High-Rate GNSS Observations. Remote Sens. 2019, 12, 79. [Google Scholar] [CrossRef]
- Wang, M.; Wang, J.; Dong, D.; Chen, W.; Li, H.; Wang, Z. Advanced Sidereal Filtering for Mitigating Multipath Effects in GNSS Short Baseline Positioning. ISPRS Int. J. Geo-Inf. 2018, 7, 228. [Google Scholar] [CrossRef]
- Dong, D.; Wang, M.; Chen, W.; Zeng, Z.; Song, L.; Zhang, Q.; Cai, M.; Cheng, Y.; Lv, J. Mitigation of multipath effect in GNSS short baseline positioning by the multipath hemispherical map. J. Geod. 2016, 90, 255–262. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, X.; Zhong, S.; Xi, K.; Shen, H. A Multipath Hemispherical Map with Strict Quality Control for Multipath Mitigation. Remote Sens. 2025, 17, 767. [Google Scholar] [CrossRef]
- Tena, Á.; Chamorro, A.; Calle, J.D. Enhancing GNSS PPP Algorithms with AI: Towards Mitigating Multipath Effects. Eng. Proc. 2025, 88, 56. [Google Scholar] [CrossRef]
- Geng, J.; Zhang, H.; Li, G.; Aoki, Y. Multipath mitigation for GPS/Galileo/BDS-3 precise point positioning with overlap-frequency signals. Satell. Navig. 2024, 5, 22. [Google Scholar] [CrossRef]
- Li, X.; Wang, H.; Li, S.; Feng, S.; Wang, X.; Liao, J. GIL: A tightly coupled GNSS PPP/INS/LiDAR method for precise vehicle navigation. Satell. Navig. 2021, 2, 26. [Google Scholar] [CrossRef]
- Kubo, N.; Kobayashi, K.; Furukawa, R. GNSS Multipath Detection Using Continuous Time-Series C/N0. Sensors 2020, 20, 4059. [Google Scholar] [CrossRef]
- Xu, P.; Zhang, G.; Yang, B.; Hsu, L.-T. Machine Learning in GNSS Multipath/NLOS Mitigation: Review and Benchmark. IEEE Aerosp. Electron. Syst. Mag. 2024, 39, 26–44. [Google Scholar] [CrossRef]
- Pan, Y.; Möller, G.; Soja, B. Machine learning-based multipath modeling in spatial domain applied to GNSS short baseline processing. GPS Solut. 2024, 28, 9. [Google Scholar] [CrossRef]
- Wu, Z.; Yue, Y.; Wu, M. An improved carrier phase-based RAIM method applied to GNSS RTK positioning integrity for landslide monitoring. Adv. Space Res. 2025, in press. [Google Scholar] [CrossRef]
- Li, Y.; Mi, J.; Xu, Y.; Li, B.; Jiang, D.; Liu, W. A Robust Adaptive Filtering Algorithm for GNSS Single-Frequency RTK of Smartphone. Remote Sens. 2022, 14, 6388. [Google Scholar] [CrossRef]
- Medina, D.; Li, H.; Vilà-Valls, J.; Closas, P. Robust Filtering Techniques for RTK Positioning in Harsh Propagation Environments. Sensors 2021, 21, 1250. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Qian, C.; Li, W.; Li, B.; Liu, H. Tightly coupled integration of vector HD map, LiDAR, GNSS, and INS for precise vehicle navigation in GNSS-challenging environment. Geospat. Inf. Sci. 2025, 28, 1341–1358. [Google Scholar] [CrossRef]
- Li, X.; Jiang, H.; Wang, B.; Gao, Z.; Shi, Y.; Li, X. Improving multipath extraction in PPP-RTK for high-precision dynamic deformation monitoring. Geospat. Inf. Sci. 2025, in press. [Google Scholar] [CrossRef]
- Elsayed, H.; El-Mowafy, A.; Allahvirdi-Zadeh, A.; Wang, K. Fast Protection Level for Precise Positioning Using PPP-RTK with Robust Adaptive Kalman Filter. Remote Sens. 2025, 17, 2924. [Google Scholar] [CrossRef]
- Li, X.; Wang, X.; Liao, J.; Li, X.; Li, S.; Lyu, H. Improving PPP-RTK-based vehicle navigation in urban environments via multilayer perceptron-based NLOS signal detection. GPS Solut. 2024, 28, 29. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Liu, G.; Feng, G.; Wang, Y.; Zhang, S.; Huang, J. Improving PPP–RTK in urban environment by tightly coupled integration of GNSS and INS. J. Geod. 2021, 95, 132. [Google Scholar] [CrossRef]
- Yang, L.; Wang, J.; Li, H.; Balz, T. Global Assessment of the GNSS Single Point Positioning Biases Produced by the Residual Tropospheric Delay. Remote Sens. 2021, 13, 1202. [Google Scholar] [CrossRef]
- Hopfield, H.S. Two-quartic tropospheric refractivity profile for correcting satellite data. J. Geophys. Res. 1969, 74, 4487–4499. [Google Scholar] [CrossRef]
- Saastamoinen, J. Introduction to practical computation of astronomical refraction. Bull. Geod. 1972, 106, 383–397. [Google Scholar] [CrossRef]
- Leandro, R.F.; Langley, R.B.; Santos, M.C. UNB3m_pack: A neutral atmosphere delay package for radiometric space techniques. GPS Solut. 2008, 12, 65–70. [Google Scholar] [CrossRef]
- Penna, N.; Dodson, A.; Chen, W. Assessment of EGNOS Tropospheric Correction Model. J. Navig. 2001, 54, 37–55. [Google Scholar] [CrossRef]
- Hofmeister, A.; Böhm, J. Application of ray-traced tropospheric slant delays to geodetic VLBI analysis. J. Geod. 2017, 91, 945–964. [Google Scholar] [CrossRef]
- Yao, Y.; Hu, Y.; Yu, C.; Zhang, B.; Guo, J. An improved global zenith tropospheric delay model GZTD2 considering diurnal variations. Nonlinear Process. Geophys. 2016, 23, 127–136. [Google Scholar] [CrossRef]
- Schüler, T. The TropGrid2 standard tropospheric correction model. GPS Solut. 2014, 18, 123–131. [Google Scholar] [CrossRef]
- Yao, Y.; Xu, C.; Shi, J.; Cao, N.; Zhang, B.; Yang, J. ITG: A New Global GNSS Tropospheric Correction Model. Sci. Rep. 2015, 5, 10273. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Chen, X.; Sun, J.; Liu, Q. An analysis of GPT2/GPT2w+Saastamoinen models for estimating zenith tropospheric delay over Asian area. Adv. Space Res. 2017, 59, 824–832. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, Y.; Li, W.; Li, Y.; Chai, Y. Assessment of Three Tropospheric Delay Models (IGGtrop, EGNOS and UNB3m) Based on Precise Point Positioning in the Chinese Region. Sensors 2016, 16, 122. [Google Scholar] [CrossRef]
- Chen, J.; Gao, Y. A Machine Learning-Based Tropospheric Prediction Approach for High-Precision Real-Time GNSS Positioning. Sensors 2024, 24, 2957. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.; Yu, C.; Hu, Y. A New Method to Accelerate PPP Convergence Time by using a Global Zenith Troposphere Delay Estimate Model. J. Navig. 2014, 67, 899–910. [Google Scholar] [CrossRef]
- Urquhart, L.; Nievinski, F.G.; Santos, M.C. Assessment of troposphere mapping functions using three-dimensional ray-tracing. GPS Solut. 2014, 18, 345–354. [Google Scholar] [CrossRef]
- Wilgan, K.; Hadas, T.; Hordyniec, P.; Bosy, J. Real-time precise point positioning augmented with high-resolution numerical weather prediction model. GPS Solut. 2017, 21, 1341–1353. [Google Scholar] [CrossRef]
- Shi, J.; Xu, C.; Guo, J.; Gao, Y. Local troposphere augmentation for real-time precise point positioning. Earth Planets Space 2014, 66, 30. [Google Scholar] [CrossRef]
- Cui, B.; Wang, J.; Li, P.; Ge, M.; Schuh, H. Modeling wide-area tropospheric delay corrections for fast PPP ambiguity resolution. GPS Solut. 2022, 26, 56. [Google Scholar] [CrossRef]
- Lou, Y.; Huang, J.; Zhang, W.; Liang, H.; Zheng, F.; Liu, J. A New Zenith Tropospheric Delay Grid Product for Real-Time PPP Applications over China. Sensors 2018, 18, 65. [Google Scholar] [CrossRef]
- Xu, C.; Yao, Y.; Shi, J.; Zhang, Q.; Peng, W. Development of Global Tropospheric Empirical Correction Model with High Temporal Resolution. Remote Sens. 2020, 12, 721. [Google Scholar] [CrossRef]
- Deng, Y.; Yang, H.; Zheng, Y.; Zhang, Y.; Wu, Z.; Li, J.; Tao, J. Improving GNSS precise point positioning with tropospheric constraints from data-driven numerical weather prediction model. Geospat. Inf. Sci. 2025; in press. [Google Scholar] [CrossRef]
- Jensen, A.B.O.; Ovstedal, O. Real Time Modelling of the Troposphere for Network RTK. In Proceedings of the 19th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2006), Fort Worth, TX, USA, 26–29 September 2006. [Google Scholar]
- Wübbena, G.; Bagge, A.; Schmitz, M. Network−Based Techniques for RTK Applications. In Proceedings of the GPS Symposium, Tokyo, Japan, 15–18 November 2001. [Google Scholar]
- Kim, B.-G.; Kim, D.; Song, J.; Kee, C. Expanding Network RTK Coverage Using an Ionospheric-Free Combination and Kriging for Tropospheric Delay. In Proceedings of the ION 2021 Pacific PNT Meeting, Honolulu, HI, USA, 19–23 April 2021. [Google Scholar]
- Xu, Y.; Wu, C.; Li, L.; Yan, L.; Liu, M.; Wang, S. GPS/BDS Medium/Long-Range RTK Constrained with Tropospheric Delay Parameters from NWP Model. Remote Sens. 2018, 10, 1113. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X.; Li, P.; Tu, R.; Lu, X.; Huang, J.; Wang, G. Performance of PPP and PPP-RTK with new-generation GNSS constellations and signals. Satell. Navig. 2025, 6, 17. [Google Scholar] [CrossRef]
- Yin, Z.; Yang, J.; Ma, Y.; Wang, S.; Chai, D.; Cui, H. A Robust Adaptive Extended Kalman Filter Based on an Improved Measurement Noise Covariance Matrix for the Monitoring and Isolation of Abnormal Disturbances in GNSS/INS Vehicle Navigation. Remote Sens. 2023, 15, 4125. [Google Scholar] [CrossRef]
- Mosavi, M.R.; Ayatollahi, A.; Emamgholipour, I. Noise Smoothing for GPS Receivers Positioning Data using Wavelet Transform. Int. J. Electr. Comput. Eng. 2011, 4, 2. [Google Scholar]
- Zhang, Q.; Zhang, L.; Sun, A.; Meng, X.; Zhao, D.; Hancock, C. GNSS Carrier-Phase Multipath Modeling and Correction: A Review and Prospect of Data Processing Methods. Remote Sens. 2024, 16, 189. [Google Scholar] [CrossRef]
- Angrisano, A.; Del Pizzo, S.; Gaglione, S.; Troisi, S.; Vultaggio, M. Using local redundancy to improve GNSS absolute positioning in harsh scenario. Acta IMEKO 2018, 7, 16. [Google Scholar] [CrossRef]
- Lotfy, A.; Abdelfatah, M.; El-Fiky, G. Improving the performance of GNSS precise point positioning by developed robust adaptive Kalman filter. Egypt. J. Remote Sens. Space Sci. 2022, 25, 919–928. [Google Scholar] [CrossRef]
- Shinghal, G.; Bisnath, S. Conditioning and PPP processing of smartphone GNSS measurements in realistic environments. Satell. Navig. 2021, 2, 10. [Google Scholar] [CrossRef] [PubMed]
- Kiliszek, D.; Kroszczyński, K.; Araszkiewicz, A. Analysis of Different Weighting Functions of Observations for GPS and Galileo Precise Point Positioning Performance. Remote Sens. 2022, 14, 2223. [Google Scholar] [CrossRef]
- Zhao, L.; Zhai, W. Assessment of PPP Using BDS PPP-B2b Products with Short-Time-Span Observations and Backward Smoothing Method. Remote Sens. 2024, 17, 25. [Google Scholar] [CrossRef]
- Watson, R.M.; Gross, J.N. Evaluation of kinematic precise point positioning convergence with an incremental graph optimizer. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; pp. 589–596. [Google Scholar] [CrossRef]
- Wang, Z.; Hou, X.; Dan, Z.; Fang, K. Adaptive Kalman filter based on integer ambiguity validation in moving base RTK. GPS Solut. 2023, 27, 34. [Google Scholar] [CrossRef]
- Wang, K.; El-Mowafy, A.; Rizos, C.; Wang, J. Integrity Monitoring for Horizontal RTK Positioning: New Weighting Model and Overbounding CDF in Open-Sky and Suburban Scenarios. Remote Sens. 2020, 12, 1173. [Google Scholar] [CrossRef]
- Wang, F.; Geng, J. GNSS PPP-RTK tightly coupled with low-cost visual-inertial odometry aiming at urban canyons. J. Geod. 2023, 97, 66. [Google Scholar] [CrossRef]
- Grewal, M.S.; Andrews, A.P.; Bartone, C.G. Global Navigation Satellite Systems, Inertial Navigation, and Integration, 1st ed.; Wiley: Hoboken, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Sabatini, R.; Moore, T.; Ramasamy, S. Global navigation satellite systems performance analysis and augmentation strategies in aviation. Prog. Aerosp. Sci. 2017, 95, 45–98. [Google Scholar] [CrossRef]
- Setlak, L.; Kowalik, R. The Basic Architecture of the System with the A-GNSS Receiver. MATEC Web Conf. 2019, 292, 04010. [Google Scholar] [CrossRef]
- Hamza, V.; Stopar, B.; Sterle, O.; Pavlovčič-Prešeren, P. Recent advances and applications of low-cost GNSS receivers: A review. GPS Solut. 2025, 29, 56. [Google Scholar] [CrossRef]
- Hamza, V.; Stopar, B.; Sterle, O.; Pavlovčič-Prešeren, P. Observations and positioning quality of low-cost GNSS receivers: A review. GPS Solut. 2024, 28, 149. [Google Scholar] [CrossRef]
- Capuano, V.; Shehaj, E.; Blunt, P.; Botteron, C.; Farine, P.-A. High accuracy GNSS based navigation in GEO. Acta Astronaut. 2017, 136, 332–341. [Google Scholar] [CrossRef]
- Kowalczyk, W.Z.; Hadas, T. A comparative analysis of the performance of various GNSS positioning concepts dedicated to precision agriculture. Rep. Geod. Geoinform. 2024, 117, 11–20. [Google Scholar] [CrossRef]
- Xu, J. Review of the GNSS’s Development and Its Civil Applications. In Proceedings of the 2022 6th International Seminar on Education, Management and Social Sciences (ISEMSS 2022), Changchun, China, 27–29 May 2022; Ali, G., Birkök, M.C., Khan, I.A., Eds.; Atlantis Press SARL: Paris, France, 2022; Volume 687, pp. 2596–2604. [Google Scholar] [CrossRef]
- Pany, T.; Kappen, G.; Hartl, L.M.; Morrison, A.; Patino Studencka, M.; Rao, A.; Stöber, C. GNSS Software-Defined Radio: History, Current Developments, and Standardization Efforts. NAVIGATION 2024, 71, navi.628. [Google Scholar] [CrossRef]
- Akeela, R.; Dezfouli, B. Software-defined Radios: Architecture, state-of-the-art, and challenges. Comput. Commun. 2018, 128, 106–125. [Google Scholar] [CrossRef]
- Schmidt, E.; Ruble, Z.; Akopian, D.; Pack, D.J. Software-Defined Radio GNSS Instrumentation for Spoofing Mitigation: A Review and a Case Study. IEEE Trans. Instrum. Meas. 2019, 68, 2768–2784. [Google Scholar] [CrossRef]
- Taylor, F.; Aguado, L.E.; Amin, M.P.; Kato, N.; Clemente, P.A. Software Defined Radio for GNSS Radio Frequency Interference Localization. Sensors 2023, 24, 72. [Google Scholar] [CrossRef]
- PocketSDR. Available online: https://github.com/tomojitakasu/PocketSDR (accessed on 1 October 2025).
- GNSS SDR Open Source Tool. Available online: https://www.academia.edu/18084392/GNSS_SDR_an_open_source_tool_for_researchers_and_developers (accessed on 1 October 2025).
- Alotaibi, A.; Chatwin, C.; Birch, P. Evaluating Global Navigation Satellite System (GNSS) Constellation Performance for Unmanned Aerial Vehicle (UAV) Navigation Precision. J. Comput. Commun. 2024, 12, 39–62. [Google Scholar] [CrossRef]
- Reuper, B.; Becker, M.; Leinen, S. Benefits of Multi-Constellation/Multi-Frequency GNSS in a Tightly Coupled GNSS/IMU/Odometry Integration Algorithm. Sensors 2018, 18, 3052. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, Q.; Yu, Z.; Hu, C.; Liu, H.; Han, S. Modeling and performance assessment of precise point positioning with multi-frequency GNSS signals. Measurement 2022, 201, 111687. [Google Scholar] [CrossRef]
- Erol, S. A Comparative Study for Performance Analysis of Kinematic Multi-Constellation GNSS PPP in Dynamic Environment. J. Mar. Sci. Eng. 2020, 8, 514. [Google Scholar] [CrossRef]
- Dutta, U.; Johansson, J. Multi-Constellation/Multi-Frequency GNSS Signal Degradation Due to Foliage and Reflective Environments. Eng. Proc. 2023, 54, 2. [Google Scholar] [CrossRef]
- Lucas-Sabola, V.; Seco-Granados, G.; Lopez-Salcedo, J.A.; Garcia-Molina, J.A.; Crisci, M. Cloud GNSS receivers: New advanced applications made possible. In Proceedings of the 2016 International Conference on Localization and GNSS (ICL-GNSS), Barcelona, Spain, 28–30 June 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Song, J.; Zhao, L.; Xu, W.; Jin, S. A Cloud-Based Solution for Real-Time PPP in GNSS Positioning: Implementation and Performance Evaluation. SSRN 2024. [Google Scholar] [CrossRef]
- Hernández Olcina, J.; Anquela Julián, A.B.; Martín Furones, Á.E. Real-time cloud computing of GNSS measurements from smartphones and mobile devices for enhanced positioning and navigation. GPS Solut. 2024, 28, 167. [Google Scholar] [CrossRef]
- Hernández Olcina, J.; Anquela Julián, A.B.; Martín Furones, Á.E. Treatment and Analysis of the GNSS Signal from Smartphones and Its Applicability to Urban Mobility. Environ. Sci. Proc. 2023, 28, 1. [Google Scholar] [CrossRef]
- Hernández Olcina, J.; Anquela Julián, A.B.; Martín Furones, Á.E. Navigating latency hurdles: An in-depth examination of a cloud-powered GNSS real-time positioning application on mobile devices. Sci. Rep. 2024, 14, 14668. [Google Scholar] [CrossRef]
- Yoshida, S. Study on Cloud-Based GNSS Positioning Architecture with Satellite Selection Algorithm and Report of Field Experiments. IEICE Trans. Commun. 2022, E105.B, 388–398. [Google Scholar] [CrossRef]
- Quezada-Gaibor, D.; Torres-Sospedra, J.; Nurmi, J.; Koucheryavy, Y.; Huerta, J. Cloud Platforms for Context-Adaptive Positioning and Localisation in GNSS-Denied Scenarios—A Systematic Review. Sensors 2021, 22, 110. [Google Scholar] [CrossRef]
- Boguspayev, N.; Akhmedov, D.; Raskaliyev, A.; Kim, A.; Sukhenko, A. A Comprehensive Review of GNSS/INS Integration Techniques for Land and Air Vehicle Applications. Appl. Sci. 2023, 13, 4819. [Google Scholar] [CrossRef]
- He, Y.; Li, J.; Liu, J. Research on GNSS INS & GNSS/INS Integrated Navigation Method for Autonomous Vehicles: A Survey. IEEE Access 2023, 11, 79033–79055. [Google Scholar] [CrossRef]
- Chang, L.; Niu, X.; Liu, T.; Tang, J.; Qian, C. GNSS/INS/LiDAR-SLAM Integrated Navigation System Based on Graph Optimization. Remote Sens. 2019, 11, 1009. [Google Scholar] [CrossRef]
- Elamin, A.; Abdelaziz, N.; El-Rabbany, A. A GNSS/INS/LiDAR Integration Scheme for UAV-Based Navigation in GNSS-Challenging Environments. Sensors 2022, 22, 9908. [Google Scholar] [CrossRef]
- Liu, J.; Gao, K.; Guo, W.; Cui, J.; Guo, C. Role, path, and vision of “5G + BDS/GNSS”. Satell. Navig. 2020, 1, 23. [Google Scholar] [CrossRef]
- Li, S.; Wang, S.; Zhou, Y.; Shen, Z.; Li, X. Tightly Coupled Integration of GNSS, INS, and LiDAR for Vehicle Navigation in Urban Environments. IEEE Internet Things J. 2022, 9, 24721–24735. [Google Scholar] [CrossRef]
- Liu, D.; Wang, H.; Xia, Q.; Jiang, C. A Low-Cost Method of Improving the GNSS/SINS Integrated Navigation System Using Multiple Receivers. Electronics 2020, 9, 1079. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Q.; Zhang, H.; Duan, X. A Low-Cost GNSS/INS integration method aided by Cascade-LSTM Pseudo-Velocity measurement for bridging GNSS outages. Measurement 2025, 240, 115518. [Google Scholar] [CrossRef]
- Wu, F.; Zhao, H.; Zhao, Y.; Zhong, H. Robust SINS/GNSS Integration Method for High Dynamic Applications. TELKOMNIKA Indones. J. Electr. Eng. 2015, 13, 292–299. [Google Scholar] [CrossRef]
- Zhao, C.; Yang, Z.; Cheng, X.; Hu, J.; Hou, X. SINS/GNSS integrated navigation system based on maximum versoria filter. Chin. J. Aeronaut. 2022, 35, 168–178. [Google Scholar] [CrossRef]
- Wen, W. 3D LiDAR Aided GNSS and Its Tightly Coupled Integration with INS Via Factor Graph Optimization. In Proceedings of the 33rd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2020), Online, 21–25 September 2020; pp. 1649–1672. [Google Scholar] [CrossRef]
- Katsumoto, T.; Takaoka, K.; Takanohashi, K.; Youssef, M. GNSS System Design and Evaluation for IoT Applications. In Proceedings of the 30th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2017), Portland, OR, USA, 25–29 September 2017; pp. 3566–3572. [Google Scholar] [CrossRef]
- Wang, J.; Garthwaite, M.C.; Wang, C.; Hellen, L. Development of a Multi-Sensor GNSS-IoT System for Precise Water Surface Elevation Measurement. Sensors 2025, 25, 3566. [Google Scholar] [CrossRef]
- Vadlamudi, M.N.; Jayanthi, N.; Swetha, G.; Nishitha, P.; Al-Salman, G.A.; Saikumar, K. IoT Empowered GNSS Tracking in Real-time via Cloud Infrastructure. In Proceedings of the 2024 IEEE 9th International Conference for Convergence in Technology (I2CT), Pune, India, 5–7 April 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Agarwal, K.; Ainapure, B.; Shukla, A. A Comprehensive Review of the GNSS with IoT Applications and Their Use Cases with Special Emphasis on Machine Learning and Deep Learning Models. Int. J. Res. Innov. Technol. Comput. Commun. 2023, 11, 220–230. [Google Scholar] [CrossRef]
- Landa, V.; Reuveni, Y. Assessment of Dynamic Mode Decomposition (DMD) Model for Ionospheric TEC Map Predictions. Remote Sens. 2023, 15, 365. [Google Scholar] [CrossRef]
- Zewdie, G.K.; Valladares, C.; Cohen, M.B.; Lary, D.J.; Ramani, D.; Tsidu, G.M. Data-Driven Forecasting of Low-Latitude Ionospheric Total Electron Content Using the Random Forest and LSTM Machine Learning Methods. Space Weather 2021, 19, e2020SW002639. [Google Scholar] [CrossRef]
- Zhang, Q.; Yao, Y.; Kong, J.; Ma, X.; Zhu, H. A New GNSS TEC Neural Network Prediction Algorithm with the Data Fusion of Physical Observation. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–12. [Google Scholar] [CrossRef]
- Linty, N.; Dovis, F.; Alfonsi, L. Software-defined radio technology for GNSS scintillation analysis: Bring Antarctica to the lab. GPS Solut. 2018, 22, 96. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sukhenko, A.; Meirambekuly, N.; Syzdykov, A.; Mukhamedgali, A.; Mellatova, Y. GNSS for High-Precision and Reliable Positioning: A Review of Correction Techniques and System Architectures. Appl. Sci. 2025, 15, 12304. https://doi.org/10.3390/app152212304
Sukhenko A, Meirambekuly N, Syzdykov A, Mukhamedgali A, Mellatova Y. GNSS for High-Precision and Reliable Positioning: A Review of Correction Techniques and System Architectures. Applied Sciences. 2025; 15(22):12304. https://doi.org/10.3390/app152212304
Chicago/Turabian StyleSukhenko, Anna, Nursultan Meirambekuly, Arman Syzdykov, Adil Mukhamedgali, and Yenglik Mellatova. 2025. "GNSS for High-Precision and Reliable Positioning: A Review of Correction Techniques and System Architectures" Applied Sciences 15, no. 22: 12304. https://doi.org/10.3390/app152212304
APA StyleSukhenko, A., Meirambekuly, N., Syzdykov, A., Mukhamedgali, A., & Mellatova, Y. (2025). GNSS for High-Precision and Reliable Positioning: A Review of Correction Techniques and System Architectures. Applied Sciences, 15(22), 12304. https://doi.org/10.3390/app152212304






