Abstract
We propose a LiDAR point-based docking spot generation system for autonomous docking using point clouds from a low-density LiDAR sensor in berthing environments. The system consists of four key stages: scan matching, 3D object detection, long-term object perception, and docking spot generation. Scan matching estimates the unmanned surface vehicle’s position within the global coordinate system using scan-to-map matching. In the 3D object detection stage, high-quality point clouds are generated from low-density LiDAR data to enhance detection performance, and detected object information is transformed into the global coordinate system. In the long-term object perception stage, object information beyond the LiDAR’s field of view is stored on the map for continuous environmental perception. Finally, the docking spot generation stage employs an algorithm to generate valid docking spots. Experimental validation in real-world environments demonstrates that the proposed system achieves an average 3D mAP improvement of 23.38 percentage points across multiple detection architectures. Notably, for small object detection, the average 3D AP improvement reaches 38.12 percentage points, demonstrating significant effectiveness in challenging scenarios. These improvements enhance long-term perception, object management, and docking spot generation stability.
1. Introduction
In recent years, unmanned surface vehicles (USVs) have become more widely used in various fields, including environmental monitoring, maritime transportation, and search and rescue operations. However, in line with the increasing awareness of climate change and the demand for marine environmental protection, there is a growing need for the development of USV technologies for maritime applications that minimize human intervention. Maritime environments are inherently unstructured and unpredictable. This complexity requires precise detection strategies and robust autonomous navigation for the successful deployment of marine USVs [1]. Autonomous docking is a particular challenge for the practical development of USVs, requiring reliable object detection, docking path planning, and accurate localization.
To achieve autonomous docking, various types of sensors can be employed, with cameras, RAdio Detection And Ranging (RADAR), and Light Detection And Ranging (LiDAR) the most commonly used options. Cameras accurately capture the colors and shapes of objects in the surrounding environment, making them highly effective for object detection [2]. Therefore, a number of researchers have taken advantage of the low-cost, high-precision localization capabilities of cameras for autonomous docking applications. For example, stereo vision-based localization systems have been combined with 3D reconstruction techniques to identify stable autonomous docking spots even in unstructured environments [3]. Self-supervised learning-based models have also been employed to predict the docking station location and orientation [4], while deep reinforcement learning employs RGB images to control the speed and posture during autonomous docking [5]. However, camera-based systems suffer from performance degradation during nighttime or under low-visibility conditions and are less reliable in complex environments. As a result, the use of cameras alone is insufficient for the establishment of stable autonomous docking systems.
RADAR is a powerful sensor capable of detecting objects over long distances and is widely used in autonomous docking systems within maritime environments. A representative approach involves first detecting targets using RADAR and then refining object tracking through electro-optical systems [6]. However, it remains difficult to use RADAR to accurately track objects in complex environments where multiple objects are densely clustered or exhibit significant shape variations [7].
LiDAR technology generates 3D point clouds to precisely detect the geometric features of an environment, and it has been widely investigated for use in autonomous docking systems [8,9,10]. For example, a LiDAR-based approach has been used to analyze the horizontal planes and pillar positions of docks and identify autonomous docking spots, and LiDAR has been combined with deep learning-based semantic segmentation with a Kalman filter to track and classify objects near rivers [11,12]. Point cloud clustering has also been utilized to separate static and dynamic objects, thus overcoming the challenges associated with dynamic object detection [13]. In localization research using LiDAR point clouds, the deep learning-based inference of coastlines and semantic information on buildings has been integrated with simultaneous localization and mapping (SLAM) or applied reinforcement learning to reduce the risk of collisions when detecting autonomous docking spots [14].
Unlike cameras and RADAR, LiDAR provides highly accurate environmental perception even in complex environments and at nighttime. However, the deployment of high-density LiDAR, which produces high-resolution, high-quality point clouds, is limited by its significantly high initial purchase cost. Therefore, research is needed to enhance object detection using low-density LiDAR and thus improve the stability and reliability of autonomous docking systems [15,16].
Point cloud density, defined as the number of points per unit area, is a critical factor affecting 3D object detection performance. While there is no universally standardized threshold distinguishing high-density from low-density point clouds, the impact of point density on detection performance can be observed in the range-based evaluation metrics of established 3D object detection benchmarks [17,18]. Due to the inherent characteristics of LiDAR sensors, point density naturally decreases with distance, as objects farther from the sensor receive fewer points per unit area, effectively becoming low-density point clouds. The evaluation results from these benchmarks consistently show that detection performance degrades significantly at longer ranges, which directly correlates with lower point density. This demonstrates the fundamental challenge of maintaining reliable object detection performance with low-density point clouds.
In the present study, we propose a method to generate high-quality point clouds from low-density LiDAR data based on point cloud registration techniques to improve object detection. The proposed approach enables the implementation of highly accurate autonomous docking systems in cost-constrained environments that rely on low-density LiDAR. In this framework, a map is constructed using scan matching to ensure precise localization within the global coordinate system, which is essential for autonomous docking. Detected objects are then continuously stored on the map to manage those that fall outside the field of view (FOV) of the LiDAR. Next, a docking spot generation (DSG) algorithm is employed to generate valid docking spots.
We applied the high-quality point clouds generated by our method to various object detection models. All models demonstrated consistent performance improvements, validating the generalizability of our approach. Real-world docking experiments further confirmed the reliability and practical utility of the proposed system. The key contributions of the present study are as follows:
- High-quality point cloud generation using low-density LiDAR sensor: We generate high-quality point clouds by registering sequential low-density LiDAR point clouds over time.
- Improved object detection accuracy based on high-quality training data: By applying the high-quality training data to various object detection models and achieving consistent performance improvements, the proposed method demonstrates its generalizability and validity.
- Long-term perception and management of objects: We store and manage object information on the map over time to improve environmental perception in docking scenarios.
- DSG algorithm: The devised algorithm identifies candidate docking spots and selects valid docking spots.
- Real-world applicability of docking technology: We validate our autonomous docking system under various real-world scenarios, demonstrating its technological efficiency and stability.
2. Related Works
Scan matching and 3D object detection are important technological components of autonomous docking systems for USVs. Scan matching utilizes LiDAR point clouds to estimate the position of a USV in the global coordinate system. LiDAR point clouds are also employed in 3D object detection to precisely estimate the positions of objects in 3D space and extract the surrounding object information necessary to generate autonomous docking spots. In the present study, we integrate these two technologies to generate autonomous docking spots using low-density LiDAR.
2.1. Scan Matching Methods
Scan matching is used to accurately estimate the position of a moving object within an environment based on LiDAR point cloud data. This method can be categorized into two types: direct point matching and feature-based matching. Direct point matching estimates the transformation between two LiDAR scan positions based on LiDAR point information. Iterative closest point (ICP) [19] minimizes the sum of the squared distance between corresponding point pairs to determine the optimal transformation of two LiDAR scan positions. Although ICP is straightforward to implement, it is highly susceptible to local minima, which can lead to significant errors, while iterative optimization can result in high computational costs.
To address these issues, several improvements have been proposed. For example, trimmed ICP (TrICP) [20] enhances the computational efficiency and robustness of ICP by employing a trimmed least-squares approach instead of the standard least-squares method. Point-to-plane ICP [21] also improves ICP performance by incorporating planar information in real-world environments. Generalized ICP (GICP) [22] extends ICP by integrating both approaches [20,21] and additionally utilizing covariance information for neighboring points to enhance performance. However, these methods still struggle to completely avoid local minima because they rely on point distance information.
As a response to these limitations, normal distributions transform (NDT) [23] was introduced to utilize point distribution information. NDT partitions the 3D space into small volumetric grid cells called voxels. Within each voxel, the point distribution is modeled as a Gaussian distribution, creating a smooth and continuous representation of the environment. NDT then uses this representation as a cost function to find the optimal transformation between the current point cloud and an existing map, providing highly reliable output in static environments. In addition, because NDT does not require explicit point correspondence, it offers superior computational efficiency and ensures stability during the registration process.
The feature-based matching approach estimates the positions of objects by extracting key structural information from LiDAR point cloud data in the form of geometric features. By using feature points instead of the entire point cloud, outliers such as noise are effectively removed, thus improving the computational speed and overall performance. LiDAR odometry and mapping (LOAM) [24] identifies and matches feature points corresponding to edges and planes by evaluating the smoothness of local surfaces and estimating the transformation between two LiDAR scan positions. This method ensures accurate feature extraction through point cloud segmentation and has been developed further to progressively determine transformations with six degrees of freedom [25]. Other research has also aimed to reduce feature detection errors for horizontal planes, particularly when using LiDAR sensors optimized for vertically sparse scanning [26]. Furthermore, surfel-based mapping (SuMa) [27] utilizes surface normals for odometry estimation by comparing vertex and normal maps rendered from the current scan with a surfel-based map. This approach has been extended to integrate semantic information to achieve more accurate odometry estimation [28].
Though feature-based matching performs well in environments where structural feature points are well-defined, it is limited in the presence of sparse features or high levels of noise. Berthing environments in particular tend to be structurally monotonous and lack distinctive feature points, complicating standardized feature extraction. Therefore, we estimate the transformation between LiDAR scan positions using the computationally efficient NDT, which effectively addresses feature sparsity and local minima.
2.2. 3D Object Detection Methods
3D object detection predicts the location of objects in 3D space by generating 3D bounding boxes with rotation based on point cloud data. This method can be categorized into two types: point-based object detection and voxel-based object detection. A representative example of point-based object detection is PointRCNN [29], which utilizes PointNet++ [30] to identify foreground points that are potential objects in the point cloud. Based on these points, it conducts the region-proposal process [31] to highlight potential object regions. The points within these regions are passed through the PointNet++ encoder to predict 3D bounding boxes.
Another point-based approach, 3DSSD [32], differs from PointRCNN in that it adopts an encoder-only structure. It utilizes Distance-based Farthest Point Sampling (D-FPS) and Feature-based Farthest Point Sampling (F-FPS) in parallel, enabling the model to efficiently sample only the most informative points. In addition, it applies a voting mechanism inspired by VoteNet [33], allowing each point to predict the center of its corresponding object, upon which 3D bounding boxes are regressed. IA-SSD [34], which also adopts an encoder-based architecture like 3DSSD, predicts in advance the likelihood of each point belonging to an object. This enables the model to preserve important points that might otherwise be discarded during the sampling process. As a result, it reduces the loss of semantically meaningful information and facilitates more robust 3D object detection.
A representative example of voxel-based object detection is PointPillars [35]. PointPillars divides the point cloud into vertical pillars and utilizes a simplified PointNet [36] to extract features from each pillar. These pillars are then converted into a pseudo-image and processed through a 2D convolutional network, where 3D bounding boxes are predicted at each pixel. This structure significantly reduces computational complexity by replacing 3D convolutions with 2D convolutions, enabling high processing speed. In contrast, SECOND [37] partitions the point cloud into 3D voxels and normalizes the points within each voxel to preserve spatial structure. To address the high computational cost of 3D convolutions, it adopts 3D sparse convolution [38,39], which greatly improves efficiency. As a result, SECOND is capable of accurately learning 3D spatial structures while maintaining both high detection performance and computational efficiency.
Voxel R-CNN [40], similar to SECOND, divides the point cloud into voxels and extracts features using 3D sparse convolution. It then generates region proposals based on the 2D feature map in the Bird’s Eye View (BEV) and defines a 3D grid of query points within each proposal region. For each query point, voxel-level features from the 3D feature map are retrieved using a voxel query mechanism, enabling the extraction of precise object information. These features are subsequently used to predict 3D bounding boxes. PillarNet [41] builds upon the lightweight architecture of PointPillars by incorporating 2D sparse convolution to improve computational efficiency. Furthermore, it enhances the utilization of 2D feature maps by improving the intermediate processing stage to integrate and emphasize multi-scale information. This allows PillarNet to maintain fast inference speed while further improving object detection accuracy.
Point-based object detection models are sensitive to the number of input points, making their configurations highly dependent on point density. These models typically filter points to a fixed number at the input layer and sample points to specific numbers at each subsequent layer, with network parameters configured according to the expected point distribution of the training dataset. This architectural dependency means that fairly comparing raw point clouds and high-quality point clouds would require designing and tuning separate network architectures for each dataset, introducing additional variables beyond point cloud quality itself. This characteristic has been consistently observed across various point-based detection architectures [32,34].
Consequently, it is difficult to fairly evaluate raw point clouds and high-quality point clouds generated by the proposed method under the same model setting. Therefore, we adopt only voxel-based object detection models, which can provide stable and consistent representations across different density conditions.
2.3. Low-Density LiDAR for 3D Object Detection
Several 3D object detection datasets [17,42] provide ground truth poses for each frame. Many detection methods [32,34,35,37] leverage these provided poses to aggregate low-density point clouds across multiple frames into a single keyframe coordinate system, generating high-quality point clouds for training. While this approach effectively demonstrates the benefits of increased point density, it fundamentally depends on dataset-provided pose information, typically obtained through high-precision global positioning system (GPS) and inertial measurement unit (IMU). This dependency creates a significant barrier for deployment in new environments where such pose information is unavailable.
In contrast, our LP-DSG system generates pose estimates directly from LiDAR point clouds through scan matching, eliminating dependency on external pose sources. This self-contained approach enables direct deployment in new berthing environments without requiring dataset specific pose information or additional sensor infrastructure while maintaining real-time performance on embedded platforms.
3. LP-DSG System
We propose a LiDAR point-based DSG (LP-DSG) system to generate autonomous docking spots for USVs in berthing environments. As shown in Figure 1, LP-DSG consists of four key stages: scan matching, 3D object detection, long-term object perception (LOP), and DSG.
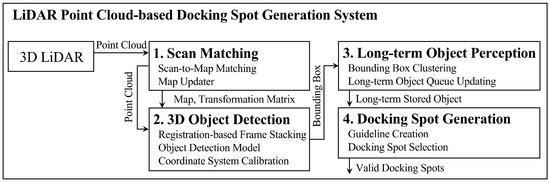
Figure 1.
Overview of the proposed LP-DSG system, which consists of four interconnected stages: scan matching, 3D object detection, LOP, and DSG.
In the scan matching stage, the system estimates the transformation matrix between the current LiDAR scan and the map through scan-to-map matching. The map is continuously updated by accumulating multiple scans in the global coordinate system. In the 3D object detection stage, low-density LiDAR point clouds are transformed into high-quality point clouds using the transformation matrix from scan matching. The object detection model then generates precise 3D bounding boxes, which are projected onto the map. In the LOP stage, bounding boxes from each frame are clustered and stored to preserve object information outside the LiDAR FOV. Finally, in the DSG stage, the system establishes guidelines using landmarks and selects valid docking spots from the generated candidates.
3.1. Scan Matching
Scan matching utilizes point clouds to estimate the transformation matrix between LiDAR scan positions, thus aligning point clouds with the global coordinate system to construct a map. As shown in Figure 2, the scan matching process consists of two stages: Scan-to-Map Matching, which accurately estimates the current position in the global coordinate system by aligning newly collected point clouds with the existing map to calculate the transformation matrix, and the Map Updater, which integrates newly collected point clouds into the map.
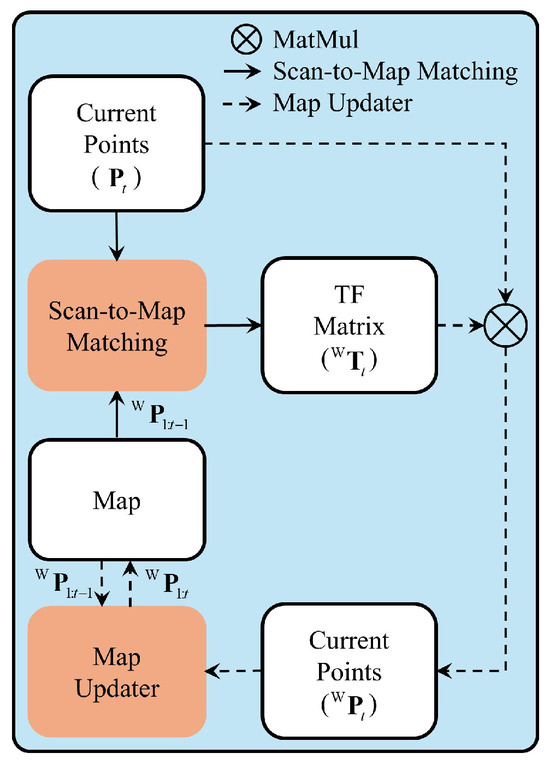
Figure 2.
Process for determining transformation matrix via scan-to-map matching and constructing a map in the global coordinate system. Scan-to-map matching takes point cloud as the source and map as the target. Through scan-to-map matching, is obtained as the output. The map updater then integrates transformed point cloud into to generate the updated map .
3.1.1. Scan-to-Map Matching
Scan-to-map matching estimates the transformation matrix , which transforms point cloud collected at time t from the LiDAR sensors into the global coordinate system, with designated as the source and map as the target.
Source is defined based on a coordinate system centered on the sensor and is expressed as
where contains points at time t, and each point is represented as a column vector that includes its position and intensity .
Target map consists of the accumulated point cloud in the global coordinate system up to time :
where k represents any time step from 1 to .
As illustrated in Figure 2, scan-to-map matching estimates at time t using and :
where the scan-to-map matching function estimates in real time. Here, rotation matrix and translation vector represent the 3D rotational state and position in the global coordinate system at time t, respectively.
3.1.2. Map Updater
As shown in Figure 2, transformed point cloud at time t in the global coordinate system is obtained by applying to :
is then merged with to update map as follows:
3.2. 3D Object Detection
3D object detection estimates the position, size, and orientation of objects in point clouds. Registration-based Frame Stacking (RFS) is conducted to align continuously collected low-density point clouds, generating high-quality point clouds. The high-quality point clouds generated using RFS compensate for the low object detection performance that results from the use of low-density point clouds. Crucially, the high-quality point clouds provide the Object Detection Model with more reliable and accurate geometric cues of the object’s true shape and volume, enabling precise detection of objects within the sensor coordinate system. These detected objects are then transformed into the global coordinate system via Coordinate System Calibration.
3.2.1. Registration-Based Frame Stacking
Figure 3 illustrates the overall process for RFS. One of scan matching output is stored in the point cloud queue for each frame. The point clouds stored in the queue are merged to generate in the global coordinate system:
where n represents the queue size . Subsequently, the other of scan matching output is inverted to obtain inverse transformation matrix . Applying to transforms it into , which represents the high-quality point cloud in the sensor coordinate system:
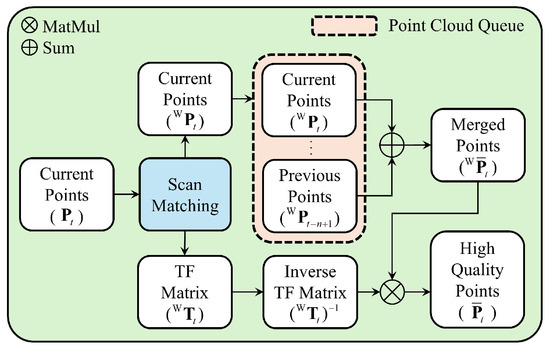
Figure 3.
Process for the generation of high-quality point cloud using RFS. One of scan matching output is stored in the point cloud queue for each frame. The merged point cloud is generated by combining previously stored point clouds in the point cloud queue. Subsequently, the other of scan matching output is inverted and applied to , generating within the sensor coordinate system.
is given by the following equation:
3.2.2. Object Detection Model
As shown in Figure 4, the high-quality point cloud obtained through the preprocessing stage is cropped to a region of interest (ROI) with dimensions , which is then divided into voxels of size . In the case of using a 2D backbone, the height of the region is set equal to . Each voxel is fed into the object detection model, which outputs a feature map of size . Each pixel in this feature image is assigned anchors, resulting in a total of anchors, which form the anchor set :
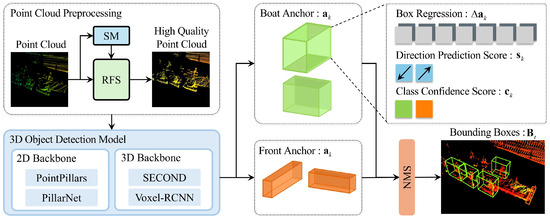
Figure 4.
Overview of the object detection model. The point cloud is transformed into a high-quality point cloud through a preprocessing stage composed of SM and RFS. The processed point cloud is then fed into a 3D object detection model with either a 2D or 3D backbone to generate a feature map. Each pixel in the generated feature map is assigned an anchor. Each anchor passes through the model’s detection head to predict a bounding box containing the object’s location and size offsets, orientation, and class. Finally, Non-Maximum Suppression (NMS) is applied to remove redundant predictions and yield the final detection results.
Each anchor is characterized by its position and anchor type . is determined by pixel location in the feature image, and is fixed as the center value of . The anchor type is defined by its size and initial rotation angle . The number of anchors assigned per pixel is determined by the product of the number of object classes and the number of initial rotation angles. As illustrated in Figure 4, two object classes are defined: the Boat and the Front. The Front represents the berth edge, which is the outermost part of the dock. The initial rotation angles are set to predefined values of and .
The object detection model predicts offset for the predefined anchors in terms of position, size, and orientation, along with direction prediction score and class confidence score . These predictions refine the anchor to generate bounding box :
where indicates whether the predicted bounding box orientation is correct:
In this context, when is 0, the bounding box orientation has been correctly predicted, as represented by the confidence score. Conversely, when is 1, the bounding box orientation has been rotated by , and the class confidence score set is formally defined as
where represents the confidence score for the n-th class among a total of classes. Finally, the bounding box is obtained via non-maximum suppression (NMS) as follows:
where only selected via the NMS function is used for bounding box generation. Each bounding box consists of position , size , Z-axis rotation angle , direction prediction score , and class confidence score as follows:
3.2.3. Coordinate System Calibration
Because contains position and orientation information within the sensor coordinate system, it must be transformed into the global coordinate system to determine the position and orientation of the objects on the map. Algorithm 1 takes and as inputs and describes the process of converting bounding boxes into within the global coordinate system.
| Algorithm 1: Coordinate System Calibration |
 |
3.3. Long-Term Object Perception
To perceive objects outside the LiDAR FOV, which is essential for DSG, we propose LOP (Algorithm 2). In berthing environments, the USV continuously moves relative to the dock, causing objects to enter and exit the LiDAR FOV. Without long-term perception, the DSG algorithm would only consider objects currently visible in the LiDAR FOV, leading to incomplete environmental understanding and potentially identifying occupied locations as valid docking spots. LOP addresses this limitation by maintaining a persistent representation of all detected objects over time, ensuring that the DSG algorithm has access to complete environmental information regardless of the current LiDAR FOV constraints. LOP stores and manages object information beyond the LiDAR FOV through two key processes: Bounding Box Clustering, which clusters bounding boxes within the global coordinate system for each frame, and Long-term Object Queue Updating, which updates the long-term object queue by storing the object information used for DSG and assigning unique identifiers to manage objects over time.
| Algorithm 2: Long-term Object Perception |
 |
3.3.1. Bounding Box Clustering
As shown in Figure 5, the process of storing in bounding box queue for each frame follows Step 1 of Algorithm 2. In this step, can store up to elements. In Step 2, density-based spatial clustering of applications with noise (DBSCAN) [43] is employed for the distance-based clustering of bounding boxes. Specifically, DBSCAN operates on the center coordinates of the detected bounding boxes across sequential frames, grouping boxes that are close in distance. This density-based approach inherently treats spatially isolated or transient false detection boxes as noise, effectively discarding them from the subsequent LOP process. Cluster distance threshold and minimum cluster points are set as DBSCAN parameters. For bounding boxes classified as the same cluster, average pooling is conducted on their positions and orientations, and the results are stored in cluster buffer .
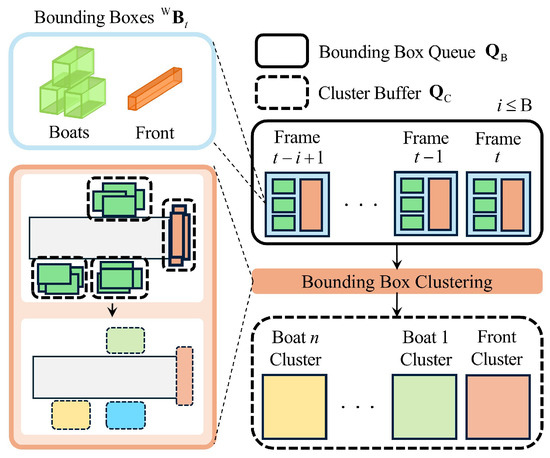
Figure 5.
Overview of the bounding box clustering process. is stored in bounding box queue for each frame, and the distance between bounding boxes is used to determine whether they belong to the same object. The results are stored in cluster buffer .
3.3.2. Long-Term Object Queue Updating
Cluster buffer is used to update the long-term object queue or to add new elements (Figure 6). In Step 3 of Algorithm 2, each element in is matched with all elements in based on matching distance threshold to determine whether matching is successful. If the matching succeeds, the information for is updated by incorporating information from in proportion to weight ratio . If the matching fails, is added to as a new object element . In this process, can store up to . Subsequently, Step 4 assigns unique identifiers to . If does not have an identifier, a new unique ID is generated and assigned. This step ensures that objects stored in can be consistently identified between frames, facilitating long-term object management.
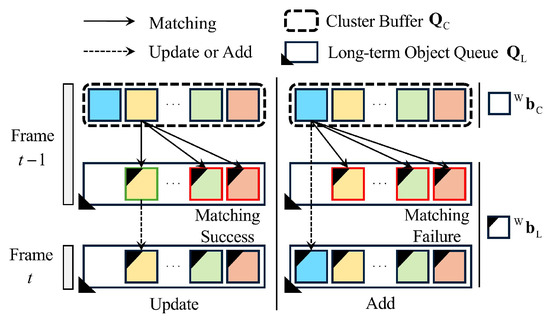
Figure 6.
Overview of the long-term object queue updating process. Elements in cluster buffer are matched with elements in long-term object queue based on distance. As shown on the left, if successfully matches with an existing in , the corresponding is updated. Conversely, as shown on the right, if matching fails, is added as a new to .
3.4. Docking Spot Generation
As illustrated in Figure 7, the DSG process utilizes object information stored in LOP to identify valid docking spots. Steps 1 to 3 correspond to guideline creation, where the Front is designated as a landmark to generate guidelines. Steps 4 and 5 correspond to docking spot selection, in which candidate docking spots are identified based on the guidelines, and valid docking spots are determined using an object matching process. The process for each step in Figure 7 is detailed in Algorithm 3.

Figure 7.
Overview of the docking spot generation (DSG) process. Steps 1 to 3 generate vertical and horizontal guidelines based on positional information for the first detected Front and Boat in . Step 4 designates the intersections of all guidelines, except for the vertical central guideline, as candidate docking spots. Step 5 determines the valid docking spots by updating all object information in .
3.4.1. Guideline Creation
Before generating the docking spots, it is necessary to configure the environmental parameters based on the structure of the dock and the size of the USV. and are both fixed constants that represent the length and width of the dock, respectively. is a user-defined variable that specifies the desired dock distance.
As LOP progresses, object information is progressively stored in . As shown in Step 1 of Figure 7, if at least one bounding box for the Boat and Front is stored in , these bounding boxes are selected to define the docking area. In Step 2, vertical guidelines are drawn based on the position of the Front. These include central vertical guideline and two vertical guidelines and , spaced on the left and right sides of the dock. The guideline information consists of vectors defined by their start and end points. The direction of the Boat is determined based on the position and orientation information of the Boat and Front, where is selected from and . To align the vertical guidelines with the dock, the vertical guidelines are then rotated around the endpoint of as the rotation axis until the center of aligns with the center of the Boat.
Step 3 defines a set of horizontal guidelines , drawn at intervals of within , extending upward and downward from the intersection of the Boat and . As a result, a grid-like pattern of guidelines covering the entire dock is generated.
3.4.2. Docking Spot Selection
In Step 4, the intersection of all elements in with and is designated as candidate docking spots. Step 5 then initiates an object matching process to determine the occupancy of each docking spot. When is updated, if the center of a Boat’s bounding box stored in is located on a candidate docking spot, that spot is marked as occupied. An occupied docking spot is no longer available, and the non-occupied docking spots become valid docking spots.
| Algorithm 3: Docking Spot Generation |
 |
4. Experimental Evaluation
4.1. Experimental Setup
To experimentally evaluate the performance of LP-DSG, a Livox MID-360 (Livox, Shenzhen, China) LiDAR sensor is used as the low-density LiDAR, and a low-power NVIDIA Jetson AGX Orin (NVIDIA, Santa Clara, CA, USA) is employed to run the algorithm. The Livox MID-360 sensor can detect objects with 80% reflectivity at a maximum range of 70 m and objects with a reflectivity of 10% at a maximum range of 40 m. It also has a horizontal FOV of and a vertical FOV that ranges from to . Sensor data is collected at 10 Hz intervals, with approximately 20,000 points per scan frame. The NVIDIA Jetson AGX Orin features an 8-core Cortex-A78AE CPU and an Ampere architecture-based GPU with 2048 CUDA cores, delivering up to 275 TOPS.
NDT is used as a scan-to-map matching technique. NDT partitions the point cloud into voxel spaces and models them as normal distributions, producing an optimal transformation matrix that minimizes the distributional differences between two LiDAR scans or between a LiDAR scan and a map. This process is used to generate the map. In LP-DSG, NDT is employed to match the LiDAR scans with the map to ensure stable map generation.
For 3D object detection, we used voxel-based PointPillars, PillarNet, SECOND and Voxel R-CNN models. Among these, PointPillars was selected as the experimental model for evaluating the entire LP-DSG system, including LOP and DSG algorithms, due to its computational efficiency suitable for real-time operation on embedded platforms while maintaining sufficient detection performance. For PointPillars, the voxel size is set to (0.16, 0.16, 6) m, and each voxel is configured to hold a maximum of 16 points for computational efficiency. The point cloud queue size in Equation (6) is set to 5, determined through systematic experiments using this PointPillars configuration. Figure 8 visualizes the effect of different queue size on voxel occupancy as a heatmap, while Table 1 provides a detailed quantitative analysis. The analysis region contains 1662 voxels from the same ground truth bounding box.

Figure 8.
Visualization of voxel occupancy for different queue sizes : The heatmap shows the number of points per voxel for RFS with Q of 1, 3, 5, 7, and 9 within the same ground truth bounding box region.

Table 1.
Effect of queue size on voxel occupancy in ground truth bounding box region: The total number of voxels in the region is 1662.
As shown in Table 1, increasing from 3 to 5 adds 90 non-empty voxels while introducing only 15 over-capacity voxels, achieving a 6 to 1 ratio. However, further increasing from 5 to 7 adds just 63 non-empty voxels but introduces 41 over-capacity voxels, resulting in a 1.5 to 1 ratio. Here, non-empty voxels represent features that capture object geometry, while over-capacity voxels require random sampling that can disrupt learning. In PointPillars, when a voxel exceeds the 16-point limit, random sampling may produce point distributions that do not represent actual object surfaces, creating unrealistic geometric patterns that hinder model training. Additionally, larger queue sizes increase computational overhead, which can compromise real-time performance on embedded platforms. Therefore, of 5 was selected as the optimal balance that maximizes geometric feature coverage while minimizing both learning interference from random sampling artifacts and computational burden for real-time operation.
Furthermore, the ROI for USV is set to [−69.12, 69.12] m, [−69.12, 69.12] m, and [−2, 4] m, respectively, to enable detection in all directions. Voxel size is determined with each model’s downsampling ratio in mind, as shown in Table 2. Because 3D backbone models preserve detailed information along the Z-axis, reducing XY resolution incurs minimal performance loss. In contrast, 2D backbone models lose some Z-axis information when projecting to BEV and therefore require higher XY resolution to maintain a fine-grained representation. Accordingly, PillarNet uses a voxel size with half the XY dimensions of the other models to ensure sufficient performance despite its 0.125 downsampling ratio. The anchor sizes for the Boat and Front are set to (2.0, 3.8, 3.6) m and (3.6, 0.8, 1.5) m, respectively, reflecting actual object dimensions. All training-related settings, including network architecture, optimizer, scheduler, learning rate, and loss function, are implemented in OpenPCDet [44] using the default hyperparameter values specified in the original publications [35,37,40,41].

Table 2.
Voxel size, feature map resolution, and downsampling ratio for each object detection model.
LOP employs DBSCAN as the clustering method. The DBSCAN parameters in Algorithm 2 are set considering the size of the USV, with the cluster distance threshold set to 1.0 m and the minimum cluster points set to 3. Because LP-DSG operates across a relatively small scale of approximately 50 m, the sizes of the bounding box queue and long-term object queue are both set to 100, allowing up to 100 objects to be stored on the map. Considering the size of the USV and registration errors, matching distance threshold between the cluster buffer and long-term object queue is set to 2.0 m. Long-term object queue update weight is set to 0.9, meaning that 90% of the information from the cluster buffer and 10% from the long-term object queue is incorporated to maintain the most up-to-date information during updates. Given the actual berthing environment for DSG, dock length is set to 32.0 m, dock width to 5.6 m, and dock distance to 4.0 m. The specific dimensions for these parameters are derived from the physical constraints of the test site and the USV, as referenced in Figure 9a.

Figure 9.
Experimental setup and dimensional information: (a) detailed dimensions of the USV used in the experiments (b) the lake test site.
4.2. Dataset Construction
As shown in Figure 9b, the experiments are conducted on a large lake using a USV, from which the necessary data for training are collected. To ensure diversity in the point cloud data collected from LiDAR, three datasets were constructed based on four scenarios (Figure 10). The first dataset consists of raw point cloud data collected directly from LiDAR (Figure 11a), while the second dataset was generated by applying frame stacking (FS) to create high-quality point cloud data. FS accumulates point clouds from previous frames in the current frame to produce a merged point cloud, without a registration process. The third dataset was constructed by registering and merging five consecutive frames of raw point cloud data, producing high-quality point cloud data using RFS (Figure 11b).
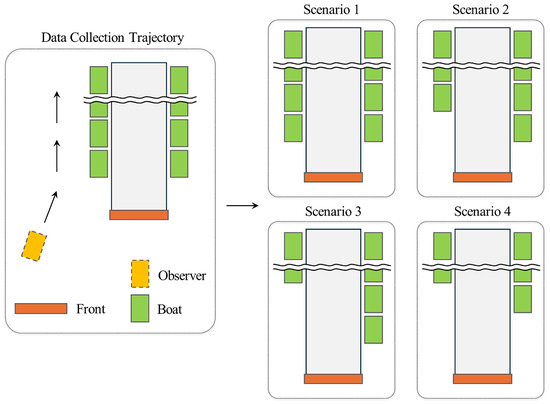
Figure 10.
USV movement path and scenario setup for the construction of the point cloud dataset. The movement path of the USV is set to traverse the left side of the dock. To ensure data diversity, raw point clouds are collected based on four different scenarios.

Figure 11.
Dataset composition: (a) raw point cloud and (b) high-quality point cloud with RFS. Colors represent distance from the sensor using a rainbow colormap.
All three datasets share the same label information, which was generated using the high-quality point clouds from RFS. This labeling approach is justified by the fact that all three datasets exist in the same sensor coordinate system and represent the same physical scenes captured at the same time. In LiDAR-based 3D object detection, bounding box annotations represent the physical dimensions and locations of objects based on surface points, independent of point density.
This follows the standard practice in major 3D detection benchmarks [17,42,45], where objects are labeled based on their physical extent regardless of point sparsity in any particular frame. Using consistent labels across all datasets ensures fair comparison by eliminating annotation variance as a confounding factor, allowing us to isolate and evaluate the effect of point cloud quality on detection performance. Each of the three datasets consists of the same 1722 scenes, and the labeled dataset is divided into 1378 and 344 scenes for training and validation, respectively.
We employ four data augmentation techniques to enhance training data diversity and reduce observation angle bias. First, we perform ground-truth sampling [37], which extracts points from labeled bounding boxes and inserts them into other scenes. We set the minimum points to sample to 5 for both Boat and Front classes, with up to 20 Boat objects and 5 Front objects inserted per scene. Second, we randomly flip each scene along the X and Y axes. Third, we apply random rotation around the Z axis within . Finally, we apply random scaling with factors between 0.95 and 1.05. These augmentations ensure that each training iteration encounters a different scene variation, allowing the model to learn from diverse inputs.
4.3. Experimental Results
Experiments are conducted to evaluate the improvement in object detection reliability and accuracy, efficiency in the long-term perception and management of objects, and the stability of DSG in real-world scenarios. In this experiment, PointPillars was selected as the experimental model for performing subsequent tasks after comparing object detection performance.
To evaluate the improvement in object detection reliability and accuracy due to the use of high-quality training data, a comparative analysis is conducted using 344 validation scenes, as shown in Table 3. For each model, the evaluation compares its baseline and extended versions incorporating FS and RFS. Table 3 presents a quantitative evaluation of detection accuracy by comparing class-wise AP and mAP for both 3D bounding boxes and BEV. For all classes, the IoU threshold is set to 0.7, and 40 recall positions are used for a more detailed performance analysis [46,47].

Table 3.
Object detection results.
As a result, compared to the single-frame baseline models, applying RFS consistently improves performance across all four model architectures. Quantitatively, RFS achieves an average 3D mAP improvement of 23.38 percentage points across all models. Specifically, PointPillars improves by 22.45 percentage points, PillarNet by 23.26 percentage points, SECOND by 26.44 percentage points, and Voxel R-CNN by 21.37 percentage points. Notably, the Front class shows particularly substantial improvements across all architectures. PointPillars achieves a 35.87 percentage point improvement, PillarNet 39.19 percentage points, SECOND 41.73 percentage points, and Voxel R-CNN 35.68 percentage points. These results indicate that high-quality point clouds generated by RFS are especially effective for detecting small objects with sparse point clouds. This consistent improvement pattern across diverse model architectures, ranging from lightweight PointPillars to complex Voxel R-CNN, validates the robustness and generalizability of our approach.
RFS produces a higher object detection performance than FS, another multi-frame model. This improvement is attributed to the multi-frame alignment process in RFS, which refines the point cloud, making it more suitable for object detection. Figure 12 visualizes the point cloud datasets generated by applying FS and RFS to the experimental model and shows the class-wise precision-recall (PR) curve results for each model. Notably, in the Front object region, indicated by the red ellipse, the FS data sample produces an unstable object shape. In contrast, with RFS, the object shape is more stable due to precise frame alignment. This is a critical factor in detecting relatively small objects such as the Front.
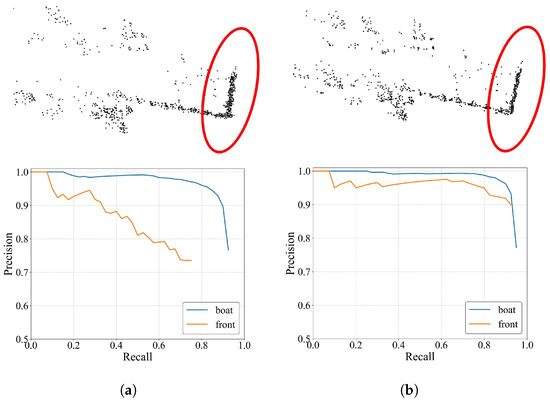
Figure 12.
Point cloud dataset generated using FS and RFS and the class-wise PR curve results derived from the experimental model training: (a) baseline with FS (b) baseline with RFS. Red circles indicate regions where point distribution stability can be observed without and with RFS in the Front class.
Figure 13 presents the inference results for the experimental model. Compared to the ground truth, the baseline and baseline with FS models (Figure 13a and Figure 13b, respectively) fail to detect the Front, while the baseline with RFS model reliably does so (Figure 13c).
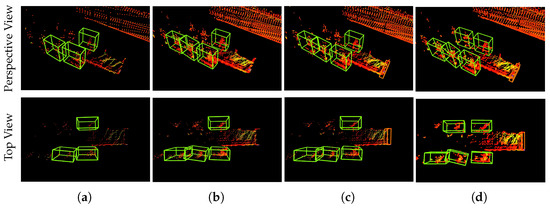
Figure 13.
Visualization of the inference results for the experimental model: (a) baseline (b) baseline with FS (c) baseline with RFS (d) the ground truth. Only bounding boxes with a class confidence score higher than 0.7 are displayed. Point colors represent LiDAR intensity values using a rainbow colormap.
To evaluate the effectiveness of long-term perception and object management, we compare the detection recall (DR) with and without LOP. Figure 14 presents the DR over time, representing the detected objects as a percentage of the total number of actual objects in Scenario 3 of Figure 10. When LOP is not employed, the DR gradually increases over time but starts to decline after reaching 60% (Figure 14a). This decline can be attributed to objects moving out of the LiDAR FOV. In addition, due to noise in the real-world environment, the DR fluctuates during the detection process. In contrast, when LOP is used, the DR steadily increases over time (Figure 14b). This is because LOP retains object information even when they move out of the LiDAR FOV. As a result, a DR of approximately 90% is achieved in Scenario 3, contributing to the stability of DSG.
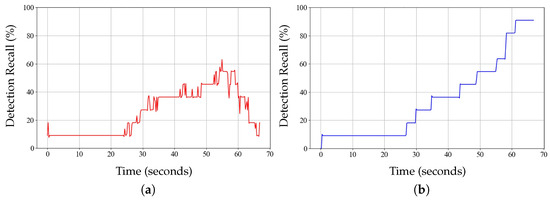
Figure 14.
Graph of DR variation over time for the experimental model: baseline (a) without and (b) with LOP.
The stability of the DSG algorithm employed in Scenario 1 of Figure 10 is also tested. Table 4 presents the DSG results for the baseline and RFS of the experimental model. Nearest-neighbor matching is performed in the XY plane between the bounding boxes of the Boat stored in LOP and the candidate docking spots generated by the DSG algorithm. The mean, standard deviation, and 95% confidence interval of the matching distances between paired points are calculated. As a result, the baseline model exhibits a mean matching distance of 0.654 m, whereas the model with RFS achieves an improved mean matching distance of 0.579 m. Additionally, when comparing the confidence intervals of both models, the baseline model has a range of [0.614, 0.693] m, while the model with RFS has a range of [0.531, 0.627] m. Because the confidence interval widths are relatively small compared to the size of the USV, which has a length of 3.8 m and a width of 1.8 m, it can be confirmed that the DSG algorithm is stable in both cases. Figure 15 visualizes the DSG results for the model with RFS, confirming that the system can reliably generate autonomous docking spots in real-world environments. A detailed visualization of the complete LP-DSG system workflow is provided in Video S1.

Table 4.
DSG results.

Figure 15.
Visualization of the DSG results. Blue points denote occupied docking spots, while green points indicate valid docking spots where no matched bounding box is present. Point colors represent LiDAR intensity values using a rainbow colormap.
5. Discussion and Conclusions
In the present study, we proposed LP-DSG, a LiDAR point-based docking spot generation system for autonomous USV docking using low-density LiDAR in berthing environments. The key innovation of LP-DSG is the integration of scan matching with registration-based frame stacking (RFS) to generate high-quality point clouds from low-density LiDAR data. This approach enables accurate object detection and long-term environmental perception, which are essential for reliable autonomous docking spot generation.
To validate the performance of LP-DSG, we conducted experiments in a large lake using a USV. The USV was equipped with low-density LiDAR and an embedded board, and its performance was evaluated under practical operating scenarios. Based on the experimental results, the proposed approach was shown to be effective in improving the accuracy of 3D object detection, the long-term perception and management of objects, and the stability of DSG. Given its practical applicability in real-world environments, LP-DSG is thus suitable for low-density LiDAR. In particular, it has the potential to be a cost-effective alternative for situations where the use of expensive high-precision sensors may not be feasible, such as with small autonomous vessels, USVs, and floating offshore structures.
While LP-DSG demonstrates effective performance in berthing environments, several limitations should be acknowledged. One limitation is that the RFS method inherently accumulates points from sequential frames over time, which limits its applicability in highly dynamic environments. When objects in the scene move significantly between frames, the point cloud registration process may introduce misalignment artifacts, potentially degrading the quality of the accumulated point cloud. Our current implementation is therefore most suitable for berthing scenarios where the environment is relatively static.
Another limitation is that the DSG algorithm relies on the successful detection of both Front and Boat objects stored in long-term object queue. The Front serves as a landmark for establishing the global coordinate system and generating guidelines, while the Boat provides directional information for determining docking orientation. If either object fails to be detected due to occlusion, sensor limitations, or challenging environmental conditions, the system cannot generate optimally oriented docking spots. However, we note that if only the Front is detected, it would be possible to generate docking spots using the Front’s orientation information as a default docking direction, though this would result in less accurate directional alignment compared to using actual Boat positions. This dependency on landmark detection represents a fundamental limitation of the current approach.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/app152212290/s1, Video S1: Visualization of the LP-DSG system workflow and processing stages.
Author Contributions
Conceptualization, Y.-C.L. and S.S.; methodology, S.S.; software, S.S.; validation, S.S.; writing—original draft, S.S. and J.J.; investigation, J.S. and J.K.; writing—review and editing, Y.-C.L. and J.S.; formal analysis, S.S. and J.K.; visualization, S.S. and J.J.; supervision, Y.-C.L.; project administration, Y.-C.L.; funding acquisition, Y.-C.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the MSIT (Ministry of Science and ICT), Korea, under the ICAN (ICT Challenge and Advanced Network of HRD) support program (IITP-2024-00436744), and the Artificial Intelligence Convergence Innovation Human Resources Development (IITP-2025-RS-2023-00254592) supervised by the IITP (Institute for Information & Communications Technology Planning & Evaluation).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Dataset available on request from the authors.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DSG | Docking spot generation |
| LOP | Long-term object perception |
| RFS | Registration-based frame stacking |
| NDT | Normal distributions transform |
| USV | Unmanned surface vehicle |
| BEV | Bird’s eye view |
| DR | Detection recall |
References
- Bai, X.; Li, B.; Xu, X.; Xiao, Y. A Review of Current Research and Advances in Unmanned Surface Vehicles. J. Mar. Sci. Appl. 2022, 21, 47–58. [Google Scholar] [CrossRef]
- Chen, Y.; Ma, X.; Wang, Q.; He, Y.; Xie, S. Research on Water Surface Object Detection Method Based on Image Fusion. J. Mar. Sci. Eng. 2025, 13, 1832. [Google Scholar] [CrossRef]
- Volden, Ø.; Stahl, A.; Fossen, T.I. Vision-based positioning system for auto-docking of unmanned surface vehicles (USVs). Int. J. Intell. Rob. Appl. 2022, 6, 86–103. [Google Scholar] [CrossRef]
- Chu, Y.; Wu, Z.; Zhu, X.; Yue, Y.; Lim, E.G.; Paoletti, P. Self-supervised Dock Pose Estimator for Unmanned Surface Vehicles Autonomous Docking. In Proceedings of the 2024 10th International Conference on Mechatronics and Robotics Engineering (ICMRE), Milan, Italy, 27–29 February 2024; pp. 189–194. [Google Scholar] [CrossRef]
- Wang, W.; Luo, X. Autonomous Docking of the USV using Deep Reinforcement Learning Combine with Observation Enhanced. In Proceedings of the 2021 IEEE International Conference on Advances in Electrical Engineering and Computer Applications (AEECA), Dalian, China, 27–28 August 2021; pp. 992–996. [Google Scholar] [CrossRef]
- Yu, Q.; Wang, B.; Su, Y. Object Detection-Tracking Algorithm for Unmanned Surface Vehicles Based on a Radar-Photoelectric System. IEEE Access 2021, 9, 57529–57541. [Google Scholar] [CrossRef]
- Qian, L.; Hu, J.; Ren, H.; Lin, J.; Luo, X.; Zou, L.; Zhou, Y. Cross-Level Adaptive Feature Aggregation Network for Arbitrary-Oriented SAR Ship Detection. Remote Sens. 2025, 17, 1770. [Google Scholar] [CrossRef]
- Zhang, W.; Jiang, F.; Yang, C.F.; Wang, Z.P.; Zhao, T.J. Research on Unmanned Surface Vehicles Environment Perception Based on the Fusion of Vision and Lidar. IEEE Access 2021, 9, 63107–63121. [Google Scholar] [CrossRef]
- Jing, Q.; Bai, M.; Yin, Y.; Guo, D. I-VoxICP: A Fast Point Cloud Registration Method for Unmanned Surface Vessels. J. Mar. Sci. Eng. 2025, 13, 1854. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Guo, H.; Zhang, Z.; Gao, Y. LiDAR Data-Driven Deep Network for Ship Berthing Behavior Prediction in Smart Port Systems. J. Mar. Sci. Eng. 2025, 13, 1396. [Google Scholar] [CrossRef]
- Esposito, J.M.; Graves, M. An algorithm to identify docking locations for autonomous surface vessels from 3-D LiDAR scans. In Proceedings of the 2014 IEEE International Conference on Technologies for Practical Robot Applications (TePRA), Boston, MA, USA, 14–15 April 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Shan, Y.; Yao, X.; Lin, H.; Zou, X.; Huang, K. Lidar-Based Stable Navigable Region Detection for Unmanned Surface Vehicles. IEEE Trans. Instrum. Meas. 2021, 70, 1–13. [Google Scholar] [CrossRef]
- Ahmed, M.; Rasheed, B.; Salloum, H.; Hegazy, M.; Bahrami, M.R.; Chuchkalov, M. Seal Pipeline: Enhancing Dynamic Object Detection and Tracking for Autonomous Unmanned Surface Vehicles in Maritime Environments. Drones 2024, 8, 561. [Google Scholar] [CrossRef]
- Pereira, M.I.; Pinto, A.M. Reinforcement learning based robot navigation using illegal actions for autonomous docking of surface vehicles in unknown environments. Eng. Appl. Artif. Intell. 2024, 133, 108506. [Google Scholar] [CrossRef]
- Zhu, Y.; Zheng, C.; Yuan, C.; Huang, X.; Hong, X. CamVox: A Low-cost and Accurate Lidar-assisted Visual SLAM System. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 5049–5055. [Google Scholar] [CrossRef]
- You, J.; Kim, Y.K. Up-Sampling Method for Low-Resolution LiDAR Point Cloud to Enhance 3D Object Detection in an Autonomous Driving Environment. Sensors 2022, 23, 322. [Google Scholar] [CrossRef] [PubMed]
- Sun, P.; Kretzschmar, H.; Dotiwalla, X.; Chouard, A.; Patnaik, V.; Tsui, P.; Guo, J.; Zhou, Y.; Chai, Y.; Caine, B.; et al. Scalability in Perception for Autonomous Driving: Waymo Open Dataset. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 2446–2454. [Google Scholar] [CrossRef]
- Mao, J.; Niu, M.; Jiang, C.; Liang, H.; Chen, J.; Liang, X.; Li, Y.; Ye, C.; Zhang, W.; Li, Z.; et al. One Million Scenes for Autonomous Driving: ONCE Dataset. arXiv 2021, arXiv:2106.11037. [Google Scholar]
- Besl, P.; McKay, N.D. A Method for Registration of 3-D Shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Chetverikov, D.; Svirko, D.; Stepanov, D.; Krsek, P. The Trimmed Iterative Closest Point algorithm. In Proceedings of the 2002 International Conference on Pattern Recognition (ICPR), Quebec City, QC, Canada, 11–15 August 2002; pp. 545–548. [Google Scholar] [CrossRef]
- Chen, Y.; Medioni, G. Object modelling by registration of multiple range images. Image Vision Comput. 1992, 10, 145–155. [Google Scholar] [CrossRef]
- Segal, A.; Haehnel, D.; Thrun, S. Generalized-icp. In Proceedings of the 2009 Robotics: Science and Systems (RSS), Seattle, WA, USA, 28 June–1 July 2009; p. 435. [Google Scholar] [CrossRef]
- Biber, P.; Straßer, W. The normal distributions transform: A new approach to laser scan matching. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 27–31 October 2003; pp. 2743–2748. [Google Scholar] [CrossRef]
- Zhang, J.; Singh, S. LOAM: Lidar odometry and mapping in real-time. In Proceedings of the 2014 Robotics: Science and Systems (RSS), Berkeley, CA, USA, 12–16 July 2014; pp. 1–9. [Google Scholar] [CrossRef]
- Shan, T.; Englot, B. LeGO-LOAM: Lightweight and Ground-Optimized Lidar Odometry and Mapping on Variable Terrain. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4758–4765. [Google Scholar] [CrossRef]
- Wang, H.; Wang, C.; Chen, C.L.; Xie, L. F-LOAM: Fast LiDAR Odometry and Mapping. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 4390–4396. [Google Scholar] [CrossRef]
- Behley, J.; Stachniss, C. Efficient surfel-based SLAM using 3D laser range data in urban environments. In Proceedings of the 2018 Robotics: Science and Systems (RSS), Pittsburgh, PA, USA, 26–30 June 2018; p. 59. [Google Scholar] [CrossRef]
- Chen, X.; Milioto, A.; Palazzolo, E.; Giguere, P.; Behley, J.; Stachniss, C. SuMa++: Efficient LiDAR-based Semantic SLAM. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 4530–4537. [Google Scholar] [CrossRef]
- Shi, S.; Wang, X.; Li, H. PointRCNN: 3D Object Proposal Generation and Detection From Point Cloud. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 770–779. [Google Scholar] [CrossRef]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. Available online: https://proceedings.neurips.cc/paper_files/paper/2017/file/d8bf84be3800d12f74d8b05e9b89836f-Paper.pdf (accessed on 17 November 2025).
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. Available online: https://proceedings.neurips.cc/paper_files/paper/2015/file/14bfa6bb14875e45bba028a21ed38046-Paper.pdf (accessed on 17 November 2025).
- Yang, Z.; Sun, Y.; Liu, S.; Jia, J. 3DSSD: Point-Based 3D Single Stage Object Detector. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 11040–11048. [Google Scholar] [CrossRef]
- Qi, C.R.; Litany, O.; He, K.; Guibas, L.J. Deep Hough Voting for 3D Object Detection in Point Clouds. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 9277–9286. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, Q.; Xu, G.; Ma, Y.; Wan, J.; Guo, Y. Not All Points Are Equal: Learning Highly Efficient Point-Based Detectors for 3D LiDAR Point Clouds. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–24 June 2022; pp. 18953–18962. [Google Scholar] [CrossRef]
- Lang, A.H.; Vora, S.; Caesar, H.; Zhou, L.; Yang, J.; Beijbom, O. PointPillars: Fast Encoders for Object Detection From Point Clouds. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 12697–12705. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar] [CrossRef]
- Yan, Y.; Mao, Y.; Li, B. SECOND: Sparsely Embedded Convolutional Detection. Sensors 2018, 18, 3337. [Google Scholar] [CrossRef] [PubMed]
- Graham, B. Spatially-sparse convolutional neural networks. arXiv 2014, arXiv:1409.6070. [Google Scholar]
- Graham, B.; Van der Maaten, L. Submanifold Sparse Convolutional Networks. arXiv 2017, arXiv:1706.01307. [Google Scholar] [PubMed]
- Deng, J.; Shi, S.; Li, P.; Zhou, W.; Zhang, Y.; Li, H. Voxel R-CNN: Towards High Performance Voxel-based 3D Object Detection. In Proceedings of the 2021 AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 2–9 February 2021; pp. 1201–1209. [Google Scholar] [CrossRef]
- Shi, G.; Li, R.; Ma, C. PillarNet: Real-Time and High-Performance Pillar-Based 3D Object Detection. In Proceedings of the 2022 European Conference on Computer Vision (ECCV), Tel-Aviv, Israel, 23–27 October 2022; pp. 35–52. [Google Scholar] [CrossRef]
- Caesar, H.; Bankiti, V.; Lang, A.H.; Vora, S.; Liong, V.E.; Xu, Q.; Krishnan, A.; Pan, Y.; Baldan, G.; Beijbom, O. nuScenes: A Multimodal Dataset for Autonomous Driving. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 11621–11631. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the 1996 Second International Conference on Knowledge Discovery and Data Mining (KDD), Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- OpenPCDet Development Team. OpenPCDet: An Open-Source Toolbox for 3D Object Detection from Point Clouds. 2020. Available online: https://github.com/open-mmlab/OpenPCDet (accessed on 17 June 2025).
- Geiger, A.; Lenz, P.; Stiller, C.; Urtasun, R. Vision meets robotics: The kitti dataset. Int. J. Rob. Res. 2013, 32, 1231–1237. [Google Scholar] [CrossRef]
- Everingham, M.; Van Gool, L.; Williams, C.K.; Winn, J.; Zisserman, A. The Pascal Visual Object Classes (VOC) Challenge. Int. J. Comput. Vision 2010, 88, 303–338. [Google Scholar] [CrossRef]
- Simonelli, A.; Bulo, S.R.; Porzi, L.; López-Antequera, M.; Kontschieder, P. Disentangling Monocular 3D Object Detection. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1991–1999. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).