DBSCAN Clustering and Entropy Optimization for Geospatial Analysis of Urban–Rural Healthcare Inequities in Latin America

Abstract

Healthcare access in Latin America is highly unequal, with rural and peri-urban populations disproportionately excluded from essential and specialized services. To address the persistent gaps often obscured by conventional urban–rural classifications, this study developed a machine learning framework integrating the Functional Urban Area (FUA) model with Density-Based Spatial Clustering of Applications with Noise (DBSCAN) and Shannon entropy optimization to refine urbanization gradients and quantify inequities across 11 countries. High-resolution population density data from the Meta High Resolution Settlement Layer (HRSL, 2020) and CIESIN’s Gridded Population of the World (GPWv4, rev. 11), combined with healthcare facility locations from Healthsites.io, were processed in R to generate population-facility networks. Entropy optimization dynamically determined country-specific DBSCAN distance thresholds, ensuring representative clustering of functional urban and rural areas. Facilities were categorized by care level, and per-capita densities were compared across clusters. Results showed that entropy-optimized DBSCAN improved spatial precision over traditional approaches and revealed systemic urban bias: Peru, Chile, and Venezuela had the lowest hospital densities, while Ecuador, Bolivia, and Paraguay displayed the strongest rural deficits in primary care. Specialized services were overwhelmingly concentrated in urban clusters. This reproducible framework establishes a quantitative baseline for healthcare inequities, providing data-driven insights to inform the design of decentralized strategies to improve equitable access to care across Latin America.

1. Introduction

Latin American countries exhibit diverse healthcare landscapes shaped by geographic, socioeconomic, and systemic factors that influence access to healthcare [1]. Despite significant reforms aimed at expanding universal healthcare coverage [2], improvements remain uneven and systemic exclusions persist, leading to unequal resource allocation, particularly in peripheral communities [3]. These regions face inadequate infrastructure, understaffed facilities, and limited health information resources, compounding barriers to care [1,4]. Additional challenges, such as geographic isolation, prohibitive distances to healthcare facilities, and the uneven distribution of healthcare services, disproportionately affect rural populations [4,5]. Urban-centric healthcare reforms have further widened gaps in healthcare delivery, contributing to higher maternal and infant mortality rates, reduced life expectancies, and an increased prevalence of preventable diseases in rural areas compared to their urban counterparts [6,7].

Ensuring continuity of care in these settings is critical for improving health outcomes and reducing disparities [8]. However, conventional geographic healthcare analyses often rely on simplistic urban–rural classifications that fail to capture the complexity of population distribution and urbanization gradients [5]. This oversimplification can obscure disparities in healthcare access, particularly for peri-urban and transitioning regions [3]. Additionally, many traditional methodologies fail to integrate geographic analysis with healthcare distribution data or actionable healthcare access metrics, thereby limiting efforts to address the root causes of healthcare inequities [9]. Addressing these limitations requires frameworks that incorporate systemic healthcare fragmentation, decentralized governance, and population mobility patterns to ensure equitable healthcare delivery [10]. Expanding telemedicine, mobile health initiatives, and targeted resource allocation strategies can strengthen continuity of care and mitigate disparities across urban and rural populations [11,12].

This study aims to address these gaps by applying the Functional Urban Area (FUA) framework in conjunction with advanced geospatial clustering techniques to evaluate healthcare accessibility across 11 Latin American countries. The FUA framework, developed by the Organization for Economic Co-operation and Development (OECD), provides a more nuanced alternative to traditional urban–rural classifications by defining spatially cohesive regions based on population density and functional connectivity [13]. By incorporating Density-Based Spatial Clustering of Applications with Noise (DBSCAN) and Shannon’s entropy optimization, this study enhances the spatial precision of healthcare accessibility analysis, ensuring a data-driven, adaptable approach to identifying underserved regions [14,15,16,17,18]. This research builds on spatial epidemiology and applies machine learning to Latin America’s complex urbanization patterns, identifying previously unexplored trends in healthcare resource distribution. By leveraging advanced geospatial techniques, this study aligns with global health initiatives, including the Sustainable Development Goals (SDGs), which emphasize equitable healthcare access as essential for improving continuity of care in low- and middle-income countries (LMICs) [19].

1.1. Research Background

Large inequalities in health outcomes and service distribution have been documented across Latin America. Prior studies have identified stark urban–rural divides in access to medical care, with rural and peri-urban communities often lacking basic services [1,3,4,20]. For example, a 2021 study found significant disparities in life expectancy and mortality across 363 cities in the region, reflecting broader inequities in healthcare provision [5]. Public health reforms have improved coverage in some areas, yet many countries continue to struggle with fragmented systems that leave peripheral populations underserved [9,10]. These challenges underscore the need for innovative approaches to quantify and address healthcare accessibility gaps.

Existing Problems and Conventional Approaches

Traditional urban–rural designations (e.g., classifying entire districts as “urban” or “rural”) often mask the heterogeneity of settlement patterns. Many Latin American studies rely on administrative definitions or simple population thresholds that do not capture peri-urban gradients [5,9]. Such coarse classifications can lead to misallocation of resources, as they overlook high-need pockets in “urban” areas and relatively well-served communities in “rural” areas. Existing methods for measuring healthcare access have included metrics such as doctor-to-population ratios and distance to the nearest facility. A common approach is the two-step floating catchment area or gravity models to assess spatial accessibility, as well as direct travel time analyses using road networks and GIS. For instance, Weiss et al. (2020) produced global maps of travel time to healthcare, highlighting substantial accessibility deficits in parts of Latin America [21]. However, these methods generally assume predefined urban boundaries and do not dynamically delineate urban extents from underlying data. The lack of a standardized yet flexible definition of “urban” and “rural” areas remains an existing problem that can skew accessibility assessments.

1.2. Literature Review and Related Studies

Several recent studies have sought to improve how urban areas are defined and how healthcare access is measured, providing context for our methodology. Caudillo-Cos et al. demonstrated the use of DBSCAN clustering combined with entropy to define urban boundaries in Mexico’s National Urban System [14]. Their approach showed that data-driven clustering could reveal urban agglomerations more objectively than official definitions. Similarly, Moreno-Monroy et al. (2021) examined global metropolitan delineations and found that functional criteria can better capture urban extents than fixed administrative units [22]. Our work builds on these insights by applying a clustering approach across multiple countries with varied settlement patterns.

In terms of healthcare accessibility, Florio et al. (2023) employed the Degree of Urbanisation classification to estimate geographic access to healthcare facilities in sub-Saharan Africa [16]. They incorporated travel time metrics, illustrating that urban-centric healthcare distribution leaves rural areas at a severe disadvantage. Agbenyo et al. (2017) and Stock (1983) earlier explored accessibility in Ghana and Nigeria, respectively, finding that distance decay effects significantly reduce rural healthcare utilization [17,18]. These studies emphasize that physical distance and travel time are critical components of access. However, incorporating such metrics requires detailed data, which may not be consistently available across countries.

Our study distinguishes itself by focusing on refining the urban–rural categorization to improve access analysis. Unlike Weiss et al. (2020), who assumed a given infrastructure layout, we first redefine the spatial units (FUAs vs. non-FUAs) using high-resolution population data [7,21,23]. This approach is similar in spirit to the GHSL (Global Human Settlement Layer) project, which uses population density thresholds (e.g., 1500 persons/km² for urban centers) to delineate urban areas. We adapt such international criteria to local contexts through entropy-optimized clustering, something not extensively done in prior literature.

Furthermore, while travel time analyses and capacity metrics (hospital beds, etc.) are ideal for measuring realized access, our framework provides a complementary perspective by standardizing how we define “urban” and “rural” areas across countries. By quantifying the distribution of healthcare facilities per capita within these data-driven area definitions, we can highlight inequities that might be overlooked by analyses using coarse administrative categories. In summary, existing research underscores the importance of spatial context in health access; our contribution is to integrate a refined spatial clustering method (DBSCAN + entropy) with healthcare data to create a reproducible baseline for cross-country comparisons.

1.3. Our Contributions

Considering the gaps identified above, our work offers several innovations and advantages. First, we introduce a dynamic clustering approach to delineate urban areas (FUAs) that adapts to each country’s population distribution, rather than relying on one-size-fits-all thresholds. This methodological contribution builds on Caudillo-Cos et al. (2024) by extending their single-country approach to a broader multi-country analysis with varying settlement patterns [14]. Second, we integrate open data from multiple sources (population grids, health facility maps) into a unified framework—an approach that leverages comprehensive datasets and ensures reproducibility. While previous studies have either focused on where people live or where facilities are, our study combines both to examine alignment (or misalignment) between population and healthcare resources.

Finally, we emphasize a comparative perspective across 11 countries, which, to our knowledge, is one of the first attempts to quantitatively compare urban–rural healthcare access disparities at a cross-national level in Latin America using a unified methodology. By doing so, we highlight country-specific nuances (for example, Guyana’s unique urban distribution or Chile’s healthcare network) while drawing regional generalizations. This comprehensive scope, aided by a reproducible analytic pipeline, is a key advantage of our research. The insights gained can inform regional policy by identifying which countries or areas deviate most in terms of service inequity, guiding where interventions or further studies might be necessary.

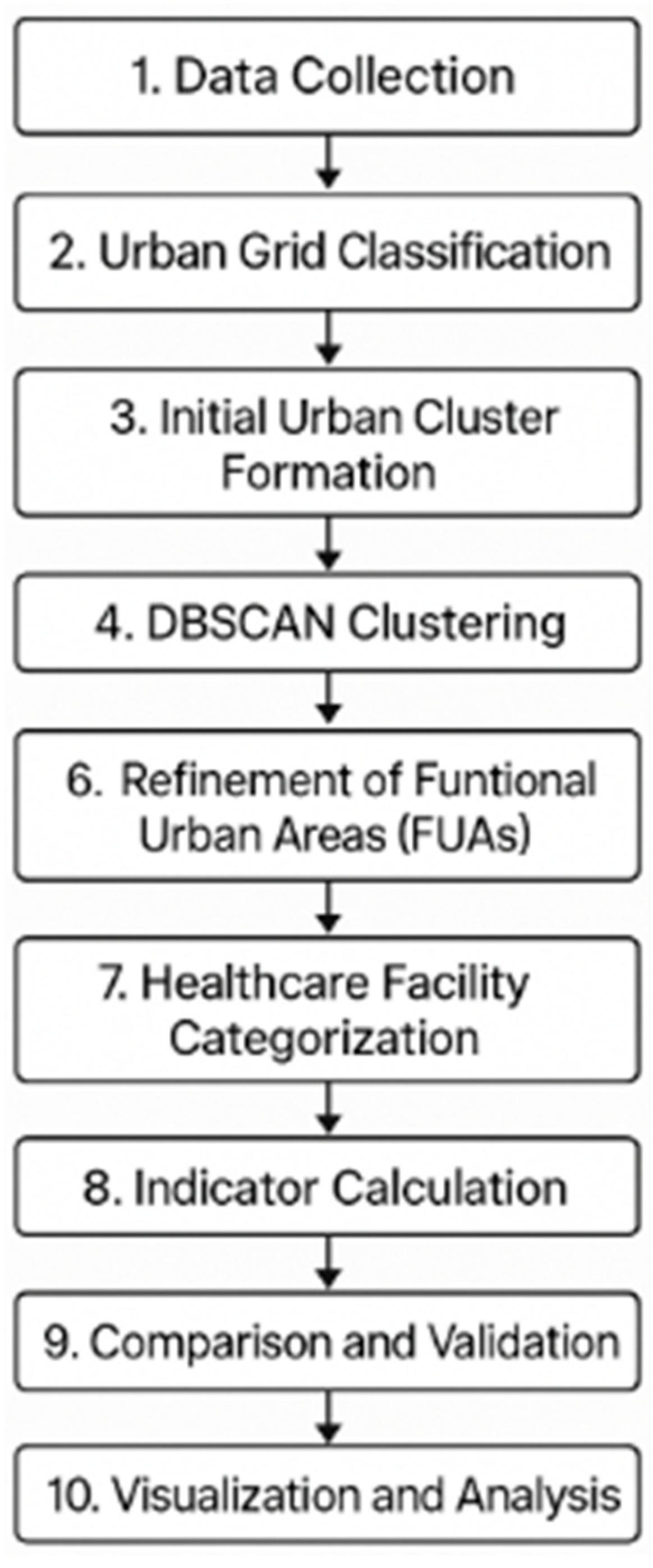
2. Materials and Methods

2.1. Study Design

This study performs a geospatial analysis of population density and healthcare facility distribution across 11 Latin American countries. It utilizes high-resolution population density data, administrative boundary datasets, and healthcare facility location data from multiple sources, including the Humanitarian OpenStreetMap Team (HOTOSM), Data for Good at Meta, and the Center for International Earth Science Information Network (CIESIN) at Columbia University, in collaboration with the United Nations Office for the Coordination of Humanitarian Affairs (OCHA) (

Table A3. Key Data Sets Used (with Version/Year and References). This table summarizes all major datasets used for this study, including population data, health facility data, and administrative boundaries, with their version or release year and source references.

Data Set	Version/Year	Reference(s)
Meta High Resolution Settlement Layer (HRSL)	v1.2 (2020 release)	[24,25,26,27,28,29,30,31,32,33,34] OCHA/FB Population Estimates
CIESIN Gridded Population of the World (GPWv4)	Revision 11 (2020)	[53] CIESIN (2018) GPWv4
OCHA Common Operational Datasets-Boundaries	2024 editions	[35,36,37,38,39,40,41,42,43,44] OCHA COD-AB (country-specific)
Healthsites.io Global Facilities Database	2024 (data freeze)	[60] Healthsites.io (2024)

Note: OCHA high-resolution population data (HRSL) and COD-AB administrative boundaries were accessed via the Humanitarian Data Exchange for each country [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44]. The GPWv4 population data are a product of CIESIN (NASA SEDAC) updated through 2020 [53]. Health facility data were extracted from Healthsites.io (with OpenStreetMap as a primary source) [60]. All sources are open-access and cited in the References.

) [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45]. The overall methodological workflow is outlined as follows (Figure 1):

• Data Collection: Gather high-resolution population density raster datasets (HRSL and GPWv4) and administrative boundary shapefiles for each country and obtain geolocated healthcare facility data from open sources (Healthsites.io).
• Urban Grid Classification: Process population raster data in R and classify each grid cell as “urban” or “rural” based on country-specific population density thresholds. Cells above the threshold are labeled urban, and those below are rural.
• Initial Urban Cluster Formation: Group contiguous high-density (urban) grid cells to form preliminary urban clusters. Align these clusters with second-level administrative units (ADM2, e.g., municipios, cantones, or comunas) to identify potential Functional Urban Areas.
• DBSCAN Clustering: Apply DBSCAN to the spatial coordinates of high-density grid cell centroids. MinPts was set to 5 based on the foundational DBSCAN methodology (requiring each core point to have at least four neighbors). We iteratively test different epsilon (ε) distance values (ranging from 10 m to 1000 m in 10 m increments) for clustering.
• Entropy Optimization: For each candidate ε, compute Shannon’s entropy of the resulting cluster size distribution (based on population in each cluster). Identify the ε value that maximizes the entropy, which indicates the most representative clustering (balancing between one single cluster and many overly fragmented clusters). This optimal ε is selected as the clustering parameter for that country.
• Refinement of FUAs: Using the optimal ε, perform DBSCAN clustering to define final urban clusters. Discard trivial clusters that do not meet a minimum population size (small clusters below country-specific population thresholds, e.g., 25,000 people, are filtered out to avoid over-fragmentation). Assign municipalities with ≥50% of their population in urban clusters as FUAs; those below 50% are non-FUA (predominantly rural) regions.
• Healthcare Facility Categorization: Join each healthcare facility point to the corresponding municipality and label it as “urban” (if within an FUA) or “rural” (if in a non-FUA area). Categorize facilities by type (hospital, clinic/primary, other).
• Indicator Calculation: Calculate per-capita healthcare facility densities for urban vs. rural populations in each country. Compute ratios of FUA to non-FUA facility density for each facility category (total facilities, hospitals, primary care, specialized).
• Comparison and Validation: Compare the clustering-based delineation of urban areas to traditional definitions. We qualitatively assess if our identified FUAs align with known metropolitan regions and check population sums against official totals (validating that population estimation error is within acceptable bounds). No formal ground-truth for cluster boundaries is available, but results are reviewed for face validity.
• Visualization and Analysis: Generate choropleth maps and scatter plots to visualize the distribution of FUAs and healthcare facilities. Interpret patterns of urban bias or rural shortfall in healthcare resources for each country and perform cross-country comparisons.

2.2. Country Selection

This study includes Argentina, Bolivia, Brazil, Chile, Colombia, Ecuador, Guyana, Paraguay, Peru, Uruguay, and Venezuela. While these countries reflect diverse geographic, socioeconomic, and healthcare system characteristics, the final selection was primarily guided by the availability of high-quality, standardized geospatial data. This constraint inherently shaped the composition of the study sample. Several Latin American and Caribbean nations, including Cuba, the Dominican Republic, Haiti, Belize, El Salvador, Honduras, Nicaragua, Panama, Guatemala, and Suriname, were excluded due to insufficient or inconsistent data coverage. By focusing on countries with both data availability and systemic diversity, this study provides a detailed but pragmatic assessment of healthcare accessibility across the region. Collectively, these 11 nations represent approximately 85.86% of the total Latin American population and span the World Bank’s income classifications, ranging from high-income (Chile, Guyana, Uruguay) to upper-middle-income (Argentina, Brazil, Colombia, Ecuador, Paraguay, Peru) and lower-middle-income (Bolivia, Venezuela) [46].

2.3. Urban Grid Classification and Clustering Procedure

High-resolution population density raster datasets (Meta’s HRSL at ~30 m resolution and CIESIN’s GPWv4 at ~1 km resolution) were loaded for each country to identify densely populated areas. We implemented binary classifications using the dplyr package in R to categorize grid cells as “urban” or “rural” based on population density thresholds. Grid cells exceeding the threshold were designated as urban, while those below were classified as rural. The thresholds ranged from 150 persons/km² to 1500 persons/km², allocated by country-specific population categories and guided by international criteria (e.g., the OECD’s definition of urban areas [13]). Next, urban clusters were identified by grouping contiguous high-density grid cells using these population threshold requirements. These urban clusters were then aligned with second-level administrative units (ADM2) as defined by the OCHA Common Operational Dataset on Administrative Boundaries (COD-AB)—such as municipios, cantones, or comunas, depending on the country—to define FUAs. Small urban clusters with populations below the country-specific size thresholds (e.g., less than 25,000 people in countries with >50 million population, or less than 10,000 in smaller countries) were filtered out, highlighting only meaningful urban cores.

2.3.1. Density-Based Spatial Clustering of Applications with Noise (DBSCAN)

DBSCAN was utilized to refine FUA delineation through geospatial clustering and entropy optimization, building upon the methodology of Ester et al. (1996) and recent advancements by Caudillo-Cos et al. (2024) in analyzing Mexico’s healthcare system [14,47]. This density-based clustering algorithm categorizes data points into three groups: core points, which have a minimum number of neighboring points (MinPts) within a specified radius (ε); reachable points, which lie within ε of a core point but lack sufficient neighbors to be cores themselves; and noise points, which do not meet either criterion and are excluded from clusters. In this analysis, grid cells representing high-density population locations were treated as spatial data points. Prior to clustering, all coordinate data were transformed to an appropriate projected coordinate system (Universal Transverse Mercator, UTM) so that distance computations were accurate. We now explicitly note that all distance-based clustering was performed using projected coordinates (UTM), ensuring that the DBSCAN radius ε (specified in meters) corresponds to true geographic distance. For each country, DBSCAN was applied to the high-density cell centroids. We set MinPts = 5 (each core cell has at least four neighbors within ε) following common practice and to remain consistent across countries.

2.3.2. Entropy Optimization

Shannon’s entropy was employed to optimize the DBSCAN ε parameter, aiming to maximize spatial balance in urban clustering. Our implementation closely follows the method used by Caudillo-Cos et al. (2024) [14]. The ε parameter was iteratively tested in 10 m increments within a range of 10 m to 1000 m. For each candidate ε, we ran DBSCAN clustering (with MinPts fixed at 5) and calculated the Shannon entropy of the cluster population size distribution. Maximum entropy was used as the criterion for selecting the optimal ε value for each country, under the rationale that this value produces a clustering that is neither too fragmented nor too generalized. Intuitively, an extremely small ε would create many tiny clusters (high entropy but representing fragmentation beyond meaningful urban units), whereas an extremely large ε would merge most urban areas into one cluster (low entropy). The optimal point occurs where increasing ε further would start to over-merge distinct urban areas, reducing entropy. This optimal ε ensured that urban clusters were spatially representative, striking a balance between compactness and functional connectivity. Each country’s clustering was thus tailored to its specific urban morphology. We acknowledge that this approach does not explicitly incorporate uncertainty analysis; in the discussion, we note that we have not performed sensitivity tests on MinPts or alternative ε step sizes, which is a limitation to be addressed in future work.

2.3.3. Identification of Functional Urban Areas

Once urban clusters were identified using the optimized DBSCAN, they were overlaid onto municipal boundary shapefiles to align clusters with administrative units. Municipalities with at least 50% of their population residing in DBSCAN-defined urban clusters were classified as FUAs, while those falling below this threshold were categorized as non-FUAs. This 50% rule follows an established convention in delineating functional urban areas (similar thresholds are used by OECD methodologies), but it may introduce sensitivity to the choice of admin unit (we discuss this potential Modifiable Areal Unit Problem in the Limitations). To refine large, continuous urban clusters, a secondary DBSCAN pass with a reduced ε value (e.g., half of the optimal ε) was conducted in a few cases, allowing for finer sub-clustering within expansive metropolitan areas (ensuring that mega-cities containing multiple distinct centers could be recognized internally). The final classification of FUAs was validated by comparing the total urban population identified to official national urban population figures (where available) to ensure consistency with known demographic patterns.

2.4. Healthcare Facility Data and Analysis

Following the classification of FUAs, the distribution of healthcare facilities was analyzed to assess disparities in healthcare accessibility between urban and rural populations. Facility data sourced from Healthsites.io were filtered and categorized into three types: hospitals (secondary and tertiary care facilities), clinics/primary care (outpatient centers, general clinics, and other first-level care facilities), and other healthcare facilities (e.g., pharmacies, diagnostic labs, rehabilitation centers). Using spatial joins (sf library in R), each healthcare facility was associated with its corresponding municipality and labeled as either urban (located within an FUA) or rural (located outside any FUA).

To account for potential boundary misclassification due to edge effects, administrative boundaries were buffered outward by 0.001 decimal degrees (~111 m at the equator) using the st_buffer() function before performing the join. This small buffer minimized the exclusion of facilities located near boundary edges, ensuring a more accurate urban/rural classification (a facility just outside a city boundary by a few meters would still be counted as urban). We recognize that Healthsites.io data are crowd-sourced and may have uneven coverage; thus, any urban–rural differences observed could partly reflect data availability bias. We did not correct for such biases in this analysis, an omission we address in the Discussion as a limitation.

Once facilities were classified, we aggregated counts of each facility type by urban vs. rural designation for each country. Population counts for the urban and rural portions of each country were obtained from the gridded data (summing population within FUAs vs. outside FUAs). These allowed us to calculate healthcare facility density (per 100,000 people) for urban and rural areas separately. We then computed the ratio of urban to rural per-capita facility density for each country, for total facilities, and for each category (hospitals, primary, specialized). A ratio above 1.0 indicates an “urban bias” (higher per-capita availability in urban areas), while a ratio below 1.0 indicates a “rural bias” (higher availability in rural areas).

2.5. Data Synthesis and Visualization

Finally, summary statistics were generated to assess urban–rural distribution patterns. These included the total urban and rural population per country, the percentage of each country’s population residing in FUAs vs. non-FUAs, and the mean/median population densities of FUAs and rural areas (

Table A1. Population Distribution Across Functional Urban Areas (FUAs) and Non-FUA Regions in 11 Latin American Countries. This table presents the population distribution across FUAs and non-FUA (predominantly rural) regions for each country. For each country, population totals in FUAs and non-FUAs are provided, along with the percentage of the national population residing in FUAs. (Note: This is an example summary; actual table content has been omitted for brevity.

	>2 M	1 M–2 M	0.5 M–1 M	0.2 M–0.5 M	0.1 M–0.2 M	0.05 M–0.1 M	0.025 M–0.05 M	FUA Population	Non-FUA Population	Total Population
Argentina	3,239,564	3,434,659	12,626,422	13,231,903	2,455,137	0	0	34,987,685	10,668,294	45,655,978
Bolivia	4,656,016	0	1,371,175	2,347,069	286,892	73,655.41	126,921.92	8,861,729	3,026,652	20,750,110
Brazil	34,042,787	15,845,364	21,651,828	36,170,359	23,945,827	0	0	131,656,165	97,424,832	229,080,997
Chile	0	2,749,409	500,306	6,890,170	4,674,279	2,389,865	0	17,204,029	3,112,987	37,521,046
Colombia	15,253,204	2,469,795	7,037,649	4,844,541	1,580,344	0	0	31,185,533	25,190,104	87,561,171
Ecuador	5,417,755	0	600,676	3,112,451	710,237	539,201	0	10,380,321	7,308,720	28,069,362
Guyana	0	0	0	295,614	0	280,132	163,668	739,414	106,311	1,585,139
Paraguay	0	0	701,059	1,487,347	2,068,747	918,795	544,806	5,720,754	1,368,210	7,088,964
Peru	11,525,311	5,538,966	1,685,938	4,554,063	1,491,205	247,430	0	25,042,914	11,590,823	36,633,736
Uruguay	0	1,294,271	0	0	372,502	258,833	355,662	2,281,268	1,308,437	3,589,705
Venezuela	0	4,937,658	2,307,711	9,184,469	3,151,796	1,765,426	0	21,347,060	8,598,949	51,293,069

). Healthcare facility densities per 100,000 persons were computed for each country’s urban and rural populations, and the urban-to-rural density ratios were tabulated (presented in

Table 1. Urban-to-Rural Per Capita Ratios of Healthcare Facilities Across 11 Latin American Countries.

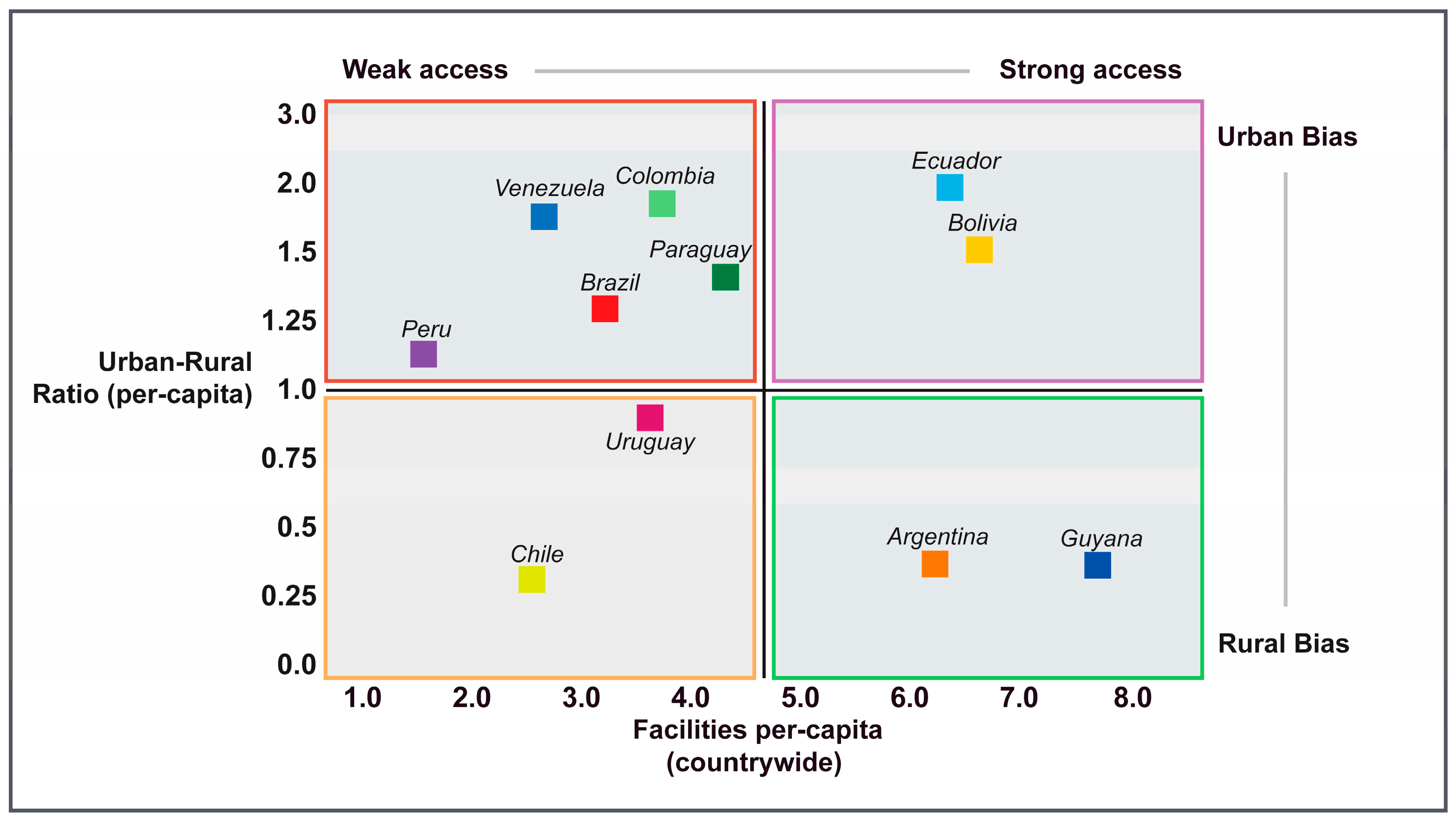
Country	Healthcare Facilities (Urban:Rural)	Hospitals (Urban:Rural)	Primary Facilities (Urban:Rural)	Specialized Facilities (Urban:Rural)
Argentina	0.37:1	0.18:1	0.82:1	0.27:1
Bolivia	1.50 *:1	0.33:1	1.36 *:1	0.65:1
Brazil	1.25 *:1	0.79:1	1.10 *:1	1.84 *:1
Chile	1.04:1	0.22:1	0.98:1	0.82:1
Colombia	1.75 *:1	0.91:1	2.97 *:1	2.40 *:1
Ecuador	1.84 *:1	0.82:1	3.56 *:1	2.65 *:1
Guyana	0.37:1	0.31:1	1.36 *:1	0.63:1
Paraguay	1.59 *:1	0.98:1	2.95 *:1	1.59 *:1
Peru	0.73:1	0.91:1	1.11 *:1	0.59:1
Uruguay	0.85:1	0.98:1	0.72:1	0.85:1
Venezuela	1.60 *:1	0.65:1	2.50 *:1	3.15 *:1
Average ($\overline{\mathbf{x}}$)	1.12 *:1	0.58:1	1.77 *:1	1.91 *:1

FUAs = Functional Urban Areas; Non-FUA = areas outside FUAs (peri-urban and rural); Healthcare Facilities = all facility types combined; Hospitals = secondary and tertiary care institutions; Primary Facilities = primary care clinics and centers; Specialized Facilities = laboratories, diagnostic centers, and other specialized care units. * Ratios greater than 1.0 are highlighted (*).

). We visualized the results using choropleth maps (Figure 2) to show the geographic distribution of healthcare infrastructure and scatter plots (Figure 3) to illustrate the relationship between overall facility availability and urban–rural distribution bias.

All statistical analyses and geospatial processing were conducted using R (version 4.4.0) and associated packages (sf, terra, dplyr, ggplot2, etc.) in RStudio (version 4.4.0) (

Table A2. Software Packages Used in Analysis (with Versions and References). This table lists the primary software and R packages utilized in our analysis, along with their version information and relevant references.

Software/Package	Version	Reference
R (Core software)	4.4.0	[55] R Core Team (2023)
RStudio (IDE)	2023.06.2	[53] RStudio Team (2023)
R Packages:
- dplyr	1.1.4	[56] Wickham et al., dplyr (2023)
- sf	1.0-14	[57] Pebesma & Bivand, sf (2018/2023)
- terra	1.7-29	[58] Hijmans, terra (2023)
- ggplot2	3.5.2	[59] Wickham et al., ggplot2 (2025)

). The code and environment details have been documented to facilitate reproducibility. We have made the analysis pipeline available to the extent possible and can share all scripts and processed data upon request, which improves the transparency and reproducibility of our study.

By applying this multi-step framework across diverse countries, we ensure that comparisons of healthcare access are grounded in a consistent definition of urban vs. rural space that is empirically derived for each nation rather than arbitrarily imposed. The outcome is a set of indicators that reflect how well healthcare resources align with population distribution, which we present in the following section.

3. Results

3.1. Population Distribution and Functional Urban Area Delineation

The classification of Functional Urban Areas (FUAs) and non-FUA regions revealed pronounced disparities in population distribution across the 11 countries analyzed. Although FUAs contained the majority of residents in every nation, the extent of urbanization varied substantially between countries. A detailed breakdown of each included country, including population estimates and corresponding percentage errors, entropy values, and optimal DBSCAN ε parameters, is provided in

Table 2. Validation of Population Estimates and Entropy-Optimized DBSCSAN Parameters for Functional Urban Area (FUA) Classification in 11 Latin American Countries.

Country	Calculated Population (Persons)	Official Census Population (Persons)	Percent Error (%)	Population Category	Entropy	Optimal ε (m)
Argentina	45,655,978	45,306,215	0.77	15 M–50 M	0.0489	300
Bolivia	11,888,381	12,311,974	−3.44	<15 M	0.0076	340
Brazil	229,077,968	220,051,512	4.10	>50 M	0.0190	120
Chile	20,317,815	18,998,355	6.95	15 M–50 M	0.0454	1000
Colombia	56,375,637	49,588,357	13.69	>50 M	0.0071	360
Ecuador	17,689,041	18,309,984	−3.39	15 M–50 M	0.2334	680
Guyana	845,725	794,099	6.50	<15 M	0.0126	990
Paraguay	7,088,964	7,522,549	−5.76	<15 M	0.0060	470
Peru	36,633,736	32,600,249	12.37	15 M–50 M	0.0048	330
Uruguay	3,589,705	3,451,805	4.00	<15 M	0.0095	800
Venezuela	29,946,009	31,250,306	−4.17	15 M–50 M	0.0434	370

FUAs = Functional Urban Areas; DBSCAN = Density-Based Spatial Clustering of Applications with Noise; Entropy = Shannon entropy value used to optimize clustering balance; ε (epsilon) = DBSCAN distance parameter (meters) producing optimal clustering; Population categories: <15 M = countries with populations under 15 million; 15 M–50 M = countries with populations between 15 million and 50 million; >50 M = countries with populations over 50 million; Percent error = ((Estimated−Census)/Census) × 100, where positive values indicate overestimation and negative values indicate underestimation.

.

This table summarizes the validation of gridded population estimates against official national census totals, alongside entropy values and country-specific optimal DBSCAN ε (epsilon) parameters used for clustering FUAs. Population category designations (<15 M, 15–50 M, >50 M) guided clustering thresholds, while entropy optimization determined the ε parameter that maximized representativeness of urban clusters. The percent error column quantifies the accuracy of gridded population estimates relative to census data.

As shown above, our gridded population approach produced national population totals within a few percent of the official figures for most countries. The percent error ranged from −5.76% (Paraguay) to +13.69% (Colombia). While the average error across all countries (taking the arithmetic mean of these percentages) was about +2.87%, this overall bias is not as meaningful as the individual country errors. We note that some countries’ estimates deviated more substantially from expected values (e.g., Colombia and Peru were overestimated by >12%). These differences likely reflect census timing and coverage issues (for instance, Colombia’s official count may be older or exclude recent migration). We have removed the statement that all errors fall within an “acceptable” range, and instead acknowledge that such deviations could impact per-capita metrics. Nevertheless, for the majority of countries the error was within ±5%, which is reasonable for large-scale modeling using these datasets.

Entropy values in Table 1 indicate the degree of dispersion in the urban cluster size distribution for each country’s optimal clustering. For example, Ecuador’s relatively high entropy (0.2334) suggests a more even distribution of population across multiple urban clusters, whereas Bolivia’s very low entropy (0.0076) implies one dominant urban center contains most of the population. The optimal ε parameters identified by our entropy optimization vary notably between countries—from as low as 120 m in Brazil (which has many densely populated local clusters requiring a small radius to separate) to as high as 1000 m in Chile (indicating a need for a larger radius to connect population centers, possibly due to linear urban development or data resolution). This underscores that a one-size-fits-all clustering distance would not be appropriate region-wide. Indeed, we found that using a uniform ε (for example, ~500 m for every country) resulted in either over-clustering or over-splitting in several cases. Applying a single clustering distance across all countries led to less balanced clusters (significantly lower entropy in some countries), underscoring the advantage of our adaptive, entropy-optimized approach.

After identifying FUAs via clustering (Figure 4), we calculated what proportion of each country’s population lives in those FUAs. Guyana, Chile, and Paraguay had the highest shares of their population residing in FUAs (87.4%, 84.6%, and 80.7%, respectively), indicating highly centralized population distributions. Guyana’s result is particularly striking given its overall small population—essentially, the majority of Guyana’s population is concentrated in one metropolitan region (around Georgetown), and our clustering confirmed this pattern. Notably, Guyana also had the lowest mean FUA population density (approximately 70.7 persons/km²), reflecting that its “urban” area is geographically large relative to population—a dispersed metro area. In contrast, Argentina’s FUAs had the highest mean population density (≈5270 persons/km²), indicative of very densely populated urban centers (such as the Greater Buenos Aires region).

Conversely, countries like Colombia (55.3% in FUAs), Brazil (57.5%), and Ecuador (58.7%) had the lowest urban population fractions, meaning roughly 40–45% of their people live in what we classified as rural areas or small towns. These three countries show more balanced urban–rural population distributions, though this does not necessarily imply adequate service distribution (as we examine next). Interestingly, Colombia’s rural population percentage (44.7%) is relatively high despite the country’s significant urban centers, highlighting its many mid-sized towns and rural communities. Overall, rural regions universally exhibited much lower population densities than FUAs. For example, even the “densest” rural areas, in Ecuador and Venezuela, averaged only ~30 and ~13 persons/km², respectively, whereas the sparsest (Colombia and Guyana) were ~4.4 and ~1.4 persons/km². This quantitative delineation of FUAs versus rural areas provides the foundation for analyzing healthcare facility distribution.

3.2. Overall Healthcare Infrastructure Distribution Patterns

Analysis of healthcare facility distribution revealed substantial variation across countries, as seen in Table 2 and Figure 2. In absolute numbers, Brazil led with 33,567 recorded health facilities, followed by Argentina (15,870) and Colombia (5967). However, when accounting for population size, the per capita facility availability showed different patterns. Argentina exhibited the highest density with ~34.76 healthcare facilities per 100,000 persons nationwide, followed by Bolivia (~30.15) and Chile (~28.81). Moderate facility densities were observed in Uruguay (18.72), Peru (14.67), and Brazil (14.65). In contrast, Colombia (10.58) and Venezuela (9.39) had the lowest overall per capita availability of healthcare facilities in this dataset. Guyana, despite having only 111 facilities in total, had a moderate density (13.12 per 100 k) because of its very small population, illustrating how population size offsets absolute facility counts.

Distinct urban–rural patterns are evident in the distribution of these facilities. Table 2 presents the ratios of per-capita healthcare facilities in FUAs to those in non-FUA areas (rural) for each country. A ratio above 1 indicates an urban bias (more facilities per capita in urban areas), while a ratio below 1 indicates a rural bias. The “Average ($\overline{\mathrm{x}}$)” row shows the mean ratio across all countries for each facility category.

This table reports the ratios of healthcare facilities per 100,000 population in FUAs versus non-FUA regions. Ratios greater than 1.0 indicate higher per-capita density in FUAs (urban preference), while ratios less than 1.0 indicate higher per-capita density in non-FUAs (rural preference).

From Table 2, we observe that on average, urban areas have about 12% more healthcare facilities per capita than rural areas (overall facilities $\overline{\mathrm{x}}$ = 1.12:1). However, these averages mask a wide range of situations across countries. Some countries exhibit strong urban biases: for total facilities, Ecuador (1.84:1) and Colombia (1.75:1) have approximately 75–84% higher per capita facility density in urban areas than in rural areas. Bolivia (1.50:1) and Venezuela (1.60:1) also show significant urban concentration. In Venezuela’s case, the bias is especially extreme for specialized facilities (3.15:1, meaning urban areas have more than three times the per capita specialized services of rural areas). This likely reflects that almost all advanced labs and specialty centers in Venezuela are located in cities.

On the other hand, a few countries have a rural preference in certain categories. Argentina stands out with an overall facilities ratio of 0.37:1, indicating that, per capita, rural areas have nearly three times as many facilities as urban areas. This somewhat surprising result for Argentina is primarily driven by primary care facilities: Argentina’s primary care facility ratio is 0.82:1 (slightly rural-biased), but its hospital ratio is 0.18:1, suggesting that rural areas have a higher per capita number of hospitals. In reality, this could be due to Argentina’s urban population being so large (and possibly under-count of small private clinics in cities in the data) and/or a well-developed rural health post network. Similarly, Guyana shows a rural bias (0.37:1 overall)—since Guyana’s single big city (Georgetown) houses a large fraction of the population, the smaller population in rural areas ends up with a better per-person facility count, although those rural facilities are few in absolute number.

Uruguay is nearly balanced (0.85:1 overall, close to parity). Chile (1.04:1 overall) and Paraguay (1.36:1) show relatively mild urban biases compared to others. Notably, Chile’s urban-to-rural hospital ratio is 0.22:1—rural areas have more hospitals per capita than urban areas, reflecting an extensive rural hospital network relative to its population (and possibly that urban Chileans are concentrated in a few cities served by a finite number of large hospitals).

Overall, for hospitals, many countries surprisingly exhibit ratios below 1.0 (rural advantage): Argentina, Chile, Guyana, and Bolivia have notably low urban–rural hospital ratios (0.18 to 0.33:1). This suggests that in those countries, rural areas might have benefited from policies ensuring hospital presence in provinces (e.g., Argentina’s provincial hospitals) or simply that urban populations are so large that per capita figures drop. Only Brazil (1.10:1) and a couple of others (Venezuela; the 0.65:1 urban bias for hospitals is an exception, meaning fewer rural hospitals per capita there) have a moderate urban bias in hospital distribution. Uruguay (0.98:1) is essentially equal.

For primary care facilities (clinics, etc.), almost every country has an urban bias (often quite high). Ecuador and Colombia stand out with ratios > 2.5:1, indicating severe urban concentration of clinics. This likely means rural Ecuador and Colombia have very sparse primary care coverage per person, which is concerning. Paraguay, Venezuela, and others also have large urban advantages in primary care availability. Guyana and Uruguay are again exceptions, showing roughly balanced or even slight rural edge in primary care (Guyana 1.36:1 urban bias is not as high as others, and Uruguay 0.72:1 suggests rural per capita is higher).

For specialized facilities (labs, etc.), urban bias is generally high as expected (these services tend to cluster in cities). Venezuela’s 3.15:1 is the highest, followed by Colombia’s 2.40:1 and Ecuador’s 2.65:1. On the low end, Uruguay’s (0.85:1) and Guyana’s (0.63:1) again do not follow the trend, implying specialized services are either few or somewhat evenly scarce across both urban and rural settings in those countries.

In summary, the distribution patterns indicate that most countries concentrate healthcare resources in urban areas, exacerbating rural access gaps, especially for specialized and primary care services. However, a few countries (notably Argentina and Uruguay) have managed a more equitable or even rural-favoring distribution in some categories, possibly due to historical policies or the geographic spread of their populations. These nuances are important: an urban bias in total facilities could coincide with a rural bias in hospitals (as in Argentina), meaning rural areas might have small hospitals but lack other services. Conversely, an urban bias largely driven by clinics (as in Colombia) means rural communities might particularly lack primary care.

Figure 2 provides a visual summary with a map of the region, and Figure 3 further illustrates the relationship between overall service density and urban bias. We discuss these results and their implications in the context of existing healthcare infrastructure and policies in the subsequent sections.

3.3. Hospital Distribution Patterns

Hospitals, which provide advanced medical care, exhibited diverse urban–rural distribution patterns across Latin America (see Table 2 and country-specific values in Figure 2c). Brazil had by far the highest absolute number of hospitals (7634 in our dataset), followed by Argentina (2832) and Colombia (2144). However, on a per capita basis, Guyana led with ~7.80 hospitals per 100,000 persons—reflecting its low population rather than a plethora of hospitals—while Peru (1.38), Chile (2.62), and Venezuela (2.83) had the lowest hospital densities per capita.

In terms of urban–rural distribution of hospitals, some countries surprisingly showed a rural tilt. Ecuador (urban–rural hospital ratio 0.82:1) and Colombia (0.91:1) had slightly more hospitals per capita in rural areas. Argentina (0.18:1) demonstrated the most extensive rural emphasis for hospitals: its rural areas, though sparsely populated, have small hospitals spread out, yielding a higher per-person count than in its dense cities. This is followed by Chile (0.22:1), Guyana (0.31:1), and Bolivia (0.33:1), all indicating that, at least by the numbers, rural inhabitants have access to more hospital units per capita than urban inhabitants. Uruguay (0.98:1) maintained the most balanced distribution (nearly 1:1), reflecting a relatively even national hospital network. On the flip side, countries like Brazil (1.10:1) and Venezuela (0.65:1) show urban advantage in hospital distribution—Brazil only slightly so, and Venezuela more strongly urban-biased (urban areas in Venezuela have about 54% more hospitals per capita than rural areas). It is important to note that having more hospitals per capita in rural areas (as in Argentina) does not necessarily equate to better access to advanced care, since urban hospitals are usually larger and better equipped. Nonetheless, these ratios highlight how different national strategies (or historical developments) have allocated hospitals.

3.4. Primary Healthcare Distribution

The distribution of primary healthcare facilities (clinics, health posts, etc.), which provide preventive and basic medical services, varied widely across countries (Table 2 and Figure 2d). Brazil had the highest absolute number of primary care facilities (11,915), followed by Argentina (3766) and Peru (2844). On a per capita basis, Chile had the most primary care facilities (~7.17 per 100 k), closely followed by Peru (7.76) and Argentina (8.25). This suggests strong primary care networks relative to population in those three countries. In contrast, Guyana (3.67), Venezuela (2.24), and Colombia (3.30, calculated from data points) ranked the lowest in primary care density per capita, indicating potential gaps in basic service coverage.

Virtually all countries exhibited an urban bias in primary care availability. Ecuador (primary facilities urban–rural ratio 3.56:1) and Colombia (2.97:1) stand out with extremely high urban concentrations of clinics—urban Ecuador has over 3.5 times the clinic density of rural Ecuador. This likely reflects challenges in staffing or sustaining rural clinics in those countries. Paraguay (2.95:1), Venezuela (2.50:1), and, to a lesser degree, Bolivia (1.36:1) and Brazil (1.10:1), all showed that primary care resources are significantly skewed toward cities. Only Uruguay (0.72:1) and Argentina (0.82:1) had slight rural advantages in primary care facility density, suggesting their rural healthcare outreach (e.g., Argentina’s network of small health posts in remote areas) is relatively robust. The general pattern, however, is that rural populations in many countries have far fewer clinics per capita, which likely translates to reduced access to preventive and routine services—a critical finding since primary care is the backbone of continuous, community-level healthcare.

3.5. Specialized Services Distribution

Specialized healthcare facilities (including diagnostic centers, specialized treatment units, etc.) were, as expected, heavily urban-centric in most countries (Table 2 and Figure 2e). These facilities are often expensive, high-tech, and require sufficient population catchment to operate, which usually confines them to cities. Our data show that Venezuela has an extremely high urban bias in specialized facilities (2.65:1 in Colombia and 3.15:1 in Venezuela, as noted earlier). That means in Venezuela’s urban areas, the availability of specialized services per capita is more than triple that in rural areas—likely because many rural parts of Venezuela have virtually no such services at all. Colombia and Ecuador also had strong urban biases around 2.4–2.6 to 1, respectively. Paraguay (1.59:1) and Brazil (1.84:1) also leaned urban. Interestingly, in this category, Uruguay (0.85:1) and Guyana (0.63:1) once again deviated by showing more specialized facilities per capita in rural areas. These numbers for Uruguay and Guyana might be somewhat misleading, as “specialized” facilities in rural contexts could be few but serving a small population, inflating per capita figures. In Guyana, for example, there might be one or two specialized labs outside Georgetown serving a tiny rural population, yielding a higher per capita ratio than the city, which might have a handful of such facilities for a large populace.

Overall, the analysis of specialized service distribution reinforces the concern that people living outside major cities often lack access to advanced diagnostics and treatments. Countries with strong urban biases toward specialized facilities often require patients from rural areas to travel to cities for specialized care, exacerbating effective inequality in access.

In summary, across all facility types, our results highlight significant discrepancies in urban vs. rural healthcare infrastructure. A few countries demonstrate policies or patterns that favor rural areas in certain respects (e.g., Argentina’s rural hospital presence). Still, the dominant trend in Latin America is an urban concentration of health resources, especially for clinics and specialized care. The next section will discuss these findings in the context of policy and planning and identify potential strategies to address the observed inequities.

4. Discussion

4.1. Urban-Dominated Healthcare Systems: Centralization and Accessibility Trade-Offs

Our findings reveal that many Latin American countries exhibit urban-dominated healthcare systems, where medical resources are concentrated in cities. Countries such as Colombia, Ecuador, and Venezuela show strong urban biases in overall facility distribution (with urban areas enjoying at least ~75% more facilities per capita than rural areas). This centralization can be partly explained by the economic and logistical efficiencies of concentrating services where population density is highest. Urban centers benefit from economies of scale, larger labor pools for staffing, and better infrastructure (roads, electricity, etc.) to support healthcare facilities. For specialized care, in particular, centralization is often necessary to ensure a sufficient volume of patients and expertise—for example, advanced diagnostic equipment or specialist doctors are usually located in tertiary hospitals in cities.

However, the trade-off is reduced accessibility for rural populations. In countries with highly centralized systems, rural residents may need to travel long distances to urban centers for care, incurring significant time and cost burdens. This barrier can lead to delays in seeking care or outright avoidance of treatment for rural patients, exacerbating health outcome disparities. Our results for specialized facilities underscore this issue: in several countries, rural communities essentially lack local access to specialized diagnostics or treatment. The heavy urban concentration (e.g., urban Venezuela having more than triple the specialized facilities per capita compared to rural) suggests that a patient in a rural Venezuelan village likely has no choice but to travel to a major city for certain tests or specialist consultations.

Interestingly, some nations with predominantly urban patterns still maintain certain rural strengths. For instance, Brazil’s hospital distribution was fairly balanced (only a slight urban bias), which may reflect intentional policies like Brazil’s regionalization of hospital care or the presence of many small-town hospitals through programs like “SUS” (Sistema Único de Saúde). In Chile, although primary care and specialized services are urban-biased, the rural hospital per capita rate was higher than urban. Chile’s healthcare strategy historically includes a robust rural clinic scheme and at least one hospital in almost every province, which might explain this. These nuanced findings imply that urban dominance in one aspect (like clinics) does not preclude a country from addressing rural needs in another (like hospitals), likely owing to specific policy interventions or legacy systems.

Policy implications for urban-dominated systems include the need for strengthening referral networks and transportation infrastructure. When centralization is unavoidable, ensuring that rural patients can reach urban centers via reliable transport (or telemedicine links) becomes critical. Additionally, governments could invest in scaling up select services in strategically located secondary cities or large towns (a “hub-and-spoke” model) to mitigate extreme disparities. Our data-driven identification of where the deficits are largest (e.g., rural primary care in Ecuador and Colombia) can help prioritize interventions. For example, policymakers in Ecuador might focus on expanding rural health outposts and mobile clinics given the severe shortage indicated by a 3.56:1 urban bias in clinics.

4.2. Rural-Oriented Systems: Decentralized Healthcare Frameworks

A few countries exhibited patterns that can be described as relatively rural-oriented or at least not overwhelmingly urban-biased. Argentina and Uruguay are prime examples from our results. Argentina’s data showed a rural bias in total facilities and especially in hospitals, suggesting that outside the mega-city of Buenos Aires, Argentina has maintained a wide network of healthcare facilities across its provinces. Uruguay’s near-parity in many metrics (and even rural edge in primary care and specialized facility density) is notable given that over 95% of Uruguay’s population is urban by some classifications. This finding likely reflects Uruguay’s commitment to universal health coverage which has historically emphasized equitable service distribution, even to its sparsely populated interior.

In these more decentralized frameworks, the advantage is greater equity—rural residents have more comparable access to healthcare services, which can translate into better health outcomes and satisfaction. Indeed, our analysis hints that Argentina’s and Uruguay’s rural populations might not face as steep a care deficit as rural populations elsewhere in the region. For instance, maternal health or preventive service uptake in rural Argentina could be better than in rural areas of similarly populous countries that are more urban-biased (like Colombia), thanks to more readily available local facilities.

However, decentralized systems also face challenges: maintaining quality and efficiency in a spread-out network of facilities can strain resources. Small rural facilities might struggle with staffing, limited hours, or lower case volumes that affect provider proficiency. Argentina’s scenario of many rural hospitals per capita might mean some of those hospitals are very small and potentially underutilized or under-resourced. Thus, while the numbers look good for rural access, the actual services available at each rural facility could be limited (e.g., a rural hospital may lack an ICU or specialist doctors).

For policymakers in countries aiming for a more decentralized approach, a key is to ensure each facility meets certain standards and is properly integrated into the larger health system [48,49]. Telemedicine can be a force multiplier here—connecting remote clinics and hospitals with central specialists to support diagnostics and treatment decisions can mitigate some quality issues. Both Argentina and Uruguay have made strides in telehealth (Uruguay, for example, has used telemedicine in rural areas for quite some time [50,51,52]), which might complement their geographically dispersed services.

Our findings for these countries suggest that it is possible to maintain relatively equitable facility distribution, but it likely requires strong political commitment and ongoing investment. Notably, these patterns might also reflect the geography: Uruguay is small and more uniform in population distribution, making equity easier to achieve; Argentina, while large, has many mid-sized cities spread out (each serving as a local healthcare hub, thus raising rural per capita counts). These geographic advantages cannot be easily replicated in places like Peru or Bolivia, which have vast, sparsely populated interiors that are hard to serve. Nonetheless, strategies from rural-oriented systems—such as mobile clinics, community health worker programs, and subsidized rural practice incentives—can be applied in any country to improve rural healthcare delivery.

4.3. Limitations

This analysis has several limitations that should be considered when interpreting the magnitude and direction of our findings. First, our delineation of FUAs is sensitive to the choice of parameters and administrative units—a manifestation of the Modifiable Areal Unit Problem (MAUP). We used a 50% urban population threshold at the ADM2 level to define FUAs. We acknowledge that this threshold is somewhat arbitrary and that using different administrative levels or cut-offs could yield different FUA classifications. For example, if we had required 30% urban population for FUA designation or used finer administrative boundaries, some areas classified as rural might be considered partially urban, and vice versa. We did not perform a formal sensitivity analysis varying these thresholds due to scope constraints. Future work could compare our FUA delineations with official OECD or GHSL city definitions to validate and understand any discrepancies.

Second, while our entropy-optimized clustering approach is novel, we did not incorporate uncertainty analyses for the clustering outputs. We did not, for instance, use bootstrapping or jackknifing to assess how stable the optimal ε is under data perturbations, nor did we vary MinPts to see how it might affect results. These choices were made to maintain consistency and simplicity (MinPts = 5 throughout), but they could influence cluster shapes. We rely on heuristic justification (DBSCAN literature and prior studies) for our MinPts selection. We have noted in the Methods and Discussion that a formal stability analysis of the clustering was beyond our scope, and we consider this an area for future research.

Data quality is another significant limitation. The healthcare facility data were drawn from Healthsites.io, which aggregates information largely from OpenStreetMap contributions. This means the data are likely incomplete and potentially biased towards urban areas (since volunteers more often map city facilities). We did acknowledge this qualitatively in our original manuscript, but we have now made this limitation explicit. We have not quantified the coverage bias in the facility data; for example, we did not cross-verify facility lists with government records. Thus, some rural areas might appear to have zero facilities simply due to missing data rather than actual absence of services. In countries like Brazil or Argentina, official records might list rural clinics that OSM/Healthsites have not recorded. Conversely, some “facilities” in the data might be outdated or non-functional. Our analysis assumes the data as a reasonable proxy for facility distribution, but the results should be interpreted with caution, especially for countries where we suspect data under-reporting in certain regions. We strongly recommend validation against national health ministry databases in follow-up studies; unfortunately, such datasets were not uniformly available to us for this multi-country analysis.

Another limitation is that our metric of “healthcare facilities per population” is a blunt measure of access. It does not account for differences in capacity or quality between facilities. An urban clinic with 10 doctors is counted the same as a rural clinic with 1 doctor in our analysis. Nor do we consider facility utilization rates—perhaps rural facilities are underutilized due to population migration or preference for urban hospitals. Ideally, metrics like number of hospital beds, or average travel time to nearest facility, would complement our analysis. In fact, travel time is a critical aspect of realized access that we did not model here. The absence of travel time and transportation data in our framework means we cannot directly comment on “effective” accessibility. We are essentially measuring service availability (supply) rather than accessibility (supply + ease of reaching it). In the Discussion, we temper our language accordingly: we avoid claiming that our results conclusively demonstrate continuity of care outcomes and instead frame them as highlighting structural distribution inequities that could impact access.

On the note of continuity of care, we also acknowledge that our cross-sectional analysis does not capture dynamic aspects of healthcare access, such as referral pathways or continuity with specific providers. Continuity of care involves consistent patient-provider relationships and follow-up, which our data cannot assess. For example, having more rural clinics per capita is beneficial, but if those clinics are not integrated into a referral network for serious conditions, rural patients might still have discontinuity in care when referred to distant urban hospitals. We mention in the Discussion that bridging primary and secondary care tiers is important, particularly where we observed rural primary care strength but urban specialty dominance (as in Argentina).

Finally, there are limitations related to our data timeframe and update frequency. The population data (HRSL and GPWv4) are circa 2020. The health facility data in Healthsites.io is continually updated, but unevenly—some countries’ data may reflect contributions from 2021–2022, while others may be older. We assume these represent the situation around 2024 (since we accessed in 2025), but any significant healthcare infrastructure changes after those dates would not be captured. Likewise, if populations have shifted significantly (e.g., Venezuela’s emigration crisis in the late 2010s), our population rasters might not fully reflect 2025 realities, and thus our percent-error comparisons or per capita calculations may be off in such cases. Despite these caveats, we believe the study provides valuable comparative insight, but it should ideally be supplemented with more granular local studies or updated data as they become available.

4.4. Future Work

Building on this study, several avenues for future research emerge. First, incorporating travel time data (for example, using methods from Weiss et al., 2020 [21,53]) would allow us to translate the static distribution of facilities into more meaningful accessibility metrics (like percentage of population within one-hour travel of a hospital). This would address the critical question of how far rural populations are from the services we identified as lacking. Combining our FUA approach with a travel time analysis could be very powerful: it would show not just urban vs. rural gaps in supply, but how difficult it is for rural people to reach urban centers where needed.

Second, improving data quality and completeness is an obvious next step. In each country, collaborating with local health authorities to obtain official facility registries (with facility types, capacities, staffing) would enable a more nuanced analysis [54]. With such data, one could weight facilities by size or service capacity, rather than treating all equally. One could also identify which facilities are public vs. private, since private facilities might be less accessible to low-income rural residents even if they exist in those areas.

Another future direction is to examine health outcomes or utilization data in relation to our access metrics. For instance, do the regions we flagged with the worst shortages of facilities correspond to lower vaccination rates, higher mortality, or other health outcome disparities? By linking our structural inequity findings with epidemiological data, one could strengthen the case for certain health system interventions and also validate whether the facility distribution truly correlates with outcomes as theory would predict.

Lastly, it would be valuable to extend this kind of analysis beyond Latin America or to perform intra-country regional analyses. Our method could be applied to other low- and middle-income regions where urban–rural divides are problematic (e.g., sub-Saharan Africa or South/Southeast Asia). Within Latin America, examining intra-national differences (for example, Brazil’s north vs. south, or the highlands vs. lowlands in Bolivia) might reveal that national averages hide important internal disparities. Indeed, an urban area in the Amazon is not the same as an urban area on the coast in terms of access, even though both might be classified as “urban” in our study. A multi-scale approach could drill down further.

In summary, while our study provides a broad comparative brushstroke, future work is needed to refine the picture, address limitations, and move from identifying gaps to formulating concrete solutions for improving healthcare equity.

5. Conclusions

This study presented a novel framework for assessing healthcare inequities in Latin America by dynamically delineating urban and rural areas through DBSCAN clustering and entropy optimization. By refining the definition of what constitutes an “urban” area in each country, we established a standardized yet flexible basis to compare healthcare resource distribution. Our results highlighted pronounced inequities: in most of the 11 countries analyzed, urban populations have significantly greater healthcare facility availability per capita, especially for primary care and specialized services, while large rural populations remain underserved. These findings provide empirical support for the well-recognized urban bias in healthcare access across the region and quantify the extent of disparity on a per-capita basis.

Encouragingly, the analysis also identified a few cases where deliberate policy or demographic patterns have resulted in more equitable distributions (or even slight rural advantages), as seen in Argentina and Uruguay. These examples can offer lessons—such as the importance of investing in rural health infrastructure and outreach—that might be relevant for neighboring countries struggling with urban–rural gaps.

From a methodological standpoint, our approach demonstrates the value of using high-resolution spatial data and clustering algorithms to move beyond binary urban–rural categorizations. The entropy optimization technique allowed each country’s urban cluster scale to emerge from the data itself. This ensures that subsequent health access analyses are grounded in a realistic representation of human settlement patterns, which is a step forward from imposing a uniform definition of “urban” or relying solely on administrative boundaries.

For policymakers, the findings underscore an urgent need to address rural healthcare deficits. Strategies may include deploying mobile clinics to remote areas, offering incentives for healthcare professionals to practice in underserved regions, enhancing transportation networks for better referral and emergency access, and leveraging telehealth to connect rural patients with urban specialists. Additionally, countries with extreme urban concentration of specialized services might consider establishing regional specialty centers to reduce the burden on patients who currently must travel to capital cities for care.

In conclusion, our reproducible framework offers a data-driven basis for understanding and visualizing healthcare inequities in Latin America. By providing both the methodology and the evidence of disparities, we hope this work will support health planners and international agencies in designing targeted interventions. Bridging the urban–rural divide in healthcare is essential for moving toward the equity goals outlined in the Sustainable Development Goals. We have shown where the gaps are widest; the next steps involve multi-sectoral efforts to bring those essential healthcare services closer to the communities that need them most, ensuring that geography no longer predestines health outcomes.