Load-Sensitive Tire–Road Friction Modeling and Dynamic Stability Analysis of Multi-Axle Trucks

Abstract

This study addresses the accurate estimation of safe driving speeds for multi-axle trucks negotiating curved road segments by explicitly incorporating dynamic axle load transfer and load-sensitive tire–road friction characteristics. Conventional standards that assume a constant friction coefficient fail to capture wheel-specific load variations, leading to underestimation of rollover and skidding risks. To overcome these limitations, a load-sensitive friction model is integrated with the friction ellipse and static rollover threshold (SRT), and a forward–backward algorithm is applied to compute dynamically feasible speed trajectories. The proposed framework is demonstrated through accident reconstruction of a ramp rollover scenario using TruckSim–Simulink co-simulation with reported geometric and vehicle parameters. The results reveal that neglecting load sensitivity systematically overestimates safe speeds and underestimates lateral deviation. Furthermore, SRT variation analysis illustrates a trade-off between structural stability and frictional constraints, where rollover dominates under low stability and skidding under high stability conditions. These findings emphasize the necessity of accounting for dynamic load distribution and load-sensitive friction in truck safety speed estimation, providing a foundation for autonomous truck speed control strategies and enhanced road design standards.

1. Introduction

Tire–road interaction plays a fundamental role in vehicle safety because braking capability, cornering stability, and loss-of-control events are ultimately limited by the friction available at the tire–pavement interface. Numerous studies have shown that insufficient friction—whether caused by wet pavement, surface wear, or load-induced friction reduction—contributes to skidding and roadway-departure crashes across all vehicle types. Importantly, the effective friction coefficient ($\mu$) is not constant; it decreases nonlinearly with increasing vertical load, meaning that traction can be reduced precisely when dynamic load transfer increases the normal force on the outer tires during cornering. Neglecting this load sensitivity can therefore lead to overly optimistic assessments of vehicle stability.

Although this mechanism affects passenger cars, buses, and trucks alike, its consequences are considerably more severe in heavy trucks because of their large gross weight, high center of gravity, and long wheelbase, which amplify the effects of dynamic load transfer. As automated and semi-autonomous heavy trucks move toward commercial deployment in freight transport, ensuring safe operation on curved road segments has become a critical research issue.

These vehicles, characterized by large mass, high center of gravity, and long wheelbase, present unique challenges compared to passenger cars, especially in dynamically complex conditions such as curves, ramps, and uneven surfaces. According to the FMCSA [1], approximately 8–10% of fatal large-truck crashes occurred under adverse weather conditions, such as rain or snow. These weather-related crashes are often associated with skidding or rollover, which are primarily induced by excessive speed and reduced tire–road friction. Such factors significantly affect the braking and steering performance of heavy trucks, making them more vulnerable to lateral instability. The need for accurate and adaptive safe-speed estimation is therefore evident, particularly on curved road segments where combined lateral and longitudinal tire forces under reduced friction conditions can easily lead to instability and loss of control.

Conventional road design standards, such as the AASHTO Green Book [2] and FHWA guidelines [3], determine safe speeds primarily from road curvature, superelevation, and a constant design side-friction factor ($\mu$). These standards provide tabulated friction values that are treated as fixed inputs for geometric design and do not account for dynamic axle-load transfer or the load-dependent reduction in tire–road friction observed in real driving. However, in practice, $\mu$ is not constant—it varies with vertical load, slip, temperature, and pavement conditions. Despite this, many simulation-based studies have also adopted a fixed $\mu$ for simplicity. For example, Du et al. [4] analyzed tractor–trailer stability on curved slopes in TruckSim using a uniform adhesion coefficient ($\mu$ = 0.3), ignoring wheel-specific friction degradation under load. Such assumptions neglect the friction loss and lateral-grip imbalance caused by dynamic load transfer, leading to optimistic or physically inconsistent safe-speed predictions.

To overcome such limitations, vehicle dynamics research has focused on more precise tire–road interaction modeling. Wong [5] and Rajamani [6] analyzed vehicle limit behavior considering slip angle, slip ratio, and combined-slip dynamics. Pacejka’s Magic Formula [7] introduced a nonlinear representation of tire forces, which has since become a standard tool in handling-limit and control studies. Subsequent experimental research [8,9] further demonstrated that the friction coefficient decreases nonlinearly with increasing normal load, confirming load sensitivity as a significant and measurable physical phenomenon that must be considered in vehicle stability analysis. However, this effect is not uniform, as friction behavior can vary with pavement and environmental conditions.

Truck-oriented studies have provided additional insight. Segel and Ervin [10] reported that heavy truck tires exhibit a more pronounced reduction in friction coefficient than passenger car tires under the same load increase, which contributes to degraded handling and higher rollover tendency. More recently, Zhang et al. [11] reconstructed real rollover accidents using TruckSim-based simulations and showed that an increase in center-of-gravity (CG) height significantly amplifies the Lateral Load Transfer Ratio (LTR), thus raising rollover risk. These studies highlight the necessity of jointly considering load-sensitive friction, dynamic load transfer, and geometric curvature effects when evaluating curve safety for heavy trucks.

Recent research has also advanced real-time safety technologies. Chen and Peng [12] developed an LTR-based rollover warning system, while Kamnik et al. [13] established the Static Rollover Threshold (SRT) as a fundamental indicator of structural stability. Non-contact friction estimation methods using video, radar, and infrared sensors have been proposed [14,15,16], and machine learning–based $\mu$ prediction models have also been developed [17,18] to improve adaptability under varying road conditions. In addition, curve speed planning has been formulated as an optimization problem to enable real-time implementation in automated systems [19,20], while predictive indices such as the PLTR [21] have been introduced for proactive rollover-preventive control.

However, approaches that simultaneously incorporate wheel-level dynamic load transfer and load-sensitive friction modeling for safe-speed estimation in multi-axle trucks remain scarce. To address this gap, the present study proposes a new framework that integrates structural stability (SRT), dynamic load transfer, and load-sensitive friction modeling in a unified formulation. The framework employs the friction ellipse theory to capture trade-offs among traction, braking, and steering demands under combined-slip conditions. It is implemented within a TruckSim–Simulink co-simulation environment, which couples realistic multi-axle vehicle dynamics with the proposed friction and control logics, enabling physically consistent evaluation of dynamic load transfer and stability on curved roads. Furthermore, the framework’s validity is examined through reconstructed curved ramp scenarios based on real accident data. The proposed method provides a generalized and physically consistent procedure for safe-speed assessment that considers both rollover and skidding constraints, offering practical implications for real-time speed control in autonomous heavy trucks and for the refinement of future road design standards.

2. Materials and Methods

2.1. Problem Definition and Overview

The maximum safe speed of a heavy truck negotiating a curved road segment is primarily governed by two mechanisms: friction utilization leading to skidding and excessive lateral load transfer leading to rollover. Both phenomena represent critical safety limits, and a realistic speed profile must satisfy both simultaneously.

In this study, we propose a method that computes wheel-level normal loads, applies a load-sensitive friction coefficient $\mu \left(N\right)$, and determines the available lateral and longitudinal forces at each wheel. These available forces are compared against the required tire forces using the friction ellipse constraint to check for incipient skidding. In parallel, the Load Transfer Ratio (LTR) is evaluated to assess rollover risk. The maximum speed at each station is numerically determined as the largest speed that satisfies both constraints, and a forward–backward speed shaping procedure is performed to account for realistic longitudinal dynamics and yield a feasible speed profile. In this framework, two quantitative stability metrics are used to evaluate the limiting condition at each road station: (1) the maximum Lateral Load Transfer Ratio (LTR) for rollover risk, and (2) the minimum wheel-level friction coefficient $\mu \left(N\right)$, computed from the load-sensitive friction model, for skidding risk. The governing safe speed is defined as the highest speed at which both criteria remain below their respective thresholds.

2.2. Road Geometry and Required Tire Forces

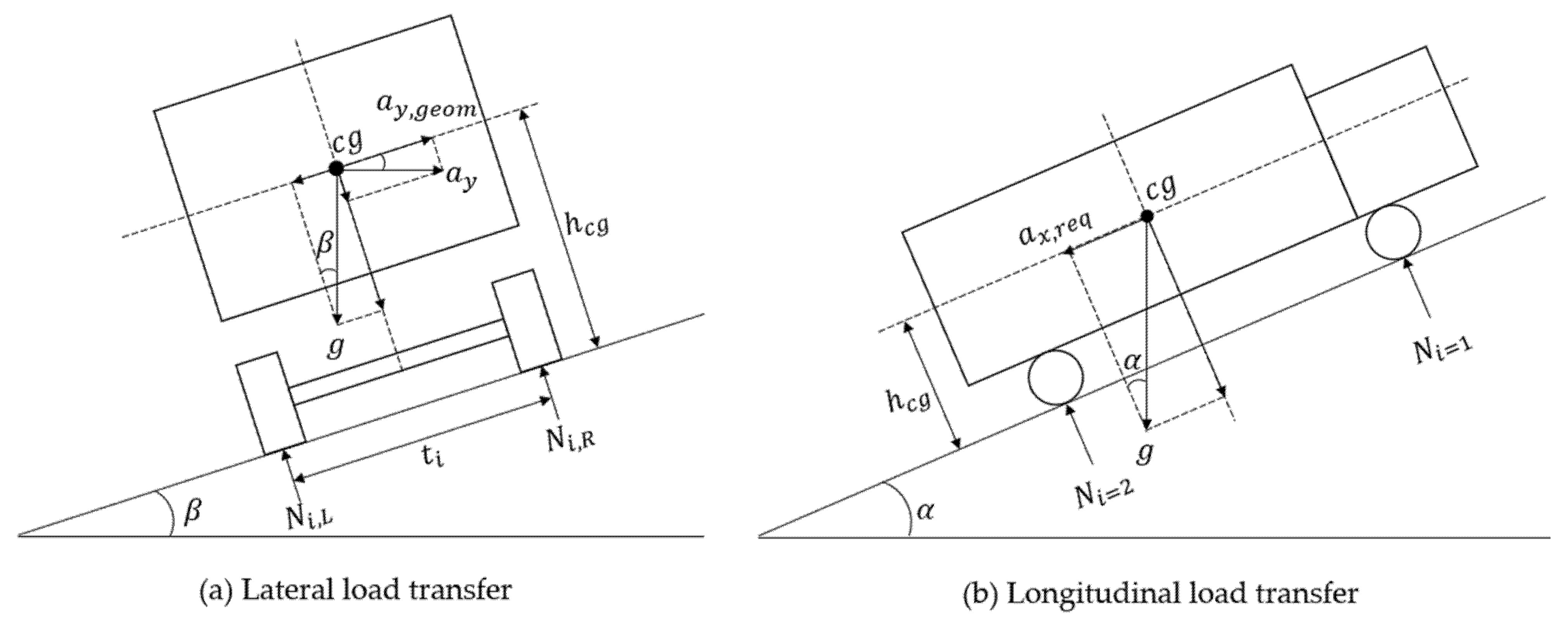
Figure 1 illustrates the fundamental load-transfer mechanisms that occur in multi-axle trucks while negotiating curved road segments. Figure 1a shows the lateral load transfer generated by centrifugal effects on a banked curve, whereas Figure 1b depicts the longitudinal load transfer induced by acceleration or braking on an inclined surface. These physical mechanisms establish the basis for the mathematical formulation of dynamic axle loads developed later in this section.

The road is parameterized by station coordinate $\mathrm{s}$, curvature $\mathsf{\kappa }\left(\mathrm{s}\right)$, radius $\mathrm{R}\left(\mathrm{s}\right)=1/\mathsf{\kappa }\left(\mathrm{s}\right)$, longitudinal grade $\mathsf{\alpha }\left(\mathrm{s}\right)$, and superelevation $\mathsf{\beta }\left(\mathrm{s}\right)$. For a given speed $\mathrm{v}$, the geometric and effective lateral accelerations are

$$a_{y,\mathrm{g}\mathrm{e}\mathrm{o}\mathrm{m}}={\displaystyle \frac{v^2}{R}}\mathrm{c}\mathrm{o}\mathrm{s}\beta , a_{y,\mathrm{e}\mathrm{f}\mathrm{f}}=a_{y,\mathrm{g}\mathrm{e}\mathrm{o}\mathrm{m}}-g\mathrm{s}\mathrm{i}\mathrm{n}\beta ,$$

(1)

and the required longitudinal acceleration due to grade is

$$a_{x,\mathrm{r}\mathrm{e}\mathrm{q}}=-g\mathrm{s}\mathrm{i}\mathrm{n}\alpha .$$

(2)

The corresponding total lateral and longitudinal force demands are

$$F_y^{\mathrm{n}\mathrm{e}\mathrm{e}\mathrm{d}}=m|a_{y,\mathrm{e}\mathrm{f}\mathrm{f}}|, F_x^{\mathrm{n}\mathrm{e}\mathrm{e}\mathrm{d}}=m{a}_{x,\mathrm{r}\mathrm{e}\mathrm{q}}.$$

(3)

Static axle loads $N_{i,\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}}$ are computed from the total vehicle mass, payload distribution, and axle shares. The dynamic left–right load transfer at axle $i$ is modeled as

$${\Delta }_i=k_i|a_{y,\mathrm{e}\mathrm{f}\mathrm{f}}|, k_i={\rho }_i{\displaystyle \frac{m{h}_{\mathrm{c}\mathrm{g}}}{t_i}},$$

(4)

where $t_i$ is the track width and ${\rho }_i$ is the fractional load transfer share of axle $i$ (${\sum }_i{\rho }_i\approx 1$). The instantaneous left and right axle loads are then

$$N_{i,\mathrm{R}/\mathrm{L}}={\displaystyle \frac{N_{i,\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}}\mathrm{c}\mathrm{o}\mathrm{s}\alpha \mathrm{c}\mathrm{o}\mathrm{s}\beta }{2}}\pm {\displaystyle \frac{{\Delta }_i}{2}}.$$

(5)

For tandem or dual tires, these loads are evenly split to obtain wheel-level normal loads $N_w$, which serve as the basis for computing available tire forces.

2.3. Load-Sensitive Friction and Skid Constraint

The friction behavior between the tire and the road surface is not constant but varies nonlinearly with the applied normal load. Numerous experimental studies have shown that the effective friction coefficient decreases as the vertical load increases, due to the combined effects of rubber viscoelasticity, contact pressure redistribution, and thermo-mechanical coupling at the tire–road interface. This load-sensitivity phenomenon has been documented over several decades: Segel and Ervin [10] reported a clear reduction in peak friction levels for heavy-truck tires under increasing wheel load, while Liu et al. [9] observed similar nonlinear trends in controlled thermo-mechanical tests on tread rubber. These results indicate that $\mu$ should be treated as a function of the per-wheel normal load rather than as a fixed constant, particularly for multi-axle trucks experiencing significant dynamic load transfer during cornering. To represent this dependence in a compact analytical form suitable for vehicle-level simulation, the present study adopts the following empirical power-law model [5,6,7,10,22]:

$$\mu (N_w)={\mu }_0{\left({\displaystyle \frac{N_w}{N_0}}\right)}^{c-1}, {\mu }_{\mathrm{m}\mathrm{i}\mathrm{n}}\le \mu (N_w)\le {\mu }_{\mathrm{m}\mathrm{a}\mathrm{x}},$$

(6)

where $N_w$ is the normal load acting on each tire, ${\mu }_0$ is the reference friction coefficient at the nominal load $N_0$, and $c$ is an empirical parameter describing the degree of load sensitivity.

This power-law formulation effectively reflects the experimentally observed trend that the friction coefficient decreases with load, while maintaining computational simplicity for dynamic vehicle stability analysis.

Given the instantaneous wheel loads and the corresponding $\mu \left(N_w\right)$, the combined longitudinal and lateral force that each tire can generate is limited by the classical friction ellipse. Introducing a safety margin factor $(1-\delta )$, the admissible force boundary for each wheel $w$ is written as

$${\left({\displaystyle \frac{F_{x,w}}{(1-\delta )\mu \left(N_w\right)N_w}}\right)}^2+{\left({\displaystyle \frac{F_{y,w}}{(1-\delta )\mu \left(N_w\right)N_w}}\right)}^2\le 1.$$

(7)

The total lateral force required for steady-state cornering, $F_y^{\mathrm{n}\mathrm{e}\mathrm{e}\mathrm{d}}$, is then distributed across wheels in proportion to their vertical loads, reflecting the fact that lateral force capacity scales with normal load:

$$F_{y,w}^{\mathrm{d}\mathrm{e}\mathrm{m}}=F_y^{\mathrm{n}\mathrm{e}\mathrm{e}\mathrm{d}}{\displaystyle \frac{N_w}{{\sum }_u{N}_u}}.$$

(8)

Using this allocation, the remaining longitudinal force capacity at each wheel becomes

$$F_{x,w}^{\mathrm{r}\mathrm{e}\mathrm{s}}=(1-\delta )\mu (N_w)N_w\sqrt{1-{\left({\displaystyle \frac{F_{y,w}^{\mathrm{d}\mathrm{e}\mathrm{m}}}{(1-\delta )\mu \left(N_w\right)N_w}}\right)}^2} .$$

(9)

A skid event is predicted when the demanded traction or braking force $F_{x,w}$ exceeds the residual capacity $F_{x,w}^{\mathrm{r}\mathrm{e}\mathrm{s}}$ on any wheel. Accordingly, the friction-limited safe speed at a given road station is defined as the maximum speed at which the total lateral force demand can still be satisfied by the sum of available tire forces across all wheels.

2.4. Rollover Criterion and Safe Speed Determination

The rollover propensity of a multi-axle truck is evaluated using the Load Transfer Ratio (LTR), defined as

$$\mathrm{L}\mathrm{T}\mathrm{R}={\displaystyle \frac{{\sum }_i(N_{i,\mathrm{o}\mathrm{u}\mathrm{t}}-N_{i,\mathrm{i}\mathrm{n}})}{{\sum }_i(N_{i,\mathrm{o}\mathrm{u}\mathrm{t}}+N_{i,\mathrm{i}\mathrm{n}})}},$$

(10)

where $N_{i,\mathrm{o}\mathrm{u}\mathrm{t}}$ and $N_{i,\mathrm{i}\mathrm{n}}$ denote the normal loads on the outer and inner wheels of the $i$-th axle, respectively. An LTR of 1.0 indicates that all inner wheels are completely unloaded, corresponding to incipient rollover. To maintain rollover safety, the following condition must be satisfied at every station $s$ along the path:

$$\mathrm{L}\mathrm{T}\mathrm{R}(v,R,\mathsf{\alpha },\beta )\le {\mathrm{L}\mathrm{T}\mathrm{R}}_{\mathrm{m}\mathrm{a}\mathrm{x}},$$

(11)

where $v$ is the vehicle speed, $R$ the curvature radius, $\alpha$ the road grade and $\beta$ the superelevation angle. In this study, a nominal threshold of ${\mathrm{L}\mathrm{T}\mathrm{R}}_{\mathrm{m}\mathrm{a}\mathrm{x}}=0.8$ was initially adopted, which is widely used in rollover studies to represent the onset of wheel lift with a safety margin before complete rollover [23].

Since the absolute value of LTR depends on model assumptions such as suspension roll stiffness distribution, center-of-gravity height, and payload configuration, a calibration procedure was introduced to ensure physical consistency. Specifically, the Static Rollover Threshold (SRT) of the model was obtained by gradually increasing the steady-state lateral acceleration $a_y$ on a level surface until LTR reached unity, yielding

$${\mathrm{S}\mathrm{R}\mathrm{T}}_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}={\displaystyle \frac{a_{y,\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}}{g}}, \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} \mathrm{L}\mathrm{T}\mathrm{R}\left(a_{y,\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}\right)=1.$$

(12)

The SRT is numerically equivalent (in g-units) to the Static Stability Factor (SSF = T/2 h). Drawing on well-known UMTRI data [24], typical tractor–semitrailer combinations exhibit static rollover thresholds on the order of 0.25–0.50 g depending on configuration and loading, petroleum or cryogenic tankers generally lie in the ~0.30–0.45 g band, while light trucks/SUVs commonly reach ~0.8–1.2 g. These values make clear that rollover resistance depends strongly on CG height, suspension geometry, and payload distribution. In light of this established spread, and based on the rollover threshold ranges reported in UMTRI datasets and subsequent experimental studies, we select three representative SRT target levels—0.3 g, 0.5 g, and 0.7 g—to span low-, moderate-, and high-stability configurations encountered in practice: (i) 0.3 g reflects fully loaded or high-CG conditions typical of tank or container semitrailers; (ii) 0.5 g represents medium-load multi-axle trucks; and (iii) 0.7 g approximates light/unladen configurations comparable to small rigid trucks or SUV-like upper bounds. This triplet provides a consistent basis to study how structural stability interacts with friction limits in safe-speed estimation.

When the computed ${\mathrm{S}\mathrm{R}\mathrm{T}}_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}$ exceeded the selected target value, a global scaling factor was applied to the roll moment distribution so that ${\mathrm{S}\mathrm{R}\mathrm{T}}_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}$ exactly matched ${\mathrm{S}\mathrm{R}\mathrm{T}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}$. This calibration step aligns the model with standardized safety metrics such as the Static Stability Factor (SSF), which is numerically equivalent to SRT expressed in g-units, thereby ensuring that the predicted rollover speeds are neither overly conservative nor overly optimistic.

Finally, the safe speed envelope $v_{\mathrm{s}\mathrm{a}\mathrm{f}\mathrm{e}}\left(s\right)$ is determined by solving for the maximum speed at each station that satisfies the calibrated rollover criterion:

$$v_{\mathrm{s}\mathrm{a}\mathrm{f}\mathrm{e}}\left(s\right)=\mathrm{m}\mathrm{a}\mathrm{x}\{v\hspace{0.17em}\left|\hspace{0.17em}\mathrm{L}\mathrm{T}\mathrm{R}(v,R(s),\beta (s),\varphi (s\left)\right)\le {\mathrm{L}\mathrm{T}\mathrm{R}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right\}.$$

(13)

2.5. Longitudinal Dynamics and Final Speed Shaping

The lateral-stability-based speed profile $v_{safe}\left(s\right)$ defines the maximum allowable speed envelope considering only tire force saturation and rollover constraints. In practice, vehicles are also limited by engine power, drivetrain efficiency, aerodynamic drag, rolling resistance, and comfort limits on acceleration and braking. To produce a realizable speed trajectory, these longitudinal effects are incorporated through a forward–backward pass.

2.5.1. Residual Longitudinal Capacity

At each station $s$, the remaining tire force capacity after satisfying the lateral demand is converted into an equivalent longitudinal acceleration:

$$a_{\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g}}={\displaystyle \frac{{\sum }_w{F}_{x,w}^{\mathrm{r}\mathrm{e}\mathrm{s}}}{m}}.$$

(14)

After subtracting aerodynamic drag $F_{\mathrm{a}\mathrm{e}\mathrm{r}\mathrm{o}}$, rolling resistance $F_{\mathrm{r}\mathrm{o}\mathrm{l}\mathrm{l}}$, and grade resistance $mg\mathrm{s}\mathrm{i}\mathrm{n}\alpha$, the net available acceleration is further limited by the powertrain:

$$a_{\mathrm{p}\mathrm{o}\mathrm{w}}={\displaystyle \frac{P_{\mathrm{m}\mathrm{a}\mathrm{x}}}{m\hspace{0.17em}\mathrm{m}\mathrm{a}\mathrm{x}(v,\epsilon )}}.$$

(15)

The final feasible acceleration and braking deceleration are

$$a_{\mathrm{a}\mathrm{c}\mathrm{c}}=\mathrm{m}\mathrm{i}\mathrm{n}\left(a_{\mathrm{a}\mathrm{c}\mathrm{c},\mathrm{t}\mathrm{i}\mathrm{r}\mathrm{e}},\hspace{0.17em}{a}_{\mathrm{p}\mathrm{o}\mathrm{w}},\hspace{0.17em}{a}_{\mathrm{a}\mathrm{c}\mathrm{c},\mathrm{c}\mathrm{a}\mathrm{p}}\right),$$

(16)

$$a_{\mathrm{b}\mathrm{r}\mathrm{k}}=\mathrm{m}\mathrm{i}\mathrm{n}\left(a_{\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g}}+g\mathrm{s}\mathrm{i}\mathrm{n}\alpha ,\hspace{0.17em}{a}_{\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{t}}\right).$$

(17)

Here $a_{\mathrm{a}\mathrm{c}\mathrm{c},\mathrm{c}\mathrm{a}\mathrm{p}}$ and $a_{\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{t}}$ are driver-imposed comfort limits.

2.5.2. Final Speed Shaping

Once the tire-limited longitudinal acceleration and braking capabilities have been computed, a forward–backward pass algorithm is applied to shape a dynamically feasible speed trajectory along the path.

In the forward pass, each station’s speed is updated by propagating the maximum allowable acceleration without exceeding the local lateral stability envelope:

$$v_i\leftarrow \mathrm{m}\mathrm{i}\mathrm{n}\left(v_{\mathrm{s}\mathrm{a}\mathrm{f}\mathrm{e},\mathrm{i}}, \sqrt{v_{i-1}^2+2a_{acc,i-1}\Delta s}\right),$$

(18)

are feasible by iteratively adjusting the speed profile in the reverse direction:

$$v_i\leftarrow \mathrm{m}\mathrm{i}\mathrm{n}\left(v_{\mathrm{s}\mathrm{a}\mathrm{f}\mathrm{e},\mathrm{i}}, \sqrt{v_{i+1}^2+2a_{brk,i+1}\Delta s}\right).$$

(19)

This forward–backward iteration continues until the profile converges within a predefined tolerance. The resulting trajectory $v_{final}\left(s\right)$ satisfies friction, rollover, and longitudinal acceleration constraints, providing a smooth and physically realizable speed profile for trajectory planning or intelligent speed advisory applications.

3. Results

This section presents the validation results of the proposed dynamic load–sensitive friction coefficient model and safe speed estimation framework using TruckSim–Simulink co-simulation. For comparison, two cases were considered: one assuming a constant friction coefficient and the other applying the proposed $\mu \left(N\right)$-based load-sensitive friction model. The validation scenario was reconstructed from an actual accident case involving a curved ramp.

3.1. Simulation Setup

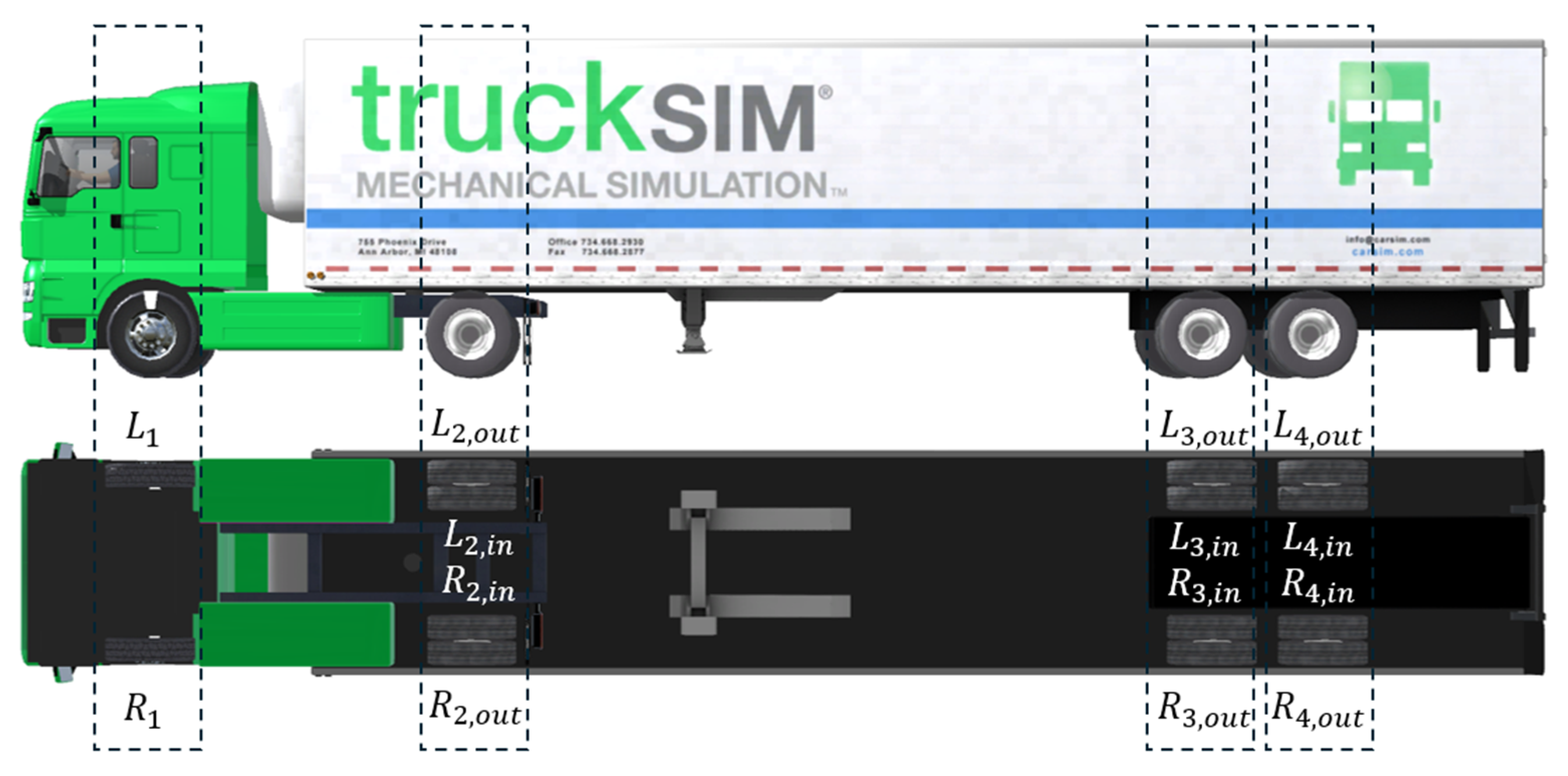
The simulation was conducted using a co-simulation environment linking TruckSim (version 2021) with MATLAB/Simulink (version 2023b). The test vehicle was a four-axle rigid truck, with its configuration shown in Figure 2. Figure 3 illustrates the curved ramp section reconstructed from a fatal rollover accident of a multi-axle truck [11]. The simulation route incorporated the actual geometric conditions of the accident site, including curve radius and longitudinal/lateral slope.

The major physical parameters—including gross vehicle weight, axle load distribution ratio, center of gravity (CG) height, axle track width, roll stiffness distribution ratio, and load-sensitive friction parameters—were derived from the accident vehicle data [11], and their detailed values are summarized in

Table 1. Vehicle parameters and load-sensitive friction model inputs.

Section	Parameter	Value	Unit
Vehicle Mass & CG	Tractor empty mass	$6.8$	ton
	Trailer empty mass	$10.7$	ton
	Payload mass	$17.2$	ton
	CG height (empty)	1.60	m
	CG height (full)	2.725	m
Axle & Load	Axle load distribution ratio	[0.21, 0.30, 0.25, 0.24]	—
Distribution	Track width per axle	[2.04, 1.82, 1.82, 1.82]	m
	Roll stiffness distribution ratio	[0.15, 0.20, 0.30, 0.35]	—
Friction Parameters	Reference load ($N_0$)	4000.0	N
	Load-sensitivity exponent (c)	0.4–1.0	—
	Safety margin factor ($\delta$)	0.2	—
	Minimum friction coefficient (${\mu }_{min}$)	0.05	—
	Maximum friction coefficient (${\mu }_{max}$)	0.95	—
Stability Thresholds	LTR threshold	0.80	—
	Target SRT	0.3–0.5	g
	SRT tolerance	0.005	g
Longitudinal	Air density	1.225	kg/m3
Dynamics	Drag area (CdA)	8.5	m2
	Rolling resistance coefficient	0.008	—
	Engine maximum power	300.0	kW
	Driver acceleration comfort limit	0.5	m/s2

.

As shown in Table 1, the gross vehicle weight was set to approximately 32 tons, and the CG height increased from about 1.60 m (empty) to 2.73 m (full), which is a critical factor influencing the Static Rollover Threshold (SRT). The axle load distribution ratio [0.21, 0.30, 0.25, 0.24] reflects the fact that load transfer during cornering may be concentrated on specific axles. The axle track width (2.04–1.82 m) and the roll stiffness distribution ratio [0.15, 0.20, 0.30, 0.35] serve as important inputs in calculating the Lateral Load Transfer Ratio (LTR).

In particular, the proposed $\mu \left(N\right)$ formulation employs a reference normal load $N_0=4000\hspace{0.17em}\mathrm{N}$ and a load-sensitivity exponent $c$ to characterize how the tire–road friction coefficient varies with vertical load. The chosen $N_0$ corresponds to the average static wheel load of the vehicle under a half-loaded condition, approximately representing the midpoint between the curb-weight and fully loaded wheel loads obtained from TruckSim’s static analysis. With this setup, the simulation environment enables a quantitative assessment of rollover and skidding risks of multi-axle trucks negotiating curved ramps.

3.2. Dominant Constraints in Safe Speed Determination

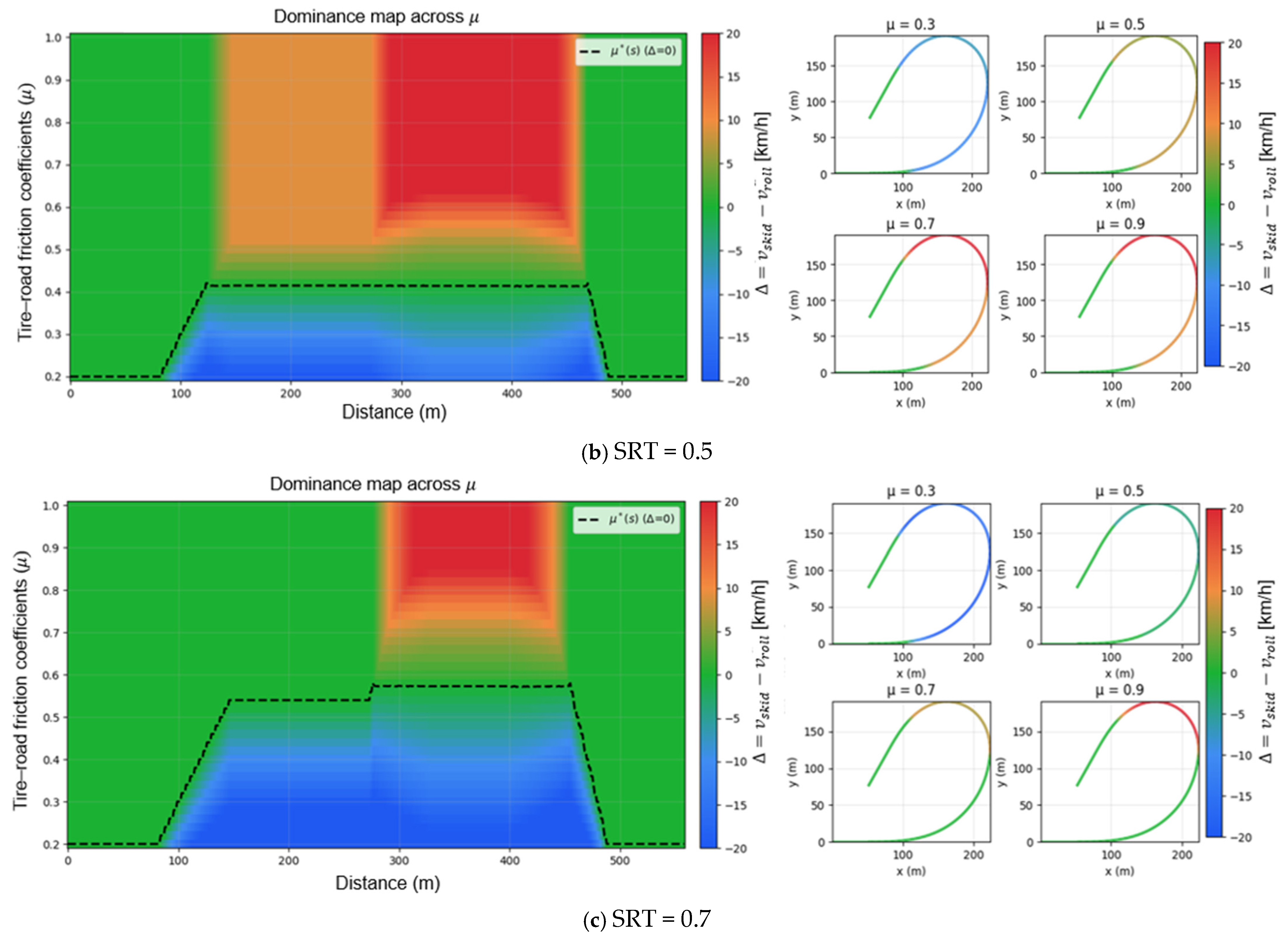
Figure 4 illustrates how the dominant constraint on safe speed varies along the curved ramp as a function of the tire–road friction coefficient ($\mu$). The color shading distinguishes whether rollover or skidding governs the speed limit, and each panel corresponds to a different Static Rollover Threshold (SRT) setting: 0.3, 0.5, and 0.7. The ramp consists of an entry straight, spiral-in (increasing curvature), circular arc (apex), spiral-out (decreasing curvature), and exit straight, with the governing factor shifting as the lateral demand changes with curvature.

When the SRT is low (Figure 4a, SRT = 0.3), rollover dominates across the entire ramp due to poor structural stability, and the apex region is governed by rollover even under high friction. This indicates that, for vehicles with high centers of gravity or weak roll stiffness, rollover remains the critical constraint regardless of road surface conditions. At a moderate SRT (Figure 4b, SRT = 0.5), skidding governs at low friction ($\mu$ = 0.3–0.5), but rollover becomes dominant at the apex once $\mu$ exceeds 0.7. With a high SRT (Figure 4c, SRT = 0.7), skidding is the prevailing constraint under most friction conditions, and rollover appears only locally near the apex under very high $\mu$.

These results confirm that safe speed cannot be explained by a single factor. At low SRT values, rollover is the dominant constraint; at intermediate levels, the governing factor alternates between skidding and rollover depending on $\mu$; and at high SRT values, skidding dominates except under extreme friction. Therefore, both vehicle structural stability (SRT) and road surface conditions ($\mu$) must be jointly considered in safe speed estimation. Neglecting either factor risks overestimating or underestimating the true safe speed. This finding underscores the necessity of integrated approaches in curve safety assessment and the design of speed control algorithms for autonomous multi-axle trucks.

3.3. Effects of the Load-Sensitivity Exponent

As discussed in Section 3.2, the safe speed of a multi-axle truck on curved ramps is governed by the interplay between rollover and skidding constraints. This section investigates the quantitative influence of the load-sensitivity coefficient (c) in the proposed load-sensitive friction model, defined as $\mu \left(N\right)={\mu }_0{(N/N_0)}^{c-1}$, hereafter referred to as the $\mu \left(N\right) model$. The exponent c represents the rate at which the tire–road friction coefficient decreases with increasing vertical load.

To validate the proposed model, experimental data from Segel and Ervin [10] were analyzed for both passenger-car and heavy-truck tires. Their experiments were conducted on dry Portland cement concrete with coarse surface texture, where vertical load was incrementally varied while measuring the tire–road friction coefficient ($\mu$). The measured data were normalized by a reference load ($N_0$) to enable comparison across vehicle types. Figure 5 presents the fitting results obtained using the proposed model. For passenger-car tires, ${\mu }_0=0.880$ and $c=0.893$, showing a relatively mild reduction in friction with increasing load. For heavy-truck tires, ${\mu }_0=0.749$ and $c=0.821$ were identified, indicating a stronger load sensitivity.

While Segel and Ervin’s data [10] provide the experimental evidence for this difference, the stronger $\mu$–N decay in heavy-truck tires can be interpreted in light of general rubber friction theory, which attributes load-dependent friction reduction to contact-area saturation, reduced adhesion, and frictional heating under high normal force [22]. Because heavy-truck tires typically operate at higher inflation pressures and exhibit stiffer carcass constructions than passenger-car tires, these mechanisms are likely to be more pronounced, resulting in a faster decrease in usable friction with increasing load. This interpretation is consistent with both the fitted c-values and the experimentally observed trends.

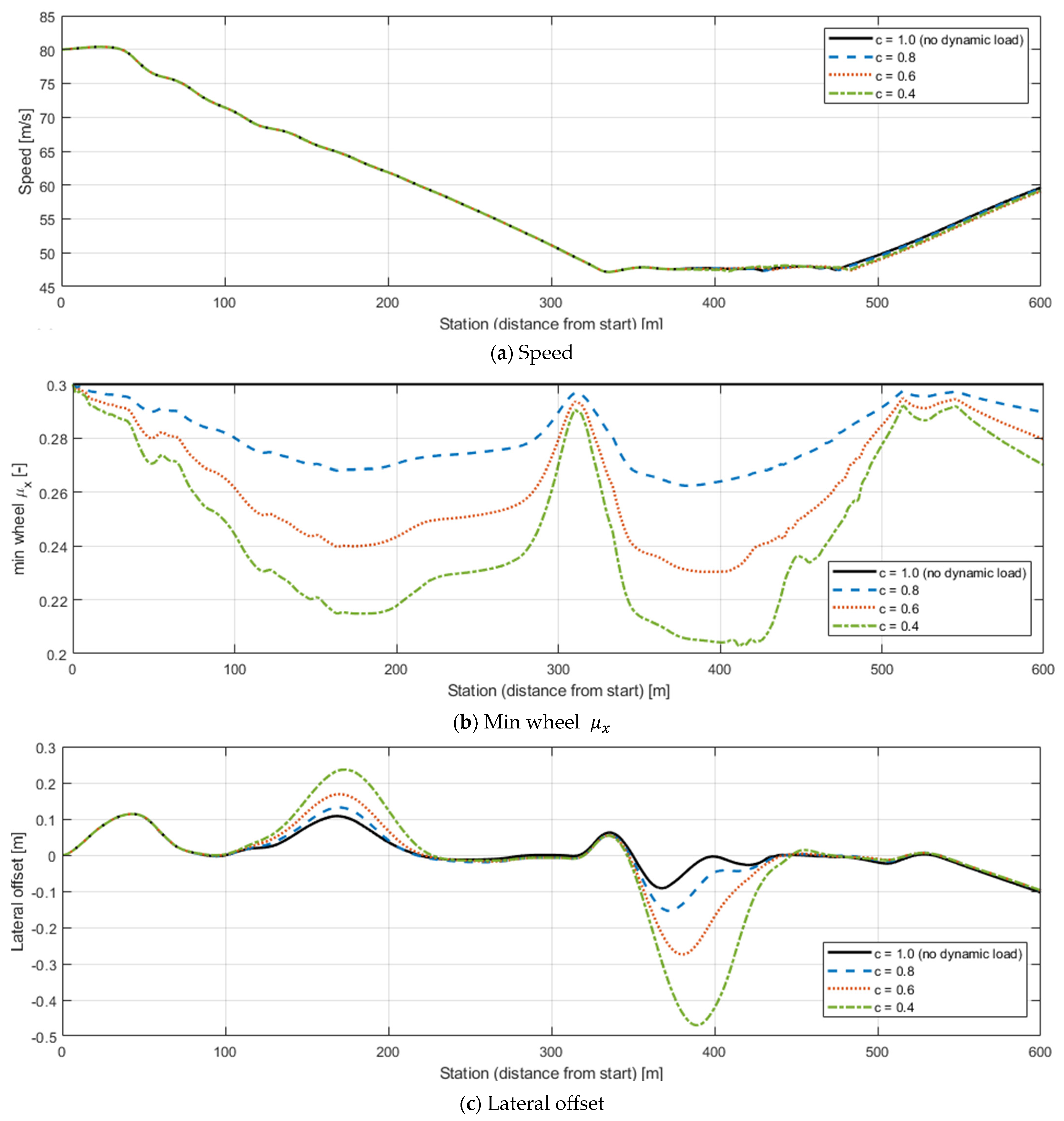
Based on this validation, the effect of varying $c$ on the vehicle’s dynamic behavior was further analyzed. Figure 6 illustrates the simulation results for c values ranging from 0.4 to 1.0, with SRT fixed at 0.5 and $\mu$₀ at 0.3. Here, $c=1.0$ corresponds to the idealized case with no variation in friction regardless of load. Figure 6a shows the simulated vehicle speed under the same reference safe-speed condition, Figure 6b presents the minimum friction coefficient among all wheels, and Figure 6c displays the lateral offset from the lane centerline.

The results indicate that as $c$ decreases, friction on the outer wheels drops more sharply due to higher vertical loads, leading to increased lateral deviation. Particularly at $c=0.4$, pronounced outward displacement occurred, whereas for $c=1.0$, friction remained uniform across wheels, resulting in minimal deviation and stable trajectory tracking. In other words, higher load sensitivity (smaller $c$) significantly degrades vehicle stability even at the same nominal speed.

Figure 7 provides a detailed view of dynamic wheel loads and the corresponding friction variations during ramp negotiation under SRT = 0.5, μ₀ = 0.3, and c = 0.4. Figure 7a shows the left–right wheel load distribution, where the outer wheels experience load increases while the inner wheels unload due to centrifugal effects. Wheel positions correspond to those defined in Figure 2 and Table 1. Figure 7b applies the $\mu \left(N\right)$ model to calculate the resulting friction coefficients. For the outer wheels, the friction coefficient dropped markedly with increasing load: for instance, the L4 wheel decreased from $\mu$₀ = 0.3 to a minimum of 0.229 (a 23.5% reduction), while the L3 and L1 wheels fell to 0.236 and 0.237, respectively (approximately 21% reduction). In contrast, the R1 wheel showed only a 6% reduction ($\mu$ = 0.281). These results quantitatively demonstrate that load redistribution during cornering directly translates into asymmetric friction loss, where the minimum $\mu$ among wheels governs overall vehicle stability.

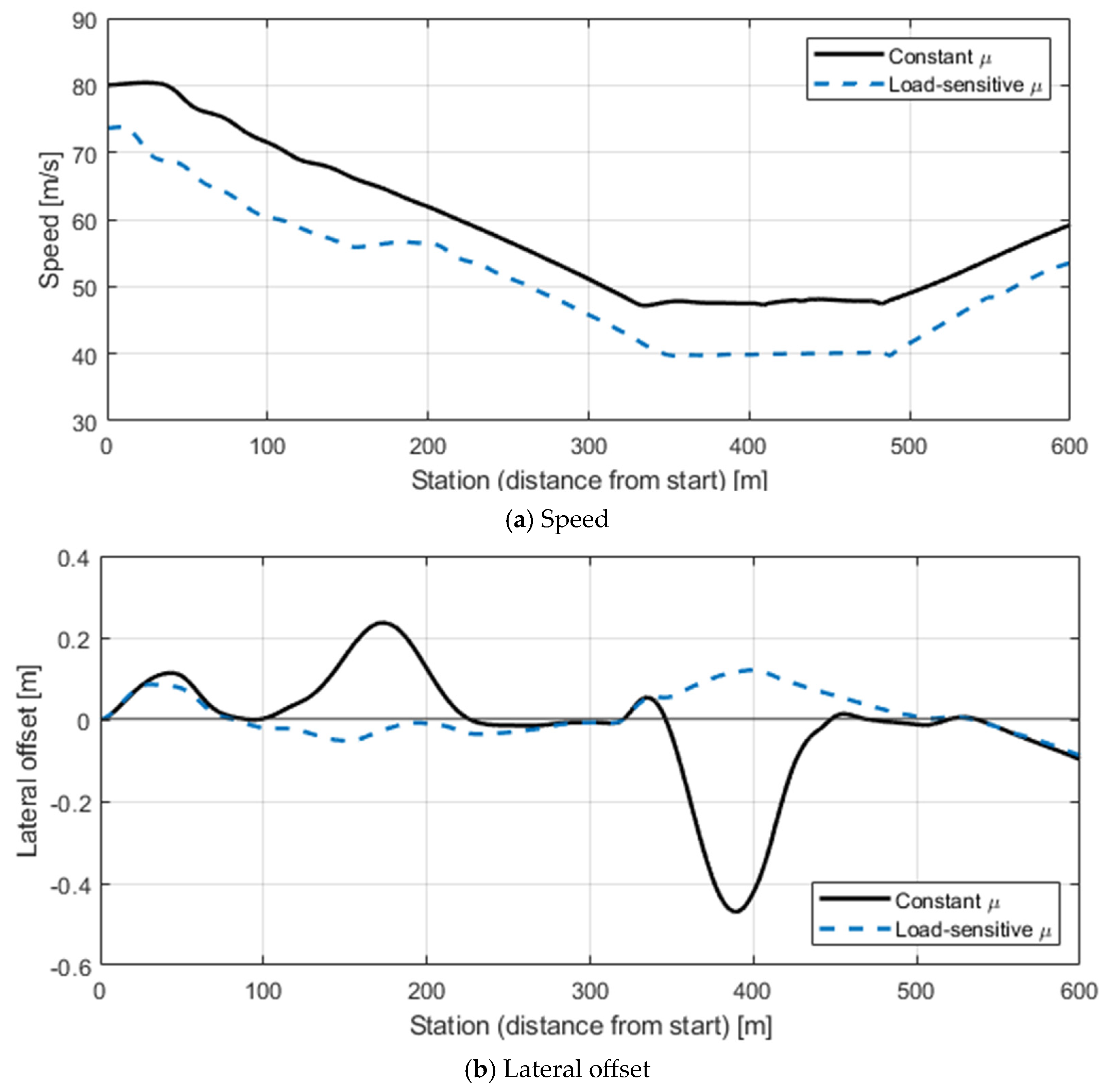
Figure 8 compares the simulation results between cases with and without load sensitivity (c = 0.4). Following the procedure established in Section 2, the safe speed was calculated by considering vertical loads at each wheel, applying the $\mu \left(N\right)$ model, and incorporating both the friction ellipse and LTR-based rollover constraints. Figure 8a compares the safe-speed profiles for the two cases. When assuming a constant $\mu$, the estimated safe speed remained relatively high even in sharp curvature sections. In contrast, applying the $\mu \left(N\right)$ model produced lower safe-speed estimates as the reduced friction on the outer wheels became dominant in the friction-limited zones. Quantitatively, the average difference between the two cases was approximately 7.5 km/h. Figure 8b shows the corresponding lateral offset. With load sensitivity considered, the average offset increased to +0.080 m (standard deviation 0.163 m), and the maximum reached 0.52 m. Without load sensitivity, the average offset was −0.044 m (standard deviation 0.075 m) with a maximum of only 0.12 m. This indicates that neglecting load sensitivity leads to underestimation of trajectory deviation and overestimation of stability, whereas including it reflects the actual instability and risk more realistically.

Overall, the results demonstrate that incorporating the load-sensitive friction model $\mu \left(N\right)$ enables a more realistic estimation of safe speed and lateral behavior during cornering. Conversely, assuming a constant friction coefficient leads to optimistic and potentially unsafe predictions. Therefore, accounting for load sensitivity is essential for accurate stability evaluation and for improving real-time speed control algorithms and road design standards for autonomous heavy trucks.

4. Discussion

This section discusses the physical implications and practical significance of dynamic load transfer and load-sensitive friction characteristics regarding the estimation of safe speed for multi-axle trucks negotiating curved road segments.

First, the Static Rollover Threshold (SRT) served as a key parameter determining the absolute level of safe speed, as it represents the vehicle’s inherent structural stability. When SRT = 0.3, rollover dominated throughout the curve, and the safe speed remained around 50–55 km/h. As SRT increased to 0.5, rollover and skidding constraints alternated, expanding the safe-speed range to 55–70 km/h. At SRT = 0.7, skidding became the dominant constraint, allowing speeds exceeding 75 km/h. These results indicate that, even under identical geometric conditions, differences in structural stability can lead to more than a 20 km/h variation in the estimated safe speed.

Second, the load-sensitivity coefficient (c) proved to be a critical factor explaining the stability differences among vehicle types. Based on the fitting results from [10], the value of c was estimated as 0.893 for passenger-car tires and 0.821 for heavy-truck tires, demonstrating that truck tires experience a greater friction reduction under equivalent load increases. Importantly, when an appropriate c value is chosen, the proposed $\mu$(N) formulation reproduces the experimentally observed friction–load relationship with high fidelity, confirming the physical validity and accuracy of the model. Consistent with this finding, the simulation results of the present study showed that when c = 0.4, the friction coefficient of the outer wheels decreased by more than 20% from its nominal value, while the lateral offset increased to an average of 0.080 m and a maximum of 0.52 m. In contrast, when c = 1.0, no friction degradation occurred with varying load, and the trajectory deviation was negligible. These results empirically confirm that the minimum outer-wheel friction coefficient governs the overall vehicle stability during curve negotiation.

Third, a systematic difference was observed between the constant-$\mu$ and $\mu \left(N\right)$-based models in both safe-speed estimation and trajectory stability evaluation. The constant-$\mu$ model overestimated the safe speed by an average of approximately 7.5 km/h and underestimated the lateral deviation. In contrast, the $\mu \left(N\right)$ model, which incorporated the load increase on the outer wheels and the corresponding friction reduction, yielded more realistic results. This clearly indicates that the constant-$\mu$ assumption tends to underestimate the actual driving risk on curved ramps.

Overall, these findings suggest that integrating dynamic load transfer and load-sensitive friction characteristics provides a quantitatively more accurate representation of the actual driving risk during curve negotiation than the traditional constant-friction assumption. The present discussion provides strong evidence supporting the adoption of load-sensitive friction models in real-time speed control algorithms for autonomous heavy trucks and in the development of improved road design standards.

5. Conclusions

This study proposed a unified framework for realistic safe-speed estimation of multi-axle heavy trucks on curved road segments by integrating dynamic axle-load transfer and load-sensitive tire–road friction within a TruckSim–Simulink co-simulation environment. The proposed $\mu$(N) model more accurately reproduces the rollover–skidding boundary than constant-$\mu$ approaches, demonstrating that jointly modeling load dynamics and friction degradation is essential for physically consistent safety assessment. The framework assumes that the friction state is provided in real time through external sensing or estimation and therefore does not yet address uncertainty in $\mu$, stochastic variation in road conditions, or frequency-dependent tire behavior under oscillatory load variations. Future work should focus on online estimation of load and friction parameters, integration with optimal or stochastic speed-control architectures, and extension of the tire model to represent oscillatory loading more accurately [25]. The framework offers a physically grounded basis for safe-speed evaluation that accounts for both rollover and skidding limits and may support real-time control in autonomous heavy trucks as well as the refinement of road safety standards.