Synthetic Data Generation Pipeline for Multi-Task Deep Learning-Based Catheter 3D Reconstruction and Segmentation from Biplanar X-Ray Images
Abstract
1. Introduction
2. Materials and Methods
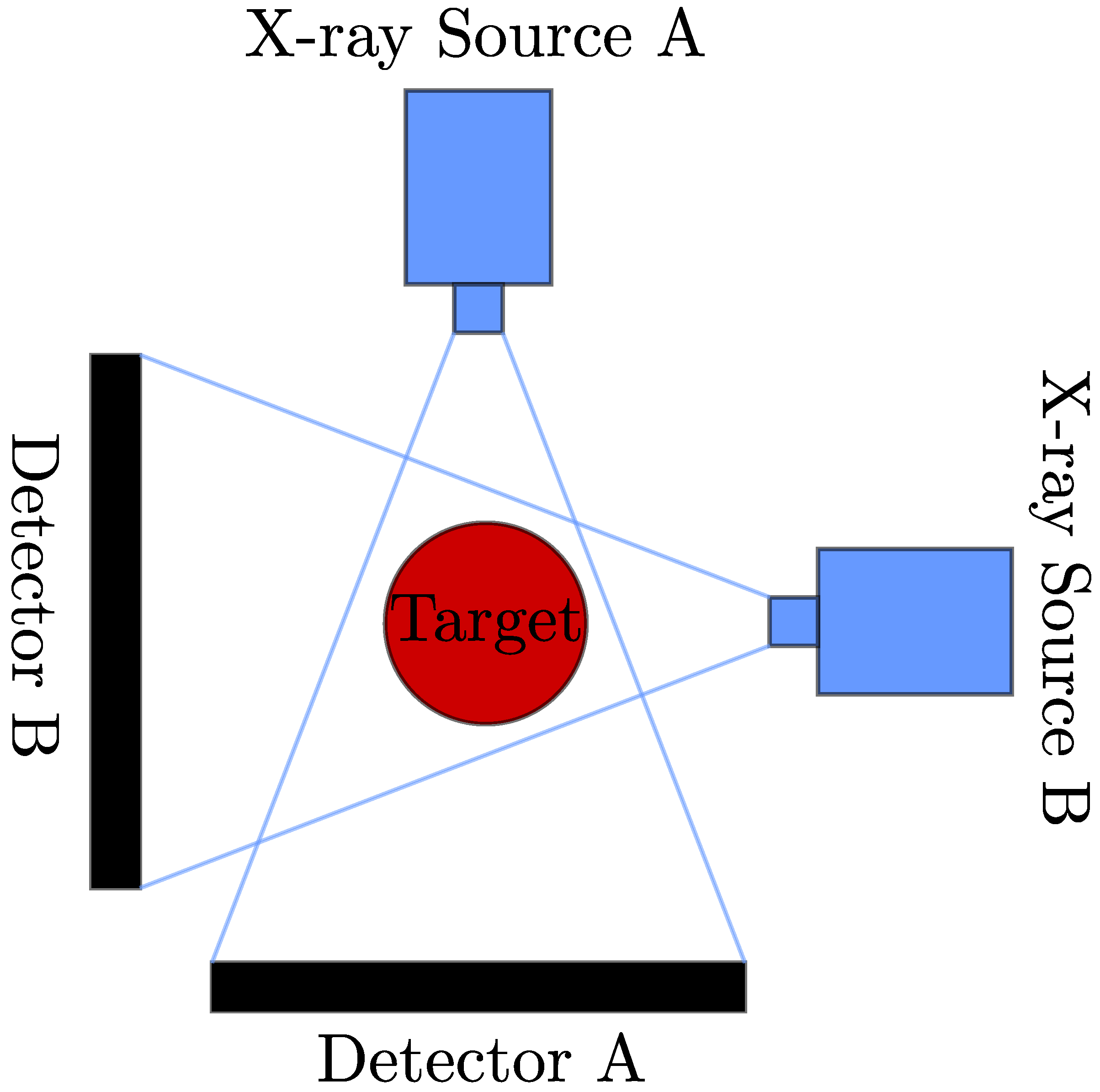
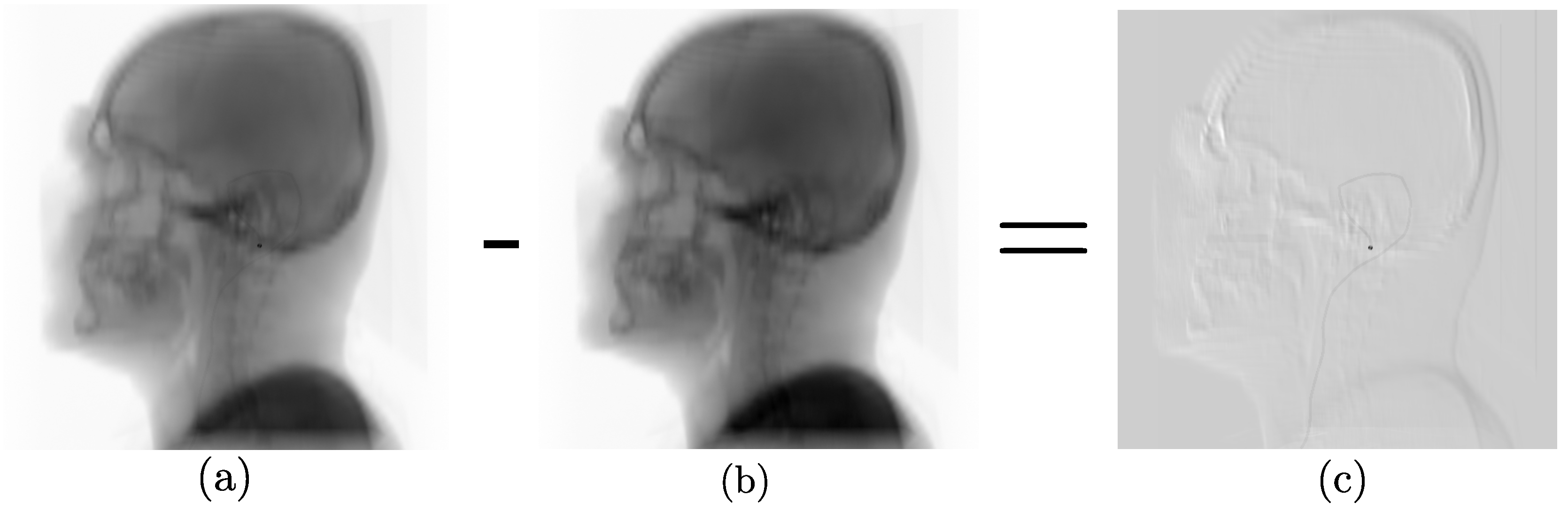
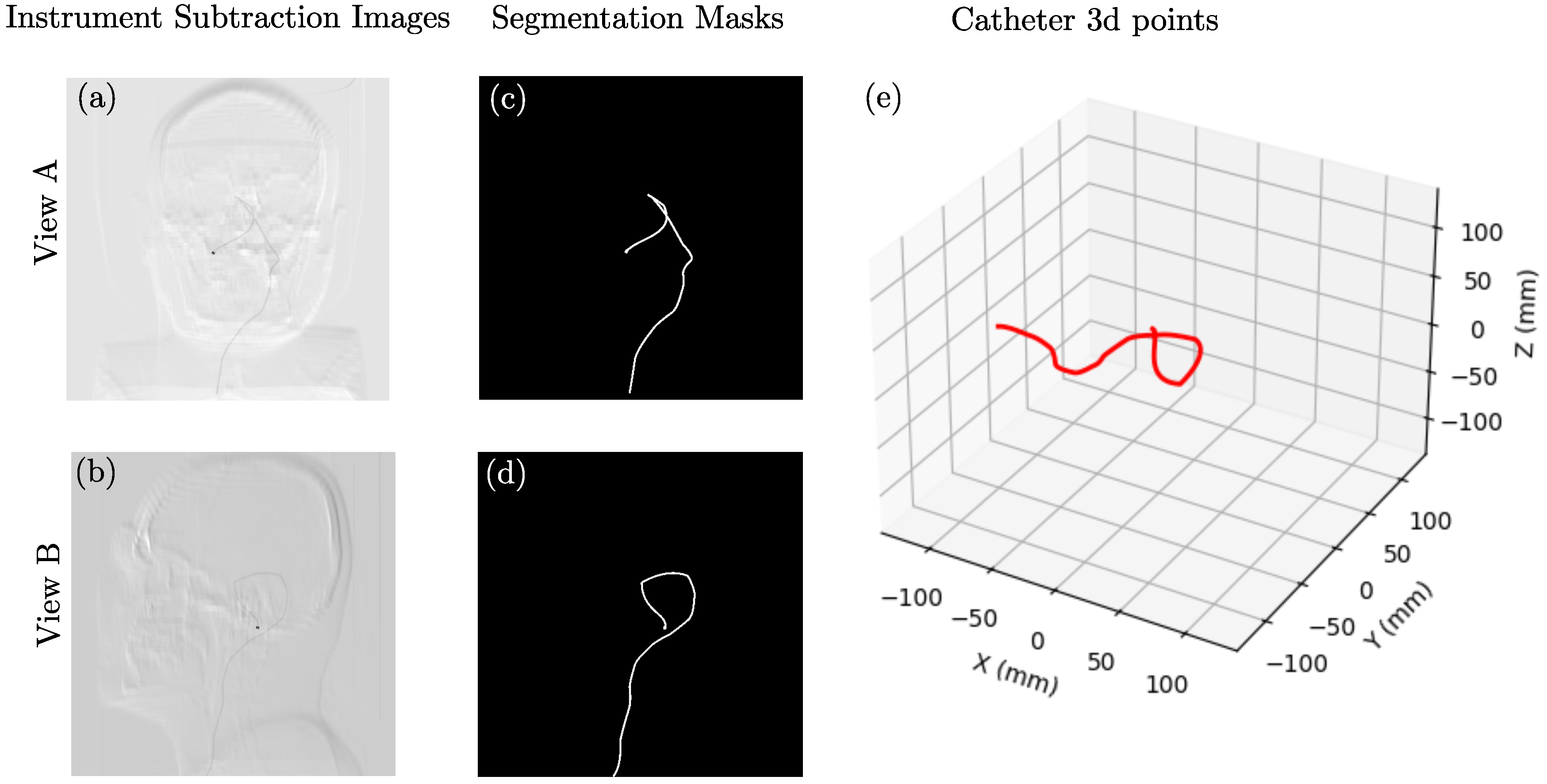
2.1. Data Synthesis
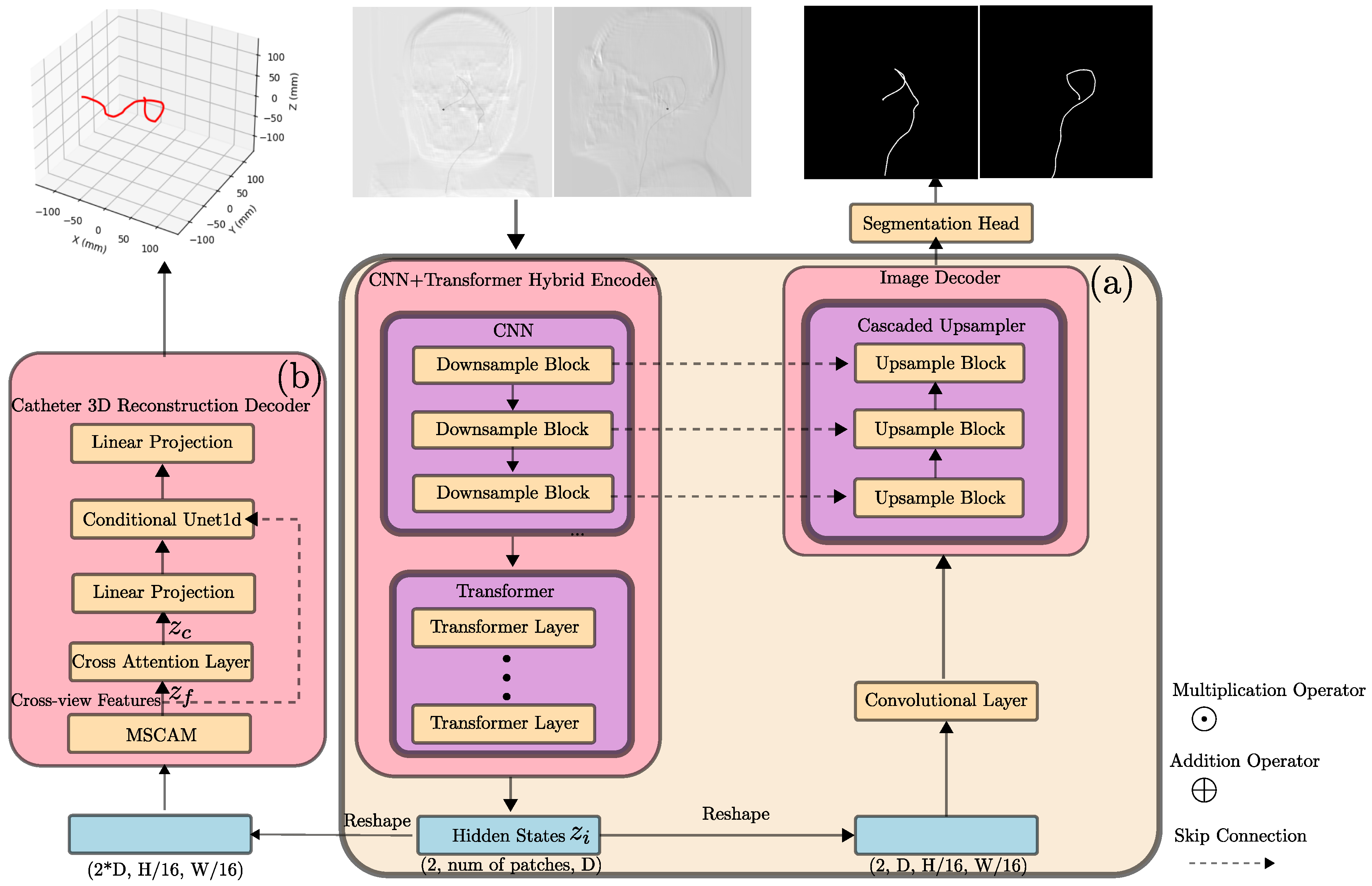
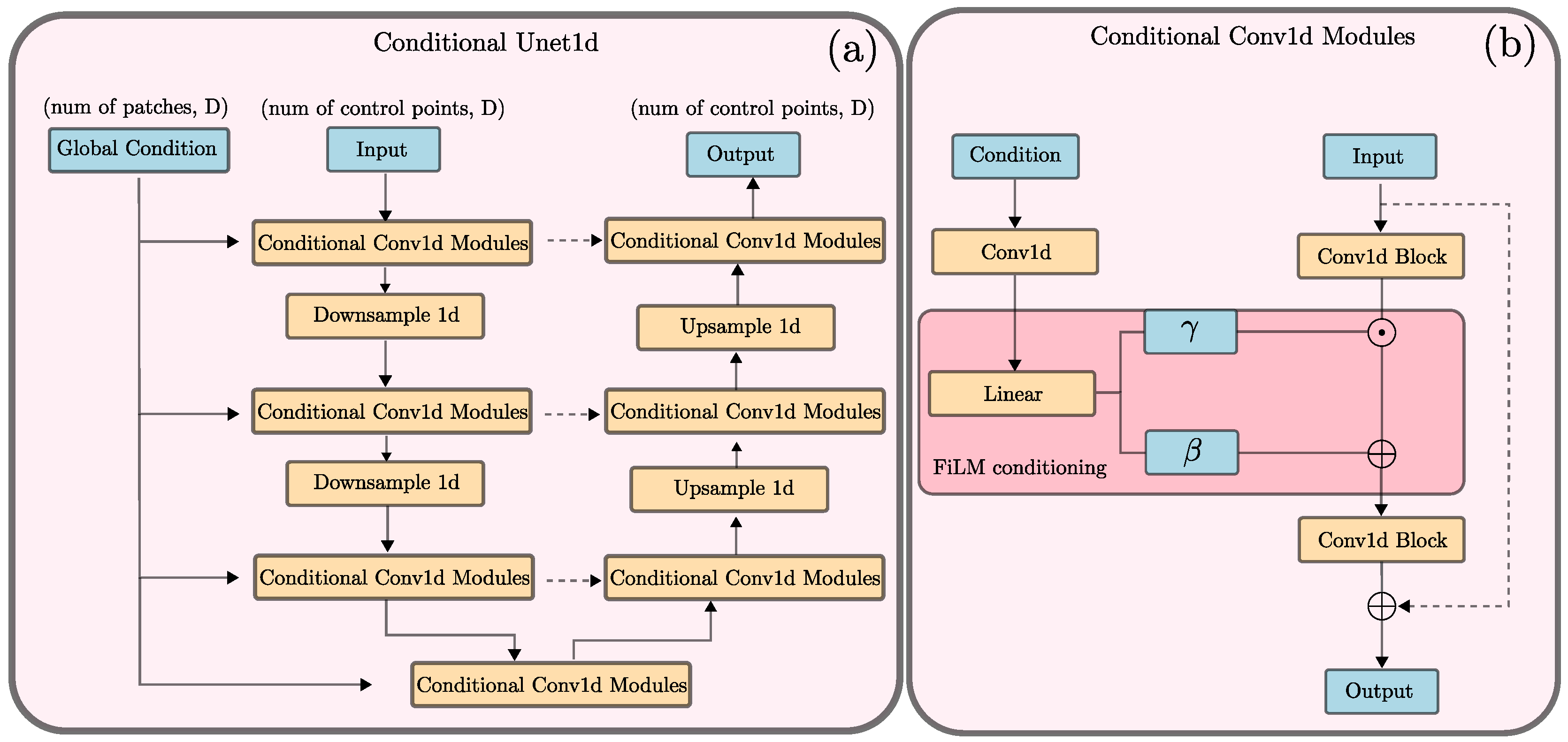
2.2. Neural Network Architecture
2.3. Loss Function
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NdFeB | Neodymium Iron Boron |
| PTFE | polytetrafluoroethylene |
| SID | Source-to-Image Distance |
| SOD | Source-to-Object Distance |
| CT | Computed Tomography |
| HU | Hounsfied Unit |
| CNN | Convolutional Neural Network |
| MSCAM | Multi-Scale Convolutional Attention Module |
| FiLM | Feature-wire Linear Modulation |
References
- Kummer, M.P.; Abbott, J.J.; Kratochvil, B.E.; Borer, R.; Sengul, A.; Nelson, B.J. OctoMag: An electromagnetic system for 5-DOF wireless micromanipulation. IEEE Trans. Robot. 2010, 26, 1006–1017. [Google Scholar] [CrossRef]
- Le, V.N.; Nguyen, N.H.; Alameh, K.; Weerasooriya, R.; Pratten, P. Accurate modeling and positioning of a magnetically controlled catheter tip. Med. Phys. 2016, 43, 650–663. [Google Scholar] [CrossRef] [PubMed]
- Sikorski, J.; Dawson, I.; Denasi, A.; Hekman, E.E.; Misra, S. Introducing BigMag—A novel system for 3D magnetic actuation of flexible surgical manipulators. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3594–3599. [Google Scholar]
- Fu, S.; Chen, B.; Li, D.; Han, J.; Xu, S.; Wang, S.; Huang, C.; Qiu, M.; Cheng, S.; Wu, X.; et al. A magnetically controlled guidewire robot system with steering and propulsion capabilities for vascular interventional surgery. Adv. Intell. Syst. 2023, 5, 2300267. [Google Scholar] [CrossRef]
- Kim, Y.; Parada, G.A.; Liu, S.; Zhao, X. Ferromagnetic soft continuum robots. Sci. Robot. 2019, 4, eaax7329. [Google Scholar] [CrossRef] [PubMed]
- Dreyfus, R.; Boehler, Q.; Lyttle, S.; Gruber, P.; Lussi, J.; Chautems, C.; Gervasoni, S.; Seibold, D.; Ochsenbein-Kölble, N.; Reinehr, M.; et al. Dexterous helical magnetic robot for improved endovascular access. Sci. Robot. 2024, 9, eadh0298. [Google Scholar] [CrossRef] [PubMed]
- Torlakcik, H.; Sevim, S.; Alves, P.; Mattmann, M.; Llacer-Wintle, J.; Pinto, M.; Moreira, R.; Flouris, A.; Landers, F.; Chen, X.; et al. Magnetically guided microcatheter for targeted injection of magnetic particle swarms. Adv. Sci. 2024, 11, 2404061. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, M.; Brost, A.; Jakob, C.; Bourier, F.; Koch, M.; Kurzidim, K.; Hornegger, J.; Strobel, N. Semi-automatic catheter reconstruction from two views. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention, Nice, France, 1–5 October 2012; pp. 584–591. [Google Scholar]
- Hoffmann, M.; Brost, A.; Jakob, C.; Koch, M.; Bourier, F.; Kurzidim, K.; Hornegger, J.; Strobel, N. Reconstruction method for curvilinear structures from two views. In Proceedings of the Medical Imaging 2013: Image-Guided Procedures, Robotic Interventions, and Modeling, Lake Buena Vista, FL, USA, 9–14 February 2013; Volume 8671, pp. 630–637. [Google Scholar]
- Hoffmann, M.; Brost, A.; Koch, M.; Bourier, F.; Maier, A.; Kurzidim, K.; Strobel, N.; Hornegger, J. Electrophysiology catheter detection and reconstruction from two views in fluoroscopic images. IEEE Trans. Med. Imaging 2015, 35, 567–579. [Google Scholar] [CrossRef] [PubMed]
- Delmas, C.; Berger, M.O.; Kerrien, E.; Riddell, C.; Trousset, Y.; Anxionnat, R.; Bracard, S. Three-dimensional curvilinear device reconstruction from two fluoroscopic views. In Proceedings of the Medical Imaging 2015: Image-Guided Procedures, Robotic Interventions, and Modeling, Orlando, FL, USA, 21–26 February 2015; Volume 9415, pp. 100–110. [Google Scholar]
- Petković, T.; Homan, R.; Lončarić, S. Real-time 3D position reconstruction of guidewire for monoplane X-ray. Comput. Med. Imaging Graph. 2014, 38, 211–223. [Google Scholar] [CrossRef] [PubMed]
- Wagner, M.; Schafer, S.; Strother, C.; Mistretta, C. 4D interventional device reconstruction from biplane fluoroscopy. Med. Phys. 2016, 43, 1324–1334. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Ambrosini, P.; Ruijters, D.; Niessen, W.J.; Moelker, A.; van Walsum, T. Fully automatic and real-time catheter segmentation in X-ray fluoroscopy. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention, Quebec City, QC, Canada, 11–13 September 2017; pp. 577–585. [Google Scholar]
- Nguyen, A.; Kundrat, D.; Dagnino, G.; Chi, W.; Abdelaziz, M.E.; Guo, Y.; Ma, Y.; Kwok, T.; Riga, C.; Yang, G.Z. End-to-end real-time catheter segmentation with optical flow-guided warping during endovascular intervention. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 9967–9973. [Google Scholar]
- Zhou, Y.J.; Xie, X.L.; Zhou, X.H.; Liu, S.Q.; Bian, G.B.; Hou, Z.G. Pyramid attention recurrent networks for real-time guidewire segmentation and tracking in intraoperative X-ray fluoroscopy. Comput. Med. Imaging Graph. 2020, 83, 101734. [Google Scholar] [CrossRef] [PubMed]
- Ullah, I.; Chikontwe, P.; Park, S.H. Real-time tracking of guidewire robot tips using deep convolutional neural networks on successive localized frames. IEEE Access 2019, 7, 159743–159753. [Google Scholar] [CrossRef]
- Zhou, Y.J.; Liu, S.Q.; Xie, X.L.; Zhou, X.H.; Wang, G.A.; Hou, Z.G.; Li, R.-Q.; Ni, Z.-L.; Fan, C.C. A real-time multi-task framework for guidewire segmentation and endpoint localization in endovascular interventions. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 13784–13790. [Google Scholar]
- Jianu, T.; Huang, B.; Berthet-Rayne, P.; Fichera, S.; Nguyen, A. 3D guidewire shape reconstruction from monoplane fluoroscopic images. In Proceedings of the International Conference on Robot Intelligence Technology and Applications, Taicang, China, 6–8 December 2023; pp. 84–94. [Google Scholar]
- Jianu, T.; Huang, B.; Nguyen, H.; Bhattarai, B.; Do, T.; Tjiputra, E.; Tran, Q.; Berthet-Rayne, P.; Le, N.; Fichera, S.; et al. Guide3D: A biplanar X-ray Dataset for Guidewire Segmentation and 3D Reconstruction. In Proceedings of the Computer Vision—ACCV 2024: 17th Asian Conference on Computer Vision, Hanoi, Vietnam, 8–12 December 2024; pp. 1549–1565. [Google Scholar]
- Community, B.O. 2018. Blender—A 3D Modelling and Rendering Package. Stichting Blender Foundation, Amsterdam. Available online: http://www.blender.org (accessed on 6 August 2025).
- Vidal, F.P.; Afshari, S.; Ahmed, S.; Atkins, C.; Béchet, É.; Bellot, A.C.; Bosse, S.; Chahid, Y.; Chou, C.-Y.; Culver, R.; et al. X-ray simulations with gVXR as a useful tool for education, data analysis, set-up of CT scans, and scanner development. Dev. X-Ray Tomogr. XV 2024, 13152, 30–49. [Google Scholar]
- Biguri, A.; Dosanjh, M.; Hancock, S.; Soleimani, M. TIGRE: A MATLAB-GPU toolbox for CBCT image reconstruction. Biomed. Phys. Eng. Express 2016, 2, 055010. [Google Scholar] [CrossRef]
- Hubbell, J.H.; Seltzer, S.M. Tables of X-Ray Mass Attenuation Coefficients and Mass Energy-Absorption Coefficients (Version 1.4); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2004. Available online: http://physics.nist.gov/xaamdi (accessed on 7 August 2025).
- Hssayeni, M. Computed Tomography Images for Intracranial Hemorrhage Detection and Segmentation (Version 1.3.1). PhysioNet. RRID:SCR_007345. 2020. Available online: https://doi.org/10.13026/4nae-zg36 (accessed on 7 August 2025).
- Hssayeni, M.D.; Croock, M.S.; Salman, A.D.; Al-Khafaji, H.F.; Yahya, Z.A.; Ghoraani, B. Intracranial Hemorrhage Segmentation Using A Deep Convolutional Model. Data 2020, 5, 14. [Google Scholar] [CrossRef]
- Goldberger, A.; Amaral, L.; Glass, L.; Hausdorff, J.; Ivanov, P.C.; Mark, R.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef] [PubMed]
- Cardoso, M.J.; Li, W.; Brown, R.; Ma, N.; Kerfoot, E.; Wang, Y.; Murrey, B.; Myronenko, A.; Zhao, C.; Yang, D.; et al. Monai: An open-source framework for deep learning in healthcare. arXiv 2022, arXiv:2211.02701. [Google Scholar] [CrossRef]
- Chen, J.; Lu, Y.; Yu, Q.; Luo, X.; Adeli, E.; Wang, Y.; Lu, L.; Yuille, A.; Zhou, Y. Transunet: Transformers make strong encoders for medical image segmentation. arXiv 2021, arXiv:2102.04306. [Google Scholar] [CrossRef]
- Rahman, M.M.; Munir, M.; Marculescu, R. Emcad: Efficient multi-scale convolutional attention decoding for medical image segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 11769–11779. [Google Scholar]
- Cao, H.; Wang, Y.; Chen, J.; Jiang, D.; Zhang, X.; Tian, Q.; Wang, M. Swin-unet: Unet-like pure transformer for medical image segmentation. In Proceedings of the Computer Vision–ECCV 2022 Workshops, Tel Aviv, Israel, 23–27 October 2022; pp. 205–218. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 1–11. [Google Scholar] [CrossRef]
- Chi, C.; Xu, Z.; Feng, S.; Cousineau, E.; Du, Y.; Burchfiel, B.; Tedrake, R.; Song, S. Diffusion policy: Visuomotor policy learning via action diffusion. Int. J. Robot. Res. 2025, 44, 1684–1704. [Google Scholar] [CrossRef]
- Perez, E.; Strub, F.; De Vries, H.; Dumoulin, V.; Courville, A. Film: Visual reasoning with a general conditioning layer. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; p. 32. [Google Scholar]
- Boor, C.D. Subroutine Package for Calculating with b-Splines; Los Alamos Scientific Laboratory: Los Alamos, NM, USA, 1971. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled weight decay regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Smith, L.N.; Topin, N. Super-convergence: Very fast training of neural networks using large learning rates. In Proceedings of the Artificial Intelligence and Machine Learning for Multi-Domain Operations Applications, Baltimore, MD, USA, 14–18 April 2019; Volume 11006, pp. 369–386. [Google Scholar]




| Dataset | Dice | RMSE | RP-DICE |
|---|---|---|---|
| Validation Dataset | 0.91 | 5.5 | 0.40 |
| Experimental Dataset | 0.83 | / | 0.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Zhang, G.; Yang, W.; Wang, C.; Yang, J. Synthetic Data Generation Pipeline for Multi-Task Deep Learning-Based Catheter 3D Reconstruction and Segmentation from Biplanar X-Ray Images. Appl. Sci. 2025, 15, 12247. https://doi.org/10.3390/app152212247
Wang J, Zhang G, Yang W, Wang C, Yang J. Synthetic Data Generation Pipeline for Multi-Task Deep Learning-Based Catheter 3D Reconstruction and Segmentation from Biplanar X-Ray Images. Applied Sciences. 2025; 15(22):12247. https://doi.org/10.3390/app152212247
Chicago/Turabian StyleWang, Junang, Guixiang Zhang, Wenyun Yang, Changsheng Wang, and Jinbo Yang. 2025. "Synthetic Data Generation Pipeline for Multi-Task Deep Learning-Based Catheter 3D Reconstruction and Segmentation from Biplanar X-Ray Images" Applied Sciences 15, no. 22: 12247. https://doi.org/10.3390/app152212247
APA StyleWang, J., Zhang, G., Yang, W., Wang, C., & Yang, J. (2025). Synthetic Data Generation Pipeline for Multi-Task Deep Learning-Based Catheter 3D Reconstruction and Segmentation from Biplanar X-Ray Images. Applied Sciences, 15(22), 12247. https://doi.org/10.3390/app152212247






