Study on Determining the Ranges of the Inner Wheel Difference Zone for the Right Turns of Large Vehicles

Abstract

To effectively reduce traffic accidents caused by inner wheel differences during large vehicles’ right turns at intersections, this study proposes a quantitative method to calculate the range of inner wheel difference areas. Typical intersections in Nanjing and Taiyuan were selected for field tests using rigid-body and articulated vehicles with different parameters. Dynamic data during turning were collected, revealing a significant linear correlation between the number of steering wheel rotations and the geometric parameters of the intersection as well as the structural dimensions of the vehicle. On the basis of Ackermann’s steering geometry theory, trajectory prediction models for both vehicle types were constructed. Verification with actual trajectory data extracted by Tracker software revealed that the rigid-body vehicle model had a maximum relative error of 8.12% and an average of 5.39%, whereas the articulated vehicle model had a maximum of 8.32% and an average of 5.12%, confirming high model accuracy. A Python-based visualization program for inner wheel difference areas was developed. The results provide technical support for scientifically marking warning areas at intersections and improving the refined management of traffic safety.

1. Introduction

The inner wheel difference refers to the difference between the turning radii of the front and rear inner wheels of a vehicle when it is turning. The closed area resulting from the inner wheel difference is called the inner wheel difference zone. When a vehicle is making a turn, road users located within the inner wheel difference zone are at a significantly elevated risk of accidents. The potential conflicts between right-turning motor vehicle traffic and the movements of pedestrians and nonmotorized vehicles represent significant safety risks at urban intersections [1], presenting a major challenge to road traffic safety [2]. According to incomplete statistics, more than 70% of traffic accidents involving large vehicles (including rigid vehicles and hinge vehicles) are related to inner wheel differences [3], in particular, the collision accidents between large vehicles and vulnerable road users [VRUs (pedestrians, bicyclists, motorcycle riders, etc.). VRUs (pedestrians, bicyclists, motorcycle riders, etc.)] caused by inner wheel differences at intersections have a very high frequency and fatality rate [4,5,6]. Petr et al. [7,8,9] investigated and analyzed large vehicle–bicycle accidents in Norway, and the results revealed that from 2000 to 2014, cyclists who died due to collisions between turning vehicles and bicycles going straight accounted for 20% of the total number of urban cyclist deaths. Since the smaller the turning radius of a vehicle is, the greater its inner wheel difference, in China, where right-hand driving rules are followed, scrapes and crushes of pedestrians or nonmotor vehicles caused by the inner wheel differences produced when large vehicles turn right at intersections are among the main forms of large-vehicle traffic accidents [10].

Existing studies [11,12,13] have explored traffic safety for VRUs [14,15] and large vehicles (e.g., trucks) by assessing topics such as accident causes, severity levels, collision reconstruction simulations, and prevention/early warning systems. The key influencing factors identified are vehicle speeds, trajectories, collision locations [16] and the field of view [17]: a higher speed increases the severity of inner wheel difference accidents [18]; a smaller turning radius for a large vehicle increases its inner wheel difference, increasing the accident risk [19]; cyclists are more likely to be fatally crushed when the initial collision point is near the cab [20]; and the larger the blind spot, the more likely it is to have an inner wheel difference accident [21,22]. Assessing the effects of these factors on such accidents requires substantial statistical data, but data collection is a time-consuming and error-prone process. Thus, model-based simulations are widely used to examine the influences of these factors and summarize collision patterns [23].

This study focuses on the scenario of large vehicles making right turns at intersections. Through in-depth analysis of on-site survey data, it quantifies the correlation between the geometric parameters of vehicles and intersections and the steering wheel rotation count during the right-turn maneuver. On this basis, with reference to the Ackermann steering geometry theory, a calculation model for the inner wheel difference area range of large vehicles turning right at intersections is established, and a user-friendly program interface is developed. By inputting the geometric parameters of intersections and vehicles into this interface, the maximum inner wheel difference value and boundary coordinates of inner wheel difference area can be automatically computed. Finally, the model accuracy is validated through experimental verification. A key advantage of this model is that the inner wheel difference area range can be directly derived solely based on the known geometric dimensions of intersections and vehicles. This proposed model not only significantly reduces the complexity of inner wheel difference area range calculation but also exhibits excellent adaptability to diverse intersection and vehicle scenarios.

2. Literature Review

Regarding traffic accidents caused by the inner wheel difference when large vehicles turn right, some scholars have determined the scope of the inner wheel difference area by establishing a calculation model for the inner wheel difference. On the basis of an established multi-rigid-body model, Wei et al. simulated the dynamic response processes of collisions and rollovers between rigid trucks and electric bicycles under different conditions, and the differences among these processes revealed the laws of accidents [13]. Compared with that for rigid vehicles, the calculation of the inner wheel difference zones for articulated vehicles is a more complex task. Tsai and Sung proposed an algebraic analytical method to derive the inner wheel differences of semitrailers and established equations based on vehicle dimensions and steering conditions. This method can predict the steering trajectory of a vehicle almost in real time but involves numerous parameters and a complex calculation process [24]. Wang et al. modeled the wheel difference on the basis of the relationship between the angular and linear velocities of the wheels during turning; however, the inner wheel difference of the trailer part was determined on the basis of the calculation results of the tractor, and the calculation model still needs further research [13]. Compared with traditional schemes, the introduction of steerable axles in truck semitrailers can significantly improve the traction performance of these semitrailers and enhance their operational safety [25]; however, this scheme is too complex and significantly increases the cost of vehicle manufacturing. After the model is established, further visual presentation is required. Integrating the model into a simulation platform can reproduce the random behaviors of vehicles and Vulnerable Road Users (VRUs) under different geometric layouts and operating conditions [26].

Some scholars have used the PC-CRASH 8.0 simulation software (a Windows-based 3D collision and trajectory simulation tool developed by Steffan Datentechnik GmbH in Linz, Austria) to simulate right-turn inner wheel difference accidents of large vehicles. This software can simulate the complete collision process with high resolution and predict the dynamic response processes such as the movement trajectories of accident participants, and has high accuracy [27]. Yang et al. obtained wheel trajectory information through PC-CRASH, and by setting appropriate initial conditions, the simulation could effectively reflect the movement trajectory of the accident vehicle [28], it can also relatively accurately predict the dynamic response processes such as the movement trajectories of accident participants [29,30]. Although the method of obtaining right-turn collision patterns through PC-CRASH is effective, simulations rarely consider the contingencies and complexities of real collisions. Moreover, differences among the road conditions, vehicles, and human models in different countries and regions should be considered [31]. Therefore, some scholars have used target detection models and recurrent neural network models to predict the inner wheel trajectories of large vehicles from the perspective of motorcycle riders by means of image recognition technology in deep learning [32]. Recurrent Neural Networks (RNNs), represented by Long Short-Term Memory (LSTM) networks, have inherent advantages in processing time-series data, which have greatly promoted research related to vehicle trajectory prediction [33,34]. This helps develop early warning devices for installation on large vehicles [35].

In addition, advanced driver assistance systems (ADASs) are expected to prevent or mitigate such collisions [36], and their development requires a detailed understanding of the behavioral characteristics of truck drivers [37]. Studies have shown that general anticipatory driving training that combines theory, workshops, and on-road practice helps increase the attention given by truck drivers to cyclists [38]. In particular, the size of the blind zone formed by the inner wheel difference zone is closely related to the height of the driver’s eye point from the ground [39] and changes dynamically as the vehicle turns [40]. Furthermore, increasing the possibility of positive interaction between large vehicle drivers and Vulnerable Road Users (VRUs)—that is, large vehicles staying behind VRUs when approaching intersections—can eliminate collision risks [41]. All of these factors need to be included in driver training. Researchers compared drivers before and after they received training and observed that the results were highly consistent with the drivers’ views and feelings about the training process, as expressed in the interviews. Therefore, driver training can serve as a supplementary solution [42].

These studies indicate that traffic accidents caused by inner wheel differences during the right turns of large vehicles have received widespread attention. Researchers have produced abundant results by focusing on accident causes, accident severity levels, collision reconstruction simulations, and accident prevention and early warning techniques. These achievements are all based on the inner wheel difference zones of large vehicles, which shows that determining their scope is key to addressing related accidents. The inner wheel difference zones produced during the right turns of large vehicles are affected by the geometric parameters of the intersections. Without considering this influence, adjusting the scope of the inner wheel difference zone during the right turns of a large vehicle in a timely manner according to the different geometric parameters of intersections is impossible.

Therefore, this paper proposes a calculation method that combines the geometric characteristics of intersections and vehicles to determine the scope of the inner wheel difference zone and establishes a mathematical model for the actual turning of vehicles. First, by analyzing field survey data, a relational model between the geometric dimensions of intersections and vehicles and the number of steering wheel rotations during vehicle right turns was established. Then, based on the kinematic geometry theory of vehicle steering, trajectory prediction models for rigid-body vehicles and articulated vehicles during right turns were constructed. With the help of the Python 3.11 platform, coordinate images of the inner wheel difference area range were generated. Finally, the accuracy of the model-predicted trajectory data was verified using real trajectory data of vehicle right turns extracted by Tracker software 6.2.0.

The models and customer-oriented interface program developed on this basis greatly improve the efficiency of calculating the inner wheel difference area formed by large vehicles of different geometric dimensions when turning right at any intersection, and can provide references for road design and the marking of dangerous areas at intersections. However, the research results are applicable only to standard (perpendicularly intersecting) intersections. For irregular intersections, further research is needed to enhance applicability.

The rest of this paper is organized as follows: Section 3 describes the research on the right-turn behaviors of large vehicles, identifies the influencing factors of steering wheel rotation during large vehicles’ right turns, and a linear fitting relationship is derived—with the vehicle wheelbase as the independent variable and the number of steering wheel revolutions as the dependent variable; Section 4, based on the conclusions of Section 3, develops a program for the inner wheel difference area model using the Python platform, which generates images of the inner wheel difference area at intersections according to given data; Section 5 conducts a credibility analysis of the aforementioned model program. The driving trajectories of the inner wheels of large vehicles before and after right turns at intersections are obtained from video data captured by UAVs and high-point cameras. After trajectory extraction and coordinate conversion, the actual trajectory data are acquired. Numerical analysis is then performed by taking the inner wheel trajectory coordinate values at the same time points as evaluation indicators, comparing the actual data with the data obtained from the program in Section 4; Section 6 and Section 7 present the discussion and conclusions of this paper.

3. Research of Large Vehicles Turning Right

To further investigate the formation mechanism of the inner wheel difference zone during the right turn of large vehicles, this section employs the observational method to collect relevant data through on-site filming of intersection geometric parameters and the steering wheel operation of large vehicle drivers using handheld cameras and unmanned aerial vehicles (UAVs). Finally, the collected data are analyzed in conjunction with the inherent parameters of the surveyed vehicles, providing a scientific basis for the subsequent determination of the inner wheel difference zone scope and the formulation of safety countermeasures.

3.1. Research Methods and Procedures

Since the inner wheel difference zone produced during the right turn of a vehicle is mainly controlled by the number of steering wheel rotations, the experiment aims to clarify how the dimensions of large vehicles and the geometric parameters of intersections influence the number of steering wheel rotation when drivers maneuver large vehicles to make right turns at intersections.

The observational method refers to a data collection approach wherein researchers conduct purposeful and systematic observations through sensory perception or specialized instruments to identify inherent patterns and characteristics. It is characterized by simplicity, intuitiveness, and suitability for on-site data acquisition. Therefore, this study adopts the video-based observational method—a specific type of observational research: handheld cameras are used to record the number of steering wheel revolutions during driver steering operations, while unmanned aerial vehicles (UAVs) capture the geometric parameters of intersections and the entire process of vehicle turning maneuvers. Subsequently, the control variable method is employed to analyze the relationships between vehicle parameters, intersection geometric parameters, and the number of steering wheel revolutions. The experimental process is shown in Figure 1.

3.2. Research Object

Large vehicles are classified into rigid vehicles and articulated vehicles based on their body structures. Considering road commonality, accident risk, market share and research practicality, the research objects of the two types of vehicles and their selection basis are as follows:

First, rigid vehicles refer to those with the engine cab fixedly connected to the vehicle body, such as large trucks and buses commonly seen on urban roads. Buses are selected as the research carrier because they operate on fixed routes, have high popularity and are suitable for video surveys.

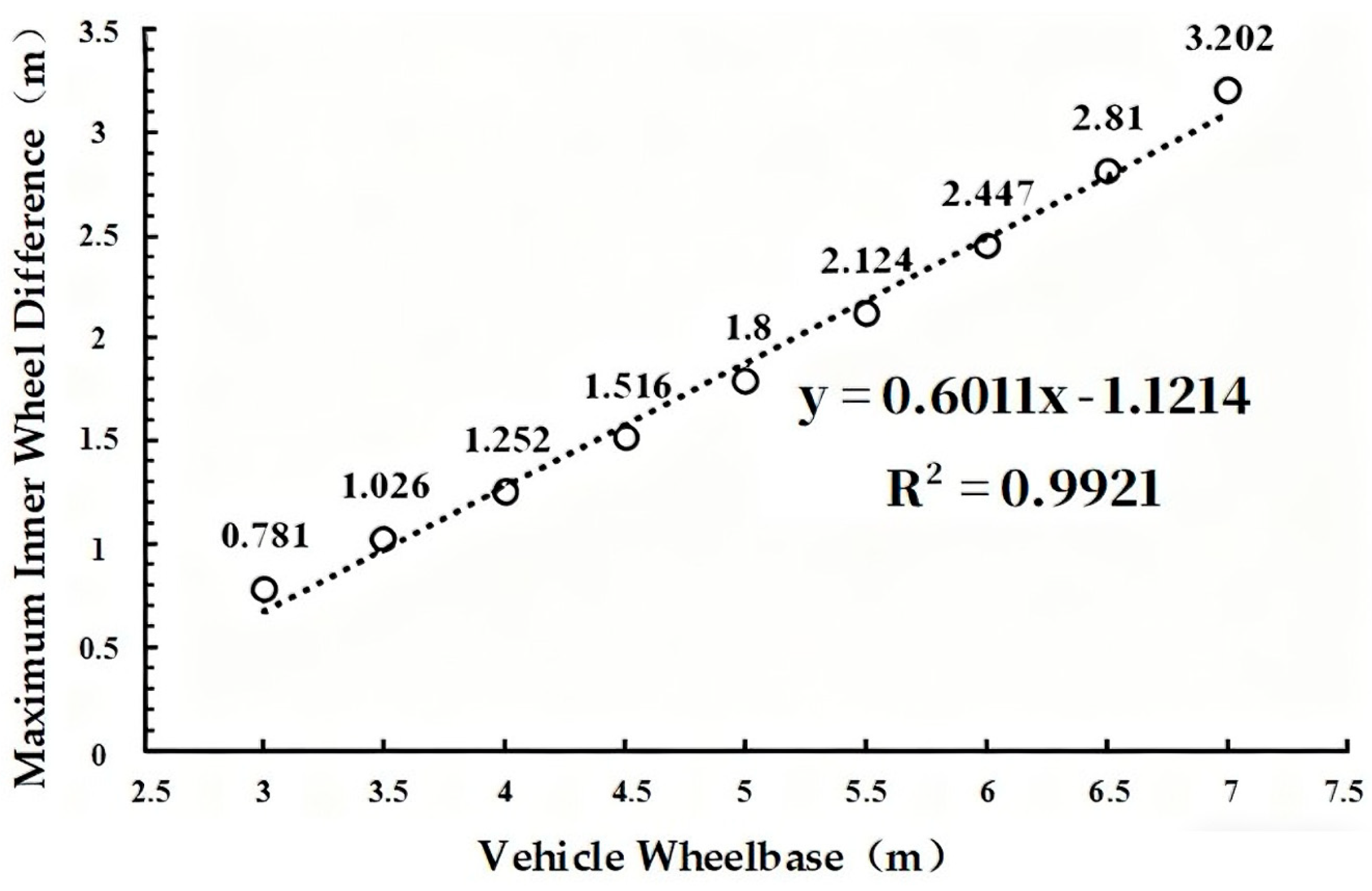
Buses are categorized by length into small (3.5–7 m), medium (7–10 m), large (10–12 m) and extra-large (13–18 m, articulated). Studies have shown [43,44] that the wheelbase is positively correlated with the inner wheel difference, and the data fitting of the maximum inner wheel difference caused by the vehicle wheelbase is shown in Figure 2. Large buses have a wheelbase of 4.4–6.2 m, which results in a larger inner wheel difference and higher accident risk. Therefore, the research on rigid vehicles focuses on the inner wheel difference of large buses when turning right.

Second, articulated vehicles, which consist of a tractor and a trailer. In the data collection areas (Jinyuan District and Qingxu County of Taiyuan City), FAW Jiefang tractors account for 64% of the total tractors (main models: Han V500/J6 series). Therefore, FAW Jiefang heavy-duty truck models Han V500 and J6 series were selected as the research objects. During the right turn of vehicles at intersections, the wheelbase and track width of the trailer not only affect driving performance such as vehicle pass ability but also significantly influence the area scope of the inner wheel difference for large vehicles when turning right. Based on domestic and international trailer data, the wheelbase of trailers is mostly 7000~10,000 mm, and the track width is usually standardized at 1820 mm, with a small number of trailers using 2240 mm. Considering the on-site conditions of the research areas, 11 mstake trucks and 13 m box trailers were selected as the trailer models for data collection.

3.3. Date Collection

To accurately capture steering behavior data of large vehicles during right turns and characterize intersection environmental attributes, it is imperative to first define the selection criteria for test equipment and the principles of scenario configuration—prerequisites for the precise extraction of target data parameters. This section details the data collection methodology by elucidating the selection rationale and specific parameters from three core dimensions: “Camera Selection”, “Large Vehicle Sampling”, and “Test Intersection Selection”. From these three dimensions, three key variables—“steering wheel revolutions”, “vehicle wheelbase”, and “intersection aspect ratio”—were extracted, laying a robust foundation for ensuring the scientific rigor and representativeness of subsequent data acquisition.

3.3.1. Selection of Cameras

The selection of cameras is crucial to ensuring data accuracy. The following factors were considered during the selection and shooting: in terms of image sensors, the CMOS type was preferred due to its small size and high flexibility, which make it suitable for field survey shooting; the video frame rate was set to 60 frames per second, which provides clearer and more realistic images than 30 frames per second; the aperture parameter was adjusted according to the shooting distance: a small F-number aperture was used for close-range shooting to ensure sufficient light, while a large F-number aperture was adopted for long-range shooting.

1. Video Shooting of Rigid-Body Vehicles

A dual-lens camera with 12 million + 20 million pixels, featuring an f/1.8 aperture and a CMOS sensor was selected. CMOS sensors, which have the advantages of small size and high flexibility, are suitable for field surveys and imaging. The video shooting resolution is 1080 p (3840 × 2160 pixels) at 30 frames per second.

2. Video Shooting of Articulated Vehicles

A main lens with 48 million pixels, equipped with an f/1.79 aperture and a CMOS sensor was adopted. The video was shot at 4K resolution (3840 × 2160 pixels) at 30 frames per second.

3. Video Shooting of Intersection Environments

A Sony Exmor R CMOS sensor, sourced from Sony Group Corporation, Tokyo, Japan.With an effective pixel count of 20 million (total pixels: 20.48 million) was adopted, paired with an f/2.8 wide-angle autofocus lens with an equivalent focal length of 24 mm. Video shooting with H.264 encoding can reach a maximum resolution of C4K (4096 × 2160 pixels) at 60 frames per second.

3.3.2. Large Vehicle Selection

1. Rigid-Body Vehicles

Various types of 10 m and 12 m class large buses in Nanjing and Taiyuan were used as test vehicles, and the corresponding vehicle parameters were collected, as shown in

Table 1. Parameters of large-scale bus vehicles in Nanjing and Taiyuan.

Vehicle Brand and Model	Vehicle Length/m	Vehicle Width/m	Maximum Turning Angle/°	Front Track/m	Rear Track/m
BYD6121LGEV4	12	2.55	6.05	2.11	1.9
LCK6120EVG3A11	12	2.55	6.1	2.03	1.83
LCK6106EVGA2	10.5	2.55	5.8	2.03	1.83
JK6126GBEVQ4	11.99	2.55	6	2.02	1.83
TEG6129BEV11	11.95	2.54	5.9	2.1	1.86
TEG6105BEV11	10.5	2.5	5.8	2.06	1.86
CKZ6106NA3	10.2	2.5	4.7	2.02	1.8

.

2. Articulated Vehicles

Articulated vehicles operate mainly at intersections on urban fringes, which makes research investigations relatively difficult. Therefore, 5 male long-distance freight articulated vehicle drivers, each from Jinyuan District and Qingxu County of Taiyuan, were selected as subjects. Their personal codes are A–E, they are aged between 35 and 45, and all have more than 8 years of driving experience. Before starting the experiment, all the subjects were informed of the specific operation procedures of the experiment, After the test drive, each driver completed one right-turn maneuver.

Data collection was conducted through a case study in a simulated intersection established in a large parking lot in Jinyuan District, Taiyuan. The intersection was designed as a right-angled cross intersection without a dedicated right-turn lane. The collected articulated vehicles travel from south to north and turn right from the proposed south entrance of the intersection to the east exit. The vehicle parameters are shown in

Table 2. Draft intersection geometry parameters and vehicle parameters.

Parameter Name	Jinyuan District, Taiyuan	Qingxu County, Taiyuan
vehicle brand and model	FAW Jiefang Han V500 Tractor Unit	FAW Jiefang J6P Series Tractor Unit
Tractor Length/m	6.675	6.945
Tractor Wheelbase/m	3.15 + 1.35	3.30 + 1.35
Trailer Wheelbase/m	5.38 + 1.31 + 1.31	5.60 + 1.31 + 1.31
Tractor Front Track/mm	2020	2020
Trailer Rear Track/mm	1847	1830

.

3.3.3. Selecting Test Intersections

Priority was given to intersections without dedicated right-turn lanes, where motor vehicles and nonmotor vehicles share the same road, which leads to a high incidence of inner wheel difference accidents. In this test urban intersections without dedicated right-turn lanes were investigated. For the selection of test intersections, factors such as the volume of passing large vehicles and geometric characteristics of intersections should be considered. Intersections in mixed traffic areas such as old urban districts and suburban fringe areas were chosen to ensure the representativeness of the selected intersections and their right-turn lanes.

When UAV video collection is used to obtain trajectory data of large rigid-body vehicles turning right at urban intersections, special attention should be given to potential obstructions in the shooting area, such as street trees and traffic signal signs. For safety reasons, a simulated intersection was built on a dedicated site for articulated vehicle data collection. The surrounding area was open to facilitate the construction of the simulated intersection.

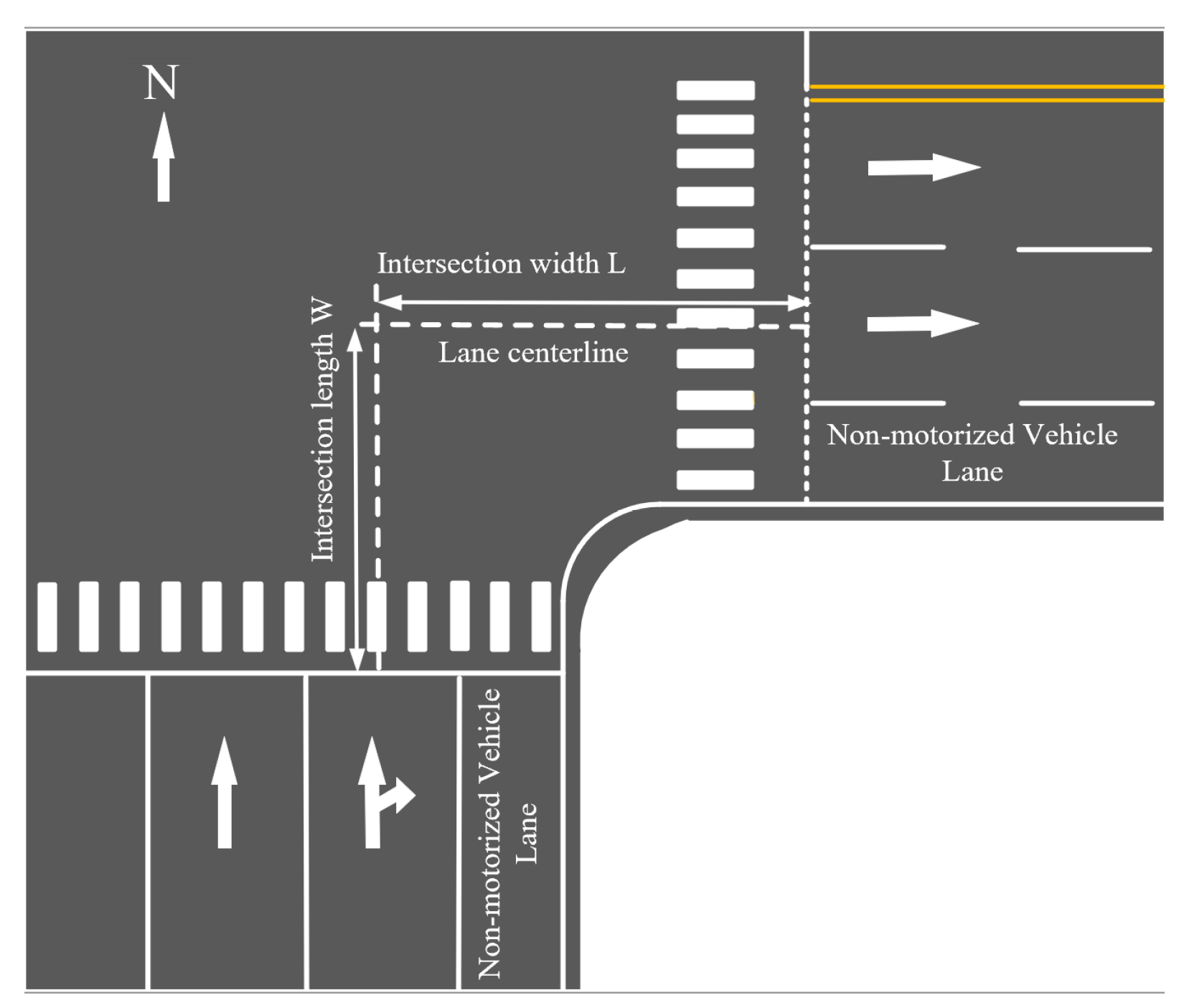
The vertical distance from the stop line of the south entrance lane to the extension line of the centerline of the rightmost lane of the east exit of the intersection is taken as the width W/m of the right-turn area of the intersection entrance, while the vertical distance from the extension line of the centerline of the rightmost lane of the south entrance to the stop line of the east exit is taken as the length L/m of the right-turn area of the intersection entrance, as shown in Figure 3. The aspect ratio M of the right-turn area of the intersection entrance is as follows:

$$M={\displaystyle \frac{W}{L}}$$

(1)

3.4. Date Processing

For rigid vehicles, on the basis of the control variable method, the intersection aspect ratio and vehicle wheelbase are taken as the corresponding control variables, and the survey data are analyzed in the following two ways: one is to fix the intersection and investigate the numbers of steering wheel rotations made by different vehicle drivers when passing through the intersection; the other is to fix the vehicle and investigate the number of steering wheel rotations made by drivers when passing through different intersections.

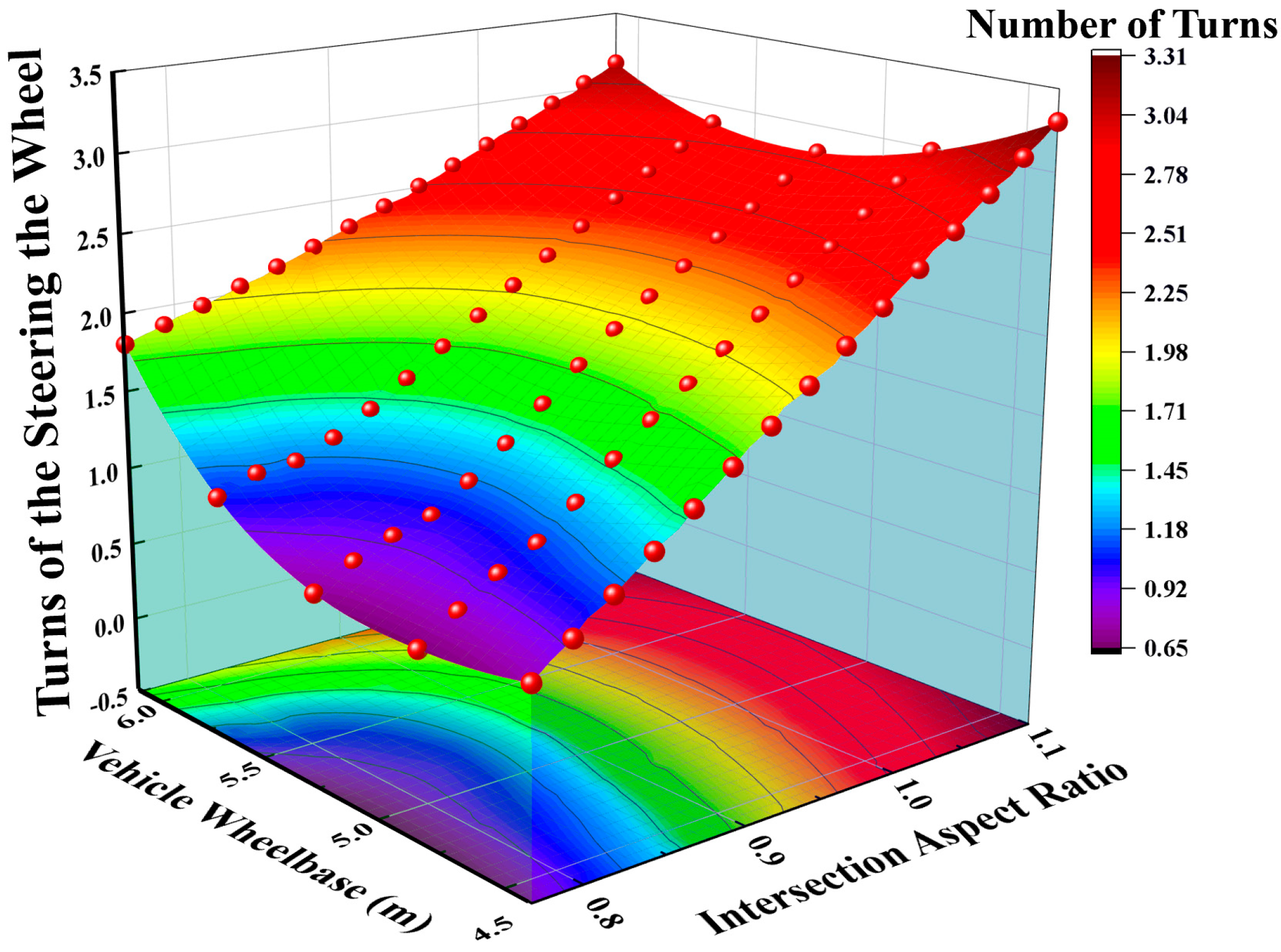
With the vehicle wheelbase and intersection aspect ratio as the x-axis and y-axis of the three-dimensional image, respectively, and the number of steering wheel rotations as the z-axis, three-dimensional smooth fitting is performed on the survey data, as shown in Figure 4. The results show that when a rigid vehicle turns right at an intersection, the number of steering wheel rotations is related to the intersection aspect ratio and the vehicle wheelbase. An analysis of the x-axis data reveals that with the same intersection aspect ratio, the number of steering wheel rotations increases linearly with increasing vehicle wheelbase; an analysis of the y-axis data reveals that with the same vehicle wheelbase, the number of steering wheel rotations increases linearly with increasing intersection aspect ratio. In conclusion, the relationships among the three factors can be approximately expressed by linear fitting.

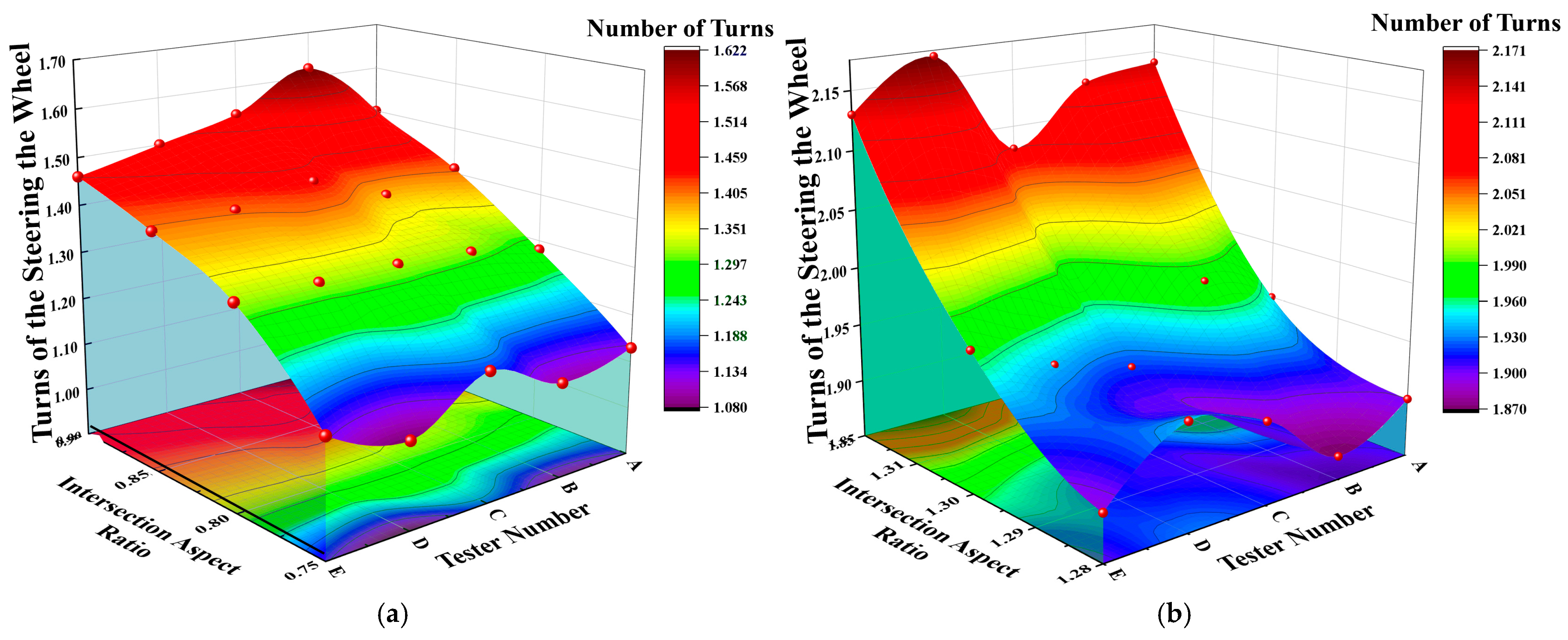
For articulated vehicles, on the basis of the utilized control variable method, the driver, intersection aspect ratio, and vehicle wheelbase are taken as the corresponding control variables, and the survey data are analyzed as follows. Firstly, fix the intersection and investigate the numbers of steering wheel rotations made by different drivers when passing through an intersection with the same vehicle. Secondly, fix the vehicle and investigate the numbers of steering wheel rotations made by the same driver when passing through different intersections. Finally, record the numbers of steering wheel rotations made when drivers from the two regions drive different vehicles. With the intersection aspect ratio and subject code as the x-axis and y-axis of the three-dimensional image, respectively, and the number of steering wheel rotations as the z-axis, three-dimensional smooth fitting is performed on the survey data, as shown in Figure 5.

The data analysis results reveal that when an articulated vehicle turns right at an intersection, the number of steering wheel rotations is related to the intersection aspect ratio and the vehicle wheelbase. For a single graph, an analysis of the x-axis data shows that with the same driver, the number of steering wheel rotations increases linearly with increasing intersection aspect ratio; an analysis of the y-axis data shows that with the same intersection aspect ratio, the number of steering wheel rotations is essentially the same when the driver changes. A comparison of the data derived from the two graphs reveals that for the same driver, the numbers of steering wheel rotations made when driving different vehicles differ. In conclusion, the number of steering wheel rotations made when an articulated vehicle turns right is affected by the intersection aspect ratio, the tractor wheelbase, and the trailer wheelbase, and these factors exhibit a linear relationship.

4. Model Development

On the basis of the relationships between vehicle parameters, the intersection aspect ratio, and the number of steering wheel rotations obtained in the previous data collection phase, this section focuses on the construction of a multilevel model framework to transform from the “basis parameters” to the “inner wheel difference area range”.

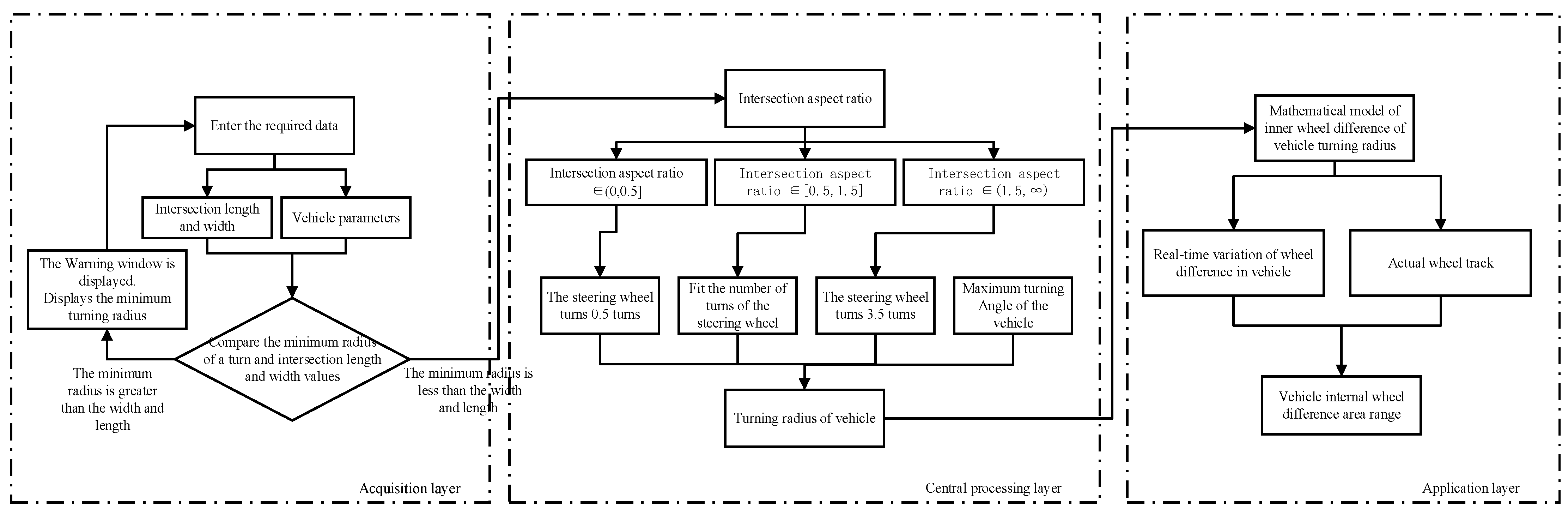
The model consists of three layers: the collection layer, the central processing layer, and the application layer. These layers undertake the functions of data input verification, turning radius fitting, and inner wheel difference calculation, respectively. This layered design not only ensures the clarity of the model logic but also provides a structured solution for subsequent algorithm implementation and practical application.

4.1. Model Framework

On the basis of field investigations, the number of steering wheel rotations made when large vehicles turn right at intersections is directly affected by the intersection aspect ratio and vehicle wheelbase. Furthermore, the front wheel angle of the tractor of such a vehicle can be derived from the intersection aspect ratio and the parameters of the vehicle itself. The mathematical model constructed on this basis starts with quantitative traffic parameters, fits the turning radius and inner wheel difference zone of the vehicle during right turns, and reflects the driver’s understanding of the interaction rules. The model includes the following three layers: an acquisition layer, a central processing layer, and an application layer. The overall framework is shown in Figure 6.

The overall steps are as follows: The acquisition layer first obtains various onsite parameters through road traffic personnel and judges whether the method can be used for fitting. Afterward, the central processing layer provides corresponding control parameters to fit the vehicle turning radius for different actual situations and outputs them to the application layer. Finally, the application layer calculates the actual inner wheel difference area range in combination with the centerline of the actual intersection lane.

4.1.1. Acquisition Layer

The acquisition layer obtains two types of data: the geometric parameters of the intersection (the intersection aspect ratio M) and the intrinsic parameters of large vehicles. The intrinsic parameters collected for rigid vehicles include the front and rear tracks, wheelbase, and maximum front wheel turning angle of each vehicle; the intrinsic parameters of articulated vehicles include the front track of the tractor, rear track of the trailer, wheelbase of the tractor, wheelbase of the trailer, maximum front wheel turning angle of the tractor, and distance of the fifth wheel.

By obtaining the above parameters, the minimum turning radius of large vehicles can be calculated according to the cosine formula. The formula for calculating the minimum turning radius of a rigid vehicle is shown in Equation (2).

$$D_0=\sqrt{{({\displaystyle \frac{d_0}{2}})}^2+({\displaystyle \frac{L_0}{\sin {\beta }_0}}{)}^2-{\displaystyle \frac{d_0{L}_0}{\sin {\beta }_0}}\cos (180°-{\beta }_0)}$$

(2)

where D₀ is the minimum turning radius of the rigid vehicle (m); L₀ is the vehicle wheelbase (m); β₀ is the maximum turning angle of the front wheels of the vehicle (°); and d₀ is the front track of the vehicle (m). The calculation of the minimum turning radius of the articulated vehicle is shown in Equation (3).

$$D_1=\sqrt{{\left(L_1\cot {\beta }_1\right)}^2+k^2-{L_2}^2}-{\displaystyle \frac{{d_3}^2}{2}}$$

(3)

where D₁ is the minimum turning radius of the articulated vehicle (m), L₁ is the tractor wheelbase (m), L₂ is the trailer wheelbase (m), β₁ is the maximum turning angle of the front wheels of the tractor (°), d₃ is the rear track of the trailer (m), and k is the distance between the kingpin centers of the two steering wheels of the tractor (m).

If the obtained length and width of the intersection are smaller than the minimum turning radius of the vehicle, the acquisition layer determines that this method cannot be used to predict the range of the inner wheel difference area and reports an error to alert the user. Otherwise, the data are transferred to the central processing layer.

4.1.2. Central Processing Layer

The central processing layer uses the intersection aspect ratio as an evaluation index and formulates three criteria for evaluating the planned trajectory of the vehicle: (1) intersection aspect ratio M ∈ (0, 0.5]; (2) intersection aspect ratio M ∈ [0.5, 1.5]; and (3) intersection aspect ratio M ∈ [1.5, ∞). For the first and third criteria, a fixed number of steering wheel rotations is directly set for the vehicle. For the second criterion, the number of steering wheel rotations is fitted according to the intersection aspect ratio and the vehicle wheelbase. Afterward, the vehicle turning radius is fitted on the basis of the obtained number of steering wheel rotations.

For case 1, where the intersection aspect ratio M ∈ [0.5, 1.5]:

According to the survey data, intersections with aspect ratios M ∈ [0.5, 1.5] account for a relatively large proportion. For such intersections, the number of steering wheel rotations made by the vehicle can be linearly fitted based on the intersection aspect ratio and the vehicle wheelbase.

For rigid vehicles, binary linear fitting is performed using the intersection aspect ratio and the vehicle wheelbase. Taking O₀ as the number of rotations of the steering wheel of the rigid vehicle for fitting to obtain the experimental data, the resulting binary linear fitting equation is as shown in Equation (4):

$$O_0=4.007M+0.467L_0-4.13$$

(4)

For articulated vehicles, ternary linear fitting is performed using the intersection aspect ratio, tractor wheelbase, and trailer wheelbase. Taking O₁ as the number of steering wheel rotations made by the articulated vehicle for fitting to obtain the experimental data, the resulting ternary linear fitting equation is as shown in Equation (5):

$$O_1=2.65M-2.57L_1-1.60L_2+23.67$$

(5)

A total correlation coefficient test is conducted on the linear fitting equations of the above two types of large vehicles. The test coefficients for rigid vehicles and articulated vehicles are 0.969 and 0.976, respectively, which meet the requirements of this paper and allow for further program processing.

For case 2, where the intersection aspect ratio M ∈ [0, 0.5]:

When large vehicle drivers turn right at such intersections, the number of steering wheel rotations is relatively small, and the range of the inner wheel difference area during right turns is small. Based on the data obtained from the survey, the number of steering wheel rotations is set to 0.5 turns.

For case 3, where the intersection aspect ratio M ∈ [1.5, ∞):

When the drivers of large vehicles turn right at such intersections, the number of steering wheel rotations reaches the maximum value, and the range of the inner wheel difference area during right turns also reaches a peak. Based on the data obtained from the survey, the number of steering wheel rotations is set to 3.5 turns for rigid vehicles and 3.0 turns for articulated vehicles.

After the number of steering wheel rotations is determined, to obtain the rotation status of the vehicle and further fit its turning radius, it is necessary to conduct further research on the corresponding process of steering wheel rotation when large vehicles turn right.

Through a video analysis, the process of steering wheel rotation performed when rigid vehicles turn right at intersections can be summarized into the following three parts. ① At the start of the right turn of a vehicle, continuous steering wheel rotation is performed until the maximum number of rotations required to pass through the intersection is reached. ② This number of rotations is maintained (unchanged). ③ When the right turn of the vehicle is nearly complete, the steering wheel is continuously returned to its original position, at which point the vehicle completes the entire right turn process. In a traffic environment without the influence of other road users, the time ratio of the three parts can be approximated as 2:2:1. Furthermore, the step sizes of the number of turning rotations for the three parts can be set to 0.01, 0.01, and 0.02, and the sum of the step sizes of the three parts can be calculated. On the basis of the obtained maximum turning angle of the front wheels of the vehicle, combined with the number of steering wheel rotations, the real-time front inner wheel angle and vehicle turning radius are obtained, as shown in Equations (6) and (7), respectively.

$${\theta }_0={\beta }_0{\displaystyle \frac{O_0}{3.5}}$$

(6)

$$R_0={\displaystyle \frac{L_0}{\sin {\theta }_0}}$$

(7)

where θ₀ is the front inner wheel angle of the vehicle (°), and R₀ is the turning radius of the rigid vehicle (m).

Through a video analysis, the process of steering wheel rotation performed when articulated vehicles turn right at intersections can be summarized into the following two parts. ① At the start of the right turn of the vehicle, continuous steering wheel rotation is performed until the maximum number of rotations required to pass through the intersection is reached. ② When the right turn of the vehicle is nearly complete, the steering wheel is continuously returned to its original position, at which point the vehicle completes the entire right turn process. In a traffic environment without the influence of other road users, the time ratio of the two parts can be approximated as 2:1. Furthermore, the step sizes of the number of turning rotations for the two parts can be set to 0.01 and 0.02, and the sum of these step sizes is calculated. On the basis of the obtained maximum turning angle of the front wheels of the tractor, combined with the number of steering wheel rotations, the real-time front inner wheel angle of the tractor and the vehicle turning radius are subsequently obtained, as shown in Equations (8) and (9), respectively.

$${\theta }_1={\beta }_1{\displaystyle \frac{O_1}{3.0}}$$

(8)

$$R_1={\displaystyle \frac{L_1}{\sin {\theta }_1}}$$

(9)

where θ₁ is the front inner wheel angle of the tractor (°), and R₁ is the turning radius of the articulated vehicle (m).

4.1.3. Application Layer

The application layer stores calculation modules that are related to the inner wheel difference during the right turns of large vehicles with respect to the lane centerline. After the turning radius of a vehicle is obtained, these calculation modules calculate the movement radii of the front and rear inner wheels of the vehicle, thereby obtaining the range of the inner wheel difference area.

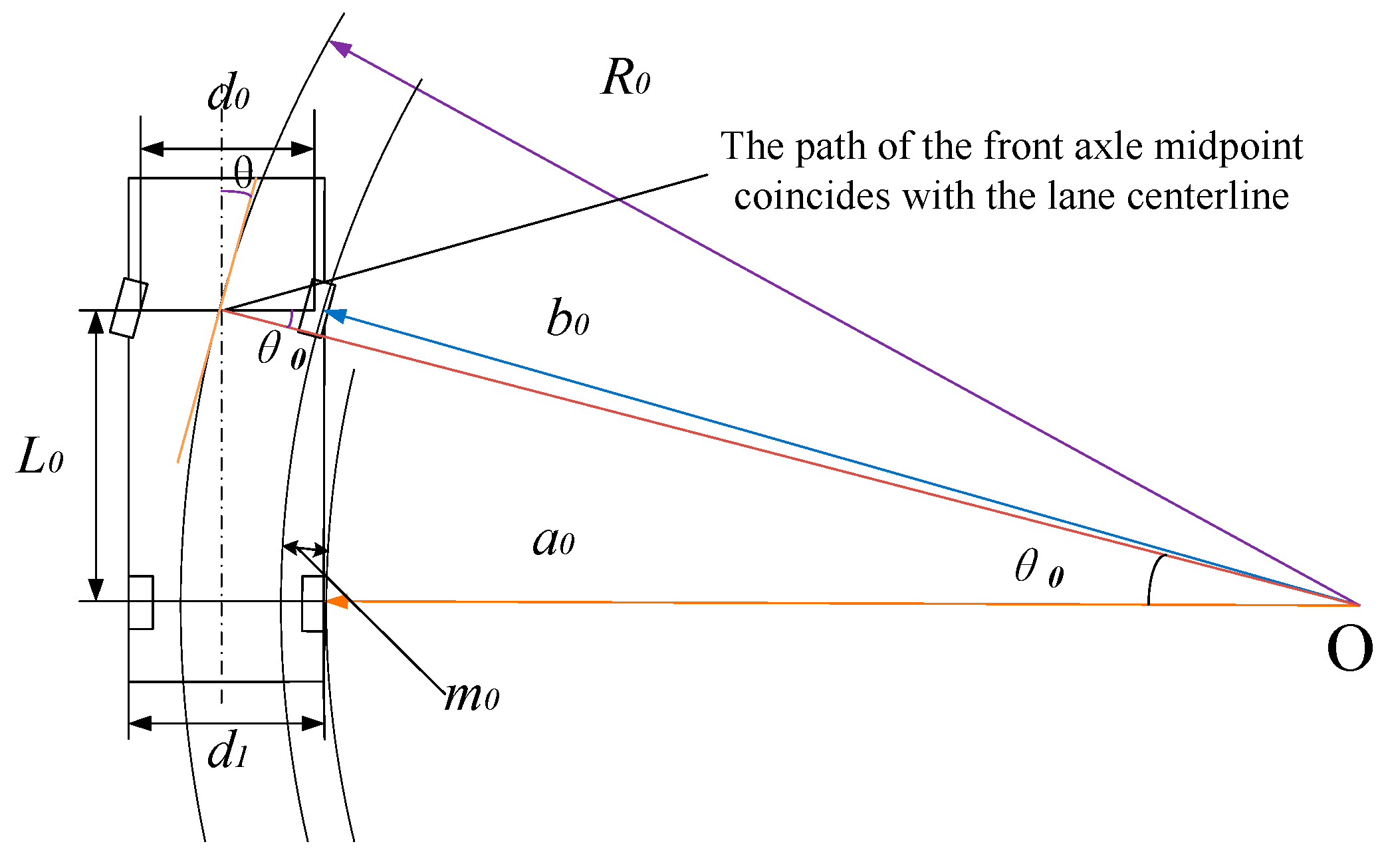
For rigid vehicles, an inner wheel difference fitting model diagram with a straight line, where the rear wheels of the vehicle are located as the turning center, is constructed, as shown in Figure 7.

In the figure, d₁ is the rear track of the rigid vehicle (m), and m₀ is the inner wheel difference of the rigid vehicle (m).

Since the motion trajectory of the midpoint of the front axle of a rigid vehicle mostly coincides with the lane centerline and the vehicle wheelbase is fixed, the motion radius of the front inner wheel of the vehicle, as well as the motion radius of the rear inner wheel of the vehicle, can be calculated according to the trigonometric function formula. The inner wheel difference of the rigid vehicle can be obtained by subtracting these two components.

$$a_0=R_0\cos {\theta }_0-{\displaystyle \frac{d_1}{2}}$$

(10)

$$b_0=\sqrt{{R_0}^2+{({\displaystyle \frac{d_0}{2}})}^2-d_0{R}_0\cos {\theta }_0}$$

(11)

$$m_0=b_0-a_0$$

(12)

where b₀ is the motion radius of the front inner wheel of the rigid vehicle (m), and a₀ is the motion radius of the rear inner wheel of the rigid vehicle (m).

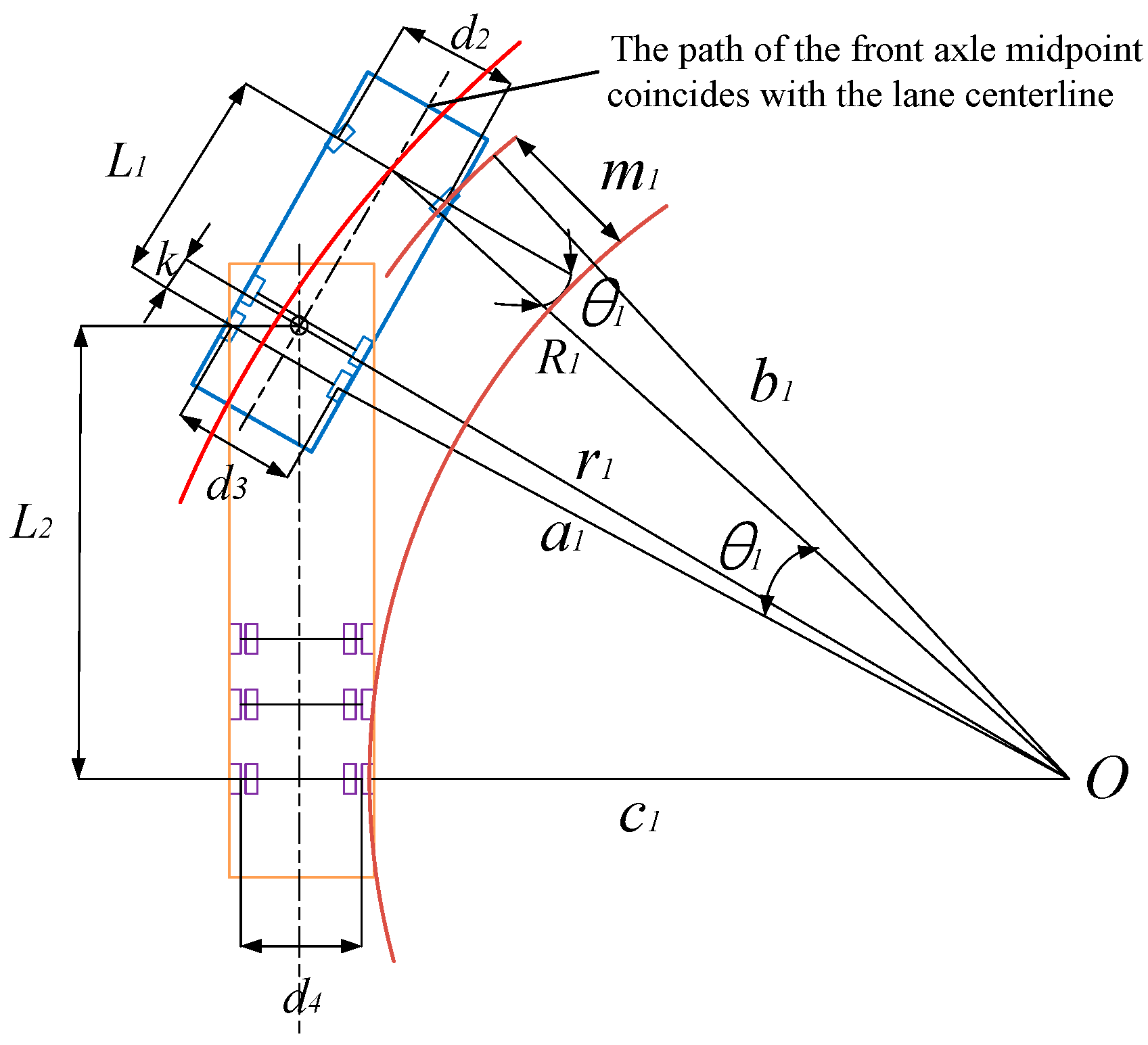
For articulated vehicles, an inner wheel difference fitting model diagram with a straight line, where the rear wheels of the trailer are located as the turning center, is constructed, as shown in Figure 8.

In the figure, d₂ is the front track of the tractor (m), and m₁ is the inner wheel difference of the articulated vehicle (m).

Since the motion trajectory of the midpoint of the front axle of the articulated vehicle mostly coincides with the lane centerline and the wheelbases of the tractor and trailer are fixed, the motion radius of the front inner wheel of the tractor, as well as the motion radius of the rear wheel of the trailer, can be calculated according to the trigonometric function formula. The inner wheel difference of the articulated vehicle can be obtained by subtracting these two components.

$$b_1=\sqrt{{R_1}^2+{\left({\displaystyle \frac{d_2}{2}}\right)}^2-d_2{R}_1\cos {\theta }_1}$$

(13)

$$c_1=\sqrt{(R_1\cos {\theta }_1{)}^2+k^2-{L_2}^2}-{\displaystyle \frac{d_4}{2}}$$

(14)

$$m_1=b_1-c_1$$

(15)

where b₁ is the motion radius of the front inner wheel of the tractor (m), and c₁ is the motion radius of the rear wheel of the trailer (m).

For a rigid vehicle, the trajectory trend of the front inner wheel of the vehicle is an ellipse, where A₀ = X − d₁ and B₀ = Y − d₁. In the planar coordinate system, the trajectory of the rear inner wheel of the vehicle is calculated through the inner wheel difference corresponding to each point:

$$x_0=-{\displaystyle \frac{A_0{B}_0}{\sqrt{{B_0}^2+({A_0}^2{\tan }^2\mu )}}}+A_0$$

(16)

$$y_0=-{\displaystyle \frac{A_0{B}_0\tan \mu }{\sqrt{{B_0}^2+({A_0}^2{\tan }^2\mu )}}}$$

(17)

$$x_1=x_0$$

(18)

$${\mathrm{y}}_1=y_0-m_0$$

(19)

where μ is the angle value with a starting point of 0.5π and an ending point of π (°); x₀ and y₀ are the coordinate values of the rear inner wheel of the vehicle (m); and x₁ and y₁ are the coordinate values of the front inner wheel of the vehicle (m).

For articulated vehicles, the trajectory trend of the rear wheel of the trailer is an ellipse, where A₁ = X − d₄ and B₁ = Y − d₄. In the planar coordinate system, the trajectory of the front inner wheel of the tractor is calculated through the inner wheel difference corresponding to each point:

$$x_2=-{\displaystyle \frac{A_1{B}_1}{\sqrt{{B_1}^2+({A_1}^2{\tan }^2\mu )}}}+A_1$$

(20)

$$y_2=-{\displaystyle \frac{A_1{B}_1\tan \mu }{\sqrt{{B_1}^2+({A_1}^2{\tan }^2\mu )}}}$$

(21)

$$x_3=x_2$$

(22)

$$y_3=y_2+m_1$$

(23)

where μ is the angle value with a starting point of 0.5π and an ending point of π (°); x₂ and y₂ are the coordinate values of the rear wheel of the trailer (m); and x₃ and y₃ are the coordinate values of the front inner wheel of the tractor (m).

4.2. Model Algorithm

To enable computer language to simulate the range of the inner wheel difference area during the right turns of large vehicles at urban intersections, the above concepts and methods are integrated into an executable algorithm. The right-turn inner wheel difference model for large vehicles is programmed out through the Python platform, which can simulate the complete process of a large vehicle turning right into and exiting an intersection. The specific algorithm is shown in Algorithm 1.

Algorithm 1. Specific algorithm of the system component model

Step 1: (Acquisition Layer)

Step 1.1: (Parameter Acquisition)

Input the length and width values of the actual road intersection (X/m and Y/m, respectively); vehicle parameters (classified into rigid vehicles and articulated vehicles); and data such as the maximum turning angle of the front wheels of the vehicle, the vehicle wheelbase, and the vehicle track.

Step 1.2: (Judgment on whether one-time turning is possible)

Calculate the length–width ratio M of the intersection according to Equation (1); calculate the minimum turning radius of rigid vehicles according to Equation (2); calculate the minimum turning radius of articulated vehicles according to Equation (3). If D ≥ Min(W, Y), pop up a warning window to display the minimum turning radius, and return to Step 1.1; otherwise, proceed to Step 2.

Step 2: (Central Processing Layer)

Step 2.1: (Number of Steering Wheel Rotations)

Step 2.1.1: (Fitting Criterion 1)

If the obtained length–width ratio of the intersection is <0.5, set the number of steering wheel rotations O = 0.5, and then proceed to Step 2.2.

Step 2.1.2: (Fitting Criterion 2)

If the obtained length–width ratio of the intersection is >1.5, set the number of steering wheel rotations for rigid vehicles to O0 = 3.5 and that for articulated vehicles to O1 = 3.0, and then proceed to Step 2.2.

Step 2.1.3: (Fitting Criterion 3)

If the length–width ratio of the intersection is between 0.5 and 1.5, calculate the number of steering wheel rotations for rigid vehicles according to Equation (4) and that for articulated vehicles according to Equation (5), and then proceed to Step 2.2.

Step 2.2: (Vehicle Turning Radius)

For the three stages of rigid vehicles turning right, set lists f0, f1, and f2, respectively. For f0: with 0.01 as the starting point, O0 as the ending point, and 0.01 as the step size, obtain the number of elements q0 in the list; for f1: the number of elements q1 = q0, and the element value is O0; for f2: with O0 as the starting point, 0.02 as the ending point, and 0.02 as the step size, obtain the number of elements q2 in the list. Merge the three lists into a list F0, and the total number of elements in the three lists is Q0 = q0 + q1 + q2.    Traverse each element in list F0, combine the information with the maximum turning angle of the front wheels of the vehicle, correlate the number of steering wheel rotations with the length–width ratio of the intersection and the number of steering wheel rotations made by the driver according to Equation (6) to obtain the real-time front wheel angle of the vehicle, derive the turning radius of the vehicle during the turning process according to Equation (7), and then proceed to Step 3.    For the two stages of articulated vehicles turning right, set lists f3 and f4, respectively. For f3: with 0.01 as the starting point, O1 as the ending point, and 0.01 as the step size, obtain the number of elements q3 in the list; for f4: with O1 as the starting point, 0.02 as the ending point, and 0.02 as the step size, obtain the number of elements q4 in the list. Merge the two lists into list F1, and the total number of elements in the two lists is Q1 = q3 + q4.    Traverse each element in list F1, combine this information with the maximum turning angle of the front wheels of the tractor, correlate the number of steering wheel rotations with the length–width ratio of the intersection and the number of steering wheel rotations made by the driver according to Equation (8) to obtain the real-time front wheel angle of the vehicle, derive the turning radius of the vehicle during the turning process according to Equation (9), and then proceed to Step 3.

Step 3: (Application Layer)

Step 3.1: (Mathematical Model of the Inner Wheel Difference)

Establish mathematical fitting models of the right-turn inner wheel differences for rigid vehicles and articulated vehicles (Figure 6 and Figure 7, respectively). Calculate the actual trajectory and changes exhibited by the inner wheel differences of rigid vehicles through Equations (10)–(12), and calculate the actual trajectory and changes exhibited by the inner wheel differences of articulated vehicles through Equations (13)–(15).

Step 3.2: (Delineation of the Actual Inner Wheel Difference Area)

Within [0.5π, π], set points for rigid vehicles with a step size of 0.5π/Q0. Set the trajectory of the front inner wheel of the vehicle as an ellipse, and calculate the range of the inner wheel difference area for rigid vehicles through Equations (16)–(19) in combination with the inner wheel difference of the vehicles. Set points for articulated vehicles with a step size of 0.5π/Q1. Set the trajectory of the rear wheel of the trailer as an ellipse, and calculate the range of the inner wheel difference area for articulated vehicles through Equations (20)–(23) in combination with the inner wheel difference of the vehicles.

5. Model Validation

To verify the accuracy of the model, the selected intersection and vehicle geometric parameters were input into the model program to obtain the inner wheel difference area range (predicted trajectories of the front and rear inner wheels) of rigid-body vehicles and articulated vehicles during right turns.

Tracker software was subsequently used to extract the trajectory data of the front and rear inner wheels in real time from the recorded videos of the right turns of rigid-body and articulated vehicles. Based on the camera’s video imaging principle, the extracted real-time trajectory data were further mapped to the actual road.

Finally, the predicted trajectory data of the front and rear inner wheels were compared and analyzed with the real trajectory data for both types of vehicles during right turns to verify the model’s accuracy.

5.1. Model Calculation Results

A specific intersection and a vehicle type obtained during the data collection phase are selected and input into the model for fitting. For rigid vehicles, the intersection of Shuixiguan Street and Taoyuan North Road in Yingze District, Taiyuan, is chosen, using the video data collected on Bus Route 809 traveling from south to north and turning right from the south entrance to the east exit of the intersection, with various parameters shown in

Table 3. Road parameters of the intersection and parameters of the bus vehicle.

Intersection Width/m	Intersection Length/m	Maximum Turning Angle/°	Wheelbase/m	Front Track/m	Rear Track/m
17.75	18.35	33	6.10	2.03	1.83

. For articulated vehicles, the video data of a simulated intersection test case established in a large parking lot in Jinyuan District, Taiyuan, are selected, with various parameters as shown in

Table 4. Road parameters of the intersection and parameters of the articulated vehicle.

Intersection Width/m	Intersection Length/m	Maximum Turning Angle/°	Tractor Wheelbase/m	Trailer Wheelbase/m	Fifth Wheel Distance/m	Tractor Front Track/m	Trailer Rear Track/m
14	18	30	4.5	8.08	1.0	2.02	1.847

.

After the geometric feature data of the intersection and various data concerning rigid vehicles and articulated vehicles are input into the model, the turning radii of the rigid vehicles and articulated vehicles are calculated by combining Equations (6)–(9). Then, the inner wheel differences of the rigid vehicles and articulated vehicles when turning right at intersections can be obtained by combining Equations (10)–(15), and the predicted trajectory diagrams of the inner wheel differences of the rigid vehicles and articulated vehicles can be obtained by combining Equations (16)–(23), as shown in Figure 9.

5.2. Actual Measurement Results

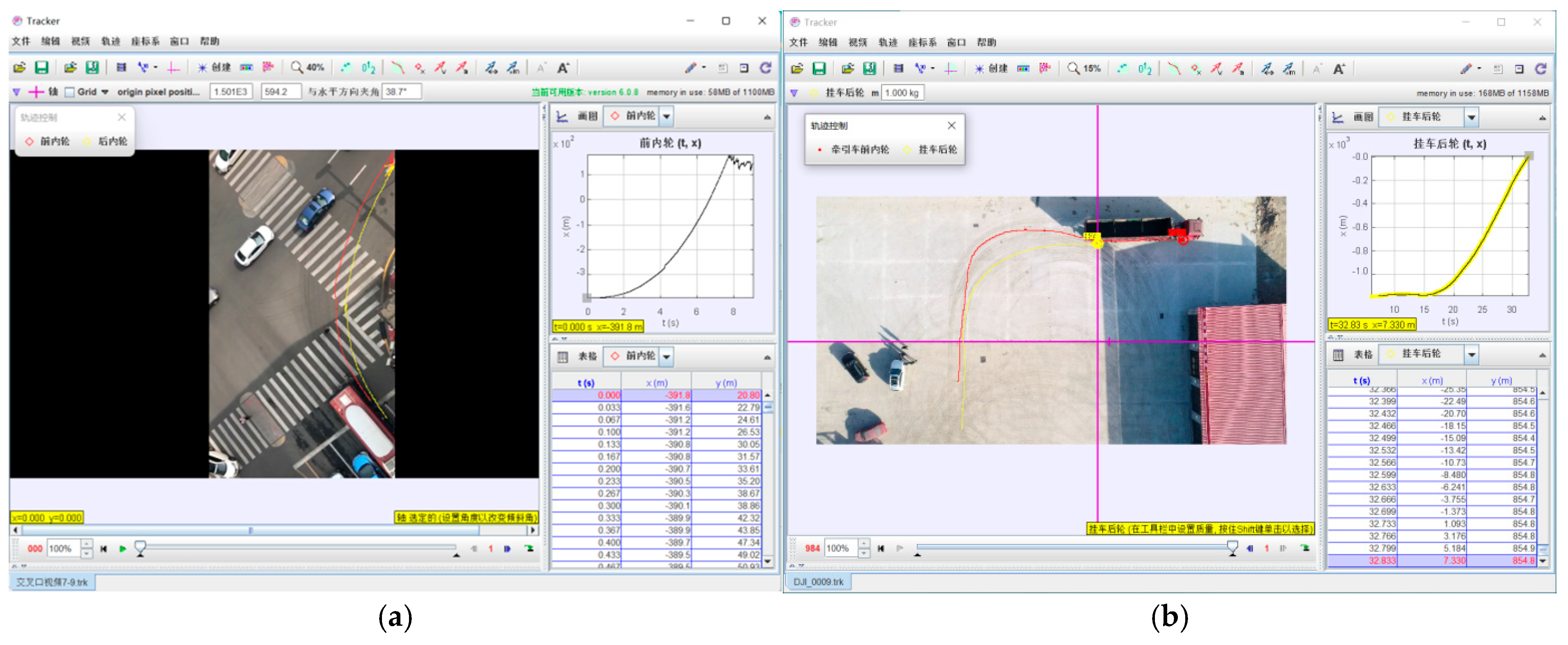
The inner wheel difference trajectory data of vehicle driving are extracted via Tracker software, and the model-calculated inner wheel difference zone is compared with the actual inner wheel difference zone to verify the accuracy of the model.

First, with the help of Tracker, a physical experiment trajectory capture and analysis software, the collected video clips are analyzed. The right-turn movement trajectories of selected rigid vehicles and articulated vehicles at intersections are tracked, and three columns of data (“time-X coordinate-Y coordinate”) are exported to record the position information of each frame of the vehicle. After smoothing, the coordinate values of the front and rear inner wheels at the same time points in the program and the Tracker analysis curve are extracted, as shown in Figure 10.

Second, according to the camera imaging principle, a conversion matrix is established to convert the coordinate system in the video into the coordinate system in the real world, and then the coordinate values of the front and rear inner wheels of the two systems are compared. In the experiment, the camera shooting angle is approximately vertical, and a simplified fixed matrix transformation relationship exists as follows:

$$X_r={\displaystyle \frac{C_1+C_2{X}_S+C_3{Y}_S}{1+C_7{X}_S+C_8{Y}_S}}$$

(24)

$$Y_r={\displaystyle \frac{C_4+C_5{X}_S+C_6{Y}_S}{1+C_7{X}_S+C_8{Y}_S}}$$

(25)

where X_s and Y_s are the image coordinates of the target object; X_r and Y_r are the actual spatial coordinates of the measured object; and C₁, C₂, C₃, C₄, C₅, C₆, C₇, and C₈ are constant coefficients.

To calibrate the 8 constant coefficients, 8 special points that can be easily used to measure actual coordinates need to be selected as feature points (i.e., points A, B, C, D, E, F, G, and H in Figure 11a; and points A, B, C, D, E, F, O, and G in Figure 11b). These points are divided into two groups with four points each, and the feature points in each group should not be collinear.

D and E in Figure 11b were selected to measure their actual 3D spatial coordinates and the 2D planar coordinates in the Tracker video. These coordinate data were substituted into Equations (24) and (25) to calculate the 8 constant coefficients.

The other group of feature coordinate points (i.e., points E, F, G, and H in Figure 10a and points B, F, O and G in Figure 11b) was used for verification. Their 2D planar coordinates in the Tracker video were measured, and their actual 3D spatial coordinates were calculated using Equations (24) and (25) on the basis of the video’s 2D planar coordinates.

The actual 3D spatial coordinates of points E, F, G, H in Figure 10a and points B, F, O, G in Figure 11b were measured and compared with the calculated coordinates to determine the reliability of the obtained constant coefficients.

Relative error was used as the indicator for the reliability of trajectory coordinate conversion. The calculation results for rigid-body vehicles and articulated vehicles are shown in

Table 5. Statistical Results of Coordinate Conversion Errors for Fitted Calibration Points at Intersections of Rigid-Body Vehicles.

Feature Point	Xs	Ys	Xr	Xm	Error	Yr	Ym	Error
A	994	118	0	0	/	0	0	/
B	1401	138	9.5	9.5	/	0	0	/
C	834	651	9.5	9.5	/	42.4	42.4	/
D	509	669	0	0	/	44.4	44.4	/
E	1552	137	−6.67	−6.7	0.45%	0.06	0	0.06
F	711	102	3.24	3.2	1.25%	0.09	0	0.09
G	1079	122	3.27	3.2	2.2%	42.35	42.4	0.12%
H	1228	129	−3.15	−3.2	1.56%	44.34	44.4	0.14%

and

Table 6. Statistical Results of Coordinate Conversion Errors for Fitted Calibration Points at Intersections of Articulated Vehicles.

Feature Point	Xs	Ys	Xr	Xm	Error	Yr	Ym	Error
A	−813.6	−0.324	−13.475	−13.475	/	0	0	/
B	−573	2.676	−9.549	−9.6	0.53%	0.042	0	0.042
C	0.12	128.1	0	0	/	2	2	/
D	−333.3	0.176	−5.6	−5.6	/	0	0	/
E	−6.755	368.6	0	0	/	6	6	/
O	0.13	0.01	−0.055	0	0.055	−0.008	0	0.008
F	−208	−0.218	−3.524	−3.6	2.12%	−0.008	0	0.008
G	−3.37	248	0.001	0	0.001	3.955	4	1.12%

Note: X_s and Y_s represent the coordinates of the selected feature points in the video; X_r and Y_r represent the real coordinates of the selected feature points calculated according to the aforementioned matrix transformation formula; and X_m and Y_m represent the actual measured coordinates of the selected feature points. For verification points whose relative error cannot be calculated on the coordinate axis, the absolute error is calculated, in meters.

, respectively. As shown in the tables, the relative error of the results is less than 5%, and the absolute error is less than 0.1 m, which meets the required accuracy.

5.3. Result Comparison and Verification

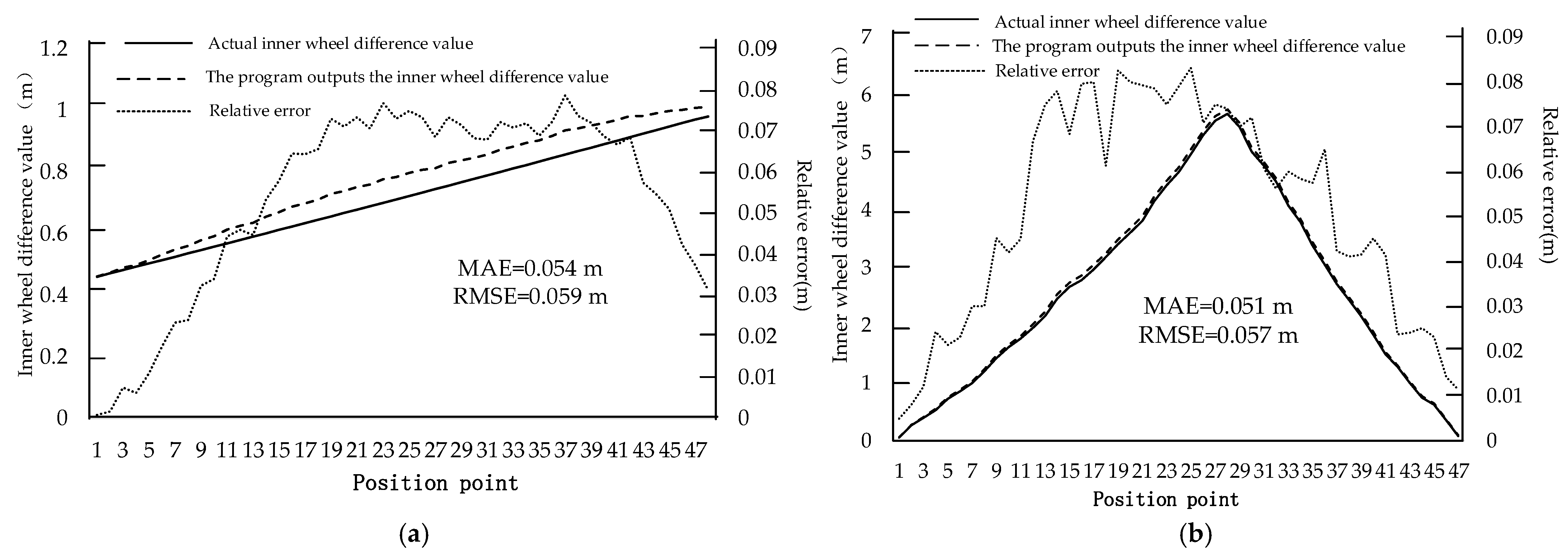
The field-measured data were input into the program. For rigid-body vehicles, the data calculated by the program were compared with the smoothed data exported from Tracker through the above steps. The comparison parameters were the coordinate values of the front and rear inner wheels of the vehicle. The calculation of the relative error between the two sets of data revealed that the maximum value was 8.12% and the average value was 5.39%, as shown in Figure 12a.

For articulated vehicles, the data calculated by the program were compared with the smoothed data exported from Tracker through the above steps. The comparison parameters were the coordinate values of the front inner wheel of the tractor and the rear wheel of the trailer. The calculation of the relative error between the two sets of data revealed that the maximum value was 8.32% and the average value was 5.12%, as shown in Figure 12b.

The real vehicle verification results indicate that the model-calculated inner wheel difference area range is in good agreement with the actual inner wheel difference area range. Therefore, the established program model can be used to calculate the inner wheel difference area range of large vehicles turning right at urban intersections.

6. Discussion

The construction, calculation, and accuracy verification of the inner wheel difference model have been completed in the previous chapters. On this basis, this section further explores the in-depth influence mechanism of the inner wheel difference area and the practical application value of the model. It focuses on analyzing the synergistic effect of intersection geometric characteristics and vehicle geometric characteristics on the inner wheel difference, as well as targeted accident prevention and control measures based on the research results. This discussion not only explains the rationality of the model design logic but also expands the application scenarios of the research, combining theoretical results with the actual needs of traffic safety management.

6.1. The Combined Effect of Intersection Geometry and Vehicle Geometry

The size of the turning radius of a vehicle is restricted by the geometric dimensions of the encountered intersection. Compared with a small turning radius, a large turning radius reduces the maximum width of the inner wheel difference zone but increases the length of the inner wheel difference zone range. Therefore, it is necessary to comprehensively consider the geometric design of the intersection and actual operation conditions. When the vehicle is turning, the turning radius is variable. To determine the situation in which a driver turns the steering wheel during vehicle turning, we record videos of the driver turning the steering wheel inside the vehicle and obtain the rotation angle of the steering wheel through video processing. We find that the rotation angle of the steering wheel significantly differs when the same driver turns at intersections with different geometric dimensions.

We take the vertical distance from the stop line of the entrance lane of the intersection to the extension line of the centerline of the rightmost lane of the right-turn exit lane as the width of the right-turn area of the entrance lane of the intersection, denoted as M/m, and the vertical distance from the extension line of the centerline of the rightmost lane of the entrance lane to the stop line of the right-turn exit lane as the length of the right-turn area of the entrance lane of the intersection, denoted as L/m. Let the aspect ratio of the right-turn area of the entrance lane of the intersection be M = M/L; then, the rotation angle of the steering wheel when the vehicle is turning has a linear relationship with M. After multiple verifications, it is found that when different drivers drive vehicles with different geometric sizes to turn at intersections with different aspect ratios M, the rotation angle of the steering wheel always has a linear relationship with M. This finding simplifies the complexity of the model caused by the need to consider the influences of multiple factors on the steering wheel rotation angle when calculating the inner wheel difference zones of large vehicles.

In addition to the rotation angle of the steering wheel, the angular velocity of its rotation also impacts the inner wheel difference area. Our research reveals that the angular velocity of the rotation of the steering wheel is affected by the speed of the vehicle when turning. During the process of establishing the model, we do not consider the vehicle speed factor. This is because the turning speed of the vehicle is also affected by the aspect ratio of the intersection M. The larger M is, the greater the turning angle of the vehicle when turning, and the lower the safe speed. Although drivers have different driving speeds, an excessively low safe speed limits the variability of driving speeds; the smaller M is, the smaller the turning angle of the vehicle when turning, and the higher the safe speed. However, the inner wheel difference is also smaller at this time, and the probability of traffic accidents caused by the inner wheel difference area is also lower.

By establishing the relationship between the geometric dimensions of intersections and vehicles, and the steering wheel rotation angle and angular velocity during vehicle right turns, we avoided the difficulty of real-time collection of steering wheel rotation angle and angular velocity. Compared with similar models developed by other researchers [45], the complexity of the proposed model is greatly reduced.

Compared with simulation technology [31] and video detection technology [32], the model developed in this study improves the adaptability in solving inner wheel difference accidents of large vehicles during right turns and reduces the cost.

6.2. Right-Turn Inner Wheel Difference-Based Accident Prevention and Control

Large vehicle right-turn inner wheel difference-based accidents are among the main types of urban traffic accidents and have attracted increasing attention from scholars, traffic managers, and relevant practitioners. Their prevention and control measures can start from the three elements of a traffic system: people, vehicles, and roads.

With respect to people, it is necessary to make road users aware of the inner wheel difference zone and the serious accident risks it poses through publicity and training. For large vehicle drivers, the formation of the inner wheel difference zone and similar accidents should be included in the mandatory test items of the driver’s license examination. For nonmotorized vehicle riders, corresponding publicity and safety education should be carried out to increase their awareness of these dangerous scenarios.

With respect to vehicles, the number of rear-view mirrors should be increased according to the blind spots caused by the inner wheel difference zone to eliminate these visual blind spots. In addition, the blind spot warning system should be improved, and the accuracy of the warning system should be enhanced through the use of various sensors, such as radar, infrared, and ultrasonic sensors. For example, in China, to reduce the number of right-turn collision accidents caused by blind spots, the government has formulated relevant specifications (such as a series of standards issued by the State Administration for Market Regulation in 2020), requiring vehicles to be equipped with right-turn behavior detection and warning devices. Warning devices should alert not only drivers but also surrounding road users.

With respect to roads, additional road facilities can be added to improve the traffic environment. For example, warning signs should be established on the roadside, as shown in Figure 13. “Stop” signs can also be added. In addition, the inner wheel difference zones of large vehicles can be marked with colors on the road surface at intersections to warn road users located in the potential area. Roads with suitable conditions can set up dedicated right-turn lanes or dedicated right-turn traffic lights to separate large vehicles and vulnerable groups in space or time.

7. Conclusions

(1) The observation method is used to analyze video-collected data, and the relationships between vehicle parameters, the aspect ratios of intersections, and the numbers of steering wheel rotations made by vehicles are derived. The results show that there is a linear relationship among the three factors; thus, a linear fitting equation with the vehicle wheelbase and intersection aspect ratio as independent variables is constructed to fit the number of right-turn steering wheel rotations made by the drivers of large vehicles, and a model is established to calculate the right-turn inner wheel difference areas of the vehicles.

(2) Large vehicles (large rigid vehicles and large articulated vehicles) with different vehicle type parameters from multiple locations, such as Nanjing and Taiyuan, are selected as research objects to study the changes exhibited by their right-turn inner wheel differences at different types of intersections. The results show that the driving behaviors displayed by drivers when large vehicles turn right can be fitted by the inner wheel difference based on the geometric characteristics of intersections and the vehicle wheelbase. For rigid vehicles, combined with the maximum bus turning angle, the driving trajectories of the front and rear inner wheels and the range of the inner wheel difference area during the right turns of the bus can be obtained. For articulated vehicles, combined with the maximum turning angle of the front wheels of the tractor, the driving trajectories of the front inner wheels of the tractor and the rear wheels of the trailer, as well as the range of the inner wheel difference area, can be obtained. The results provide a theoretical basis for determining the range of the inner wheel difference zone at actual intersections.

(3) Tracker trajectory capture and analysis software is used to analyze and verify the inner wheel differences between actual vehicles during right turns. The results show that for rigid vehicles that conform to the basic principles of the model when turning right, the maximum relative error between the model and the actual right-turn inner wheel difference is 8.12%, with an average relative error of 5.39%; for articulated vehicles that conform to the basic principles of the model when turning right, the maximum relative error between the model and the actual right-turn inner wheel difference is 8.32%, with an average relative error of 5.12%.

(4) Based on the research results, targeted prevention and control measures can be proposed. In terms of road infrastructure, areas with large vehicle right-turn inner wheel differences can be marked, and warning signs can be established. At intersections with suitable conditions, dedicated right-turn lanes can be installed, or traffic signs requiring large vehicles to stop when turning right can be added. In terms of vehicle design, early warning devices can be designed and installed to mitigate the blind spots of large vehicles. Most importantly, the education and management of road users should be promoted. For instance, content related to the inner wheel differences should be incorporated into the testing process for obtaining driving permits, and the traffic safety awareness of road users should be enhanced through a combination of educational activities and online accident reports.