Optimizing Vehicle Emission Estimation of On-Road Vehicles Using Deep Learning Frameworks
Abstract
1. Introduction
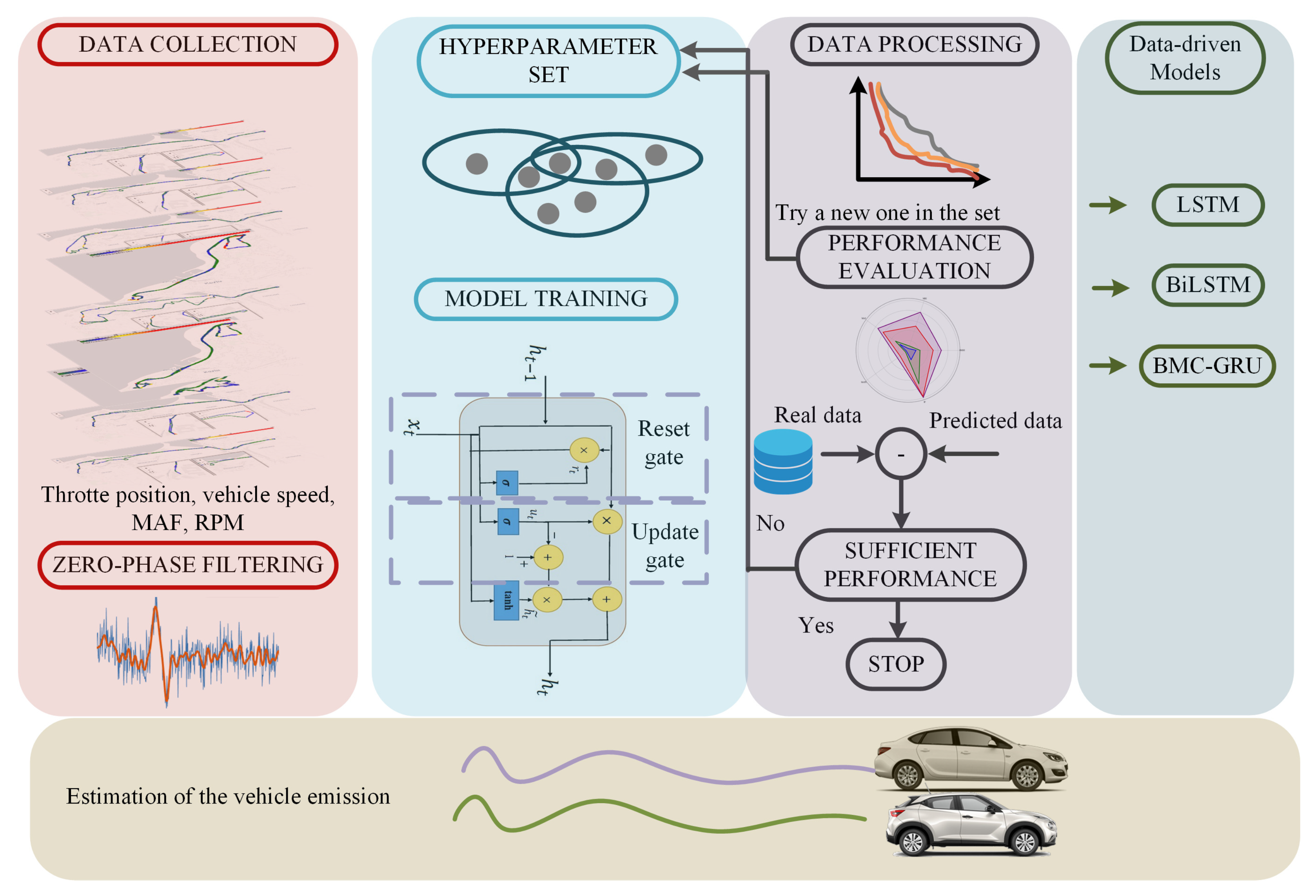
- We propose a Bayesian GRU-network-based estimation method to optimize probabilistically the hyperparameters of the network, i.e., learning rate, batch size, number of hidden layers, and number of nodes in each hidden layer.
- The method uses an uncertainty-aware emission estimation model that uses MC-Dropout to quantify epistemic uncertainty and Bayesian optimization to probabilistically tune hyperparameters, resulting in calibrated predictions and dependability against distribution drift.
- The estimation model can achieve high-resolution performance accuracy using the velocity, revolutions per minute (RPM), throttle position, and mass air flow (MAF) sensor data of the vehicle from the OBD system. The dataset is collected under real road conditions, i.e., rough country roads, stopped traffic, and free-flow roads, using multiple vehicles.
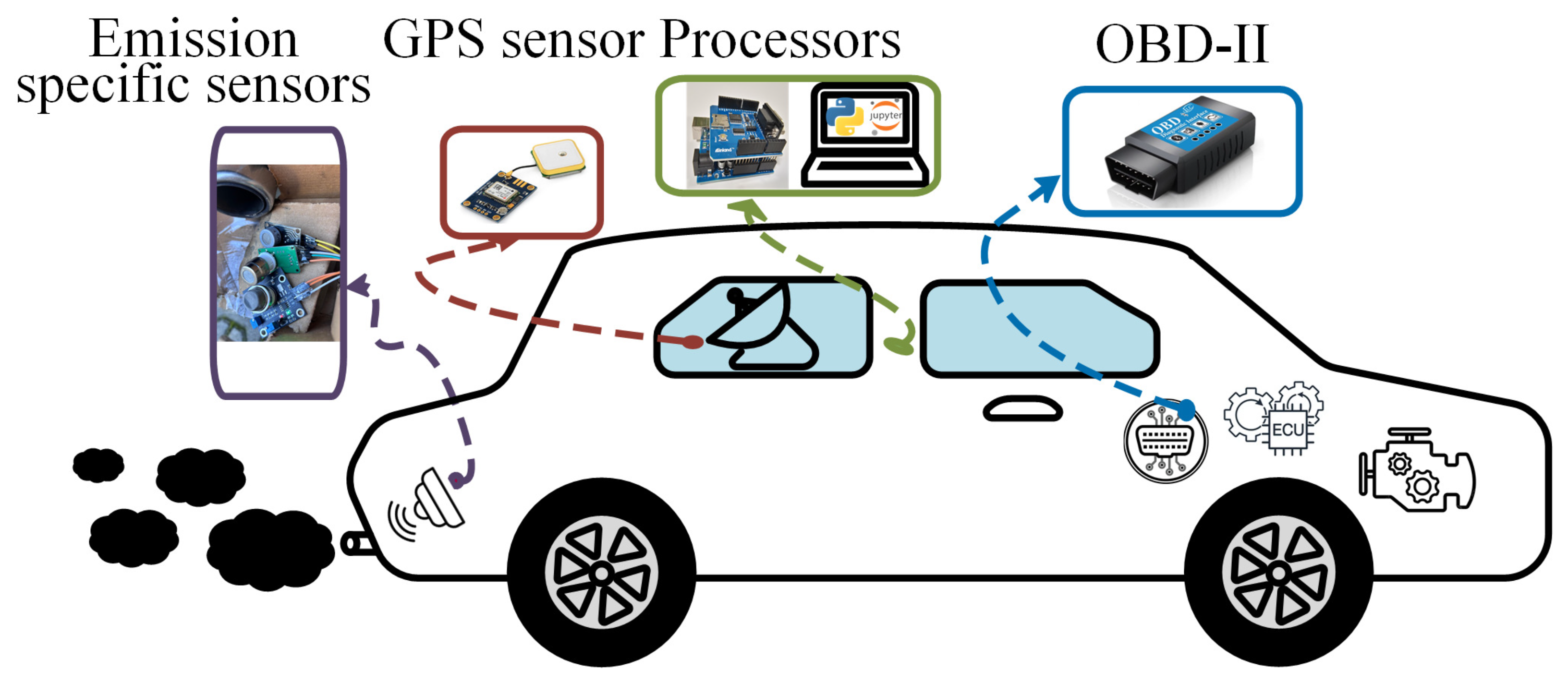
2. System Description and Problem Formulation
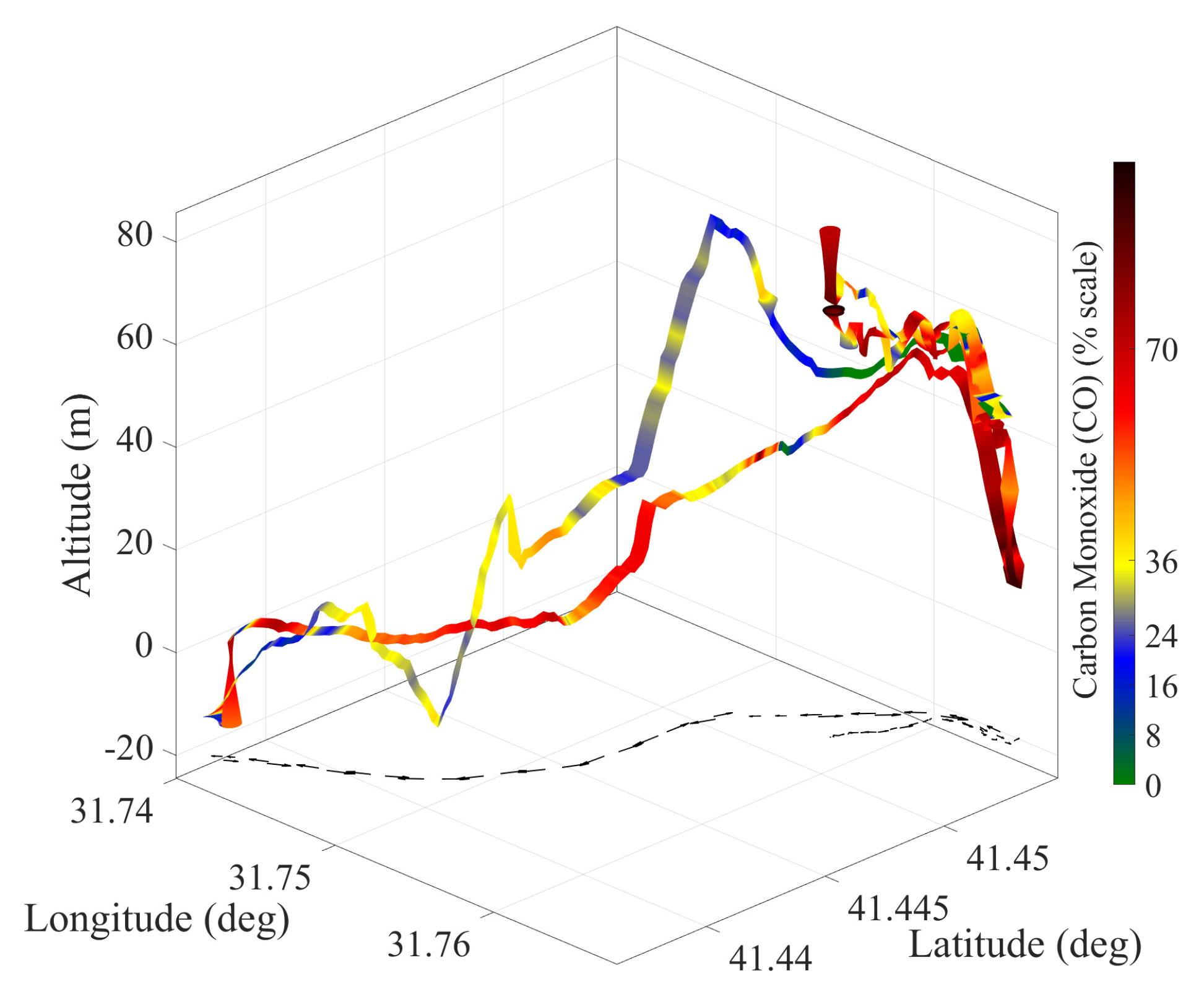
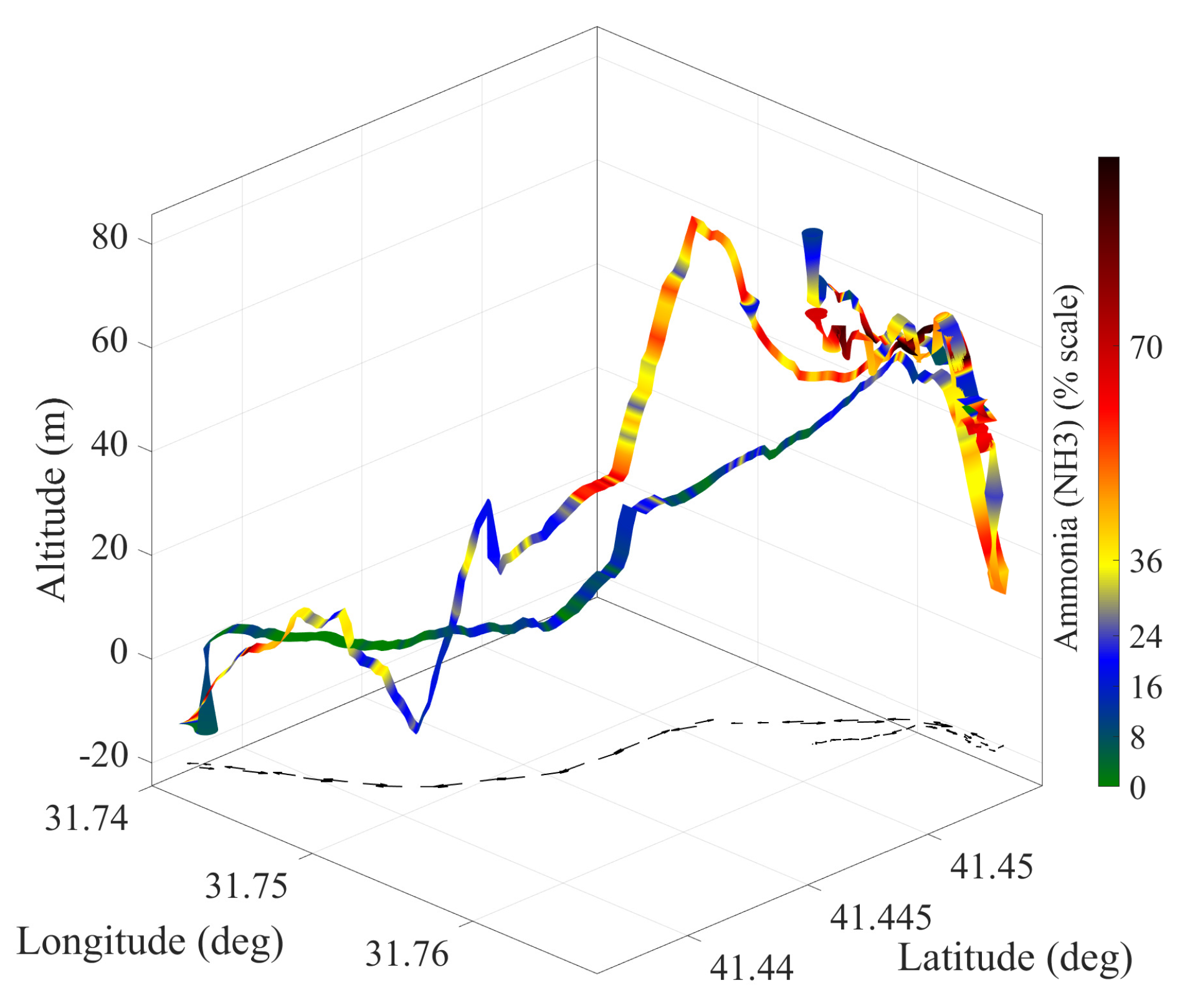
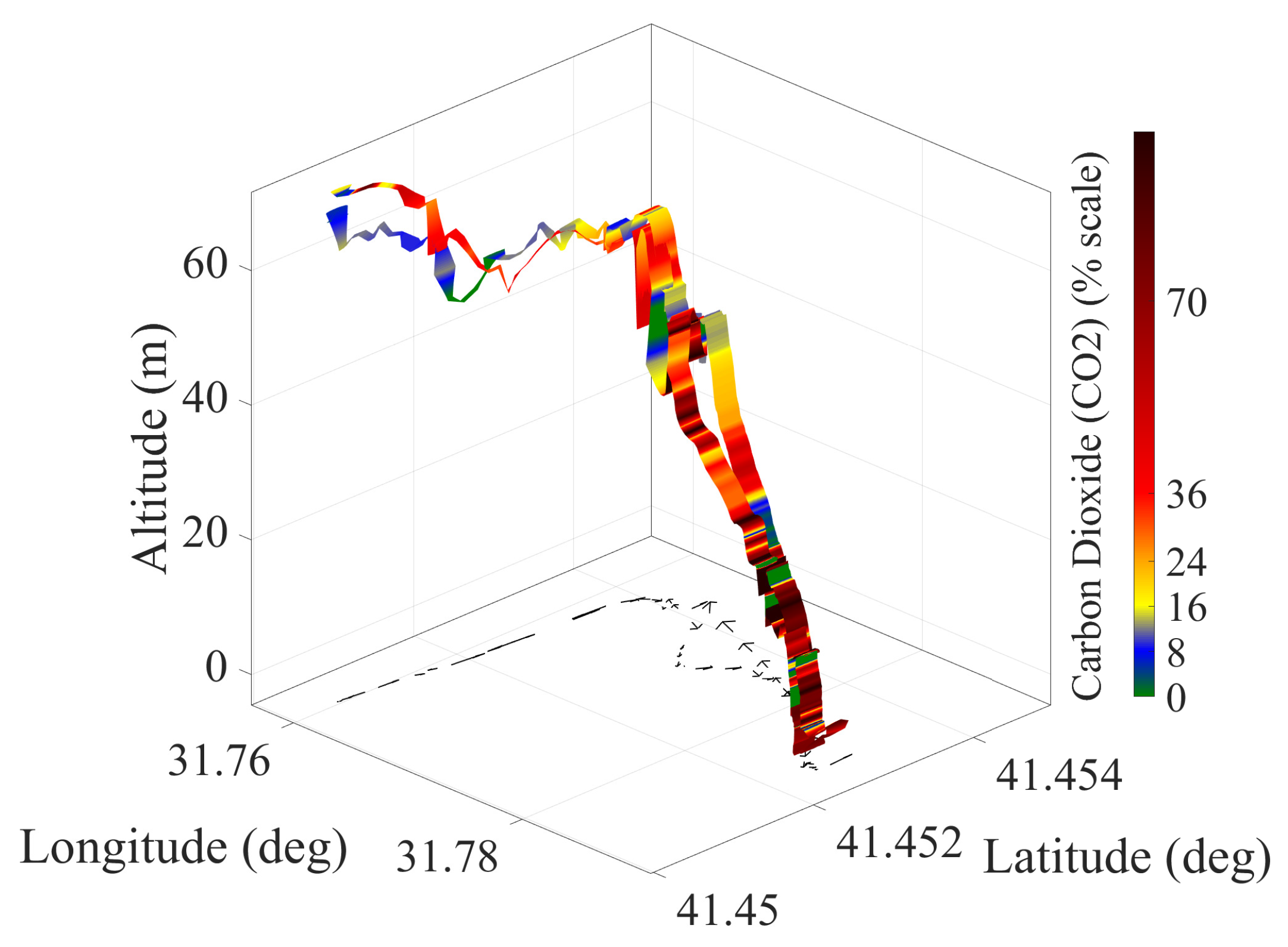
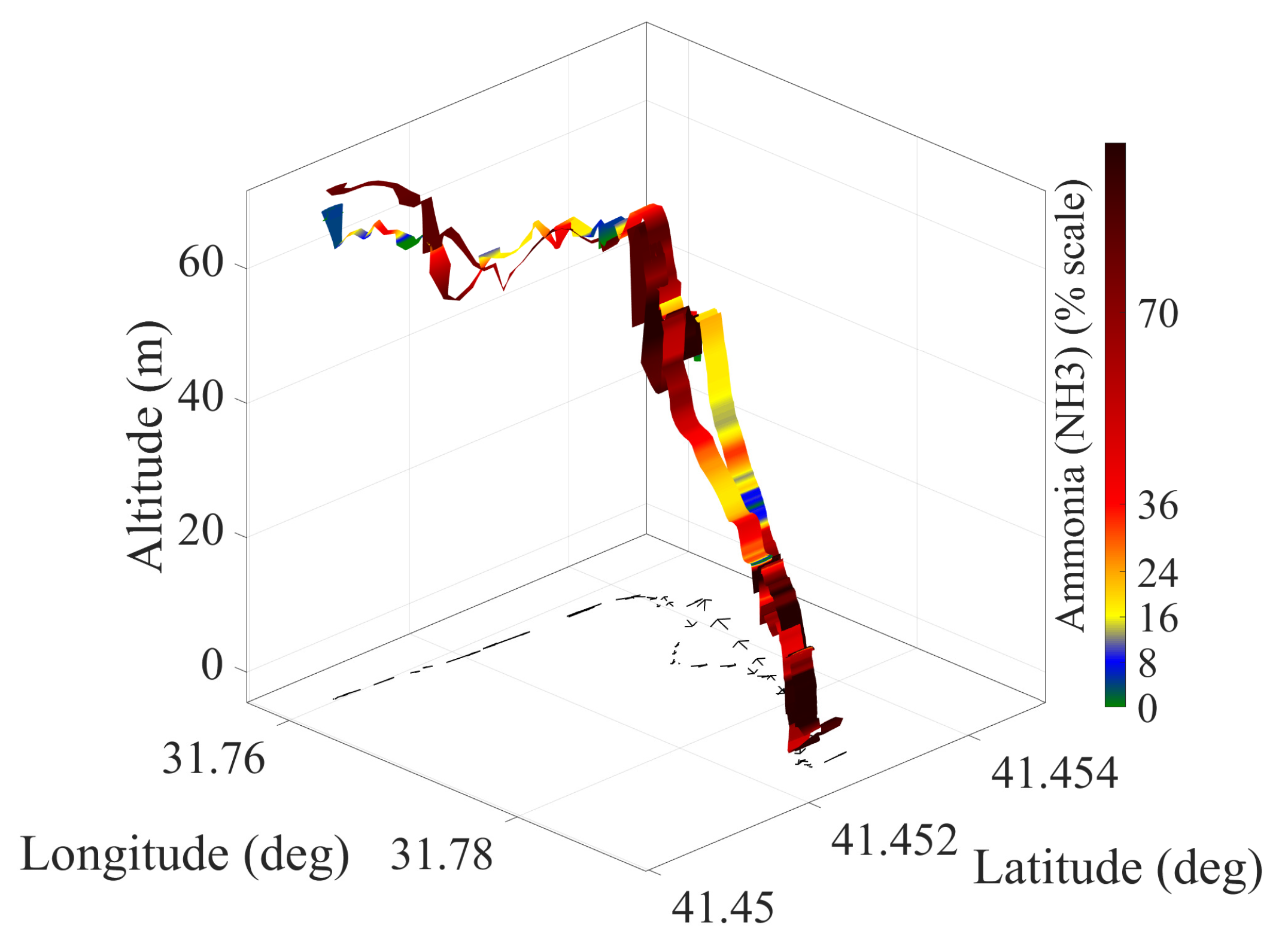
Data Collection
3. Deep Learning-Based Prediction Model
3.1. Bayesian Method-Based Hyperparameter Optimization
3.2. Monte Carlo Dropout Method
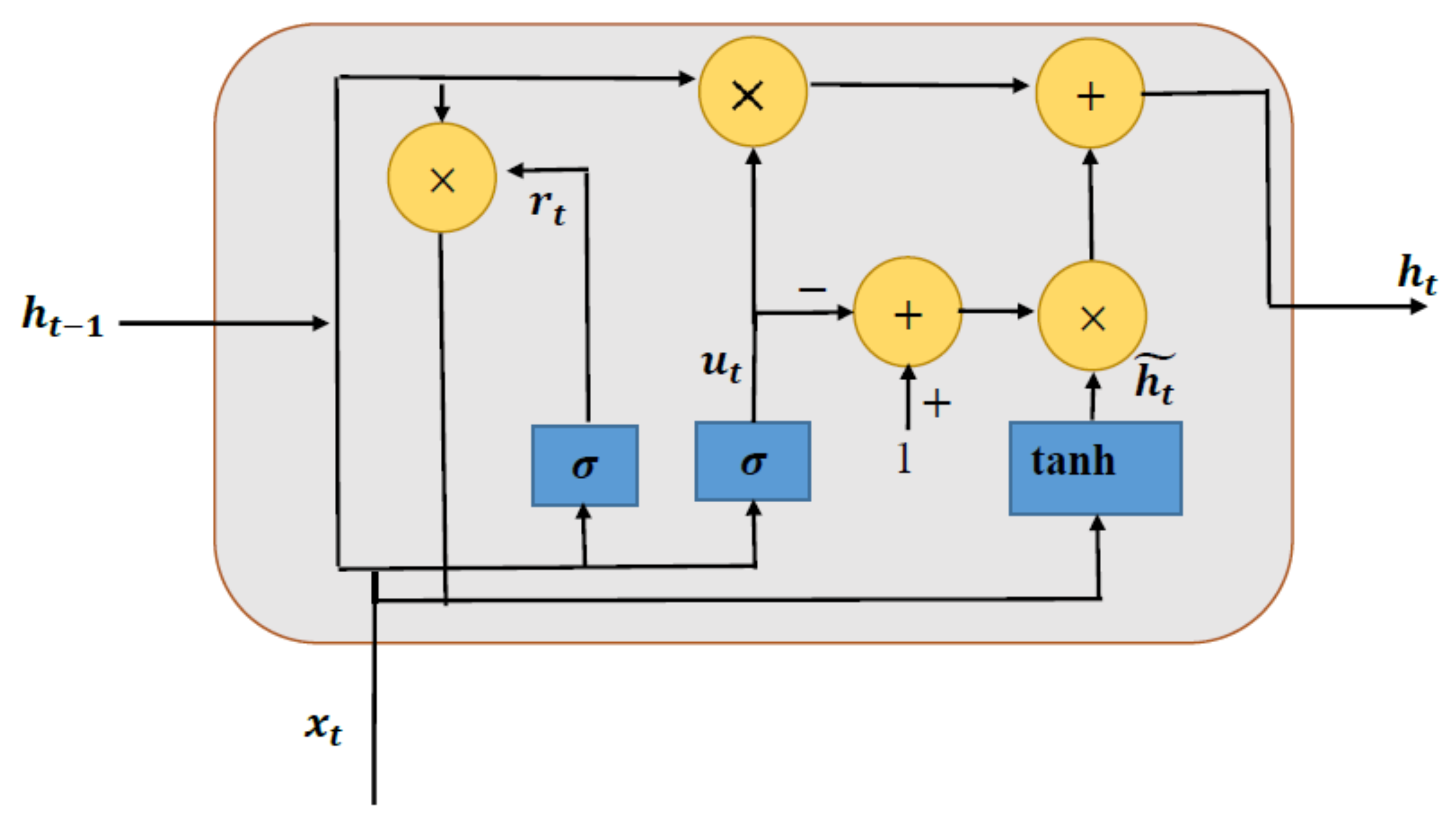
3.3. Gated Recurrent Unit
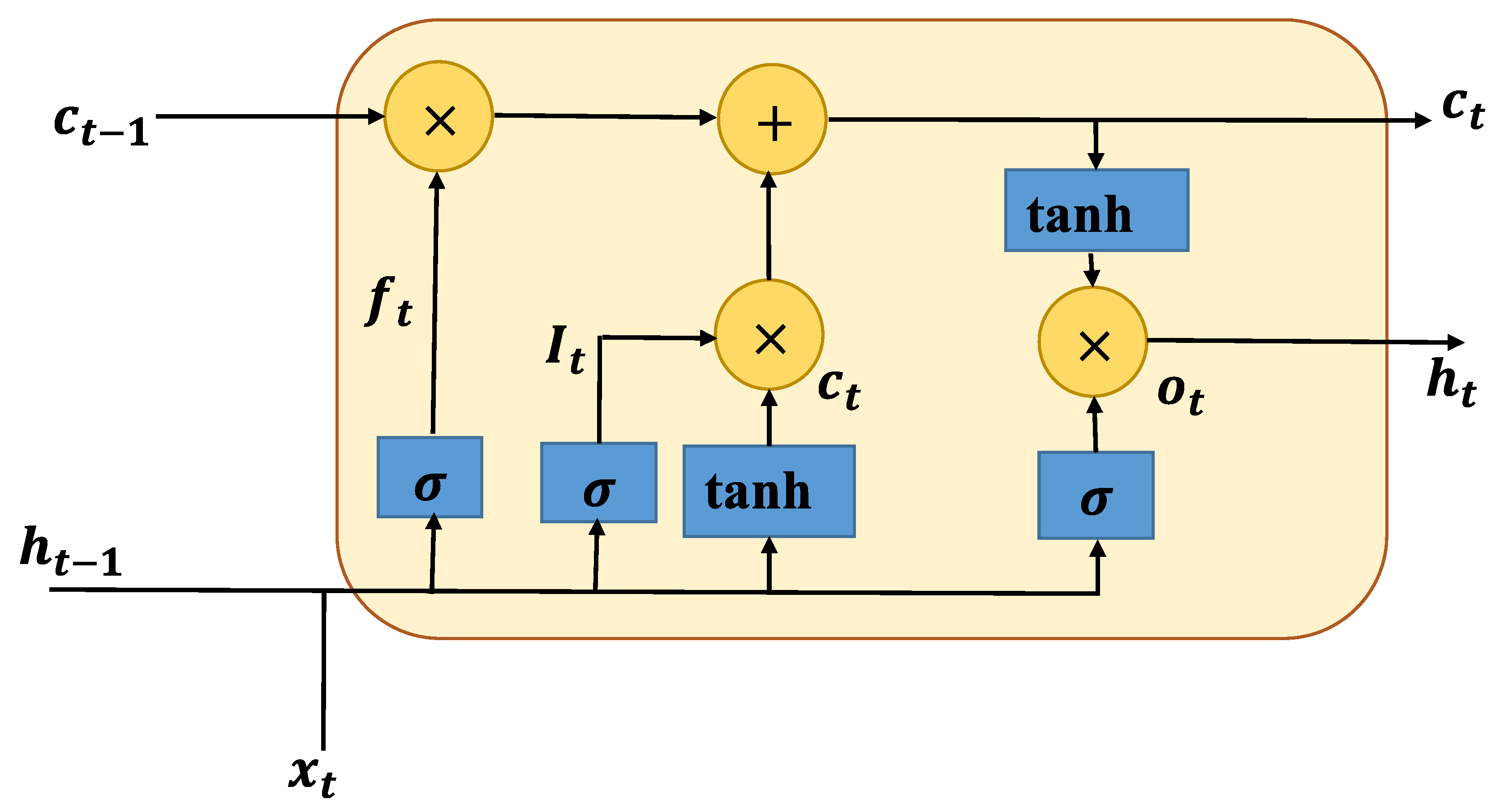
3.4. Long Short-Term Memory
3.5. Bidirectional LSTM
3.6. Ridge Regression-Based Prediction Model
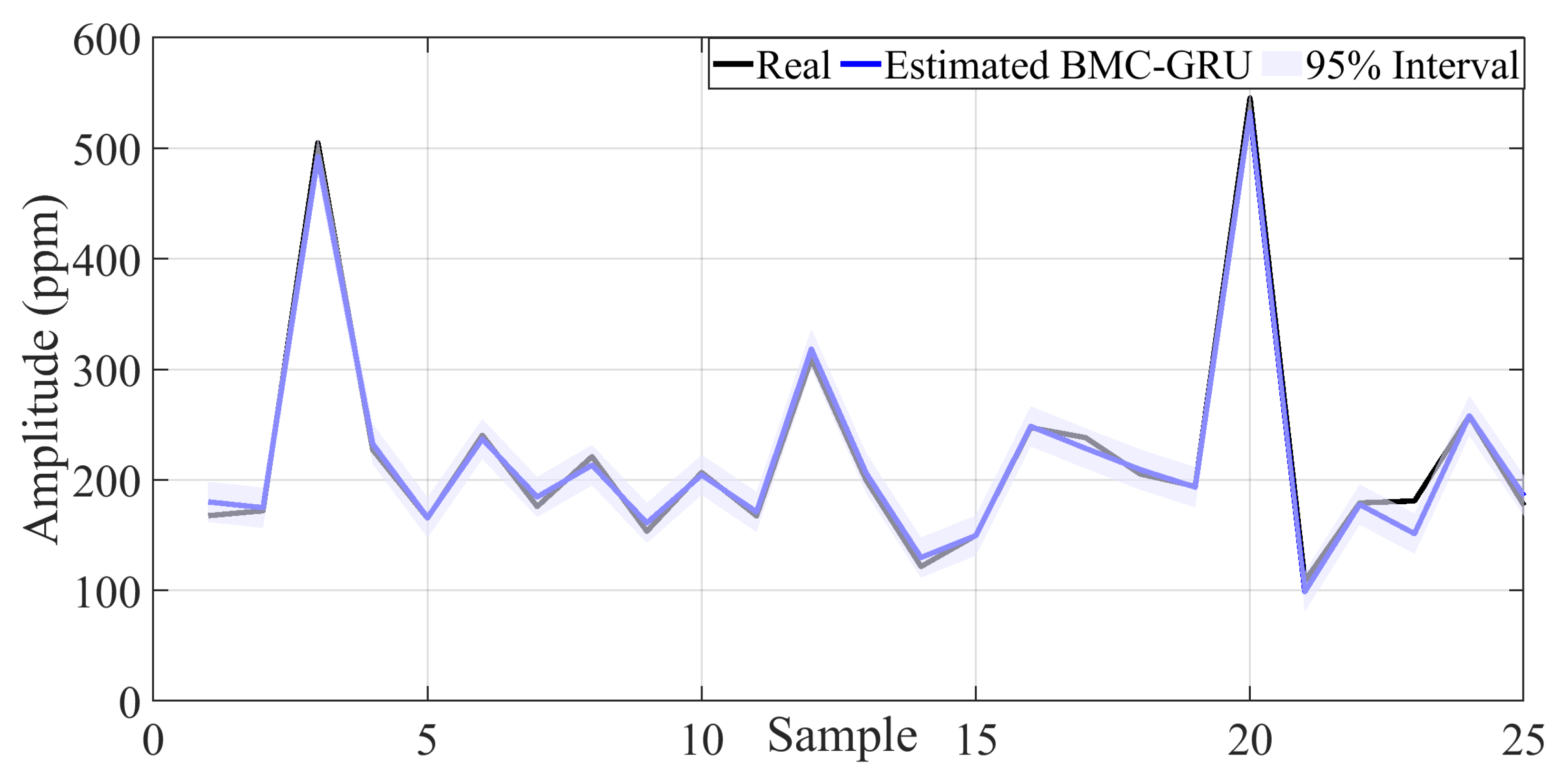
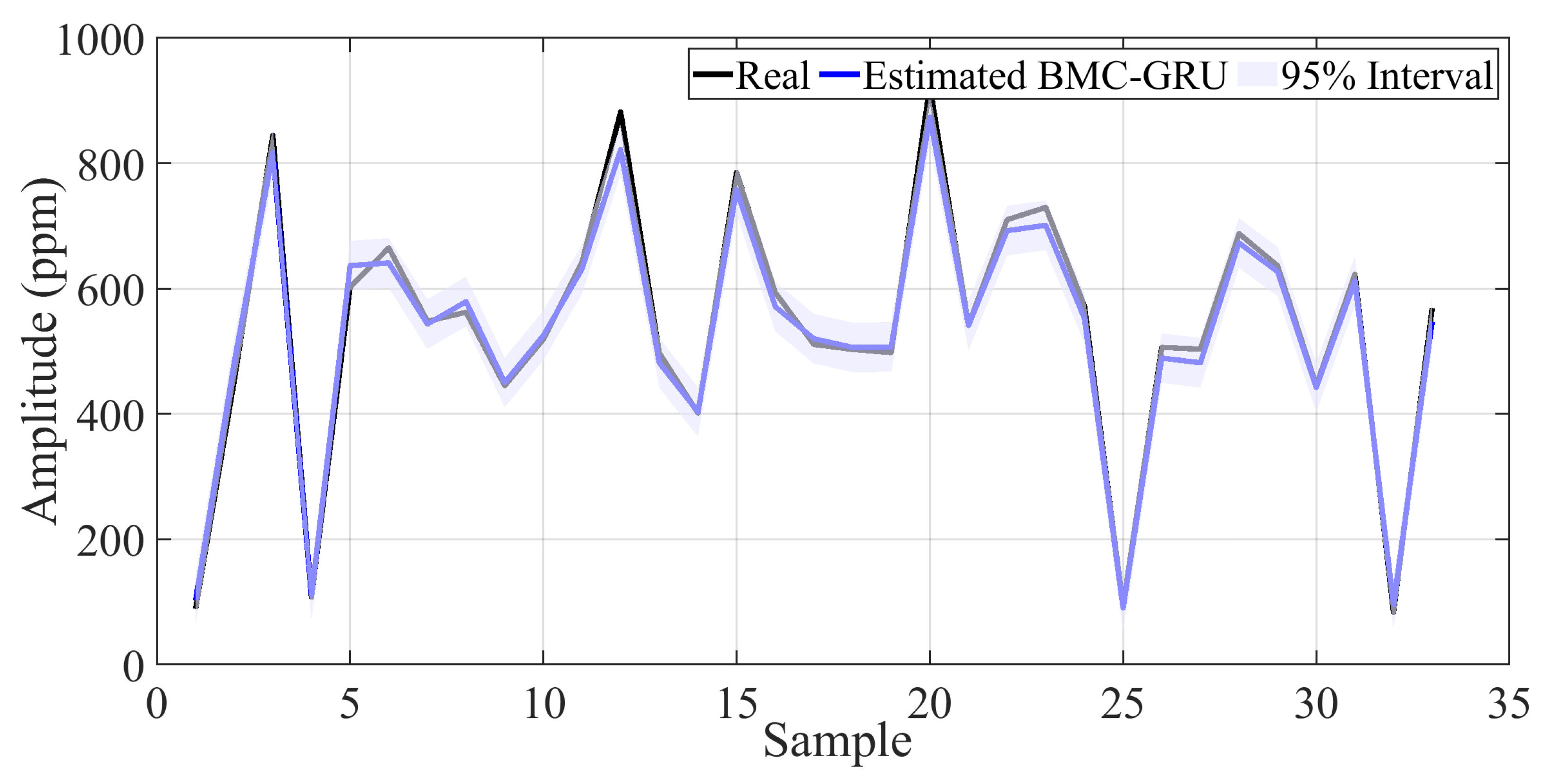
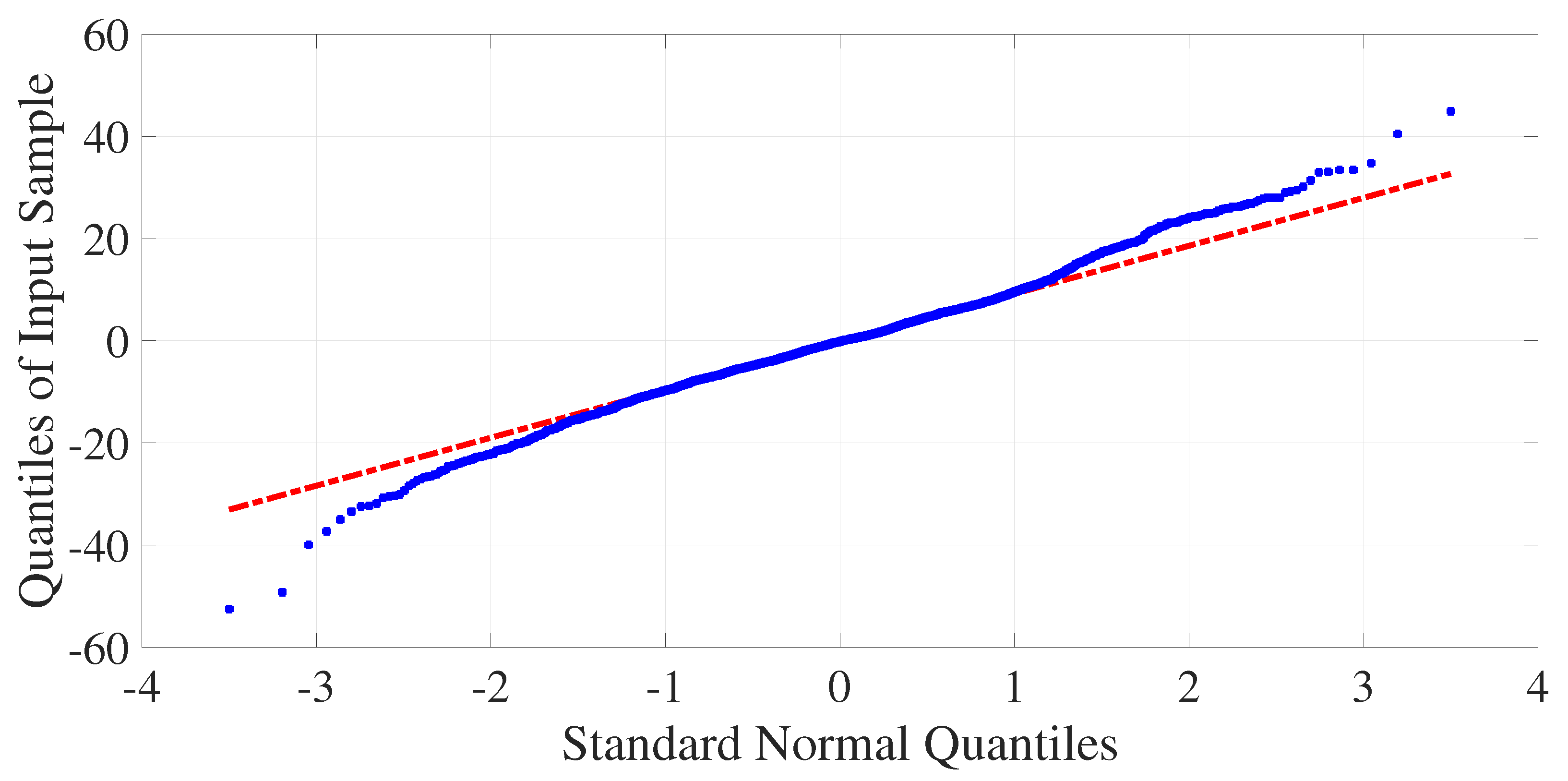
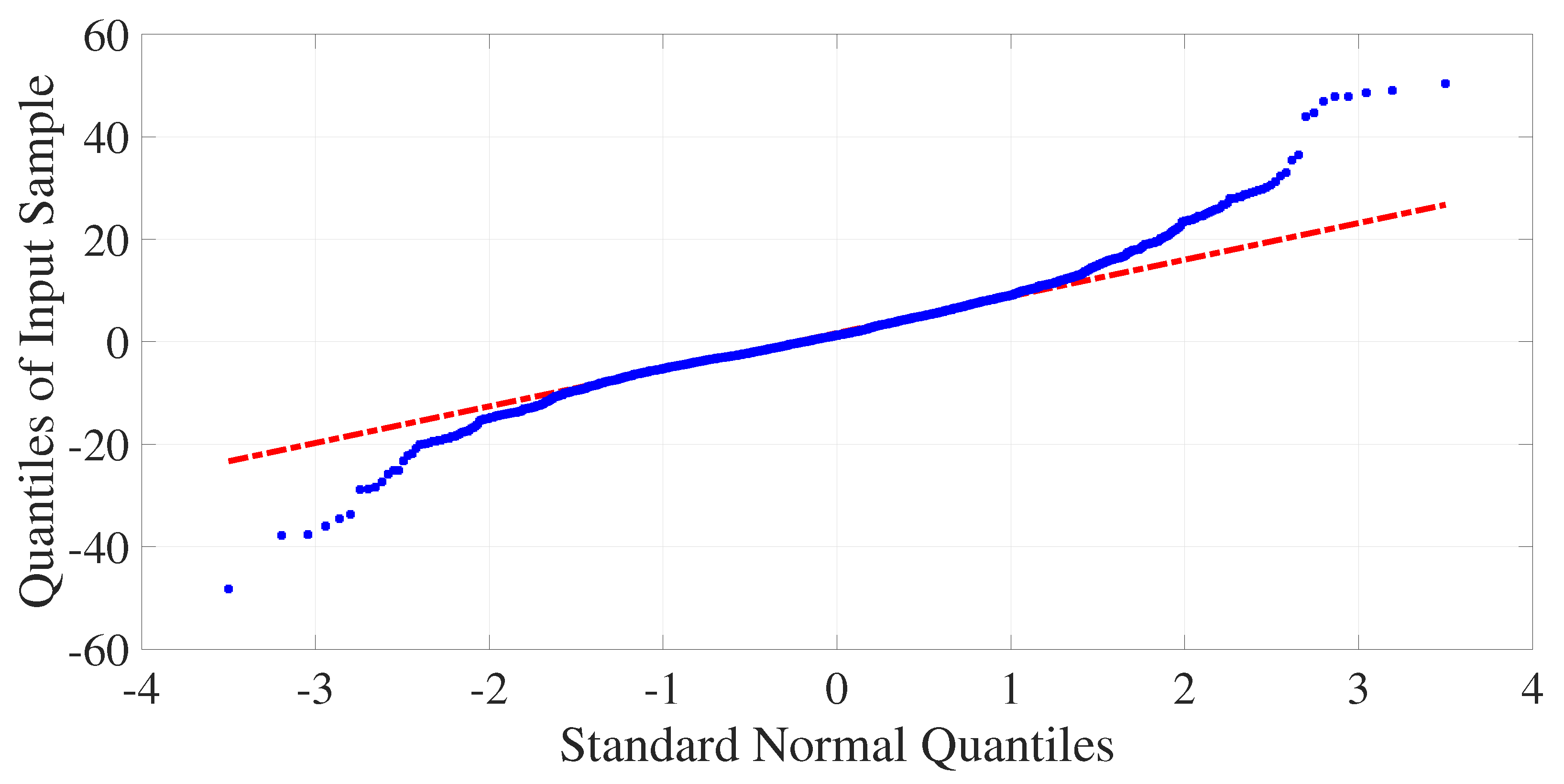
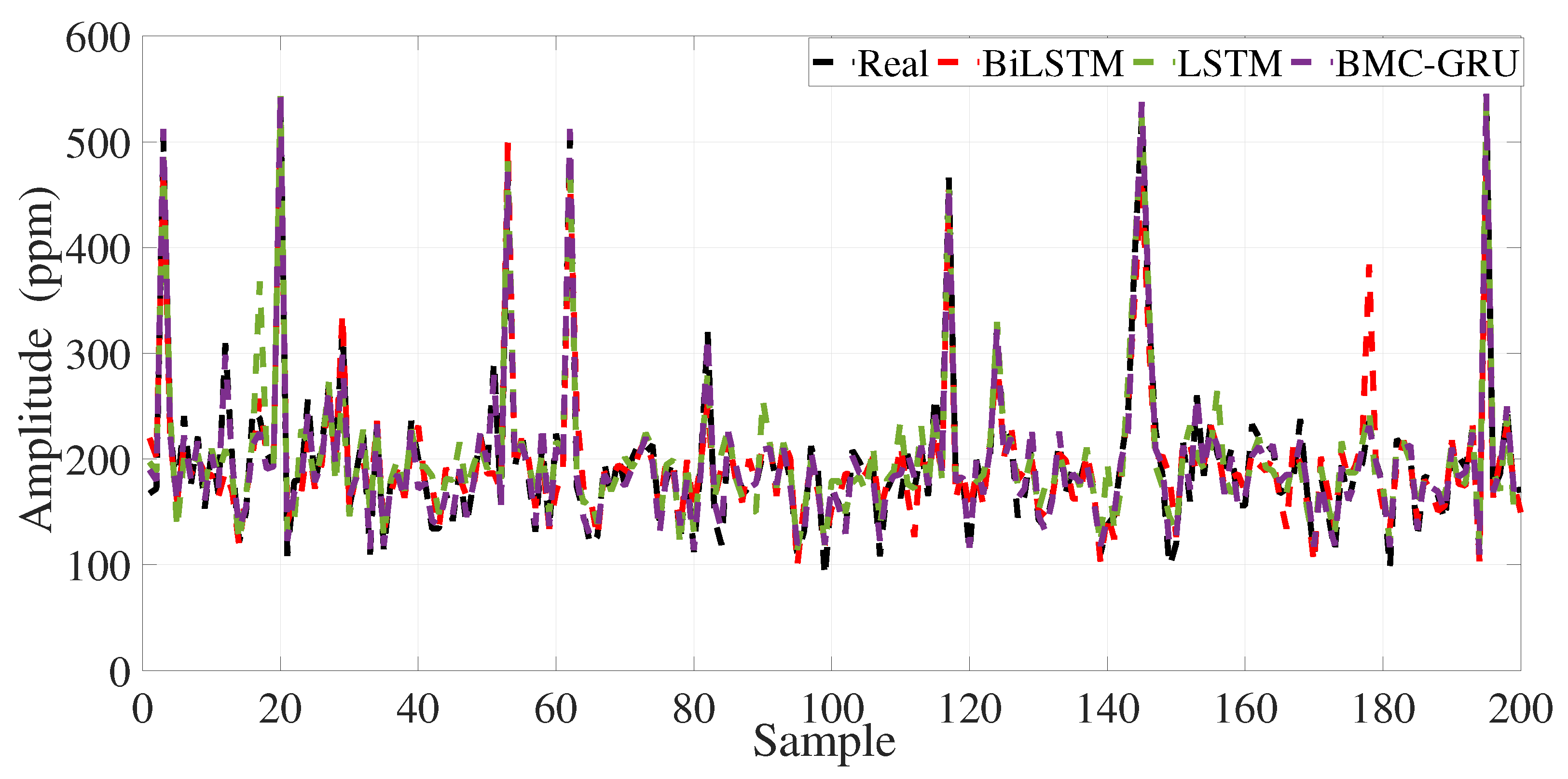
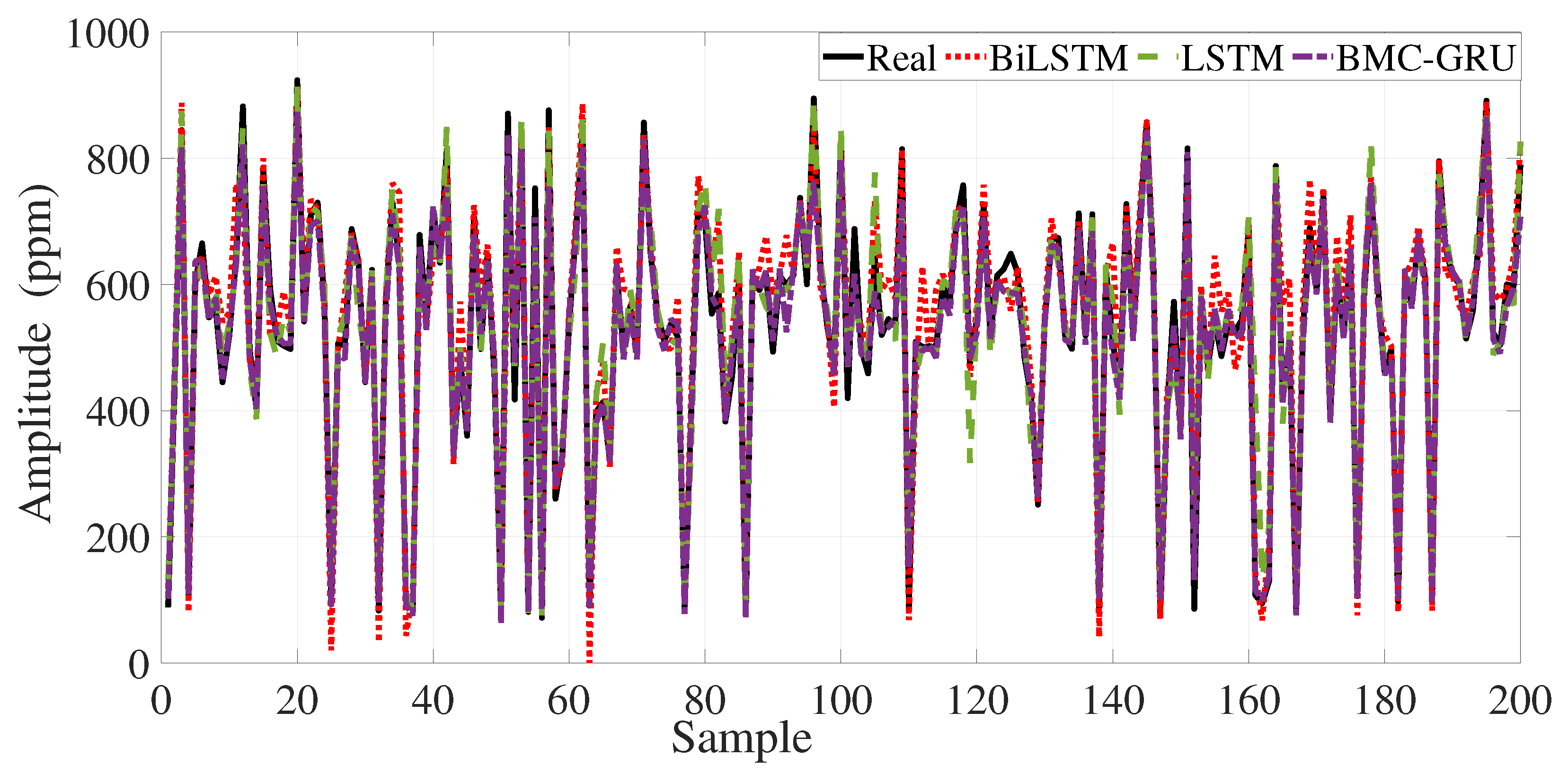
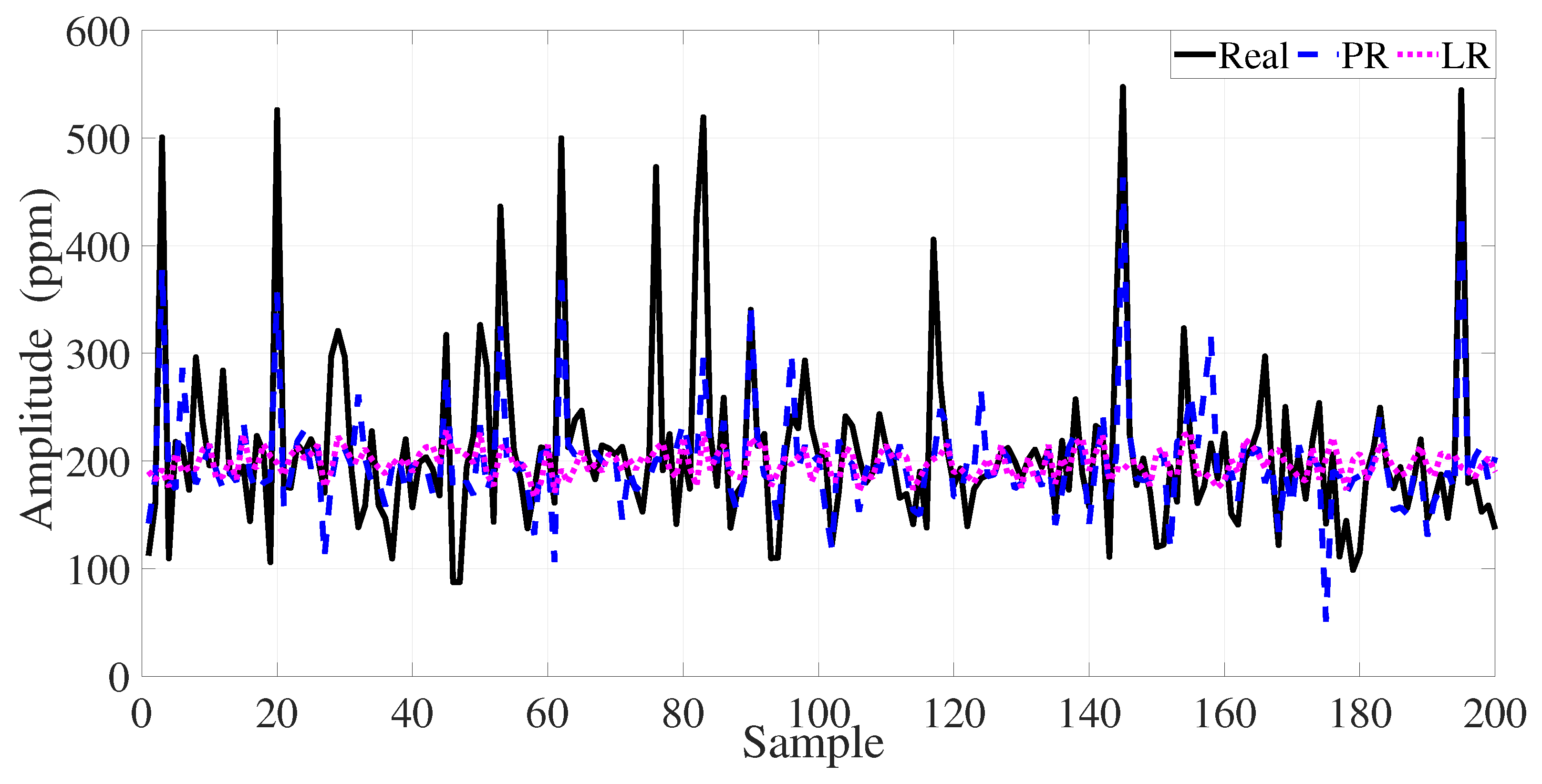
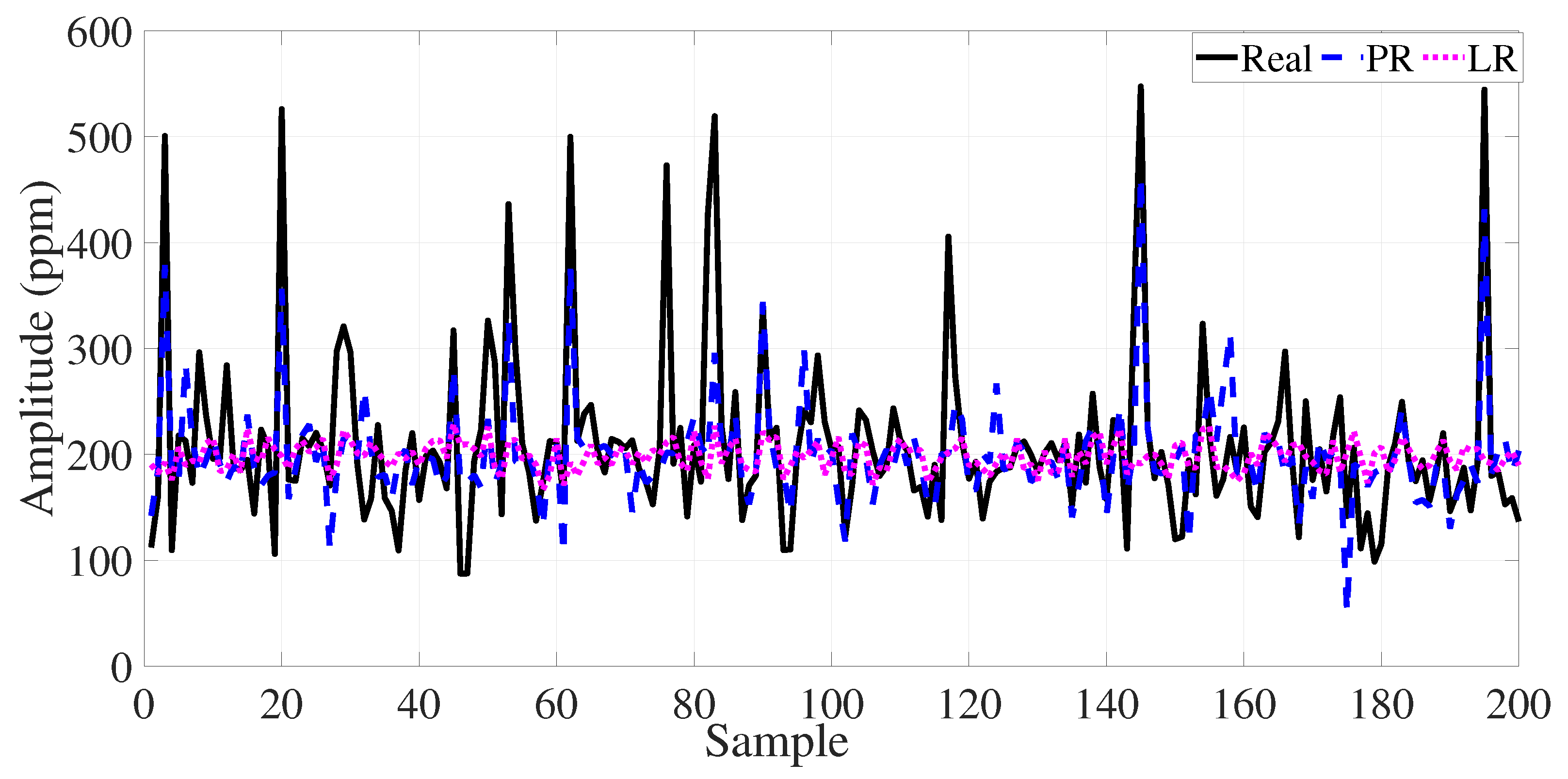
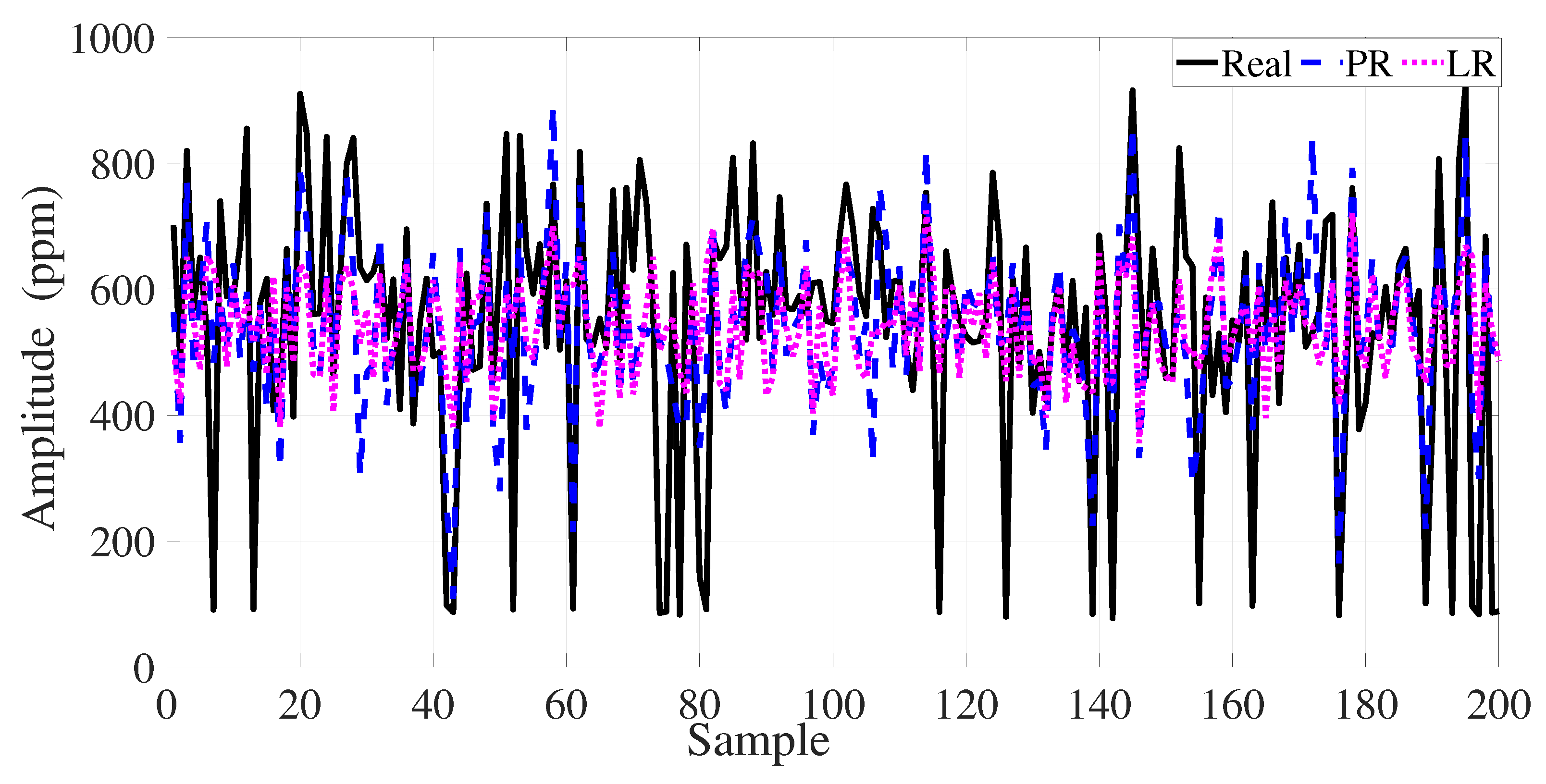
4. Performance Results of the Data-Driven Estimation Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hu, X.; Hao, X.; Zhang, K.; Wang, L.; Wang, C. Investigating the effect of estimating urban air pollution considering transportation infrastructure layouts. Transp. Res. Part D Transp. Environ. 2025, 139, 104569. [Google Scholar] [CrossRef]
- Mubeen, M.; He, S.; Rahman, M.S.; Wang, L.; Zhang, X.; Ahmed, B.; He, Z.; Han, Y. Smart prediction and optimization of air quality index with artificial intelligence. J. Environ. Sci. 2025, 158, 761–775. [Google Scholar] [CrossRef]
- Pan, R.; Zhu, J.; Chen, D.; Cheng, H.; Huang, L.; Wang, Y.; Li, L. Integrated analysis of air quality-vegetation-health effects of near-future air pollution control strategies. Environ. Pollut. 2025, 366, 125407. [Google Scholar] [CrossRef] [PubMed]
- Račić, N.; Petrić, V.; Mureddu, F.; Portin, H.; Niemi, J.V.; Hussein, T.; Lovrić, M. A Proxy Model for Traffic Related Air Pollution Indicators Based on Traffic Count. Atmosphere 2025, 16, 538. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, S.; Li, M.; Ge, Y.; Shu, J.; Zhou, Y.; Xu, Y.; Hu, J.; Liu, H.; Fu, L.; et al. The challenge to NO x emission control for heavy-duty diesel vehicles in China. Atmos. Chem. Phys. 2012, 12, 9365–9379. [Google Scholar] [CrossRef]
- Ahmed, M.; Zhang, X.; Shen, Y.; Ahmed, T.; Ali, S.; Ali, A.; Gulakhmadov, A.; Nam, W.H.; Chen, N. Low-cost video-based air quality estimation system using structured deep learning with selective state space modeling. Environ. Int. 2025, 199, 109496. [Google Scholar] [CrossRef] [PubMed]
- Hao, X.; Hu, X.; Liu, T.; Wang, C.; Wang, L. Estimating urban PM2. 5 concentration: An analysis on the nonlinear effects of explanatory variables based on gradient boosted regression tree. Urban Clim. 2022, 44, 101172. [Google Scholar] [CrossRef]
- Smit, R.; Ntziachristos, L.; Boulter, P. Validation of road vehicle and traffic emission models–A review and meta-analysis. Atmos. Environ. 2010, 44, 2943–2953. [Google Scholar] [CrossRef]
- Wang, J.; Wang, R.; Yin, H.; Wang, Y.; Wang, H.; He, C.; Liang, J.; He, D.; Yin, H.; He, K. Assessing heavy-duty vehicles (HDVs) on-road NOx emission in China from on-board diagnostics (OBD) remote report data. Sci. Total Environ. 2022, 846, 157209. [Google Scholar] [CrossRef]
- Zhao, D.; Li, H.; Hou, J.; Gong, P.; Zhong, Y.; He, W.; Fu, Z. A review of the data-driven prediction method of vehicle fuel consumption. Energies 2023, 16, 5258. [Google Scholar] [CrossRef]
- Qu, L.; Wang, W.; Li, M.; Xu, X.; Shi, Z.; Mao, H.; Jin, T. Dependence of pollutant emission factors and fuel consumption on driving conditions and gasoline vehicle types. Atmos. Pollut. Res. 2021, 12, 137–146. [Google Scholar] [CrossRef]
- Smit, R.; Dia, H.; Morawska, L. Road traffic emission and fuel consumption modelling: Trends, new developments and future challenges. In Traffic Related Air Pollution and Internal Combustion Engines; Nova Science Publishers, Inc.: New York, NY, USA, 2009; pp. 29–68. [Google Scholar]
- Chan, K.; Matthews, P.; Munir, K. Time Series Forecasting for Air Quality with Structured and Unstructured Data Using Artificial Neural Networks. Atmosphere 2025, 16, 320. [Google Scholar] [CrossRef]
- Vallamsundar, S.; Lin, J. MOVES versus MOBILE: Comparison of greenhouse gas and criterion pollutant emissions. Transp. Res. Rec. 2011, 2233, 27–35. [Google Scholar] [CrossRef]
- Kota, S.H.; Zhang, H.; Chen, G.; Schade, G.W.; Ying, Q. Evaluation of on-road vehicle CO and NOx National Emission Inventories using an urban-scale source-oriented air quality model. Atmos. Environ. 2014, 85, 99–108. [Google Scholar] [CrossRef]
- Fujita, E.M.; Campbell, D.E.; Zielinska, B.; Chow, J.C.; Lindhjem, C.E.; DenBleyker, A.; Bishop, G.A.; Schuchmann, B.G.; Stedman, D.H.; Lawson, D.R. Comparison of the MOVES2010a, MOBILE6. 2, and EMFAC2007 mobile source emission models with on-road traffic tunnel and remote sensing measurements. J. Air Waste Manag. Assoc. 2012, 62, 1134–1149. [Google Scholar] [CrossRef]
- Kota, S.H.; Ying, Q.; Schade, G.W. MOVES vs. MOBILE6. 2: Differences in emission factors and regional air quality predictions. In Proceedings of the 91st Annual Meeting of the Transportation Research Board, Washington, DC, USA, 22–26 January 2012. [Google Scholar]
- Boriboonsomsin, K.; Uddin, W. Simplified methodology to estimate emissions from mobile sources for ambient air quality assessment. J. Transp. Eng. 2006, 132, 817–828. [Google Scholar] [CrossRef]
- Jimenez-Palacios, J.L. Understanding and Quantifying Motor Vehicle Emissions with Vehicle Specific Power and TILDAS Remote Sensing. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1998. [Google Scholar]
- Frey, H.C.; Unal, A.; Chen, J.; Li, S. Modeling mobile source emissions based upon in-use and second-by-second data: Development of conceptual approaches for EPA’s new moves model. In Proceedings of the Annual Meeting of the Air and Waste Management Association, Pittsburgh, PA, USA, 22–24 October 2003. [Google Scholar]
- Wang, H.; Chen, C.; Huang, C.; Fu, L. On-road vehicle emission inventory and its uncertainty analysis for Shanghai, China. Sci. Total Environ. 2008, 398, 60–67. [Google Scholar] [CrossRef]
- Lindhjem, C.E.; Pollack, A.K.; Slott, R.S.; Sawyer, R.F. Analysis of EPA’s Draft Plan for Emissions Modeling in MOVES and MOVES GHG; Research Report# CRC Project E-68; Environ International Corporation: Novato, CA, USA, 2004. [Google Scholar]
- Mendes, M.; Duarte, G.; Baptista, P. Introducing specific power to bicycles and motorcycles: Application to electric mobility. Transp. Res. Part C Emerg. Technol. 2015, 51, 120–135. [Google Scholar] [CrossRef]
- Liang, Y.C.; Maimury, Y.; Chen, A.H.L.; Juarez, J.R.C. Machine learning-based prediction of air quality. Appl. Sci. 2020, 10, 9151. [Google Scholar] [CrossRef]
- Matthaios, V.N.; Knibbs, L.D.; Kramer, L.J.; Crilley, L.R.; Bloss, W.J. Predicting real-time within-vehicle air pollution exposure with mass-balance and machine learning approaches using on-road and air quality data. Atmos. Environ. 2024, 318, 120233. [Google Scholar] [CrossRef]
- Wai, K.M.; Yu, P.K. Application of a machine learning method for prediction of urban neighborhood-scale air pollution. Int. J. Environ. Res. Public Health 2023, 20, 2412. [Google Scholar] [CrossRef]
- Seo, J.; Lim, Y.; Han, J.; Park, S. Machine learning-based estimation of gaseous and particulate emissions using internally observable vehicle operating parameters. Urban Clim. 2023, 52, 101734. [Google Scholar] [CrossRef]
- Azeez, O.S.; Pradhan, B.; Shafri, H.Z. Vehicular CO emission prediction using support vector regression model and GIS. Sustainability 2018, 10, 3434. [Google Scholar] [CrossRef]
- Yap, W.K.; Karri, V. ANN virtual sensors for emissions prediction and control. Appl. Energy 2011, 88, 4505–4516. [Google Scholar] [CrossRef]
- Azeez, O.S.; Pradhan, B.; Shafri, H.Z.; Shukla, N.; Lee, C.W.; Rizeei, H.M. Modeling of CO emissions from traffic vehicles using artificial neural networks. Appl. Sci. 2019, 9, 313. [Google Scholar] [CrossRef]
- Jida, S.N.; Hetet, J.F.; Chesse, P.; Guadie, A. Roadside vehicle particulate matter concentration estimation using artificial neural network model in Addis Ababa, Ethiopia. J. Environ. Sci. 2021, 101, 428–439. [Google Scholar] [CrossRef]
- Seo, J.; Yun, B.; Park, J.; Park, J.; Shin, M.; Park, S. Prediction of instantaneous real-world emissions from diesel light-duty vehicles based on an integrated artificial neural network and vehicle dynamics model. Sci. Total Environ. 2021, 786, 147359. [Google Scholar] [CrossRef] [PubMed]
- Suri, R.S.; Jain, A.K.; Kapoor, N.R.; Kumar, A.; Arora, H.C.; Kumar, K.; Jahangir, H. Air quality prediction-a study using neural network based approach. J. Soft Comput. Civ. Eng. 2023, 7, 93–113. [Google Scholar]
- Antanasijević, D.Z.; Pocajt, V.V.; Povrenović, D.S.; Ristić, M.Đ.; Perić-Grujić, A.A. PM10 emission forecasting using artificial neural networks and genetic algorithm input variable optimization. Sci. Total Environ. 2013, 443, 511–519. [Google Scholar] [CrossRef]
- Li, Y.; Jia, M.; Han, X.; Bai, X.S. Towards a comprehensive optimization of engine efficiency and emissions by coupling artificial neural network (ANN) with genetic algorithm (GA). Energy 2021, 225, 120331. [Google Scholar] [CrossRef]
- Chang, Y.S.; Chiao, H.T.; Abimannan, S.; Huang, Y.P.; Tsai, Y.T.; Lin, K.M. An LSTM-based aggregated model for air pollution forecasting. Atmos. Pollut. Res. 2020, 11, 1451–1463. [Google Scholar] [CrossRef]
- Xie, H.; Zhang, Y.; He, Y.; You, K.; Fan, B.; Yu, D.; Lei, B.; Zhang, W. Parallel attention-based LSTM for building a prediction model of vehicle emissions using PEMS and OBD. Measurement 2021, 185, 110074. [Google Scholar] [CrossRef]
- Seng, D.; Zhang, Q.; Zhang, X.; Chen, G.; Chen, X. Spatiotemporal prediction of air quality based on LSTM neural network. Alex. Eng. J. 2021, 60, 2021–2032. [Google Scholar] [CrossRef]
- Dalal, S.; Lilhore, U.K.; Faujdar, N.; Samiya, S.; Jaglan, V.; Alroobaea, R.; Shaheen, M.; Ahmad, F. Optimising air quality prediction in smart cities with hybrid particle swarm optimization-long-short term memory-recurrent neural network model. IET Smart Cities 2024, 6, 156–179. [Google Scholar] [CrossRef]
- Hu, L.; Wang, C.; Ye, Z.; Wang, S. Estimating gaseous pollutants from bus emissions: A hybrid model based on GRU and XGBoost. Sci. Total Environ. 2021, 783, 146870. [Google Scholar] [CrossRef]
- Huang, H.; Qian, C. Modeling PM2. 5 forecast using a self-weighted ensemble GRU network: Method optimization and evaluation. Ecol. Indic. 2023, 156, 111138. [Google Scholar] [CrossRef]
- Yang, L.; Ge, Y.; Lyu, L.; Tan, J.; Hao, L.; Wang, X.; Yin, H.; Wang, J. Enhancing vehicular emissions monitoring: A GA-GRU-based soft sensors approach for HDDVs. Environ. Res. 2024, 247, 118190. [Google Scholar] [CrossRef]
- Araújo, T.; Silva, L.; Moreira, A. Evaluation of low-cost sensors for weather and carbon dioxide monitoring in internet of things context. IoT 2020, 1, 286–308. [Google Scholar] [CrossRef]
- Kanarachos, S.; Mathew, J.; Fitzpatrick, M.E. Instantaneous vehicle fuel consumption estimation using smartphones and recurrent neural networks. Expert Syst. Appl. 2019, 120, 436–447. [Google Scholar] [CrossRef]
- Bengio, Y. Practical recommendations for gradient-based training of deep architectures. In Neural Networks: Tricks of the Trade, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 437–478. [Google Scholar]
- Seoh, R. Qualitative analysis of monte carlo dropout. arXiv 2020, arXiv:2007.01720. [Google Scholar] [CrossRef]
- Martínez-Ramón, M.; Ajith, M.; Kurup, A.R. Deep Learning: A Practical Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2024. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; pp. 1050–1059. [Google Scholar]
- Folgoc, L.L.; Baltatzis, V.; Desai, S.; Devaraj, A.; Ellis, S.; Manzanera, O.E.M.; Nair, A.; Qiu, H.; Schnabel, J.; Glocker, B. Is MC dropout bayesian? arXiv 2021, arXiv:2110.04286. [Google Scholar] [CrossRef]
- Padarian, J.; Minasny, B.; McBratney, A. Assessing the uncertainty of deep learning soil spectral models using Monte Carlo dropout. Geoderma 2022, 425, 116063. [Google Scholar] [CrossRef]
- Waqas, M.; Humphries, U.W. A critical review of RNN and LSTM variants in hydrological time series predictions. MethodsX 2024, 13, 102946. [Google Scholar] [CrossRef] [PubMed]
- Rezazadeh, N.; de Oliveira, M.; Perfetto, D.; De Luca, A.; Caputo, F. Classification of unbalanced and bowed rotors under uncertainty using wavelet time scattering, LSTM, and SVM. Appl. Sci. 2023, 13, 6861. [Google Scholar] [CrossRef]
- Ławryńczuk, M.; Zarzycki, K. LSTM and GRU type recurrent neural networks in model predictive control: A Review. Neurocomputing 2025, 632, 129712. [Google Scholar] [CrossRef]
- Singla, P.; Duhan, M.; Saroha, S. An ensemble method to forecast 24-h ahead solar irradiance using wavelet decomposition and BiLSTM deep learning network. Earth Sci. Inform. 2022, 15, 291–306. [Google Scholar] [CrossRef]
- Sang, S.; Li, L. A stock prediction method based on heterogeneous bidirectional LSTM. Appl. Sci. 2024, 14, 9158. [Google Scholar] [CrossRef]
- Peng, S.; Zhu, J.; Wu, T.; Yuan, C.; Cang, J.; Zhang, K.; Pecht, M. Prediction of wind and PV power by fusing the multi-stage feature extraction and a PSO-BiLSTM model. Energy 2024, 298, 131345. [Google Scholar] [CrossRef]
- Michael, N.E.; Hasan, S.; Al-Durra, A.; Mishra, M. Short-term solar irradiance forecasting based on a novel Bayesian optimized deep Long Short-Term Memory neural network. Appl. Energy 2022, 324, 119727. [Google Scholar] [CrossRef]
- Cui, P.; Wang, J. Out-of-distribution (ood) detection based on deep learning: A review. Electronics 2022, 11, 3500. [Google Scholar] [CrossRef]
- Yang, J.; Chen, L.; Chen, H.; Liu, J.; Han, B. Constructing prediction intervals to explore uncertainty based on deep neural networks. J. Intell. Fuzzy Syst. 2024, 46, 10441–10456. [Google Scholar] [CrossRef]






| Model | Hidden Layers (First and Second) | Layers | Dropout | Learning Rate | Epochs | Batch Size |
|---|---|---|---|---|---|---|
| BiLSTM | 128–128 | 4 | 0 | 0.001 | 60 | 16 |
| 2-Layer LSTM | 128–128 | 4 | 0 | 0.001 | 60 | 16 |
| BMC-GRU | [64–180], [64–180] | 4 | [0.1–0.5] | [0.0001–0.01] | 60 | 16 |
| Metric | CO | ||
|---|---|---|---|
| PICP | 92.5% | 96% | 93.94% |
| NLL | 3.88 | 3.63 | 4.49 |
| OOD | 7.5% | 4% | 6.06% |
| Pollutant Type | Model | RMSE | MSE | MAE | |
|---|---|---|---|---|---|
| BiLSTM | 31.3839 | 984.9479 | 21.8114 | 0.8175 | |
| 2-Layer LSTM | 27.3329 | 747.0852 | 19.4289 | 0.8616 | |
| PR (4th) | 57.8295 | 3344.2469 | 38.4257 | 0.3567 | |
| LR (1st) | 70.9923 | 5039.9049 | 42.5329 | 0.0305 | |
| BMC-GRU | 10.7605 | 115.7878 | 8.1643 | 0.9785 | |
| BiLSTM | 10.6735 | 113.9227 | 7.5959 | 0.9789 | |
| 2-Layer LSTM | 46.9525 | 2204.5388 | 29.0457 | 0.5915 | |
| PR (4th) | 57.8295 | 3344.2469 | 38.4257 | 0.3567 | |
| LR (1st) | 70.9923 | 5039.9049 | 42.5329 | 0.0305 | |
| BMC-GRU | 9.1997 | 84.6347 | 6.5613 | 0.9843 | |
| BiLSTM | 54.1117 | 2928.0795 | 39.6300 | 0.9236 | |
| 2-Layer LSTM | 43.8469 | 1922.5493 | 30.9648 | 0.9499 | |
| PR (4th) | 151.1623 | 22,850.0524 | 114.9986 | 0.4024 | |
| LR (1st) | 176.6161 | 31,193.2329 | 134.5648 | 0.1842 | |
| BMC-GRU | 27.0893 | 733.8281 | 19.9770 | 0.9809 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belge, E.; Keskin, R.; Kutoglu, S.H. Optimizing Vehicle Emission Estimation of On-Road Vehicles Using Deep Learning Frameworks. Appl. Sci. 2025, 15, 12235. https://doi.org/10.3390/app152212235
Belge E, Keskin R, Kutoglu SH. Optimizing Vehicle Emission Estimation of On-Road Vehicles Using Deep Learning Frameworks. Applied Sciences. 2025; 15(22):12235. https://doi.org/10.3390/app152212235
Chicago/Turabian StyleBelge, Egemen, Rıdvan Keskin, and Senol Hakan Kutoglu. 2025. "Optimizing Vehicle Emission Estimation of On-Road Vehicles Using Deep Learning Frameworks" Applied Sciences 15, no. 22: 12235. https://doi.org/10.3390/app152212235
APA StyleBelge, E., Keskin, R., & Kutoglu, S. H. (2025). Optimizing Vehicle Emission Estimation of On-Road Vehicles Using Deep Learning Frameworks. Applied Sciences, 15(22), 12235. https://doi.org/10.3390/app152212235







