Stress-Based Optimization of Components and Supports for Sinter-Based Additive Manufacturing
Abstract
1. Introduction
2. Theoretical Background and Methods Used
2.1. Sinter-Based Additive Manufacturing
2.2. Sinter Supports
2.3. Optimization Algorithms
2.4. Experimental Setup
3. Applied Stress-Based Optimization for Sinter-Based Additive Manufacturing
3.1. Optimization of Components
3.2. Optimization of Sinter Supports
- Break down the geometries (component and component with support) into planes
- Derive the intersection curves of geometries and the respective plane
- Overlay the intersection curves in the respective layer
- Offset the intersection curve of the pure geometry by the thickness of the support coating
- Subtract the enclosed area of this modified intersection curve from the area enclosed by the intersection curve of the optimized geometry
3.3. Optimization with Respect to Stiffness
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BESO | Bi-directional Evolutionary Structural Optimization |
| CAD | Computer-Aided Design |
| CMF | Cold Metal Fusion |
| DED | Directed Energy Deposition |
| ESO | Evolutionary Structural Optimization |
| FEA | Finite Element Analysis |
| LPBF | Laser Powder Bed Fusion |
| MBJ | Metal Binder Jetting |
| MFFF | Metal Fused Filament Fabrication |
| MIM | Metal Injection Molding |
| PM | Powder Metallurgy |
| SBAM | Sinter-based Additive Manufacturing |
| SIMP | Solid Isotropic Material with Penalization |
| SLS | Selective Laser Sintering |
Appendix A
| ID | ||||
|---|---|---|---|---|
| Low_1 | 6.71 | 8.53 | 1.82 | 1.35 |
| Low_2 | 4.55 | 5.95 | 1.39 | |
| Low_3 | 4.54 | 5.41 | 0.87 | |
| Low_4 | 7.51 | 9.16 | 1.65 | |
| Low_5 | 5.82 | 6.59 | 0.77 | |
| Low_6 | 4.12 | 5.32 | 1.20 | |
| Low_7 | 3.83 | 5.16 | 1.32 | |
| Low_8 | 6.30 | 8.07 | 1.77 | |
| Medium_1 | 4.19 | 4.61 | 0.42 | 0.77 |
| Medium_2 | 3.43 | 4.37 | 0.94 | |
| Medium_3 | 1.65 | 2.18 | 0.53 | |
| Medium_4 | 3.52 | 4.73 | 1.21 | |
| Medium_5 | 6.09 | 6.26 | 0.17 | |
| Medium_6 * | 8.00 | 4.08 | −3.92 | |
| Medium_7 | 3.26 | 4.20 | 0.94 | |
| Medium_8 | 4.57 | 5.74 | 1.17 | |
| High_1 | 1.39 | 1.43 | 0.03 | 0.09 |
| High_2 | 0.75 | 0.76 | 0.01 | |
| High_3 | 1.08 | 0.84 | −0.24 | |
| High_4 | 2.01 | 2.43 | 0.42 | |
| High_5 | 1.05 | 1.30 | 0.25 | |
| High_6 | 0.67 | 0.77 | 0.10 | |
| High_7 | 0.72 | 0.59 | −0.13 | |
| High_8 | 1.93 | 2.22 | 0.28 |
References
- Gibson, I.; Rosen, D.; Stucker, B.; Khorasani, M. Additive Manufacturing Technologies; Springer International Publishing: Cham, Switzerland, 2021; ISBN 978-3-030-56126-0. [Google Scholar]
- Presciutti, A.; Gebennini, E.; Liberti, F.; Nanni, F.; Bragaglia, M. Comparative Life Cycle Assessment of SLS and mFFF Additive Manufacturing Techniques for the Production of a Metal Specimen. Materials 2023, 17, 78. [Google Scholar] [CrossRef] [PubMed]
- Mostafaei, A.; Elliott, A.M.; Barnes, J.E.; Li, F.; Tan, W.; Cramer, C.L.; Nandwana, P.; Chmielus, M. Binder Jet 3D Printing—Process Parameters, Materials, Properties, Modeling, and Challenges. Prog. Mater. Sci. 2021, 119, 100707. [Google Scholar] [CrossRef]
- Zhu, B.; Li, R.; Yuan, T.; Li, W.; Cai, D.; Kang, N. Metal Binder Jetting Additive Manufacturing: An Overview of the Process, Materials and Reinforcement Methods. J. Alloys Compd. 2025, 1037, 182196. [Google Scholar] [CrossRef]
- Paudel, B.J.; Conover, D.; Lee, J.-K.; To, A.C. A Computational Framework for Modeling Distortion during Sintering of Binder Jet Printed Parts. J. Micromech. Mol. Phys. 2021, 06, 95–102. [Google Scholar] [CrossRef]
- Paudel, B.J.; Deng, H.; To, A.C. A Physics-Based Data-Driven Distortion Compensation Model for Sintered Binder Jet Parts Considering Size Effects. Addit. Manuf. 2023, 68, 103517. [Google Scholar] [CrossRef]
- Li, Z.-J.; Xiao, P.; Dai, H.-L.; Yao, Y.; Luo, W.-F. Modelling of Geometrical Deformation and Compensation during Sintering of Binder Jetting. Virtual Phys. Prototyp. 2025, 20, e2443958. [Google Scholar] [CrossRef]
- Gözüküçük, F.; Telgkamp, J.; Scharowsky, T.; Tenelsen, C. Sintering Simulation and Validation for the Sinter-Based Fused Filament Fabrication Process Route. Prog. Addit. Manuf. 2025, 10, 10091–10109. [Google Scholar] [CrossRef]
- Stachg, D.; Marter, T.; Telgkamp, J. Green Part Properties as Design Driver for “First Time Right” within Sinter-Based Additive Manufacturing Introduced on the Examples of Cold Metal Fusion and Metal FFF. RTe J. 2025. [Google Scholar] [CrossRef]
- Raether, F.; Seifert, G.; Ziebold, H. Simulation of Sintering across Scales. Adv. Theory Simul. 2019, 2, 1900048. [Google Scholar] [CrossRef]
- Tyflopoulos, E.; Steinert, M. Topology and Parametric Optimization-Based Design Processes for Lightweight Structures. Appl. Sci. 2020, 10, 4496. [Google Scholar] [CrossRef]
- Rosso, S.; Uriati, F.; Grigolato, L.; Meneghello, R.; Concheri, G.; Savio, G. An Optimization Workflow in Design for Additive Manufacturing. Appl. Sci. 2021, 11, 2572. [Google Scholar] [CrossRef]
- Kaschube, D.; Pawlowitz, T.; Solterbeck, C.-H.; Schloesser, J.; Malekan, M.; Bohlmann, B. Fatigue Behavior of Ti-6Al-4 V Alloy Manufactured by Cold Metal Fusion. Fatigue Fract. Eng. Mater. Struct. 2024, 47, 647–661. [Google Scholar] [CrossRef]
- Munsch, M. Reduzierung von Eigenspannungen und Verzug in der Laseradditiven Fertigung. Ph.D. Thesis, Technische Universität Hamburg, Hamburg, Germany, 2013. [Google Scholar]
- Shen, F.; Zhu, W.; Zhou, K.; Ke, L.-L. Modeling the Temperature, Crystallization, and Residual Stress for Selective Laser Sintering of Polymeric Powder. Acta Mech. 2021, 232, 3635–3653. [Google Scholar] [CrossRef]
- Banerjee, S.; Joens, C.J. Debinding and Sintering of Metal Injection Molding (MIM) Components. In Handbook of Metal Injection Molding; Elsevier: Amsterdam, The Netherlands, 2012; pp. 133–180. ISBN 978-0-85709-066-9. [Google Scholar]
- Blunk, H.; Seibel, A. Reduction of Sintering Distortion in Metal Binder Jetting: Measuring Friction under Sintering Conditions. J. Jpn. Soc. Powder Powder Metall. 2025, 72, S1475–S1479. [Google Scholar] [CrossRef]
- Blunk, H.; Huber, N. Resource-Efficient Sintering Supports for the Metal Binder Jetting Process. In Innovative Product Development by Additive Manufacturing 2022; Lachmayer, R., Bode, B., Kaierle, S., Eds.; Springer International Publishing: Cham, Switzerland, 2023; pp. 110–120. ISBN 978-3-031-27260-8. [Google Scholar]
- Meng, L.; Zhang, W.; Quan, D.; Shi, G.; Tang, L.; Hou, Y.; Breitkopf, P.; Zhu, J.; Gao, T. From Topology Optimization Design to Additive Manufacturing: Today’s Success and Tomorrow’s Roadmap. Arch. Computat. Methods Eng. 2020, 27, 805–830. [Google Scholar] [CrossRef]
- Reiher, T.; Deppe, G.; Maasjost, L.; Yu, X. Topology Optimization of Submodels within MSC Nastran Assembly Context Using a Voxel-Based Engineering Approach. In Proceedings of the NAFEMS World Congress 2025, Salzburg, Austria, 19–22 May 2025. [Google Scholar]
- Sauer, A. Bionik in der Strukturoptimierung: Praxishandbuch für Ressourceneffizienten Leichtbau; Vogel Business Media: Würzburg, Germany, 2018; ISBN 978-3-8343-3381-0. [Google Scholar]
- Huang, X.; Xie, Y.-M. A Further Review of ESO Type Methods for Topology Optimization. Struct. Multidisc. Optim. 2010, 41, 671–683. [Google Scholar] [CrossRef]
- Abbey, T. Topology Optimization (Part 2)—FE Training. Available online: https://fetraining.net/topology-optimization-part-2/ (accessed on 26 September 2025).
- ASTM International B988-18R22; Standard Specification for Powder Metallurgy (PM) Titanium and Titanium Alloy Structural Components. ASTM: West Conshohocken, PN, USA, 2022.
- Ibhadode, O.; Zhang, Z.; Sixt, J.; Nsiempba, K.M.; Orakwe, J.; Martinez-Marchese, A.; Ero, O.; Shahabad, S.I.; Bonakdar, A.; Toyserkani, E. Topology Optimization for Metal Additive Manufacturing: Current Trends, Challenges, and Future Outlook. Virtual Phys. Prototyp. 2023, 18, e2181192. [Google Scholar] [CrossRef]
- El Khadiri, I.; Zemzami, M.; Nguyen, N.-Q.; Abouelmajd, M.; Hmina, N.; Belhouideg, S. Topology Optimization Methods for Additive Manufacturing: A Review. Int. J. Simul. Multidisci. Des. Optim. 2023, 14, 12. [Google Scholar] [CrossRef]
- Forward AM Debinding Simulation Guidelines for 3D Printed Parts Using Ultrafuse® 316L. Available online: https://forward-am.com/material-portfolio/ultrafuse-filaments-for-fused-filaments-fabrication-fff/metal-filaments/ultrafuse-316l/ (accessed on 1 September 2025).
- Tang, T.; Wang, L.; Zhu, M.; Zhang, H.; Dong, J.; Yue, W.; Xia, H. Topology Optimization: A Review for Structural Designs Under Statics Problems. Materials 2024, 17, 5970. [Google Scholar] [CrossRef]
- Hexagon AB MSC Apex GD—Stresses, Failure Criteria & Resolution Levels. Available online: https://amendate.atlassian.net/wiki/spaces/ApexGD/pages/3776185310/Stresses+Failure+Criteria+Resolution+Levels (accessed on 15 September 2025).
- Schmidt-Lehr, M.; Führer, T. Design Guideline for Sinter-Based Additive Manufacturing; AMPOWER Insights: Hamburg, Germany, 2021. [Google Scholar]
- Devine, E.; Lester, M.; McElroy, T.; Valenzuela, T.; LePage, W. Mechanical Characterization of Additive-Manufactured Ti-6Al-4V Processed via Bound Metal Deposition. Exp. Mech. 2025, 65, 573–596. [Google Scholar] [CrossRef]
- Urick, B.; Marussig, B.; Cohen, E.; Crawford, R.H.; Hughes, T.J.R.; Riesenfeld, R.F. Watertight Boolean Operations: A Framework for Creating CAD-Compatible Gap-Free Editable Solid Models. Comput.-Aided Des. 2019, 115, 147–160. [Google Scholar] [CrossRef]
- Al-Zuhairi, A.; Nouzille, D.; Teutsch, R. Systematical Redesign Method for Topology Optimized Results Using 3D-Printing. Discov. Mech. Eng. 2023, 2, 11. [Google Scholar] [CrossRef]
- Boissonnat, J.-D. Shape Reconstruction from Planar Cross Sections. Comput. Vis. Graph. Image Process. 1988, 44, 1–29. [Google Scholar] [CrossRef]
- Klein, B.; Gänsicke, T. Leichtbau-Konstruktion: Dimensionierung, Strukturen, Werkstoffe und Gestaltung; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2019; ISBN 978-3-658-26845-9. [Google Scholar]
- Heaney, D.F. Designing for Metal Injection Molding (MIM). In Handbook of Metal Injection Molding; Elsevier: Amsterdam, The Netherlands, 2012; pp. 29–49. ISBN 978-0-85709-066-9. [Google Scholar]
- Mittelstedt, C. Buckling of Beams, Plates and Shells; Springer: Berlin/Heidelberg, Germany, 2024; ISBN 978-3-662-69095-6. [Google Scholar]
- DIN EN ISO 1101:2017; Geometrical Product Specifications (GPS)—Geometrical Tolerancing—Tolerances of Form, Orientation, location and Run-Out (ISO 1101:2017). Deutsches Institut für Normung: Berlin, Germany, 2017. [CrossRef]
- Giraldo-Londoño, O.; Russ, J.B.; Aguiló, M.A.; Paulino, G.H. Limiting the First Principal Stress in Topology Optimization: A Local and Consistent Approach. Struct. Multidisc. Optim. 2022, 65, 254. [Google Scholar] [CrossRef]
- Sadeghi Borujeni, S.; Shad, A.; Abburi Venkata, K.; Günther, N.; Ploshikhin, V. Numerical Simulation of Shrinkage and Deformation during Sintering in Metal Binder Jetting with Experimental Validation. Mater. Des. 2022, 216, 110490. [Google Scholar] [CrossRef]
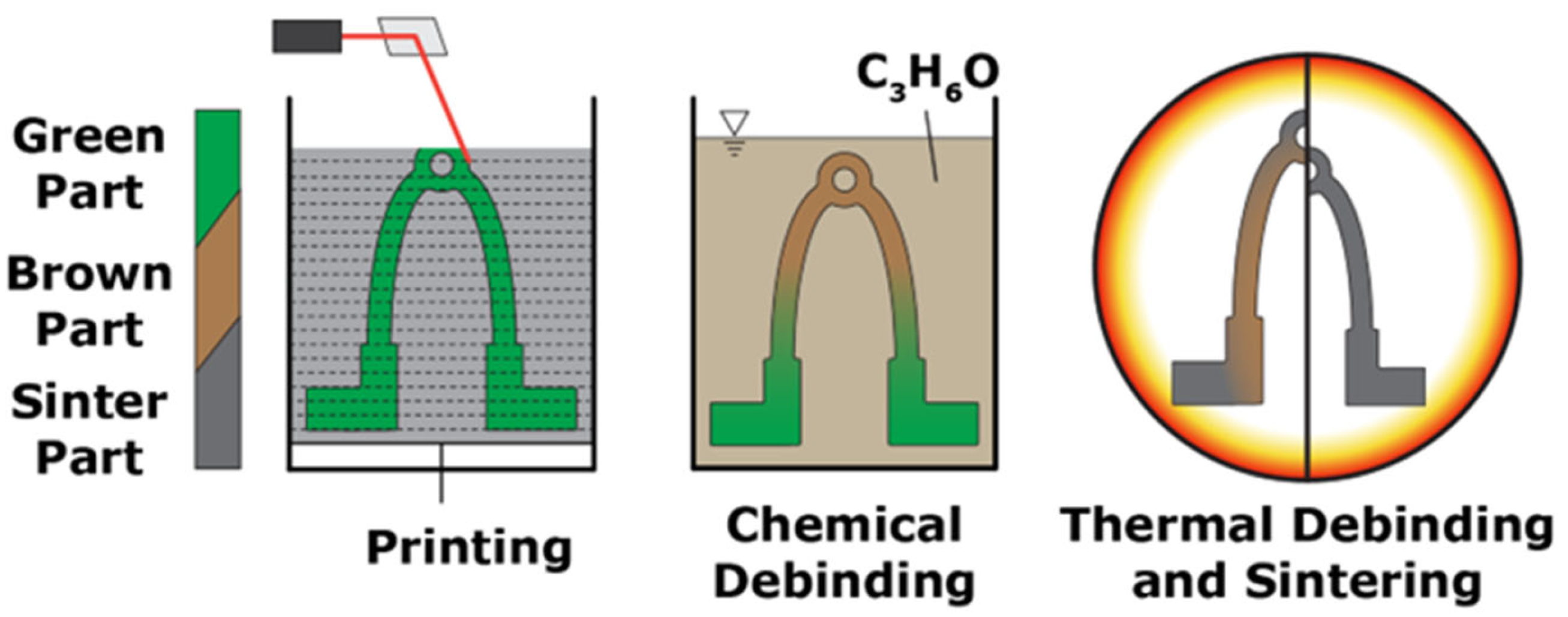


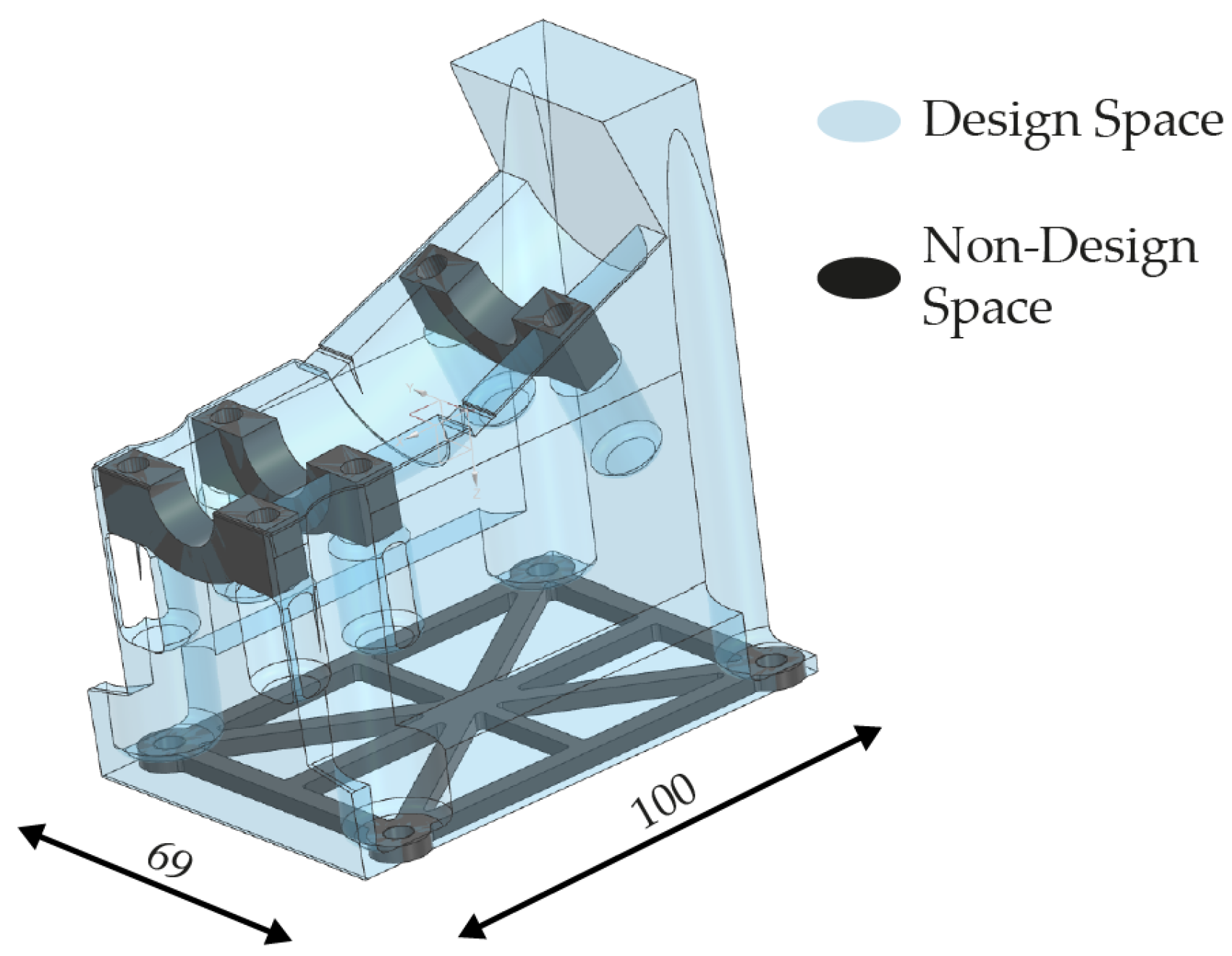
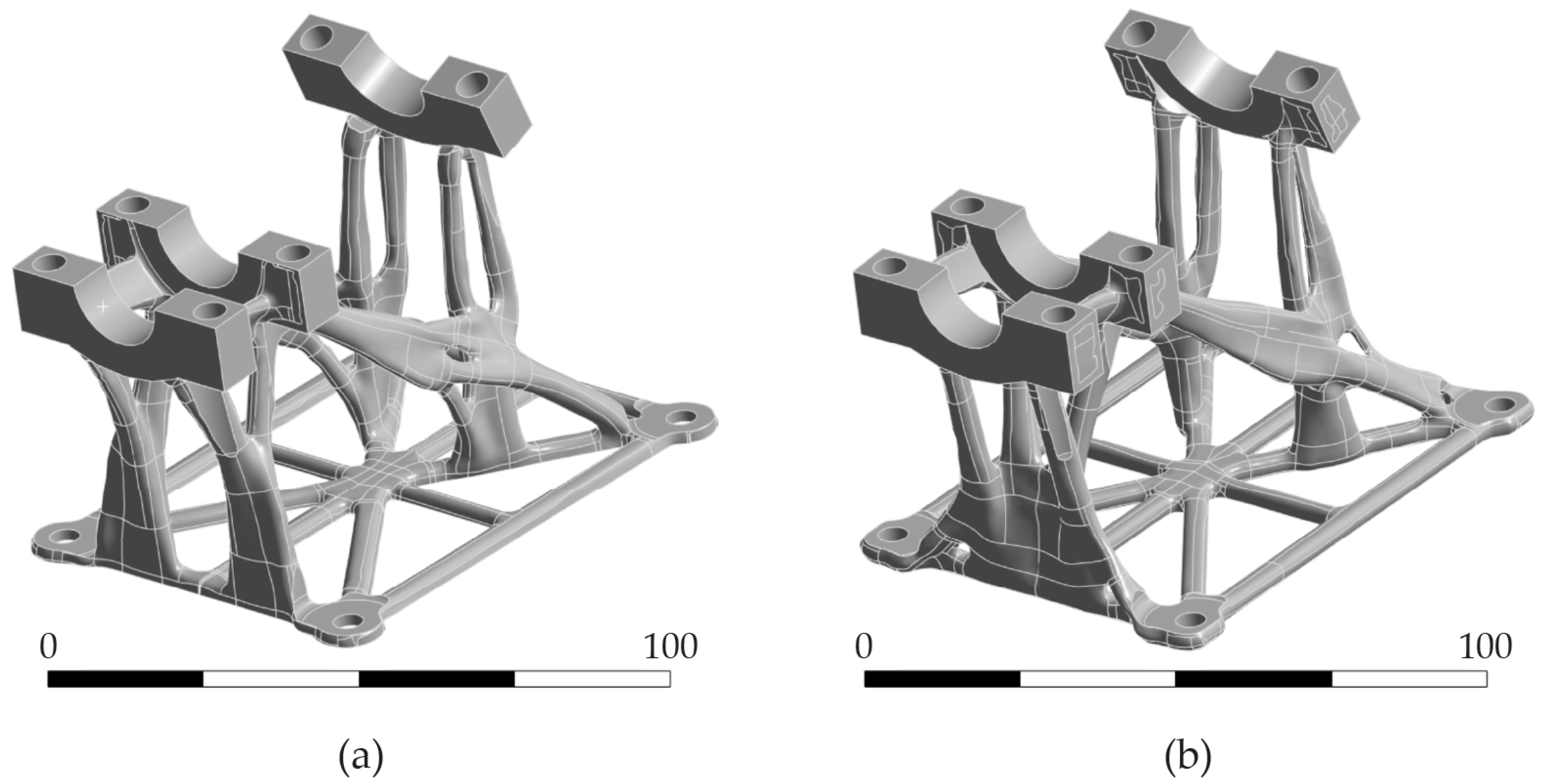

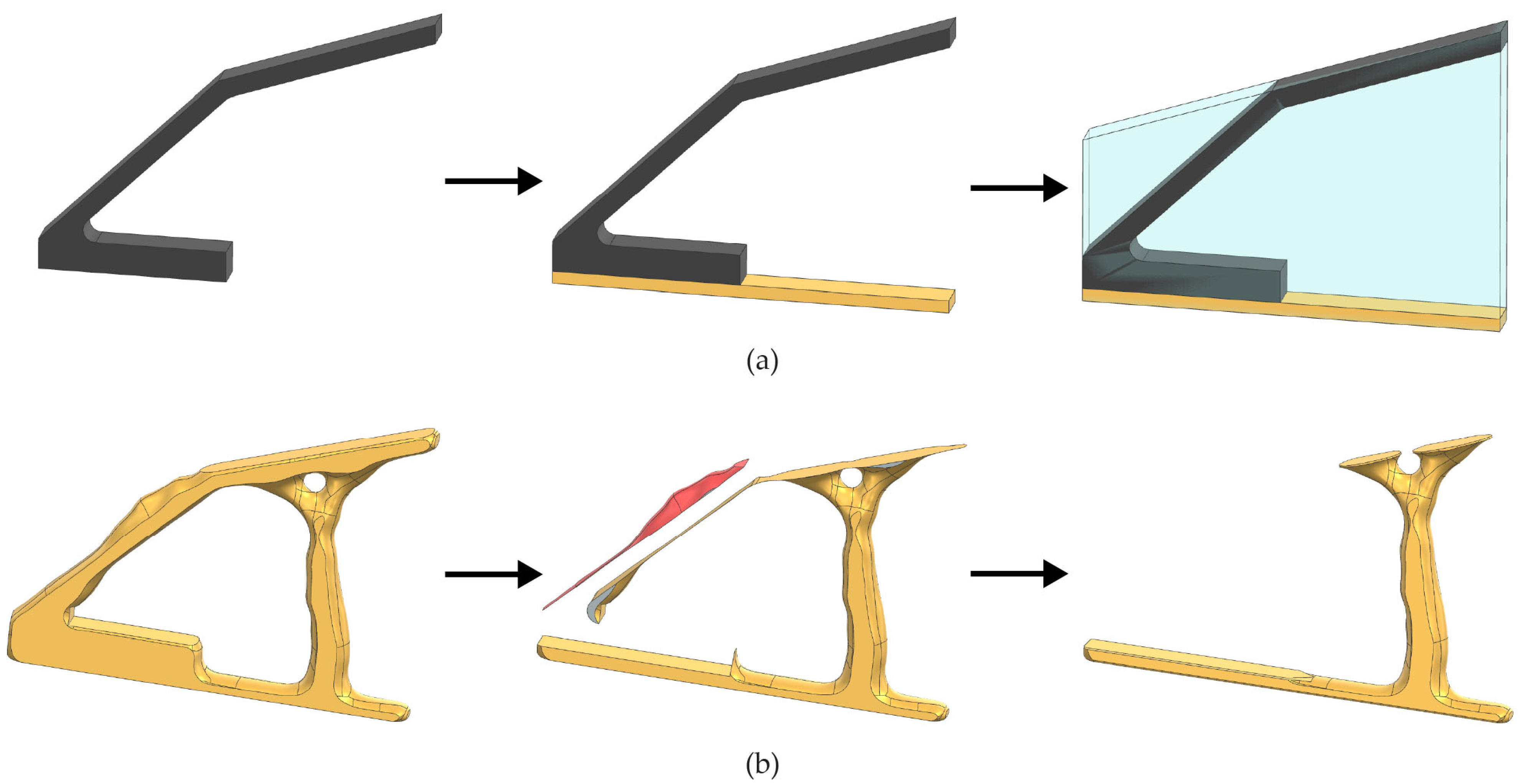

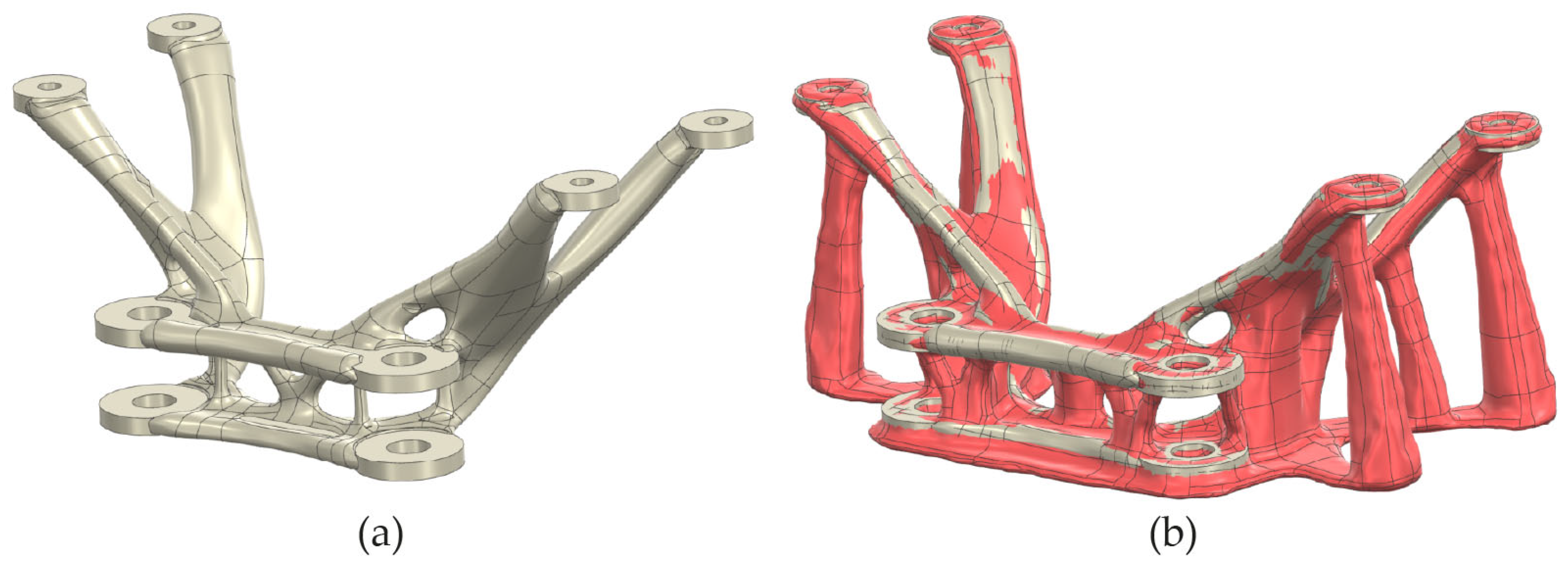
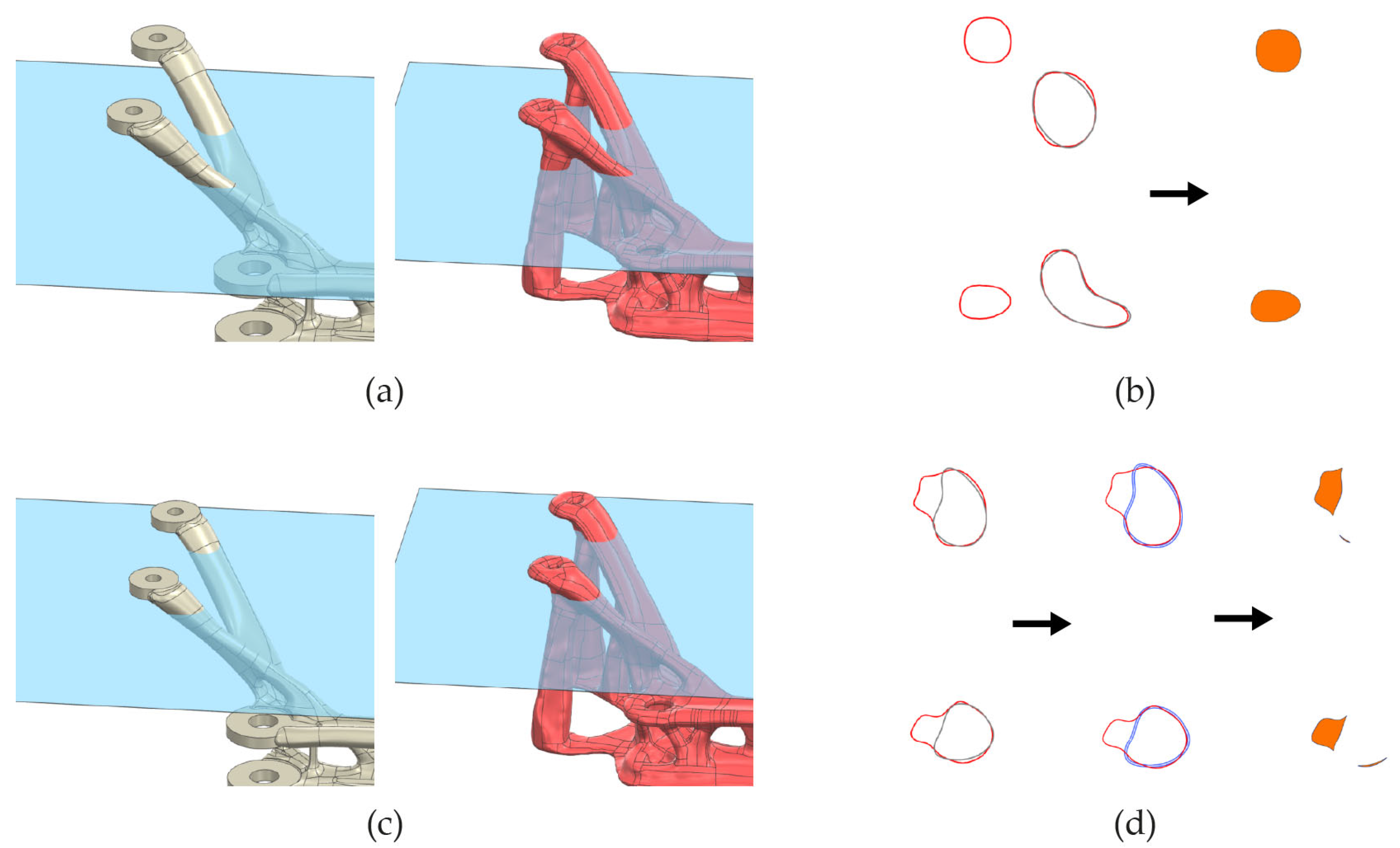

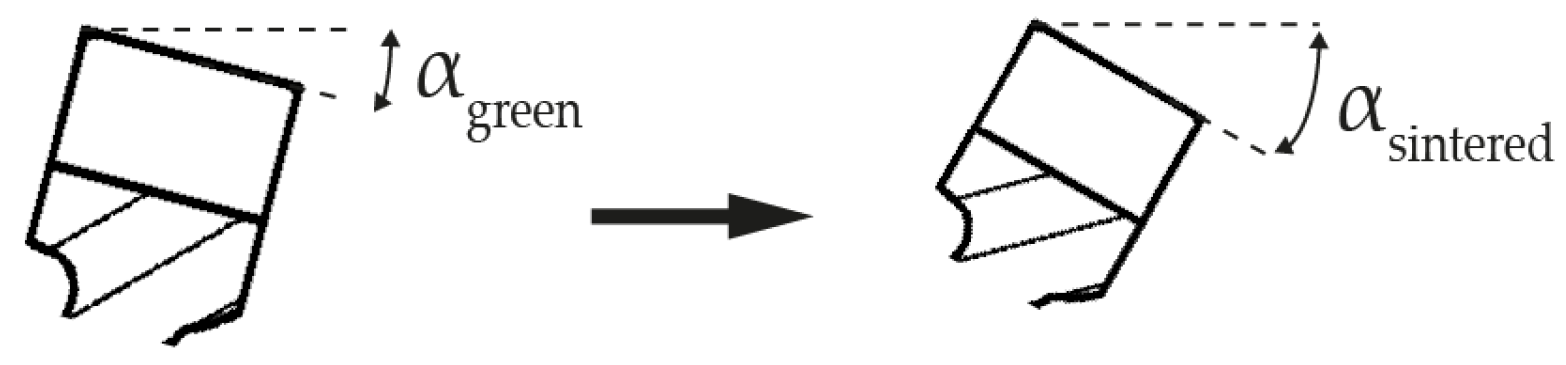
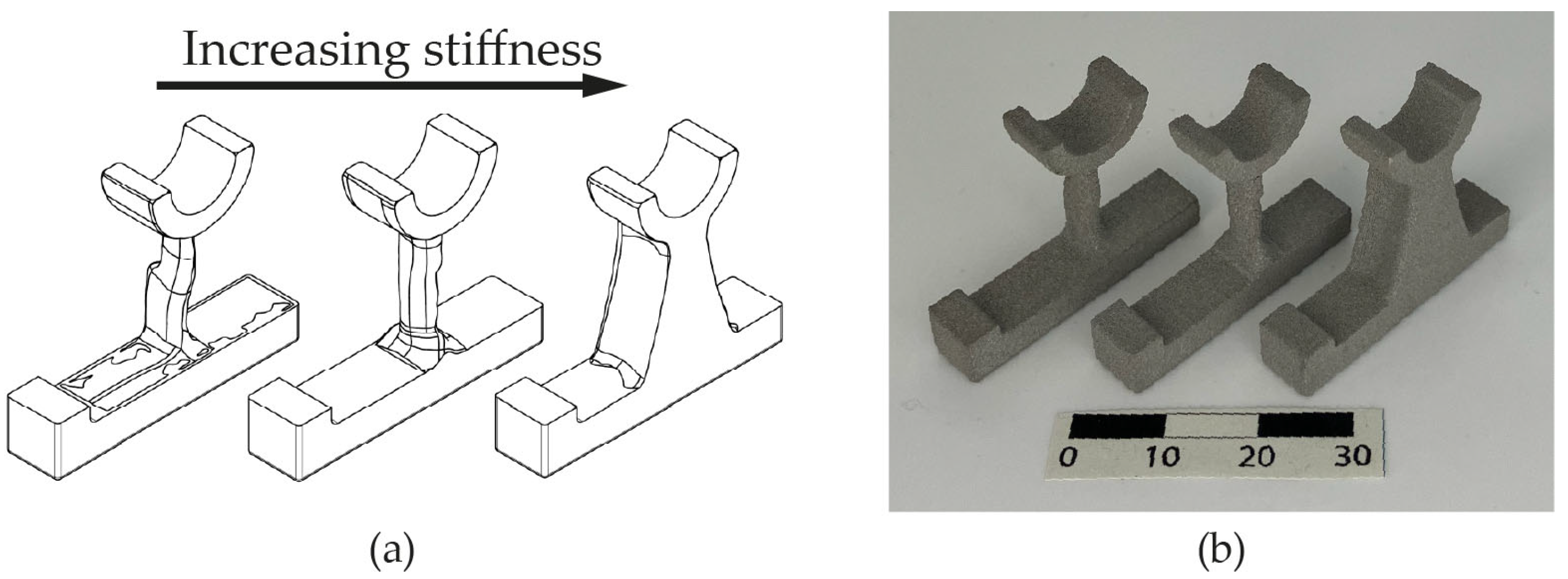
| Alloying Elements in Percent by Weight (%) | ||||||
|---|---|---|---|---|---|---|
| Ti | Al | V | O | Fe | C | N |
| Low | 5.5–6.75 | 3.5–4.5 | ≤0.30 | ≤0.30 | ≤0.05 | ≤0.05 |
| Component | Stress with Respect to Dead Load | Stress with Respect to Critical Load Case | Mass |
|---|---|---|---|
| Previous Workflow | 21.3 kPa | 1251.1 MPa | 116.6 g |
| Revised Workflow | 16.8 kPa | 893.4 MPa | 123.5 g |
| Requirement | Approach |
|---|---|
| Low material consumption | Specimens with few structural elements |
| Deformation/error must be clearly evaluable | Regular/non-freeform geometry as the evaluation object |
| Results should be evaluable in a practical context | Evaluation context: tolerancing |
| Configuration | Results | |||
|---|---|---|---|---|
| Stiffness | Displacement Under Virtual Load (mm) | (°) | SD (°) | (mm) |
| Low | 0.10 | 1.35 | 0.39 | 0.16 |
| Medium | 0.05 | 0.77 | 0.40 | 0.09 |
| High | 0.01 | 0.09 | 0.22 | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stachg, D.; Beckmann, J.; Telgkamp, J. Stress-Based Optimization of Components and Supports for Sinter-Based Additive Manufacturing. Appl. Sci. 2025, 15, 12198. https://doi.org/10.3390/app152212198
Stachg D, Beckmann J, Telgkamp J. Stress-Based Optimization of Components and Supports for Sinter-Based Additive Manufacturing. Applied Sciences. 2025; 15(22):12198. https://doi.org/10.3390/app152212198
Chicago/Turabian StyleStachg, David, Jaco Beckmann, and Jens Telgkamp. 2025. "Stress-Based Optimization of Components and Supports for Sinter-Based Additive Manufacturing" Applied Sciences 15, no. 22: 12198. https://doi.org/10.3390/app152212198
APA StyleStachg, D., Beckmann, J., & Telgkamp, J. (2025). Stress-Based Optimization of Components and Supports for Sinter-Based Additive Manufacturing. Applied Sciences, 15(22), 12198. https://doi.org/10.3390/app152212198






