Experimental Investigation of Local Wind Effects on Façade Scaffolding Structures
Abstract
1. Introduction
2. Materials and Methods
2.1. Scaffolding Structures
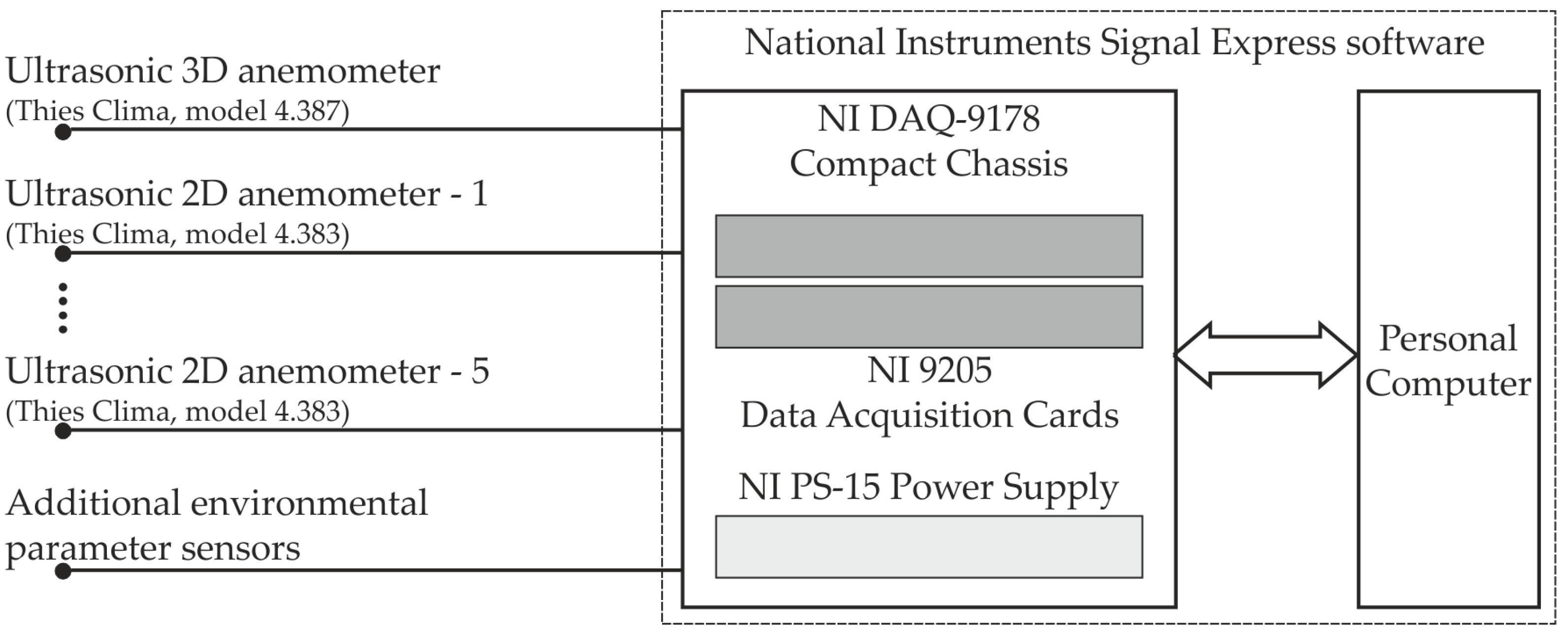
2.2. Instrumentation and Data Collection
3. Results
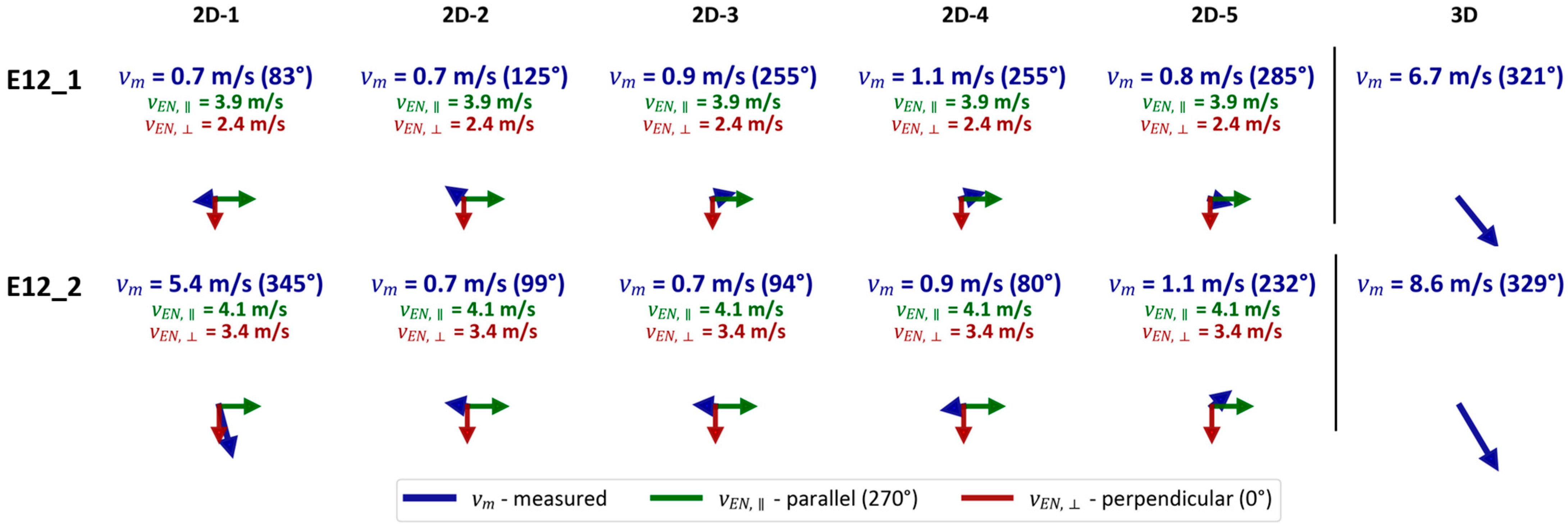
3.1. Instantaneous Time Histories
3.2. Data Processing and Directional Analysis
3.3. Normative Comparison Methodology
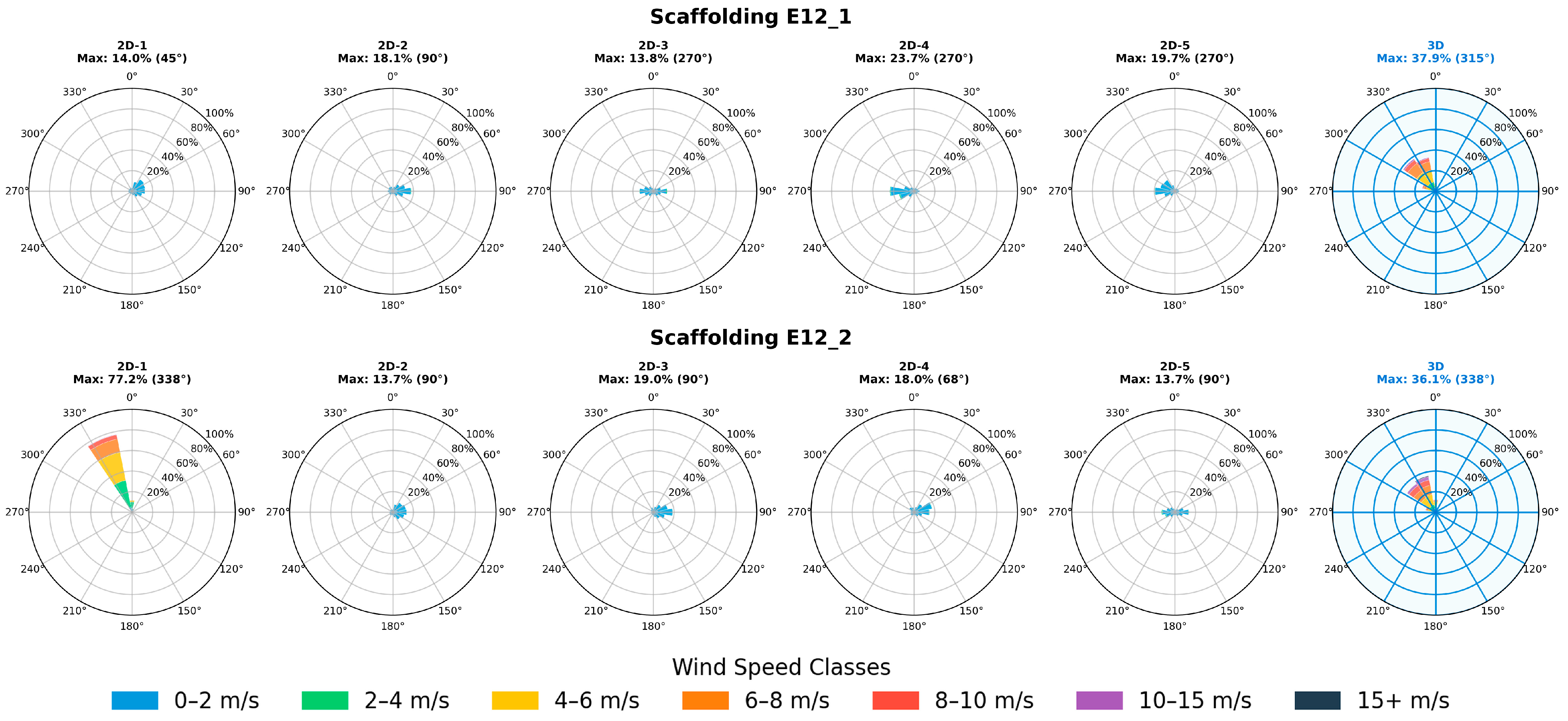
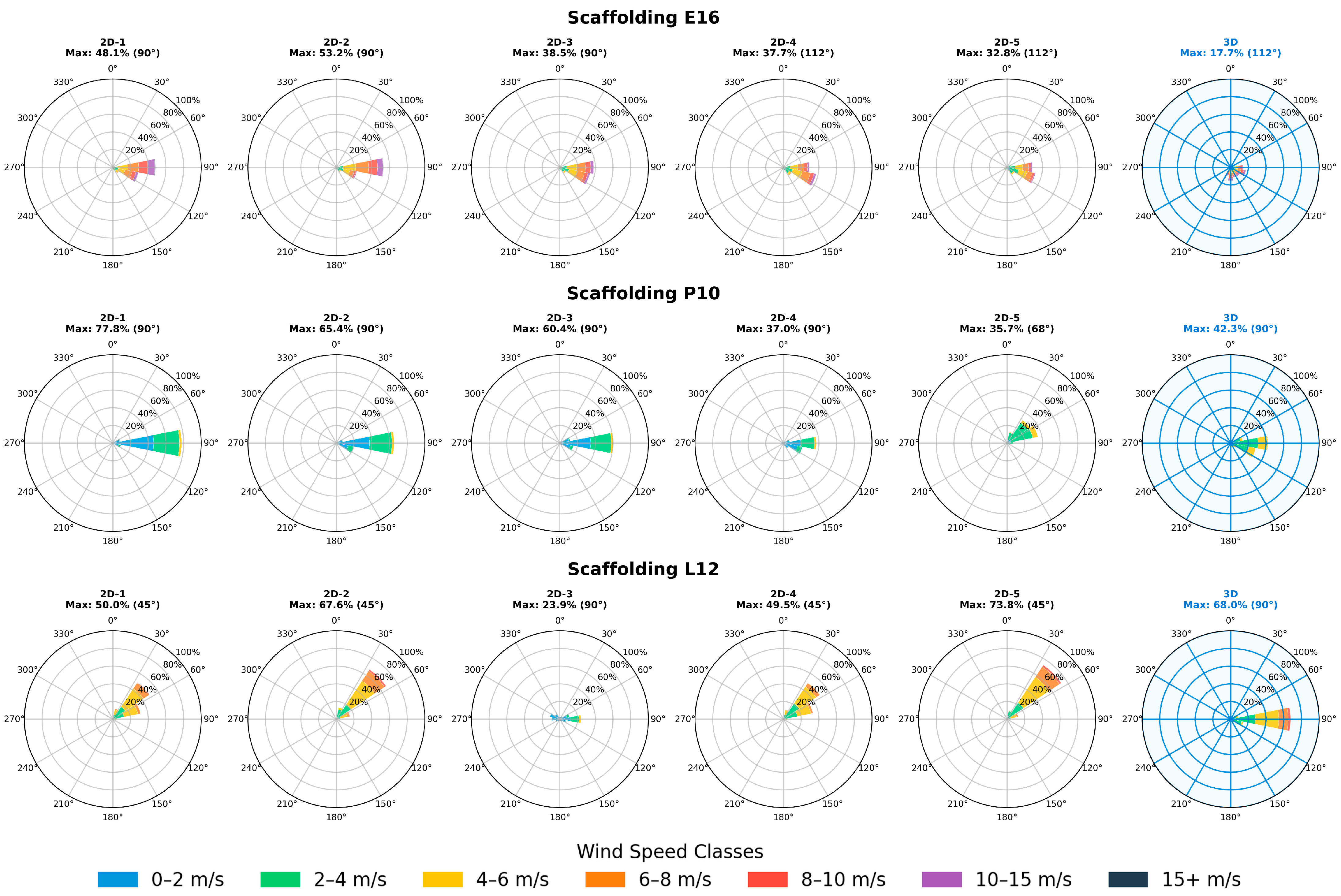
3.4. Case Studies: Wind Velocity Patterns
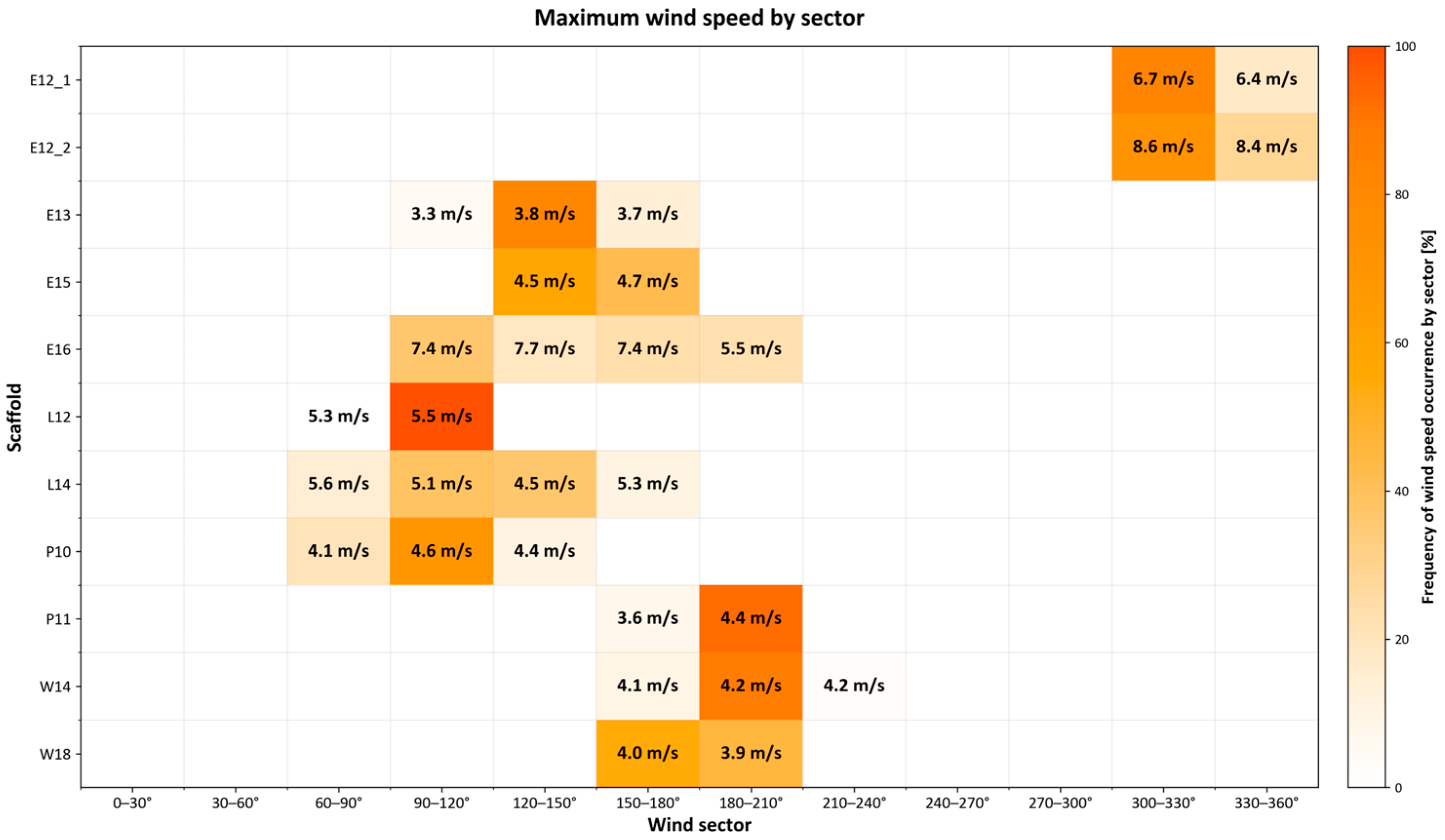
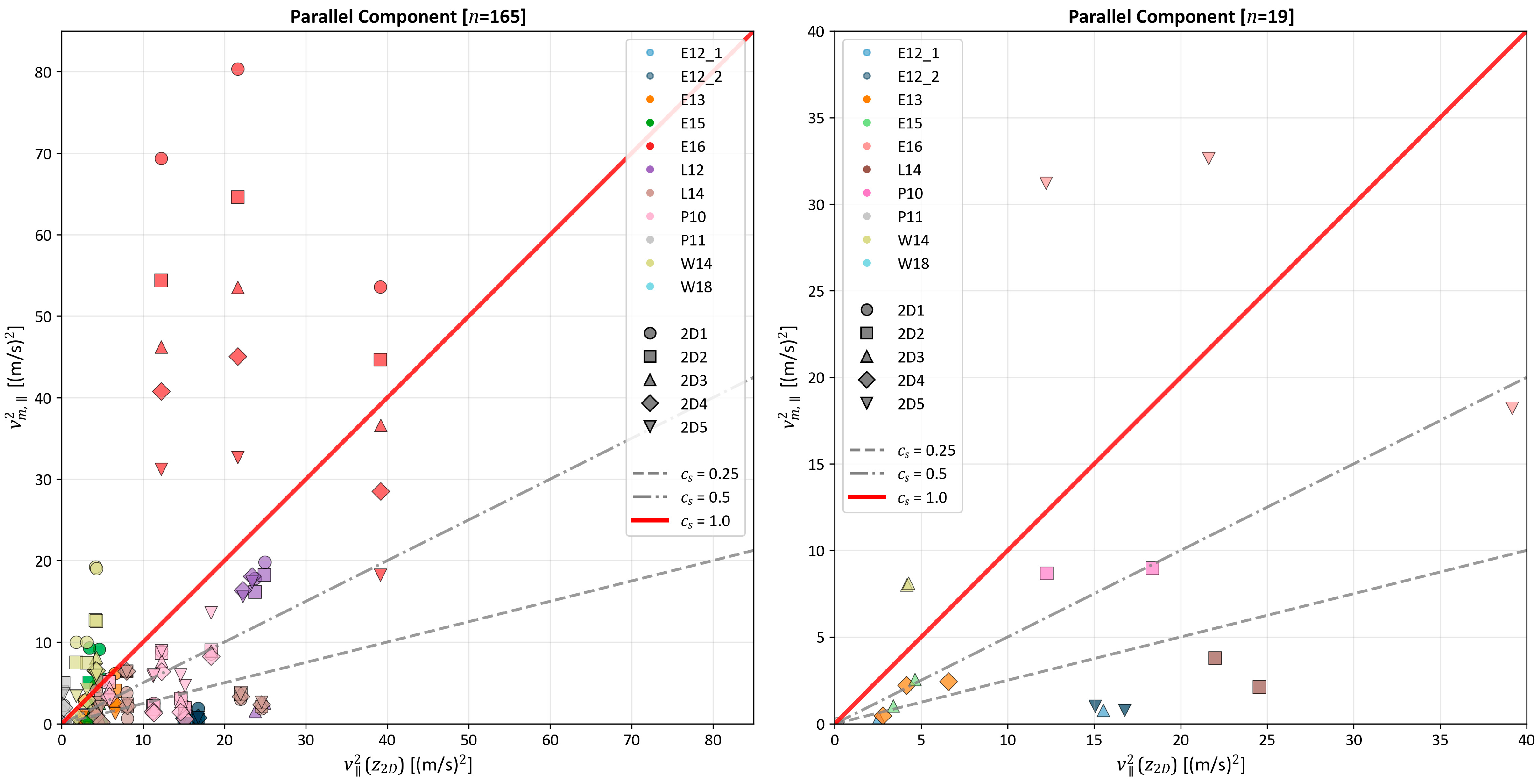
3.5. Assessment of Normative Site Coefficients
4. Discussion
4.1. Physical Mechanisms and Limitations of Normative Model
4.2. Component-Specific Flow Characteristics
4.3. Effectiveness of Protective Netting
4.4. Design and Safety Implications
4.5. Limitations and Future Research
- High-frequency measurements to characterise peak gust factors and their spatial variation across scaffold surfaces.
- Systematic investigation of net performance under varying wind velocities to quantify their impact on pressures on scaffold surfaces.
- Extended measurement campaigns across diverse building types, heights, and climatic regions to develop generalised position-dependent site factor relationships.
- Validation of computational fluid dynamics models against the full-scale dataset to establish best practices for numerical prediction.
5. Conclusions
- Wind velocities across scaffold surfaces exhibit extreme spatial variability. The squared velocity ratios ranged from below 0.1 in sheltered mid-façade positions to above 1.0 at windward corners and edges. Flow acceleration occurs at exposed corners and edges, while mid-façade and recessed zones experience velocity reduction and strong directional deviations due to boundary layer and flow separation effects.
- Current normative site factors [1] provide generally conservative estimates for mid-façade positions under typical wind conditions. For parallel and perpendicular wind directions, 79% and 83% of mid-façade measurements fell below the code-prescribed values, respectively. However, at windward corners and edges, the actual wind loads frequently exceeded the code predictions, with exceedances up to 20% under normal conditions and over 100% during storm events. For scaffolds with protective netting, the nominal does not consistently the capture observed reductions in wind velocities, particularly in more exposed positions.
- The parallel flow component exhibits substantial scatter and site-dependent variability, whereas the perpendicular component is strongly damped by the façade presence and netting. Mid-façade perpendicular velocities were generally below the normative reference. Edge and corner positions remained exceptions due to local acceleration effects.
- The results demonstrate that a uniform site factor is insufficient to describe the spatially variable aerodynamic environment of scaffolds. Position-specific site factors are recommended. Site-specific analyses should be considered for large or complex structures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- EN 12811-1:2003; Temporary Works Equipment—Part 1: Scaffolds—Performance and General Design. PKN: Warsaw, Poland, 2003.
- Richards, P.J.; Hoxey, R.P. Pressures on a Cubic Building-Part 1: Full-Scale Results. J. Wind Eng. Ind. Aerodyn. 2012, 102, 72–86. [Google Scholar] [CrossRef]
- Li, Q.S.; Xiao, Y.Q.; Wong, C.K.; Jeary, A.P. Field Measurements of Wind Effects on the Tallest Building in Hong Kong. Struct. Des. Tall Spec. Build. 2003, 12, 67–82. [Google Scholar] [CrossRef]
- Li, Q.S.; Xiao, Y.Q.; Wong, C.K.; Jeary, A.P. Field Measurements of Typhoon Effects on a Super Tall Building. Eng. Struct. 2004, 26, 233–244. [Google Scholar] [CrossRef]
- Yang, L.; Gurley, K.R.; Prevatt, D.O. Probabilistic Modeling of Wind Pressure on Low-Rise Buildings. J. Wind Eng. Ind. Aerodyn. 2013, 114, 18–26. [Google Scholar] [CrossRef]
- Goliber, M.; Sritharan, S.; Sarkar, P. An Investigation of the Accuracy of Pressure Measurements and Pressure Interpolation on the Roof of a Low-Rise Building; Iowa State University: Ames, IA, USA, 2010. [Google Scholar]
- Charisi, S.; Thiis, T.K.; Aurlien, T. Full-Scale Measurements of Wind-Pressure Coefficients in Twin Medium-Rise Buildings. Buildings 2019, 9, 63. [Google Scholar] [CrossRef]
- Zhou, L.; Zhu, Q.; Tse, K.T.; Ning, X.; Ai, Y.; Zhang, H. Flow Pattern- and Forces-Susceptibility to Small Attack Angles for a Rectangular Cylinder. Ocean Eng. 2024, 300, 117376. [Google Scholar] [CrossRef]
- Richardson, G.M.; Hoxey, R.P.; Robertson, A.P.; Short, J.L. The Silsoe Structures Building: Comparisons of Pressures Measured at Full Scale and in Two Wind Tunnels. J. Wind Eng. Ind. Aerodyn. 1997, 72, 187–197. [Google Scholar] [CrossRef]
- Irtaza, H.; Beale, R.G.; Godley, M.H.R. A Wind-Tunnel Investigation into the Pressure Distribution around Sheet-Clad Scaffolds. J. Wind Eng. Ind. Aerodyn. 2012, 103, 86–95. [Google Scholar] [CrossRef]
- Geurts, C.P.W. Full-Scale and Wind-Tunnel Measurements of the Wind and Wind-Induced Pressures over Suburban Terrain. J. Wind Eng. Ind. Aerodyn. 1996, 64, 89–100. [Google Scholar] [CrossRef]
- Liu, J.; Hui, Y.; Yang, Q.; Zhang, R. LES Evaluation of the Aerodynamic Characteristics of High-Rise Building with Horizontal Ribs under Atmospheric Boundary Layer Flow. J. Build. Eng. 2023, 71, 106487. [Google Scholar] [CrossRef]
- Elshaer, A.; Aboshosha, H.; Bitsuamlak, G.; El Damatty, A.; Dagnew, A. LES Evaluation of Wind-Induced Responses for an Isolated and a Surrounded Tall Building. Eng. Struct. 2016, 115, 179–195. [Google Scholar] [CrossRef]
- Yu, X.; Xie, Z.; Gu, M. Interference Effects between Two Tall Buildings with Different Section Sizes on Wind-Induced Acceleration. J. Wind Eng. Ind. Aerodyn. 2018, 182, 16–26. [Google Scholar] [CrossRef]
- Montazeri, H.; Blocken, B. CFD Simulation of Wind-Induced Pressure Coefficients on Buildings with and without Balconies: Validation and Sensitivity Analysis. Build. Environ. 2013, 60, 137–149. [Google Scholar] [CrossRef]
- Zhang, A.; Gao, C.; Zhang, L. Numerical Simulation of the Wind Field around Different Building Arrangements. J. Wind Eng. Ind. Aerodyn. 2005, 93, 891–904. [Google Scholar] [CrossRef]
- Xia, Y.; Shen, Y.; Yuan, J.; Chen, S. Numerical and Experimental Study on Flow Field around Slab-Type High-Rise Residential Buildings. Sustainability 2023, 15, 12685. [Google Scholar] [CrossRef]
- Wang, F.; Tamura, Y.; Yoshida, A. Wind Loads on Clad Scaffolding with Different Geometries and Building Opening Ratios. J. Wind Eng. Ind. Aerodyn. 2013, 120, 37–50. [Google Scholar] [CrossRef]
- Wang, F.; Tamura, Y.; Yoshida, A. Interference Effects of a Neighboring Building on Wind Loads on Scaffolding. J. Wind Eng. Ind. Aerodyn. 2014, 125, 1–12. [Google Scholar] [CrossRef]
- Yang, Z.; Xie, Q.; Li, Y.; He, C.; Yang, Z.; Xie, Q.; Li, Y.; He, C. Wind Load Parameters and Performance of an Integral Steel Platform Scaffold System. Wind Struct. 2023, 36, 263. [Google Scholar] [CrossRef]
- Fang, T.; Gong, J.; Dong, X.; Li, Y.; Cui, W.; Feng, Y. Aerodynamic Characteristics and Structural Effects of Suspending Scaffolds for Super High-Rise Building Construction. J. Build. Eng. 2025, 107, 112718. [Google Scholar] [CrossRef]
- Fang, F.M.; Chang, S.X.; Chung, C.Y.; Li, Y.C.; Lin, C.C.; Huang, C.H. Investigations on the Wind Force and Flow of a Scaffolding System. J. Chin. Inst. Eng. 2021, 44, 305–318. [Google Scholar] [CrossRef]
- Irtaza, H. Experimental and Computational Determination of Wind Loads on Netted/Sheeted Scaffold. Ph.D. Thesis, Oxford Brookes University, Oxford, UK, 2009. [Google Scholar]
- Hrischev, L.; Slavchev, V.; Tepeliev, V.; Dinev, D.; Angelova, R. Influence of Wind Loads on Façade Scaffolds Covered with Different Types of Nets. IOP Conf. Ser. Mater. Sci. Eng. 2020, 951, 012024. [Google Scholar] [CrossRef]
- Agarwal, A.; Irtaza, H. Turbulent Wind Flow through Permeable Claddings Mounted on Elevated Scaffold Using CFD Simulation. Eng. Rep. 2020, 3, e12350. [Google Scholar] [CrossRef]
- Cao, Q.; Huang, Y.; Chen, B.; Wu, P.; Zhang, S.; Liang, M.; Wei, L.; Huang, L. Performance Study of External Scaffolding under Wind-Induced Action. J. Phys. Conf. Ser. 2023, 2458, 012029. [Google Scholar] [CrossRef]
- Isobe, D.; Tago, T. One-Way Fluid–Structure Coupled Analysis of a Construction Scaffolding under Wind Loads. J. Civ. Eng. Constr. 2025, 14, 71–87. [Google Scholar] [CrossRef]
- Pieńko, M.; Błazik-Borowa, E. Verification of the Numerical Model of Insert-Type Joint of Scaffolding in Relation to Experimental Research. AIP Conf. Proc. 2018, 1922, 80003. [Google Scholar] [CrossRef]
- Abdel-Jaber, M.; Abdel-Jaber, M.S.; Beale, R.G. An Experimental Study into the Behaviour of Tube and Fitting Scaffold Structures under Cyclic Side and Vertical Loads. Metals 2022, 12, 40. [Google Scholar] [CrossRef]
- Błazik-Borowa, E.; Robak, A.; Pieńko, M.; Czepiżak, D. The Measurement of Axial Forces in Scaffolding Standards. Measurement 2023, 223, 113770. [Google Scholar] [CrossRef]
- Bęc, J.; Błazik-Borowa, E.; Szer, J. Analysis of Scaffolding Harmonic Excitation. Bull. Pol. Acad. Sci. Tech. Sci. 2023, 71, e144577. [Google Scholar] [CrossRef]
- Bęc, J. Influence of Anchoring and Bracing System on Dynamic Characteristics of Façade Scaffolding. Arch. Civ. Eng. 2023, 69, 493–506. [Google Scholar] [CrossRef]
- Yue, F.; Yuan, Y.; Li, G.; Ye, K.; Chen, Z.; Wang, Z. Wind Load on Integral-Lift Scaffolds for Tall Building Construction. J. Struct. Eng. 2005, 131, 816–824. [Google Scholar] [CrossRef]
- Lipecki, T.; Jamińska-Gadomska, P.; Bęc, J.; Błazik-Borowa, E. Façade Scaffolding Behaviour under Wind Action. Arch. Civ. Mech. Eng. 2020, 20, 27. [Google Scholar] [CrossRef]
- Lipecki, T.; Jamińska-Gadomska, P.; Błazik-Borowa, E. Wind Load on Façade Scaffolding without Protective Cover—Eurocode and in-Situ Measurement Approaches. J. Build. Eng. 2021, 42, 102516. [Google Scholar] [CrossRef]
- Ohdo, K. Introduction. In Specific Research Reports (SRR-No.31); National Institute of Industrial Safety: Tokyo, Japan, 2005; pp. 1–8. Available online: https://www.jniosh.johas.go.jp/en/publication/srr/srr-no31.html (accessed on 28 October 2025).
- Ohdo, K.; Takanashi, S.; Hino, Y.; Saito, K. Measurement of Wind Load Acting on the Scaffolds. In Specific Research Reports (SRR-No.31); National Institute of Industrial Safety: Tokyo, Japan, 2005; pp. 9–18. Available online: https://www.jniosh.johas.go.jp/en/publication/srr/srr-no31.html (accessed on 28 October 2025).
- Hino, Y.; Sato, N.; Phongkumsing, S.; Ohdo, K.; Takanashi, S. The Predictability of Wind Pressure Acting on the Actual Scaffolds by the Wind Tunnel Test. In Specific Research Reports (SRR-No.31); National Institute of Industrial Safety: Tokyo, Japan, 2005; pp. 19–26. Available online: https://www.jniosh.johas.go.jp/en/publication/srr/srr-no31.html (accessed on 28 October 2025).
- Hino, Y.; Ohdo, K. Study on a New Reinforcement Method of Temporary Scaffolds. In Specific Research Reports (SRR-No.31); National Institute of Industrial Safety: Tokyo, Japan, 2005; pp. 43–50. Available online: https://www.jniosh.johas.go.jp/en/publication/srr/srr-no31.html (accessed on 28 October 2025).
- Wang, J.; Wang, F.; Chen, X.; Wei, J.; Ma, J. Investigation of Wind Load Characteristics of Cantilevered Scaffolding of a High-Rise Building Based on Field Measurement. Energy Build. 2025, 328, 115123. [Google Scholar] [CrossRef]
- Sumorek, A. The measurement system of wind load of facade scaffolding. Inform. Control Meas. Econ. Environ. Prot. 2016, 6, 37–42. [Google Scholar] [CrossRef]
- Lipecki, T.; Jamińska, P.; Sumorek, A.; Błazik-Borowa, E.; Bęc, J. A System for Measuring Environmental Data in Full-Scale. J. Phys. Conf. Ser. 2018, 1101, 012019. [Google Scholar] [CrossRef]
- Lipecki, T.; Jamińska-Gadomska, P.; Sumorek, A. Influence of Ultrasonic Wind Sensor Position on Measurement Accuracy under Full-Scale Conditions. Sensors 2020, 20, 5640. [Google Scholar] [CrossRef] [PubMed]
- EN 1991-1-4:2008; Eurocode 1: Actions on Structures. Part 1–4: General Actions-Wind Actions. PKN: Warsaw, Poland, 2008.
- Wieringa, J. Gust Factors over Open Water and Built-up Country. Bound. Layer Meteorol. 1973, 3, 424–441. [Google Scholar] [CrossRef]





| Scaffold | Location Along the Wall | Photo | Location of 2D Sensors | Hmax [m] | L [m] |
|---|---|---|---|---|---|
| E12 |  |  | 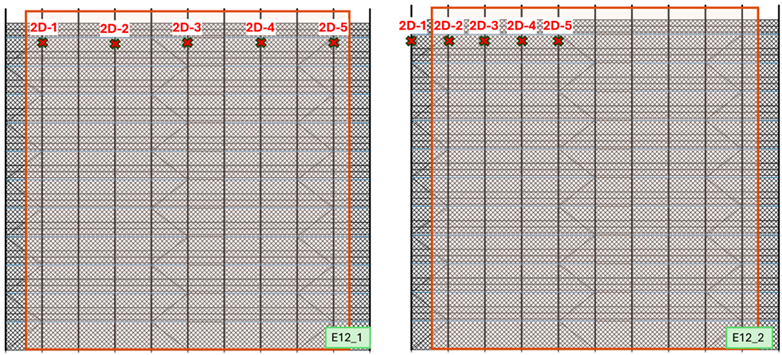 | 24.2 | 25.7 |
| E13 |  |  | 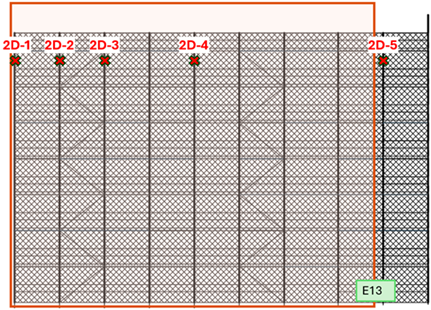 | 15.3 | 23.0 |
| E16 |  |  | 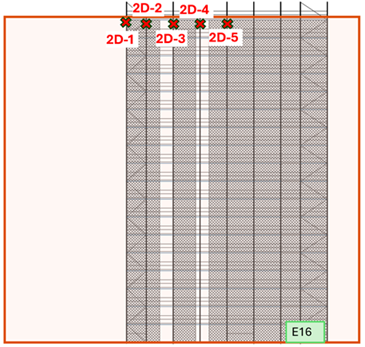 | 38.2 | 22.5 |
| Scaffold | Location Along the Wall | Photo | Location of 2D Sensors | Hmax [m] | L [m] |
|---|---|---|---|---|---|
| E15 |  |  | 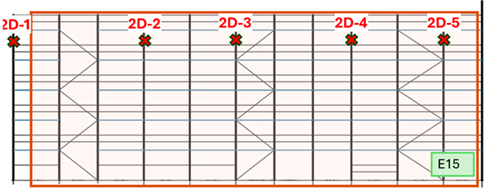 | 11.4 | 31.3 |
| L12 |  |  | 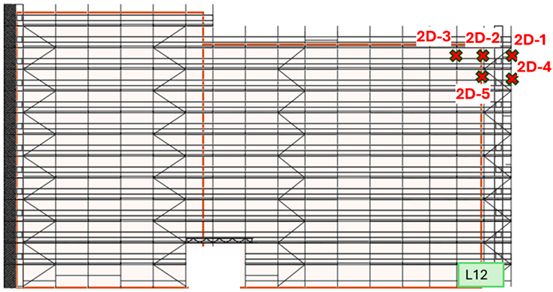 | 32.0 | 45.0 |
| L14 |  |  | 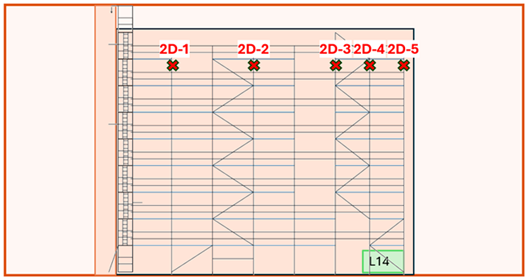 | 18.0 | 20.0 |
| P10 |  |  | 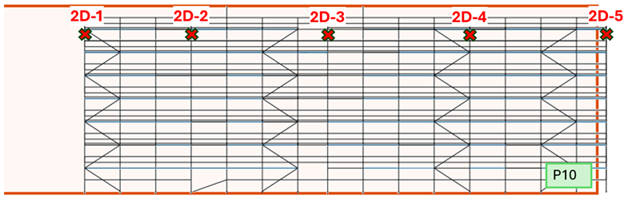 | 16.2 | 45.1 |
| P11 |  |  | 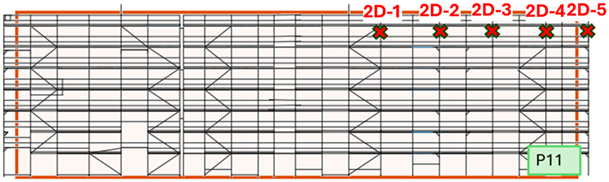 | 16.2 | 54.9 |
| W14 |  |  | 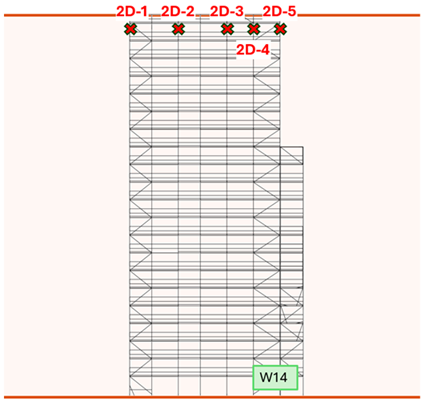 | 43.1 | 17.0 |
| W18 |  |  |  | 53.8 | 23.6 |
| Speed Range | Speed Accuracy v [m/s] | Speed Resolution | Direction Accuracy v [m/s] | Direction Resolution | |
|---|---|---|---|---|---|
| 2D | 0.01–75 m/s | ±0.2 m/s (v < 5) ±2% (5 < v < 60) | 0.01 m/s | ±2° (v > 1) | 0.1° |
| 3D | 0.01–85 m/s | ±0.1 m/s (v < 5) ±1% (5 < v < 35) ±2% (35 < v < 85) | 0.01 m/s | ±1° (1 < v < 35) ±2° (35 < v < 65) ±4° (65 < v < 85) ±2° (v > 1) | 0.1° |
| Terrain Category | [m] | [m] | [m] | Net | [-] | [-] | |
|---|---|---|---|---|---|---|---|
| E12 | IV | 1 | 26.3 | 21 | + | 0.25 | 0.25 |
| E13 | IV | 1 | 18 | 13 | + | 0.25 | 0.25 |
| E15 | IV | 1 | 13.5 | 9 | − | 1 | 0.25 |
| E16 | IV | 1 | 40 | 33 | + | 0.25 | 0.25 |
| L12 | IV | 1 | 29 | 21.5 | − | 1 | 0.25 |
| L14 | IV | 1 | 20 | 15.5 | − | 1 | 0.25 |
| P10 | II | 0.05 | 19 | 13.5 | − | 1 | 0.25 |
| P11 | IV | 1 | 17 | 13.5 | − | 1 | 0.25 |
| W14 | IV | 1 | 46 | 41 | − | 1 | 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jamińska-Gadomska, P.; Sumorek, A. Experimental Investigation of Local Wind Effects on Façade Scaffolding Structures. Appl. Sci. 2025, 15, 12196. https://doi.org/10.3390/app152212196
Jamińska-Gadomska P, Sumorek A. Experimental Investigation of Local Wind Effects on Façade Scaffolding Structures. Applied Sciences. 2025; 15(22):12196. https://doi.org/10.3390/app152212196
Chicago/Turabian StyleJamińska-Gadomska, Paulina, and Andrzej Sumorek. 2025. "Experimental Investigation of Local Wind Effects on Façade Scaffolding Structures" Applied Sciences 15, no. 22: 12196. https://doi.org/10.3390/app152212196
APA StyleJamińska-Gadomska, P., & Sumorek, A. (2025). Experimental Investigation of Local Wind Effects on Façade Scaffolding Structures. Applied Sciences, 15(22), 12196. https://doi.org/10.3390/app152212196






