Viola–Jones Algorithm in a Bioindicative Holographic Experiment with Daphnia magna Population

Abstract

This study considers the applicability and effectiveness of the Viola–Jones method to automatically distinguish zooplankton particles from the background in images reconstructed from digital holograms obtained in natural conditions. For the first time, this algorithm is applied to holographic images containing coherent noise and residual defocusing. The method was trained on 880 annotated (marked) holographic images of Daphnia magna along with 120 background frames. It was then tested on independent laboratory and field datasets, including morphologically related taxa. With optimized settings, the precision of the algorithm reached ~90% and F1~85% on noisy holographic images, and the algorithm also demonstrated the preliminary ability to recognize similar taxa without retraining. The algorithm is well suited for analyzing holographic data as a fast and resource-efficient pre-filter—it effectively separates particles from the background and thereby allows subsequent classification or its application in real-time aquatic environment monitoring systems. The article presents experimental results demonstrating the efficiency of this algorithm during plankton monitoring in situ.

1. Introduction

Zooplankton is a sensitive bioindicator of water quality and may be used as a sensor of ecological monitoring in an aquatic medium. Changes in the behavioral parameters of plankton reflect changes in the environment already at the early stages of their appearance, including water temperature fluctuations, presence of pollutants, availability of nutrients and the general state of ecosystems [1,2,3].

Continuous monitoring of zooplankton ensures adequate interpretation of the dynamics of marine ecosystems and their response to anthropogenic and natural impacts [4,5]. This confirms the need for automated noninvasive methods of analysis to monitor zooplankton in the habitat and in real time. Indicator responses of plankton to external impacts differ depending on the species present in the biocenosis, which causes the need for automatic classification of plankton individuals.

One of the traditional bioindication methods is the daphnia test. Daphnia magna, a member of the Cladocera superorder, is an important model organism in ecological and evolutionary studies due to its prevalence, ease of cultivation, and high sensitivity to invasive environmental changes. It can be used to monitor the ecological state of water bodies and identify potential environmental threats [6,7].

The study of the behavioral responses of zooplankton in the habitat causes the need to process a large amount of data with high accuracy and speed of analysis [8]. The paper [9] compares the traditional net catching (MOCNESS) and the optical recording (UVP) methods and shows that net catching provides a higher taxonomic resolution during the study of small forms of zooplankton—less than 1 mm (in particular, Copepods and Ostracods), which are difficult to identify through UVP images. At the same time, for large and fragile taxa, the net catching method gives distorted results due to the destruction of organisms during trawling and fixation and requires considerable time to obtain further information on plankton particles in laboratory conditions. On the other hand, in case of optical recording, the use of a trawl leads to turbulence that may affect the quality of obtained images. In this regard, for the purpose of generating a reliable data flow and providing sufficient image quality for automatic classification it is more advisable to use a stationary in situ positioning of a holographic recorder that minimizes mechanical effects on objects and allows real-time observations.

2. Literature Review

Traditional methods used in the analysis of images of plankton particles reconstructed from digital holograms are time-consuming and labor-intensive, making them less effective in real-time conditions. Therefore, the use of modern technologies for the registration of images of plankton individuals using optoelectronic systems, in particular digital holography, alongside AI technologies, especially recognition algorithms based on neural networks, is becoming more relevant. Convolutional neural networks are one of the most effective tools for image and video analysis. They are able to automatically identify key features of objects in images, which makes it possible to achieve high registration speed with high recognition accuracy [10]. In most cases, deep convolutional models require well-focused optical images to ensure stable extraction of features and convergence during training. However, such techniques may be difficult to directly apply to raw holographic images containing strong coherent noise.

Recent developments in deep learning reveal several promising directions for improving the robustness of image recognition models under challenging imaging conditions.

For example, the work [11] proposes a structure for training topological features, which includes continuous homology in convolutional networks, thus making it possible to distinguish objects primarily by structural features of a form, rather than by texture at the pixel level. This concept may be relevant for holographical analysis of plankton, where external morphological characters play a major role in the recognition of the taxonomic group of zooplankton.

The FlexUOD model [12] is a flexible, uncontrolled approach to detecting outliers in noisy real images that can be useful for coherent noise filtration.

Another direction is based on the introduction of models of real physical processes into the network architecture. The DAFNet [13] serves such a network. It demonstrates how the introduction of physical constraints into neural architectures can improve the understanding of complex spatial structures—an idea that could potentially be transferred to holography.

Recent studies have shown a growing interest in combining digital holography with machine learning for plankton detection. Convolutional networks and YOLO-type detectors have been successfully trained to recognize plankton on reconstructed holographic images, achieving good accuracy in both laboratory and field experiments [14]. A recent review highlights several common challenges faced by such methods: limited annotated data, high noise levels, differences between imaging instruments, and a wide diversity of particle types [15]. Other works aim to simplify the reconstruction of holographic images and include physical constraints into neural models, which improves their stability under noisy conditions [16].

Although these approaches are quite promising, at the current stage simple performance-based methods remain more practical for low-power systems, which operate in real time, serving as effective tools for preliminary detection and segmentation of objects. Performance-based algorithms can operate on partially defocused images without explicit phase reconstruction, making them attractive for resource-constrained holographic applications [17].

However, the use of such images in digital plankton holography requires several stages of image preprocessing, in particular, reconstruction and search for the position of sharp images of plankton particles (virtual or digital focusing). Let us briefly describe the standard process for obtaining and processing holographic images.

Traditionally we use the DHC technology [18] (DHC—Digital Holographic Camera) to study plankton, which includes recording a hologram of the medium volume with plankton, numerical (using a diffraction integral) layer-by-layer reconstruction of holographic images of the medium volume cross sections, detection of focused images of plankton particles at appropriate distances (z₁, z₂, …,) and their location on a separate plane. The reconstruction of holographic images of particles and the formation of a 2D display is shown schematically and visually in Figure 1.

Thus, a 2D display of a three-dimensional image of the medium volume is formed. It contains sharp images of all plankton and other particles that were in the volume of the medium at the time of hologram recording.

This 2D display can be used to simultaneously improve the image quality of all particles using a sequence of corresponding algorithms, as well as for further analysis, similar to typical optical images. All the above processes are automated in the DHC.

Correct focusing (adjustment for a sharp image of a particle) allows obtaining clear contours of each particle, a detailed image of the structure of its section and provides accurate measurements of its size and shape. This is particularly important in the analysis of microscopic objects, where even a small deviation from a focused image may lead to significant image distortions. The main problems in the automated search for the plane where a sharp image of a particle is located are mainly associated with coherent noise and interference due to various reasons. These interferences hamper the automatic focusing, and hence, the measurement algorithms may fail to provide a correct result [19].

The main difficulty is the fact that autofocusing algorithms can wrongly interpret coherent and other noises as indicators of a sharp image plane. This causes the reconstructed image of a particle to shift from its actual position (from the best focus plane) and reduce its sharpness. We call this deviation a residual defocusing.

It should be emphasized that the residual defocusing used in this article differs from the classical twin image effect typical for in-line holography. This effect is caused by the simultaneous reconstruction of a virtual and real image from a hologram. In the considered in-line holography scheme, the waves forming these images are co-directional, coherent and form an interference pattern circumscribing the particle image and deteriorating its quality. Residual defocusing is an algorithmic focusing error that may occur due to the presence of twin images, coherent noise, and imperfect sharpness criteria. This results in subsequent classification errors for various recognition algorithms that are traditionally designed to analyze sharp images, or errors of neural networks trained on a dataset containing sharp images when analyzing images reconstructed from real holograms.

There are several metrics for determining the best focusing plane of a particle image, each of which has its advantages and disadvantages. The papers [20,21] pays great attention to the problems of automation of the focusing process, considers the accuracy of various criteria for different stage depths. The most successful was the boundary contrast algorithm, which is used to search for the best image plane of a particle and the formation of a 2D display for the studied volume [22].

The presence of a focused image is particularly important for automated particle recognition and classification by machine learning and image processing algorithms. Blurred images may reduce the classification accuracy and increase the error probability.

This study considers the Viola–Jones method for the classification of images of plankton particles reconstructed from digital holograms. The method is based on the use of cascade classifiers and integral images and is regarded one of the first and most well-known algorithms for image recognition [23,24,25,26,27]. At the same time, this algorithm is used for the first time to recognize holographic images under conditions of coherent noise and residual defocusing. The morphological features of Daphnia magna, including fairly clear body features and the configuration of the appendages, remain recognizable with little residual defocusing, which allows reliable detection of plankton particles based on geometric characteristics. At the same time, coherent noise, which inevitably appears in natural recording conditions, mainly affects low-frequency background components and does not significantly affect the morphological features of particles, which form the basis of Haar characteristics. The Viola–Jones algorithm retains its recognition ability even in partially defocused and noisy holographic images.

We considered the possibility of using the Viola–Jones algorithm to identify the representatives of the chosen taxon among the mixed biocenosis of plankton presented as 2D images using the example of Daphnia magna individuals.

Examples from other fields of science and technology confirm the applicability of manual development of characteristics in tasks with a high level of noise and limited resources. In particular, a CNN architecture with the “focus on characteristics” was proposed for portable medical imaging, where manually extracted characteristics are used as indicators for a neural network, while noise is suppressed and details important for diagnosis are preserved [28]. The authors show that with limited resources and high noise levels, clear edges/features improve the ability to reconstruct important local structures. This idea is similar to the use of Haar features in cascade detectors: both approaches rely on local contrast/gradient invariants, which turn out to be more resistant to background interference and reduce the computational load during preliminary filtration.

The paper presents the estimates of precision and recall of the trained algorithm, as well as estimates of the stability of the algorithm to residual defocusing in a 2D display of the studied volume when plankton is analyzed using a submersible digital holographic camera. It also presents the comparison with other machine learning algorithms.

3. Materials and Methods

3.1. Indicator Species

The Cladocera superorder from the Branchiopoda subclass are small plankton crustaceans, one of the most massive and extremely diverse animals in terms of the external structure of plankton, benthos and neustone of inland water bodies of all types and all continents, including Antarctica. The most well-known representatives of the order are Daphnia crustaceans, which mainly live in fresh water, although a number of species live even in hypersaline reservoirs and seas. Most species filter large masses of water during nutrition, thereby cleaning water bodies from pollution.

Daphnia magna was chosen as an object of study due to its widespread distribution and key role in freshwater ecosystems. These zooplankton species are widely used in environmental and toxicological studies as an indicator of water quality. The legs with multiple bristles of the most cladocerans serve to filter out fine food particles from water. Their legs have gill appendages that perform a respiratory function. Daphnia magna actively filters out large volumes of water, thus catching bacteria and microalgae, which makes it especially sensitive to even minimal concentrations of pollutants, such as heavy metals, pesticides and other toxic compounds [29,30,31]. Consequently, the daphnia test has become a popular method to assess water toxicity based on changes in behavior and survival of Daphnia magna exposed to pollutants, which makes it possible to quickly and effectively identify the potential environmental threats.

Since a digital holographic camera was used for recording, it is important to understand the specific features of the obtained holographic reconstructions for subsequent image processing and classification. Figure 2 presents coherent holographic images of several Cladocera species that illustrate their general morphology as observed in holographic reconstructions.

Figure 2 shows that the reconstructed holographic images contain information about the outer contours and the general morphology of organisms. Unlike conventional optical microscopic images of daphnia [32], reconstructed holographic images usually do not contain information about the internal structure and small morphological details, small-scale anatomical elements described in [33] remain unresolved. Therefore, the analysis of such holographic images focuses mainly on the external shape characteristics and sizes of certain zooplankton individuals. This sometimes makes it difficult to accurately identify species, since interspecies differences are often associated with internal anatomy. However, for bioindication purposes, it is usually enough to assess the total number and distribution of organisms in large taxonomic groups (orders or superorders).

3.2. Zooplanktonad Registration Method

Sampling using nets similar to the Juday net with subsequent manual classification using a microscope or laboratory instruments is increasingly being replaced by the registration of zooplankton in its natural habitat [34,35]. Traditional net catching has a number of significant constraints caused by high labor costs both during sampling and processing, as well as by a physical impact on plankton due to net catching. Registration of plankton in situ preserves natural conditions and dynamics, which provides more accurate data on the behavior and distribution of these organisms in space.

Such methods as digital holography and automated image analysis make it possible not only to accurately identify plankton species, but also to collect data on their spatial and temporal distribution, as well as on the dynamics of their relative speed of movement. This is particularly important in understanding the ecological processes and interactions in marine ecosystems. Holography in a natural environment allows monitoring plankton responses to environmental changes in real time, which is also critical in the assessment of natural and anthropogenic impacts.

The additional use of a neural network or other algorithms for the analysis of obtained holographic images of particles makes it possible to significantly speed up and automate the classification and monitoring, thus minimizing the human factor and increasing the accuracy of results. Thus, the integration of holographic registration of zooplankton in its natural environment with modern data processing algorithms provides researchers with the most complete understanding of the state and dynamics of marine ecosystems.

The optical scheme of digital hologram recording (in-line scheme or Gabor scheme) is shown in Figure 3.

Laser illumination of the studied medium volume with particles forms an interference pattern of a reference wave (radiation that passed by the particles) and the object wave (radiation scattered on the particles). The camera registers this interference pattern as a two-dimensional array of discrete intensity values, which is a digital volume hologram. The hologram is transferred to the computer memory, followed by numerical reconstruction of a holographic image of the medium with particles. In this case, information on each particle (plankton individual, settling non-living particle, gas bubble, etc.) contained in the recorded volume of the water medium is reproduced [36].

The Laboratory of Radiophysical and Optical Methods for Environmental Research of National Research Tomsk State University developed a submersible digital holographic camera to study plankton in its habitat. Figure 4 shows a 3D model of this device.

It is noteworthy that the in-line scheme here is implemented in a folded configuration using prisms.

3.3. Plankton Classification Method

Modern automated methods for plankton classification according to its holographic images are based on image processing algorithms. Typically, the analysis includes the stages of preprocessing, identification of characteristics, and further classification of objects. In recent years, machine learning and artificial intelligence have expanded the classification capabilities, including through the use of convolutional neural networks that are able to automatically extract hierarchical features, thus providing high recognition accuracy even if noise is present. However, along with neural network methods, there are other approaches that demonstrate high efficiency in object detection. One of them is the Viola–Jones algorithm, which provides fast and accurate detection of objects in images using simple Haar features and a cascade of classifiers. In the present study, this algorithm is used to detect and classify plankton images from holographic data, which are specific to this algorithm as they are characterized by coherent noise and residual defocusing.

3.3.1. Viola–Jones Method

One of the most well-known object recognition algorithms is the Viola–Jones method, which was developed for fast and accurate recognition of objects in images and videos [37,38]. The Viola–Jones method is based on the use of integral images and cascade classifiers, which ensures quick and efficient detection of objects in images. The main stages of the method include the calculation of Haar features, application of cascade classifiers and filtration of false alarms [39].

The mathematical formulation of the main elements of the method is presented below.

The integral representation of the image $I\left(x,y\right)$ is the sum of all pixel intensities above and to the left of the point $\left(x,y\right)$:

$$I\left(x,y\right)=\sum _{i=0,j=0}^{i\le x,j\le y}I\left(i,j\right),$$

Each Haar feature f_i is defined as the difference between the sum of the pixel intensities of the light ($R_1$) and dark ($R_2$) parts of the rectangular features:

$${\mathrm{f}}_{\mathrm{i}}\left(\mathrm{x},\mathrm{y}\right)=\sum _{(x,y)\in R_1}I(x,y)-\sum _{(x,y)\in R_2}I(x,y)$$

These characteristics describe the local changes in contrast typical of object edges and textures.

In the present study, the Viola–Jones method was first used to classify plankton individuals based on their holographic images.

3.3.2. Dataset Composition

The dataset used for the training consisted of reconstructed holographic images that clearly showed the contours and structures of Daphnia magna particles. A dataset consisting of 880 reconstructed digital holographic images of Daphnia magna was used for training. Daphnia magna was cultivated under standard conditions [40] at the Biotest-Nano Center of Tomsk State University. A set of digital holograms of the water medium with Daphnia magna individuals was recorded in the laboratory using the DHC.

It should be noted that all images are obtained under different conditions, and include typical variations in shape, size, angle of rotation and density of objects. The body length of Daphnia magna in the reconstructed holographic images ranged from about 0.2 to 2 mm. The density of particles in the frame ranged from 1 to >20. Although the volume of the training dataset may seem insufficient according to modern machine learning standards, it adequately reflects the complexity of real holographic data. Each image corresponds to a unique holographic registration of a living plankton organism in the presence of coherent noise, which makes this dataset quite diverse and representative enough, despite its limited size. In addition, the Viola–Jones algorithm is well suited for such small and heterogeneous datasets. Unlike deep convolutional networks, which require a large amount of annotated (marked) data, this method is based on manually developed Haar functions and advanced weak classifiers, which allows for stable recognition even with a relatively small set of training data. The resulting dataset was marked manually by highlighting the focused images of individuals with circumscribed rectangles. Training was conducted using the OpenCV library tools.

Preprocessing included the grayscale conversion of all plankton particle images. The training of the model involved the adjustment of the following hyperparameters.

The minHitRate parameter sets the minimum desired accuracy for each stage of a cascade classifier [41], which determines the main features of holographic images of plankton particles. This parameter sets the proportion of particle images the classifier should correctly recognize. The value of minHitRate ranges from 0 to 1, where 1 is 100% accuracy. For example, 0.995 means that the classifier must correctly recognize at least 99.5% of objects at each stage.

The maxFalseAlarmRate parameter determines the maximum allowed false alarm rate for each stage of a cascade classifier. This parameter sets the proportion of regions that are incorrectly classified as containing an image of a particle, when in fact they do not contain it. The maxFalseAlarmRate also lies within a range from 0 to 1, where 0 means no false alarms. For example, 0.5 means that the classifier allows up to 50% false alarms at each stage.

These two parameters were chosen empirically by comparing the precision of the model at the output after training. The optimal values of these parameters, at which the highest precision was achieved, were 0.99 and 0.5, respectively.

The neighborhood parameter or minNeighbors in the Viola–Jones algorithm determines how many intersecting detections there must be for a region to be finally accepted as containing a particle image. This parameter is used to filter false alarms and improve recognition accuracy. The empirical fitting of this parameter, or statistical evaluation, makes it possible to form a test dataset and build the graphs of the dependence of the precision, recall and F1 on the neighborhood parameter, as will be shown below.

To improve the quality of recognition, 120 background images of the water medium volume without plankton particles, which are marked as images without particles, were added to the training dataset. The size of the scanning window was 40 × 40 pixels.

4. Results

4.1. Algorithm Testing

Both reconstructed images with residual defocusing and unprocessed holograms, without additional network retraining, were used for testing and evaluation, which made it possible to assess the ability of the algorithm to recognize particles, including directly from holograms.

To assess the efficiency of the detection algorithm, precision, recall and F1 metrics [42] were used. Precision (TPR = TP/(TP + FP)) characterizes the proportion of primarily detected particles among all detections, recall (REC = TP/(TP + FN)) reflects the completeness of detection, and F1 = 2PR/(TP + TR) gives their harmonic mean. Precision in this article refers to the overall accuracy of detection based on validation data. It should be noted that the algorithm was tested in two modes: with the use of 2D images, which may contain residual defocusing, to assess the efficiency of the classifier under standard conditions of the DHC station, and with the use of the holograms themselves to assess the ability to recognize particles without reconstruction of their images from holograms.

The dataset used in this study consisted of three subsets. The training subset included 880 images of Daphnia magna and 120 background images. A separate validation subset was formed from the same species and imaging conditions to monitor model convergence and evaluate its accuracy. In addition, several independent test datasets were used, each corresponding to different recording conditions or plankton taxa. These datasets were employed to assess the generalization capability of the trained classifier.

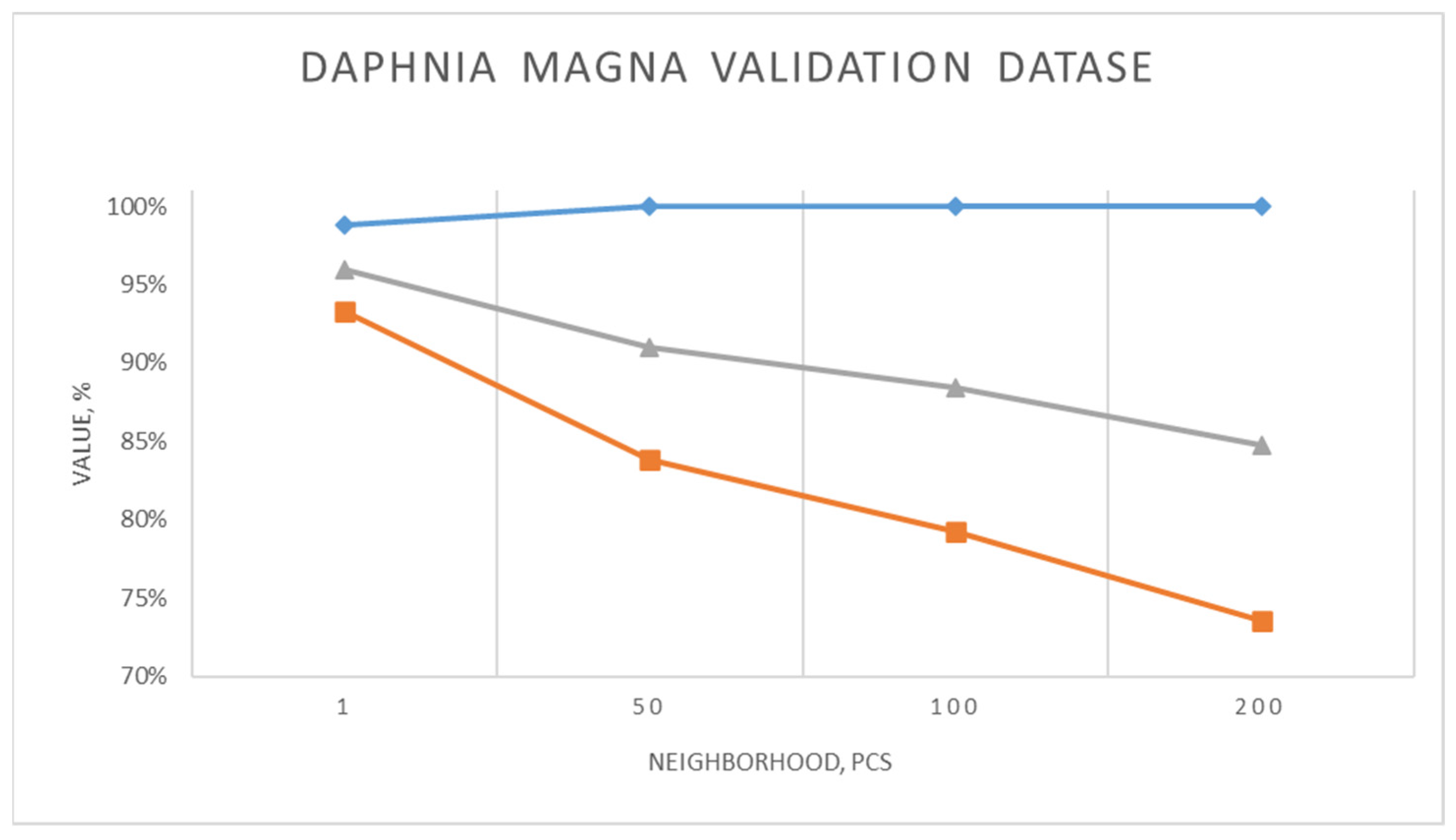
When Daphnia magna was recognized from the validation set the precision (TPR), recall (REC) and F1 showed the following values (Figure 5) for different neighborhood parameters.

With a decrease in the neighborhood parameter in the Viola–Jones algorithm, the recall and F1 increase, reaching the maximum values with minNeighbors = 1 (93% and 96%, respectively), which indicates better object detection. At the same time, the precision remains at a high level (about 100%), only slightly decreasing to 99% with minNeighbors = 1. High values of minNeighbors increase detection precision but reduce recall and do not recognize some objects. Such precision data show quite a good result, given the fact that in traditional methods of estimating plankton the errors of 30% and even 50% are considered acceptable. The examples of recognized images are shown in Figure 6.

In the course of working with a trained neural network cascade, we revealed its resistance to residual defocusing. Digital holography allows registering the volume of the measuring medium with zooplankton particles in the form of a two-dimensional distribution of the intensity of the interference field. However, to obtain visual images of particles, numerical reconstruction of holographic images of cross sections of the volume is required, followed by selection of the best (sharp) image plane of a particular particle. The best image plane is chosen using autofocusing algorithms based on various sharpness criteria (quality indicators). The best image plane determines the longitudinal coordinate of a particle. Thus, a three-dimensional display of the zooplankton distribution in the recorded volume is formed. However, errors in determining the best focus plane due to diffraction and algorithmic limitation may lead not only to errors in determining the coordinates, but also to a decrease in the quality of subsequent analysis, since blurred images deteriorate the accuracy of detection and classification of objects. In view of the above, the work additionally tested the possibility of the algorithm operation avoiding the process of finding the best image plane and reconstructing focused holographic images. Hence, a laboratory experiment was conducted on the holographic registration of Daphnia magna. The volume of water with daphnia was in a 25 mm long cuvette, which was located at a distance of 90 mm from the matrix recording the digital hologram. The algorithm is tested on a sample of defocused Daphnia magna images reconstructed from holograms. 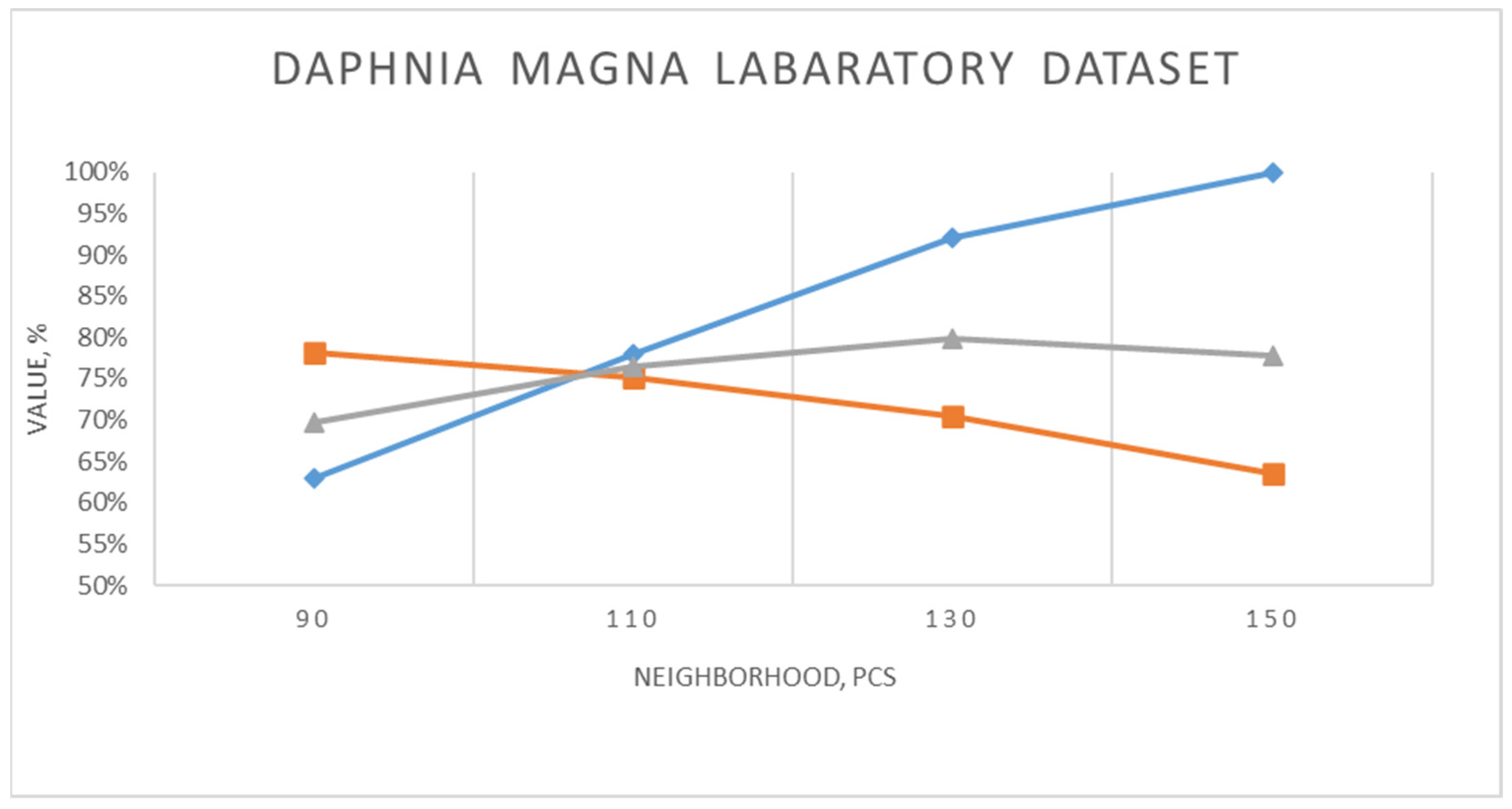Test results are shown in Figure 7.

Figure 7 shows that with a decrease in the neighborhood parameter, the precision drops from 100% to 63%, while the recall increases from 64% to 78%. F1 reaches the maximum with minNeighbors = 130 (80%), which is the optimal value. This indicates that at lower parameter values, the sensitivity of the algorithm to the detection of plankton individuals increases, but the number of false alarms increases, which primarily decreases precision. This also confirms the fact that the algorithm is able to recognize an object with a precision of ~90% at optimal neighborhood values. The examples of holograms included in the test dataset and an example of recognition using them are shown in Figure 8.

Note that the test dataset considered here has a significantly lower contrast compared to Figure 6, and despite this difference, the recognition results were quite high.

Next, the algorithm was tested for selectivity to a certain type of plankton particles used for training. For this, a test dataset was compiled from holograms of the Black Sea zooplankton, which included the following taxa: Copepoda, Cirripedia, Chaetognatha, Noctiluca, Larvae, Penilia. Some of the above taxa have morphological features similar to Daphnia magna, especially Cirripedia and Penilia, so when the metrics were calculated, the result of recognizing any of these taxa was considered correct, while the others not. Testing results are shown in Figure 9.

The testing results confirm that the algorithm demonstrates significant non-selectivity to morphologically similar zooplankton taxa. Initially trained on Daphnia magna images, the algorithm had not previously dealt with zooplankton presented in the test dataset; however, it showed a high ability to recognize such taxa as Cirripedia Copepoda and Penilia, which have similar features to Daphnia magna training taxon particles.

At the same time, the testing showed that with small values of the neighborhood parameter, the algorithm successfully classifies plankton particles, thus reaching 83% accuracy, 79% recall and 81% F1.

Next, the algorithm was tested on a taxon significantly different from the training taxon. For this, two test sets of holographic images of Artemia salina individuals were compiled. The first set of images contained 2D images of Artemia salina belonging to the same order with Dafnidae—Crustacea, Branchiopoda of various age groups ranging from the beginning of hatching to adult species. Testing results are shown in Figure 10.

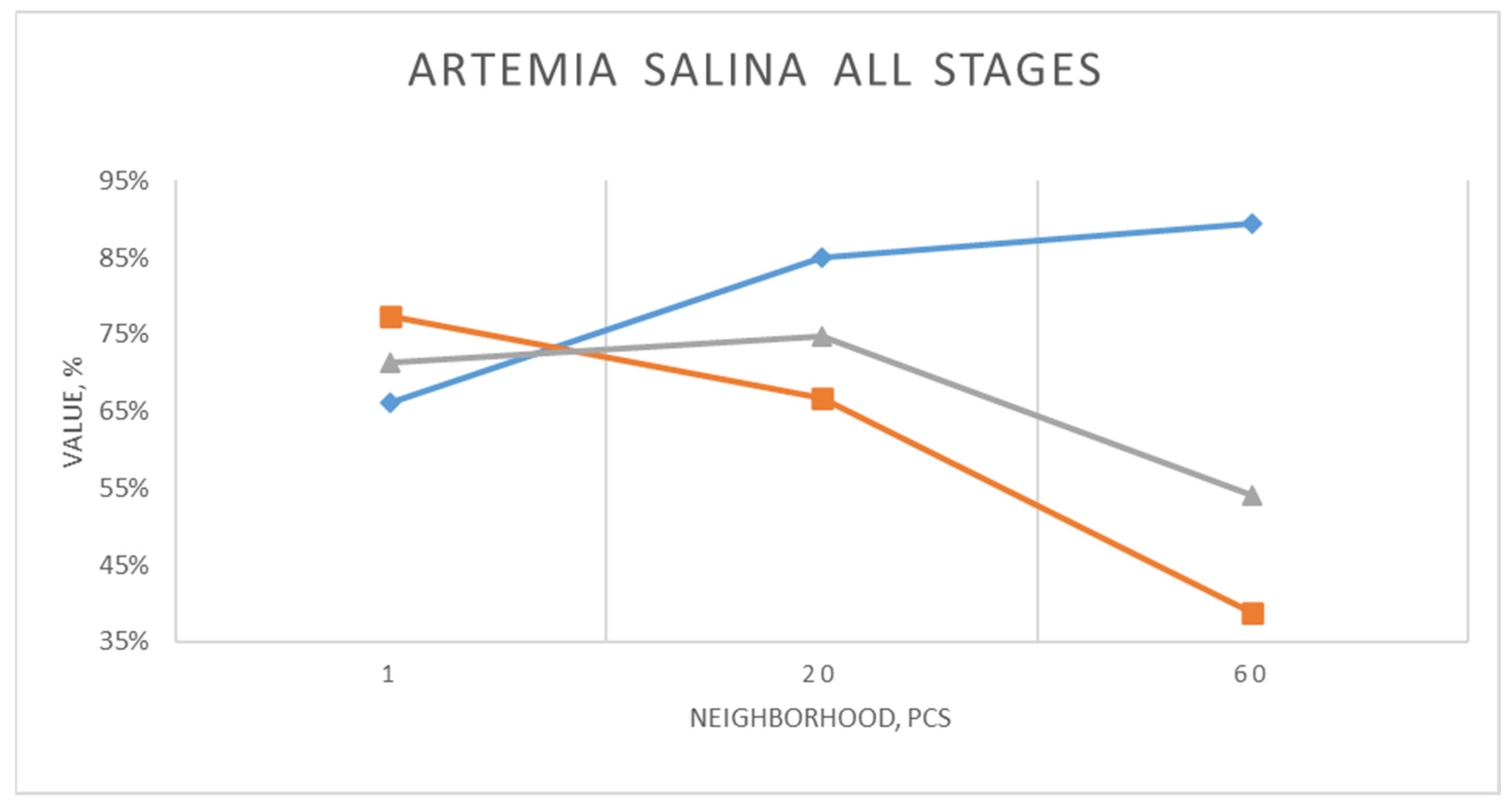
Here, there is a similar situation regarding the dependence of metrics on the neighborhood value. F1 reaches the best value (75%) with the average value of the neighborhood parameter (20). In this particular case this indicates the most optimal relationship between high precision and satisfactory recall.

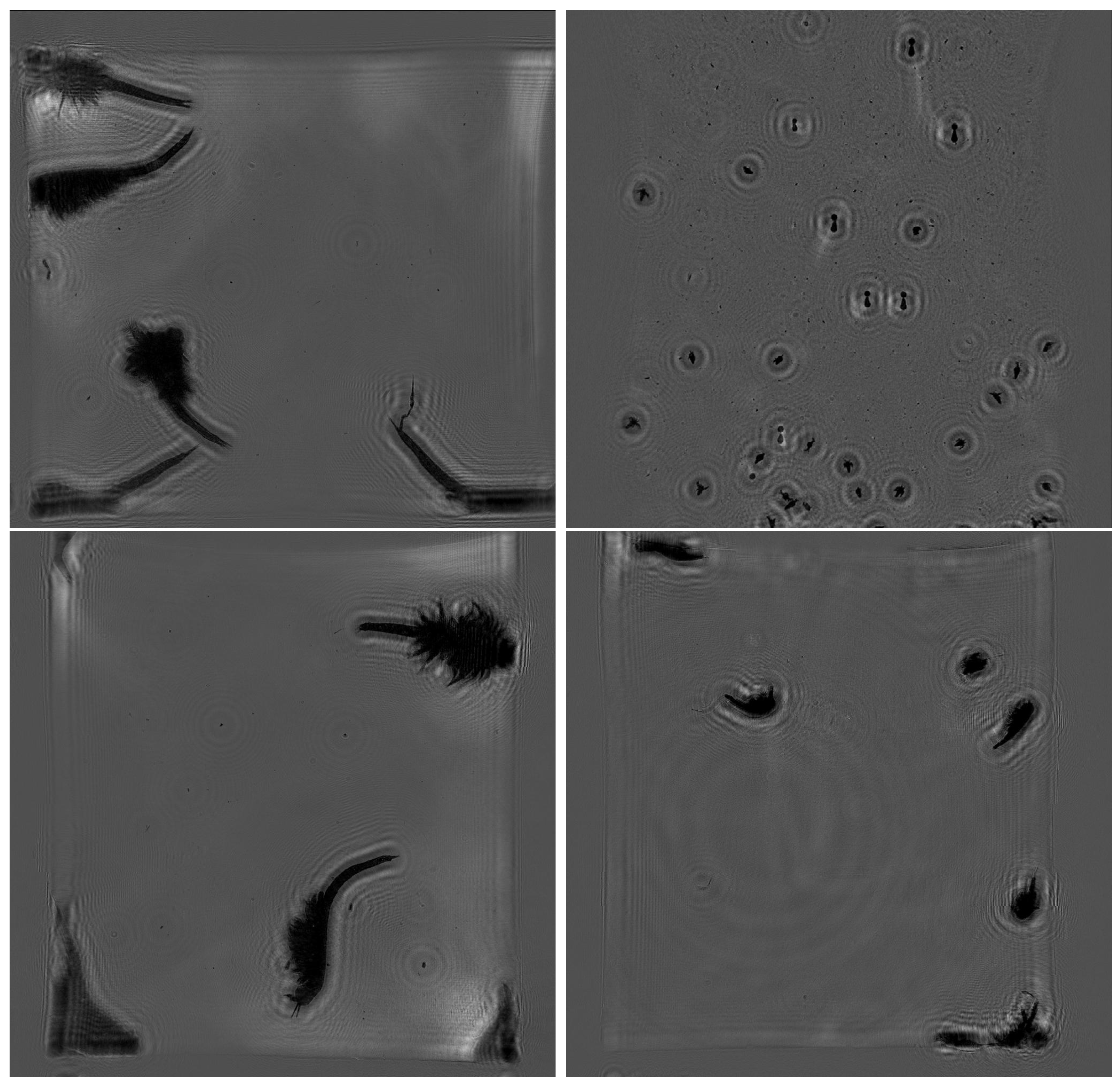
The examples of images included in the test dataset are shown in Figure 11.

During the processing of a set of images, the algorithm clearly distinguished the stage of the early juvenile Artemia salina, so it was decided to test it for the possibility of recognizing this stage according to a hologram. Testing results are shown in Figure 12.

An identical dependence of the metrics on the neighborhood value is quite obvious; however, the average result for hologram recognition of the Artemia salina monoculture turned out to be even greater. F1 reaches the best value (87%) with the average value of the neighborhood parameter (30). The examples of images included in the test dataset are shown in Figure 13.

4.2. Performance Evaluation

The processing speed was assessed on a laptop with the Intel Core i5-8250U processor (1.6 GHz, 4 cores, 8 threads) and 8 GB RAM. The algorithm was implemented in C# using the standard functions of the OpenCV cascade detector and integrated into the Windows Forms app. The mean time to detect was approximately 0.043 s per particle detected, which means that for an image containing n particles, the total processing time can be estimated as (0.043 × n) seconds. These experiments demonstrate that the Viola–Jones algorithm, due to its cascaded structure, ensures high speed of detection even on low-power processors without GPU acceleration.

4.3. Comparison with the Results of the Dimensional Algorithm

A morphological algorithm, which determines the correlation of the size of a rectangle circumscribed around a particle, is quite effective for the analysis of spatial and temporal distributions of plankton and other marine particles in real time in situ [43]. However, its accuracy of particle classification at the species level is lower compared to the Viola–Jones method. In particular, the classification error in determining mesoplankton at the level of systematic order is about 30%.

The Viola–Jones method provides faster and more accurate recognition of particles such as Daphnia magna, Cirripedia, Copepoda, Penilia, and Artemia salina in their juvenile stage and reaches up to 90% precision. However, this method requires careful adjustment of some parameters, such as the neighborhood, to maintain a reasonable balance between precision and recall.

A dimensional algorithm is better suited for various tasks of ecological monitoring. It provides reliable but less accurate measurements of particle distributions. Despite its reliability, the method can hardly differentiate species with similar morphological characteristics. In addition, it cannot directly analyze the holograms of particles, unlike the Viola–Jones method, which demonstrates its resistance to defocusing.

5. Discussion

The experiments showed that the Viola–Jones algorithm trained on a dataset of Daphnia magna images demonstrates high precision and recall in recognizing this species. High recall indicates the ability of the algorithm to effectively identify Daphnia magna among other objects, which is critical for bioindication purposes.

The studies showed that the Viola–Jones algorithm is resistant to residual defocusing which means that it recognizes plankton images out of the best focus plane almost as well as it does with fully focused particle images. In this regard, the study makes it possible to conclude that the algorithm can process holograms thus neglecting the reconstruction of particle images. In order to numerically assess the accuracy of hologram processing, the algorithm was tested to recognize laboratory-grown Daphnia magna on a hologram without image reconstruction. The analysis of the dependence of precision, recall and F1 on the neighborhood parameter showed that with a decrease in the neighborhood parameter, recall increases, but at the same time the precision decreases, which indicates an increase in the number of false recognitions. The most balanced results are achieved with a neighborhood parameter of about 130, which corresponds to the maximum F1 (80%). However, the optimal value shall be selected again for each new experiment.

The experiments also showed that the Viola–Jones algorithm demonstrates a high degree of non-selectivity to various species of zooplankton, in particular, Daphnia magna, Cirripedia, Copepoda, Penilia, and Artemia salina. This means that the algorithm is able to recognize taxa that have similar and not quite similar morphological characteristics almost as efficiently as Daphnia magna. For example, with a neighborhood parameter of 20, the recognition precision of Artemia salina is 85%, recall—68%, and F1—75%, which is comparable to the results for Daphnia magna (92%, 80% 71%, respectively). The decrease in accuracy for Artemia salina is explained by the fact that this taxonomic group was not included in the training sample containing only Daphnia magna and background. Nevertheless, the algorithm shows a partial generalizing ability even to previously undetected taxa, which emphasizes the practical potential of the method as a primary filter for separating zooplankton particles from background structures.

The results show that the Viola–Jones algorithm can be used to work with holograms without reconstructing particle images, thus making it possible to effectively recognize a wide range of morphologically similar taxa.

6. Comparative Analysis

Let us compare the effectiveness of automatic analysis of holographic images of zooplankton using a relatively simple and inexpensive Viola–Jones algorithm with deep convolutional neural networks. Thus, the work [44] presents an algorithm for detecting and tracking plankton organisms using unprocessed holograms in real time. The algorithm is based on the use of YOLOv5 in conjunction with the SORT tracker. The authors were able to achieve high detection accuracy—mAP@0.5 = 97.6% at a processing speed of 44 frames per second (FPS), thus demonstrating the applicability of modern CNN in the monitoring of biological particles. However, a crucial point here is that this study was carried out on synthesized holographic images that do not contain parasitic interference noise, coherent background and other optical distortions characteristic of underwater holography under natural conditions.

At the same time, the use of synthetic data to train models in digital holography cannot be considered solely as a limitation. Modern research shows that physical-optical modeling of holograms can be an effective way to form scalable and controlled datasets, especially in cases of insufficiency of marked real images. This approach makes it possible to vary the parameters of lighting, noise and optical distortion, thus forming more stable models. However, this requires domain adaptation or additional training on real data, since a fully synthetic dataset does not always reflect the statistics of background interference and artifacts in situ [45,46].

A similar approach was applied in [47], where convolutional neural networks were used to classify zooplankton particles on holograms. The authors reached the precision of about 92% when classifying objects on holograms; however, they used data obtained under controlled conditions, without noise typical for natural recording. This makes this approach different from our studies, where digital holograms were recorded in situ, taking into account all the features of the real water volume, including residual defocusing, coherent noise and varying contrast.

In our study, the classic Viola–Jones algorithm was adapted (in a simple way—by matching the neighborhood parameter) to recognize Daphnia magna images reconstructed from holograms, including cases of residual defocusing. With optimal neighborhood parameters, the algorithm achieved the precision of up to 90%, recall—80%, F1-score—85%, which, despite the lower absolute accuracy compared to YOLOv5(AP_0.5~97.6%) and AlexNet(F1~88.5%), DTL_ResNet18(F1~92.0%) and VGG(F1~90.5%), is a high result for non-reconstructed or noisy data. In addition, the advantage of the considered algorithm is its resistance to image distortion and low computational requirements, which allows it to be used in resource-limited conditions.

Thus, despite the fact that modern deep neural network architectures demonstrate higher precision in ideal conditions, their reliability and generalization ability in noisy holographic images is quite doubtful. In contrast, the proposed cascade classifier demonstrates stability in real conditions and may also be used as the first stage of data filtering before being transferred to more complex classifiers.

7. Conclusions

The study is based on 880 holographic images of Daphnia magna and 120 background holographic images. Despite the limited set, it reflects real shooting conditions and covers the typical variability of shapes, poses and lighting conditions. We tested the algorithm on other taxa (Penilia, Artemia, Cirripedia) to assess the generalization ability of the algorithm without retraining. Moreover, this confirms the applicability of the basic approach.

Indeed, the Viola–Jones algorithm has not previously been applied to holographic images of zooplankton. The paper shows that even basic algorithms can be reliable in conditions of limited computing resources characteristic of autonomous sensors. In addition, the study demonstrated its ability to generalize for other taxa without retraining, which is quite interesting for monitoring tasks from a practical perspective.

The studies demonstrate the efficiency of the Viola–Jones algorithm for recognizing various types of zooplankton, such as Daphnia magna and Artemia salina, in bioindication studies. Despite the presence of coherent noise, the algorithm is able to effectively separate objects from the background (up to 90% precision). The algorithm shows high precision and recall, which indicates its ability to reliably distinguish objects even in the presence of residual defocusing. This allows the algorithm to be used for the analysis of holographic data without reconstructing particle images, which greatly speeds up the data processing.

The main limitation of this study is the need for complex empirical selection of the neighborhood parameters for each type of conditions. This complicates automation and reduces the processing speed when holographic conditions change. Nevertheless, the obtained results demonstrate the possibility of using the considered algorithms for rapid preliminary processing of holographic images and the holograms themselves, and for the localization of the studied particles. Future research will focus on expanding the dataset with a wider variety of plankton taxa and visualization conditions, as well as on the integration of modern deep learning architectures, including neural networks with complex values for direct phase reconstruction and end-to-end analysis of holographic images. Such hybrid approaches can combine the interpretability and efficiency of methods based on features with the adaptability of data-based models.

A distinctive feature of the considered algorithm is the simplicity of its optimization to the measurement conditions. The optimization of the neighborhood parameter allows finding a balance between precision and recall, thus adapting the algorithm to the specific conditions of each experiment. As a result, the Viola–Jones algorithm can serve as a universal tool for automated analysis of zooplankton holographic images.