A Shallow Foundation Settlement Prediction Method Considering Uncertainty Based on Machine Learning and CPT Data
Abstract
1. Introduction
2. Traditional Method
3. Case Study Records
4. Modeling Process
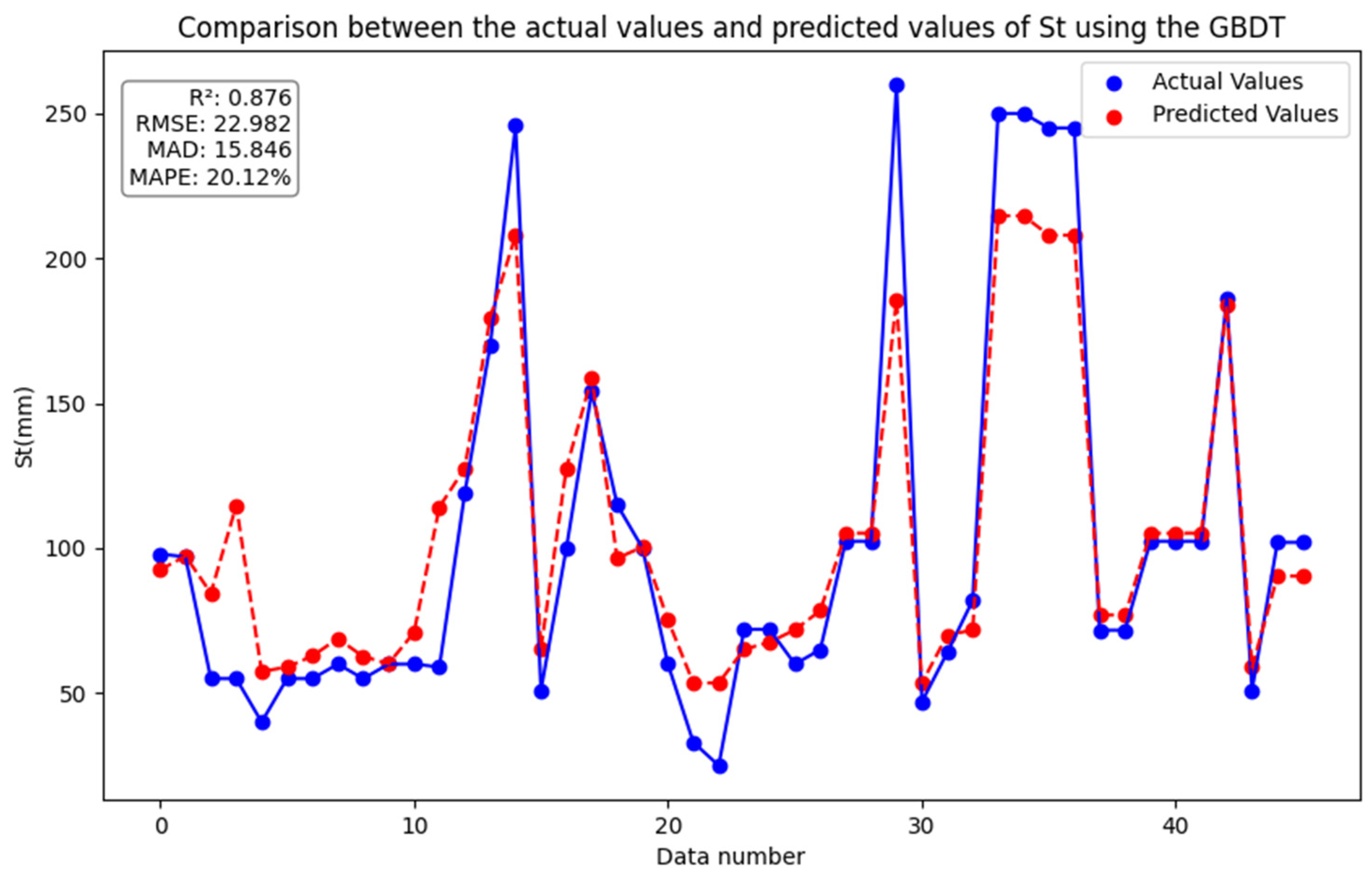
4.1. Gradient Boosting Decision Tree (GBDT)
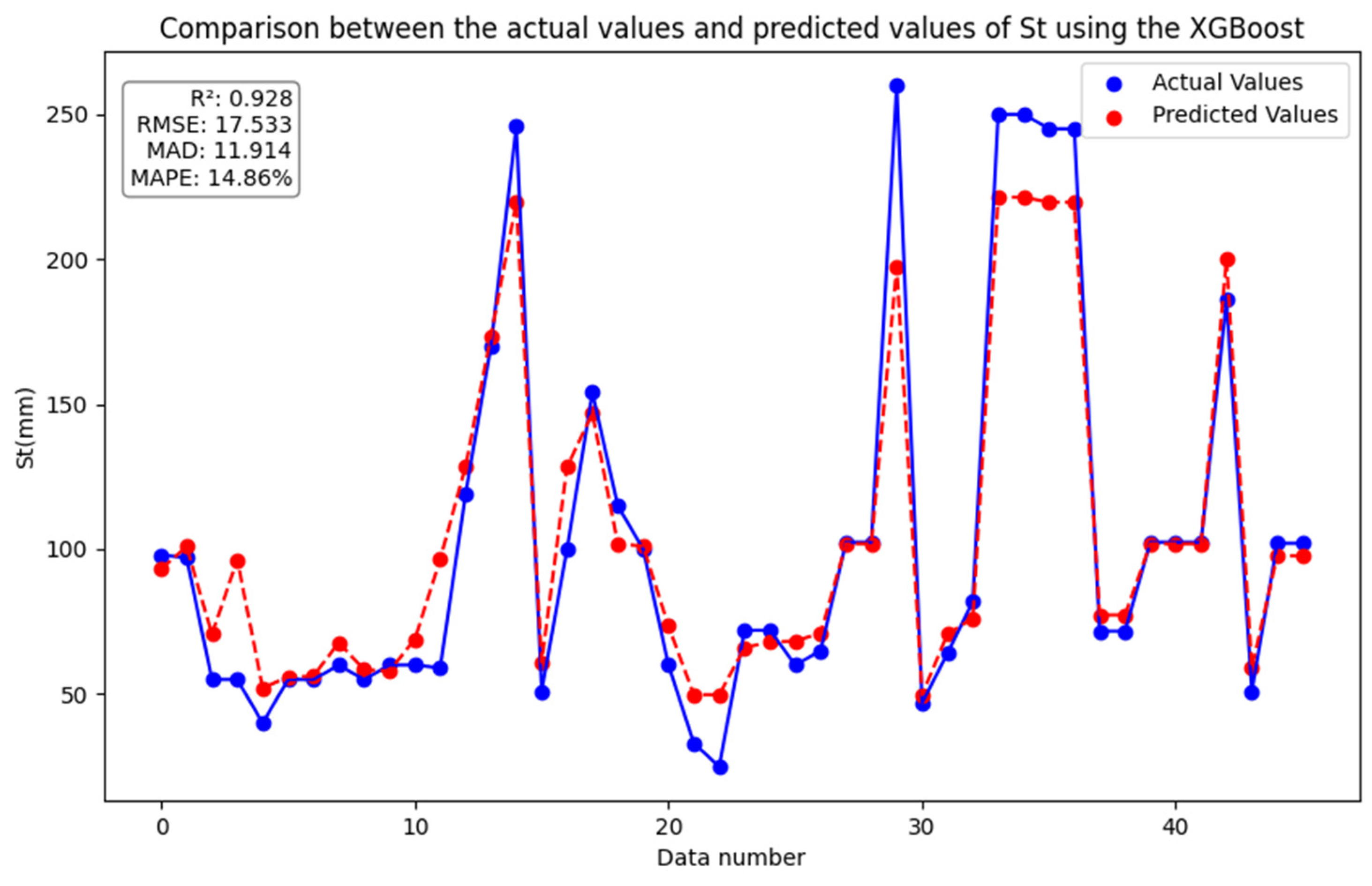
4.2. Extreme Gradient Boosting (XGBoost)
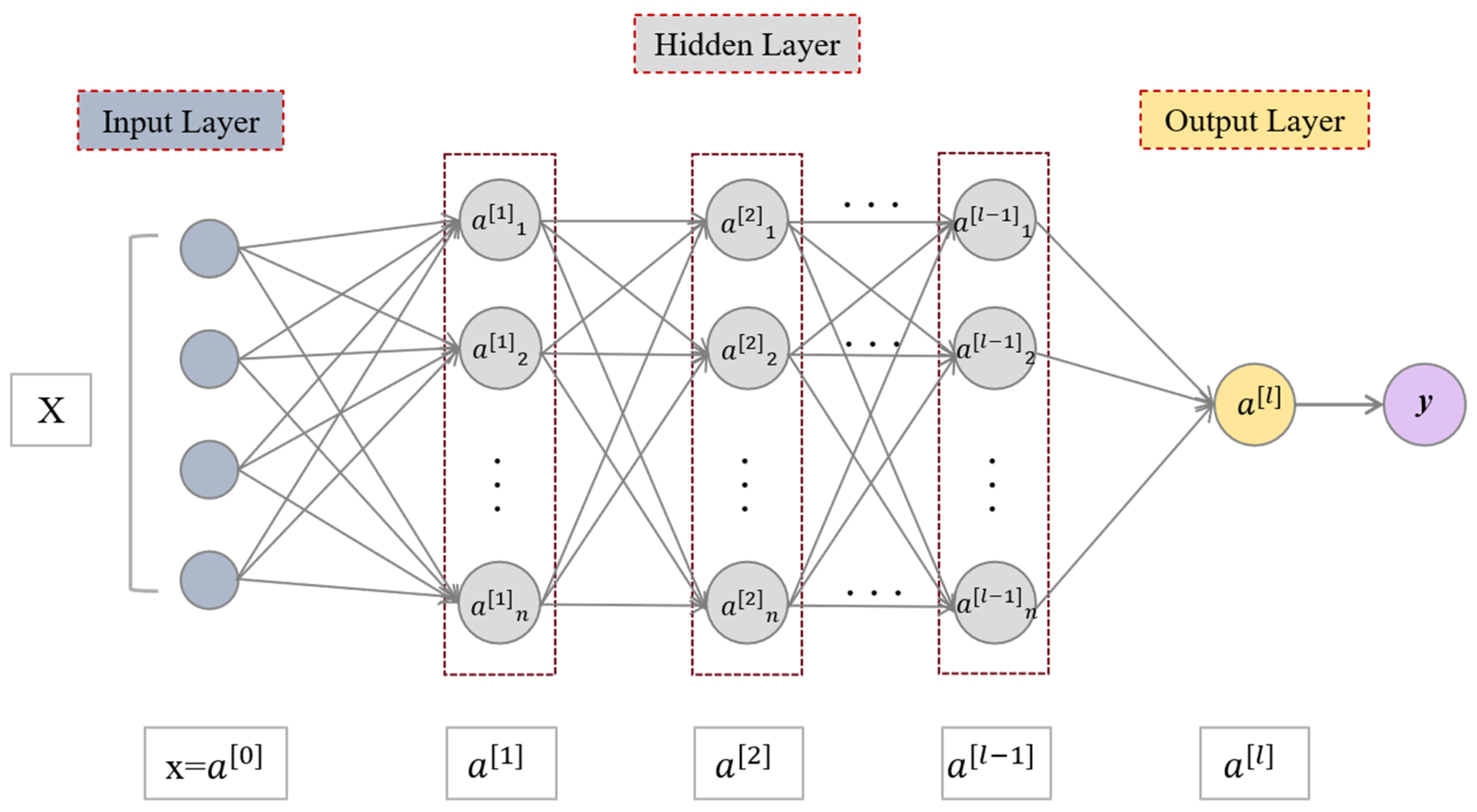
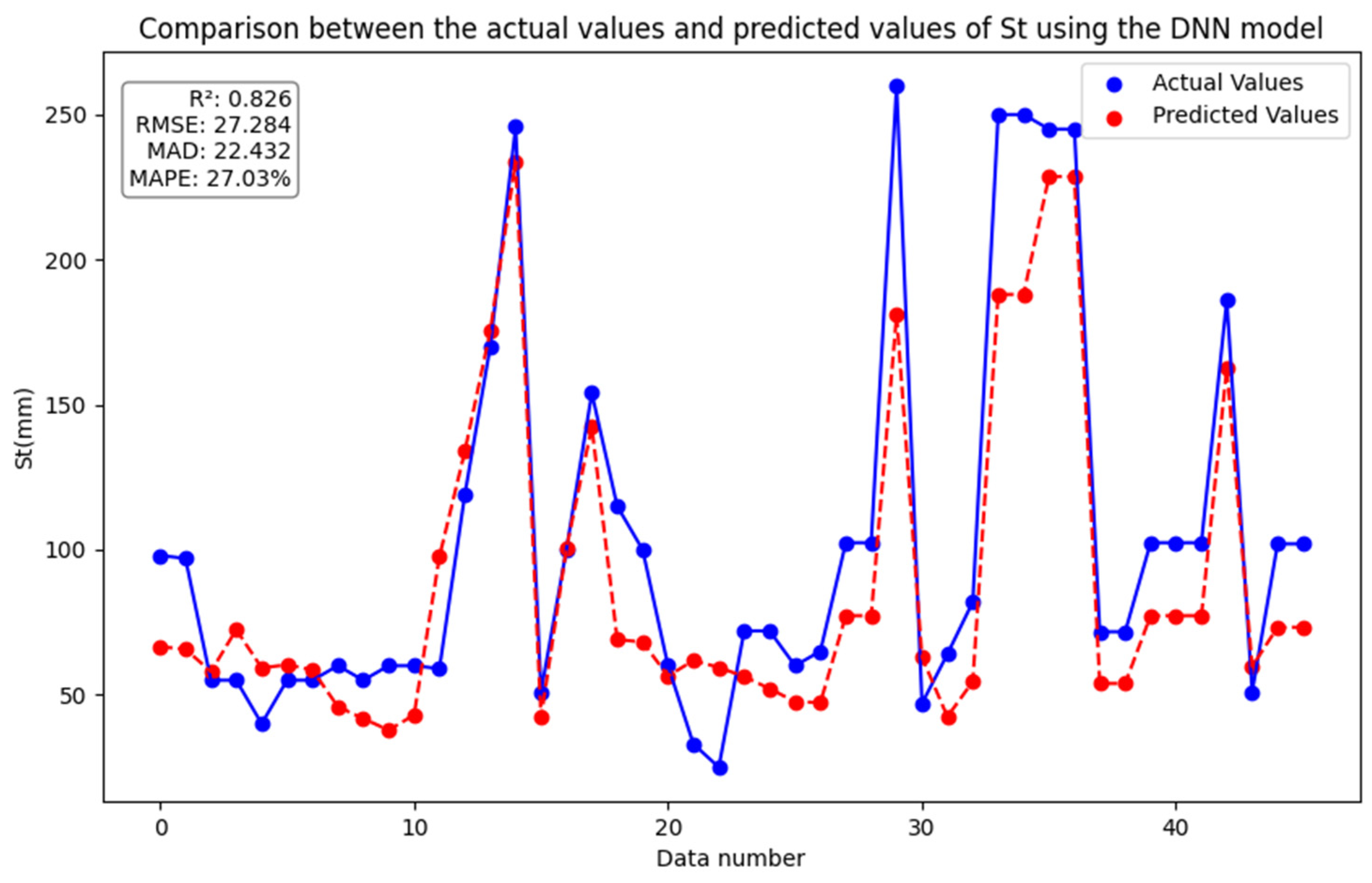
4.3. Deep Neural Network (DNN)
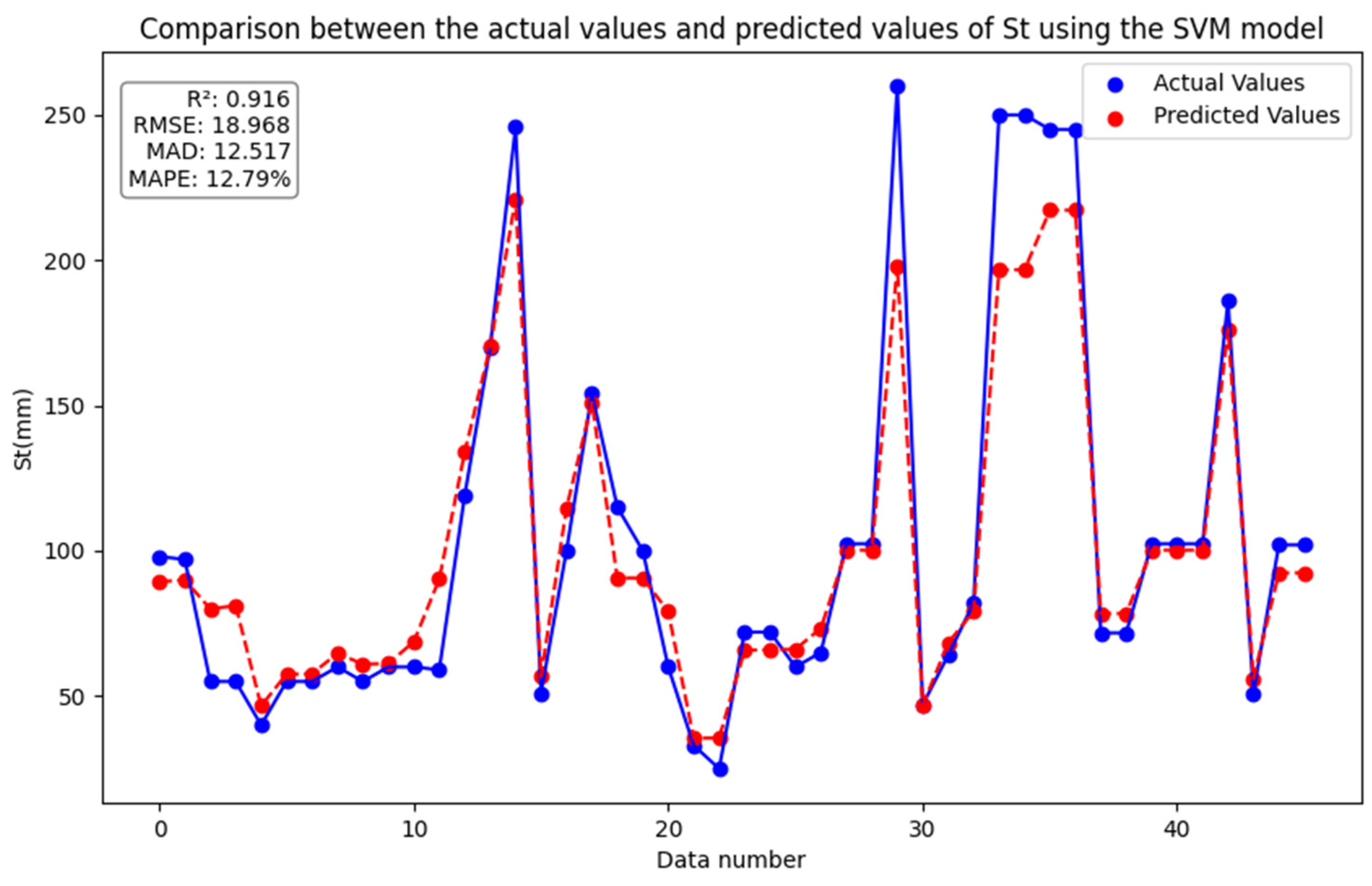
4.4. Support Vector Machines (SVM)
4.5. Random Forest (RF)
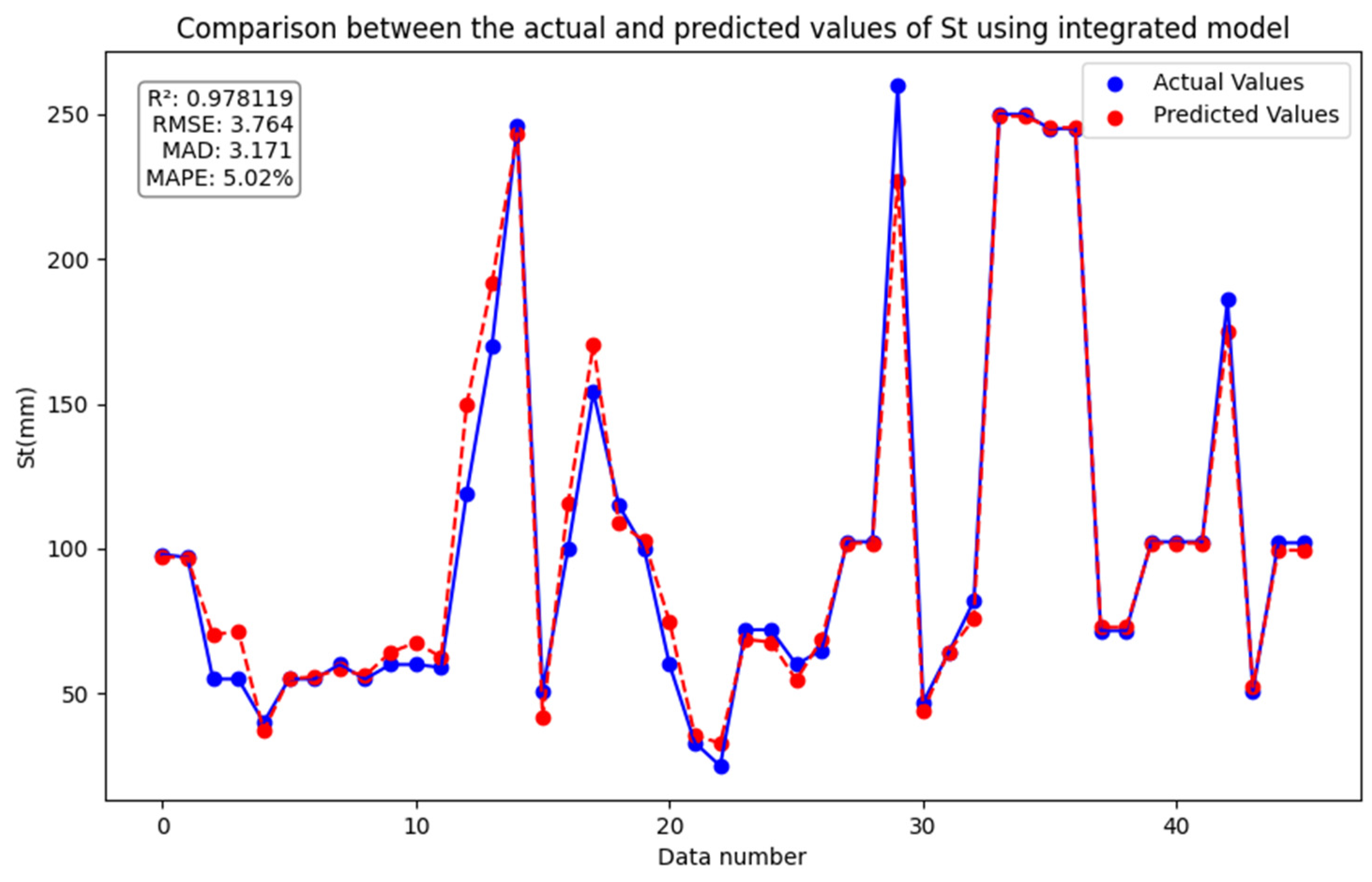
4.6. Integration of SVM and RF
4.7. Code Implementation Framework and Development Environment
5. Results
5.1. Evaluation Indicators
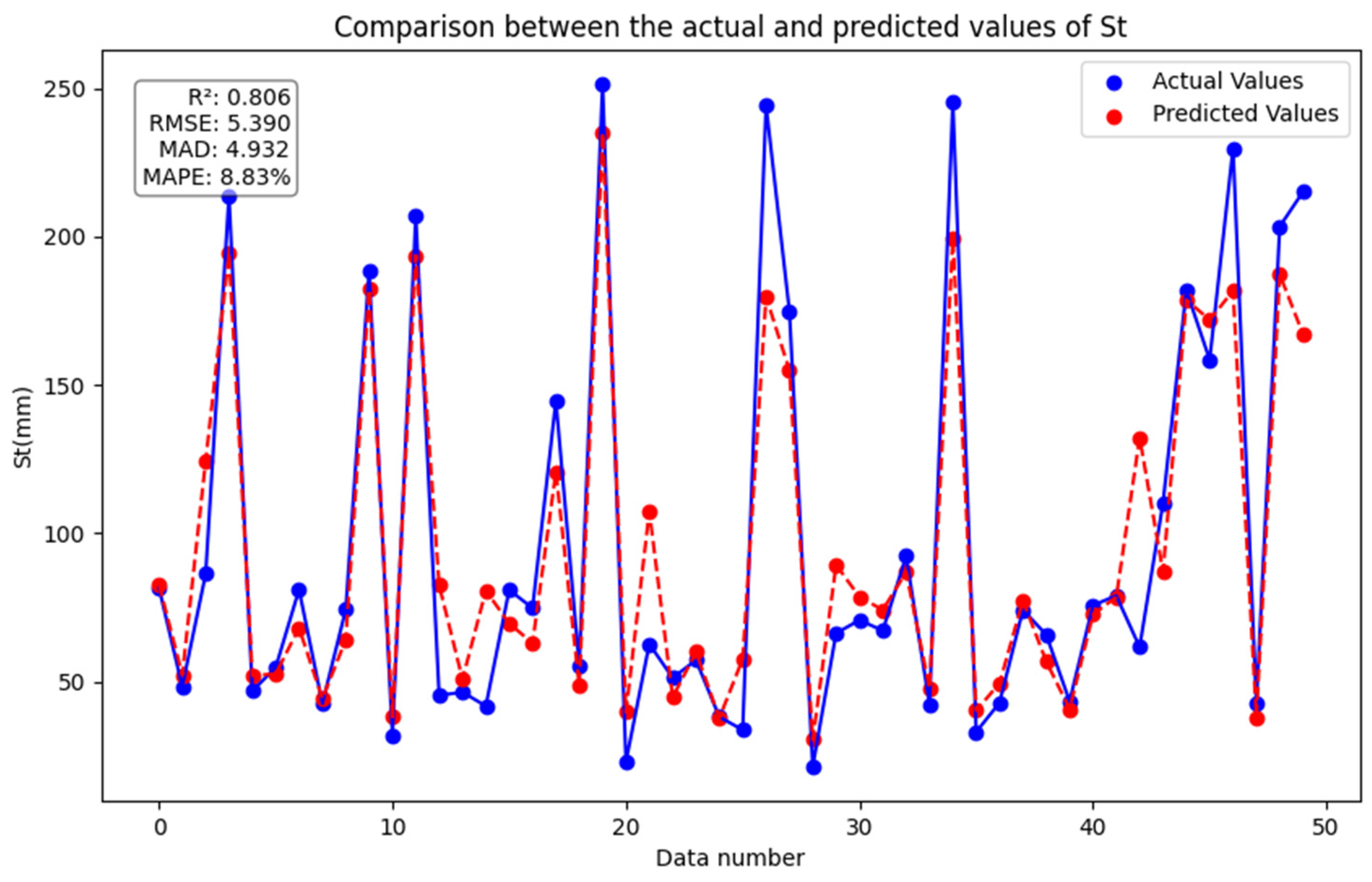
5.2. St Prediction
5.2.1. GBDT, XGBoost and DNN Model
5.2.2. SVM Model and RF Model
5.2.3. Integrated Model
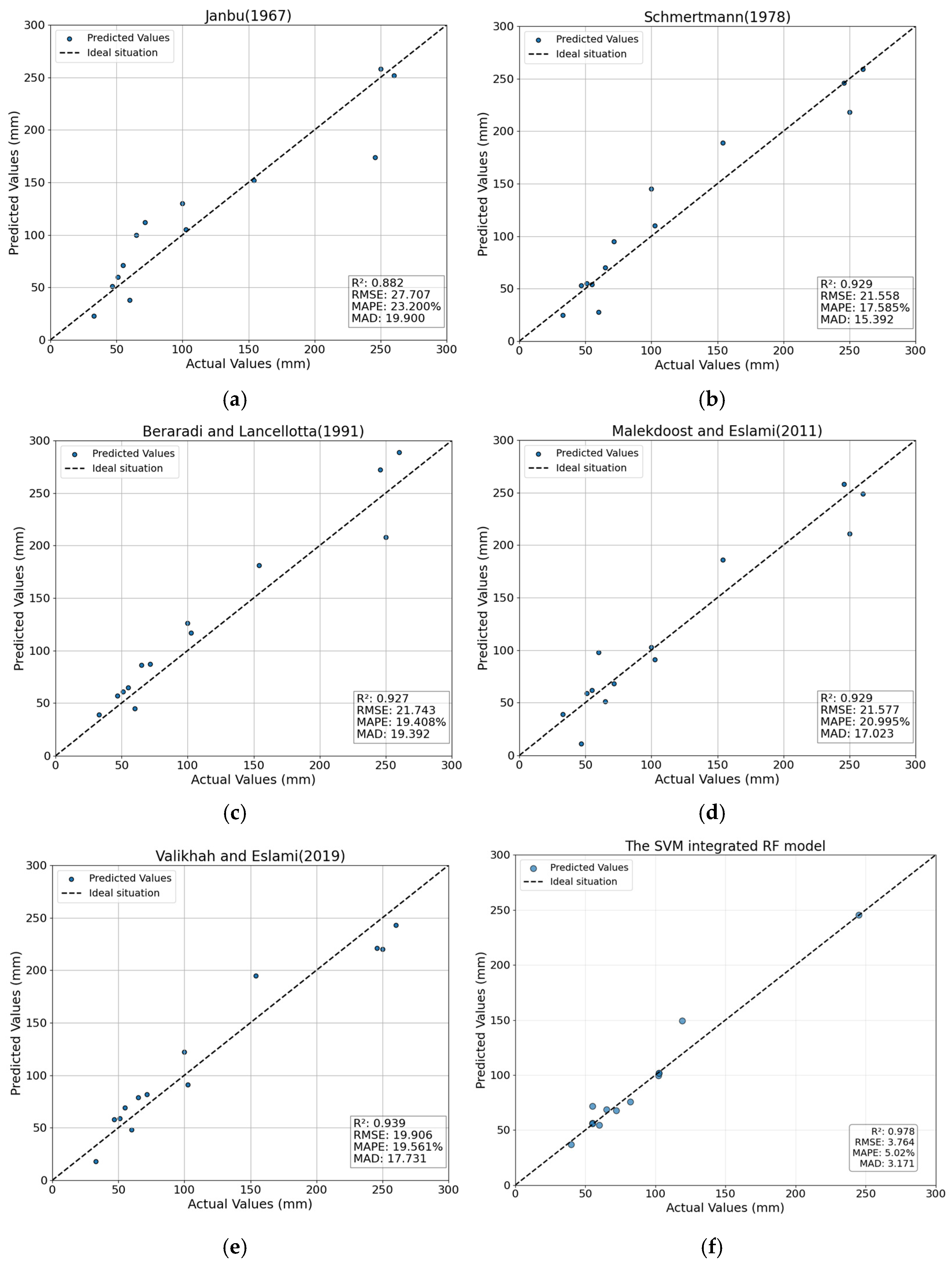
5.3. Comparison Between the Integrated Model and the Existing Equations
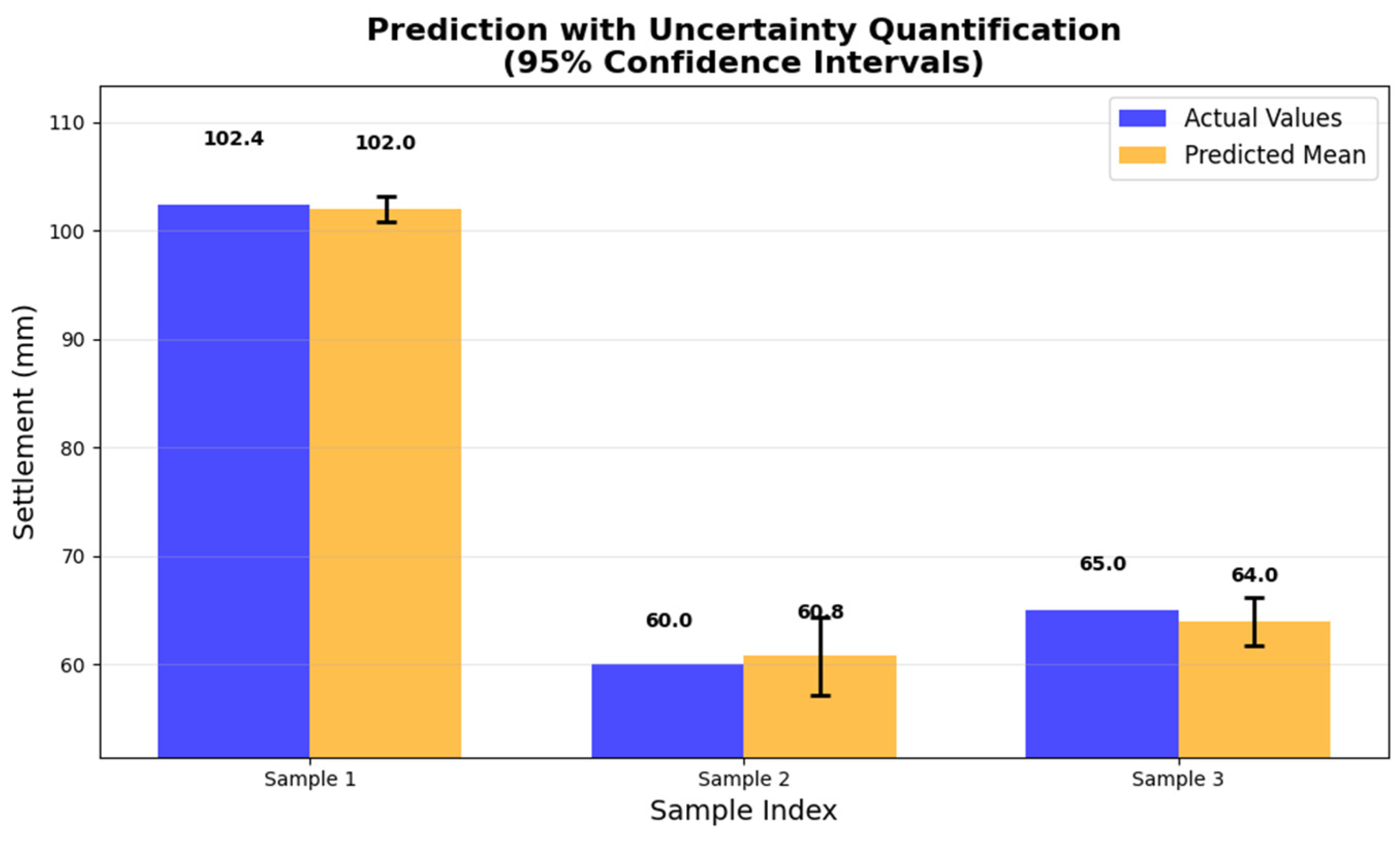
5.4. Uncertainty Analysis of Integrated Models
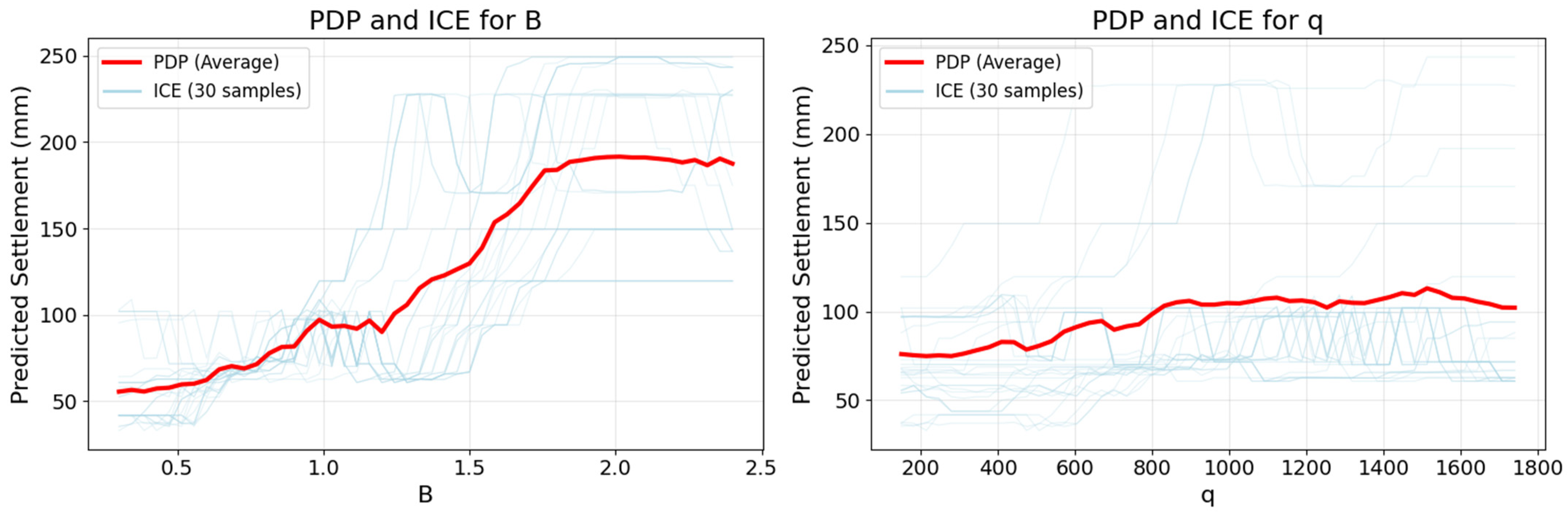
5.5. Sensitivity Analysis of Integrated Models
6. Model Validation
7. Conclusions
- (1)
- The SVM-ensemble RF model proposed in this study predicts values that closely match the actual values and outperforms the other models, followed by XGBoost, SVM, RF, GBDT, and DNN. Therefore, the proposed ensemble model has very high predictive capability and can effectively capture the complex nonlinear relationships between soil layer characteristics and settlement.
- (2)
- This study compared the SVM-ensemble RF model with traditional methods and single machine learning models. The results showed that the SVM-ensemble RF model performed best across all evaluation metrics. This further validates that the integrated model proposed in this study can achieve more realistic and accurate settlement predictions, providing a reference for geotechnical engineering practice.
- (3)
- This study employs Monte Carlo simulation to quantify the uncertainty of the ensemble model’s prediction results and conducts a sensitivity analysis. The results of uncertainty quantification all fall within the 95% confidence interval. The sensitivity analysis shows that, when using an SVM-integrated RF model to predict settlement values (St), the foundation width (B) has the greatest influence, followed by foundation load (q), and finally corrected cone tip resistance ().
- (4)
- Finally, based on the 46 sets of data collected from the literature, 50 new datasets were generated using a Generative Adversarial Network (GAN) and applied to the ensemble model proposed in this study. The results indicate that the ensemble model demonstrates good generalization ability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Holtz, R.D.; Kovacs, W.D.; Sheahan, T.C. An Introduction to Geotechnical Engineering; Prentice-hall: Englewood Cliffs, NJ, USA, 1981. [Google Scholar]
- Paikowsky, S.G.; Fu, Y.; Amatya, S.; Canniff, M.C. Uncertainty in shallow foundations settlement analysis and its utilization in SLS design specifications. In Proceedings of the 17th International Conference on Soil Mechanics and Geotechnical Engineering (Volumes 1, 2, 3 and 4), Alexandria, Egypt, 5–9 October 2009; pp. 1317–1320. [Google Scholar]
- Valikhah, F.; Eslami, A. CPT-Based Nonlinear Stress–Strain Approach for Evaluating Foundation Settlement: Analytical and Numerical Analysis. Arab. J. Sci. Eng. 2019, 44, 8819–8834. [Google Scholar] [CrossRef]
- Omer, J.R.; Delpak, R.; Robinson, R.B. A new computer program for pile capacity prediction using CPT data. Geotech. Geol. Eng. 2006, 24, 399–426. [Google Scholar] [CrossRef]
- Moshfeghi, S.; Eslami, A. Reliability-based assessment of drilled displacement piles bearing capacity using CPT records. Mar. Georesources Geotechnol. 2019, 37, 67–80. [Google Scholar] [CrossRef]
- Robertson, P.K. Soil behaviour type from the CPT: An update. In Proceedings of the 2nd International Symposium on Cone Penetration Testing, Huntington Beach, CA, USA, 9–11 May 2010; Volume 2, pp. 575–583. [Google Scholar]
- Mayne, P.W. Cone Penetration Testing; Transportation Research Board: Washington, DC, USA, 2007. [Google Scholar]
- Lunne, T.; Powell, J.J.M.; Robertson, P.K. Cone Penetration Testing in Geotechnical Practice; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Jefferies, M.G.; Davies, M.P. Use of CPTU to estimate equivalent SPT N 60. Geotech. Test. J. 1993, 16, 458–468. [Google Scholar] [CrossRef]
- Samui, P. Support vector machine applied to settlement of shallow foundations on cohesionless soils. Comput. Geotech. 2008, 35, 419–427. [Google Scholar] [CrossRef]
- Kaveh, A. Applications of Artificial Neural Networks and Machine Learning in Civil Engineering; Studies in Computational Intelligence; Springer: Cham, Switzerland, 2024; Volume 1168. [Google Scholar]
- Kourehpaz, P.; Molina Hutt, C. Machine learning for enhanced regional seismic risk assessments. J. Struct. Eng. 2022, 148, 04022126. [Google Scholar] [CrossRef]
- Ahmed, M.O.; Khalef, R.; Ali, G.G.; El-Adaway, I.H. Evaluating deterioration of tunnels using computational machine learning algorithms. J. Constr. Eng. Manag. 2021, 147, 04021125. [Google Scholar] [CrossRef]
- Faraz Athar, M.; Khoshnevisan, S.; Sadik, L. CPT-Based Soil Classification through Machine Learning Techniques. In Proceedings of the Geo-Congress 2023, Los Angeles, CA, USA, 26–29 March 2023; pp. 277–292. [Google Scholar]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Xu, X. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; Volume 1, pp. 278–282. [Google Scholar]
- Cervantes, J.; Garcia-Lamont, F.; Rodríguez-Mazahua, L.; Lopez, A. A comprehensive survey on support vector machine classification: Applications, challenges and trends. Neurocomputing 2020, 408, 189–215. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Asgarkhani, N.; Kazemi, F.; Jankowski, R.; Formisano, A. Dynamic ensemble-learning model for seismic risk assessment of masonry infilled steel structures incorporating soil-foundation-structure interaction. Reliab. Eng. Syst. Saf. 2025, 267, 111839. [Google Scholar] [CrossRef]
- Benker, M.; Furtner, L.; Semm, T.; Zaeh, M.F. Utilizing uncertainty information in remaining useful life estimation via Bayesian neural networks and Hamiltonian Monte Carlo. J. Manuf. Syst. 2021, 61, 799–807. [Google Scholar] [CrossRef]
- Padarian, J.; Minasny, B.; McBratney, A.B. Assessing the uncertainty of deep learning soil spectral models using Monte Carlo dropout. Geoderma 2022, 425, 116063. [Google Scholar] [CrossRef]
- Nguyen, H.T.T.; Cao, H.Q.; Nguyen, K.V.T.; Pham, N.D.K. Evaluation of explainable artificial intelligence: Shap, lime, and cam. In Proceedings of the FPT AI Conference, Ha Noi, Vietnam, 6–7 May 2021; pp. 1–6. [Google Scholar]
- Lundberg, S.M.; Erion, G.G.; Lee, S.I. Consistent individualized feature attribution for tree ensembles. arXiv 2018, arXiv:1802.03888. [Google Scholar]
- Cracknell, M.J.; Reading, A.M. Geological mapping using remote sensing data: A comparison of five machine learning algorithms, their response to variations in the spatial distribution of training data and the use of explicit spatial information. Comput. Geosci. 2014, 63, 22–33. [Google Scholar] [CrossRef]
- Wang, W.; Xue, C.; Zhao, J.; Yuan, C.; Tang, J. Machine learning-based field geological mapping: A new exploration of geological survey data acquisition strategy. Ore Geol. Rev. 2024, 166, 105959. [Google Scholar] [CrossRef]
- Ishihara, K.; Yoshimine, M. Evaluation of settlements in sand deposits following liquefaction during earthquakes. Soils Found. 1992, 32, 173–188. [Google Scholar] [CrossRef]
- Janbu, N. Settlement Calculations Based on the Tangent Modulus Concept; Technical University of Norway: Trondheim, Norway, 1967. [Google Scholar]
- Schmertmann, J.H. Guidelines for Cone Test, Performance, and Design; Report FHWA-TS-78209; Federal Highway Administration: Washington, DC, USA, 1978; p. 145. [Google Scholar]
- Berardi, R.; Lancellotta, R. Stiffness of granular soils from field performance. Geotechnique 1991, 41, 149–157. [Google Scholar] [CrossRef]
- Malekdoost, M.; Eslami, A. Application of CPT data for estimating foundations settlement-case histories. Sharif J. Civ. Eng. 2011, 1, 75–85. [Google Scholar]
- MolaAbasi, H.; Saberian, M.; Khajeh, A.; Li, J.; Chenari, R.J. Settlement predictions of shallow foundations for non-cohesive soils based on CPT records-polynomial model. Comput. Geotech. 2020, 128, 103811. [Google Scholar] [CrossRef]
- Eslami, A.; Gholami, M. Bearing capacity analysis of shallow foundations from CPT data. In Proceedings of the 16th International Conference on Soil Mechanics and Geotechnical Engineering, Osaka, Japan, 12–16 September 2005; pp. 1463–1466. [Google Scholar]
- Mayne, P.W.; Illingworth, F. Direct CPT method for footing response in sands using a database approach. In Proceedings of the 2nd International Symposium on Cone Penetration Testing, Huntington Beach, CA, USA, 9–11 May 2010. [Google Scholar]
- Briaud, J.L.; Gibbens, R. Behavior of five large spread footings in sand. J. Geotech. Geoenviron. Eng. 1999, 125, 787–796. [Google Scholar] [CrossRef]
- Eslami, A.A.; Gholami, A.M. Analytical model for the ultimate bearing capacity of foundations from cone resistance. Sci. Iran. 2006, 13, 223–233. [Google Scholar]
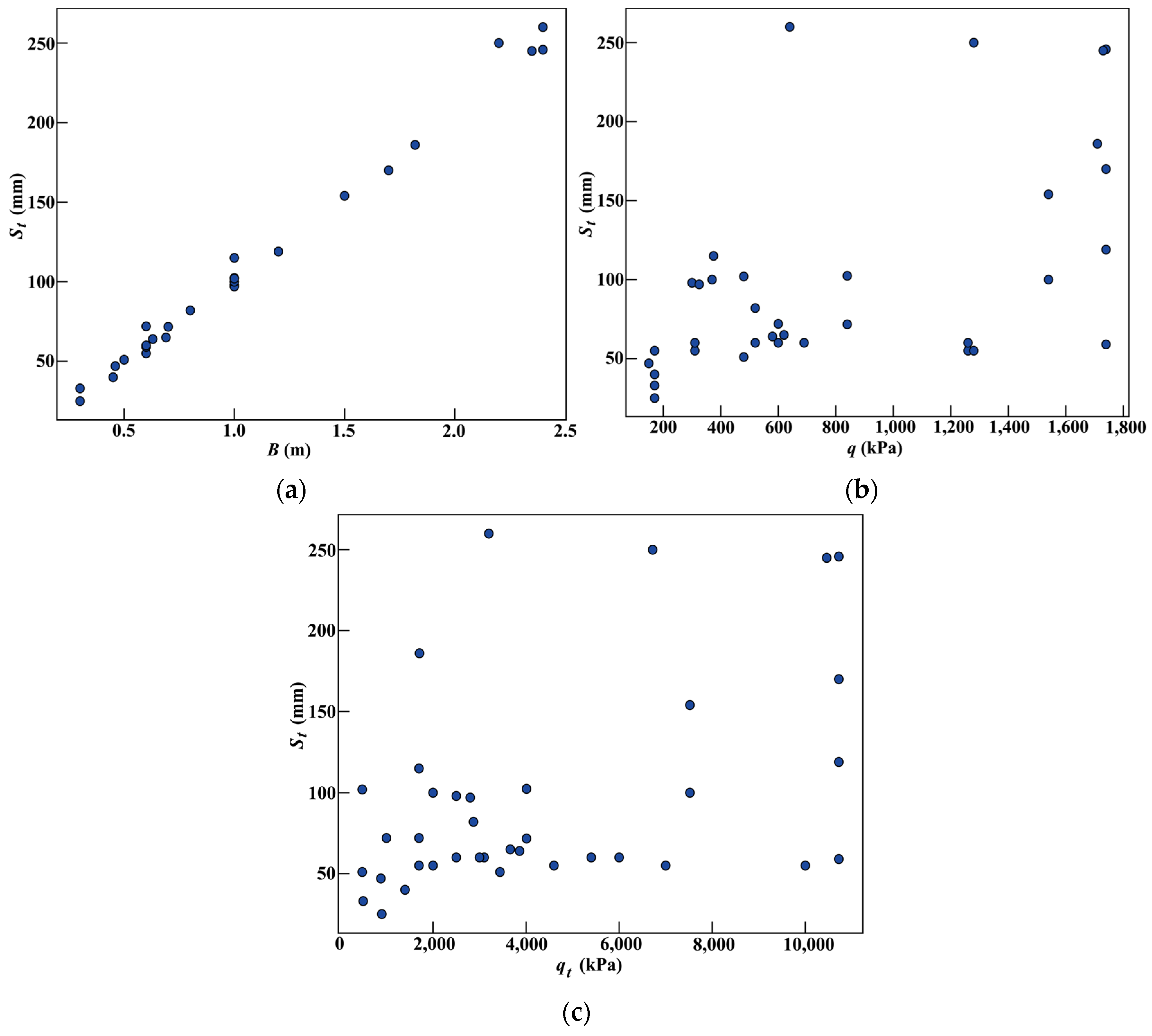




| No | Methods | Equation | Remarks |
|---|---|---|---|
| 1 | Janbu (1967) [31] | : foundation settlement, : strain induced by effective stress increase, : initial effective stress, : increase in effective stress under applied stress, m: modulus number, H: the thickness of the target layer, j: stress exponent = 0.5, : constant stress equal to 100 kPa | |
| 2 | Schmertmann (1978) [32] | : a correction factor for the depth of foundation embedment = , : a correction factor to account for creep in soil (t is time in year) = , : strain influence factor, E = 2 | |
| 3 | Berardi and Lancellotta (1991) [33] | , : modulus number, = 0.63, 0.69, and 0.88 for circle, square, and rectangular foundations, respectively | |
| 4 | Malekdoost and Eslami (2011) [34] | m = 2, , : cone tip resistance, : friction ratio = | |
| 5 | Valikhah and Eslami (2019) [3] | , B: foundation width, b: penetration cone diameter, , , |
| Soil Type | Case No. | Footing Shape | (kPa) | (m) | B (m) | (kPa) | (mm) | Reference | |
|---|---|---|---|---|---|---|---|---|---|
| Silt | 1 | Square | 2500 | 0.5 | 0 | 1 | 300 | 98 | Eslami and Gholami (2005) [36] |
| 2 | 2800 | 0.5 | 0 | 1 | 325 | 97 | |||
| Silt Sand | 3 | Square | 7000 | 0.5 | 0 | 0.6 | 1260 | 55 | |
| 4 | 10,000 | 0.5 | 0 | 0.6 | 1280 | 55 | |||
| Silt Clay | 5 | Circular | 1400 | 0.6 | 0 | 0.45 | 170 | 40 | |
| 6 | 1700 | 0.6 | 0 | 0.6 | 170 | 55 | |||
| 7 | 2000 | 0.6 | 0 | 0.6 | 170 | 55 | |||
| Silt Clay | 8 | Circular | 3100 | 0.6 | 1.5 | 0.6 | 520 | 60 | |
| 9 | 4600 | 0.6 | 1.5 | 0.6 | 310 | 55 | |||
| 10 | 5400 | 0.6 | 1.5 | 0.6 | 310 | 60 | |||
| 11 | 6000 | 0.6 | 1.5 | 0.6 | 690 | 60 | |||
| Glaciofluvial Sand | 12 | Rectangular | 10,720 | 0.51 | 0.4 | 0.6 | 1740 | 59 | Mayne and Illingworth (2010) [37] |
| 13 | 10,720 | 0.51 | 0.6 | 1.2 | 1740 | 119 | |||
| 14 | 10,720 | 0.51 | 0.8 | 1.7 | 1740 | 170 | |||
| 15 | 10,720 | 0.51 | 1.1 | 2.4 | 1740 | 245.8 | |||
| Siliceous Sand | 16 | Square | 3440 | 0.44 | 0.5 | 0.5 | 480 | 51 | |
| Sand, Silty Sand | 17 | Square | 7520 | 0.65 | 0.76 | 1 | 1540 | 100 | Briaud and Gibbens (1999) [38] |
| 18 | 7520 | 0.65 | 0.76 | 1.5 | 1540 | 154 | |||
| Silt | 19 | Square | 1700 | 0.5 | 0 | 1 | 375 | 115 | Eslami and Gholami (2006) [39] |
| 20 | 2000 | 0.5 | 0 | 1 | 370 | 100 | |||
| Silt Sand | 21 | Square | 3000 | 0.5 | 0 | 0.6 | 1260 | 60 | |
| Silt Clay | 22 | Circular | 500 | 0.6 | 0 | 0.3 | 170 | 33 | |
| 23 | 900 | 0.6 | 0 | 0.3 | 170 | 25 | |||
| Silt Clay | 24 | Circular | 1000 | 0.6 | 1.5 | 0.6 | 600 | 72 | |
| 25 | 1700 | 0.6 | 1.5 | 0.6 | 600 | 72 | |||
| 26 | 2500 | 0.6 | 1.5 | 0.6 | 600 | 60 | |||
| White Fine Sand | 27 | Square | 3660 | 0.54 | 0 | 0.69 | 620 | 65 | Mayne and Illingworth (2010) [37] |
| Glaciofluvial Sand | 28 | Rectangular | 4010 | 0.63 | 0 | 1 | 840 | 102.4 | |
| 29 | 4010 | 0.63 | 0 | 1 | 840 | 102.4 | |||
| 30 | 3200 | 0.63 | 1.1 | 2.4 | 640 | 260 | |||
| Compacted Fill | 31 | Square | 880 | 0.53 | 0 | 0.46 | 150 | 47 | |
| 32 | 3860 | 0.48 | 0 | 0.63 | 580 | 64 | |||
| 33 | 2870 | 0.58 | 0 | 0.8 | 520 | 82 | |||
| Alluvial Sand | 34 | Circular | 6720 | 0.6 | 2.2 | 2.2 | 1280 | 250 | |
| 35 | 6720 | 0.6 | 2.2 | 2.2 | 1280 | 250 | |||
| 36 | 10,460 | 0.52 | 2.35 | 2.35 | 1730 | 245 | |||
| 37 | 10,460 | 0.52 | 2.35 | 2.35 | 1730 | 245 | |||
| Dune Sand | 38 | Square | 4010 | 0.66 | 0 | 0.7 | 840 | 71.7 | |
| 39 | 4010 | 0.66 | 0 | 0.7 | 840 | 71.7 | |||
| 40 | 4010 | 0.66 | 0 | 1 | 840 | 102.4 | |||
| 41 | 4010 | 0.66 | 0 | 1 | 840 | 102.4 | |||
| 42 | 4010 | 0.66 | 0 | 1 | 840 | 102.4 | |||
| Silty Sand | 43 | Circular | 1710 | 0.55 | 0.6 | 1.82 | 1710 | 186 | |
| Siliceous Dune Sand | 44 | Square | 480 | 0.44 | 0.5 | 0.5 | 480 | 51 | |
| 45 | 480 | 0.44 | 1 | 1 | 480 | 102 | |||
| 46 | 480 | 0.44 | 1 | 1 | 480 | 102 |
| Model | RMSE | MAD | MAPE | |
|---|---|---|---|---|
| GBDT | 0.876 ± 0.009 | 22.982 ± 0.43 | 15.846 ± 0.43 | 20.12% ± 0.40% |
| XGBoost | 0.926 ± 0.007 | 17.533 ± 0.48 | 11.914 ± 0.39 | 14.86% ± 0.35% |
| DNN | 0.826 ± 0.015 | 27.284 ± 0.68 | 22.432 ± 0.52 | 27.03% ± 0.48% |
| SVM | 0.916 ± 0.008 | 18.968 ± 0.52 | 12.517 ± 0.41 | 12.79% ± 0.38% |
| RF | 0.901 ± 0.012 | 20.570 ± 0.61 | 13.458 ± 0.49 | 15.87% ± 0.45% |
| SVM-integrated RF | 0.978 ± 0.005 | 3.764 ± 0.45 | 3.171 ± 0.38 | 5.02% ± 0.32% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Zhang, W. A Shallow Foundation Settlement Prediction Method Considering Uncertainty Based on Machine Learning and CPT Data. Appl. Sci. 2025, 15, 12174. https://doi.org/10.3390/app152212174
Zhang R, Zhang W. A Shallow Foundation Settlement Prediction Method Considering Uncertainty Based on Machine Learning and CPT Data. Applied Sciences. 2025; 15(22):12174. https://doi.org/10.3390/app152212174
Chicago/Turabian StyleZhang, Rui, and Wuyu Zhang. 2025. "A Shallow Foundation Settlement Prediction Method Considering Uncertainty Based on Machine Learning and CPT Data" Applied Sciences 15, no. 22: 12174. https://doi.org/10.3390/app152212174
APA StyleZhang, R., & Zhang, W. (2025). A Shallow Foundation Settlement Prediction Method Considering Uncertainty Based on Machine Learning and CPT Data. Applied Sciences, 15(22), 12174. https://doi.org/10.3390/app152212174





