From First Life to Second Life: Advances and Research Gaps in Prognosis Techniques for Lithium-Ion Batteries
Abstract
1. Introduction
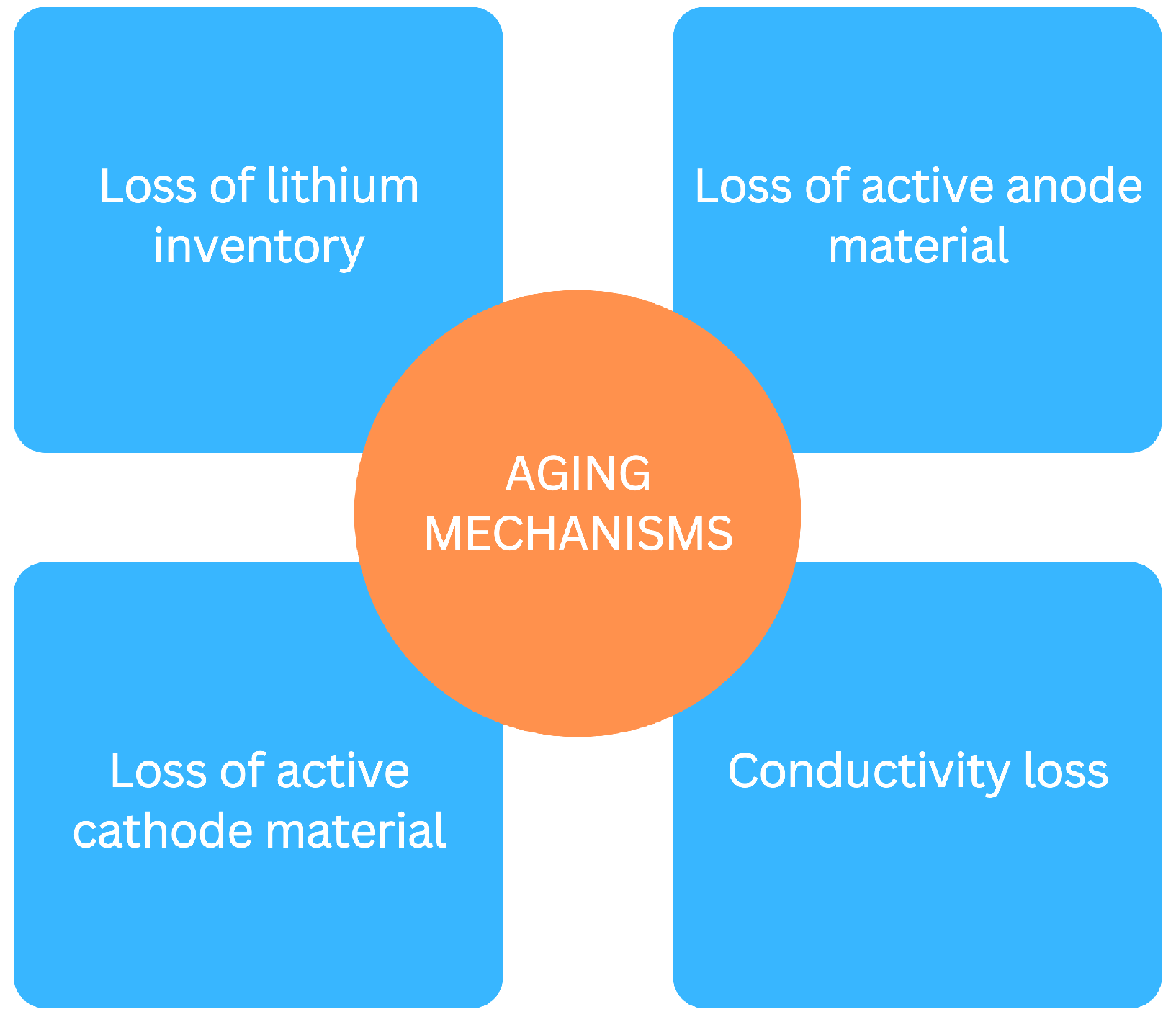
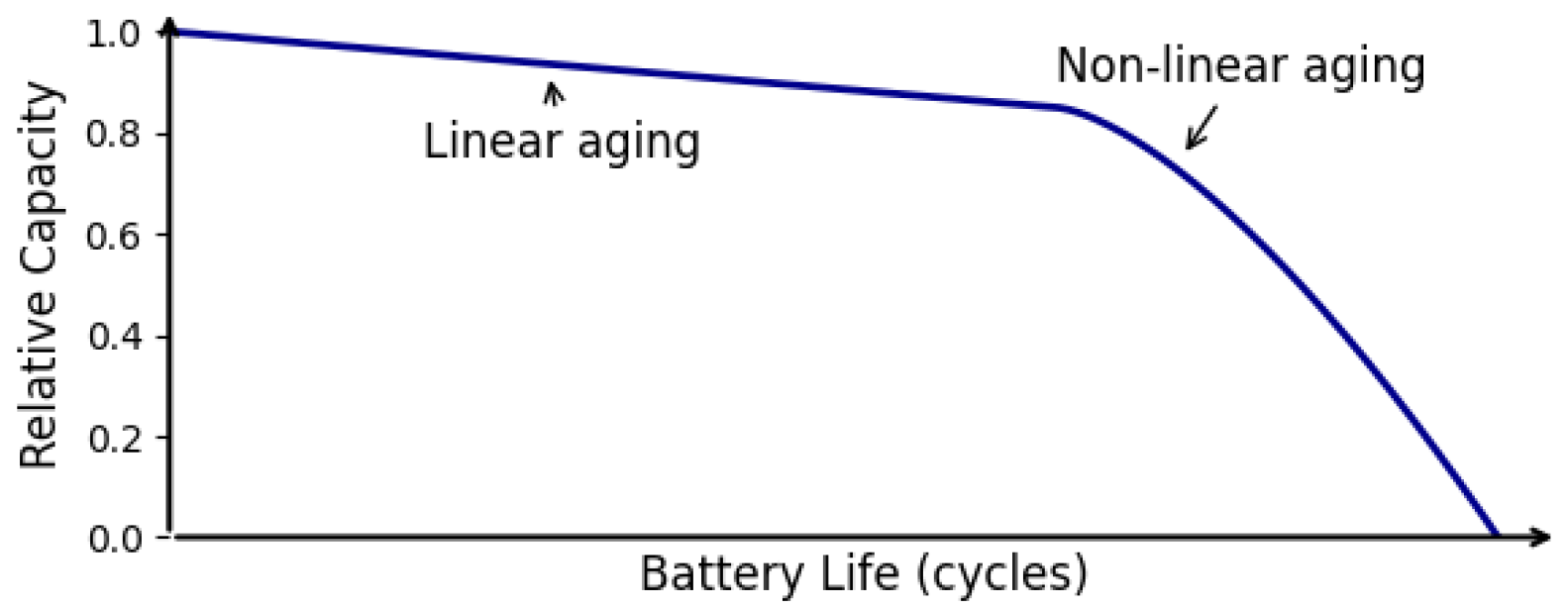
2. Degradation Mechanisms of Lithium-Ion Batteries
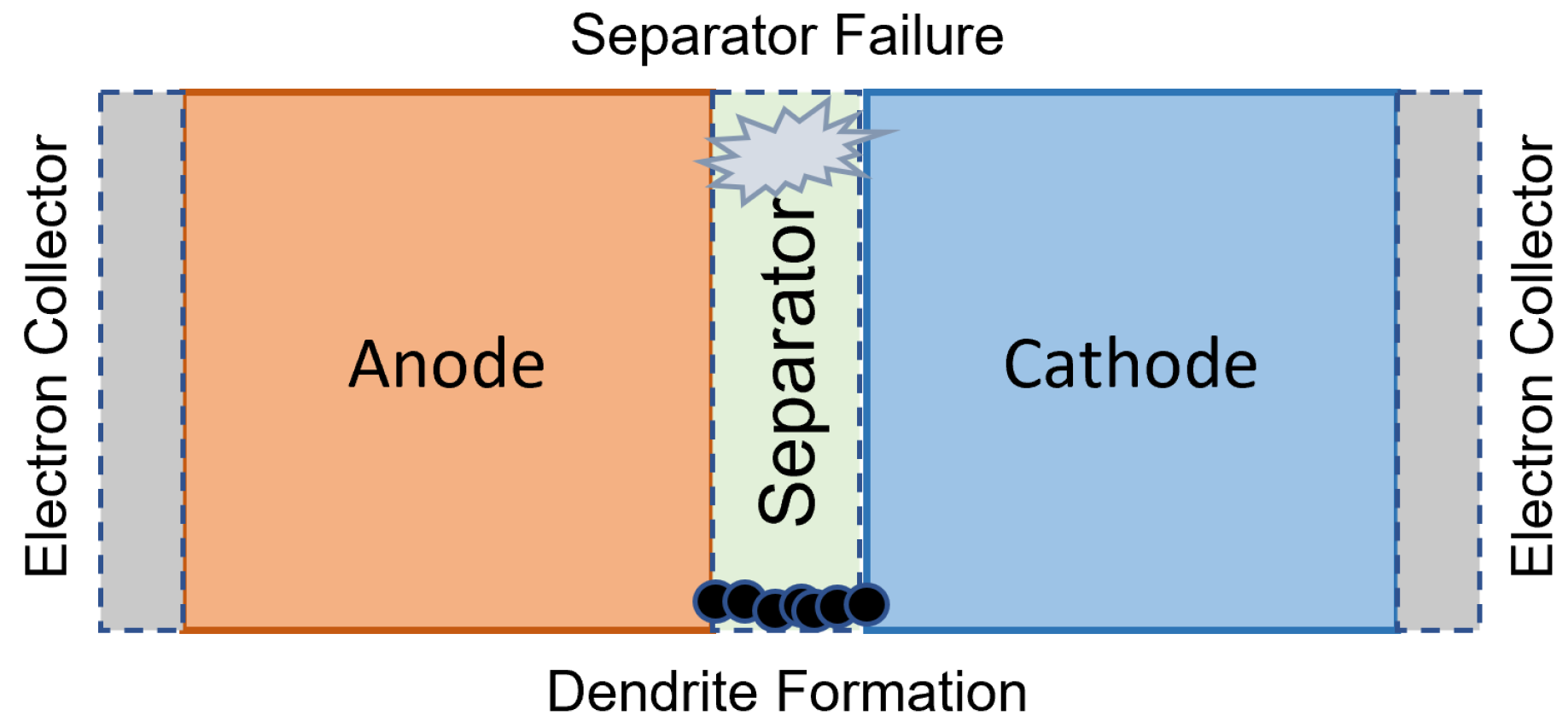
2.1. Internal Short Circuit
2.2. External Short Circuit
2.3. Voltage Deviations
2.4. Thermal Runaway
3. Second-Life Batteries: Opportunities and Challenges
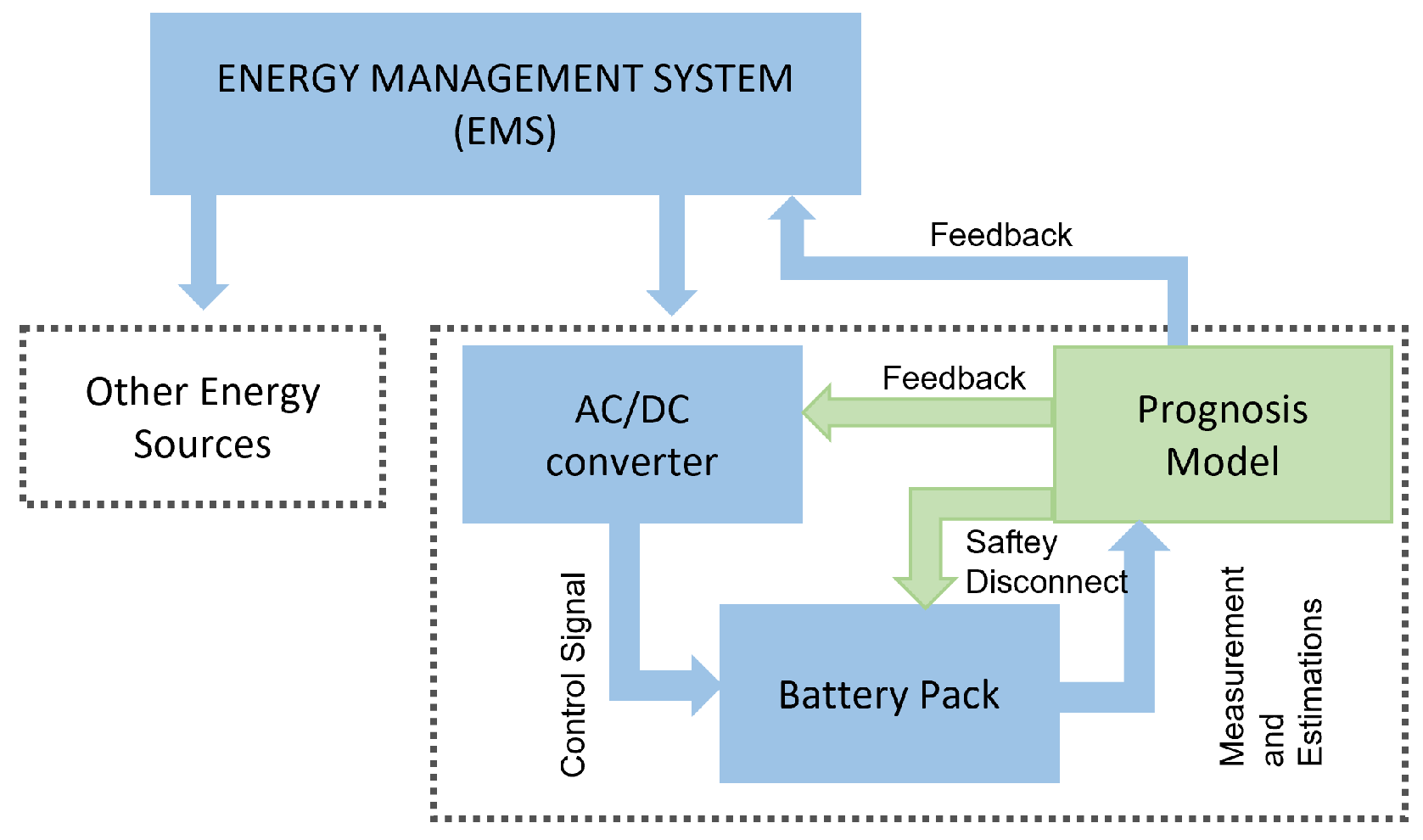
4. Battery Prognosis and Second-Life Applications
4.1. Physics-Informed and Hybrid Models
4.2. Data-Driven Neural Networks and Regression Models
4.3. Transfer Learning and Feature Extraction
5. Comparative Analysis and Health Management
6. Conclusions and Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | Alternating Current |
| ADMD | Adaptive Differential Model Decomposition |
| APE | Absolute Percentage Error |
| BESS | Battery Energy Storage System |
| BiGRU | Bidirectional Gate Recurrent Unit |
| BiLSTM | Bidirectional Long Short-Term Memory |
| BMS | Battery Management System |
| BPNN | Back-Propagation Neural Network |
| BR | Bayesian Regularization |
| CC | Constant Current |
| CL | Cell Level |
| CNN | Convolutional Neural Network |
| CV | Constant Voltage |
| CWT | Continuous Wavelet Transform |
| DC | Direct Current |
| DMD | Dynamic Mode Decomposition |
| DWT | Discrete Wavelet Transform |
| ECM | Equivalent Circuit Model |
| EIS | Electrochemical Impedance Spectroscopy |
| EOL | End of Life |
| EMS | Energy Management System |
| ESN | Echo State Network |
| EST | Exponential Smoothing Transformer |
| EU | European Union |
| EV | Electric Vehicle |
| FC | Fully Connected |
| FFA | Fennec Fox Algorithm |
| FFNN | Feedforward Neural Network |
| FPCA | Functional Principal Component Analysis |
| FT | Fourier Transform |
| GAN | Generative Adversarial Network |
| GP | Gaussian Process |
| GPR | Gaussian Process Regression |
| GRU | Gated Recurrent Unit |
| HI | Health Indicator |
| LAM | Loss of Active Material |
| LFP | Lithium Iron Phosphate |
| LIB | Lithium-Ion Battery |
| LIBs | Lithium-Ion Batteries |
| LM | Levenberg–Marquardt |
| LSTM | Long Short-Term Memory |
| MAE | Mean Absolute Error |
| MCC | Multistage Constant Current |
| MMD | Maximum Mean Discrepancy |
| MSE | Mean Square Error |
| NASA | National Aeronautics and Space Administration |
| NCB | Nickel Cobalt Battery |
| OAI | Online Accuracy Index |
| P2D | Pseudo-two-dimensional |
| PGAS | Particle Gibbs with Ancestor Sampling |
| PHM | Prognostics and Health Management |
| PIF | Physics-Informed Framework |
| PI-TNET | Physics-Informed Neural Network integrated with a transformer |
| PIML | Physics-Informed Machine Learning |
| PITC | Partially Independent Training Conditional |
| PLDP | Pseudo-Label Distribution Perturbation |
| RCGAN | Recurrent Conditional Generative Adversarial Network |
| Coefficient of Determination | |
| RF | Random Forest |
| RL | Reinforcement Learning |
| RMSE | Root Mean Square Error |
| RUL | Remaining Useful Life |
| SCG | Scaled Conjugate Gradient |
| SEI | Solid Electrolyte Interphase |
| SFE | Salient Frequency Extraction |
| SOC | State of Charge |
| SOH | State of Health |
| TCN | Temporal Convolutional Network |
| TDC | Temporal Distribution Characteristics |
| TRIBD | Transfer Recurrent Information-Based Decomposition |
| UADA | Uncertainty-Aware Domain Adaptation |
References
- Cochran, J.; Mai, T.; Bazilian, M. Meta-analysis of high penetration renewable energy scenarios. Renew. Sustain. Energy Rev. 2014, 29, 246–253. [Google Scholar] [CrossRef]
- Giacomarra, M.; Bono, F. European Union commitment towards RES market penetration: From the first legislative acts to the publication of the recent guidelines on State aid 2014/2020. Renew. Sustain. Energy Rev. 2015, 47, 218–232. [Google Scholar] [CrossRef]
- Liu, H.; Li, L.; Duan, B.; Kang, Y.; Zhang, C. Multi-fault detection and diagnosis method for battery packs based on statistical analysis. Energy 2024, 293, 130465. [Google Scholar] [CrossRef]
- Samanta, A.; Chowdhuri, S.; Williamson, S.S. Machine Learning-Based Data-Driven Fault Detection/Diagnosis of Lithium-Ion Battery: A Critical Review. Electronics 2021, 10, 1309. [Google Scholar] [CrossRef]
- Zhao, J.; Feng, X.; Pang, Q.; Wang, J.; Lian, Y.; Ouyang, M.; Burke, A.F. Battery prognostics and health management from a machine learning perspective. J. Power Sources 2023, 581, 233474. [Google Scholar] [CrossRef]
- Xiao, Y.; Wen, J.; Yao, L.; Zheng, J.; Fang, Z.; Shen, Y. A comprehensive review of the lithium-ion battery state of health prognosis methods combining aging mechanism analysis. J. Energy Storage 2023, 65, 107347. [Google Scholar] [CrossRef]
- Madani, S.S.; Shabeer, Y.; Allard, F.; Fowler, M.; Ziebert, C.; Wang, Z.; Panchal, S.; Chaoui, H.; Mekhilef, S.; Dou, S.X.; et al. A Comprehensive Review on Lithium-Ion Battery Lifetime Prediction and Aging Mechanism Analysis. Batteries 2025, 11, 127. [Google Scholar] [CrossRef]
- Hu, X.; Xu, L.; Lin, X.; Pecht, M. Battery Lifetime Prognostics. Joule 2020, 4, 310–346. [Google Scholar] [CrossRef]
- Che, Y.; Hu, X.; Lin, X.; Guo, J.; Teodorescu, R. Health prognostics for lithium-ion batteries: Mechanisms, methods, and prospects. Energy Environ. Sci. 2023, 16, 338–371. [Google Scholar] [CrossRef]
- Kumar, R.; Das, K. Lithium battery prognostics and health management for electric vehicle application—A perspective review. Sustain. Energy Technol. Assess. 2024, 65, 103766. [Google Scholar] [CrossRef]
- Xu, J.; Sun, C.; Ni, Y.; Lyu, C.; Wu, C.; Zhang, H.; Yang, Q.; Feng, F. Fast Identification of Micro-Health Parameters for Retired Batteries Based on a Simplified P2D Model by Using Padé Approximation. Batteries 2023, 9, 64. [Google Scholar] [CrossRef]
- Zhao, J.; Feng, X.; Pang, Q.; Fowler, M.; Lian, Y.; Ouyang, M.; Burke, A.F. Battery safety: Machine learning-based prognostics. Prog. Energy Combust. Sci. 2024, 102, 101142. [Google Scholar] [CrossRef]
- Finegan, D.P.; Zhu, J.; Feng, X.; Keyser, M.; Ulmefors, M.; Li, W.; Bazant, M.Z.; Cooper, S.J. The Application of Data-Driven Methods and Physics-Based Learning for Improving Battery Safety. Joule 2021, 5, 316–329. [Google Scholar] [CrossRef]
- Wang, Y.; Xiang, H.; Soo, Y.Y.; Fan, X. Aging mechanisms, prognostics and management for lithium-ion batteries: Recent advances. Renew. Sustain. Energy Rev. 2025, 207, 114915. [Google Scholar] [CrossRef]
- Wheeler, W.; Venet, P.; Bultel, Y.; Sari, A.; Riviere, E. Aging in First and Second Life of G/LFP 18650 Cells: Diagnosis and Evolution of the State of Health of the Cell and the Negative Electrode under Cycling. Batteries 2024, 10, 137. [Google Scholar] [CrossRef]
- Li, H.; Kaleem, M.B.; Liu, K.; Wu, Y.; Liu, W.; Peng, Q. Fault prognosis of Li-ion batteries in electric vehicles: Recent progress, challenges and prospects. J. Energy Storage 2025, 116, 116002. [Google Scholar] [CrossRef]
- Korthauer, R. (Ed.) Lithium-Ion Batteries: Basics and Applications; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Plett, G.L. Battery Management Systems, Volume 1: Battery Modeling; Artech House: Boston, MA, USA, 2015. [Google Scholar]
- Hogrefe, C.; Waldmann, T.; Hölzle, M.; Wohlfahrt-Mehrens, M. Direct observation of internal short circuits by lithium dendrites in cross-sectional lithium-ion in situ full cells. J. Power Sources 2023, 556, 232391. [Google Scholar] [CrossRef]
- Setta, J.; Lecocq, A.; Desprez, P.; Origuchi, M.; Destriau, L.; Marlair, G.; Carlier, D.; Croguennec, L.; Bordes, A. Internal short circuits in lithium-ion batteries; origins, detection, and experimental reproduction: A review. J. Power Sources 2025, 658, 238265. [Google Scholar] [CrossRef]
- Liu, B.; Jia, Y.; Li, J.; Yin, S.; Yuan, C.; Hu, Z.; Wang, L.; Li, Y.; Xu, J. Safety issues caused by internal short circuits in lithium-ion batteries. J. Mater. Chem. A 2018, 6, 21475–21484. [Google Scholar] [CrossRef]
- Zhao, J.; Guan, X.; Li, C.; Mou, Q.; Chen, Z. Comprehensive Evaluation of Inter-Turn Short Circuit Faults in PMSM Used for Electric Vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 22, 611–621. [Google Scholar] [CrossRef]
- Devarapu, C.P.; Vital, M.; Lanke, K.; Kade, P.; Chinmaya, K.P. Battery Management System using Cell Charge Balancing Topology in Electric Vehicle. In Proceedings of the 2023 International Conference on Inventive Computation Technologies (ICICT), Lalitpur, Nepal, 18–23 April 2023; pp. 1547–1552. [Google Scholar] [CrossRef]
- Yu, H.; Niu, S.; Shang, Y.; Shao, Z.; Jia, Y.; Jian, L. Electric vehicles integration and vehicle-to-grid operation in active distribution grids: A comprehensive review on power architectures, grid connection standards and typical applications. Renew. Sustain. Energy Rev. 2022, 168, 112812. [Google Scholar] [CrossRef]
- Plett, G.L. Battery Management Systems, Volume 2: Equivalent-Circuit Methods; Artech House: Boston, MA, USA, 2016. [Google Scholar]
- Xu, B.; Lee, J.; Kwon, D.; Kong, L.; Pecht, M. Mitigation strategies for Li-ion battery thermal runaway: A review. Renew. Sustain. Energy Rev. 2021, 150, 111437. [Google Scholar] [CrossRef]
- Gayathri, A.; Manimegalai, V.; Krishnakumar, P. Challenging Issues and Solutions on Battery Thermal Management for Electric Vehicles. In Electrical and Electronic Devices, Circuits, and Materials, 1 ed.; Tripathi, S.L., Alvi, P.A., Subramaniam, U., Eds.; Wiley: Hoboken, NJ, USA, 2021; pp. 535–553. [Google Scholar] [CrossRef]
- Zhang, R.; Li, X.; Sun, C.; Yang, S.; Tian, Y.; Tian, J. State of Charge and Temperature Joint Estimation Based on Ultrasonic Reflection Waves for Lithium-Ion Battery Applications. Batteries 2023, 9, 335. [Google Scholar] [CrossRef]
- Hossain, E.; Murtaugh, D.; Mody, J.; Faruque, H.M.R.; Haque Sunny, M.S.; Mohammad, N. A Comprehensive Review on Second-Life Batteries: Current State, Manufacturing Considerations, Applications, Impacts, Barriers & Potential Solutions, Business Strategies, and Policies. IEEE Access 2019, 7, 73215–73252. [Google Scholar] [CrossRef]
- Shahjalal, M.; Roy, P.K.; Shams, T.; Fly, A.; Chowdhury, J.I.; Ahmed, M.R.; Liu, K. A review on second-life of Li-ion batteries: Prospects, challenges, and issues. Energy 2022, 241, 122881. [Google Scholar] [CrossRef]
- The Glasgow Climate Pact: Key Outcomes from COP26. 2021. Available online: https://unfccc.int/process-and-meetings/the-paris-agreement/the-glasgow-climate-pact-key-outcomes-from-cop26 (accessed on 17 October 2025).
- Orangi, S.; Manjong, N.; Clos, D.P.; Usai, L.; Burheim, O.S.; Strømman, A.H. Historical and prospective lithium-ion battery cost trajectories from a bottom-up production modeling perspective. J. Energy Storage 2024, 76, 109800. [Google Scholar] [CrossRef]
- Cui, X.; Zhang, J.; Zhang, D.; Wei, Y.; Qi, H. Joint Prediction of Li-Ion Battery Cycle Life and Knee Point Based on Early Charging Performance. Symmetry 2025, 17, 351. [Google Scholar] [CrossRef]
- Li, S.; Shironita, S.; Hosono, E.; Asakura, D.; Sone, Y.; Umeda, M. A Dynamic Analysis of Reversible/Irreversible Capacity Fading of Li-ion Cells Owing to Low-temperature Operation by Differential Capacity Profile. Electrochemistry 2024, 92, 097007. [Google Scholar] [CrossRef]
- Fermín-Cueto, P.; McTurk, E.; Allerhand, M.; Medina-Lopez, E.; Anjos, M.F.; Sylvester, J.; Dos Reis, G. Identification and machine learning prediction of knee-point and knee-onset in capacity degradation curves of lithium-ion cells. Energy AI 2020, 1, 100006. [Google Scholar] [CrossRef]
- Martinez-Laserna, E.; Gandiaga, I.; Sarasketa-Zabala, E.; Badeda, J.; Stroe, D.I.; Swierczynski, M.; Goikoetxea, A. Battery second life: Hype, hope or reality? A critical review of the state of the art. Renew. Sustain. Energy Rev. 2018, 93, 701–718. [Google Scholar] [CrossRef]
- Elmahallawy, M.; Elfouly, T.; Alouani, A.; Massoud, A.M. A Comprehensive Review of Lithium-Ion Batteries Modeling, and State of Health and Remaining Useful Lifetime Prediction. IEEE Access 2022, 10, 119040–119070. [Google Scholar] [CrossRef]
- Allam, A.; Onori, S. Online Capacity Estimation for Lithium-Ion Battery Cells via an Electrochemical Model-Based Adaptive Interconnected Observer. IEEE Trans. Control Syst. Technol. 2021, 29, 1636–1651. [Google Scholar] [CrossRef]
- Lyu, C.; Lai, Q.; Ge, T.; Yu, H.; Wang, L.; Ma, N. A lead-acid battery’s remaining useful life prediction by using electrochemical model in the Particle Filtering framework. Energy 2017, 120, 975–984. [Google Scholar] [CrossRef]
- Zhang, H.; Miao, Q.; Zhang, X.; Liu, Z. An improved unscented particle filter approach for lithium-ion battery remaining useful life prediction. Microelectron. Reliab. 2018, 81, 288–298. [Google Scholar] [CrossRef]
- Ahwiadi, M.; Wang, W. An enhanced particle filter technology for battery system state estimation and RUL prediction. Measurement 2022, 191, 110817. [Google Scholar] [CrossRef]
- Zheng, X.; Fang, H. An integrated unscented kalman filter and relevance vector regression approach for lithium-ion battery remaining useful life and short-term capacity prediction. Reliab. Eng. Syst. Saf. 2015, 144, 74–82. [Google Scholar] [CrossRef]
- Cong, X.; Zhang, C.; Jiang, J.; Zhang, W.; Jiang, Y.; Jia, X. An Improved Unscented Particle Filter Method for Remaining Useful Life Prognostic of Lithium-ion Batteries With Li(NiMnCo)O2 Cathode With Capacity Diving. IEEE Access 2020, 8, 58717–58729. [Google Scholar] [CrossRef]
- Guo, W.; Sun, Z.; Vilsen, S.B.; Meng, J.; Stroe, D.I. Review of “grey box” lifetime modeling for lithium-ion battery: Combining physics and data-driven methods. J. Energy Storage 2022, 56, 105992. [Google Scholar] [CrossRef]
- Deng, W.; Le, H.; Nguyen, K.T.; Gogu, C.; Medjaher, K.; Morio, J.; Wu, D. A Generic physics-informed machine learning framework for battery remaining useful life prediction using small early-stage lifecycle data. Appl. Energy 2025, 384, 125314. [Google Scholar] [CrossRef]
- Li, K.; Xie, N.; Li, H. A hybrid grey approach for battery remaining useful life prediction considering capacity regeneration. Expert Syst. Appl. 2025, 274, 126905. [Google Scholar] [CrossRef]
- Zhan, Y.; Yan, K.; Zheng, X. Integrating Transformers into Physics-Informed Neural Networks: An Approach to Lithium-Ion Battery State of Health Prognostics. Int. J. Electr. Power Energy Syst. 2025, 172, 111173. [Google Scholar] [CrossRef]
- Peleg, M.; Corradini, M.G.; Normand, M.D. The logistic (Verhulst) model for sigmoid microbial growth curves revisited. Food Res. Int. 2007, 40, 808–818. [Google Scholar] [CrossRef]
- NASA. NASA Open Data Portal. Available online: https://data.nasa.gov/ (accessed on 15 October 2025).
- Liu, K.Y.; Wang, T.T.; Zou, B.B.; Peng, H.J.; Liu, X. TELL-Me: A time-series-decomposition-based ensembled lightweight learning model for diverse battery prognosis and diagnosis. J. Energy Chem. 2025, 106, 1–8. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Liu, C.; Chen, Z. A novel approach of battery pack state of health estimation using artificial intelligence optimization algorithm. J. Power Sources 2018, 376, 191–199. [Google Scholar] [CrossRef]
- Lyu, D.; Liu, E.; Chen, H.; Zhang, B.; Xiang, J. Transfer-driven prognosis from battery cells to packs: An application with adaptive differential model decomposition. Appl. Energy 2025, 377, 124290. [Google Scholar] [CrossRef]
- Lyu, D.; Niu, G.; Liu, E.; Zhang, B.; Chen, G.; Yang, T.; Zio, E. Time space modelling for fault diagnosis and prognosis with uncertainty management: A general theoretical formulation. Reliab. Eng. Syst. Saf. 2022, 226, 108686. [Google Scholar] [CrossRef]
- Zhang, H.; Niu, G.; Zhang, B.; Miao, Q. Cost-Effective Lebesgue Sampling Long Short-Term Memory Networks for Lithium-Ion Batteries Diagnosis and Prognosis. IEEE Trans. Ind. Electron. 2022, 69, 1958–1967. [Google Scholar] [CrossRef]
- Lyu, D.; Niu, G.; Liu, E.; Yang, T.; Chen, G.; Zhang, B. Uncertainty Management and Differential Model Decomposition for Fault Diagnosis and Prognosis. IEEE Trans. Ind. Electron. 2022, 69, 5235–5246. [Google Scholar] [CrossRef]
- Thomas, H.; Weatherspoon, M.H. Capacity and State-of-Health Prediction of Lithium-Ion Batteries Using Reduced Equivalent Circuit Models. Batteries 2025, 11, 162. [Google Scholar] [CrossRef]
- Shao, J.; Li, J.; Yuan, W.; Dai, C.; Wang, Z.; Zhao, M.; Pecht, M. A novel method of discharge capacity prediction based on simplified electrochemical model-aging mechanism for lithium-ion batteries. J. Energy Storage 2023, 61, 106788. [Google Scholar] [CrossRef]
- Li, C.; Yang, L.; Li, Q.; Zhang, Q.; Zhou, Z.; Meng, Y.; Zhao, X.; Wang, L.; Zhang, S.; Li, Y.; et al. SOH estimation method for lithium-ion batteries based on an improved equivalent circuit model via electrochemical impedance spectroscopy. J. Energy Storage 2024, 86, 111167. [Google Scholar] [CrossRef]
- Rodriguez-Cea, A.I.; Morinigo-Sotelo, D.; Tinaut, F.V. A procedure for evaluating the SOH of Li-ion batteries from data during the constant voltage charge phase and the use of an ECM with internal resistance. J. Energy Storage 2025, 108, 115074. [Google Scholar] [CrossRef]
- Lee, S.H. Performance Evaluation of Machine Learning and Deep Learning-Based Models for Predicting Remaining Capacity of Lithium-Ion Batteries. Appl. Sci. 2023, 13, 9127. [Google Scholar] [CrossRef]
- Thomas, H.; Weatherspoon, M.H.; Nelson, R. Localized EIS Data for Capacity and SOH Prediction With Neural Networks. Battery Energy 2025, 4, e70021. [Google Scholar] [CrossRef]
- Soo, Y.Y.; Wang, Y.; Xiang, H.; Chen, Z. A novel transfer learning model for battery state of health prediction based on driving behavior classification. J. Energy Storage 2025, 111, 115409. [Google Scholar] [CrossRef]
- Li, X.; Chu, J. Lithium Battery Life Prediction for Electric Vehicles Using Enhanced TCN and SVN Quantile Regression. IEEE Access 2025, 13, 12581–12595. [Google Scholar] [CrossRef]
- Kamişli, K.; Taş, Ç. Estimation of Battery Remaining Life-time with Deep Learning Methods. Int. J. New Find. Eng. Sci. Technol. 2025, 3, 32–43. [Google Scholar] [CrossRef]
- Xie, S.; Dong, G.; Chen, H.; Sun, L.; Lou, Y. Data-Driven Battery Health Prognostics Using Time-Frequency Feature Maps and Spatial-Temporal Neural Network. IEEE Trans. Veh. Technol. 2025, 74, 8226–8237. [Google Scholar] [CrossRef]
- Cheng, G.; Wang, X.; He, Y. Remaining useful life and state of health prediction for lithium batteries based on empirical mode decomposition and a long and short memory neural network. Energy 2021, 232, 121022. [Google Scholar] [CrossRef]
- Liu, K.; Tang, X.; Teodorescu, R.; Gao, F.; Meng, J. Future Ageing Trajectory Prediction for Lithium-Ion Battery Considering the Knee Point Effect. IEEE Trans. Energy Convers. 2022, 37, 1282–1291. [Google Scholar] [CrossRef]
- Chen, H.; Dong, G.; Wang, Y.; Yu, J.; Wu, L.; Lou, Y. Data-Driven Battery Health Prognosis Using Scalable Deep Recurrent Structure and Partial Fast-Charging Profiles. IEEE Trans. Veh. Technol. 2025; early access. [Google Scholar] [CrossRef]
- Fei, Z.; Zhang, Z.; Tsui, K.L. Deep Learning Powered Online Battery Health Estimation Considering Multitimescale Aging Dynamics and Partial Charging Information. IEEE Trans. Transp. Electrif. 2024, 10, 42–54. [Google Scholar] [CrossRef]
- Ansari, S.; Ayob, A.; Hossain Lipu, M.; Hussain, A.; Md Saad, M.H. Jellyfish optimized recurrent neural network for state of health estimation of lithium-ion batteries. Expert Syst. Appl. 2024, 238, 121904. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, Z.; Liu, P.; Wang, Q.; She, C.; Bauer, P.; Qin, Z. Multistep Fast Charging-Based State of Health Estimation of Lithium-Ion Batteries. IEEE Trans. Transp. Electrif. 2024, 10, 4640–4652. [Google Scholar] [CrossRef]
- Deng, Z.; Lin, X.; Cai, J.; Hu, X. Battery health estimation with degradation pattern recognition and transfer learning. J. Power Sources 2022, 525, 231027. [Google Scholar] [CrossRef]
- Sun, J.; Wang, H. Enhanced state of health estimation of lithium-ion batteries through advanced feature selection and self-developed datasets. J. Energy Storage 2025, 114, 115713. [Google Scholar] [CrossRef]
- Xu, J.; Qu, J.; Xu, H. Capacity estimation of lithium-ion batteries with automatic feature extraction and graph-enhanced LSTM. J. Energy Storage 2024, 85, 111131. [Google Scholar] [CrossRef]
- Li, N.; Wang, M.; Lei, Y.; Yang, B.; Li, X.; Si, X. Remaining useful life prediction of lithium-ion battery with nonparametric degradation modeling and incomplete data. Reliab. Eng. Syst. Saf. 2025, 256, 110721. [Google Scholar] [CrossRef]
- Li, N.; Wang, M.; Lei, Y.; Si, X.; Yang, B.; Li, X. A nonparametric degradation modeling method for remaining useful life prediction with fragment data. Reliab. Eng. Syst. Saf. 2024, 249, 110224. [Google Scholar] [CrossRef]
- Chowdhury, M.A.; Modekwe, G.; Lu, Q. Lithium-ion Battery Capacity Prediction via Conditional Recurrent Generative Adversarial Network-based Time-Series Regeneration. arXiv 2025, arXiv:2503.12258. [Google Scholar] [CrossRef]
- Rajasekaran, E.; Venkatanarayanan, S. State-of-Health (SoH) prediction for electric vehicle battery systems using GAN-based models with triple attention mechanisms. J. Energy Storage 2025, 134, 118143. [Google Scholar] [CrossRef]
- Chao, X.; Cao, J.; Lu, Y.; Dai, Q.; Liang, S. Constrained Generative Adversarial Networks. IEEE Access 2021, 9, 19208–19218. [Google Scholar] [CrossRef]
- Min, Y.; Azizan, N. HardNet: Hard-Constrained Neural Networks with Universal Approximation Guarantees. arXiv 2025, arXiv:2410.10807. [Google Scholar] [CrossRef]
- Gu, X.; See, K.; Liu, Y.; Arshad, B.; Zhao, L.; Wang, Y. A time-series Wasserstein GAN method for state-of-charge estimation of lithium-ion batteries. J. Power Sources 2023, 581, 233472. [Google Scholar] [CrossRef]
- Li, Y.; Li, K.; Liu, X.; Wang, Y.; Zhang, L. Lithium-ion battery capacity estimation—A pruned convolutional neural network approach assisted with transfer learning. Appl. Energy 2021, 285, 116410. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, J.; Cao, L.; Gopaluni, B.; Cao, Y. Long Short-Term Memory Network with Transfer Learning for Lithium-ion Battery Capacity Fade and Cycle Life Prediction. Appl. Energy 2023, 350, 121660. [Google Scholar] [CrossRef]
- Shen, S.; Sadoughi, M.; Li, M.; Wang, Z.; Hu, C. Deep convolutional neural networks with ensemble learning and transfer learning for capacity estimation of lithium-ion batteries. Appl. Energy 2020, 260, 114296. [Google Scholar] [CrossRef]
- Pan, D.; Li, H.; Wang, S. Transfer Learning-Based Hybrid Remaining Useful Life Prediction for Lithium-Ion Batteries Under Different Stresses. IEEE Trans. Instrum. Meas. 2022, 71, 3501810. [Google Scholar] [CrossRef]
- Chen, J.; Han, X.; Sun, T.; Zheng, Y. Analysis and prediction of battery aging modes based on transfer learning. Appl. Energy 2024, 356, 122330. [Google Scholar] [CrossRef]
- Oyewole, I.; Chehade, A.; Kim, Y. A controllable deep transfer learning network with multiple domain adaptation for battery state-of-charge estimation. Appl. Energy 2022, 312, 118726. [Google Scholar] [CrossRef]
- Zhu, Y.; Gu, X.; Liu, K.; Zhao, W.; Shang, Y. Rapid Test and Assessment of Lithium-Ion Battery Cycle Life Based on Transfer Learning. IEEE Trans. Transp. Electrif. 2024, 10, 9133–9143. [Google Scholar] [CrossRef]
- Fu, S.; Tao, S.; Fan, H.; He, K.; Liu, X.; Tao, Y.; Zuo, J.; Zhang, X.; Wang, Y.; Sun, Y. Data-driven capacity estimation for lithium-ion batteries with feature matching based transfer learning method. Appl. Energy 2024, 353, 121991. [Google Scholar] [CrossRef]
- Ji, S.; Zhu, J.; Lyu, Z.; You, H.; Zhou, Y.; Gu, L.; Qu, J.; Xia, Z.; Zhang, Z.; Dai, H. Deep learning enhanced lithium-ion battery nonlinear fading prognosis. J. Energy Chem. 2023, 78, 565–573. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, Y.; Nie, Y.; Li, J.; Liu, S.; Zhao, L.; Yu, Q.; Zhang, C. Deep transfer learning enables battery state of charge and state of health estimation. Energy 2024, 294, 130779. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, X.; Altaf, F.; Wik, T. A Transferable Physics-Informed Framework for Battery Degradation Diagnosis, Knee-Onset Detection and Knee Prediction. arXiv 2025, arXiv:2501.14573. [Google Scholar] [CrossRef]
- Greenbank, S.; Howey, D. Automated Feature Extraction and Selection for Data-Driven Models of Rapid Battery Capacity Fade and End of Life. IEEE Trans. Ind. Inform. 2022, 18, 2965–2973. [Google Scholar] [CrossRef]
- Zhang, H.; Altaf, F.; Wik, T. Scenario-Aware Machine Learning Pipeline for Battery Lifetime Prediction. In Proceedings of the 2024 European Control Conference (ECC), Stockholm, Sweden, 25–28 June 2024; pp. 212–217. [Google Scholar] [CrossRef]
- Sugiarto, L.; Huang, Z.; Lu, Y.C. Battery lifetime prediction using surface temperature features from early cycle data. Energy Environ. Sci. 2025, 18, 2511–2523. [Google Scholar] [CrossRef]
- Wu, W.; Chen, Z.; Liu, W.; Zhou, D.; Xia, T.; Pan, E. Battery health prognosis in data-deficient practical scenarios via reconstructed voltage-based machine learning. Cell Rep. Phys. Sci. 2025, 6, 102442. [Google Scholar] [CrossRef]
- Khatib, A.R.E.; Hoblos, G.; Langueh, K.; Duviella, E. Robust Polytopic Luenberger Observer for SOC Estimation of a Battery Cell. In Proceedings of the 2025 International Conference on Control, Automation and Diagnosis (ICCAD), Barcelona, Spain, 18–20 June 2025; pp. 1–6. [Google Scholar] [CrossRef]
- Ji, S.; Zhu, J.; Zhang, Z.; Xia, Z. Degradation Prognosis for Fast-Charging Batteries via Improved Domain Adaptation. IEEE Trans. Ind. Inf. 2025, 21, 1743. [Google Scholar] [CrossRef]
- Schaltz, E.; Stroe, D.I.; Norregaard, K.; Ingvardsen, L.S.; Christensen, A. Incremental Capacity Analysis Applied on Electric Vehicles for Battery State-of-Health Estimation. IEEE Trans. Ind. Appl. 2021, 57, 1810–1817. [Google Scholar] [CrossRef]
- Jiang, B.; Dai, H.; Wei, X. Incremental capacity analysis based adaptive capacity estimation for lithium-ion battery considering charging condition. Appl. Energy 2020, 269, 115074. [Google Scholar] [CrossRef]
- Ji, S.; Zhang, Z.; Stein, H.S.; Zhu, J. Flexible health prognosis of battery nonlinear aging using temporal transfer learning. Appl. Energy 2025, 377, 124766. [Google Scholar] [CrossRef]
- Haskara, I.; Hegde, B.; Chang, C.F. Reinforcement learning based EV energy management for integrated traction and cabin thermal management considering battery aging. IFAC-PapersOnLine 2022, 55, 348–353. [Google Scholar] [CrossRef]
- Suanpang, P.; Jamjuntr, P. Optimal Electric Vehicle Battery Management Using Q-learning for Sustainability. Sustainability 2024, 16, 7180. [Google Scholar] [CrossRef]
- Usama, M.; Salaje, A.; Chevet, T.; Langlois, N. Optimal Weighting Factors Design for Model Predictive Current Controller for Enhanced Dynamic Performance of PMSM Employing Deep Reinforcement Learning. Appl. Sci. 2025, 15, 5874. [Google Scholar] [CrossRef]
- Namdari, A.; Samani, M.A.; Durrani, T.S. Lithium-Ion Battery Prognostics through Reinforcement Learning Based on Entropy Measures. Algorithms 2022, 15, 393. [Google Scholar] [CrossRef]
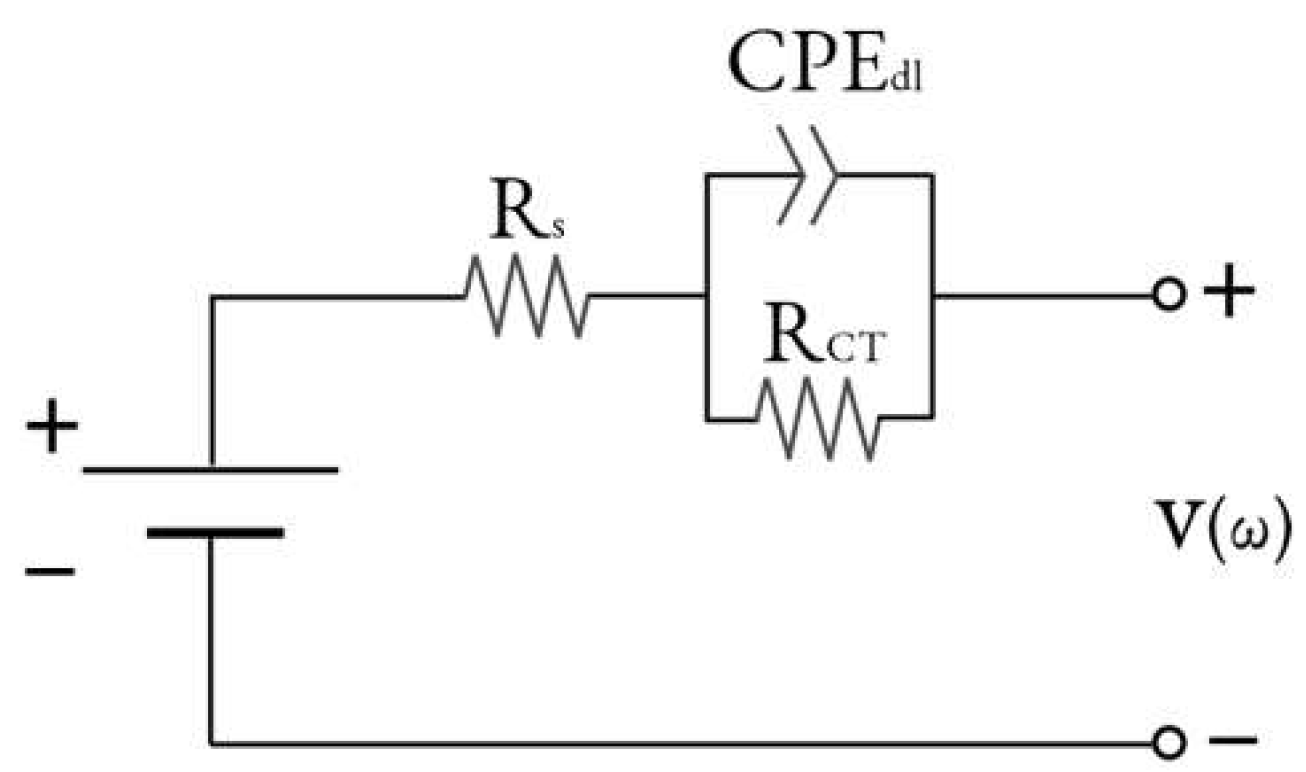
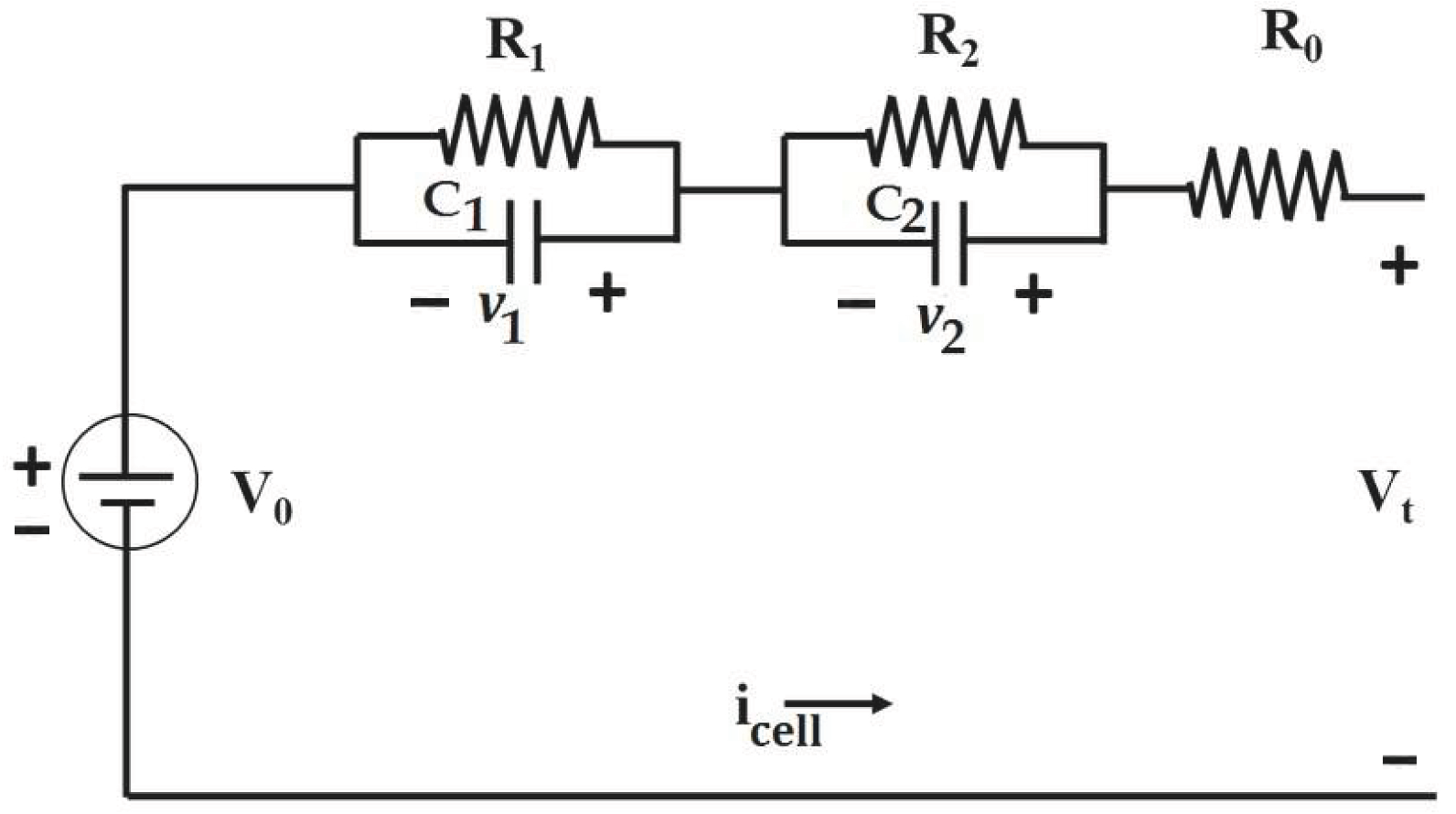
| Approach | Features/Metrics Used | Predicted Quantity + Error | Datasets/Validation | Adequacy for Second-Life Batteries |
|---|---|---|---|---|
| Physics-informed ML (CNN + SEI dynamics) [45] | SEI growth dynamics + voltage/current cycles | RUL; superior accuracy using only 4 initial cycles (MAE = 8.3–8.4%) | Stanford–MIT–Toyota dataset | Limited: requires explicit SEI modeling, which is complicated in repurposed packs |
| Hybrid Grey + ensemble Kalman filter [46] | Quasi-exponential degradation + random regeneration; correction via EnKF | RUL; improved prediction vs. benchmarks (MAPE = 0.65–0.93%) | NASA dataset; 4 cells | Limited: sensitive to noise and depends heavily on early-cycle data |
| PI-TNet [47] | Voltage, current, temperature time series | SOH; MAE improved up to 94.69% vs. baselines | NASA dataset; validated on 4 cells | Limited: constraints require physical knowledge not tracked by BMS |
| Tell-me model (dual data-driven hybrid) [50] | Discharge-curve features + gradient module (voltage and capacity) | SOH + EOL; higher accuracy than benchmarks (MAPE = 3.27–7.94%) | 3 public datasets (LIB + other chemistries) | Promising: relies on discharge features that can be extracted from BMS data, handles inconsistencies |
| Transfer-driven ADMD for packs [52] | Degradation trajectory vectors + adaptive differential model decomposition | RUL; MPE = 5% | NASA dataset; pack-level validation | Promising: explicitly considers cell heterogeneity in packs, relevant for second-life scenarios |
| ECM + BPNN hybrid [56] | Mid/high-frequency EIS parameters from 1st-order ECM | SOH + capacity; average error 1.4% | 4 cells; reduced training time vs. normal EIS | Limited: requires EIS measurements, rarely feasible in second-life |
| Approach | Features/Metrics Used | Predicted Quantity + Error | Datasets | Adequacy for Second-Life Batteries |
|---|---|---|---|---|
| BPNN with Salient Frequency Extraction [61] | Impedance (EIS salient frequencies) | SOH = 4.36%, Capacity = 1.16% | 4 cells (EIS) | Limited: requires EIS, less feasible for aged packs |
| ETSformer [62] | Driving behavior and discharge profiles | SOH, = 0.061% | Driving datasets (EV) | Limited: relies on driving behavior (EV) |
| Quantile Regression + TCN [63] | Time-series current/voltage cycles | SOH (88% accuracy) + RUL (extended by 45 cycles) | TRIBD + NASA datasets | Promising: robust under uncertainty and protocol variation |
| FFNN (Trained using SCG) [64] | Voltage/current features | RUL; MAE = 0.0295% | NASA dataset | Promising: robust with limited data |
| FFNN (Trained using RF) [64] | Voltage/current features | RUL; MSE = 0.0020% | NASA dataset | Promising: robust with limited data |
| CNN-BiLSTM-Attention [65] | CWT time–frequency maps | SOH; RMSE = 0.74% | 124 LFP cells + NASA + CALCE | Promising: handles nonlinear degradation and fast charging |
| GPR-LSTM [68] | DWT features from MCC voltage charging profiles + health indicators | SOH (RMSE = 0.91–1.02%, MAE = 0.79–0.81%); RUL | 140 cells (1- and 2-step MCC) | Promising: scalable, uncertainty-aware, fits heterogeneous data |
| FPCA + Bayesian Updating [75] | Functional principal components of degradation data (discharge capacity) | RUL distribution (median error lowest among 3 baselines) | Multiple sparse datasets | Promising: robust under incomplete or sparse data |
| RCGAN [77] | Voltage, current, temperature (synthetic cycles via GAN) | Capacity prediction; GRU+GAN RMSE = 0.0077%, MAE = 0.0061% | NASA + MIT datasets | Promising: accurate prediction with limited data |
| GAN (CNN-LSTM Generator + ESN) [78] | SOH trajectories (synthetic via GAN) | SOH; MAE = 0.0075%, RMSE = 0.0113%, MAPE = 1.1% | NASA dataset (4 cells) | Promising: accurate prediction with limited data |
| Approach | Features/Metrics Used | Predicted Quantity + Error | Datasets | Adequacy for Second-Life Batteries |
|---|---|---|---|---|
| DeepHPM + XGBoost [92] | Voltage–current histograms | SOH + knee point (Accuracy = 82–89%) | Multiple LIB datasets; few-shot transfer validation | Promising: requires few samples and is adaptable across different scenarios |
| Linear + Elastic Net Regression [95] | Early surface temperature (first 10 cycles) | RUL; MAPE as low as 14.2% | TRI dataset with multiple chemistries | Promising: chemistry-agnostic health indicators and robust early prediction |
| LSTM + MAML [96] | Reconstructed discharge voltage curves | SOH; MAE < 0.2% across fragmented datasets | Real-world fragmented datasets | Promising: effectively handles incomplete or fragmented data |
| BiGRU + ICA [98] | Incremental capacity (dQ/dV) curves | LLI (RMSE = 3.93%) + LAM (RMSE = 9.31%) | EV fast-charging datasets | Promising: fast, robust, handles uncertainty well |
| BiGRU + TDC [101] | Temporal distribution characteristics of IC and voltage curves | SOH (MAPE = 0.55–2.42%, RMSE = 0.72–2.52%); Knee point (MAPE = 0.54–1.44%, RMSE = 0.72–1.38%) | 151 cells; multi-chemistry datasets | Promising: adapts to nonlinear regimes and generalizes across chemistries |
| Method | Robust to Uncertainty | Handles Heterogeneous or Sparse Data | High Data Efficiency |
|---|---|---|---|
| Tell-me model [50] | X | ||
| Transfer-driven ADMD [52] | X | X | |
| Quantile+TCN [63] | X | ||
| FFNN(SCG) [64] | X | ||
| FFNN(RF) [64] | X | ||
| CNN-BiLSTM-Attention [65] | X | ||
| GPR-LSTM [68] | X | X | |
| FPCA+Bayesian [75] | X | ||
| RCGAN [77] | X | ||
| GAN(CNN-LSTM+ESN) [78] | X | ||
| DeepHPM+XGBoost [92] | X | X | |
| Linear+Elastic Net [95] | X | X | |
| LSTM+MAML [96] | X | ||
| BiGRU+ICA [98] | X | X | X |
| BiGRU+TDC [101] | X | X |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Khatib, A.R.; Hoblos, G.; Langueh, K.; Duviella, E. From First Life to Second Life: Advances and Research Gaps in Prognosis Techniques for Lithium-Ion Batteries. Appl. Sci. 2025, 15, 12171. https://doi.org/10.3390/app152212171
El Khatib AR, Hoblos G, Langueh K, Duviella E. From First Life to Second Life: Advances and Research Gaps in Prognosis Techniques for Lithium-Ion Batteries. Applied Sciences. 2025; 15(22):12171. https://doi.org/10.3390/app152212171
Chicago/Turabian StyleEl Khatib, Abdel Rahman, Ghaleb Hoblos, Kokou Langueh, and Eric Duviella. 2025. "From First Life to Second Life: Advances and Research Gaps in Prognosis Techniques for Lithium-Ion Batteries" Applied Sciences 15, no. 22: 12171. https://doi.org/10.3390/app152212171
APA StyleEl Khatib, A. R., Hoblos, G., Langueh, K., & Duviella, E. (2025). From First Life to Second Life: Advances and Research Gaps in Prognosis Techniques for Lithium-Ion Batteries. Applied Sciences, 15(22), 12171. https://doi.org/10.3390/app152212171







