Landslide Susceptibility Mapping Optimization for Improved Risk Assessment Using Multicollinearity Analysis and Machine Learning Technique
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
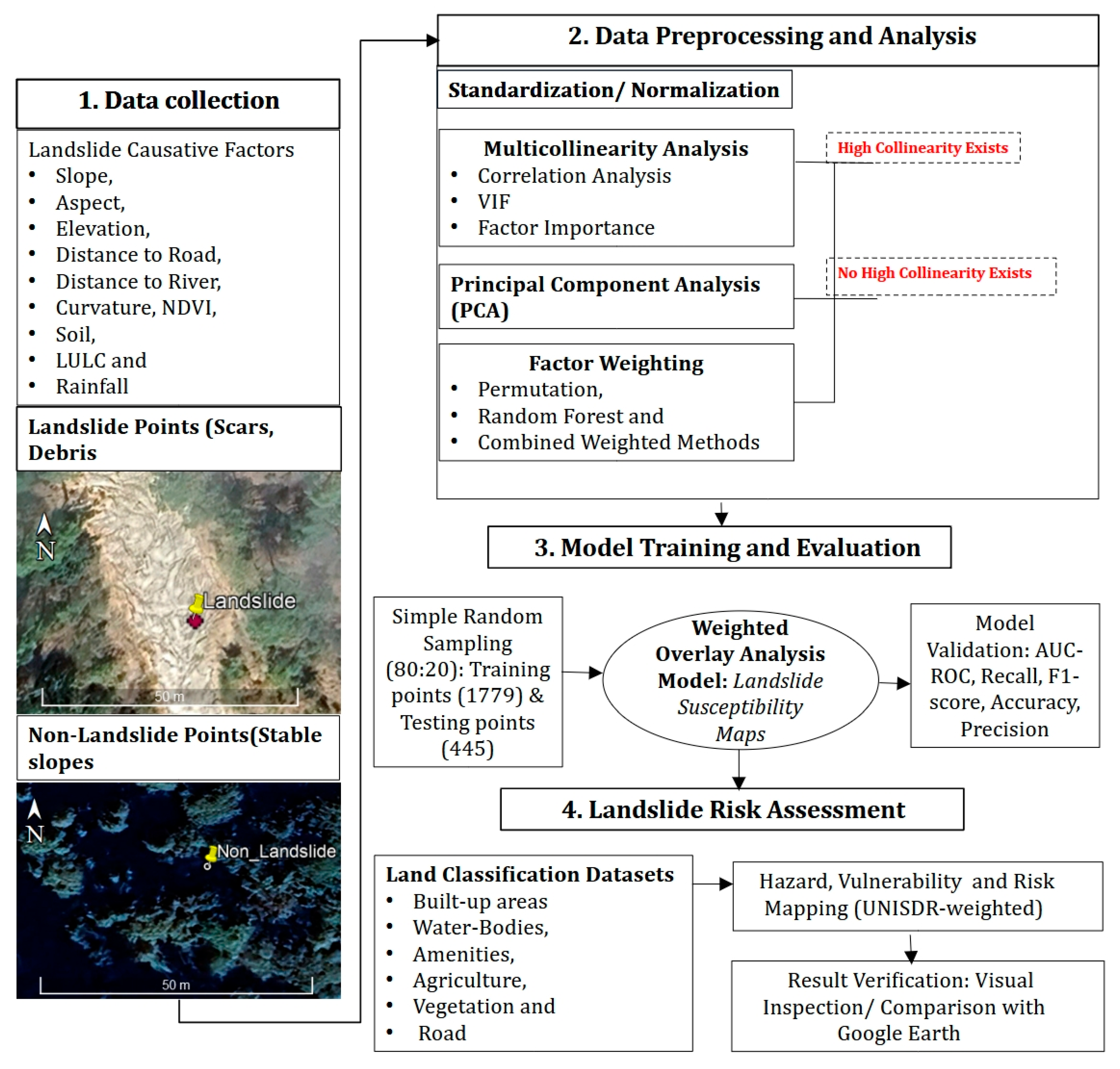
2.2. Computational Framework and Implementation
2.3. Landslide Inventory: Compilation and Validation
2.4. Landslide Causative Factors: Standardization and Normalization
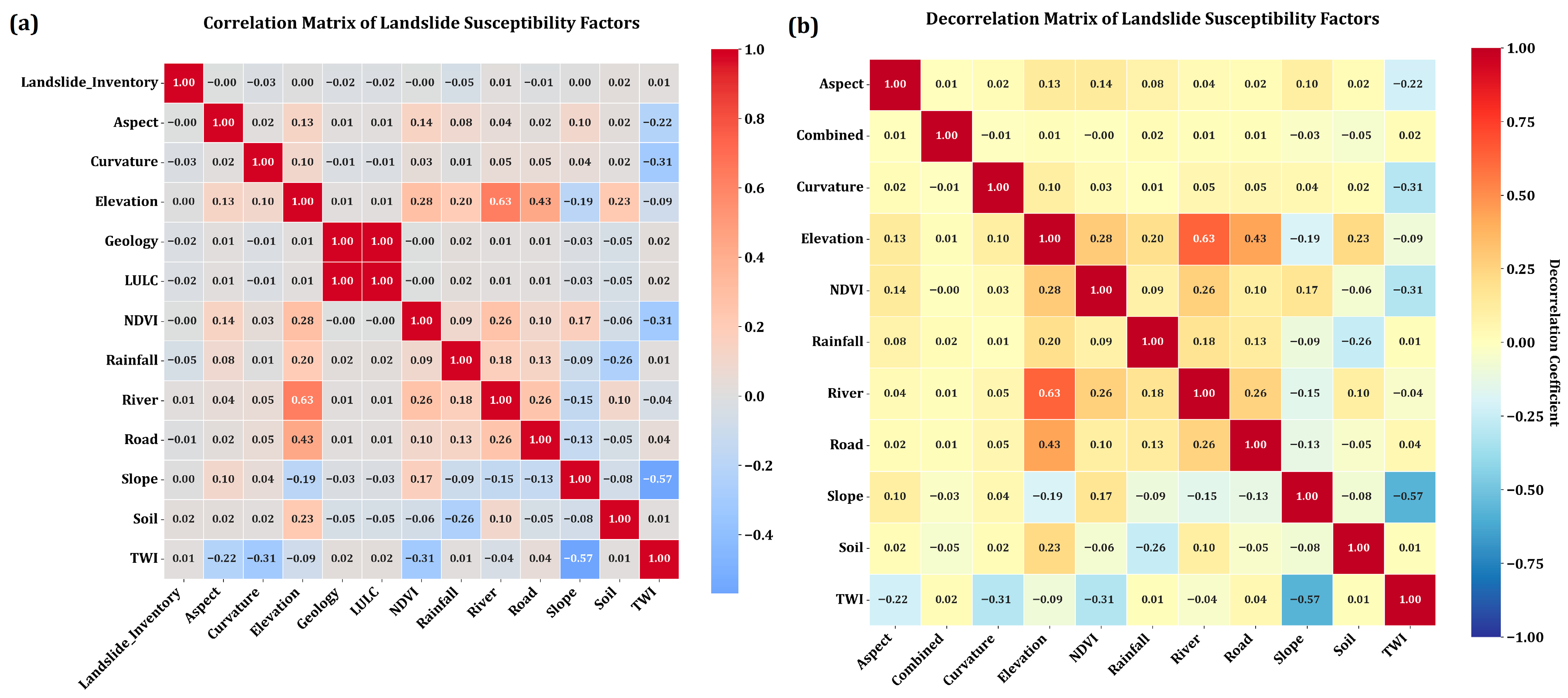
2.5. Multicollinearity Assessment
2.5.1. Correlation Analysis
2.5.2. Principal Component Analysis (PCA)
2.5.3. Variation Inflation Factor (VIF) Analysis
2.6. Feature Importance Analysis
2.6.1. Random Forest Feature Importance (Gini Importance)
2.6.2. Permutation Importance
2.6.3. Combined Average Importance
2.7. Landslide Susceptibility Mapping
2.7.1. Random Forest Weight Calculation
2.7.2. Permutation Importance Weight Calculation
2.7.3. Combined Weight Derivation
2.8. Model Evaluation and Validation
2.9. Landslide Risk Assessment
2.9.1. Clipping and Normalization
2.9.2. Quantile Classification
3. Results
3.1. Multicollinearity Analysis and Estimating Weightage
3.1.1. Multicollinearity Analysis
3.1.2. PCA Application
3.1.3. Factor Importance Assessment
3.2. Comparative Analysis of Landslide Susceptibility Models
3.3. Accuracy Assessment and Model Performance Evaluation
3.4. Verification of Landslide Risk Assessment Outcomes
4. Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| SN | LCF | Class No. | Class | Class Pixels Count | % Class Pixels (a) | Landslide Pixels Count | % Landslide in Class (b) | IV = ln(b/a) | Normalized Weightage | Label Encoding |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Geology | 1 | Ba | 2095 | 0.000919868 | 0 | 0 | 0 | 0.596528535 | 10 |
| 2 | Basic Rocks | 58,7000 | 0.257738749 | 242 | 0.217625899 | −0.169168939 | 0.547434951 | 12 | ||
| 3 | Bu | 146,842 | 0.064475082 | 82 | 0.073741007 | 0.134280223 | 0.635497257 | 6 | ||
| 4 | Damgad Formation | 105,566 | 0.046351701 | 207 | 0.186151079 | 1.390300598 | 1 | 1 | ||
| 5 | Galyang Formation | 39,634 | 0.017402415 | 21 | 0.018884892 | 0.081753256 | 0.620253696 | 8 | ||
| 6 | Gh | 571 | 0.000250714 | 0 | 0 | 0 | 0.596528535 | 10 | ||
| 7 | Gn | 15,998 | 0.007024369 | 1 | 0.000899281 | −2.05554556 | 0 | 17 | ||
| 8 | Granites | 130,080 | 0.057115258 | 11 | 0.009892086 | −1.753336219 | 0.087702505 | 16 | ||
| 9 | Lakharpata Formation | 48,682 | 0.021375192 | 44 | 0.039568345 | 0.615798436 | 0.775236001 | 4 | ||
| 10 | Melmura Formation | 74,079 | 0.032526454 | 30 | 0.026978417 | −0.187016555 | 0.542255492 | 13 | ||
| 11 | Ranimatta Formation | 245,922 | 0.107978924 | 124 | 0.111510791 | 0.032185307 | 0.605868855 | 9 | ||
| 12 | Sallyani Gad Formation | 606,247 | 0.266189682 | 78 | 0.070143885 | −1.333660513 | 0.209494276 | 14 | ||
| 13 | Sangram Formation | 10,920 | 0.004794731 | 6 | 0.005395683 | 0.118081653 | 0.63079636 | 7 | ||
| 14 | Siwalik | 46,439 | 0.02039034 | 33 | 0.029676259 | 0.375286092 | 0.705438241 | 5 | ||
| 15 | Suntar Formation | 56,922 | 0.024993194 | 55 | 0.049460432 | 0.68256943 | 0.794613243 | 3 | ||
| 16 | Swat Formation | 8829 | 0.003876619 | 1 | 0.000899281 | −1.461123604 | 0.172503916 | 15 | ||
| 17 | Syangja Formation | 151,674 | 0.066596707 | 177 | 0.159172662 | 0.871334406 | 0.849393685 | 2 | ||
| 2,277,500 | 1112 | |||||||||
| 2 | Soil types | 1 | CMe | 1,603,043 | 0.703860812 | 835 | 0.750899281 | 0.064690902 | 0.656216582 | 3 |
| 2 | CMg | 17,326 | 0.007607464 | 7 | 0.006294964 | −0.18937996 | 0.543835365 | 5 | ||
| 3 | Cmo | 1765 | 0.000774973 | 2 | 0.001798561 | 0.841914644 | 1 | 1 | ||
| 4 | CMu | 44,609 | 0.019586828 | 1 | 0.000899281 | 0 | 0.627602351 | 4 | ||
| 5 | CMx | 483,921 | 0.212479034 | 172 | 0.154676259 | −0.317509039 | 0.487161012 | 6 | ||
| 6 | RGd | 84,517 | 0.03710955 | 90 | 0.080935252 | 0.779775127 | 0.972514304 | 2 | ||
| 7 | RGe | 42,319 | 0.018581339 | 5 | 0.004496403 | −1.418880091 | 0 | 7 | ||
| 2,277,500 | 1112 | |||||||||
| 3 | LULC types | 1 | Agricultural Land | 269,422 | 0.118297256 | 158 | 0.142086331 | 0.183234264 | 0.111840933 | 6 |
| 2 | Bareland | 44,015 | 0.019326015 | 41 | 0.036870504 | 0.645959736 | 0.394275273 | 4 | ||
| 3 | Builtup Area | 98,953 | 0.043448079 | 136 | 0.122302158 | 1.03492805 | 0.631690362 | 3 | ||
| 4 | Forests | 1,373,235 | 0.60295719 | 314 | 0.282374101 | 0 | 0 | 7 | ||
| 5 | Grassland | 451,609 | 0.198291548 | 384 | 0.345323741 | 0.554743946 | 0.338599774 | 5 | ||
| 6 | Riverbed | 15,918 | 0.006989243 | 40 | 0.035971223 | 1.638347064 | 1 | 1 | ||
| 7 | Waterbody | 24,348 | 0.01069067 | 39 | 0.035071942 | 1.18803009 | 0.725139451 | 2 | ||
| 2,277,500 | 1112 |
| Causative Factors | Random Forest_Importance | Permutation Importance | Std_Dev. | Average Importance |
|---|---|---|---|---|
| Slope | 0.59 | 0.44 | 0.01 | 0.52 |
| TWI | 0.11 | 0.02 | 0 | 0.07 |
| Elevation | 0.06 | 0.01 | 0 | 0.03 |
| Combined | 0.05 | 0.01 | 0 | 0.03 |
| Curvature | 0.04 | 0.02 | 0 | 0.03 |
| Rainfall | 0.03 | 0.01 | 0 | 0.02 |
| Aspect | 0.04 | 0.01 | 0 | 0.02 |
| Distance to River | 0.03 | 0.01 | 0 | 0.02 |
| NDVI | 0.03 | 0.01 | 0 | 0.02 |
| Distance to Road | 0.02 | 0.01 | 0 | 0.01 |
| Soil | 0 | 0 | 0 | 0 |
References
- Petley, D. Global Patterns of Loss of Life from Landslides. Geology 2012, 40, 927–930. [Google Scholar] [CrossRef]
- Froude, M.J.; Petley, D.N. Global Fatal Landslide Occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef]
- Kargel, J.S.; Leonard, G.J.; Shugar, D.H.; Haritashya, U.K.; Bevington, A.; Fielding, E.J.; Young, N. Geomorphic and Geologic Controls of Geohazards Induced by Nepal’s 2015 Gorkha Earthquake. Science 2016, 351, aac8353. [Google Scholar] [CrossRef] [PubMed]
- Lamichhane, K.; Biswakarma, K.; Acharya, B.; Karki, S.; KC, R.; Subedi, M.; Sharma, K. Preliminary Assessment of September 2024 Extreme Rainfall–Induced Landslides in Central Nepal. Landslides 2025, 22, 3281–3295. [Google Scholar] [CrossRef]
- Gariano, S.L.; Guzzetti, F. Landslides in a Changing Climate. Earth Sci. Rev. 2016, 162, 227–252. [Google Scholar] [CrossRef]
- Haque, U.; Blum, P.; Da Silva, P.F.; Andersen, P.; Pilz, J.; Chalov, S.R.; Keellings, D. Fatal Landslides in Europe. Landslides 2016, 13, 1545–1554. [Google Scholar] [CrossRef]
- Deuba, T. More than 250 Families Displaced by Landslides in Doti. The Himalayan Times. 2015. Available online: https://thehimalayantimes.com/nepal/more-than-250-families-displaced-by-landslides-in-doti/ (accessed on 8 October 2025).
- Deuba, T. Haliya Settlement at Risk in Doti. The Himalayan Times. 2018. Available online: https://thehimalayantimes.com/nepal/haliya-settlement-at-risk-in-doti (accessed on 10 October 2025).
- RSS. Landslide Displaces Eight Families in Doti. Ratopati. 2020. Available online: https://english.ratopati.com/story/13941 (accessed on 10 October 2025).
- Deuba, T. Landslide Obstructs Bhimdutta Highway in Sudurpaschim. The Himalayan Times. 2021. Available online: https://thehimalayantimes.com/nepal/landslide-obstructs-bhimdutta-highway-in-sudurpaschim (accessed on 10 October 2025).
- Bist, D.B.; Thapa, M.S.; Bista, U.; Awasthi, N. Analytical Hierarchy Process (AHP) Based Landslide Susceptibility Mapping of Kaligandaki Hydro-Catchment of Syangja, Nepal. Available online: Agric. For. J. 2020, 4, 80–90. [Google Scholar]
- Regmi, A.D.; Devkota, K.C.; Yoshida, K.; Pradhan, B.; Pourghasemi, H.R.; Kumamoto, T.; Akgun, A. Application of Frequency Ratio, Statistical Index, and Weights-of-Evidence Models and Their Comparison in Landslide Susceptibility Mapping in Central Nepal Himalaya. Arab. J. Geosci. 2014, 7, 725–742. [Google Scholar] [CrossRef]
- Polykretis, C.; Chalkias, C. Comparison and Evaluation of Landslide Susceptibility Maps Obtained from Weight of Evidence, Logistic Regression, and Artificial Neural Network Models. Nat. Hazards 2018, 93, 249–274. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Singh, S.K.; Shirzadi, A.; Shahabi, H.; Tran, T.T.T.; Bui, D.T. Landslide Susceptibility Modeling Using Reduced Error Pruning Trees and Different Ensemble Techniques: Hybrid Machine Learning Approaches. Catena 2019, 175, 203–218. [Google Scholar] [CrossRef]
- Merghadi, A.; Yunus, A.P.; Dou, J.; Whiteley, J.; ThaiPham, B.; Bui, D.T.; Abderrahmane, B. Machine Learning Methods for Landslide Susceptibility Studies: A Comparative Overview of Algorithm Performance. Earth-Sci. Rev. 2020, 207, 103225. [Google Scholar] [CrossRef]
- Pandey, V.K.; Pourghasemi, H.R.; Sharma, M.C. Landslide Susceptibility Mapping Using Maximum Entropy and Support Vector Machine Models along the Highway Corridor, Garhwal Himalaya. Geocarto Int. 2020, 35, 168–187. [Google Scholar] [CrossRef]
- Mandal, B.; Mondal, S.; Mandal, S. GIS-Based Landslide Susceptibility Zonation (LSZ) Mapping of Darjeeling Himalaya, India Using Weights of Evidence (WoE) Model. Arab. J. Geosci. 2023, 16, 421. [Google Scholar] [CrossRef]
- Aboutaib, F.; Krimissa, S.; Pradhan, B.; Elaloui, A.; Ismaili, M.; Abdelrahman, K.; Namous, M. Evaluating the Effectiveness and Robustness of Machine Learning Models with Varied Geo-Environmental Factors for Determining Vulnerability to Water Flow-Induced Gully Erosion. Front. Environ. Sci. 2023, 11, 1207027. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Blaschke, T. GIS-Multicriteria Decision Analysis for Landslide Susceptibility Mapping: Comparing Three Methods for the Urmia Lake Basin, Iran. Nat. Hazards 2013, 65, 2105–2128. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Rossi, M. Landslide Susceptibility Modeling in a Landslide Prone Area in Mazandarn Province, North of Iran: A Comparison between GLM, GAM, MARS, and M-AHP Methods. Theor. Appl. Climatol. 2017, 130, 609–633. [Google Scholar] [CrossRef]
- Kappes, M.S.; Papathoma-Köhle, M.; Keiler, M. Assessing Physical Vulnerability for Multi-Hazards Using an Indicator-Based Methodology. Appl. Geogr. 2012, 32, 577–590. [Google Scholar] [CrossRef]
- Glade, T. Vulnerability Assessment in Landslide Risk Analysis. Erde 2003, 134, 123–146. [Google Scholar]
- Saba, S.B.; van der Meijde, M.; van der Werff, H. Spatiotemporal Landslide Detection for the 2005 Kashmir Earthquake Region. Geomorphology 2010, 124, 17–25. [Google Scholar] [CrossRef]
- Wei, X.; Zhang, L.; Gardoni, P.; Chen, Y.; Tan, L.; Liu, D.; Li, H. Comparison of Hybrid Data-Driven and Physical Models for Landslide Susceptibility Mapping at Regional Scales. Acta Geotech. 2023, 18, 4453–4476. [Google Scholar] [CrossRef]
- Steger, S.; Brenning, A.; Bell, R.; Glade, T. The Influence of Systematically Incomplete Shallow Landslide Inventories on Statistical Susceptibility Models and Suggestions for Improvements. Landslides 2017, 14, 1767–1781. [Google Scholar] [CrossRef]
- Zhang, W.; Li, H.; Li, Y.; Liu, H.; Chen, Y.; Ding, X. Application of Deep Learning Algorithms in Geotechnical Engineering: A Short Critical Review. Artif. Intell. Rev. 2021, 54, 5633–5673. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Liu, S.; Han, L.; Zhang, W.; Hong, L.; Zhu, X. Region Similarity Assessment for Empowering Physics-Informed Transfer Learning-Based Landslide Susceptibility Mapping. J. Rock Mech. Geotech. Eng. 2025, in press. [CrossRef]
- Cui, H.Z.; Tong, B.; Wang, T.; Dou, J.; Ji, J. A Hybrid Data-Driven Approach for Rainfall-Induced Landslide Susceptibility Mapping: Physically Based Probabilistic Model with Convolutional Neural Network. J. Rock Mech. Geotech. Eng. 2024, 17, 4933–4951. [Google Scholar] [CrossRef]
- Wang, Y.H.; Wang, L.Q.; Zhang, W.G.; Liu, S.L.; Sun, W.X.; Hong, L.; Zhu, Z.W. A Physics-Informed Machine Learning Solution for Landslide Susceptibility Mapping Based on Three-Dimensional Slope Stability Evaluation. J. Cent. South Univ. 2024, 31, 3838–3853. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Liu, S.; Liu, P.; Zhu, Z.; Zhang, W. A Comparative Study of Regional Landslide Susceptibility Mapping with Multiple Machine Learning Models. Geol. J. 2024, 59, 2383–2400. [Google Scholar] [CrossRef]
- Singh, A.; Dhiman, N.; KC, N.; Shukla, D.P. Improving ML-Based Landslide Susceptibility Using Ensemble Method for Sample Selection: A Case Study of Kangra District in Himachal Pradesh, India. Environ. Sci. Pollut. Res. 2024, 31, 1–24. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.; Dhiman, N.; Niraj, K.C.; Shukla, D.P. Ensembled Transfer Learning Approach for Error Reduction in Landslide Susceptibility Mapping of the Data Scare Region. Sci. Rep. 2024, 14, 29060. [Google Scholar] [CrossRef]
- Kincey, M.E.; Rosser, N.J.; Swirad, Z.M.; Robinson, T.R.; Shrestha, R.; Pujara, D.S.; Basyal, G.K.; Densmore, M.E.; Arrell, K.; Oven, K.J.; et al. National-Scale Rainfall-Triggered Landslide Susceptibility and Exposure in Nepal. Earth’s Future 2024, 12, e2023EF004102. [Google Scholar] [CrossRef]
- Niraj, K.C.; Singh, A.; Shukla, D.P. Effect of the Normalized Difference Vegetation Index (NDVI) on GIS-Enabled Bivariate and Multivariate Statistical Models for Landslide Susceptibility Mapping. J. Indian Soc. Remote Sens. 2023, 51, 1739–1756. [Google Scholar] [CrossRef]
- Hayashi, D. Geological Reconnaissance around Silgarhi-Doti, West Central Nepal. Bull. Coll. Sci. Univ. Ryukyus 1984, 38, 103–116. [Google Scholar]
- Tiwari, R.K.; Paudyal, H. Spatial Mapping of b-Value and Fractal Dimension Prior to November 8, 2022, Doti Earthquake, Nepal. PLoS ONE 2023, 18, e0289673. [Google Scholar] [CrossRef] [PubMed]
- Bhandari, G. Trends in Seasonal Precipitation and Temperature–A Review in Doti and Surkhet Districts of Nepal. Int. J. Environ. 2013, 2, 269–279. [Google Scholar] [CrossRef]
- Paudyal, N.; Khadka, R.B.; Khadka, R. Agricultural Perspectives of Climate Change Induced Disasters in Doti, Nepal. J. Agric. Environ. 2013, 14, 149–159. [Google Scholar] [CrossRef]
- Wagle, N.; Acharya, T.D.; Kolluru, V.; Huang, H.; Lee, D.H. Multi-Temporal Land Cover Change Mapping Using Google Earth Engine and Ensemble Learning Methods. Appl. Sci. 2020, 10, 8083. [Google Scholar] [CrossRef]
- Chao, Z.; Gan, L.; Cao, Y.; Wang, Y.; Segoni, S.; Shi, X.; Motagh, M.; Singh, R.P. Landslide Susceptibility Assessment of the Wanzhou District: Merging Landslide Susceptibility Modelling (LSM) with InSAR-Derived Ground Deformation Map. Int. J. Appl. Earth Obs. Geoinf. 2025, 136, 104365. [Google Scholar] [CrossRef]
- Phuyal, B.; Thapa, P.B.; Devkota, K.C. Characterization of Large-Scale Landslides and Their Susceptibility Evaluation in Central Nepal Himalaya. J. Nepal Geol. Soc. 2022, 63, 109–122. [Google Scholar] [CrossRef]
- Zighmi, K.; Zahri, F.; Faqeih, K.; Al Amri, A.; Riheb, H.; Alamri, S.M.; Alamery, E. AHP Multi Criteria Analysis for Landslide Susceptibility Mapping in the Tellian Atlas Chain. Sci. Rep. 2025, 15, 25747. [Google Scholar] [CrossRef]
- Ali, P.J.M.; Faraj, R.H.; Koya, E. Data Normalization and Standardization: A Technical Report. Mach. Learn. Tech. Rep. 2014, 1, 1–6. [Google Scholar]
- Asuero, A.G.; Sayago, A.; González, A.G. The Correlation Coefficient: An Overview. Crit. Rev. Anal. Chem. 2006, 36, 41–59. [Google Scholar] [CrossRef]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Lautenbach, S. Collinearity: A Review of Methods to Deal with It and a Simulation Study Evaluating Their Performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Parhizkar, T.; Rafieipour, E.; Parhizkar, A. Evaluation and Improvement of Energy Consumption Prediction Models Using Principal Component Analysis Based Feature Reduction. J. Clean. Prod. 2021, 279, 123866. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Bui, D.T.; Merghadi, A.; Sahana, M.; Zhu, Z.; Chen, C.-W.; Khosravi, K.; Yang, Y.; Pham, B.T. Assessment of Advanced Random Forest and Decision Tree Algorithms for Modeling Rainfall-Induced Landslide Susceptibility in the Izu-Oshima Volcanic Island, Japan. Sci. Total Environ. 2019, 662, 332–346. [Google Scholar] [CrossRef]
- Xia, D.; Tang, H.; Sun, S.; Tang, C.; Zhang, B. Landslide Susceptibility Mapping Based on the Germinal Center Optimization Algorithm and Support Vector Classification. Remote Sens. 2022, 14, 2707. [Google Scholar] [CrossRef]
- Wang, H.; Yang, F.; Luo, Z. An Experimental Study of the Intrinsic Stability of Random Forest Variable Importance Measures. BMC Bioinform. 2016, 17, 60. [Google Scholar] [CrossRef]
- Altmann, A.; Toloşi, L.; Sander, O.; Lengauer, T. Permutation Importance: A Corrected Feature Importance Measure. Bioinformatics 2010, 26, 1340–1347. [Google Scholar] [CrossRef]
- Newey, W.K.; Stoker, T.M. Efficiency of Weighted Average Derivative Estimators and Index Models. Econometrica 1993, 61, 1199–1223. [Google Scholar] [CrossRef]
- Fawcett, T. An Introduction to ROC Analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Huang, F.; Cao, Z.; Guo, J.; Jiang, S.-H.; Li, S.; Guo, Z. Comparisons of Heuristic, General Statistical and Machine Learning Models for Landslide Susceptibility Prediction and Mapping. Catena 2020, 191, 104580. [Google Scholar] [CrossRef]
- Koks, E.E.; Jongman, B.; Husby, T.G.; Botzen, W.J. Combining Hazard, Exposure, and Social Vulnerability to Provide Lessons for Flood Risk Management. Environ. Sci. Policy 2015, 47, 42–52. [Google Scholar] [CrossRef]
- Abdiweli, A.J. Simulation Study on the Performance of Robust Outlier Labelling Methods. Ph.D. Thesis, Kampala International University, Kampala, Uganda, October 2023. Available online: https://irbackend.kiu.ac.ug/server/api/core/bitstreams/86d8fd79-e3c5-408a-98f1-48de5057c608/content (accessed on 10 October 2025).
- Ma, S.; Shao, X.; Xu, C. Delineating Non-Susceptible Landslide Areas in China Based on Topographic Index and Quantile Non-Linear Model. Forests 2024, 15, 678. [Google Scholar] [CrossRef]
- Wannous, C.; Velasquez, G. United Nations Office for Disaster Risk Reduction (UNISDR)—UNISDR’s Contribution to Science and Technology for Disaster Risk Reduction and the Role of the International Consortium on Landslides (ICL). In Advancing Culture of Living with Landslides: Volume 1 ISDR-ICL Sendai Partnerships 2015–2025; Sassa, K., Mikos, M., Yin, Y., Eds.; Springer: Cham, Switzerland, 2017; pp. 109–115. [Google Scholar] [CrossRef]
- Maini, R.; Clarke, L.; Blanchard, K.; Murray, V. The Sendai Framework for Disaster Risk Reduction and Its Indicators—Where Does Health Fit In? Int. J. Disaster Risk Sci. 2017, 8, 150–155. [Google Scholar] [CrossRef]
- Michael, E.A.; Samanta, S. Landslide Vulnerability Mapping (LVM) Using Weighted Linear Combination (WLC) Model through Remote Sensing and GIS Techniques. Model. Earth Syst. Environ. 2016, 2, 88. [Google Scholar] [CrossRef]
- Devkota, K.C.; Regmi, A.D.; Pourghasemi, H.R.; Yoshida, K.; Pradhan, B.; Ryu, I.C.; Althuwaynee, O.F. Landslide Susceptibility Mapping Using Certainty Factor, Index of Entropy and Logistic Regression Models in GIS and Their Comparison at Mugling–Narayanghat Road Section in Nepal Himalaya. Nat. Hazards 2013, 65, 135–165. [Google Scholar] [CrossRef]
- Das, S.; Pandit, K.; Sarkar, S.; Kanungo, D.P. Stability and Hazard Assessment of the Progressive Zero Landslide in the Kalimpong Region of Darjeeling Himalaya, India. Geotech. Geol. Eng. 2024, 42, 1693–1709. [Google Scholar] [CrossRef]
- Okalp, K.; Akgün, H. Assessing Landslide Susceptibility of Türkiye at Drainage Basin Scale: A Semi-Quantitative Approach. Nat. Hazards 2025, 121, 20099–20127. [Google Scholar] [CrossRef]
- Zeraatpisheh, M.; Ayoubi, S.; Sulieman, M.; Rodrigo-Comino, J. Determining the Spatial Distribution of Soil Properties Using the Environmental Covariates and Multivariate Statistical Analysis: A Case Study in Semi-Arid Regions of Iran. J. Arid Land 2019, 11, 551–566. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Kornejady, A.; Zhang, N. Landslide Spatial Modeling: Introducing New Ensembles of ANN, MaxEnt, and SVM Machine Learning Techniques. Geoderma 2017, 305, 314–327. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, L.; Yin, K.; Luo, H.; Li, J. Landslide Identification Using Machine Learning. Geosci. Front. 2021, 12, 351–364. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A Review of Statistically-Based Landslide Susceptibility Models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Hong, H.; Liu, J.; Bui, D.T.; Pradhan, B.; Acharya, T.D.; Pham, B.T.; Ahmad, B.B. Landslide Susceptibility Mapping Using J48 Decision Tree with AdaBoost, Bagging and Rotation Forest Ensembles in the Guangchang Area (China). Catena 2018, 163, 399–413. [Google Scholar] [CrossRef]
- Frattini, P.; Crosta, G.; Carrara, A. Techniques for Evaluating the Performance of Landslide Susceptibility Models. Eng. Geol. 2010, 111, 62–72. [Google Scholar] [CrossRef]
- Huang, F.; Cao, Z.; Jiang, S.-H.; Zhou, C.; Huang, J.; Guo, Z. Landslide Susceptibility Prediction Based on a Semi-Supervised Multiple-Layer Perceptron Model. Landslides 2020, 17, 2919–2930. [Google Scholar] [CrossRef]

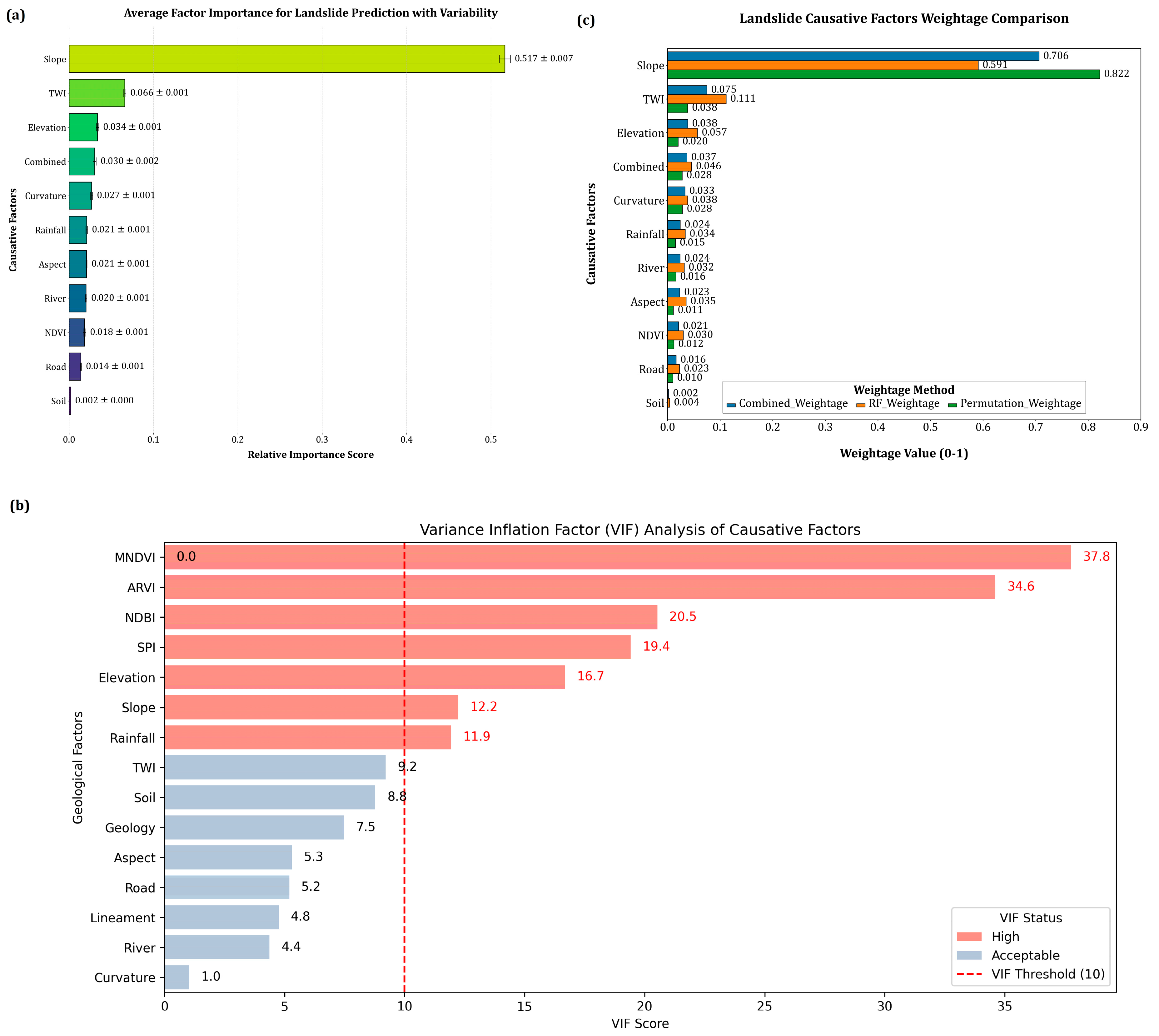
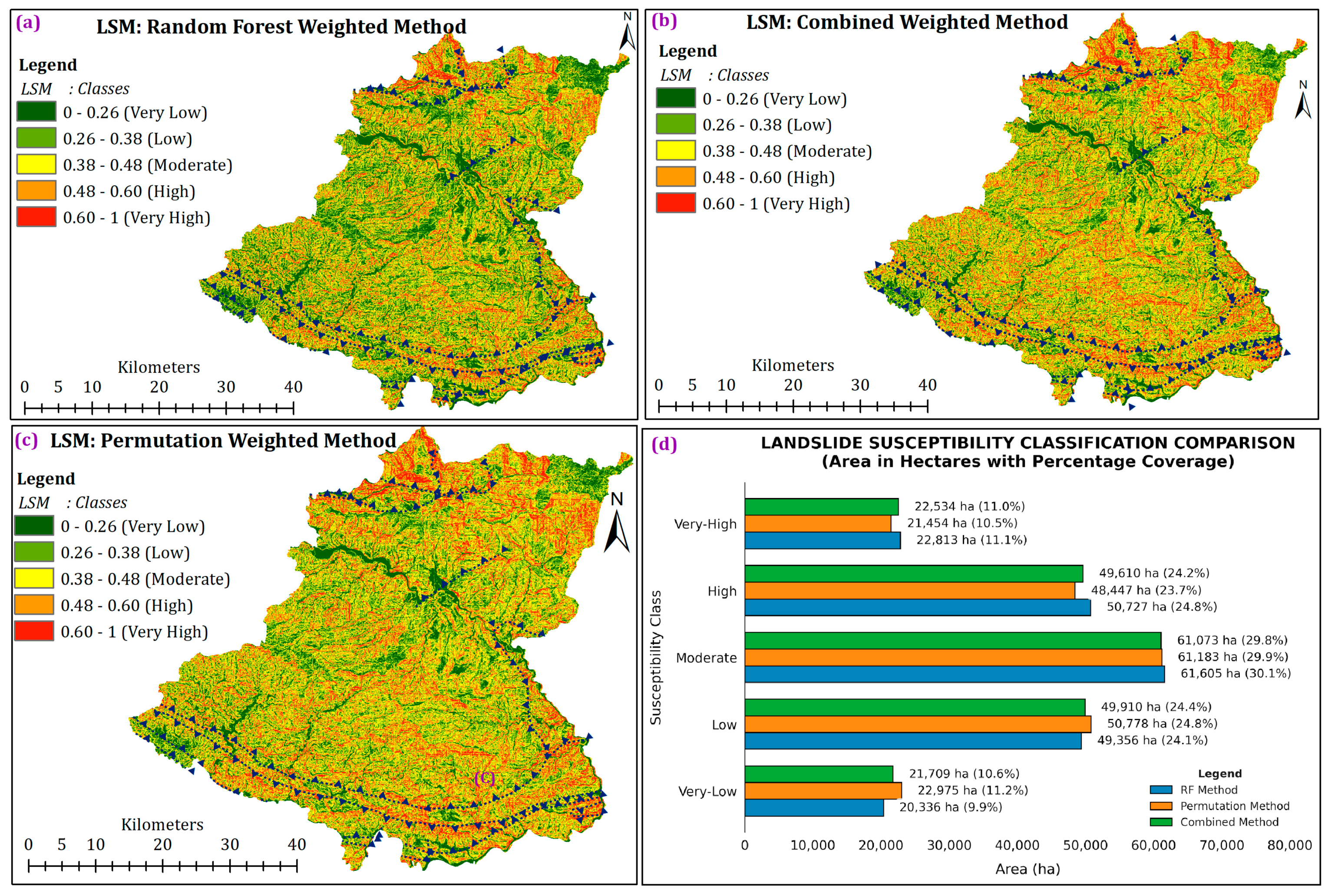
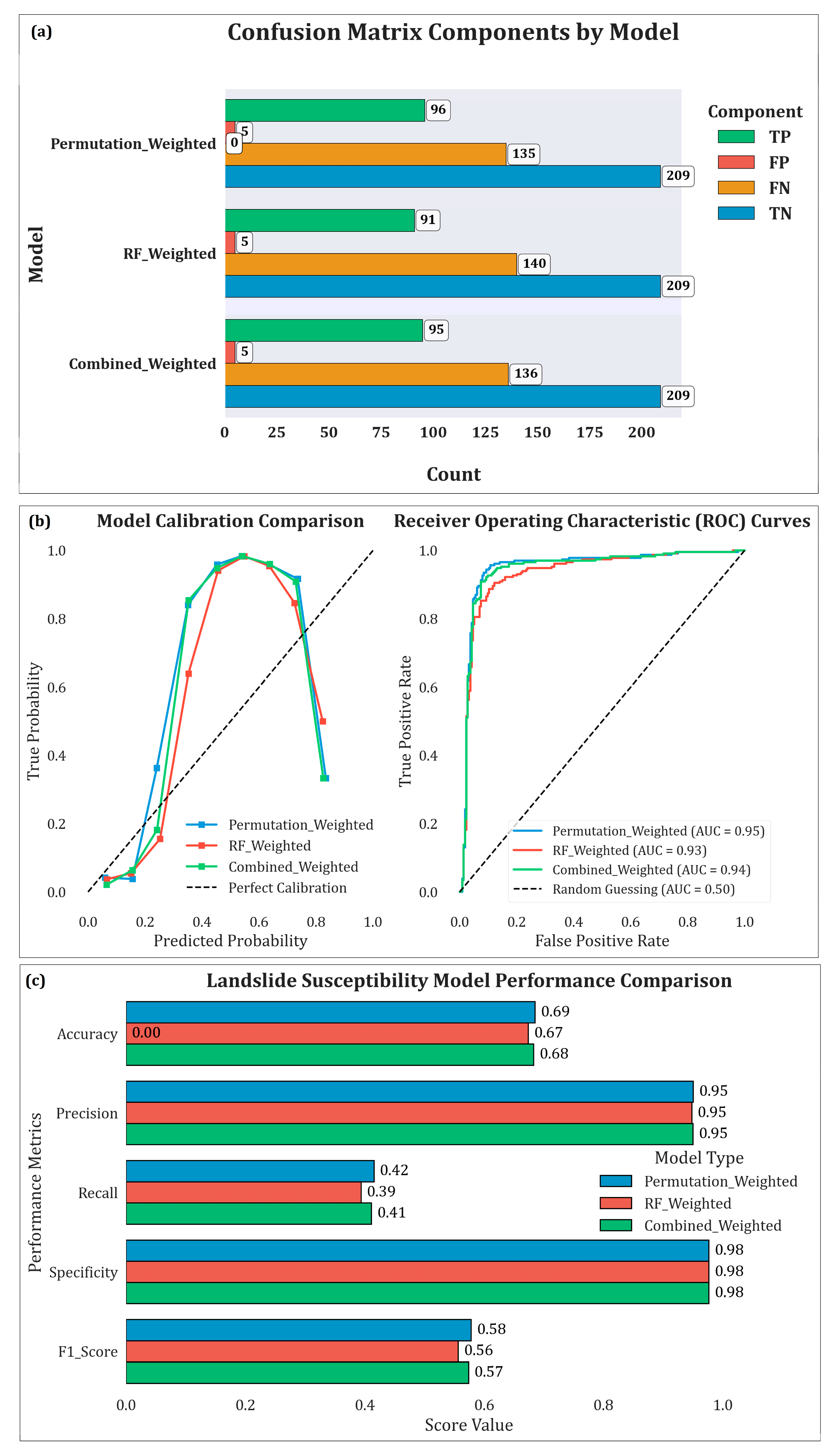
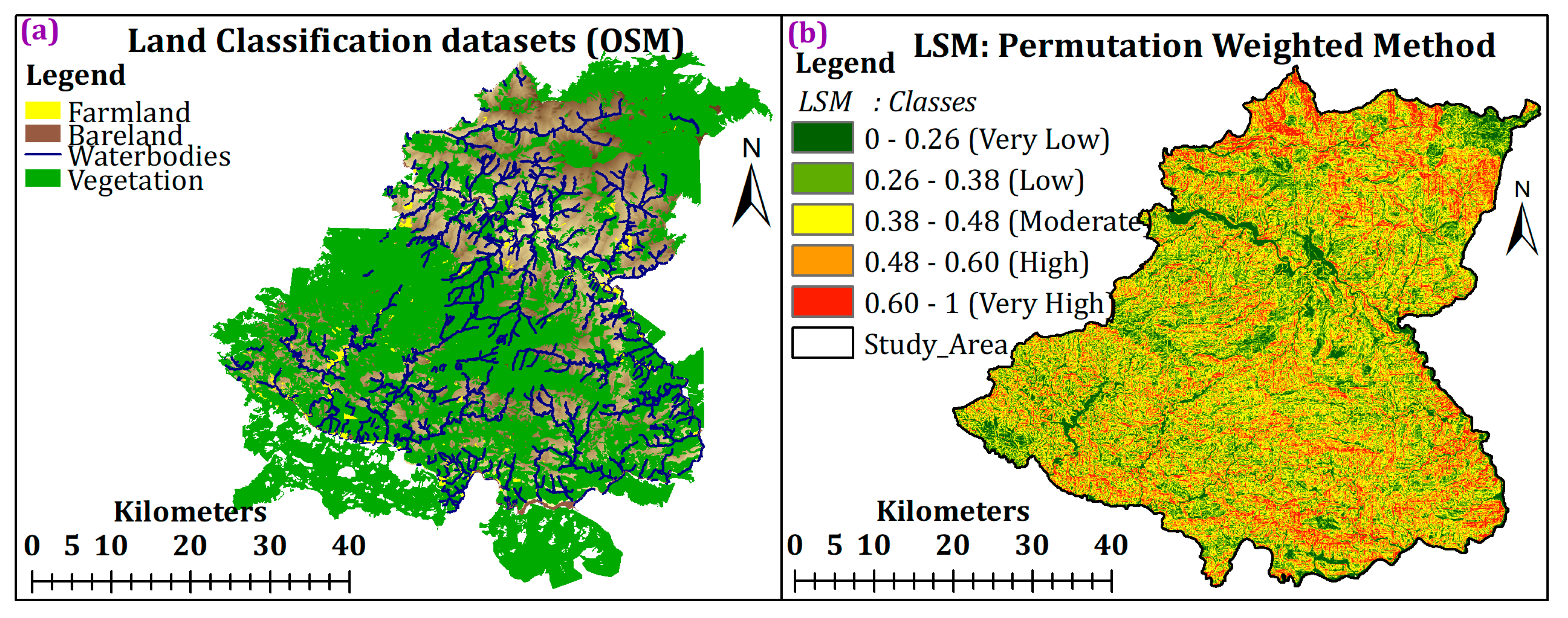
| Rank | Landslide Causative Factors | Combined Weightage | Random Forest Weightage | Permutation Weightage |
|---|---|---|---|---|
| 1 | Slope | 0.7064 | 0.5907 | 0.8218 |
| 2 | TWI | 0.0748 | 0.1114 | 0.0382 |
| 3 | Elevation | 0.0384 | 0.0567 | 0.0201 |
| 4 | Combined | 0.0367 | 0.0457 | 0.0278 |
| 5 | Curvature | 0.0332 | 0.0381 | 0.0283 |
| 6 | Rainfall | 0.0243 | 0.0337 | 0.0149 |
| 7 | Distance to River | 0.0238 | 0.0318 | 0.0158 |
| 8 | Aspect | 0.0232 | 0.0354 | 0.0111 |
| 9 | NDVI | 0.021 | 0.0301 | 0.012 |
| 10 | Distance to Road | 0.0163 | 0.0226 | 0.01 |
| 11 | Soil | 0.0019 | 0.0039 | 0 |
| Model | AUC (±Std) | Accuracy (±Std) | Precision (±Std) | Recall (±Std) | F1-Score (±Std) |
|---|---|---|---|---|---|
| Random Forest | 0.92 (±0.02) | 0.65 (±0.03) | 0.90 (±0.02) | 0.60 (±0.04) | 0.72 (±0.03) |
| Permutation-Weighted | 0.95 (±0.01) | 0.69 (±0.02) | 0.95 (±0.01) | 0.66 (±0.03) | 0.78 (±0.02) |
| Combined | 0.93 (±0.02) | 0.67 (±0.02) | 0.92 (±0.02) | 0.63 (±0.03) | 0.75 (±0.02) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Joshi, B.R.; Bhandary, N.P.; Acharya, I.P.; KC, N.; Bhandari, C. Landslide Susceptibility Mapping Optimization for Improved Risk Assessment Using Multicollinearity Analysis and Machine Learning Technique. Appl. Sci. 2025, 15, 12152. https://doi.org/10.3390/app152212152
Joshi BR, Bhandary NP, Acharya IP, KC N, Bhandari C. Landslide Susceptibility Mapping Optimization for Improved Risk Assessment Using Multicollinearity Analysis and Machine Learning Technique. Applied Sciences. 2025; 15(22):12152. https://doi.org/10.3390/app152212152
Chicago/Turabian StyleJoshi, Buddhi Raj, Netra Prakash Bhandary, Indra Prasad Acharya, Niraj KC, and Chakra Bhandari. 2025. "Landslide Susceptibility Mapping Optimization for Improved Risk Assessment Using Multicollinearity Analysis and Machine Learning Technique" Applied Sciences 15, no. 22: 12152. https://doi.org/10.3390/app152212152
APA StyleJoshi, B. R., Bhandary, N. P., Acharya, I. P., KC, N., & Bhandari, C. (2025). Landslide Susceptibility Mapping Optimization for Improved Risk Assessment Using Multicollinearity Analysis and Machine Learning Technique. Applied Sciences, 15(22), 12152. https://doi.org/10.3390/app152212152








