An Entropy–Envelope Approach for the Detection and Quantification of Power Quality Disturbances
Abstract
1. Introduction
- We use entropy features to characterize a PQD, allowing us to obtain a good description of the disturbances, even in noisy environments.
- We perform an analysis of the raw electrical signal but also of the signal envelope, enhancing the performance in the detection of amplitude-related disturbances like sag and swell.
- We reduce the computation burden by using a reduced number of features and LDA.
- The proposed methodology can automatically detect, classify, and quantify the disturbance present in the power grid.
2. Theoretical Background
2.1. Power Quality
2.2. Hilbert–Huang Transform
2.3. Entropy Features
2.4. Dimensionality Reduction
2.5. Magnitude of the PQD
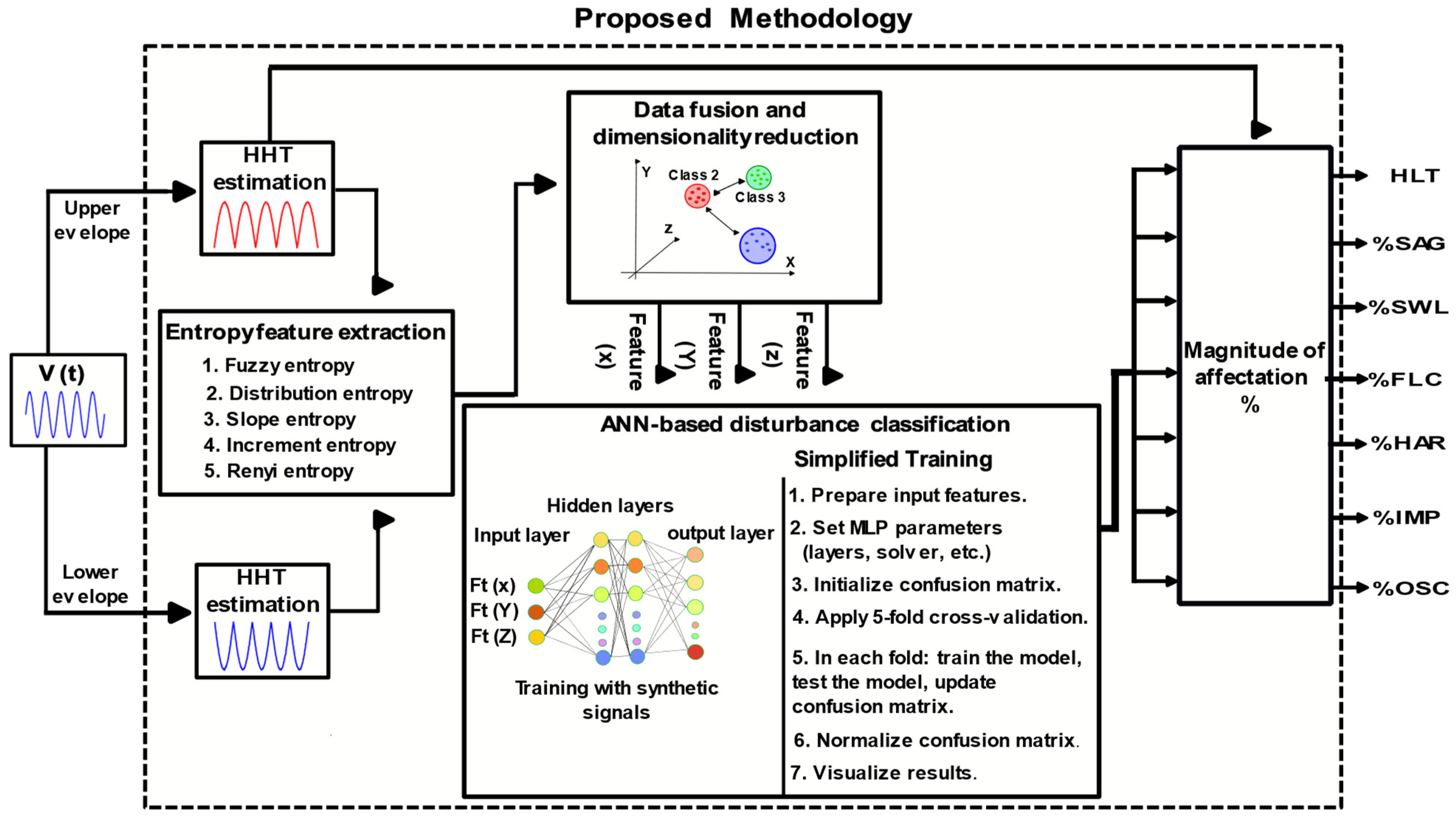
3. Methodology
3.1. Envelope Calculation
3.2. Entropy Feature Extraction
3.3. Data Fusion and Dimensionality Reduction
3.4. ANN-Based Disturbance Classification
3.5. Disturbance Quantification
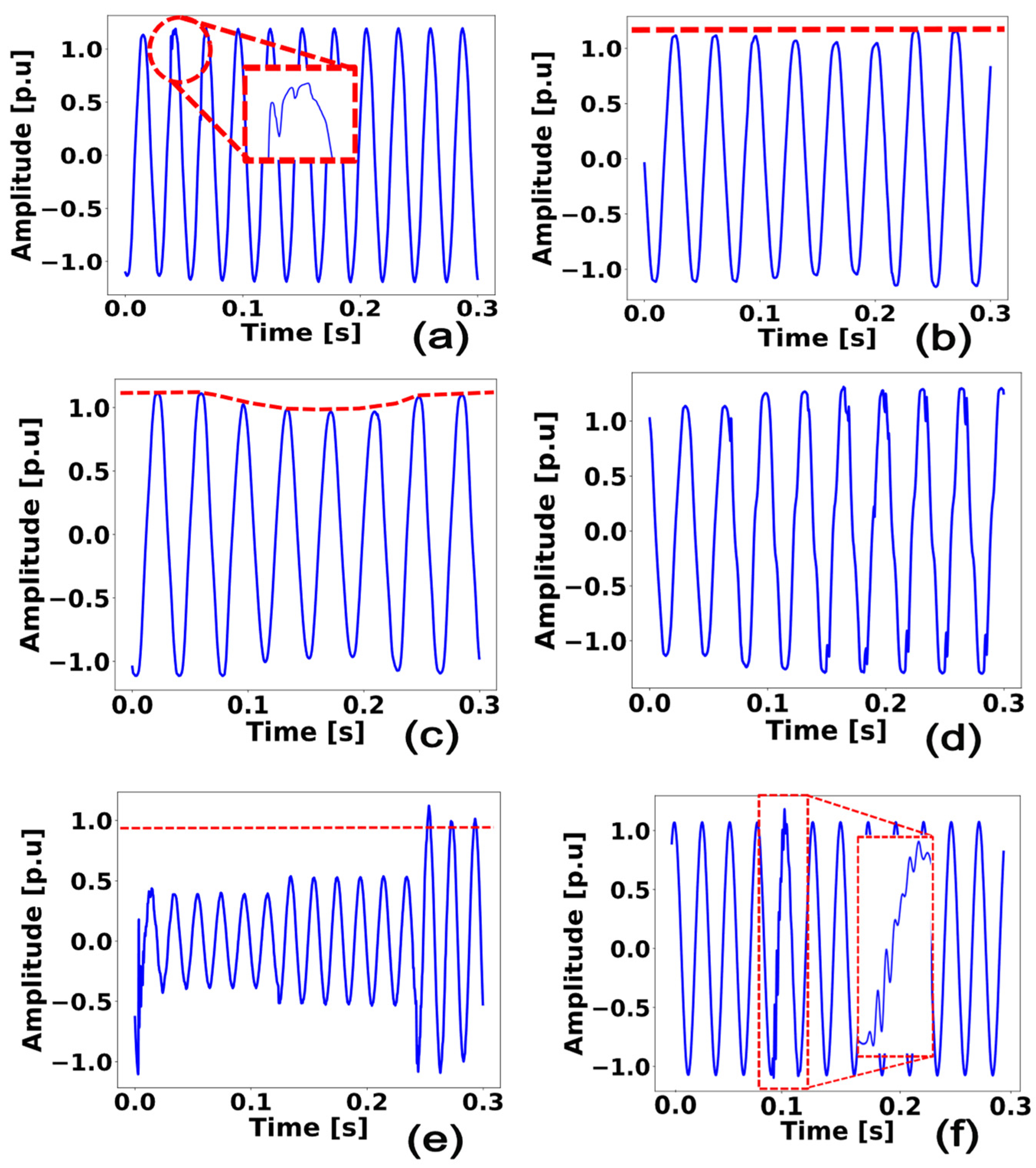
4. Results and Discussion
4.1. Study Case I: Synthetic Signals
4.2. Study Case II: Real Signals from the IEEE Working Group and the PV Generation Plant
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ayadi, F.; Colak, I.; Garip, I.; Bulbul, H.I. Targets of Countries in Renewable Energy. In Proceedings of the 2020 9th International Conference on Renewable Energy Research and Application (ICRERA), Glasgow, UK, 27–30 September 2020; pp. 394–398. [Google Scholar]
- Li, B.; Delpha, C.; Diallo, D.; Migan-Dubois, A. Application of Artificial Neural Networks to Photovoltaic Fault Detection and Diagnosis: A Review. Renew. Sustain. Energy Rev. 2021, 138, 110512. [Google Scholar] [CrossRef]
- IEEE Std 1159-2019; IEEE Recommended Practice for Monitoring Electric Power Quality. (Revision of IEEE Std 1159-2009). IEEE: Piscataway, NJ, USA, 2019; pp. 1–98.
- Priyadarshini, M.S.; Bajaj, M.; Prokop, L.; Berhanu, M. Perception of Power Quality Disturbances Using Fourier, Short-Time Fourier, Continuous and Discrete Wavelet Transforms. Sci. Rep. 2024, 14, 3443. [Google Scholar] [CrossRef] [PubMed]
- Hukampal, S.R.; Mohanty, S.R. Hardware Implementation of Ensemble Empirical Mode Decomposition for Critical PQ Disturbances Detection. In Proceedings of the 2020 IEEE 7th Uttar Pradesh Section International Conference on Electrical, Electronics and Computer Engineering (UPCON), Online, 27–29 November 2020; pp. 1–6. [Google Scholar]
- Chen, S.; Li, Z.; Pan, G.; Xu, F. Power Quality Disturbance Recognition Using Empirical Wavelet Transform and Feature Selection. Electronics 2022, 11, 174. [Google Scholar] [CrossRef]
- Sahani, M.; Choudhury, S.; Rout, S.K.; Gadanayak, D.A. DSP-Based Online Power Quality Events Detection and Classification Using Hilbert-Huang Transform and Random Forest Method. In Proceedings of the 2020 International Conference on Computational Intelligence for Smart Power System and Sustainable Energy (CISPSSE), Keonjhar, India, 29–31 July 2020. [Google Scholar]
- Liang, C.; Teng, Z.; Li, J.; Yao, W.; Wang, L.; He, Q.; Hu, S. Improved S-Transform for Time-Frequency Analysis for Power Quality Disturbances. IEEE Trans. Power Del. 2022, 37, 2942–2952. [Google Scholar] [CrossRef]
- Salles, R.S.; Ribeiro, P.F. The Use of Deep Learning and 2-D Wavelet Scalograms for Power Quality Disturbance Classification. Electr. Power Syst. Res. 2023, 214, 108834. [Google Scholar] [CrossRef]
- Liu, Y.; Jin, T.; Mohamed, M.A.; Wang, Q. A Novel Three-Step Classification Approach Based on Time-Dependent Spectral Features for Complex Power Quality Disturbances. IEEE Trans. Instrum. Meas. 2021, 70, 3000814. [Google Scholar] [CrossRef]
- Gonzalez-Abreu, A.-D.; Delgado-Prieto, M.; Osornio-Rios, R.-A.; Saucedo-Dorantes, J.-J.; Romero-Troncoso, R.-J. A Novel Deep Learning-Based Diagnosis Method Applied to Power Quality Disturbances. Energies 2021, 14, 2839. [Google Scholar] [CrossRef]
- Akter, M.S. Multiband Entropy-Based Feature-Extraction Method for Automatic Identification of Epileptic Focus Based on High-Frequency Components in Interictal EEG. IEEE Access 2020, 10, 7044. [Google Scholar]
- Henry, M.; Judge, G. Permutation Entropy and Information Recovery in Nonlinear Dynamic Economic Time Series. Econometrics 2019, 7, 10. [Google Scholar] [CrossRef]
- Shang, Y.; Lu, G.; Kang, Y.; Zhou, Z.; Duan, B.; Zhang, C. A Multifault Diagnosis Method Based on Modified Sample Entropy for Lithium-Ion Battery Strings. J. Power Sources 2020, 466, 250–275. [Google Scholar]
- Sandoval, D.; Leturiondo, U.; Vidal, Y.; Pozo, F. Entropy Indicators: An Approach for Low-Speed Bearing Diagnosis. Sensors 2021, 21, 849. [Google Scholar] [CrossRef] [PubMed]
- Yadav, R.; Pradhan, A.K.; Kamwa, I. Spectral Continuity and Subspace Change Detection for Recovery of Missing Harmonic Features in Power Quality. IEEE Trans. Power Del. 2024, 39, 180–191. [Google Scholar] [CrossRef]
- Malhotra, A.; Minhas, A.S.; Singh, S.; Zuo, M.J.; Kumar, R.; Kankar, P.K. Bearing Fault Diagnosis Based on Flexible Analytical Wavelet Transform and Fuzzy Entropy Approach. Mater. Today Proc. 2021, 43, 629–635. [Google Scholar] [CrossRef]
- Lee, D.Y.; Choi, Y. Multiscale Distribution Entropy Analysis of Rate Variability Using Differential Inter-Beat Intervals. IEEE Access 2020, 8, 48761–48773. [Google Scholar] [CrossRef]
- Li, Y.; Tang, B.; Huang, B.; Xue, X. A Dual-Optimization Fault Diagnosis Method for Rolling Bearings Based on Hierarchical Slope Entropy and SVM Synergized with Shark Optimization Algorithm. Sensors 2023, 23, 12. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Sun, Y. Role of Entropy in Fault Diagnosis of Mechanical Equipment: A Review. Eng. Res. Express 2023, 5, 032004. [Google Scholar] [CrossRef]
- Girault, J.-M.; Humeau-Heurtier, A. Centered and Averaged Fuzzy Entropy to Improve Fuzzy Entropy Precision. Entropy 2018, 20, 287. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Guerrero, M.A.; Carranza-Lopez-Padilla, R.; Osornio-Rios, R.A.; Romero-Troncoso, R.J. A Novel Methodology for Modeling Waveforms for Power Quality Disturbance Analysis. Electr. Power Syst. Res. 2017, 143, 14–24. [Google Scholar] [CrossRef]



| No. | Entropy Feature | Equation | Description |
|---|---|---|---|
| (2–3) | Fuzzy Entropy | Ps1 is the average value of the fuzzy similarities for length m, and Ps2 helps to capture the regularity on an extended scale. N is the length of the time series, m is the length of the pattern, and r is the tolerance threshold which determines the scale of similarity of the patterns. is the fuzzy similarity function for patterns of length m [21]. | |
| (4) | Distribution Entropy | indicates the number of dimensions of the matrix and is the number of histograms, while is estimated as the probability of each element. | |
| (5) | Slope Entropy | is the time series to be developed, according to size ; and represent the limits of the partitions for each dimension conformed by and represents the total number of patterns vs. times of the number of occurrences. | |
| (6) | Increment Entropy | is the order of the function, quantifies the resolution of the function, and is the relative frequency for each element evaluated. | |
| (7) | Renyi Entropy | is the distribution measure, represents the frequency discrete variable and the temporal discrete variable, and is the probability of the distribution along the discrete signal. |
| No. | PQ | Equation | Description |
|---|---|---|---|
| (8) | SAG | The value of is the value of the upper envelope, and the is the mean of the upper envelope of the HLT signal. | |
| (9) | SWELL | The value of is the value of the upper envelope, and the is the mean upper envelope of the HLT signal. | |
| (10) | FLC | % | The value of represents the standard deviation of the upper envelope, and is the mean upper envelope of the healthy signal. |
| (11) | HAR | Here, represents the RMS value of the fundamental frequency, while denotes the RMS value of the h-th harmonic component obtained through spectral decomposition (e.g., FFT). indicates the highest harmonic order. The THD expresses the degree of waveform distortion. | |
| (12) | IMP | calculates the percentage reduction in peak voltage by comparing the maximum value of the IMP signal to that of the HLT signal . | |
| (13–14) | OSC | Here, calculates the max value in the upper envelope, and calculates the maximum value of the healthy upper envelope; this gives the peak magnitude affectation. In the case of , it measures the relative change in energy between the OSC and the HLT signal. |
| True Class | Classification Report | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| HLT | SAG | SWL | FLC | HAR | IMP | OSC | Precision | Recall | F1-Score | ||
| Assigned Class | HLT | 98.2 | 0.4 | 1.4 | 0 | 0 | 0 | 0 | 0.9592 | 0.9400 | 0.9600 |
| SAG | 0.8 | 99.0 | 0.2 | 0 | 0 | 0 | 0 | 0.9800 | 0.9800 | 0.9851 | |
| SWL | 2.6 | 0 | 97.0 | .04 | 0 | 0 | 0 | 0.9505 | 0.9600 | 0.9697 | |
| FLC | 0 | 0 | 0.2 | 99.4 | 0.4 | 0 | 0 | 0.9900 | 0.9900 | 0.9849 | |
| HAR | 0 | 0 | 0 | 0 | 99.6 | 0.4 | 0 | 0.9901 | 1.0 | 0.9901 | |
| IMP | 0 | 0 | 0 | 0 | 0 | 99.6 | 0.4 | 1.0 | 1.0 | 1.0 | |
| OSC | 0 | 0 | 0 | 0 | 0 | 0 | 100 | 1.0 | 1.0 | 1.0 | |
| F1-SCORE | ||||||||
|---|---|---|---|---|---|---|---|---|
| FuzzEn (Ps1) | FuzzEn (Ps2) | DistEn | SlopeEn | IncreEn | RenyiEn | Proposed | ||
| Assigned Class | HLT | 0.3636 | 0.6552 | 0.0000 | 0.7280 | 0.2895 | 0.7901 | 0.9600 |
| SAG | 0.8776 | 0.8586 | 0.3030 | 0.7861 | 0.7162 | 0.6502 | 0.9851 | |
| SWL | 0.9314 | 0.9366 | 0.2196 | 0.3478 | 0.6911 | 0.2336 | 0.9697 | |
| FLC | 0.7042 | 0.7909 | 0.0198 | 0.5381 | 0.4593 | 0.5283 | 0.9849 | |
| HAR | 0.9694 | 0.9694 | 0.0571 | 0.5899 | 0.6173 | 0.9950 | 0.9901 | |
| IMP | 0.8475 | 0.9014 | 0.5929 | 0.8070 | 0.9901 | 0.6111 | 1.0 | |
| OSC | 0.9851 | 0.9851 | 0.6755 | 0.7570 | 0.9800 | 0.9851 | 1.0 | |
| ACCURACY | 0.8257 | 0.8743 | 0.3143 | 0.6586 | 0.6929 | 0.7114 | 0.9843 | |
| Ref. | PQD | Data Type | Technique | Advantage | Dis-Advantage | Total Performance % |
|---|---|---|---|---|---|---|
| [7] | Transient, sag, swell, harmonics, notch, flicker, DC offset. | Synthetic/Emulated | EMD/HHT/ Random Forest Technique | Higher learning speed; superior classification accuracy. | It is necessary to process the magnitude response, frequency response, phase response, and Hilbert energy spectrum for a good response of the methodology. | 97.40% |
| [9] | Normal, impulsive, interruption, oscillatory, sag, swell. | Synthetic | CWT/2D-CNN | High precision, time, and frequency information that characterizes several PQ issues. | Network training time is extensive and requires lots of computational power. | 96.67% |
| [10] | Normal, interruption, swell, sag, flicker, harmonics, oscillatory transient. | Synthetic/Emulated | EMD/Feature extraction/LDA/K-nearest neighbor | Robustness and high accuracy even under different conditions of noise. | IMFs will affect the classifier’s accuracy, such as noise and pseudo. At the same time, the overall computation time will increase. | 97.40% |
| [11] | Normal, sag, swell, interruption. flicker, harmonics, oscillatory transient. | Synthetic/Real | FFT/EMD/NN | Robustness and high accuracy even under different conditions of noise. | It is necessary to tune of the corresponding hyperparameters. | 99.47% |
| Proposed | Normal, sag, swell, flicker, harmonics, impulsive, oscillatory. | Synthetic/Real | HHT/Entropy/LDA/NN | Higher learning speed; superior classification accuracy. | Some of the techniques applied may be difficult to apply in systems with low processing power, making them difficult to apply in microprocessors. | 98.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perez-Anaya, E.; Saucedo-Dorantes, J.J.; Jaen-Cuellar, A.Y.; Romero-Troncoso, R.d.J.; Elvira-Ortiz, D.A. An Entropy–Envelope Approach for the Detection and Quantification of Power Quality Disturbances. Appl. Sci. 2025, 15, 12101. https://doi.org/10.3390/app152212101
Perez-Anaya E, Saucedo-Dorantes JJ, Jaen-Cuellar AY, Romero-Troncoso RdJ, Elvira-Ortiz DA. An Entropy–Envelope Approach for the Detection and Quantification of Power Quality Disturbances. Applied Sciences. 2025; 15(22):12101. https://doi.org/10.3390/app152212101
Chicago/Turabian StylePerez-Anaya, Eduardo, Juan Jose Saucedo-Dorantes, Arturo Yosimar Jaen-Cuellar, Rene de Jesus Romero-Troncoso, and David Alejandro Elvira-Ortiz. 2025. "An Entropy–Envelope Approach for the Detection and Quantification of Power Quality Disturbances" Applied Sciences 15, no. 22: 12101. https://doi.org/10.3390/app152212101
APA StylePerez-Anaya, E., Saucedo-Dorantes, J. J., Jaen-Cuellar, A. Y., Romero-Troncoso, R. d. J., & Elvira-Ortiz, D. A. (2025). An Entropy–Envelope Approach for the Detection and Quantification of Power Quality Disturbances. Applied Sciences, 15(22), 12101. https://doi.org/10.3390/app152212101










