Prefabricated Reinforced Guide Walls for Mountainous River Locks: Numerical Analysis and Performance Evaluation
Abstract
1. Introduction
2. Design and Assembly of the Prefabricated Reinforced Guide Wall
- Carry out river channel foundation treatment, pour the concrete base plate, and reserve rebar holes during pouring. The distribution of rebar holes must be consistent with the positions of the rebar holes in the first layer of concrete units, and appropriate tolerance should be considered to ensure alignment accuracy during assembly.
- According to the positions of the rebar holes reserved in Step 1, hoist and install the first layer of concrete units in sequence, making different concrete units arranged in a staggered manner. Install connecting bolts on the concrete units to enhance the intra-layer integrity.
- Fill rocks into each concrete unit and make the rocks flush with the top of the concrete unit. On this basis, hoist and install the second layer of concrete units, so that the protrusions on the top of the first layer of concrete units are inserted into the grooves at the bottom of the second layer.
- Repeat Steps 2 and 3 until the guide wall reaches the designed cross-section and height. The stepped backfill area is formed between the wall and the shore.
- Place rebars downward from the reserved rebar holes at the top protrusions of each concrete unit in the uppermost layer, and penetrate them into the rebar holes reserved in the base plate in Step 1 to form the main body of the guide wall.
- Depending on actual usage requirements, waste rockfill can be filled into the backfill area between the guide wall and the shore in Step 4 to perform the functions of soil retaining and slope protection.
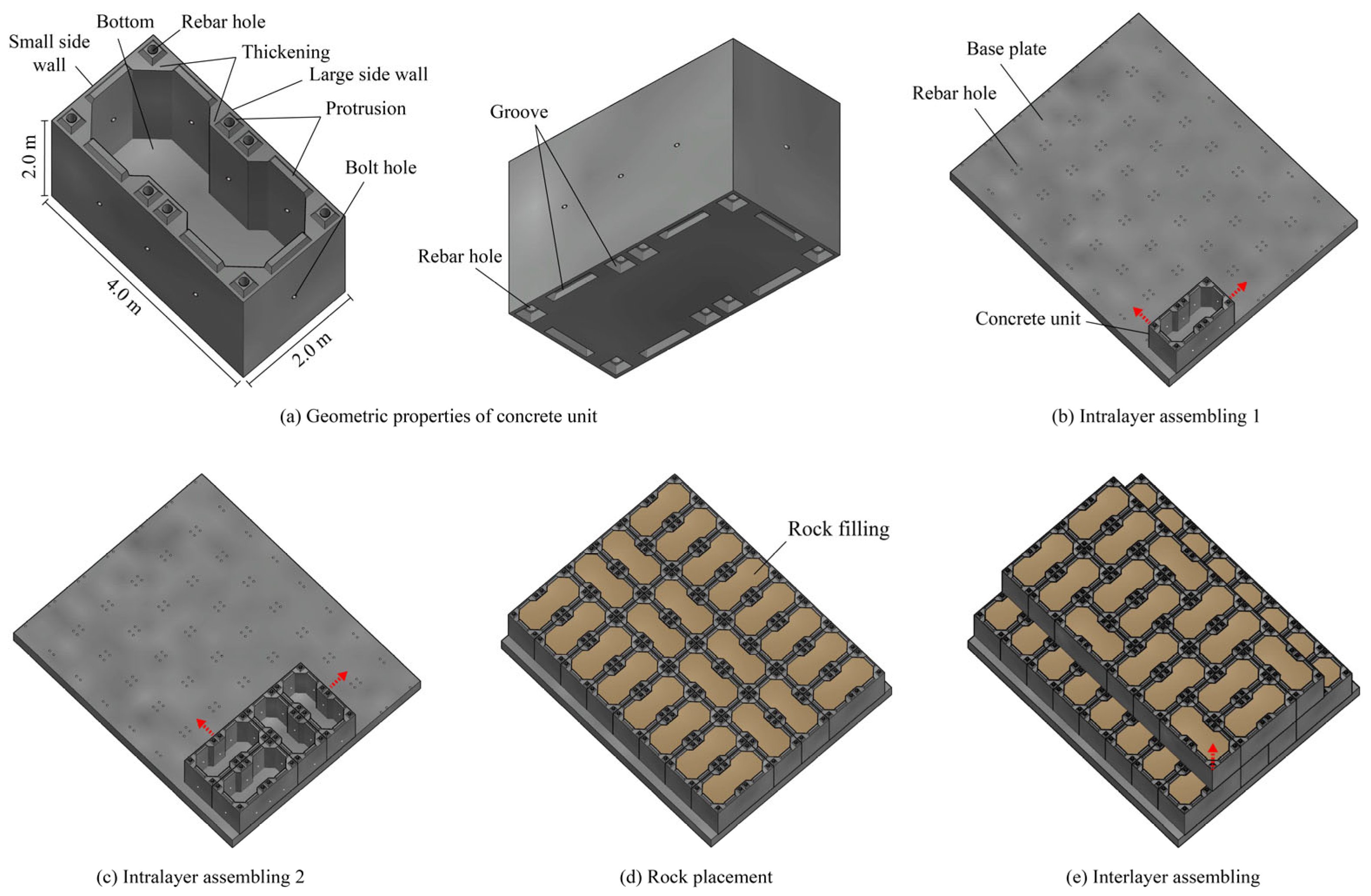
3. Methodology
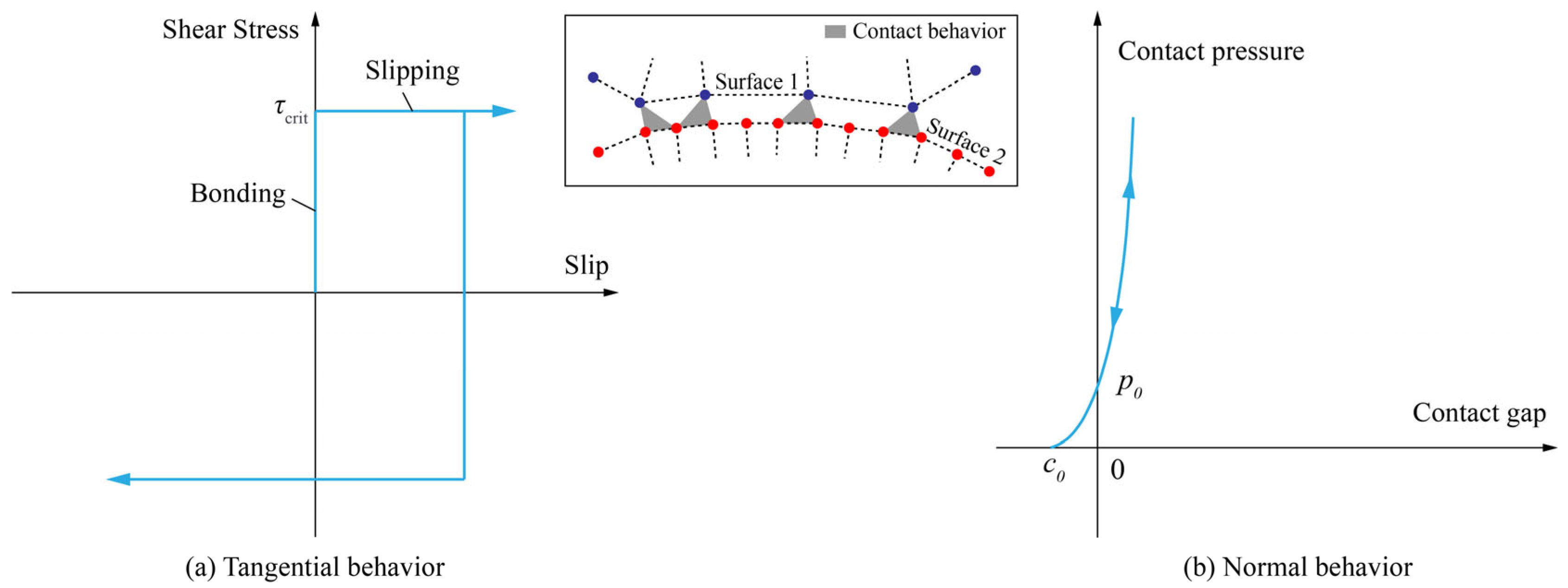
3.1. Nonlinear Contact Model and Metal Plasticity Model
3.2. Analysis Method of Structural Stress–Deformation–Stability
4. Analysis of the Performance and Its Influencing Factors of the Prefabricated Reinforced Guide Wall
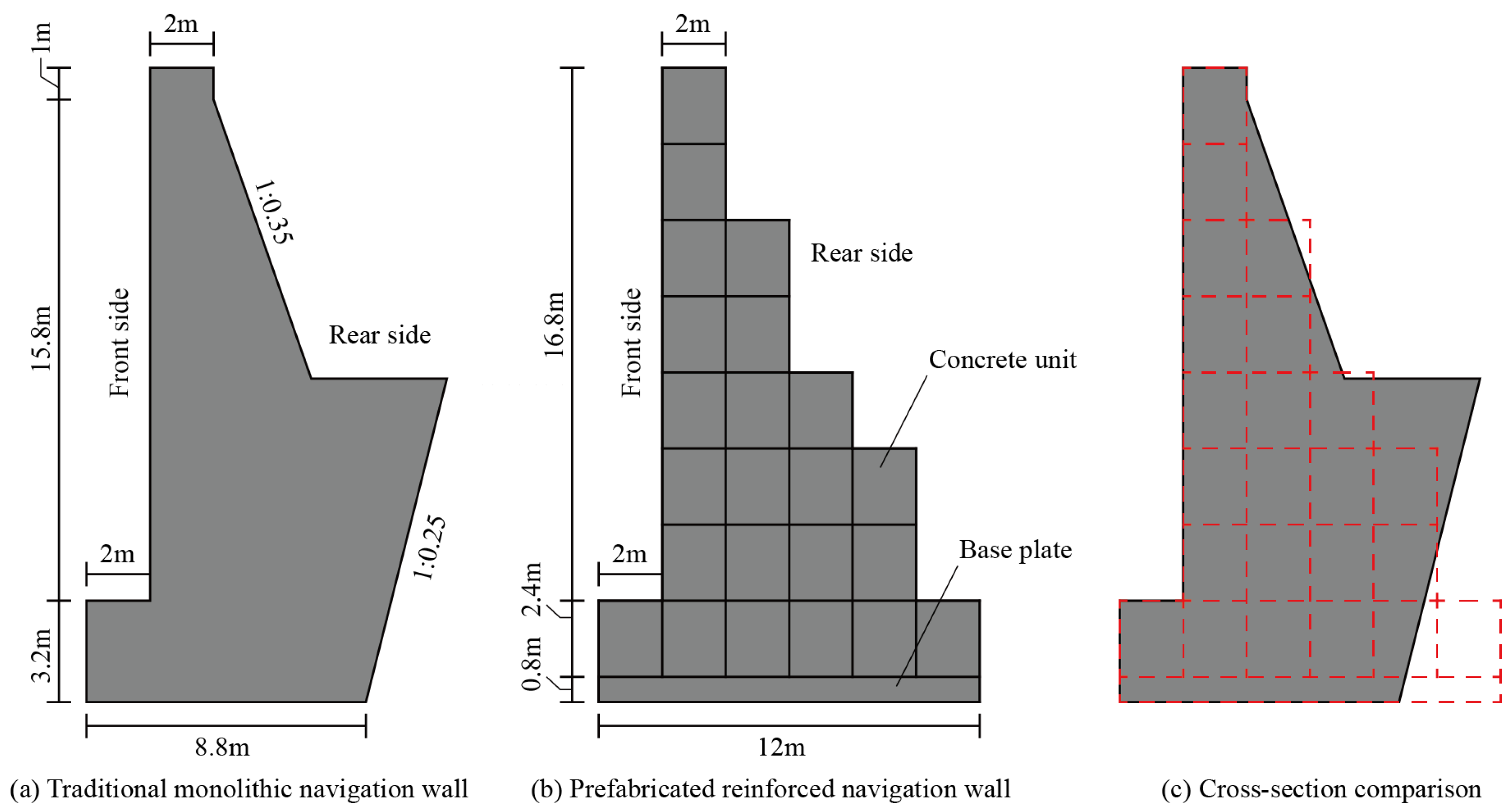
4.1. Structural Geometry and Configuration
4.2. Model and Parameters
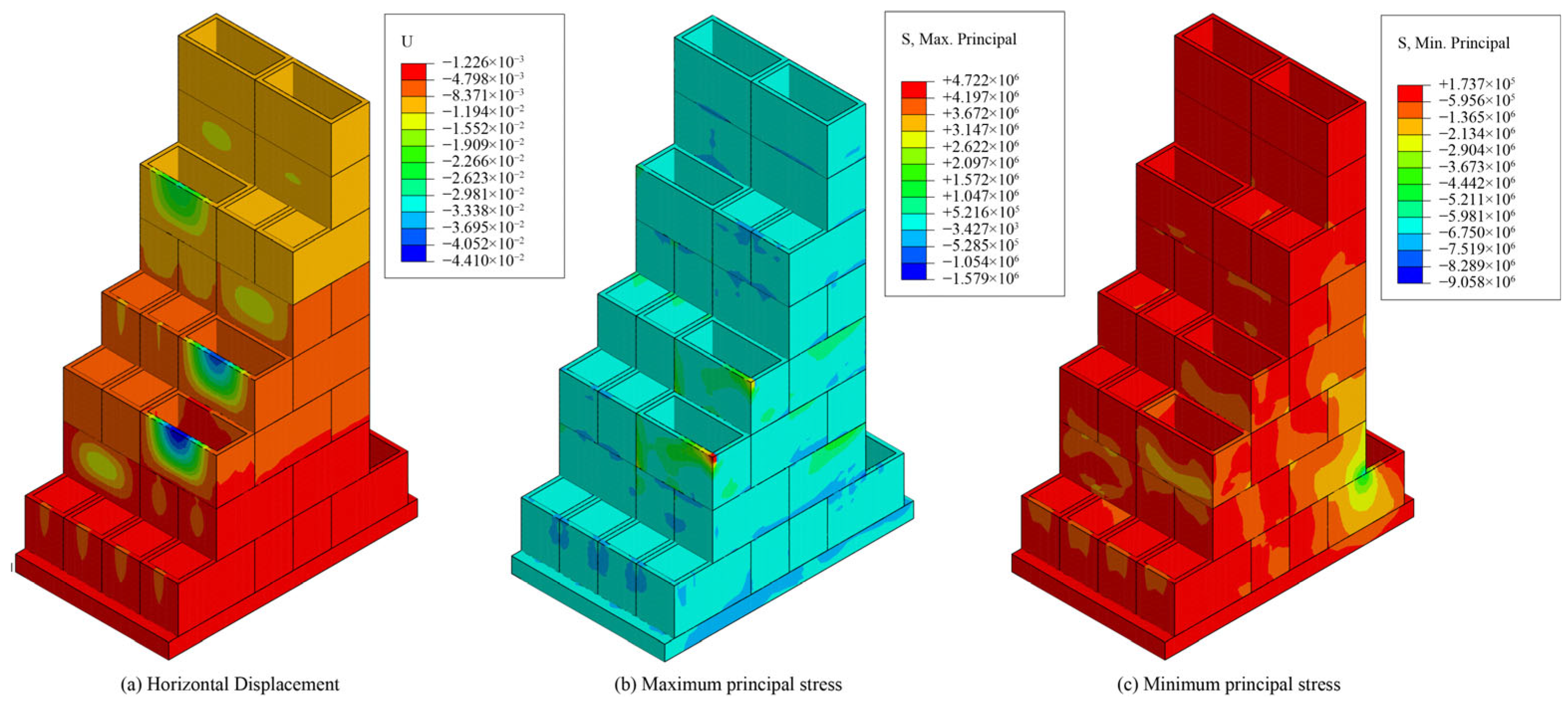
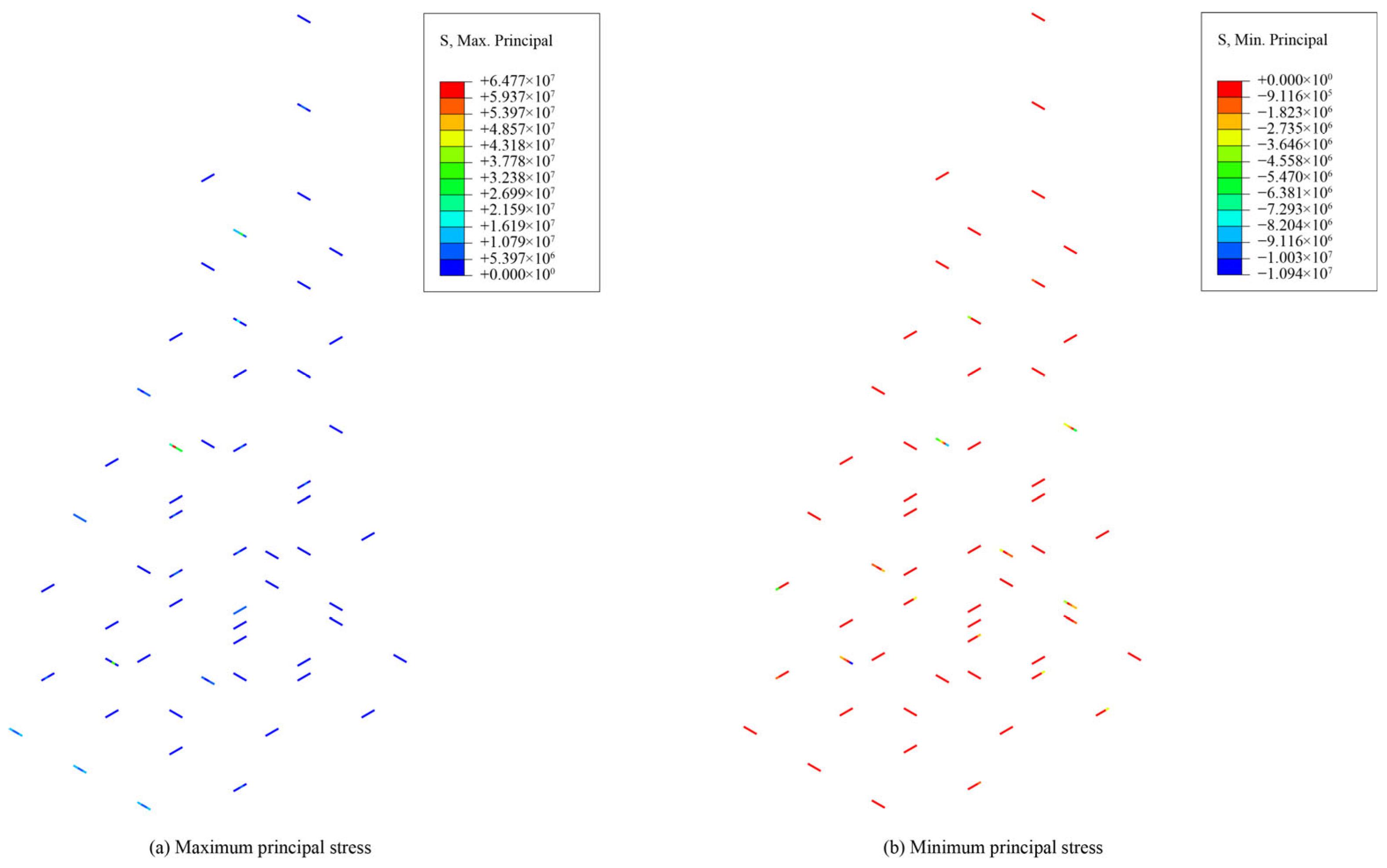
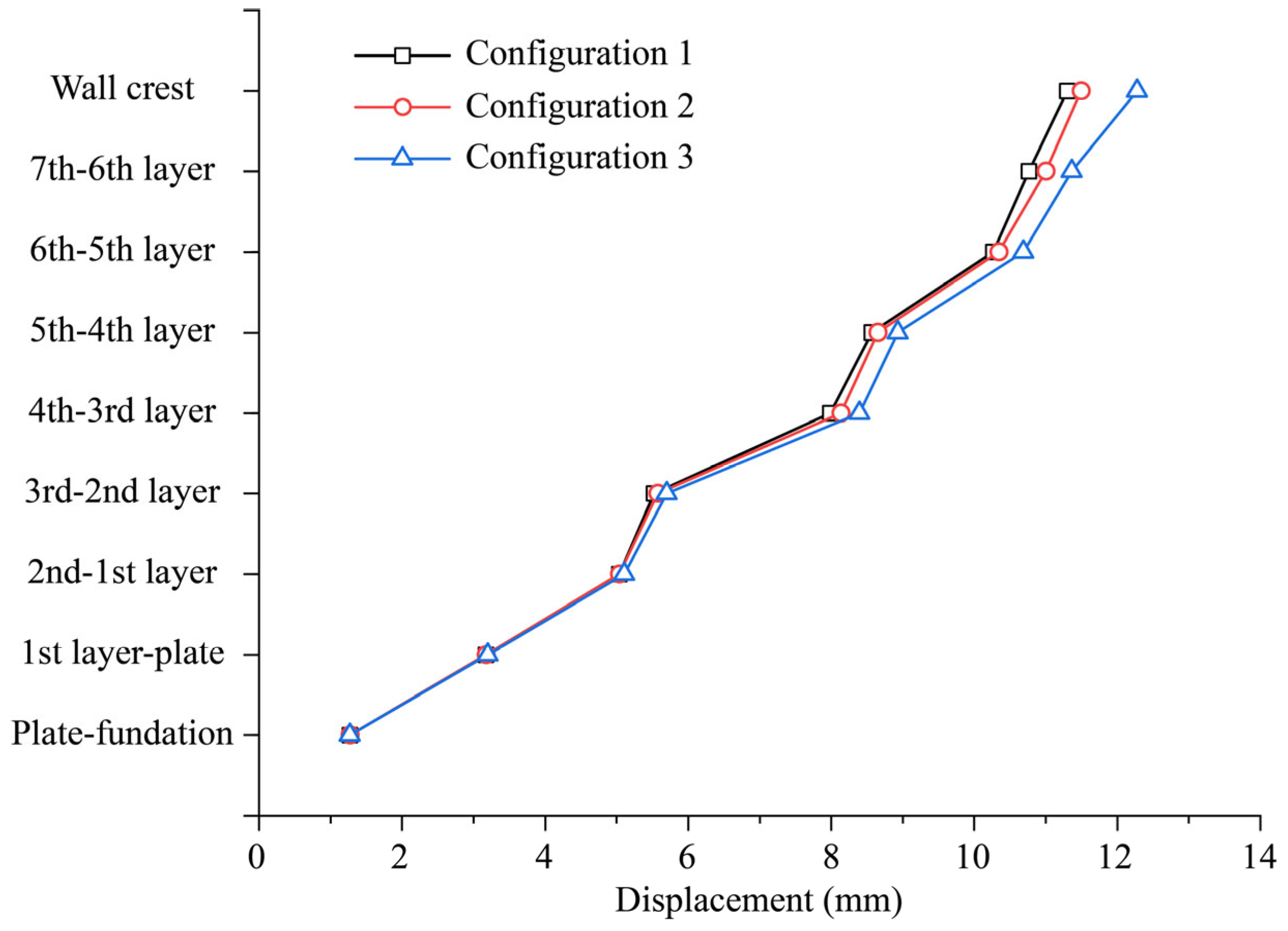
4.3. Mechanical Behavior Analysis
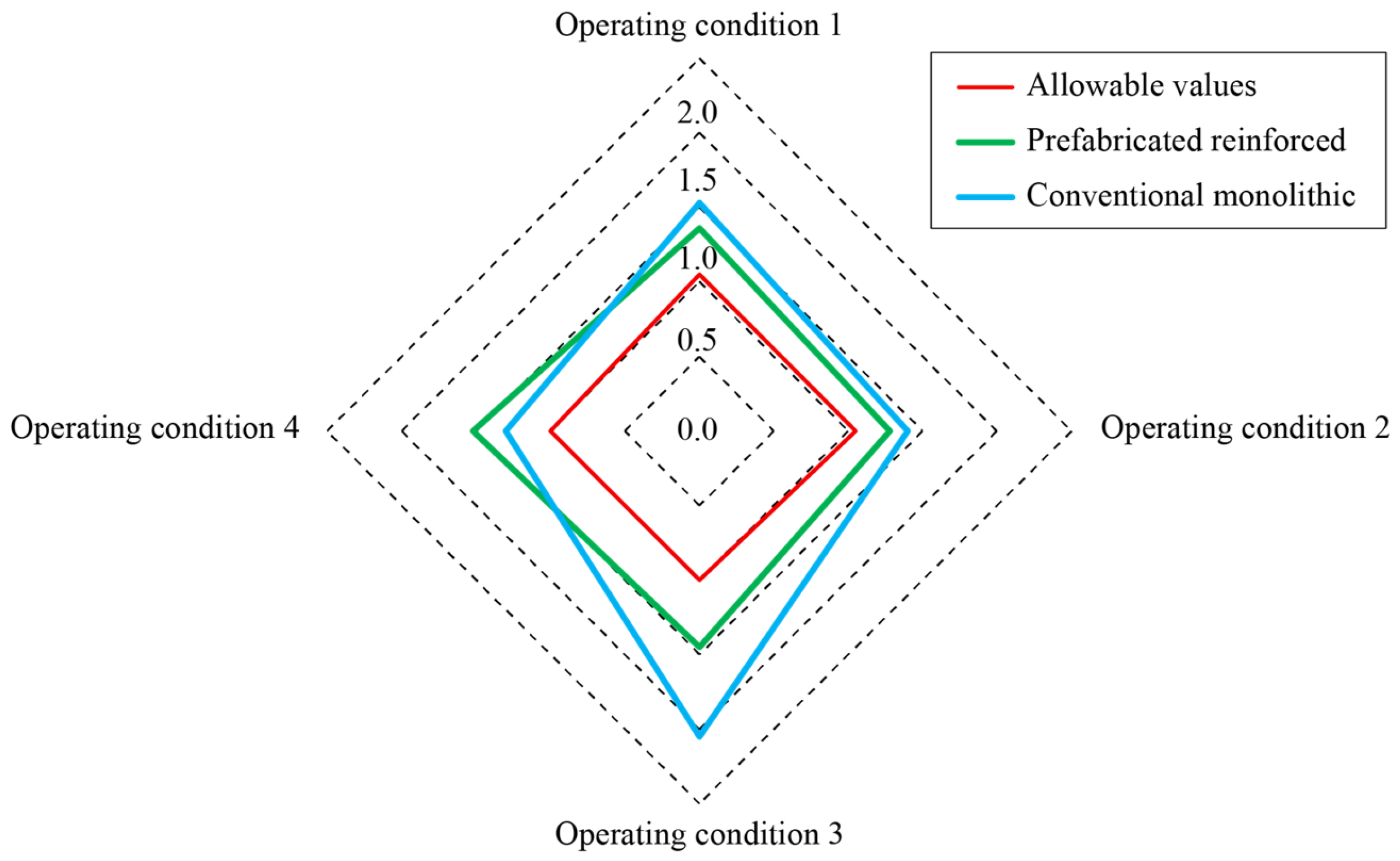
4.4. Analysis of the Impact of Different Design Schemes
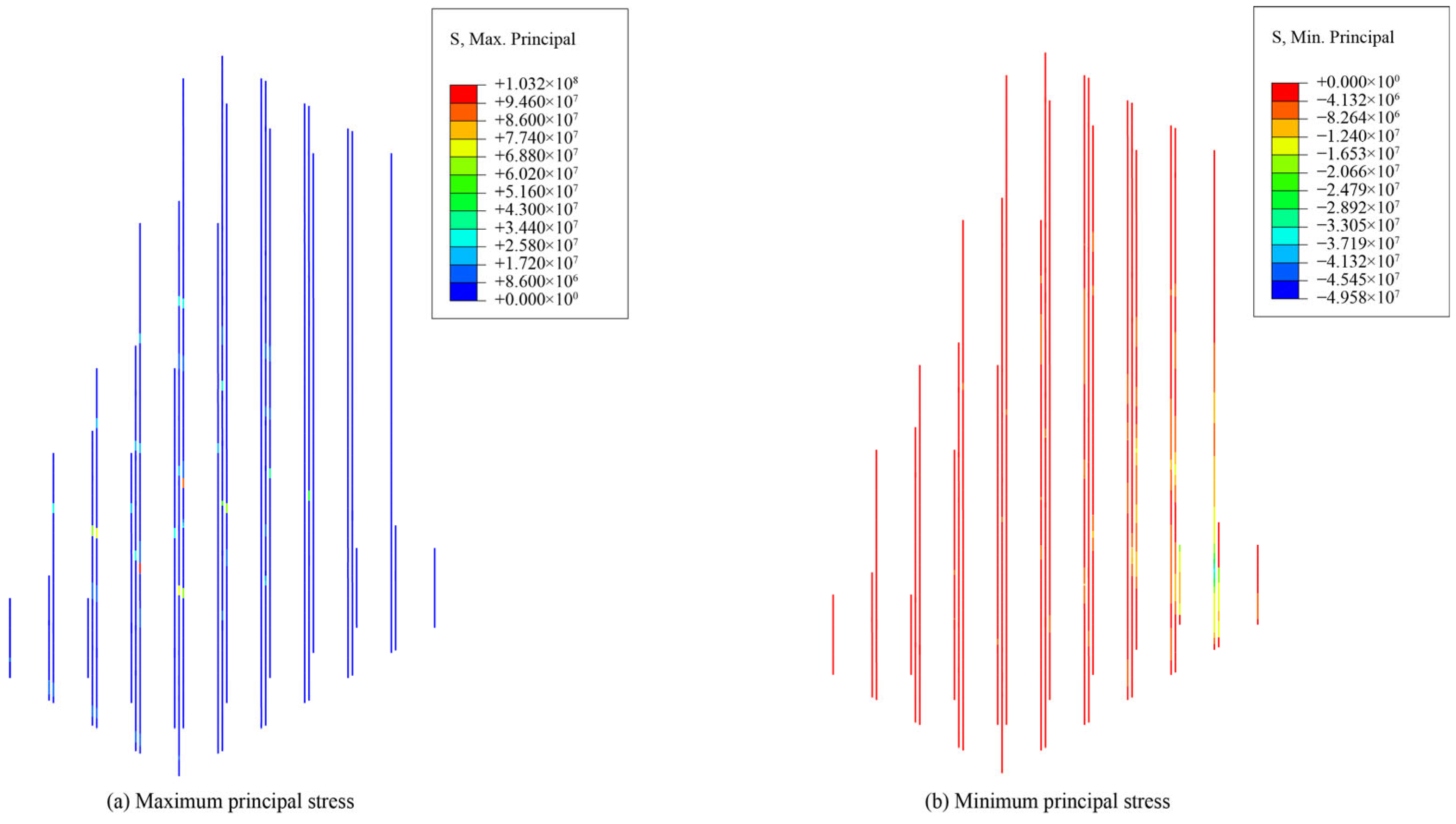
4.4.1. Influence of Bolt and Rebar Configurations
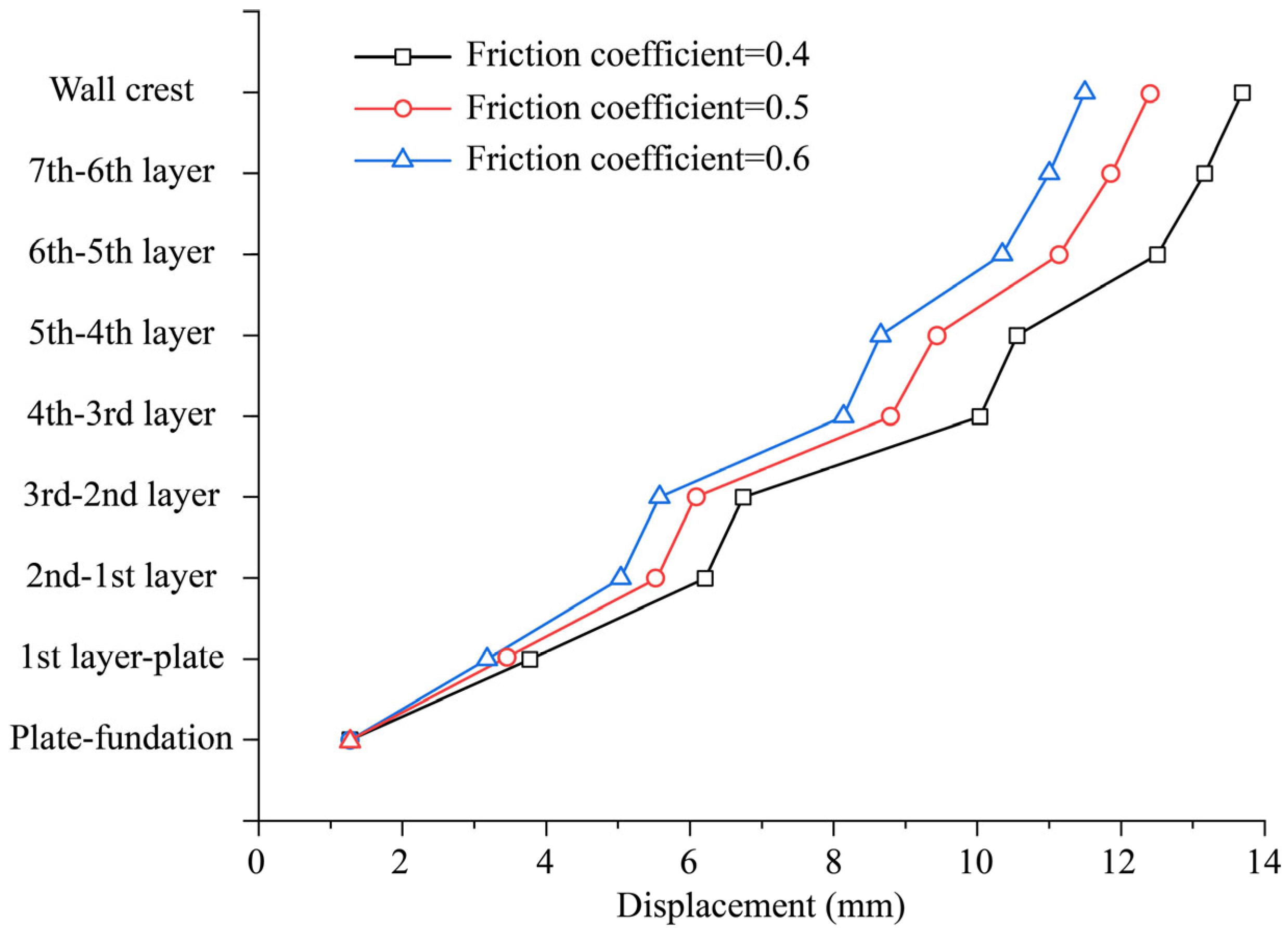
4.4.2. Influence of Contact Surface Friction Coefficient
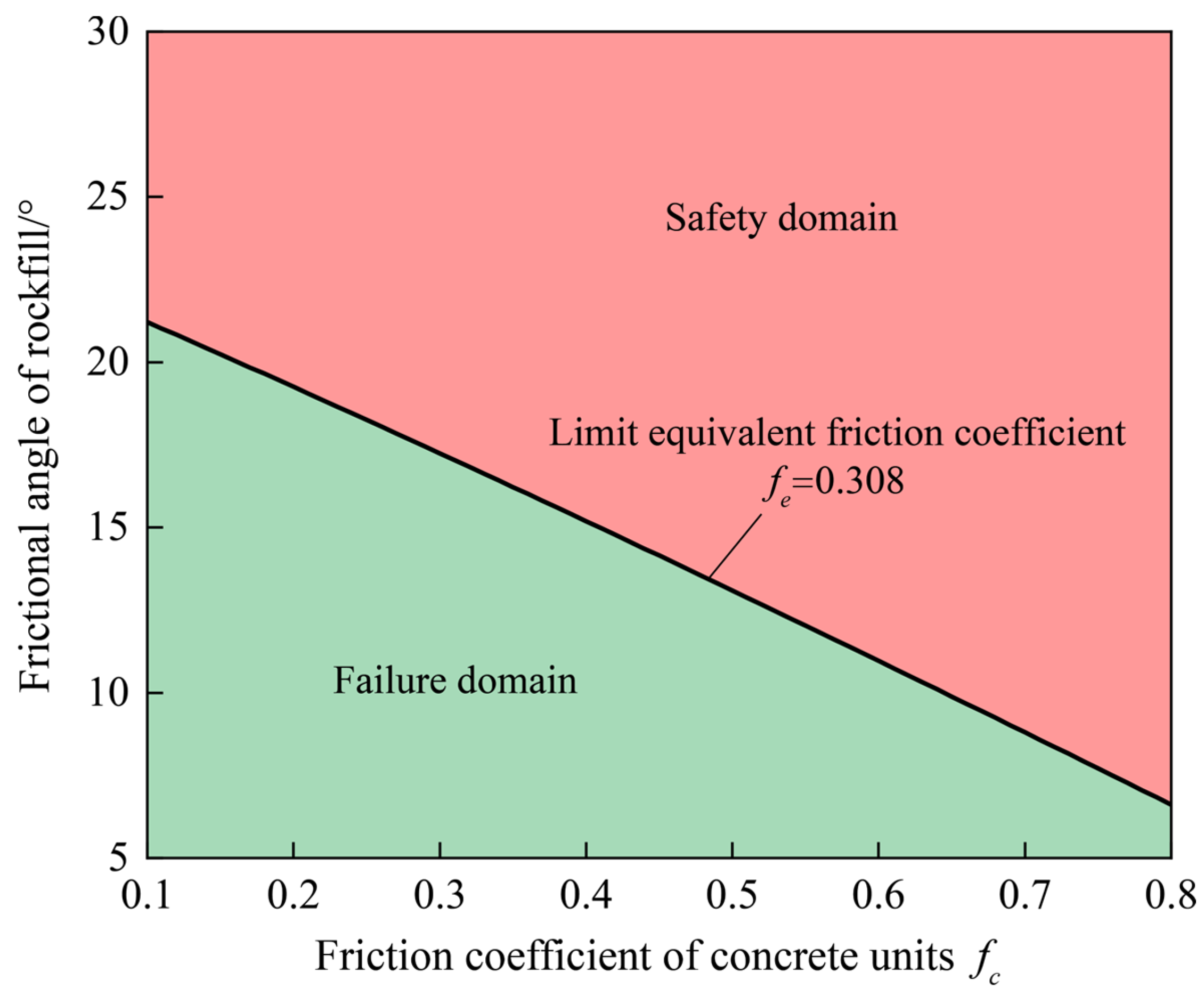
4.4.3. Discussion on Bottomless Concrete Units
5. Future Work
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hulagabali, A.; Solanki, C.; Dodagoudar, G.; Anitha. Finite Element Analysis of Segmental Precast Concrete Panel Reinforced Earth Retaining Wall. Jordan J. Civ. Eng. 2023, 17, 582–597. [Google Scholar] [CrossRef]
- Ferdous, W.; Bai, Y.; Almutairi, A.D.; Satasivam, S.; Jeske, J. Modular Assembly of Water-Retaining Walls Using GFRP Hollow Profiles: Components and Connection Performance. Compos. Struct. 2018, 194, 1–11. [Google Scholar] [CrossRef]
- Yu, X.; Cheng, J. Prefabricated Reinforced Concrete Wall Protection. In Lecture Notes in Civil Engineering, Proceedings of the 2nd International Conference on Advanced Civil Engineering and Smart Structures, Chengdu, China, 25–26 November 2023; Springer: Singapore, 2024; pp. 303–308. [Google Scholar]
- Zhao, J.; Liu, R.; Zhou, B.; Fu, Y.; Li, Y.; Zhang, W. Thermal performance and passive energy saving optimization of prefabricated houses in Xinjiang region. Case Stud. Therm. Eng. 2025, 70, 106082. [Google Scholar] [CrossRef]
- Yang, X.; Huang, M.; Peng, Z.; Lin, F. Calculation of dynamic assembly and tensioning loads at multiple points of prefabricated structure. Tunn. Undergr. Space Technol. 2022, 126, 104564. [Google Scholar] [CrossRef]
- Yang, X.; Lin, F. Research on prefabricated metro station structure and key assembly technologies. Tunn. Undergr. Space Technol. 2024, 153, 106029. [Google Scholar] [CrossRef]
- Ma, S.; Li, Z.; Fu, R. A Fully Prefabricated Pile-Wall Composite Scheme of Open-Cut Tunnel and the Mechanical Behavior of the Composite Structure during Construction. Buildings 2024, 14, 1693. [Google Scholar] [CrossRef]
- Chen, L.; Xie, H.; Xiang, N.; Zhang, K.; Yang, S.; Hu, Z. Optimized evaluation of ground motion intensity measures for the prefabricated cantilevered roadbed structure in mountainous areas. Structures 2024, 70, 107701. [Google Scholar] [CrossRef]
- Huang, Z.; Yang, Y. Vibration Response Characteristics of Prefabricated Frame Structures Around the Subway. Appl. Sci. 2025, 15, 6419. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, C.; Diao, H.; Ning, Y. Structural Behavior of Prefabricated Ecological Grid Retaining Walls and Application in a Highway in China. Symmetry 2021, 13, 746. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, C. Examining Pipe-Borehole Wall Contact and Pullback Loads for Horizontal Directional Drilling. Appl. Sci. 2024, 14, 8841. [Google Scholar] [CrossRef]
- Borekci, M. Influence of Friction Models on the Seismic Response of Box-Girder RC Bridges with Double Concave Friction Pendulum Bearings under Varying Deck Aspect and Mass Ratios. Buildings 2025, 15, 556. [Google Scholar] [CrossRef]
- Fan, X.; Wang, T. Formulation and Implementation of a Hypoplastic Constitutive Model for Interface Behavior of Mechanical Joints. Mech. Syst. Signal Process. 2023, 204, 110735. [Google Scholar] [CrossRef]
- Wang, G.; Wang, Y.; Lu, W.; Yu, M.; Wang, C. Deterministic 3D Seismic Damage Analysis of Guandi Concrete Gravity Dam: A Case Study. Eng. Struct. 2017, 148, 263–276. [Google Scholar] [CrossRef]
- Zhang, A.; Ma, L.; Liu, X.; Jiang, Z. Finite Element Analysis on Mechanical Performance of Steel Frame Structure with Prefabricated External Wall Panel. J. Build. Struct. 2016, 37, 152–157. [Google Scholar] [CrossRef]
- Li, W.; Jing, Y.; Xing, G.; Ma, Z. A Lode-Dependent Plasticity Model for High-Strength Structural Steel. J. Constr. Steel Res. 2023, 211, 108202. [Google Scholar] [CrossRef]
- Mohsenali, S.; Pouria, Z.; Parsa Jelokhani, N.; Eskandari, A. Force-Displacement Relation for Lumped Plasticity Model of Compact Square Concrete-Filled Steel Tube Columns. Results Eng. 2024, 23, 102619. [Google Scholar]
- Moallemi, M.; Kim, S.; Abbas, Z.; Farabi, E. Strain Hardening Analysis and Deformation Micromechanisms in High Strength-High Ductility Metastable Duplex Stainless Steels: Role of Sustained Stacking Faults in the Work Hardening. Mater. Charact. 2023, 197, 112662. [Google Scholar] [CrossRef]
- Syroka-Korol, E.; Tejchman, J.; Mróz, Z. FE Analysis of Size Effects in Reinforced Concrete Beams without Shear Reinforcement Based on Stochastic Elasto-Plasticity with Non-Local Softening. Finite Elem. Anal. Des. 2014, 88, 25–41. [Google Scholar] [CrossRef]
- Li, S.; Ding, W.; Zhang, Q. Development of a New Temperature-Dependent Yield Criterion for Stainless and High-Strength Alloy Steels in Construction Engineering. Case Stud. Constr. Mater. 2023, 18, e02149. [Google Scholar] [CrossRef]
- Koksal, H.; Doran, B.; Kuruscu, A.; Kocak, A. Elastoplastic Finite Element Analysis of Masonry Shear Walls. KSCE J. Civ. Eng. 2015, 20, 784–791. [Google Scholar] [CrossRef]
- Keawsawasvong, S.; Ukritchon, B. Finite Element Analysis of Undrained Stability of Cantilever Flood Walls. Int. J. Geotech. Eng. 2016, 11, 355–367. [Google Scholar] [CrossRef]
- Li, Z.; Wu, Z.; Chen, J.; Li, Y.; Huang, H.; Lu, Y.; Lu, X.; Li, J. Inverse Analysis of Deformation Moduli for High Arch Dams Using the Displacement Reconstruction Technique and Multi-Objective Optimization. Comput. Aided Civ. Infrastruct. Eng. 2023, 39, 1507–1529. [Google Scholar] [CrossRef]
- Xue, J.; Zhang, P.; Li, J.; Lu, X.; Li, Z.; Li, Y.; Chen, J.; Kuang, C. A deep learning methodology for rapid identification of slab damage in concrete face rockfill dams. Comput. Aided Civ. Infrastruct. Eng. 2025, online. [Google Scholar] [CrossRef]
- Lu, Z.; Fan, Q.; Tian, W.; Li, J. Seismic Performance Analysis of Steel Frame Installed with Prefabricated External Walls and New Connection Type. J. Build. Eng. 2024, 84, 108471. [Google Scholar] [CrossRef]
- Liu, J.; Bao, Y.; Qin, K. Experimental and Finite Element Analysis on the Structural Performance of Lightweight Hollow Slab Prefabricated Staircases. Buildings 2025, 15, 245. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, G.; Liu, G.; Xin, H.; Cai, J.; Satyanaga, A.; Zhang, R.; Dai, G. Seismic Behavior of Cluster-Connected Prefabricated Shear Walls under Different Axial Compression Ratios. Buildings 2024, 14, 2768. [Google Scholar] [CrossRef]
- Greco, V. Active thrust on retaining walls of narrow backfill width. Comput. Geotech. 2013, 50, 66–78. [Google Scholar] [CrossRef]
- Shi, H.; Gong, J.; Zhang, Y. Earth pressure of layered soil on retaining structures. Soil Dyn. Earthq. Eng. 2016, 83, 33–52. [Google Scholar] [CrossRef]


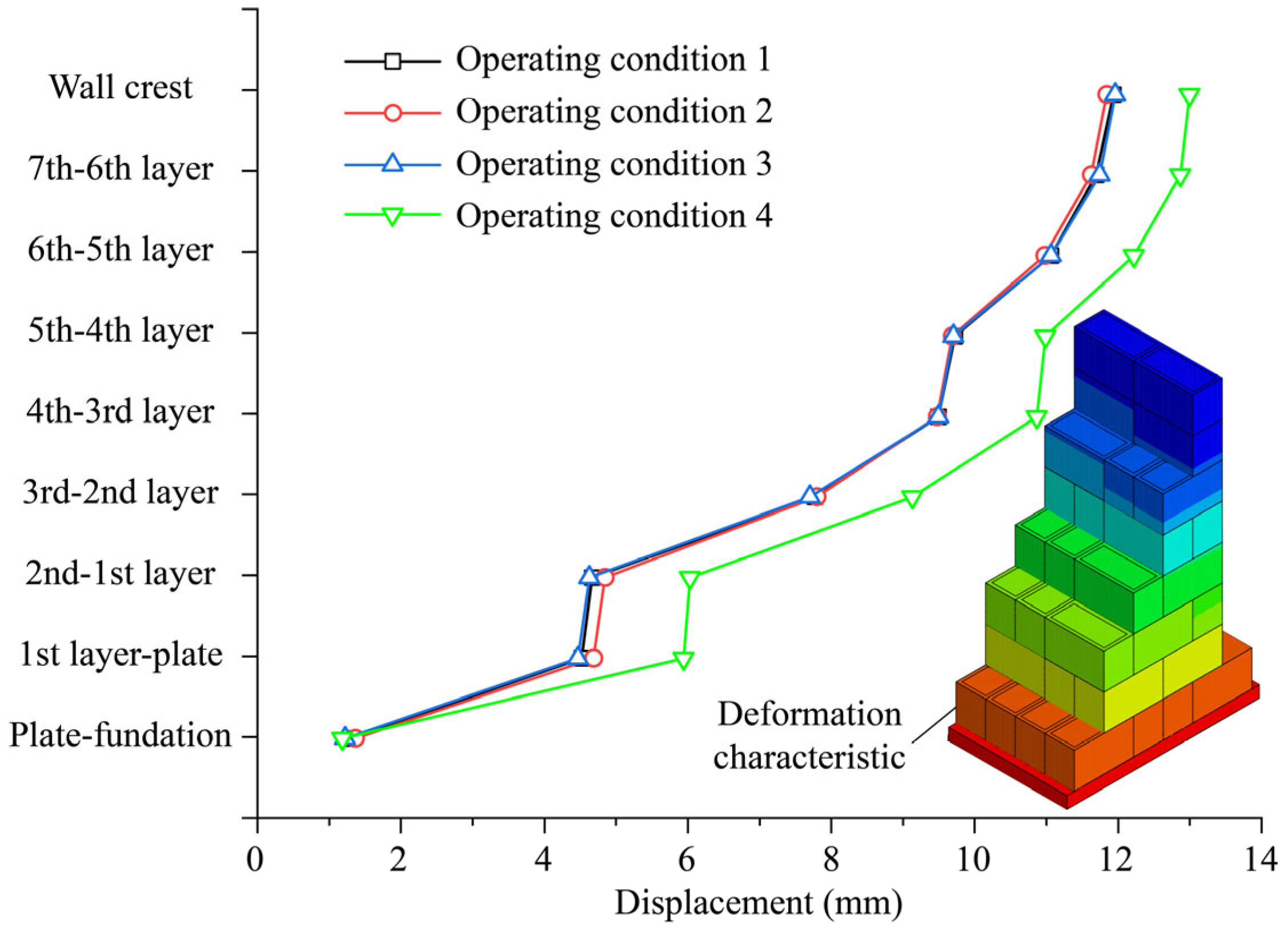
| Condition | Scenario | Water Level (Front)/m | Water Level (Behind)/m | Backfill Elevation (Front)/m | Backfill Elevation (Behind)/m |
|---|---|---|---|---|---|
| 1 | High water level | 346.44 | 346.94 | 338.00 | 350.00 |
| 2 | Low water level | 340.5 | 342.5 | 338.00 | 350.00 |
| 3 | Final Constructed | / | / | 338.00 | 350.00 |
| 4 | Check water level | 353.99 | 353.99 | 338.00 | 350.00 |
| Number | Material or Contact Surface | Parameter | Value |
|---|---|---|---|
| 1 | Concrete unit | Elastic modulus (GPa) | 30 |
| Density (kg/m3) | 2380 | ||
| Poisson’s ratio | 0.167 | ||
| Tensile strength (MPa) | 2.2 | ||
| Compressive strength (MPa) | 23.4 | ||
| 2 | Concrete base plate | Elastic modulus (GPa) | 28 |
| Density (kg/m3) | 2380 | ||
| Poisson’s ratio | 0.167 | ||
| Tensile strength (MPa) | 1.78 | ||
| Compressive strength (MPa) | 16.7 | ||
| 3 | Bolts and rebars | Elastic modulus (GPa) | 210 |
| Density (kg/m3) | 7850 | ||
| Poisson’s ratio | 0.258 | ||
| Yield strength (MPa) | 320 (Bolts)/300 (Rebars) | ||
| 4 | Rockfill | Density (kg/m3) | 7850 |
| Friction angle (°) | 2000 | ||
| 5 | Unit–unit | Friction coefficient | 0.6 |
| 6 | Unit–plate | Friction coefficient | 0.6 |
| 7 | Plate–foundation | Friction coefficient | 0.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.; Li, Y.; Lu, X.; Wu, Z. Prefabricated Reinforced Guide Walls for Mountainous River Locks: Numerical Analysis and Performance Evaluation. Appl. Sci. 2025, 15, 12083. https://doi.org/10.3390/app152212083
Wu L, Li Y, Lu X, Wu Z. Prefabricated Reinforced Guide Walls for Mountainous River Locks: Numerical Analysis and Performance Evaluation. Applied Sciences. 2025; 15(22):12083. https://doi.org/10.3390/app152212083
Chicago/Turabian StyleWu, Liguo, Yonglong Li, Xiang Lu, and Zhenyu Wu. 2025. "Prefabricated Reinforced Guide Walls for Mountainous River Locks: Numerical Analysis and Performance Evaluation" Applied Sciences 15, no. 22: 12083. https://doi.org/10.3390/app152212083
APA StyleWu, L., Li, Y., Lu, X., & Wu, Z. (2025). Prefabricated Reinforced Guide Walls for Mountainous River Locks: Numerical Analysis and Performance Evaluation. Applied Sciences, 15(22), 12083. https://doi.org/10.3390/app152212083







