Corrosion and Fracture Localization in Grounding Grids and State Evaluation Based on Analysis of the Evolution of Magnetic Field Distributions

Abstract

The grounding grid of a substation is a crucial component for ensuring normal operation. However, since it is buried underground for long periods, it is highly susceptible to electrochemical corrosion. This corrosion leads to a reduction in its grounding performance, and severe corrosion may endanger the reliable operation of high-voltage equipment and secondary relay-protection equipment, as well as the safety of personnel. In this paper, the electromagnetic field analysis method is used to conduct simulation modeling of the grounding grid. A different-frequency current is injected into the grounding grid to study the variation law of the surface magnetic field distribution when corrosion occurs to different degrees at different positions in the grounding grid. Through the analysis of the evolutionary characteristics of the magnetic field distribution, the corrosion-induced breakages in the grounding grid are located and a comprehensive state evaluation is carried out. The results show that when a fault occurs in a conductor at the same position, the variation amplitude of the surface magnetic field gradually increases with increased corrosion. Based on this finding, an online monitoring algorithm for the location of corrosion-induced breakages and state evaluation of the grounding grid is proposed. A comprehensive evaluation model is constructed by combining the grounding resistance value and corrosion characteristic value to accurately locate the fault.

1. Introduction

As traction substations serve as energy-conversion hubs in the power system, their operating status directly determines the stability and safety of the entire power supply [1]. The grounding system, as a core component of substation facilities, has the dual functions of equipment grounding and safety protection. Through a network of metal conductors, it establishes a reliable equipotential connection between the on-site facilities and the earth. This not only safeguards the stable operation of the power system but also effectively reduces the risk of electric shock to humans and thus serves as a crucial foundation for the safe and efficient operation of substation facilities [2,3,4].

In recent years, substation burnout accidents have occurred frequently. Investigations have found that abnormal grounding grids are the root cause of such accidents [5,6,7].

The root cause of the vast majority of grounding-grid failures is the corrosion of grounding grids. Since the grounding-grid conductors are buried underground for long periods, their diameter gradually decreases under the continuous influence of factors such as the humid soil environment and corrosive substances in saline–alkali soil. According to research conducted in China and internationally, the annual corrosion rate of some soils can reach 2.1 mm/year, and in more severe cases, the annual corrosion rate can reach 7.99 mm/year [8]. When a branch of the grounding grid is corroded, the resistance of that branch increases significantly, which in turn leads to a rise in the grounding resistance of the entire grounding grid, resulting in reduced grounding performance and weakened current-discharge capacity [9]. Changes in ground resistance not only affect the potential distribution of the existing power grid but also alter the distribution of the surface magnetic field, potentially leading to accidents or injuries [10]. Under such circumstances, the flow of current is likely to cause a localized potential rise that not only damages electrical equipment but also poses a serious threat to the safety of staff [11,12,13].

Since grounding grids are deeply buried underground, information on their status is difficult to obtain directly. Currently, indirect evaluation mainly relies on electrical and magnetic signals. Common characteristic signals include grounding-grid resistance, variation in earth potential, maximum touch voltage, and maximum step voltage [14,15,16]. Previously, the potential-drop method was used to assess the condition of grounding grids. However, this method requires circuit disconnection, making it unsuitable for monitoring live substations [17]. Subsequently, researchers began evaluating grounding-grid status based on ground resistance values. While this approach is simple and direct, it is not well suited to localized detection of corrosion within the grounding grid [18]. Researchers in [19] evaluated the condition of grounding grids by measuring transient magnetic fields at the ground surface, achieving good results. However, this study measured only the magnetic field distribution across the entire observation surface, and the conclusions are largely qualitative and thus cannot provide further explanations based on actual data. The authors in reference [20] investigated the grounding methods for overhead lines or transformer neutral points, as well as the fluctuations in grounding-grid potential under multiple current-injection conditions during ground faults. This method exhibits an ideal response to external faults, mainly due to the interconnection properties of grounding conductors. Nevertheless, it is difficult to determine the specific fault location when a ground fault or breakage occurs in internal conductors. Therefore, some scholars have analyzed the potential changes that occur when grounding impedance decreases using the finite element method, verifying the feasibility of replacing the actual conductor radius with an equivalent radius [21]. However, this method still has certain limitations: relying solely on potential variation makes it impossible to accurately locate the specific position of a grounding-conductor fault. Some researchers have identified integrity failures in the grounding grid by establishing grounding-grid models and calculating contact resistance and voltage [22,23]. However, treating the entire grid as a single flat plate makes it difficult to identify local faults.

The electromagnetic field analysis method can relatively intuitively detect corrosion faults in grounding grids. Its principle mechanism involves injecting current into a conductor that connects the grounding grid to the ground, which induces an electromagnetic field on the ground surface above the grounding grid. Then, the surface electromagnetic field signals are collected and the relationship between the distribution of the surface electromagnetic field and the corrosion or breakage faults in the grounding grid is thus analyzed. This method does not require consideration of the structural design of the grounding grid, but it has obvious limitations: it involves the need to arrange a large number of monitoring points for the electromagnetic field, is vulnerable to interference from the internal electromagnetic environment of the substation, and has high requirements for the accuracy of the equipment used to monitor the electromagnetic field. F.P. Dawalibi, was the first to discover the characteristics of the electromagnetic field of grounding grids; they later developed CDEGS software (https://www.sestech.com/en/Product/Package/CDEGS (Accessed on 6 November 2025)) [24,25]. This software is currently recognized worldwide for grounding-grid electromagnetic field simulation. To reduce the impact caused by power-frequency current, some scholars have changed the injected current to a different-frequency current [26,27]. In addition to the steady-state research on the electromagnetic field of grounding grids, some scholars have studied the transient characteristics of grounding grids using antenna theory [28]. Scholars at home and abroad have used the transient characteristics of the grounding-grid electromagnetic field to study fault-state diagnosis methods and conducted effective analyses using relevant simulation software [29,30]. Therefore, some scholars have investigated the characteristics of variation in grounding resistance in grounding grids under the influence of impulse currents, as well as the patterns of current variation during fault occurrence, in order to further pinpoint specific fault locations [31].

This paper combines the finite-element electromagnetic analysis method with CDEGS simulation software and, in addition to the conventional overall observation plane, simultaneously observes the electromagnetic changes along conductor lines and at discrete observation points. By classifying the conductors, the paper examines the variation patterns of three types of electromagnetic field observation results under different fault severities. It then derives a method that can effectively analyze fault locations for grounding conductors and proposes an optimized distribution scheme for the observation points of the grounding grid based on these results.

Research findings indicate that under normal conditions, the surface magnetic field exhibits a symmetrical distribution. When a conductor experiences corrosion failure, the magnitude of the surface magnetic field at each monitoring point on the grounding grid changes. The monitoring point with the highest rate of change will be that located nearest to the corroded conductor. Under mild corrosion, the maximum rate of change reaches 30%. As corrosion severity increases, this rate further escalates to a maximum of 275%. By selecting a reference conductor and utilizing the characteristics of the variation in the magnetic field of parallel and perpendicular conductor branches, the location of the corrosion can be pinpointed. Furthermore, this paper analyzes patterns of variation in the magnetic field to eliminate monitoring points with negligible impact, thereby reducing costs. Finally, it proposes an evaluation method using Manhattan distance to assess the corrosion status of grounding grids. Compared to traditional methods such as the potential-drop method and impedance measurement, this approach achieves higher measurement accuracy without affecting the existing grounding grid during the installation of monitoring points. It can also be used in conjunction with conventional methods. Leveraging the characteristics of the transient magnetic fields generated under pulsed current allows localized corrosion to be precisely located. Furthermore, costs associated with distributed monitoring are reduced through conductor classification and the elimination of monitoring points, with minimal impact on results.

2. Design of a Grounding-Grid Simulation Model

2.1. Establishment of a Grounding-Unit Model

As an effective method for numerical calculation, the finite element method (FEM) can conveniently take into account the influences of various factors such as soil structure, soil resistivity, grounding-grid burial depth, and current-injection point when analyzing the grounding performance of grounding grids.

To avoid interference from power-frequency magnetic fields, this paper injects a sinusoidal current of a different frequency through the down-conductor of the grounding grid. A detection coil measures the magnetic induction intensity on the ground surface induced by the excitation current. The corrosion state of the grounding-grid mesh conductors is diagnosed based on the spatial distribution of the magnetic-induction intensity, enabling monitoring of both corrosion and breakage faults in the grounding grid. Based on the principle of electromagnetic induction, when the frequency of the excitation current is low, the problem of the substation grounding grid can be described by the Laplace equation, as shown in Equation (1):

$$\nabla ·(\sigma \nabla \phi )=0$$

(1)

Its boundary conditions are described by Equations (2) and (3):

$${\displaystyle \frac{\partial \phi }{\partial n}}=0$$

(2)

$$\phi =0$$

(3)

where φ is the scalar potential and σ is the soil conductivity.

The soil region is discretized using a three-dimensional eight-node hexahedral cell, and finite element Equations (4) and (5) can be obtained by using the weighted residual method, as follows:

$${\displaystyle \sum _e{\displaystyle {\iiint }_{{\mathrm{\Omega }}_e}{\sigma }_s^e}}(\nabla N_i^e)·(\nabla {\varphi }_s^e)d\mathrm{\Omega }=0$$

(4)

$${\varphi }_s^e={\displaystyle \sum _{j=1}^8{N}_j^e}{\varphi }_j^e$$

(5)

where Ω_e is the soil cell and ${\sigma }_e^s$, $N_i^e$, ${\phi }_s^e$, and ${\phi }_j^e$, are the conductivity, interpolation function, scalar potential function, and nodal scalar potential of the soil cell, respectively.

The grounding-grid conductor is discretized using a one-dimensional two-node unit, which yields the finite element equations given in Equations (6) and (7):

$${\displaystyle \sum _e{S}_e}{\displaystyle {\int }_{l_e}{\sigma }_c^e}(\nabla N_i^e)·(\nabla {\varphi }_c^e)dl=0$$

(6)

$${\varphi }_c^e={\displaystyle \sum _{j=1}^2{N}_j^e}{\varphi }_j^e$$

(7)

where l_e, S_e, and ${\sigma }_c^e$ are the length, cross-sectional area, and conductivity of the conductor unit of the grounding network; $N_i^e$, ${\phi }_c^e$, and ${\phi }_j^e$ are the interpolation function of the conductor unit, the scalar potential function, and the nodal scalar potential.

The soil and conductor fields are discretized; the corresponding unit stiffness array is derived, and the total stiffness matrix is obtained by synthesizing the unit stiffness array of each unit as a whole. In order to ensure high accuracy in the calculation, the zero-potential boundary is applied in an area seven times the size of the grounding grid. The soil and the grounding grid are discretized uniformly to ensure that one prong of the grounding-grid conductor unit and the soil unit are completely coincident and that the nodes and their numbers are the same. As shown in Figure 1, the one-dimensional unit of the grounding-grid conductor exactly coincides with one prong of the three-dimensional hexahedral unit of the soil, and the two units share two nodes, i.e., node 1 and node 2.

For this eight-node rectangular cell, the cell stiffness array is given by Equation (8):

$$K_e={\displaystyle \frac{{\sigma }_s^e{h}_y^e{h}_z^e}{36h_x^e}}{K}_{ex}+{\displaystyle \frac{{\sigma }_s^e{h}_x^e{h}_z^e}{36h_y^e}}{K}_{ey}+{\displaystyle \frac{{\sigma }_s^e{h}_x^e{h}_y^e}{36h_z^e}}{K}_{ez}$$

(8)

where ${\sigma }_c^e$ denotes the conductivity of the soil cell and $h_x^e$, $h_y^e$, and $h_z^e$ denote the edge lengths of the soil cell in each direction. The unit stiffness in each direction is converted to a uniform form of the unit-stiffness array as in Equation (9):

$$K_e={\displaystyle \frac{1}{Z^e{l}_e}}\left[\begin{array}{cc}1& -1\\ -1& 1\end{array}\right]$$

(9)

where Z^e is the unit-length impedance of the grounding network conductor.

In order to study the effect of frequency on the grounding performance of a substation grounding network, we ignore the frequency-variable characteristics of the soil unit and consider only the frequency-variable characteristics of the conductor unit. For the circular cross-section radius of the grounding network conductor, unit-length impedance can be calculated via Equations (10)–(14):

$$Z^e=Z_i^e+Z_o^e$$

(10)

$$Z_i^e={\displaystyle \frac{m_c}{2\pi r{\sigma }_c}}\coth (0.777m_{c}r)+{\displaystyle \frac{0.356}{\pi r^2{\sigma }_c}}$$

(11)

$$m_c=\sqrt{j2\pi f\mu {\sigma }_c}$$

(12)

$$Z_o^e=jf{\mu }_0[K_0(m_{s}r)+{\displaystyle \frac{2e^{-2h{m}_s}}{4+{(m_{s}r)}^2}}]$$

(13)

$$m_s=\sqrt{j2\pi f{\mu }_0{\sigma }_s}$$

(14)

where $Z_i^e$ and $Z_o^e$ are the unit-length internal external impedances of the conductor; σ_c and μ are the conductor’s electrical and magnetic permeabilities, respectively; σ_s is the soil conductivity; h is the burial depth of the conductor; and K₀ is the second type of zero-order Bessel function.

2.2. Grounding-Grid Model

Most of the substation grounding nets are welded from metal conductors in a mesh. In the establishment of the grounding network model, we consider only the horizontal grounding conductor, ignoring the vertical grounding conductor. In order to facilitate the study and enhance the generalizability of the results, this paper considers a 40 × 40 mesh grounding network with the following parameters: the network contains 4 × 4 mesh holes, and each conductor is 40 m long and is divided into four 10 m long sections. The specific structure of the grounding network is shown in Figure 2.

In this paper, the distribution of the surface magnetic field is monitored by placing nine observation points on each line, with a distance between neighboring points of 5 m; a total of 65 observation points are set on the surface, and the numbering of the points is as shown in Figure 3.

Most actual grounding network use flat steel as the conductor material. For the rectangular 40 × 40 mesh considered here, the equivalent conductor radius is 14.006 mm; the conductor material is uniformly flat steel; the burial depth of the grounding network is of 0.6 m; and the soil is assumed to be uniform, with a resistivity of 100 Ω·m.

As the frequency of the current injection increases, the capacitance value of the ground becomes non-negligible, which causes difficulties in measuring the surface magnetic field signal. The effect is such that the surface magnetic field distribution gradually becomes uniform and the amplitude of the surface magnetic field decreases. Specifically, we simulated the magnetic field values measurable from the injected current at different frequencies, with the results shown in Figure 4.

As shown in the figure, the strength of the surface magnetic field reaches maxima at 50 Hz and 70 Hz, facilitating signal acquisition. To prevent interference from the 50 Hz current during normal operation, we therefore employ a 70 Hz frequency as the injection-current source. Furthermore, simulation tests were conducted to analyze the magnetic field distribution at different current levels under 70 Hz conditions. The simulation results are shown in Figure 5.

As shown in the figure, the strength of the surface magnetic field decreases as the injected current increases. Therefore, in order to collect a stronger magnetic field signal and at the same time to avoid interference from the industrial frequency, this paper uses a 10 A current of 70 Hz as the injection current.

2.3. Grounding-Grid Corrosion and Breakage Model

Assume the grounding-grid resistance model shown in Figure 2 consists of N nodes, K branches, and N accessible nodes. A voltage source is connected between two accessible nodes i and j, and a new branch numbered K + 1 is added. Then, the relationship given below, in Equation (15), can be derived:

$$\left\{\begin{array}{l}{G}_N=AG{A}^T\\ U_N=-G^{-1}AG{U}_S\\ U=A^T{U}_N\\ I=G{A}^T{U}_N\end{array}\right.$$

(15)

In the equation, G_N represents the node admittance matrix, A denotes the equivalent grounded network association matrix, G signifies the branch admittance matrix, U_N indicates the node voltage matrix, and I represents the branch current matrix.

From Equation (15), the resistance between nodes can be calculated as in Equation (16), where K is the total number of branches; R₁, R₂, …, R_k are the circuit values of the respective grounded branches; and U_k+1 and I_k+1 are elements in U and I, respectively, corresponding to the voltage and current of the K + 1th branch.

$$R_{ij}=U_{k-1}/I_{k+1}=f(R_1,R_2,\dots ,R_k)$$

(16)

A series of nonlinear equations can be obtained based on different accessible nodes, as shown in Equation (17):

$$\left\{\begin{array}{l}{R}_{i,j1}=f_1(R_1,R_2,\dots ,R_k)\hfill \\ R_{i,j2}=f_2(R_1,R_2,\dots ,R_k)\hfill \\ ⋮\hfill \\ R_{i,jg}=f_g(R_1,R_2,\dots ,R_k)\hfill \end{array}\right.$$

(17)

The optimal solution subject to constraints is given by Equation (18):

$$\left\{\begin{array}{l}\mathrm{Min}\hspace{0.33em}f(\mathrm{\Delta }{R}_i^{(n)},\hspace{0.33em}\mathrm{\Delta }{R}_2^{(n)},\dots ,\mathrm{\Delta }{R}_k^{(n)})={\displaystyle \sum _{i=1}^M{(\mathrm{\Delta }{R}_{i,w}^{(n)}-\mathrm{\Delta }{R}_{i,c})}^2}\hfill \\ 0\le \mathrm{\Delta }{R}_b^{(n)}\le \mathrm{\Delta }{R}_b^{(n-1)}+R_b^{(0)}\hspace{1em}(b=1,2,3,\dots ,K)\hfill \end{array}\right.$$

(18)

where $\mathrm{\Delta }{R}_k^{(n)}$ is the increment in ground conductor resistance and $\mathrm{\Delta }{R}_{i,w}^{(n)}$ is the increment in port resistance. Then, the expansion factor Pn for the nth conductor branch is defined as in Equation (19):

$$P_n={\displaystyle \frac{R_a}{R_b}}$$

(19)

In the equation, Ra denotes the resistance matrix after the ground fault and Rb denotes the resistance matrix before the ground fault. When P_n ≤ 2, the corrosion is mild; when 2 < P_n ≤ 10, the corrosion is moderate. In CDEGS, it is not possible to set the branch resistance directly, but it is possible to change the resistance value of the branch indirectly by changing the radius of the branch. For the 40 × 40 m grounding network, the conductor has an equivalent radius of 14.006 mm. In fault simulation, this value is reduced to 9.9037 mm for mild corrosion or to 4.4291–9.9037 mm for moderate corrosion and is truncated entirely to simulate conductor fracture. Figure 6 illustrates the distribution of faulty conductors in the grounding network.

3. Grounding-Grid Corrosion and Breakage Localization

3.1. Algorithm Research

The conversion of the 2-9-4-11 branches in the grounding-grid model shown in Figure 6 to a circuit model is shown in Figure 7.

In the figure, C_g2, C_g4, C_g9, and C_g11 denote the capacitance to ground of each branch, and C_9-11 and C_2-4 denote the phase-to-phase capacitance of the two branches. Therefore, the injected current can be expressed as in Equation (20):

$$I_{Input}=I_{output}+I_g$$

(20)

I_input denotes the current injected along the reference conductor, while I_output denotes the current flowing out along the reference conductor. I_g denotes the total leakage current to ground.

The impedance matrix of a unit can be established as in Equation (21):

$$Z_{2-4-9-11}=\left[\begin{array}{cccc}{Z}_2& {\displaystyle \frac{1}{j2\omega C_{2-4}}}& & \\ {\displaystyle \frac{1}{j2\omega C_{2-4}}}& Z_4& & \\ & & Z_9& {\displaystyle \frac{1}{j2\omega C_{9-11}}}\\ & & {\displaystyle \frac{1}{j2\omega C_{9-11}}}& Z_{11}\end{array}\right]$$

(21)

After the impedance matrix has been extended to the entire grounding network, its impedance matrix is expressed in terms of Z_b. The final transformation into the node impedance matrix Z establishes the Equations (22) and (23):

$$J_n{Z}_n=V_n$$

(22)

$$V_n=\left[V_y|V_x\right]$$

(23)

where J_n is the node current injection and V_n is the voltage at that node. This represents the portion of the circuit that is used for the injected current. V_x and V_y denote the node voltages in the x and y directions, respectively.

Thus, the electromagnetic field for a particular branch can be expressed in Equation (24):

$$B={\displaystyle \frac{{\mu }_0}{4\pi }}{\displaystyle \iiint \frac{(\mathrm{\Delta }{V}_x/Z_x)}{r^3}}dv+{\displaystyle \frac{{\mu }_0}{4\pi }}{\displaystyle \iiint \frac{(V_x\omega C_x)}{r^3}}dv$$

(24)

In the above equation, the first term represents the magnetic field generated by the injected current and the second term represents the magnetic field generated by the earth current in the soil. It can be seen that, with the injected current remaining constant, corrosion and breakage reduce the equivalent radius of the material, which in turn increases the resistance value, thereby reducing the magnetic field generated in this branch. However, the magnetic field generated by the leakage current is not affected by changes in resistance and remains unchanged. When a breakage fault occurs in a branch, since the resistance approaches infinity, the only magnetic field generated by this branch at this time is the soil electromagnetic field.

The electromagnetic field on one branch is affected not only by its own electromagnetic field but also by all surrounding branches. Based on the distance between conductors, we classify each branch into one of two categories according to the intensity of the electromagnetic field acting on the conductor:

a. Parallel branches, i.e., branches parallel to the location of the branch, are assumed to be m in total. The total electromagnetic field can be expressed as in Equation (25):

$$B={\displaystyle \frac{{\mu }_0}{4\pi }}{\displaystyle \iiint \frac{(\mathrm{\Delta }{V}_x/Z_x+V_x\omega C_x)}{{r_0}^3}}dv+{\displaystyle \frac{{\mu }_0}{4\pi }}{\displaystyle \iiint {\displaystyle \sum \frac{(\mathrm{\Delta }{V}_{xm}/Z_{xm}+V_{xm}\omega C_{xm})}{{r_m}^3}}}dv$$

(25)

b. Vertical branches, i.e., branches perpendicular to the location of this branch, are assuming to number n, and the total EMF can be expressed as in Equation (26):

$$B=\sqrt{{\left({\displaystyle \frac{{\mu }_0}{4\pi }}{\displaystyle \iiint \frac{(\mathrm{\Delta }{V}_x/Z_x+V_x\omega C_x)}{{r_0}^3}}dv\right)}^2+{\left({\displaystyle \frac{{\mu }_0}{4\pi }}{\displaystyle \iiint {\displaystyle \sum \frac{(\mathrm{\Delta }{V}_{xn}/Z_{xn}+V_{xn}\omega C_{xn})}{{r_n}^3}}}dv\right)}^2}$$

(26)

Combining the two cases above, the total magnetic field is expressed in Equation (27);

$$B=\sqrt{\begin{array}{l}{\left({\displaystyle \frac{{\mu }_0}{4\pi }}{\displaystyle \iiint \frac{(\mathrm{\Delta }{V}_x/Z_x+V_x\omega C_x)}{{r_0}^3}}dv+{\displaystyle \sum \frac{(\mathrm{\Delta }{V}_{xm}/Z_{xm}+V_{xm}\omega C_{xm})}{{r_m}^3}}\right)}^2\\ +{\left({\displaystyle \frac{{\mu }_0}{4\pi }}{\displaystyle \iiint {\displaystyle \sum \frac{(\mathrm{\Delta }{V}_{xn}/Z_{xn}+V_{xn}\omega C_{xn})}{{r_n}^3}}}dv\right)}^2\end{array}}$$

(27)

Assuming a neighboring branch distance of 10 m, a parallel conductor at a distance of 20 m contributes only one-eighth the effect of the neighboring conductor; the influence of conductors at greater distances is even weaker, so the influence of conductors outside the 20 m radius can be ignored. Similarly, for vertical branches, only up to four connected branches are considered. This reduces the total number of branches of both types, simplifying the calculation.

3.2. Simulation Analysis

The surface magnetic field distribution of the grounding network under no-fault conditions is simulated, and the observation results are shown in Figure 8; from the figure, it can be seen that the branch magnetic field along the x-axis is significantly stronger than the branch magnetic field along the y-axis. The strength of the magnetic field is much greater along the x-axis where current is injected than it is on the other x-axis, and the overall distribution of the magnetic field shows symmetry.

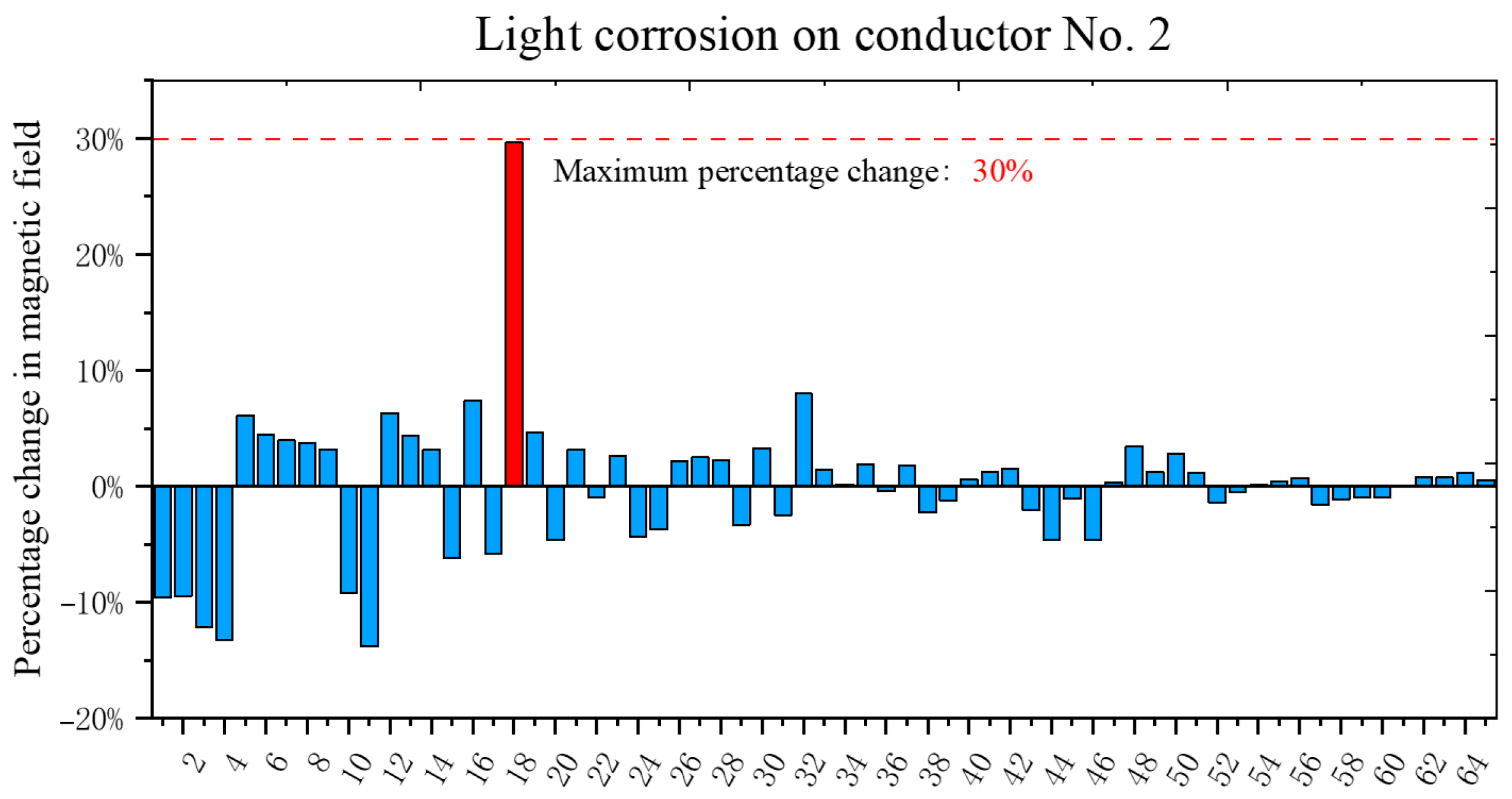
The percent change in magnetic-field strength at each point when mild corrosion occurs in Conductor No. 2 is shown in Figure 9. Blue indicates the magnitude of magnetic field variation at each point, while red indicates the point with the greatest magnetic field variation.

Here, points 1, 3, 4, 11 and 18 have a variation of more than 10%, while Point 18 shows the largest variation, at 30%.

The percent change in magnetic field at each point when moderate corrosion occurs in Conductor No. 2 is shown in Figure 10. Blue indicates the magnitude of magnetic field variation at each point, while red indicates the point with the greatest magnetic field variation.

It can be observed that here, points 3, 4, 11, 18, and 32 change by more than 40%, with Point 18 showing the largest change, at 108%.

When Conductor No. 2 undergoes a corrosion fracture, the magnitude of the change in magnetic field at each point is shown in Figure 11. Blue indicates the magnitude of magnetic field variation at each point, while red indicates the point with the greatest magnetic field variation.

Here, Points 1, 2, 3, 4, 5, 10, 11, 12, 15, 16, 18, 30, 32, and 34 change by more than 50%; Point 18 shows the largest change, at 275%.

The comprehensive simulation results above represent the effects of light corrosion, moderate corrosion, and corrosion fracture in the conductor; the effects on the grounding-network surface magnetic field distribution are shown to be basically similar, but the more serious the corrosion of the conductor, the greater the degree of change in the surface magnetic field. This correlation indicates that the degree of corrosion significantly affects both the magnitude of the surface magnetic field size and its distribution.

3.3. Impact of Damage to Parallel Branches

This section analyzes the situations in which a corrosion fracture occurs in Conductors No. 4, 5, or 6, which are parallel branches of Conductor No. 2.

The magnitude of the change in magnetic field that occurs at each point when light corrosion occurs in Conductor No. 4 is shown in Figure 12. Blue indicates the magnitude of magnetic field variation at each point, while red indicates the point with the greatest magnetic field variation.

Here, only point 18 changes more by than 10%, to −13%.

The magnitude of change in the magnetic field at each point when light corrosion occurs in Conductor No. 5 is shown in Figure 13.

Here, there is no point where the magnetic field changes, indicating that light corrosion in Conductor 5 has no effect on the distribution of the surface magnetic field. Since Conductor 5 is located in the center of the grounding network, its impedance structure resembles a bridge, so the amplitude of the current flowing through the conductor is minimally affected by small unbalanced impedances and its thus basically unaffected by corrosion.

For further verification, we also measured Conductor No. 6. The magnitude of the change in magnetic field at each point that results when light corrosion occurs in Conductor No. 6 is shown in Figure 14.

It can be observed that here, there are no points at which the magnetic field changes, indicating that light corrosion in Conductor 6 also has no effect on the surface magnetic field distribution.

Conductors No. 2, 4, 6 are the closest to the center of the injected current. Under conditions of light corrosion, changes in the magnetic field along the observation line are small and amplitude variations are relatively small and symmetrical.

Based on statistics describing the magnetic field at its various points, it can be seen that when corrosion occurs in Conductor No. 2, the magnetic field at monitoring points 1 to 5 decreases and the magnetic field at points 6 to 9 increases, with monitoring point 18 showing the greatest magnitude of change. The degree of change in the magnetic field decreases with distance from the fault point. A comparison of the diagrams showing the changes in magnetic field for No. 2 and No. 4 is shown in Figure 15. Red indicates that when conductor No. 2 experiences light corrosion, the magnetic field variation at this point reaches its maximum value; Pink indicates that when conductor No. 4 experiences light corrosion, the magnetic field variation at this point reaches its maximum value.

As can be seen from the figure, the change in magnetic field at each point occurs by column. When Conductor No. 2 undergoes light corrosion, in the first column of monitoring points, Points 1 to 4, the strength of the magnetic field decreases; in the second column of monitoring points, points 5 to 9, the strength of the magnetic field increases; at points 11 and 12, the strength of the magnetic field decreases; at points 13 to 15, the strength of the magnetic field increases. In the third column of monitoring points, the maximum change in the strength of the magnetic field occurs at point 18. The first two columns show opposite-direction changes in the strength of the magnetic field when Conductor No. 4 and Conductor No. 2 undergo light corrosion. The third column of monitoring points also shows maximum values. In the fourth and fifth columns, the strength of the magnetic field changes in the same direction.

Therefore, we conclude that a grounding network is divided into left and right zones, where the corrosion of the conductor in one zone will not affect the other zone. If corrosion occurs in a conductor in the same zone, the grounding network can be again divided into upper and lower parts. In this case, changes in the strength of the magnetic field in the first and third columns will occur along the center line, while in the second column, the changes in the strength of the magnetic field occur in the vicinity of the corroded conductor. By combining the points with maximum change in the amplitude of the magnetic field, you can obtain a cross-shaped pattern of branches corresponding to the location of the corroded conductor.

For further verification, we take Conductors No. 1 and No. 3 as a comparison, and the results are shown in Figure 16. Based on those results, the change characteristics are the same as in the first two columns in the left zone. Since Conductors No. 1 and No. 3 are located in the topmost part of the grounding network, the magnetic field does not change at the lowest monitoring point. The point at which maximum change occurs remains in the third column, corresponding to the centerline of the grounding network, but its position has been shifted upward to be closer to the corroded conductor. At the same time, in the second column, the 10th and 11th monitoring points show opposite-direction changes in the strength of the magnetic field near the corroded conductor. The 16th monitoring point exhibits the largest amplitude change, producing a cross pattern corresponding to Conductors No. 1 and No. 3. Red indicates that when conductor No. 1 experiences light corrosion, the magnetic field variation at this point reaches its maximum value; Pink indicates that when conductor No. 3 experiences light corrosion, the magnetic field variation at this point reaches its maximum value.

3.4. Impact of Damage to Vertical Branches

In this section, the changes in the strength of the magnetic field under corrosion of Conductors No. 7, 8, 9, 10, 11, and 12 are analyzed and discussed. The magnitudes of the changes in the magnetic field at various points when Conductor No. 7 has been subjected to light corrosion are shown in Figure 17. Blue indicates the magnitude of magnetic field variation at each point, while red indicates the point with the greatest magnetic field variation.

Here, Points 1, 2, 10, and 16 change by more than 10%, and Point 16 exhibits the largest change, at 19%.

A noticeable change in symmetry can be observed along the magnetic field line of No. 7 by comparing the position changes of the magnetic field at points No. 7 and No. 8, as shown in Figure 18. Red indicates that the magnetic field change at this point reaches its maximum when conductor No. 7 experiences light corrosion; pink indicates that the magnetic field change at this point reaches its maximum when conductor No. 8 experiences light corrosion.

For vertical branch conductors in the same row experiencing light corrosion, the direction of magnetic field change at each point is basically the same. In the second column, the magnetic field changes in the vicinity of the corroded conductor, but the points of maximum change point will be different, being located near one corroded conductor in the third column and near another corroded conductor for the fourth column.

The results of the comparison of the strength of the changes in the magnetic field for Conductors 7, 9, and 11 are shown in Figure 19. In the figure, the blue box shows Points 10, 11, and 12, which correspond to the second column of monitoring points near the corroded conductor. Each monitoring point has two nearby vertical conductor branches on the left and right, and the point with the largest value change can be used as a secondary basis for judgment. The conductor branch intersecting the two points is the corroded branch. Red indicates that the magnetic field change at this point reaches its maximum when conductor No. 7 experiences light corrosion; Light purple indicates that the magnetic field change at this point reaches its maximum when conductor No. 9 experiences light corrosion; Cyan indicates that the magnetic field change at this point reaches its maximum when conductor No. 11 experiences light corrosion.

4. Optimization of Grounding Network Monitoring Locations

The simulation results for Conductors 1–12 under light corrosion, moderate corrosion, and corrosion fracture were compiled and analyzed. It was found that Points 1, 5, 12, 16, 18, 30, and 32 changed more significantly when various faults occurred. Specific changes are shown in

Table 1. Percentage change in the strength of the magnetic field at observation points for various corrosion conditions.

Fault Type	Percentage Change
	Point 1	Point 5	Point 12	Point 16	Point 18	Point 30	Point 32
Corrosive breakage.1	−70%	7%	7%	189%	18%	77%	17%
Corrosive breakage.2	−78%	80%	57%	71%	275%	93%	232%
Corrosive breakage.3	20%	−1%	−1%	−52%	−15%	49%	1%
Corrosive breakage.4	4%	−6%	−7%	−31%	−54%	5%	58%
Corrosive breakage.5	0%	0%	0%	0%	0%	0%	0%
Corrosive breakage.6	0%	0%	0%	0%	0%	0%	0%
Corrosive breakage.7	−70%	7%	7%	189%	19%	77%	17%
Corrosive breakage.8	−46%	5%	4%	108%	−40%	522%	58%
Corrosive breakage.9	80%	21%	19%	−16%	106%	15%	36%
Corrosive breakage.10	14%	3%	3%	172%	−24%	315%	303%
Corrosive breakage.11	56%	−97%	−83%	−62%	57%	33%	91%
Corrosive breakage.12	17%	−15%	−18%	55%	153%	49%	384%
Mild corrosion.1	−11%	1%	1%	19%	2%	3%	0%
Mild corrosion.2	−10%	6%	6%	7%	30%	3%	8%
Mild corrosion.3	3%	0%	0%	−14%	−2%	3%	0%
Mild corrosion.4	1%	−1%	−1%	−5%	−13%	1%	3%
Mild corrosion.5	0%	0%	0%	0%	0%	0%	0%
Mild corrosion.6	0%	0%	0%	0%	0%	0%	0%
Mild corrosion.7	−11%	1%	1%	19%	2%	3%	0%
Mild corrosion.8	−5%	0%	0%	−24%	−5%	29%	1%
Mild corrosion.9	11%	2%	3%	−23%	15%	−1%	2%
Mild corrosion.10	2%	0%	0%	23%	−15%	9%	20%
Mild corrosion.11	7%	−15%	−17%	−10%	−31%	0%	1%
Mild corrosion.12	2%	−2%	−3%	7%	22%	−1%	19%
Moderate corrosion.1	−40%	2%	3%	69%	7%	17%	3%
Moderate corrosion.2	−34%	26%	22%	28%	108%	23%	64%
Moderate corrosion.3	9%	0%	0%	−42%	−7%	16%	0%
Moderate corrosion.4	2%	−3%	−3%	−16%	−41%	2%	18%
Moderate corrosion.5	0%	0%	0%	0%	0%	0%	0%
Moderate corrosion.6	0%	0%	0%	0%	0%	0%	0%
Moderate corrosion.7	−40%	2%	3%	69%	7%	17%	3%
Moderate corrosion.8	−19%	2%	2%	−34%	−17%	173%	12%
Moderate corrosion.9	37%	9%	9%	−65%	49%	1%	11%
Moderate corrosion.10	6%	1%	1%	79%	−40%	109%	117%
Moderate corrosion.11	26%	−48%	−55%	−31%	−54%	6%	24%
Moderate corrosion.12	8%	−7%	−9%	26%	72%	10%	147%

, where the red data represent the maximum values of the change in the amplitude of the magnetic field under the fault. Under “Fault Type”, the first word indicates the degree of failure and the number indicates which conductor failed.

From the table, it can be seen that Points 1, 5, 12, 16, 18, 30 and 32 can be used to accurately determine the type and location of the fault of the grounding network; due to the symmetry of the grounding network, so only some of the points need to be monitored for signs of corrosion. A preliminary determination of optimal point locations is shown in Figure 20.

Since the currents through Conductors 5 and 6 are too small to produce a noticeable effect on the monitored points, the current injection method was adjusted for another round of fault localization. The new injection position is (0, 20), and the withdrawal position is (0, −20). The rest of the conditions remain unchanged. Surface magnetic field simulations were then conducted for Conductor 5 and Conductor 6 under conditions of light corrosion, moderate corrosion, and corrosion fracture, and the results were compared with the fault-free surface magnetic field under the adjusted injection positions. The results from Points 29, 39, and 40 are shown in

Table 2. Amplitude of Magnetic Field Changes at Various Points During Conductor 5 and 6 Faults.

Fault Type	Percentage Change
	Point 29	Point 39	Point 40
Corrosive breakage.5	−96.96%	56.98%	90.97%
Corrosive breakage.6	−15.49%	153.49%	384.38%
Mild corrosion.5	−14.72%	−30.81%	1.39%
Mild corrosion.6	−2.29%	21.51%	18.92%
Moderate corrosion.5	−48.18%	−53.90%	23.61%
Moderate corrosion.6	−7.46%	72.09%	146.53%

.

As can be seen from the table, the changes in the amplitude of the magnetic field at Points 29, 39, and 40 can clearly indicate the fault location and type (The highlighted data represents the maximum amplitude of magnetic field variation.). Here, Conductors 5 and 6 correspond to Conductors 11 and 12 in the original injection scheme, and according to the principle of symmetry, they can be effectively monitored through points 29, 37, 39, 40, and 41. The final monitoring-point installation scheme is shown in Figure 21. The results demonstrate the rationality of the optimized design for point installation. The original 65 observation points were successfully reduced to 25 points, minimizing the need to install monitoring points.

5. Method for Grounding Grid Condition Assessment

When conducting condition assessment of a grounding grid, a comprehensive judgment must encompass its overall grounding resistance and local corrosion/breakage faults. To this end, this paper defines characteristic fault values as the performance parameters for grounding-grid condition assessment. The amplitude variation of the grounding grid’s surface magnetic field is used as the fault characteristic information and is analyzed in combination with the Manhattan distance function. Meanwhile, the Manhattan distance function is used to define the corrosion characteristic value M_f, which is employed to characterize the cumulative effect of surface magnetic field intensity variations corresponding to the corroded conductor segments. The definition of M_f is given by Equation (28):

$$M_f={\displaystyle \sum _{i=0}^n\frac{\left|Y_i-F_i\right|}{Y_i}}$$

(28)

where Y_i represents the intensity of the surface magnetic field at point i in the fault-free grounding grid; F_i represents the intensity of the surface magnetic field at point i in the grounding grid after corrosion occurs; and n represents the number of sampling points.

The M_f values of a 40 × 40 mesh grounding grid under mild corrosion, moderate corrosion, and severe corrosion were calculated, and the specific values are shown in

Table 3. Summary of M_f values for a 40 × 40 grounding grid.

Fault Location	Mild Corrosion	Moderate Corrosion	Corrosive Breakage
Conductor 1	0.958158	3.677575	9.0969777
Conductor 2	2.449257	9.331216	23.344007
Conductor 3	0.460438	1.524947	3.0149211
Conductor 4	0.617513	2.050086	4.1613752
Conductor 5	0	0	0
Conductor 6	0	0	0
Conductor 7	0.958158	3.669528	9.0989096
Conductor 8	1.747068	6.444285	16.728551
Conductor 9	1.494734	4.900457	9.443291
Conductor 10	2.013926	7.878544	17.423657
Conductor 11	3.036678	9.609934	20.293575
Conductor 12	2.605763	10.51044	23.931548

.

It can be seen that the fault in Conductor No. 11 has the greatest impact on the grounding grid. Moreover, there is a proportional relationship between the M_f values under mild corrosion, moderate corrosion, and corrosive breakage. Through summary and calculation, it is found that the M_f value under mild corrosion is 12.53% of that under corrosive breakage and that the M_f value under moderate corrosion is 44.75% of that under corrosive breakage.

Due to the relatively complex structure of the actual grounding grid, it is difficult to simulate mild corrosion and moderate corrosion of the grid. Therefore, in the early stage, only corrosive breakage was simulated and analyzed. Based on the patterns of mild corrosion and moderate corrosion relative to corrosive breakage in the mesh grounding grid, the M_f values of the actual grounding grid under mild corrosion and moderate corrosion can be deduced. Define M_f1 as the M_f value when extracting from the upper-right corner and M_f2 as the M_f value when extracting from the lower-right corner. Based on the calculated values of M_f1 and M_f2, the values given in

Table 4. Probabilities of various faults corresponding to different M_f values in the actual grounding grid.

Range of Mf1	Probability of Mild Corrosion	Probability of Moderate Corrosion	Probability of Corrosive Breakage	Range of Mf2	Probability of Mild Corrosion	Probability of Moderate Corrosion	Probability of Corrosive Breakage
$M_{f1}>70$	0%	0%	100%	$M_{f2}>50$	0%	0%	100%
$19 < M_{f1}<70$	0%	52.63%	47.37%	$17 < M_{f2}<50$	0%	67%	33%
$0.7 < M_{f1}<19$	55%	45%	0%	$0.5 < M_{f2}<17$	50%	50%	0%
$0.2 < M_{f1}<0.7$	100%	0%	0%	$0.15 < M_{f2}<0.5$	100%	0%	0%
$M_{f1}<0.2$	0%	0%	0%	$M_{f2}<0.15$	0%	0%	0%

can be obtained.

A grounding-grid condition-assessment method can be designed by combining the characteristic parameters and grounding resistance values, and the specific process is shown in Figure 22.

The condition-assessment method for grounding grids combines overall assessment and fault location. The overall assessment mainly monitors the grounding resistance of the grounding grid and the corrosion characteristic values M_f1 and M_f2. When the grounding resistance value of the grounding grid is greater than 1 Ω, or M_f1 > 70, or M_f2 > 50, the grounding grid has a breakage fault. This is judged as a severe fault, and excavation and maintenance must be carried out immediately. When the grounding resistance value is greater than 200 mΩ but less than 1 Ω, or 19 < M_f1 < 70, or 17 < M_f2 < 50, the probability of breakage and moderate corrosion of the grounding grid is very high. The grounding grid is judged to be in a poor condition at this time, and excavation and maintenance should be planned according to specific circumstances. When the grounding resistance value is greater than 50 mΩ but less than 200 mΩ, or 0.2 < M_f1 < 19, or 0.15 < M_f2 < 17, the grounding grid may be suffering from moderate corrosion or mild corrosion. Under these circumstances, the grounding grid is in acceptable condition, and continuous monitoring is required to prevent further corrosion and breakage. When the grounding resistance value is less than 50 mΩ, or M_f1 < 0.2, or M_f2 < 0.15, the grounding grid is free of faults and judged to be in a normal condition. The judgment logic is shown in Figure 23.

If the overall assessment determines that there is a fault in the grounding grid, the fault can be located by combining the data with the results of local detection, thereby effectively reducing the costs of excavation and maintenance. The assessment of local corrosion and breakage mainly locates faults by collecting data on the amplitude of surface magnetic field changes. Specifically, the process is as follows: first, inject a different-frequency current into the grounding grid, where the current-injection point is the center of the grounding grid and the extraction points are at the upper-right corner and lower-right corner. After injecting the different-frequency current, collect the surface magnetic field signals acquired by the fluxgate sensors installed on the ground surface and compare these signals with the previously stored surface magnetic field signals from the grounding grid in the fault-free state. Fault location is achieved as a result.

6. Conclusions

Since the grounding grid of a substation needs to be buried underground for a long time and usually covers a large area, it is often difficult to accurately determine the positions of local corrosion and breakage. In such cases, the entire grounding grid has to be replaced, which not only wastes a large quantity of human and material resources but also affects the normal operation of the electric traction system. Studies have shown that when a different-frequency current is passed through the grounding grid, a different-frequency magnetic field can be generated on the ground surface. When a section of the conductor in the grounding grid suffers from corrosion and breakage faults, the ground surface magnetic field changes accordingly. Based on this principle, the corrosion and breakage faults of the grounding grid can be located. This paper studies the localization of corrosion and breakage and the condition assessment of substation grounding grids and draws the following conclusions:

(1). The structure of a substation grounding grid is usually approximately symmetric, and the distribution of the surface magnetic field generated during normal operation also exhibits corresponding symmetric characteristics. When a conductor in the grounding grid is corroded, this inherent magnetic field symmetry is disrupted, and this regular change can serve as a key basis for locating the fault in the grounding grid. It should be noted in particular that there is a special case: for conductors located on the perpendicular bisector of the injected current, due to the influence of the bridge effect, only an extremely weak current flows through such conductors. Therefore, even if such conductors suffer from corrosion and breakage faults, the magnetic field changes caused by the faults are very slight, making it difficult to effectively identify the fault characteristics.

(2). When a conductor of the grounding grid perpendicular to the direction of the injected current suffers from corrosion and breakage faults, it will directly disrupt the original balanced state of the magnetic field distribution along the observation line. For the deployed observation points, with the center line of the injected current as the boundary, the direction of change in the strength of the magnetic field at each column of observation points within a zone should remain consistent. If the direction of change in the strength of a magnetic field at a certain column of observation points does not conform to this rule, then the corroded conductor is most likely located in the area adjacent to this column of observation points. The observation point with the largest amplitude of change in the strength of the magnetic field is usually closest to the corroded conductor.

(3). When a conductor parallel to the direction of the injected current suffers from corrosion and breakage faults, the distribution of the magnetic field along the observation line will also become unbalanced. As in Conclusion (2), by analyzing the direction of magnetic field change at each column of observation points on non-center lines, specific observation points where the change in the strength of the magnetic field does not conform to the rule can be located. Since the conductors in the grounding grid that are perpendicular to the current direction are arranged horizontally, the observation points with abnormal changes in the magnetic field can directly correspond to the positions of the corresponding horizontal conductors. On this basis, by further combining the position of the observation point with the largest amplitude of change in the magnetic field and conducting spatial correlation analysis on these key points, conductors potentially affected by corrosion faults can be identified.

(4). It can be seen from the simulation results different fault locations and degrees in the grounding grid have significantly different effects on the surface magnetic field distribution. For example, the amplitude of the change in the magnetic field at some observation points when a fault occurs is relatively large; such points can be used as core monitoring points to realize effective monitoring of corrosion and breakage faults in the grounding grid. At the same time, by utilizing the characteristic that the distance between adjacent vertical conductors is small, a single observation point can be used to cover the area that originally required monitoring by four points, which greatly improves monitoring efficiency. Combined with the analysis of data with the most significant change in the strength of the magnetic field under various fault scenarios, after further optimization and adjustment, the initial 65 observation points can be finally streamlined to 25, which significantly reduces the cost at the actual engineering installation stage.

(5). By combining the optimized placement of monitoring points with the simulation results, a method for grounding-grid condition assessment was designed. This method is divided into two parts: overall assessment and fault location. The overall assessment mainly assesses two key parameters, namely the grounding resistance value and the corrosion characteristic value M_f, to construct a comprehensive assessment model and classifies the grounding-grid conditions into four levels: normal condition, acceptable condition, poor condition, and severe fault. When the overall assessment determines that there is a fault in the grounding grid, the fault is located by monitoring the variation in the amplitude of the surface magnetic field.