Multispectral-NeRF: A Multispectral Modeling Approach Based on Neural Radiance Fields
Abstract
1. Introduction
2. Related Work
2.1. Traditional Multispectral-Integrated 3D Reconstruction Methods
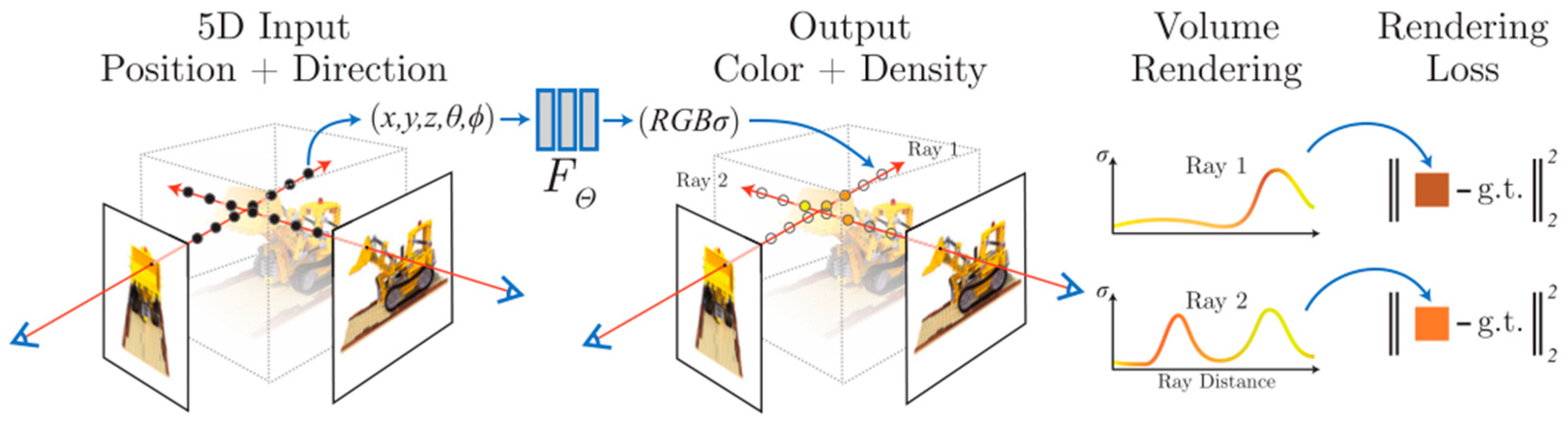
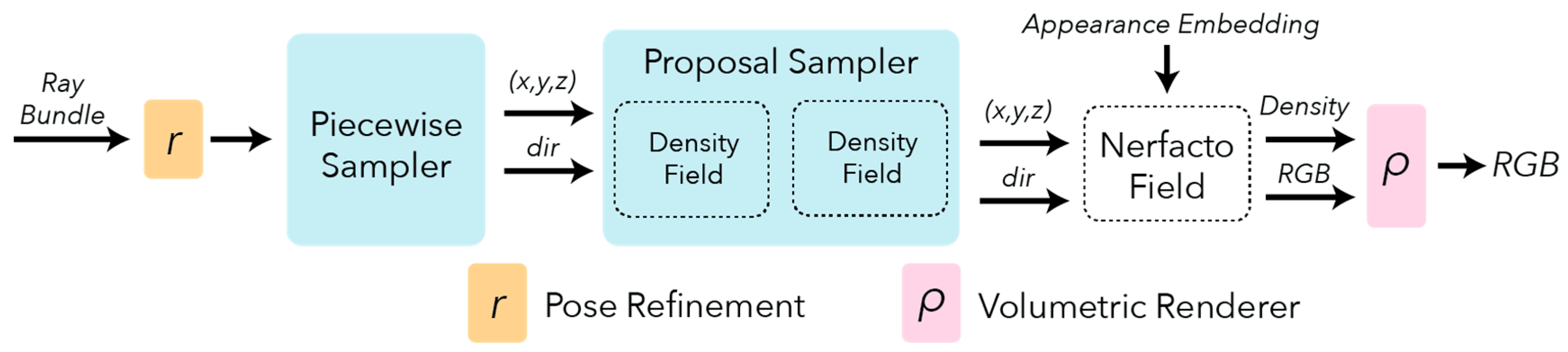
2.2. NeRF-Based 3D Reconstruction Methods
3. Methodology
3.1. Model Improvements
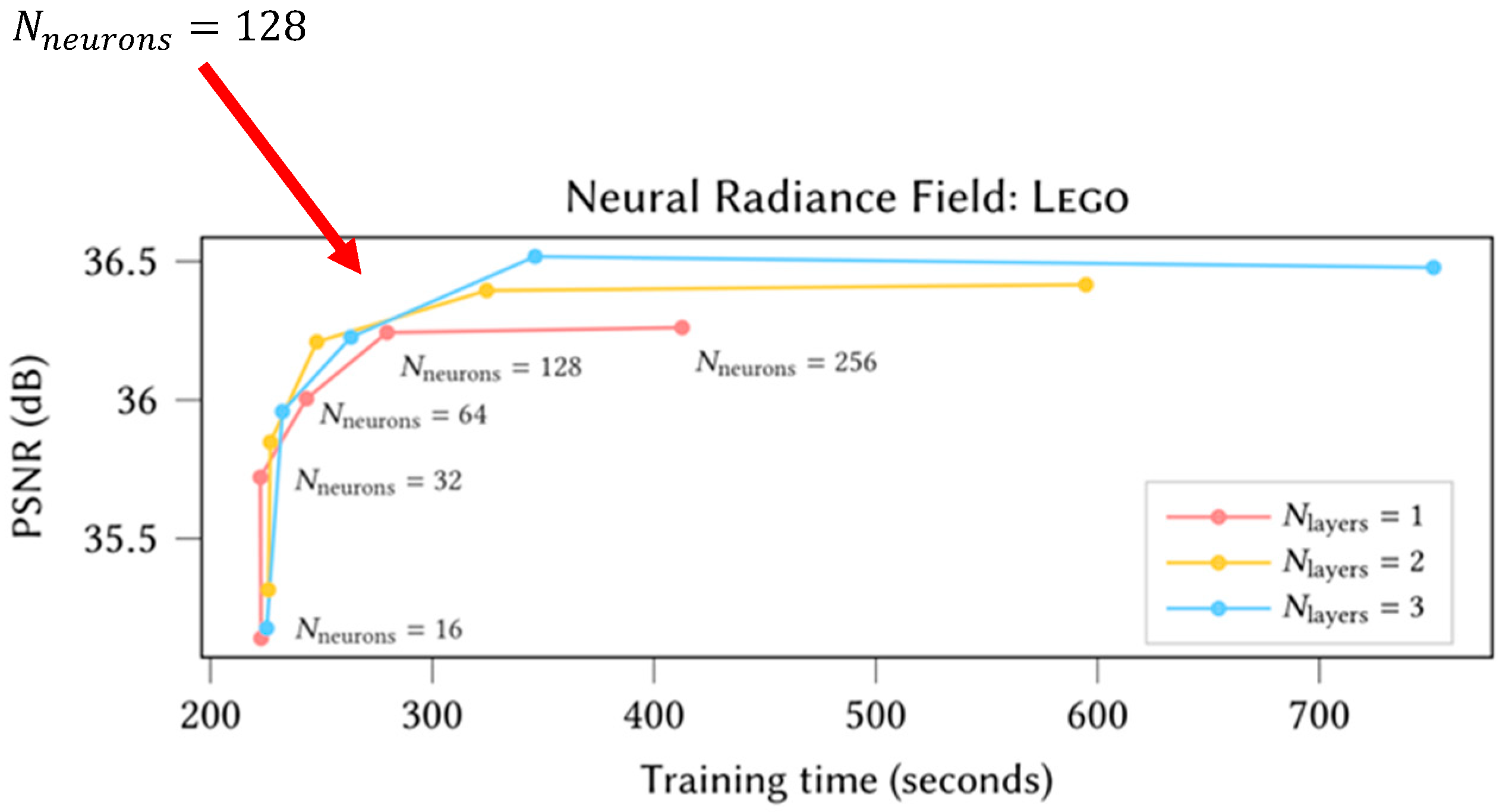
3.2. Model Parameter Selection
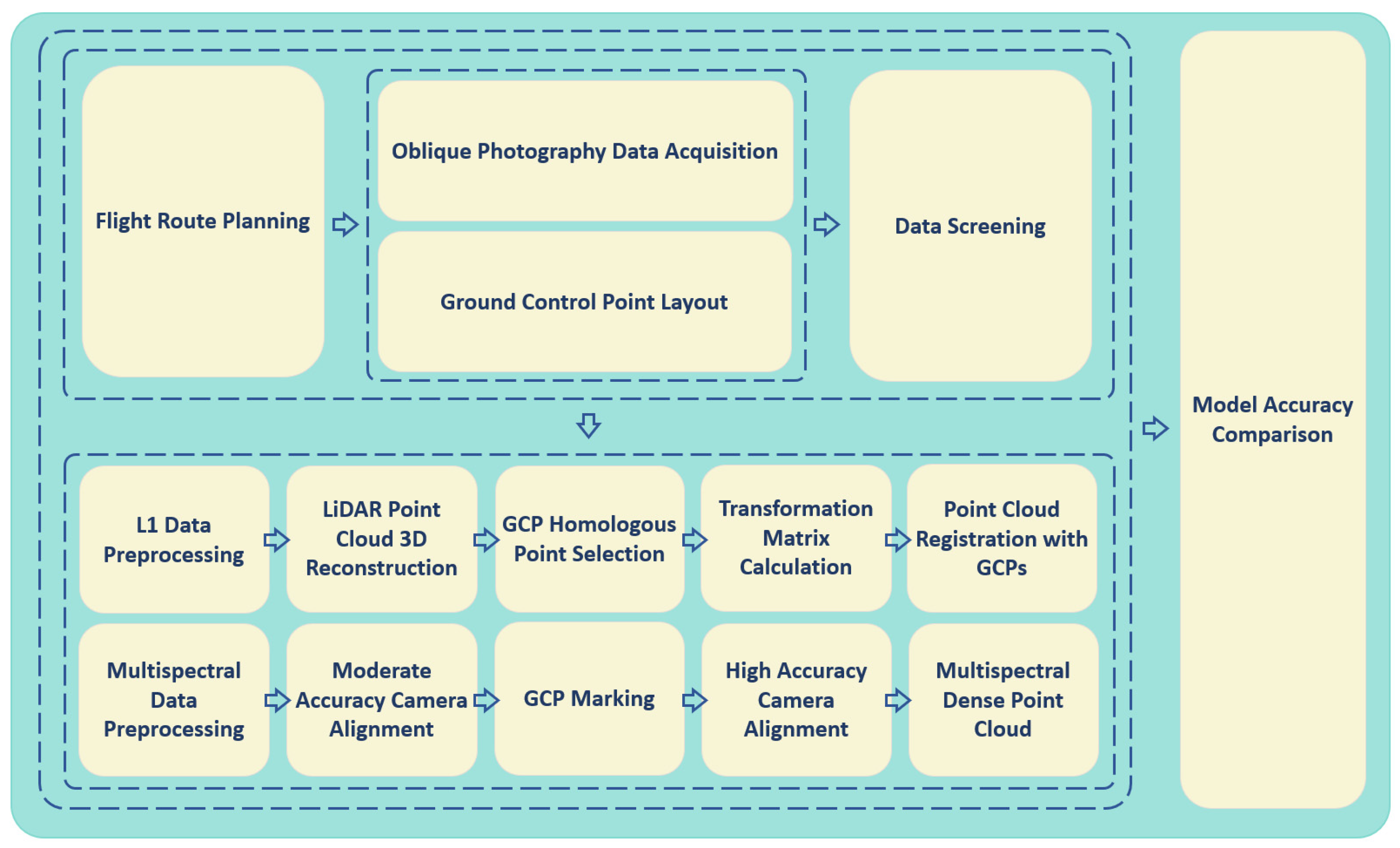
4. Experiments and Data
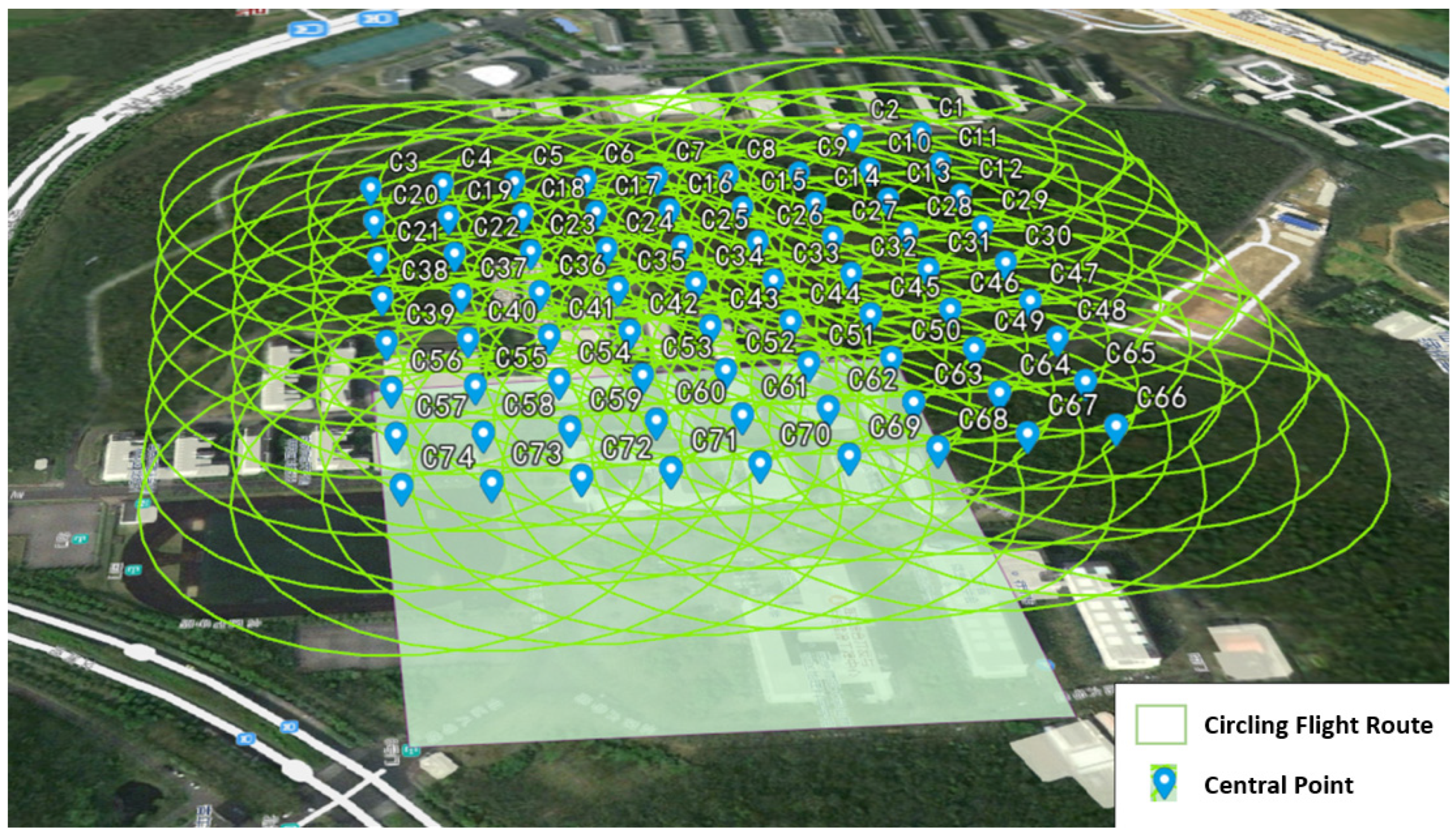
4.1. Study Area
4.2. Experimental Setup
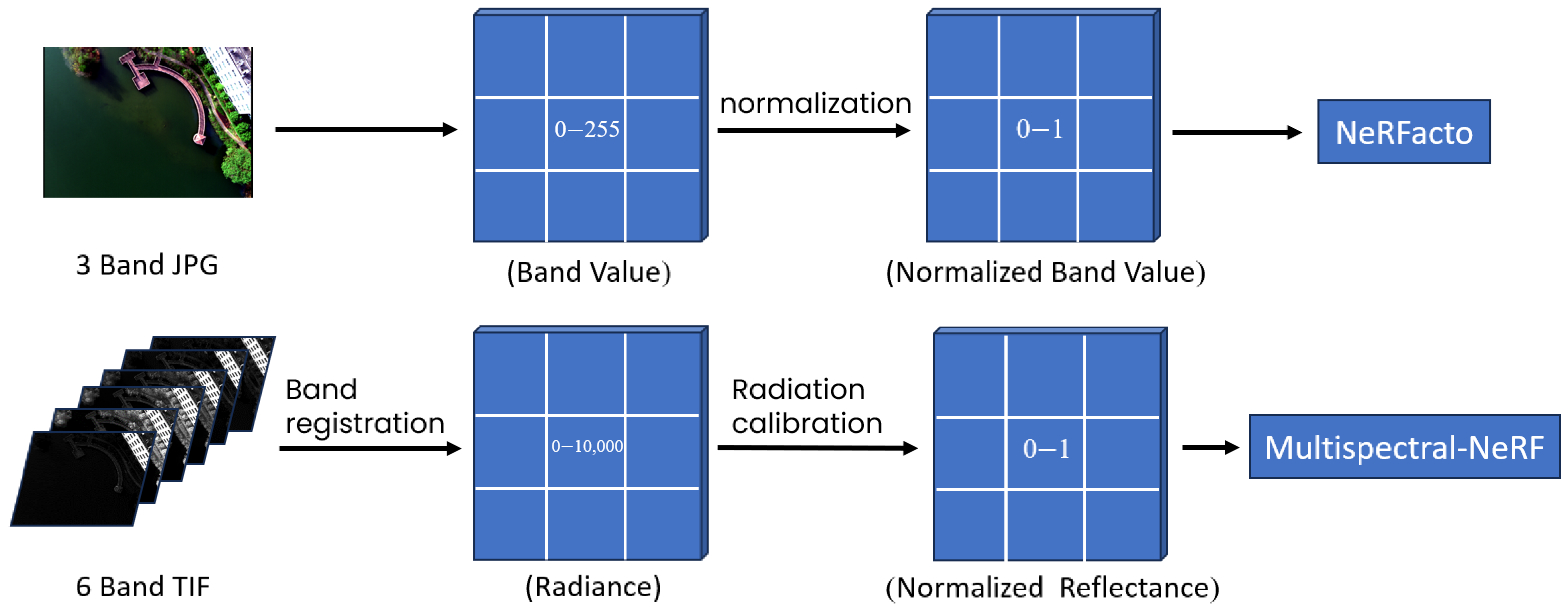
4.3. Experimental Data Acquisition and Processing
4.4. Data Feasibility Analysis
5. Results
5.1. Accuracy Evaluation Metrics
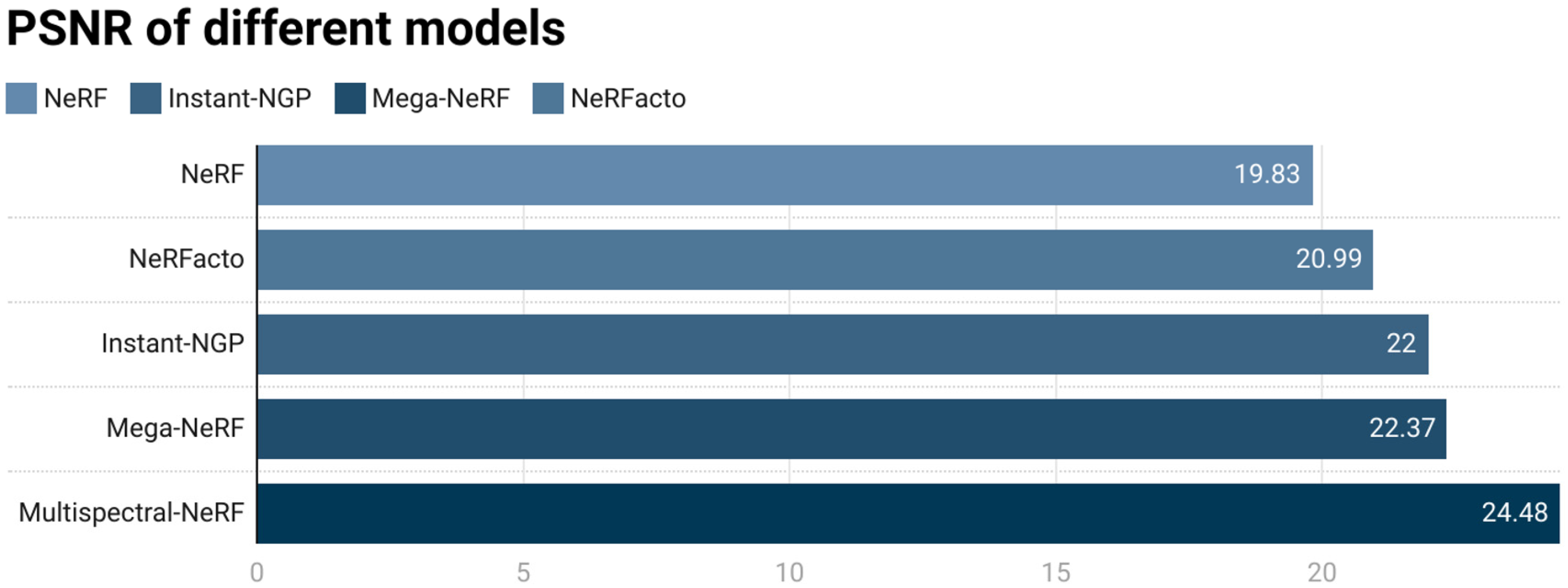
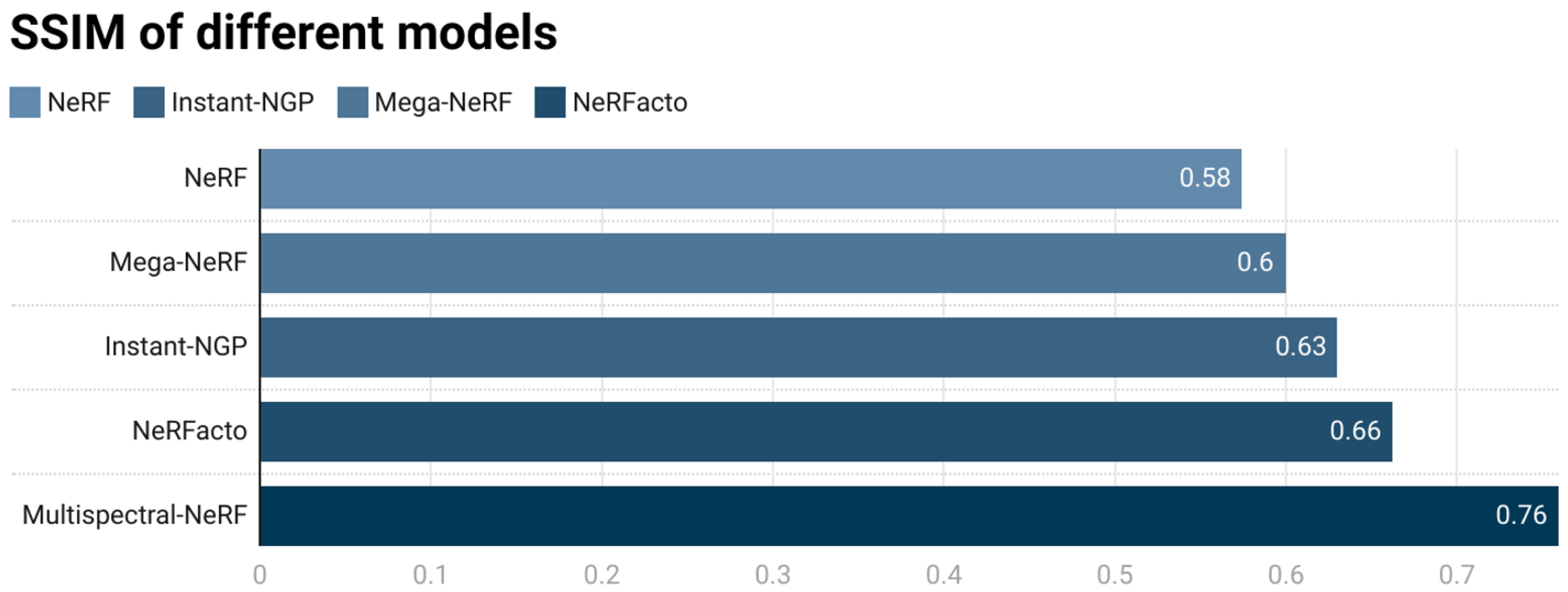
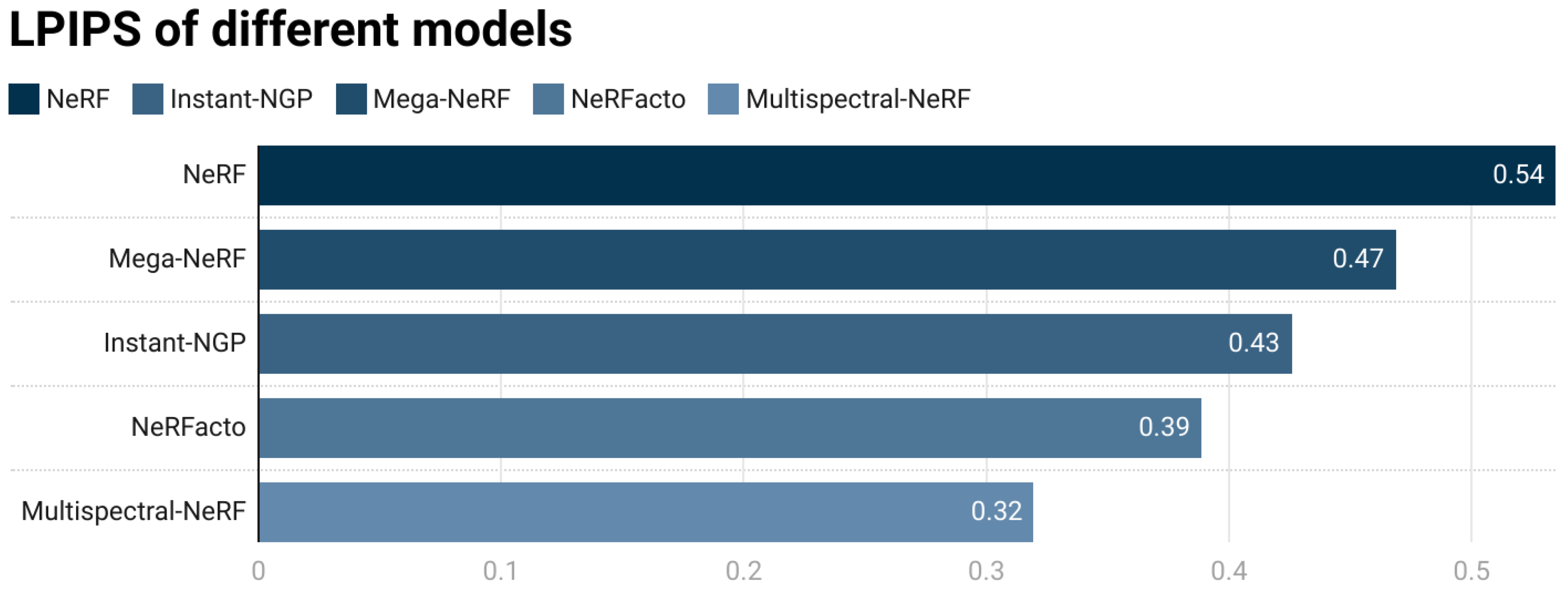
5.2. Analysis of Training Results
6. Discussion
6.1. CPU Parameter Selection
6.2. GPU Parameter Selection
6.3. Shortcomings and Prospects
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pollefeys, M.; Nistér, D.; Frahm, J.-M.; Akbarzadeh, A.; Mordohai, P.; Clipp, B.; Engels, C.; Gallup, D.; Kim, S.-J.; Merrell, P.; et al. Detailed Real-Time Urban 3D Reconstruction from Video. Int. J. Comput. Vis. 2007, 78, 143–167. [Google Scholar] [CrossRef]
- Wu, J.; Wyman, O.; Tang, Y.; Pasini, D.; Wang, W. Multi-View 3D Reconstruction Based on Deep Learning: A Survey and Comparison of Methods. Neurocomputing 2024, 582, 127553. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, S.; Fan, S.; Lu, J.; Li, P.; Tang, P. Image-Based 3D Reconstruction for Multi-Scale Civil and Infrastructure Projects: A Review from 2012 to 2022 with New Perspective from Deep Learning Methods. Adv. Eng. Inform. 2024, 59, 102268. [Google Scholar] [CrossRef]
- Shiode, N. 3D urban models: Recent developments in the digital modelling of urban environments in three-dimensions. GeoJournal 2000, 52, 263–269. [Google Scholar] [CrossRef]
- Fruh, C.; Zakhor, A. 3D model generation for cities using aerial photographs and ground level laser scans. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, CVPR 2001, Kauai, HI, USA, 8–14 December 2021; Volume 2, pp. II-31–I-38. [Google Scholar]
- Xie, F.; Lin, Z.; Gui, D.; Lin, H. Study on Construction OF 3D Building Based on Uav Images. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, XXXIX-B1, 469–473. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, H.; Wang, C. Considerations on Geospatial Big Data. IOP Conf. Ser. Earth Environ. Sci. 2016, 46, 012058. [Google Scholar] [CrossRef]
- Zainuddin, K.; Majid, Z.; Ariff, M.F.M.; Idris, K.M.; Abbas, M.A.; Darwin, N. 3D Modeling for Rock Art Documentation Using Lightweight Multispectral Camera. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2/W9, 787–793. [Google Scholar] [CrossRef]
- Li, Z.; Schaefer, M.; Strahler, A.; Schaaf, C.; Jupp, D. On the Utilization of Novel Spectral Laser Scanning for Three-Dimensional Classification of Vegetation Elements. Interface Focus 2018, 8, 20170039. [Google Scholar] [CrossRef]
- Nijland, W.; Coops, N.C.; Nielsen, S.E.; Stenhouse, G. Integrating Optical Satellite Data and Airborne Laser Scanning in Habitat Classification for Wildlife Management. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 242–250. [Google Scholar] [CrossRef]
- Over, J.-S.R.; Ritchie, A.C.; Kranenburg, C.J.; Brown, J.A.; Buscombe, D.D.; Noble, T.; Sherwood, C.R.; Warrick, J.A.; Wernette, P.A. Processing coastal imagery with Agisoft Metashape Professional Edition, version 1.6—Structure from motion workflow documentation. In Open-File Report; US Geological Survey: Reston, VA, USA, 2021. [Google Scholar]
- Wan, Q.; Guan, Y.; Zhao, Q.; Wen, X.; She, J. Constraining the Geometry of NeRFs for Accurate DSM Generation from Multi-View Satellite Images. ISPRS Int. J. Geo-Inf. 2024, 13, 243. [Google Scholar] [CrossRef]
- Johari, M.M.; Lepoittevin, Y.; Fleuret, F. GeoNeRF: Generalizing NeRF with Geometry Priors. arXiv 2021, arXiv:2111.13539. [Google Scholar]
- Mokssit, S.; Licea, D.B.; Guermah, B.; Ghogho, M. Deep Learning Techniques for Visual SLAM: A Survey. IEEE Access 2023, 11, 20026–20050. [Google Scholar] [CrossRef]
- Li, Y.; Ma, L.; Zhong, Z.; Liu, F.; Chapman, M.A.; Cao, D.; Li, J. Deep Learning for LiDAR Point Clouds in Autonomous Driving: A Review. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3412–3432. [Google Scholar] [CrossRef]
- Delegido, J.; Verrelst, J.; Meza, C.M.; Rivera, J.P.; Alonso, L.; Moreno, J. A Red-Edge Spectral Index for Remote Sensing Estimation of Green LAI over Agroecosystems. Eur. J. Agron. 2013, 46, 42–52. [Google Scholar] [CrossRef]
- Zhang, Y.; Migliavacca, M.; Penuelas, J.; Ju, W. Advances in Hyperspectral Remote Sensing of Vegetation Traits and Functions. Remote Sens. Environ. 2021, 252, 112121. [Google Scholar] [CrossRef]
- Rall, J.A.; Knox, R.G. Spectral ratio biospheric Lidar. In Proceedings of the 2004 IEEE International Geoscience and Remote Sensing Symposium, IGARSS ’04, Anchorage, AK, USA, 20–24 September 2004; Volume 3, pp. 1951–1954. [Google Scholar]
- Decker, K.T.; Borghetti, B.J. Composite Style Pixel and Point Convolution-Based Deep Fusion Neural Network Architecture for the Semantic Segmentation of Hyperspectral and Lidar Data. Remote Sens. 2022, 14, 2113. [Google Scholar] [CrossRef]
- Vlaminck, M.; Diels, L.; Philips, W.; Maes, W.; Heim, R.; Wit, B.D.; Luong, H. A Multisensor UAV Payload and Processing Pipeline for Generating Multispectral Point Clouds. Remote Sens. 2023, 15, 1524. [Google Scholar] [CrossRef]
- Murtiyoso, A.; Landes, T.; Grussenmeyer, P. A Novel and Automatic Photogrammetric Workflow for 3D Point Cloud Ai-Based Semantic Segmentation. In Proceedings of the International Symposium on Applied Geoinformatics (ISAG2021), Riga, Latvia, 2–3 December 2021. [Google Scholar]
- Karantanellis, E.; Arav, R.; Dille, A.; Lippl, S.; Marsy, G.; Torresani, L.; Oude Elberink, S. Evaluating the Quality of Photogrammetric Point-Clouds In Challenging Geo-Environments—A Case Study in an Alpine Valley. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, XLIII-B2-2020, 1099–1105. [Google Scholar] [CrossRef]
- Mildenhall, B.; Srinivasan, P.P.; Tancik, M.; Barron, J.T.; Ramamoorthi, R.; Ng, R. NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis. In Computer Vision—ECCV 2020, Proceedings of the Lecture Notes in Computer Science, Amsterdam, The Netherlands, 3–5 June 2020; Springer International Publishing: Cham, Switzerland, 2020; pp. 405–421. [Google Scholar] [CrossRef]
- Yang, B.; Rosa, S.; Markham, A.; Trigoni, N.; Wen, H. Dense 3D Object Reconstruction from a Single Depth View. arXiv 2018, arXiv:1802.00411. [Google Scholar] [CrossRef]
- Tatarchenko, M.; Dosovitskiy, A.; Brox, T. Octree Generating Networks: Efficient Convolutional Architectures for High-Resolution 3D Outputs. arXiv 2017, arXiv:1703.09438. [Google Scholar] [CrossRef]
- Yagubbayli, F.; Wang, Y.; Tonioni, A.; Tombari, F. LegoFormer: Transformers for Block-by-Block Multi-View 3D Reconstruction. arXiv 2021, arXiv:2106.12102. [Google Scholar]
- Mandikal, P.; Navaneet, K.L.; Agarwal, M.; Babu, R.V. 3D-LMNet: Latent Embedding Matching for Accurate and Diverse 3D Point Cloud Reconstruction from a Single Image. arXiv 2018, arXiv:1807.07796. [Google Scholar]
- Tancik, M.; Weber, E.; Ng, E.; Li, R.; Yi, B.; Kerr, J.; Wang, T.; Kristoffersen, A.; Austin, J.; Salahi, K.; et al. Nerfstudio: A Modular Framework for Neural Radiance Field Development. arXiv 2023, arXiv:2302.04264. [Google Scholar] [CrossRef]
- Verbin, D.; Hedman, P.; Mildenhall, B.; Zickler, T.; Barron, J.T.; Srinivasan, P.P. Ref-NeRF: Structured View-Dependent Appearance for Neural Radiance Fields. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 47, 9426–9437. [Google Scholar] [CrossRef]
- Müller, T.; Evans, A.; Schied, C.; Keller, A. Instant Neural Graphics Primitives with a Multiresolution Hash Encoding. arXiv 2022, arXiv:2201.05989. [Google Scholar] [CrossRef]
- Chen, A.; Xu, Z.; Geiger, A.; Yu, J.; Su, H. TensoRF: Tensorial Radiance Fields. arXiv 2022, arXiv:2203.09517. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, S.; Xie, W.; Chen, M.; Prisacariu, V.A. NeRF: Neural Radiance Fields Without Known Camera Parameters. arXiv 2021, arXiv:2102.07064. [Google Scholar]
- Lin, C.-H.; Ma, W.-C.; Torralba, A.; Lucey, S. BARF: Bundle-Adjusting Neural Radiance Fields. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 5721–5731. [Google Scholar] [CrossRef]
- Li, J.; Li, Y.; Sun, C.; Wang, C.; Xiang, J. Spec-NeRF: Multi-spectral Neural Radiance Fields (Version 1). arXiv 2023, arXiv:2310.12987. [Google Scholar]
- Poggi, M.; Ramirez, P.Z.; Tosi, F.; Salti, S.; Mattoccia, S.; Di Stefano, L. Cross-spectral neural radiance fields. In Proceedings of the 2022 International Conference on 3D Vision (3DV), Prague, Czech Republic, 12–16 September 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 606–616. [Google Scholar]
- Tulsiani, S.; Zhou, T.; Efros, A.A.; Malik, J. Multi-View Supervision for Single-View Reconstruction via Differentiable Ray Consistency. arXiv 2017, arXiv:1704.06254. [Google Scholar]
- Kerbl, B.; Kopanas, G.; Leimkuehler, T.; Drettakis, G. 3D Gaussian Splatting for Real-Time Radiance Field Rendering. ACM Trans. Graph. 2023, 42, 1–14. [Google Scholar] [CrossRef]
- Xie, Y.; Takikawa, T.; Saito, S.; Litany, O.; Yan, S.; Khan, N.; Tombari, F.; Tompkin, J.; Sitzmann, V.; Sridhar, S. Neural Fields in Visual Computing and Beyond. Comput. Graph. Forum 2022, 41, 641–676. [Google Scholar] [CrossRef]
- Xiao, W.; Chierchia, R.; Cruz, R.S.; Li, X.; Ahmedt-Aristizabal, D.; Salvado, O.; Fookes, C.; Lebrat, L. Neural Radiance Fields for the Real World: A Survey. arXiv 2025, arXiv:2501.13104. [Google Scholar] [CrossRef]
- Cai, J.; Lu, H. Nerf-based multi-view synthesis techniques: A survey. In Proceedings of the 2024 International Wireless Communications and Mobile Computing (IWCMC), Ayia Napa, Cyprus, 27-31 May 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 208–213. [Google Scholar]
- Wu, T.; Yuan, Y.-J.; Zhang, L.-X.; Yang, J.; Cao, Y.-P.; Yan, L.-Q.; Gao, L. Recent advances in 3D Gaussian splatting. Comput. Vis. Media 2024, 10, 613–642. [Google Scholar] [CrossRef]
- Hu, R.; He, Q.; Du, D.; Jin, X. ScatterSplatting: Enhanced View Synthesis in Scattering Scenarios via Joint NeRF and Gaussian Splatting. In Proceedings of the 2025 IEEE International Symposium on Circuits and Systems (ISCAS), London, UK, 25–28 May 2025; pp. 1–5. [Google Scholar] [CrossRef]
- Furukawa, Y.; Ponce, J. Accurate, Dense, and Robust Multiview Stereopsis. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1362–1376. [Google Scholar] [CrossRef]
- Ramamoorthi, R.; Hanrahan, P. An efficient representation for irradiance environment maps. In Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 12–17 August 2001; pp. 497–500. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, X.; Ni, X.; Dong, F.; Tang, L.; Sun, J.; Wang, Y. Neural radiance fields for multi-scale constraint-free 3D reconstruction and rendering in orchard scenes. Comput. Electron. Agric. 2024, 217, 108629. [Google Scholar] [CrossRef]
- CH/T 9016-2012; Fundamental Geographic Information—Specifications for the Producing of Three-Dimensional Model. Surveying and Mapping Press: Beijing, China, 2012.
- Turki, H.; Ramanan, D.; Satyanarayanan, M. Mega-NeRF: Scalable Construction of Large-Scale NeRFs for Virtual Fly-Throughs (Version 2). arXiv 2021, arXiv:2112.10703. [Google Scholar]
- Gu, J.; Jiang, M.; Li, H.; Lu, X.; Zhu, G.; Shah, S.A.A.; Zhang, L.; Bennamoun, M. UE4-NeRF: Neural Radiance Field for Real-Time Rendering of Large-Scale Scene (Version 1). arXiv 2023, arXiv:2310.13263. [Google Scholar]
- Xu, L.; Xiangli, Y.; Peng, S.; Pan, X.; Zhao, N.; Theobalt, C.; Dai, B.; Lin, D. Grid-guided neural radiance fields for large urban scenes. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 8296–8306. [Google Scholar]
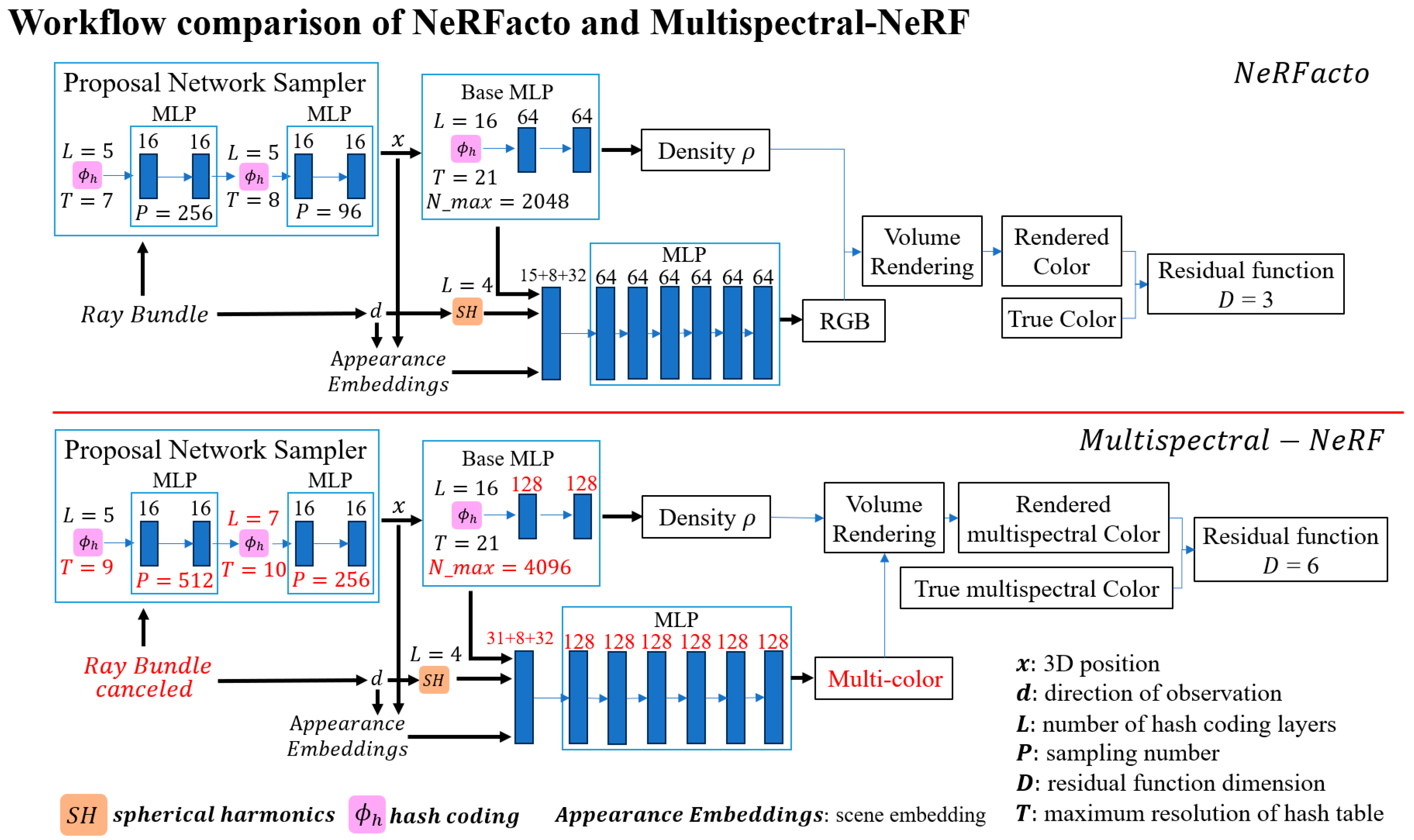







| Parameters | NeRFacto | Multispectral-NeRF |
|---|---|---|
| Hidden Layer Dimension | 64 | 128 |
| Spectral Network Hidden Layer Dimension | 64 | 128 |
| Base MLP Hash Table Max Resolution | 2048 | 4096 |
| Base MLP Hash Table Size | 219 | 221 |
| Base MLP Output Geometric Feature Dimension | 15 | 31 |
| Proposal Network Sampler Sample Points | 256, 96 | 512, 256 |
| Proposal Network Sampler Hash Table Max Resolution | 128, 256 | 512, 1024 |
| Proposal Network Sampler Hash Table Max Levels | 5, 5 | 5, 7 |
| Technical Parameters | Value |
|---|---|
| Effective Pixel of Sensor | 1.2 million pixels |
| Quantization Bit | 12 bit |
| Field of View | HFOV: 49.6° VFOV: 38° |
| Focal Length | 5.2 mm |
| Ground Sample Distance | 8.65 cm@h = 120 m translation: ±320° |
| Spectral Band Range | B: 450 nm, G: 555 nm, R: 660 nm, RE1: 720 nm, RE2: 750 nm, NIR: 840 nm |
| Swath Width | 110 m × 83 m@h = 120 m |
| Route Parameter | Value |
|---|---|
| Relative Flying Height | 100 m |
| Inter-Circumaviation Overlap Rate | 75% |
| Intra-Circumaviation Overlap Rate | 75% |
| Gimbal Tilt Angle | −60° |
| Boundary Buffer | 15 m |
| Data Type | Number of Photographs | Data Size |
|---|---|---|
| Multispectral images | 3171 | 92.9 GB |
| Lidar point cloud | / | 15.7 GB |
| Number of GCP | X Error (mm) | Y Error (mm) | Z Error (mm) | Aggregate (mm) | Image Pixel Error (pi) | Projected Quantity |
|---|---|---|---|---|---|---|
| 1 | 10.03 | −7.95 | 0.23 | 12.80 | 0.38 | 41 |
| 2 | −7.70 | 1.77 | 1.06 | 7.98 | 0.39 | 28 |
| 3 | −4.68 | 3.38 | −0.19 | 5.78 | 0.39 | 17 |
| 4 | 1.95 | 3.20 | 0.84 | 3.85 | 0.41 | 30 |
| 5 | −0.27 | −0.21 | −0.51 | 0.61 | 0.42 | 26 |
| 6 | −4.84 | −1.76 | −0.38 | 5.16 | 0.43 | 21 |
| 7 | 5.17 | 0.03 | −0.87 | 5.23 | 0.33 | 25 |
| 8 | 0.78 | 0.37 | 0.82 | 1.19 | 0.38 | 16 |
| 9 | −12.82 | 8.92 | −5.49 | 16.56 | 0.44 | 61 |
| 10 | 10.76 | −1.78 | 3.34 | 11.41 | 0.44 | 36 |
| 11 | 5.00 | −5.89 | −1.37 | 7.85 | 0.44 | 25 |
| 12 | −3.39 | −0.07 | 2.57 | 4.26 | 0.41 | 41 |
| Average | 6.79 | 4.17 | 2.11 | 8.24 | 0.41 | 31 |
| Point Cloud Category | Mean Euclidean Distance Error (m) |
|---|---|
| L1 Raw Unregistered Point Cloud | 0.178 |
| Multispectral Point Cloud via SFM Algorithm | 0.241 |
| Point Cloud Category | Mean Plane Distance Error (m) | Mean Elevation Distance Error (m) |
|---|---|---|
| L1 Raw Unregistered Point Cloud | 0.196 | 0.092 |
| Multispectral Point Cloud via SFM Algorithm | 0.261 | 0.123 |
| CPU Configuration | Number of Photos | N | M | Max | Memory Usage |
|---|---|---|---|---|---|
| 256 G | 4000 | 1000 | 2000 | 120,000 | 180~240 G |
| 512 G | 4000 | 2000 | 4000 | 60,000 | 340~460 G |
| GPU | Training Ray Batch Size | Evaluation Ray Batch Size | Video Memory Usage |
|---|---|---|---|
| GeForce RTX 2080Ti (11 GB) | 16,384 | 8192 | 10 G |
| NVIDIA A100 (80 GB) | 32,768 | 16,384 | 16 G |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Guo, F.; Xie, Z.; Yao, D. Multispectral-NeRF: A Multispectral Modeling Approach Based on Neural Radiance Fields. Appl. Sci. 2025, 15, 12080. https://doi.org/10.3390/app152212080
Zhang H, Guo F, Xie Z, Yao D. Multispectral-NeRF: A Multispectral Modeling Approach Based on Neural Radiance Fields. Applied Sciences. 2025; 15(22):12080. https://doi.org/10.3390/app152212080
Chicago/Turabian StyleZhang, Hong, Fei Guo, Zihan Xie, and Dizhao Yao. 2025. "Multispectral-NeRF: A Multispectral Modeling Approach Based on Neural Radiance Fields" Applied Sciences 15, no. 22: 12080. https://doi.org/10.3390/app152212080
APA StyleZhang, H., Guo, F., Xie, Z., & Yao, D. (2025). Multispectral-NeRF: A Multispectral Modeling Approach Based on Neural Radiance Fields. Applied Sciences, 15(22), 12080. https://doi.org/10.3390/app152212080






