Quantitative Assessment of the Reliability Index in the Safety Analysis of Spatial Truss Domes
Abstract
1. Introduction
2. Materials and Methods
2.1. Finite-Element Method as a Training Data Generator
2.2. Neural Network (NN) as a Limit-State Function Approximator
- The input layer—corresponding to the random variables Xi;
- One or more hidden layers—performing the nonlinear transformation of data;
- The output layer—corresponding to the value of the limit-state function G(X).
2.3. Applied Methods of Reliability Analysis
2.3.1. The FORM Method Combined with an Explicit Limit-State Function
2.3.2. The FORM Method Combined with an Implicit Limit-State Function
2.3.3. Classical and Hybrid Monte Carlo Method in Structural Reliability Analysis
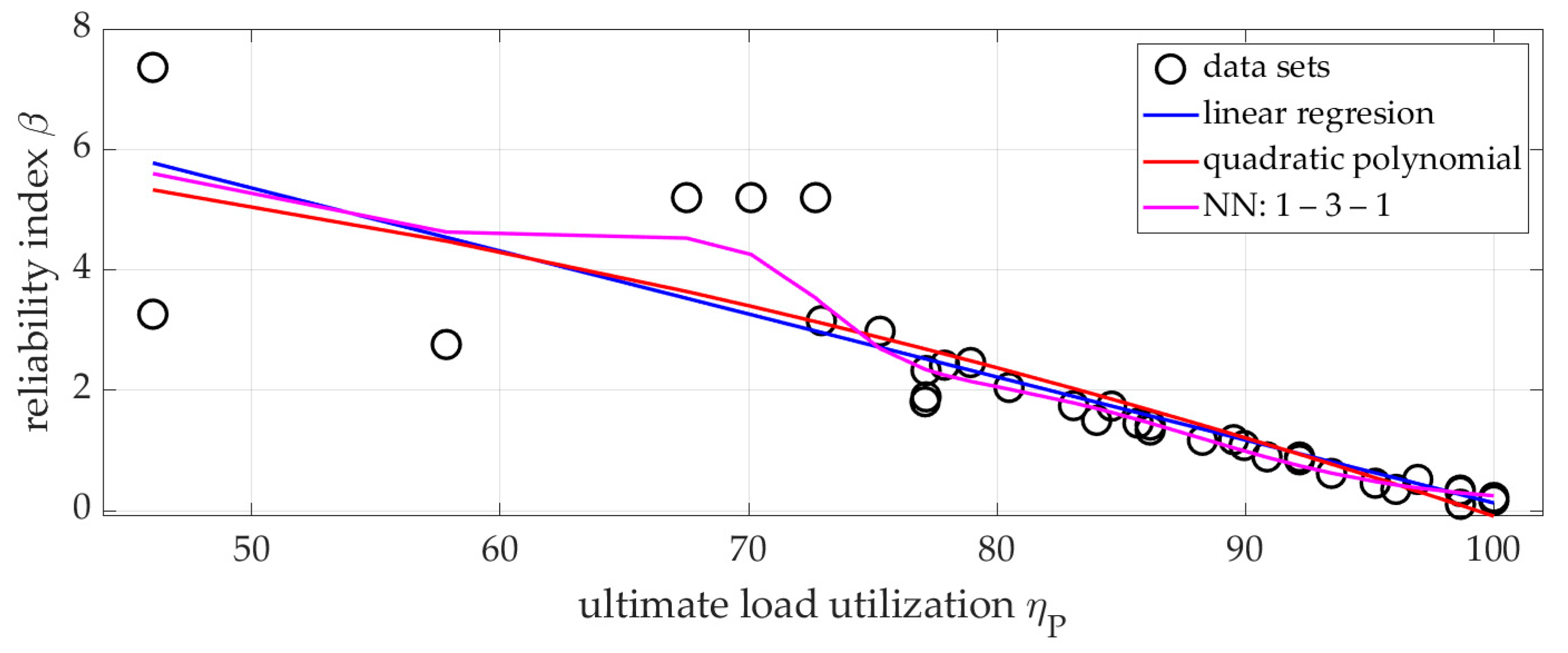
2.4. Methods of Approximation of the Reliability Index
- Full Data: Containing all 36 computational points in the range ⟨46%, 100%⟩ of Pult.
- Reduced Data: A subset limited to ⟨73%, 100%⟩ of Pult, introduced to minimize the dispersion of β values observed for lower load levels.
- Linear regression, expressed as
- 2.
- Quadratic polynomial, expressed as
- 3.
- Simple feedforward neural network (NN), with an adaptive architecture of the form 1–H–1, where H denotes the number of neurons in the hidden layer. The network was trained using the back-propagation algorithm, and the model parameters were selected adaptively so that the Mean Squared Eror (MSE) for training and testing datasets remained comparable, thus avoiding overfitting.
3. Results and Discussion
3.1. Description of Analyzed Structures
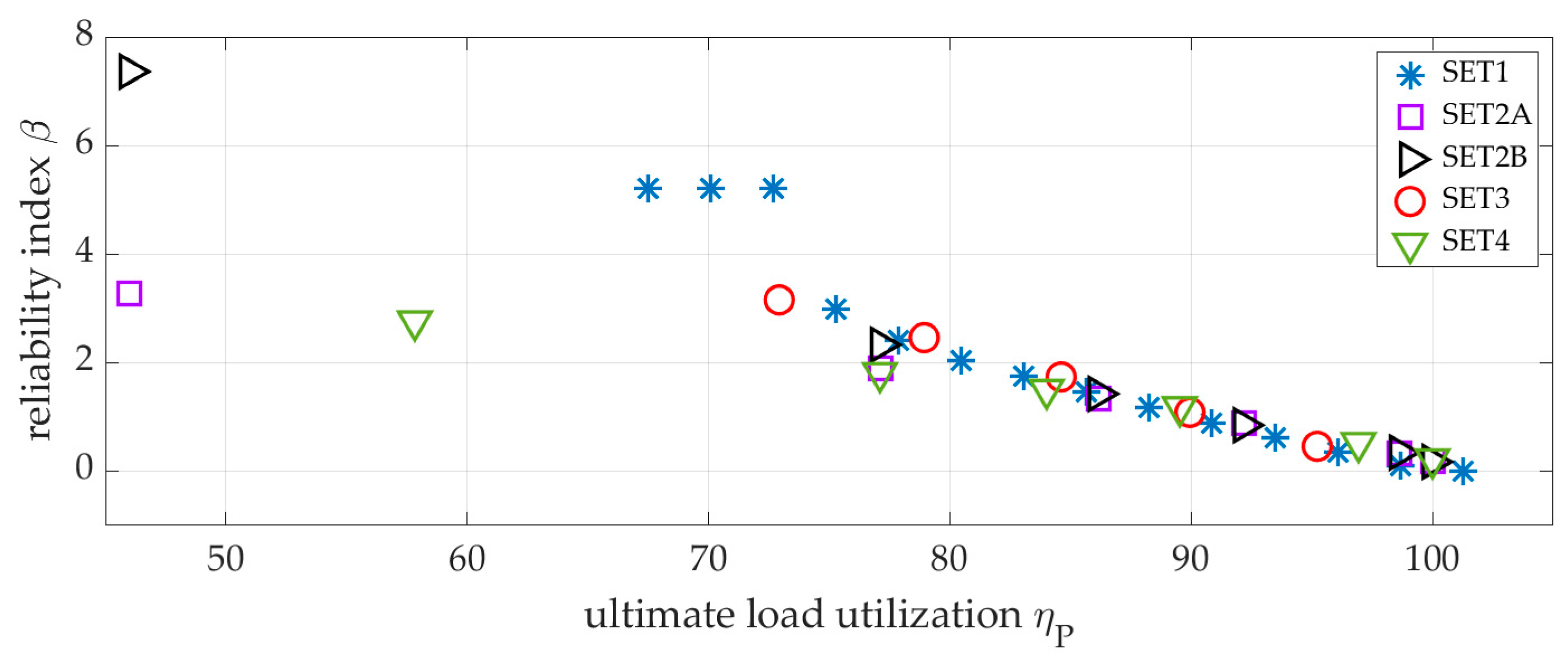
3.2. Reliability Assessment Results
3.2.1. SET1
3.2.2. SET2
3.2.3. SET3
3.2.4. SET4
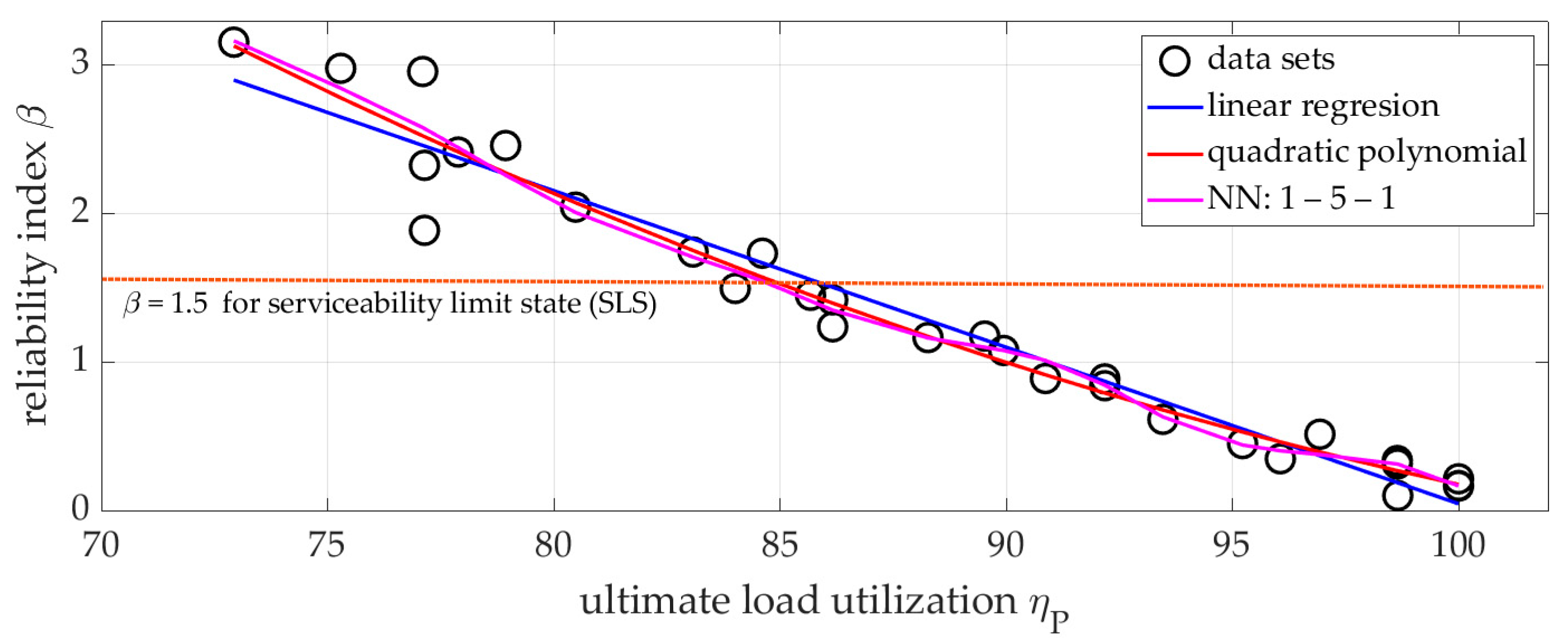
3.3. Reliability Assessment and Approximation of the Reliability Index
- Full Data—Including all results within the range ⟨46%, 100%⟩ of Pult.
- Reduced Data—Limited to ⟨73%, 100%⟩ of Pult, introduced to minimize the dispersion of reliability index (β) values at low load levels.
Analysis of the Causes of Differences
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| BPNN | Back-Propagation Neural Network |
| FORM | First-Order Reliability Method |
| FEM | Finite-Element Method |
| GNA | Geometrically Nonlinear Analysis |
| HMC | Hybrid Monte Carlo Method |
| LA | Linear Static Analysis |
| LBA | Linear Buckling Analysis |
| MC | Classical Monte Carlo Method |
| MSE | Mean Squared Eror |
| SLS | Serviceability Limit State |
References
- Ditlevsen, O.; Madsen, H. Structural Reliability Methods; John Wiley & Sons: Chichester, UK, 1996. [Google Scholar]
- Melchers, R.E. Structural Reliability Analysis and Predictions, 2nd ed.; John Wiley & Sons: Chichester, UK, 1999. [Google Scholar]
- Nowak, A.; Collins, K. Reliability of Structures, 2nd ed.; CRC Press: New York, NY, USA, 2013. [Google Scholar]
- Harr, M.E. Reliability-Based Design in Civil Engineering; Dover Publications Inc.: New York, NY, USA, 2000. [Google Scholar]
- Dudzik, A.; Potrzeszcz-Sut, B. The Structural Reliability Analysis Using Explicit Neural State Functions. MATEC Web Conf. 2019, 262, 10002. [Google Scholar] [CrossRef][Green Version]
- Dudzik, A.; Potrzeszcz-Sut, B. Hybrid Approach to the First Order Reliability Method in the Reliability Analysis of a Spatial Structure. Appl. Sci. 2021, 11, 648. [Google Scholar] [CrossRef]
- Dudzik, A. Reliability Assessment of Steel-Aluminium Lattice Tower. IOP Conf. Ser. Mater. Sci. Eng. 2017, 245, 032072. [Google Scholar] [CrossRef]
- Zabojszcza, P.; Radoń, U. The Impact of Node Location Imperfections on the Reliability of Single-Layer Steel Domes. Appl. Sci. 2019, 9, 2742. [Google Scholar] [CrossRef]
- Radoń, U.; Szaniec, W.; Zabojszcza, P. Probabilistic Approach to Limit States of a Steel Dome. Materials 2021, 14, 5528. [Google Scholar] [CrossRef]
- Potrzeszcz-Sut, B. Reliability Analysis of Shell Truss Structure by Hybrid Monte Carlo Method. J. Theor. Appl. Mech. 2020, 58, 469–482. [Google Scholar] [CrossRef]
- Grubišić, M.; Ivošević, J.; Grubišić, A. Reliability Analysis of Reinforced Concrete Frame by Finite Element Method with Implicit Limit State Functions. Buildings 2019, 9, 119. [Google Scholar] [CrossRef]
- Kubicka, K.; Obara, P.; Radoń, U.; Szaniec, W. Assessment of Steel Truss Fire Safety in Terms of the System Reliability Analysis. Arch. Civ. Mech. Eng. 2019, 19, 417–427. [Google Scholar] [CrossRef]
- Kubicka, K.; Radoń, U. The Impact of Support Type on the Reliability of Steel Trusses Subjected to the Action of a Fire. Appl. Sci. 2020, 10, 7916. [Google Scholar] [CrossRef]
- PN-EN 1993; Eurocode 3: Design of Steel Structures. European Committee for Standardization (CEN): Brussels, Belgium, 2006.
- Hasofer, A.; Lind, N. Exact and Invariant Second-Moment Code Format. J. Eng. Mech. Div. ASCE 1974, 100, 111–121. [Google Scholar] [CrossRef]
- Rackwitz, R.; Fiessler, B. Structural Reliability under Combined Random Load Sequences. Comput. Struct. 1978, 9, 489–494. [Google Scholar] [CrossRef]
- Cornell, A. A Probability-Based Structural Code. J. Am. Concr. Inst. 1969, 66, 974–985. [Google Scholar]
- Hohenbichler, M.; Gollwitzer, S.; Kruse, W.; Rackwitz, R. New Light on First and Second Order Reliability Methods. Struct. Saf. 1987, 4, 267–284. [Google Scholar] [CrossRef]
- Der Kiureghian, A.; De Stefano, M. Efficient Algorithm for Second-Order Reliability Analysis. J. Eng. Mech. 1991, 117, 2904–2923. [Google Scholar] [CrossRef]
- Yan-Gang, Z.; Tetsuro, O. A General Procedure for First/Second-Order Reliability Method (FORM/SORM). Struct. Saf. 1999, 21, 95–112. [Google Scholar]
- Rossi, L.; Winands, M.H.M.; Butenweg, C. Monte Carlo Tree Search as an Intelligent Search Tool in Structural Design Problems. Eng. Comput. 2021, 38, 3219–3236. [Google Scholar] [CrossRef]
- Metropolis, N. The Beginning of the Monte Carlo Method; Los Alamos Science: Los Alamos, NM, USA, 1987; Special Issue; pp. 125–130. [Google Scholar]
- Cardoso, J.; Almeida, J.; Dias, J.; Coelho, P. Structural Reliability Analysis Using Monte Carlo Simulation and Neural Networks. Adv. Eng. Softw. 2008, 39, 505–513. [Google Scholar] [CrossRef]
- Hasani, H.; Freddi, F. Artificial Neural Network-Based Automated Finite Element Model Updating with an Integrated Graphical User Interface for Operational Modal Analysis of Structures. Buildings 2024, 14, 3039. [Google Scholar] [CrossRef]
- Beskopylny, A.; Lyapin, A.; Anysz, H.; Meskhi, B.; Veremeenko, A.; Mozgovoy, A. Artificial Neural Networks in Classification of Steel Grades Based on Non-Destructive Tests. Materials 2020, 13, 2445. [Google Scholar] [CrossRef]
- Kaliszuk, J. Hybrid Monte Carlo Method in the Reliability Analysis of Structures. Comput. Assist. Mech. Eng. Sci. 2011, 18, 205–216. [Google Scholar]
- Deng, J.; Gu, D.; Li, X.; Qi Yue, Z. Structural Reliability Analysis for Implicit Performance Functions Using Neural Network. Struct. Saf. 2005, 27, 25–48. [Google Scholar] [CrossRef]
- Mises, R.V.; Ratzersdorfer, J. Die Knicksicherheit von Fachwerken. ZAMM J. Appl. Math. Mech. Z. Für Angew. Math. Und Mech. 1925, 5, 218–235. [Google Scholar] [CrossRef]
- Mirski, J.Z. The Origin and Morphology of Bar Domes in the Context of Geometric Shaping of Architectural Forms. Ph.D. Dissertation, Kielce University of Technology Publishing House, Kielce, Poland, 2003. (In Polish). [Google Scholar]
- Thai, H.-T. Machine Learning for Structural Engineering: A State-of-the-Art Review. Structures 2022, 38, 448–491. [Google Scholar] [CrossRef]
- Đorđević, F.; Marinković, M. PINN Surrogate Model for Nonlinear Equilibrium Path Analysis of von Mises Shallow Truss. J. Big Data 2025, 12, 103. [Google Scholar] [CrossRef]
- Mai, H.T.; Lieu, Q.X.; Kang, J.; Lee, J. A Robust Unsupervised Neural Network Framework for Geometrically Nonlinear Analysis of Inelastic Truss Structures. Appl. Math. Model. 2022, 107, 332–352. [Google Scholar] [CrossRef]
- Manguri, A.; Magisano, D.; Jankowski, R. Gradient-Based Weight Minimization of Nonlinear Truss Structures with Displacement, Stress, and Stability Constraints. Int. J. Numer. Methods Eng. 2025, 126, e70096. [Google Scholar] [CrossRef]
- Mai, H.T.; Lee, S.; Kang, J.; Lee, J. A Damage-Informed Neural Network Framework for Structural Damage Identification. Comput. Struct. 2024, 292, 107232. [Google Scholar] [CrossRef]
- Ojha, V.; Pantò, B.; Nicosia, G. Adaptive Search Space Decomposition Method for Pre- and Post- Buckling Analyses of Space Truss Structures. Eng. Appl. Artif. Intell. 2023, 117, 105593. [Google Scholar] [CrossRef]
- Kowalczyk, P.; Rojek, J.; Stocki, R.; Bednarek, T.; Tauzowski, P.; Lasota, R.; Lumelskyy, D.; Wawrzyk, K. NUMPRESS−Integrated Computer System for Analysis and Optimization of Industrial Sheet Metal Forming Processes. Hut. Wiadomości Hut. 2014, 81, 55–63. [Google Scholar]
- Radoń, U. Zastosowanie Metody FORM w Analizie Niezawodności Konstrukcji Kratowych Podatnych Na Przeskok; Wydawnictwo Politechniki Świętokrzyskiej: Kielce, Poland, 2012. [Google Scholar]
- Metropolis, N.; Ulam, S. The Monte Carlo Method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef]
- Hurd, C. A Note on Early Monte Carlo Computations and Scientific Meetings. Ann. Hist. Comput. 1985, 7, 141–155. [Google Scholar] [CrossRef]
- Robert, C.; Casella, G. Monte Carlo Statistical Methods; Springer: New York, NY, USA, 1999. [Google Scholar]
- Rubinstein, R.; Kroese, D. Simulation and the Monte Carlo Method; Wiley-Interscience: New York, NY, USA, 2008; ISBN 0-470-17794-2. [Google Scholar]
- Kallenberg, O. Foundations of Modern Probability; Springer: New York, NY, USA, 2002. [Google Scholar]
- Olofsson, P.; Andersson, M. Probability, Statistics, and Stochastic Processes, 2nd ed.; Wiley-Interscience: New York, NY, USA, 2012. [Google Scholar]
- Jelic, A.; Baitsch, M.; Hartmann, D.; Spitzlei, K.; Ballnus, D. Distributed Computing of Failure Probabilities for Structures in Civil Engineering. In Proceedings of the X. International Conference on Computing in Civil and Building Engineering, Weimar, Germany, 2–4 June 2004. [Google Scholar]
- Doliński, K. Importance Sampling Techniques in Reliability Calculation; IPPT PAN: Warszawa, Poland, 1988; Volume 37. [Google Scholar]
- Carpentier, A.; Munos, R. Adaptive Stratified Sampling for Monte-Carlo Integration of Differentiable Functions. In Proceedings of the Advances in Neural Information Processing Systems 25 (NIPS 2012), Lake Tahoe, NV, USA, 3–6 December 2012. [Google Scholar]
- Papadrakakis, M.; Lagaros, N. Reliability-Based Structural Optimization Using Neural Networks and Monte Carlo Simulation. Comput. Methods Appl. Mech. Eng. 2002, 191, 3491–3507. [Google Scholar] [CrossRef]
- Hurtado, J.; Alvarez, D. Reliability Assessment of Structural Systems Using Neural Networks. In Proceedings of the (CDROM) European Congress on Computational Methods in Applied Sciences and Engineering, ECCOMAS-2000, Barcelona, Spain, 11–14 September 2000. [Google Scholar]
- Kaliszuk, J.; Waszczyszyn, Z. Reliability Analysis of a Steel Girder by the Hybrid Monte Carlo Method. Progress in steel, composite and aluminium structures. In Proceedings of the 11th International Conference on Metal Structures, Rzeszów, Poland, 21–23 June 2006; pp. 843–847. [Google Scholar]
- Waszczyszyn, Z.; Cichoń, C.; Radwańska, M. Stability of Structures by Finite Element Methods; Elsevier: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Dudzik, A. Impact of the Mathematical Model Description on the Assessment of the Reliability of Structural Elements. IOP Conf. Ser. Mater. Sci. Eng. 2017, 245, 062055. [Google Scholar] [CrossRef]
- Radoń, U.; Zabojszcza, P. Stability Analysis of the Single-Layer Dome in Probabilistic Description by the Monte Carlo Method. J. Theor. Appl. Mech. 2020, 58, 425–436. [Google Scholar] [CrossRef]
- Dudzik, A.; Radoń, U. The Evaluation of Algorithms for Determination of the Reliability Index. Arch. Civ. Eng. 2015, LXI, 133–147. [Google Scholar] [CrossRef]

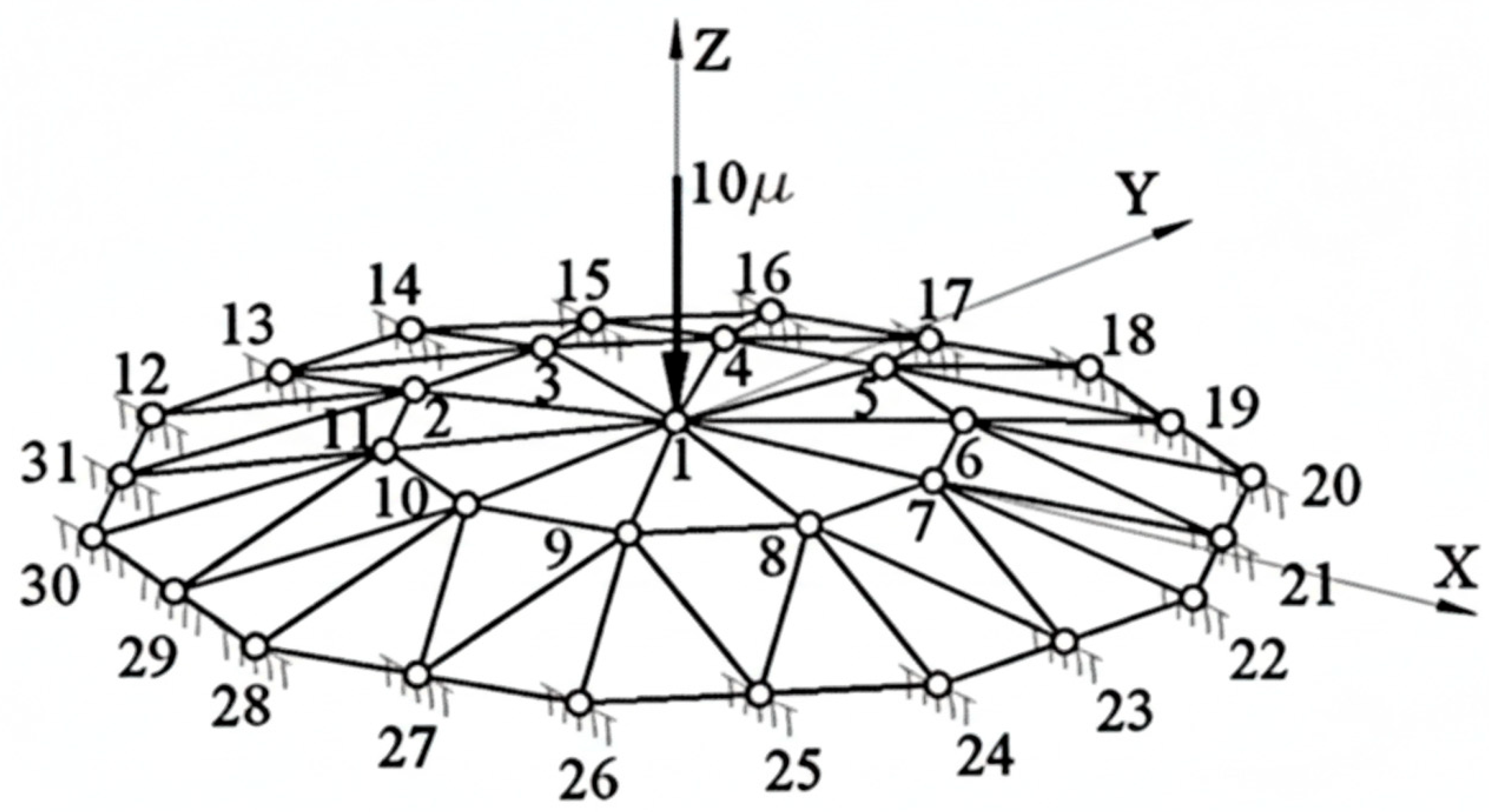
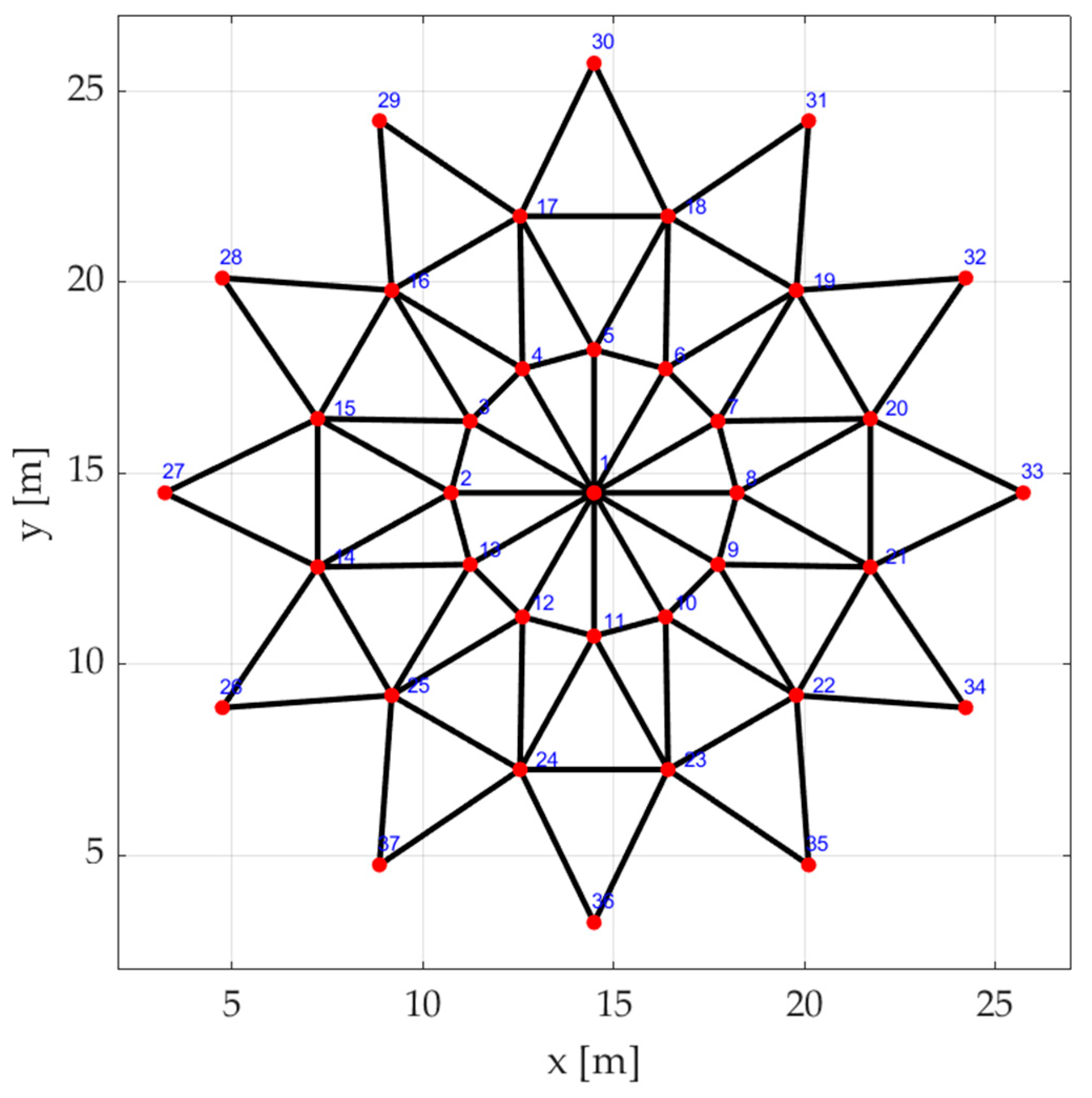

| SET1 | SET2 | SET3 | SET4 | |
|---|---|---|---|---|
| Number of nodes | 13 | 31 | 37 | 61 |
| Number of bars | 24 | 70 | 120 | 150 |
| Span (X) [m] | 80.60 | 20.00 | 22.50 | 30.00 |
| Width (Y) [m] | 100.00 | 19.02 | 22.50 | 28.54 |
| Height (Z) [m] | 8.22 | 0.52 | 0.90 | 1.49 |
| Computation Point | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| P [kN] | 207.40 | 212.73 | 200.90 | 189.09 | 188.47 | 177.27 |
| ηP | 100.00 | 102.57 | 96.87 | 91.17 | 90.87 | 85.47 |
| reliability index (β) | - | 1.44 | 2.056 | 3.128 | 3.431 | 5.199 |
| Computation Point | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| μ | 6.65 | 6.56 | 6.13 | 5.73 | 5.13 | 3.06 |
| ηP | 100 | 98.65 | 92.18 | 86.17 | 77.14 | 45.98 |
| reliability index βA | 0.177 | 0.320 | 0.892 | 1.340 | 1.891 | 3.264 |
| reliability index βB | 0.171 | 0.343 | 0.846 | 1.423 | 2.238 | 7.361 |
| Computation Point | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| P [kN] | 11.10 | 10.57 | 9.984 | 9.392 | 8.762 | 8.095 |
| ηP | 100.00 | 95.23 | 89.95 | 84.61 | 78.94 | 72.93 |
| reliability index (β) | - | 0.457 | 1.083 | 1.737 | 2.461 | 3.156 |
| Computation Point | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| μ | 17.95 | 17.40 | 16.07 | 15.08 | 13.84 | 10.38 |
| ηP | 100.00 | 97.05 | 89.01 | 84.01 | 77.07 | 57.83 |
| reliability index (β) | 0.19 | 0.48 | 1.10 | 1.48 | 1.89 | 2.81 |
| Approx Method | Mean Ep % | Correlation R | Proposed Formula |
|---|---|---|---|
| Linear function | 25.9806 | 0.8649 | β(ηP) = 10.5866 − 0.1046 ηP |
| Quadratic polynomial | 27.8116 | 0.8708 | β(ηP) = 6.8551 − 0.0023 ηP + 0.0007 (ηP)2 |
| Simple NN | 21.1510 | 0.9096 | Hidden formula of NN: 1–3–1 |
| Approx Method | Mean Ep % | Correlation R | Proposed Formula |
|---|---|---|---|
| Linear function | 3.42 | 0.9761 | β(ηP) = 10.5761 − 0.1052 ∙ ηP |
| Quadratic polynomial | 4.89 | 0.9887 | β(ηP) = 22.5385 − 0.3808 ∙ ηP + 0.0016 ∙ ηP 2 |
| Simple NN | 4.03 | 0.9758 | Hidden formula of NN: 1–5–1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Potrzeszcz-Sut, B.; Dudzik, A.; Kossakowski, P.G. Quantitative Assessment of the Reliability Index in the Safety Analysis of Spatial Truss Domes. Appl. Sci. 2025, 15, 12060. https://doi.org/10.3390/app152212060
Potrzeszcz-Sut B, Dudzik A, Kossakowski PG. Quantitative Assessment of the Reliability Index in the Safety Analysis of Spatial Truss Domes. Applied Sciences. 2025; 15(22):12060. https://doi.org/10.3390/app152212060
Chicago/Turabian StylePotrzeszcz-Sut, Beata, Agnieszka Dudzik, and Paweł Grzegorz Kossakowski. 2025. "Quantitative Assessment of the Reliability Index in the Safety Analysis of Spatial Truss Domes" Applied Sciences 15, no. 22: 12060. https://doi.org/10.3390/app152212060
APA StylePotrzeszcz-Sut, B., Dudzik, A., & Kossakowski, P. G. (2025). Quantitative Assessment of the Reliability Index in the Safety Analysis of Spatial Truss Domes. Applied Sciences, 15(22), 12060. https://doi.org/10.3390/app152212060








