Neural ODE-Based Frequency Stability Assessment and Control of Energy Storage Systems

Abstract

Frequency stability becomes more and more important with the increase in inverter-based resources in power systems. To enhance the frequency stability, this paper proposes a novel data-driven method for frequency stability assessment and control for energy storage systems (ESSs). Leveraging the neural ordinary differential Equation (ODE) framework, the method learns a continuous-time model of the system frequency dynamics. A neural-network-based controller is then designed according to the learned neural ODE model to enhance frequency stability. The training process involves an alternating optimization algorithm that updates both the neural ODE model and the controller parameters via the adjoint sensitivity method. Simulation results demonstrate that the proposed method accurately predicts frequency trajectories. Moreover, the designed controller reduces frequency deviation by 53%.

1. Introduction

A high penetration of inverter-based resources (IBRs), including renewable energy sources (RESs), energy storage systems (ESSs), high-voltage DC transmission systems, etc., has introduced more complexity into the power system. Due to the lack of physical inertia and damping compared with thermal synchronous generators, IBRs pose a significant impact to the frequency stability of power systems [1]. Moreover, uncertainty and fluctuation of RESs further cause large frequency deviation and oscillation [2]. Hence, it is necessary to build an accurate power system dynamics model and improve the ability of the frequency stability assessment and control.

It requires the frequency stability assessment to judge the reliability of power systems. Some methods output the decision-making results directly according to the system measurement [3], while other methods build the frequency dynamics model and evaluate the system stability indirectly [4]. Existing methods for the frequency stability assessment can be commonly divided into model-based methods and data-driven methods, as shown in Table 1. Model-based methods depend on the mathematical modeling or physical mechanism of power systems. The common model-based method is to build the models of the speed governor and the prime mover of the generating unit [5], but it is not suitable for inverter-dominated power systems that include many IBRs with various response characteristics. Reference [6] builds a state–space frequency prediction equation of voltage source converters and further designs a model predictive controller for fast frequency response. However, the tradeoff between accuracy and efficiency limits the application of the model-based method in power systems, as the accuracy usually depends on complex modeling that needs more computation resources [4].

The data-driven methods include statistical analysis [7], system identification [8], decision-tree learning [9], support vector machines (SVM) [10], etc. Recently, deep learning has achieved significant success in many research fields. Deep learning appears to be a promising method for predicting frequency dynamics and stability analysis, which can reduce online computational burden by learning historical data offline. In [11], an extreme learning machine method is utilized to design a stability assessment model considering various system topologies. In [12], a deep belief network (DBN)-based nonlinear representation learning method is proposed to assess the stability according to the power flow and voltage measurement. Reference [13] uses deep Koopman-based inference network to learn the power system dynamics and model predictive control (MPC) to enhance frequency stability.

The assessment method that learns the system dynamics is more beneficial for controller design. However, typical neural networks can only learn discrete-time dynamics. The discretization step size decides the accuracy of the assessment method, resulting in a tradeoff between accuracy and computational cost. Recently, neural ordinary differential Equation (ODE) models [14] have demonstrated the ability to model continuous-time systems, which provides an approach for solving continuous-time control tasks efficiently and accurately.

Table 1. Comparison of frequency stability assessment methods.

Category	Method	Modeling Approach
Model-based methods	State–space model [6], physical modeling [5], etc.	Physics-based equations
Data-driven methods	Decision tree [9], SVM [10], DBN [12], etc.	Discrete-time black-box models
Hybrid methods	Model and data-driven [4]	Partial modeling and data completion

Table 1. Comparison of frequency stability assessment methods.

Category	Method	Modeling Approach
Model-based methods	State–space model [6], physical modeling [5], etc.	Physics-based equations
Data-driven methods	Decision tree [9], SVM [10], DBN [12], etc.	Discrete-time black-box models
Hybrid methods	Model and data-driven [4]	Partial modeling and data completion

Currently, using neural controllers is a dominant approach in reinforcement learning [15], relying on the universal approximation capacity of neural networks [16]. However, the RL training usually requires lots of trajectory samplings to estimate the objective to be optimized. If the system dynamics is known, it is possible to optimize the controller efficiently based on an optimal control method [17].

To this end, this paper proposes a neural ODE-based frequency stability assessment and control method for ESSs. First, two neural networks are utilized to build the frequency dynamics model and frequency controller, respectively. Then, the frequency dynamics model can learn the true dynamics of the system through the ODE solver and adjoint method. Further, the frequency dynamics model is used to evaluate the performance of the neural controller, which provides optimization direction to update the controller. Thereafter, an alternative optimization algorithm for the neural ODE model and the controller is designed to improve the performance of the frequency stability assessment and control.

The rest of this paper is organized as follows. Section 2 describes the proposed method for the frequency stability assessment and control. Section 3 presents the simulation results of the proposed method. Finally, the paper concludes in Section 4.

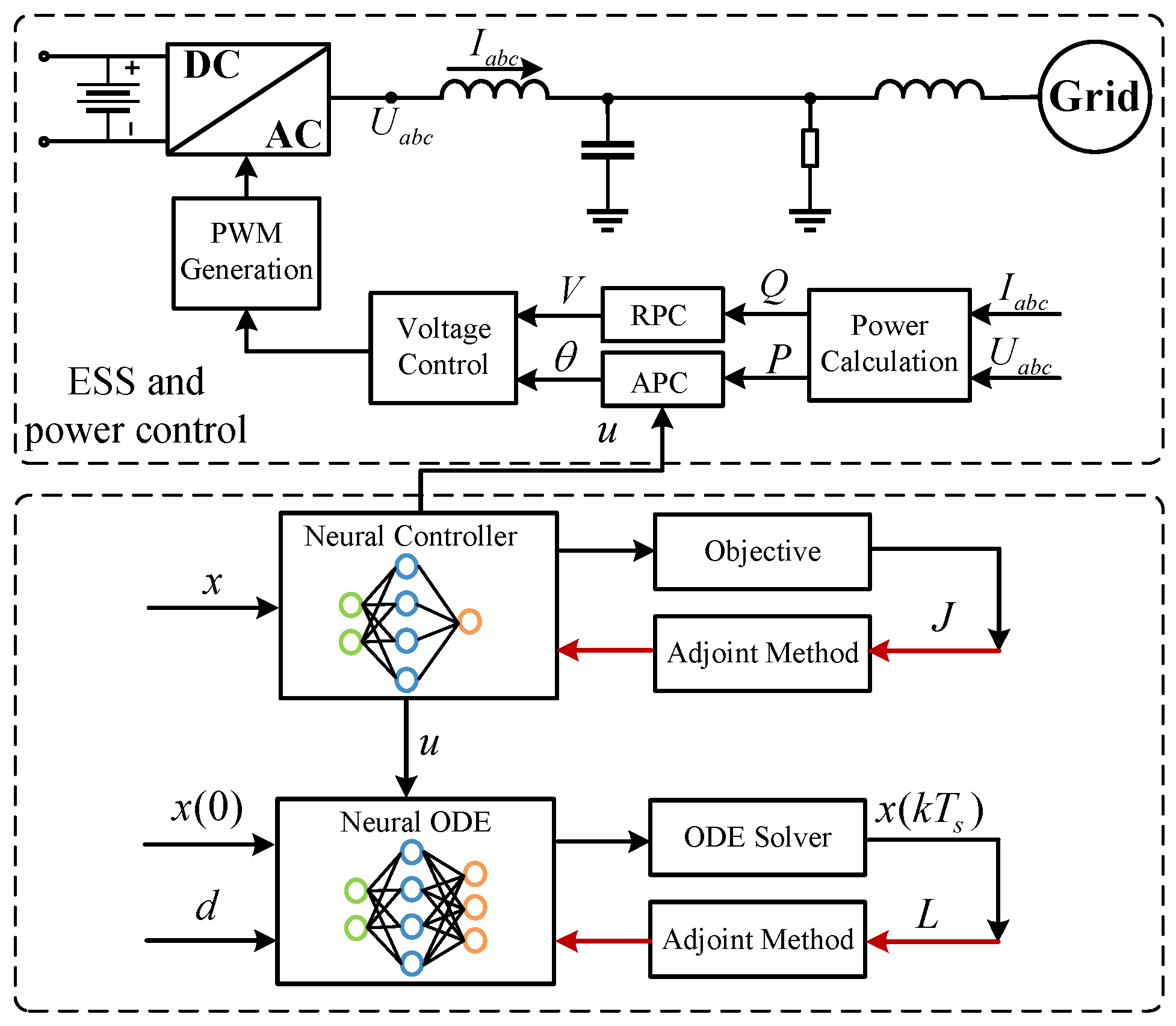
2. Methodology

The framework of the proposed method is shown in Figure 1. The primary control of the ESS consists of the active power control (APC) and the reactive power control (RPC). The APC regulates the active power output through changing the power angle of the ESS, while the RPC regulates the reactive power through changing the voltage magnitude. The proposed method learns the frequency dynamics of the ESS and regulates APC to enhance frequency stability.

2.1. Frequency Stability Assessment

The APC of the ESS based on a typical virtual synchronous generator method can be expressed as

$$\begin{array}{cc}\hfill \dot{\delta }& =\omega \hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill 2H\dot{\omega }& =-D\omega +P-P_e+u,\hfill \end{array}$$

(2)

where $\delta$ is the angle difference between the converter and the power grid, $\omega$ is the frequency deviation, u is the control input to provide additional frequency response, H, D, P and $P_e$ are the emulated inertia, damping coefficient, active power reference and active power output, respectively. The above model is decided by the control law of the converter and does not consider the response of the converter. Hence, we use the neural ODE method [14] to learn the system frequency dynamics:

$$\dot{x}=f(x,u,d),$$

(3)

where $x={[\delta ,\omega ]}^{\top }$ represents the state and d represents the system disturbance, including the change in the active power reference and load.

A neural ODE model $f_{\theta }$ parameterized by $\theta$ is designed to approximate f. If the system sampling period $T_s$, the optimization problem of the model is as follows:

$$\begin{array}{cc}\hfill \underset{\theta }{\min }& L=\sum _{k=0}^N\parallel x\left(k{T}_s\right)-y_k\parallel \hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}& x\left(k{T}_s\right)=x\left(0\right)+{\int }_0^{k{T}_s}{f}_{\theta }(x\left(t\right),u\left(t\right),d)\mathrm{d}t,\hfill \end{array}$$

(5)

where $y_k$ is the measured state from the system at time step k. In practice, the estimated state is the result of an ODE solver, so the main challenge in solving the problem (4) and (5) is performing the backpropagation through the ODE solver, which requires the gradients with respect to $\theta$. The backpropagation of the neural ODE is achieved by the adjoint method. Define the adjoint $a\left(t\right)$ and its dynamics:

$$\dot{a}\left(t\right)=-a{\left(t\right)}^{\top }{\displaystyle \frac{\partial f_{\theta }(x\left(t\right),u\left(t\right),d)}{\partial x}}.$$

(6)

The adjoint can be solved by the ODE solver with the initial value $a\left(k{T}_s\right)=$$\partial x\left(k{T}_s\right)/\partial x\left(k{T}_s\right)=1$. According to the adjoint sensitivity method, the gradient with respect to the parameters $\theta$ is

$${\displaystyle \frac{\mathrm{d}x\left(k{T}_s\right)}{\mathrm{d}\theta }}={\int }_{k{T}_s}^{0}a{\left(t\right)}^{\top }{\displaystyle \frac{\partial f_{\theta }(x\left(t\right),u\left(t\right),d)}{\partial \theta }}\mathrm{d}t.$$

(7)

As a result, the gradient of L with respect to the parameter $\theta$ can be obtained by the chain rule

$${\displaystyle \frac{\mathrm{d}L}{\mathrm{d}\theta }}=\sum _{k=0}^N{\displaystyle \frac{\mathrm{d}L}{\mathrm{d}x\left(k{T}_s\right)}}{\displaystyle \frac{\mathrm{d}x\left(k{T}_s\right)}{\mathrm{d}\theta }}.$$

(8)

Hence, the parameter $\theta$ can be adjusted by the gradient (8) to minimize the objective (4).

After the training, the frequency dynamics can be predicted by the neural ODE model $f_{\theta }$ to assess the frequency stability when changing the active power reference or occurring load disturbances. To predict the frequency response under the load disturbances, it is necessary to measure the disturbance signal previously. According to the relationship between the maximum RoCoF ${\dot{\omega }}_{max}$ and the disturbance, the disturbance magnitude can be estimated by ${\dot{\omega }}_{max}=d/2H$ [18]. The maximum RoCoF ${\dot{\omega }}_{max}$ is measured at the instant of frequency change, before any control input is implemented.

2.2. Neural Frequency Control

To further reduce the frequency deviation, a neural controller $u_{\rho }\left(x\right)$ parameterized by $\rho$ is designed to decide the control input u. Hence, the frequency dynamics can be predicted by a coupled neural ODE model:

$$\dot{x}=f_{\theta }(x,u_{\rho }\left(x\right),d).$$

(9)

The control objective is to minimize the frequency deviation:

$$\underset{\rho }{min}J=\sum _{k=0}^N{T}_s(\parallel x\left(k{T}_s\right){\parallel }_Q+\parallel u\left(k{T}_s\right){\parallel }_R),$$

(10)

where Q and R are the state cost matrix and control cost matrix, respectively. Similarly to the optimization method for problem (4) and (5), the gradient of J with respect to the parameter $\rho$ is

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}L}{\mathrm{d}\rho }}& =\sum _{k=0}^N{\displaystyle \frac{\mathrm{d}J}{\mathrm{d}x\left(k{T}_s\right)}}{\displaystyle \frac{\mathrm{d}x\left(k{T}_s\right)}{\mathrm{d}\rho }}\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}x\left(k{T}_s\right)}{\mathrm{d}\rho }}& ={\int }_{k{T}_s}^{0}a{\left(t\right)}^{\top }{\displaystyle \frac{\partial f_{\theta }(x\left(t\right),u_{\rho }\left(x\right),d)}{\partial \rho }}\mathrm{d}t.\hfill \end{array}$$

(12)

Hence, the controller can be updated by the gradient (11).

In the frequency control task, the control input u can not affect the steady state of the system, i.e., $u=0$ when the system frequency deviation $\omega =0$. To satisfy the condition, each layer of the neural controller has no biases and uses the tanh activation function.

2.3. Algorithm

The neural ODE model $f_{\theta }$ and the controller $u_{\rho }$ are optimized alternately. The accuracy of the model $f_{\theta }$ determines the effectiveness of the controller optimization. Hence, it is necessary to update the model $f_{\theta }$ first according to the real trajectories. On the other hand, the controller may change the distribution of the state space, thus the neural ODE model needs to be trained again. As the controller $u_{\rho }$ is optimized, the model $f_{\theta }$ still needs to be further updated. Overall, the optimization method is as shown in Algorithm 1.

In each epoch, the algorithm collects the trajectory in I episodes and then updates the neural ODE model and controller. The number of episodes I is chosen to provide a sufficiently large dataset to optimize the model. The length of each episode N allows the model to capture the complete dynamics, which should be large enough. The learning rates for the model and controller should be relatively small to ensure stable convergence.

Algorithm 1 Optimizing neural ODE model and controller

Input: Power system environment f; Output: Parameters of neural ODE model $\theta$ and $\rho$;   1: Initialize the parameters $\theta$ and $\rho$;   2: for epoch $=1:E$ do   3:       for episode $=1:I$ do   4:             Obtain the initial state $y_0$ and system disturbance d;   5:             for $k=0:N$ do   6:                   Execute control input $u=u_{\rho }\left(y_k\right)$;   7:                   Observe the next state $y_{k+1}$;   8:             end for   9:             Store the trajectory $[y_0,..,y_N]$ in the buffer; 10:       end for 11:      for $i=0:I$ do 12:             Sampling a trajectory $[y_0,..,y_N]$ from buffer; 13:             Predict the trajectory $x\left(k{T}_s\right)$ through $f_{\theta }$ with the inital value $x\left(0\right)=y_0$; 14:             Compute the loss function L; 15:             Compute the gradient $g_1=\mathrm{d}L/\mathrm{d}\theta$; 16:             $\theta \leftarrow \theta -{\alpha }_1{g}_1$; 17:      end for 18:      for $i=0:I$ do 19:             Predict the trajectory $x\left(k{T}_s\right)$ through $f_{\theta }$ with the inital value $x\left(0\right)=y_0$; 20:             Compute the objective function J; 21:            Compute the gradient $g_2=\mathrm{d}x\left(k{T}_s\right)/\mathrm{d}\rho$; 22:            $\rho \leftarrow \rho -{\alpha }_2{g}_2$; 23:      end for 24: end for

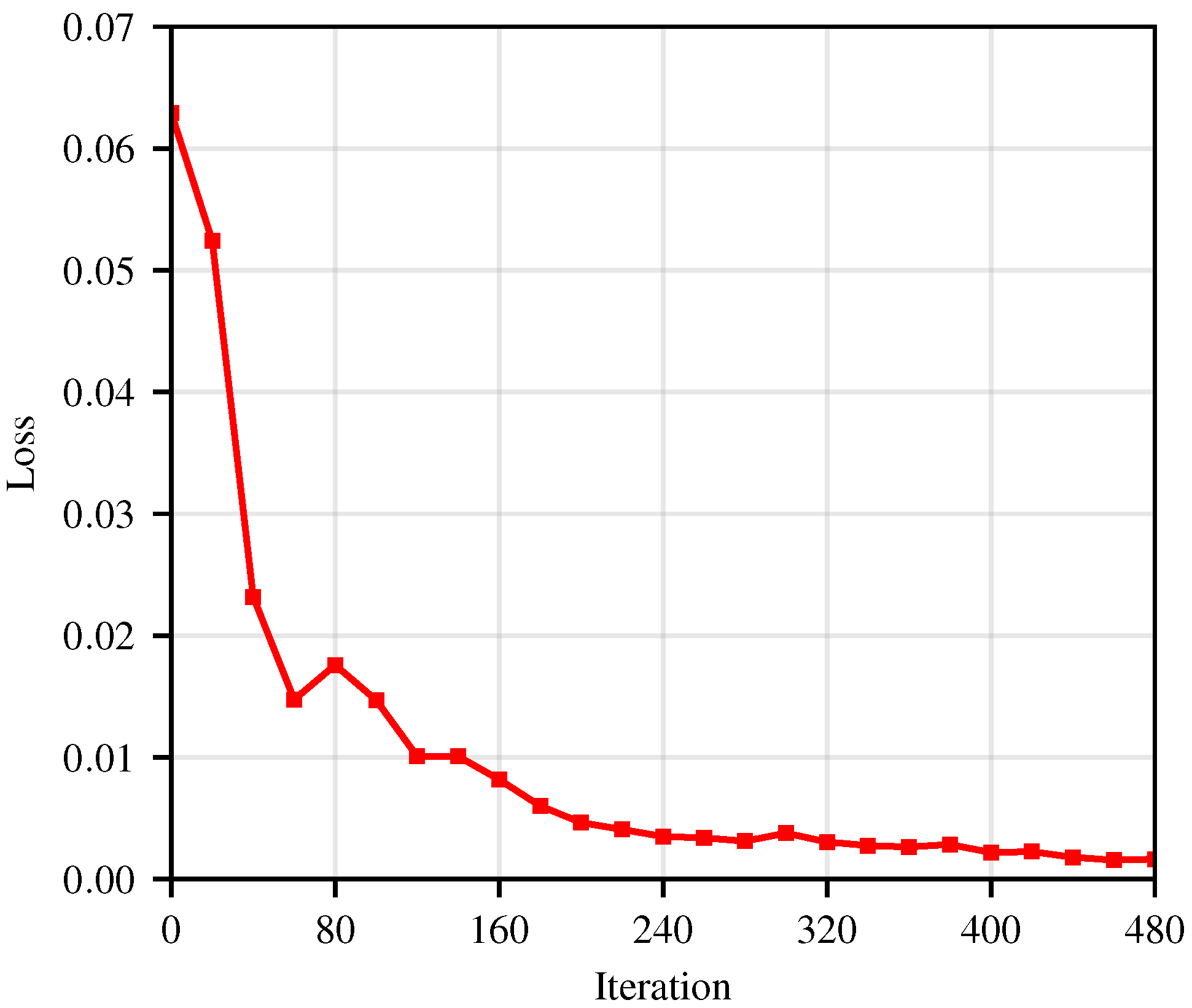
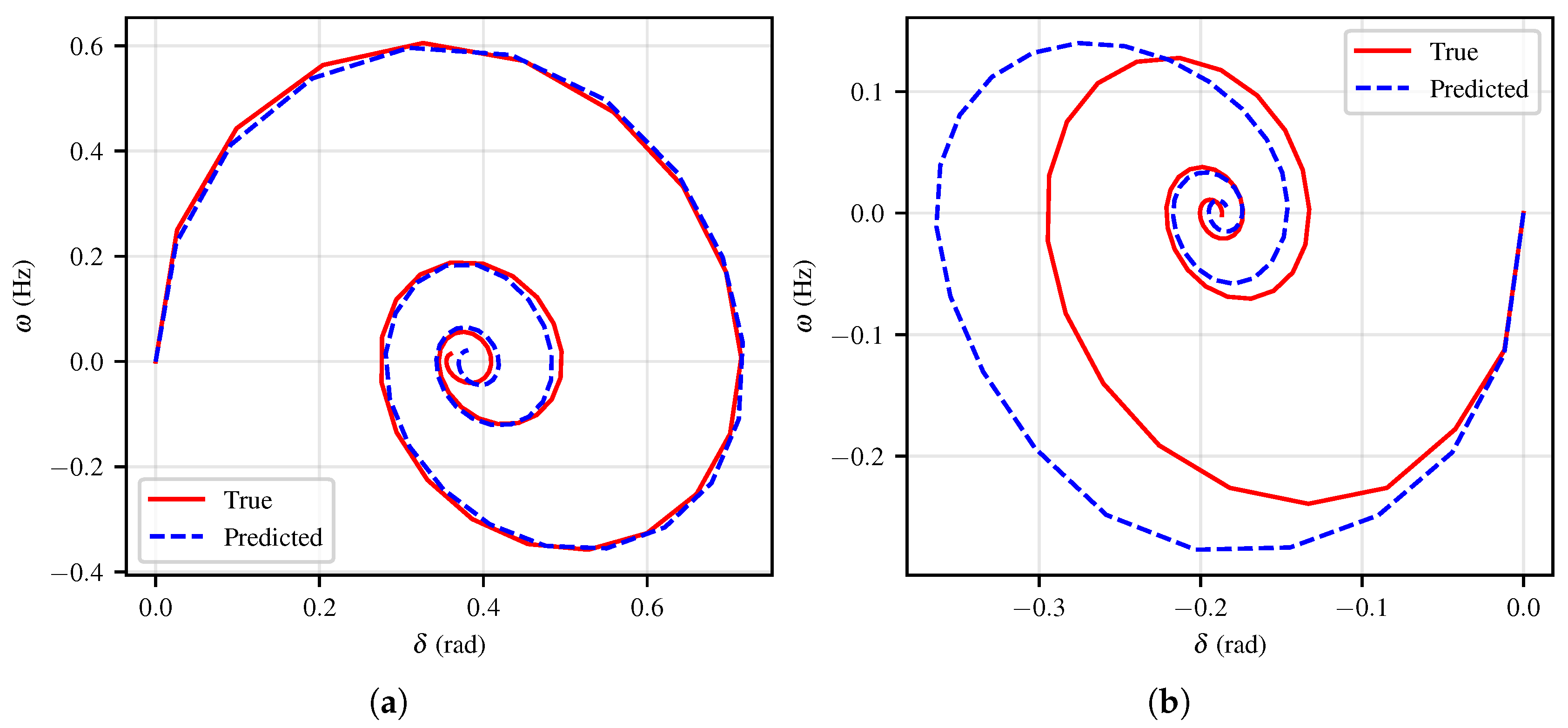
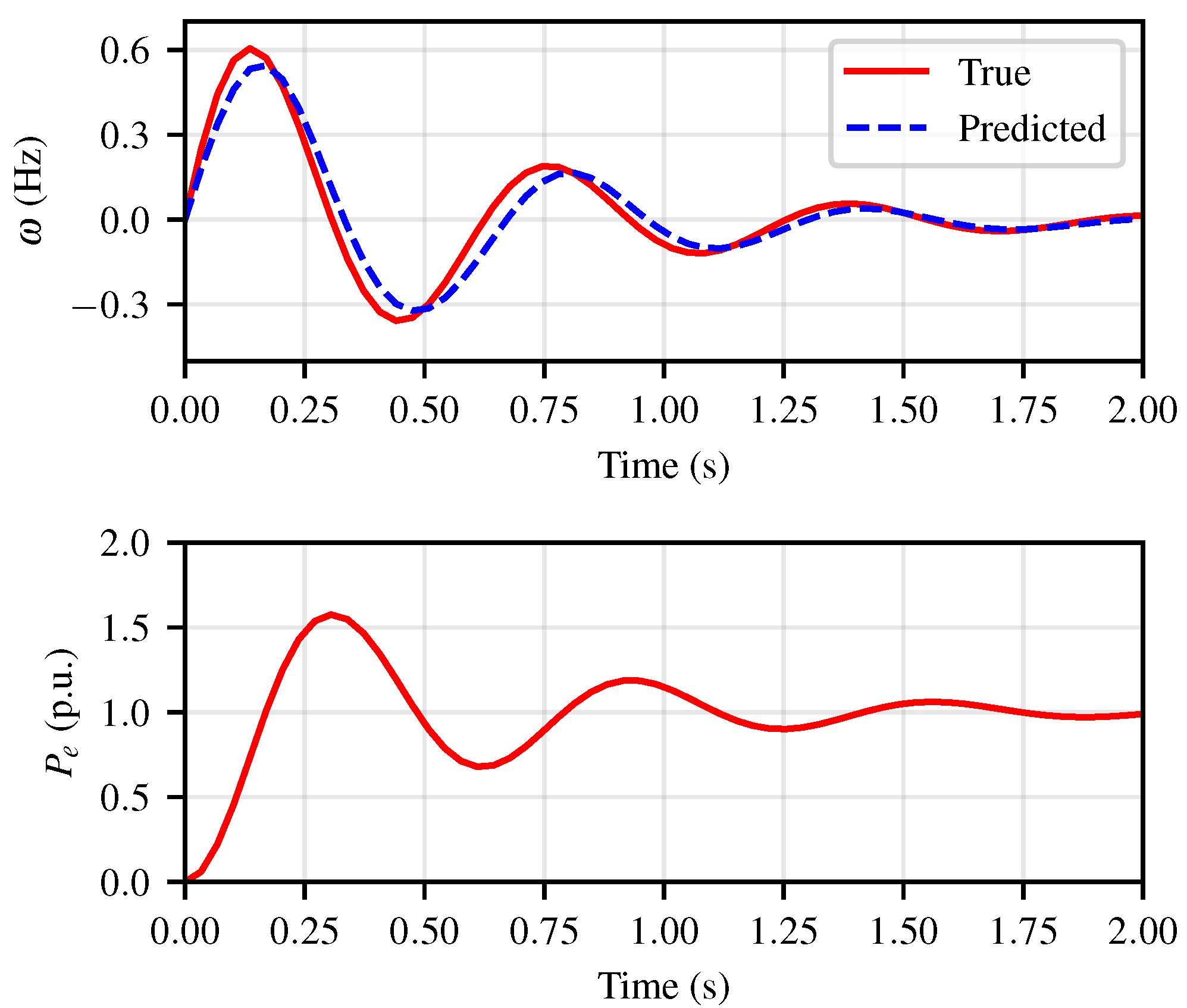
3. Simulation Results

The proposed method is validated on the ESS connected with an infinite bus. The ESS implements the virtual synchronous generator control method as shown in Equation (1), where $H=4$ and $D=40$. The ODE model $f_{\theta }$ is employed with four hidden layers consisting of 50 neurons each and a controller $u_{\rho }$ with one hidden layer consisting of 50 neurons. All hidden layers use the tanh activation function.

To train the model in Algorithm 1, the number of episodes I and the length of each episode N are set as 100 and 60, respectively. The length of each episode is large enough to capture complete frequency dynamics. Satisfactory control performance is achieved in two epochs of the alternative training. The state cost matrix Q and control cost matrix R are set as $[0,0;0,1]$ and $0.01$, respectively.

The step lengths ${\alpha }_1$ and ${\alpha }_2$ are all set as $0.003$. The sampling period $T_s$ is $1/30$ s. The real trajectories of the power system environment are obtained from the simulation in Python 3.11 and Andes [19], a software for symbolic power system modeling and numerical analysis.

To improve the training efficiency of the algorithm, the neural ODE model is initialized by the trajectories without controllers. The system dynamics data is collected to train the neural ODE model. The loss function L through the training is shown in Figure 2. It can be seen that the training error of the neural ODE model decreases gradually.

After the initialization, the trajectories of the ESS under two different cases are collected. The first case is to regulate the active power references from 0 to 1 p.u., and the other case is 1 p.u. step load increase. The true trajectories are compared with the predicted trajectories by the model $f_{\theta }$. Figure 3a illustrates the system dynamics when regulating the active power references at $t=0$ s. The neural ODE model can predict the system dynamics accurately, which can be utilized to evaluate the frequency nadir and RoCoF before regulating the output power of ESS. Figure 3b illustrates the system dynamics in the case of the step load increase occurring at $t=0$ s. There exists a certain approximate error, which may be caused by the inaccurate load disturbance estimation.

To illustrate the optimization process, the control performance of the controller $u_{\rho }$ at the end of each epoch is tested. At $t=0$ s, the active power reference of the ESS is adjusted from 0 to 1 p.u. The frequency and control input response after each epoch are shown in Figure 4 and Figure 5. Comparing Figure 4 and Figure 5, the controller reduces the frequency deviation and suppresses overshoot of the active power output of the ESS effectively. In addition, the neural ODE still predicts frequency dynamics well. In Figure 5b, it can be seen that the controller is further optimized and the frequency deviation becomes smaller.

The frequency dynamics and control performance when occurring 1 p.u. step load increase are tested in the simulation. The control performance of the MPC-based method [12] and the proposed method is evaluated by the integral absolute error and nadir of the frequency deviation in

Table 2. Comparisons of control performance.

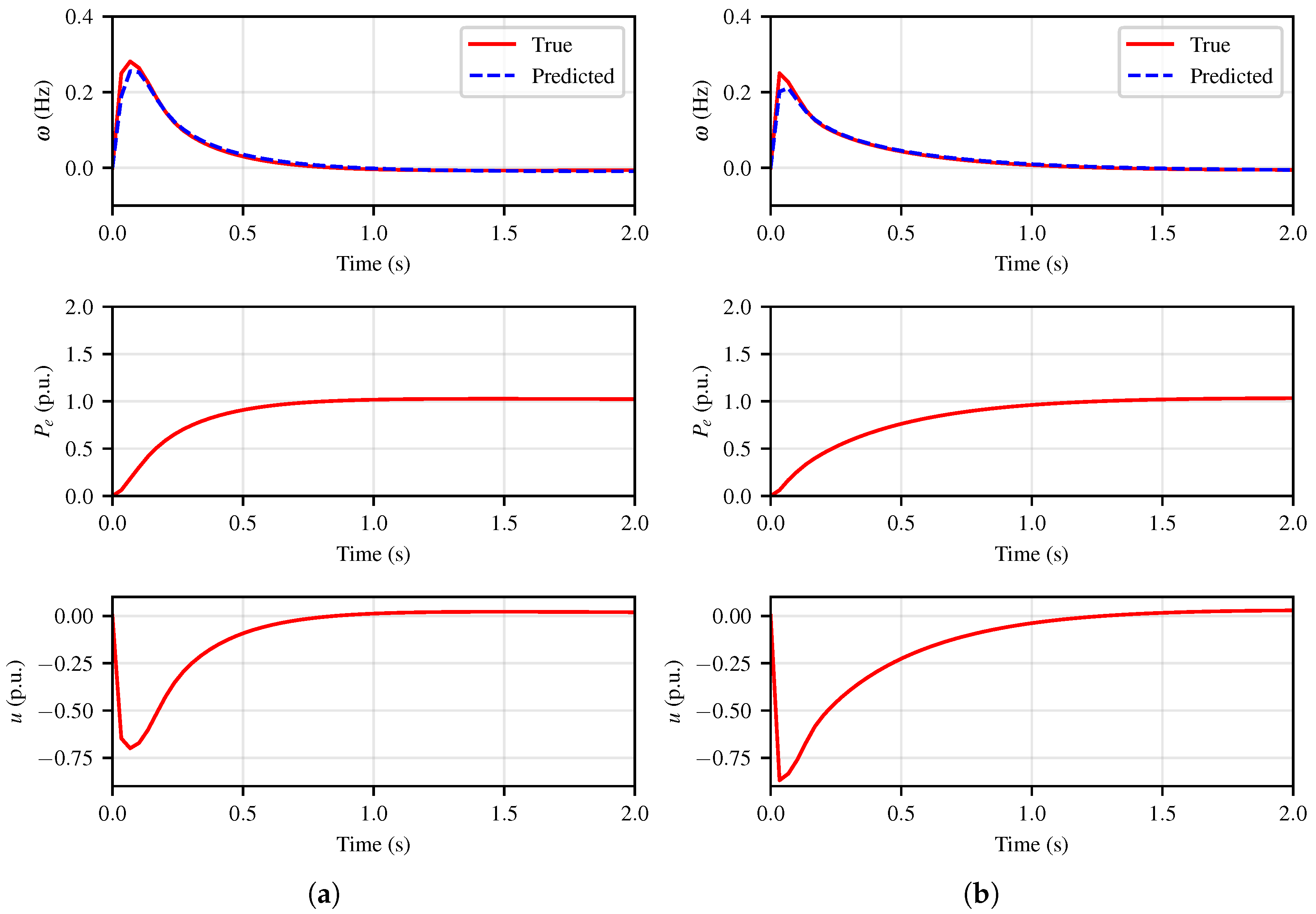
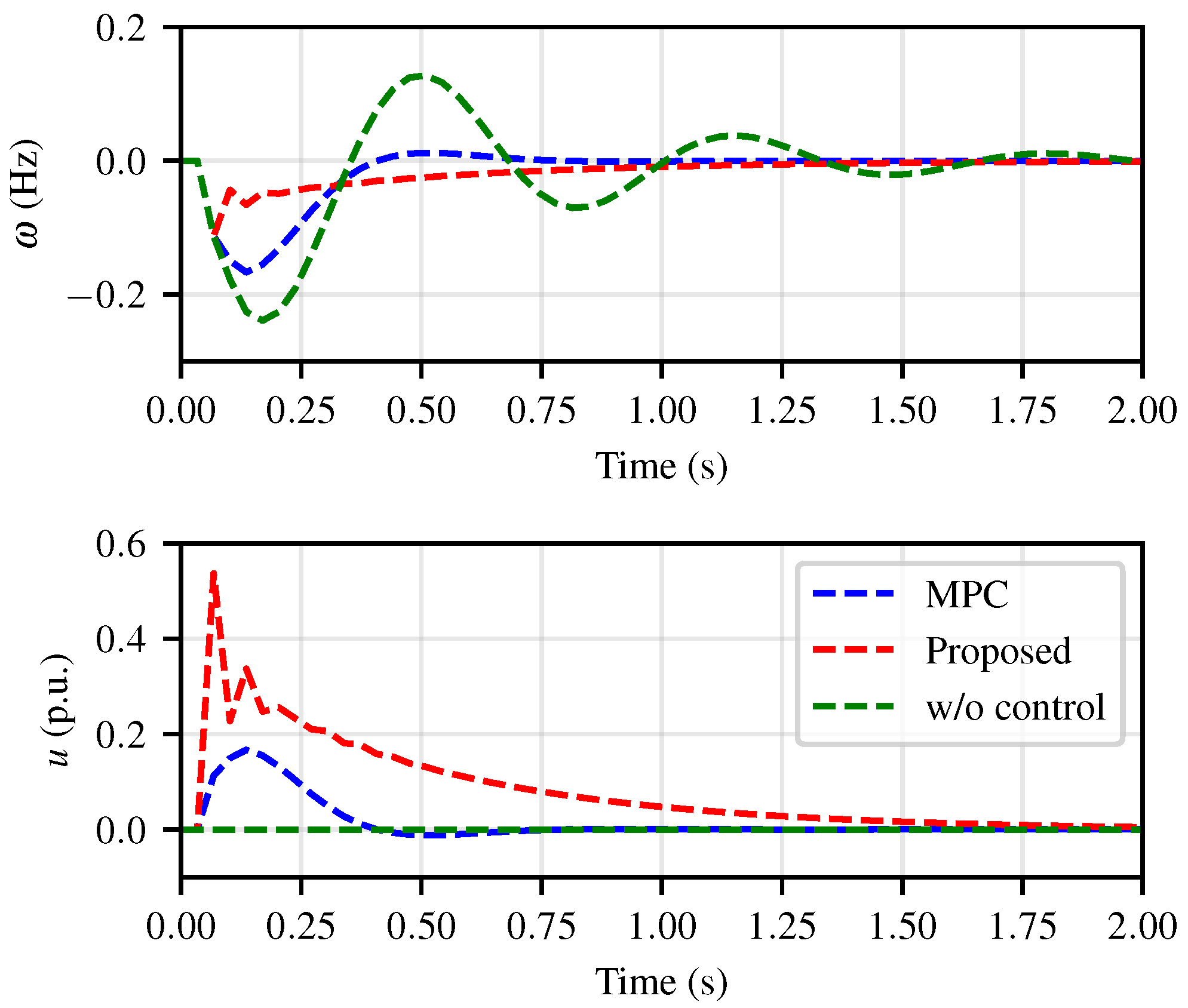
Controller	IAE (Hz)	Nadir (Hz)
MPC [12]	0.0356	−0.1670
Proposed	0.0314	−0.1127
w/o control	0.1019	−0.2392

. It can be seen that the proposed method achieves the smallest frequency deviation and nadir. As shown in Figure 6, the frequency deviation is reduced by the optimized controller, which demonstrates the effectiveness of the proposed method.

4. Conclusions

This paper has presented a neural ODE-based framework for frequency stability assessment and control of ESSs. The proposed method predicts the frequency dynamics accurately and provides the reference model for the controller optimization. The optimized controller reduces the frequency deviation and oscillation effectively. The effectiveness of the proposed method lies in the combination of the neural ODE model with the neural controller. In the proposed framework, an alternative training algorithm for the neural ODE model and controller is designed to reduce the prediction error of the system frequency and improve the control performance. The proposed algorithm is tested on the simulation to validate its outstanding performance.

Future work should include building neural stochastic ODEs to improve the robustness of the controller and neural differential algebraic equations for large power systems.