Orderly Charging Scheduling for EVs with a Novel Queuing Model Under Power Capacity Constraints
Abstract
1. Introduction
1.1. Background
1.2. Literature Review
1.3. Contributions and Organization
- Inaccurate Queueing Modeling: Traditional queueing theory often fails to precisely calculate waiting times from the station’s perspective under dynamic charging states and power constraints. A more granular model that captures the real-time state of the charging queue is needed for realistic user satisfaction evaluation.
- Uncoordinated Objectives: A significant limitation is the frequent disconnect between the objectives of minimizing grid load fluctuations and minimizing user queue times. An integrated framework that simultaneously addresses both operational and user-centric goals is lacking.
- Computational Inefficiency for Integrated Models: The integration of detailed queueing models with multi-stage, power-constrained scheduling leads to complex problems. There remains a need for efficient solution methods that can handle this integrated complexity for practical-scale problems.
- We introduce a novel queuing model with virtual charging piles and state variables to accurately calculate EV waiting times, addressing the first gap.
- We formulate a bi-level optimization model that explicitly co-optimizes the goal of flattening the station’s load profile with the objective of minimizing user queue times, thereby bridging the second gap.
- We develop an adaptive large-neighborhood search (ALNS) algorithm, which hybridizes heuristics with a mathematical solver, to solve the resulting complex model efficiently, which addresses the third gap.
2. Problem Formulation for EV Charging Scheduling
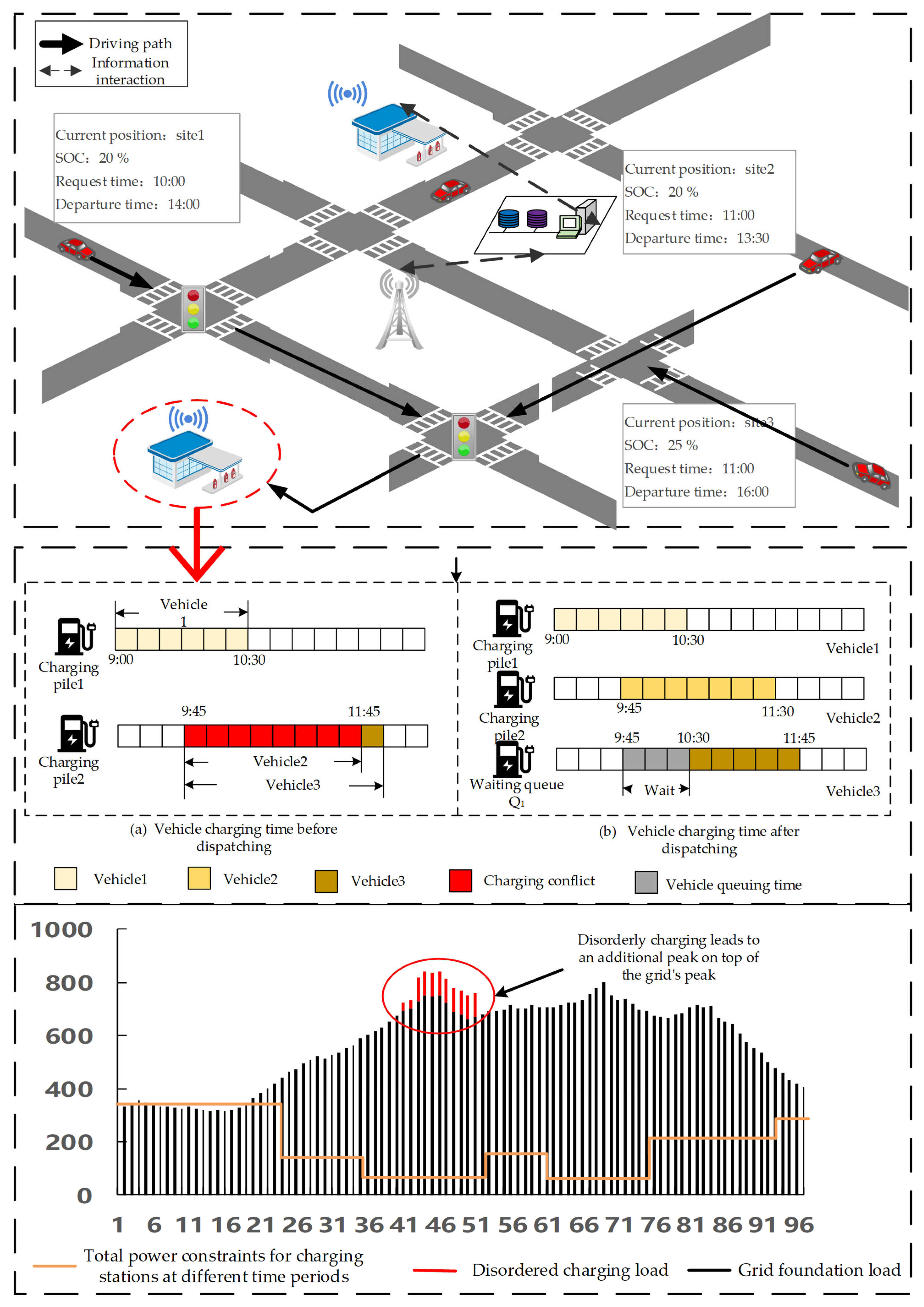
2.1. Problem Description
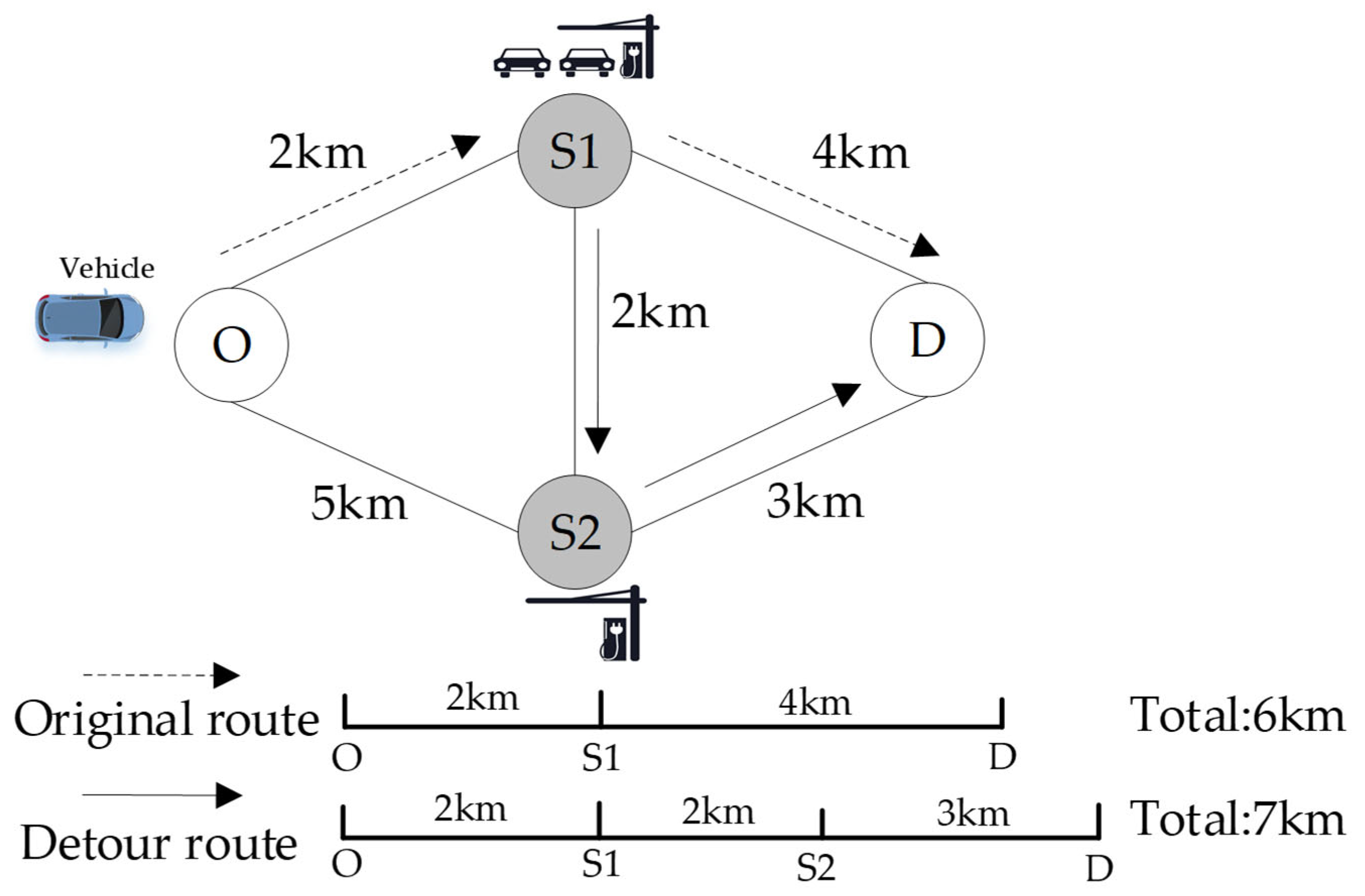
2.2. Charging Scheduling Process and Detour Compensation
- The shortest path from the user’s origin to destination that includes any suitable charging station.
- The shortest path from the origin to destination that includes the specifically assigned charging station.
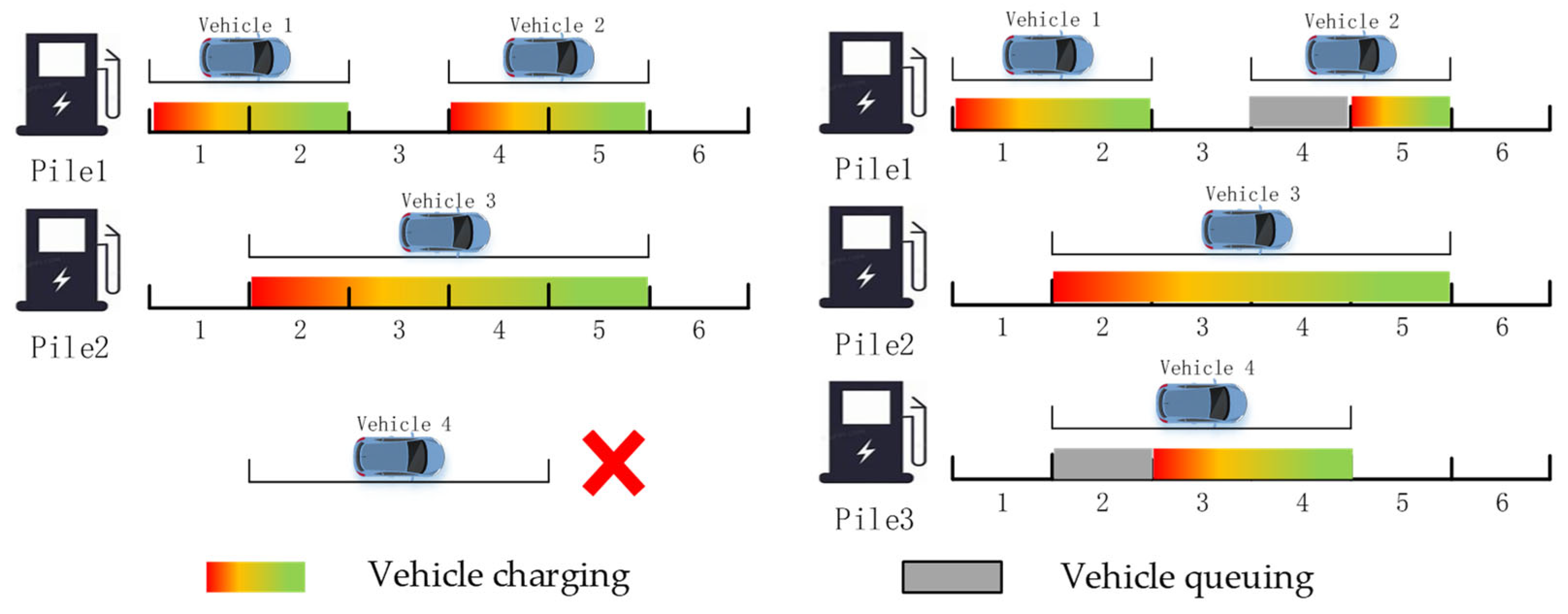
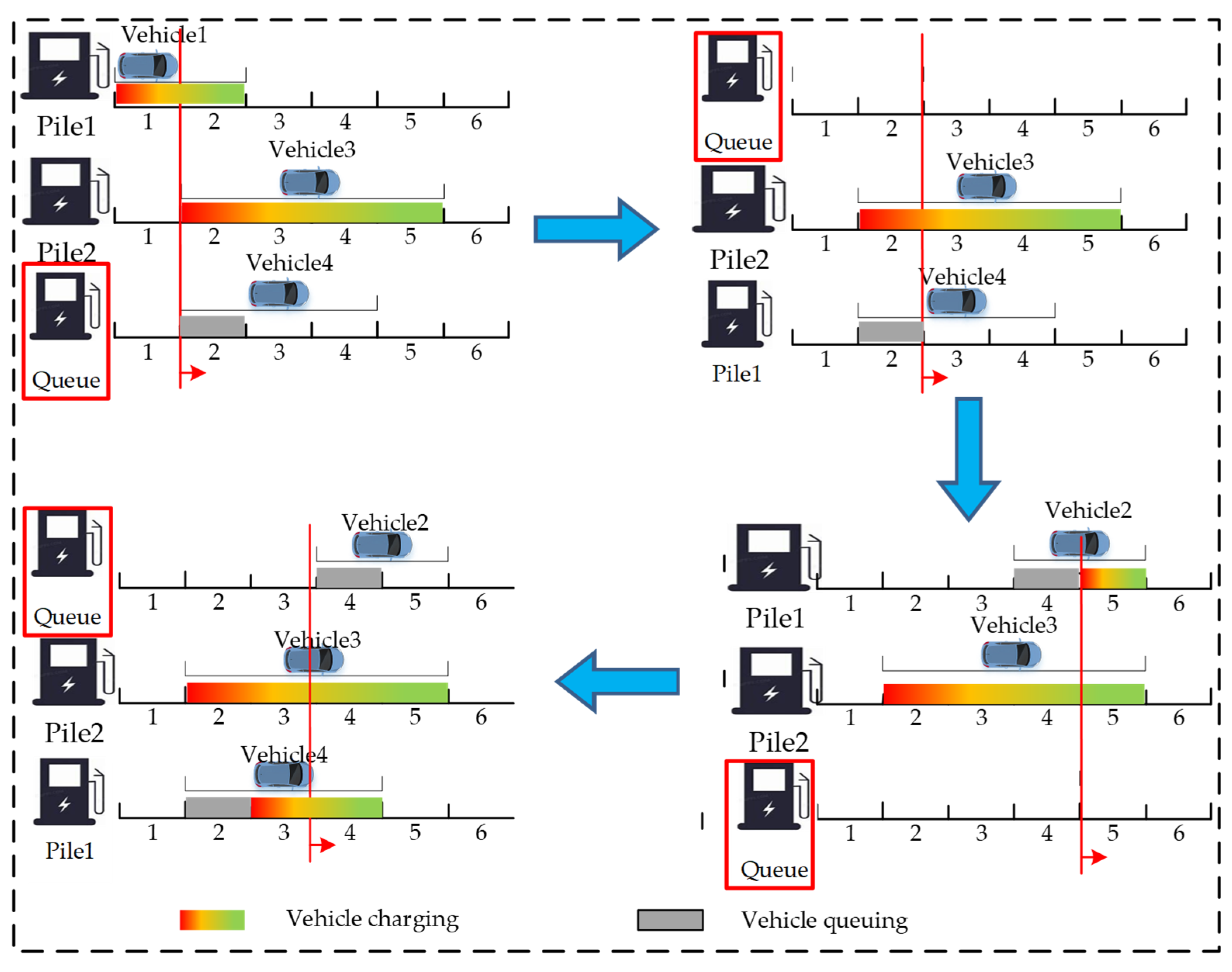
2.3. Modeling Approach for EV Charging Queue Status
3. Model Formulation
3.1. Model Assumptions and Notation
3.2. Formalization of the Queuing Discipline and Causality
3.3. Optimization Model
3.3.1. Upper-Level Model
3.3.2. Lower-Level Model
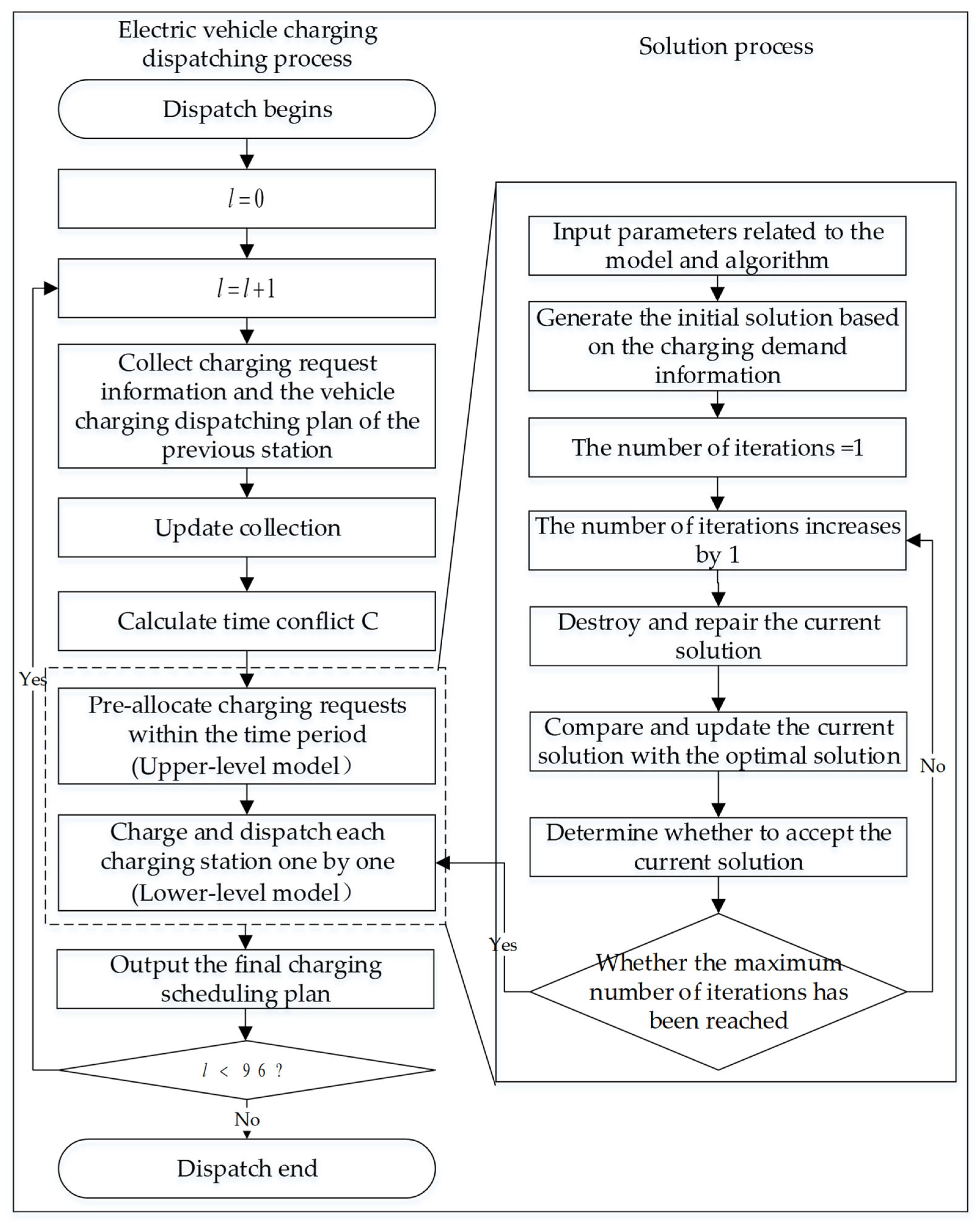
4. Solution Methodology
4.1. Model Analysis and Solution Framework
4.2. Initial Solution Generation
4.3. Removal Operators
- (1)
- Random Removal Operator
- (2)
- Longest Queue Removal Operator
- (3)
- Maximum Conflict Removal Operator
- (4)
- Maximum Detour Cost Removal Operator
- (5)
- Maximum Unserved Users Removal Operator
4.4. Insertion Operators
- (1)
- Random Insertion Operator
- (2)
- Shortest Queue Insertion Operator
- (3)
- Minimum Conflict Insertion Operator
4.5. Solution Feasibility Repair
4.6. Search Weight Adjustment
4.7. Algorithm Solution Procedure
| Algorithm 1. Improved Adaptive Large Neighborhood Search | |
| Input: Network data, EV data, ALNS parameters. | |
| Output: Best scheduling scheme , | |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | do |
| 6 | Select removal operator and insertion operator via roulette wheel |
| 7 | |
| 8 | |
| 9 | |
| 10 | then |
| 11 | |
| 12 | end if |
| 13 | then |
| 14 | |
| 15 | |
| 16 | then |
| 17 | |
| 18 | end if |
| 19 | moddecayInterval == 0 then |
| 20 | |
| 21 | end if |
| 22 | |
| 23 | end for |
| 24 | |
5. Computational Experiments and Results Analysis
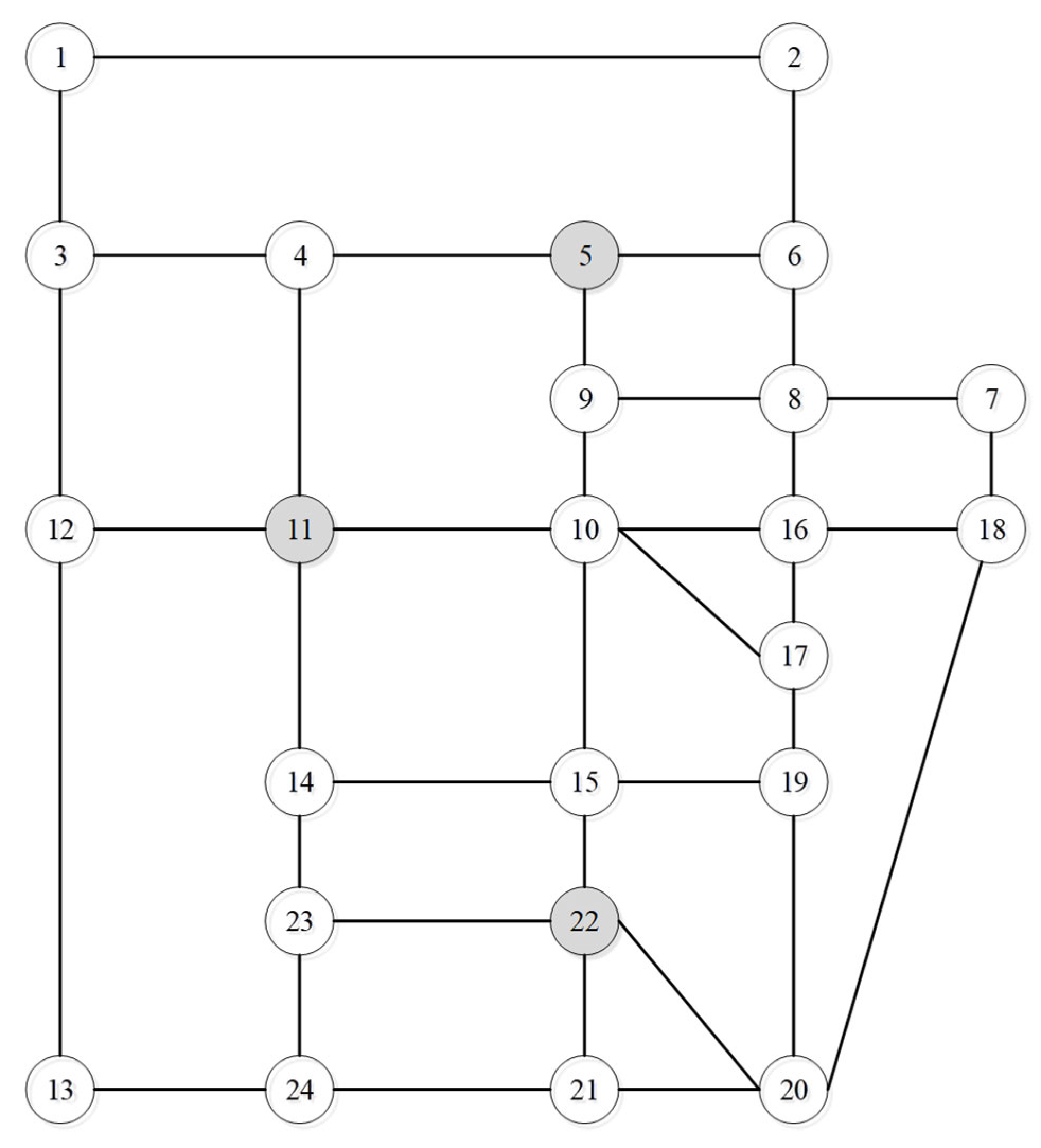
5.1. Small-Scale Instances
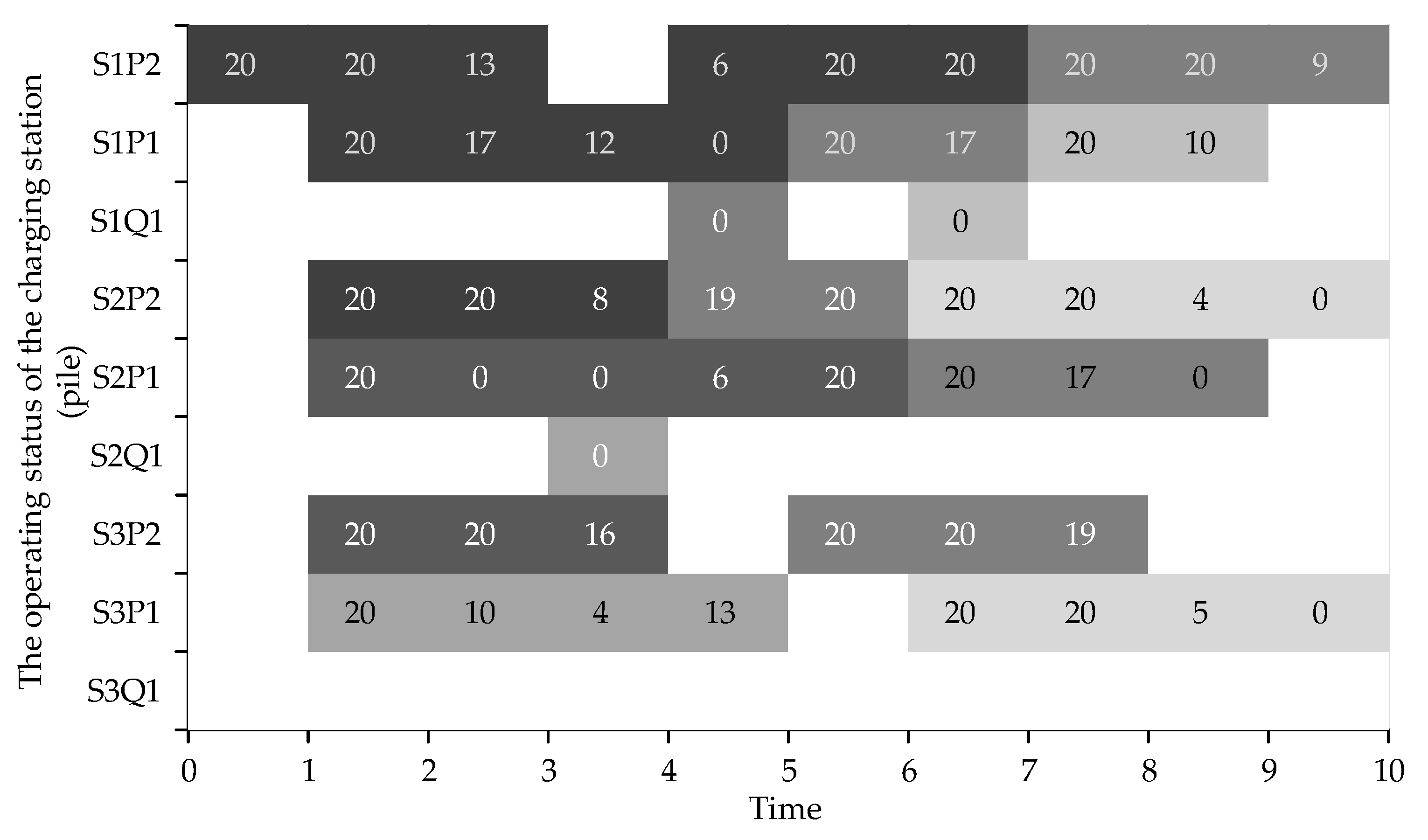
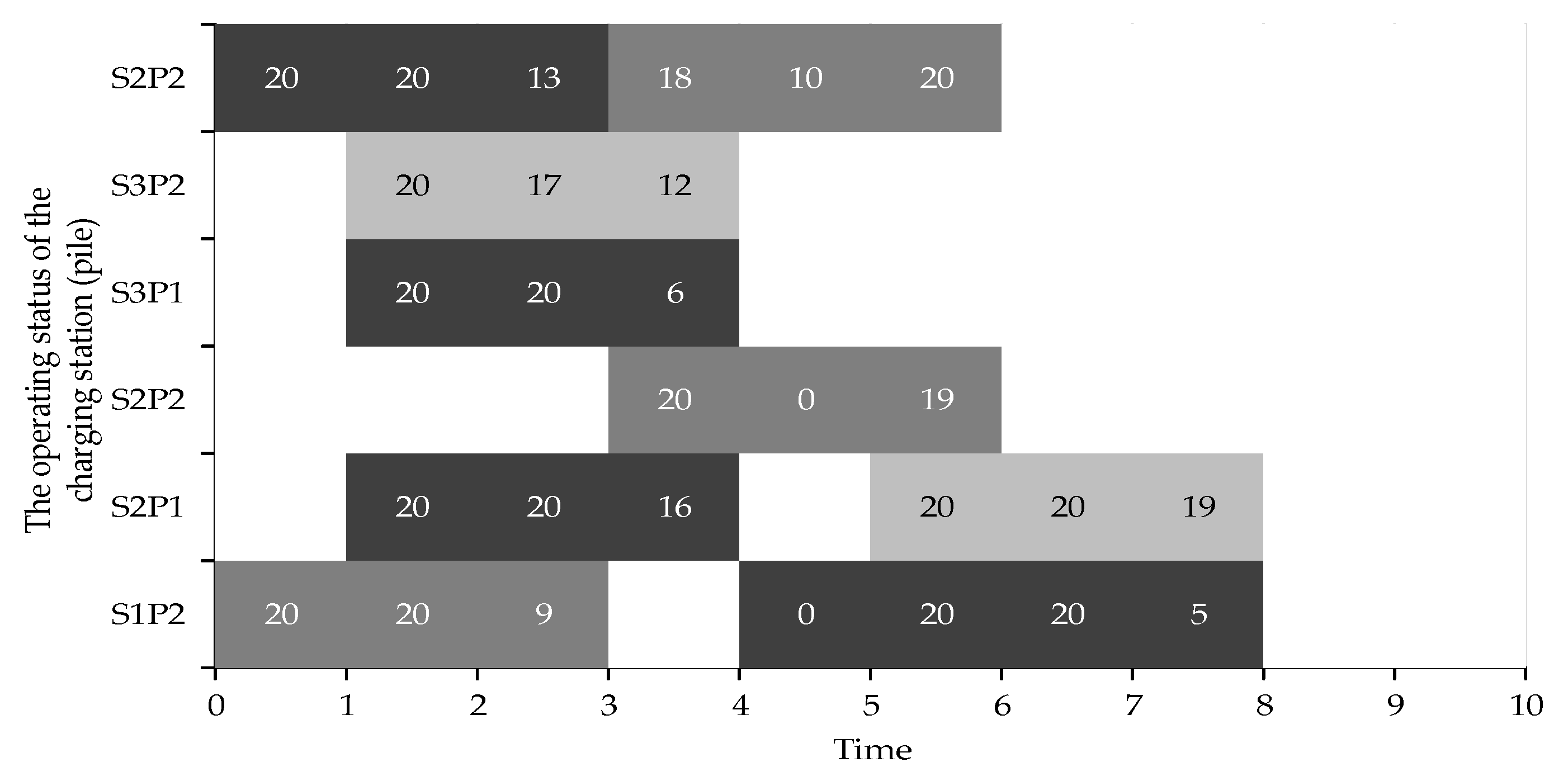
5.2. Case Study
5.2.1. Case Background and Experimental Setup
- The period from 14:00 to 17:00 is designated as the peak period, with a charging price of 1.59 CNY/kWh.
- The period from 17:00 to 20:00 is designated as the off-peak period, with a charging price of 0.99 CNY/kWh.
- Scenario 1: The proposed integrated approach, considering both coordinated EV charging scheduling and station queuing.
- Scenario 2: A partially coordinated scenario considering station queuing, but where EV users simply choose the nearest charging station without system-level reassignment.
- Scenario 3: A baseline, uncoordinated scenario where EV users only choose the nearest charging station and are unwilling to queue, leaving immediately if no pile is available.
5.2.2. Effectiveness Validation of the Scheduling Strategy
5.2.3. Analysis of ALNS Operator Contributions
5.3. Sensitivity Analysis
5.3.1. Analysis of the Number of Time Intervals on Scheduling Results
5.3.2. Analysis of Different Cost Coefficients on Scheduling Results
5.3.3. Analysis of the Impact of the Detour Value Coefficient on Scheduling Results
5.3.4. Analysis of the Incentive Effect of Time-of-Use Electricity Pricing on Station Operations
5.3.5. Analysis of Heterogeneous and Non-Linear Charging Characteristics of Electric Vehicles
- (1)
- Analysis of EV Parameter Heterogeneity
- (2)
- Impact of Non-linear Charging Curves
5.4. Extended Experiments with Time-Varying Traffic Congestion
5.4.1. Small-Scale Network Experiment
5.4.2. Large-Scale Case Study
6. Discussion
6.1. Interpretation of Principal Findings
6.2. Algorithmic Performance and Managerial Insights
6.3. Limitations and Future Research
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lemme, R.F.F.; Arruda, E.F.; Bahiense, L. Optimization model to assess electric vehicles as an alternative for fleet composition in station-based car sharing systems. Transp. Res. Part D Transp. Environ. 2019, 67, 173–196. [Google Scholar] [CrossRef]
- Xiao, Y.; Dong, Y.; Xue, R.; Meng, Z.; Li, B.; Hu, Y.; Wang, Z. Tech-policy integrated validation of spatiotemporal energy-emissions efficiency in public bus systems. Transp. Res. Part D Transp. Environ. 2025, 147, 104967. [Google Scholar] [CrossRef]
- Licari, J.; Rhaili, S.E.; Micallef, A.; Staines, C.S. Addressing voltage regulation challenges in low voltage distribution networks with high renewable energy and electrical vehicles: A critical review. Energy Rep. 2025, 14, 2977–2997. [Google Scholar] [CrossRef]
- Motlagh, S.G.; Oladigbolu, J.; Li, L. A review on electric vehicle charging station operation considering market dynamics and grid interaction. Appl. Energy 2025, 392, 126058. [Google Scholar] [CrossRef]
- Ikram, M.K.; Seyedmehmoudian, M.; Thirunavukkarasu, G.S.; Mekhilef, S.; Stojcevski, A. A two-stage fuzzy-informed optimization framework for reduced peak load and hierarchical EV management in smart grids. J. Energy Storage 2025, 136, 118308. [Google Scholar] [CrossRef]
- Savari, G.F.; Sathik, M.J.; Raman, L.A.; El-Shahat, A.; Hasanien, H.M.; Almakhles, D.; Aleem, S.H.E.A.; Omar, A.I. Assessment of charging technologies, infrastructure and charging station recommendation schemes of electric vehicles: A review. Ain Shams Eng. J. 2023, 14, 101938. [Google Scholar] [CrossRef]
- Ki, Y.; Kim, B.I.; Ko, Y.M.; Jeong, H.; Koo, J. Charging scheduling problem of an M-to-N electric vehicle charger. Appl. Math. Model. 2018, 64, 603–614. [Google Scholar] [CrossRef]
- Yin, W.; Ming, Z.; Wen, T. Scheduling strategy of electric vehicle charging considering different requirements of grid and users. Energy 2021, 232, 121118. [Google Scholar] [CrossRef]
- Kumar, K.N.; Sivaneasan, B.; So, P.L. Impact of priority criteria on electric vehicle charge scheduling. IEEE Trans. Transp. Electrif. 2015, 1, 200–210. [Google Scholar] [CrossRef]
- Al-Hanahi, B.; Ahmad, I.; Habibi, D.; Masoum, M.A.S. Smart charging strategies for heavy electric vehicles. eTransportation 2022, 13, 100182. [Google Scholar] [CrossRef]
- Wu, O.Q.; Yücel, S.; Zhou, Y.F. Smart charging of electric vehicles: An innovative business model for utility firms. Manuf. Serv. Oper. Manag. 2022, 24, 2481–2499. [Google Scholar] [CrossRef]
- Alexeenko, P.; Bitar, E. Achieving reliable coordination of residential plug-in electric vehicle charging: A pilot study. Transp. Res. Part D Transp. Environ. 2023, 118, 103658. [Google Scholar] [CrossRef]
- Cao, Y.; Liu, S.; He, Z.M.; Dai, X.; Xie, X.; Wang, R.; Yu, S. Electric vehicle charging reservation under preemptive service. In Proceedings of the 2019 1st International Conference on Industrial Artificial Intelligence (IAI), Shenyang, China, 23–27 July 2019; pp. 1–6. [Google Scholar]
- Liu, S.; Xia, X.; Cao, Y.; Ni, Q.; Zhang, X.; Xu, L. Reservation-based EV charging recommendation concerning charging urgency policy. Sustain. Cities Soc. 2021, 74, 103150. [Google Scholar] [CrossRef]
- Yue, Z.; Zhou, Y.; Li, Y.; Sun, H.; Zhong, Y.; Li, Y. Research on an Orderly Charging Strategy for New Energy Charging Stations Based on Dynamic Electricity Prices and a Reservation Charging Mechanism for Electric Vehicles. In Proceedings of the 2022 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Shanghai, China, 8–11 July 2022; pp. 1525–1531. [Google Scholar]
- Kumar, N.; Chaudhry, R.; Kaiwartya, O.; Kumar, N. ChaseMe: A heuristic scheme for electric vehicles mobility management on charging stations in a smart city scenario. IEEE Trans. Intell. Transp. Syst. 2022, 23, 16048–16058. [Google Scholar] [CrossRef]
- Zhang, X.; Cao, Y.; Peng, L.; Li, J.; Ahmad, N.; Yu, S. Mobile charging as a service: A reservation-based approach. IEEE Trans. Autom. Sci. Eng. 2020, 17, 1976–1988. [Google Scholar] [CrossRef]
- Yazdani, M.; Estebsari, A.; Estebsari, M.; Rajabi, R. Markov Chain Modelling-Based Approach to Reserve Electric Vehicles in Parking Lots for Distribution System Energy Management. In Proceedings of the 2019 IEEE International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Genova, Italy, 11–14 June 2019; pp. 1–5. [Google Scholar]
- Latinopoulos, C.; Sivakumar, A.; Polak, J. Response of electric vehicle drivers to dynamic pricing of parking and charging services: Risky choice in early reservations. Transp. Res. Part C Emerg. Technol. 2017, 80, 175–189. [Google Scholar] [CrossRef]
- Fernandez, G.S.; Krishnasamy, V.; Kuppusamy, S.; Ali, J.S. Optimal dynamic scheduling of electric vehicles in a parking lot using particle swarm optimization and shuffled frog leaping algorithm. Energies 2020, 13, 6384. [Google Scholar] [CrossRef]
- Wu, H.; Pang, G.K.; Choy, K.L.; Lam, H.Y. Dynamic resource allocation for parking lot electric vehicle recharging using heuristic fuzzy particle swarm optimization algorithm. Appl. Soft Comput. 2018, 71, 538–552. [Google Scholar] [CrossRef]
- Liu, S.; Ni, Q.; Cao, Y.; Cui, J.; Tian, D.; Zhuang, Y. A reservation-based vehicle-to-vehicle charging service under constraint of parking duration. IEEE Syst. J. 2022, 17, 176–187. [Google Scholar] [CrossRef]
- Bernal, R.; Olivares, D.; Negrete, P.; LORCA, Á. Management of EV charging stations under advance reservations schemes in electricity markets. Sustain. Energy Grids Netw. 2020, 24, 100388. [Google Scholar] [CrossRef]
- Hou, L.; Wang, C.; Yan, J. Bidding for preferred timing: An auction design for electric vehicle charging station scheduling. IEEE Trans. Intell. Transp. Syst. 2019, 21, 3332–3343. [Google Scholar] [CrossRef]
- Popiolek, A.; Dimitrova, Z.; Hassler, J.; Petit, M.; Dessante, P. Comparison of decentralised fast-charging strategies for long-distance trips with electric vehicles. Transp. Res. Part D Transp. Environ. 2023, 124, 103953. [Google Scholar] [CrossRef]
- Tan, M.; Ren, Y.; Pan, R.; Wang, L.; Chen, J. Fair and efficient electric vehicle charging scheduling optimization considering the maximum individual waiting time and operating cost. IEEE Trans. Veh. Technol. 2023, 72, 9808–9820. [Google Scholar] [CrossRef]
- Mokhtar, M.; Shaaban, M.F.; Zeineldin, H.; El-Saadany, E.F. A customer-centered smart charging strategy considering virtual charging system. IEEE Access 2021, 9, 117993–118004. [Google Scholar] [CrossRef]
- Li, X.; Wang, W.; Jin, K.; Gu, H. A blockchain-enabled personalized charging system for electric vehicles. Transp. Res. Part C Emerg. Technol. 2024, 161, 104549. [Google Scholar] [CrossRef]
- Arias, N.B.; Sabillón, C.; Franco, J.F.; Quirós-Tortós, J.; Rider, M.J. Hierarchical optimization for user-satisfaction-driven electric vehicles charging coordination in integrated Mv/Lv networks. IEEE Syst. J. 2023, 17, 1247–1258. [Google Scholar] [CrossRef]
- Kumar, V.M.; Chokkalingam, B.; Mihet-Popa, L. Mitigation of complexity in charging station allocation for evs using chaotic harris hawks optimization charge scheduling algorithm. IEEE Access 2023, 11, 130466–130482. [Google Scholar] [CrossRef]
- Shi, X.; Xu, Y.; Guo, Q.; Sun, H.; Gu, W. A distributed ev navigation strategy considering the interaction between power system and traffic network. IEEE Trans. Smart Grid 2020, 11, 3545–3557. [Google Scholar] [CrossRef]
- Wang, Y.X.; Bi, J.; Lu, C.R.; Ding, C. Route guidance strategies for electric vehicles by considering stochastic charging demands in a time-varying road network. Energies 2020, 13, 2287. [Google Scholar] [CrossRef]
- Häusler, F.; Crisostomi, E.; Schlote, A.; Radusch, I.; Shorten, R. Stochastic park-and-charge balancing for fully electric and plug-in hybrid vehicles. IEEE Trans. Intell. Transp. Syst. 2013, 15, 895–901. [Google Scholar] [CrossRef]
- Zaidi, I.; Oulamara, A.; Idoumghar, L.; Basset, M. Minimizing grid capacity in preemptive electric vehicle charging orchestration: Complexity, exact and heuristic approaches. Eur. J. Oper. Res. 2024, 312, 22–37. [Google Scholar] [CrossRef]
- Liu, W.L.; Gong, Y.J.; Chen, W.N.; Liu, Z.; Wang, H.; Zhang, J. Coordinated charging scheduling of electric vehicles: A mixed-variable differential evolution approach. IEEE Trans. Intell. Transp. Syst. 2020, 21, 5094–5109. [Google Scholar] [CrossRef]
- Chen, J.; Huang, X.; Cao, Y.; Li, L.; Yan, K.; Wu, L.; Liang, K. Electric vehicle charging schedule considering shared charging pile based on Generalized Nash Game. Int. J. Electr. Power Energy Syst. 2022, 136, 107579. [Google Scholar] [CrossRef]
- Li, B.B. Stochastic modeling and adaptive forecasting for parking space availability with drivers? time-varying arrival/departure behavior. Transp. Res. Part B Methodol. 2022, 166, 313–332. [Google Scholar] [CrossRef]
- Wu, J.; Su, H.; Meng, J.; Lin, M. Electric vehicle charging scheduling considering infrastructure constraints. Energy 2023, 278, 127806. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, K.; Du, C.; Cai, W.; Lu, Y.; Feng, Y. Learning-based scheduling of integrated charging-storage-discharging station for minimizing electric vehicle users’ cost. J. Energy Storage 2024, 81, 110474. [Google Scholar] [CrossRef]
- Shao, S.P.; Sartipizadeh, H.; Gupta, A. Scheduling ev charging having demand with different reliability constraints. IEEE Trans. Intell. Transp. Syst. 2023, 24, 11018–11029. [Google Scholar] [CrossRef]
- Chongqing Municipal Development and Reform Commission. Notice on Establishing a Time-of-Use Electricity Pricing Mechanism for Residents. 2023. Available online: https://fzggw.cq.gov.cn/zwgk/zfxxgkml/zcwj/xzgfxwj/sfzggwxzgfxwj/202305/t20230516_11968210.html (accessed on 13 May 2023).
| Notation | Definition | Domain |
|---|---|---|
| Set | ||
| The collection of nodes in the urban road network | - | |
| The collection of road sections in the urban road network | - | |
| A collection of charging stations | - | |
| The collection of charging piles in charging station i | - | |
| A collection of EV users | - | |
| A collection of time periods | - | |
| Parameter | ||
| The number of charging piles in the charging station i | ||
| The maximum number of vehicles queuing at the charging station i | ||
| Maximum waiting time for EV users k | ||
| The total time length of scheduling optimization | ||
| The number of time periods | ||
| The total number of EV users | ||
| The distance between EV users k and charging stations i | ||
| The distance between the EV user and the nearest charging station i | ||
| The time that EV users k stay at charging stations | ||
| The driving speed of EVs | ||
| The maximum remaining range for EV users k | ||
| The total power output constraint of the charging station i in the first time period | ||
| The maximum charging power of EVs | ||
| The maximum charge capacity of an EV | ||
| The amount of charging required by EV users k | ||
| The electricity purchase price for the first time period at the charging station i | ||
| The fixed charging price per kilowatt-hour at the charging station i | ||
| The time when EV users k arrive at the charging station i | ||
| The value coefficient of detour costs for EV users | ||
| The value coefficient of queuing waiting time for EV users | ||
| Variable | ||
| The 0–1 variable takes a value of 1 if the dispatching user k charges at the charging station i, and 0 otherwise | Binary | |
| A positive integer variable refers to the amount of EVs k charged by charging piles j within a charging station i during a certain period l If the charging time of the user’s vehicle conflicts with that of the user’s vehicle, the value is 1; otherwise, it is 0 | Non-negative Integer | |
| Auxiliary variable | ||
| If the charging time of the user’s vehicle k conflicts with that of the user’s vehicle k′, the value is 1; otherwise, it is 0 | Binary | |
| The 0–1 variable takes a value of 1 if both the user k and the user k′ are charging at the charging pile j; otherwise, it takes a value of 0 | Binary | |
| The 0–1 variable, if the user’s vehicle k occupies the charging pile j during a certain period l of time, the value is 1; otherwise, it is 0 | Binary | |
| The 0–1 variable takes the value 1 if the user’s vehicle k remains at the charging station i during the time period l; otherwise, it takes the value 0 | Binary | |
| The 0–1 variable takes a value of 1 when a user k charges at a charging pile j within a charging station i; otherwise, it takes a value of 0 | Binary | |
| The 0–1 variable, within the charging station i, takes a value of 1 if users k queue at the charging pile j during a certain period l; otherwise, it takes a value of 0 | Binary | |
| Parameter | Value | Description |
|---|---|---|
| Maximum Iterations | 3000 | Main stopping criterion |
| Max No-Improve | 30 | Early stopping criterion |
| Initial Operator Weight | 10 | Starting weight for all operators |
| Score 1 () | 1 | Reward for a solution that improves the current one |
| Score 2 () | 3 | Reward for finding a new global best solution |
| Pairwise Score () | 2 | Reward for a successful operator pair |
| Cooling Rate | 0.9995 | Simulated annealing cooling rate |
| Start Temperature | 500 | Initial temperature for SA acceptance |
| Weight Decay Interval | 500 | Iterations between weight decay |
| Random Seed | 12,345 | Seed for reproducible results |
| Time Period | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Power constraint | 40 | 40 | 30 | 30 | 30 | 40 | 40 | 40 | 30 | 30 |
| The electricity purchase price | 0.2 | 0.2 | 0.5 | 0.5 | 0.5 | 0.2 | 0.2 | 0.2 | 0.5 | 0.5 |
| The electricity sales price | 0.8 | 0.8 | 1.3 | 1.3 | 1.3 | 0.8 | 0.8 | 0.8 | 1.3 | 1.3 |
| EV Count | Scenario 1 | Scenario 2 | Scenario 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Charging Revenue (CNY) | Detour Distance (km) | Queuing Time (min) | EVs Served | Charging Revenue (CNY) | Queuing Time (min) | EVs Served | Charging Revenue (CNY) | EVs Served | |
| 15 | 861.9 | 0 | 0 | 15 | 861.9 | 0 | 15 | 861.9 | 15 |
| 20 | 1105.5 | 0 | 0 | 20 | 1105.5 | 15 | 20 | 1023.4 | 19 |
| 25 | 1527.8 | 3.4 | 0 | 25 | 1575.9 | 30 | 25 | 1481.6 | 23 |
| 30 | 1914.9 | 3.8 | 0 | 30 | 1959.1 | 60 | 30 | 1695.8 | 26 |
| 35 | 2270.7 | 4.8 | 30 | 35 | 2201.9 | 90 | 33 | 1854.9 | 28 |
| 40 | 2627.5 | 7.1 | 75 | 40 | 2415.0 | 150 | 36 | 1961.3 | 28 |
| 45 | 2928.7 | 8.4 | 120 | 45 | 2535.2 | 195 | 38 | 1964.1 | 29 |
| 50 | 3314.9 | 11.1 | 195 | 50 | 2547.5 | 240 | 39 | 2105.0 | 32 |
| 55 | 3790.9 | 16.4 | 255 | 55 | 2581.6 | 270 | 40 | 2226.5 | 33 |
| 60 | 4114.1 | 19.5 | 345 | 58 | 2754.8 | 270 | 41 | 2397.6 | 36 |
| Configuration (Disabled Operator) | Average Final Objective Value (CNY) | Performance Drop vs. Full ALNS |
|---|---|---|
| Full ALNS (All Operators) | 3314.9 | - |
| Without Random Removal | 3278.5 | −1.1% |
| Without Longest Queue Removal | 3156.3 | −4.8% |
| Without Max Conflict Removal | 3223.7 | −2.7% |
| Without Max Detour Cost Removal | 3291.1 | −0.7% |
| Without Max Unserved Users Removal | 3098.4 | −6.5% |
| Number of Time Intervals | Time Step (min) | Charging Revenue (CNY) | Relative Error in Charging Revenue (%) | Detour Distance (km) | Relative Error in Detour Distance (%) | Queuing Time (min) | Relative Error in Queuing Time (%) | Solving Time (s) |
|---|---|---|---|---|---|---|---|---|
| 12 | 30 | 3283.1 | 2.52 | 12.7 | 42.70 | 210 | 23.53 | 361.4 |
| 18 | 20 | 3314.9 | 1.58 | 12.0 | 34.83 | 200 | 17.65 | 477.1 |
| 24 | 15 | 3332.9 | 1.04 | 11.1 | 24.72 | 195 | 14.71 | 873.9 |
| 36 (Benchmark) | 10 | 3368.0 | - | 8.9 | - | 170 | - | 2790.7 |
| Number of Nodes | Computation Time (s) | Speed-Up | Parallel Efficiency (%) |
|---|---|---|---|
| 1 (Baseline) | 873.9 | 1.00 | 100 |
| 2 | 477.1 | 1.83 | 91.5 |
| 4 | 256.3 | 3.41 | 85.3 |
| Priority Queuing | Priority Detouring | Neutral Preference | |
|---|---|---|---|
| Preference Combination 1 | 25.0% | 25.0% | 50.0% |
| Preference Combination 2 | 25.0% | 50.0% | 25.0% |
| Preference Combination 3 | 50.0% | 25.0% | 25.0% |
| Preference Combination 4 | 33.3% | 33.3% | 33.4% |
| Preference Intensity (γ) | Preference Combination 3 | Preference Combination 4 | ||||
|---|---|---|---|---|---|---|
| Charging Revenue (CNY) | Detour Distance (km) | Queuing Time (min) | Charging Revenue (CNY) | Detour Distance (km) | Queuing Time (min) | |
| 10% | 3275.6 | 12.0 | 195 | 3359.1 | 10.9 | 195 |
| 30% | 3258.2 | 12.3 | 180 | 3403.3 | 10.3 | 210 |
| 50% | 3223.1 | 12.7 | 165 | 3469.6 | 9.7 | 225 |
| 70% | 3171.9 | 13.2 | 165 | 3513.8 | 9.3 | 240 |
| 10% | 3210.1 | 12.3 | 195 | 3292.8 | 11.9 | 195 |
| 30% | 3165.3 | 13.6 | 195 | 3270.7 | 12.1 | 180 |
| 50% | 3063.0 | 14.5 | 180 | 3226.5 | 12.4 | 180 |
| 70% | 2911.9 | 15.7 | 165 | 3182.3 | 12.8 | 165 |
| Detour Value Coefficient (λ) | Total Station Revenue (CNY) | Detour Compensation Cost (CNY) | Revenue Improvement (%) |
|---|---|---|---|
| 0.50 | 1515.45 | 32.79 | 21.12 |
| 0.75 | 1398.12 | 50.9 | 18.96 |
| 1.00 | 1385.72 | 76.53 | 17.41 |
| 1.25 | 1386.05 | 92.64 | 15.88 |
| 1.50 | 1344.97 | 119.31 | 13.96 |
| 1.75 | 1271.41 | 124.22 | 10.49 |
| 2.00 | 1246.81 | 168.16 | 9.07 |
| 2.25 | 1291.87 | 183.06 | 7.92 |
| 2.50 | 1302.44 | 168.16 | 5.57 |
| 2.75 | 1324.86 | 140.47 | 3.61 |
| Peak Price (CNY/kWh) | Off-Peak Price (CNY/kWh) | Price Gap (CNY/kWh) | Compliance Rate (%) | Station Revenue (CNY) | Service Rate (%) | Scheduling Cost (CNY) |
|---|---|---|---|---|---|---|
| 0.5 | 0.3 | 0.2 | 15 | 1493.90 | 71 | 89.75 |
| 0.6 | 0.3 | 0.3 | 15 | 1490.74 | 73 | 94.96 |
| 0.7 | 0.3 | 0.4 | 15 | 1377.61 | 74 | 104.995 |
| 0.8 | 0.3 | 0.5 | 15 | 1325.36 | 76 | 101.15 |
| 0.9 | 0.4 | 0.5 | 30 | 1225.31 | 68 | 212.63 |
| 0.9 | 0.5 | 0.4 | 30 | 1118.52 | 70 | 209.88 |
| 0.9 | 0.6 | 0.3 | 30 | 1052.97 | 70 | 195.03 |
| 0.9 | 0.7 | 0.2 | 30 | 870.37 | 70 | 187.19 |
| 0.5 | 0.3 | 0.2 | 15 | 1493.90 | 71 | 89.75 |
| Scenario | Scheduling Strategy | Revenue (CNY) | EVs Served | Avg. Queuing Time (min) | Detour Distance (km) |
|---|---|---|---|---|---|
| Baseline (Homogeneous) | Scenario 1 | 3314.9 | 50 | 195 | 11.1 |
| Scenario 2 | 2547.5 | 39 | 240 | - | |
| Scenario 3 | 2105.0 | 32 | 0 | - | |
| H1 (Het. Capacity) | Scenario 1 | 3298.3 (−0.5%) | 50 | 203 (+4.1%) | 10.8 |
| Scenario 2 | 2515.1 (−1.3%) | 38 | 255 (+6.3%) | - | |
| Scenario 3 | 2087.2 (−0.8%) | 32 | 0 | - | |
| H2 (Het. Power) | Scenario 1 | 3357.1 (+1.3%) | 50 | 181 (−7.2%) | 11.6 |
| Scenario 2 | 2490.5 (−2.2%) | 38 | 262 (+9.2%) | - | |
| Scenario 3 | 2053.7 (−2.4%) | 31 | 0 | - | |
| H3 (Mixed Het.) | Scenario 1 | 3320.5 (+0.2%) | 50 | 189 (−3.1%) | 11.3 |
| Scenario 2 | 2501.8 (−1.8%) | 38 | 258 (+7.5%) | - | |
| Scenario 3 | 2075.4 (−1.4%) | 31 | 0 | - |
| Vehicle | Initial SOC | Target SOC | Battery Capacity (kWh) | Linear Model Time (min) | CC/CV Model Time (min) | Absolute Error (min) | Relative Error (%) |
|---|---|---|---|---|---|---|---|
| A | 20% | 95% | 60 | 77.1 | 81.3 | +4.2 | +5.4% |
| B | 40% | 90% | 60 | 51.4 | 53.6 | +2.2 | +4.3% |
| C | 15% | 100% | 60 | 85.7 | 92.5 | +6.8 | +7.9% |
| Scheduling Strategy | Charging Revenue (CNY) | EVs Served | Total System Travel Time (min) | Total Compensation Cost (CNY) |
|---|---|---|---|---|
| Scenario 1 (Proposed) | 655.8 | 15 | 338.5 | 24.7 |
| Scenario 2 | 641.2 | 14 | 351.2 | - |
| Scenario 3 | 598.5 | 12 | 325.1 | - |
| Scenario | Scheduling Strategy | Charging Revenue (CNY) | EVs Served | Total System Travel Time (Hours) | Avg. Compensation (CNY/veh) |
|---|---|---|---|---|---|
| Ideal scenario | Scenario 1 | 3314.9 | 50 | 9.8 | 12.5 |
| Scenario 2 | 2547.5 | 39 | 10.5 | - | |
| Scenario 3 | 2105.0 | 32 | 8.2 | - | |
| Congestion scenario | Scenario 1 | 3285.7 (−0.9%) | 50 | 12.7 (+29.6%) | 16.8 (+34.4%) |
| Scenario 2 | 2509.3 (−1.5%) | 38 | 14.1 (+34.3%) | - | |
| Scenario 3 | 2078.1 (−1.3%) | 31 | 10.5 (+28.0%) | - |
| EV Number | Current Node | Duration of Stay | Charging Demand | Destination Node |
|---|---|---|---|---|
| 1 | 4 | 2 | 53% | 7 |
| 2 | 6 | 3 | 49% | 10 |
| 3 | 18 | 2 | 46% | 1 |
| 4 | 14 | 2 | 37% | 6 |
| 5 | 22 | 2 | 30% | 2 |
| 6 | 21 | 2 | 49% | 2 |
| 7 | 10 | 2 | 48% | 5 |
| 8 | 13 | 2 | 39% | 9 |
| 9 | 2 | 3 | 44% | 23 |
| 10 | 20 | 2 | 37% | 12 |
| 11 | 10 | 4 | 46% | 13 |
| 12 | 20 | 2 | 56% | 16 |
| 13 | 8 | 2 | 59% | 21 |
| 14 | 24 | 3 | 47% | 9 |
| 15 | 7 | 3 | 45% | 21 |
| EV Count | This Paper | Gurobi | Gap | ||
|---|---|---|---|---|---|
| Optimal Value (CNY) | Solving Time (s) | Optimal Value (CNY) | Solving Time (s) | ||
| 6 | 239.5 | 118.2 | 239.5 | 5.8 | 0.0 |
| 7 | 293.2 | 140.7 | 293.2 | 28.9 | 0.0 |
| 8 | 345.6 | 167.1 | 345.6 | 125.6 | 0.0 |
| 9 | 386.3 | 239.9 | 386.3 | 353.4 | 0.0 |
| 10 | 423.5 | 291.1 | 423.5 | 882.9 | 0.0 |
| 11 | 453.1 | 355.4 | 453.1 | 1345.5 | 0.0 |
| 12 | 492.9 | 413.8 | 492.9 | 2682.4 | 0.0 |
| 13 | 557.7 | 478.4 | 557.7 | 6548.3 | 0.0 |
| 14 | 605.9 | 501.7 | — | — | — |
| 15 | 677.0 | 543.9 | — | — | — |
| 16 | 716.0 | 589.0 | — | — | — |
| 17 | 757.4 | 632.8 | — | — | — |
| 18 | 766.4 | 672.4 | — | — | — |
| 19 | 861.9 | 763.8 | — | — | — |
| 20 | 861.9 | 856.4 | — | — | — |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Ge, X.; Jin, Y.; Xu, M.; Huang, Z. Orderly Charging Scheduling for EVs with a Novel Queuing Model Under Power Capacity Constraints. Appl. Sci. 2025, 15, 12038. https://doi.org/10.3390/app152212038
Wang B, Ge X, Jin Y, Xu M, Huang Z. Orderly Charging Scheduling for EVs with a Novel Queuing Model Under Power Capacity Constraints. Applied Sciences. 2025; 15(22):12038. https://doi.org/10.3390/app152212038
Chicago/Turabian StyleWang, Bo, Xianlong Ge, Yuanzhi Jin, Mushun Xu, and Zhuoran Huang. 2025. "Orderly Charging Scheduling for EVs with a Novel Queuing Model Under Power Capacity Constraints" Applied Sciences 15, no. 22: 12038. https://doi.org/10.3390/app152212038
APA StyleWang, B., Ge, X., Jin, Y., Xu, M., & Huang, Z. (2025). Orderly Charging Scheduling for EVs with a Novel Queuing Model Under Power Capacity Constraints. Applied Sciences, 15(22), 12038. https://doi.org/10.3390/app152212038





