Green AI for Energy-Efficient Ground Investigation: A Greedy Algorithm-Optimized AI Model for Subsurface Data Prediction
Abstract
1. Introduction
2. Dataset Obtained from Traditional Ground Investigation
2.1. Soil Parameters in Dataset
2.2. Energy Consumption Comparison Among Soil Parameters
2.3. Determination of Model Inputs and Outputs
3. Green AI Model Optimized with Greedy Algorithm
3.1. General Model Architecture
3.2. Three-Stage Oprimization with Greedy Algorithm
4. Results and Discussion
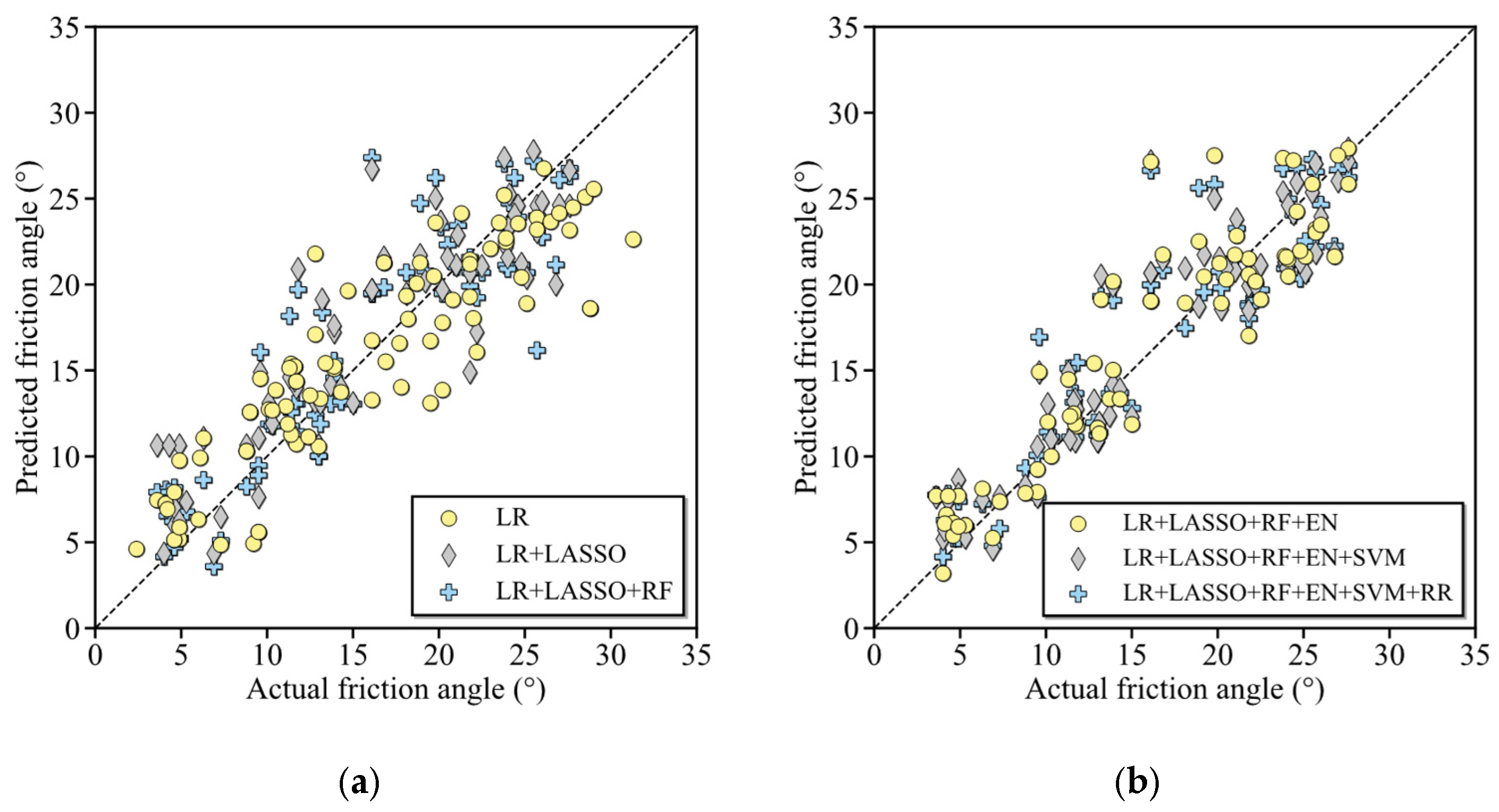
4.1. Results by 1st Stage Optimization on Baser Learner Prioritization
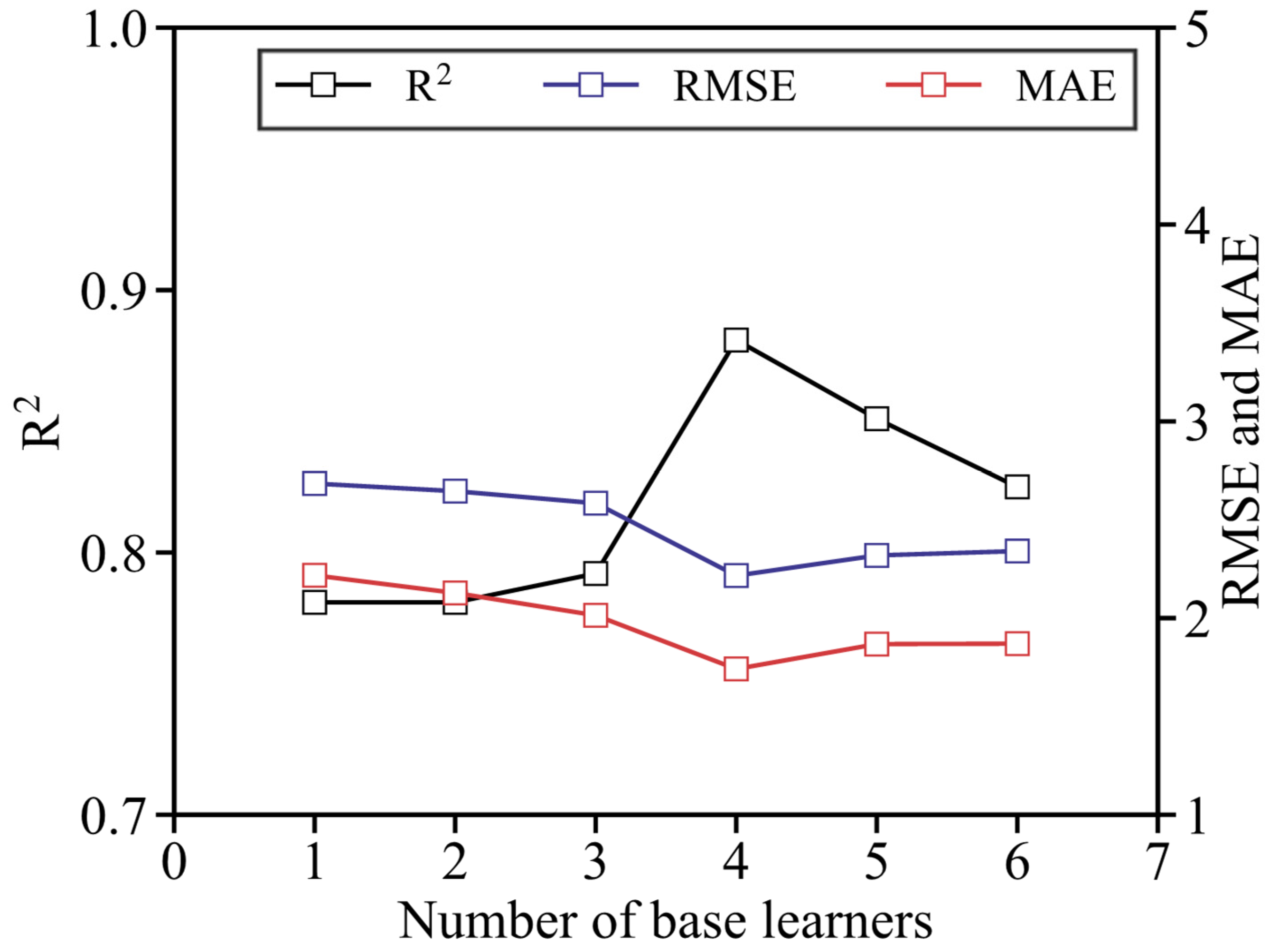
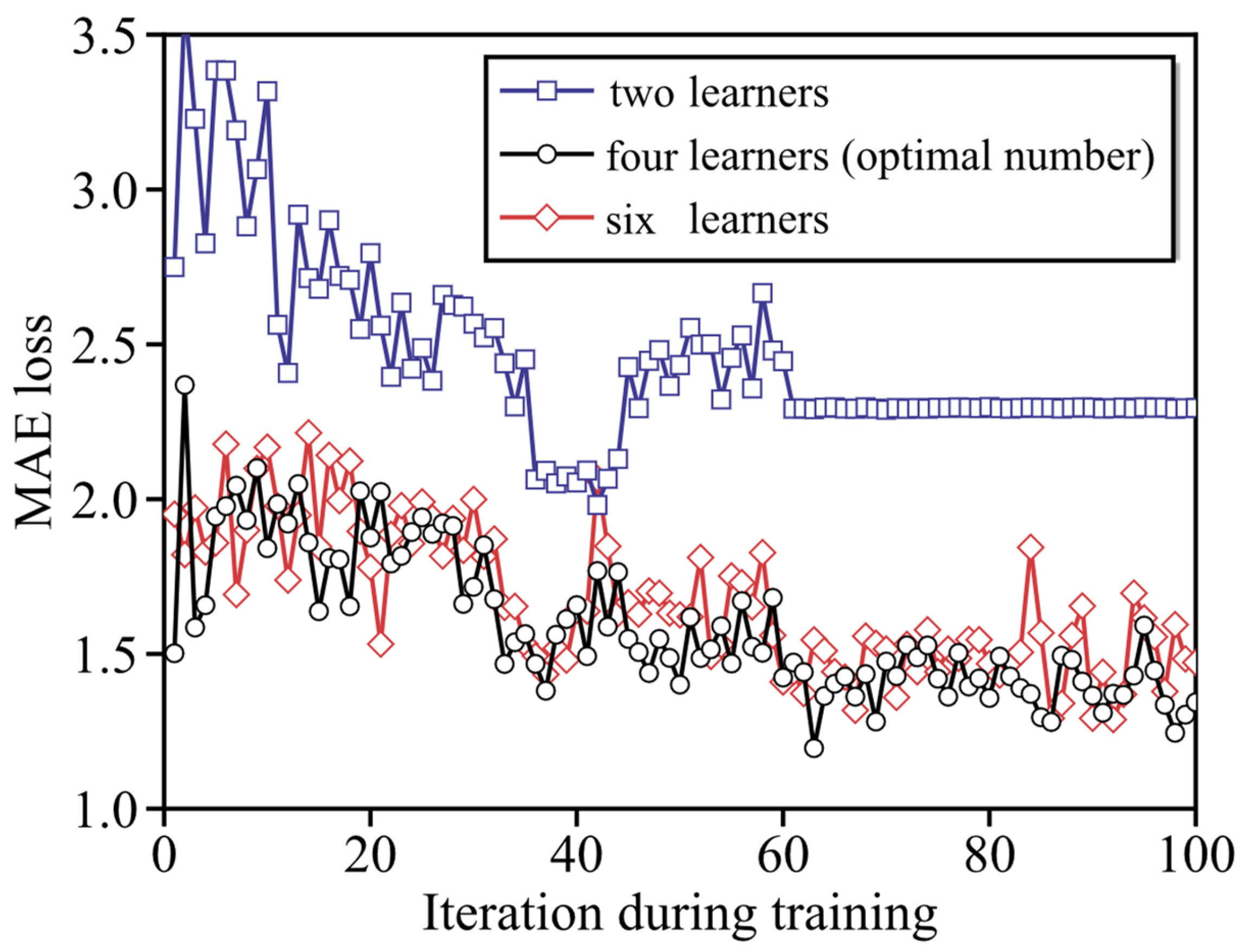
4.2. Results by 2nd Stage Optimization on Base Learner Number
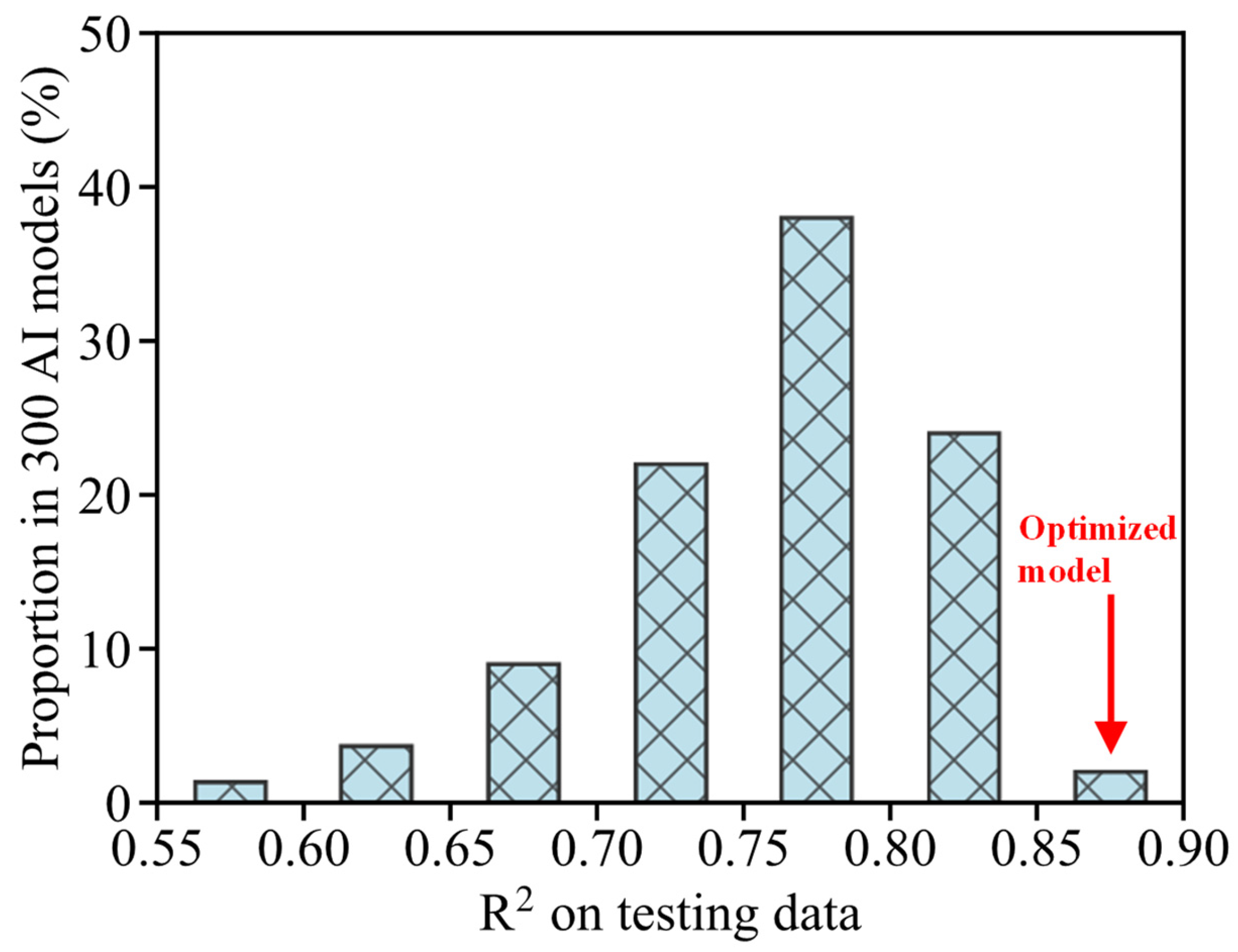
4.3. Results by 3rd Optimization of Ensemble Stragety and Energy-Saving Estimation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Das, B.M.; Sivakugan, N. Fundamentals of Geotechnical Engineering; Cengage Learning: Independence, KY, USA, 2017. [Google Scholar]
- Ng, C.W.; Liu, J.; Chen, R. Numerical investigation on gas emission from three landfill soil covers under dry weather conditions. Vadose Zone J. 2015, 14, vzj2014-12. [Google Scholar] [CrossRef]
- Liu, L.-L.; Xu, Y.-B.; Zhu, W.-Q.; Zhang, J. Effect of copula dependence structure on the failure modes of slopes in spatially variable soils. Comput. Geotech. 2024, 166, 105959. [Google Scholar] [CrossRef]
- Shi, X.; Liu, K.; Yin, J. Effect of initial density, particle shape, and confining stress on the critical state behavior of weathered gap-graded granular soils. J. Geotech. Geoenviron. Eng. 2021, 147, 04020160. [Google Scholar] [CrossRef]
- Härtl, J.; Ooi, J.Y. Experiments and simulations of direct shear tests: Porosity, contact friction and bulk friction. Granul. Matter 2008, 10, 263–271. [Google Scholar] [CrossRef]
- Tai, P.; Indraratna, B.; Rujikiatkamjorn, C.; Chen, R.; Li, Z. Cyclic behaviour of stone column reinforced subgrade under partially drained condition. Transp. Geotech. 2024, 47, 101281. [Google Scholar] [CrossRef]
- Chen, R.; Luo, Z.; Zhang, L.; Li, Z.; Tan, R. A new flexible-wall triaxial permeameter for localized characterizations of soil suffusion. Q. J. Eng. Geol. Hydrogeol. 2025, 58, qjegh2023-124. [Google Scholar] [CrossRef]
- Ladd, R. Preparing test specimens using undercompaction. Geotech. Test. J. 1978, 1, 16–23. [Google Scholar] [CrossRef]
- Ng, C.W.; Liu, J.; Chen, R.; Xu, J. Physical and numerical modeling of an inclined three-layer (silt/gravelly sand/clay) capillary barrier cover system under extreme rainfall. Waste Manag. 2015, 38, 210–221. [Google Scholar] [CrossRef]
- Zeng, Y.; Shi, X.; Zhao, J.; Bian, X.; Liu, J. Estimation of compression behavior of granular soils considering initial density effect based on equivalent concept. Acta Geotech. 2025, 20, 1035–1048. [Google Scholar] [CrossRef]
- Chen, R.; Ng, C.W.W. Impact of wetting–drying cycles on hydro-mechanical behavior of an unsaturated compacted clay. Appl. Clay Sci. 2013, 86, 38–46. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, W.; Yu, Q.; Zhu, Q.-Z.; Shao, J.-F. A micromechanical model for induced anisotropic damage-friction in rock materials under cyclic loading. Int. J. Rock Mech. Min. Sci. 2025, 186, 106014. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Y.; Chen, R.; Tai, P.; Zhang, Z. Numerical investigation of morphological effects on crushing characteristics of single calcareous sand particle by finite-discrete element method. Powder Technol. 2025, 453, 120592. [Google Scholar] [CrossRef]
- Shi, X.; Zhao, J. Practical estimation of compression behavior of clayey/silty sands using equivalent void-ratio concept. J. Geotech. Geoenviron. Eng. 2020, 146, 04020046. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, W.; Zhu, Q.; Shao, J.-F. A novel elastic–plastic damage model for rock materials considering micro-structural degradation due to cyclic fatigue. Int. J. Plast. 2023, 160, 103496. [Google Scholar] [CrossRef]
- Niu, Q.; Revil, A.; Li, Z.; Wang, Y.-H. Relationship between electrical conductivity anisotropy and fabric anisotropy in granular materials during drained triaxial compressive tests: A numerical approach. Geophys. J. Int. 2017, 210, 1–17. [Google Scholar] [CrossRef]
- Sivrikaya, O.; Toğrol, E. Determination of undrained strength of fine-grained soils by means of SPT and its application in Turkey. Eng. Geol. 2006, 86, 52–69. [Google Scholar] [CrossRef]
- Jamiolkowski, M.; Lo Presti, D.; Manassero, M. Evaluation of relative density and shear strength of sands from CPT and DMT. In Soil Behavior and Soft Ground Construction; American Society of Civil Engineers: Reston, VA, USA, 2003; pp. 201–238. [Google Scholar]
- Shi, X.; Xu, J.; Guo, N.; Bian, X.; Zeng, Y. A novel approach for describing gradation curves of rockfill materials based on the mixture concept. Comput. Geotech. 2025, 177, 106911. [Google Scholar] [CrossRef]
- Wang, H.; Chen, R.; Leung, A.K.; Garg, A.; Jiang, Z. Pore-based modeling of hydraulic conductivity function of unsaturated rooted soils. Int. J. Numer. Anal. Methods Geomech. 2025, 49, 1790–1803. [Google Scholar] [CrossRef]
- Pentoś, K.; Mbah, J.T.; Pieczarka, K.; Niedbała, G.; Wojciechowski, T. Evaluation of multiple linear regression and machine learning approaches to predict soil compaction and shear stress based on electrical parameters. Appl. Sci. 2022, 12, 8791. [Google Scholar] [CrossRef]
- Puri, N.; Prasad, H.D.; Jain, A. Prediction of geotechnical parameters using machine learning techniques. Procedia Comput. Sci. 2018, 125, 509–517. [Google Scholar] [CrossRef]
- Tziachris, P.; Aschonitis, V.; Chatzistathis, T.; Papadopoulou, M.; Doukas, I.D. Comparing machine learning models and hybrid geostatistical methods using environmental and soil covariates for soil pH prediction. ISPRS Int. J. Geo-Inf. 2020, 9, 276. [Google Scholar] [CrossRef]
- Li, J.; Sun, J.; Zhang, Z.; Li, Z. Comparative investigation of torsional interactive behaviours between suction anchors and clayey ground by centrifugal tests. Ocean Eng. 2025, 341, 122676. [Google Scholar] [CrossRef]
- Li, K.-Q.; Liu, Y.; Kang, Q. Estimating the thermal conductivity of soils using six machine learning algorithms. Int. Commun. Heat Mass Transf. 2022, 136, 106139. [Google Scholar] [CrossRef]
- Feng, Y.; Cui, N.; Hao, W.; Gao, L.; Gong, D. Estimation of soil temperature from meteorological data using different machine learning models. Geoderma 2019, 338, 67–77. [Google Scholar] [CrossRef]
- Araya, S.N.; Ghezzehei, T.A. Using machine learning for prediction of saturated hydraulic conductivity and its sensitivity to soil structural perturbations. Water Resour. Res. 2019, 55, 5715–5737. [Google Scholar] [CrossRef]
- Samui, P.; Sitharam, T. Machine learning modelling for predicting soil liquefaction susceptibility. Nat. Hazards Earth Syst. Sci. 2011, 11, 1–9. [Google Scholar] [CrossRef]
- Achieng, K.O. Modelling of soil moisture retention curve using machine learning techniques: Artificial and deep neural networks vs support vector regression models. Comput. Geosci. 2019, 133, 104320. [Google Scholar] [CrossRef]
- Zhang, P.; Yin, Z.-Y.; Jin, Y.-F. Machine learning-based modelling of soil properties for geotechnical design: Review, tool development and comparison. Arch. Comput. Methods Eng. 2022, 29, 1229–1245. [Google Scholar] [CrossRef]
- Li, Z.; Qi, Z.; Ling, J.; Liu, Y.; Guo, H.; Xu, T. A pragmatic modelling framework for long-term deformation analyses of urban tunnel under multi-source cyclic loads. Tunn. Undergr. Space Technol. 2026, 167, 107029. [Google Scholar] [CrossRef]
- Das, S.K.; Basudhar, P.K. Prediction of residual friction angle of clays using artificial neural network. Eng. Geol. 2008, 100, 142–145. [Google Scholar] [CrossRef]
- Pham, B.T.; Nguyen-Thoi, T.; Ly, H.-B.; Nguyen, M.D.; Al-Ansari, N.; Tran, V.-Q.; Le, T.-T. Extreme learning machine based prediction of soil shear strength: A sensitivity analysis using Monte Carlo simulations and feature backward elimination. Sustainability 2020, 12, 2339. [Google Scholar] [CrossRef]
- Pham, B.T.; Hoang, T.-A.; Nguyen, D.-M.; Bui, D.T. Prediction of shear strength of soft soil using machine learning methods. Catena 2018, 166, 181–191. [Google Scholar] [CrossRef]
- Zhu, L.; Liao, Q.; Wang, Z.; Chen, J.; Chen, Z.; Bian, Q.; Zhang, Q. Prediction of soil shear Strength parameters using combined data and different machine learning models. Appl. Sci. 2022, 12, 5100. [Google Scholar] [CrossRef]
- Verdecchia, R.; Sallou, J.; Cruz, L. A systematic review of Green AI. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2023, 13, e1507. [Google Scholar] [CrossRef]
- Li, Y.; Rahardjo, H.; Satyanaga, A.; Rangarajan, S.; Lee, D.T.-T. Soil database development with the application of machine learning methods in soil properties prediction. Eng. Geol. 2022, 306, 106769. [Google Scholar] [CrossRef]
- Chow, J.K.; Li, Z.; Su, Z.; Wang, Y.-H. Characterization of particle orientation of kaolinite samples using the deep learning-based technique. Acta Geotech. 2022, 17, 1097–1110. [Google Scholar] [CrossRef]
- Hengl, T.; Mendes de Jesus, J.; Heuvelink, G.B.; Ruiperez Gonzalez, M.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B. SoilGrids250m: Global gridded soil information based on machine learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Z.; Sui, Y.; Liu, C.; Li, Z. Hybrid soil strength prediction model for geotechnical ground investigation using convolutional neural network and ensemble learning. J. Phys.: Conf. Ser. 2024, 2816, 012066. [Google Scholar] [CrossRef]
- Cao, M.-T.; Hoang, N.-D.; Nhu, V.H.; Bui, D.T. An advanced meta-learner based on artificial electric field algorithm optimized stacking ensemble techniques for enhancing prediction accuracy of soil shear strength. Eng. Comput. 2022, 38, 2185–2207. [Google Scholar] [CrossRef]
- Liu, L.-L.; Yin, H.-D.; Xiao, T.; Huang, L.; Cheng, Y.-M. Dynamic prediction of landslide life expectancy using ensemble system incorporating classical prediction models and machine learning. Geosci. Front. 2024, 15, 101758. [Google Scholar] [CrossRef]
- Lin, S.; Zheng, H.; Han, B.; Li, Y.; Han, C.; Li, W. Comparative performance of eight ensemble learning approaches for the development of models of slope stability prediction. Acta Geotech. 2022, 17, 1477–1502. [Google Scholar] [CrossRef]
- Bian, X.; Fan, Z.; Liu, J.; Li, X.; Zhao, P. Regional 3D geological modeling along metro lines based on stacking ensemble model. Undergr. Space 2024, 18, 65–82. [Google Scholar] [CrossRef]
- Rabbani, A.; Samui, P.; Kumari, S. Implementing ensemble learning models for the prediction of shear strength of soil. Asian J. Civ. Eng. 2023, 24, 2103–2119. [Google Scholar] [CrossRef]
- Schwartz, R.; Dodge, J.; Smith, N.A.; Etzioni, O. Green AI. Commun. ACM 2020, 63, 54–63. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Z.; Zhang, S.; Sui, Y.; Liu, C.; Xue, Z.; Li, Z. Comparative Investigation of Axial Bearing Performance and Mechanism of Continuous Flight Auger Pile in Weathered Granitic Soils. Buildings 2023, 13, 2707. [Google Scholar] [CrossRef]
- Bian, X.; Gao, Z.; Zhao, P.; Li, X. Quantitative analysis of low carbon effect of urban underground space in Xinjiekou district of Nanjing city, China. Tunn. Undergr. Space Technol. 2024, 143, 105502. [Google Scholar] [CrossRef]
- Shi, X.; Nie, J.; Zhao, J.; Gao, Y. A homogenization equation for the small strain stiffness of gap-graded granular materials. Comput. Geotech. 2020, 121, 103440. [Google Scholar] [CrossRef]
- Henderi, H.; Wahyuningsih, T.; Rahwanto, E. Comparison of Min-Max normalization and Z-Score Normalization in the K-nearest neighbor (kNN) Algorithm to Test the Accuracy of Types of Breast Cancer. Int. J. Inform. Inf. Syst. 2021, 4, 13–20. [Google Scholar] [CrossRef]
- Bian, X.; Ren, Z.; Zeng, L.; Zhao, F.; Yao, Y.; Li, X. Effects of biochar on the compressibility of soil with high water content. J. Clean. Prod. 2024, 434, 140032. [Google Scholar] [CrossRef]
- Lin, S.; Liang, Z.; Zhao, S.; Dong, M.; Guo, H.; Zheng, H. A comprehensive evaluation of ensemble machine learning in geotechnical stability analysis and explainability. Int. J. Mech. Mater. Des. 2024, 20, 331–352. [Google Scholar] [CrossRef]
- Susan, S.; Kumar, A.; Jain, A. Evaluating heterogeneous ensembles with boosting meta-learner. In Proceedings of the Inventive Communication and Computational Technologies: Proceedings of ICICCT 2020, Namakkal, India, 28–29 May 2020; pp. 699–710. [Google Scholar]
- Ministry of Ecology and Environment of the People’s Republic of China. Announcement on the Release of 2023 Power Carbon Footprint Factor Data. 2025. Available online: https://www.mee.gov.cn/xxgk2018/xxgk/xxgk01/202501/t20250123_1101226.html (accessed on 11 August 2025).

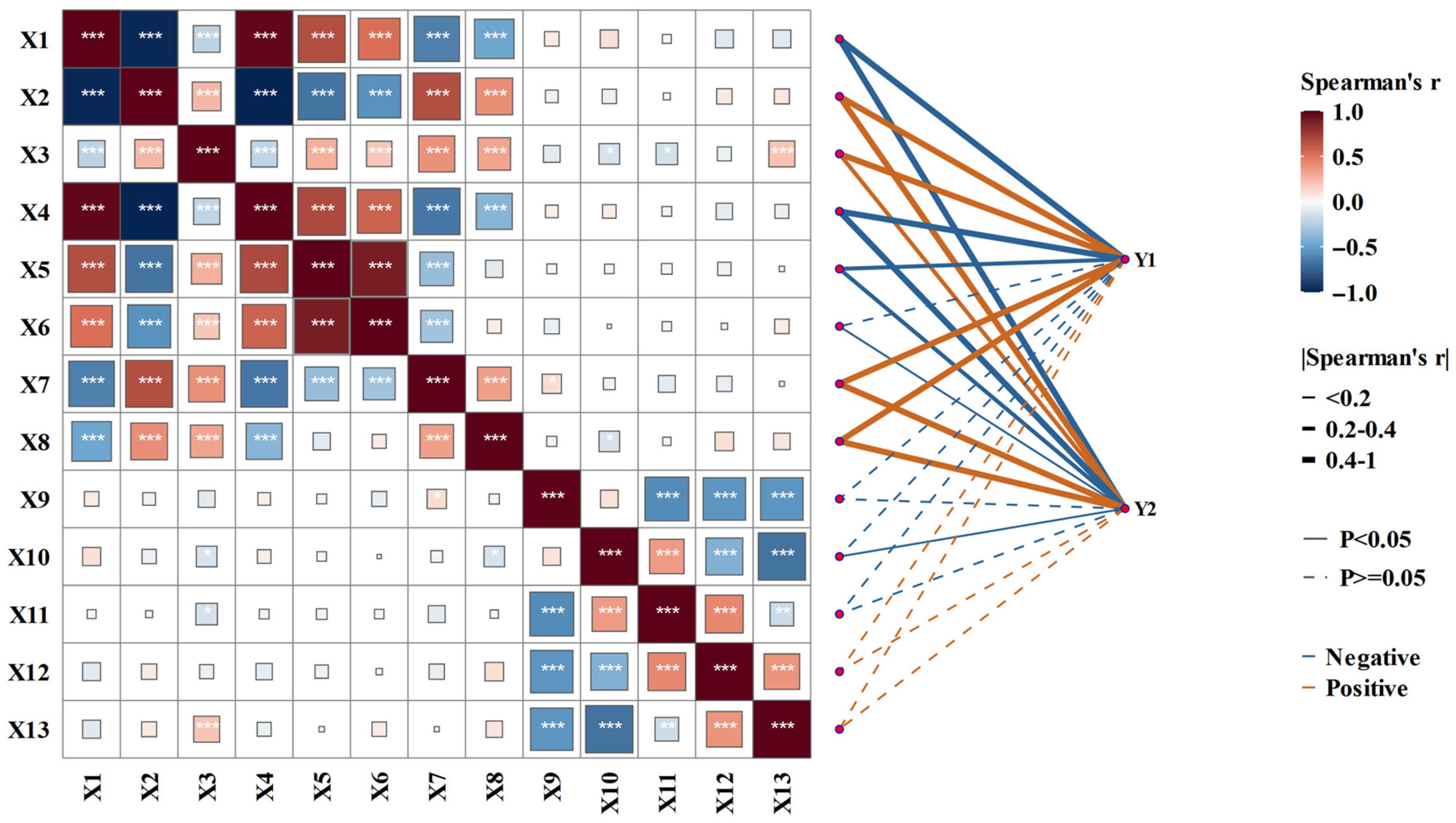
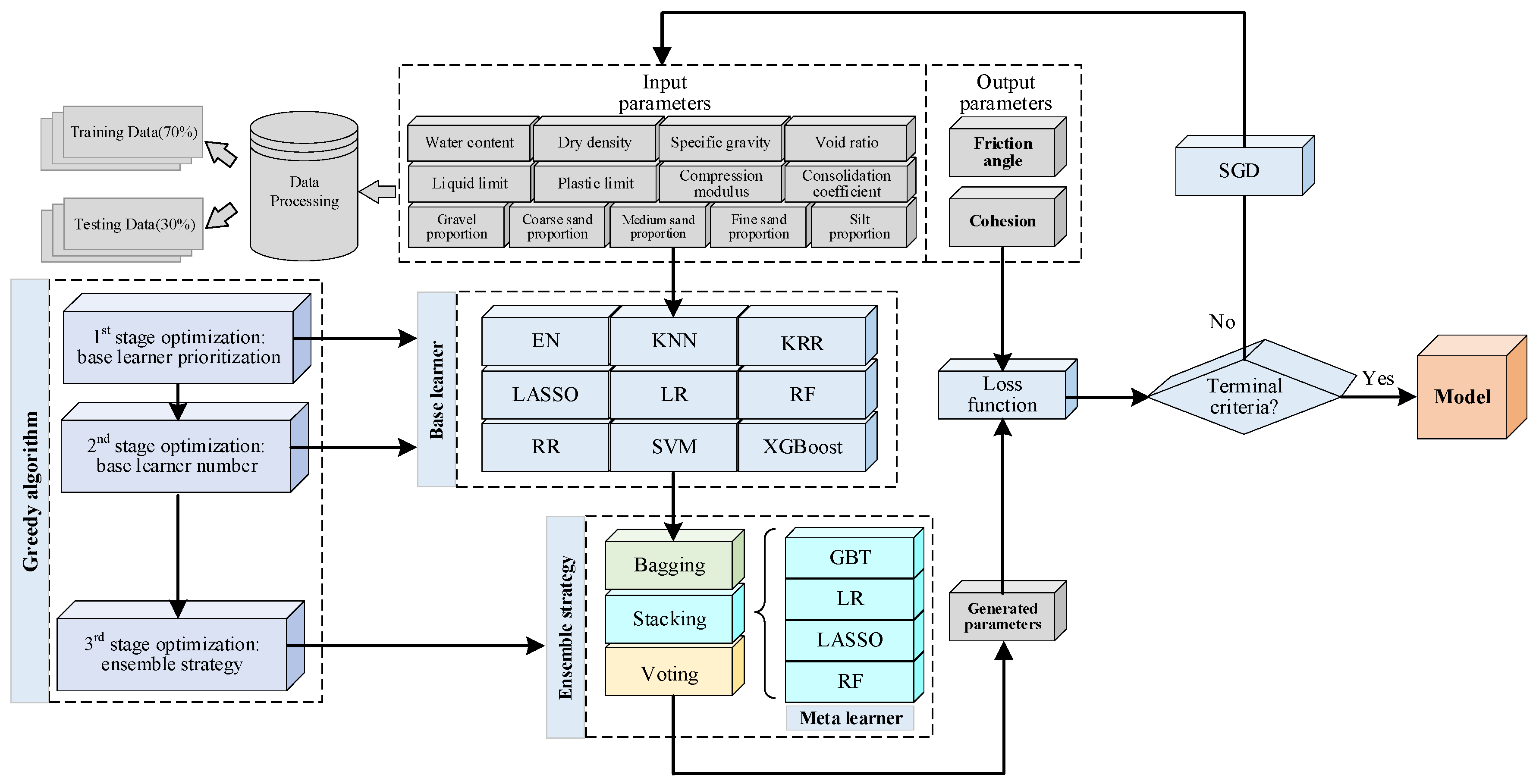
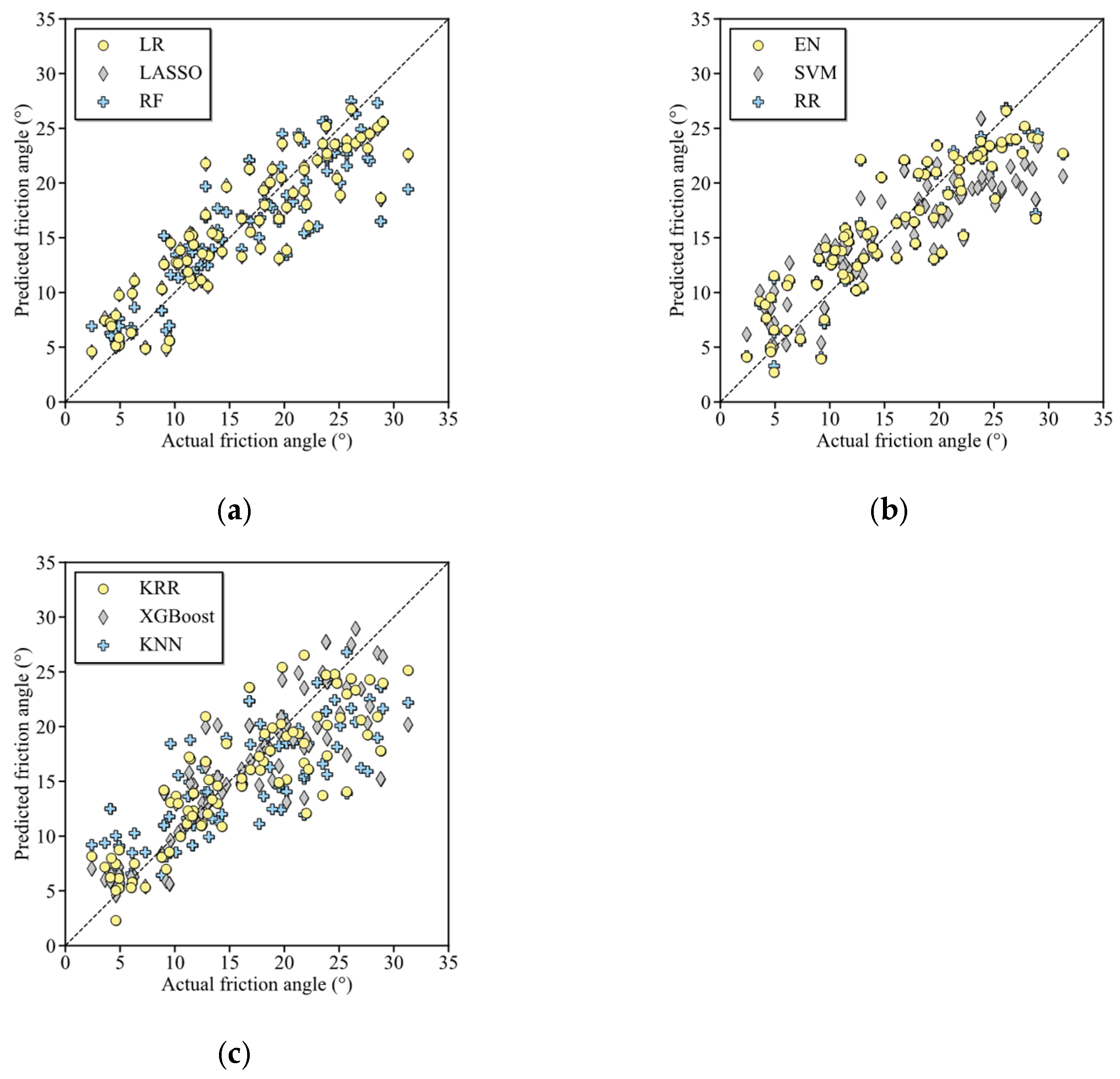
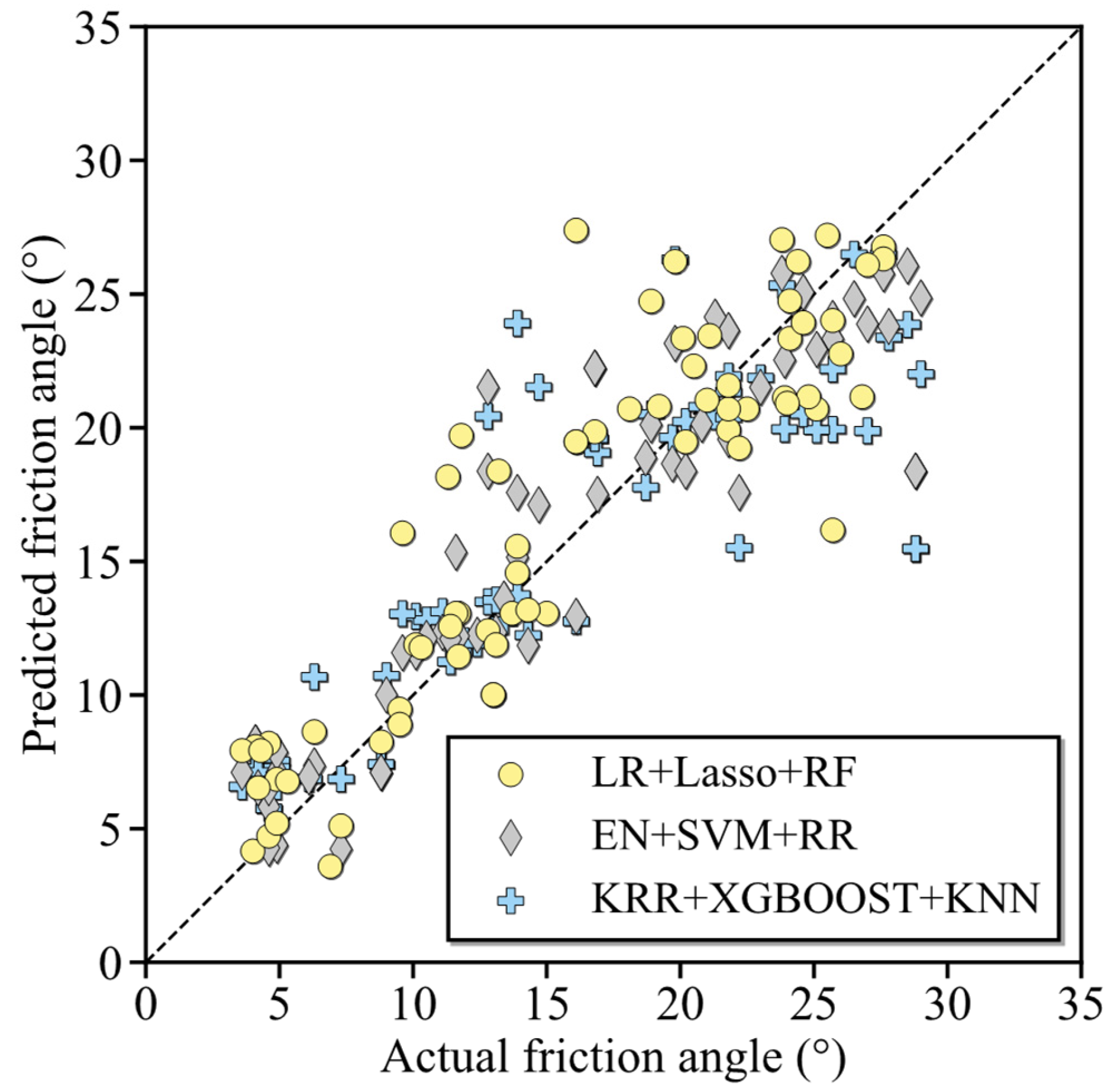
| No. | Outputs | Compared Models | Best Model | Performance | Reference |
|---|---|---|---|---|---|
| 1 | Compatibility | MLR, ANN, SA, SVM | SVM | R = 0.709 | Pentoś et al. [21] |
| 2 | pH value | MLR, RK, RF, GB, NN | RF | R2 = 0.784 | Tziachris et al. [23] |
| 3 | Thermal conductivity | MLR, GPR, SVM, DT, RF, AdaBoost | AdaBoost | RMSE = 0.099 | Li et al. [25] |
| 4 | Hydraulic conductivity | KNN, SVR, RF, BRT | BRT | RMSE = 0.295 | Araya and Ghezzehei [27] |
| 5 | Liquefaction susceptibility | ANN, SVM | SVM | 94.55% data accurately predicted | Samui and Sitharam [28] |
| 6 | Moisture content | ANN, DNN, SVR | SVR | R2 = 0.97 | Achieng [29] |
| 7 | Shear strength | PANFIS, GANFIS, SVR, ANN | PANFIS | RMSE = 0.038 | Pham et al. [34] |
| 8 | Shear strength | Ensemble learning | - | R2 = 0.7934, outperform other models | Rabbani et al. [36] |
| No. | Property | Unit | Var | Min | Max | Mean | Median | Std |
|---|---|---|---|---|---|---|---|---|
| 1 | Water content | % | X1 | 10.80 | 73.80 | 33.58 | 31.80 | 13.40 |
| 2 | Dry density | g/cm3 | X2 | 0.89 | 1.93 | 1.41 | 1.42 | 0.23 |
| 3 | Void ratio | - | X4 | 0.40 | 1.95 | 0.95 | 0.91 | 0.33 |
| 4 | Specific gravity | - | X3 | 2.60 | 2.75 | 2.69 | 2.70 | 0.03 |
| 5 | Liquid limit | % | X5 | 19.70 | 66.20 | 38.18 | 37.90 | 8.24 |
| 6 | Plastic limit | % | X6 | 9.30 | 40.40 | 23.16 | 22.70 | 5.26 |
| 7 | Compression modulus | MPa | X7 | 1.40 | 9.70 | 4.48 | 4.30 | 1.65 |
| 8 | Consolidation coefficient | 10−7 m2/s | X8 | 0.15 | 10.28 | 4.11 | 3.58 | 3.00 |
| 9 | Gravel proportion | % | X9 | 0.10 | 65.90 | 25.38 | 25.70 | 15.37 |
| 10 | Coarse sand proportion | % | X10 | 0.10 | 55.40 | 26.85 | 27.40 | 11.77 |
| 11 | Medium sand proportion | % | X11 | 2.20 | 40.80 | 14.39 | 12.20 | 7.74 |
| 12 | Fine sand proportion | % | X12 | 1.70 | 32.60 | 7.36 | 5.60 | 6.30 |
| 13 | Silt proportion | % | X13 | 2.50 | 82.60 | 26.02 | 20.50 | 16.90 |
| 14 | Friction angle | ° | Y1 | 2.40 | 31.30 | 15.33 | 13.90 | 7.23 |
| 15 | Cohesion | kPa | Y2 | 1.20 | 55.60 | 17.47 | 15.90 | 8.88 |
| No. | Type of Test | Device | Power (W) | Time (h) | Samples (/) | Parameters (/) | Energy Rate (Wh/S/P) |
|---|---|---|---|---|---|---|---|
| 1 | Water content test (oven dry method) | 101-4QB3 | 500 | 12 | 200 | X1–X3 | 10 |
| 2 | Specific gravity test (pycnometer method) | 101-4QB3 | 500 | 12 | 200 | X4 | 30 |
| 3 | Liquid-plastic limit combined test | LP-100D | 25 | 0.1 | 1 | X5–X6 | 1.25 |
| 4 | Consolidation test | GZQ-1A | 0 | 1.95 | 1 | X7–X8 | 0 |
| 5 | Sieving test | ZBSX_92A | 370 | 0.16 | 3 | X9–X13 | 3.95 |
| 6 | Direct shear test | ZJ-A | 100 | 2 | 1 | Y1–Y2 | 100 |
| Learners | R2 | RMSE (°) | MAE (°) |
|---|---|---|---|
| LR | 0.781 | 3.526 | 2.826 |
| LASSO | 0.778 | 3.549 | 2.841 |
| RF | 0.758 | 3.704 | 2.765 |
| EN | 0.738 | 3.853 | 2.990 |
| SVM | 0.718 | 3.933 | 3.252 |
| RR | 0.711 | 3.856 | 2.962 |
| KRR | 0.692 | 4.179 | 3.124 |
| XGBoost | 0.689 | 4.004 | 2.858 |
| KNN | 0.596 | 4.785 | 3.806 |
| Base Learners | Ensemble Strategy | R2 | RMSE (°) | MAE (°) |
|---|---|---|---|---|
| LR (Baseline) | - | 0.781 | 3.526 | 2.826 |
| LR + LASSO + RF | Stacking (GBT) | 0.812 | 3.377 | 2.522 |
| EN + SVM + RR | Stacking (GBT) | 0.786 | 3.682 | 2.780 |
| KRR + XGBoost + KNN | Stacking (GBT) | 0.729 | 4.065 | 3.029 |
| Ensemble Strategy | Base Learner | R2 | RMSE (°) | MAE (°) |
|---|---|---|---|---|
| - | LR (Baseline) | 0.781 | 3.526 | 2.826 |
| Stacking (GBT) | LR + LASSO + RF + EN | 0.881 | 2.954 | 2.222 |
| Stacking (LR) | LR + LASSO + RF + EN | 0.859 | 3.109 | 2.338 |
| Stacking (LASSO) | LR + LASSO + RF + EN | 0.855 | 3.134 | 2.384 |
| Stacking (RF) | LR + LASSO + RF + EN | 0.794 | 3.699 | 2.645 |
| Voting | LR + LASSO + RF + EN | 0.831 | 3.363 | 2.596 |
| Bagging | LR + LASSO + RF + EN | 0.782 | 3.809 | 2.881 |
| Direct Shear Test | Green AI Model | All Tests | AI Model + Other Tests | |
|---|---|---|---|---|
| Obtained parameters | Y1–Y2 | Y1–Y2 | X1–X13, Y1–Y2 | X1–X13, Y1–Y2 |
| Device | ZJ-A | Dell PowerEdge R760 | / | / |
| Power per sample (W) | 100 | 1400 | / | / |
| Time per sample (h) | 2 | 2 × 10−4 | / | / |
| Consumed energy (Wh) | 183,600 | 257 | 259,090 | 75,747 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Li, Z.; Qiu, X.; Sui, Y.; Lan, Z.; Tai, P. Green AI for Energy-Efficient Ground Investigation: A Greedy Algorithm-Optimized AI Model for Subsurface Data Prediction. Appl. Sci. 2025, 15, 12012. https://doi.org/10.3390/app152212012
Zhang S, Li Z, Qiu X, Sui Y, Lan Z, Tai P. Green AI for Energy-Efficient Ground Investigation: A Greedy Algorithm-Optimized AI Model for Subsurface Data Prediction. Applied Sciences. 2025; 15(22):12012. https://doi.org/10.3390/app152212012
Chicago/Turabian StyleZhang, Siyuan, Zhili Li, Xiang Qiu, Yaohua Sui, Zhi Lan, and Pei Tai. 2025. "Green AI for Energy-Efficient Ground Investigation: A Greedy Algorithm-Optimized AI Model for Subsurface Data Prediction" Applied Sciences 15, no. 22: 12012. https://doi.org/10.3390/app152212012
APA StyleZhang, S., Li, Z., Qiu, X., Sui, Y., Lan, Z., & Tai, P. (2025). Green AI for Energy-Efficient Ground Investigation: A Greedy Algorithm-Optimized AI Model for Subsurface Data Prediction. Applied Sciences, 15(22), 12012. https://doi.org/10.3390/app152212012





