Assessing the Risk of Damage to Underground Utilities Caused by Spatial Data Quality with Fuzzy Logic
Abstract
1. Introduction
Probabilistic, Bayesian, and Fuzzy Approaches—ACritical Synthesis
2. Materials and Methods
2.1. Probabilistic Risk Assessment (PRA)—Method Outline
- 1.
- Hazard and scenario identification—building a set of scenarios Si leading to damage (e.g., utility strike, mislocation).
- 2.
- Logical modelling—constructing event trees and/or fault trees that describe the sequences from initiators to consequences.
- 3.
- Probability quantification—estimating P(Si) based on historical data, failure statistics, activity frequencies and—where data are lacking—structured expert judgement; accounting for uncertainty (e.g., distributions, intervals, Monte Carlo simulation).
- 4.
- Consequence assessment—estimating I(Si) (e.g., costs, delays, health and safety/environmental impact).
- 5.
- Risk aggregation and presentation—computing risk metrics, e.g., R = ∑i P(Si)·I(Si), frequency–consequence curves, risk maps.
- 6.
- Sensitivity analysis and decisions—deriving importance measures, comparing alternatives, and selecting risk-reduction actions (e.g., more accurate utility detection, additional surveys, changes in work organisation).
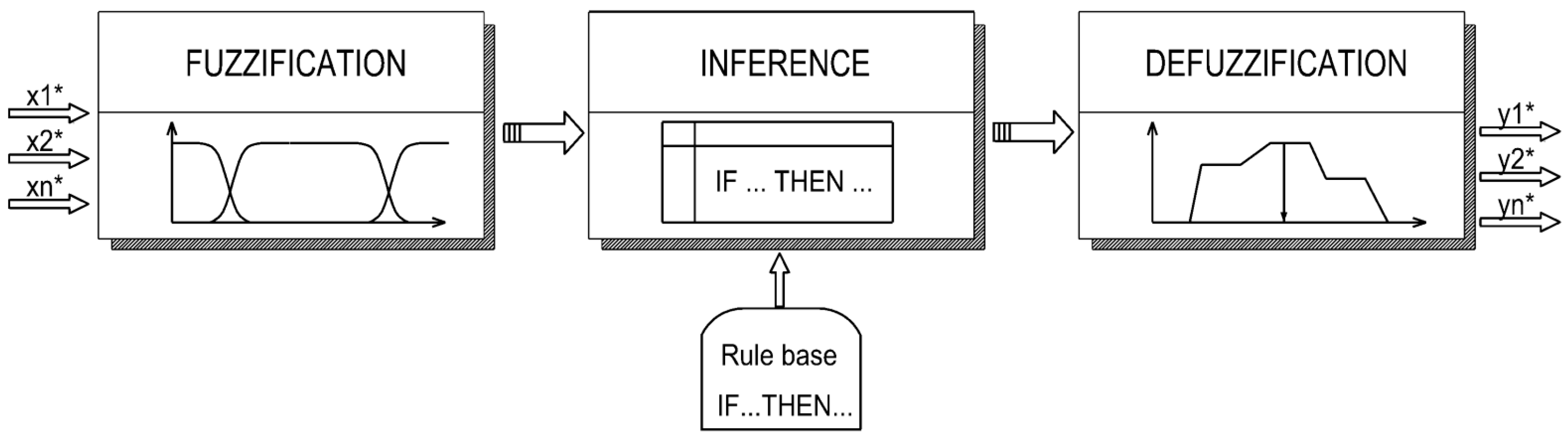
2.2. Fuzzy Risk Model for Damage to Underground Utilities
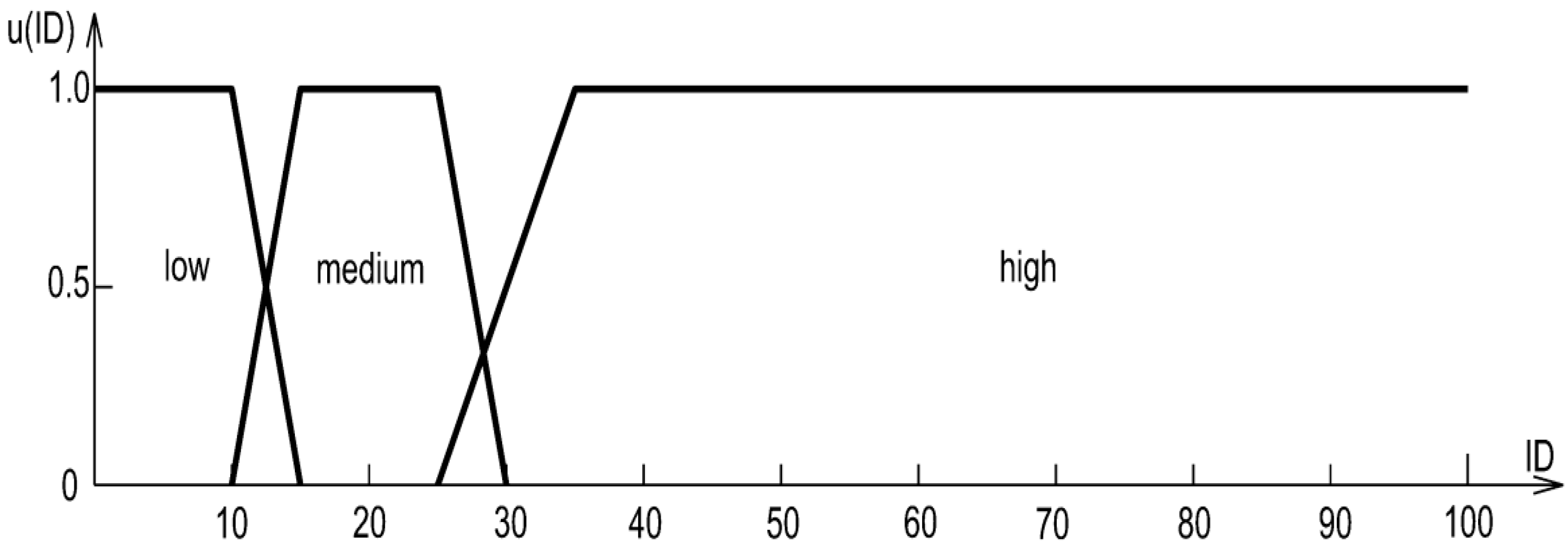
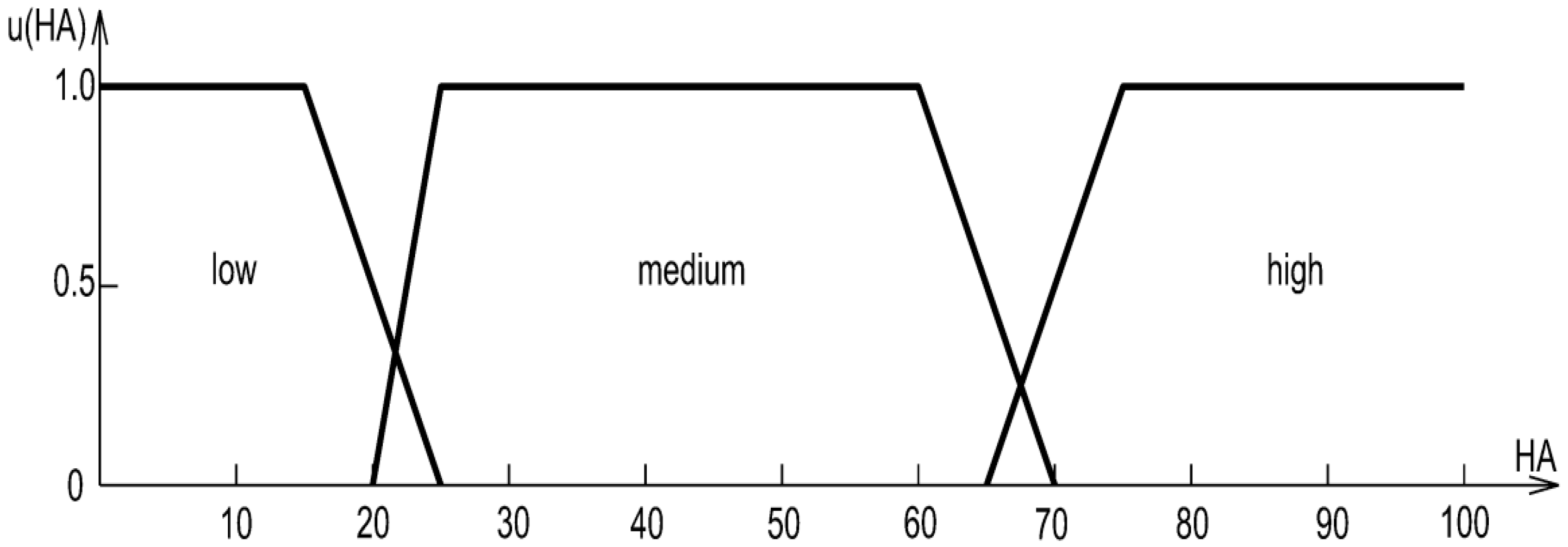
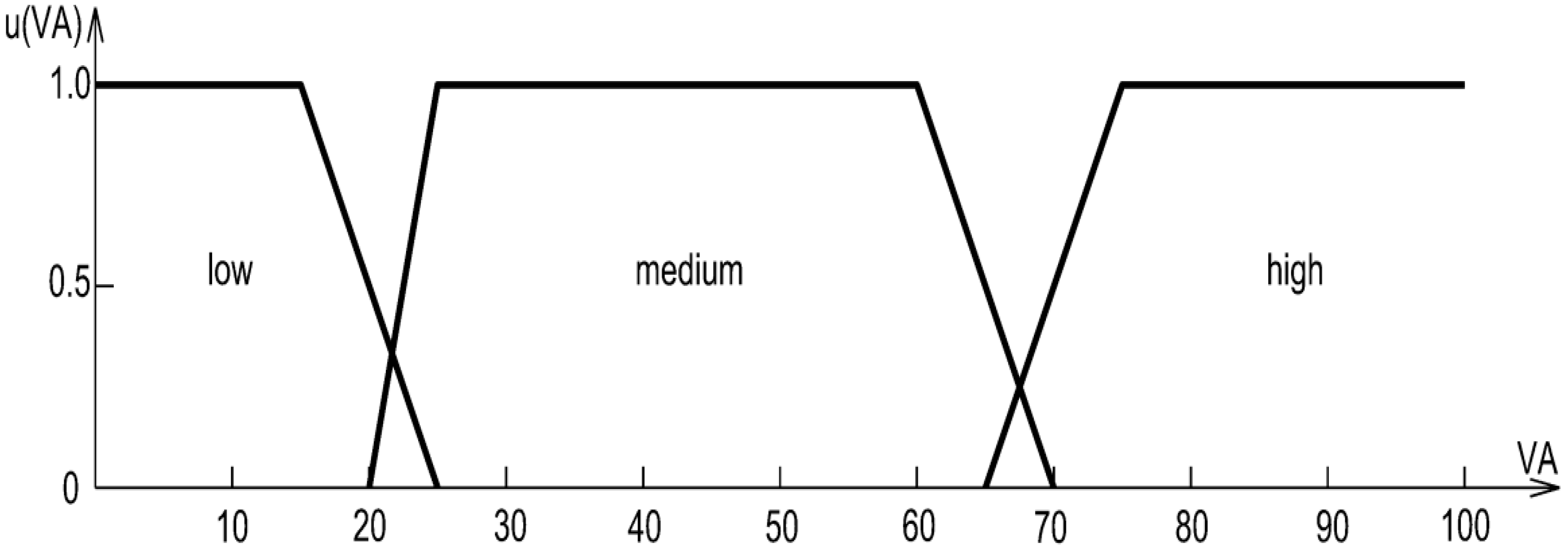
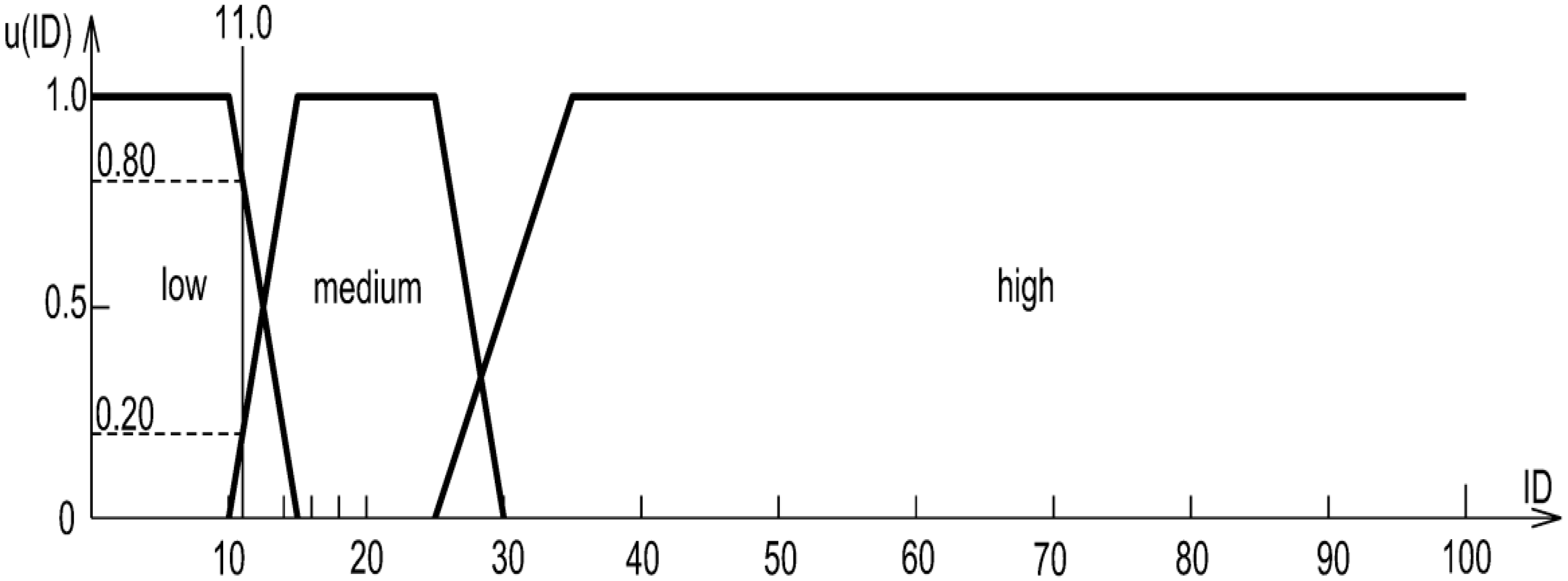
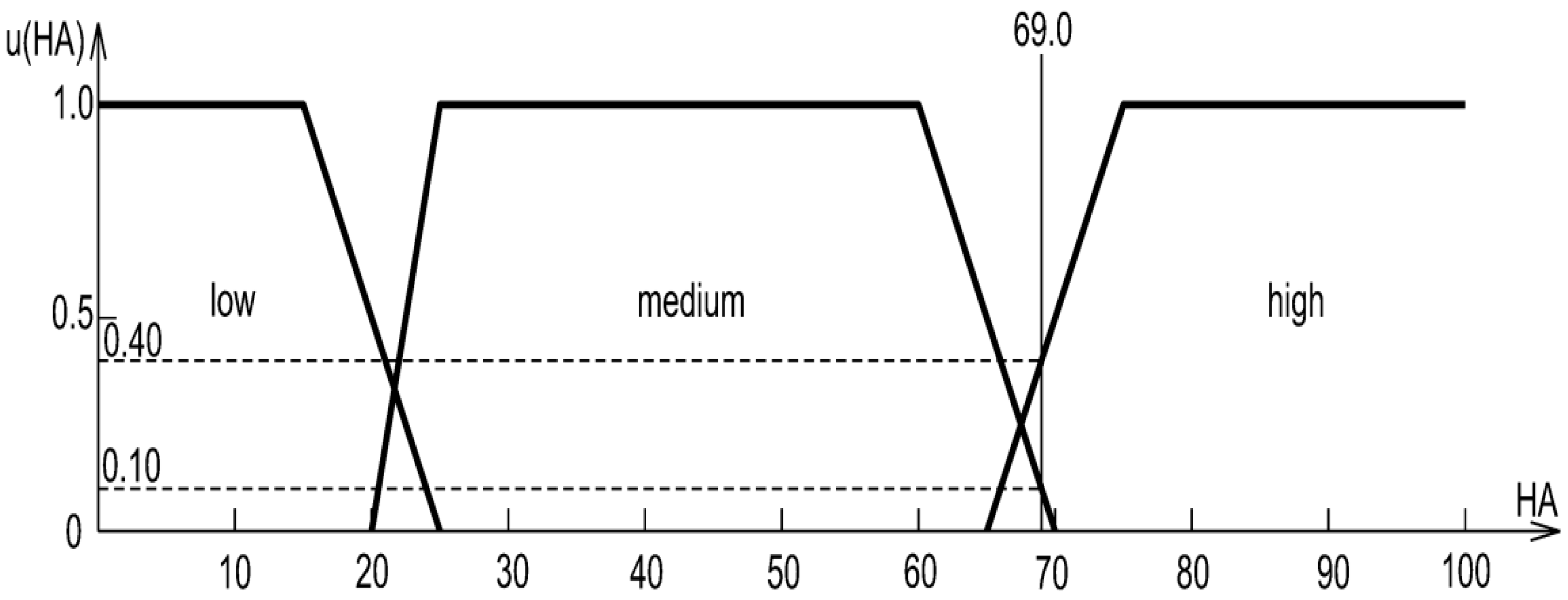
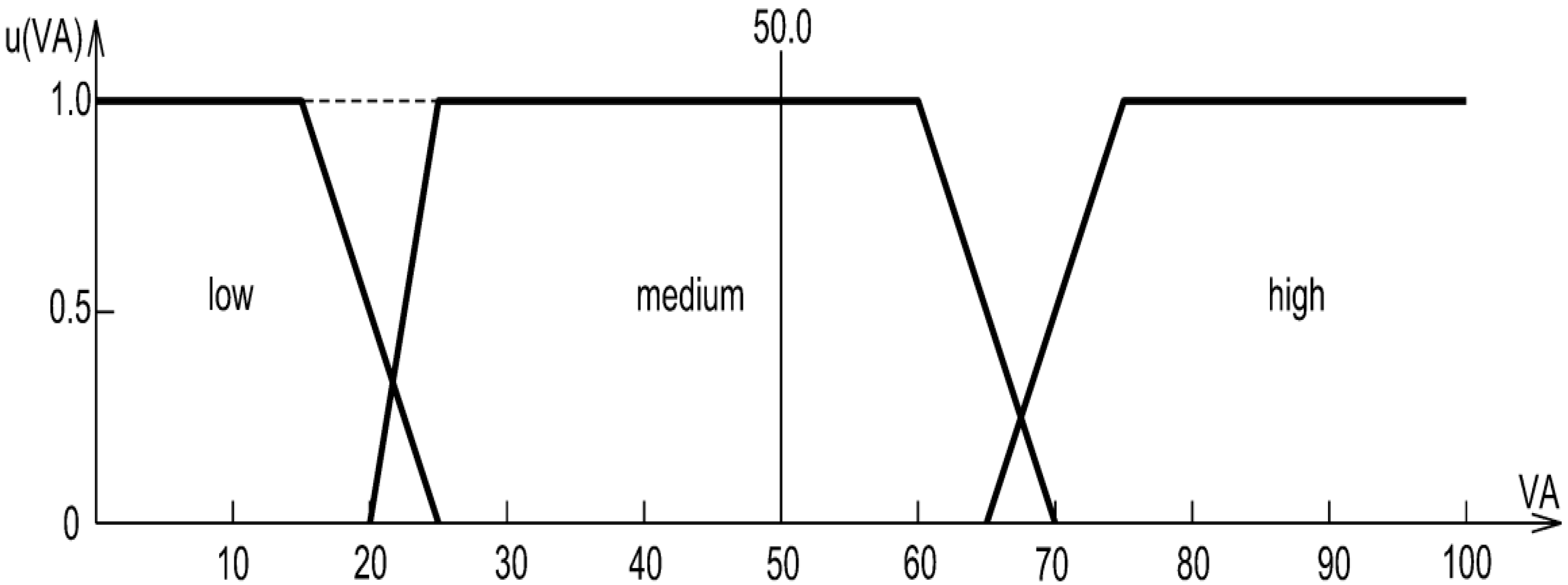
- Elicitation and sample. We conducted a structured questionnaire among practitioner–experts (site/works managers involved in linear projects near underground utilities) working in urbanised areas where 1:500 base maps and official databases are standard. N = 50 completed questionnaires. Each respondent was asked to indicate threshold values (in %) that separate low/medium/high classes for three risk factors: incompleteness of underground utility data (ID), horizontal accuracy (HA), and vertical accuracy (VA).
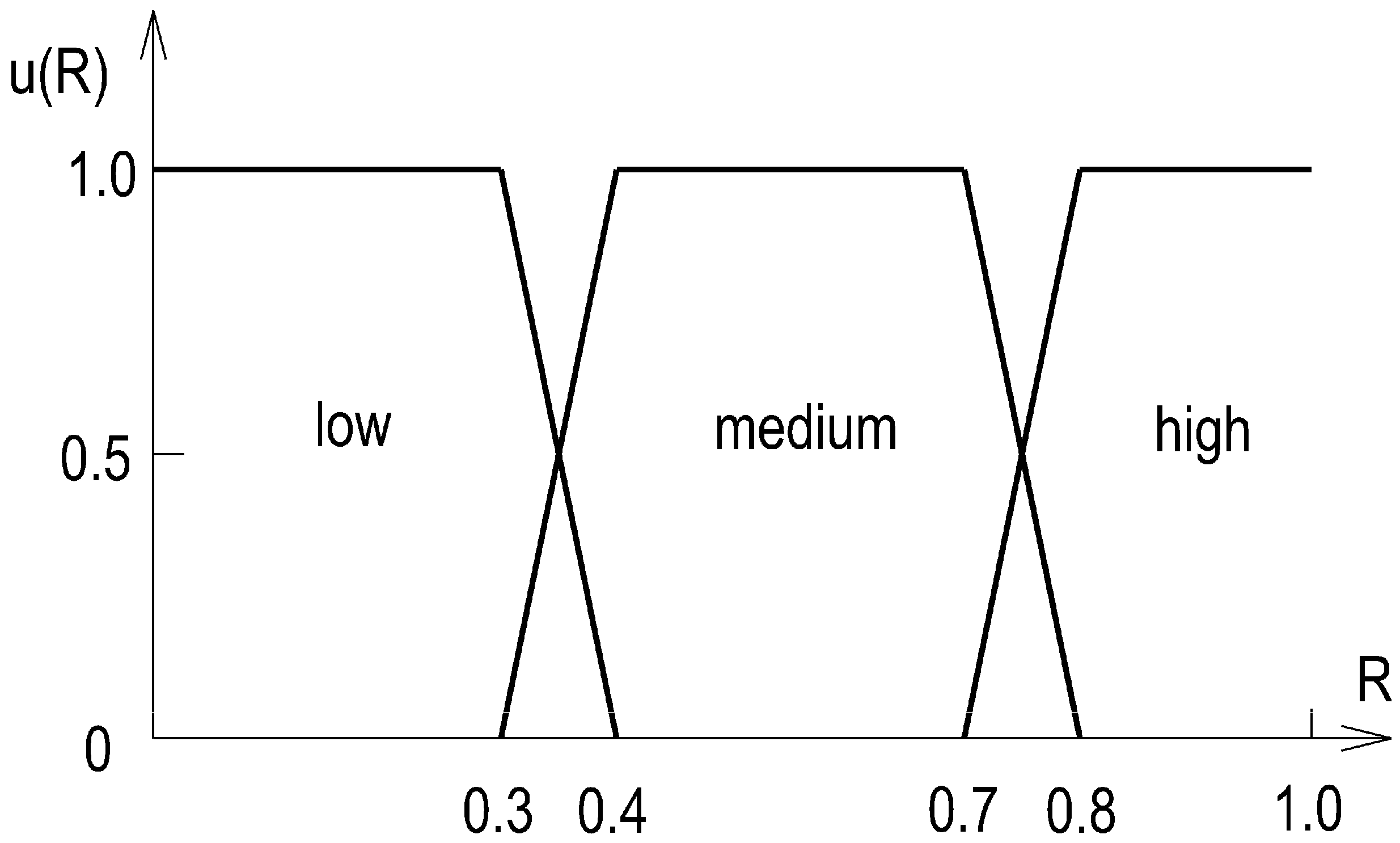
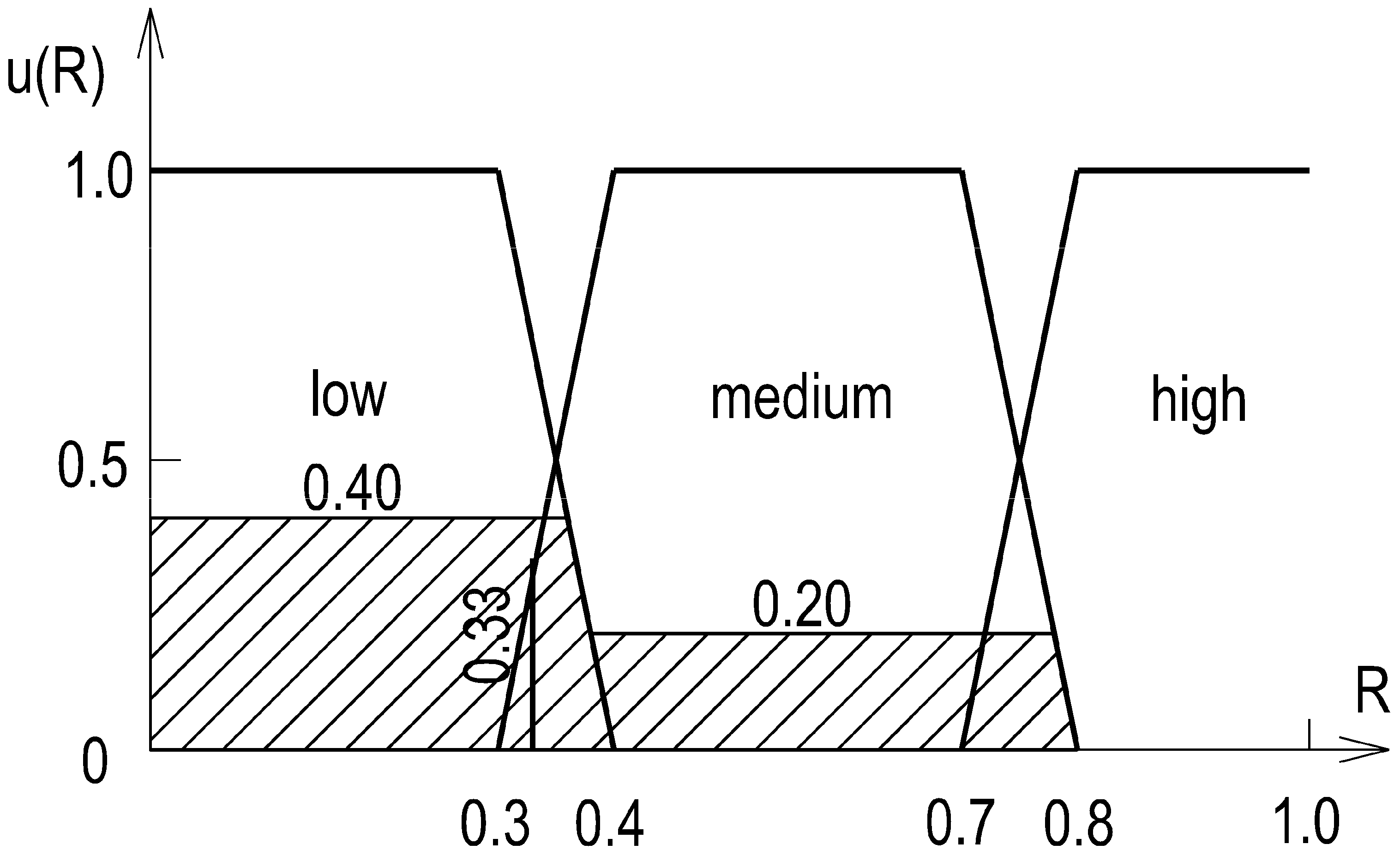
- Aggregation to objective parameters. Individual thresholds were aggregated to determine the four breakpoints (a, b, c, d) of trapezoidal membership functions for each factor. During aggregation, we enforced two mathematical conditions that guarantee internal consistency of the scales: partition of unity and continuity across adjacent classes; extreme outliers were smoothed to avoid non-physical transitions. The resulting distributions and parameters are reported in Table 3 and Table 4 and by closed-form formulas for u(ID), u(HA), and u(VA). Trapezoids were selected because experts provided interval cores of full membership, which this shape naturally captures.
- Rule base from expert knowledge. Expert reasoning was encoded as 27 intuitive IF–THEN rules in a Mamdani controller. Inference uses Zadeh min–max composition with standard t-norm/s-norm operators; this turns linguistic premises into fuzzy consequences in a reproducible way. The full rule base (Table 6) and operators are specified in the manuscript.
- From fuzzy to crisp indicators. Given any triplet (ID, HA, VA), fuzzification yields degrees of membership (example shown in Table 5), the rule base computes the output membership (Figure 9), and centre-of-gravity defuzzification produces a single numeric risk R ∈ [0, 1], which we map to low/medium/high classes. Worked examples for urban, suburban, and rural settings are reported (e.g., R = 0.33/0.55/0.86 for illustrative inputs). This pipeline makes the translation from subjective inputs to an objective, repeatable indicator explicit.
- We mitigated individual–expert idiosyncrasies by aggregating across N = 50 practitioners and by constraining the aggregated scales with partition-of-unity and continuity, which prevents any single respondent from dominating the class boundaries.
- The explicit publication of (a, b, c, d) parameters, rule base, and operators enables independent replication or recalibration with another expert panel, turning subjective inputs into auditable model components.
- The functions should satisfy the condition of partition of unity. A point in a transition zone belonging to one area to degree p belongs to the neighbouring area to degree 1 – p.
- Membership functions u(x) should be continuous in the entire universe of discourse X.
3. Results and Discussion
3.1. Sensitivity of Membership Thresholds
3.2. Methodological Recommendations and Reduction in Epistemic Uncertainty
- Standardised expert elicitation—a brief calibration training, a shared glossary, reporting of thresholds (a, b, c, d) with confidence intervals and an agreement protocol. (In our case, elicitation already underpins the parameterization of membership functions; we are now clarifying the reporting and archiving procedure.)
- Sensitivity analysis of membership functions—systematic variation in breakpoints (a, b, c, d) and observation of the impact on R; identification of stable and unstable ranges.
- Validation of the rule base—consistency/monotonicity tests and a “leave-one-scenario-out” procedure on available cases (urban/suburban/rural) with reporting of activated rules.
- Triangulation of data sources—combining GIS databases with field observation and non-invasive surveys (e.g., scanning/test trenches in line with the quality thresholds: ID, HA, VA). We added triggers for field verification: ID > 25% or HA/VA > 65% → mandatory in situ verification.
- Model updating and versioning—maintaining versioned parameters (membership functions, rules), a change log, and a “rolling update” mechanism after each project iteration.
- Limits of applicability and method selection—a decision matrix: FIS is recommended when epistemic uncertainty dominates and data are scarce (ID incompleteness, lack of failure statistics); PRA or hybrid models are preferred when stable quantitative time series are available. We supplemented the Conclusions with this explicit directive.
- Feedback from implementation—recording damage incidents and “as-built” data for cyclical recalibration of membership functions and rule revision.
3.3. Applications/Practical Guidance
- Network-wide planning (owners and cities): Use (R) maps to prioritise corridors/segments for data improvement and target budgets to locations where risk from data quality is highest. (“It will be employed to generate large-scale risk maps.”)
- Design and clash management (designers): Focus desktop reviews and clash checks on high-(R) segments; defer low-(R) segments to routine QA/QC.
- Construction means and methods (contractors): Tie potholing/vacuum excavation and utility locating intensity to (R): more intensive where (R) is high, standard practice where (R) is low/medium.
- Permitting and governance (authorities): Use (R) thresholds to set evidence requirements in permits (e.g., require verification before excavation in high-(R) zones).
- Continuous improvement: After works, ingest as-built/pothole logs to recalibrate membership breakpoints for the next programme cycle. (The paper notes that membership function distributions can be shifted for other data quality classes).
- R ≲ 0.4 (Low): Proceed with standard controls; no mandatory verification beyond routine QA/QC.
- 0.4 ≲ R ≲ 0.7 (Medium): Targeted upgrades: additional locating in conflict areas/crossings; selective verification where design clearances are tight.
- R ≳ 0.8 (High): Mandatory verification (e.g., test pits/utility exposure) before excavation and/or design changes to increase clearances.
4. Conclusions
4.1. Integration with Spatial Databases and the Digital Twin
4.2. Future Work
- Carry out external validation and calibration of the model on empirical data (records of actual strikes, as-built surveys), together with global sensitivity and uncertainty analyses of the membership functions and rules.
- Expand the factor space to include network density, depth and type of conduits, map/source class, age and reliability of records, detection method (e.g., GPR), and geotechnical–environmental conditions.
- Compare alternative inference frameworks (Mamdani vs. Sugeno), t-norm/s-norm operators and defuzzification methods, and explore type-2 fuzzy and hybrid fuzzy–PRA (Probabilistic Risk Assessment)/Bayesian models to better capture epistemic uncertainty.
- Learn parameters and reduce the rule base using ANFIS (Adaptive Neuro-Fuzzy Inference System) and evolutionary algorithms to improve transferability and limit expert bias.
- Integrate with 3D GIS/BIM (IFC/CityGML) for continuous city-/region-scale risk mapping and near-real-time “permit-to-dig” decision support.
- Link risk ratings to cost, schedule, and occupational health and safety (OHS) consequences and to cost–benefit analyses of additional surveying.
- Assess model transferability across jurisdictions and data quality classes (e.g., national utility registers) and develop implementation guidance for authorities and contractors.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gleim, I.N. CIA Review—Part I—The Internal Audit Activity’s Role in Governance, Risk and Control, Certified Internal Auditor; Gleim Publications Inc.: Gainesville, FL, USA, 2004. [Google Scholar]
- Kaplan, S.; Garrick, B.J. On the quantitative definition of risk. Risk Anal. 1981, 1, 11–27. [Google Scholar] [CrossRef]
- Fayaz, M.; Ahmad, S.; Ullah, I.; Kim, D. A Blended Risk Index Modeling and Visualization Based on Hierarchical Fuzzy Logic for Water Supply Pipelines Assessment and Management. Processes 2018, 6, 61. [Google Scholar] [CrossRef]
- Fayaz, M.; Ahmad, S.; Hang, L.; Kim, D. Water Supply Pipeline Risk Index Assessment Based on Cohesive Hierarchical Fuzzy Inference System. Processes 2019, 7, 182. [Google Scholar] [CrossRef]
- Fayaz, M.; Ullah, I.; Park, D.-H.; Kim, K.; Kim, D. An Integrated Risk Index Model Based on Hierarchical Fuzzy Logic for Underground Risk Assessment. Appl. Sci. 2017, 7, 1037. [Google Scholar] [CrossRef]
- Malinowska, A.; Cui, X.; Salmi, E.F.; Hejmanowski, R. A novel fuzzy approach to gas pipeline risk assessment under influence of ground movement. Int. J. Coal Sci. Technol. 2022, 9, 47. [Google Scholar] [CrossRef]
- Fayaz, M.; Pham, Q.B.; Linh, N.T.T.; Nhi, P.T.T.; Khoi, D.N.; Qureshi, M.S.; Shah, A.S.; Khalid, S. A Water Supply Pipeline Risk Analysis Methodology Based on DIY and Hierarchical Fuzzy Inference. Symmetry 2020, 12, 44. [Google Scholar] [CrossRef]
- Zhang, P.; Qin, G.; Wang, Y. Risk Assessment System for Oil and Gas Pipelines Laid in One Ditch Based on Quantitative Risk Analysis. Energies 2019, 12, 981. [Google Scholar] [CrossRef]
- Fu, X.; Gu, C.-S.; Su, H.-Z.; Qin, X.-N. Risk Analysis of Earth-Rock Dam Failures Based on Fuzzy Event Tree Method. Int. J. Environ. Res. Public Health 2018, 15, 886. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Z.; Li, W.; Song, Z.; Ge, W.; Han, R.; Wang, T. Risk Analysis of Instability Failure of Earth–Rock Dams Based on the Fuzzy Set Theory. Water 2021, 13, 3088. [Google Scholar] [CrossRef]
- Topal, S.; Atasoylu, E. A Fuzzy Risk Assessment Model for Small Scale Construction Work. Sustainability 2022, 14, 4442. [Google Scholar] [CrossRef]
- Zhang, W.; Huang, Z.; Zhang, J.; Zhang, R.; Ma, S. Multifactor Uncertainty Analysis of Construction Risk for Deep Foundation Pits. Appl. Sci. 2022, 12, 8122. [Google Scholar] [CrossRef]
- Jin, H.; Goodrum, P.M. Optimal Fall Protection System Selection Using a Fuzzy Multi-Criteria Decision-Making Approach for Construction Sites. Appl. Sci. 2021, 11, 5296. [Google Scholar] [CrossRef]
- Jiang, W.; Zhang, Z.; Deng, X. A Novel Failure Mode and Effects Analysis Method Based on Fuzzy Evidential Reasoning Rules. IEEE Access 2019, 7, 113605–113615. [Google Scholar] [CrossRef]
- Heidary Dahooie, J.; Vanaki, A.S.; Firoozfar, H.R.; Zavadskas, E.K.; Čereška, A. An Extension of the Failure Mode and Effect Analysis with Hesitant Fuzzy Sets to Assess the Occupational Hazards in the Construction Industry. Int. J. Environ. Res. Public Health 2020, 17, 1442. [Google Scholar] [CrossRef]
- Biswas, T.K.; Zaman, K. A Fuzzy-Based Risk Assessment Methodology for Construction Projects Under Epistemic Uncertainty. Int. J. Fuzzy Syst. 2019, 21, 1221–1240. [Google Scholar] [CrossRef]
- Shi, B.; Zeng, T.; Tang, C.; Zhang, L.; Xie, Z.; Lv, G.; Wu, Q. Landslide Risk Assessment Using Granular Fuzzy Rule-Based Modeling: A Case Study on Earthquake-Triggered Landslides. IEEE Access 2021, 9, 135790–135802. [Google Scholar] [CrossRef]
- Cárdenas, G.J.R.; Nebot, À.; Mugica, F. Integral Seismic Risk Assessment through Fuzzy Models. Appl. Sci. 2020, 10, 3017. [Google Scholar] [CrossRef]
- Bianchini, S.; Solari, L.; Del Soldato, M.; Raspini, F.; Montalti, R.; Ciampalini, A.; Casagli, N. Ground Subsidence Susceptibility (GSS) Mapping in Grosseto Plain (Tuscany, Italy) Based on Satellite InSAR Data Using Frequency Ratio and Fuzzy Logic. Remote Sens. 2019, 11, 2015. [Google Scholar] [CrossRef]
- Uzhga-Rebrov, O.; Grabusts, P. Methodology for Environmental Risk Analysis Based on Intuitionistic Fuzzy Values. Risks 2023, 11, 88. [Google Scholar] [CrossRef]
- Gul, M.; Guneri, A.F.; Nasirli, S.M. A fuzzy-based model for risk assessment of routes in oil transportation. Int. J. Environ. Sci. Technol. 2019, 16, 4671–4686. [Google Scholar] [CrossRef]
- Zhou, H.; Yue, X.; Chen, Y.; Liu, Y.; Gong, G. Comprehensive Environmental and Health Risk Assessment of Soil Heavy Metal(loid)s Considering Uncertainties: The Case of a Typical Metal Mining Area in Daye City, China. Minerals 2023, 13, 1389. [Google Scholar] [CrossRef]
- Lisboa, É.G.; Mendes, R.L.R.; Figueiredo, M.M.P.; Bello, L.A.L. Fuzzy-Probabilistic Model for a Risk Assessment of Groundwater Contamination: Application to an Urban Zone in the City of Belém, Pará, Brazil. Water 2020, 12, 1437. [Google Scholar] [CrossRef]
- Ramirez, R.; Martí, V.; Darbra, R.M. Environmental Risk Assessment of Silver Nanoparticles in Aquatic Ecosystems Using Fuzzy Logic. Water 2022, 14, 1885. [Google Scholar] [CrossRef]
- Chen, X.; Li, F.; Zhang, J.; Liu, S.; Ou, C.; Yan, J.; Sun, T. Status, fuzzy integrated risk assessment, and hierarchical risk management of soil heavy metals across China: A systematic review. Sci. Total. Environ. 2021, 785, 147180. [Google Scholar] [CrossRef]
- Wijitkosum, S.; Sriburi, T. Fuzzy AHP Integrated with GIS Analyses for Drought Risk Assessment: A Case Study from Upper Phetchaburi River Basin, Thailand. Water 2019, 11, 939. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y.; Liu, X.; Shen, C. A Multiple Model Approach for Flood Forecasting, Simulation, and Evaluation Coupling in Zhouqu County. Water 2023, 15, 4246. [Google Scholar] [CrossRef]
- Noori, A.; Bonakdari, H.; Morovati, K.; Gharabaghi, B. Development of optimal water supply plan using integratedfuzzy Delphi and fuzzy ELECTRE III methods—Case study of the Gamasiab basin. Expert Syst. 2020, 37, e12568. [Google Scholar] [CrossRef]
- Chen, H.; Xu, Z.; Liu, Y.; Huang, Y.; Yang, F. Urban Flood Risk Assessment Based on Dynamic Population Distribution and Fuzzy Comprehensive Evaluation. Int. J. Environ. Res. Public Health 2022, 19, 16406. [Google Scholar] [CrossRef] [PubMed]
- Msabi, M.M.; Makonyo, M. Flood susceptibility mapping using GIS and multi-criteria decision analysis: A case of Dodoma region, central Tanzania. Remote. Sens. Appl. Soc. Environ. 2021, 21, 100445. [Google Scholar] [CrossRef]
- Noori, A.; Bonakdari, H. A GIS-Based Fuzzy Hierarchical Modeling for Flood Susceptibility Mapping: A Case Study in Ontario, Eastern Canada. Environ. Sci. Proc. 2023, 25, 62. [Google Scholar] [CrossRef]
- Wang, G.; Liu, Y.; Hu, Z.; Lyu, Y.; Zhang, G.; Liu, J.; Liu, Y.; Gu, Y.; Huang, X.; Zheng, H.; et al. Flood Risk Assessment Based on Fuzzy Synthetic Evaluation Method in the Beijing-Tianjin-Hebei Metropolitan Area, China. Sustainability 2020, 12, 1451. [Google Scholar] [CrossRef]
- Zhou, C.; Chen, M.; Chen, J.; Chen, Y.; Chen, W. A Multi-Hazard Risk Assessment Model for a Road Network Based on Neural Networks and Fuzzy Comprehensive Evaluation. Sustainability 2024, 16, 2429. [Google Scholar] [CrossRef]
- Rodríguez-Pérez, Á.M.; Rodríguez, C.A.; Márquez-Rodríguez, A.; Caparros Mancera, J.J. Viability Analysis of Tidal Turbine Installation Using Fuzzy Logic: Case Study and Design Considerations. Axioms 2023, 12, 778. [Google Scholar] [CrossRef]
- Rodríguez Pérez, Á.M.; Rodríguez, C.A.; Olmo Rodríguez, L.; Caparros Mancera, J.J. Revitalizing the Canal de Castilla: A Community Approach to Sustainable Hydropower Assessed through Fuzzy Logic. Appl. Sci. 2024, 14, 1828. [Google Scholar] [CrossRef]
- Oort, P. Spatial Data Quality: From Description to Application; Publications on Geodesy 60; Netherlands Geodetic Commission: Delft, The Netherlands, 2005; p. 140. [Google Scholar]
- Zadeh, L.A.; Aliev, R.A. Fuzzy Logic Theory and Applications: Part I and Part II; World Scientific Publishing Company: Singapore, 2018. [Google Scholar]
- Carter, J.; Chiclana, F.; Khuman, A.S. Fuzzy Logic: Recent Applications and Developments; Springer International Publishing: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Ross, T.J. Fuzzy Logic with Engineering Applications; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Piegat, A. Fuzzy Modeling and Control; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Tchórzewska-Cieślak, B. Characterization of risk function in the analysis and assessment of water supply systems safety. Tech. Trans. 2018, 3, 187–196. [Google Scholar]
| Criterion | Probabilistic (PRA) | Bayesian | Fuzzy (FIS) |
|---|---|---|---|
| Dominant uncertainty type | Aleatory | Aleatory + epistemic (via priors) | Epistemic (vagueness) |
| Data requirements | High (historical, stable) | Moderate–high (model + priors) | Low–moderate (experts, quality thresholds) |
| Representation of expert knowledge | Indirect (scenarios, weights) | Explicit (priors, hierarchies) | Explicit (membership functions, rules |
| Output | Probabilities/risk measures | Posterior distributions | Linguistic ratings + crisp value |
| Interpretability for practitioners | Moderate | Moderate | High |
| Suitability for underground utility data quality (gaps, ambiguity) | Limited | Good, if model is well specified | Very good |
| Membership Function | ||
|---|---|---|
| Name | Plot | Equation |
| Trapezoidal | 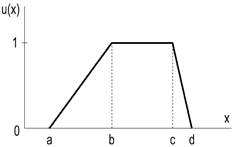 | |
| Risk Factors | Linguistic Values: Statistical Values | Count and Rate of Linguistic Values of Risk Factors | |
|---|---|---|---|
| Count | [%] | ||
| Incomplete underground utility data (ID) | low: under 5% | 27 | 54 |
| low: under 10% | 23 | 46 | |
| low: under 15% | 0 | 0 | |
| medium: 10% to 15% | 0 | 0 | |
| medium: 15% to 25% | 50 | 100 | |
| medium: 15% to 30% | 0 | 0 | |
| high: over 25% | 0 | 0 | |
| high: over 35% | 27 | 54 | |
| high: over 40% | 23 | 46 | |
| Horizontal accuracy (HA) and vertical accuracy (VA) of underground utilities | low: under 10% | 27 | 54 |
| low: under 15% | 23 | 46 | |
| low: under 25% | 0 | 0 | |
| medium: 10% to 20% | 0 | 0 | |
| medium: 25% to 60% | 50 | 100 | |
| medium: 25% to 75% | 0 | 0 | |
| high: over 65% | 0 | 0 | |
| high: over 75% | 27 | 54 | |
| high: over 80% | 23 | 46 | |
| Risk Factors | Linguistic Values | Statistical Values | ||||
|---|---|---|---|---|---|---|
| Incomplete underground utility data (ID) | low | x | 0.0 | 10.0 | 15.0 | - |
| u(x) | 1.0 | 1.0 | 0.0 | |||
| medium | x | 10.0 | 15.0 | 25.0 | 30.0 | |
| u(x) | 0.0 | 1.0 | 1.0 | 0.0 | ||
| high | x | 25.0 | 35.0 | 100.0 | ||
| u(x) | 0.0 | 1.0 | 1.0 | |||
| Horizontal accuracy (HA) and vertical accuracy (VA) | low | x | 0.0 | 15.0 | 25.0 | |
| u(x) | 1.0 | 1.0 | 0.0 | |||
| medium | x | 20.0 | 25.0 | 60.0 | 70.0 | |
| u(x) | 0.0 | 1.0 | 1.0 | 0.0 | ||
| high | x | 65.0 | 75.0 | 100.0 | ||
| u(x) | 0.0 | 1.0 | 1.0 | |||
| Linguistic Variable | Set | ||
|---|---|---|---|
| Low | Medium | High | |
| Incomplete underground utility data (ID) | 0.80 | 0.20 | 0.00 |
| Horizontal accuracy (HA) | 0.00 | 0.10 | 0.40 |
| Vertical accuracy (VA) | 0.00 | 1.00 | 0.00 |
| Scenario | R (Baseline) | Factor | R (−10%) | R (+10%) | ∆R (−10%) | ∆R (+10%) |
|---|---|---|---|---|---|---|
| Urban | 0.33 | ID | 0.39 | 0.274 | 0.06 | −0.056 |
| Urban | 0.33 | HA | 0.269 | 0.55 | −0.061 | 0.22 |
| Urban | 0.33 | VA | 0.33 | 0.33 | 0 | 0 |
| Suburban | 0.55 | ID | 0.55 | 0.55 | 0 | 0 |
| Suburban | 0.55 | HA | 0.55 | 0.55 | 0 | 0 |
| Suburban | 0.55 | VA | 0.55 | 0.55 | 0 | 0 |
| Rural | 0.86 | ID | 0.87 | 0.607 | 0.01 | −0.253 |
| Rural | 0.86 | HA | 0.86 | 0.86 | 0 | 0 |
| Rural | 0.86 | VA | 0.86 | 0.86 | 0 | 0 |
| Rule No. | Risk Factors | Risk Level | ||
|---|---|---|---|---|
| Incomplete Data | Horizontal Accuracy | Vertical Accuracy | ||
| 1 | ID = L | HA = L | VA = L | R = M |
| 2 | ID = L | HA = L | VA = M | R = M |
| 3 | ID = L | HA = H | VA = H | R = L |
| 4 | ID = L | HA = M | VA = L | R = M |
| 5 | ID = L | HA = M | VA = M | R = M |
| 6 | ID = L | HA = H | VA = L | R = L |
| 7 | ID = L | HA = H | VA = M | R = L |
| 8 | ID = M | HA = L | VA = L | R = H |
| 9 | ID = M | HA = M | VA = M | R = M |
| 10 | ID = M | HA = H | VA = H | R = M |
| 11 | ID = M | HA = M | VA = L | R = M |
| 12 | ID = M | HA = H | VA = L | R = M |
| 13 | ID = M | HA = H | VA = M | R = M |
| 14 | ID = H | HA = L | VA = L | R = H |
| 15 | ID = H | HA = M | VA = M | R = H |
| 16 | ID = H | HA = H | VA = H | R = H |
| 17 | ID = H | HA = M | VA = L | R = H |
| 18 | ID = H | HA = H | VA = L | R = H |
| 19 | ID = H | HA = H | VA = M | R = H |
| 20 | ID = L | HA = L | VA = H | R = L |
| 21 | ID = L | HA = M | VA = H | R = L |
| 22 | ID = M | HA = L | VA = M | R = M |
| 23 | ID = M | HA = L | VA = H | R = M |
| 24 | ID = M | HA = M | VA = H | R = M |
| 25 | ID = H | HA = L | VA = M | R = H |
| 26 | ID = H | HA = L | VA = H | R = H |
| 27 | ID = H | HA = M | VA = H | R = H |
| Numerical Value of the Risk Factor | Risk | |||
|---|---|---|---|---|
| Incomplete Data (ID) | Horizontal Accuracy (HA) | Vertical Accuracy (VA) | Quantitative R | Qualitative RL/RM/RH |
| 11.0 | 69.0 | 50.0 | 0.33 | RL |
| 22.0 | 58.0 | 40.0 | 0.55 | RM |
| 30.0 | 50.0 | 30.0 | 0.86 | RH |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ślusarski, M.; Przewięźlikowska, A. Assessing the Risk of Damage to Underground Utilities Caused by Spatial Data Quality with Fuzzy Logic. Appl. Sci. 2025, 15, 11980. https://doi.org/10.3390/app152211980
Ślusarski M, Przewięźlikowska A. Assessing the Risk of Damage to Underground Utilities Caused by Spatial Data Quality with Fuzzy Logic. Applied Sciences. 2025; 15(22):11980. https://doi.org/10.3390/app152211980
Chicago/Turabian StyleŚlusarski, Marek, and Anna Przewięźlikowska. 2025. "Assessing the Risk of Damage to Underground Utilities Caused by Spatial Data Quality with Fuzzy Logic" Applied Sciences 15, no. 22: 11980. https://doi.org/10.3390/app152211980
APA StyleŚlusarski, M., & Przewięźlikowska, A. (2025). Assessing the Risk of Damage to Underground Utilities Caused by Spatial Data Quality with Fuzzy Logic. Applied Sciences, 15(22), 11980. https://doi.org/10.3390/app152211980






