Calibration of a Multiphase Poroelasticity Model Using Genetic Algorithms
Abstract
1. Introduction
Related Works and Theoretical Background
2. Mathematical Model of Porous Medium
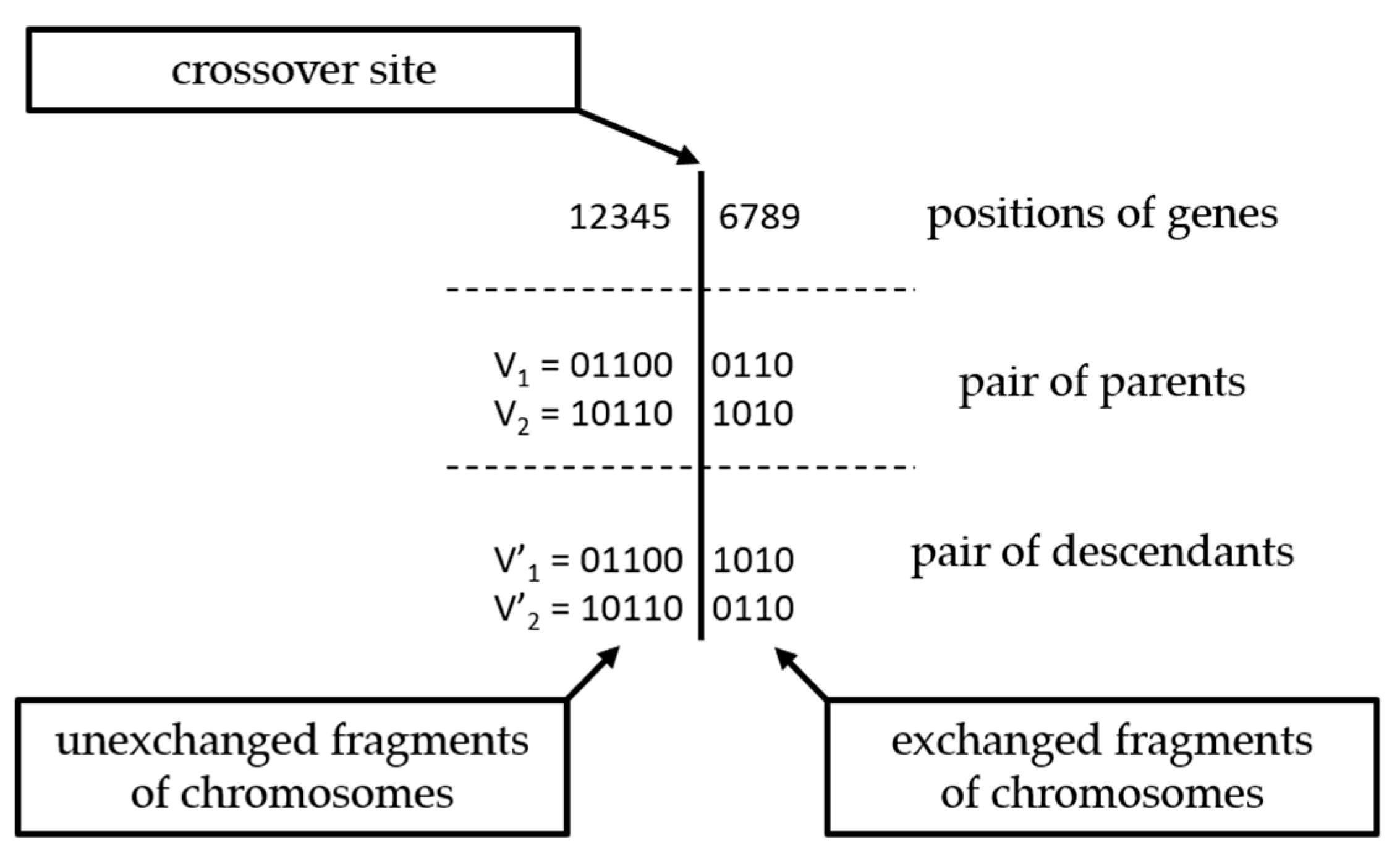
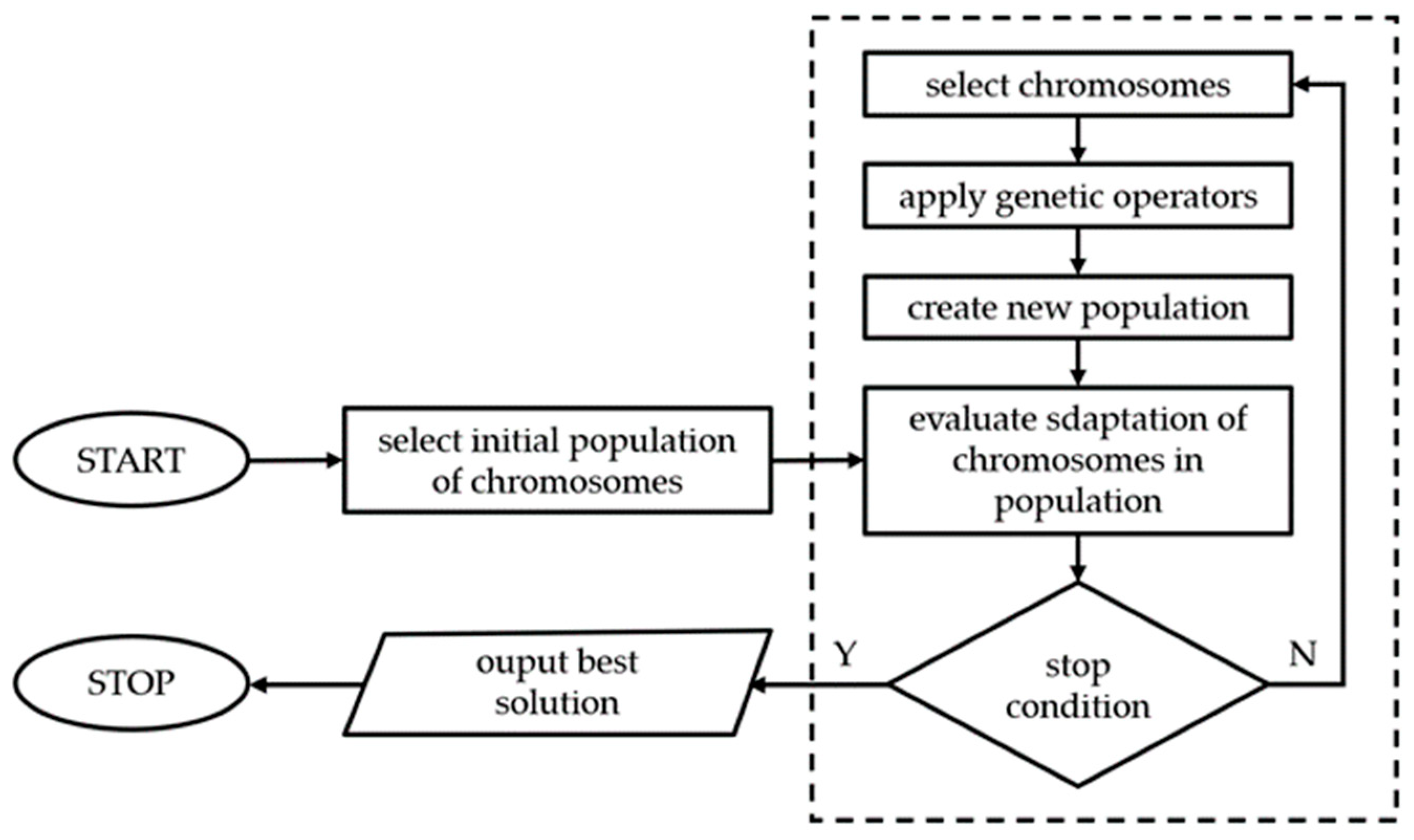
3. Genetic Algorithms
4. The Methodology Adopted
- the algorithm reads laboratory measurement results from a file;
- from the basic file for the FlexPDE program the algorithm creates a model .pde file with entered values of the calibrated parameters;
- the algorithm makes the Flex PDE program execute a simulation, the results of which are saved to a text file;
- The algorithm waits for the simulation to end and then reads the simulation results; using the simulation and measurement results, the algorithm calculates the objective function value (a standard square estimator).
5. Results of the Determination of Effective Parameters of the Biot Model
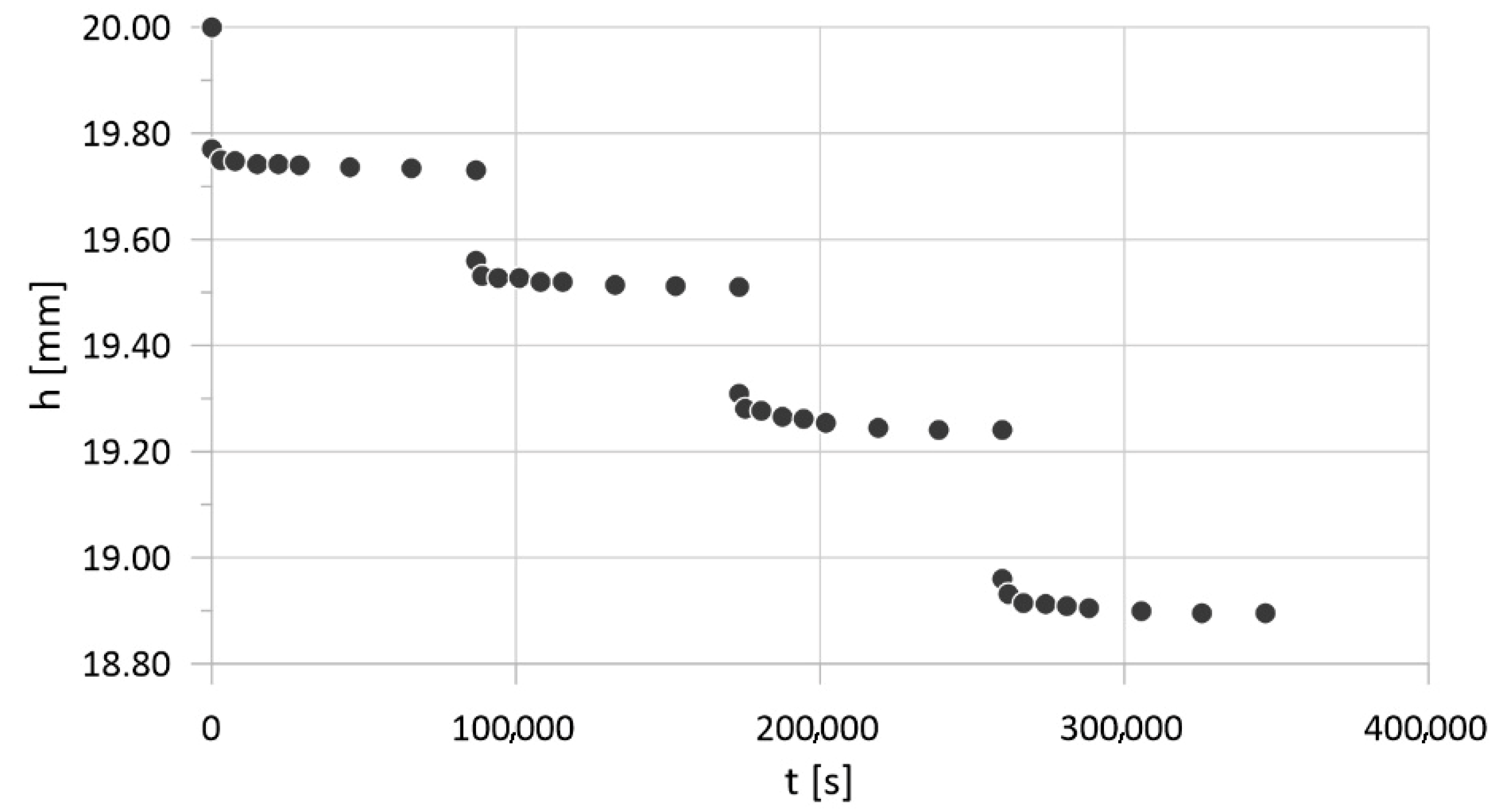
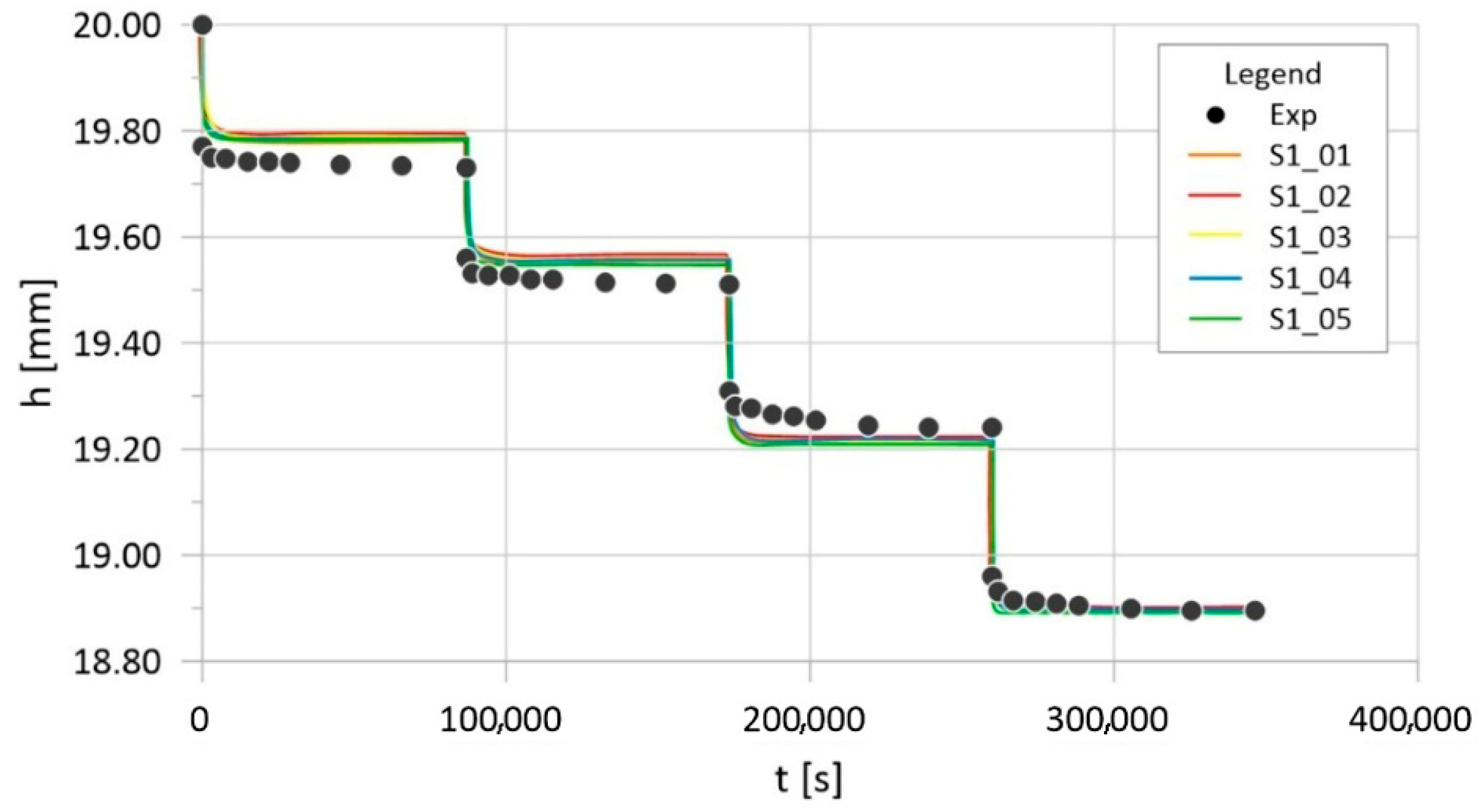
5.1. Simulation Parameters
- for the sample base—(x = 0): u = 0, θ = 0;
- for the upper surface of the sample—(x = h = 20 mm): u′ = 0, θ = T(t).
5.2. Algorithm Parameters
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bergkamp, E.A.; Verhoosel, C.V.; Remmers, J.J.C.; Smeulders, D.M.J. A staggered finite element procedure for the coupled Stokes–Biot system with fluid entry resistance. Comput. Geosci. 2019, 24, 1497–1522. [Google Scholar] [CrossRef]
- Biot, M.A. General theory of three-dimensional consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Biot, M.A. General Solutions of the Equations of Elasticity and Consolidation of a Porous Material. J. Appl. Mech. 1956, 23, 91–96. [Google Scholar] [CrossRef]
- Łydżba, D. Applications of the Asymptotic Homogenization Method in Soil and Rock Mechanics; Habilitation Thesis, Research Papers of the Institute of Geotechnics and Hydrotechnics Wrocław University of Technology; No. 23; Wrocław University of Technology Publishing House: Wrocław, Poland, 2002. (In Polish) [Google Scholar]
- Auriault, J.L. Dynamic Behavior of Porous Media. In Transport Processes in Porous Media; Springer: Dordrecht, The Netherlands, 1991; pp. 471–519. [Google Scholar]
- Bensoussan, A.; Lions, J.L.; Papanicolau, G. Asymptotic Analysis for Periodic Structures; North Holland Publishing Company: Amsterdam, The Netherlands, 1978. [Google Scholar]
- Auriault, J.L.; Sanchez Palencia, E. Etude de comportement macroscopique d’un milieu poreux sature deformable. J. Mec. 1977, 16, 575–603. [Google Scholar]
- Kröner, E. Effective elastic moduli of periodic and random media: A unification. Mech. Res. Commun. 1980, 7, 323–327. [Google Scholar] [CrossRef]
- Rubinstein, J.; Torquato, S. Flow in random porous media: Mathematical formulation, variational principles and rigorous bounds. J. Fluid Mech. 1989, 206, 25–46. [Google Scholar] [CrossRef]
- Auriault, J.L.; Strzelecki, T.; Bauer, J.; He, S. Porous deformable media by a very compressible fluid. Eur. J. Mech. A/Solid 1990, 9, 373–392. [Google Scholar]
- Uciechowska-Grakowicz, A. Temporo-Elasticity Models of a Two-Phase Medium in Mechanics of Porous Media; Strzelecki, T., Ed.; Dolnośląskie Wydawnictwo Edukacyjne: Wrocław, Poland, 2019; ISBN 978-83-7125-282-2. (In Polish) [Google Scholar]
- Uciechowska-Grakowicz, A.; Strzelecki, T. Application of the thermoporoelasticity model in numerical modelling of under-ground coal gasification influence on the surrounding medium. Stud. Geotech. Mech. 2021, 43, 116–1344. [Google Scholar] [CrossRef]
- Strzelecki, T.; Uciechowska, A. Thermal consolidation process of multiphase medium consisting of elastic skeleton, water, and water vapour. Acta Geophys. 2014, 62, 1163–1178. [Google Scholar] [CrossRef]
- Zhang, Q.; Yin, Z.; Yan, X. Material Constants of Anisotropic Poroelasticity and Its Impacts on Shale Gas Production. Energy Fuels 2023, 37, 18722–18734. [Google Scholar] [CrossRef]
- Chen, H.; Chen, Y.; Kou, J. Energy stable finite element approximations of gas flow in poroelastic media. Comput. Methods Appl. Mech. Eng. 2024, 428, 117082. [Google Scholar] [CrossRef]
- Bartlewska, M.; Strzelecki, T. One-dimensional consolidation of the porous medium with the Rheological Kelvin-Voight skeleton. Stud. Geotech. Mech. 2008, 30, 115–122. [Google Scholar]
- Bartlewska, M.; Strzelecki, T. Equations of Biot’s consolidation with Kelvin-Voight rheological frame. Stud. Geotech. Mech. 2009, 30, 3–15. [Google Scholar]
- Terzaghi, K. Theoretical Soil Mechanics; Wiley: New York, NY, USA, 1943. [Google Scholar]
- Wood, D.M. Soil Behaviour and Critical State Soil Mechanics; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Atkinson, J. The Mechanics of Soils and Foundations, 2nd ed.; CRC Press: London, UK, 2007. [Google Scholar]
- Hashash, Y.M.A.; Yao, J.I.C. Calibration of soil constitutive models for numerical analysis in geotechnical engineering. Soil Dyn. Earthq. Eng. 2005, 25, 789–798. [Google Scholar] [CrossRef][Green Version]
- Brinkgreve, R.B.J. Selection of soil models and parameters for geotechnical engineering application. In Proceedings of the PLAXIS Symposium, Paris, France, 1 August 2002; pp. 69–98. [Google Scholar][Green Version]
- Huang, T.; Yin, H.; Huang, X. Improved genetic algorithm for multi-threshold optimization in digital pathology image segmentation. Sci. Rep. 2024, 14, 22454. [Google Scholar] [CrossRef]
- Kneiding, P.; Balcells, M. Augmenting genetic algorithms with machine learning for inverse molecular design. Chem. Sci. 2024, 15, 5831–5843. [Google Scholar] [CrossRef]
- Robson, J.D.; Armstrong, D.; Cordell, J.; Pope, D.; Flint, T.F. Calibration of constitutive models using genetic algorithms. Mech. Mater. 2024, 189, 104881. [Google Scholar] [CrossRef]
- Meddahi, S. hp Error Analysis of HDG for Dynamic Poroelasticity. arXiv 2025, arXiv:2503.08360. [Google Scholar] [CrossRef]
- Bartlewska-Urban, M.; Strzelecki, T.; Urban, R. Determination of effective parameters of Biot model with the Kelvin–Voight rheological skeleton. Arch. Civ. Mech. Eng. 2015, 15, 1173–1179. [Google Scholar] [CrossRef]
- Biot, M.A.; Willis, D.G. The Elastic Coefficients of the Theory of Consolidations. J. Appl. Mech. 1957, 24, 594–601. [Google Scholar] [CrossRef]
- Coussy, O. Mechanics and Physics of Porous Solids; John Wiley & Sons: Hoboken, NJ, USA, 2011; ISBN 978-1-119-95616-7. [Google Scholar]
- Ma, Y.; Chen, X.H.; Yu, H.S. An extension of Biot’s theory with molecular influence based on mixture coupling theory: Mathematical model. Int. J. Solids Struct. 2020, 191–192, 76–86. [Google Scholar] [CrossRef]
- Srokosz, P. Selected Applications of Genetic Algorithms in Geotechnics; Wydawnictwo UWM: Olsztyn, Poland, 2012; ISBN 8372997608. (In Polish) [Google Scholar]
- Borregales, M.A.; Kumar, K.; Nordbotten, J.M.; Radu, F.A. Iterative solvers for Biot model under small and large deformations. Comput. Geosci. 2020, 25, 687–699. [Google Scholar] [CrossRef]
- Kozubal, J.V.; Kania, T.; Tarawneh, A.S.; Hassanat, A.; Lawal, R. Ultrasonic assessment of cement-stabilized soils: Deep learning experimental results. Measurement 2023, 223, 113793. [Google Scholar] [CrossRef]
- Martínez López, Y.; Oquendo Ferrer, H.; Caballero Mota, Y.; Guerra-Rodríguez, L.E.; Junco-Villegas, R.; Benítez Cortés, I.; Madera Quintana, J. Aplicación de la investigación de operaciones a la distribución de recursos relacionados con la COVID-19. Retos Dir. 2020, 14, 86–105. [Google Scholar]
- Amawi, R.M.; Al-Hussaeni, K.; Keeriath, J.J.; Ashmawy, N.S. A Machine Learning Approach to Evaluating the Impact of Natural Oils on Alzheimer’s Disease Progression. Appl. Sci. 2024, 14, 6395. [Google Scholar] [CrossRef]
- Han, J. CNN-Based Multi-Factor Authentication System for Mobile Devices Using Faces and Passwords. Appl. Sci. 2024, 14, 5019. [Google Scholar] [CrossRef]
- Villa-Pérez, M.E.; Alvarez-Carmona, M.A.; Loyola-González, O.; Medina-Pérez, M.A.; Velazco-Rossell, J.C.; Choo, K.K.R. Semi-supervised anomaly detection algorithms: A comparative summary and future research directions. Knowl.-Based Syst. 2021, 218, 106878. [Google Scholar] [CrossRef]
- Kramer, O.; Kramer, O. Genetic Algorithms; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Forrest, S. Genetic algorithms. ACM Comput. Surv. CSUR. 1996, 28, 77–80. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Forrest, S. Genetic algorithms: Principles of natural selection applied to computation. Science 1993, 261, 872–878. [Google Scholar] [CrossRef]
- Kramer, O. Genetic Algorithm Essentials; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Rutkowski, L. Computational Intelligence: Methods and Techniques; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; ISBN 978-3540762874. [Google Scholar]
- Whitley, D. A genetic algorithm tutorial. Stat. Comput. 1994, 4, 65–85. [Google Scholar] [CrossRef]
- Baker, J.E. Adaptive selection methods for genetic algorithms. In Proceedings of the 1st International Conference on Genetic Algorithms, Broadway Hillsdale, NJ, USA, 1 July 1985; pp. 101–111. [Google Scholar]
- Haupt, R.L.; Haupt, S.E. Practical Genetic Algorithms; Wiley-Interscience: Hoboken, NJ, USA, 2004. [Google Scholar]
- PDE Solutions Inc. FlexPDE 6: A Flexible Solution for Partial Differential Equations. Available online: https://www.pdesolutions.com (accessed on 12 October 2025).
- Mo, X.; Zhang, D.; Ge, F.; Huang, H.; Chen, C.; Liu, M.; Chen, H. A P-THMC Model to Solidification and Solute Separation in Saturated Freezing Soil. Water Resour. Res. 2025, 61, e2024WR038885. [Google Scholar] [CrossRef]
- Kozeny, J. Über Kapillare Leitung des Wassers im Boden; Sitzungsberichte der Akademie der Wissenschaften: Vienna, Austria, 1927; pp. 136, 271–306. [Google Scholar]
- Carman, P.C. Fluid flow through granular beds. Trans. Inst. Chem. Eng. 1937, 15, 150–166. [Google Scholar] [CrossRef]
- Carman, P.C. Flow of Gases Through Porous Media; Butterworths Scientific Publications: London, UK, 1956. [Google Scholar]
- ASTM D2435; Standard Test Methods for One-Dimensional Consolidation Properties of Soils Using Incremental Loading. ASTM: West Conshohocken, PA, USA, 2011.
- Walter, E.; Pronzato, L. Identification of Parametric Models from Experimental Data; Springer: Berlin, Germany, 1997. [Google Scholar]
- Brun, R.; Reichert, P.; Künsch, H.R. Practical identifiability analysis of large environmental simulation models. Water Resour. Res. 2001, 37, 1015–1030. [Google Scholar] [CrossRef]
- Dana, S.; Wheeler, M.F. Convergence analysis of fixed stress split iterative scheme for anisotropic poroelasticity with tensor Biot parameter. Comput. Geosci. 2019, 22, 1219–1230. [Google Scholar] [CrossRef]
- Li, S.J.; Shao, L.T.; Wang, J.Z.; Liu, Y.X. Inverse procedure for determining model parameter of soils using real-coded genetic algorithm. J. Cent. South Univ. 2012, 19, 1764–1770. [Google Scholar] [CrossRef]
- Moufida, M. Identification of soil mechanical parameters by inverse analysis using genetic algorithm and hybrid methods. Slovak J. Civ. Eng. 2022, 17, 1–12. [Google Scholar]
- Antonietti, P.F.; Bonetti, S.; Botti, M. Discontinuous Galerkin approximation of the fully-coupled thermo-poroelastic problem. SIAM J. Sci. Comput. 2023, 45, A621–A645. [Google Scholar] [CrossRef]
- Çeşmelioğlu, A.; Lee, J.J.; Rhebergen, S. Analysis of an embedded-hybridizable discontinuous Galerkin method for Biot’s consolidation model. J. Sci. Comput. 2023, 97, 1–26. [Google Scholar] [CrossRef]


| Parameter | Physical Meaning | Unit | Typical Range | Reference |
|---|---|---|---|---|
| N | Bulk modulus of the porous skeleton (elastic compressibility of the solid phase) | Pa | 106–108 | [2,27] |
| A | Shear modulus of the skeleton (resistance to shear deformation) | Pa | 107–108 | [28,29] |
| R | Bulk modulus of pore fluid | Pa | 107–109 | [3,29] |
| H | Solid–fluid coupling modulus (interaction between phases) | Pa | 107–109 | [3,27] |
| k | Darcy permeability coefficient | m/s | 10−11–10−9 | [21,30] |
| Parameter | Min | Max | The Estimation Accuracy |
|---|---|---|---|
| N [Pa] | 1 × 106 | 1 × 108 | 7 |
| A [Pa] | 1 × 107 | 1 × 108 | 7 |
| R [Pa] | 1 × 107 | 1 × 109 | 7 |
| H [Pa] | 1 × 107 | 1 × 109 | 7 |
| k [m/s] | 1 × 10−11 | 1 × 10−9 | 10 |
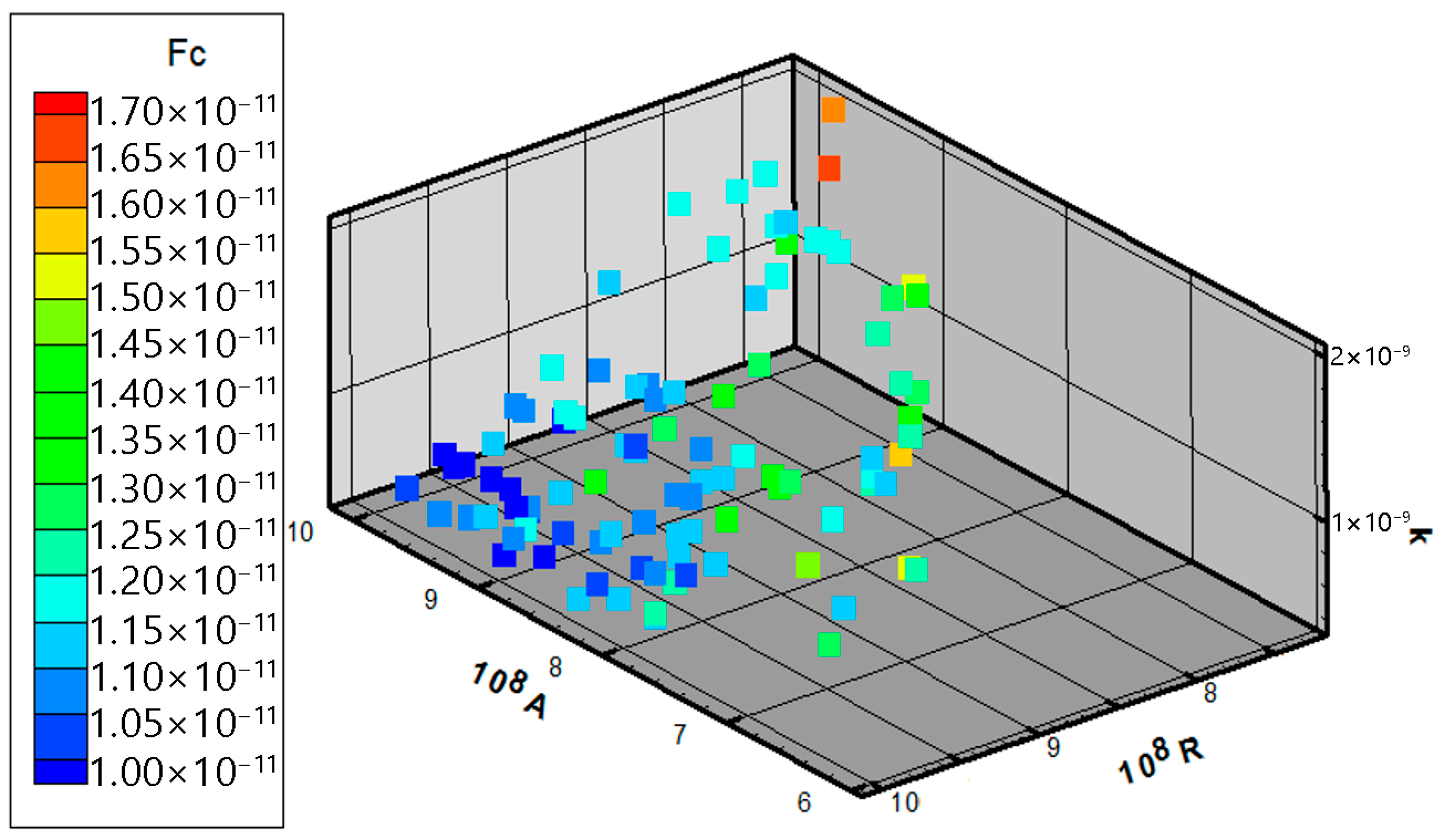
| Num | N [107 Pa] | A [108 Pa] | R [108 Pa] | H [108 Pa] | k [10−11 m/s] | Fc [108] | Δ [mm] |
|---|---|---|---|---|---|---|---|
| 1 | 1.387 | 1.820 | 1.402 | 0.698 | 14.42 | 9.91 | 0.038 |
| 2 | 1.252 | 1.776 | 0.294 | 0.145 | 91.07 | 9.42 | 0.037 |
| 3 | 1.835 | 0.534 | 1.686 | 0.923 | 82.70 | 11.44 | 0.041 |
| 4 | 1.461 | 1.970 | 0.489 | 0.265 | 36.01 | 9.78 | 0.038 |
| 5 | 1.252 | 1.147 | 1.581 | 0.549 | 12.28 | 9.90 | 0.038 |
| 6 | 1.581 | 1.387 | 1.671 | 0.728 | 4.50 | 9.44 | 0.037 |
| 7 | 1.850 | 1.028 | 1.626 | 0.923 | 38.54 | 10.30 | 0.039 |
| 8 | 1.028 | 0.668 | 1.072 | 0.250 | 7.42 | 9.82 | 0.038 |
| 9 | 0.399 | 1.820 | 0.534 | 0.145 | 39.32 | 9.43 | 0.037 |
| 10 | 1.402 | 1.087 | 1.237 | 0.444 | 7.03 | 9.82 | 0.038 |
| 11 | 1.940 | 2.000 | 0.489 | 0.414 | 26.68 | 9.48 | 0.037 |
| 12 | 1.820 | 1.641 | 1.626 | 1.028 | 34.07 | 9.90 | 0.038 |
| 13 | 1.910 | 1.177 | 1.491 | 0.893 | 31.35 | 9.59 | 0.038 |
| 14 | 1.461 | 0.863 | 1.461 | 0.564 | 27.65 | 10.45 | 0.039 |
| 15 | 1.028 | 1.581 | 1.387 | 0.549 | 48.27 | 10.96 | 0.040 |
| 16 | 1.147 | 1.461 | 1.611 | 0.564 | 8.59 | 9.36 | 0.037 |
| 17 | 1.207 | 1.910 | 0.579 | 0.265 | 16.95 | 8.96 | 0.036 |
| 18 | 1.013 | 1.835 | 1.521 | 0.624 | 30.18 | 9.99 | 0.038 |
| 18 | 1.746 | 1.850 | 1.491 | 0.938 | 24.54 | 10.20 | 0.039 |
| 19 | 0.968 | 1.521 | 1.147 | 0.444 | 53.91 | 10.74 | 0.040 |
| 20 | 1.384 | 1.454 | 1.220 | 0.567 | 31.77 | 9.94 | 0.038 |
| Avg | 0.390 | 0.436 | 0.460 | 0.269 | 22.9 | 0.585 | 0.001 |
| SD | 1.387 | 1.820 | 1.402 | 0.698 | 14.42 | 9.91 | 0.038 |
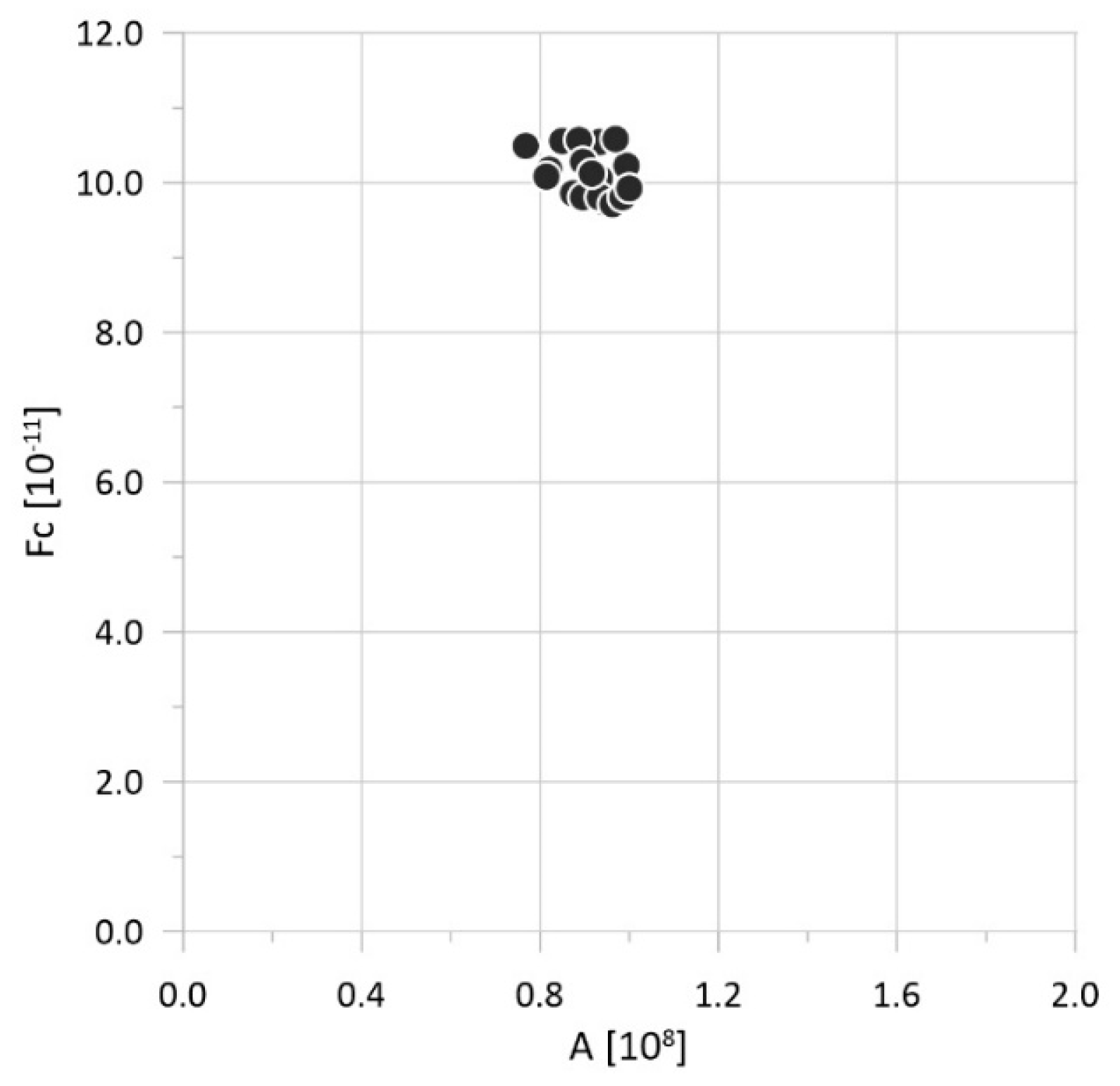
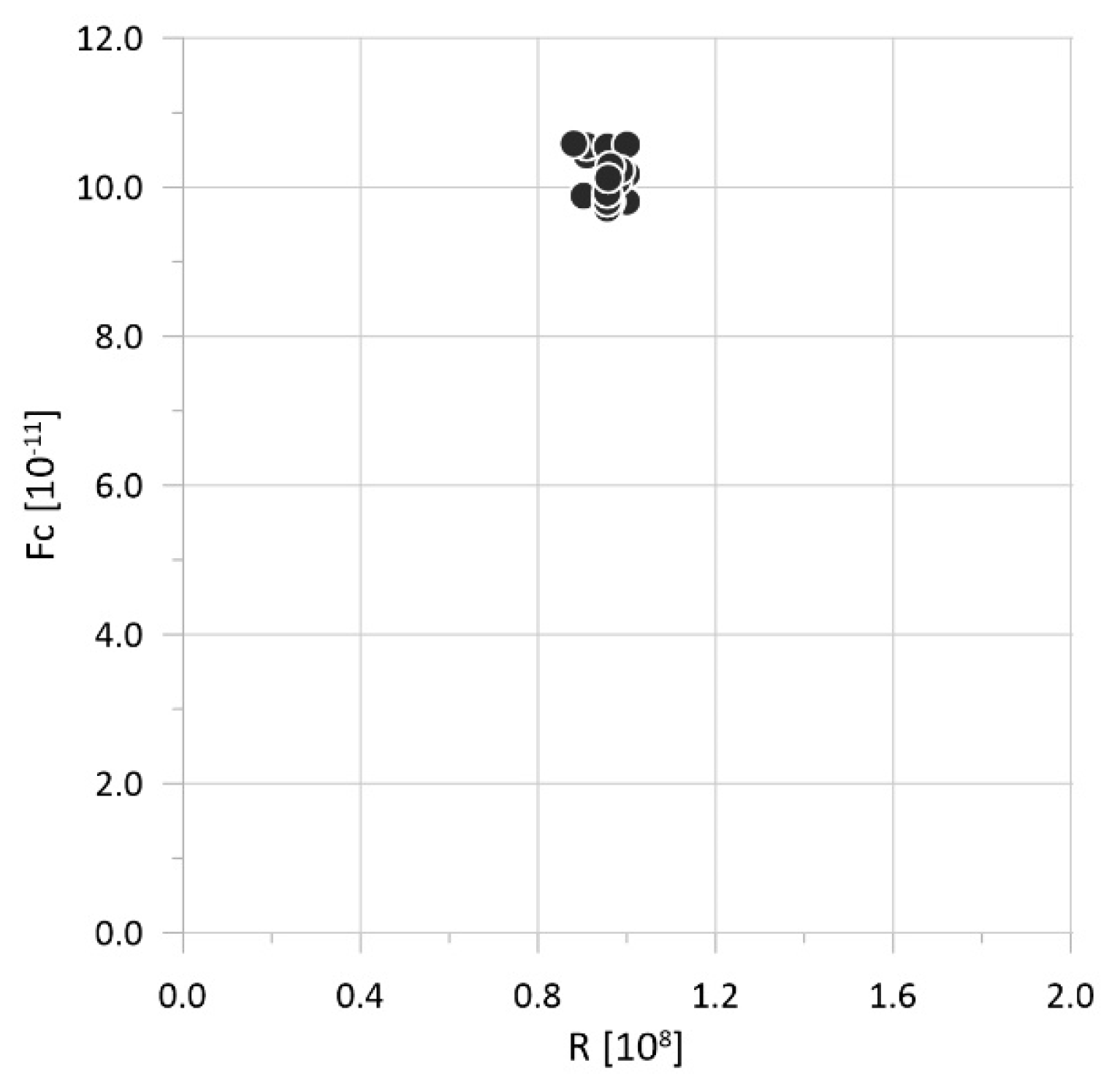
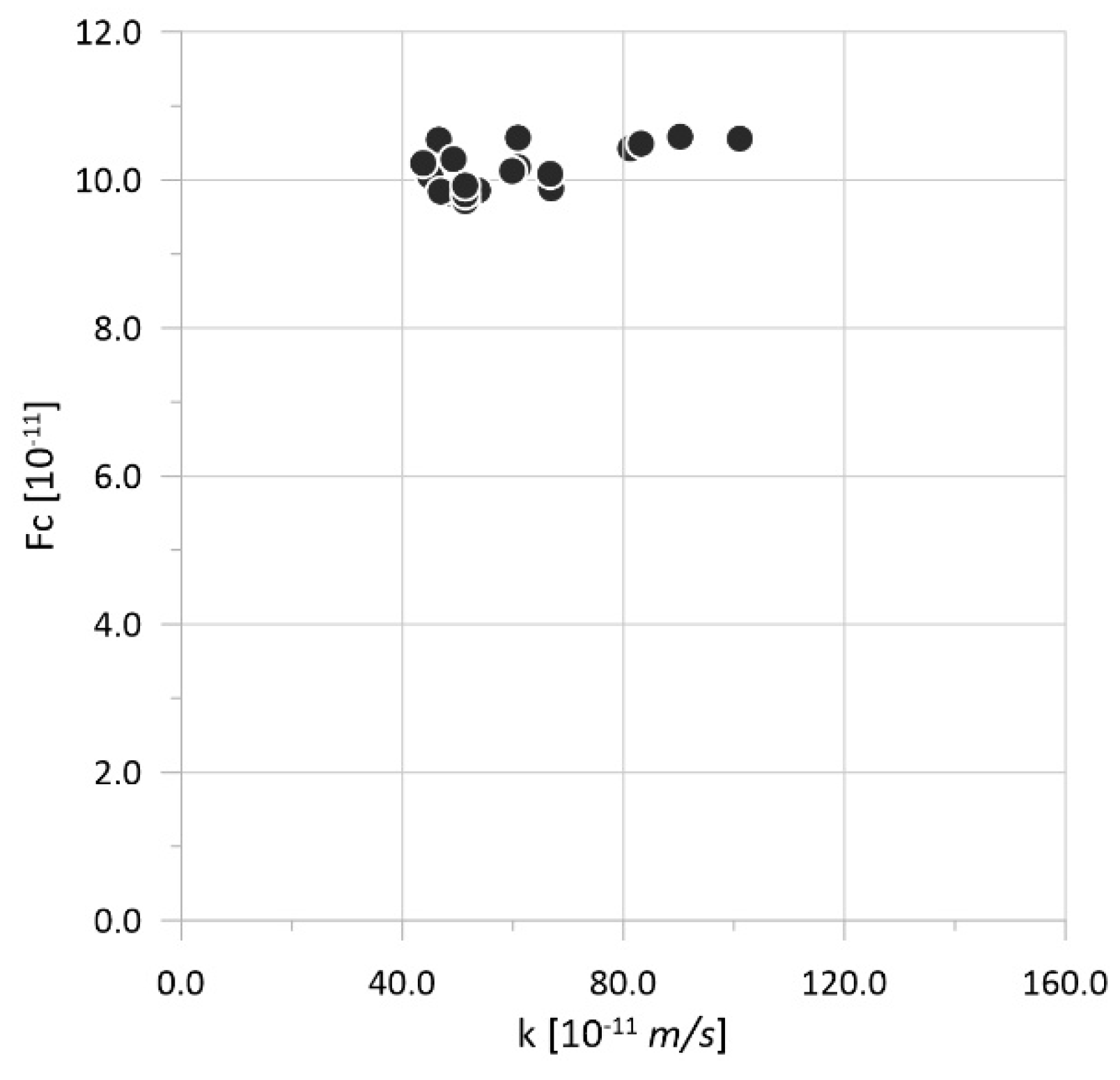
| Num | A [108 Pa] | R [108 Pa] | k [10−11 m/s] | Fc [108] | Δ [mm] |
|---|---|---|---|---|---|
| 1 | 0.903 | 0.910 | 81.34 | 10.43 | 0.039 |
| 2 | 0.873 | 0.993 | 53.72 | 9.86 | 0.038 |
| 3 | 0.895 | 1.000 | 47.69 | 9.81 | 0.038 |
| 4 | 0.970 | 0.903 | 66.94 | 9.89 | 0.038 |
| 5 | 0.948 | 0.955 | 51.38 | 9.73 | 0.038 |
| 6 | 0.768 | 0.985 | 83.28 | 10.49 | 0.039 |
| 7 | 0.933 | 0.955 | 44.96 | 10.06 | 0.038 |
| 8 | 0.821 | 1.000 | 60.91 | 10.18 | 0.039 |
| 9 | 0.813 | 0.978 | 66.75 | 10.09 | 0.039 |
| 10 | 0.933 | 0.963 | 49.24 | 9.81 | 0.038 |
| 11 | 0.963 | 0.955 | 51.38 | 9.71 | 0.038 |
| 12 | 0.850 | 0.910 | 100.99 | 10.56 | 0.039 |
| 13 | 0.993 | 0.955 | 46.91 | 9.84 | 0.038 |
| 14 | 0.933 | 0.955 | 46.52 | 10.54 | 0.039 |
| 15 | 0.888 | 1.000 | 60.91 | 10.57 | 0.039 |
| 16 | 0.993 | 0.985 | 43.80 | 10.23 | 0.039 |
| 17 | 0.895 | 0.963 | 49.24 | 10.28 | 0.039 |
| 18 | 0.985 | 0.955 | 51.38 | 9.80 | 0.038 |
| 18 | 1.000 | 0.955 | 51.38 | 9.92 | 0.038 |
| 19 | 0.970 | 0.880 | 90.29 | 10.58 | 0.039 |
| 20 | 0.916 | 0.958 | 59.95 | 10.12 | 0.039 |
| Avg | 0.064 | 0.033 | 16.20 | 0.31 | 0.001 |
| SD | 0.903 | 0.910 | 81.34 | 10.43 | 0.039 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bartlewska-Urban, M.; Bagińska, I. Calibration of a Multiphase Poroelasticity Model Using Genetic Algorithms. Appl. Sci. 2025, 15, 11972. https://doi.org/10.3390/app152211972
Bartlewska-Urban M, Bagińska I. Calibration of a Multiphase Poroelasticity Model Using Genetic Algorithms. Applied Sciences. 2025; 15(22):11972. https://doi.org/10.3390/app152211972
Chicago/Turabian StyleBartlewska-Urban, Monika, and Irena Bagińska. 2025. "Calibration of a Multiphase Poroelasticity Model Using Genetic Algorithms" Applied Sciences 15, no. 22: 11972. https://doi.org/10.3390/app152211972
APA StyleBartlewska-Urban, M., & Bagińska, I. (2025). Calibration of a Multiphase Poroelasticity Model Using Genetic Algorithms. Applied Sciences, 15(22), 11972. https://doi.org/10.3390/app152211972








