The Dynamic Behavior of Heavy Vehicles in Cornering Actions: An Assessment of the Problem
Abstract
1. Introduction
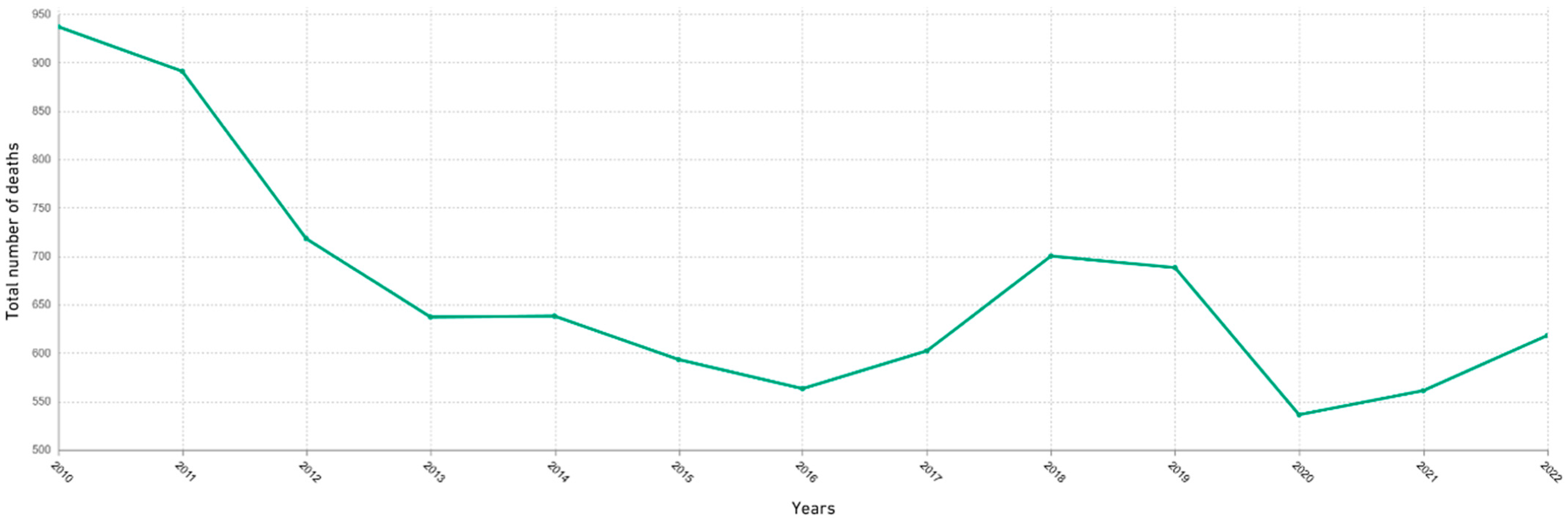
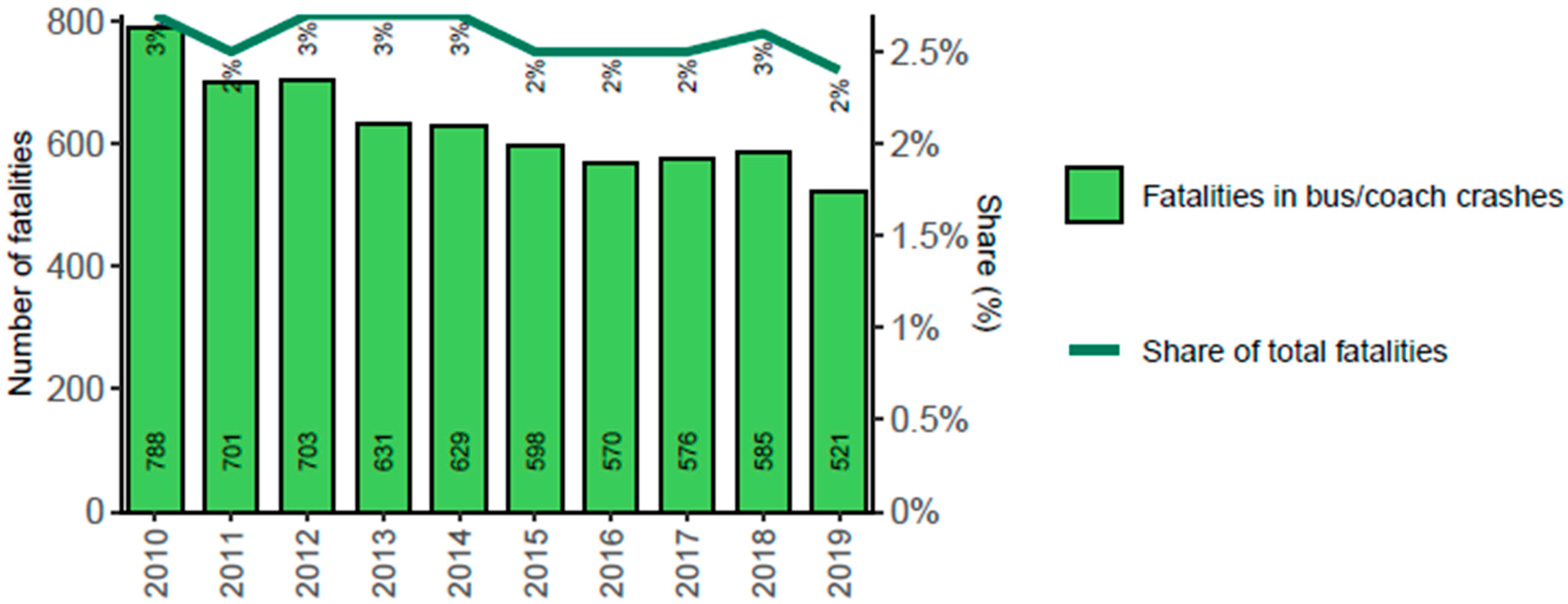
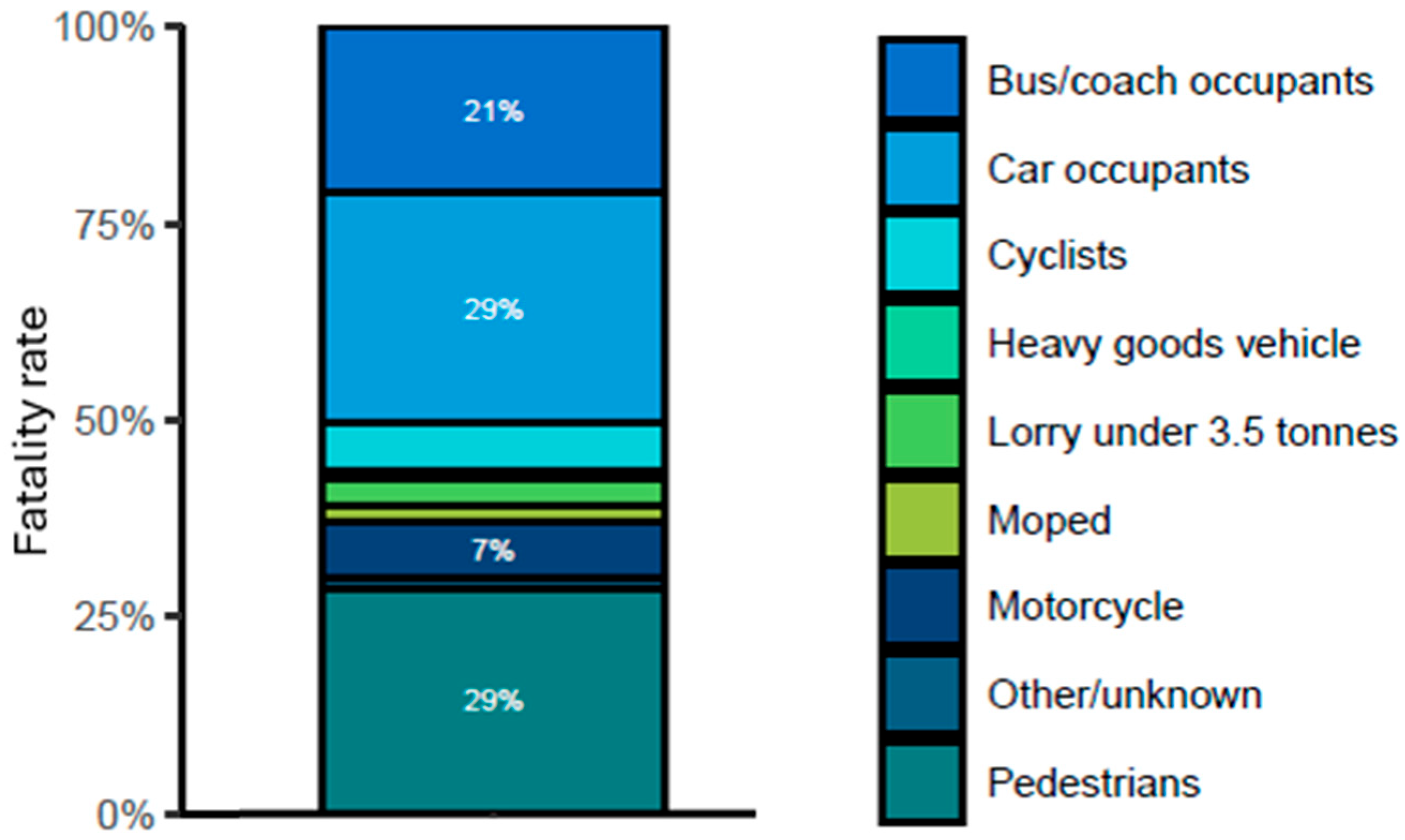
1.1. Statistics
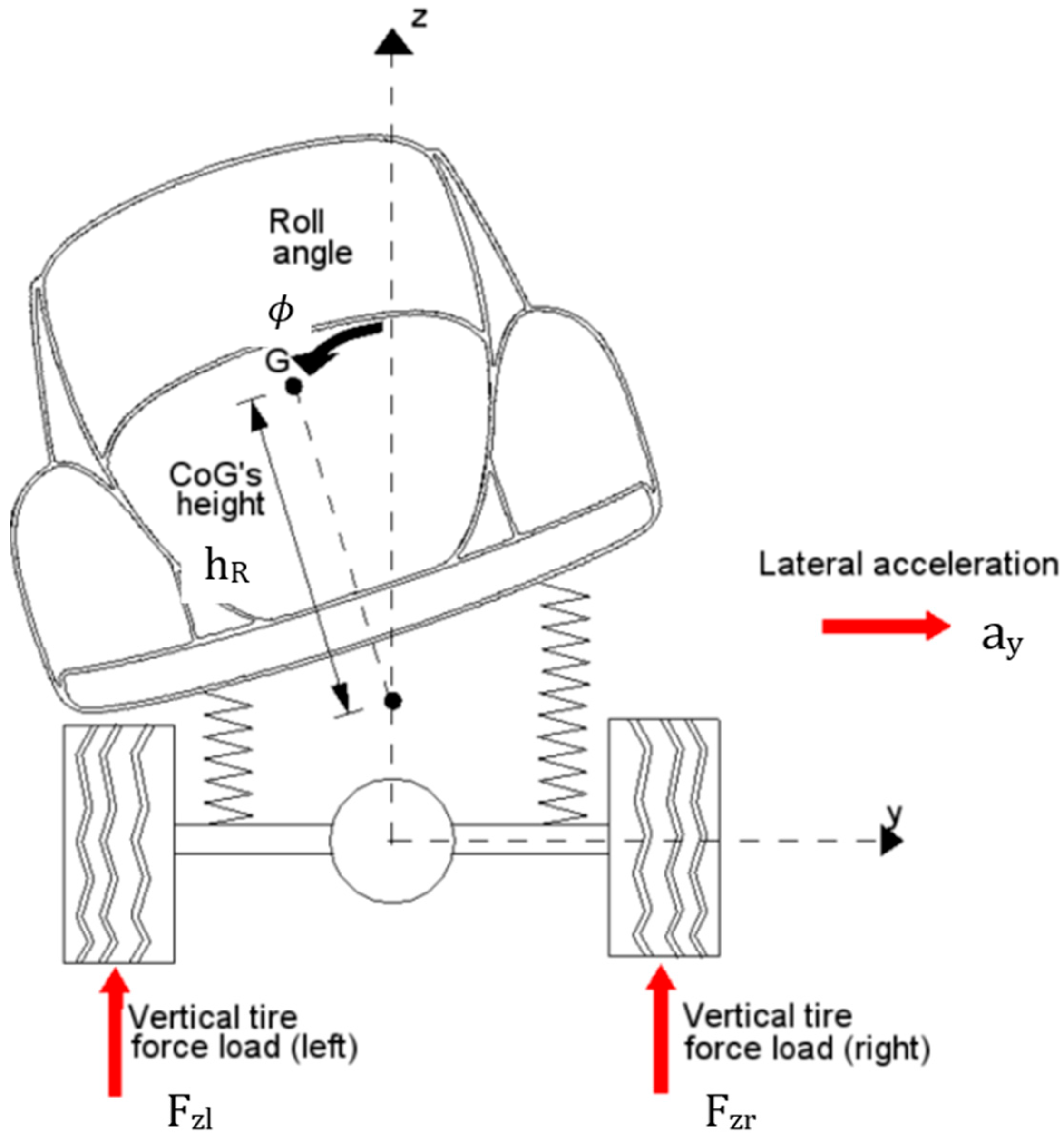
1.2. Rollover Event
1.3. Rollover Index
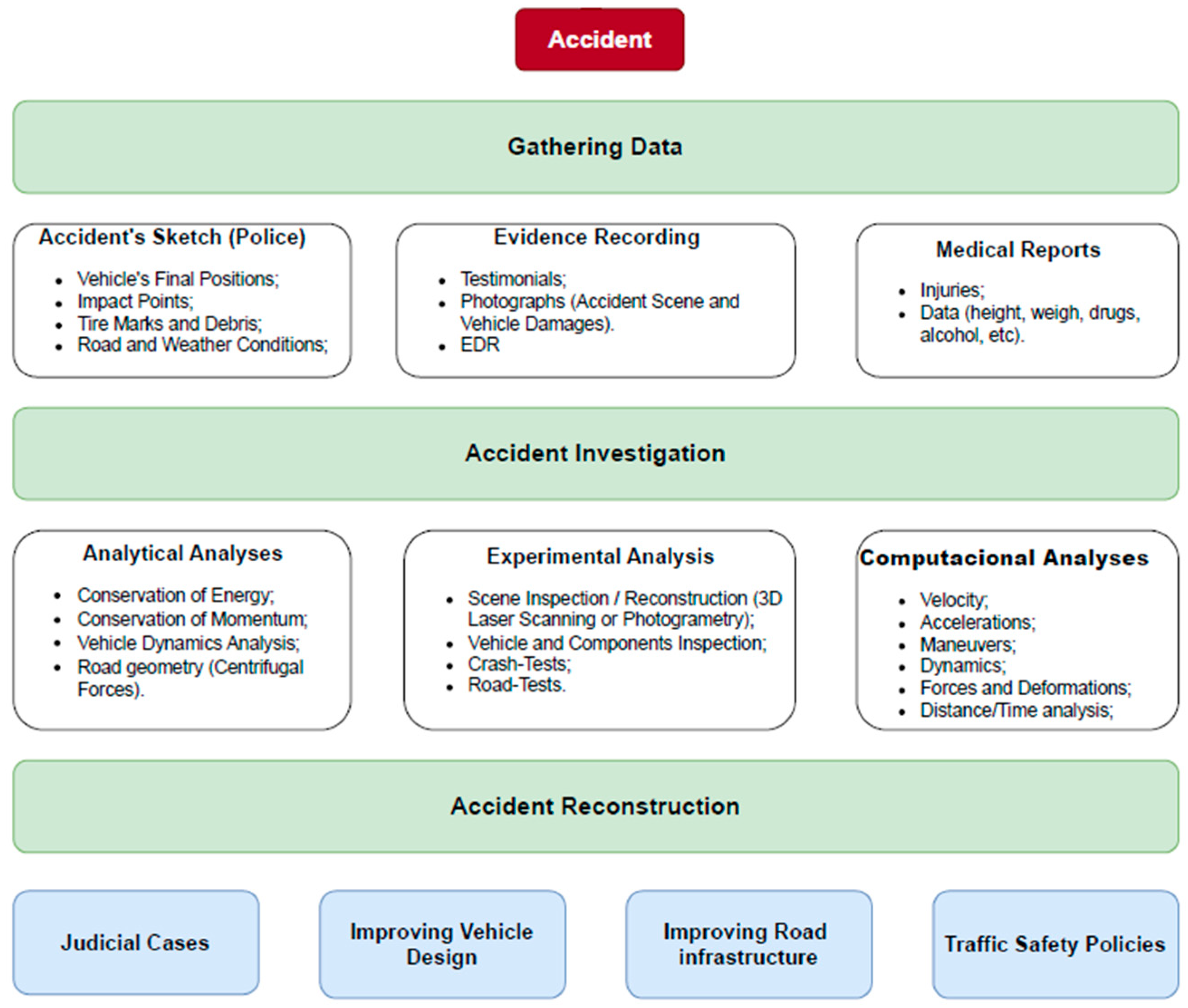
1.4. Rollover Forensic Investigation
2. Materials and Methods
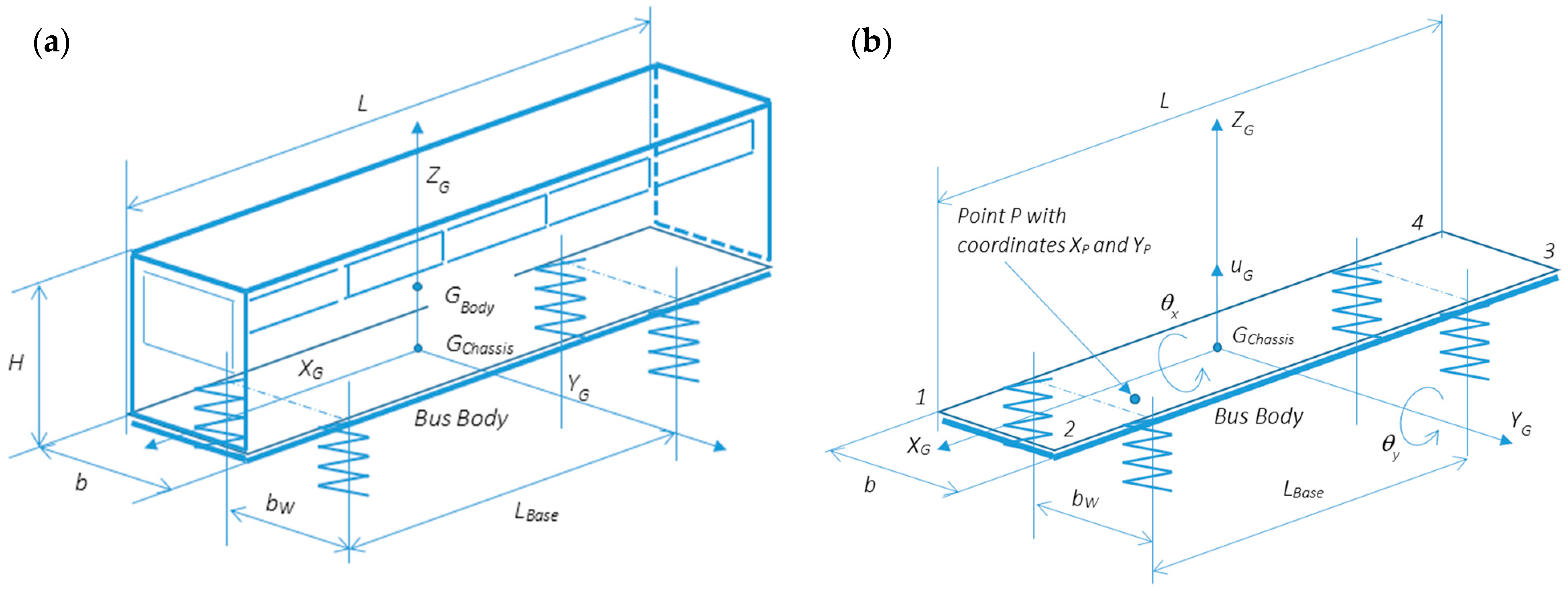
2.1. Design of a Single Macro Finite Element by Numerical Modeling
- : Vertical (or transverse) displacement of the plate’s center of mass G;
- : Plate rotation around the XG-axis;
- : Plate rotation around the YG-axis.
- The vehicle mass and respective dynamic inertial properties are assumed to be concentrated on the vehicle’s center of mass;
- The spring stiffness, (front and rear axles, respectively, if their suspension has differing stiffness values);
- The tire stiffness should be associated in series with the suspension spring. Since the tire stiffness is much higher than the stiffness of the suspension, the tire stiffness will be ignored in the series association.
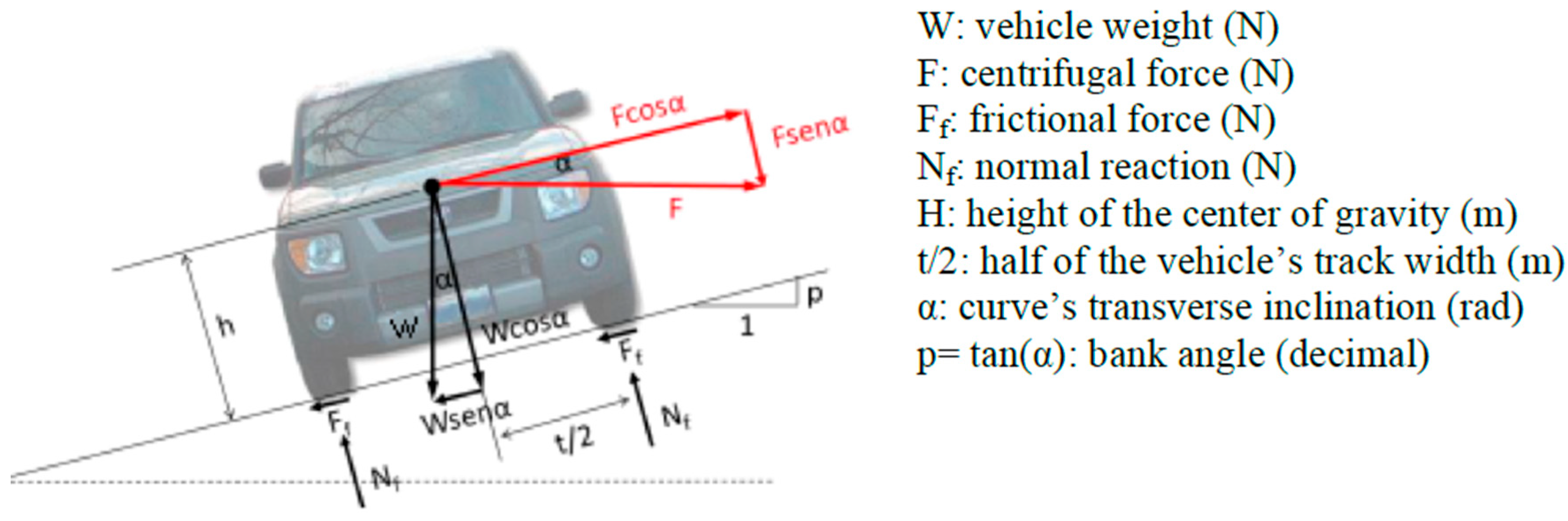
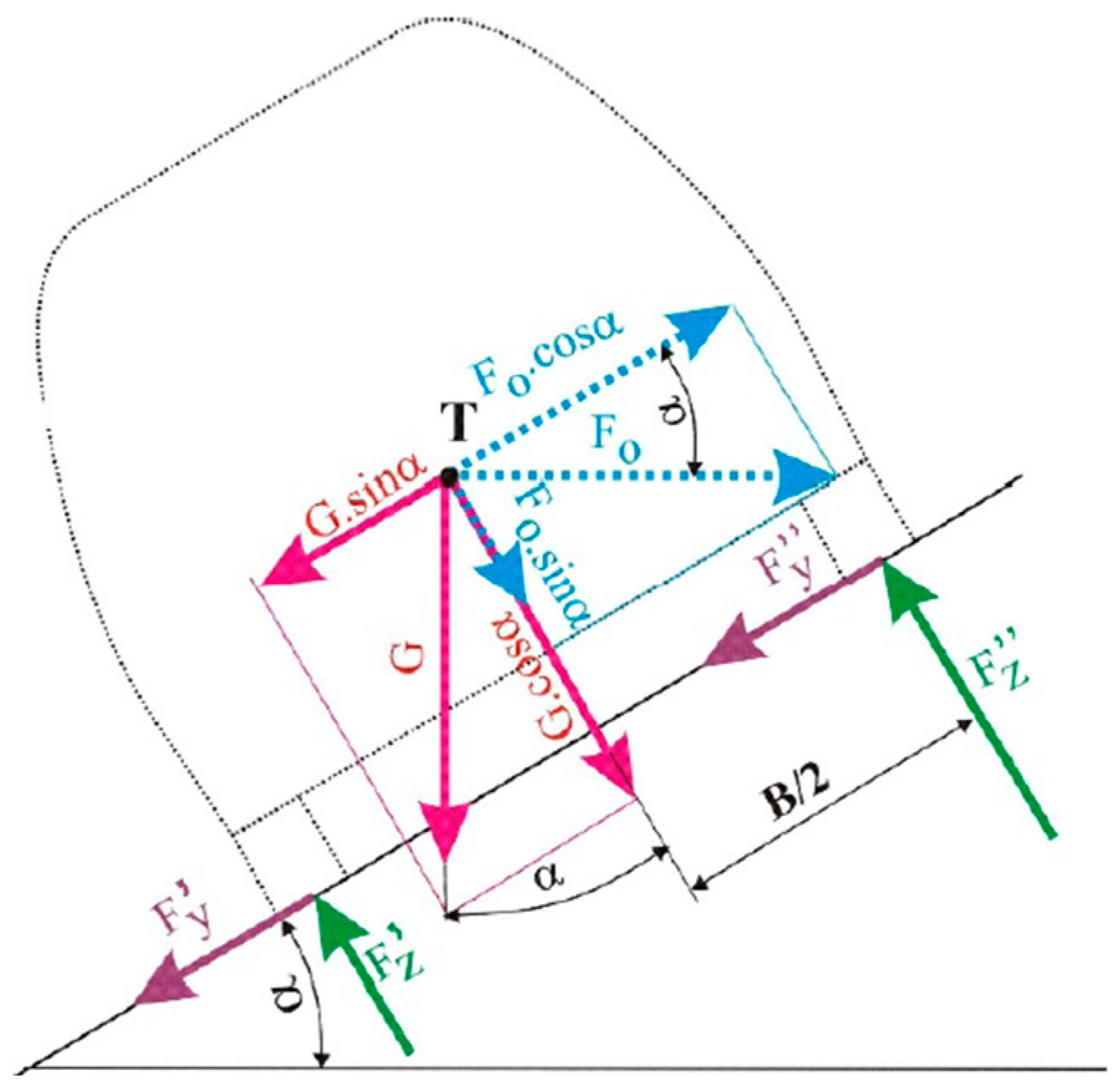
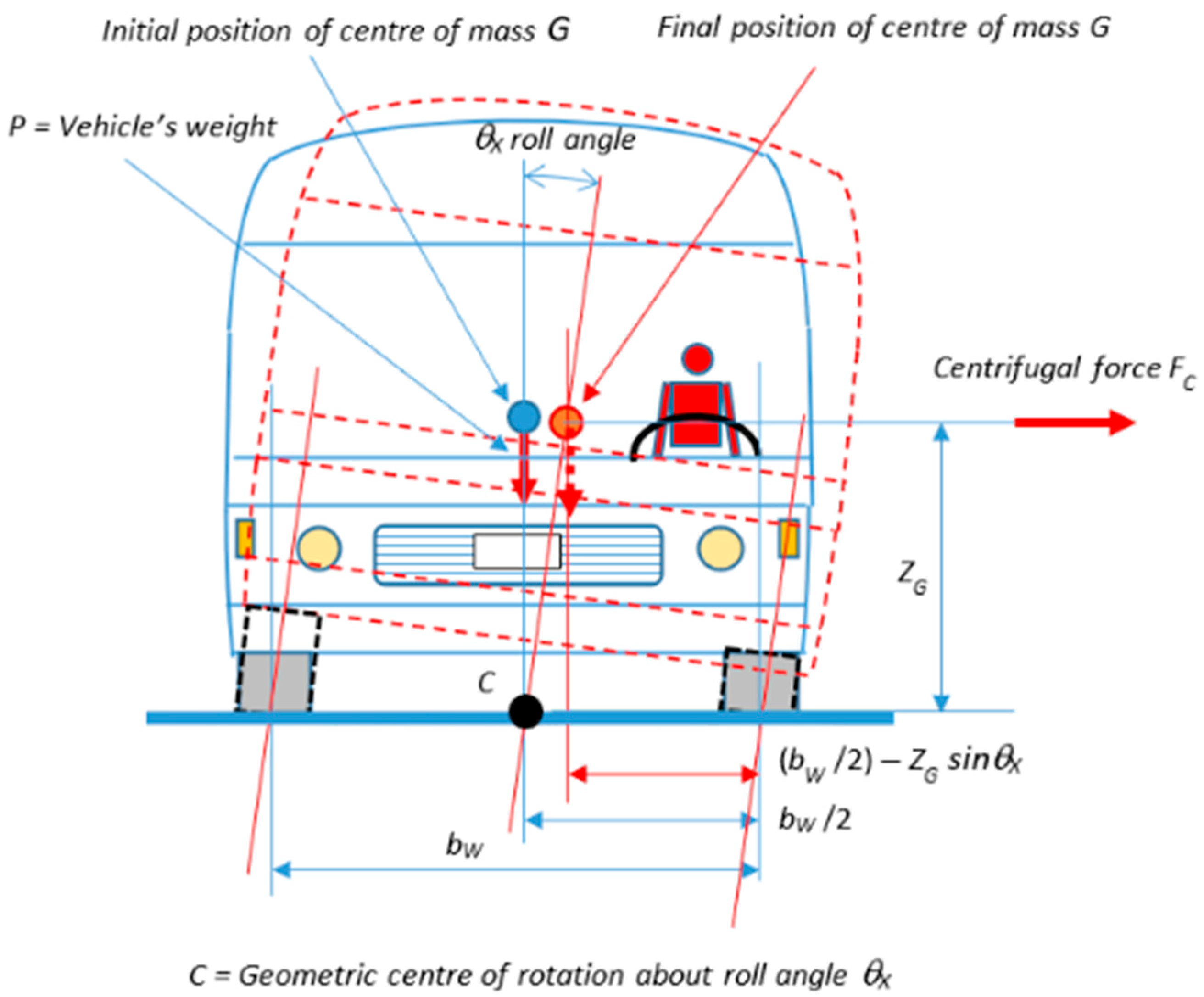
2.2. Development of an Analytical Method to Evaluate the Overturning Velocity
3. Results
3.1. Estimation of Pitch and Roll Angles
- Bus mass: 13 ton (approx. 130,000 N);
- Wheelbase : 6 m;
- Track width : 2.5 m;
- Front axis, left wheel:
- Front axis, right wheel:
- Rear axis, left wheel:
- Rear axis, right wheel:
3.2. Real-World Accident Investigation
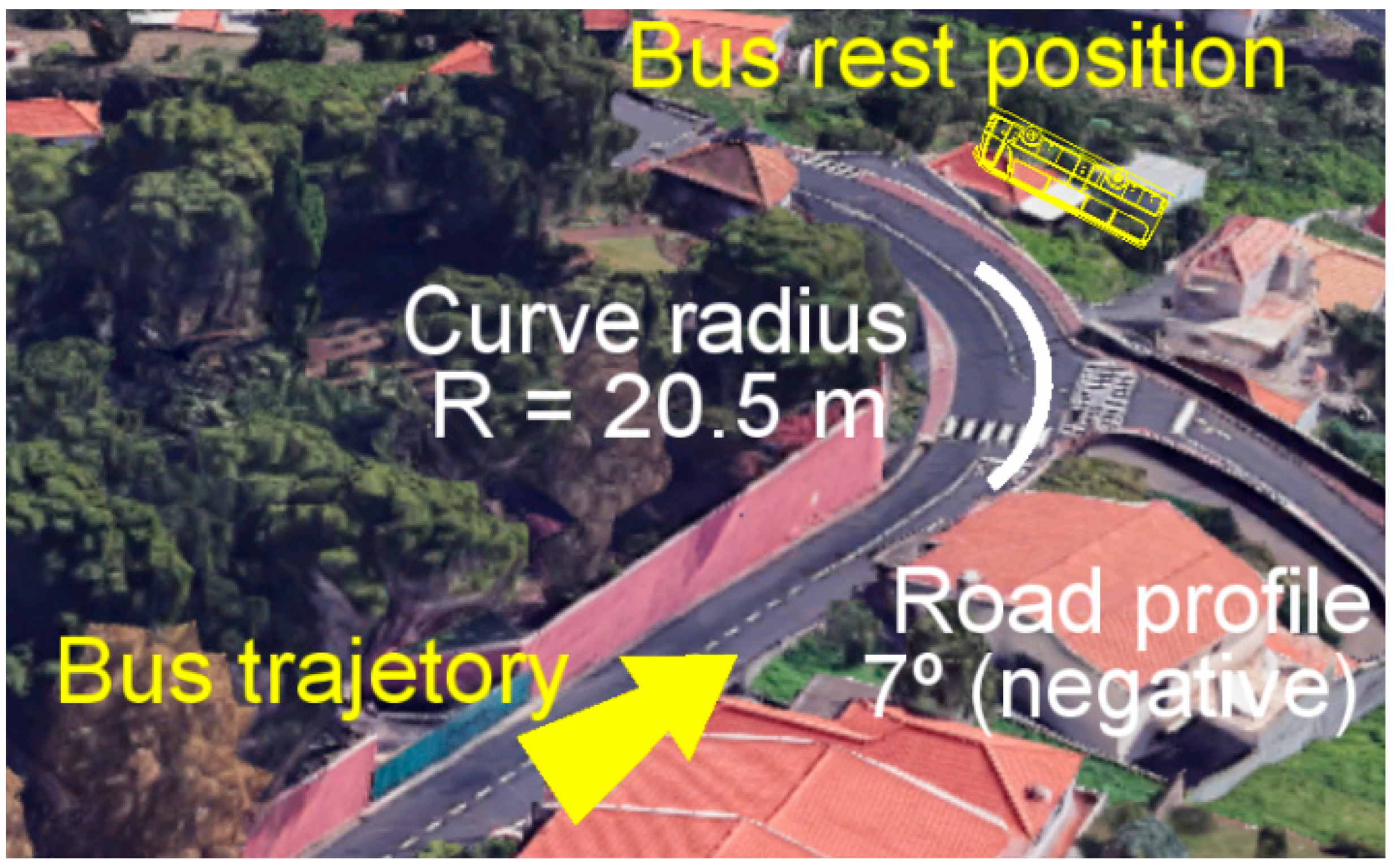
3.2.1. Accident Description: Site and Vehicle Details
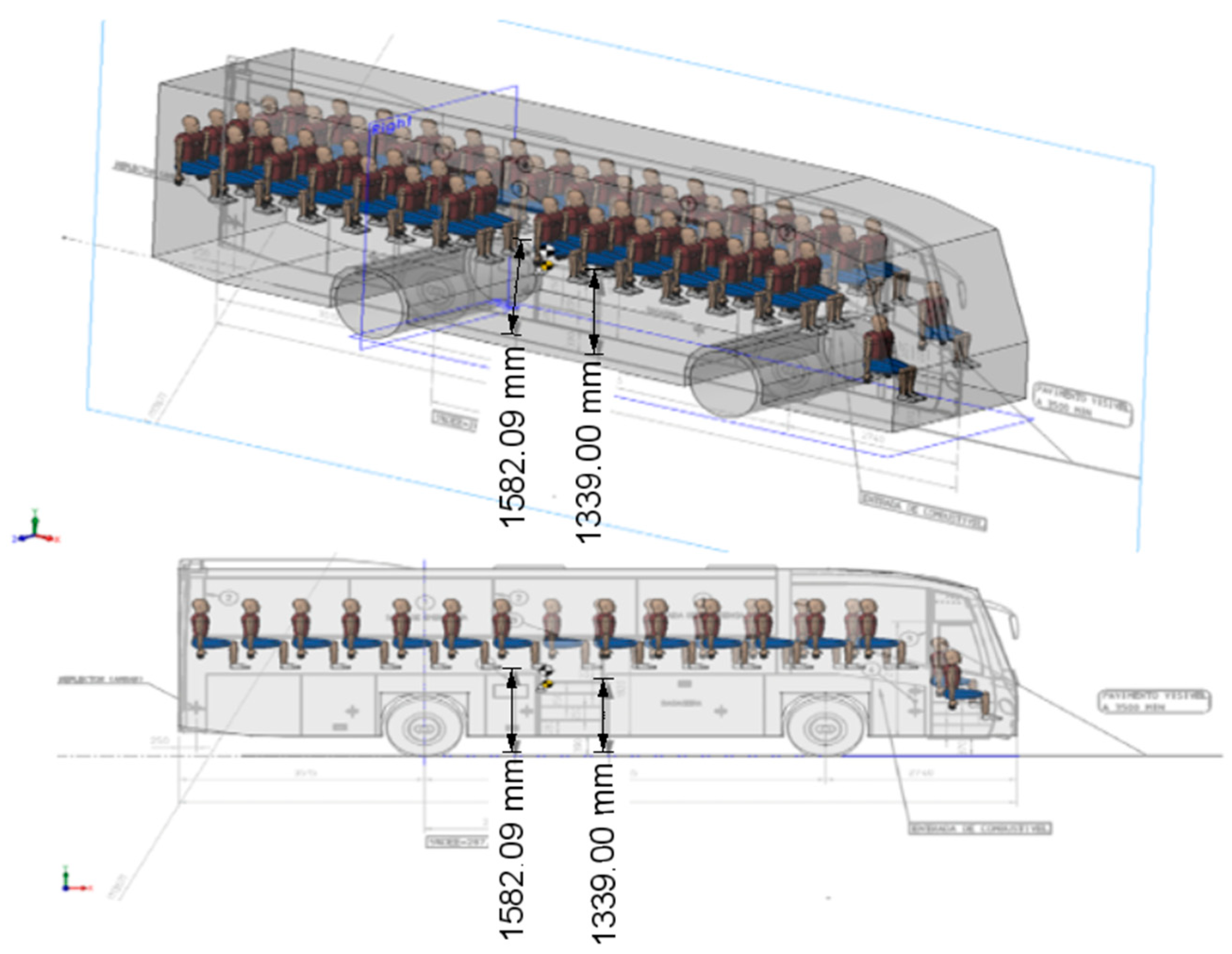
3.2.2. Reconstruction of the Accident: Analytical and Computational Analysis
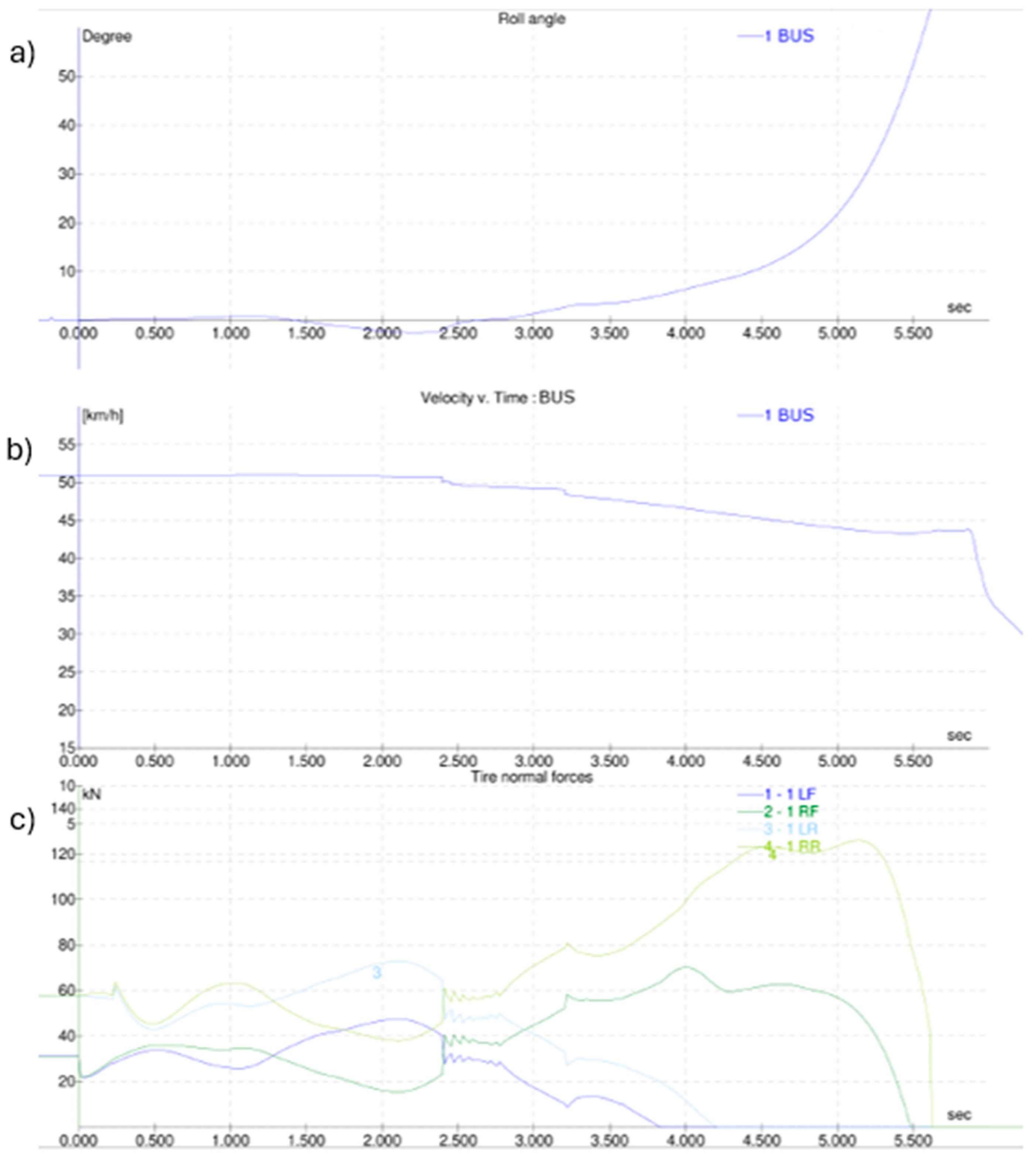
3.2.3. Numerical Modeling of the Real Case Accident Scenario
- Lower the position of the center of mass as much as possible; alternatively, design the passenger bus vehicles with a larger track base (attention should be paid to vehicle dimension rules);
- Use active suspensions, correcting for excessive vehicle roll (this is possible with pneumatic suspensions);
- Implement automatic gradual braking in case the critical cornering speed is reached;
- Introduce a movable ballast to correct for CoG deviations.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- World Health Organization. Global Status Report on Road Safety 2018; World Health Organization: Geneva, Switzerland, 2019. [Google Scholar]
- ECA. Special Report, Reaching EU road Safety Objectives; European Court of Auditors: Luxembourg, 2024. [Google Scholar]
- C. Database on Road Accidents (CARE) European Commission—Directorate-General for Mobility and Transport (MOVE). Persons Killed in Road Accidents by Age, Sex and Category of Persons involved. Available online: https://ec.europa.eu/eurostat/databrowser/view/tran_sf_roadus__custom_13407010/default/line?lang=en (accessed on 14 November 2024).
- European Commission. Facts and Figures Buses/Coaches/Heavy Goods Vehicles; European Road Safety Observatory; European Commission, Directorate General for Transport: Brussels, Belgium, 2019. [Google Scholar]
- Khan, I.U.; Vachal, K. Factors affecting injury severity of single-vehicle rollover crashes in the United States. Traffic Inj. Prev. 2020, 21, 66–71. [Google Scholar] [CrossRef]
- Wittmer, K.; Sawodny, O.; Henning, K.U. Model-Based Estimation of Vehicle Center of Gravity Height and Load. J. Dyn. Syst. Meas. Control Trans. ASME 2023, 145, 051001. [Google Scholar] [CrossRef]
- Park, G.; Choi, S.B. An Integrated Observer for Real-Time Estimation of Vehicle Center of Gravity Height. IEEE Trans. Intell. Transp. Syst. 2021, 22, 5660–5671. [Google Scholar] [CrossRef]
- Yu, K.; Watanabe, Y. Effects of Center of Gravity Position on Rollover Based Upon Detection of Three-Dimensional Center of Gravity. Toros Üniversitesi İİSBF Sos. Bilim. Derg. 2021, 70–84. [Google Scholar] [CrossRef]
- Echaveguren, T.; Cruz, P.; Echaveguren, T.; González, P. Estimation of Heavy Vehicle Rollover Potential Using Reliability Principles. 2017. Available online: www.ricuc.cl (accessed on 13 March 2025).
- Trigell, A.S.; Rothhämel, M.; Pauwelussen, J.; Kural, K. Advanced vehicle dynamics of heavy trucks with the perspective of road safety. Veh. Syst. Dyn. 2017, 55, 1572–1617. [Google Scholar] [CrossRef]
- Kühn, W. Fundamentals of Road Design; Wit Press: Southampton, UK, 2013; Volume 20. [Google Scholar]
- Gillespie, T. Fundamentals of Vehicle Dynamics; SAE International: Warrendale, PA, USA, 2021. [Google Scholar]
- Tian, J.; Whitfield, C. Effect of mass and center of gravity on vehicle speed and braking performance. J. Emerg. Investig. 2021, 4, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Wang, J. Center of gravity height real-time estimation for lightweight vehicles using tire instant effective radius. Control Eng. Pract. 2013, 21, 370–380. [Google Scholar] [CrossRef]
- Rajamani, R.; Piyabongkam, D.; Tsourapas, V.; Lew, I.Y. Real-time estimation of roll angle and CG height for active rollover prevention applications. In Proceedings of the American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 433–438. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Z.; Zhang, L.; Cao, D.; Dorrell, D.G. A Vehicle Rollover Evaluation System Based on Enabling State and Parameter Estimation. IEEE Trans. Industr. Inform. 2021, 17, 4003–4013. [Google Scholar] [CrossRef]
- Yoon, J.; Yi, K. A Rollover Mitigation Control Scheme Based on Rollover Index. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006. [Google Scholar]
- Solmaz, S.; Akar, M.; Shorten, R.; Kalkkuhl, J. Realtime Multiple-Model Estimation of Center of Gravity Position in Automotive Vehicles. Veh. Syst. Dyn. 2008, 46, 763–788. [Google Scholar] [CrossRef]
- Patel Jainish, S.G.; Topiwala, J.; Gopalbhai Patel, C. Measuring a Centre of Gravity of an Object using 4 Load Transducer Method. 2017. Available online: www.ijert.org (accessed on 13 March 2025).
- Rievaj, V.; Vrábel, J.; Synák, F.; Bartuška, L. The Effects of Vehicle Load on Driving Characteristics. Adv. Sci. Technol. Res. J. 2018, 12, 142–149. [Google Scholar] [CrossRef]
- Fabbri, A.; Molari, G. Static measurement of the centre of gravity height on narrow-track agricultural tractors. Biosyst. Eng. 2004, 87, 299–304. [Google Scholar] [CrossRef]
- Wu, F.; Sun, C.; Li, H.; Zheng, S. Real-Time Center of Gravity Estimation for Intelligent Connected Vehicle Based on HEKF-EKF. Electronics 2023, 12, 386. [Google Scholar] [CrossRef]
- Huang, X.; Wang, J. Real-time estimation of center of gravity position for lightweight vehicles using combined AKF-EKF method. IEEE Trans. Veh. Technol. 2014, 63, 4221–4231. [Google Scholar] [CrossRef]
- Germann, S.; Isermann, R. Determination of the centre of gravity height of a vehicle with parameter estimation. IFAC Proc. Vol. 1994, 27, 563–568. [Google Scholar] [CrossRef]
- Yue, H.; Zhang, L.; Shan, H.; Liu, H.; Liu, Y. Estimation of the vehicle’s centre of gravity based on a braking model. Veh. Syst. Dyn. 2015, 53, 1520–1533. [Google Scholar] [CrossRef]
- Ding, H.; Khajepour, A.; Huang, Y. A novel tripped rollover prevention system for commercial trucks with air suspensions at low speeds. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2018, 232, 1516–1527. [Google Scholar] [CrossRef]
- Kamal, M.; Shim, T. Development of Active Suspension Control for Combined Handling and Rollover Propensity Enhancement; SAE International: Warrendale, PA, USA, 2007. [Google Scholar] [CrossRef]
- Ghazali, M.; Durali, M.; Salarieh, H. Path-following in model predictive rollover prevention using front steering and braking. Veh. Syst. Dyn. 2017, 55, 121–148. [Google Scholar] [CrossRef]
- Schofield, B.; Hagglund, T. Optimal control allocation in vehicle dynamics control for rollover mitigation. In Proceedings of the American Control Conference, Seattle, WA, USA, 11–13 June 2008; pp. 3231–3236. [Google Scholar] [CrossRef]
- Rothhämel, M.; Ijkema, J.; Drugge, L. Influencing driver chosen cornering speed by means of modified steering feel. Veh. Syst. Dyn. 2013, 52, 522–538. [Google Scholar] [CrossRef]
- Woodrooffe, J.; Blower, D.; Green, P.E. Safety Performance and Benefits of Heavy Truck Stability Control: Providing Insight into Compliance Evaluation. SAE Int. J. Commer. Veh. 2012, 5, 429–440. [Google Scholar] [CrossRef]
- Blower, D.; Woodrooffe, J. Real-World Safety Effect of Roll Stability Control. In Proceedings of the SAE 2013 Commercial Vehicle Engineering Congress, Rosemont, IL, USA, 1–3 October 2013. [Google Scholar] [CrossRef]
- Franck, H.F.D. Mathematical Methods for Accident Reconstruction: A forensic Engineering Perspective; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Brach, R.M.; Brach, M.; James, M. Accident Analysis Reconstruction Methods; SAE International: Warrendale, PA, USA, 2022. [Google Scholar]
- Lopes, R.; Farahani, B.V.; de Melo, F.Q.; Moreira, P.M.G.P. A Dynamic Response Analysis of Vehicle Suspension System. Appl. Sci. 2023, 13, 2127. [Google Scholar] [CrossRef]
- Sekulić, D.; Dedović, V.; Rusov, S.; Šalinić, S.; Obradović, A. Analysis of vibration effects on the comfort of intercity bus users by oscillatory model with ten degrees of freedom. Appl. Math. Model. 2013, 37, 8629–8644. [Google Scholar] [CrossRef]
- Sekulic, D.; Dedović, V.; Sekulić, D. The Effect of Stiffness and Damping of the Suspension System Elements on the Optimisation of the Vibrational Behaviour of a Bus. 2011. Available online: https://www.researchgate.net/publication/232613306 (accessed on 6 February 2024).
- Lopes, R.; Farahani, B.V.; de Melo, F.Q.; Ramos, N.V.; Moreira, P.M.G.P. Dynamic modal analysis of a passenger bus: Theoretical and numerical studies. In Transportation Research Record; SAGE Publications Ltd.: Thousand Oaks, CA, USA, 2021; Volume 2675, pp. 264–279. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castro, F.; Melo, F.Q.d.; Faria, D.; Ramos, N.V.; Moreira, P.M.G.P.; Vaz, M.A.P. The Dynamic Behavior of Heavy Vehicles in Cornering Actions: An Assessment of the Problem. Appl. Sci. 2025, 15, 11959. https://doi.org/10.3390/app152211959
Castro F, Melo FQd, Faria D, Ramos NV, Moreira PMGP, Vaz MAP. The Dynamic Behavior of Heavy Vehicles in Cornering Actions: An Assessment of the Problem. Applied Sciences. 2025; 15(22):11959. https://doi.org/10.3390/app152211959
Chicago/Turabian StyleCastro, Francisco, Francisco Queirós de Melo, David Faria, Nuno Viriato Ramos, Pedro M. G. P. Moreira, and Mário Augusto Pires Vaz. 2025. "The Dynamic Behavior of Heavy Vehicles in Cornering Actions: An Assessment of the Problem" Applied Sciences 15, no. 22: 11959. https://doi.org/10.3390/app152211959
APA StyleCastro, F., Melo, F. Q. d., Faria, D., Ramos, N. V., Moreira, P. M. G. P., & Vaz, M. A. P. (2025). The Dynamic Behavior of Heavy Vehicles in Cornering Actions: An Assessment of the Problem. Applied Sciences, 15(22), 11959. https://doi.org/10.3390/app152211959








